Effect of Laser Ablation on Microwave Attenuation Properties of Diamond Films
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis of a Free-Standing Diamond Film by MPCVD
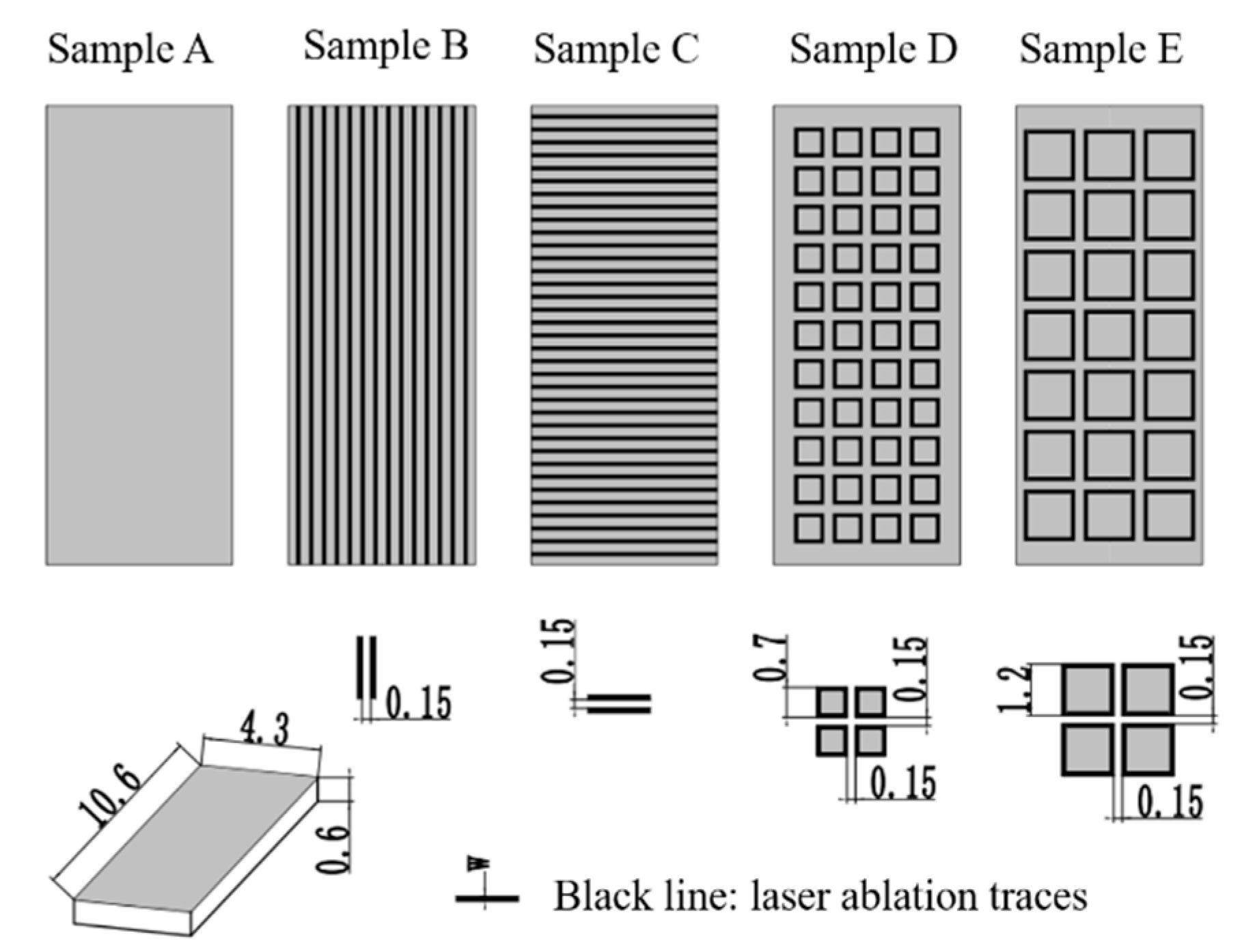
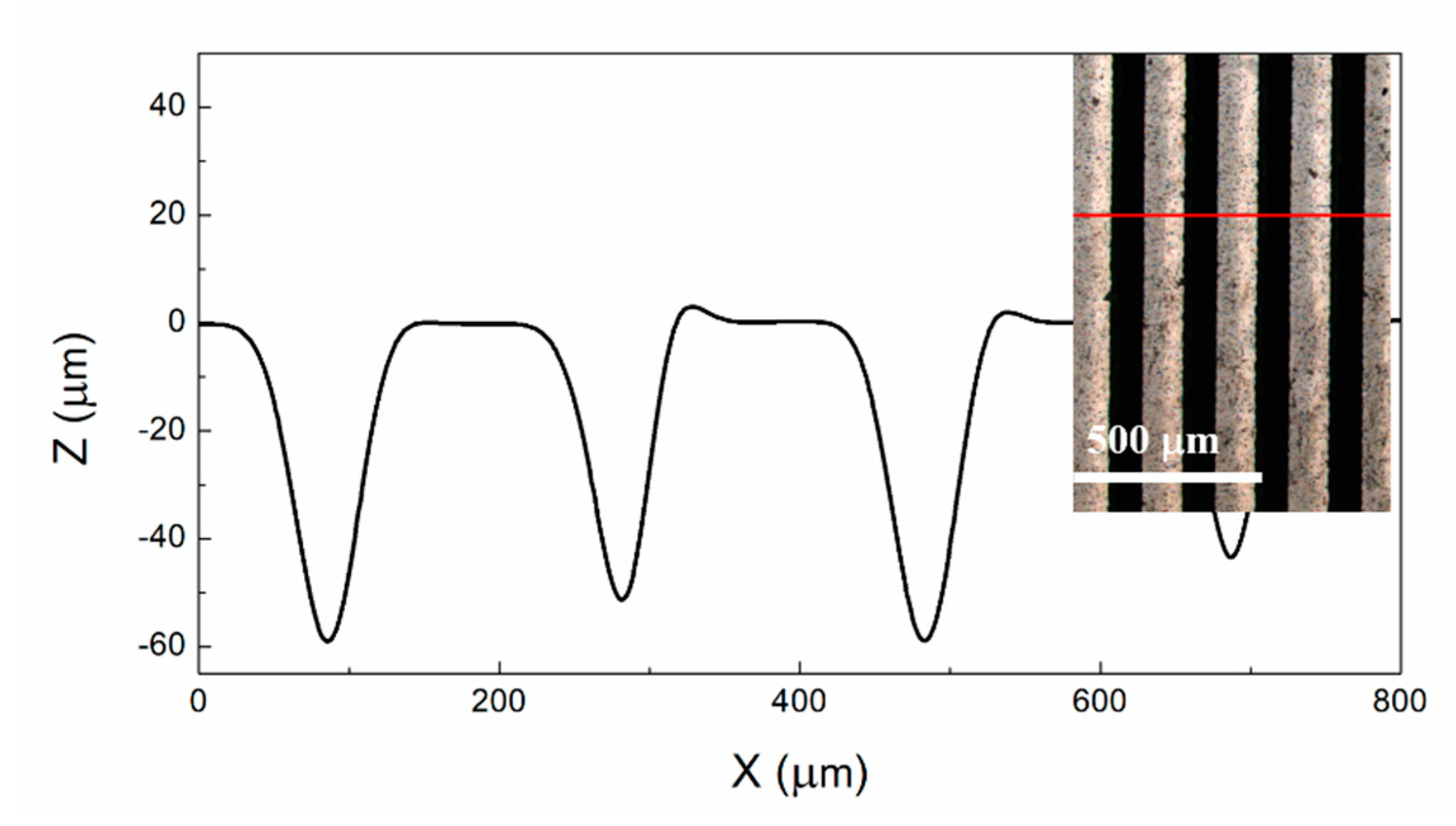
2.2. Preparation of Diamond Samples Using Laser Ablation
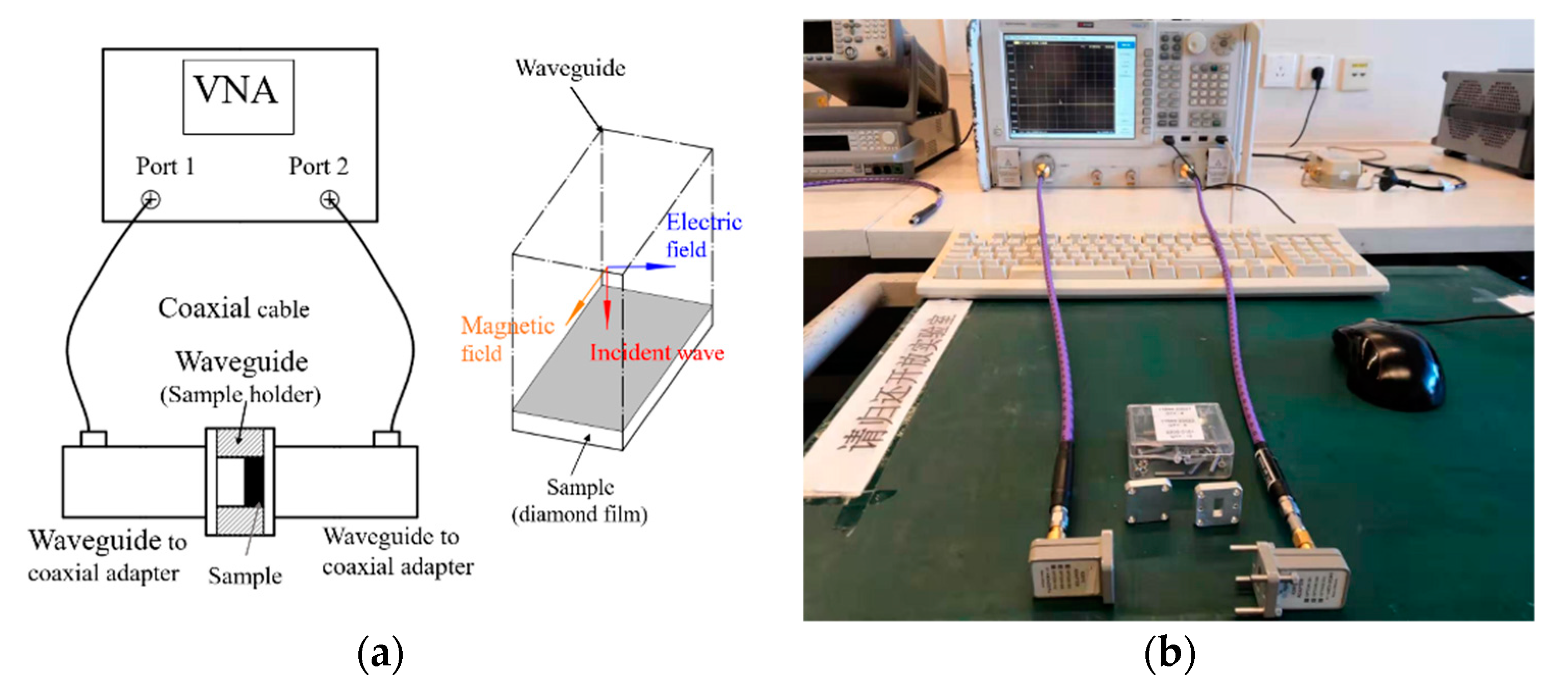
2.3. Characterization of Diamond Films
3. Results and Discussions
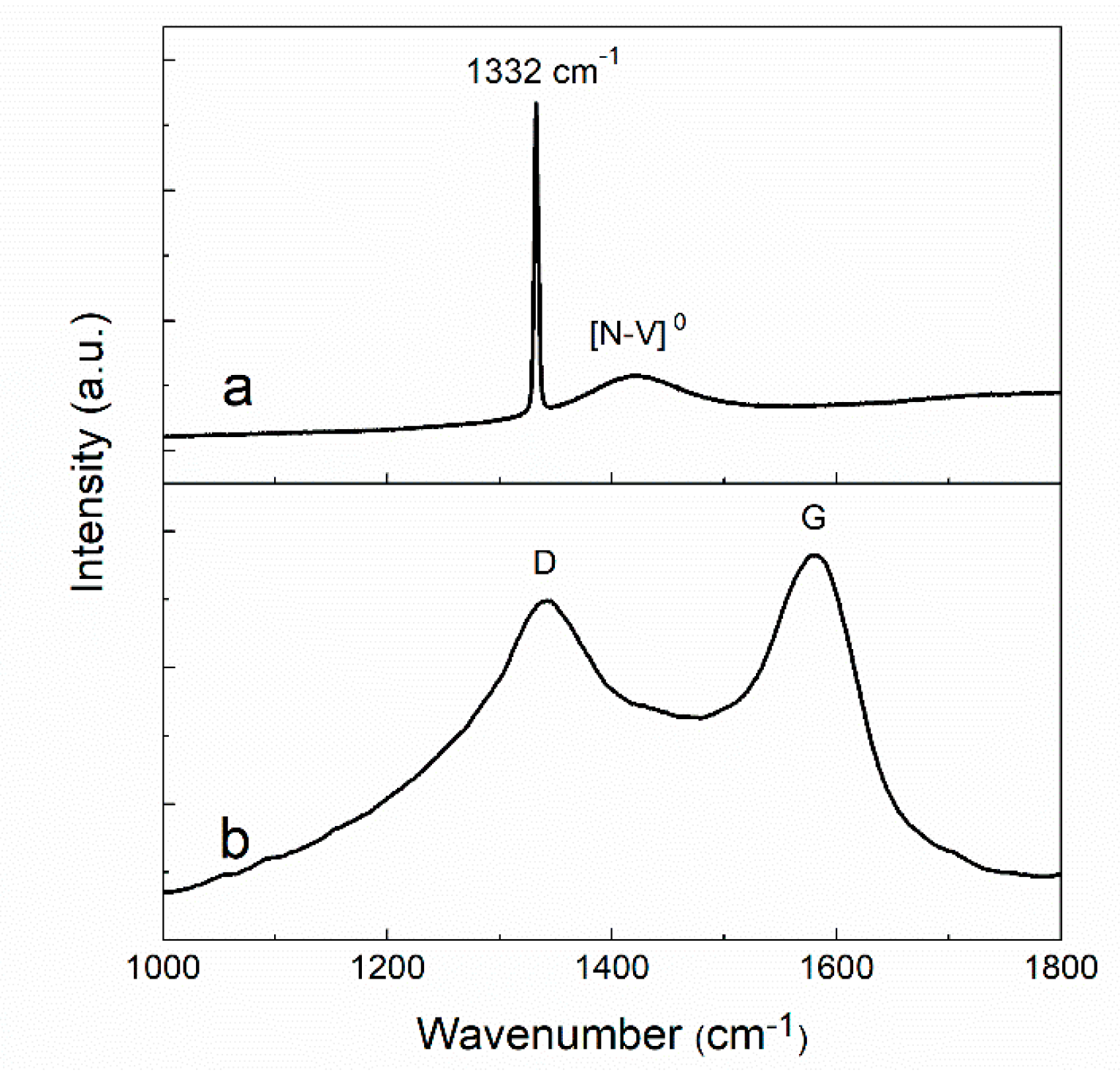
3.1. Morphologies and Raman Spectra of Diamond Films
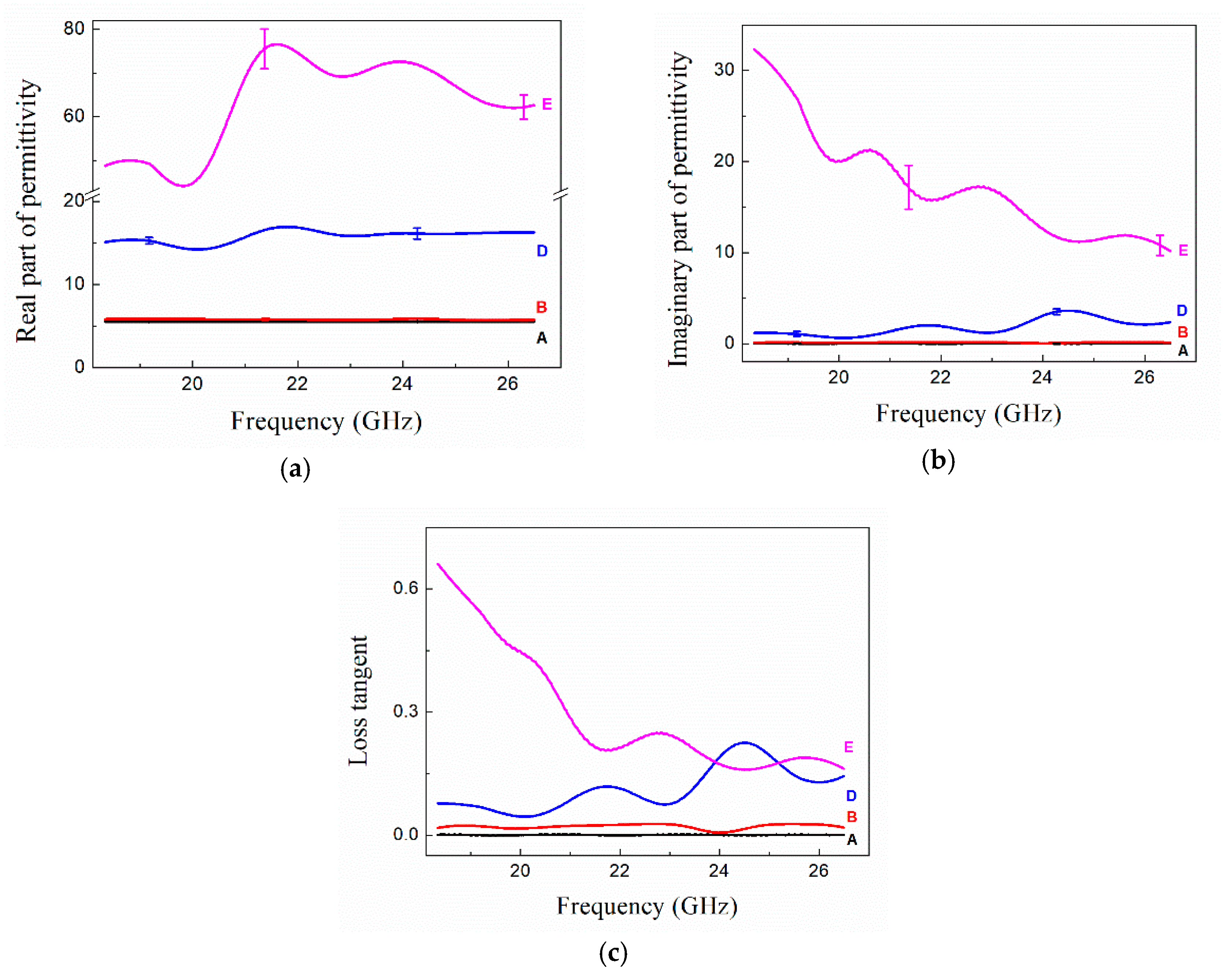
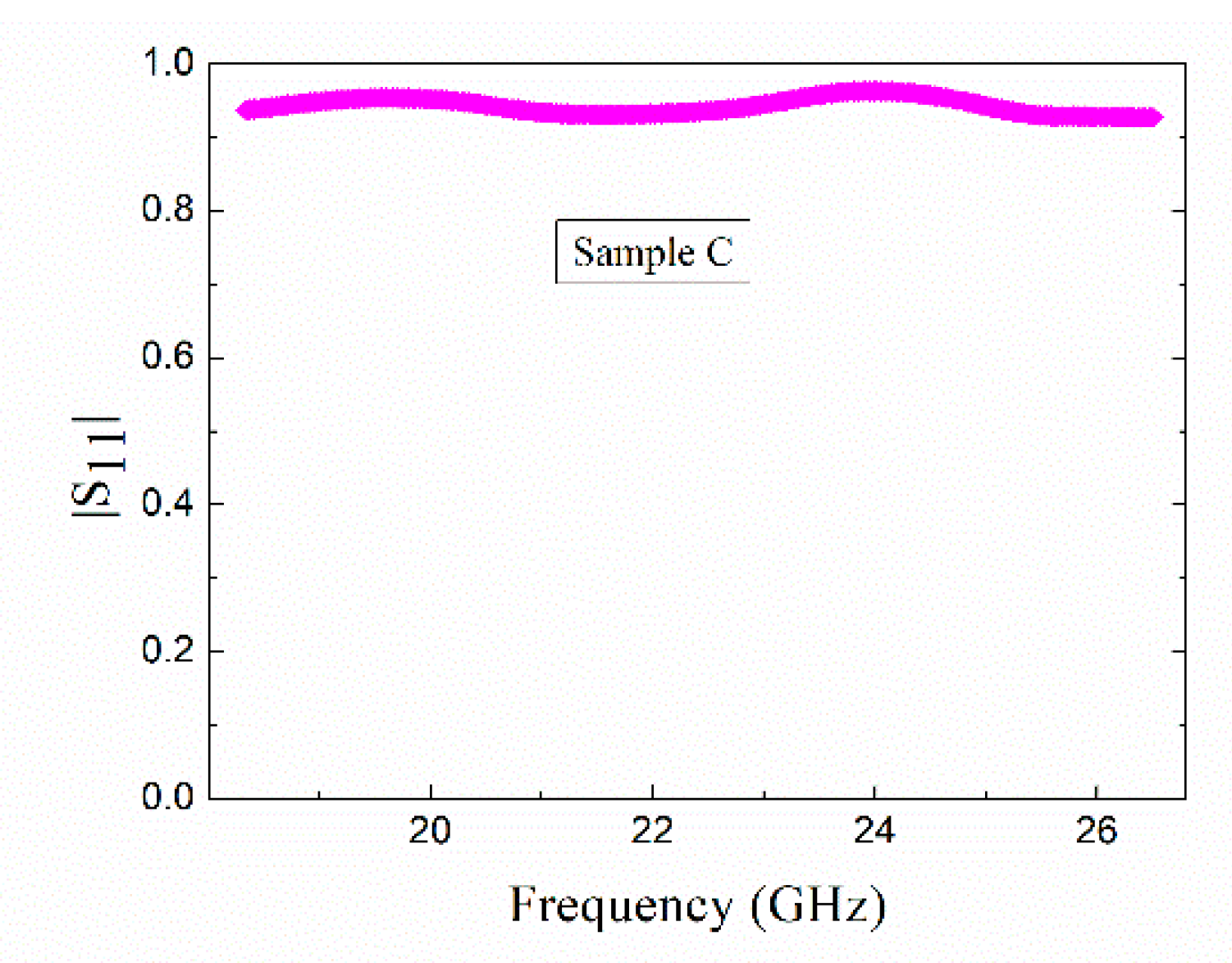
3.2. Dielectric Properties
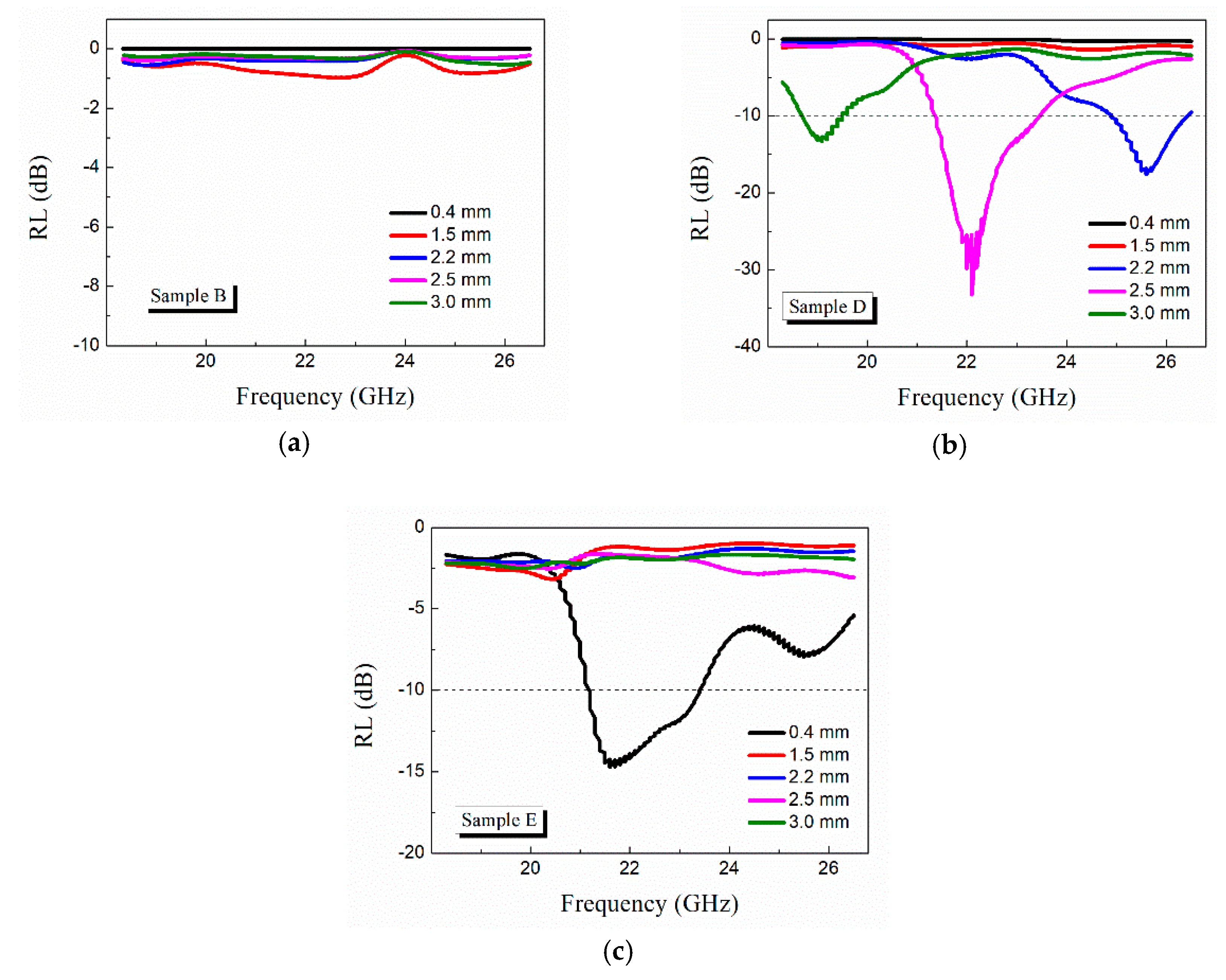
3.3. Microwave Absorbing Property
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Slack, G.A.; Austerman, S.B. Thermal conductivity of BeO single crystals. J. Appl. Phys. 1971, 42, 4713–4717. [Google Scholar] [CrossRef]
- Slack, G.A.; Tanzilli, R.A. The intrinsic thermal conductivity of AlN. J. Phys. Chem. Solids 1987, 48, 641–647. [Google Scholar] [CrossRef]
- Yuan, X.; Cheng, L.; Zhang, Y.; Guo, S.; Zhang, L. Fe-doped SiC/SiO2 composites with ordered inter-filled structure for effective high-temperature microwave attenuation. Mater. Des. 2016, 92, 563–570. [Google Scholar] [CrossRef]
- Liang, X.; Quan, B.; Chen, J.; Gu, W.; Zhang, B.; Ji, G. Nano bimetallic@carbon layer on porous carbon nanofibers with multiple interfaces for microwave absorption applications. ACS Appl. Nano Mater. 2018, 1, 5712–5721. [Google Scholar] [CrossRef]
- Shah, A.; Wang, Y.; Huang, H.; Zhang, L.; Wang, D.; Zhou, L.; Duan, Y.; Dong, X.; Zhang, Z. Microwave absorption and flexural properties of Fe nanoparticle/carbon fiber/epoxy resin composite plates. Compos. Struct. 2015, 131, 1132–1141. [Google Scholar] [CrossRef]
- Hong, W.; Xiao, P.; Luo, H.; Li, Z. Microwave axial dielectric properties of carbon fiber. Sci. Rep. 2015, 5, 14927. [Google Scholar] [CrossRef]
- Huang, S.; Zhou, W.; Luo, F.; Wei, P.; Zhu, D. Mechanical and dielectric properties of short carbon fiber reinforced Al2O3 composites with MgO additive. Ceram. Int. 2014, 40, 2785–2791. [Google Scholar] [CrossRef]
- Shi, Z.; Yang, W.; Wang, J.; Liu, G.; Qiao, G.; Jin, Z. Effect of interfacial structure on the thermal conductivity of carbon nanofibers reinforced aluminum nitride composites. Ceram. Int. 2013, 39, 3365–3370. [Google Scholar] [CrossRef]
- Calame, J.P.; Abe, D.K. Applications of advanced materials technologies to vacuum electronic devices. Proc. IEEE 1999, 87, 840–864. [Google Scholar] [CrossRef]
- Anthony, T.R. The thermal conductivity of CVD diamond films. Philos. Trans. R. Soc. A 1993, 342, 245–251. [Google Scholar]
- Yoshida, K.; Morigami, H. Thermal properties of diamond/copper composite material. Microelectron. Reliab. 2004, 44, 303–308. [Google Scholar] [CrossRef]
- Kidalov, S.; Shakhov, F. Thermal conductivity of diamond composites. Mater 2009, 2, 2467–2495. [Google Scholar] [CrossRef]
- Luo, H.; Wei, Q.; Yu, Z.M.; Wang, Y.; Long, H.; Xie, Y. Effect of film thickness on the temperature dependence of thermal conductivity for diamond/BeO composites. Ceram. Int. 2015, 41, 12052–12057. [Google Scholar] [CrossRef]
- Wen, B.; Zhao, J.; Duan, Y.; Li, T.; Zhao, Y.; Dong, C.; Liu, S.; Jin, J. Numerical analysis of effects of thickness on electromagnetic wave absorption properties of CPCCB/paraffin wax composite. Appl. Phys. B 2006, 83, 629–633. [Google Scholar] [CrossRef]
- Wen, B.; Zhao, J.; Duan, Y.; Zhang, X.; Zhao, Y.; Dong, C.; Liu, S.; Li, T. Electromagnetic wave absorption properties of carbon powder from catalysed carbon black in X and Ku bands. J. Phys. D Appl. Phys. 2006, 39, 1960–1962. [Google Scholar] [CrossRef]
- Kotsilkova, R. Design and characterization of polymer nanocomposites for microwave absorbing applications. In Proceedings of the International Semiconductor Conference, Sinaia, Romania, 4–6 October 2004. [Google Scholar]
- Bogdanov, S.; Vikharev, A.; Gorbachev, A.; Muchnikov, A.; Radishev, D.; Ovechkin, N.; Parshin, V. Growth-rate enhancement of high-quality, low-loss CVD-produced diamond disks grown for microwave windows application. Chem. Vap. Depos. 2014, 20, 32–38. [Google Scholar] [CrossRef]
- Yamada, H.; Meier, A.; Mazzocchi, F.; Schreck, S.; Scherer, T. Dielectric properties of single crystalline diamond wafers with large area at microwave wavelengths. Diam. Relat. Mater. 2015, 58, 1–4. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Ding, M.H.; Su, J.J.; Ren, H.; Lu, X.R.; Tang, W.Z. An investigation on dielectric properties of diamond films in the range of K and Ka band. Diam. Relat. Mater. 2017, 73, 114–120. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, M.; Su, J.; Li, Y.; Zhang, P.; Lu, X.; Tang, W. Dielectric properties of nitrogen-doped polycrystalline diamond films in Ka band. Diam. Relat. Mater. 2017, 76, 68–73. [Google Scholar] [CrossRef]
- Schreck, S.; Aiello, G.; Dieterle, S.; Gagliardi, M.; Meier, A.; Saibene, G.; Scherer, T.; Strauss, D. ITER ECRH Upper Launcher diamond window−Qualification and testing of a Protection Important Component. Fusion Eng. Des. 2018, 136, 472–476. [Google Scholar] [CrossRef]
- Ding, M.; Liu, Y.; Lu, X.; Li, Y.; Tang, W. Boron doped diamond films: A microwave attenuation material with high thermal conductivity. Appl. Phys. Lett. 2019, 114, 162901. [Google Scholar] [CrossRef]
- Collins, A.T.; Williams, A.W.S. The nature of the acceptor centre in semiconducting diamond. J. Phys. C Solid State Phys. 1971, 4, 1789–1800. [Google Scholar] [CrossRef]
- Fan, Y.; Yang, H.; Li, M.; Zou, G. Evaluation of the microwave absorption property of flake graphite. Mater. Chem. Phys. 2009, 115, 696–698. [Google Scholar] [CrossRef]
- Wang, C.Z.; Ho, K.M.; Shirk, M.D.; Molian, P.A. Laser-Induced Graphitization on a Diamond (111) Surface. Phys. Rev. Lett. 2000, 85, 4092–4095. [Google Scholar] [CrossRef]
- Cappelli, E.; Mattei, G.; Orlando, S.; Pinzari, F.; Ascarelli, P. Pulsed laser surface modifications of diamond thin films. Diam. Relat. Mater. 1999, 8, 257–261. [Google Scholar] [CrossRef]
- Kononenko, T.V.; Ralchenko, V.G.; Vlasov, I.I.; Garnov, S.V.; Konov, V.I. Ablation of CVD diamond with nanosecond laser pulses of UV—IR rangek. Diam. Relat. Mater. 1998, 7, 1623–1627. [Google Scholar] [CrossRef]
- Komlenok, M.S.; Kononenko, V.V.; Ralchenko, V.G.; Pimenov, S.M.; Konov, V.I. Laser induced nanoablation of diamond materials. Phys. Procedia 2011, 12, 37–45. [Google Scholar] [CrossRef]
- Qian, J.; Pantea, C.; Voronin, G.; Zerda, T.W. Partial graphitization of diamond crystals under high-pressure and high-temperature conditions. J. Appl. Phys. 2001, 90, 1632–1637. [Google Scholar] [CrossRef]
- Sun, C.Q.; Xie, H.; Zhang, W.; Ye, H.; Hing, P. Preferential oxidation of diamond {111}. J. Phys. D Appl. Phys. 2000, 33, 2196–2199. [Google Scholar] [CrossRef]
- Rothschild, M.; Arnone, C.; Ehrlich, D.J. Excimer-laser etching of diamond and hard carbon films by direct writing and optical projection. J. Vac. Sci. Technol. B 1986, 4, 310–314. [Google Scholar] [CrossRef]
- Su, J.J.; Li, Y.F.; Li, X.L.; Yao, P.L.; Liu, Y.Q.; Ding, M.H.; Tang, W.Z. A novel microwave plasma reactor with a unique structure for chemical vapor deposition of diamond films. Diam. Relat. Mater. 2014, 42, 28–32. [Google Scholar] [CrossRef]
- Qin, F.; Brosseau, C. A review and analysis of microwave absorption in polymer composites filled with carbonaceous particles. J. Appl. Phys. 2012, 111, 061301. [Google Scholar] [CrossRef]
- Shah, A.; Ding, A.; Wang, Y.; Zhang, L.; Wang, D.; Muhammad, J.; Huang, H.; Duan, Y.; Dong, X.; Zhang, Z. Enhanced microwave absorption by arrayed carbon fibers and gradient dispersion of Fe nanoparticles in epoxy resin composites. Carbon 2016, 96, 987–997. [Google Scholar] [CrossRef]
- Zhao, N.; Zou, T.; Shi, C.; Li, J.; Guo, W. Microwave absorbing properties of activated carbon-fiber felt screens (vertical-arranged carbon fibers)/epoxy resin composites. Mater. Sci. Eng. B 2006, 127, 207–211. [Google Scholar] [CrossRef]
- Fan, H.L.; Yang, W.; Chao, Z.M. Microwave absorbing composite lattice grids. Compos. Sci. Technol. 2007, 67, 3472–3479. [Google Scholar] [CrossRef]
- Bertolotti, M.; Liakhou, G.L.; Ferrari, A.; Ralchenko, V.G.; Smolin, A.A.; Obraztsova, E.; Korotoushenko, K.G.; Pimenov, S.M.; Konov, V.I. Measurements of thermal conductivity of diamond films by photothermal deflection technique. J. Appl. Phys. 1994, 75, 7795–7798. [Google Scholar] [CrossRef]
- Ding, M.; Liu, Y.; Lu, X.; Li, Y.; Tang, W. An improved algorithm for deducing complex permittivity of thin dielectric samples with the Transmission/Reflection method. Prog. Electromagn. Res. M 2019, 84, 1–9. [Google Scholar] [CrossRef]
- Chu, Z.; Cheng, H.; Xie, W.; Sun, L. Effects of diameter and hollow structure on the microwave absorption properties of short carbon fibers. Ceram. Int. 2012, 38, 4867–4873. [Google Scholar] [CrossRef]
- Zhu, R.; Liu, J.; Chen, L.; Wei, J.; Hei, L.; Li, C. Research on 1420 cm−1 characteristic peak of free-standing diamond films in Raman spectrum. J. Synth. Cryst. 2015, 44, 867–884. [Google Scholar]
- Leeds, S.M.; Davis, T.J.; May, P.W.; Pickard, C.D.O.; Ashfold, M.N.R. Use of different excitation wavelengths for the analysis of CVD diamond by laser Raman spectroscopy. Diam. Relat. Mater. 1998, 7, 233–237. [Google Scholar] [CrossRef]
- Cao, M.; Song, W.; Hou, Z.; Wen, B.; Yuan, J. The effects of temperature and frequency on the dielectric properties, electromagnetic interference shielding and microwave-absorption of short carbon fiber/silica composites. Carbon 2010, 48, 788–796. [Google Scholar] [CrossRef]
- Poolavko, Y.M.; Didenko, Y.V.; Yakimenko, Y.I. Physical mechanisms determining microwave dielectrics properties. In Proceedings of the 2015 IEEE 35th International Conference on Electronics and Nanotechnology (ELNANO), Kiev, Ukraine, 21–24 April 2015; pp. 23–28. [Google Scholar]
- Huang, Z.; Zhou, W.; Ma, R.; Tang, X.; Luo, F.; Zhu, J. Dielectric and mechanical properties of Hot-Pressed sintered Csf/Al2O3 ceramic composites. Int. J. Appl. Ceram. Tec. 2012, 9, 413–420. [Google Scholar] [CrossRef]
- Kong, L.; Yin, X.; Zhang, Y.; Yuan, X.; Li, Q.; Ye, F.; Cheng, L.; Zhang, L. Electromagnetic wave absorption properties of reduced graphene oxide modified by maghemite colloidal nanoparticle clusters. J. Phys. Chem. C 2013, 117, 19701–19711. [Google Scholar] [CrossRef]

| Power (kW) | CH4/H2 (sccm) | Temperature (°C) | Pressure (kPa) | Thickness after Polishing (mm) | Deposition Rate (μm/h) |
|---|---|---|---|---|---|
| 5.6 | 15/300 | 975 | 20 | 0.6 | 4.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, M.; Liu, Y.; Lu, X.; Tang, W. Effect of Laser Ablation on Microwave Attenuation Properties of Diamond Films. Materials 2019, 12, 3700. https://doi.org/10.3390/ma12223700
Ding M, Liu Y, Lu X, Tang W. Effect of Laser Ablation on Microwave Attenuation Properties of Diamond Films. Materials. 2019; 12(22):3700. https://doi.org/10.3390/ma12223700
Chicago/Turabian StyleDing, Minghui, Yanqing Liu, Xinru Lu, and Weizhong Tang. 2019. "Effect of Laser Ablation on Microwave Attenuation Properties of Diamond Films" Materials 12, no. 22: 3700. https://doi.org/10.3390/ma12223700
APA StyleDing, M., Liu, Y., Lu, X., & Tang, W. (2019). Effect of Laser Ablation on Microwave Attenuation Properties of Diamond Films. Materials, 12(22), 3700. https://doi.org/10.3390/ma12223700





