Asymptotic Homogenization Applied to Flexoelectric Rods
Abstract
1. Introduction
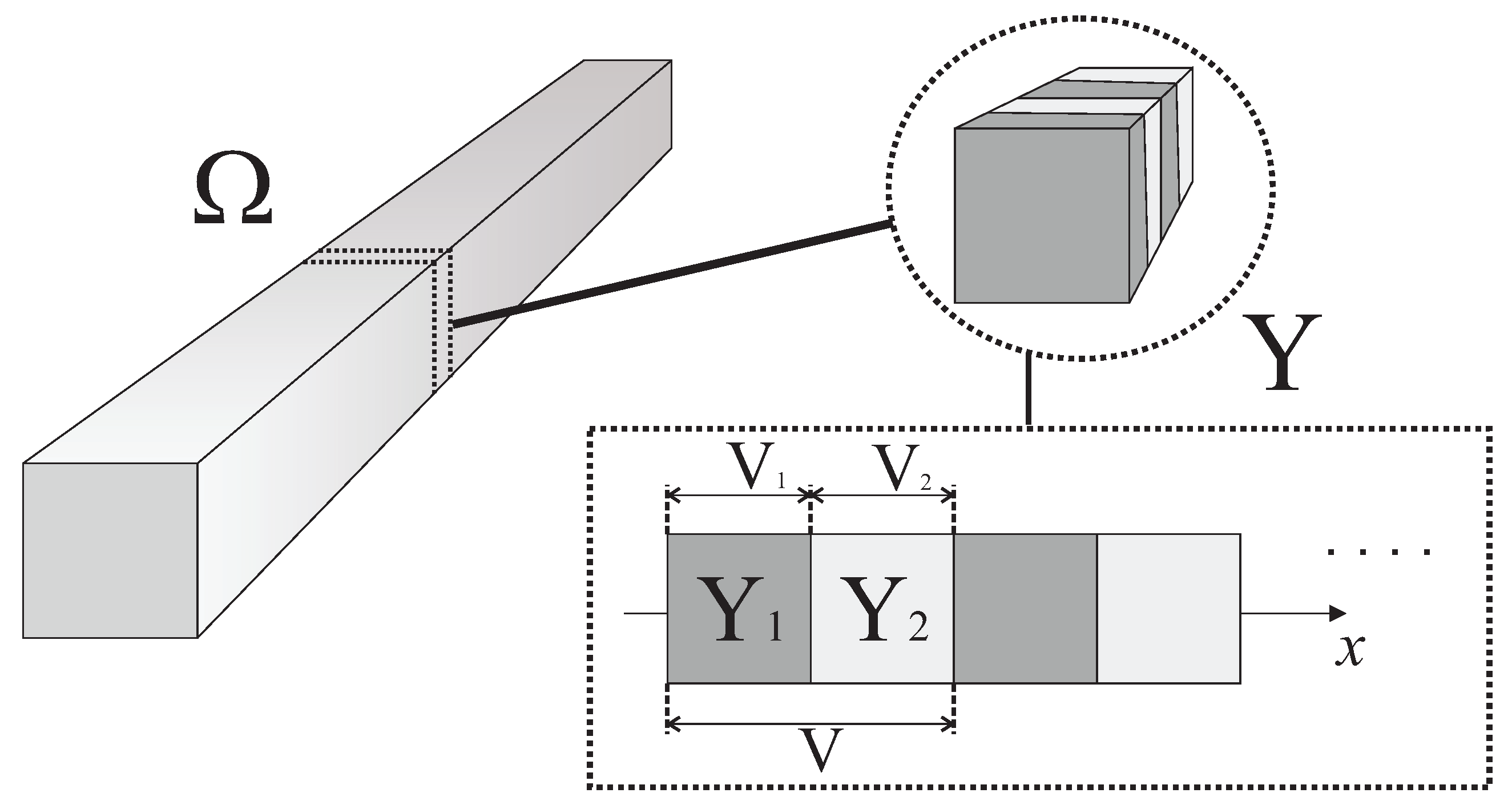
2. Flexoelectric One-Dimensional Problem
3. Asymptotic Homogenization Method
3.1. Local Problems
3.2. Methodology to Solve Local Problems Using a System of Linear Equations
3.3. Variational Formulation of the LQ System. Finite Element Method (FEM)
3.4. Effective Coefficients and Homogenized Problem
4. Analysis of Numerical Results
4.1. Model Validation with the Particular Case of Piezoelectric Materials
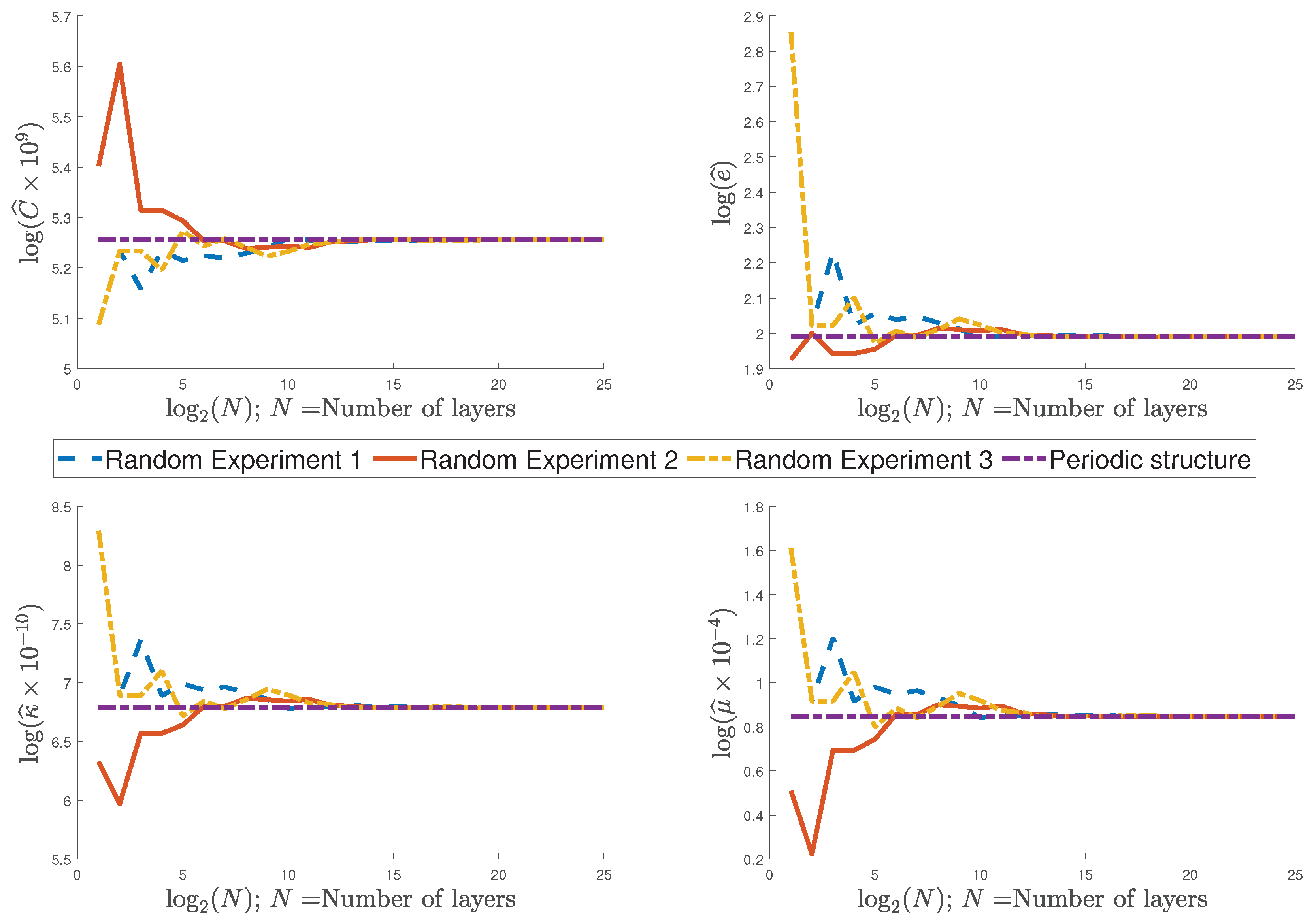
4.2. Flexoelectric Composite Rod without Ideal Periodicity
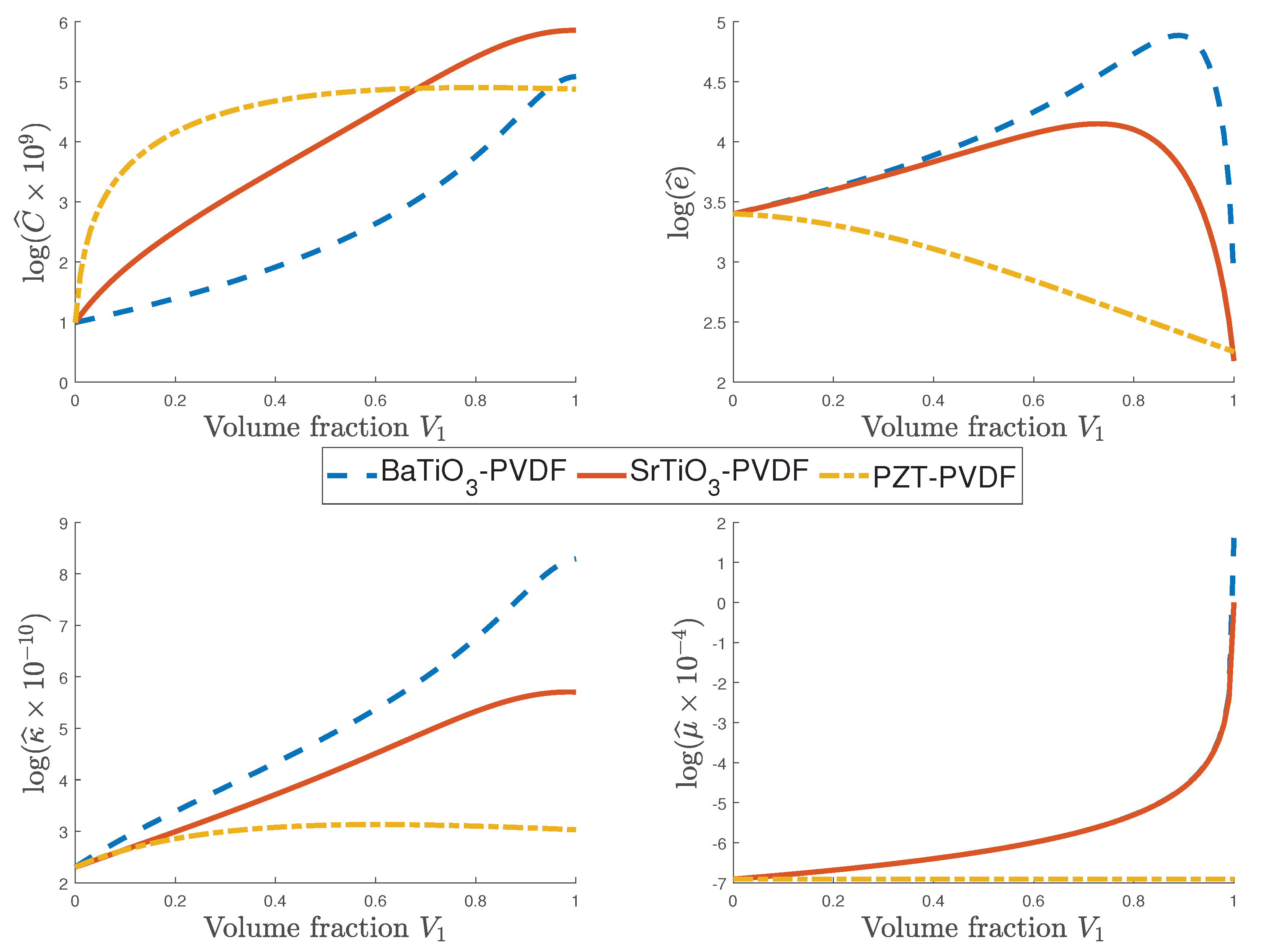
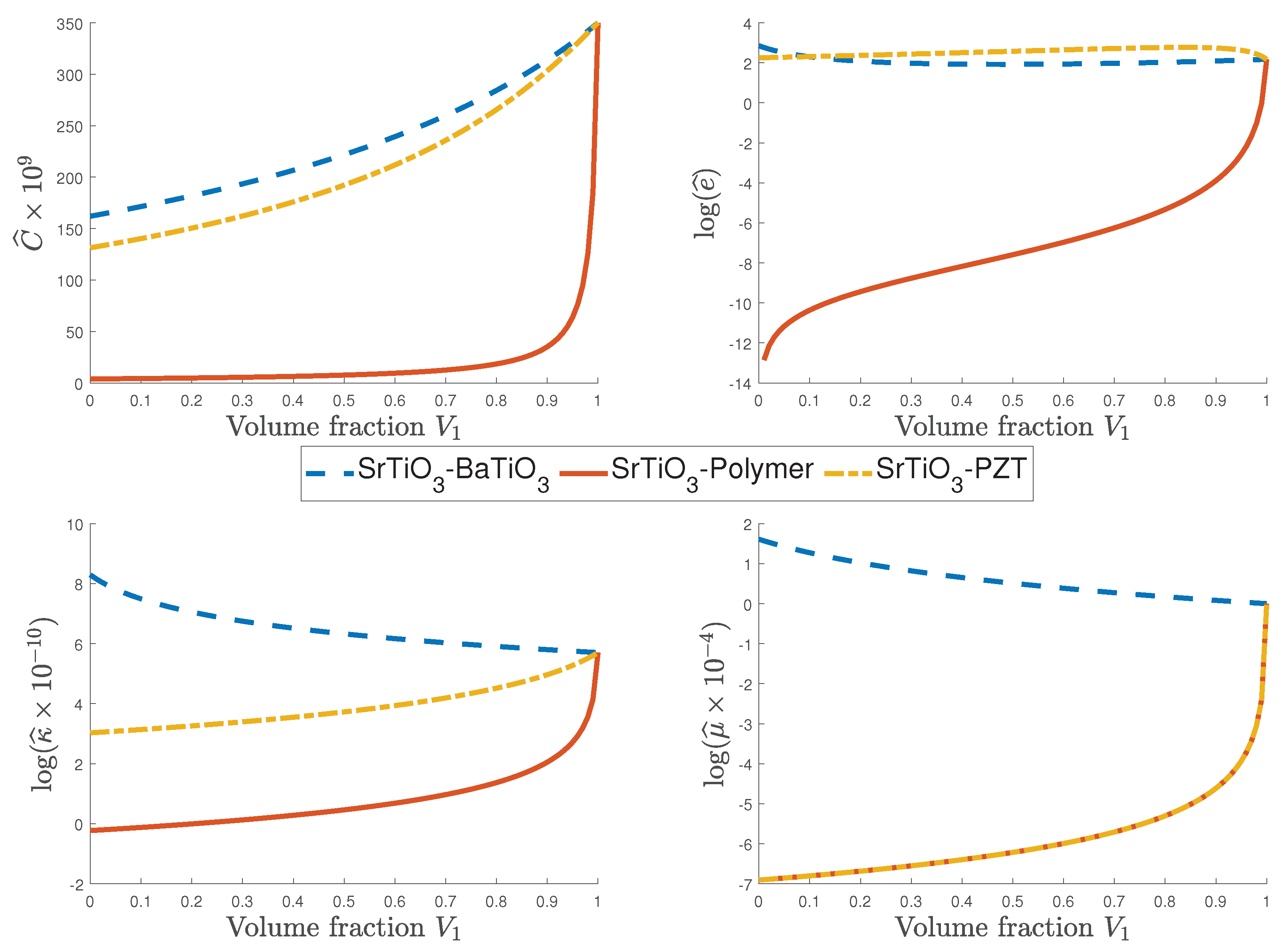
4.3. Influence of the Flexoelectric Property on the Effective Coefficients
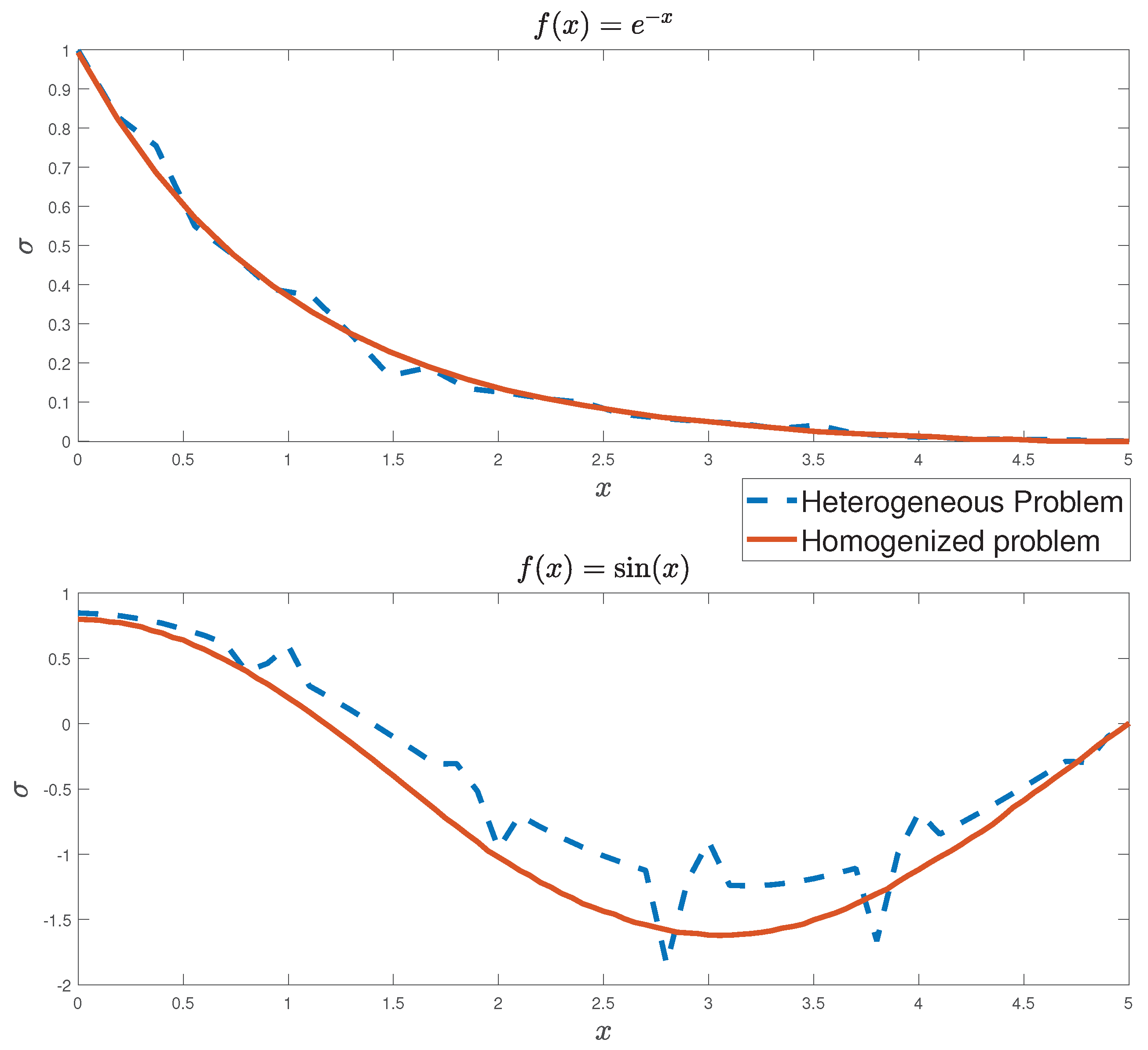
4.4. Solution of the Heterogeneous and Homogenized Problems
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BaTiO | Barium titane |
| SrTiO | Strontium titanate |
| PVDF | Polyvinylidene fluoride |
| PZT | Lead zirconate titanate |
| AHM | two-scales Asymptotic Homogenization method |
| FEM | Finite Element method |
Appendix A. Solutions of the (PR) System
References
- Ting, R.Y. Evaluation of new piezoelectric composite materials for hydrophone applications. Ferroelectrics 1986, 67, 143–157. [Google Scholar] [CrossRef]
- Gururaja, T.R.; Schulze, W.A.; Cross, L.E.; Newnham, R.E.; Auld, B.A.; Wang, Y.J. Piezoelectric Composite Materials for Ultrasonic Transducer Applications. Part I: Resonant Modes of Vibration of PZT Rod-Polymer Composites. IEEE Trans. Sonics Ultrason. 1985, 32, 481–498. [Google Scholar] [CrossRef]
- Akdogan, E.K.; Allahverdi, M.; Safari, A. Piezoelectric composites for sensor and actuator applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 746–775. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Zhou, K.; Zhang, X.; Zhang, D. Development, modeling and application of piezoelectric fiber composites. Trans. Nonferrous Met. Soc. China 2013, 23, 98–107. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Z.; Zhu, X.; Yang, B.; Fu, C. Theoretical and experimental study on the effective piezoelectric properties of 1-3 type cement-based piezoelectric composites. Materials 2018, 11, 1698. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.Q.; Huang, M.J.; Liu, J.X.; Feng, W.J. Dynamic effective property of piezoelectric composites with coated piezoelectric nano-fibers. Compos. Sci. Technol. 2014, 98, 79–85. [Google Scholar] [CrossRef]
- Yudin, P.V.; Tagantsev, A.K. Fundamentals of flexoelectricity in solids. Nanotechnology 2013, 24, 432001. [Google Scholar] [CrossRef] [PubMed]
- Mindlin, R. Polarization gradient in elastic dielectrics. Int. J. Solids Struct. 1968, 4, 637–642. [Google Scholar] [CrossRef]
- Harris, P. Mechanism for the Shock Polarization of Dielectrics. J. Appl. Phys. 1965, 36, 739–741. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric Effect in Solids. Annu. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef]
- Enakoutsa, K.; Corte, A.D.; Giorgio, I. A model for elastic flexoelectric materials including strain gradient effects. Math. Mech. Solids 2016, 21, 242–254. [Google Scholar] [CrossRef]
- Mohammadi, P.; Liu, L.; Sharma, P. A theory of flexoelectric membranes and effective properties of heterogeneous membranes. J. Appl. Mech. 2013, 81, 011007. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, L.; Sharma, P. Flexoelectricity in soft materials and biological membranes. J. Mech. Phys. Solids 2014, 62, 209–227. [Google Scholar] [CrossRef]
- Narita, F.; Shindo, Y.; Mikami, M. Analytical and experimental study of nonlinear bending response and domain wall motion in piezoelectric laminated actuators under ac electric fields. Acta Mater. 2005, 53, 4523–4529. [Google Scholar] [CrossRef]
- Krichen, S.; Sharma, P. Flexoelectricity: A Perspective on an Unusual Electromechanical Coupling. J. Appl. Mech. 2016. [Google Scholar] [CrossRef]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 2008, 77, 125424. [Google Scholar] [CrossRef]
- Nguyen, B.; Zhuang, X.; Rabczuk, T. Numerical model for the characterization of Maxwell-Wagner relaxation in piezoelectric and flexoelectric composite material. Comput. Struct. 2018, 208, 75–91. [Google Scholar] [CrossRef]
- Meguid, S.; Kalamkarov, A. Asymptotic homogenization of elastic composite materials with a regular structure. Int. J. Solids Struct. 1994, 31, 303–316. [Google Scholar] [CrossRef]
- Otero, J.; Castillero, J.; Ramos, R. Homogenization of heterogeneous piezoelectric medium. Mech. Res. Commun. 1997, 24, 75–84. [Google Scholar] [CrossRef]
- Tsalis, D.; Chatzigeorgiou, G.; Charalambakis, N. Homogenization of structures with generalized periodicity. Compos. Part B Eng. 2012, 43, 2495–2512. [Google Scholar] [CrossRef]
- Chen, C.M.; Kikuchi, N.; Rostam-Abadi, F. An enhanced asymptotic homogenization method of the static and dynamics of elastic composite laminates. Comput. Struct. 2004, 82, 373–382. [Google Scholar] [CrossRef]
- Guinovart-Díaz, R.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; Sabina, F.; Otero, J.; Maugin, G. A recursive asymptotic homogenization scheme for multi-phase fibrous elastic composites. Mech. Mater. 2005, 37, 1119–1131. [Google Scholar] [CrossRef]
- Castillero, J.; Otero, J.; Ramos, R.; Bourgeat, A. Asymptotic homogenization of laminated piezocomposite materials. Int. J. Solids Struct. 1998, 35, 527–541. [Google Scholar] [CrossRef]
- Yi, Y.M.; Park, S.H.; Youn, S.K. Asymptotic homogenization of viscoelastic composites with periodic microstructures. Int. J. Solids Struct. 1998, 35, 2039–2055. [Google Scholar] [CrossRef]
- Fantoni, F.; Bacigalupo, A.; Paggi, M. Multi-field asymptotic homogenization of thermo-piezoelectric materials with periodic microstructure. Int. J. Solids Struct. 2017, 120, 31–56. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Drygaś, P.; Mityushev, V. Effective elastic properties of random two-dimensional composites. Int. J. Solids Struct. 2016, 97-98, 543–553. [Google Scholar] [CrossRef]
- Gotlib, V.A.; Sato, T.; Beltzer, A.I. Neural computing of effective properties of random composite materials. Comput. Struct. 2001. [Google Scholar] [CrossRef]
- Levin, V.; Sabina, F.; Bravo-Castillero, J.; Guinovart-Díaz, R.; Rodríguez-Ramos, R.; Valdiviezo-Mijangos, O. Analysis of effective properties of electroelastic composites using the self-consistent and asymptotic homogenization methods. Int. J. Eng. Sci. 2008, 46, 818–834. [Google Scholar] [CrossRef]
- López-Realpozo, J.; Caballero-Pérez, R.; Rodríguez-Ramos, R.; Guinovart-Díaz, R.; Bravo-Castillero, J.; Camacho-Montes, H.; Espinosa-Almeyda, Y.; Sabina, F.; Chi-Vinh, P. Analysis of mechanical and electrical imperfect contacts in piezoelectric composites. Mech. Res. Commun. 2018, 93, 96–102. [Google Scholar] [CrossRef]
- Snarskii, A.; Bezsudnov, I.; Sevrukov, V.; Morozovskiy, A.; Malinsky, J. Transport Processes in Macroscopically Disordered Media: From Mean Field Theory to Percolation; Springer: New York, NY, USA, 2016. [Google Scholar]
- Yang, T.; Hu, T.; Liang, X.; Shen, S. On band structures of layered phononic crystals with flexoelectricity. Arch. Appl. Mech. 2018. [Google Scholar] [CrossRef]
- Della, C.N.; Shu, D. On the performance of 1–3 piezoelectric composites with a passive and active matrix. Sens. Actuators A Phys. 2007, 140, 200–206. [Google Scholar] [CrossRef]
- Erba, A.; El-Kelany, K.E.; Ferrero, M.; Baraille, I.; Rérat, M. Piezoelectricity of SrTiO3: An ab initio description. Phys. Rev. B 2013, 88, 035102. [Google Scholar] [CrossRef]
- Holmes-Siedle, A.; Wilson, P.; Verrall, A. PVdF: An electronically-active polymer for industry. Mater. Des. 1983, 4, 910–918. [Google Scholar] [CrossRef]
- Jain, A.; Sharma, A.K.; Jain, A. Dielectric and piezoelectric properties of PVDF/PZT composites: A review. Polym. Eng. Sci. 2015, 55, 1589–1616. [Google Scholar] [CrossRef]
- Berger, H.; Kari, S.; Gabbert, U.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Díaz, R. A comprehensive numerical homogenisation technique for calculating effective coefficients of uniaxial piezoelectric fibre composites. Mater. Sci. Eng. A 2005, 412, 53–60. [Google Scholar] [CrossRef]
- Berger, H.; Kari, S.; Gabbert, U.; Rodriguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Diaz, R. Calculation of effective coefficients for piezoelectric fiber composites based on a general numerical homogenization technique. Compos. Struct. 2005, 71, 397–400. [Google Scholar] [CrossRef]
- Klaasen, G.A. Existence Theorems for boundary value problems of n-th order ordinary differential equations. Rocky Mt. J. Math. 1973, 3, 457–472. [Google Scholar] [CrossRef]
- Maranganti, R.; Sharma, N.D.; Sharma, P. Electromechanical coupling in nonpiezoelectric materials due to nanoscale nonlocal size effects: Green’s function solutions and embedded inclusions. Phys. Rev. B 2006, 74, 014110. [Google Scholar] [CrossRef]
- Guinovart-Sanjuán, D.; Rizzoni, R.; Rodríguez-Ramos, R.; Guinovart-Díaz, R.; Bravo-Castillero, J.; Alfonso-Rodríguez, R.; Lebon, F.; Dumont, S.; Sevostianov, I.; Sabina, F.J. Behavior of laminated shell composite with imperfect contact between the layers. Compos. Struct. 2017, 176, 539–546. [Google Scholar] [CrossRef]
- Guinovart-Sanjuán, D.; Rodríguez-Ramos, R.; Guinovart-Díaz, R.; Bravo-Castillero, J.; Sabina, F.; Merodio, J.; Lebon, F.; Dumont, S.; Conci, A. Effective properties of regular elastic laminated shell composite. Compos. Part B Eng. 2016, 87, 12–20. [Google Scholar] [CrossRef]
- Lu, J.; Lv, J.; Liang, X.; Xu, M.; Shen, S. Improved approach to measure the direct flexoelectric coefficient of bulk polyvinylidene fluoride. J. Appl. Phys. 2016, 119, 094104. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, S.; Xu, M.; Wu, T.; Shen, S. The research of effective flexoelectric coefficient along 1123 direction in polyvinylidene fluoride. J. Appl. Phys. 2017, 121, 174104. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, K.; Xu, M.; Shen, H.; Chen, K.; Feng, B.; Shen, S. Investigation of the 2312 flexoelectric coefficient component of polyvinylidene fluoride: Deduction, simulation, and mensuration. Sci. Rep. 2017, 7, 3134. [Google Scholar] [CrossRef] [PubMed]
- Baskaran, S.; He, X.; Chen, Q.; Fu, J.Y. Experimental studies on the direct flexoelectric effect in α-phase polyvinylidene fluoride films. Appl. Phys. Lett. 2011, 98, 242901. [Google Scholar] [CrossRef]
- Bakhvalov, N.; Panasenko, G. Homogenisation: Averaging Processes in Periodic Media: Mathematical Problems in the Mechanics of Composite Materials; Mathematics and its Applications; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
| Effective Coefficient (10 N/m) | ||||
|---|---|---|---|---|
| Present Model | FEM | Ref. [30] | Ref. [19] | |
| 0.0 | 118.300 | 118.300 | 118.299 | 118.300 |
| 0.4 | 116.953 | 116.953 | 116.952 | 116.953 |
| 0.8 | 115.401 | 115.401 | 115.400 | 115.401 |
| 1.0 | 114.500 | 114.500 | 114.499 | 114.500 |
| Effective Coefficient(C/m) | ||||
| 0.0 | 26.400 | 26.400 | 26.399 | 26.400 |
| 0.4 | 24.806 | 24.806 | 24.805 | 24.806 |
| 0.8 | 22.634 | 22.863 | 22.633 | 22.634 |
| 1.0 | 21.200 | 21.200 | 21.199 | 21.200 |
| Effective Coefficient(10F/m) | ||||
| 0.0 | 110.900 | 110.900 | 110.899 | 110.900 |
| 0.4 | 148.056 | 148.056 | 148.054 | 148.056 |
| 0.8 | 200.835 | 200.836 | 200.832 | 200.835 |
| 1.0 | 236.600 | 236.600 | 236.595 | 236.600 |
| Materials | C (10 N/m) | e (C/m) | (10 F/m) | (10 C/m) |
|---|---|---|---|---|
| BaTiO | 162 [32] | 17.36 [33] | 4000 [32] | 5 [32] |
| SrTiO | 350 [32] | 8.82 [34] | 300 [32] | 1 [32] |
| PVDF | 2.7 [35] | 30 [36] | 10 [36] | 0 |
| Polymer | 3.86 [37] | 0 [37] | 0.7965 [37] | 0 |
| PZT-7A | 131.4 [38] | 9.522 [38] | 0.372 [38] | 0 |
| Materials | (10 N/m) | (C/m) | (10 F/m) | (10C/m) |
|---|---|---|---|---|
| 221.8664 | 6.8629 | 560.04 | 1.6667 | |
| 181.8374 | 8.0288 | 1158.11 | 2.7778 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guinovart-Sanjuán, D.; Merodio, J.; López-Realpozo, J.C.; Vajravelu, K.; Rodríguez-Ramos, R.; Guinovart-Díaz, R.; Bravo-Castillero, J.; Sabina, F.J. Asymptotic Homogenization Applied to Flexoelectric Rods. Materials 2019, 12, 232. https://doi.org/10.3390/ma12020232
Guinovart-Sanjuán D, Merodio J, López-Realpozo JC, Vajravelu K, Rodríguez-Ramos R, Guinovart-Díaz R, Bravo-Castillero J, Sabina FJ. Asymptotic Homogenization Applied to Flexoelectric Rods. Materials. 2019; 12(2):232. https://doi.org/10.3390/ma12020232
Chicago/Turabian StyleGuinovart-Sanjuán, David, Jose Merodio, Juan Carlos López-Realpozo, Kuppalapalle Vajravelu, Reinaldo Rodríguez-Ramos, Raúl Guinovart-Díaz, Julián Bravo-Castillero, and Federico J. Sabina. 2019. "Asymptotic Homogenization Applied to Flexoelectric Rods" Materials 12, no. 2: 232. https://doi.org/10.3390/ma12020232
APA StyleGuinovart-Sanjuán, D., Merodio, J., López-Realpozo, J. C., Vajravelu, K., Rodríguez-Ramos, R., Guinovart-Díaz, R., Bravo-Castillero, J., & Sabina, F. J. (2019). Asymptotic Homogenization Applied to Flexoelectric Rods. Materials, 12(2), 232. https://doi.org/10.3390/ma12020232






