Parallel Finite Element Model for Multispecies Transport in Nonsaturated Concrete Structures
Abstract
1. Introduction
2. Basic Transport Formulation of Unsaturated Concrete
2.1. Governing Equation
2.2. Material Parameters
2.3. Capacity and Diffusivity Coefficients of Multispecies in Nonsaturated Concrete
2.4. Coupling Parameters
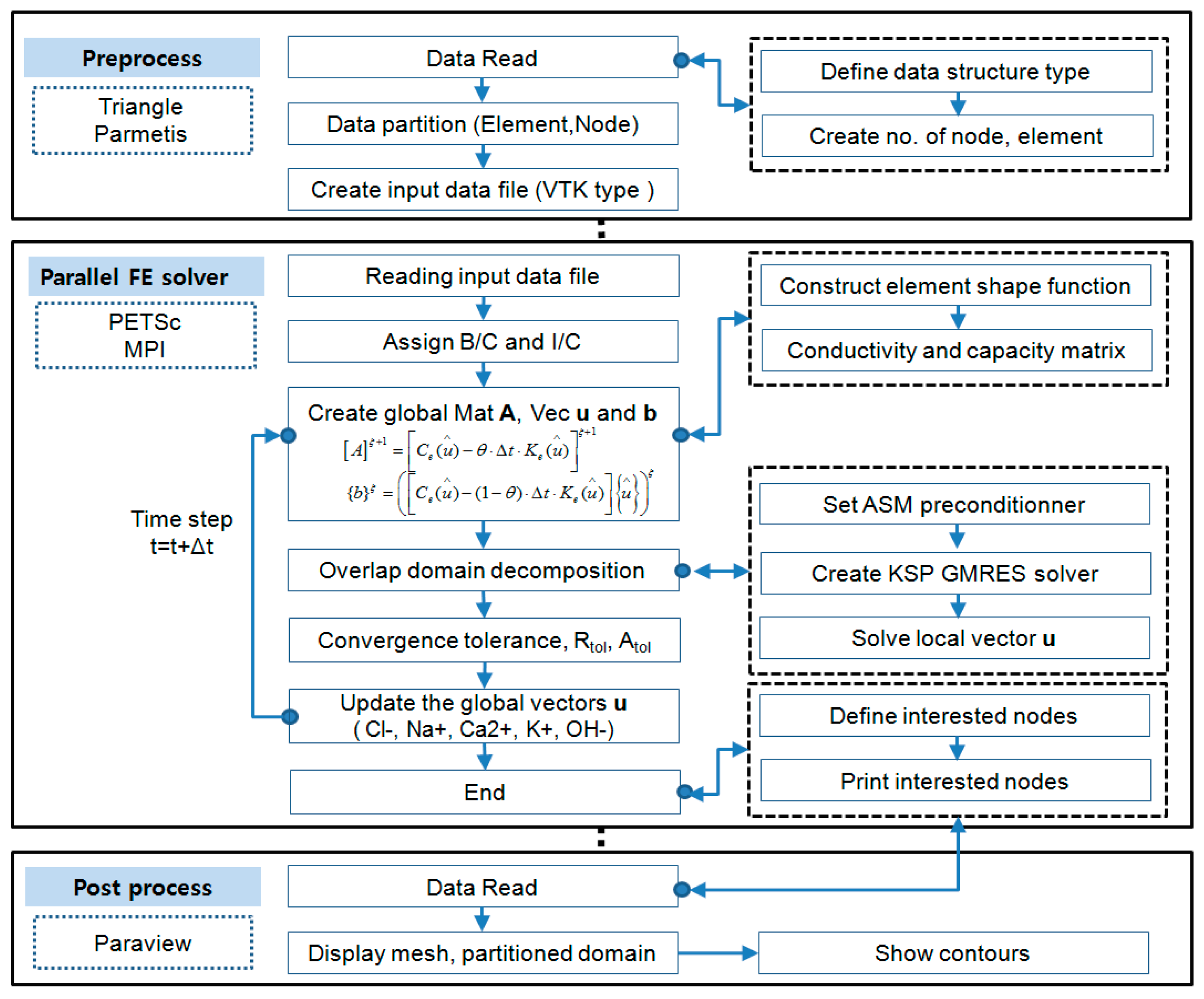
3. Parallel Finite Element Formulation
3.1. Numerical Modeling with Finite Element Method
3.2. Overlapping Domain Decomposition Method
3.3. Implementation of Parallel Finite Element Method
4. Numerical Results
4.1. Validation of Parallel Finite Element Model
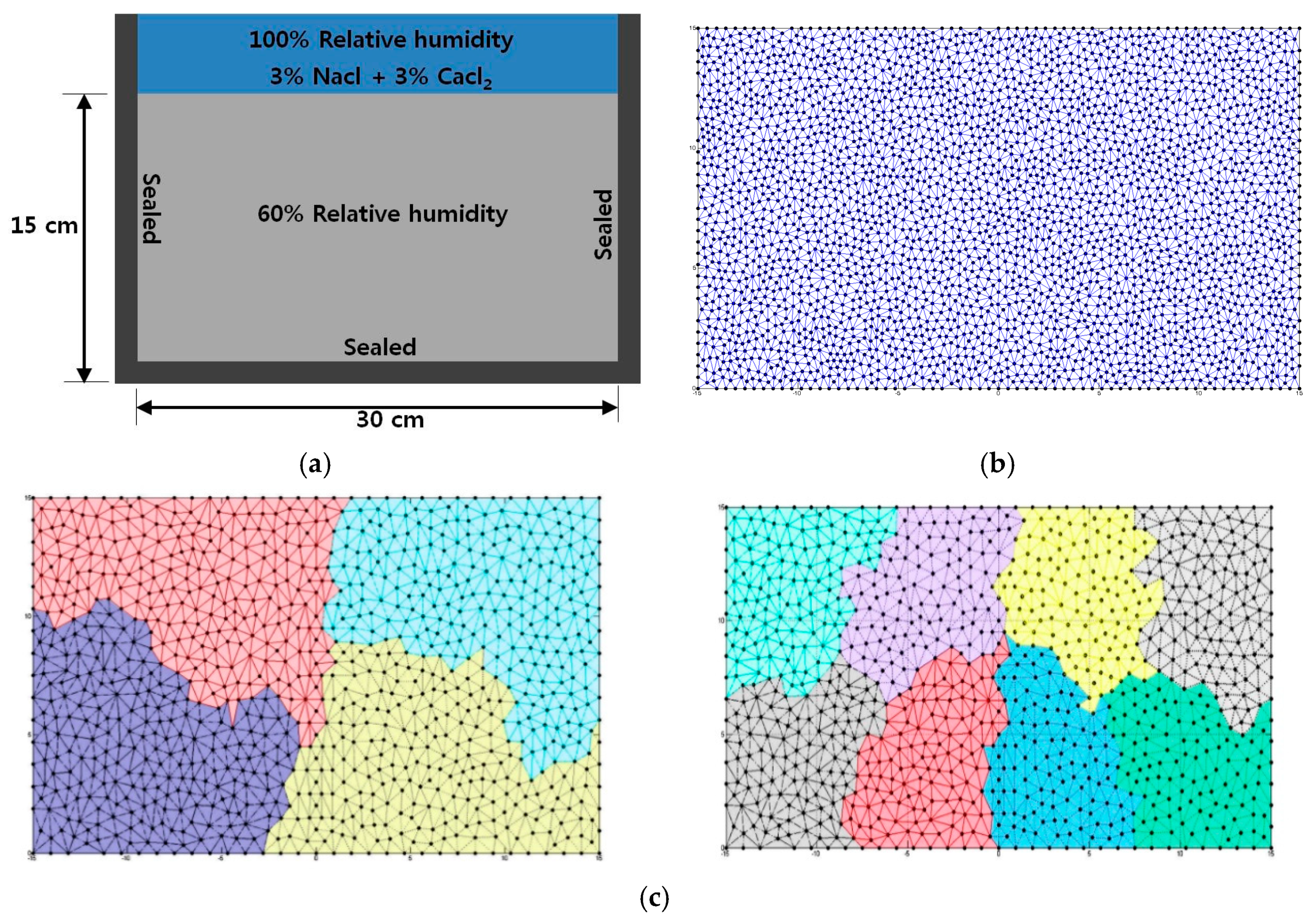
4.1.1. Test Plan for Deicing Solution Ponding Test
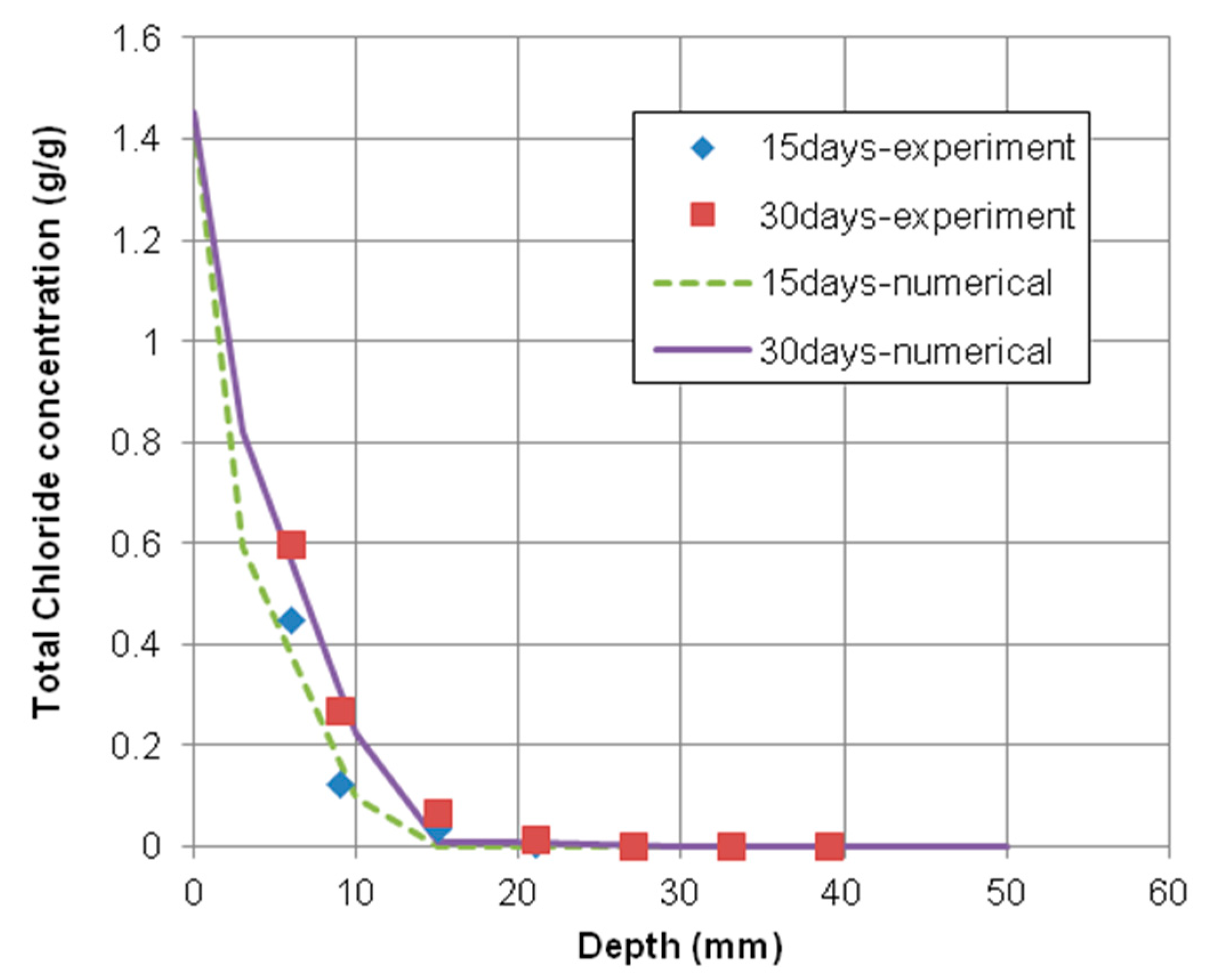
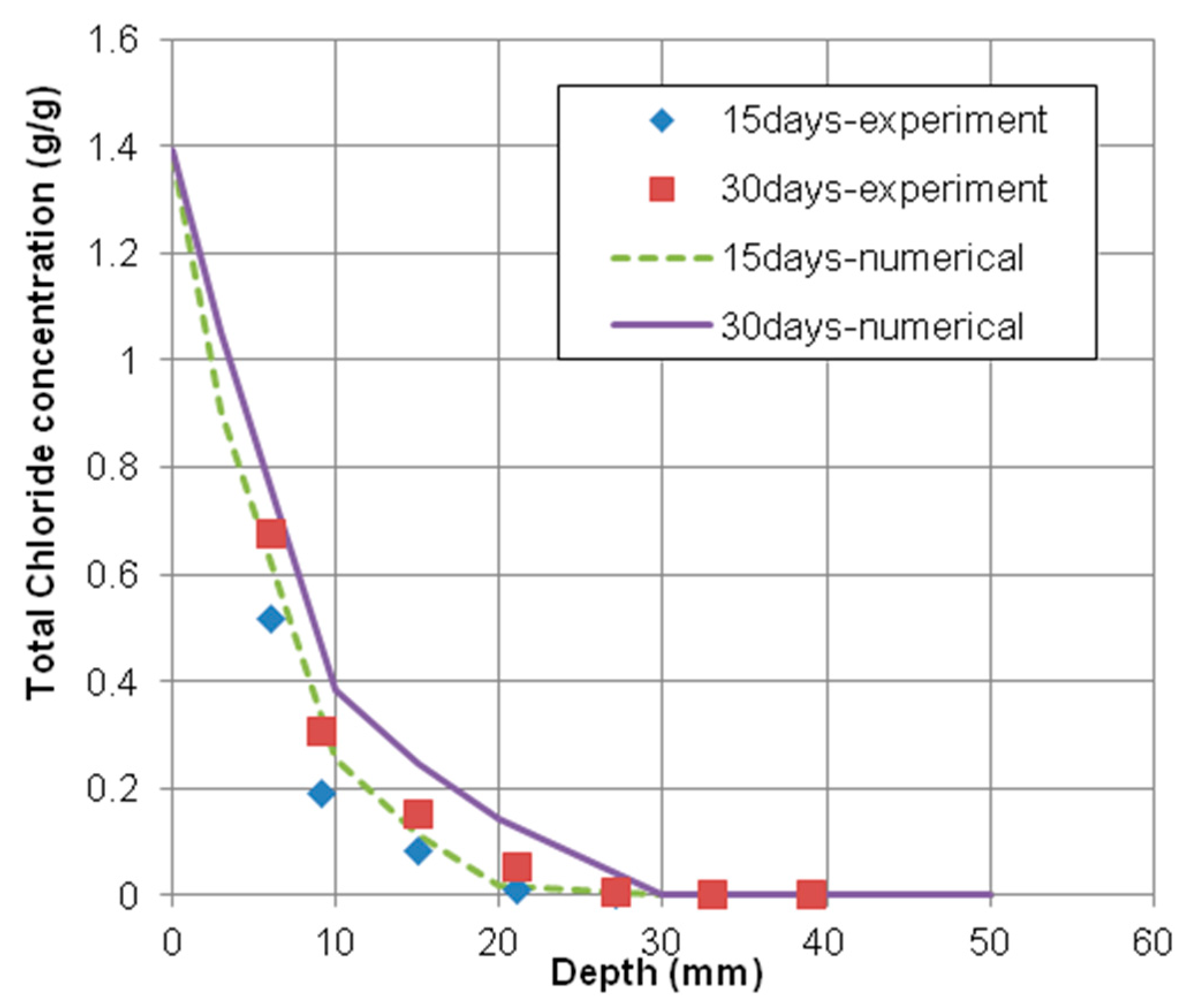
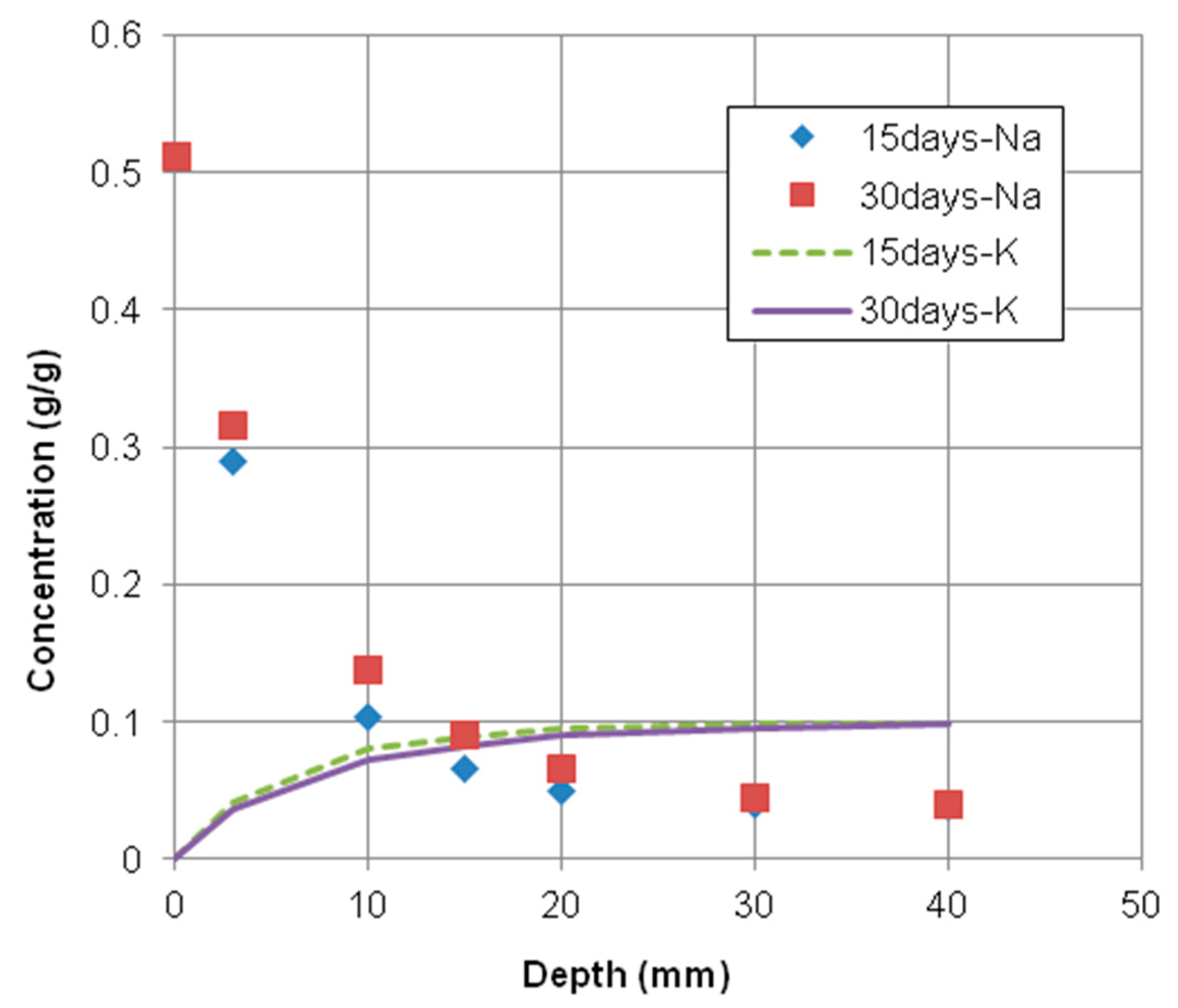
4.1.2. Comparison of Numerical Results with Test Results
4.2. Prediction for Multispecies Transport in Nonsaturated Concrete
4.2.1. Numerical Example
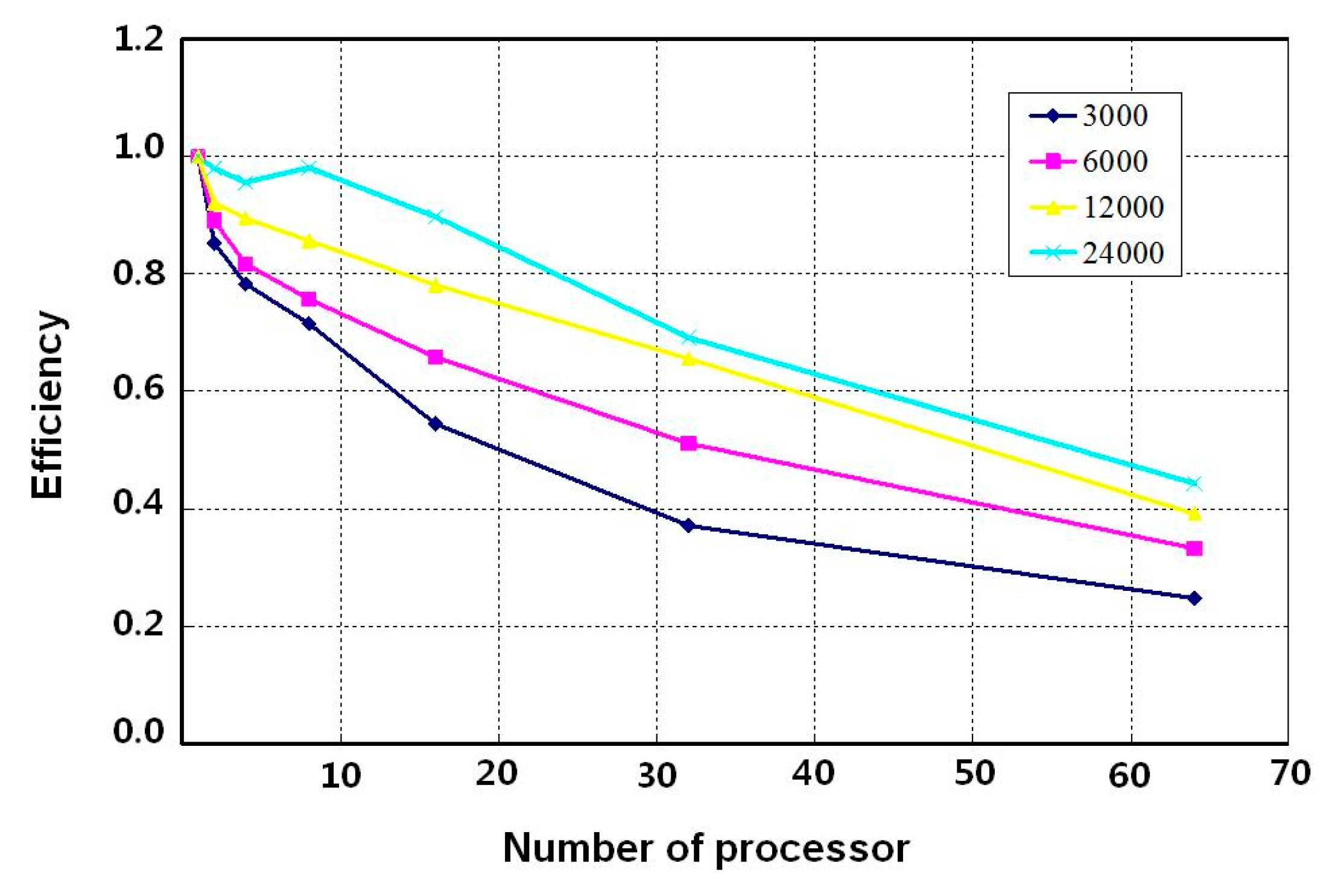
4.2.2. Performance of Parallel Finite Element Model
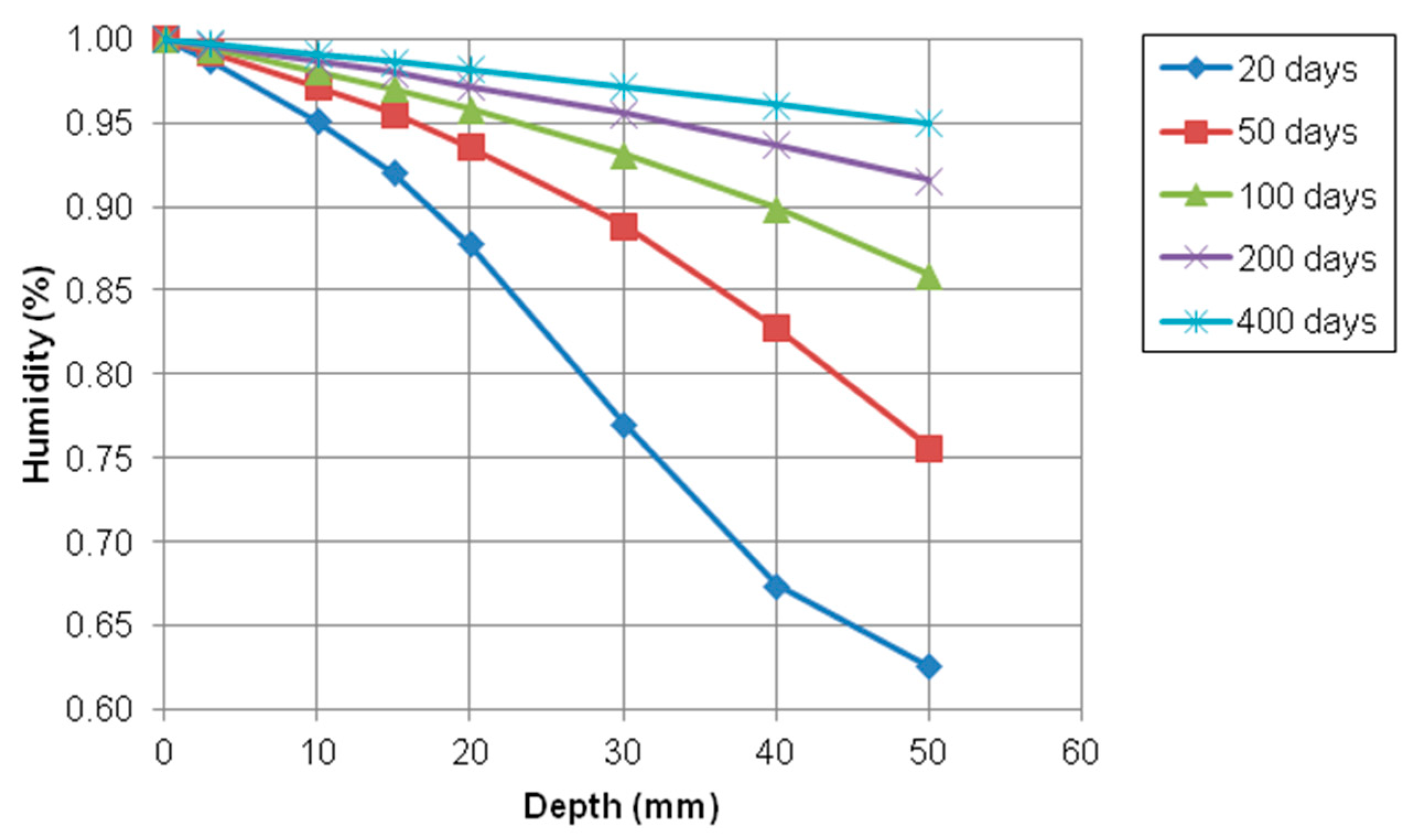
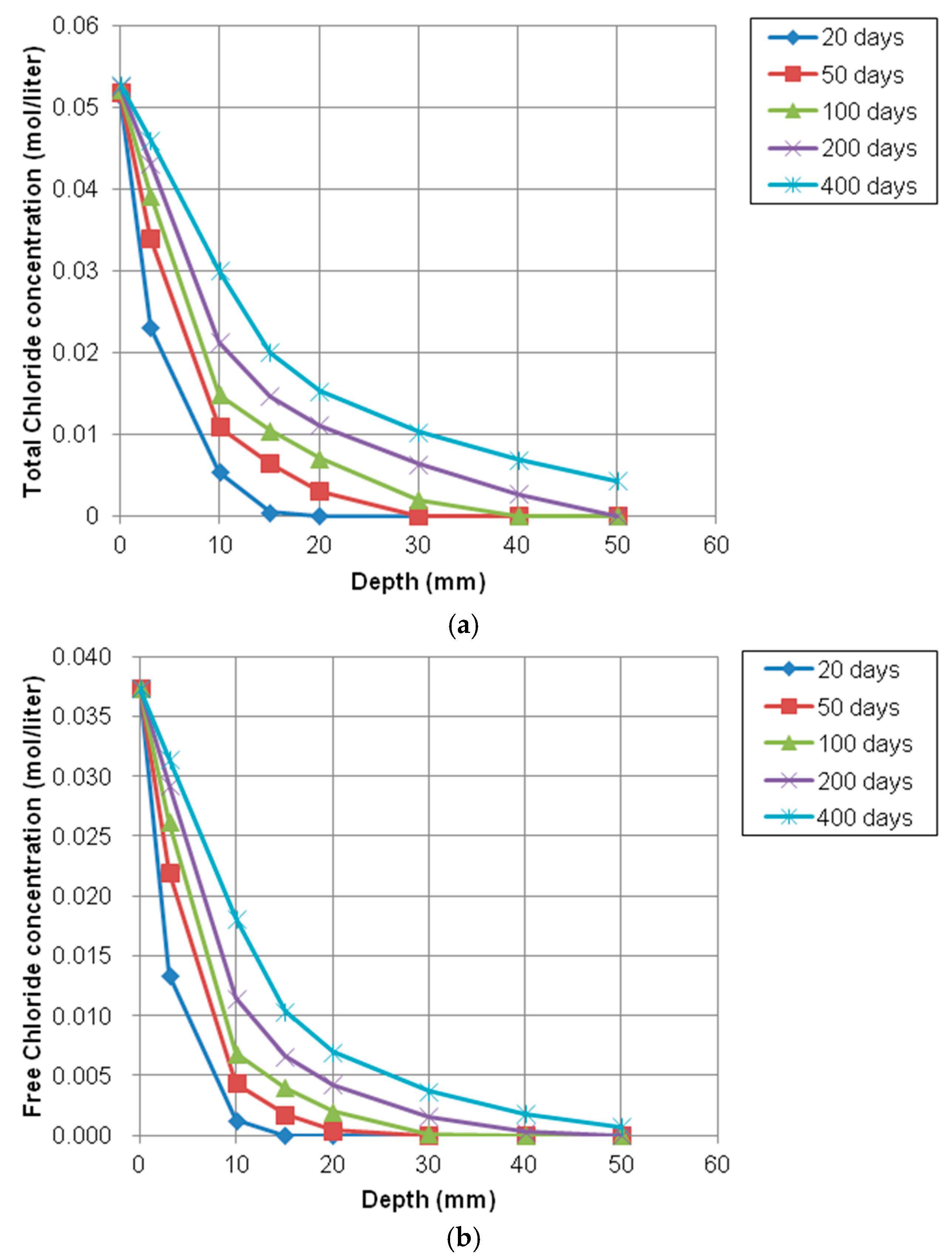
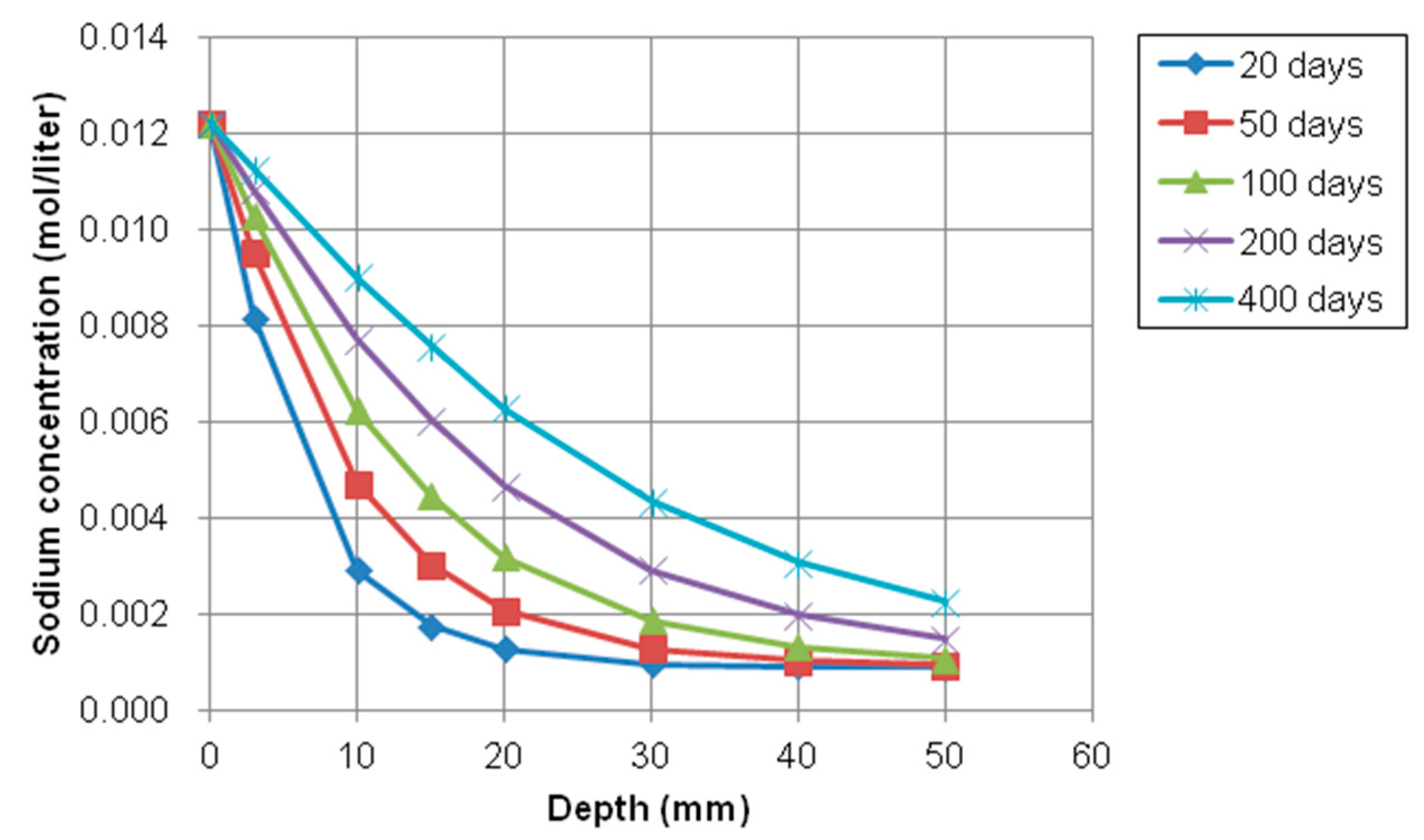
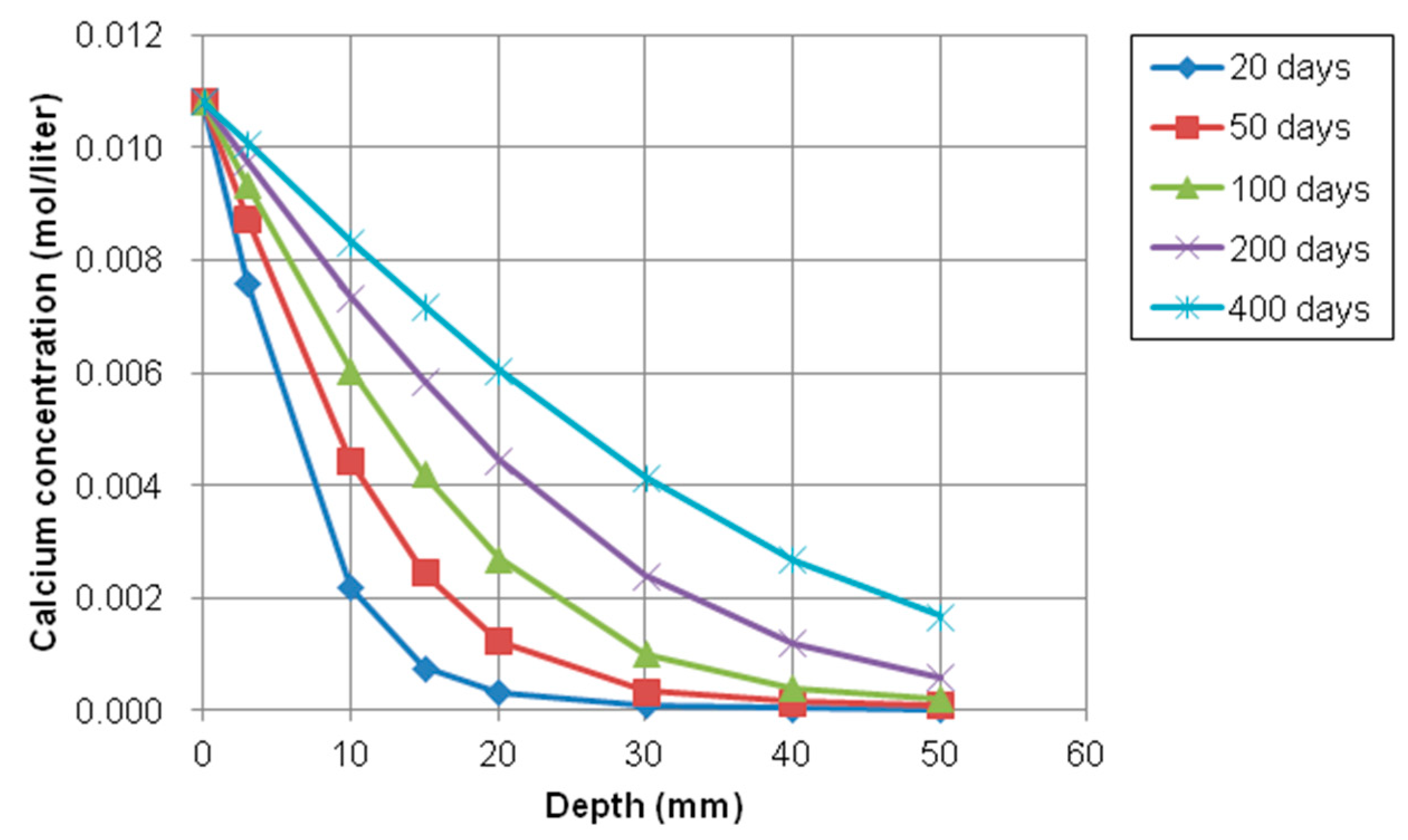
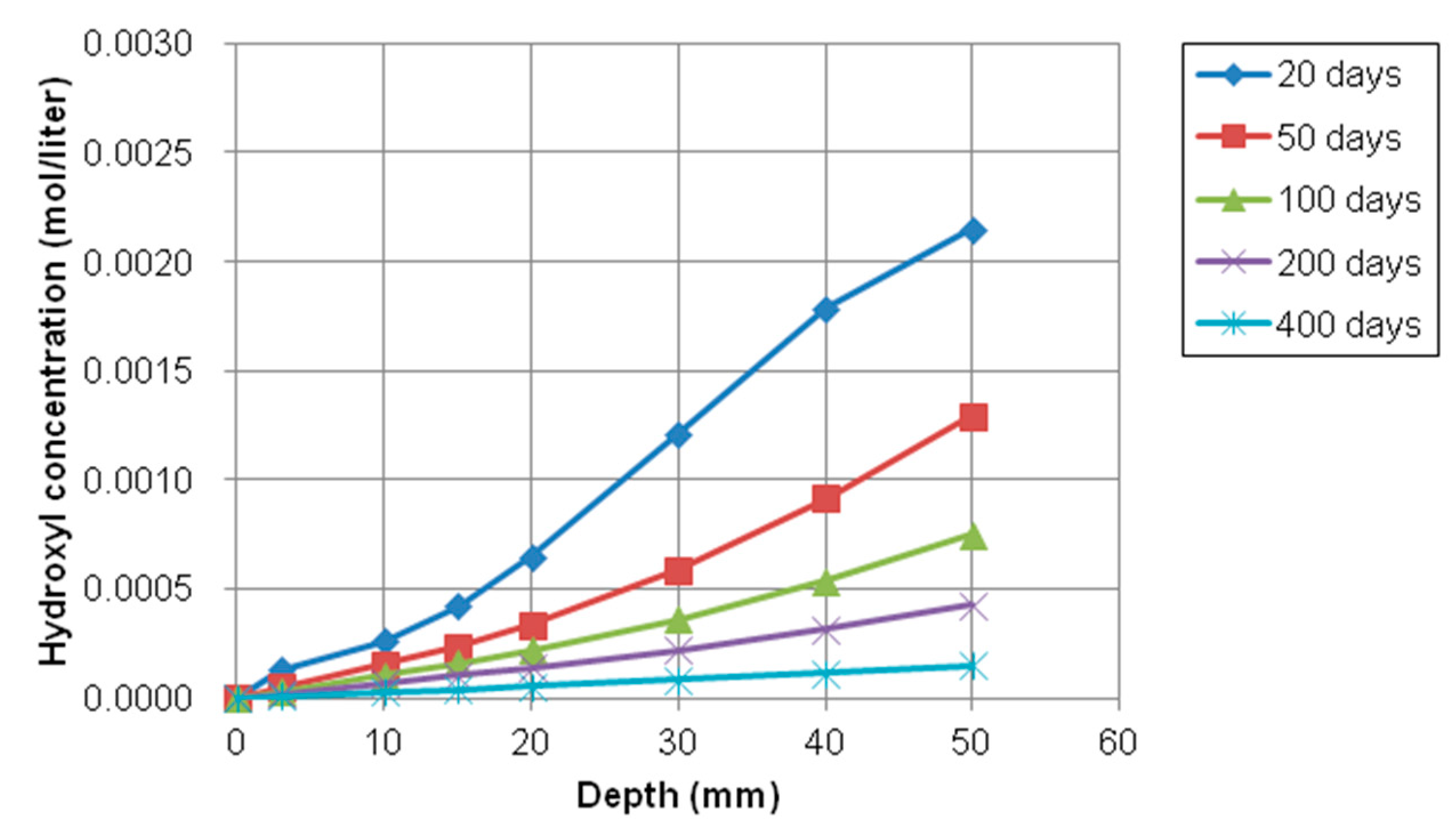
4.2.3. Numerical Results of Multispecies Transport in Nonsaturated Concrete
5. Conclusions
- The parallel finite element model was implemented with higher level library, PETSc (Portable, Extensible Toolkit for Scientific Computation) and MPI (Massage Passing Interface), based on C++ program language. For the easier implementation in algebraic approach as well as faster convergence, the overlapping DD method was employed to solve the linear sparse matrix. To improve the convergence of multispecies transport problem, the additive Schwarz preconditioner was applied and GMRES (Generalized Minimal Residual method) as an iterative solver was mainly adopted because of its ability to solve nonsymmetric linear system of global and local matrix.
- The new mathematical model was developed based on the Nernst–Planck equation and null current condition to solve the ionic-induced electrostatic potential. This model included the material models of transport mechanisms in cement paste and aggregates. The model can be used to simulate the multispecies penetration into concrete structures by considering the effect of moisture gradient.
- Moisture transport has significant effect on penetration of deicing salts into concrete by accelerating the penetration rate of chloride, sodium, and calcium ions. The coupling parameter was assumed because of no experimental data or material models of coupling parameters for other species. The parameter considering the effect of moisture on ionic transport was assumed by the same as used for the chloride ions due to carrying any other ions as it carries the chloride ions. The coupling parameter of each species can be estimated by the ratio between a specific ionic species and the chloride ions.
- In order to verify the new mathematical model, the parallel finite element program was developed and the numerical results were compared with the experimental results about the penetration of multi-types of deicing solutions into saturated concrete. The comparisons showed good results and the accuracy of the new mathematical model for the transport mechanism of the multispecies was proven effectively.
- The model prediction for the ionic transport in partially saturated concrete was conducted to investigate the transport of ionic species such as chloride, sodium, calcium, hydroxyl, and potassium. The penetration of chloride, sodium, and calcium increased over time because the initial concentration outside concrete was much higher and the moisture gradient had an effect on accelerating the transport rate of ions. However, the concentration of hydroxyl and potassium was decreased due to opposite reason. This model can be used satisfactorily to predict the penetration of aggressive chemicals, such as deicing salts into nonsaturated condition.
- For more robust verification, additional deicing ponding tests under nonsaturated conditions are needed in the future. More material models are needed to take into account the effects of mineral additives such as fly ash and silica fume on chloride penetration and ion transport in concrete. Additionally, the temperature effect is to be considered as one of the crucial parameters.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Derivation of Diffusivity Matrix
References
- Han, S.-H. Influence of diffusion coefficient on chloride ion penetration of concrete structure. Constr. Build. Mater. 2007, 21, 370–378. [Google Scholar] [CrossRef]
- Song, H.-W.; Lee, C.-H.; Ann, K.Y. Factors influencing chloride transport in concrete structures exposed to marine environments. Cem. Concr. Compos. 2008, 30, 113–121. [Google Scholar] [CrossRef]
- Tamimi, A.K.; Abdalla, J.A.; Sakka, Z.I. Prediction of long term chloride diffusion of concrete in harsh environment. Constr. Build. Mater. 2007, 22, 829–836. [Google Scholar] [CrossRef]
- Na, O.; Cai, X.-C.; Xi, Y. Corrosion Prediction with Parallel Finite Element Modeling for Coupled Hygro-Chemo Transport into Concrete under Chloride-Rich Environment. Materials 2017, 10, 350. [Google Scholar] [CrossRef]
- Khitab, A.; Anwar, W.; Arshad, M.T. Predictive Models of Chloride Penetration in concrete: An Overview. MUST J. Eng. Appl. Sci. 2017, 1, 1–14. [Google Scholar] [CrossRef][Green Version]
- Liu, Q. Multi-Phase Modelling of Multi-Species Ionic Migration in Concrete. Ph.D. Thesis, University of Plymouth, Plymouth, UK, 2013. [Google Scholar]
- Chatterji, S. Transportation of ions through cement based materials. Part 1 fundamental equations and basic measurement techniques. Cem. Concr. Res. 1994, 24, 907–912. [Google Scholar] [CrossRef]
- Li, L.; Page, C. Modelling of electrochemical chloride extraction from concrete: Influence of ionic activity coefficients. Comput. Mater. Sci. 1998, 9, 303–308. [Google Scholar] [CrossRef]
- Li, L.; Page, C. Finite element modelling of chloride removal from concrete by an electrochemical method. Corros. Sci. 2000, 42, 2145–2165. [Google Scholar] [CrossRef]
- Truc, O.; Ollivier, J.-P.; Nilsson, L.O. Numerical simulation of multi-species diffusion. Mater. Struct. 2000, 33, 566–573. [Google Scholar] [CrossRef]
- Lorente, S.; Carcassè, M.; Ollivier, J. Penetration of ionic species into saturated porous media: the case of concrete. Int. J. Energy Res. 2003, 27, 907–917. [Google Scholar] [CrossRef]
- Nguyen, T.; Baroghel-Bouny, V.; Dangla, P. Prediction of chloride ingress into saturated concrete on the basis of a multi-species model by numerical calculations. Comput. Concr. 2006, 3, 401–422. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.-Y.; Page, C. A two-dimensional model of electrochemical chloride removal from concrete. Comput. Mater. Sci. 2001, 20, 196–212. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.-Y.; Page, C. Modelling of chloride ingress into concrete from a saline environment. Build. Environ. 2005, 40, 1573–1582. [Google Scholar] [CrossRef]
- Samson, E.; Lemaire, G.; Marchand, J.; Beaudoin, J. Modeling chemical activity effects in strong ionic solutions. Comput. Mater. Sci. 1999, 15, 285–294. [Google Scholar] [CrossRef]
- Samson, E.; Marchand, J. Numerical Solution of the Extended Nernst–Planck Model. J. Colloid Interface Sci. 1999, 215, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Samson, E.; Marchand, J. Modeling the transport of ions in unsaturated cement-based materials. Comput. Struct. 2007, 85, 1740–1756. [Google Scholar] [CrossRef]
- Liu, Q.-F.; Easterbrook, D.; Yang, J.; Li, L.-Y. A three-phase, multi-component ionic transport model for simulation of chloride penetration in concrete. Eng. Struct. 2015, 86, 122–133. [Google Scholar] [CrossRef]
- Ukrainczyk, N.; Koenders, E.A.B. Numerical Model for chloride ingress in cement based materials: Method of lines implementation for solving coupled multi-species diffusion with binding. Comput. Mater. Civ. Eng. 2016, 1, 109–119. [Google Scholar]
- Liu, Q.-F.; Easterbrook, D.; Li, L.-Y.; Li, D. Prediction of chloride diffusion coefficients using multi-phase models. Mag. Concr. Res. 2017, 69, 134–144. [Google Scholar] [CrossRef]
- Suwito, S.; Cai, X.C.; Xi, Y. Parallel finite element method for coupled chloride moisture diffusion in concrete. Int. J. Numer. Anal. Model. 2006, 3, 481–503. [Google Scholar]
- Herndon, B.; Aluru, N.; Raefsky, A.; Goossens, R.J.G.; Law, K.H.; Dutton, R.W. A Methodology for Parallelizing PDE Solvers: Applications to Semiconductor Device Simulation. In Proceedings of the 7th SIAM Conference on Parallel Processing for Scientific Computing, SIAM, San Francisco, CA, USA, 15–17 Feburary 1995. [Google Scholar]
- McKenna, F. Object Oriented Finite Element Analysis: Frameworks for Analysis Algorithms and Parallel Computing. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1997. [Google Scholar]
- Ababneh, A.; Benboudjema, F.; Xi, Y. Chloride Penetration in Nonsaturated Concrete. J. Mater. Civ. Eng. 2003, 15, 183–191. [Google Scholar] [CrossRef]
- Xi, Y.; Willam, K.; Frangopol, D.M. Multiscale modeling of interactive diffusion processes in concrete. J. Eng. Mech. 2003, 126, 258–265. [Google Scholar] [CrossRef]
- Xi, Y.; Bazant, Z.P.; Molina, L.; Jennings, H.M. Moisture diffusion in cementitious materials: Adsorption isotherm. Adv. Cem. Based Mater. 1994, 1, 248–257. [Google Scholar] [CrossRef]
- Xi, Y.; Bazant, Z.P.; Molina, L.; Jennings, H.M. Moisture diffusion in cementitious materials: Moisture capacity and diffusivity. Adv. Cem. Based Mater. 1994, 1, 258–266. [Google Scholar] [CrossRef]
- Xi, Y. A model for moisture capacities of composite materials. I: Formulation. Comput. Mater. Sci. 1995, 4, 65–77. [Google Scholar] [CrossRef]
- Xi, Y. A model for moisture capacities of composite materials. II: Application to concrete. Comput. Mater. Sci. 1995, 4, 78–92. [Google Scholar] [CrossRef]
- Xi, Y.; Bažant, Z.P. Modeling Chloride Penetration in Saturated Concrete. J. Mater. Civ. Eng. 1999, 11, 58–65. [Google Scholar] [CrossRef]
- Christensen, R.M. Mechanics of Composite Materials; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Ababneh, A. An experimental study on the effect of chloride penetration on moisture diffusion in concrete. Mater. Struct. 2002, 35, 659–663. [Google Scholar] [CrossRef]
- Abarr, L. The Effect of Moisture Diffusion on Chloride Penetration. Master’s Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2005. [Google Scholar]
- Cai, X.-C.; Saad, Y. Overlapping domain decomposition algorithms for general sparse matrices. Numer. Linear Algebra Appl. 1996, 3, 221–237. [Google Scholar] [CrossRef]
- Cai, X.-C. Overlapping domain decomposition methods. In Advanced Topics in Computational Partial Differential Equations; Springer-Verlag Berlin and Heidelberg GmbH & Co. KG: Berlin, Germany, 2003; Chapter 2; pp. 57–95. [Google Scholar]
- Balay, S.; Buschelman, K.; Eijkhout, V.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; McInnes, L.C.; Smith, B.F.; Zhang, H. PETSc-Users Manual; Technical Report ANL-95/11—Revision 2.1.5; Argonne National Laboratory: Lemont, IL, USA, 2008.
- MPI Forum. MPI: A Message Passing Interface Standard. International Journal of Supercomputer Applications; University of Tennessee: Knoxville, TN, USA, 1994; pp. 159–416. [Google Scholar]
- MPI Forum. MPI2: A Message Passing Interface Standard. High Performance Computing Applications; University of Stuttgart: Stuttgart, Germany, 1998; pp. 1–299. [Google Scholar]
- MPICH Team, MPICH: A portable implementation of MPI. 1996–2005. Available online: http://wwwunix. mcs.anl.gov/mpi/mpich/.Karypis (accessed on 27 August 2019).
- Karypis, G. ParMETIS: Parallel Graph Partitioning and Sparse Matrix Ordering. 1996–2005. Available online: http://glaros.dtc.umn.edu/gkhome/metis/parmetis/overview (accessed on 27 August 2019).
- Dalcin, L.D.; Paz, R.R.; Anca, A.; Storti, M.A.; D’Elia, J. Parallel FEM application development in Python. In Proceedings of the VIII Congreso Argentino de Mecánica Computacional, Buenos Aires, Argentina, 1 November 2005. [Google Scholar]
- Mackay, D.R. Solution Methods for Static and Dynamic Structural Analysis on Distributed Memory Computers. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1992. [Google Scholar]
- Law, K.H. Large Scale Engineering Computations on Distributed Memory Parallel Computers and Distributed Workstations. In Proceedings of the NSF Workshop on Scientific Supercomputing, Visualization and Animation in Geotechnical Earthquake Engineering and Engineering Seismology, Pittsburgh, PA, USA, October 1994. [Google Scholar]
- Suarjana, M. Conjugate Gradient Method for Linear and Nonlinear Structural Analysis on Sequential and Parallel Computers. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1994. [Google Scholar]
- Aluru, N.R. Parallel and Stabilized Finite Element Methods for the Hydrodynamic Transport Model of Semiconductor Devices. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1995. [Google Scholar]
- Triangle. Available online: https://www.cs.cmu.edu/~quake/triangle.html (accessed on 27 August 2019).
- PETSc. Available online: https://www.mcs.anl.gov/petsc/ (accessed on 27 August 2019).
- Damrongwiriyanupap, N. Modeling the Penetration of Multi-Species Aggressive Chemicals into Concrete Structures. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2010. [Google Scholar]
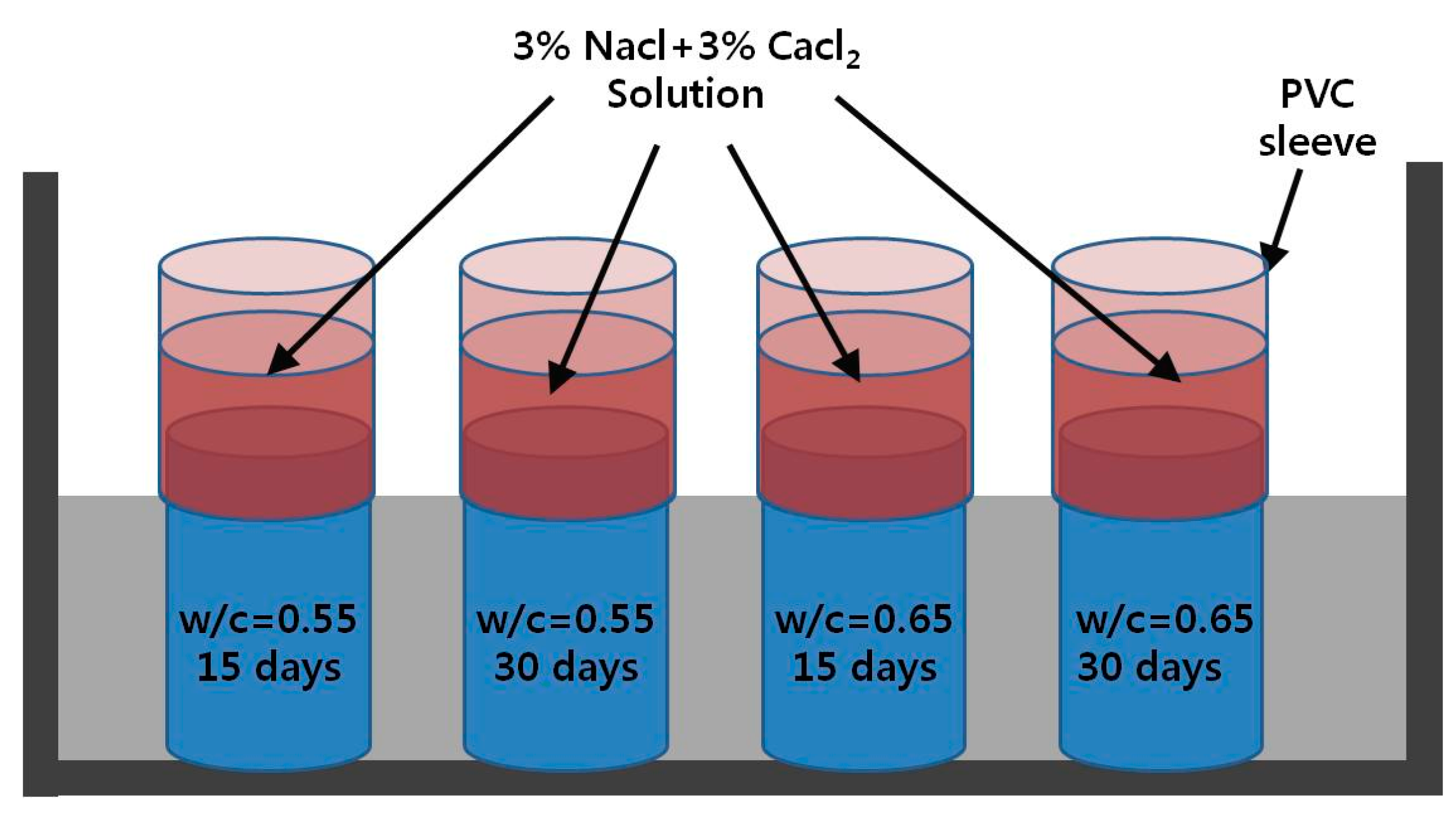



| W/C | Time (days) | Depth (mm) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0–6 | 6–12 | 12–18 | 18–24 | 24–30 | 30–36 | 36–42 | ||
| 0.55 | 15 | 0.450 | 0.125 | 0.036 | 0.006 | 0.003 | 0.003 | 0.002 |
| 30 | 0.599 | 0.269 | 0.068 | 0.014 | 0.004 | 0.003 | 0.002 | |
| 0.65 | 15 | 0.517 | 0.193 | 0.085 | 0.011 | 0.004 | 0.002 | 0.002 |
| 30 | 0.677 | 0.31 | 0.153 | 0.055 | 0.008 | 0.003 | 0.003 | |
| Species | Unit | K | Na | Cl | OH | Ca | |
|---|---|---|---|---|---|---|---|
| Charge number | +1 | +1 | −1 | −1 | +2 | ||
| Diffusion coefficient | m2/s | 4.0 × 10−11 | 2.8 × 10−11 | Refer to Equation (14) | 5.3 × 10−10 | 1.6 × 10−11 | |
| Initial condition | at top surface | mol/L | 0 | 0.513 | 1.053 | 0 | 0.27 |
| in pore solution | mol/L | 0.0995 | 0.0389 | 0 | 0.1384 | 0 | |
| Cement type | I/II | ||||||
| Water–cement ratio | 0.55 | ||||||
| Volume fraction of aggregate | 0.65 | ||||||
| Outside RH | % | 100 | |||||
| Inside RH | % | 60 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, O.; Xi, Y. Parallel Finite Element Model for Multispecies Transport in Nonsaturated Concrete Structures. Materials 2019, 12, 2764. https://doi.org/10.3390/ma12172764
Na O, Xi Y. Parallel Finite Element Model for Multispecies Transport in Nonsaturated Concrete Structures. Materials. 2019; 12(17):2764. https://doi.org/10.3390/ma12172764
Chicago/Turabian StyleNa, Okpin, and Yunping Xi. 2019. "Parallel Finite Element Model for Multispecies Transport in Nonsaturated Concrete Structures" Materials 12, no. 17: 2764. https://doi.org/10.3390/ma12172764
APA StyleNa, O., & Xi, Y. (2019). Parallel Finite Element Model for Multispecies Transport in Nonsaturated Concrete Structures. Materials, 12(17), 2764. https://doi.org/10.3390/ma12172764




