Properties of Cracking Patterns of Multi-Walled Carbon Nanotube-Reinforced Cement Matrix
Abstract
1. Introduction
2. Materials and Methods
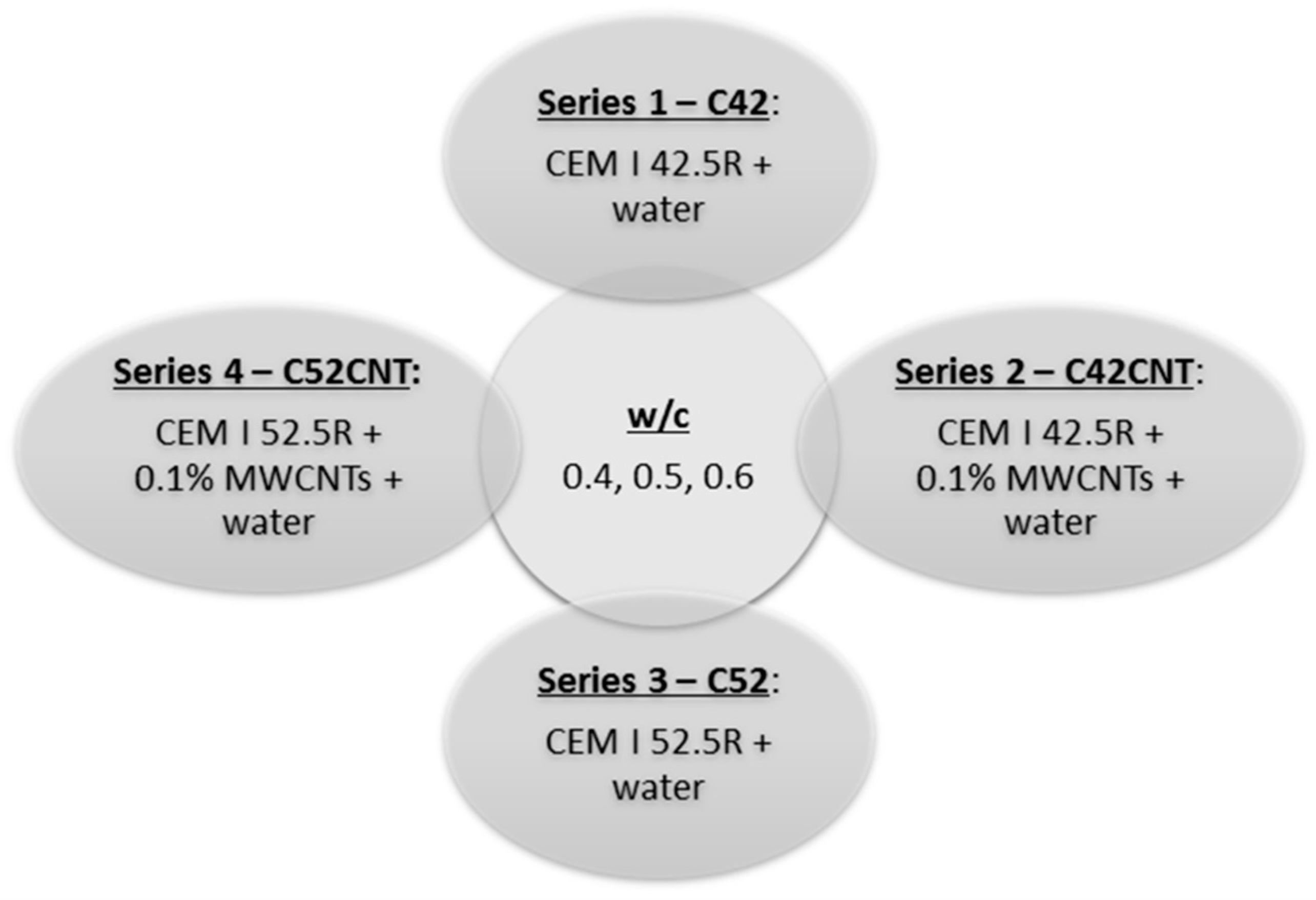
2.1. Components Used and Mixtures
2.2. Procedure of the Mixture Preparation
- the cement and water mixture was mechanically mixed until it obtained a uniform consistency,
- MWCNTs was used as the aqueous solution with surfactant (SDS); then this aqueous solution was mechanically mixed with cement,
- the MWCNTs/SDS weight ratio was 1:5,
- an aqueous MWCNTs-SDS solution was sonicated for a period of 30 min; sonication took place in a glass jar, which was placed in a bucket of cold water to remove excess heat resulting from ultrasonic mixing; the amount of the solution produced at one time was sufficient to produce six samples of the cement paste,
- for the sonication, the UP400S ultrasonic homogenizer of the HIELSCHER Ultrasound Technology company (Teltow, Germany) was used, it was equipped with the H22 horn sonotrode with a tip diameter of 22 mm, maximum amplitude—100 μm, sound power density—85 W/cm2, operating frequency—24 kHz; sonication took place in the continuous mode of the device operation, with maximum power, which in connection with the H22 sonotrode giving 300 W of power,
- test samples were made as 40 × 40 × 160 mm beams, which is in line with the requirements for testing cement pastes and mortars; the mix was laid in molds in two layers, successively compacted, using a standardized shaker, in accordance with the EN 196-1 [52], and
- samples were demolded 24 h after forming; maturation took place in dry-air conditions (average air temperature—22 °C, average relative air humidity—50%; maturation period was equal to 28 days).
2.3. Cracking Patterns Formation Process
- Phase I—preheating the furnace to 250 °C,
- Phase II—placing the samples in the furnace and heating them at the above temperature (250 °C) for a period of 4 h, and
- Phase III—removing samples from the furnace and cooling them as a result of a natural decrease in the samples temperature under laboratory conditions (average air temperature—20 °C, average relative air humidity—50%); the samples reached ambient temperature within two hours of being removed from the furnace.
2.4. Basic Physico-Mechanical Properties of the Cement Matrix
2.5. Quantitative Analysis of the Cracking Patterns—Image Analysis
- —the average cluster area (mm2),
- —the average cluster perimeter (mm),
- —the average crack width (mm),
- CD—the crack density (m−1).
3. Results
4. Discussion
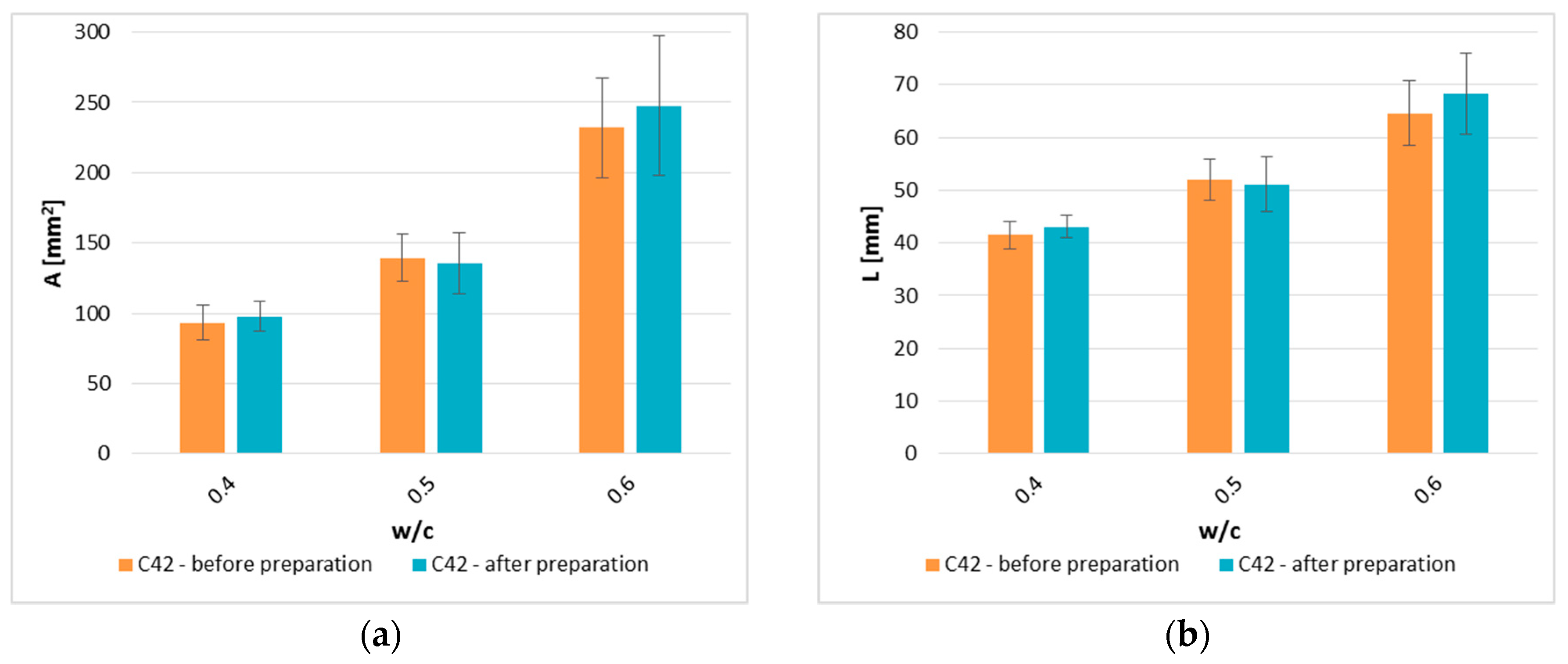
4.1. Assessment of the Impact of the Surface Preparation Method on the Correctness of the Results Obtained from the Image Analysis
4.2. Characteristics of the Cracking Patterns
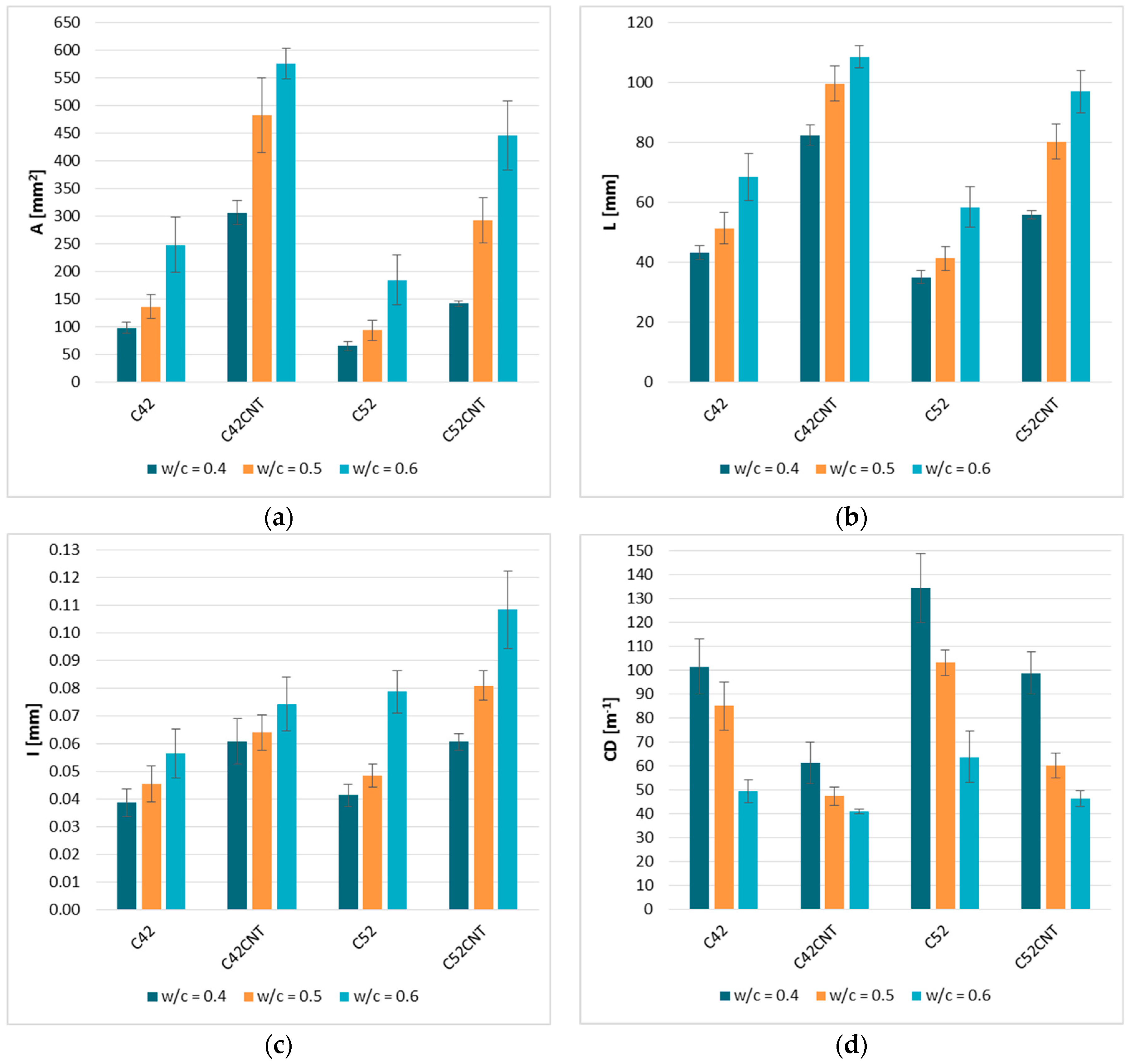
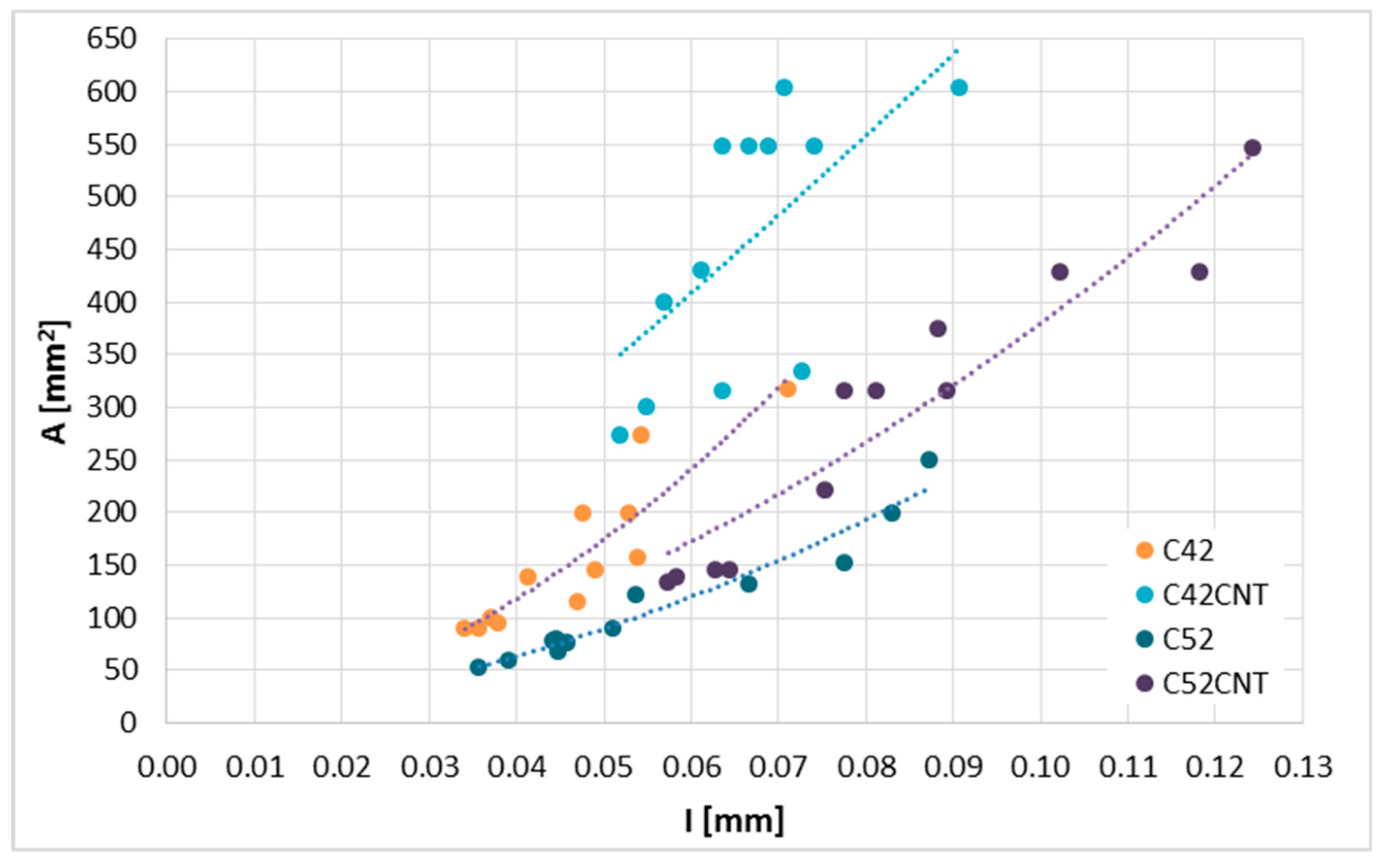
4.2.1. —The Average Cluster Area
4.2.2. —The Average Cluster Perimeter
4.2.3. —The Average Crack Width
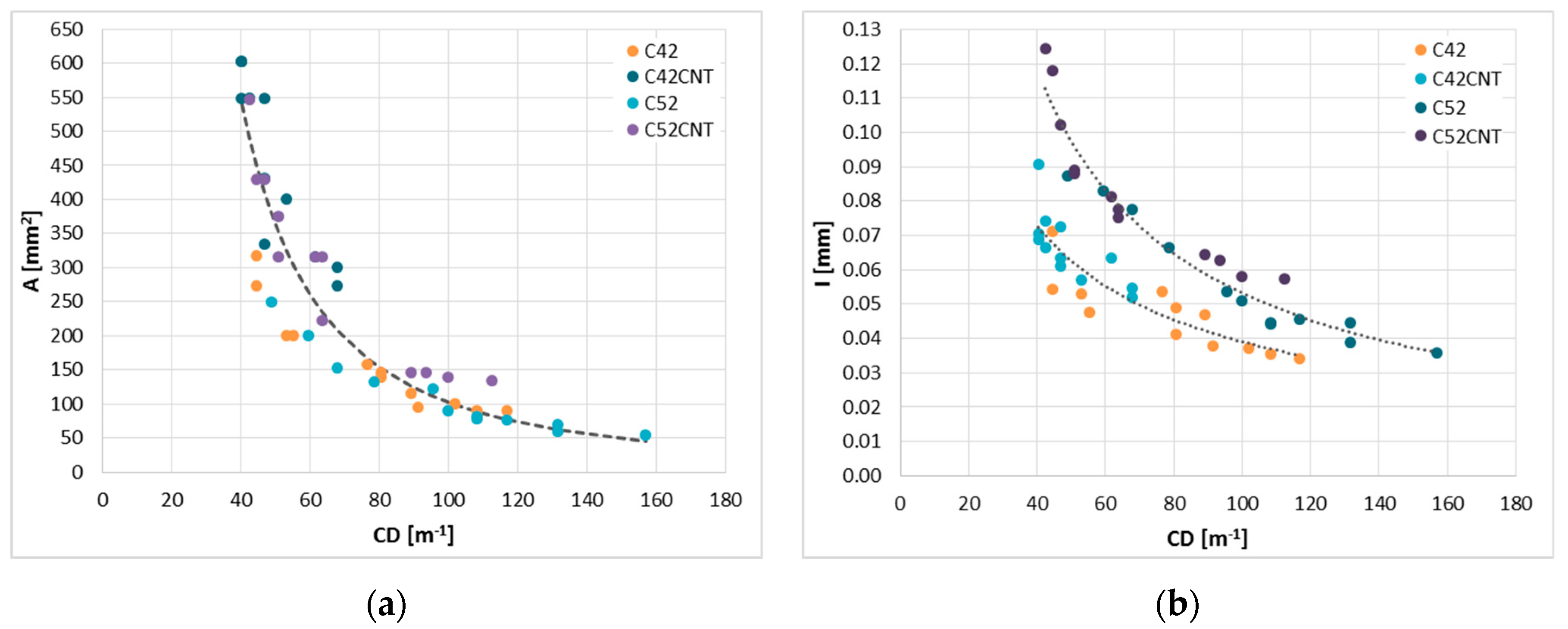
4.2.4. —The Crack Density
4.3. Correlations between the Properties of the Cracking Patterns and Physico-Mechanical Features of the Cement Matrix
5. Conclusions
- In order to facilitate the image analysis process, the samples were subjected to the preparation, which consisted in applying the thin white acrylic film to the scanned surface. The statistical analyses carried out have shown that the preparation method applied does not affect the correctness of the results obtained from the image analysis.
- As the w/c ratio increased, the , , and also increased, and CD decreased. Cement pastes made of cement with greater fineness (C52 and C52CNT) were characterized by smaller values of and , higher values of CD, while in the case of no clear influence of the cement class was observed. The presence of MWCNTs resulted in a significant increase in the , , and , and a decrease in CD.
- The use of MWCNTs in the form of an aqueous dispersion in the presence of a surfactant, which is SDS, resulted in foaming of the cement matrix during mechanical mixing. The result was a significant reduction in the cement matrix density and, thus, an increase in porosity. This is the main reason for the changes in the physico-mechanical properties of the cement matrix and it also had a key impact on the characteristics of the cracking patterns. The conclusions drawn from this work concern the combined effect of using MWCNTs and SDS, not the MWCNT addition itself.
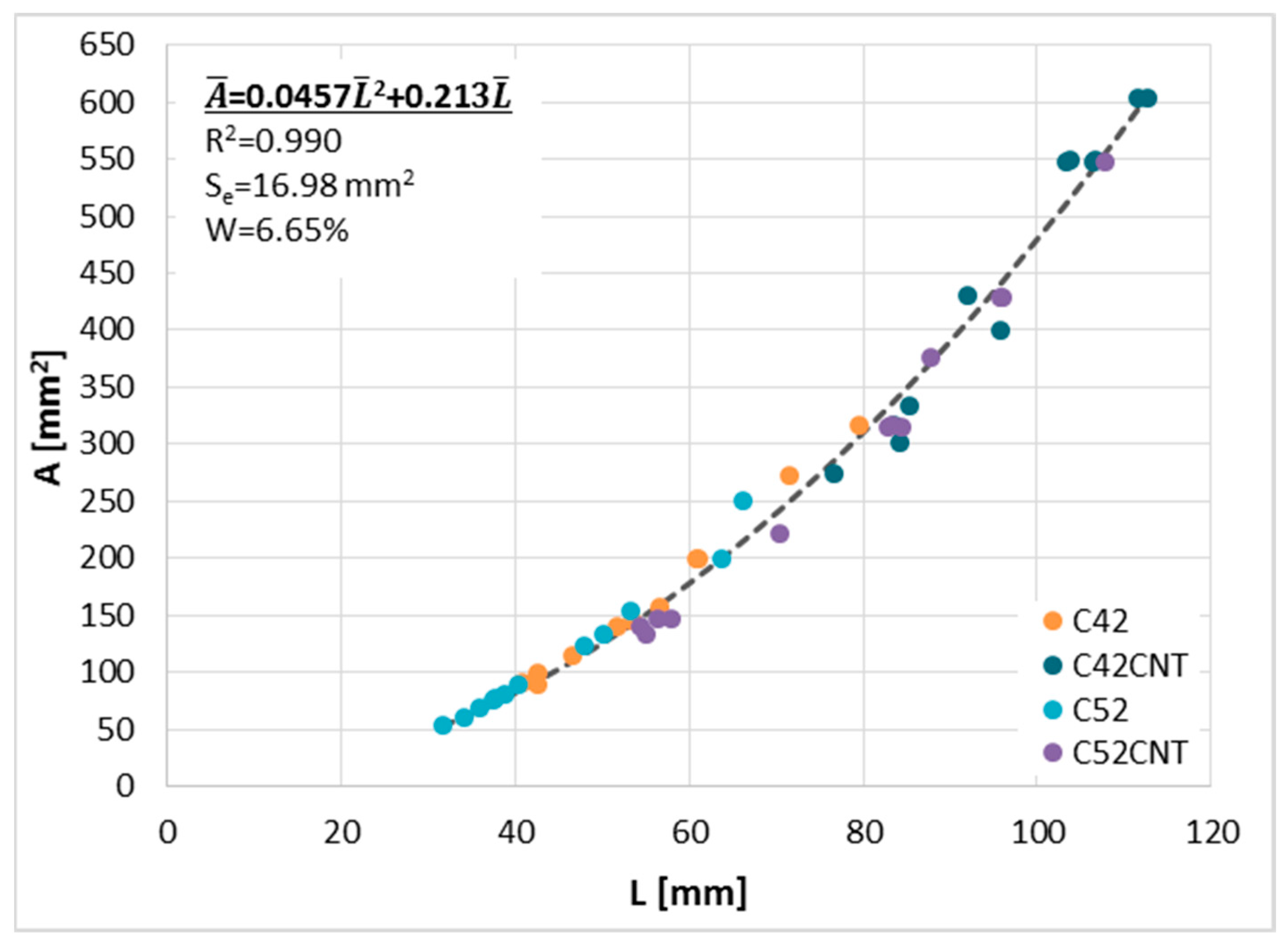
- The relationship between the parameters of the cracking patterns was assessed. There is a very strong relationship between and , and the global correlation coefficient between these parameters is up to 0.98. This relationship is constant and independent of technological variables of the material and confirms the fractal nature of the cracking patterns.
- The relationship between and largely depends on the series, i.e., mainly on the class of cement used and the presence of MWCNTs.
- The CD relationship was assessed with both and . A global relation with a strong correlation was noted between CD and . However, in the case of the dependence between CD and , a clear effect of the cement class was found.
- The possibility of estimation of physico-mechanical properties of the cement paste based on the parameters of cracking patterns was evaluated. In the vast majority, the accuracy of the estimation would be at a very good level apart from the tensile strength estimation.
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. The and Measurement Procedure Using the ImageJ v. 1.51j8 Software
- Opening the scan (File > Open).
- Setting the image scale (Analyze > Set Scale)—in order to correctly determine the surface areas and perimeter of clusters, the value of the scan resolution should be introduced.
- Rotating the image to position the sample longitudinal axis horizontally on the screen (Image > Transform > Rotate)—it may happen that the sample was not placed on the scanner parallel to the scanning traverse, but at a small angle—this facilitates further work with the image.
- Selection of the area that will be measured with dimensions of 157 × 38.5 mm on the sample surface (Edit > Selection > Specify)—this resulted from the necessity to determine a constant surface area for each sample because as a result of a sudden increase in temperature, the cement paste was subjected to the volume deformations.
- Cropping the image to 157 × 38.5 mm (Image > Crop).
- Contrasting the image (Image > Adjust > Brighthness/Contrast or Image > Adjust > Window/Level)—in order to “display” graphically the lines forming cracks in relation to the cluster surface.
- Creation a mask from a contrasted image (Image > Overlay > Add Image), then adding the mask to the ROI Manager (Image > Overlay > To ROI Manager)—the mask at a later stage can be used as a foundation with a given clearance (in the ROI Manager: Properties > Opacity),
- Creation a binary image (Process > Binary > Make binary)—a black-and-white image of the sample surface is created. The cracks are then visible as black (0 on the histogram), and the surface of the clusters is visible as white (255 on the histogram).
- Removal of any discontinuities in the lines forming the cracks (from the toolbar: Brush with a size equal to 2 px, with a gradient value corresponding to the crack gradient, 0)—to facilitate the work, a primer from a previously created mask can be applied (in the ROI Manager: select Show All).
- Removal of noise generated on the cluster surface (from the toolbar: Brush of any size, with a gradient value corresponding to the cluster surface gradient—255).
- Selection of the quantities to be measured—that is, the area and the perimeter of the cluster (Analyze > Set Measurements > selection of: Area, Perimeter).
- Inversion of colors in the image (Edit > Invert)—this is required in order to correctly identify the cluster surfaces by the counting module, which only analyzes areas with a gradient value equal to 0 (the object tested is black, the background is white).
- Automatic measurement of the surface area and perimeter of each cluster present on the sample surface using the Analyze Particles counting module (Analyze > Analyze Particles)—in the module settings must be defined: size (mm2)—2—infinity, show: Overlay (an image is created with the identification numbers that have been assigned to each of the clusters). The cluster surface area and perimeter along with its identification number are exported to a text file—for this purpose, in the module settings, the display results option should be additionally selected.
- Calculation of average values from the and measurements, e.g., using Microsoft Excel spreadsheet software.
Appendix A.2. The Measurement Procedure Using the ImageJ v. 1.51j8 Software
- Opening the scan (File > Open).
- Setting the image scale (Analyze > Set Scale)—in order to correctly determine the width of the cracks, the value of the scan resolution should be introduced.
- Rotating the image to position the sample longitudinal axis horizontally on the screen (Image > Transform > Rotate)—it may happen that the sample was not placed on the scanner parallel to the scanning traverse, but at a small angle. This facilitates further work with the image.
- Creating a parallel line to the longitudinal axis of the specimen, in a half the beam height (from the toolbar: Straight line—stake out with the Shift key pressed creates a vertical or horizontal line).
- Using the image magnification, check that the line created does not cut any cracks with an angle of inclination less than about 45°. However, if this situation occurs, the vertical position of the line should be corrected, but in such a way that the line is not more than 5 mm from the top or bottom of the longitudinal axis of the specimen.
- Removal of noise between cracks along the line length (from the toolbar: Brush)—it may happen that in the place where the line runs, there is a discoloration on the surface of the sample, which can be mistakenly interpreted as a crack at the stage of further analysis.
- Creating a graph showing the gradient value of pixels located on the line as a function of its length (Analyze > Plot Profile)—the gradient value is the same as the image mode obtained by scanning (in this case it is a monochrome image—8-bit gray scale). By default, the line has a thickness of 1 px.
- Counting how many cracks are cut by the line—pixels with a gradient value less than 200 are considered as cracks.
- Exporting numerical data from the graph to a text file (in the graph pane: List).
- Counting the number of pixels whose gradient value is below 200 importing a text file to the Microsoft Excel spreadsheet and applying the conditional function (Countif).
- Calculation of as the quotient of the number of pixels interpreted as cracks to their total number. The average crack width can be represented in the unit (px/crack) or (mm/crack).
Appendix A.3. The CD Measurement Procedure Using the ImageJ v. 1.51j8 Software
- Opening the scan (File > Open).
- Setting the image scale (Analyze > Set Scale).
- Rotating the image to position the sample longitudinal axis horizontally on the screen (Image > Transform > Rotate)—it may happen that the sample was not placed on the scanner parallel to the scanning traverse, but at a small angle. This facilitates further work with the image.
- Selection of the area that will be measured with dimensions of 157 × 38.5 mm on the sample surface (Edit > Selection > Specify)—this resulted from the necessity to determine a constant surface area for each sample because as a result of a sudden increase in temperature, the cement paste was subjected to the volume deformations.
- Cropping the image to 157 × 38.5 mm (Image > Crop).
- To create three test lines parallel to the longitudinal axis of the beam and dividing the sample surface into four equal parts, use the Grid Overlay macro should be used (Plugins > Compile and Run).
- After running the Grid Overlay macro in the dialog box, the tiles sizes should be specified. To divide the sample surface into 4 equal parts using horizontal test lines, enter the total surface length in pixels in the Tile width field, and enter the value of the scan surface height divided by four in the Tile height field.
- Counting how many cracks are cut by each test line on the sample surface.
- Using, e.g., Microsoft Excel spreadsheet software, calculate the average number of cracks that occur over the length of test lines for a given series of samples and the w/c ratio.
- Calculation of CD as the quotient of the average number of cracks occurring on the test line to the length of the scan expressed in meters, i.e., 0.157 m.
References
- Recho, N. Fracture Mechanics and Crack Growth; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Fu, Y.F.; Wong, Y.L.; Poon, C.S.; Tang, C.A. Numerical tests of thermal cracking induced by temperature gradient in cement-based composites under thermal loads. Cem. Concr. Compos. 2007, 29, 103–116. [Google Scholar] [CrossRef]
- Fic, S.; Vyrovoy, V.N.; Dorofeev, V.S. Procesy Samoorganizacji Struktury Kompozytowych Materiałów Budowlanych; Politechnika Lubelska: Lublin, Poland, 2013. [Google Scholar]
- Sukhanov, V.; Vyrovoy, V.; Dorofeev, V. Crack’s role in structural development of the constructional composite materials. Mod. Ind. Civ. Constr. 2011, 7, 135–141. [Google Scholar]
- Fic, S.; Szelag, M. Analysis of the development of cluster cracks caused by elevated temperatures in cement paste. Constr. Build. Mater. 2015, 83, 223–229. [Google Scholar] [CrossRef]
- Vyrovoy, V.N.; Dorofeev, V.S.; Sukhanov, V.G. Composite Building Materials and Constructions. Structure, Self-Organization, Properties; Publishers TES: Odessa, TX, USA, 2010. [Google Scholar]
- Bentz, D.; Aitcin, P.C. The hidden meaning of the water-to-cement ratio. Concr. Int. 2008, 30, 51–54. [Google Scholar]
- Banfill, P.F.G.E. Rheology of Fresh Cement and Concrete: Proceedings of an International Conference; CRC Press: Liverpool, UK, 1990. [Google Scholar]
- Roussel, N. Understanding the Rheology of Concrete; Woodhead Publishing: Cambridge, UK, 2012; pp. 1–364. [Google Scholar]
- Pellenq, R.; Crespin, M.; Lequeux, N.; Menager, C.; Costalin, L.; Delville, A.; Caillol, J.; van Damme, H.; Nonat, A. A (NVT) Monte-Carlo Study of the Stability of Charged Interfaces, Application to Cement and Clay Minerals; RILEM Publications SARL: Dijon, France, 1997; pp. 63–86. [Google Scholar]
- Helmuth, R.A. Structure and rheology of fresh cement paste. In Proceedings of the 7th International Congress on the Chemistry of Cement, Paris, France, 30 June–4 July 1980. [Google Scholar]
- Mohseni, E.; Naseri, F.; Amjadi, R.; Khotbehsara, M.; Ranjbar, M. Microstructure and durability properties of cement mortars containing nano-TiO2 and rice husk ash. Constr. Build. Mater. 2016, 114, 656–664. [Google Scholar] [CrossRef]
- Mendes, T.; Hotza, D.; Repette, W. Nanoparticles in cement based materials: A review. Rev. Adv. Mater. Sci. 2015, 40, 89–96. [Google Scholar]
- Hanif, A.; Parthasarathy, P.; Ma, H.; Fan, T.; Li, Z. Properties improvement of fly ash cenosphere modified cement pastes using nano silica. Cem. Concr. Compos. 2017, 81, 35–48. [Google Scholar] [CrossRef]
- Rupasinghe, M.; Nicolas, R.; Mendis, P.; Sofi, M.; Ngo, T. Investigation of strength and hydration characteristics in nano-silica incorporated cement paste. Cem. Concr. Compos. 2017, 80, 17–30. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Metaxa, Z.S.; Shah, S.P. Highly dispersed carbon nanotube reinforced cement based materials. Cem. Concr. Res. 2010, 40, 1052–1059. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Metaxa, Z.S.; Shah, S.P. Multi-scale mechanical and fracture characteristics and early-age strain capacity of high performance carbon nanotube/cement nanocomposites. Cem. Concr. Compos. 2010, 32, 110–115. [Google Scholar] [CrossRef]
- Cwirzen, A.; Habermehl-Cwirzen, K.; Penttala, V. Surface decoration of carbon nanotubes and mechanical properties of cement/carbon nanotube composites. Adv. Cem. Res. 2008, 20, 65–73. [Google Scholar] [CrossRef]
- Wang, B.; Liu, S.; Han, Y.; Leng, P. Preparation and Durability of Cement-Based Composites Doped with Multi-Walled Carbon Nanotubes. Nanosci. Nanotechnol. Lett. 2015, 7, 411–416. [Google Scholar] [CrossRef]
- Ibragimov, R.; Izotov, V. Effect of carbon nanotubes on the structure and properties of cement composites. Inorg. Mater. 2015, 51, 834–839. [Google Scholar] [CrossRef]
- Luo, J.; Duan, Z.; Zhao, T.; Li, Q.; Jiao, S.; Jiang, Z.; Bu, J. Effect of Multi-wall Carbon Nanotube on Fracture Mechanical Property of Cement-based Composite. In Advanced Materials Research; Trans Tech Publications: Zürich, Switzerland, 2011; Volume 146, pp. 581–584. [Google Scholar]
- Manzur, T.; Yazdani, N.; Emon, M. Potential of Carbon Nanotube Reinforced Cement Composites as Concrete Repair Material. J. Nanomater. 2016. [Google Scholar] [CrossRef]
- Makar, J.; Margeson, J.; Luh, J. Carbon nanotube/cement composites—Early results and potential applications. In Proceedings of the 3rd International Conference on Construction Materials: Performance, Innovations and Structural Implications, Vancouver, BC, Canada, 22–24 August 2005; pp. 1–10. [Google Scholar]
- Li, G.Y.; Wang, P.M.; Zhao, X. Mechanical behaviour and microstructure of cement composites incorporating surface-treated multi-walled carbon nanotubes. Carbon 2005, 43, 1239–1245. [Google Scholar] [CrossRef]
- Stankiewicz, N.; Lelusz, M. Nanotechnologia w budownictwie—Przegląd zastosowań. Bud. Inżynieria Środowiska 2014, 5, 101–112. [Google Scholar]
- Czarnecki, L. Nanotechnologia w budownictwie. Przegląd Bud. 2011, 1, 40–53. [Google Scholar]
- Huczko, A. Nanorurki węglowe. In Czarne Diamenty XXI Wieku.; BEL Studio: Warszawa, Poland, 2004. [Google Scholar]
- Huczko, A. Fulereny i nanorurki. Academia 2006, 2, 16. [Google Scholar]
- Kellsall, R.W.; Hamley, I.W.; Geoghegan, M. Nanotechnologie; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2009. [Google Scholar]
- Li, G.Y.; Wang, P.M.; Zhao, X. Pressure-sensitive properties and microstructure of carbon nanotube reinforced cement composites. Cem. Concr. Res. 2007, 29, 377–382. [Google Scholar] [CrossRef]
- Vaisman, L.; Wagner, D.H.; Marom, G. The role of surfactants in dispersion of carbon nanotubes. Adv. Colloid Interface Sci. 2006, 128, 37–46. [Google Scholar] [CrossRef]
- Yu, J.; Grossiord, N.; Koning, C.E.; Loos, J. Controlling the dispersion of multi-wall carbon nanotubes in aqueous surfactant solution. Carbon 2007, 45, 618–623. [Google Scholar] [CrossRef]
- Jiang, L.; Gao, L.; Sun, J. Production of aqueous colloidal dispersions of carbon nanotubes. J. Colloid Interface Sci. 2003, 260, 89–94. [Google Scholar] [CrossRef]
- Rausch, J.; Zhuang, R.; Mader, E. Surfactant assisted dispersion of functionalized multi-walled carbon nanotubes in aqueous media. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1038–1046. [Google Scholar] [CrossRef]
- Grossiord, N.; Regev, O.; Loos, J.; Meuldijk, J.; Koning, C. Time-dependent study of the exfoliation process of carbon nanotubes in aqueous dispersions by using UV-visible spectroscopy. Anal. Chem. 2005, 77, 5135–5139. [Google Scholar] [CrossRef] [PubMed]
- Rastogi, R.; Kaushal, R.; Tripathi, S.; Sharma, A.; Kaur, I.; Bharadwaj, L. Comparative study of carbon nanotube dispersion using surfactants. J. Colloid Interface Sci. 2008, 328, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Zhang, K.; Yu, X.; Kwon, E.; Ou, J. Fabrication of Piezoresistive CNT/CNF Cementitious Composites with Superplasticizer as Dispersant. J. Mater. Civ. Eng. 2012, 24, 658–665. [Google Scholar] [CrossRef]
- Fu, Y.; Wong, Y.; Tang, C.; Poon, C. Thermal induced stress and associated crackin in cement-based composite at elevated temperatures—Part II: Thermal cracking around multiple inclusions. Cem. Concr. Compos. 2004, 26, 113–126. [Google Scholar] [CrossRef]
- Luccioni, B.; Figueroa, M.; Danesi, R. Thermo-mechanic model for concrete exposed to elevated temperatures. Eng. Struct. 2003, 25, 729–742. [Google Scholar] [CrossRef]
- Xu, Y.; Wong, Y.; Poon, C.; Anson, M. Influence of PFA on cracking of concrete and cement paste after exposure to high temperatures. Cem. Concr. Res. 2003, 33, 2009–2016. [Google Scholar] [CrossRef]
- Magalhaes, M.; Toledo, R.; Fairbairn, E. Thermal stability of PVA fiber strain hardening cement-based composites. Constr. Build. Mater. 2015, 94, 437–447. [Google Scholar] [CrossRef]
- Wagner, C.; Villmann, B.; Slowik, V.; Mechtcherine, V. Water permeability of cracked strain-hardening cement-based composites. Cem. Concr. Compos. 2017, 82, 234–241. [Google Scholar] [CrossRef]
- Mobasher, B.; Stang, H.; Shah, S. Microcracking in fiber reinforced-concrete. Cem. Concr. Res. 1990, 20, 665–676. [Google Scholar] [CrossRef]
- Kim, K.; Yun, T.; Park, K. Evaluation of pore structures and cracking in cement paste exposed to elevated temperatures by X-ray computed tomography. Cem. Concr. Res. 2013, 50, 34–40. [Google Scholar] [CrossRef]
- Wang, K.; Shah, S.; Phuaksuk, P. Plastic shrinkage cracking in concrete materials - Influence of fly ash and fibers. Mater. J. 2001, 98, 458–464. [Google Scholar]
- Bisschop, J.; Wittel, F. Contraction gradient induced microcracking in hardened cement paste. Cem. Concr. Compos. 2011, 33, 466–473. [Google Scholar] [CrossRef]
- Szelag, M. The Influence of Metakaolinite on the Development of Thermal Cracks in a Cement Matrix. Materials 2018, 11, 17. [Google Scholar] [CrossRef]
- Szelag, M. Development of Cracking Patterns in Modified Cement Matrix with Microsilica. Materials 2018, 11, 19. [Google Scholar] [CrossRef]
- Szelag, M. Evaluation of cracking patterns of cement paste containing polypropylene fibers. Compos. Struct. 2019, 220, 402–411. [Google Scholar] [CrossRef]
- Szelag, M. Mechano-Physical Properties and Microstructure of Carbon Nanotube Reinforced Cement Paste after Thermal Load. Nanomaterials 2017, 7, 267. [Google Scholar] [CrossRef]
- Bogue, R.H. The Chemistry of Portland Cement; Reinhold Publishing Corporation: Stafford, TX, USA, 1947. [Google Scholar]
- EN, T. 196-1. Methods of Testing Cement—Part 1: Determination of Strength; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Szelag, M. Influence of specimen’s shape and size on the thermal cracks’ geometry of cement paste. Constr. Build. Mater. 2018, 189, 1155–1172. [Google Scholar] [CrossRef]
- Zaiontz, C. Real Statistics Using Excel. Available online: http://www.real-statistics.com (accessed on 1 March 2017).
- Lazzari, S.; Nicoud, L.; Jaquet, B.; Lattuada, M.; Morbidelli, M. Fractal-like structures in colloid science. Adv. Colloid Interface Sci. 2016, 235, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wolberg, J. Data Analysis Using the Method of Least Squares: Extracting the Most Information from Experiments; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Shao, J. Mathematical Statistics; Springer: New York, NY, USA, 2003. [Google Scholar]



| Series | C42 | C42CNT | C52 | C52CNT | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Water/Cement Ratio | 0.4 | 0.5 | 0.6 | 0.4 | 0.5 | 0.6 | 0.4 | 0.5 | 0.6 | 0.4 | 0.5 | 0.6 |
| fc(R) (MPa) | 61.40 | 43.43 | 34.17 | 26.70 | 19.02 | 15.22 | 69.52 | 49.67 | 39.10 | 36.49 | 27.87 | 22.62 |
| fc(T) (Mpa) | 39.26 | 23.08 | 15.90 | 16.28 | 10.94 | 8.35 | 49.29 | 30.42 | 21.13 | 27.21 | 19.92 | 15.78 |
| fcf(R) (Mpa) | 5.80 | 4.35 | 3.16 | 3.99 | 3.03 | 2.41 | 5.74 | 4.39 | 3.86 | 4.12 | 3.25 | 2.45 |
| fcf(T) (Mpa) | 2.97 | 2.59 | 1.32 | 2.56 | 1.81 | 1.33 | 1.53 | 1.35 | 1.16 | 2.02 | 1.55 | 1.18 |
| D(R) (g/cm3) | 1.692 | 1.528 | 1.416 | 1.143 | 1.062 | 0.952 | 1.750 | 1.574 | 1.432 | 1.182 | 1.110 | 0.995 |
| D(T) (g/cm3) | 1.513 | 1.376 | 1.277 | 1.025 | 0.956 | 0.865 | 1.549 | 1.388 | 1.266 | 1.035 | 0.982 | 0.883 |
| S28(R) (mm/m) | 2.25 | 2.52 | 3.23 | 3.56 | 3.77 | 4.06 | 1.69 | 2.44 | 3.13 | 3.17 | 3.75 | 4.40 |
| S28(T) (mm/m) | 5.50 | 6.35 | 7.58 | 8.60 | 10.15 | 10.92 | 4.53 | 5.90 | 7.48 | 8.67 | 10.10 | 11.06 |
| C42—Before Preparation | C42—After Preparation | ||||||
|---|---|---|---|---|---|---|---|
| w/c | 0.4 | 0.5 | 0.6 | 0.4 | 0.5 | 0.6 | |
| Population size | 260 | 174 | 107 | 248 | 182 | 101 | |
| The size of the random sample | 248 | 101 | 174 | ||||
| p-value | 2.34 × 10−5 | 7.17 × 10−4 | 1.44 × 10−3 | 2.10 × 10−4 | 4.02 × 10−8 | 3.35 × 10−3 | |
| p-value ≤ α | yes | yes | yes | yes | yes | yes | |
| p-value | 5.14 × 10−3 | 2.87 × 10−3 | 0.02 | 8.74 × 10−4 | 3.72 × 10−5 | 0.07 | |
| p-value ≤ α | yes | yes | yes | yes | yes | no | |
| C42—Before Preparation vs. C42—After Preparation | ||||||
|---|---|---|---|---|---|---|
| Parameter | ||||||
| w/c | 0.4 | 0.5 | 0.6 | 0.4 | 0.5 | 0.6 |
| U | 26,102 | 12,548 | 4738 | 26,925 | 12,806 | 4801 |
| Ucrit (two-sided test) | 25,226 | 11,754 | 4235 | 25,574 | 12,101 | 4244 |
| U ≤ Ucrit | no | no | no | no | no | no |
| Series | Equation | R2 | Se (mm2) | W (%) | ||
|---|---|---|---|---|---|---|
| C42 | 2 | 0.82 | 33.39 | 20.82 | 0.66 | 0.91 |
| C42CNT | 2 | 0.44 | 98.24 | 21.61 | 0.67 | |
| C52 | 2 | 0.94 | 15.28 | 13.42 | 0.96 | |
| C52CNT | 2 | 0.90 | 45.96 | 15.68 | 0.96 | |
| Series | Equation | R2 | Se | W (%) | ||
|---|---|---|---|---|---|---|
| All | = 470,138 · CD−1.831 | 0.86 | 63.74 mm2 | 24.95 | −0.83 | |
| C42 + C42CNT | = 0.901 · CD−0.682 | 0.78 | 0.0067 mm | 12.20 | −0.69 | −0.86 |
| C52 + C52CNT | = 2.997 · CD−0.875 | 0.94 | 0.0060 mm | 8.63 | −0.92 | |
| Parameter | fc(R) | fc(T) | fcf(R) | fcf(T) | D(R) | D(T) | s28(R) | s28(T) |
|---|---|---|---|---|---|---|---|---|
| −0.89 | −0.83 | −0.86 | −0.32 | −0.88 | −0.86 | 0.88 | 0.90 | |
| −0.94 | −0.87 | −0.88 | −0.28 | −0.93 | −0.91 | 0.94 | 0.94 | |
| −0.71 | −0.62 | −0.79 | −0.57 | −0.76 | −0.78 | 0.85 | 0.82 | |
| CD | 0.92 | 0.95 | 0.91 | 0.31 | 0.80 | 0.78 | −0.90 | −0.84 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szeląg, M. Properties of Cracking Patterns of Multi-Walled Carbon Nanotube-Reinforced Cement Matrix. Materials 2019, 12, 2942. https://doi.org/10.3390/ma12182942
Szeląg M. Properties of Cracking Patterns of Multi-Walled Carbon Nanotube-Reinforced Cement Matrix. Materials. 2019; 12(18):2942. https://doi.org/10.3390/ma12182942
Chicago/Turabian StyleSzeląg, Maciej. 2019. "Properties of Cracking Patterns of Multi-Walled Carbon Nanotube-Reinforced Cement Matrix" Materials 12, no. 18: 2942. https://doi.org/10.3390/ma12182942
APA StyleSzeląg, M. (2019). Properties of Cracking Patterns of Multi-Walled Carbon Nanotube-Reinforced Cement Matrix. Materials, 12(18), 2942. https://doi.org/10.3390/ma12182942





