1. Introduction
Additive manufacturing (AM) is a novel and revolutionary technique where it is possible to produce elements with complex geometries directly from the desired material [
1]. For thermoplastic materials, the most common AM technique is fusion deposition modeling (FDM) because it is very simple, relatively cheap, and is a kind of 3D printing [
2] that can be fully automated, which is becoming increasingly common in materials technologies [
3]. One of the disadvantages of using FDM is the low mechanical strength of the products, which can only be produced from some types of thermoplastics, which limits the usage of FDM technology [
4]. A possible solution is the application of strong materials, such as polyetheretherketone (PEEK), but such materials are very expensive and not readily available. An alternative method is the use of thermoplastic composites reinforced with hard particles or short fibers. Such FDM printed composites show much better properties, such as higher strength, improved wear resistance, and better dielectric permittivity compared with neat thermoplastics [
5,
6]. The addition of reinforcement materials can also help to solve some common problems with the 3D printing of neat polymers. For example, adding iron or copper particles to ABS reduces the distortion of printed parts [
7,
8]. Currently, composites reinforced with short fibers, long fibers, powders, or nanocomponents can be found in many solutions [
9,
10,
11] and are also applicable for 3D printing [
4,
12].
The wear behavior of 3D printed composites is a relatively new topic that has mainly been researched for ABS or PC-ABS blends [
13,
14]. The wear resistance of Nylon-6 composites has also been described [
15]. Since 3D printed parts exhibit anisotropic mechanical properties [
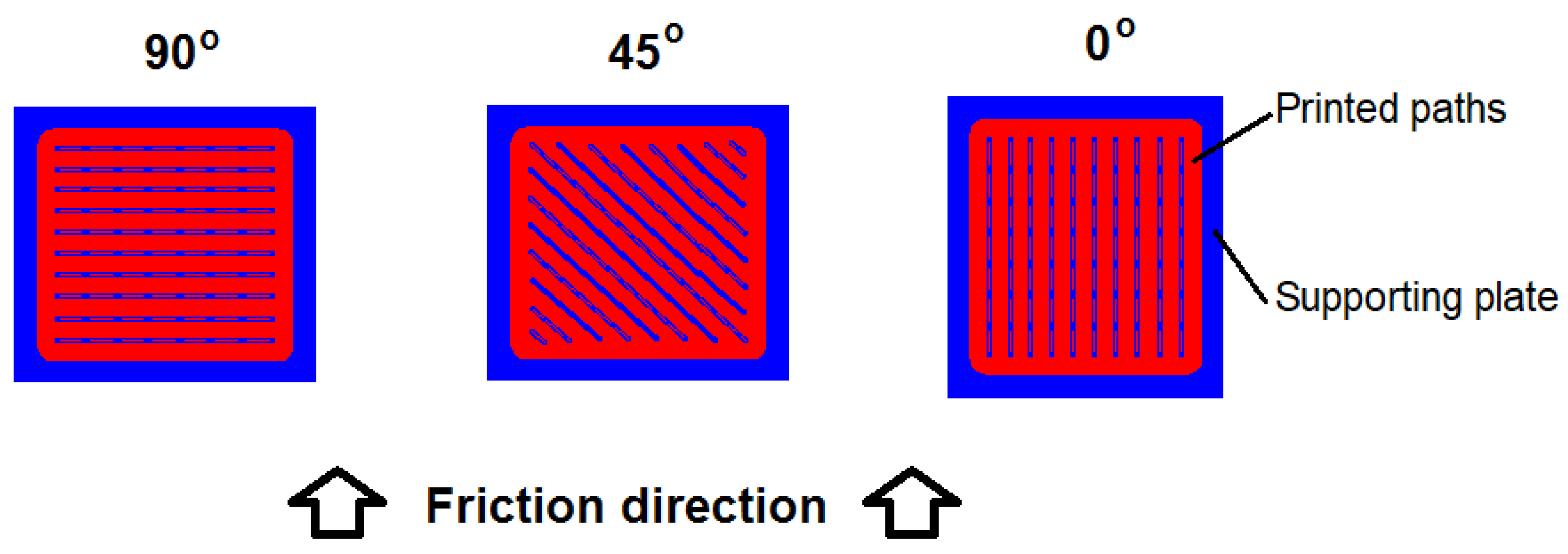
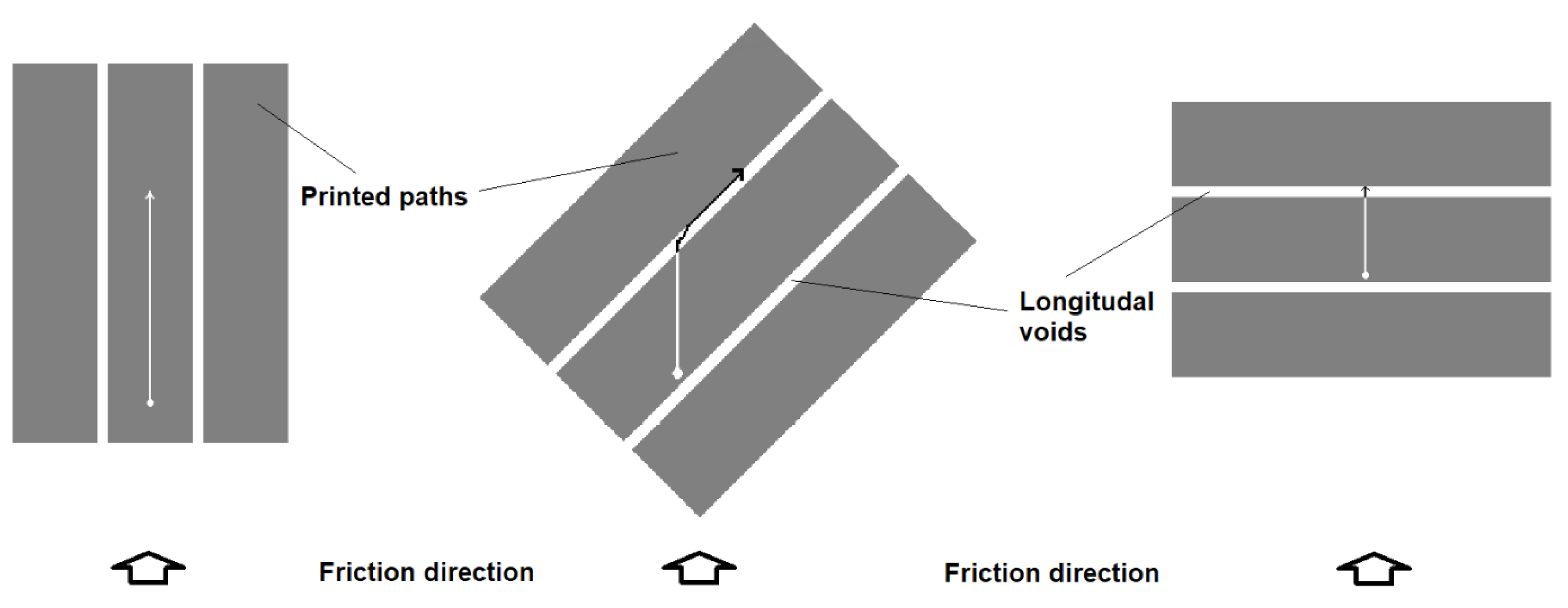
16], their wear mechanism may also vary depending on the friction direction (
Figure 1). Thus, such behavior should be more thoroughly investigated.
LDPE is an inexpensive and very popular material that is currently used mainly in packaging, toys, and everyday-use items, which generate significant waste that must be recycled. The reuse of polymer wastes as filaments for FDM printing is a relatively new and popular topic; there are works [
15] describing the use of polymer waste to obtain material for 3D printing. However, LDPE has a relatively low strength and stiffness, poor bed adhesion, and high shrinkage, which may disqualify it from being used in FDM printing. Nevertheless, some problems can be solved by reinforcing LDPE with hard particles to produce composites [
9,
17]. As mentioned before, adding ceramic or metal powders to LDPE can improve its storage modulus [
8], reduce shrinkage, and increase its mechanical properties [
7]. Currently, LDPE composites with a mold flow index (MFI) of 10 g/10 min were successfully printed [
18], so it is possible to manufacture an LDPE composite filament for FDM printing made from waste materials.
The use of LDPE as a friction material is not common, but it can be used in new applications where frictional properties and wear resistance are of great importance. An example of this is the mesosterephs in the soles of shoes, where in addition to the necessary friction properties, a low hardness, plasticity, and elasticity are important. It may also be a good carrying material for solid lubricants [
19], e.g., as a layer or near-surface filler. Other mass applications include novel high-endurance sliding pads for furniture, such as chairs and stools. In the rapidly innovating field of consumer products, many other applications for thermoplastics (e.g., [
20]) and FDM technology can be imagined [
21].
Mathematical descriptions of FDM 3D printing are still being investigated. The problem of control and performance limitations can be considered in relation to melting in a liquifier or layer deposition [
22,
23,
24,
25,
26,
27,
28]. Recent publications describing this issue have shown that mathematical modeling can be used to estimate process parameters, and to also avoid potential 3D printing failures, such as buckling or filament grinding. For example, Mackay et al. [
26] attempted to determine the minimum required temperature of feed filaments. The experimental evaluation and mathematical prediction of FFF limits were performed by Go et al. [
25] and Turner et al. [
23] previously provided a review of melt extrusion descriptions. Osswald et al. [
24] proposed a model based on the formation of a thin melt polymer film in a nozzle, which made it possible to estimate the maximum filament feed rate in which the melted polymer is pushed through a nozzle by a fed filament. The force applied by the filament was proportional to its feed rate. When the filament moves faster than its tip is melted, failure from buckling or grinding can occur. One way to prevent this is by matching the filament velocity to the feed rate. The maximum feed rate can be calculated using the least-squares method if the tensions in the filament are equal to the force necessary to push melt through the nozzle.
The aim of this study is to characterize a new composite suitable for FDM printing, which is inexpensive—making it suitable for mass production—and has enhanced wear resistance. In previous work, the authors made an LDPE composite reinforced with glass waste (an additional eco-role) as a 3D printing material [
29] with a melt flow index (MFI) of 2 g/10 min. Glass powder obtained from shredded car windscreen wastes was used as a reinforcement material to increase the printability of LDPE. In this work, the authors continue the attempts to characterize this material in two areas: its technological properties and wear resistance. A previously described mathematical model was applied to establish the buckling conditions and to estimate the maximum feed rate of the filament. Tribology tests were performed on 3D printed parts to determine whether glass wastes can be used as a reinforcement material to enhance the wear resistance of 3D printed parts and if the friction direction influences the specific wear rate of 3D printed composites.
2. Materials and Methods
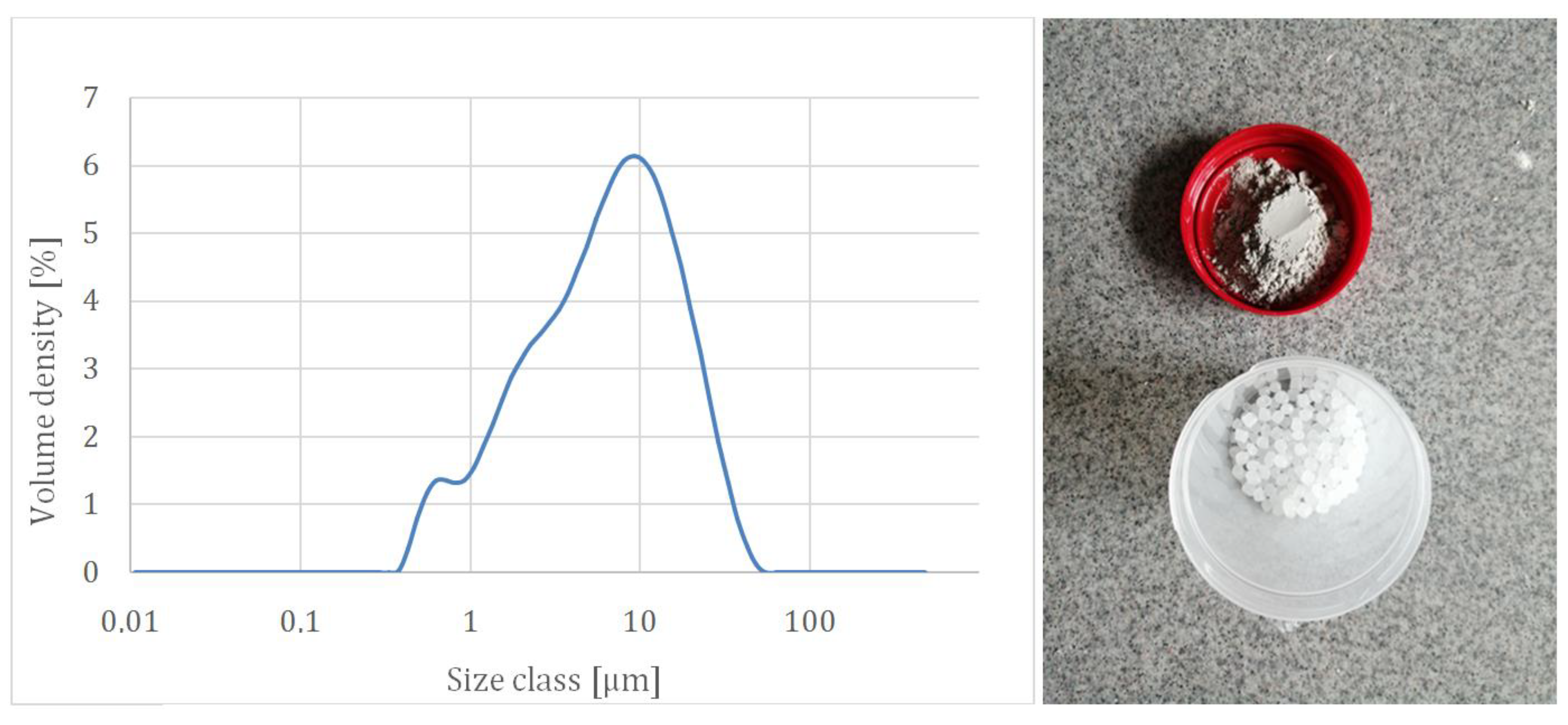
The matrix material was LDPE (Malen E FGNX 23-D022, Basell Orlen Polyolefins, Płock, Poland) with an MFI (190 °C/2.16 kg) of 1.95 g/10 min. The reinforcement material was glass powder containing polyvinyl butyral (PVB) obtained from laminated car glass waste. In this work, composites with 15 and 30 vol% of powder were made, along with neat LDPE as the reference. The glass pieces were mechanically cleaned from the outer layers of PVB foil and initially milled in a hammer grinder mill Retsch SK300 (Retsch, Haan, Germany) with a sieve mesh diameter of 0.5 mm. To obtain a fine powder, a planetary ball mill (Fritsch Pullverisser 6) was used. During milling, the powder-to-ball ratio was 1:4, and the milling speed was 600 rpm. An effective milling time of 60 min resulted in a powder of D90 = 20.1 μm with no grains larger than 100 μm (
Figure 2).
Gradual mixing is a common technique to achieve powders with a wide range of particle diameters [
10,
30]. The obtained range of particle diameters was the minimum one expected to ensure the efficiency of the FDM printing process and at the same time the smallest effect on the cost of the material.
The obtained powder was mechanically mixed with LDPE granules, dried at 70 °C for 24 h, and then extruded. Obtaining the glass used to produce the powder is relatively simple and cheap, especially compared with advanced methods such as those described in [
31] or [
32]. It is rather more similar to more massive technological methods applied for modern materials [
33,
34].
After the first extrusion using a ZAMAK DTR EHP-2x16S (Zamak Mercator, Skawina, Poland) extruder, composites were re-granulated and extruded again to obtain a homogenous material, which was extruded in the form of a filament with a diameter of 1.45 ± 0.10 mm that was suitable for 3D printing. The nozzle temperature during extrusion was 190 °C, screw speed 28 rpm and winder speed 8 rpm.
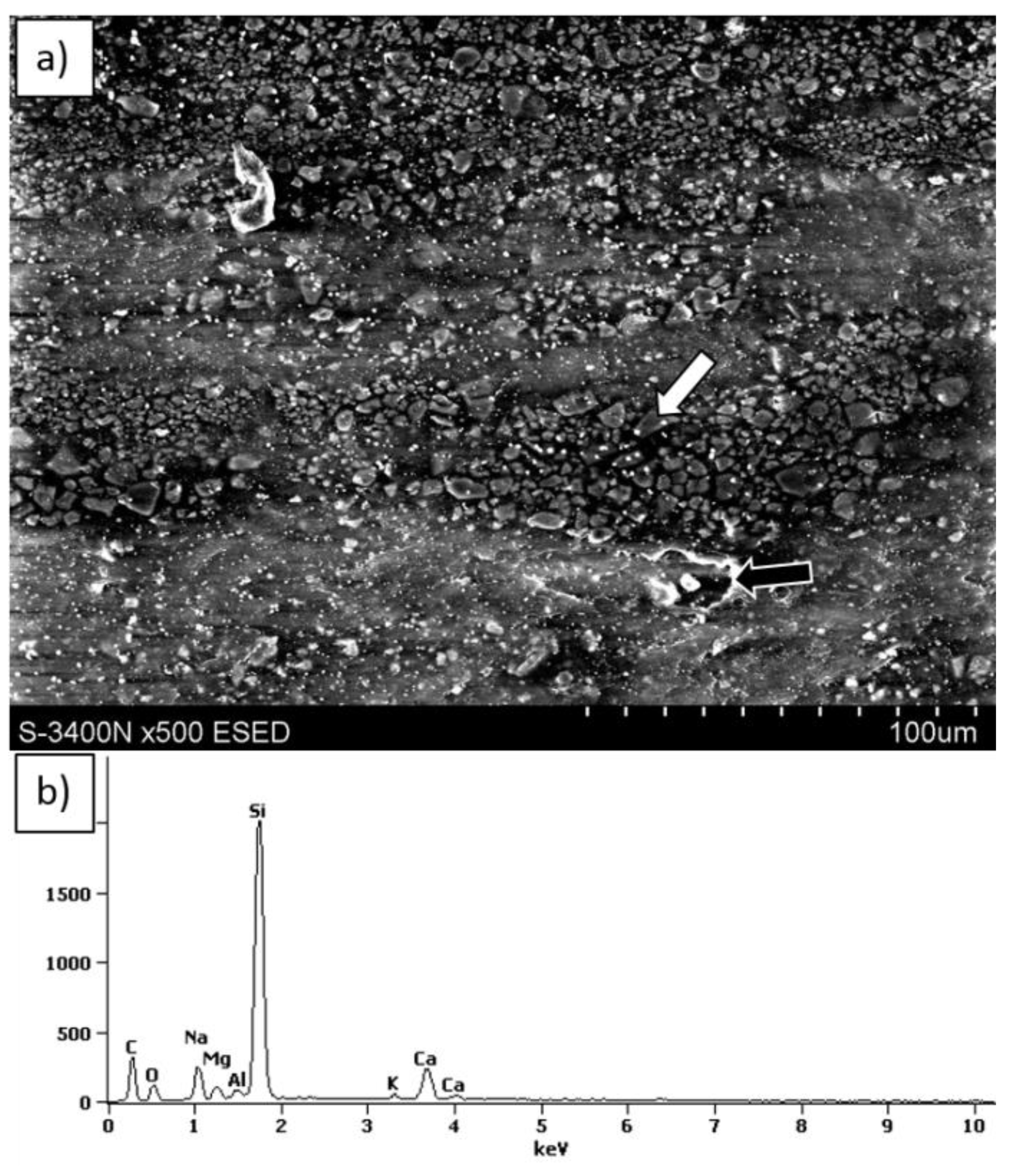
The microstructure of the obtained filament and the distribution of glass particles in the polymer matrix were evaluated using a Hitachi S-3400N (Hitachi, Tokio, Japan) scanning electron microscope (SEM).
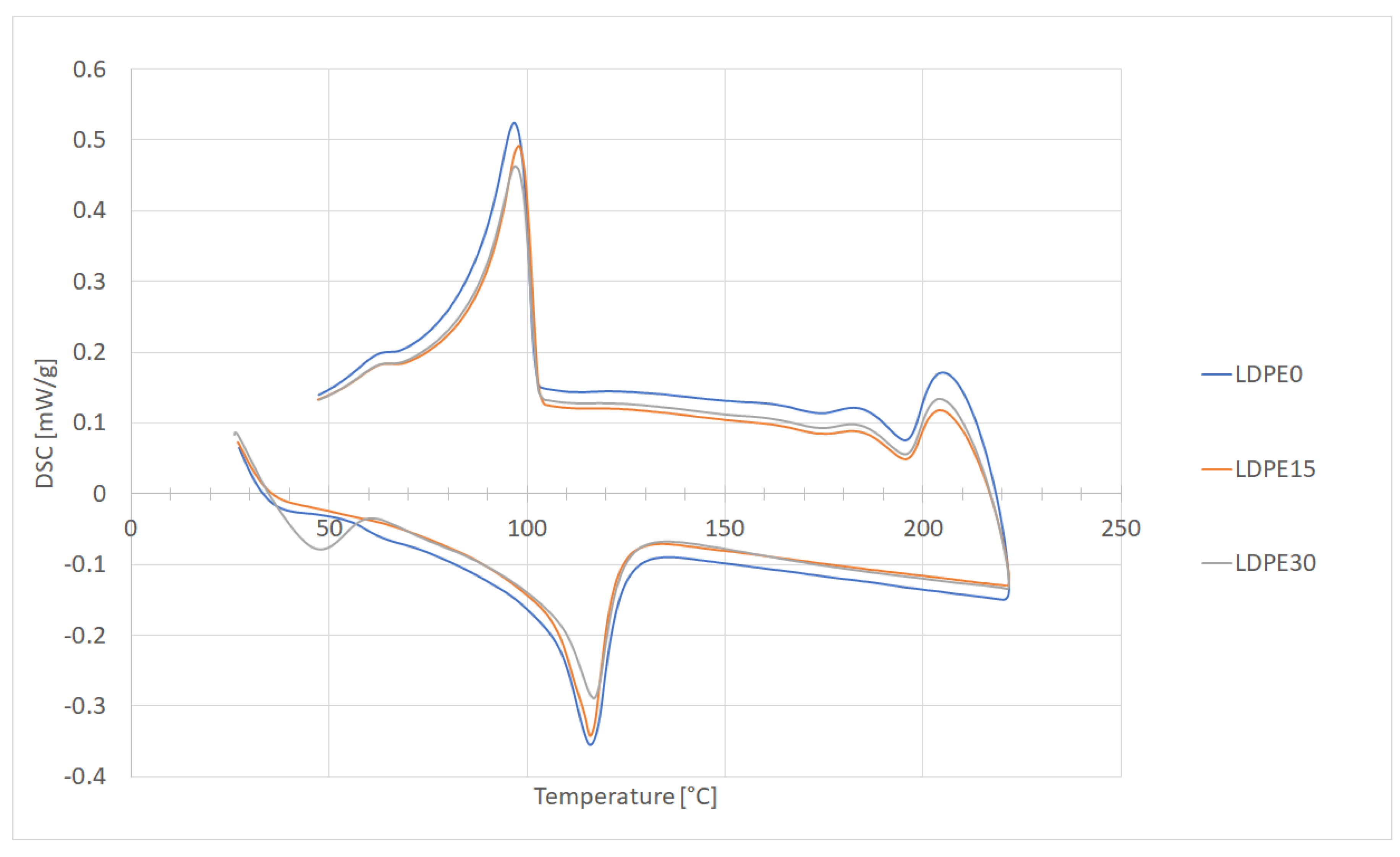
Differential scanning calorimetry NETZSCH DSC 404 F1 (Erich Netzsch GmbH, Wunsiedel, Germany) was used to determine the enthalpy of fusion to calculate the critical filament feed rate. The measurements were carried out in argon (gas flow 20 mL/min) and with heating/cooling rate 5 K/min. Along with this, the crystallinity of neat LDPE and the composites was determined using Equation (1) [
35,
36,
37,
38]:
where wt% is the mass percentage of the reinforcement, ΔH
c is the crystallization enthalpy [J/g], and ΔH
f0 is the theoretical crystallization enthalpy of 100% crystalline LDPE [293 J/g].
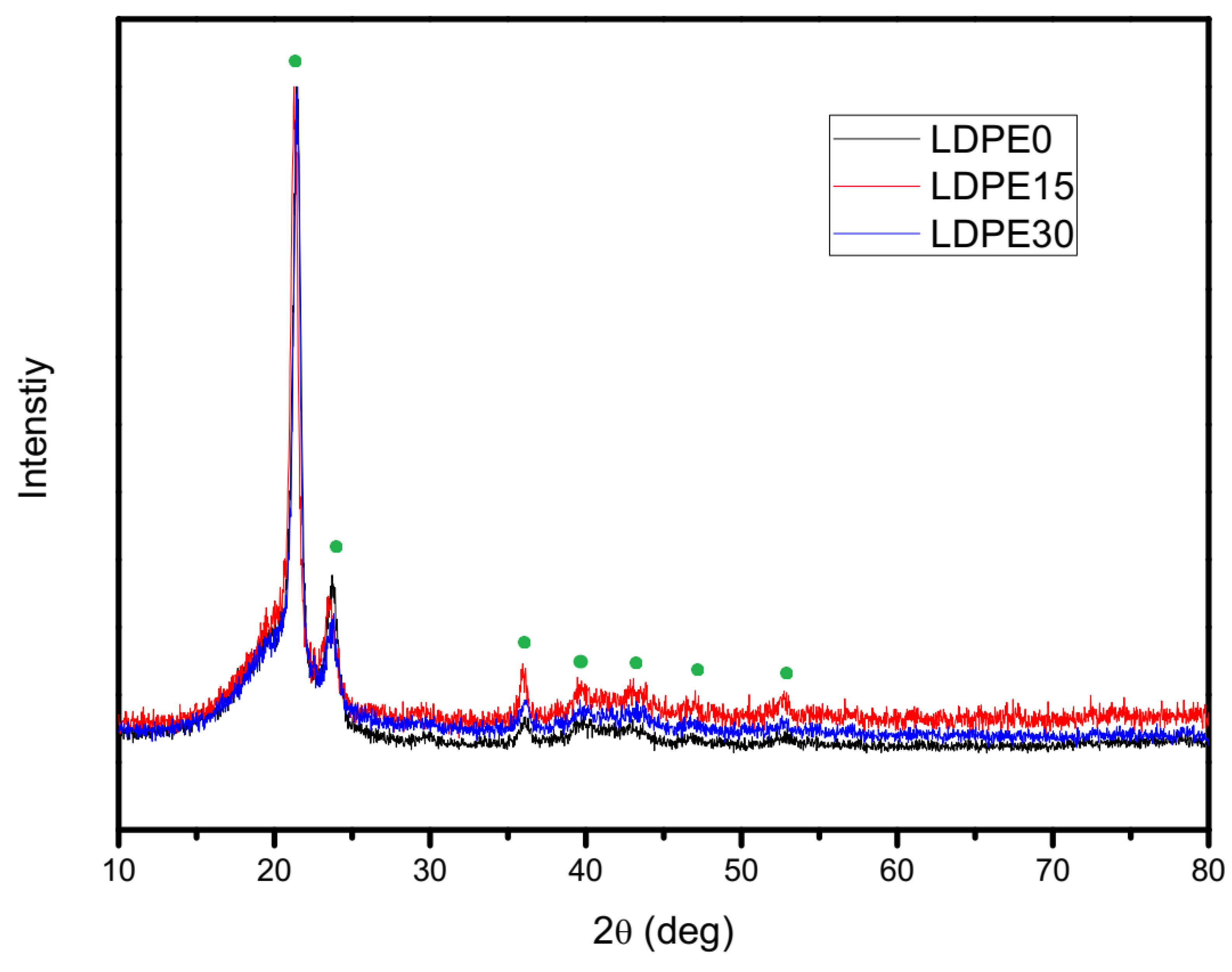
To confirm crystallinity results from DSC analysis, x-ray diffraction (XRD) tests of the neat LDPE and the composites were performed. The measurements were taken on bulk samples at Panalytical Empyreal at room temperature using Cu kα radiation (λ = 1.5405 Å), scanning step of 0.03° from 10° to 80° of 2Ɵ (Bragg angle) and 45 kV/40mA. In order to obtain reliable results, XRD curves were normalized. The crystallinity was calculated with Equation (2):
where: A
c—the area of the crystal region, A
A—the area of the amorphous region, A
c + A
A—total area.
In a previous publication [
29], the produced filaments were subjected to a static tensile test. The length of the measuring base was 100 mm, the deformation speed was 25 mm/min, and the device used was an INSTRON 4469 (Instron, Norwood, MA, USA). The results from this test were used to obtain the Young’s Modulus of all materials, and the calculated values are listed in
Table 1 and were used in further calculations.
The power-law relation for the all obtained composites was approximated from viscosity vs. shear rate curves. The values of 〈γ〉 and τ were obtained from MFI measurements performed on CEAST plastometer (Instron, Norwood, MA, USA) using the following Equations. (3) and (4):
where
RN is the nozzle radius [0.9 mm],
Rp is the piston radius [4.6 mm],
F is the applied force defined as load [L, kg],
g = 9.80665 m/s
2 and
l is the nozzle length [7.7 mm],
where
MFI is the melt flow index (210 °C) [g/10 min], and
ρ is the density [g/cm
3].
The above procedure was postulated among others in [
39]. In order to estimate the power-law coefficient, the MFI was measured at different loads. Measurements were taken at loads of 1200, 1400, 1700, 2000, 2200, 2400, and 2700 grams. The samples at each load were taken 5 times and errors for MFI, 〈γ〉, τ and η were calculated with the partial derivative of mean squared error (MSE). The obtained consistency index
K and the power-law exponents were determined from approximation curves to calculate the filament feed rate. Friction test samples were printed as in previous work [
29], and their parameters are shown in
Table 2.
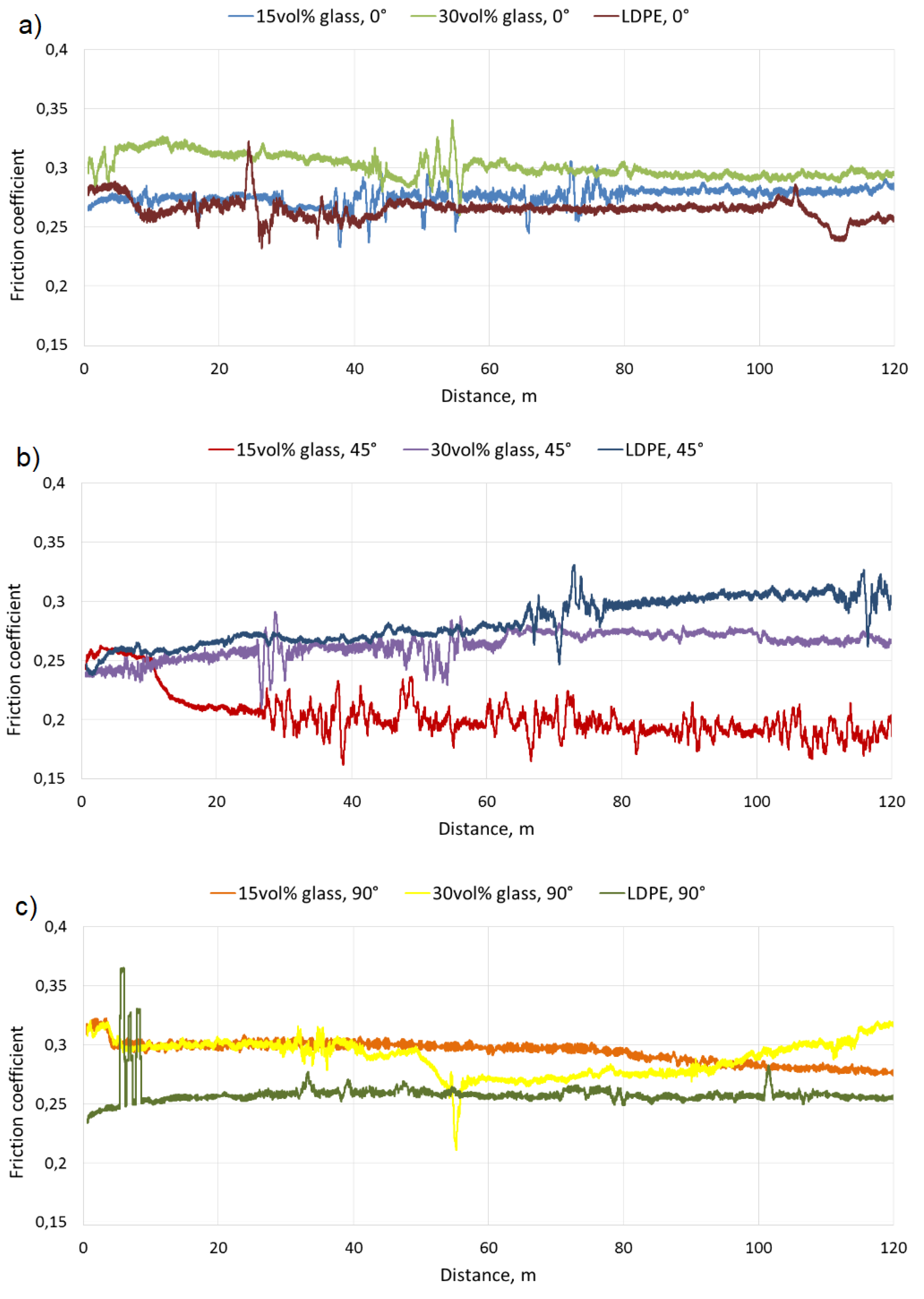
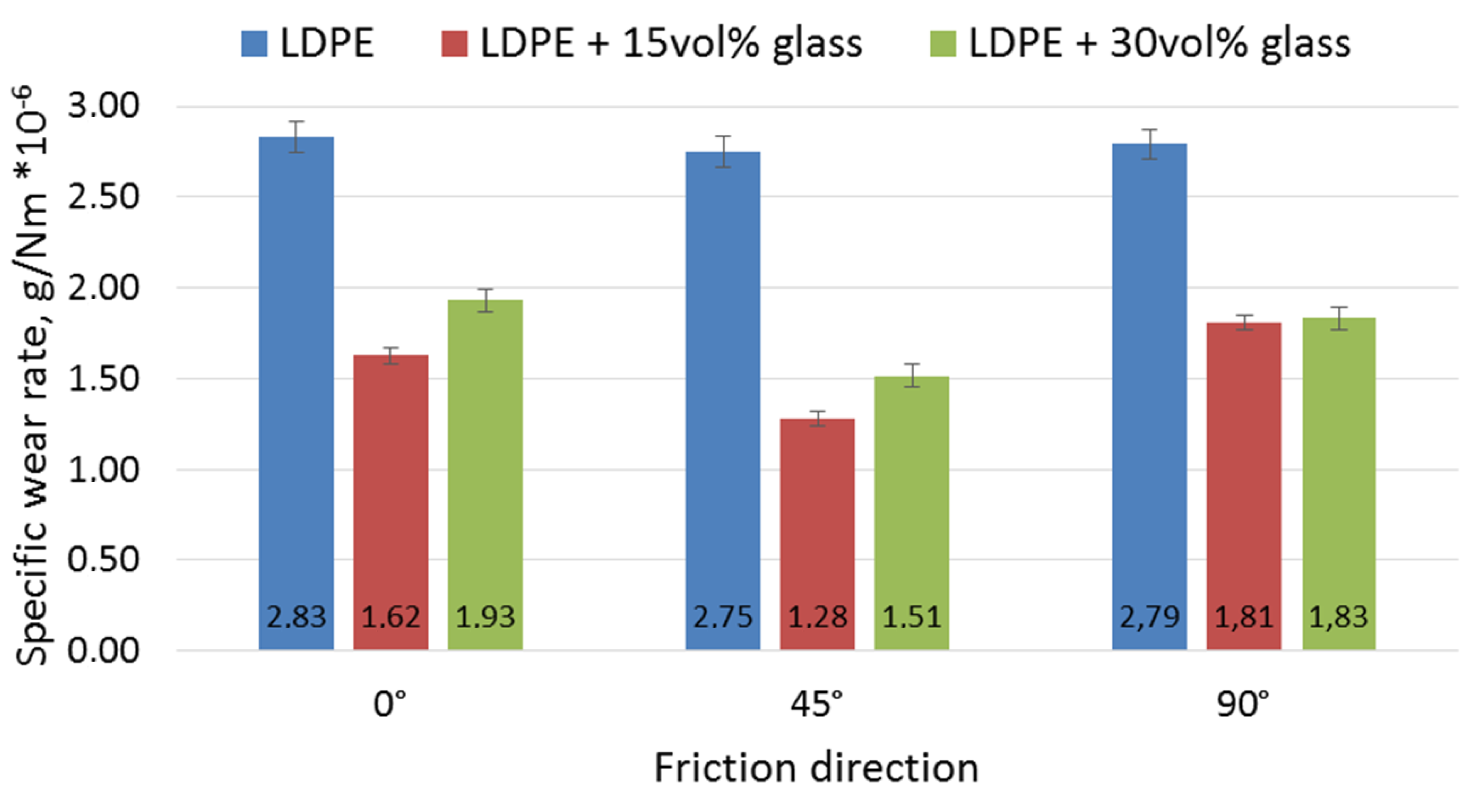
The tribological properties of the printed composites were determined using a TM-01M tester (pin-on-disc method) in dry friction conditions in reciprocating movement. Tests were carried out for a distance of 120 meters, under a 20 N load, with a velocity of 0.03 m/s, with a cast-iron countersample (φ = 3 mm). Such a friction pair was chosen as a comparative method to assess possible future applications of the composite. Moreover, the impact of the path layout was determined, and friction tests were conducted in three directions: parallel to the outer printed paths (0°), perpendicular to the paths (90°), and at 45°. Tests were performed on three specimens and the presented curves are the representative ones. The average size of wear trace was 4 mm width and 12 mm length. The specific wear rate (SWR) was calculated according to Equation (5):
where
is the mass change of a sample,
P is the load, and
L is the distance.
Finally, sample surfaces after friction tests were characterized using scanning electron microscope (SEM).
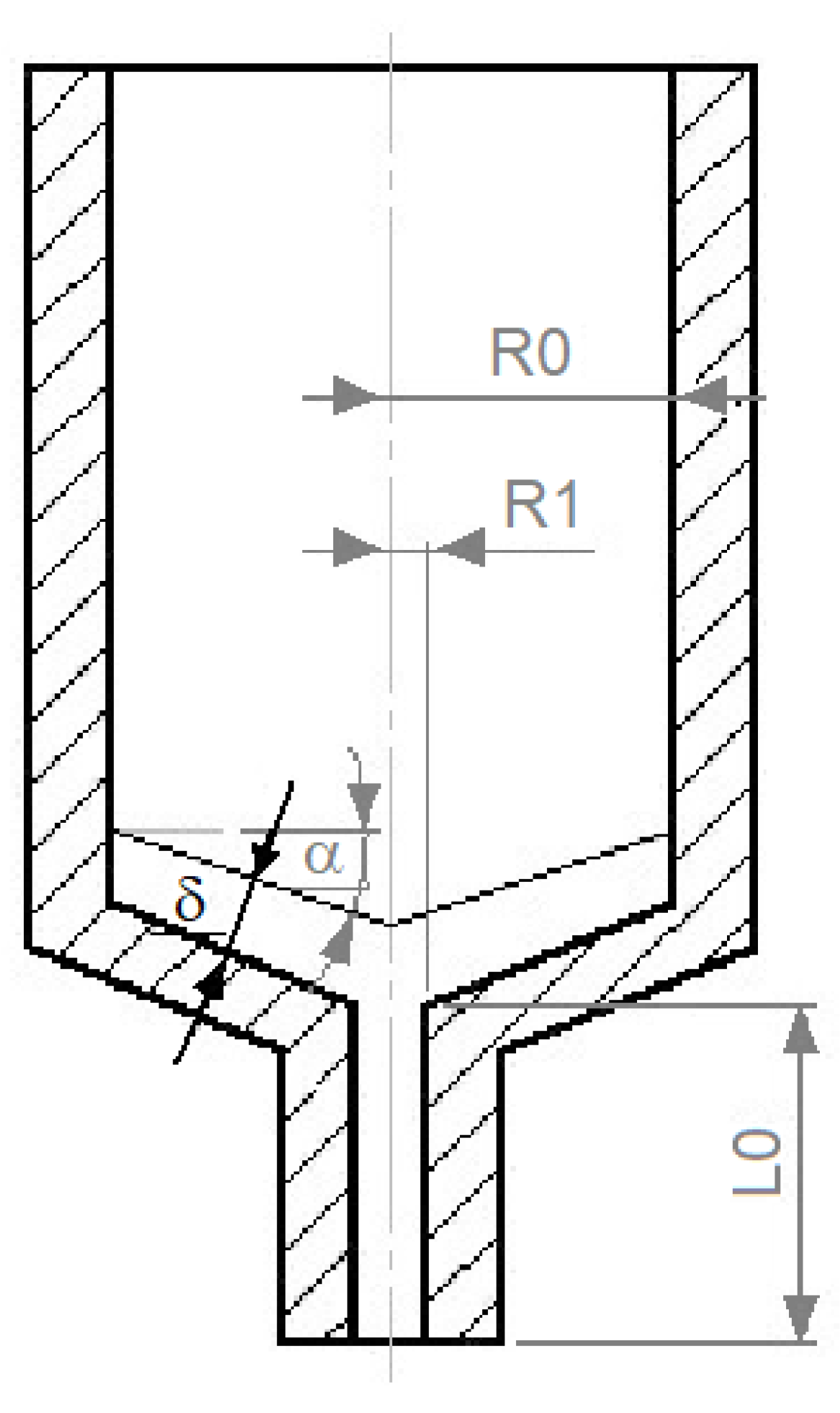
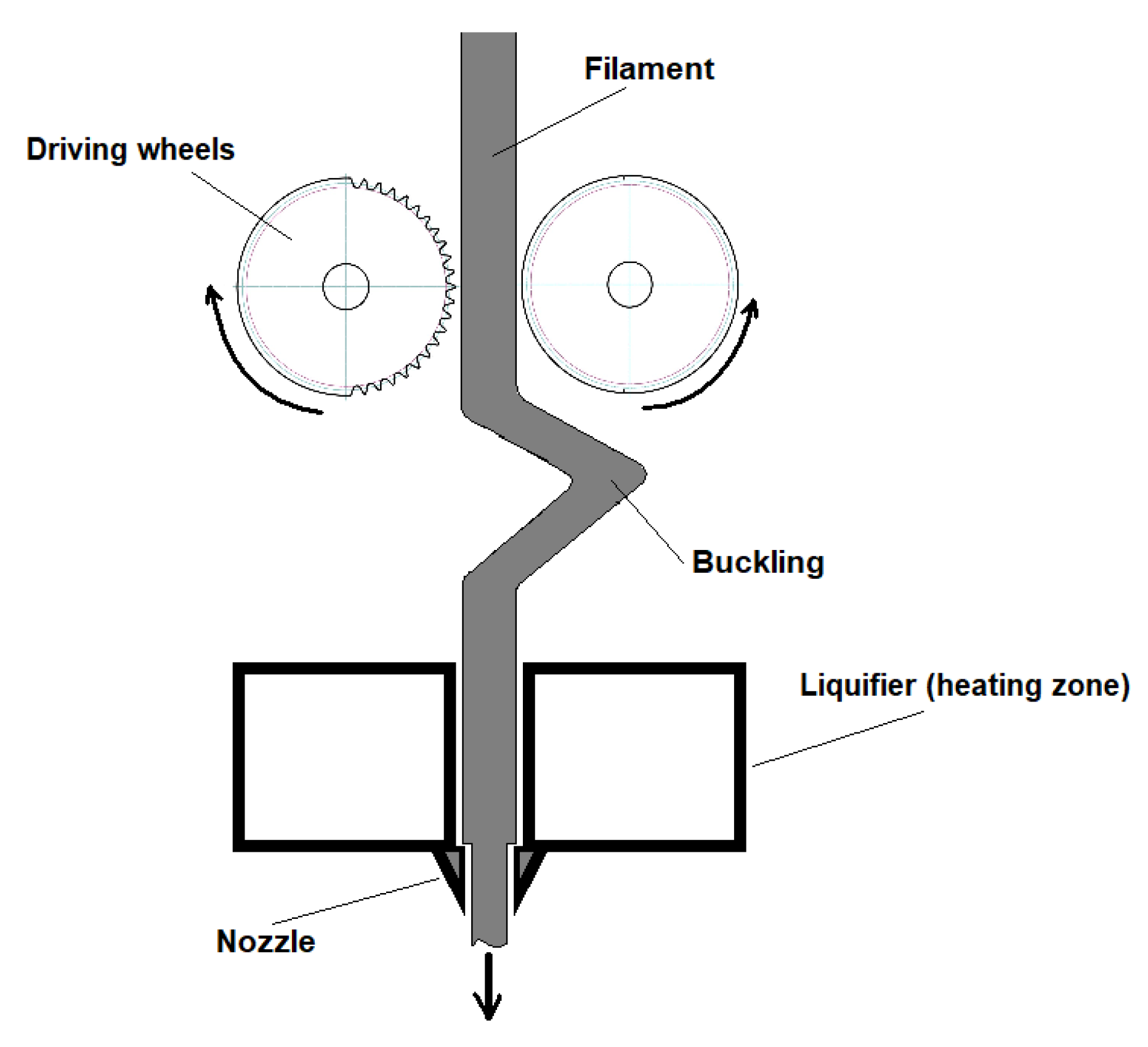
The maximum filament feed rate was calculated using the mathematical model proposed by Osswald et al. [
24] in which a melt filament is pushed towards a conical (or flat in this case) nozzle to form a thin film. The vital dimensions of the melting area of the printer are illustrated in
Figure 3.
Such an approach requires melting the material in a liquifier and simultaneously applying a force to the filament, which moves it through the nozzle. In the model, the force applied to the filament can be expressed as a function of the filament feed rate, liquifier geometry, and the material properties (Equations (6) and (7)):
where
µf is the viscosity of the melt film [Pa·s],
ρs is the filament density [g/cm
3],
ρm is the melt density [g/cm
3],
R0 is the filament radius [mm],
R1 is the nozzle radius [mm], δ is the thickness of the melt film [mm],
µc is the polymer viscosity in the nozzle [Pa·s], and
L2 is the nozzle height [mm].
where
km is the thermal conductivity of the melt [Wm
−1K
−1],
Tm is the polymer melting point [K], λ is the melt enthalpy [J/kg],
Cp is the heat capacity of the filament [Jkg
−1K
−1], and
T0 is the initial temperature of the filament [K].
To determine the maximum filament velocity, the least-squares method may be applied. As the boundary condition, a Euler buckling condition (Equation (8)) was used as proposed by Bellini et al. [
22]:
where
E is the filament’s Young’s Modulus [GPa],
d0 is the filament diameter [mm], and
L0 is the distance between the rollers and liquifier [mm].
This approach is very suitable because by changing the filament diameter, liquifier geometry, or Young’s Modulus of the material, the critical buckling pressure can be increased. This condition can also be applied for flexible filaments such as LDPE and its composites. The linear printing speed (in either the X or Y direction) was estimated from the calculated feed rate by simply assuming that the printing volume rate equals the fed filament volume.
4. Conclusions
In this preliminary work, the technological properties (filament feed rate and printing speed) and wear resistance (specific wear rate) of novel 3D-FDM printed LDPE-matrix composites were evaluated. The following general conclusions were drawn:
The applied procedure using a mathematical model was used to estimate the maximum feed rate and hence the printing speed. Such use is effective and helpful for researching new 3D printing materials.
The composites showed a higher elastic modulus compared with neat LDPE. An improvement in the elastic modulus allows a faster print speed, but failure in printed parts may be observed due to faster printing.
Composite samples exhibited a higher crystallinity than neat LDPE. However, the increase is very slight and close to the error limit.
Using a fine glass powder as a reinforcement in the thermoplastic polymer composites improved their wear resistance due to the formation of a sliding film on the sample surface.
An evident effect of the friction direction vs. the printed path direction on the wear appeared, which was probably related to differences in the removal of friction products from the friction area for different print-path layouts against the friction direction.
The LDPE composite with auto-screen glass particles is a promising material and should be studied further.