New Findings on Multilayer Silicene on Si(111)√3×√3R30°–Ag Template
Abstract
1. Introduction
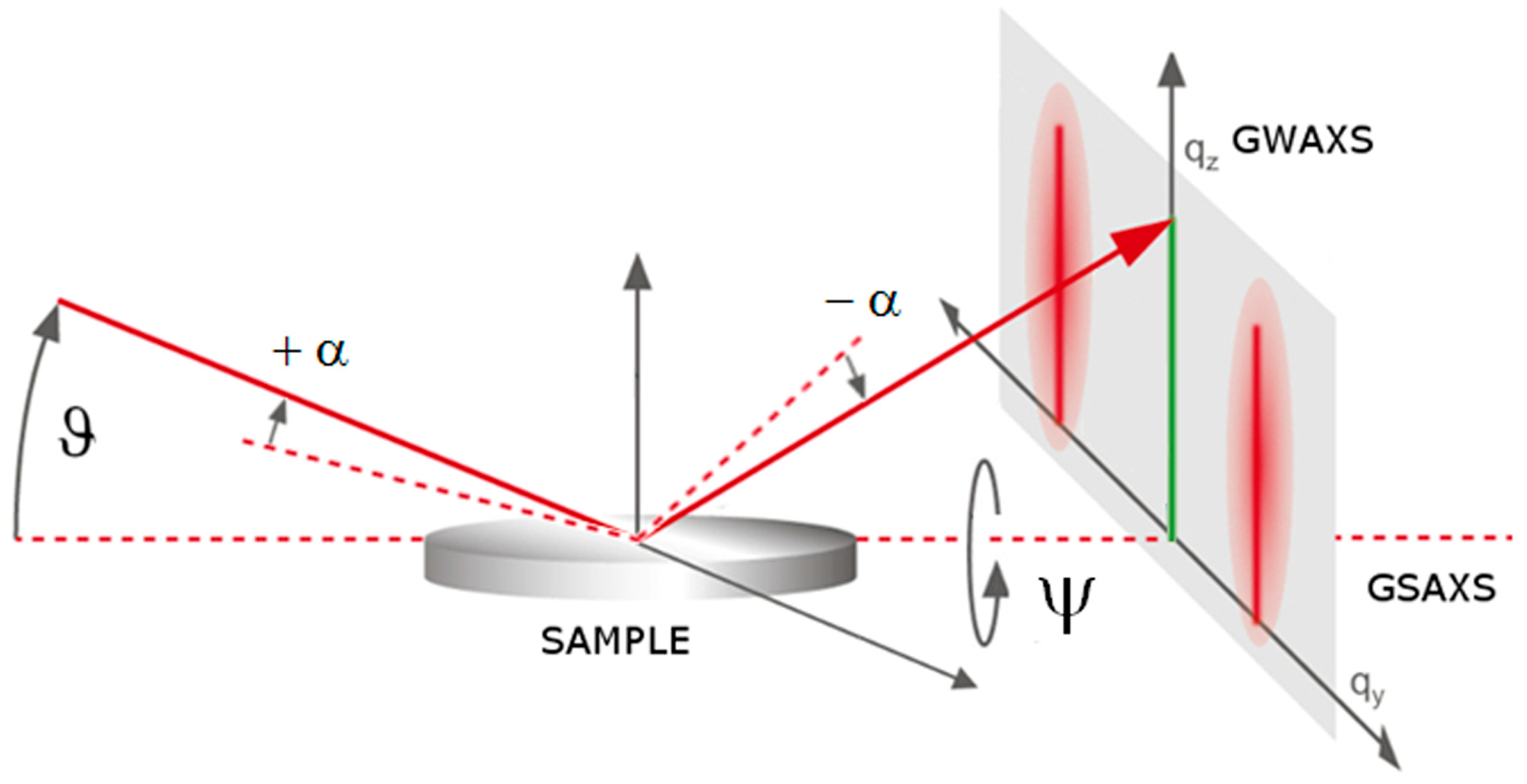
2. Materials and Methods
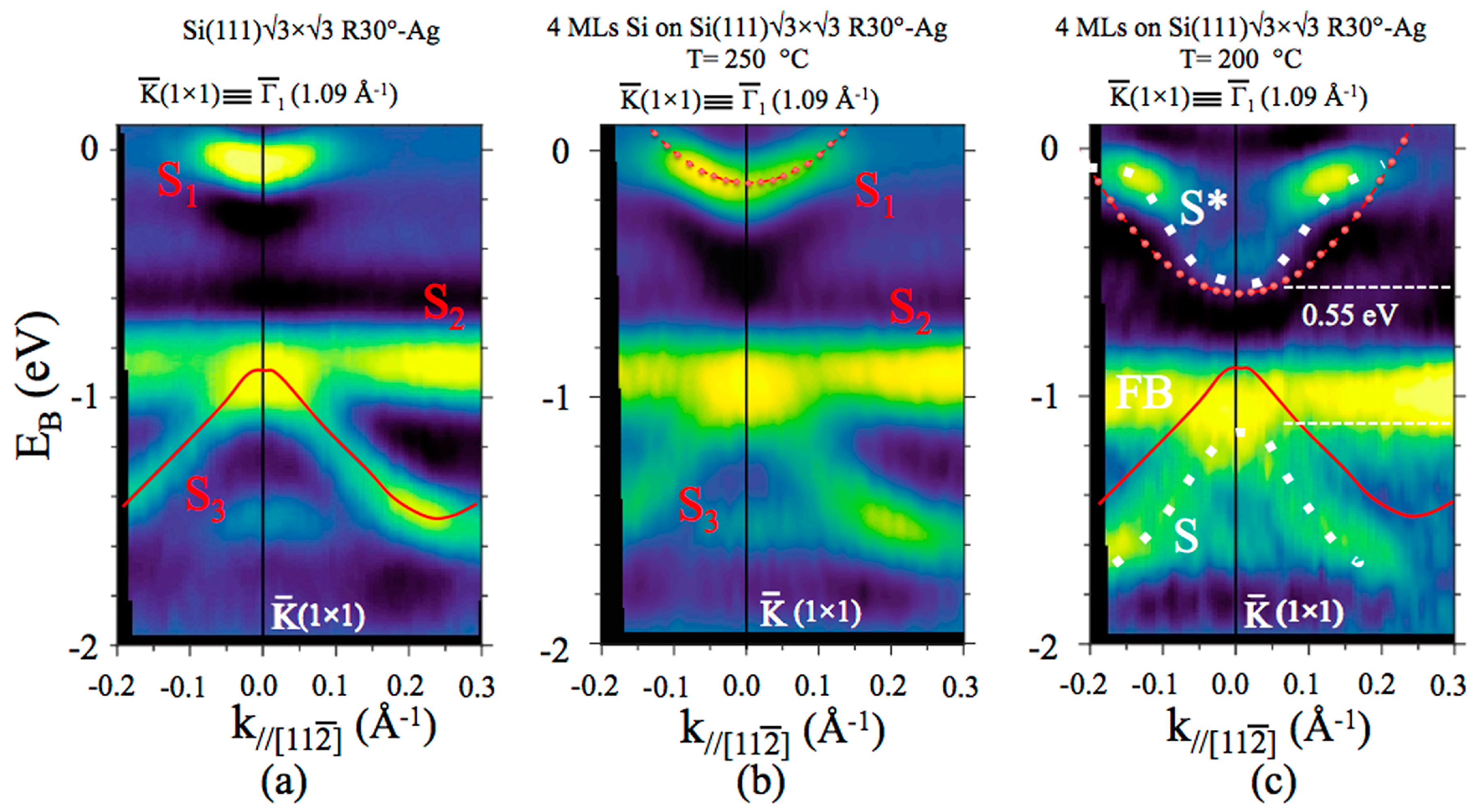
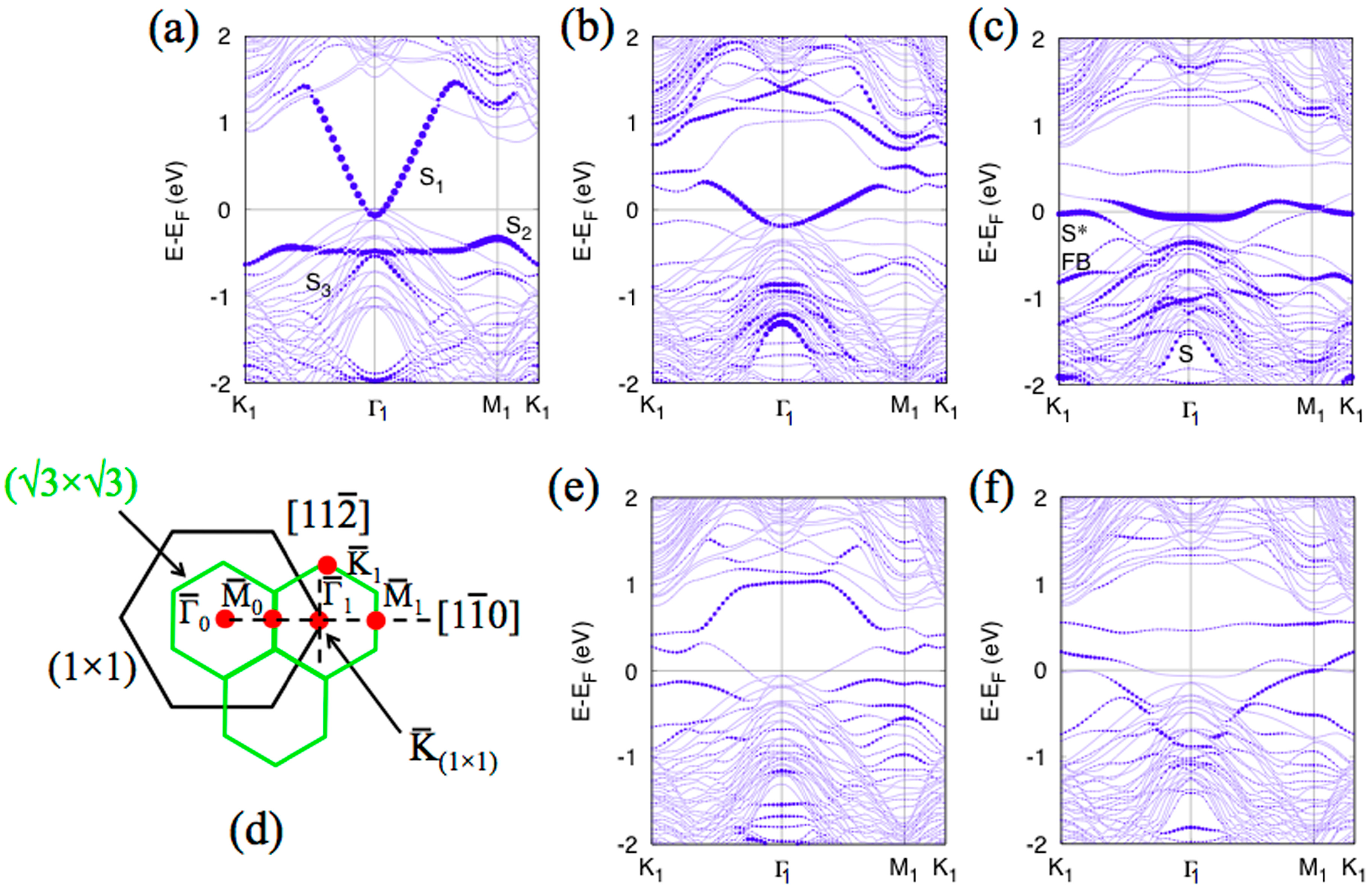
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Padova, P.; Feng, H.; Zhuang, J.; Li, Z.; Generosi, A.; Paci, B.; Ottaviani, C.; Quaresima, C.; Olivieri, B.; Krawiec, M.; et al. Synthesis of Multilayer Silicene on Si(111)√3 × √3-Ag. J. Phys. Chem. C 2017, 121, 27182–27190. [Google Scholar] [CrossRef]
- Shirai, T.; Shirasawa, T.; Hirahara, T.; Fukui, N.; Takahashi, T.; Hasegawa, S. Structure determination of multilayer silicene grown on Ag(111) films by electron diffraction: Evidence for Ag segregation at the surface. Phys. Rev. B 2014, 89, 241403-1–241403-5. [Google Scholar] [CrossRef]
- Mannix, A.J.; Kiraly, B.; Fisher, B.L.; Hersa, M.C.; Guisinger, N.P. Silicon Growth at the Two-Dimensional Limit on Ag(111). ACS Nano 2014, 8, 7538–7547. [Google Scholar] [CrossRef] [PubMed]
- Yamagami, T.; Sone, J.; Nakatsuji, K.; Hirayama, H. Surfactant Role of Ag Atoms in the Growth of Si Layers on Si(111) √ 3 × √ 3 –Ag Substrates. Appl. Phys. Lett. 2014, 105, 151603-1–151603-4. [Google Scholar] [CrossRef]
- Sone, J.; Yamagami, T.; Aoki, Y.; Nakatsuji, K.; Hirayama, H. Epitaxial Growth of Silicene on Ultra-Thin Ag(111) Films. New, J. Phys. 2014, 16, 095004-1–095004-15. [Google Scholar] [CrossRef]
- Borensztein, Y.; Curcella, A.; Royer, S.; Prévot, G. Silicene Multilayers on Ag(111) Display a Cubic Diamondlike Structure and a √3 × √3 Reconstruction Induced by Surfactant Ag Atoms. Phys. Rev. B 2015, 92, 155407-1–155407-5. [Google Scholar] [CrossRef]
- Kawahara, K.; Shirasawa, T.; Lina, C.L.; Nagao, R.; Tsukahara, N.; Takahashi, T.; Arafune, R.; Kawai, M.; Takagi, N. Determination of the Geometric Structure of “Multilayer Silicene” Grown on Ag(111) by Dynamical Low Energy Electron Diffraction and Scanning Tunneling Microscopy. Surf. Sci. 2016, 651, 70–75. [Google Scholar] [CrossRef]
- Curcella, A.; Bernard, R.; Borensztein, Y.; Lazzeri, M.; Resta, A.; Garreau, Y.; Prévot, G. Multilayer silicene: Clear evidence of Ag-terminated bulk silicon. 2D Mater 2017, 4, 025067-1–025067-9. [Google Scholar] [CrossRef][Green Version]
- Hasegawa, S.; Tong, X.; Takeda, S.; Sato, N.; Nagao, T. Structures and electronic transport on silicon surfaces. Prog. Surf. Sci. 1999, 60, 89–257. [Google Scholar] [CrossRef]
- Hasegawa, S.; Sato, N.; Shiraki, I.; Petersen, C.L.; BØggild, P.; Hansen, T.M.; Nagao, Y.; Grey, F. Structures and Electronic Transport on Silicon Surfaces. Jpn. J. Appl. Phys 2000, 39, 3815–3822. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- De Padova, P.; Vogt, P.; Resta, A.; Avila, J.; Razado-Colambo, I.; Quaresima, C.; Ottaviani, C.; Olivieri, B.; Bruhn, T.; Hirahara, T.; et al. Evidence of Dirac fermions in multilayer silicene. Appl. Phys. Lett. 2013, 102, 163106-1–163106-3. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.C.; Feng, B.; He, X.; Cheng, P.; Ding, Z.; Meng, S.; Yao, Y.; Wu, K. Evidence for Dirac Fermions in a Honeycomb Lattice Based on Silicon. Phys. Rev. Lett. 2012, 109, 056804-1–056804-5. [Google Scholar] [CrossRef]
- Salomon, E.; Ajjouri, R.E.; Le Lay, G.; Angot, T. Growth and Structural Properties of Silicene at Multilayer Coverage. J. Phys. Condens. Matter 2014, 25, 185003-1–185003-4. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, R. Small but Strong Lessons from Chemistry for Nanoscience. Angew. Chem. Int. Ed. Engl. 2013, 52, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Kamal, C.; Chakrabarti, A.; Banerjee, A.; Deb, S.K. Silicene Beyond Mono-Layers: Different Stacking Configurations and Their Properties. J. Phys. Condens. Matter 2013, 25, 085508-1–085508-10. [Google Scholar] [CrossRef]
- Cahangirov, S.; Özçelik, V.O.; Rubio, A.; Ciraci, S. The Layered Allotrope of Silicon. Phys. Rev. B 2014, 90, 085426-1–085426-5. [Google Scholar] [CrossRef]
- Feng, B.; Ding, Z.; Meng, S.; Yao, Y.; He, X.; Cheng, P.; Chen, L.; Wu, K. Evidence of Silicene in Honeycomb Structures of Silicon on Ag(111). Nano Lett. 2012, 12, 3507–3511. [Google Scholar] [CrossRef] [PubMed]
- De Padova, P.; Ottaviani, C.; Quaresima, C.; Olivieri, B.; Imperatori, P.; Salomon, E.; Angot, T.; Quagliano, L.; Romano, C.; Vona, A. 24 Hours Stability of Thick Multilayer Silicene in Air. 2D Mater 2014, 1, 021003-1–021003-11. [Google Scholar] [CrossRef]
- Vogt, P.; Capiod, P.; Berthe, M.; Resta, A.; De Padova, P.; Bruhn, T.; Le Lay, G.; Grandidier, B. Synthesis and electrical conductivity of multilayer silicene. Appl. Phys. Lett. 2014, 104, 21602. [Google Scholar] [CrossRef]
- De Padova, P.; Generosi, A.; Paci, B.; Ottaviani, C.; Quaresima, C.; Olivieri, B.; Salomon, E.; Angot, T.; Le Lay, G. Multilayer Silicene: Clear Evidence. 2D Mater 2016, 3, 031011-1–031011-7. [Google Scholar] [CrossRef]
- Du, Y.; Zhuang, J.; Wang, J.; Li, Z.; Liu, H.; Zhao, J.; Xu, X.; Feng, H.; Chen, L.; Wu, K.; et al. Quasi-freestanding Epitaxial Silicene on Ag(111) by Oxygen Intercalation. Sci. Adv. 2016, 2, 1600067-1–1600067-7. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhuang, J.; Chen, L.; Ni, Z.; Liu, C.; Wang, L.; Xu, X.; Wang, J.; Pi, X.; Wang, X.; et al. Observation of van Hove Singularities in Twisted Silicene Multilayers. ACS Central Sci. 2016, 2, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Grazianetti, C.; Cinquanta, E.; Tao, L.; De Padova, P.; Quaresima, C.; Ottaviani, C.; Akinwande, D.; Molle, A. Crossover Between Multilayer Silicene and Diamond-Like Growth Regime. ACS Nano 2017, 11, 3376–3382. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Chen, L.; Qiu, J.; Ding, Z.; Zhan, J.; Wu, K.; Li, H.; Meng, S. Multilayered Silicene: The Bottom-Up Approah for a Weakly Relaxed Si(111) with Dirac Surface States. Nanoscale 2015, 7, 15880–15885. [Google Scholar] [CrossRef]
- De Padova, P.; Olivieri, B.; Quaresima, C.; Ottaviani, C. Si nanoribbons: From 1D to 3D Nanostructures. In Silicene, Prediction, Synthesis, Application, 1st ed.; Vogt, P., Le Lay, G., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2018; Volume 1, pp. 115–128. [Google Scholar]
- Ezawa, M.; Salomon, E.; De Padova, P.; Solonenko, D.; Vogt, P.; Dávila, M.E.; Molle, A.; Angot, T.; Le Lay, G. Fundamentals and Functionalities of Silicene, Germanene, and Stanene. La Rivista del Nuovo Cimento. 2018, 41, 175–224. [Google Scholar]
- Paci, B.; Generosi, A.; Rossi Albertini, V.; Agostinelli, E.; Varvaro, G.; Fiorani, D. Structural and Morphological Characterization by Energy Dispersive X-ray Diffractometry and Reflectometry Measurements of Cr/Pt Bilayer Films. Chem. Mater. 2004, 16, 292–298. [Google Scholar] [CrossRef]
- Tajiri, H.; Sumitani, K.; Nojima, S.; Takahashi, T.; Akimoto, K.; Sugiyama, H.; Zhang, X.; Kawata, H. X-Ray Diffraction Study of the Si(111)−3√×3√−Ag Surface Structure. Phys. Rev. B 2003, 68, 035330. [Google Scholar] [CrossRef]
- Takashashi, T.; Nakatani, S. Refinement of the Si(111)√3×√3–Ag Structure by Surfce X-Ray Diffraction. Surf. Sci. 1993, 282, 17–32. [Google Scholar] [CrossRef]
- Takahashi, T.; Nakatani, S.; Okamoto, N.; Kikuta, S. Study on the Si(111) √3×√3-Ag Surface Structure by X-Ray Diffraction. Jpn. J. Appl. Phys. 1988, 27, L753–L755. [Google Scholar] [CrossRef]
- Matsuda, I.; Morikawa, H.; Liu, C.; Ohuchi, S.; Hasegawa, S.; Okuda, T.; Kinoshita, T.; Ottaviani, C.; Cricenti, A.; D’Angelo, M.; et al. Electronic evidence of asymmetry in the Si(111)3×3−Ag structure. Phys. Rev. B 2003, 68, 085407-1–085407-5. [Google Scholar] [CrossRef]
- Matsuda, I.; Hurahara, T.; Konischi, M.; Liu, C.; Morikawa, H.; D’ Angelo, M.; Hasegawa, S. Evolution of Fermi surface by electron filling into a free-electronlike surface state. Phys. Rev. B 2005, 71, 235315. [Google Scholar] [CrossRef]
- Crain, J.N.; Altmann, N.; Bromberger, C.; Himpsel, F.J. Fermi surfaces of surface states on Si(111)-Ag, Au. Phys. Rev. B 2002, 66, 205302-1–205302-11. [Google Scholar] [CrossRef]
- Zhang, H.M.; Sakamoto, K.; Uhrberg, R.I.G. Comprehensive study of the metal character of adatom-induced Ag/Si(111) reconstructions. Phys. Rev. B 2001, 64, 245421-1–245421-4. [Google Scholar] [CrossRef]
- Tong, X.; Ohuchi, S.; Sato, N.; Tanikawa, T.; Nagao, T.; Matsuda, I.; Aoyagi, Y.; Hasegawa, S. Electronic structure Ag-induced √3×√3 and √21×√21 superstructure on the si(111) surface studied by angle-resolved photoemission spectroscopy and scanning tunneling microscopy. Phys. Rev. B 2001, 64, 205316-1–205316-9. [Google Scholar] [CrossRef]
- Yokotsuka, T.; Kono, S.; Suzuki, S.; Sagawa, T. Study of Ag/Si(111) submonolayer interface, I Electronic structure by angle-resolved UPS. Surf. Sci. 1983, 127, 35–47. [Google Scholar] [CrossRef]
- Johansson, L.S.O.; Landemark, E.; Karlsson, C.J.; Uhrberg, R.I.G. Fermi–level Pinning and Surface-State Band Structure of the Si(111)-(√3×√3) R30°-Ag Surface. Phys. Rev. Lett. 1989, 63, 2092–2095. [Google Scholar] [CrossRef]
- Hirahara, T.; Matsuda, I.; Ueno, M.; Hasegawa, S. The effective mass of a free-electron-like surface of the Si(111)-(√3×√3) surface investigated by photoemission and scanning tunneling spectroscopies. Surf. Sci. 2004, 563, 191–198. [Google Scholar] [CrossRef]
- Liu, C.; Matsuda, I.; Hobara, R.; Hasegawa, S. Interaction between Adatoms-Induced Localized States and Quasi-Two Dimensional Electron Gas. Phys. Rev. Lett. 2006, 96, 036803-1–036803-4. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Xiang, H.J.; Li, B.; Zhao, A.; Xiao, X.; Yang, J.; Hou, J.G.; Zhu, Q. Detecting surface resonance states of Si(111) √3×√3-Ag with a scanning tunneling microscope. Phys. Rev. B 2004, 70, 245431-1–245431-5. [Google Scholar] [CrossRef]
- Aizawa, H.; Tsukada, M. First principle study of Ag adatoms on the Si(111)(√3×√3)-Ag surface. Phys. Rev. B 1999, 59, 10923–10927. [Google Scholar] [CrossRef]
- Jeong, H.; Yeom, H.W.; Jeong, S. Adatom-Induced variations of the atomic and electronic structure of Si(111)(√3×√3)-Ag. Phys. Rev. B 2008, 77, 235425-1–235425-8. [Google Scholar] [CrossRef]
- Crain, J.N.; Gallagher, C.; McChesney, J.L.; Bissen, M.; Himpsel, F.J. Doping of a surface band on Si(111) √3×√3-Ag. Phys. Rev. B 2005, 72, 045312. [Google Scholar] [CrossRef]
- De Padova, P.; Avila, J.; Resta, A.; Razado-Colambo, I.; Quaresima, C.; Ottaviani, C.; Olivieri, B.; Bruhn, T.; Vogt, P.; Asensio, M.C.; et al. The quasiparticles band dispersion in epitaxial multilayer silicene. J. Phys. Condens. Matter 2013, 25, 382202-1–382202-7. [Google Scholar] [CrossRef]
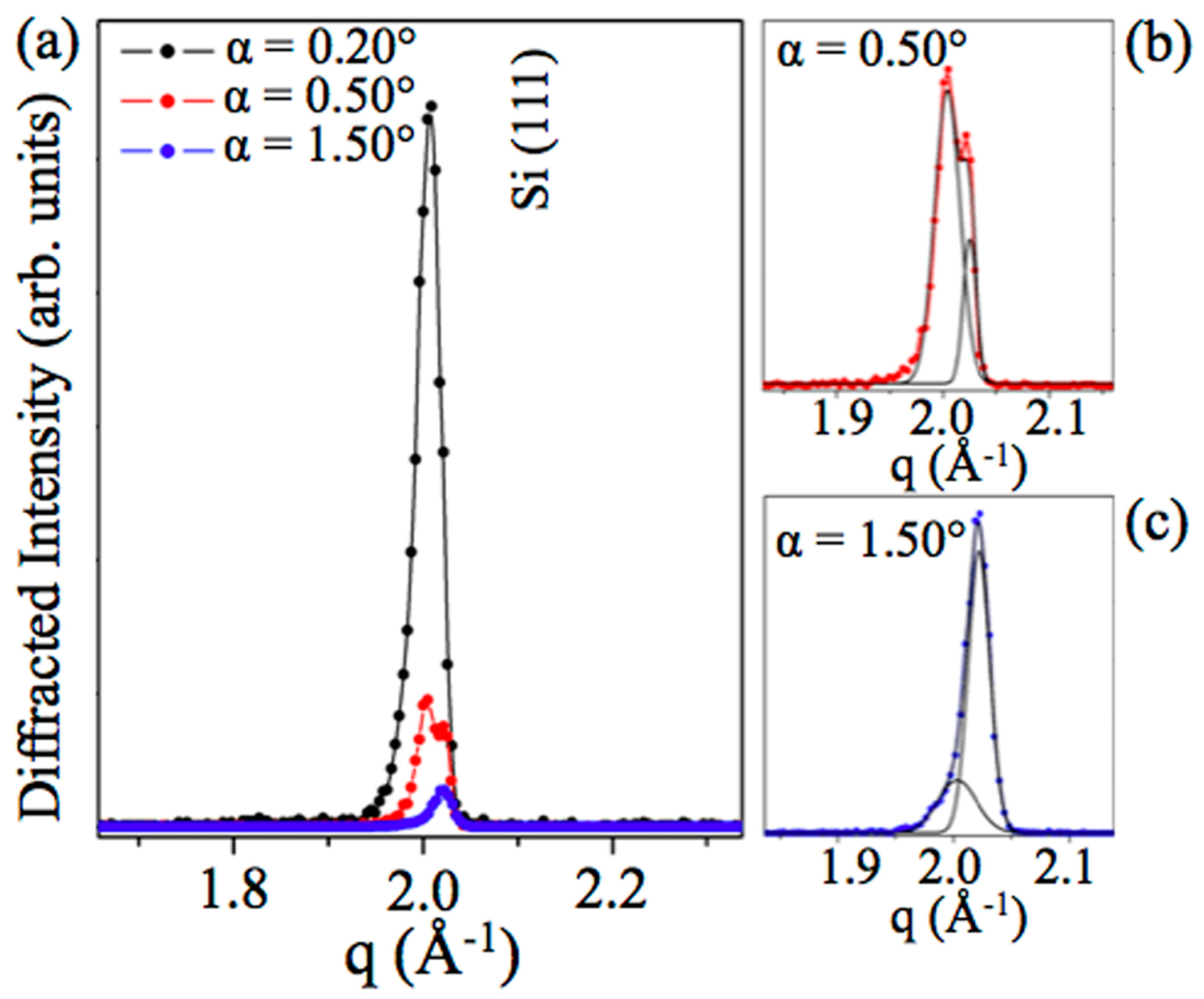


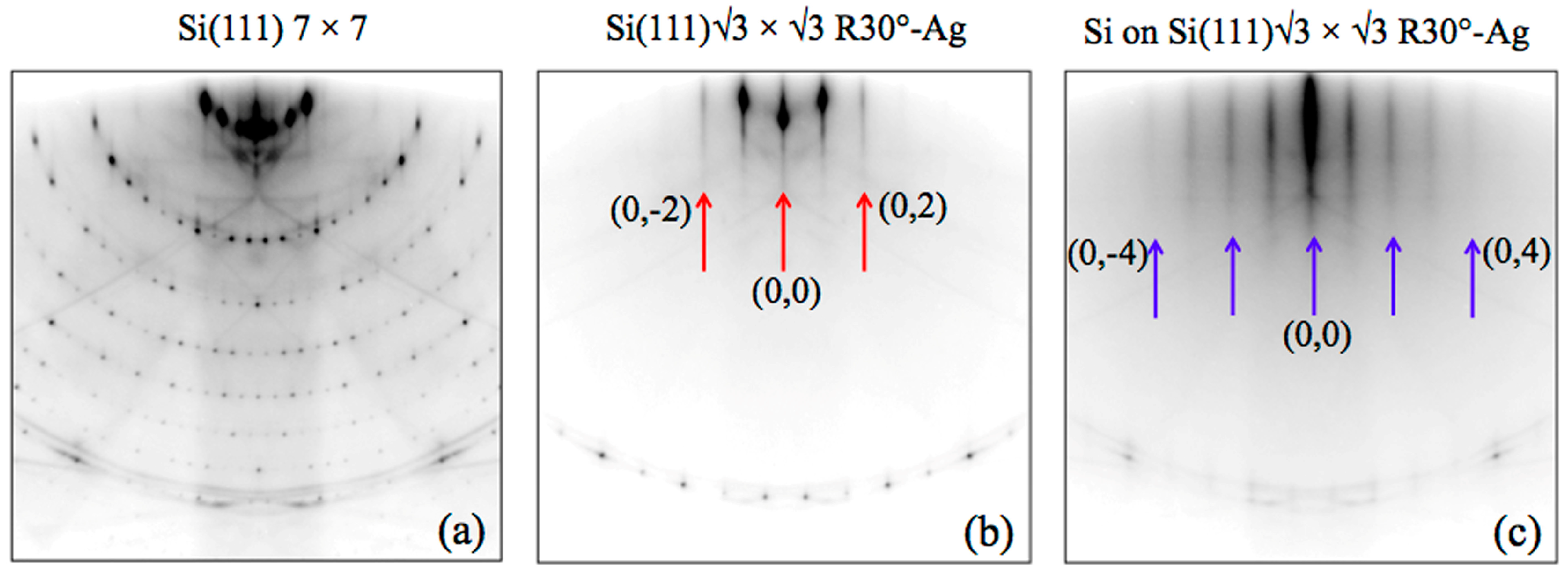
| Samples | Peakxy | qxy (Å−1) | dxy (Å) q | Peakz | qz (Å−1) | dz (Å) |
|---|---|---|---|---|---|---|
| Si(111) | (220) | 3.274 (5) | 1.919 (10) | (111) | 2.003 (5) | 3.136 (10) |
| (220) | 4.006 (5) | 1.568 (10) | ||||
| Si(111)√3–Ag | (dSi-Si Trimers) | 2.212 (5) | 2.840 (10) | |||
| (dAg-AgTriangles) | 2.910 (5) | 2.159 (10) | ||||
| dLattice parameter | 0.947 (5) | 6.640 (10) | ||||
| 10 MLs silicene | dLattice parameter | 0.969 (5) | 6.484 (15) | 2.032 (5) | 3.092 (5) | |
| 1.947 (5) 0.482 (5) | 3.240 (10) 13.030(15) 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Padova, P.; Generosi, A.; Paci, B.; Ottaviani, C.; Quaresima, C.; Olivieri, B.; Kopciuszyński, M.; Żurawek, L.; Zdyb, R.; Krawiec, M. New Findings on Multilayer Silicene on Si(111)√3×√3R30°–Ag Template. Materials 2019, 12, 2258. https://doi.org/10.3390/ma12142258
De Padova P, Generosi A, Paci B, Ottaviani C, Quaresima C, Olivieri B, Kopciuszyński M, Żurawek L, Zdyb R, Krawiec M. New Findings on Multilayer Silicene on Si(111)√3×√3R30°–Ag Template. Materials. 2019; 12(14):2258. https://doi.org/10.3390/ma12142258
Chicago/Turabian StyleDe Padova, Paola, Amanda Generosi, Barbara Paci, Carlo Ottaviani, Claudio Quaresima, Bruno Olivieri, Marek Kopciuszyński, Lucyna Żurawek, Ryszard Zdyb, and Mariusz Krawiec. 2019. "New Findings on Multilayer Silicene on Si(111)√3×√3R30°–Ag Template" Materials 12, no. 14: 2258. https://doi.org/10.3390/ma12142258
APA StyleDe Padova, P., Generosi, A., Paci, B., Ottaviani, C., Quaresima, C., Olivieri, B., Kopciuszyński, M., Żurawek, L., Zdyb, R., & Krawiec, M. (2019). New Findings on Multilayer Silicene on Si(111)√3×√3R30°–Ag Template. Materials, 12(14), 2258. https://doi.org/10.3390/ma12142258






