Generalized Softened Variable Angle Truss Model for RC Hollow Beams under Torsion
Abstract
:1. Introduction
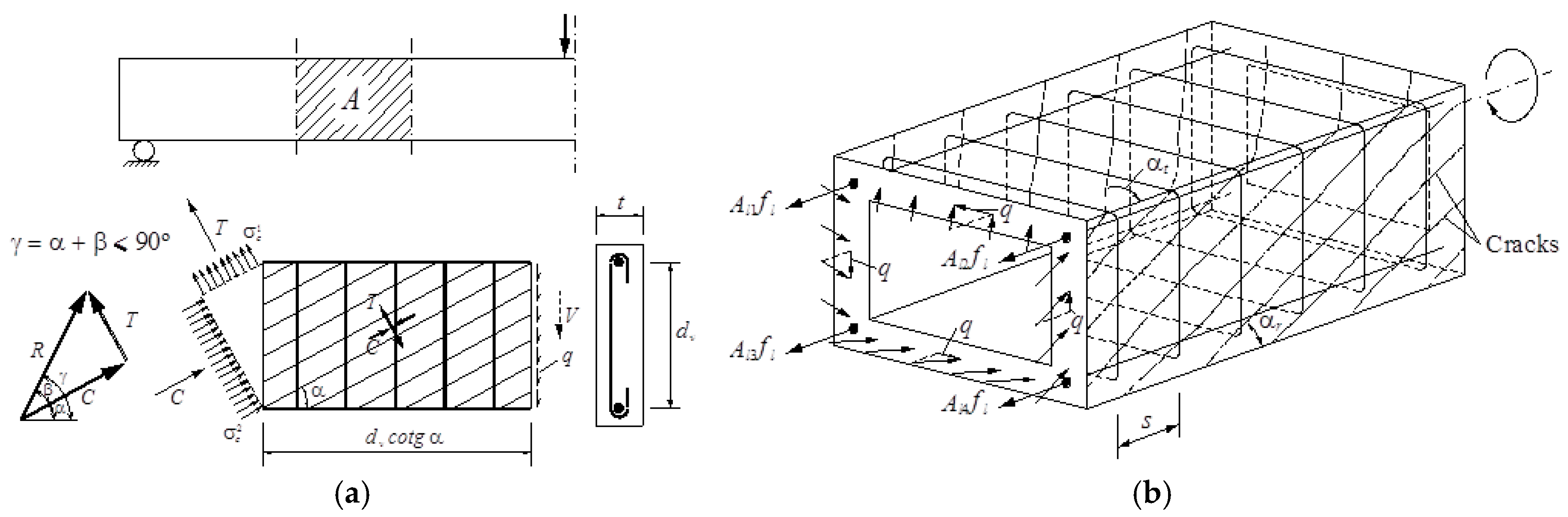
2. Brief Description of the GSVATM for RC Solid Beams
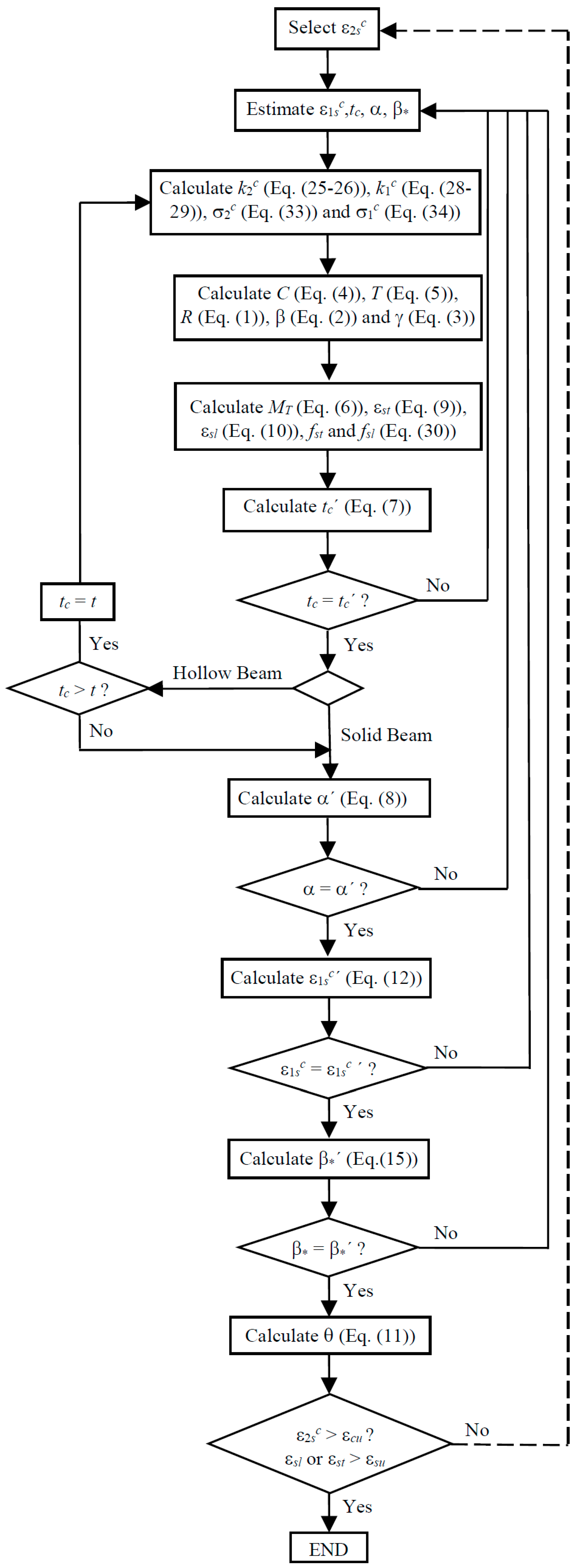
3. Calculation Procedure for RC Hollow Beams under Torsion
3.1. Introduction
3.2. Thickness of the Shear Flow
- if 0.91 the RC hollow beam has a “thin wall”;
- if 0.91 the RC hollow beam has a “thick wall”.
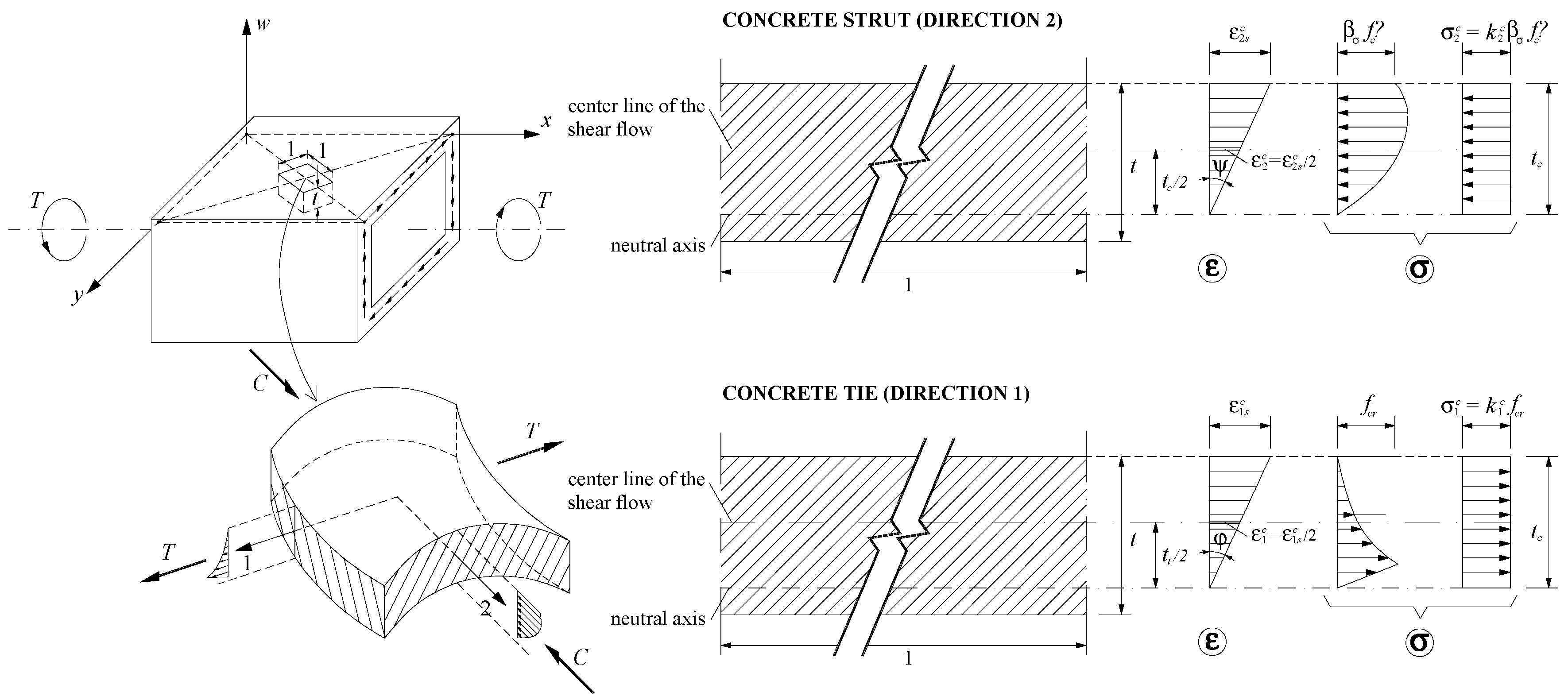
3.3. Constitutive Relationships for Concrete
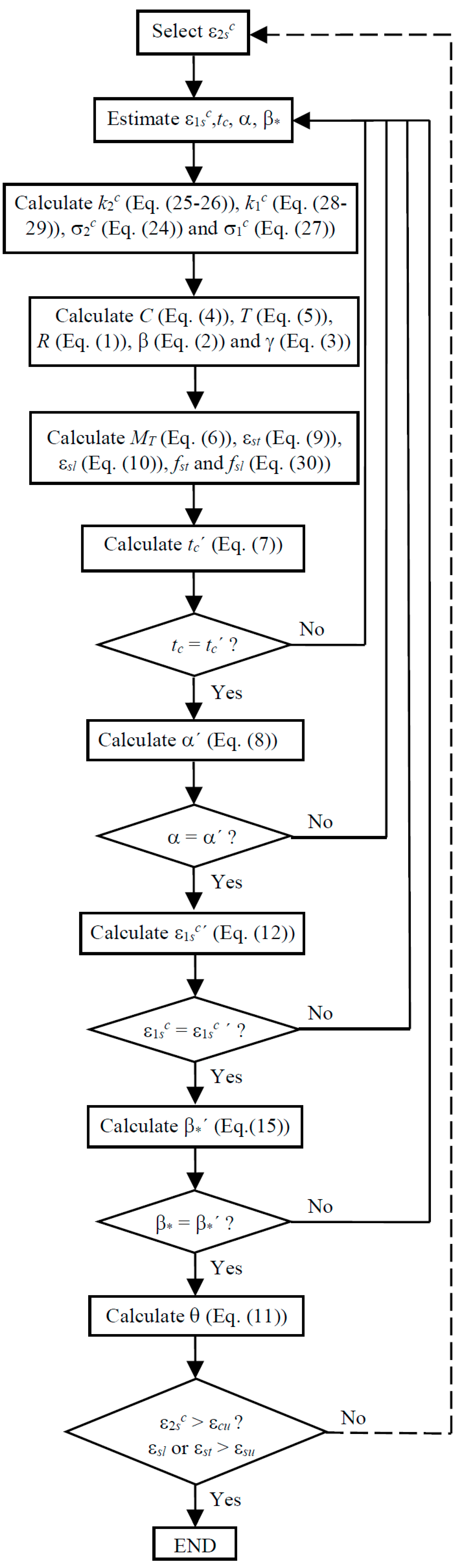
3.4. New Calculation Procedure for the GSVATM
4. Reference Beams
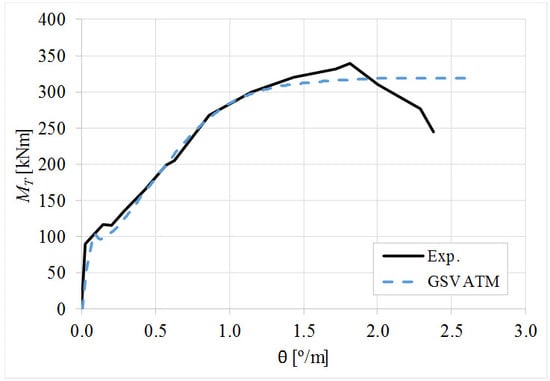
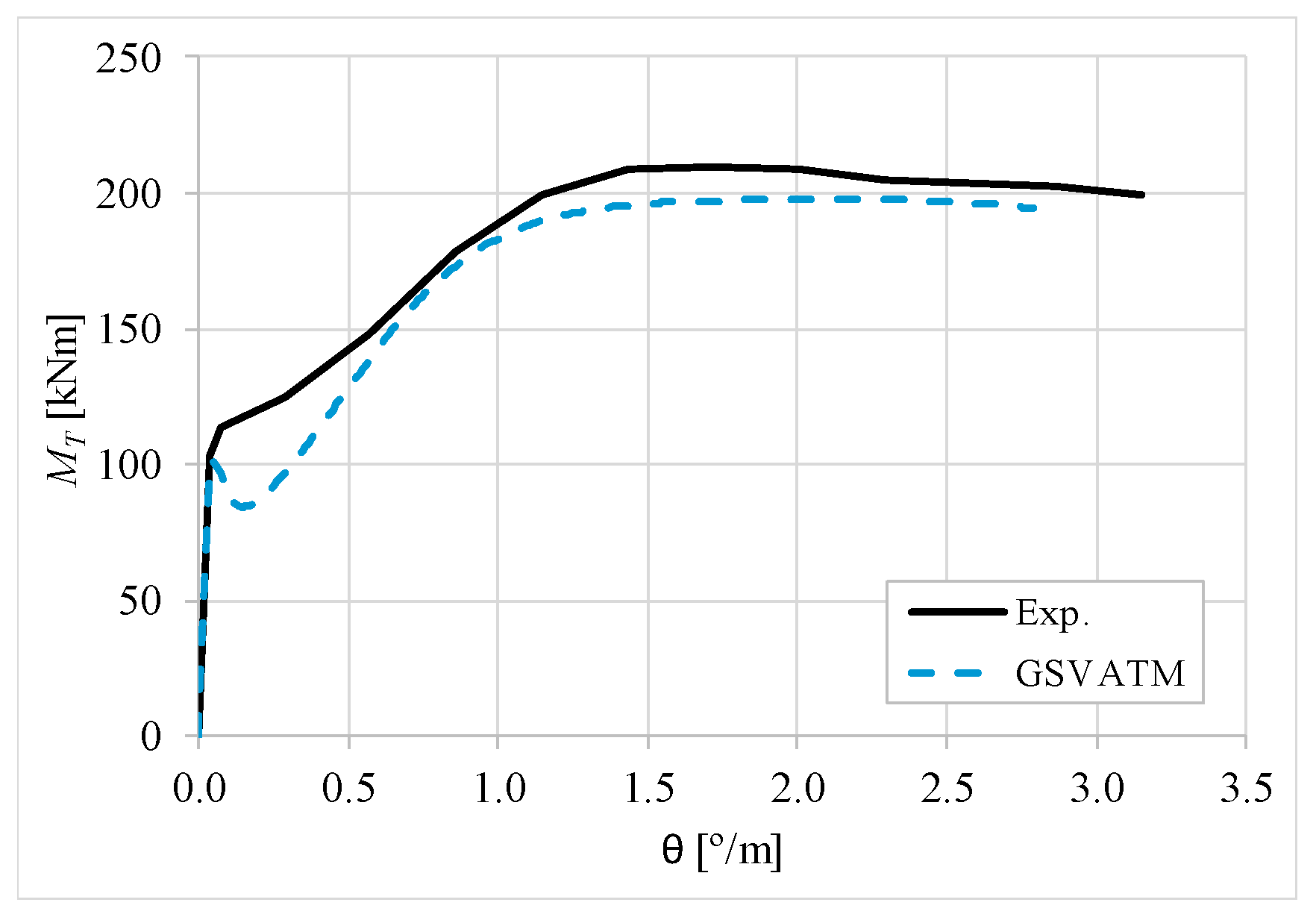
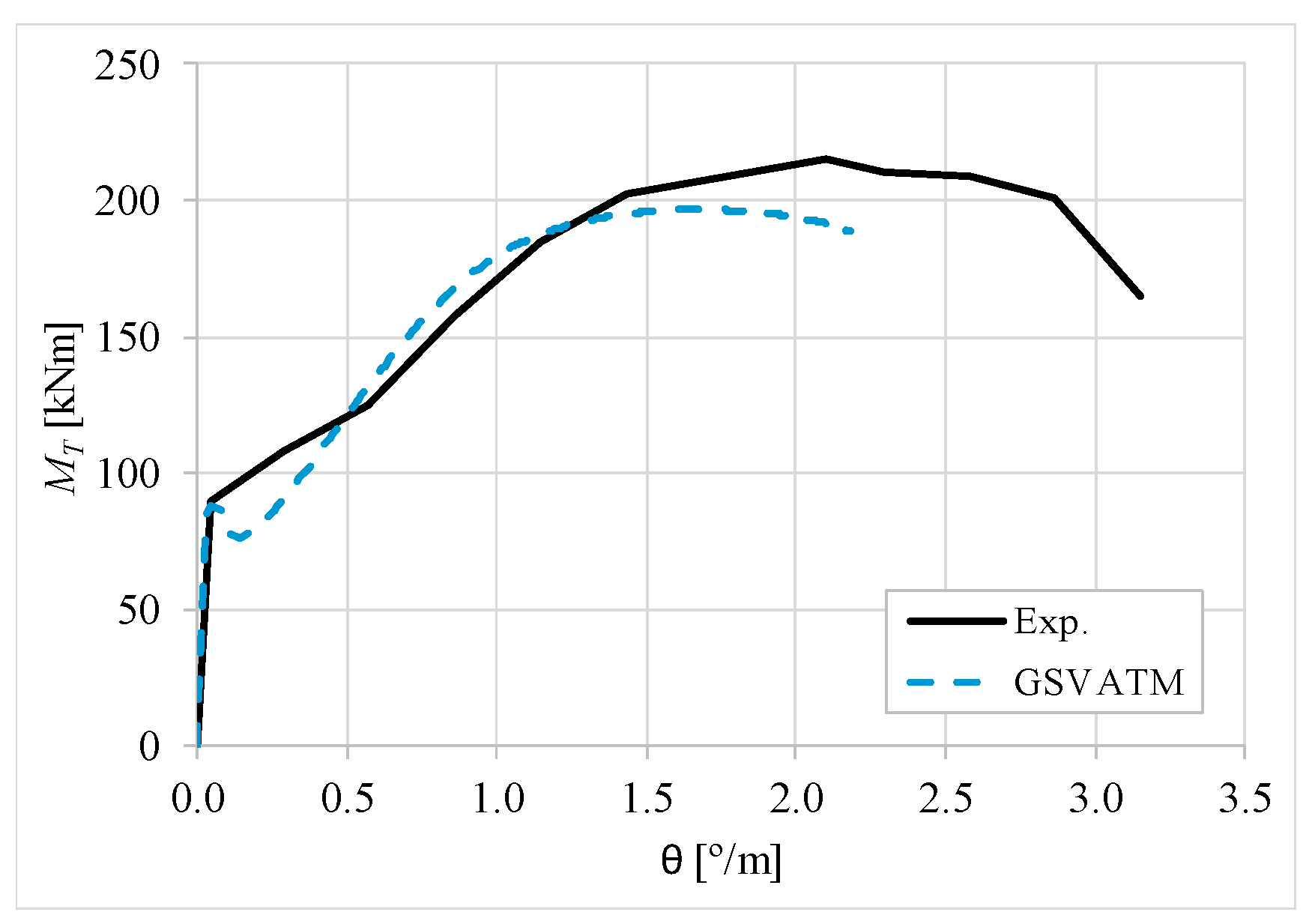
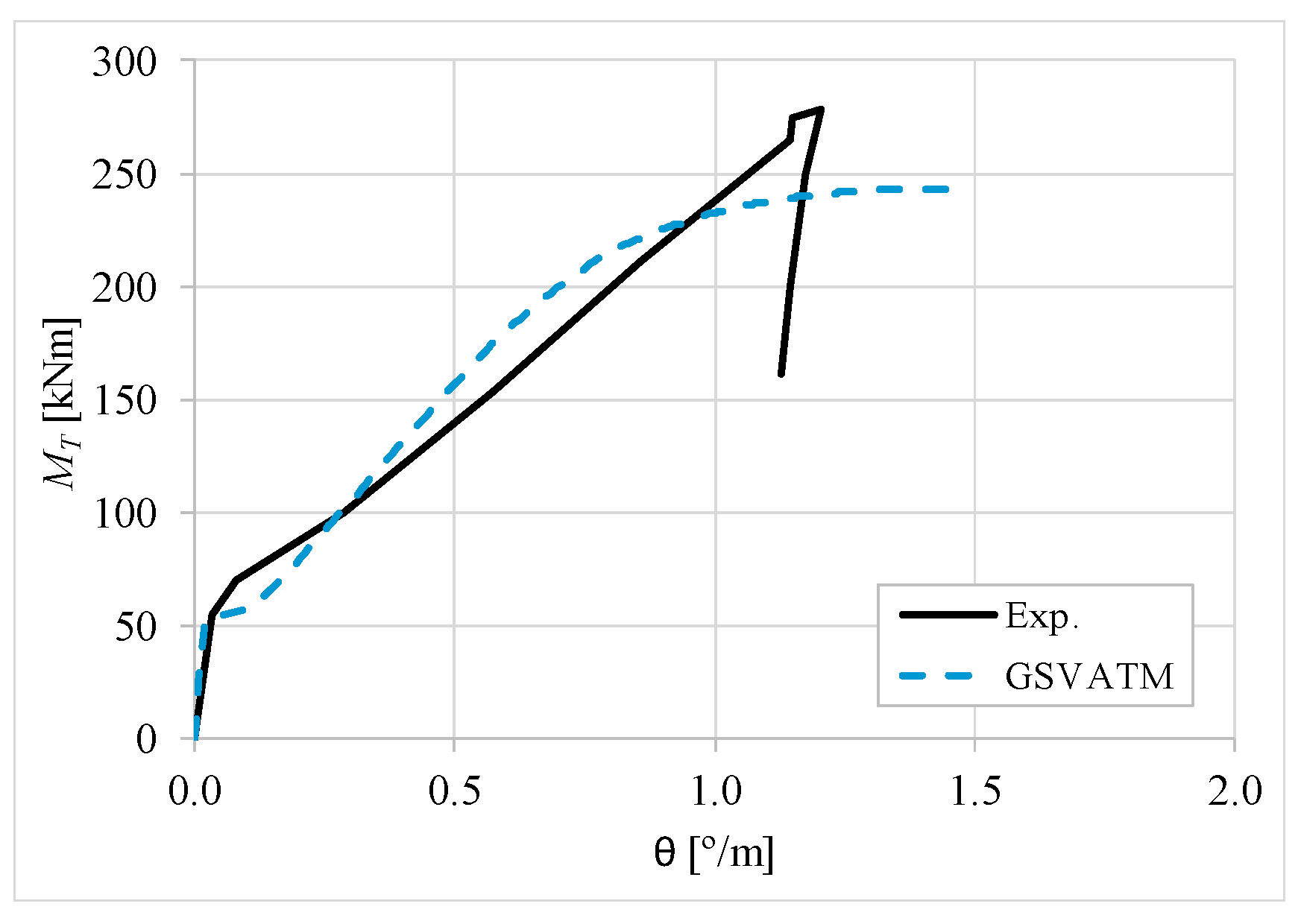
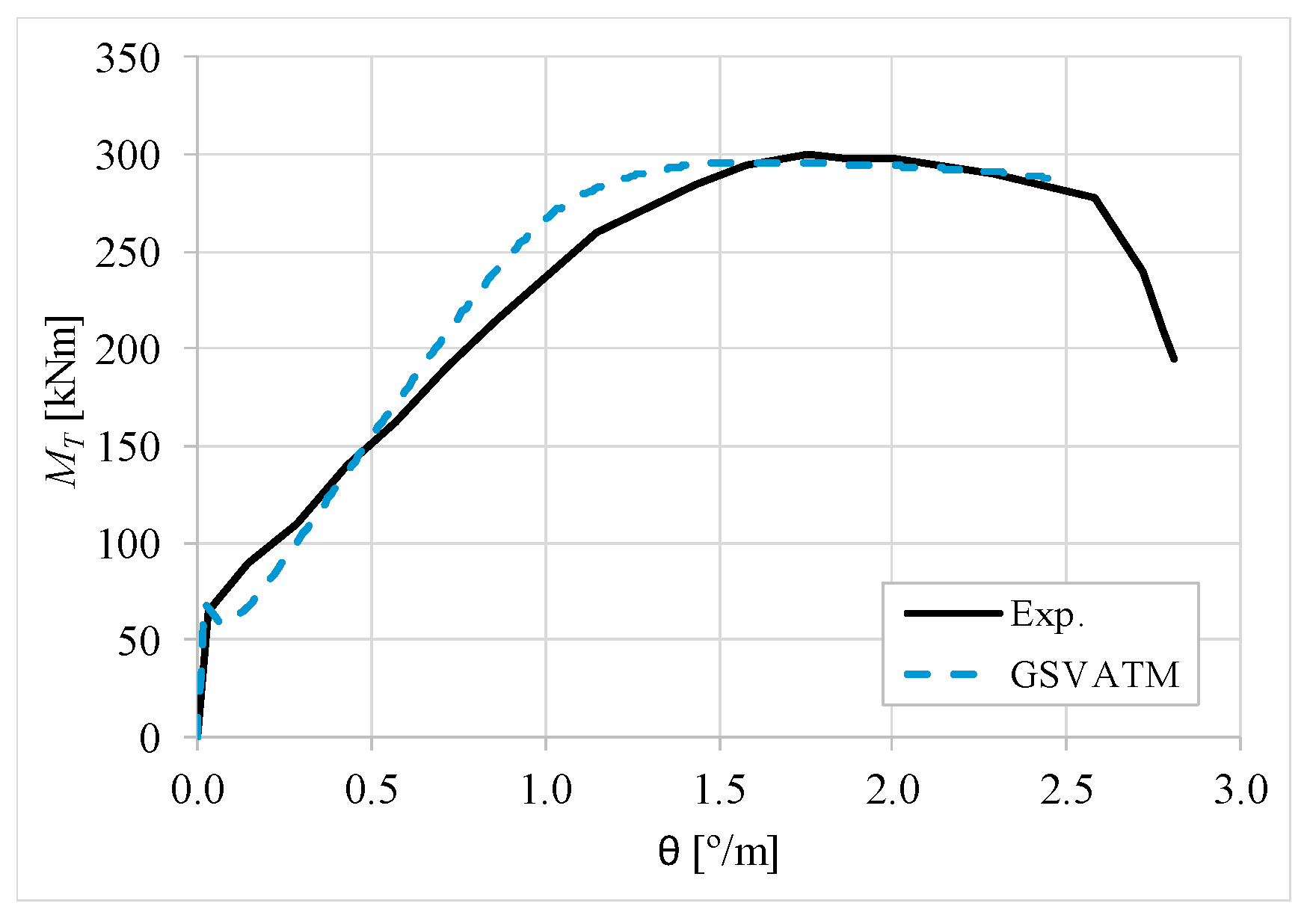
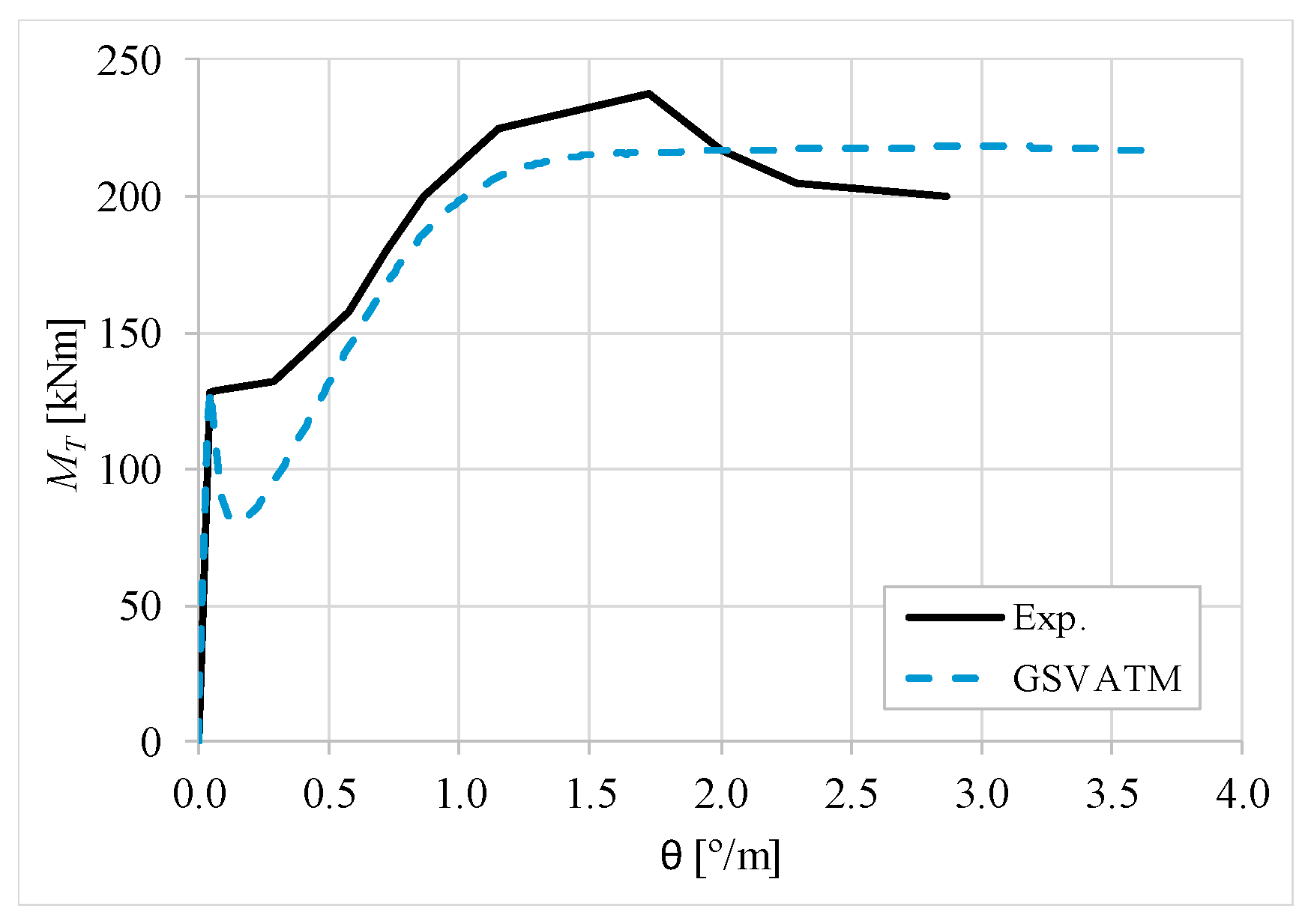
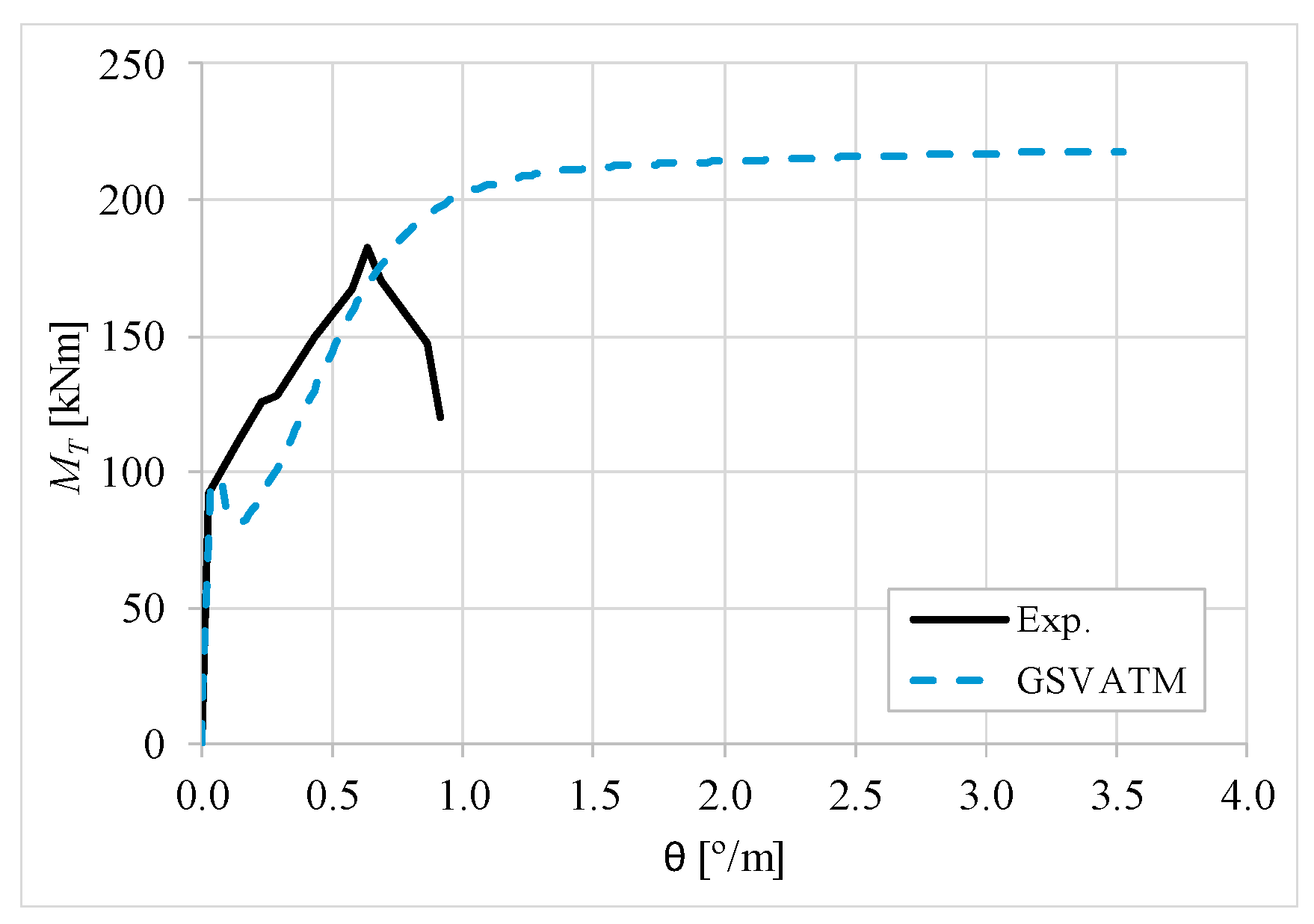
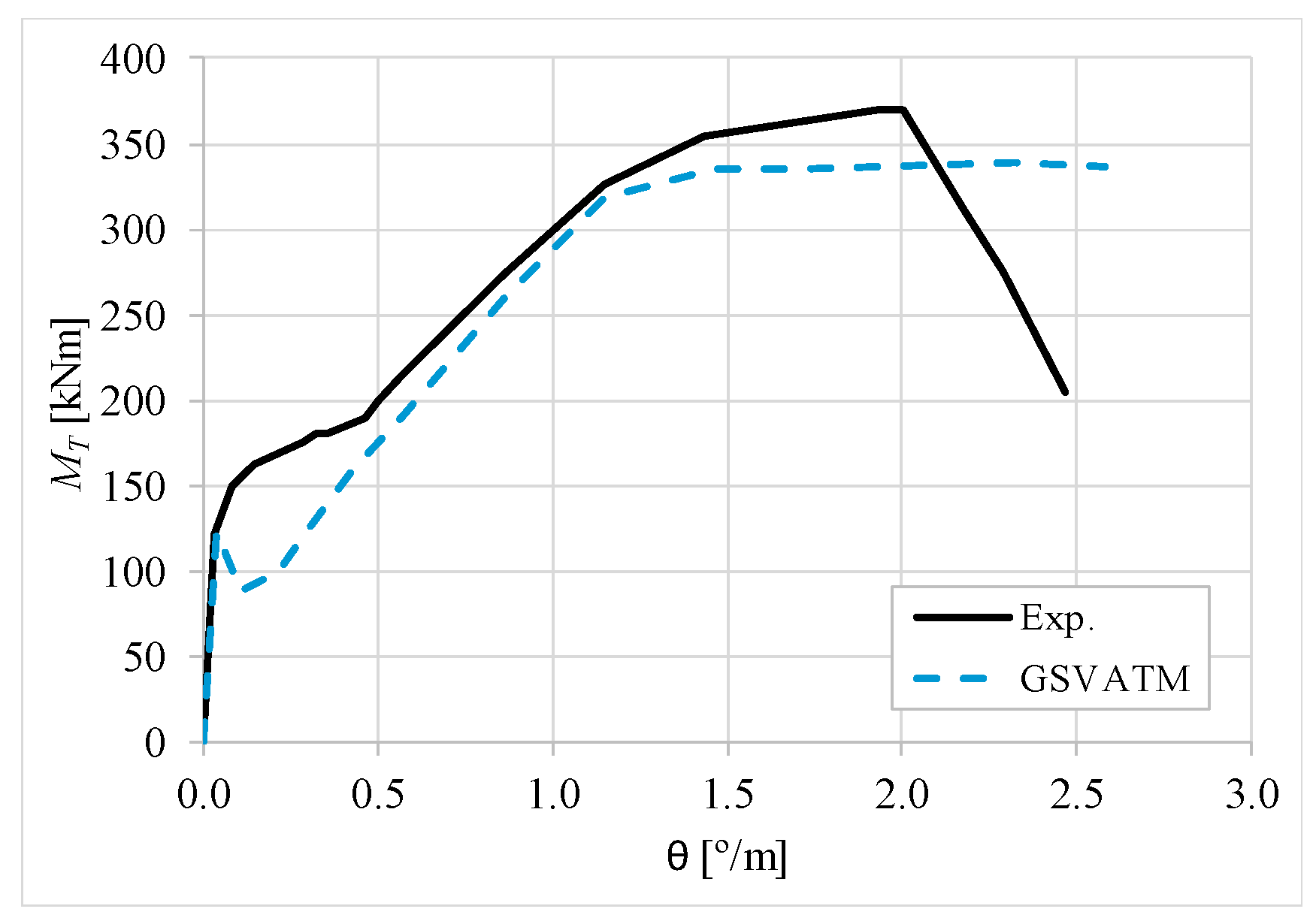
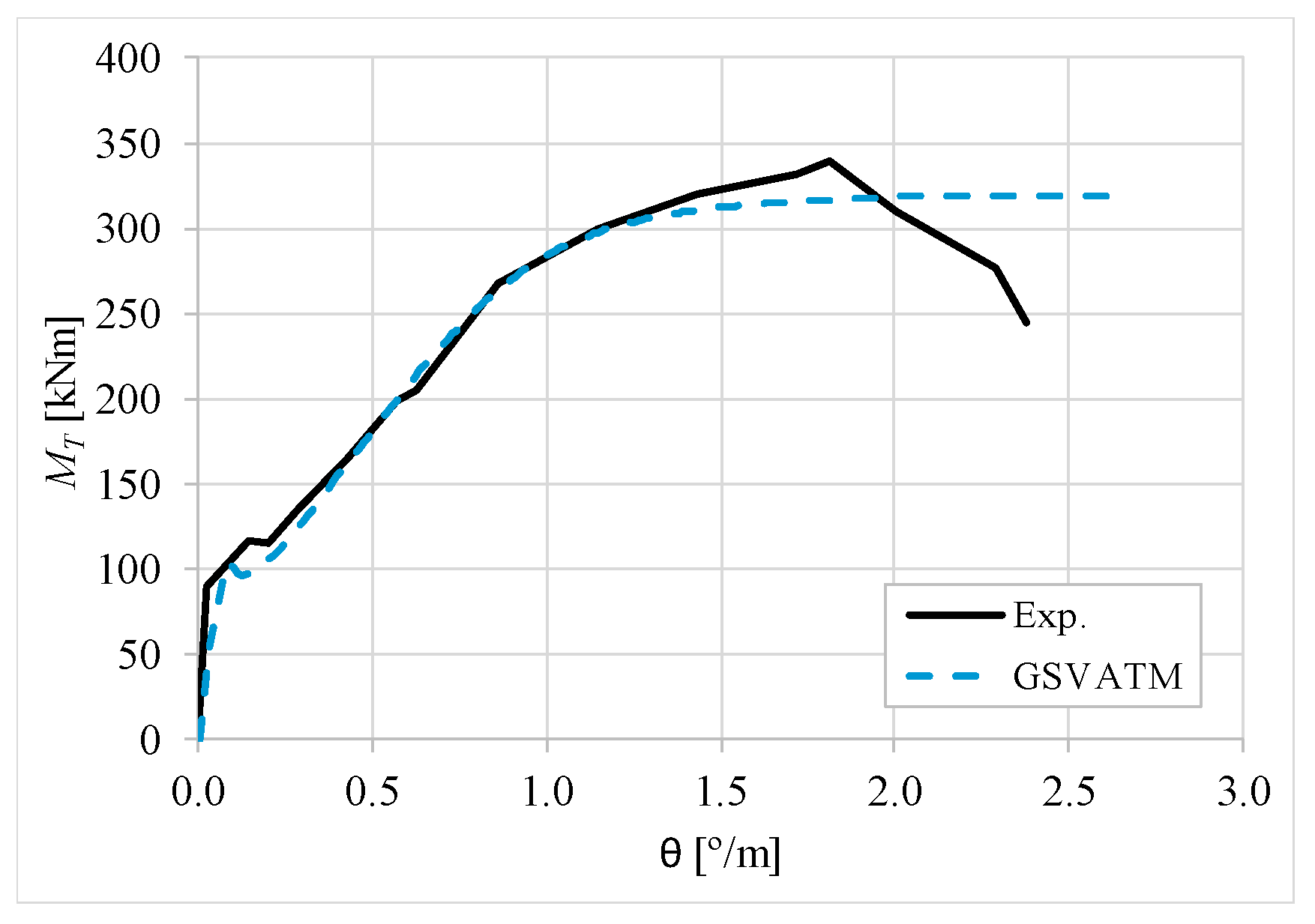
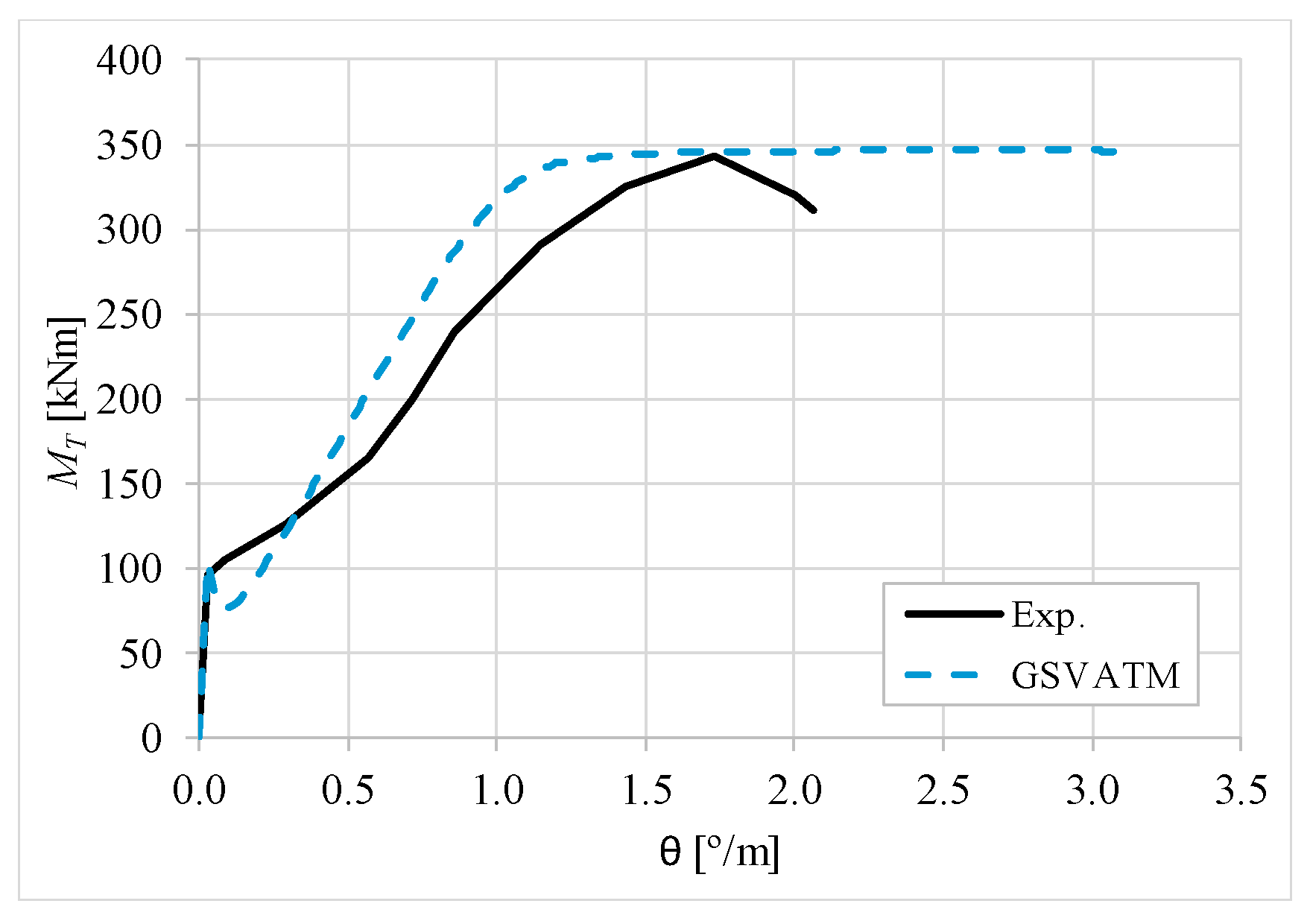
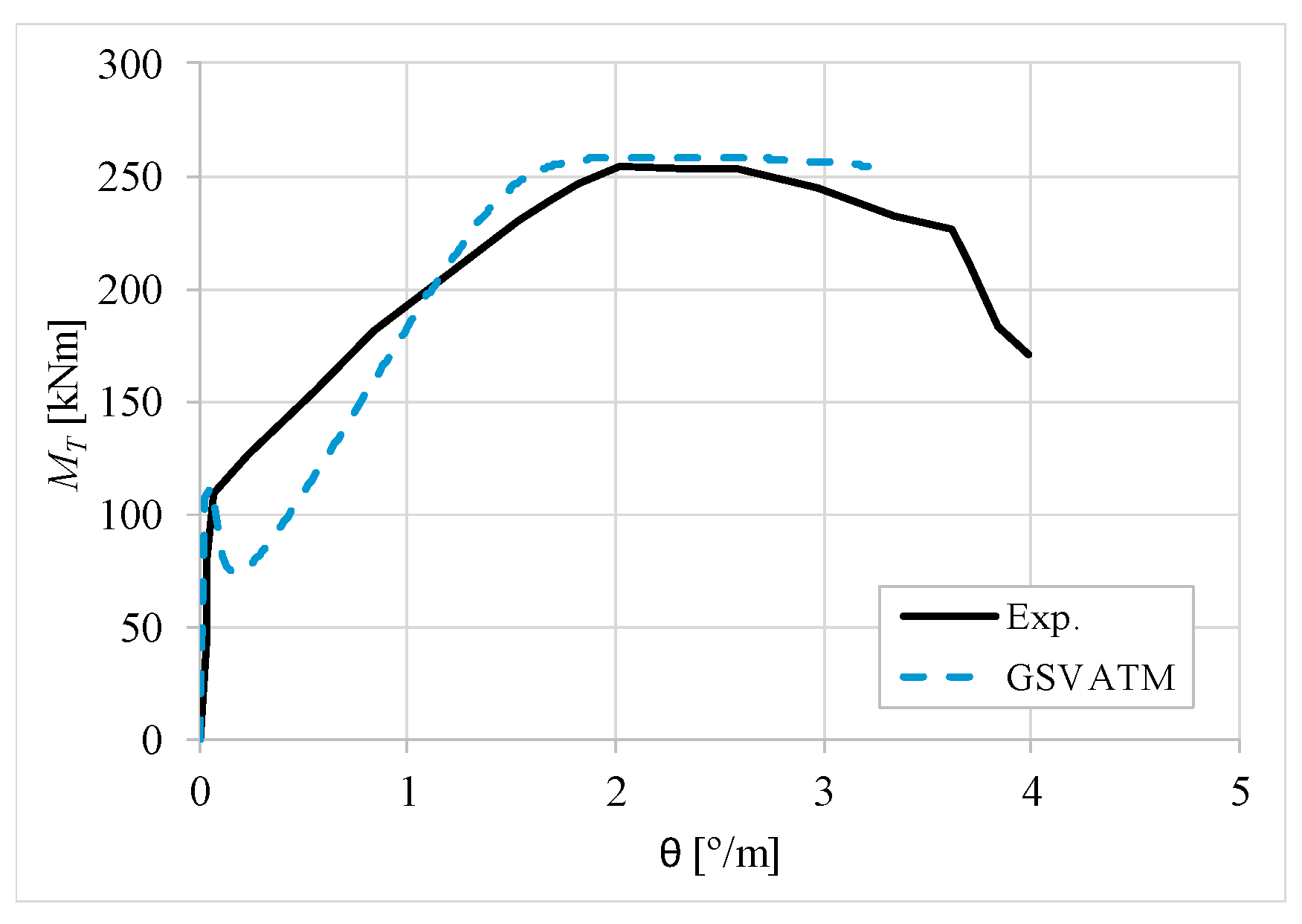
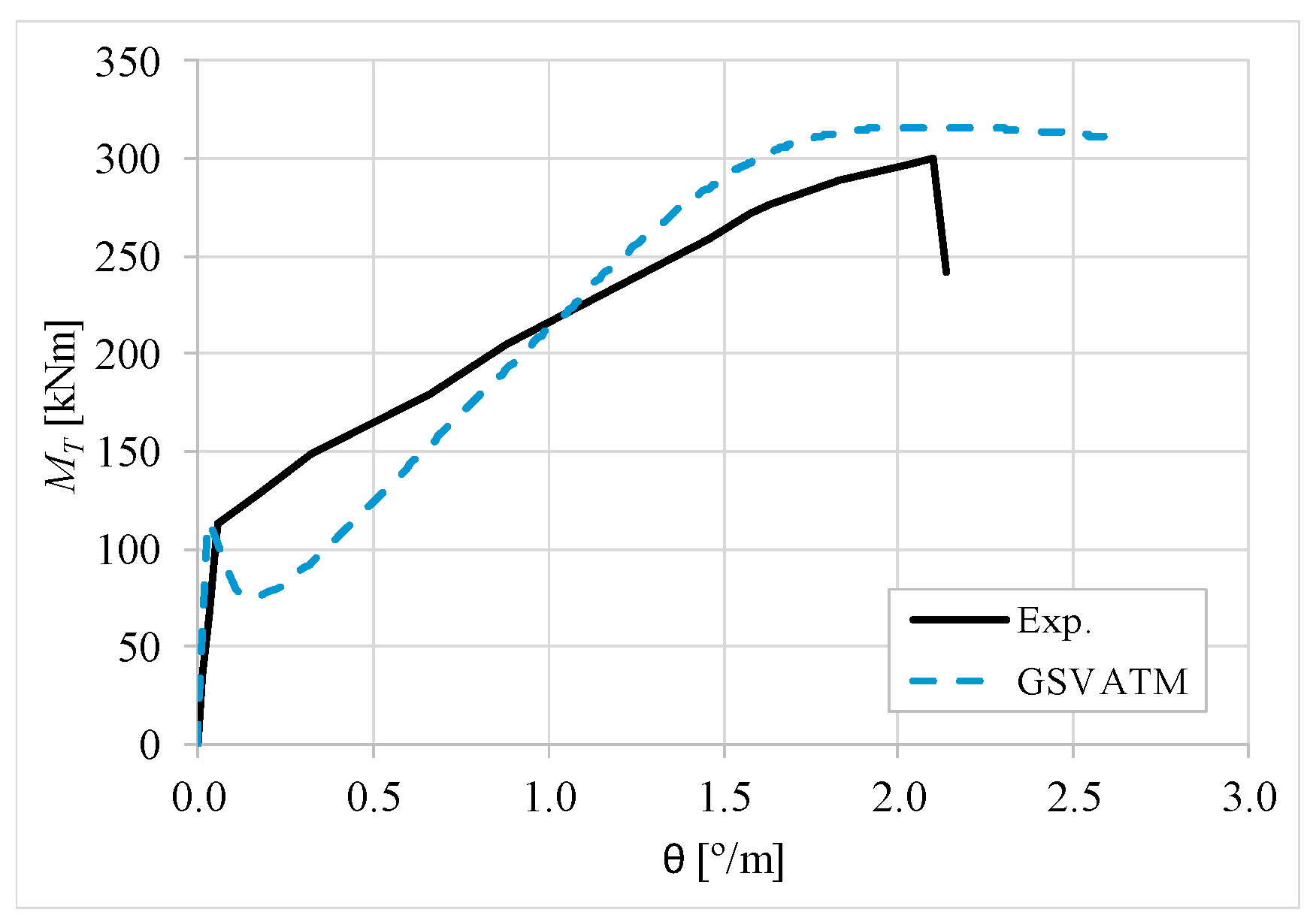
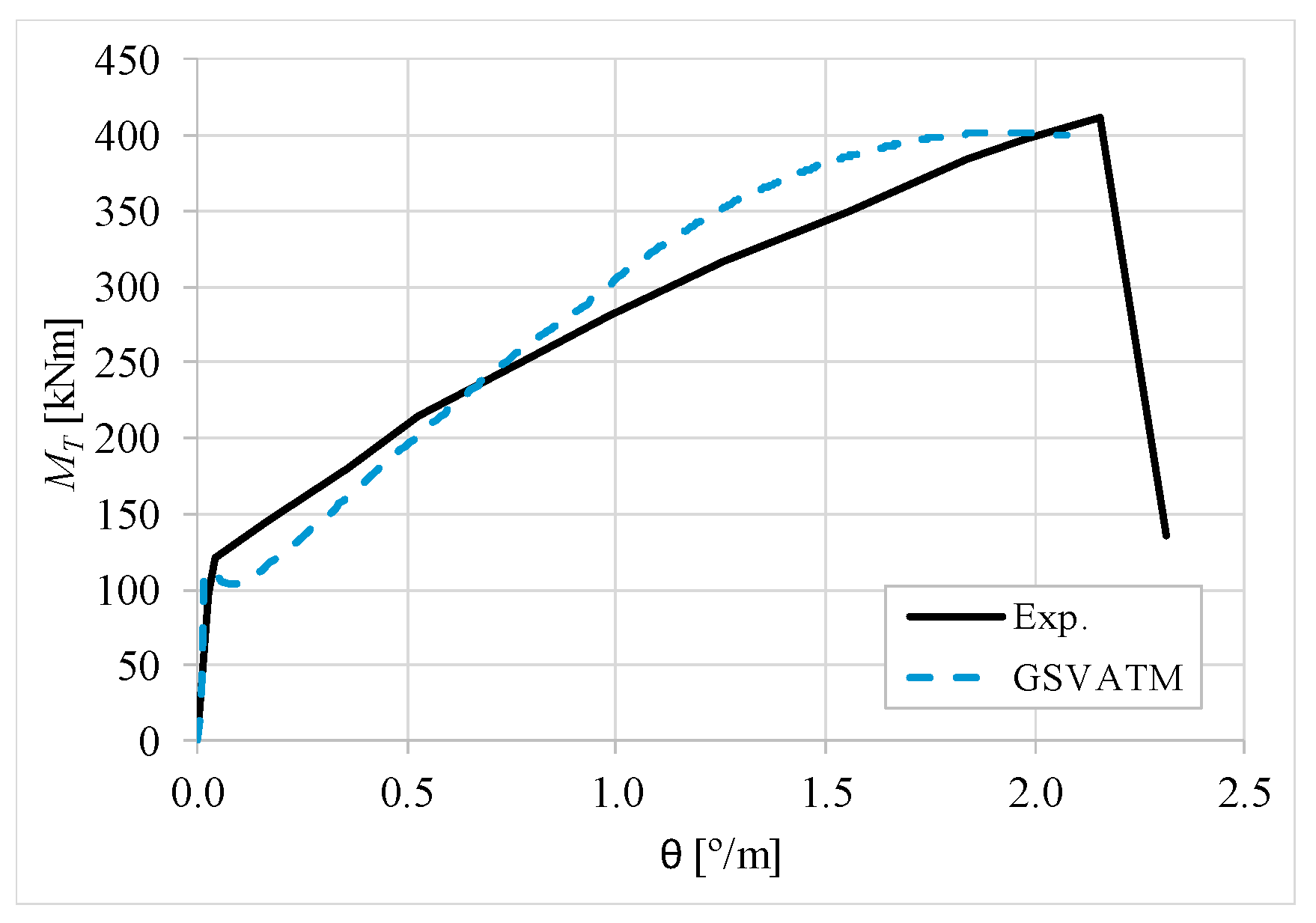
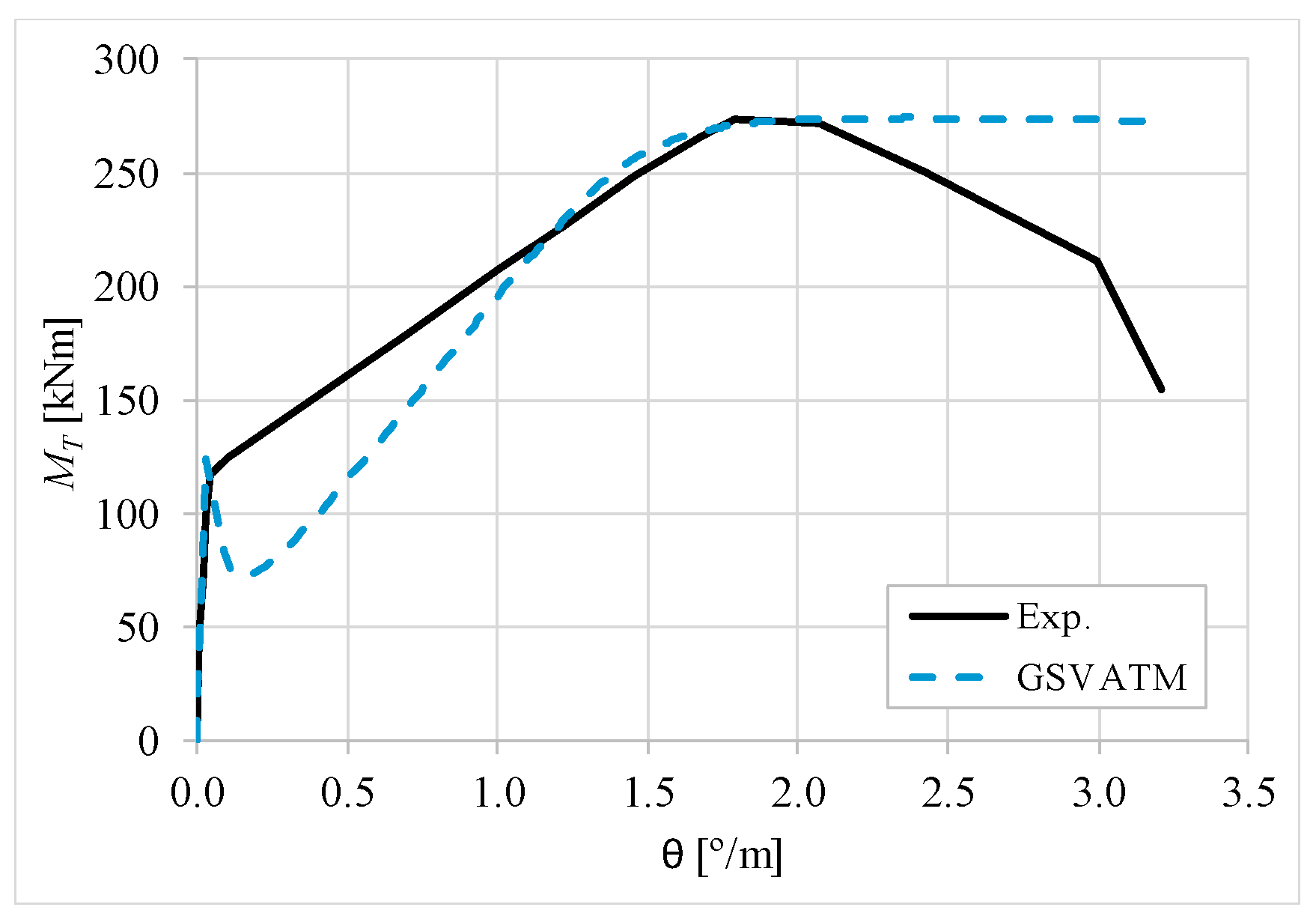
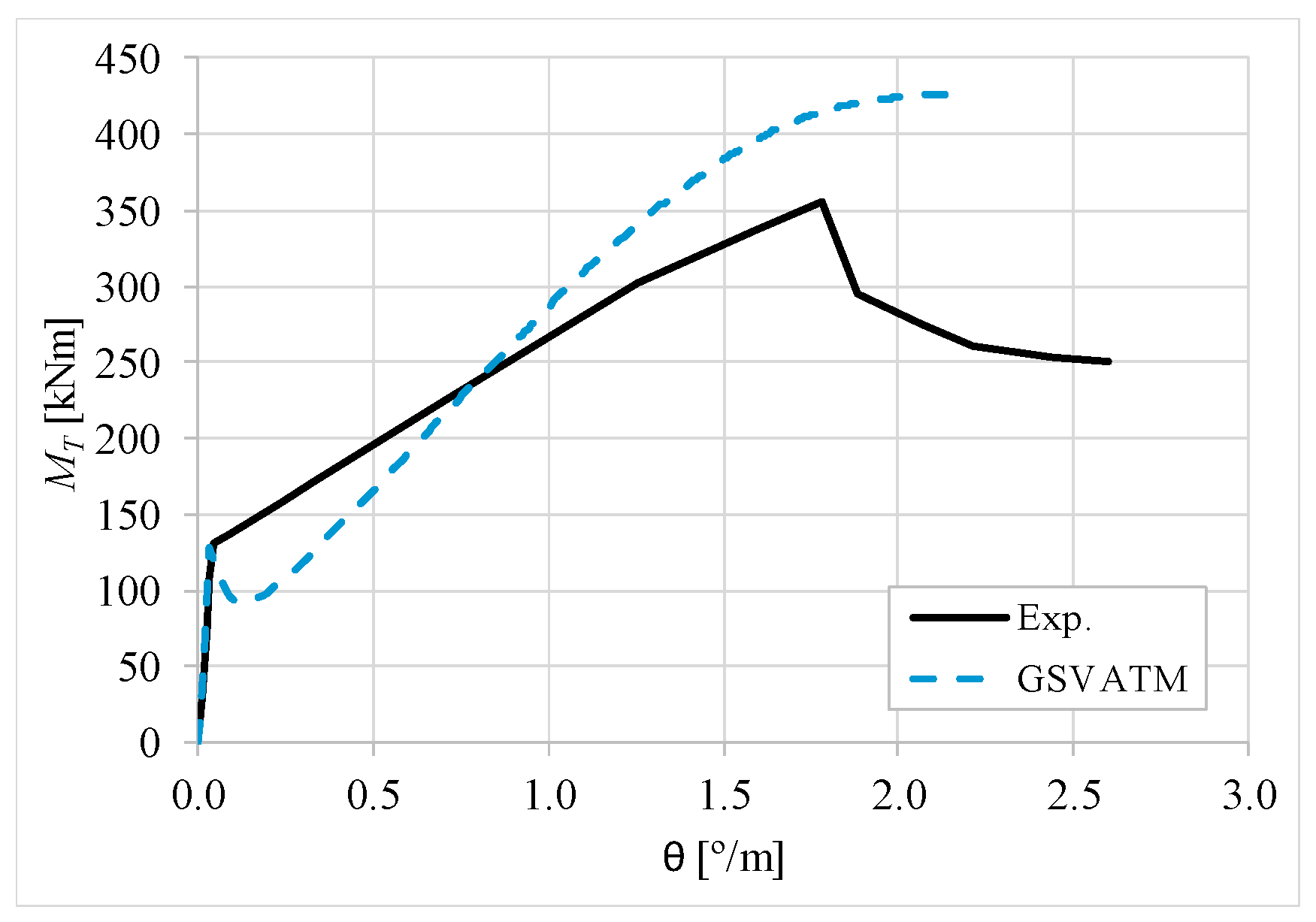
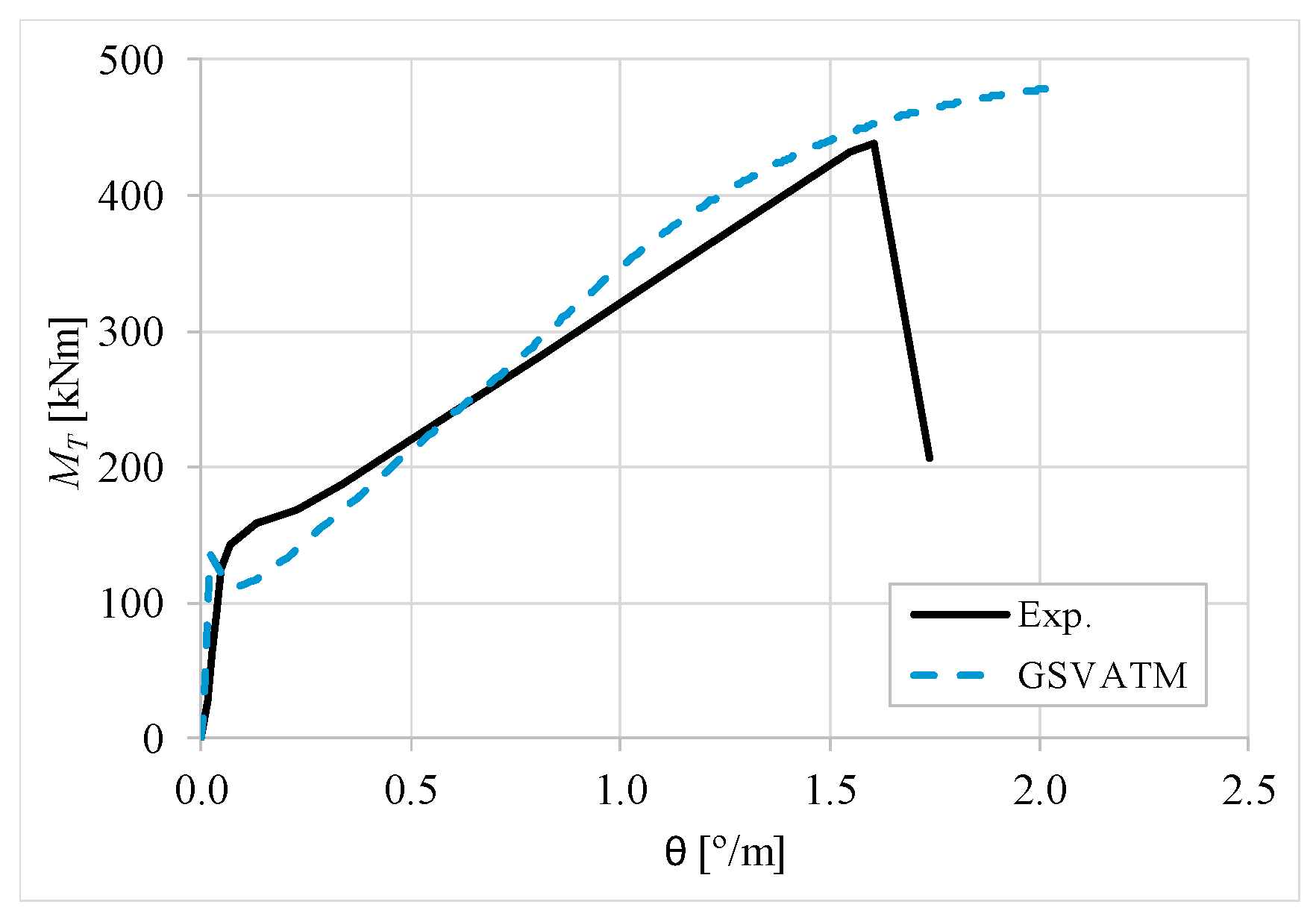
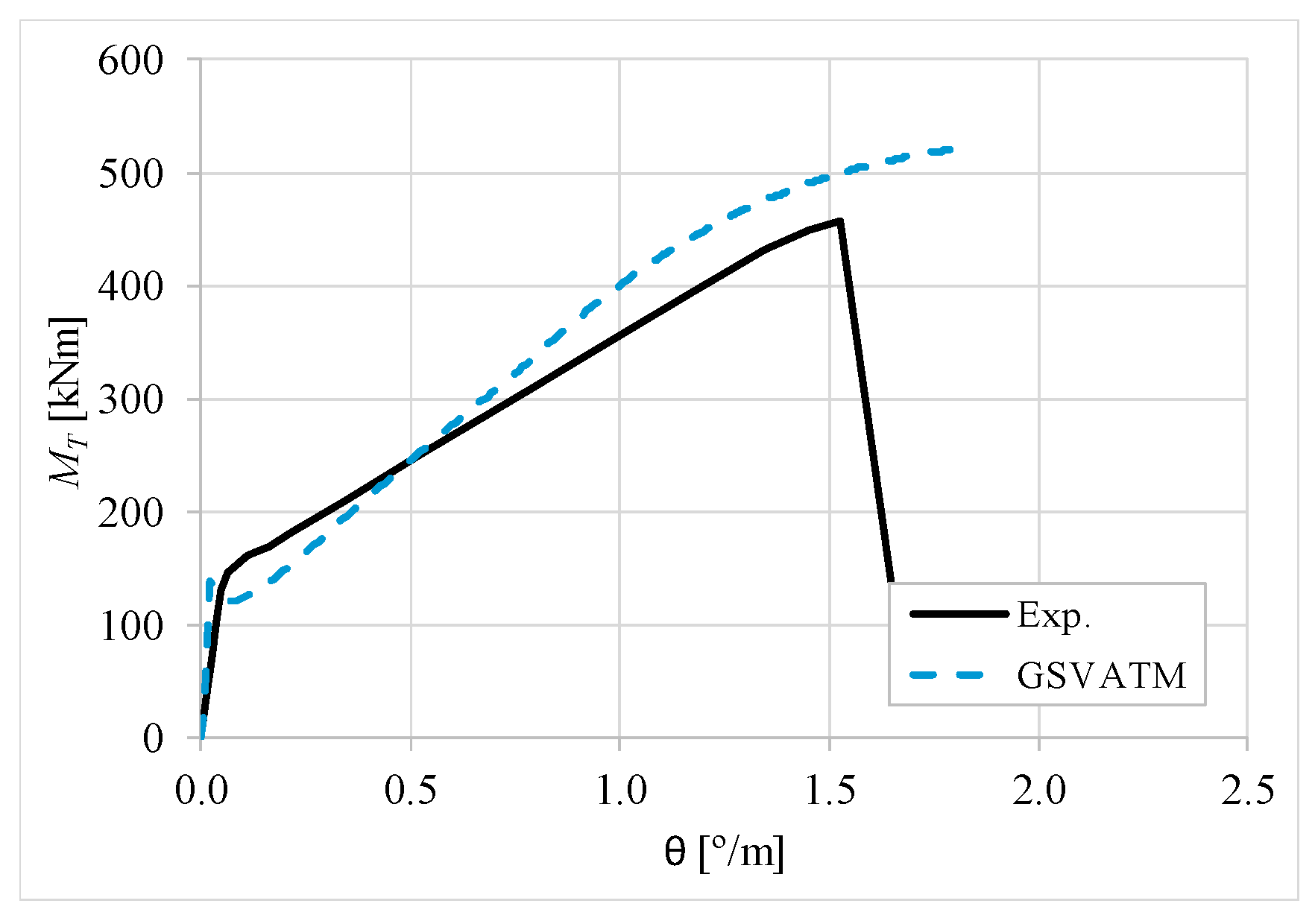
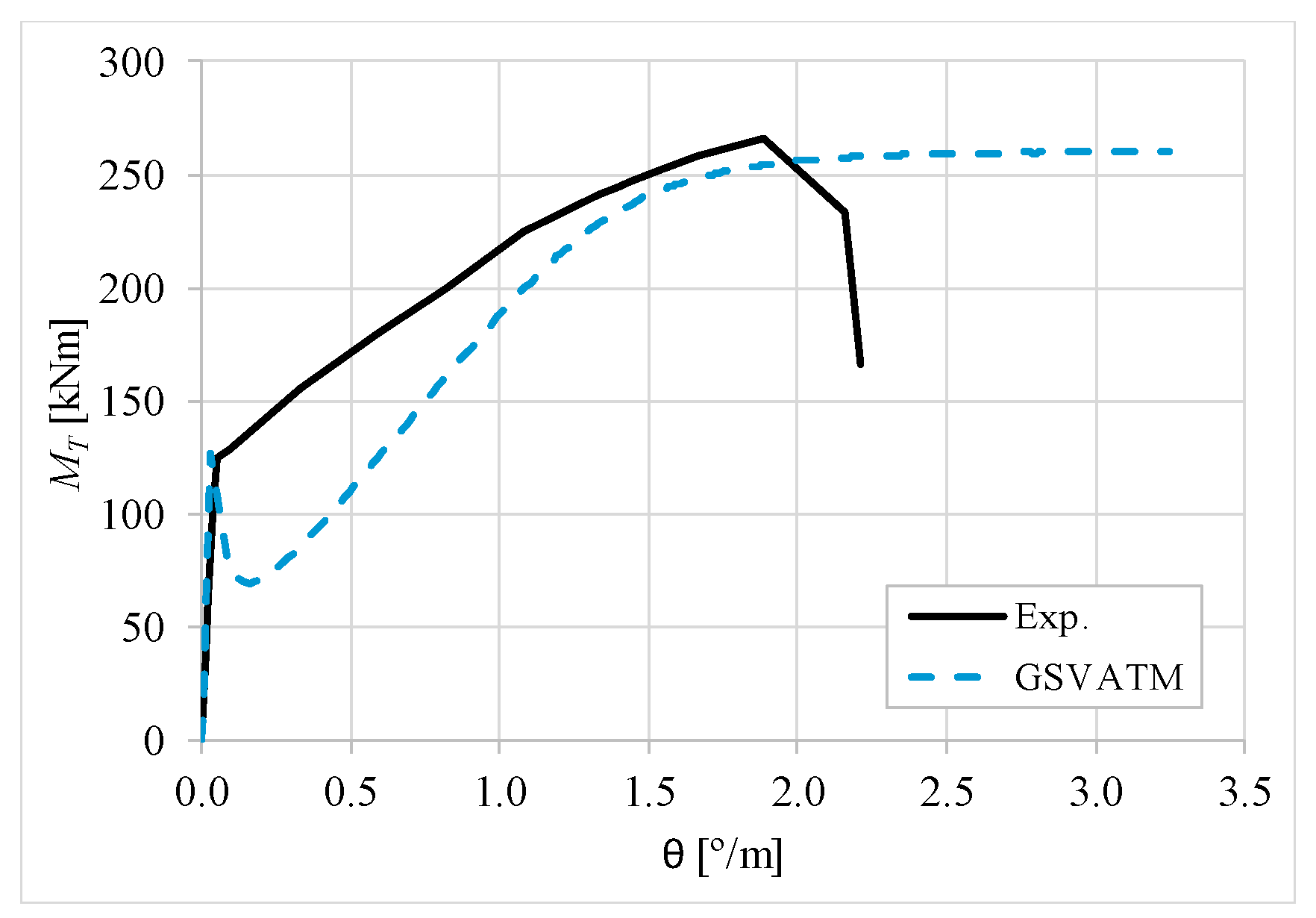
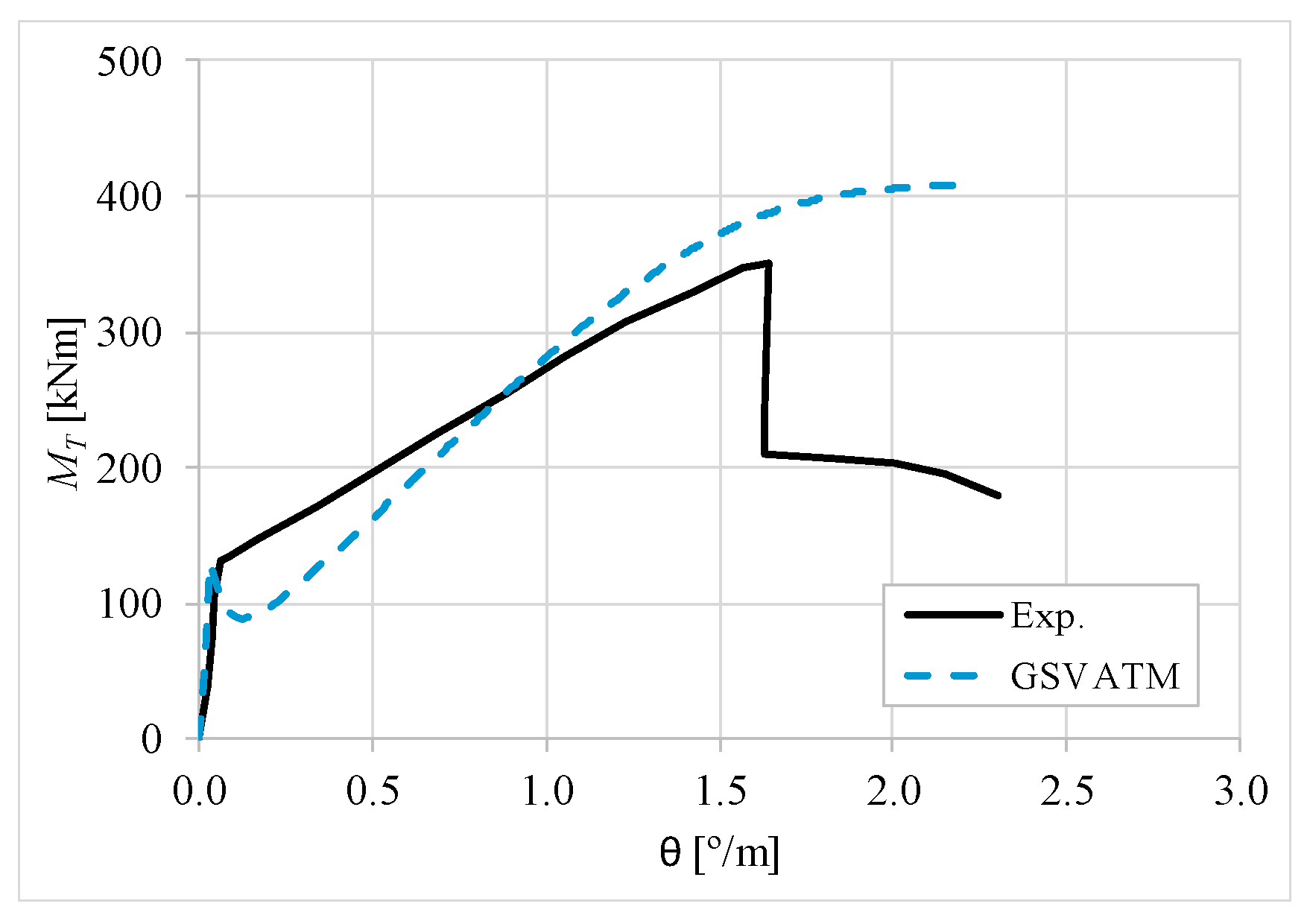
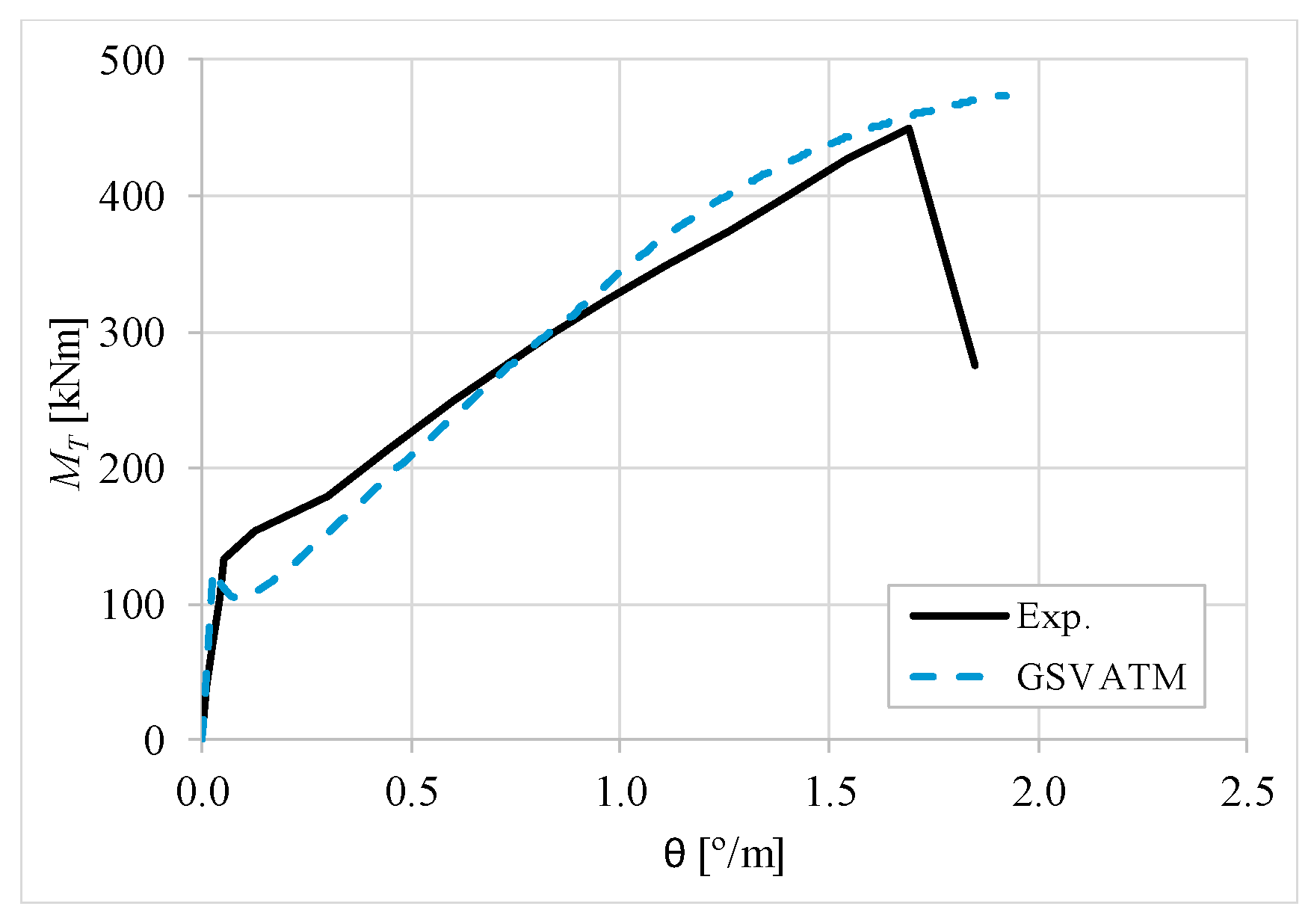
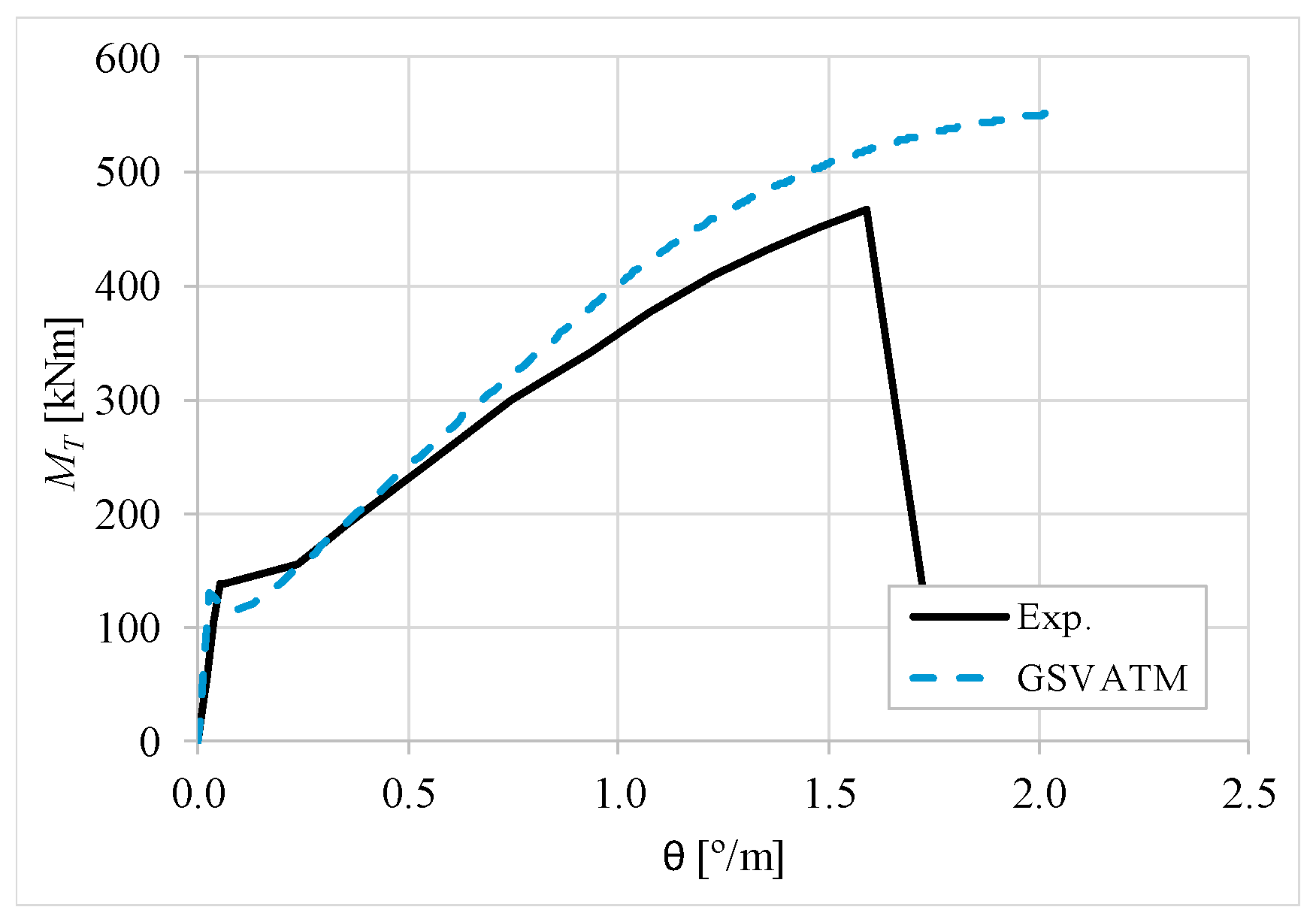
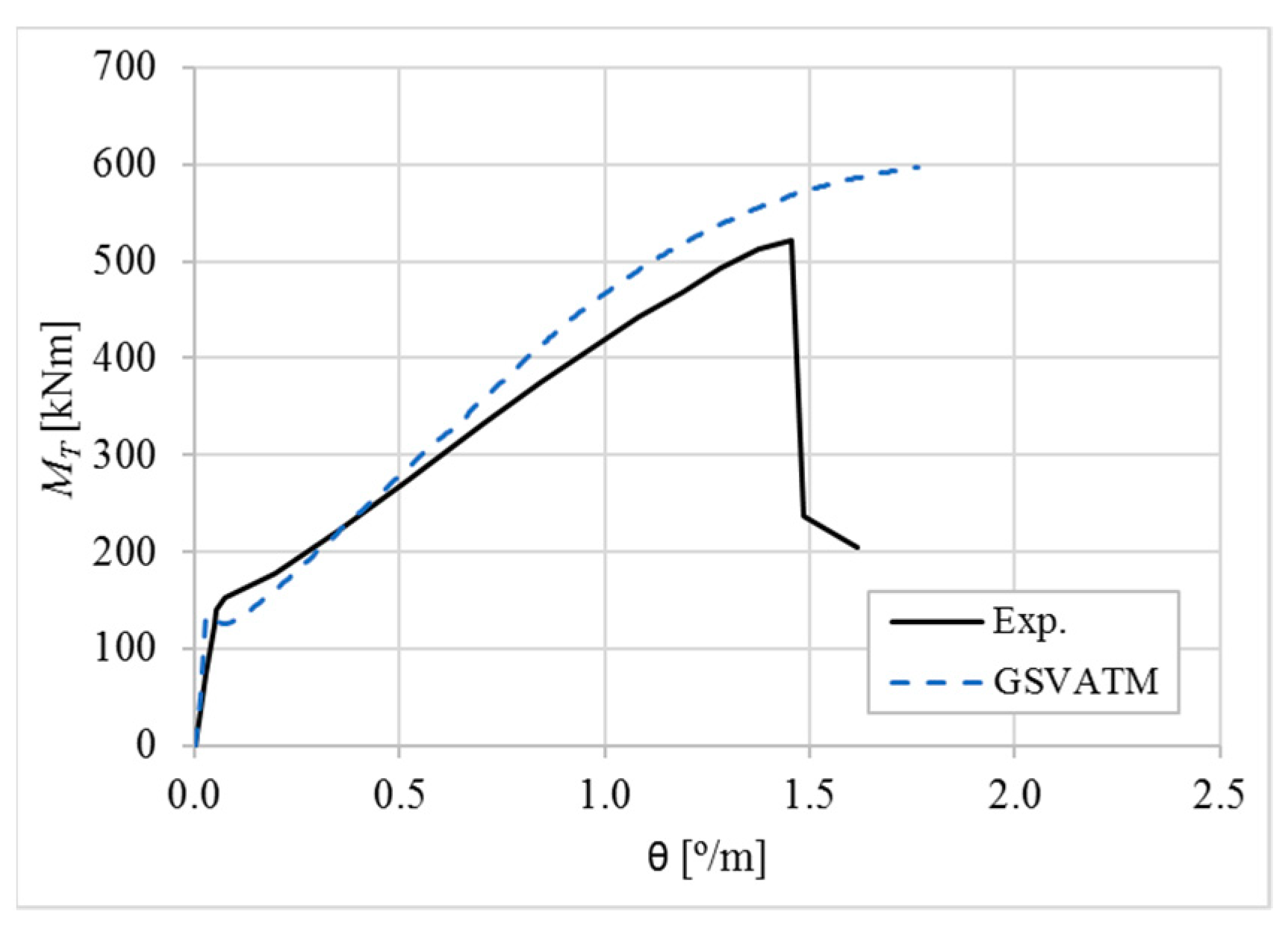
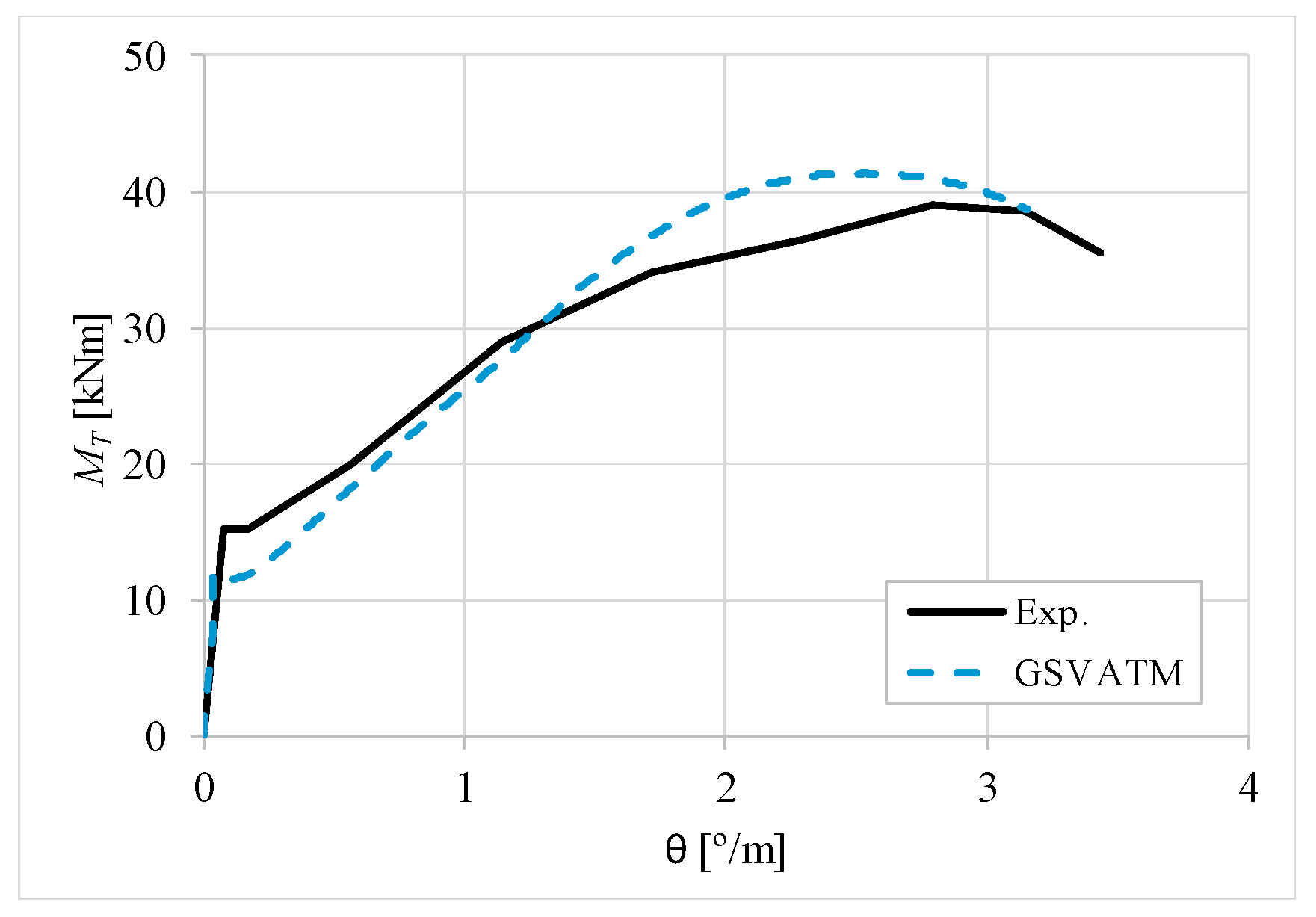
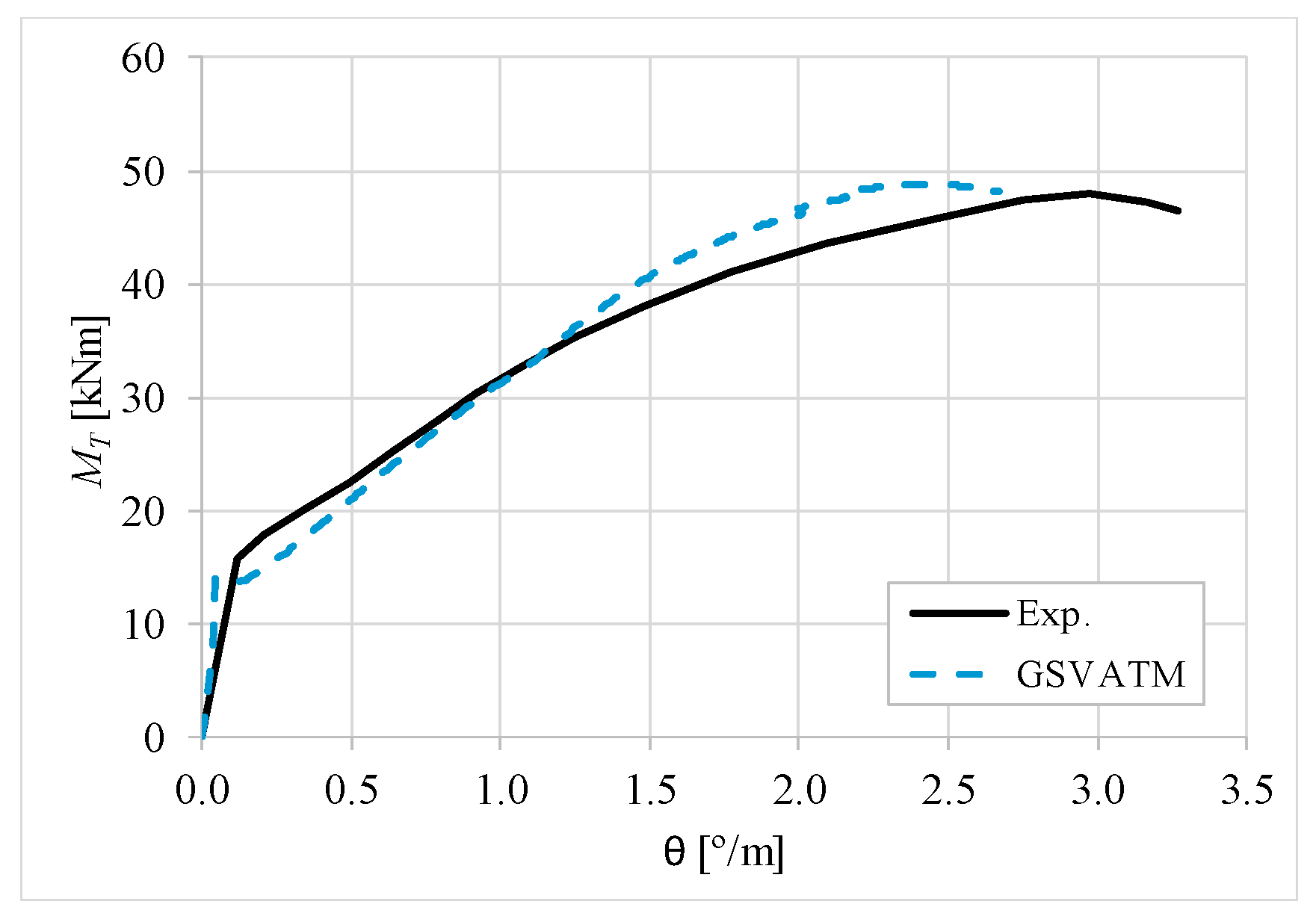
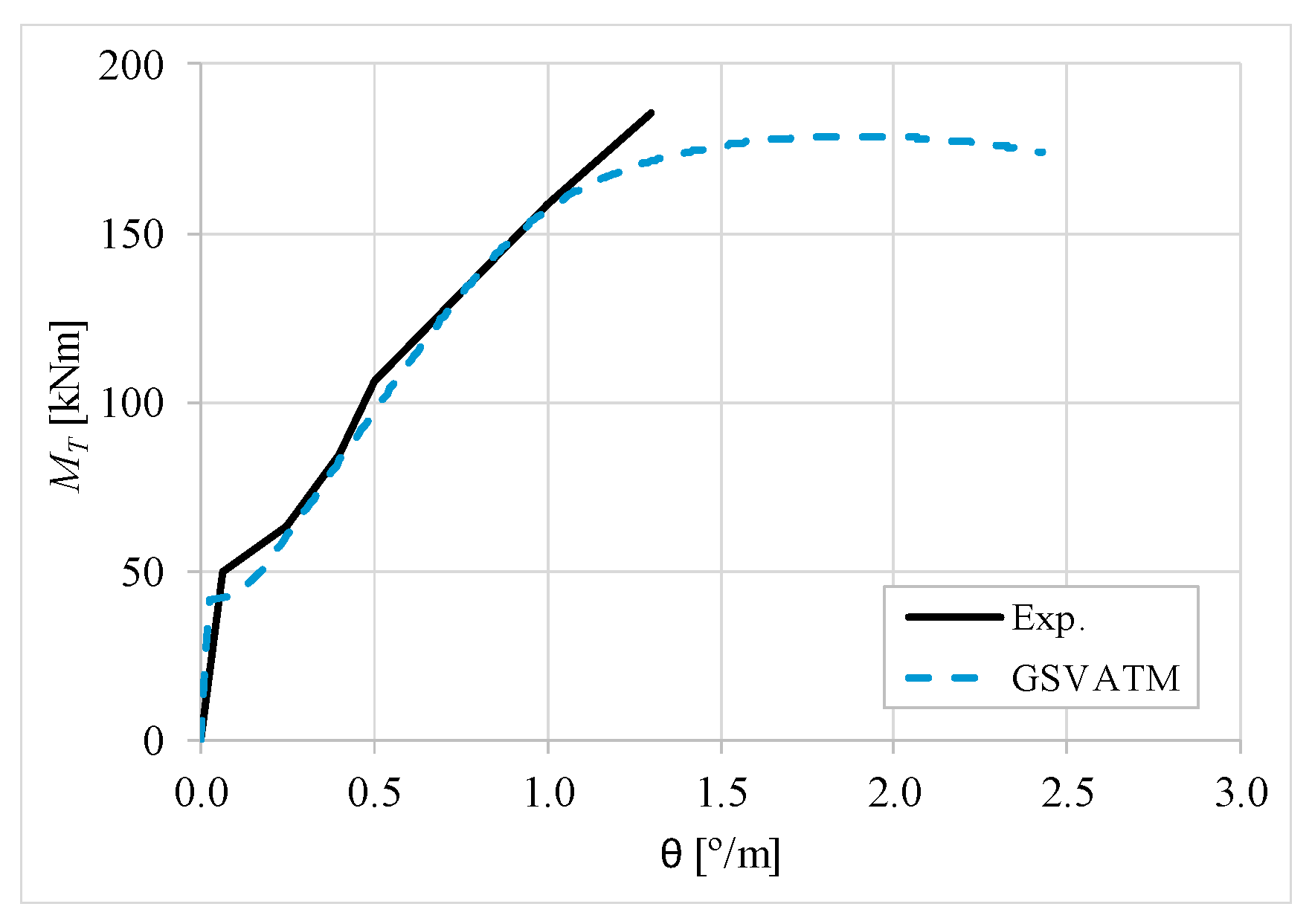
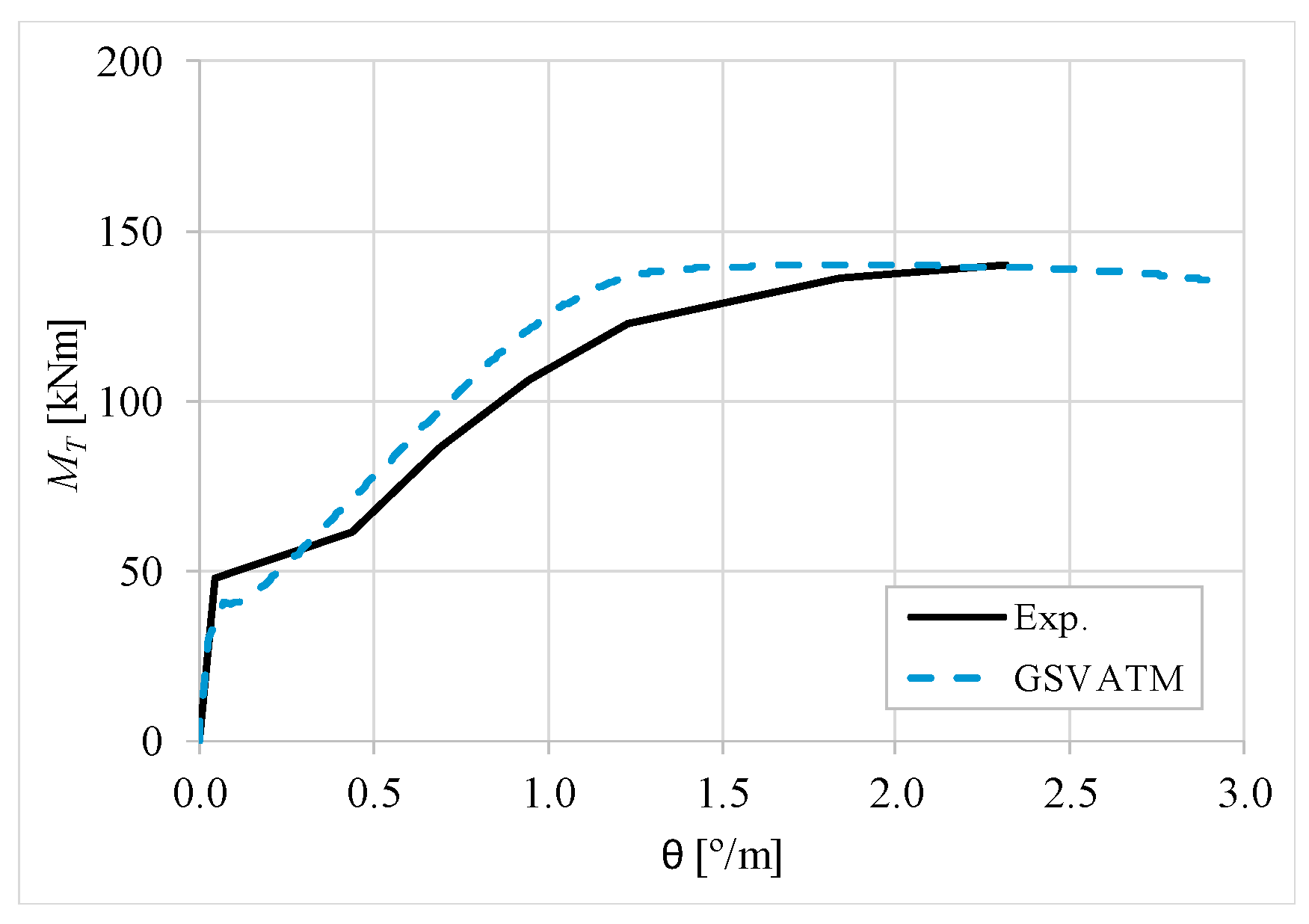
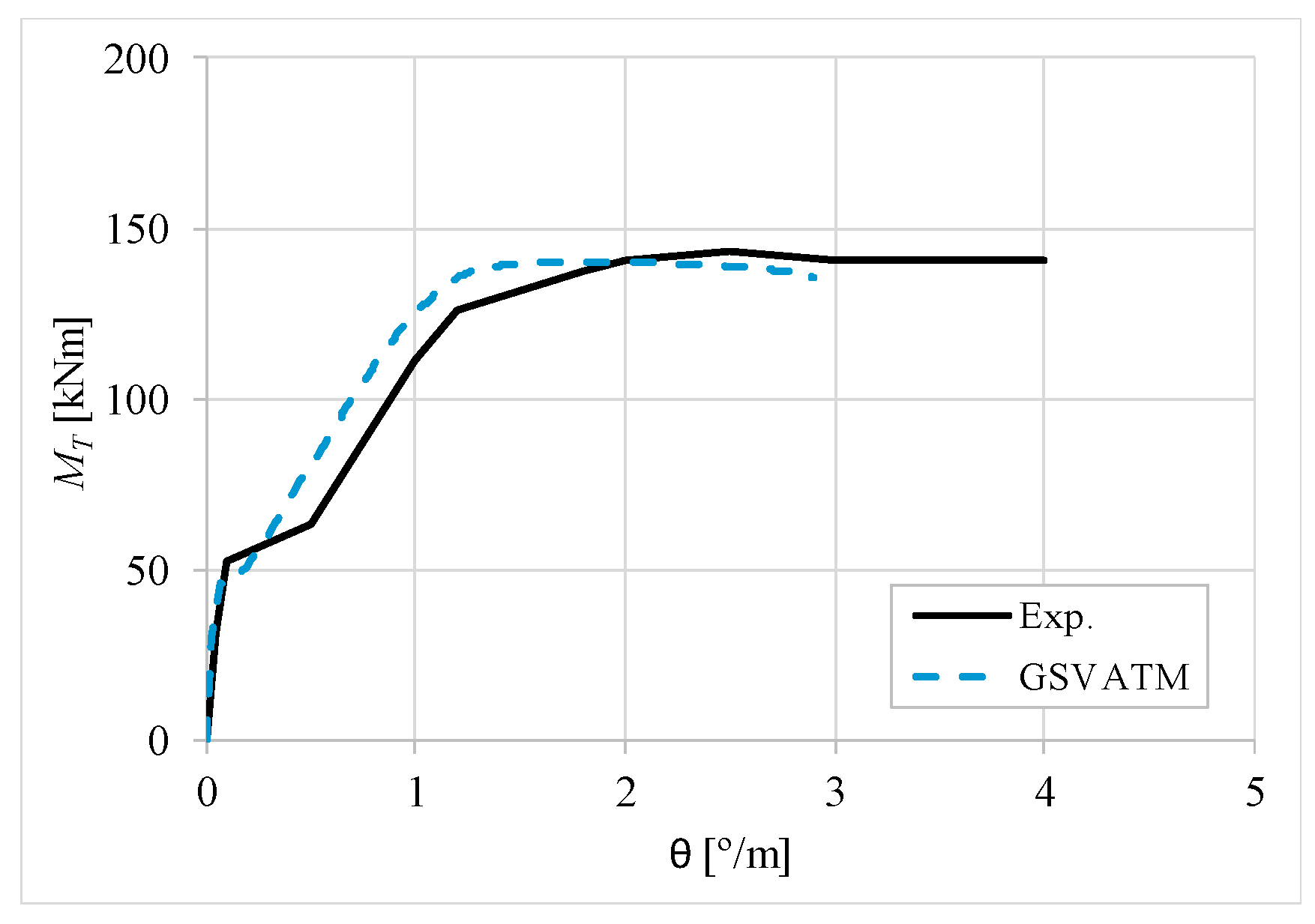
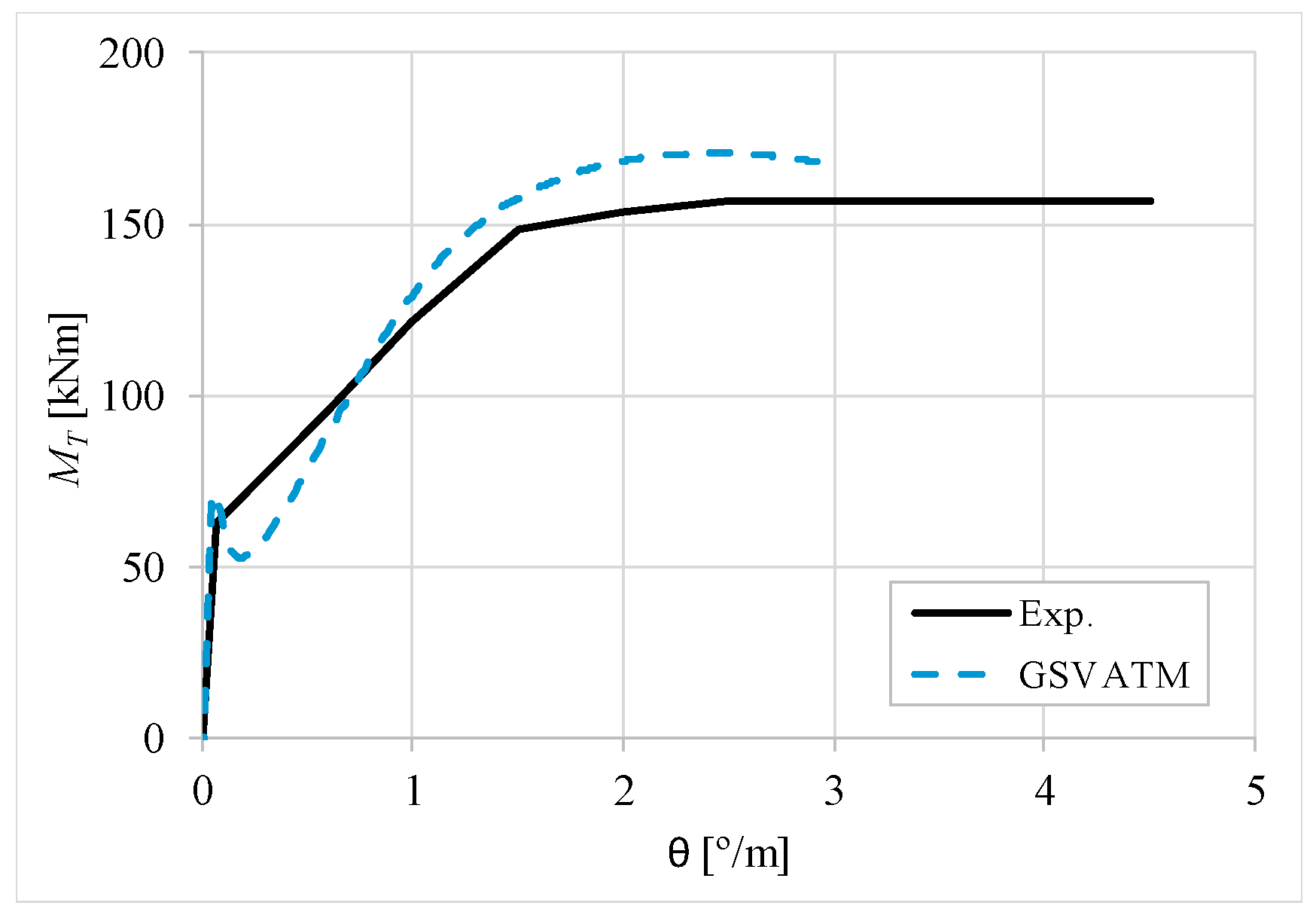
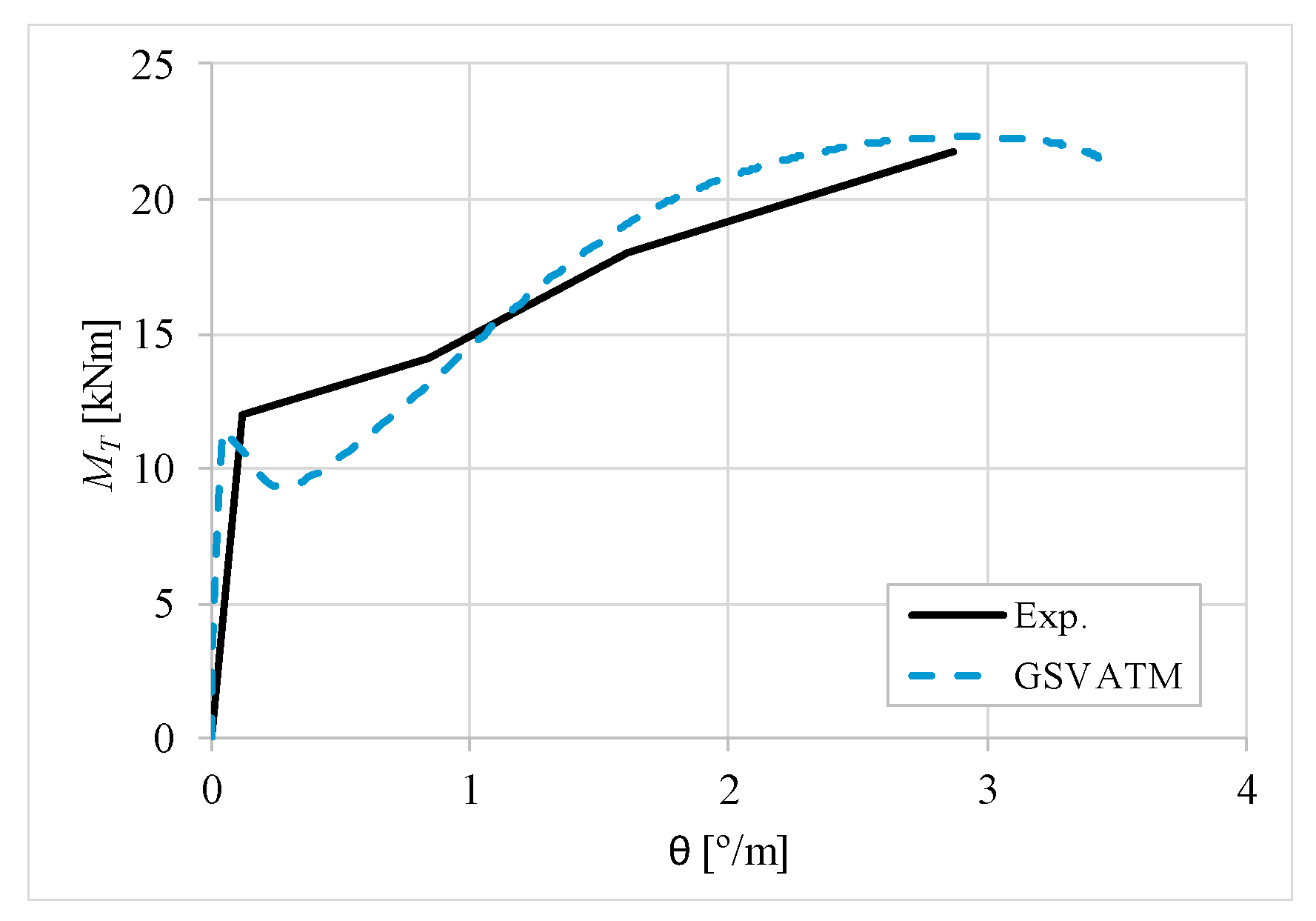
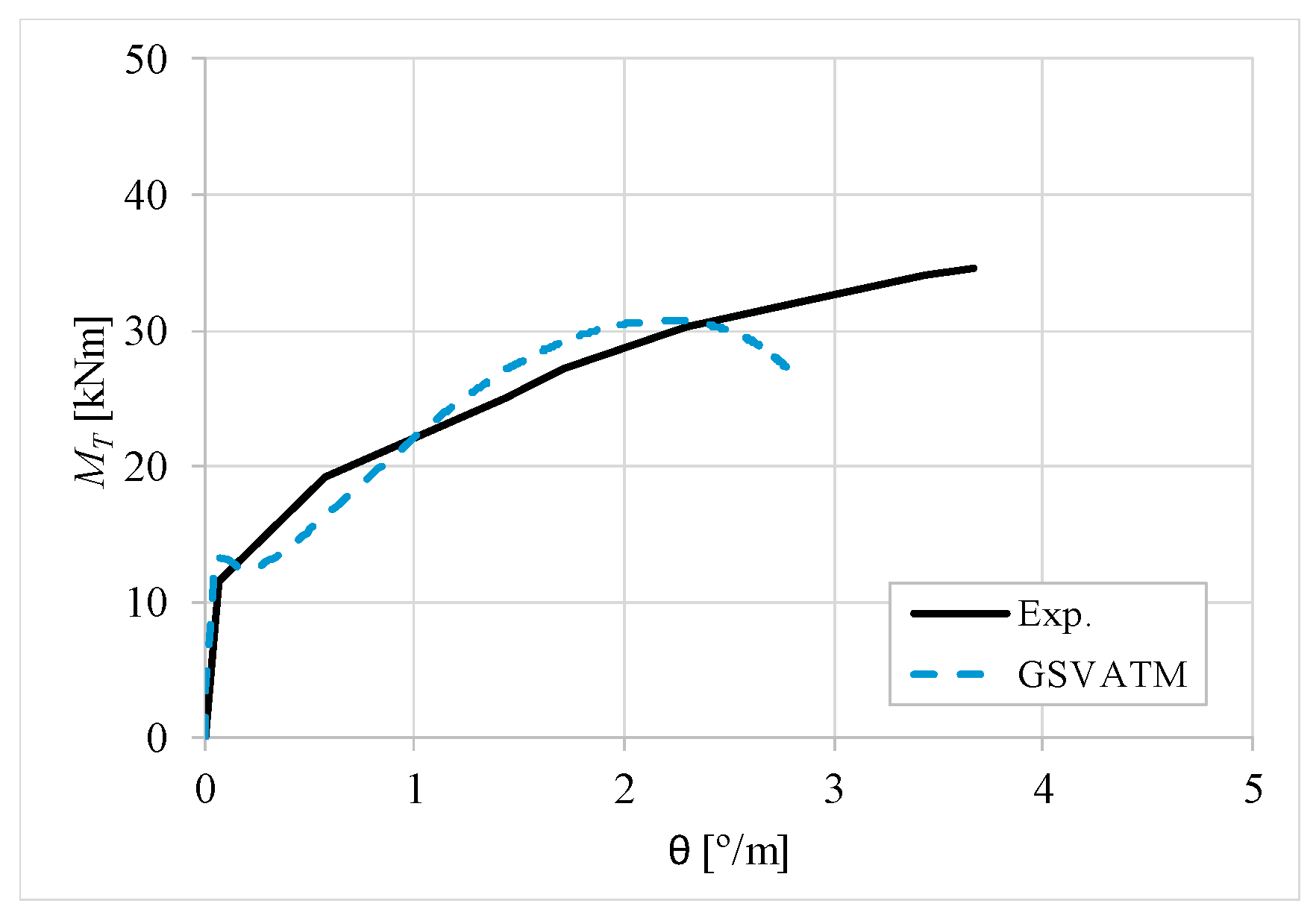
5. Comparative Analyzes
6. Conclusions
- It was found that the extended GSVATM captures well the full torsional response of RC hollow beams under torsion for all loading levels, although a drop of the torque right after the concrete cracking is predicted for most of the beams. This last observation is due to the shape of the smeared constitutive relationship used for the tensile concrete;
- Both the cracking and ultimate torque, which are important parameters for design, are very well predicted by the analytical model;
- The extended model still don´t predict very well the twists corresponding to the cracking and ultimate torque. However, since such parameters are not very important for the design, these results can be considered less important;
Funding
Acknowledgments
Conflicts of Interest
References
- Rausch, E. Design of Reinforced Concrete in Torsion. Ph.D. Thesis, Technische Hochschule, Berlin, Germany, 1929. [Google Scholar]
- Bernardo, L.F.A.; Andrade, J.M.A.; Nunes, N.C.G. Generalized softened variable angle truss-model for reinforcement concrete beams under torsion. Mater. Struct. 2015, 48, 2169–2193. [Google Scholar] [CrossRef]
- Hsu, T.T.C.; Mo, Y.L. Softening of concrete in torsional members–theory and tests. J. Am. Concr. Inst. 1985, 82, 290–303. [Google Scholar]
- Hsu, T.T.C.; Mo, Y.L. Softening of concrete in torsional members–prestressed concrete. J. Am. Concr. Inst. 1985, 82, 603–615. [Google Scholar]
- Bernardo, L.F.A.; Andrade, J.M.A.; Lopes, S.M.R. Softened truss model for reinforced NSC and HSC beams under torsion: a comparative study. Eng. Struct. 2012, 42, 278–296. [Google Scholar] [CrossRef]
- Bernardo, L.F.A.; Taborda, C.S.B.; Andrade, J.M.A. Generalized softened variable angle truss model for PC beams under torsion. Int. J. Concr. Struct. Mater. 2018. [Google Scholar] [CrossRef]
- Taborda, C.S.B.; Bernardo, L.F.A. GSVATM for RC beams under torsion combined with external axial forces. Comput. Concr. Int. J 2019. (In review) [Google Scholar]
- Jeng, C.H.; Hsu, T.T.C. A softened membrane model for torsion in reinforced concrete members. Eng. Struct. 2009, 31, 1944–1954. [Google Scholar] [CrossRef]
- Hsu, T.T.C. Torsion of Structural Concrete–Behaviour of Reinforced Concrete Rectangular Members. In Torsion of Structural Concrete; SP-18; American Concrete Institute: Detroit, MA, USA, 1968; pp. 261–306. [Google Scholar]
- Jeng, C.H.; Peng, X.; Wong, Y.L. Strain gradient effect in RC elements subjected to torsion. Mag. Concr. Res. 2011, 63, 343–356. [Google Scholar] [CrossRef]
- Jeng, C.H.; Chiu, H.J.; Peng, S.F. Design formulas for cracking torque and twist in hollow reinforced concrete members. ACI. Struct. J. 2013, 110, 457–468. [Google Scholar]
- Bernardo, L.F.A.; Andrade, J.M.A.; Oliveira, L.A.P. Reinforced and prestressed concrete hollow beams under torsion. J. Civ. Eng. Manag. 2013, 19, 141–152. [Google Scholar] [CrossRef]
- Teixeira, M.M.; Bernardo, L.F.A. Ductility of RC beams under torsion. Eng. Struct. 2018, 168, 759–769. [Google Scholar] [CrossRef]
- Jeng, C.H. Unified softened membrane model for torsion in hollow and solid reinforced concrete members - modeling the entire pre- and post- cracking behavior. J. Struct. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Belarbi, A.; Hsu, T.T.C. Constitutive laws of softened concrete in biaxial tension-compression. Struct. J. Am. Concr. Inst. 1995, 92, 562–573. [Google Scholar]
- Zhang, L.X.; Hsu, T.C. Behaviour and analysis of 100 MPa concrete membrane elements. J. Struct. Eng. 1998, 124, 24–34. [Google Scholar] [CrossRef]
- Belarbi, A.; Hsu, T.T.C. Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete. Struct. J. Am. Concr. Inst. 1994, 91, 465–474. [Google Scholar]
- Hsu, T.T.C.; Zhu, R.R.H. Softened membrane model for reinforced concrete elements in shear. ACI. Struct. J. 2002, 99, 460–469. [Google Scholar]
- Jeng, C.H. Simple rational formulas for cracking torque and twist of reinforced concrete members. ACI. Struct. J. 2010, 107, 189–198. [Google Scholar]
- Jeng, C.H. Softened membrane model for torsion in reinforced concrete members. Adv. Eng. Res 2012, 2, 251–338. [Google Scholar] [CrossRef]
- Vaz, A. Extension of the GSVATM to reinforced concrete hollow beams under torsion. Master Thesis, Department of Civil Engineering and Architecture, University of Beira Interior, Covilhã, Portugal, 2014. (In Portuguese). [Google Scholar]
- Bernardo, L.F.A.; Lopes, S.M.R. Torsion in HSC hollow beams: Strength and ductility analysis. ACI Struct. J 2009, 106, 39–48. [Google Scholar]
- Lampert, P.; Thurlimann, B. Torsionsversuche an Stanhlbetobalken (Torsion Tests of Reinforced Concrete Beams); Institute fur Baustatik, ETH: Zurich, Switzerland, 1969; Bericht, No. 6506-2. [Google Scholar]
- Leonhardt, F.; Schelling, G. Torsionsversuche an Stahlbetonbalken (Torsion Tests of Reinforced Concrete Beams); Deutcher Ausschuss fur Stahlbeton: Berlin, Germany, 1974; vol. Bulletin No. 239, p. 122. [Google Scholar]
- NP EN 1992-1-1. Eurocode 2: Design of Concrete Structures—Part 1: General Rules and Rules for Buildings; European Committee for Standardization—CEN: Brussels, Belgium, 2010. [Google Scholar]
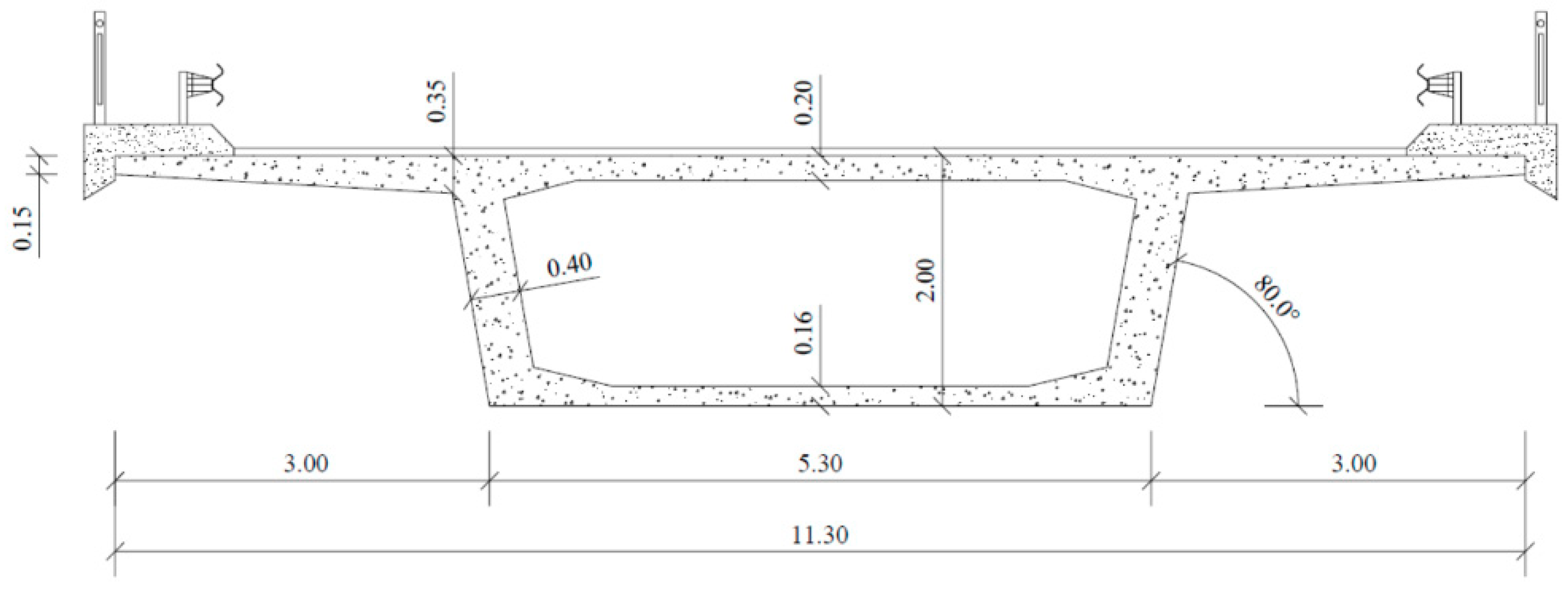


| Beam | t cm | x cm | y cm | x1 cm | y1 cm | Asl cm2 | Ast/s cm2/m | ρl % | ρt % | fly MPa | fty MPa | fc MPa |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A095c [14] | 14.5 | 49.7 | 71.1 | 43.7 | 65.1 | 13.16 | 9.93 | 0.372 | 0.611 | 371 | 381 | 35.1 |
| A120a [14] | 18.4 | 50.2 | 71.9 | 44.2 | 65.9 | 20.00 | 7.59 | 0.554 | 0.463 | 464 | 380 | 27.6 |
| B065b [14] | 9.2 | 50.3 | 71.0 | 44.3 | 65.0 | 50.97 | 9.93 | 1.427 | 0.608 | 452 | 380 | 39.2 |
| B080a [14] | 11.2 | 50.0 | 72.1 | 44.0 | 66.1 | 28.39 | 12.90 | 0.787 | 0.788 | 454 | 392 | 46.5 |
| B110a [14] | 15.5 | 49.8 | 71.0 | 43.8 | 65.0 | 20.00 | 8.60 | 0.566 | 0.529 | 453 | 369 | 48.1 |
| C065a [14] | 8.5 | 49.5 | 78.1 | 43.5 | 72.1 | 20.00 | 9.93 | 0.517 | 0.594 | 338 | 376 | 78.8 |
| C100a [14] | 12.7 | 49.9 | 72.3 | 43.9 | 66.3 | 28.39 | 12.90 | 0.787 | 0.788 | 466 | 447 | 90.6 |
| D075a [14] | 8.7 | 49.8 | 73.4 | 43.8 | 67.4 | 28.39 | 12.90 | 0.777 | 0.785 | 469 | 381 | 94.9 |
| D090a [14] | 10.5 | 50.1 | 72.2 | 44.1 | 66.2 | 28.39 | 12.90 | 0.785 | 0.787 | 466 | 447 | 105.7 |
| A2 [22] | 10.7 | 60.0 | 60.0 | 53.8 | 53.1 | 13.95 | 6.28 | 0.387 | 0.373 | 672 | 696 | 47.3 |
| A3 [22] | 10.9 | 60.0 | 60.0 | 54.0 | 53.5 | 18.10 | 8.27 | 0.503 | 0.494 | 672 | 715 | 46.2 |
| A4 [22] | 10.4 | 60.0 | 60.0 | 52.0 | 52.5 | 23.75 | 11.22 | 0.660 | 0.651 | 724 | 715 | 54.8 |
| A5 [22] | 10.4 | 60.0 | 60.0 | 52.8 | 52.8 | 30.66 | 14.14 | 0.852 | 0.829 | 724 | 672 | 53.1 |
| B2 [22] | 10.8 | 60.0 | 60.0 | 53.3 | 53.4 | 14.58 | 6.70 | 0.405 | 0.397 | 672 | 696 | 69.8 |
| B3 [22] | 10.9 | 60.0 | 60.0 | 53.5 | 53.7 | 23.75 | 11.22 | 0.660 | 0.668 | 724 | 715 | 77.8 |
| B4 [22] | 11.2 | 60.0 | 60.0 | 52.3 | 53.6 | 32.17 | 15.08 | 0.894 | 0.886 | 724 | 672 | 79.8 |
| B5 [22] | 11.7 | 60.0 | 60.0 | 51.8 | 51.8 | 40.21 | 18.85 | 1.117 | 1.085 | 724 | 672 | 76.4 |
| C2 [22] | 10.0 | 60.0 | 60.0 | 53.2 | 53.3 | 13.95 | 6.28 | 0.387 | 0.372 | 672 | 696 | 94.8 |
| C3 [22] | 10.3 | 60.0 | 60.0 | 54.5 | 54.0 | 23.75 | 10.47 | 0.660 | 0.631 | 724 | 715 | 91.6 |
| C4 [22] | 10.3 | 60.0 | 60.0 | 54.6 | 54.5 | 30.66 | 14.14 | 0.852 | 0.857 | 724 | 672 | 91.4 |
| C5 [22] | 10.4 | 60.0 | 60.0 | 54.0 | 54.3 | 36.69 | 17.40 | 1.019 | 1.047 | 724 | 672 | 96.7 |
| C6 [22] | 10.4 | 60.0 | 60.0 | 53.3 | 52.9 | 48.25 | 22.62 | 1.340 | 1.335 | 724 | 672 | 87.5 |
| D3 [9] | 6.4 | 25.4 | 38.1 | 21.6 | 34.3 | 11.36 | 10.16 | 1.173 | 1.173 | 341 | 333 | 28.4 |
| D4 [9] | 6.4 | 25.4 | 38.1 | 21.6 | 34.3 | 15.48 | 14.01 | 1.600 | 1.618 | 330 | 333 | 30.6 |
| T0 [23] | 8.0 | 50.0 | 50.0 | 43.0 | 43.0 | 32.16 | 10.28 | 1.286 | 0.707 | 345 | 357 | 45.1 |
| T1 [23] | 8.0 | 50.0 | 50.0 | 45.4 | 45.4 | 18.10 | 10.28 | 0.724 | 0.747 | 357 | 357 | 35.3 |
| T2 [23] | 8.0 | 50.0 | 50.0 | 43.0 | 43.0 | 18.10 | 10.28 | 0.724 | 0.707 | 357 | 357 | 35.3 |
| T5 [23] | 8.0 | 80.0 | 40.0 | 73.0 | 33.0 | 10.00 | 10.28 | 0.313 | 0.681 | 529 | 513 | 47.1 |
| VH1 [24] | 8.0 | 32.4 | 32.4 | 30.4 | 30.4 | 3.46 | 2.88 | 0.329 | 0.334 | 447 | 447 | 17.2 |
| VH2 [24] | 8.0 | 32.4 | 32.4 | 30.4 | 30.4 | 6.91 | 5.76 | 0.658 | 0.667 | 447 | 447 | 17.2 |
| Beam | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A095c [14] | 102.88 | 101.6 | 1.013 | 0.034 | 0.042 | 0.810 | 209.98 | 197.49 | 1.063 | 1.714 | 2.205 | 0.777 |
| A120a [14] | 89.78 | 88.38 | 1.016 | 0.048 | 0.042 | 1.143 | 215.25 | 196.61 | 1.095 | 2.1 | 1.674 | 1.254 |
| B065b [14] | 54.43 | 52.66 | 1.034 | 0.034 | 0.02 | 1.700 | 265 | 242.84 | 1.091 | 1.203 | 1.397 | 0.861 |
| B080a [14] | 65.24 | 63.97 | 1.020 | 0.033 | 0.045 | 0.733 | 300.66 | 295.9 | 1.016 | 1.756 | 1.611 | 1.090 |
| B110a [14] | 128.3 | 129.52 | 0.991 | 0.041 | 0.045 | 0.911 | 237.48 | 218.06 | 1.089 | 1.723 | 3.016 | 0.571 |
| C065a [14] | 91.68 | 96.32 | 0.952 | 0.029 | 0.033 | 0.879 | - | 217.81 | - | - | 3.527 | - |
| C100a [14] | 122.23 | 122.71 | 0.996 | 0.029 | 0.036 | 0.806 | 370.15 | 338.76 | 1.093 | 1.927 | 2.323 | 0.830 |
| D075a [14] | 90.09 | 103.95 | 0.867 | 0.028 | 0.082 | 0.341 | 339.48 | 319.11 | 1.064 | 1.815 | 2.364 | 0.768 |
| D090a [14] | 96.05 | 103.56 | 0.927 | 0.029 | 0.027 | 1.074 | 343.08 | 346.61 | 0.990 | 1.734 | 2.597 | 0.668 |
| A2 [22] | 109.49 | 112.02 | 0.977 | 0.064 | 0.053 | 1.208 | 254.08 | 258.7 | 0.982 | 2.019 | 2.178 | 0.927 |
| A3 [22] | 113.27 | 114.58 | 0.989 | 0.057 | 0.031 | 1.839 | 299.91 | 316.37 | 0.948 | 2.101 | 2.075 | 1.013 |
| A4 [22] | 120.87 | 114.29 | 1.058 | 0.063 | 0.048 | 1.313 | 368.22 | 369.96 | 0.995 | 2.295 | 2.196 | 1.045 |
| A5 [22] | 120.93 | 110.65 | 1.093 | 0.044 | 0.018 | 2.444 | 412.24 | 402.28 | 1.025 | 2.154 | 1.939 | 1.111 |
| B2 [22] | 116.72 | 124 | 0.941 | 0.044 | 0.032 | 1.375 | 273.27 | 274.07 | 0.997 | 1.787 | 2.39 | 0.748 |
| B3 [22] | 130.45 | 127.5 | 1.023 | 0.045 | 0.032 | 1.406 | - | 426.63 | - | - | 2.195 | - |
| B4 [22] | 142.93 | 136.19 | 1.049 | 0.07 | 0.025 | 2.800 | 437.85 | 478.55 | 0.915 | 1.605 | 2.03 | 0.791 |
| B5 [22] | 146.26 | 138.22 | 1.058 | 0.064 | 0.023 | 2.783 | 456.19 | 522.07 | 0.874 | 1.526 | 1.837 | 0.831 |
| C2 [22] | 124.46 | 126.53 | 0.984 | 0.049 | 0.033 | 1.485 | 266.14 | 259.94 | 1.024 | 1.884 | 3.143 | 0.599 |
| C3 [22] | 131.93 | 129.74 | 1.017 | 0.064 | 0.033 | 1.939 | - | 408.54 | - | - | 2.236 | - |
| C4 [22] | 124.77 | 102.12 | 1.222 | 0.051 | 0.026 | 1.962 | 450.3 | 474.3 | 0.949 | 1.693 | 1.922 | 0.881 |
| C5 [22] | 138.34 | 131.07 | 1.055 | 0.051 | 0.026 | 1.962 | 467.26 | 550.51 | 0.849 | 1.59 | 2.026 | 0.785 |
| C6 [22] | 139.09 | 134.39 | 1.035 | 0.054 | 0.026 | 2.077 | 521.33 | 597.04 | 0.873 | 1.456 | 1.765 | 0.825 |
| D3 [9] | 15.15 | 12.01 | 1.261 | 0.081 | 0.039 | 2.077 | 39.11 | 41.34 | 0.946 | 2.795 | 2.526 | 1.106 |
| D4 [9] | 15.82 | 14.08 | 1.124 | 0.118 | 0.042 | 2.810 | 47.92 | 48.77 | 0.983 | 2.97 | 2.453 | 1.211 |
| T0 [23] | 49.82 | 41.86 | 1.190 | 0.062 | 0.025 | 2.480 | 185.5 | 171.83 | 1.080 | 1.3 | 1.841 | 0.706 |
| T1 [23] | 47.99 | 41.15 | 1.166 | 0.043 | 0.071 | 0.606 | 140.01 | 140.04 | 1.000 | 2.316 | 1.835 | 1.262 |
| T2 [23] | 52.79 | 46.15 | 1.144 | 0.098 | 0.071 | 1.380 | 143.1 | 140.18 | 1.021 | 2.5 | 1.743 | 1.434 |
| T5 [23] | 62.54 | 71.98 | 0.869 | 0.063 | 0.049 | 1.286 | 156.88 | 170.68 | 0.919 | 2.5 | 2.436 | 1.026 |
| VH1 [24] | 11.99 | 11.41 | 1.051 | 0.123 | 0.044 | 2.795 | 21.79 | 20.3 | 1.073 | 2.865 | 2.967 | 0.966 |
| VH2 [24] | 11.5 | 13.26 | 0.867 | 0.072 | 0.045 | 1.600 | 34.5 | 30.73 | 1.123 | 3.667 | 2.186 | 1.677 |
| 1.033 | 1.601 | 1.003 | 0.954 | |||||||||
| 0.098 | 0.711 | 0.075 | 0.258 | |||||||||
| 9.46% | 44.42% | 7.52% | 27.03% | |||||||||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernardo, L. Generalized Softened Variable Angle Truss Model for RC Hollow Beams under Torsion. Materials 2019, 12, 2209. https://doi.org/10.3390/ma12132209
Bernardo L. Generalized Softened Variable Angle Truss Model for RC Hollow Beams under Torsion. Materials. 2019; 12(13):2209. https://doi.org/10.3390/ma12132209
Chicago/Turabian StyleBernardo, Luís. 2019. "Generalized Softened Variable Angle Truss Model for RC Hollow Beams under Torsion" Materials 12, no. 13: 2209. https://doi.org/10.3390/ma12132209
APA StyleBernardo, L. (2019). Generalized Softened Variable Angle Truss Model for RC Hollow Beams under Torsion. Materials, 12(13), 2209. https://doi.org/10.3390/ma12132209