Multidimensional Phononic Bandgaps in Three-Dimensional Lattices for Additive Manufacturing
Abstract
1. Introduction
2. Methods
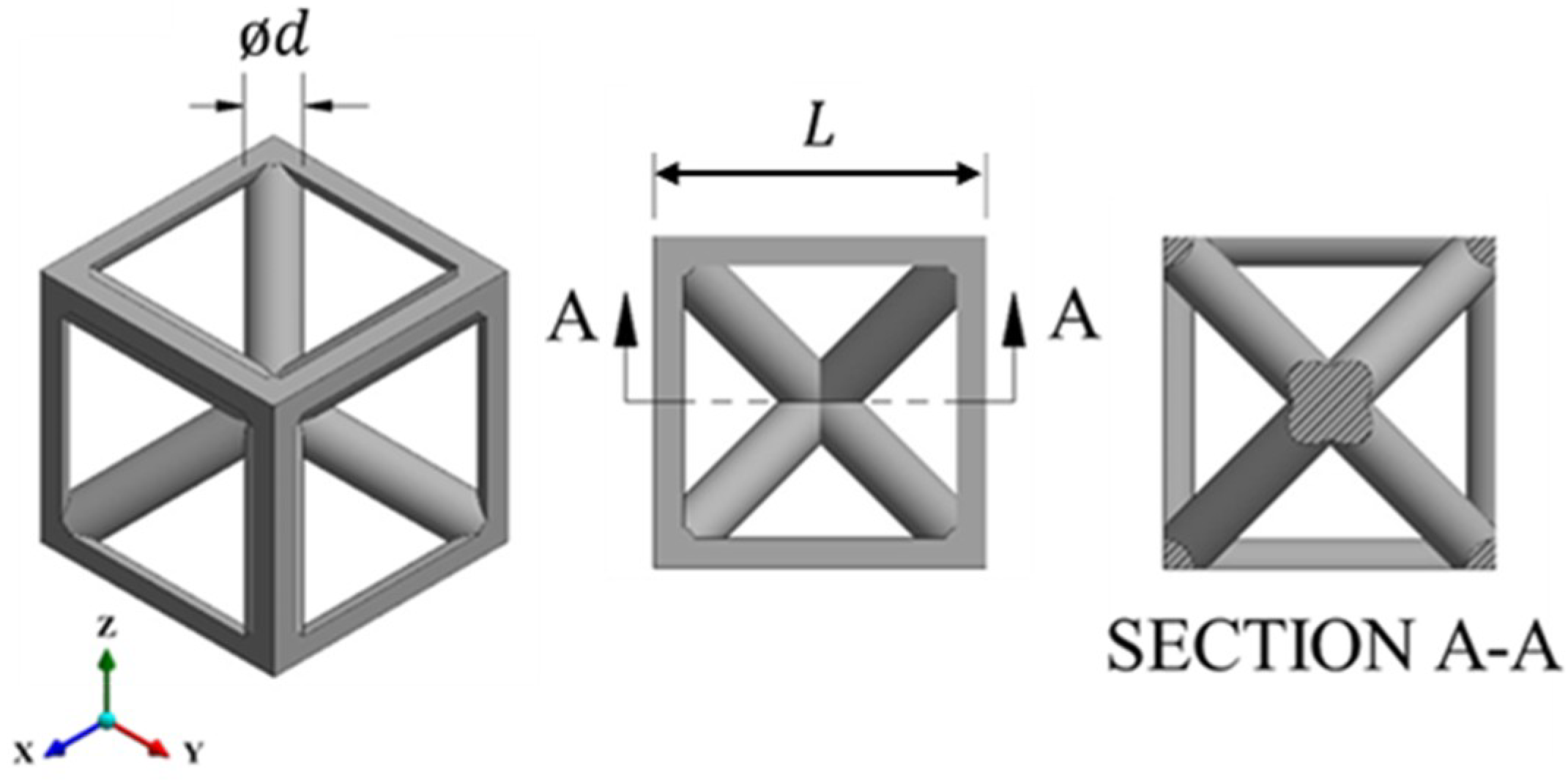
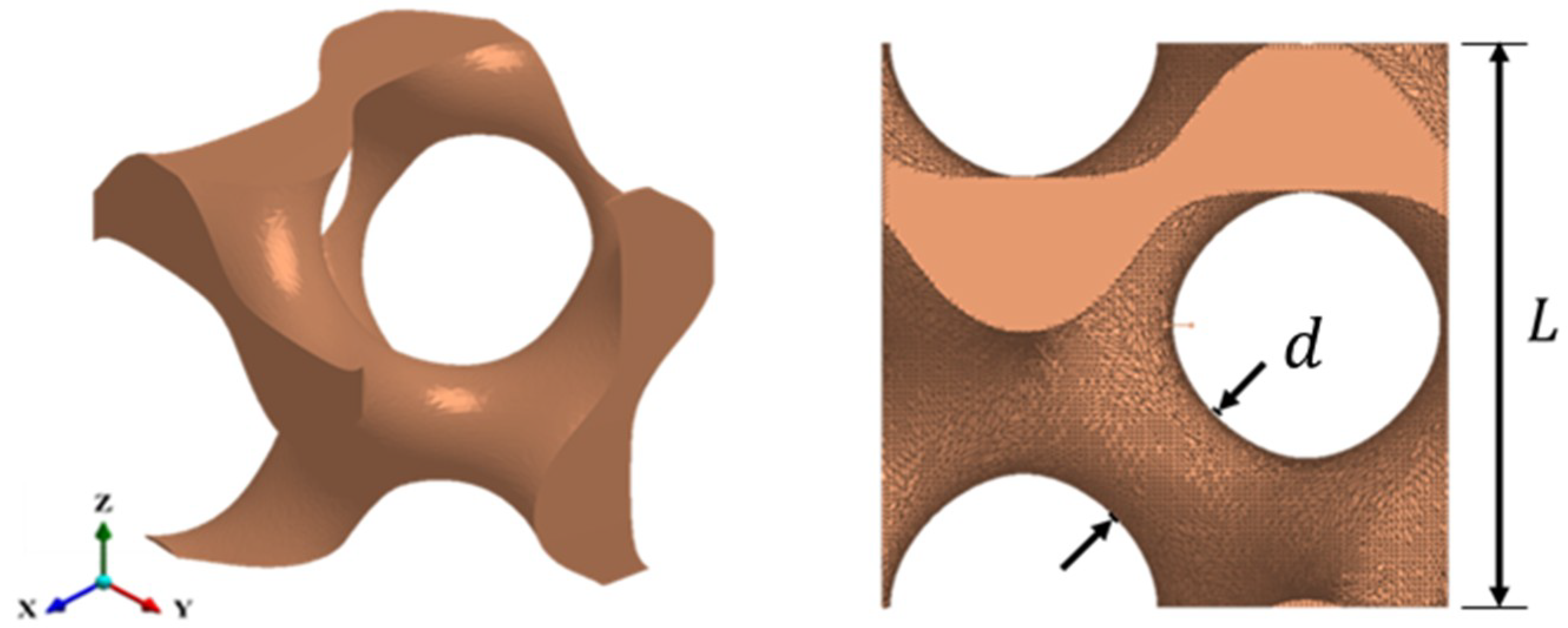
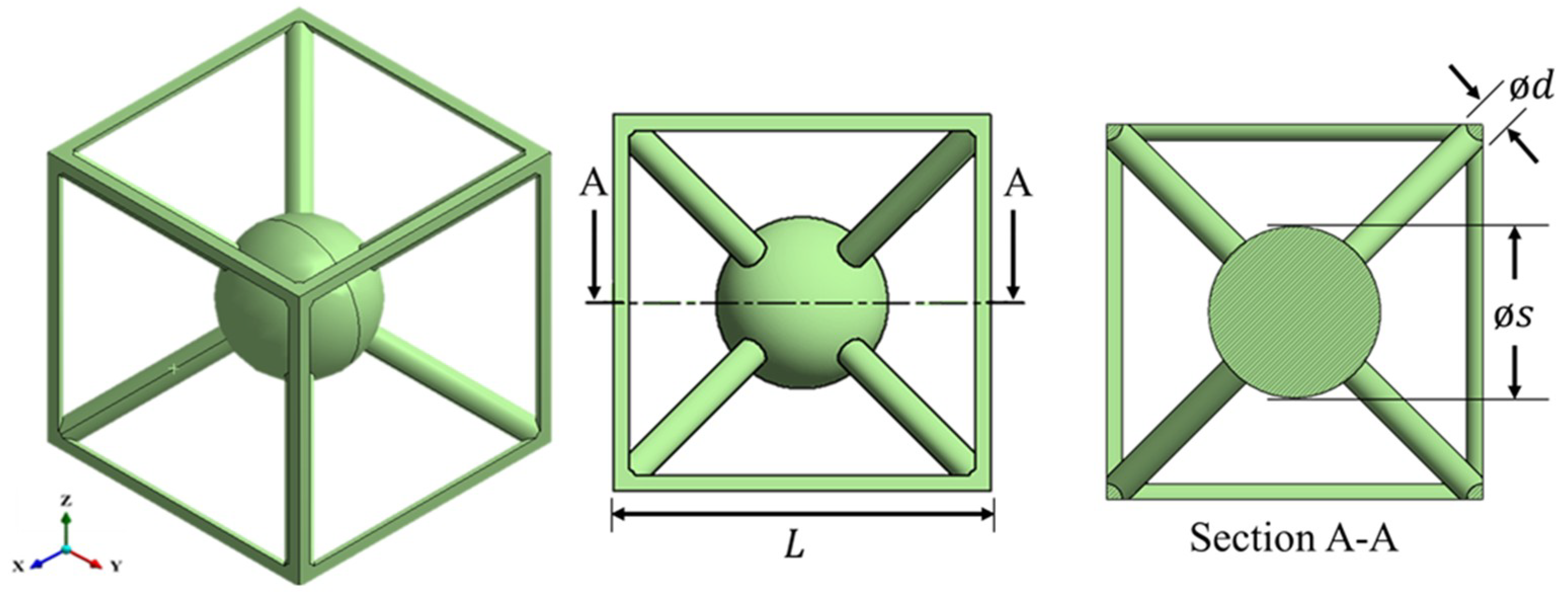
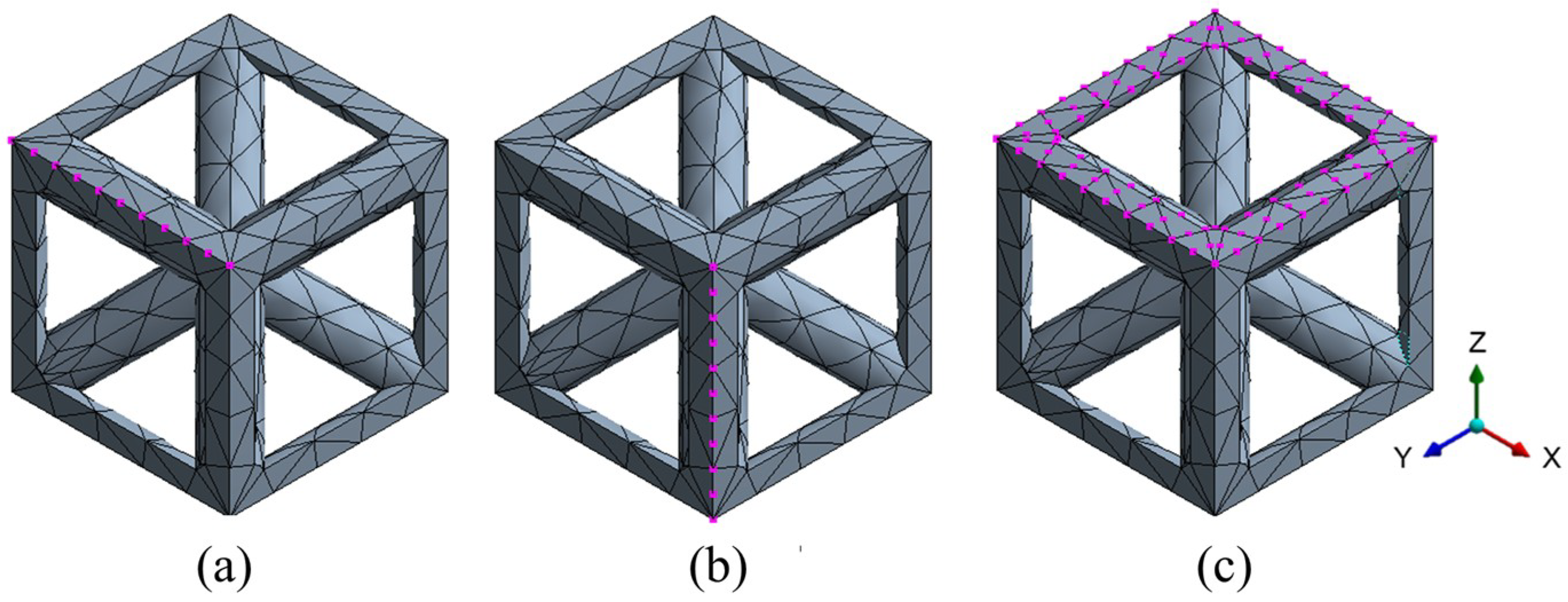
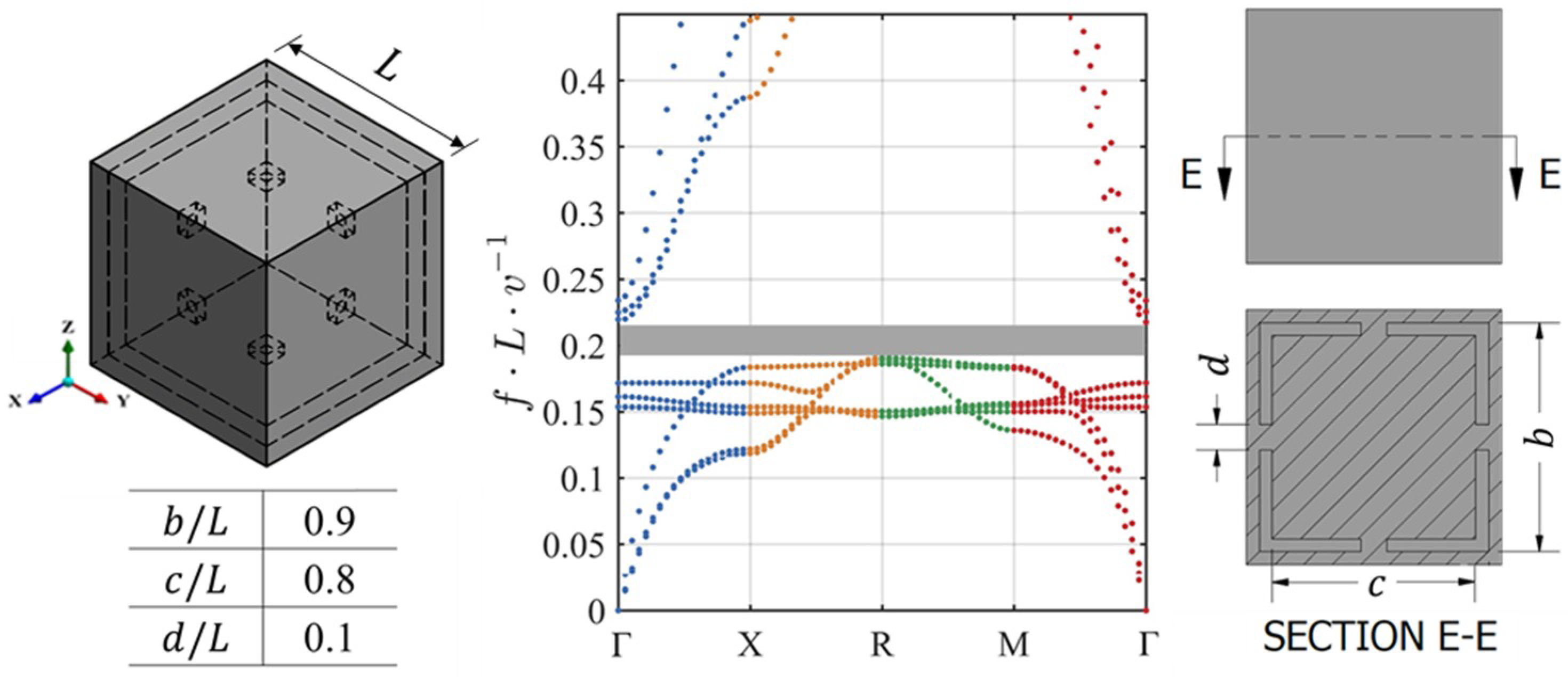
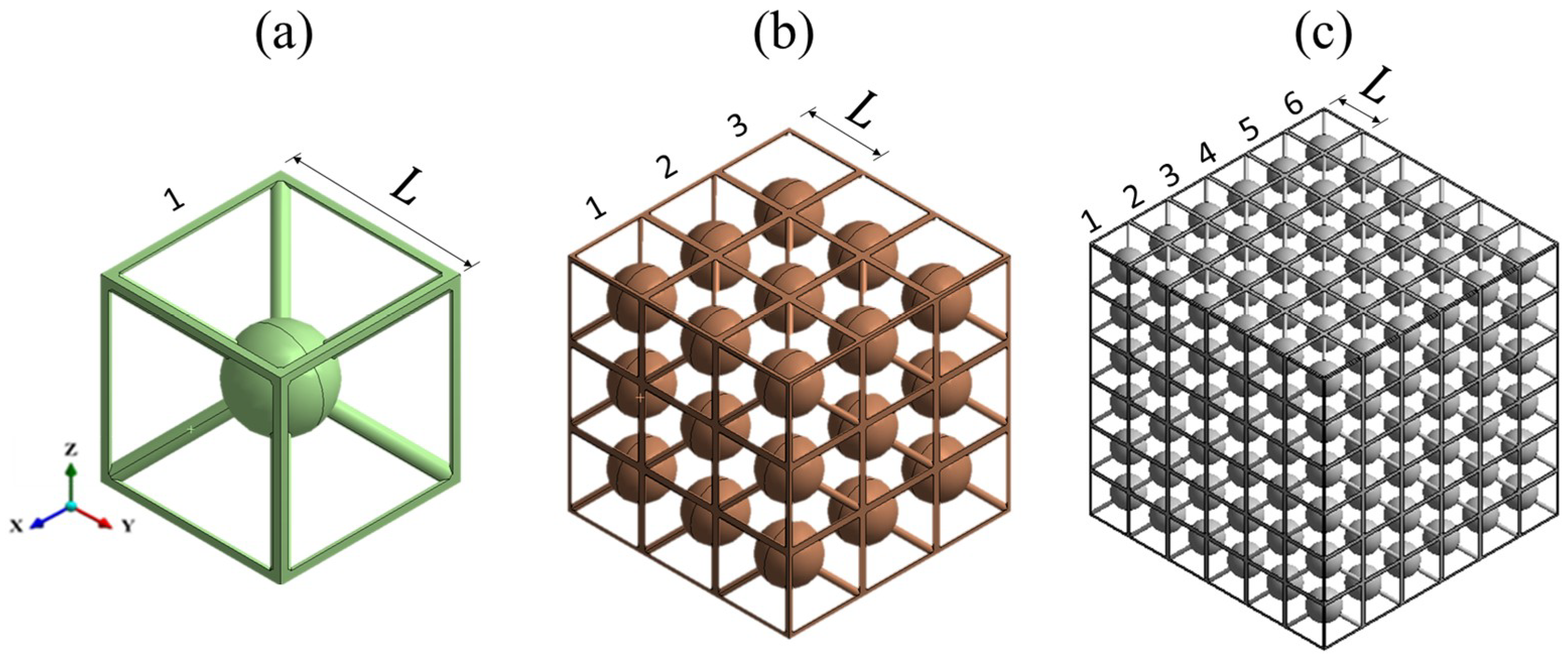
2.1. Lattice Design
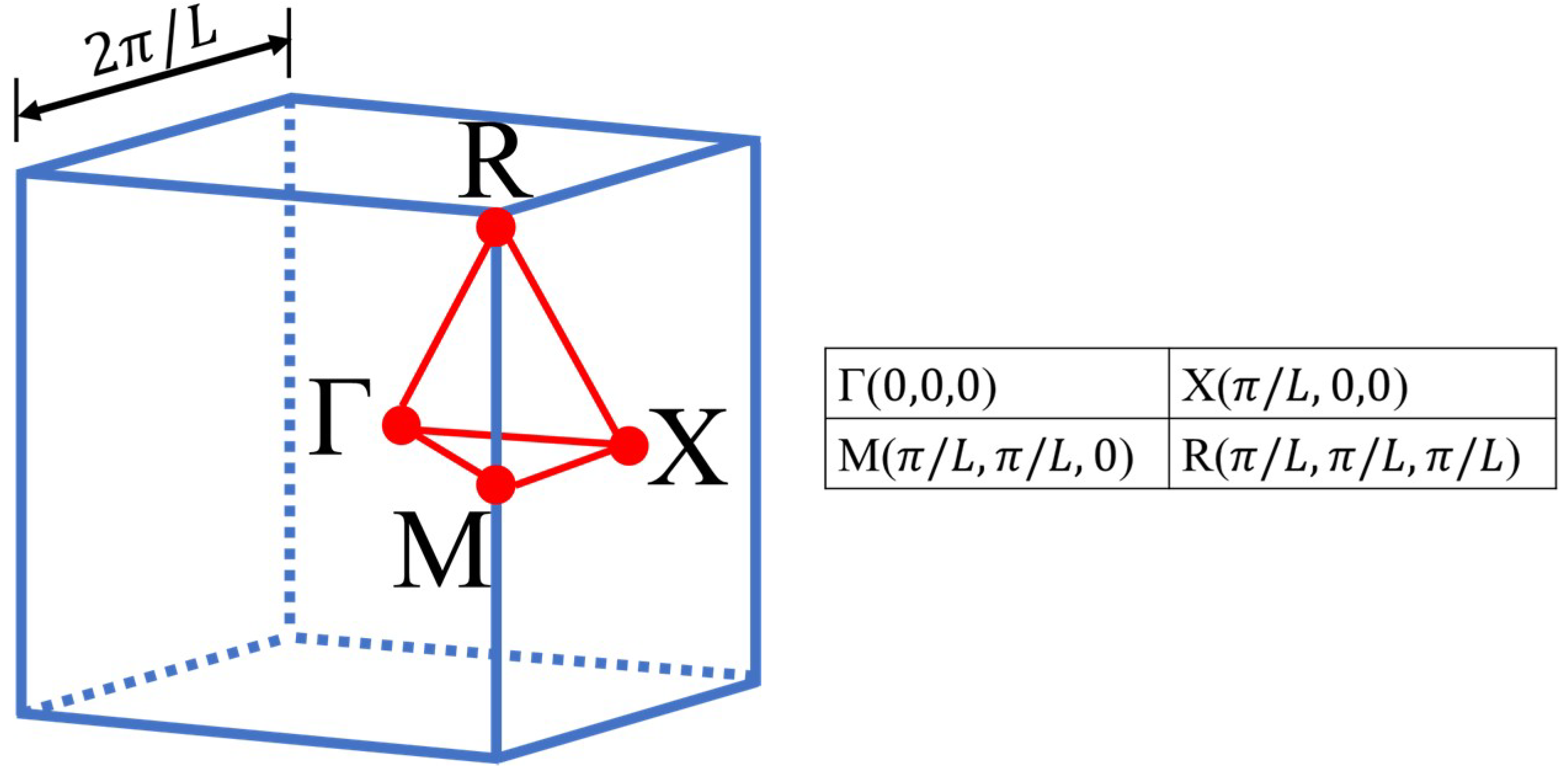
2.2. Bandgap Prediction
3. Results and Discussion
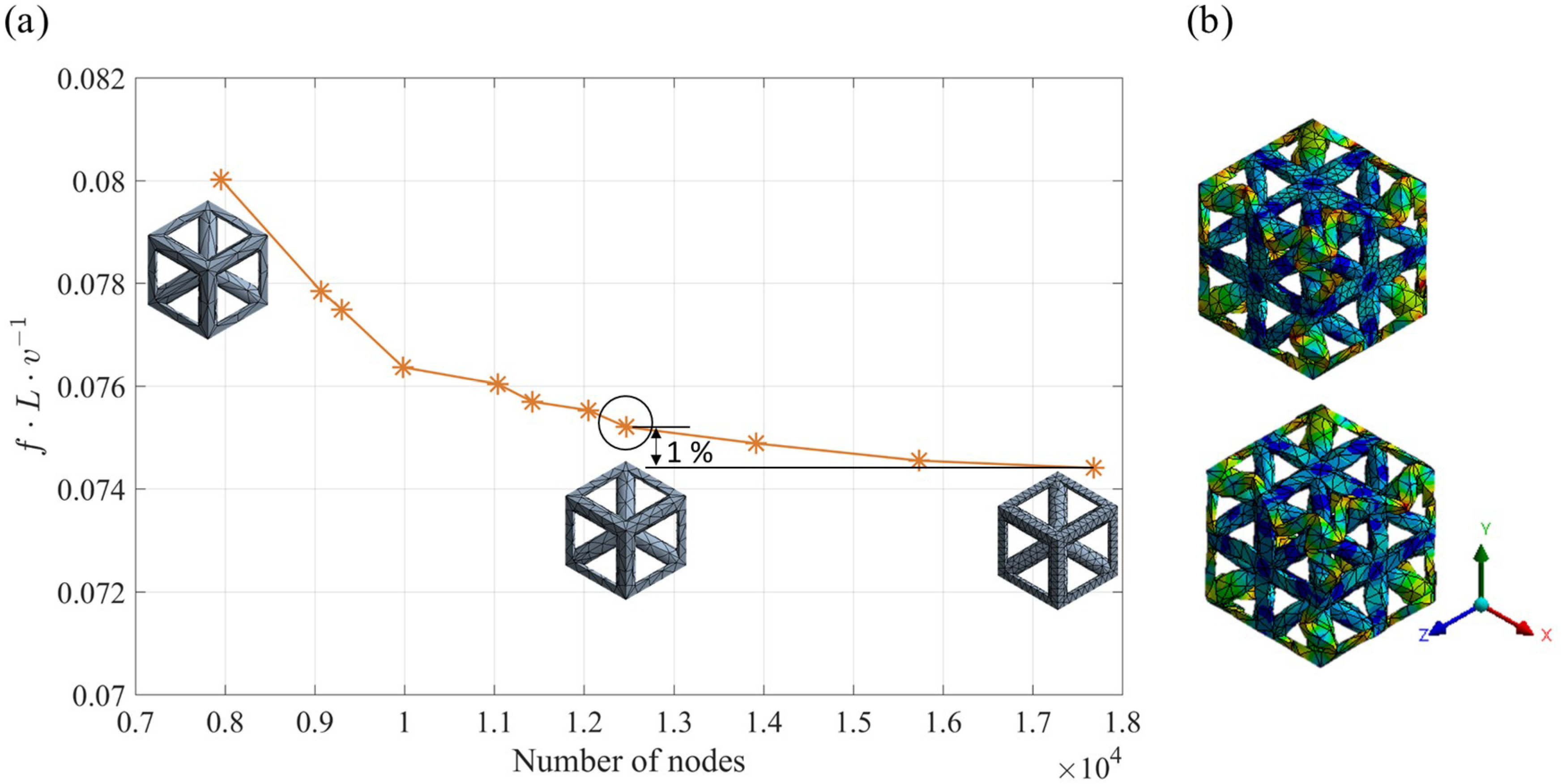
3.1. Verification of the Dispersion Curve Calculations
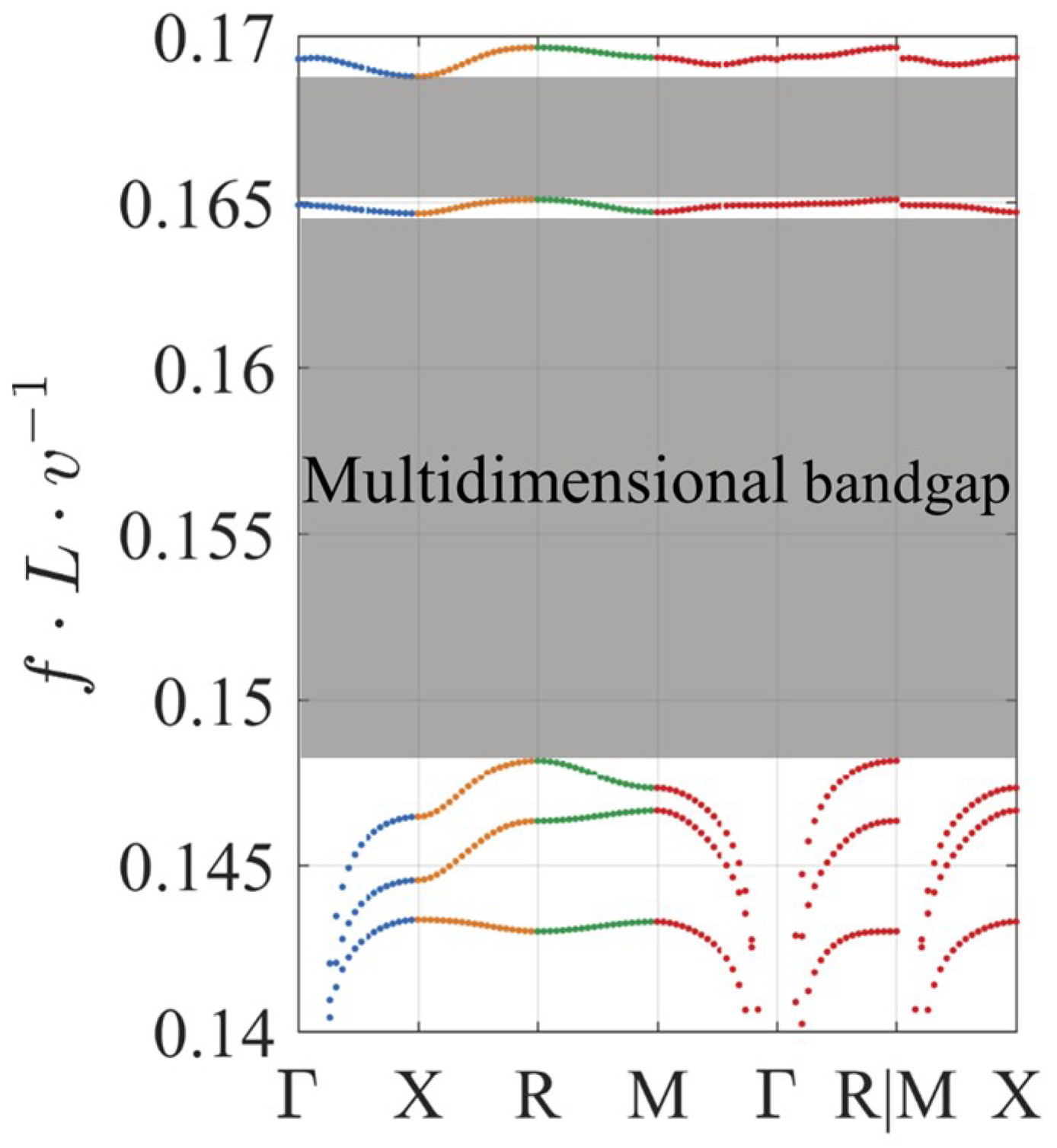
3.2. Wave Dispersion in Lattices with Infinite Periodicity
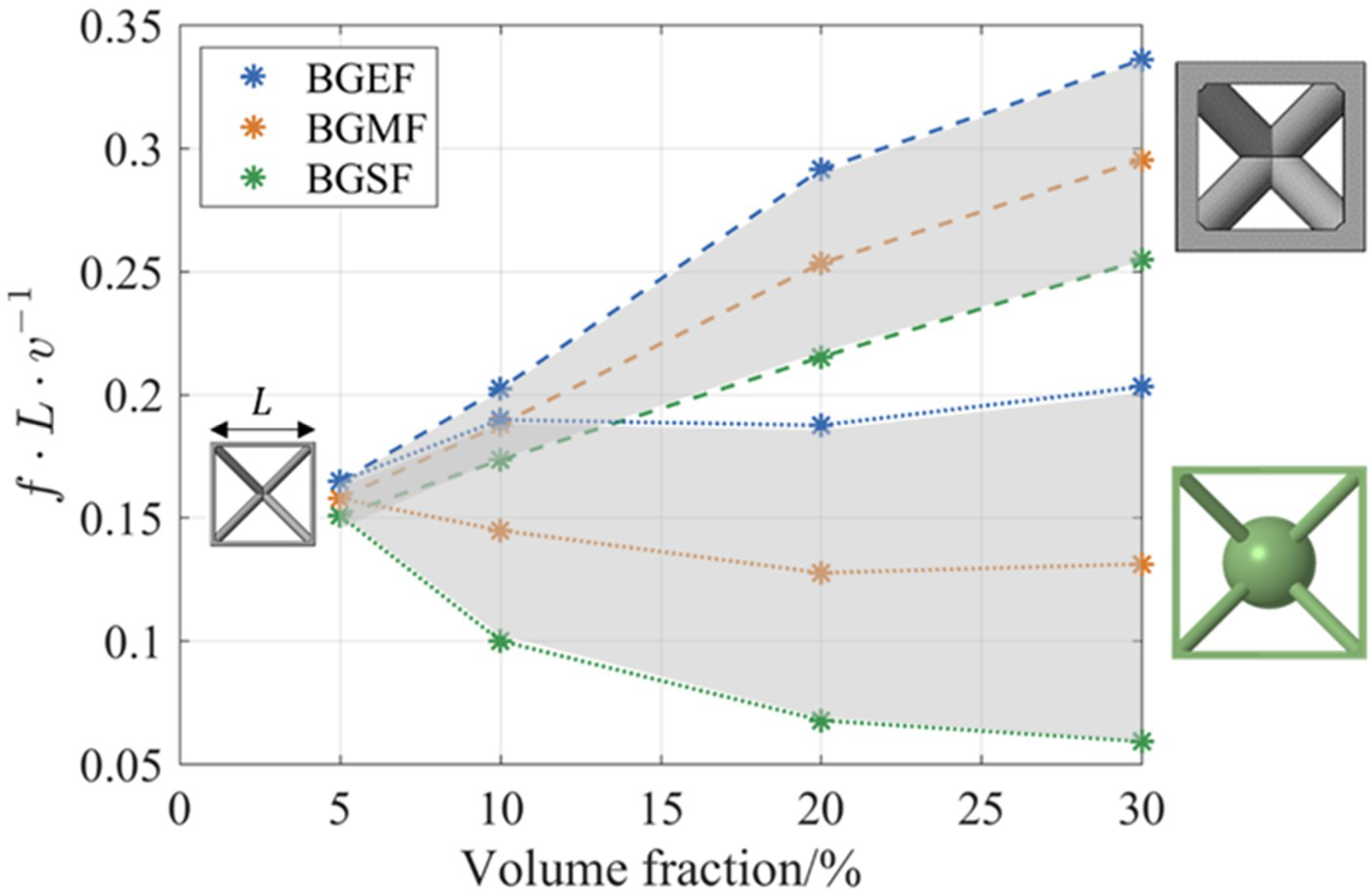
3.3. Tuning of Multidimensional BGs
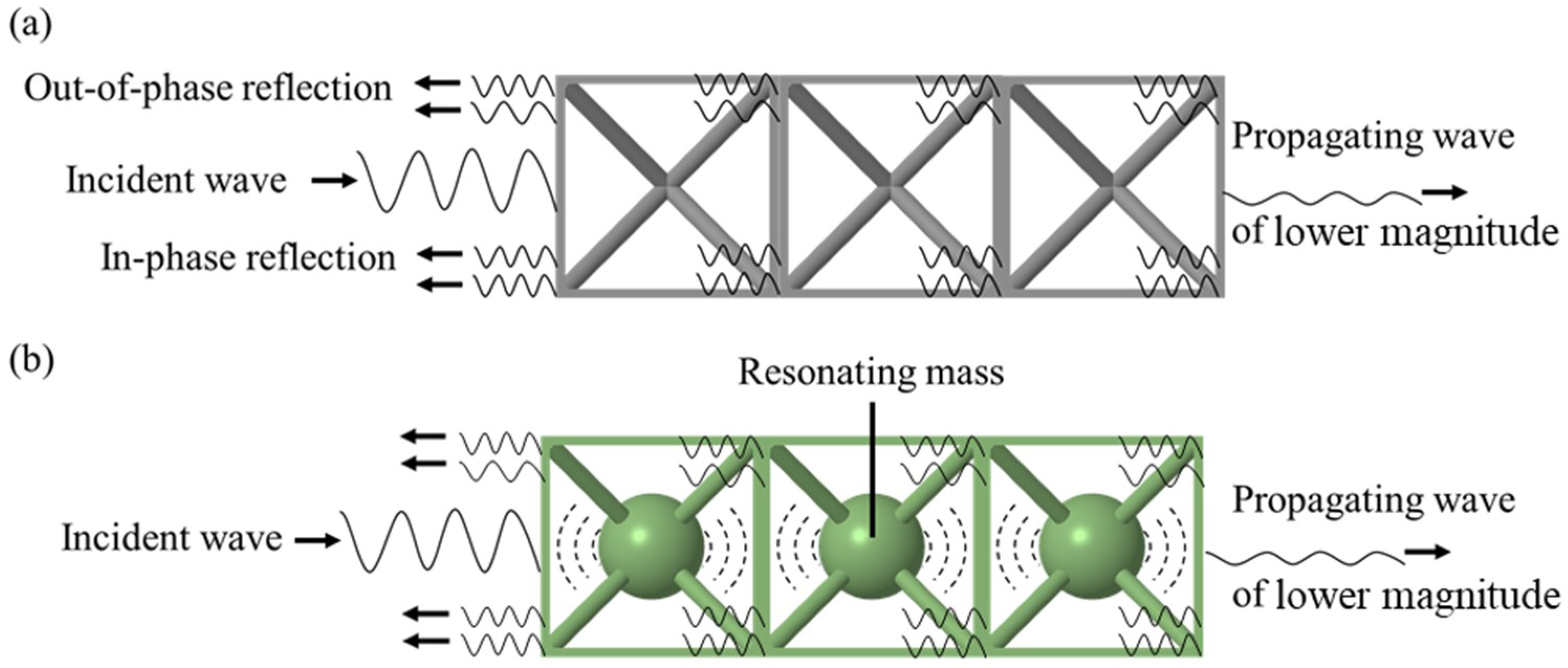
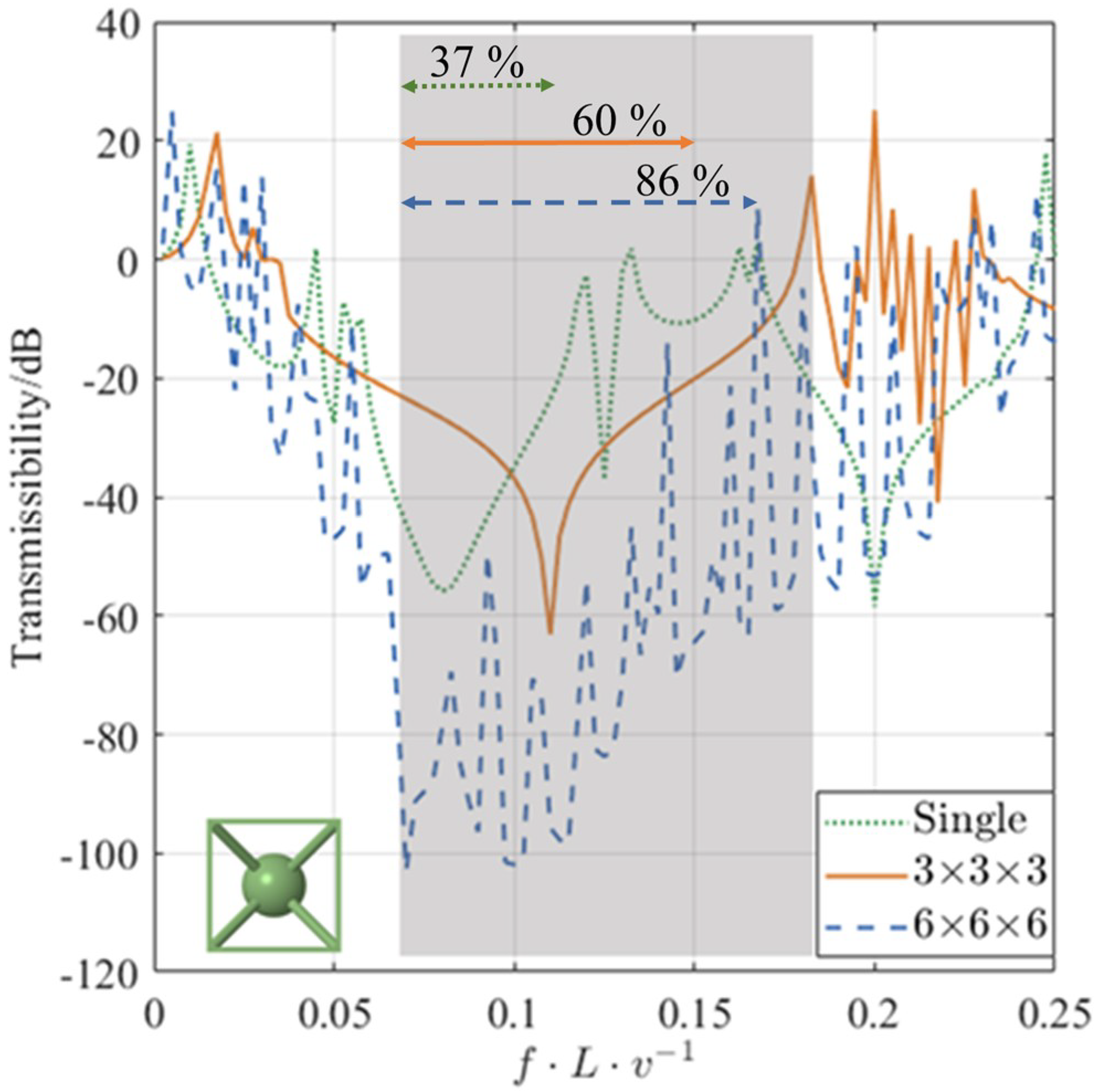
3.4. Evolution of the Wave Transmission in Lattices with Finite Periodicity
4. Conclusions
- Single material BCCxyz and res-BCCxyz lattices can provide BGs that are tunable with the volume fraction of the lattice.
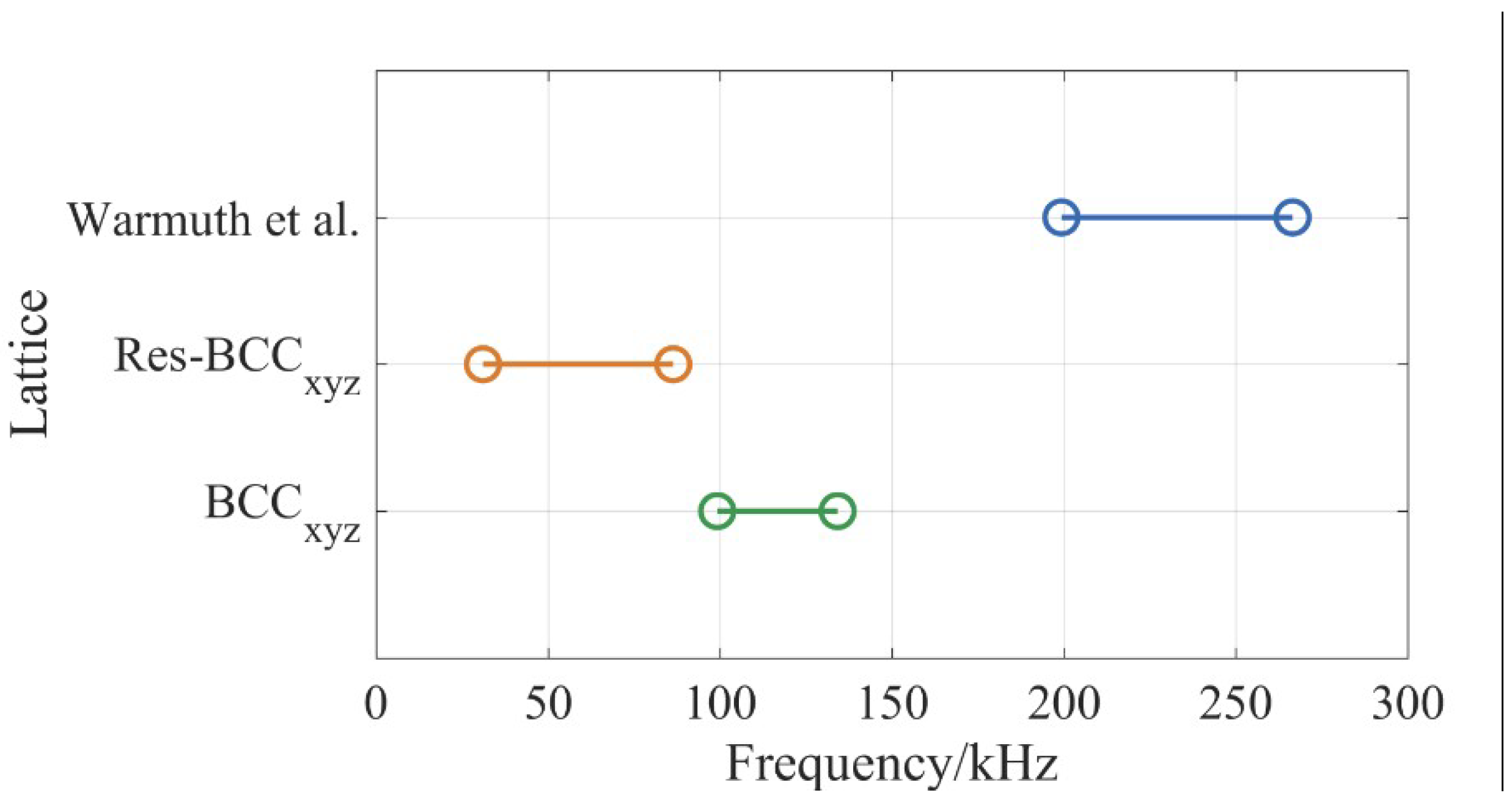
- BCCxyz and res-BCCxyz lattices have BGs of high width and intrinsically low frequency compared to results reported for similar structures in the literature.
- Although gyroid TPMS lattices are known to have 1D BGs, they do not exhibit multidimensional BGs.
- An increase in the finite periodicity of the lattice leads to an increase in the bandwidth and to a decrease in transmissibility within the BG.
- The attenuation of longitudinal waves reaches a minimum of −103 dB within the BG.
Author Contributions
Funding
Conflicts of Interest
References
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Roldán, R.; Castellanos-Gomez, A. A new bandgap tuning knob. Nat. Photonics 2017, 11, 407. [Google Scholar] [CrossRef]
- Zoorob, M.E.; Charlton, M.D.B.; Parker, G.J.; Baumberg, J.J.; Netti, M.C. Complete photonic bandgaps in 12-fold symmetric quasicrystals. Nature 2000, 404, 740. [Google Scholar] [CrossRef] [PubMed]
- Slobozhanyuk, A.; Mousavi, S.H.; Ni, X.; Smirnova, D.; Kivshar, Y.S.; Khanikaev, A.B. Three-dimensional all-dielectric photonic topological insulator. Nat. Photonics 2016, 11, 130. [Google Scholar] [CrossRef]
- Cheng, X.; Jouvaud, C.; Ni, X.; Mousavi, S.H.; Genack, A.Z.; Khanikaev, A.B. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 2016, 15, 542. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Fu, L.; Joannopoulos, J.D.; Soljačić, M. Weyl points and line nodes in gyroid photonic crystals. Nat. Photonics 2013, 7, 294. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Jasiuk, I.; Sobh, N.A. Acoustic band gaps and elastic stiffness of PMMA cellular solids based on triply periodic minimal surfaces. Mater. Des. 2018, 145, 20–27. [Google Scholar] [CrossRef]
- Khelif, A.; Hsiao, F.L.; Choujaa, A.; Benchabane, S.; Laude, V. Octave omnidirectional band gap in a three-dimensional phononic crystal. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1621–1625. [Google Scholar] [CrossRef]
- Zhou, X.Z.; Wang, Y.S.; Zhang, C.Z. Three-Dimensional sonic band gaps tunned by material parameters. Appl. Mech. Mater. 2010, 29, 1797–1802. [Google Scholar] [CrossRef]
- Phani, A.S.; Woodhouse, J.; Fleck, N.A. Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 2006, 119, 1995–2005. [Google Scholar] [CrossRef] [PubMed]
- Trainiti, G.; Rimoli, J.J.; Ruzzene, M. Wave propagation in periodically undulated beams and plates. Int. J. Solids Struct. 2015, 75, 260–276. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, Y.; Guest, J.K.; Srivastava, A. 3-D phononic crystals with ultra-wide band gaps. Sci. Rep. 2017, 7, 43407. [Google Scholar] [CrossRef] [PubMed]
- Phani, A.S. Elastodynamics of lattice materials. In Dynamics of Lattice Materials; Phani, A.S., Hussein, M.I., Eds.; John Wiley and Sons: Hoboken, NJ, USA, 2017; pp. 53–59. [Google Scholar]
- Matlack, K.H.; Bauhofer, A.; Krödel, S.; Palermo, A.; Daraio, C. Composite 3D-printed meta-structures for low frequency and broadband vibration absorption. Proc. Natl. Acad. Sci. USA 2015, 113, 8386–8390. [Google Scholar] [CrossRef] [PubMed]
- Richards, D.; Pines, D.J. Passive reduction of gear mesh vibration using a periodic drive shaft. J. Sound Vib. 2003, 2, 317–342. [Google Scholar] [CrossRef]
- Ampatzidis, T.; Leach, R.K.; Tuck, C.J.; Chronopoulos, D. Band gap behaviour of optimal composite structures with additive manufacturing inclusions. Compos. Part B Eng. 2018, 153, 26–35. [Google Scholar] [CrossRef]
- Elmadih, W.; Wahyudin, S.; Maskery, I.; Chornopolous, D.; Leach, R. Mechanical vibration bandgaps in surface-based lattices. Addit. Manuf. 2019, 25, 421–429. [Google Scholar] [CrossRef]
- Jensen, J.S. Phononic band gaps and vibrations in one- and two-dimensional mass-spring structures. J. Sound Vib. 2003, 266, 1053–1078. [Google Scholar] [CrossRef]
- Maldovan, M. Phonon wave interference and thermal bandgap materials. Nat. Mater. 2015, 14, 667. [Google Scholar] [CrossRef]
- Raghavan, L.; Phani, A.S. Local resonance bandgaps in periodic media: Theory and experiment. J. Acoust. Soc. Am. 2013, 134, 1950–1959. [Google Scholar] [CrossRef]
- Zhou, X.; Jun, W.; Wang, R.; Lin, J. Band gaps in grid structure with periodic local resonator subsystems. Mod. Phys. Lett. B 2017, 31, 1750225. [Google Scholar] [CrossRef]
- Yu, D.; Liu, Y.; Wang, G.; Zhao, H.; Qiu, J. Flexural vibration band gaps in Timoshenko beams with locally resonant structures. J. Appl. Phys. 2006, 100, 124901. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, D.; Li, L.; Zhao, H.; Wen, J.; Wen, X. Design guidelines for flexural wave attenuation of slender beams with local resonators. Phys. Lett. A 2007, 362, 344–347. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wang, Y.-S. Complete bandgap in three-dimensional holey phononic crystals with resonators. J. Vib. Acoust. 2013, 135, 41009. [Google Scholar] [CrossRef]
- Lucklum, F.; Vellekoop, M.J. Bandgap engineering of three-dimensional phononic crystals in a simple cubic lattice. Appl. Phys. Lett. 2018, 113, 201902. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Belloni, E.; Ardito, R.; Corigliano, A.; Braghin, F. Modeling and experimental verification of an ultra-wide bandgap in 3D phononic crystal. Appl. Phys. Lett. 2016, 109, 221907. [Google Scholar] [CrossRef]
- Zhang, H.; Xiao, Y.; Wen, J.; Yu, D.; Wen, X. Flexural wave band gaps in metamaterial beams with membrane-type resonators: Theory and experiment. J. Phys. D Appl. Phys. 2015, 48, 435305. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Warmuth, F.; Wormser, M.; Körner, C. Single phase 3D phononic band gap material. Sci. Rep. 2017, 7, 3843. [Google Scholar] [CrossRef]
- Wormser, M.; Warmuth, F.; Körner, C. Evolution of full phononic band gaps in periodic cellular structures. Appl. Phys. A 2017, 123, 661. [Google Scholar] [CrossRef]
- Lucklum, F.; Vellekoop, M.J. Design and fabrication challenges for millimeter-scale three-dimensional phononic crystals. Crystals 2017, 7, 348. [Google Scholar] [CrossRef]
- Kruisová, A.; Ševčík, M.; Seiner, H.; Sedlák, P.; Román-Manso, B.; Miranzo, P.; Belmonte, M.; Landa, M. Ultrasonic bandgaps in 3D-printed periodic ceramic microlattices. Ultrasonics 2018, 82, 91–100. [Google Scholar] [CrossRef]
- Yoo, D.-J. Advanced porous scaffold design using multi-void triply periodic minimal surface models with high surface area to volume ratios. Int. J. Precis. Eng. Manuf. 2014, 15, 1657–1666. [Google Scholar] [CrossRef]
- Maskery, I.; Sturm, L.; Aremu, A.O.; Panesar, A.; Williams, C.B.; Tuck, C.J.; Wildman, R.D.; Ashcroft, I.A. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer 2017, 152, 62–71. [Google Scholar] [CrossRef]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for additive manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Aremu, A.O.; Maskery, I.; Tuck, C.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.I.M. A comparative finite element study of cubic unit cells for selective laser melting. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 4–6 August 2014; pp. 1238–1249. [Google Scholar]
- Khaderi, S.N.; Deshpande, V.S.; Fleck, N.A. The stiffness and strength of the gyroid lattice. Int. J. Solids Struct. 2014, 51, 3866–3877. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Sundén, B.; Fu, J. Heat Transfer in Aerospace Applications; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Daliri, A.; Zhang, J.; Wang, C.H. 6-Hybrid polymer composites for high strain rate applications. In Lightweight Composite Structures in Transport; Njuguna, J., Ed.; Woodhead Publishing: Cambridge, UK, 2016; pp. 121–163. ISBN 978-1-78242-325-6. [Google Scholar]
- Syam, W.P.; Jianwei, W.; Zhao, B.; Maskery, I.; Elmadih, W.; Leach, R. Design and analysis of strut-based lattice structures for vibration isolation. Precis. Eng. 2017, 52, 494–506. [Google Scholar] [CrossRef]
- Hussein, A.Y. The Development of Lightweight Cellular Structures for Metal Additive Manufacturing. Ph.D. Thesis, University of Exeter, Devon, UK, 2013. [Google Scholar]
- Leary, M.; Mazur, M.; Elambasseril, J.; McMillan, M.; Chirent, T.; Sun, Y.; Qian, M.; Easton, M.; Brandt, M. Selective laser melting (SLM) of AlSi12Mg lattice structures. Mater. Des. 2016, 98, 344–357. [Google Scholar] [CrossRef]
- Hsieh, P.-F.; Wu, T.-T.; Sun, J.-H. Three-dimensional phononic band gap calculations using the FDTD method and a PC cluster system. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 148–158. [Google Scholar] [CrossRef]
- Choi, J.-W.; Kim, H.-C.; Wicker, R. Multi-material stereolithography. J. Mater. Process. Technol. 2011, 211, 318–328. [Google Scholar] [CrossRef]
- Elmadih, W.; Syam, W.; Maskery, I.; Leach, R. Additively manufactured lattice structures for precision engineering applications. In Proceedings of the 32nd Annual Meeting of American Society for Precision Engineering, Charlotte, NC, USA, 29 October–3 November 2017; pp. 164–169. [Google Scholar]
- University of Nottingham and Added Scientific FLatt Pack Modelling Software. Available online: www.Flattpack.com (accessed on 24 April 2019).
- Sigalas, M.M.; García, N. Theoretical study of three dimensional elastic band gaps with the finite-difference time-domain method. J. Appl. Phys. 2000, 87, 3122–3125. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, Y. Wavelet-based method for computing elastic band gaps of one-dimensional phononic crystals. Sci. China Ser. G. 2007, 50, 622–630. [Google Scholar]
- Yan, Z.; Wang, Y.; Zhang, C. Wavelet method for calculating the defect states of two-dimensional phononicx crystals. Acta Mech. Solida Sin. 2008, 21, 104–109. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, C.T.; Sheng, P. Three-component elastic wave band-gap material. Phys. Rev. B Condens. Matter Mater. Phys. 2002, 65, 1651161–1651166. [Google Scholar] [CrossRef]
- Marwaha, A.; Marwaha, S.; Hudiara, I.S. Analysis of Curved Boundaries by FDTD and FE Methods. IETE J. Res. 2001, 47, 301–310. [Google Scholar] [CrossRef]
- Qian, D.; Shi, Z. Using PWE/FE method to calculate the band structures of the semi-infinite beam-like PCs: Periodic in z-direction and finite in x–y plane. Phys. Lett. A 2017, 381, 1516–1524. [Google Scholar] [CrossRef]
- Collet, M.; Ouisse, M.; Ruzzene, M.; Ichchou, M.N. Floquet–Bloch decomposition for the computation of dispersion of two-dimensional periodic, damped mechanical systems. Int. J. Solids Struct. 2011, 48, 2837–2848. [Google Scholar] [CrossRef]
- Maurin, F.; Claeys, C.; Deckers, E.; Desmet, W. Probability that a band-gap extremum is located on the irreducible Brillouin-zone contour for the 17 different plane crystallographic lattices. Int. J. Solids Struct. 2017, 135, 26–36. [Google Scholar] [CrossRef]
- Craft, G.; Nussbaum, J.; Crane, N.; Harmon, J.P. Impact of extended sintering times on mechanical properties in PA-12 parts produced by powderbed fusion processes. Addit. Manuf. 2018, 22, 800–806. [Google Scholar] [CrossRef]
- King, W.E.; Anderson, A.T.; Ferencz, R.M.; Hodge, N.E.; Kamath, C.; Khairallah, S.A.; Rubenchik, A.M. Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges. Appl. Phys. Rev. 2015, 2, 41304. [Google Scholar] [CrossRef]
- Materialise PA 12 (SLS): Datasheet. Available online: http://www.materialise.com/en/manufacturing/materials/pa-12-sls (accessed on 31 January 2018).
- Agius, D.; Kourousis, K.I.; Wallbrink, C. A review of the as-built SLM Ti-6Al-4V mechanical properties towards achieving fatigue resistant designs. Metals 2018, 8, 75. [Google Scholar] [CrossRef]
- Yilmaz, C.; Hulbert, G.M. Dynamics of locally resonant and inertially amplified lattice materials. In Dynamics of Lattice Materials; Phani, A.S., Hussein, M.I., Eds.; John Wiley and Sons: Hoboken, NJ, USA, 2017; p. 233. [Google Scholar]

| Volume Fraction (%) | |
|---|---|
| 5 | 0.084 |
| 10 | 0.121 |
| 20 | 0.178 |
| 30 | 0.226 |
| Volume Fraction (%) | |
|---|---|
| 5 | 0.138 |
| 10 | 0.175 |
| 20 | 0.250 |
| 30 | 0.325 |
| Volume Fraction (%) | ||
|---|---|---|
| 10 | 0.084 | 0.480 |
| 20 | 0.084 | 0.680 |
| 30 | 0.084 | 0.796 |
| Tensile Modulus | Density | Poisson’s Ratio |
|---|---|---|
| 1500 MPa | 950 kg·m−3 | 0.3 |
| BG Property | Remodelled Structure (This Work) | Wang et al. ([25]) |
|---|---|---|
| Normalised BG start frequency | 0.19 | 0.19 |
| Normalised BG end frequency | 0.22 | 0.23 |
| Normalised BG frequency width (bandwidth) | 0.03 | 0.04 |
| Periodicity | Mean Transmissibility (dB) | Lowest Transmissibility (dB) |
|---|---|---|
| One | −23 | −56 |
| Three | −24 | −63 |
| Six | −66 | −103 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elmadih, W.; Syam, W.P.; Maskery, I.; Chronopoulos, D.; Leach, R. Multidimensional Phononic Bandgaps in Three-Dimensional Lattices for Additive Manufacturing. Materials 2019, 12, 1878. https://doi.org/10.3390/ma12111878
Elmadih W, Syam WP, Maskery I, Chronopoulos D, Leach R. Multidimensional Phononic Bandgaps in Three-Dimensional Lattices for Additive Manufacturing. Materials. 2019; 12(11):1878. https://doi.org/10.3390/ma12111878
Chicago/Turabian StyleElmadih, Waiel, Wahyudin P. Syam, Ian Maskery, Dimitrios Chronopoulos, and Richard Leach. 2019. "Multidimensional Phononic Bandgaps in Three-Dimensional Lattices for Additive Manufacturing" Materials 12, no. 11: 1878. https://doi.org/10.3390/ma12111878
APA StyleElmadih, W., Syam, W. P., Maskery, I., Chronopoulos, D., & Leach, R. (2019). Multidimensional Phononic Bandgaps in Three-Dimensional Lattices for Additive Manufacturing. Materials, 12(11), 1878. https://doi.org/10.3390/ma12111878







