Damping Enhancement Using Axially Functionally Graded Porous Structure Based on Acoustic Black Hole Effect
Abstract
1. Introduction
2. Theoretical Analysis
3. Numerical Analysis
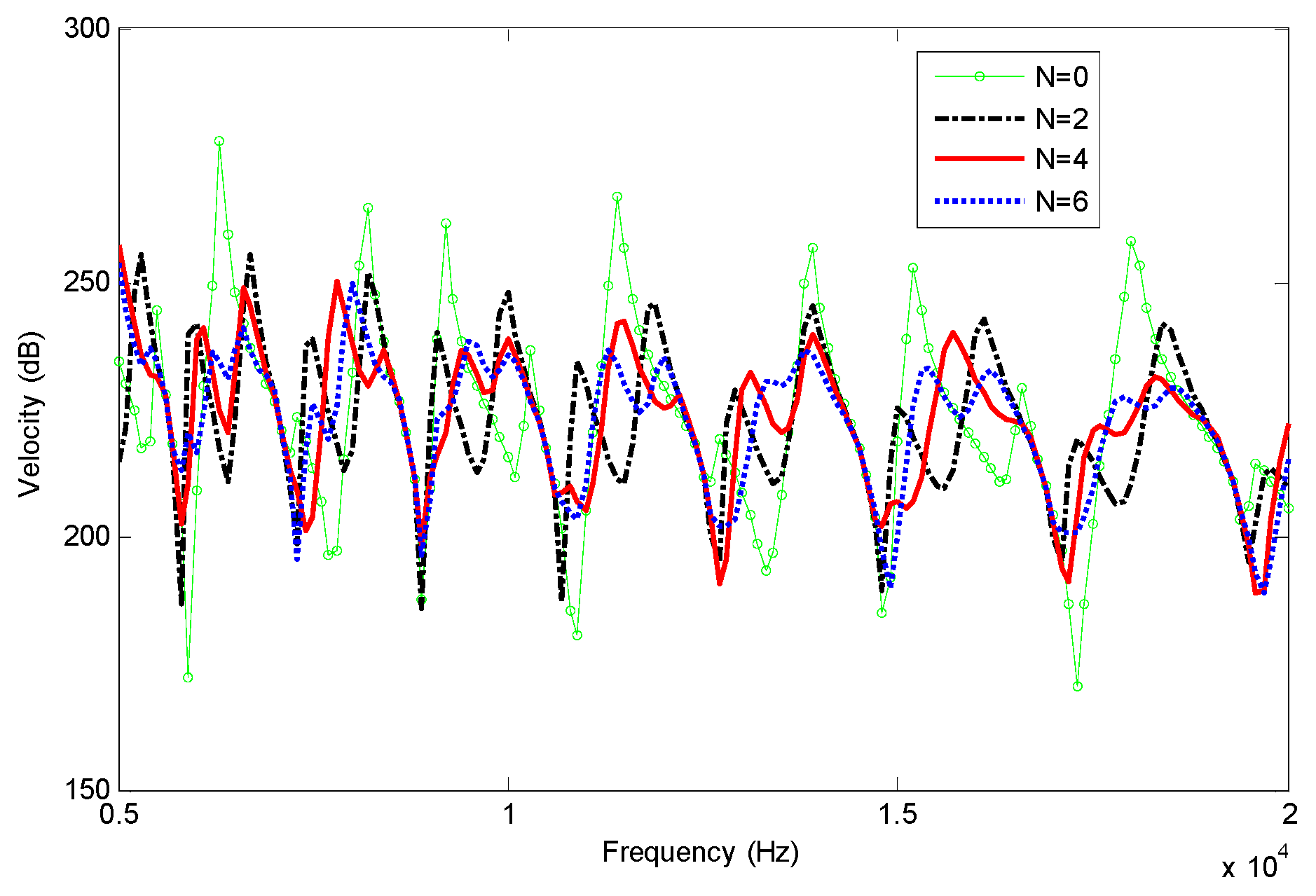
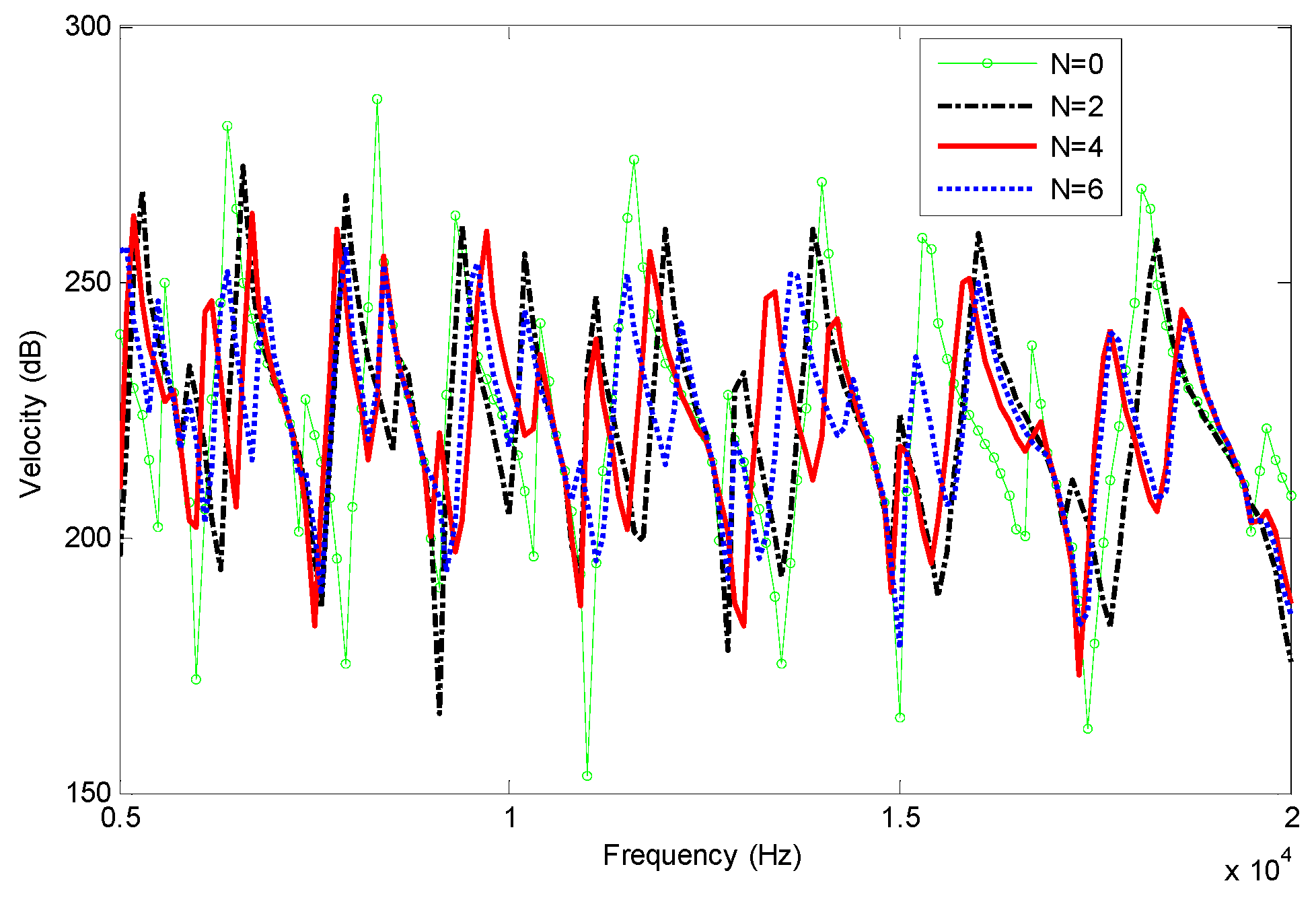
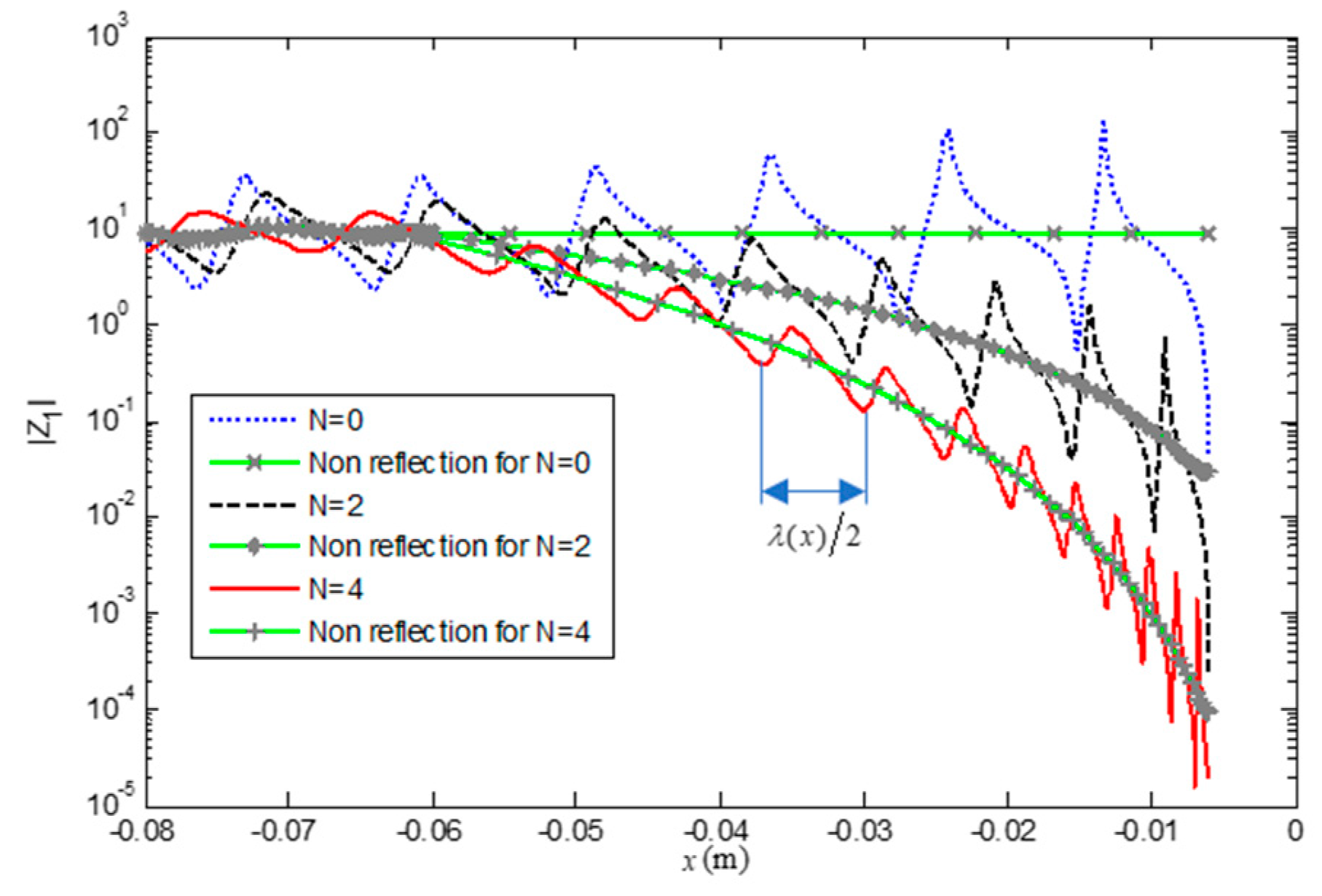
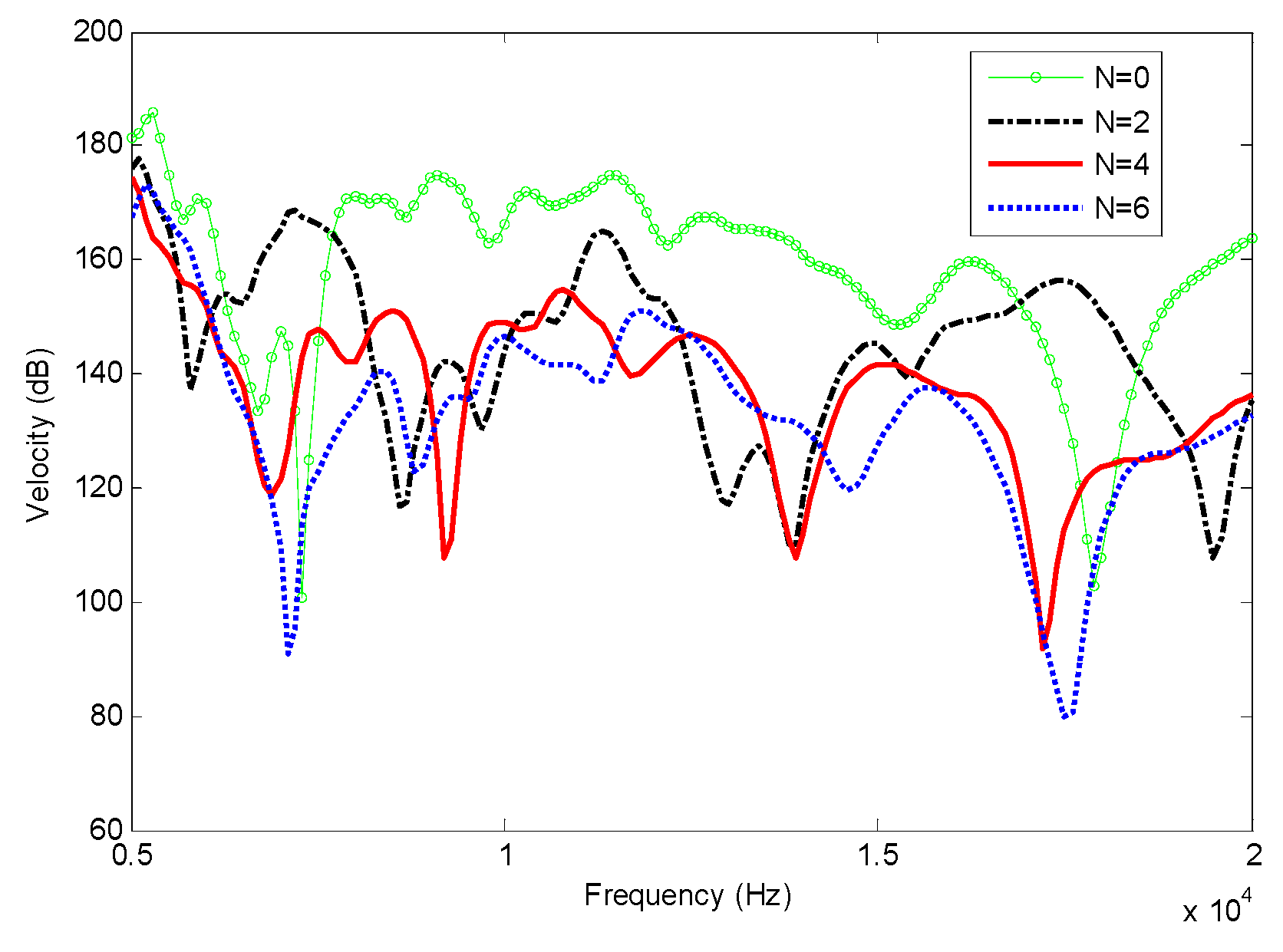
3.1. 1-D Beam with FGP End
3.2. 2D Plate Centred with FGP Disk
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Georgiev, V.B.; Cuenca, J.; Gautier, F. Damping of structural vibrations in beams and elliptical plates using the acoustic black hole effect. J. Sound Vib. 2011, 330, 2497–2508. [Google Scholar] [CrossRef]
- Feurtado, P.A.; Conlon, S.C. An experimental investigation of acoustic black hole dynamics at low, mid, and high frequencies. J. Vib. Acoust. 2016, 138, 061002. [Google Scholar] [CrossRef]
- Lee, J.Y.; Jeon, W. Vibration damping using a spiral acoustic black hole. J. Acoust. Soc. Am. 2017, 141, 1437–1445. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Tang, L.; Ji, H. Dynamic and static properties of double-layered compound acoustic black hole structures. Int. J. Appl. Mech. 2017, 9, 1750074. [Google Scholar] [CrossRef]
- Mironov, M.A. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval. Sov. Phys. Acoust. USSR 1988, 34, 318–319. [Google Scholar]
- Zhao, L.; Conlon, S.C.; Semperlotti, F. Broadband energy harvesting using acoustic black hole structural tailoring. Smart Mater. Struct. 2014, 23, 065021. [Google Scholar] [CrossRef]
- Krylov, V.V.; Tilman, F. Acoustic ‘black holes’ for flexural waves as effective vibration dampers. J. Sound Vib. 2004, 274, 605–619. [Google Scholar] [CrossRef]
- Denis, V.; Pelat, A.; Gautier, F. Scattering effects induced by imperfections on an acoustic black hole placed at a structural waveguide termination. J. Sound Vib. 2016, 362, 56–71. [Google Scholar] [CrossRef]
- Tang, L.; Cheng, L. Enhanced Acoustic Black Hole effect in beams with a modified thickness profile and extended platform. J. Sound Vib. 2017, 391, 116–126. [Google Scholar] [CrossRef]
- Georgiev, V.; Cuenca, J.; Bermudez, M.M.; Gautier, F.; Simon, L. Recent progress in vibration reduction using Acoustic Black Hole effect. In Proceedings of the 10ème Congrès Français d’Acoustique, Lyon, France, 12–16 April 2010. [Google Scholar]
- Vemula, C.; Norris, A.N.; Cody, G.D. Attenuation of waves in plates and bars using a graded impedance interface at edges. J. Sound Vib. 1996, 196, 107–127. [Google Scholar] [CrossRef]
- Birman, V.; Byrd, L.W. Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Wang, Z. Sandwich panels with layered graded aluminum honeycomb cores under blast loading. Compos. Struct. 2017, 173, 242–254. [Google Scholar] [CrossRef]
- Mosanenzadeh, S.G.; Naguib, H.E.; Park, C.B. Design and development of novel bio-based functionally graded foams for enhanced acoustic capabilities. J. Mater. Sci. 2015, 50, 1248–1256. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P. Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int. J. Mech. Sci. 2012, 62, 57–66. [Google Scholar] [CrossRef]
- Akbaş, Ş.D. Forced vibration analysis of functionally graded porous deep beams. Compos. Struct. 2018, 186, 293–302. [Google Scholar] [CrossRef]
- Simsek, M.; Kocaturk, T.; Akbas, S.D. Dynamic behavior of an axially functionally graded beam under action of a moving harmonic load. Compos. Struct. 2012, 94, 2358–2364. [Google Scholar] [CrossRef]
- Shahba, A.; Rajasekaran, S. Free vibration and stability of tapered Euler-Bernoulli beams made of axially functionally graded materials. Appl. Math. Model. 2012, 36, 3094–3111. [Google Scholar] [CrossRef]
- Shahba, A.; Attarnejad, R.; Marvi, M.; Hajilar, S. Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions. Compos. Part B 2011, 42, 801–808. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Analysis of elastic modulus of conventional foams and of re-entrant foam materials with a negative Poisson’s ratio. Int. J. Mech. Sci. 1995, 37, 51–59. [Google Scholar] [CrossRef]
- Krylov, V.V.; Shuvalov, A.L. Propagation of localized flexural vibrations along plate edges described by a power law. Proc. Inst. Acoust. 2000, 22, 263–270. [Google Scholar]
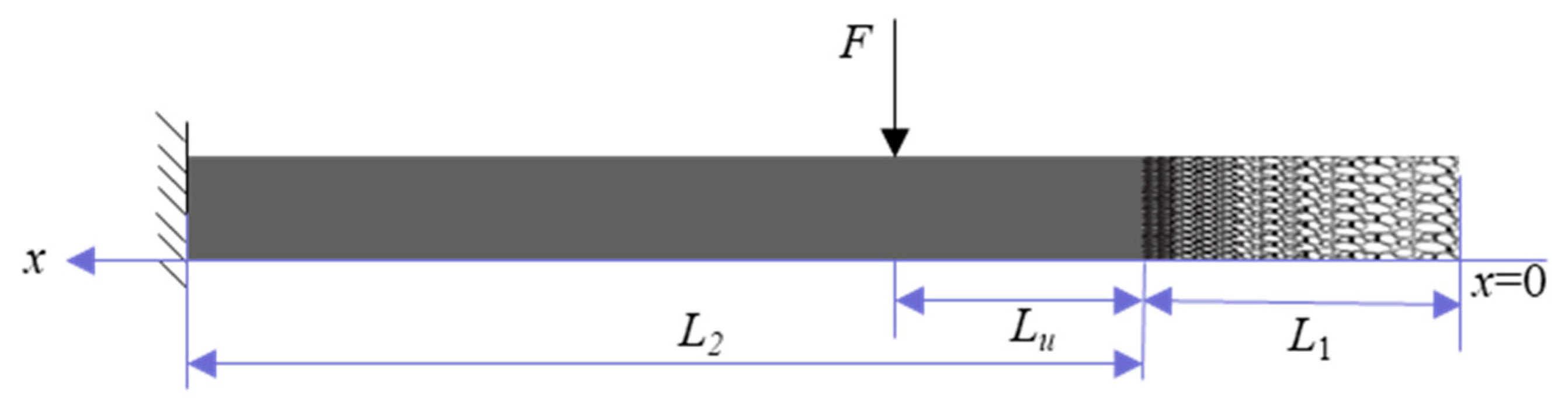




| Geometrical Characteristics | Characteristics of Material |
|---|---|
| L1 = 0.06 m | |
| Lu = 0.12 m | |
| L2 = 0.24 m | |
| h = 0.0015 m | |
| b = 0.0015 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, W.; He, S.; Tang, R.; He, S. Damping Enhancement Using Axially Functionally Graded Porous Structure Based on Acoustic Black Hole Effect. Materials 2019, 12, 2480. https://doi.org/10.3390/ma12152480
Zheng W, He S, Tang R, He S. Damping Enhancement Using Axially Functionally Graded Porous Structure Based on Acoustic Black Hole Effect. Materials. 2019; 12(15):2480. https://doi.org/10.3390/ma12152480
Chicago/Turabian StyleZheng, Weiguang, Shiming He, Rongjiang Tang, and Shuilong He. 2019. "Damping Enhancement Using Axially Functionally Graded Porous Structure Based on Acoustic Black Hole Effect" Materials 12, no. 15: 2480. https://doi.org/10.3390/ma12152480
APA StyleZheng, W., He, S., Tang, R., & He, S. (2019). Damping Enhancement Using Axially Functionally Graded Porous Structure Based on Acoustic Black Hole Effect. Materials, 12(15), 2480. https://doi.org/10.3390/ma12152480





