Fracture Resistance of Monolithic Zirconia Crowns in Implant Prostheses in Patients with Bruxism
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimens Preparation
2.2. Cyclic Loading Test
2.3. Finite Element Method
2.4. Statistical Analysis and Microstructural Observation
3. Results
3.1. Cyclic Load Test
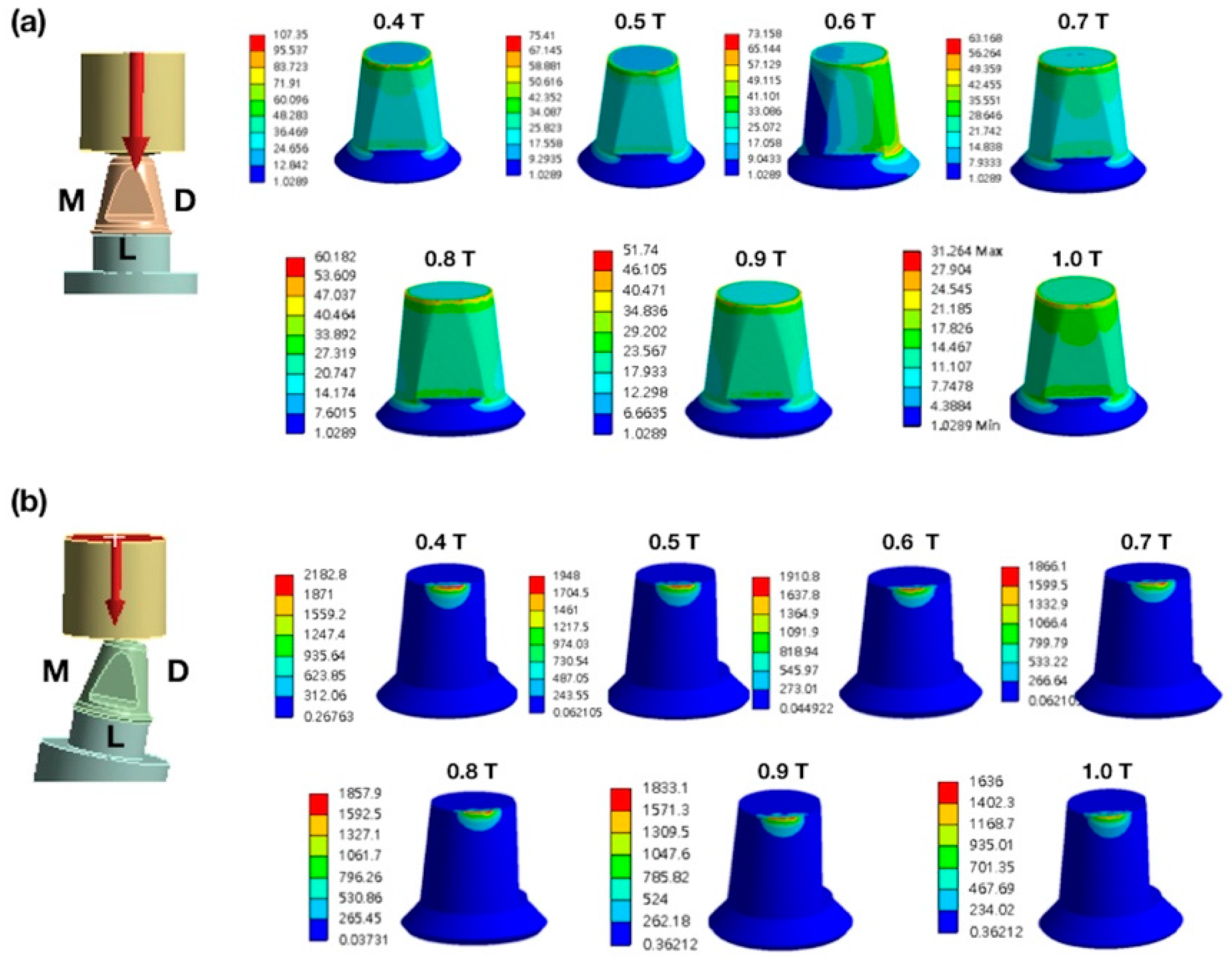
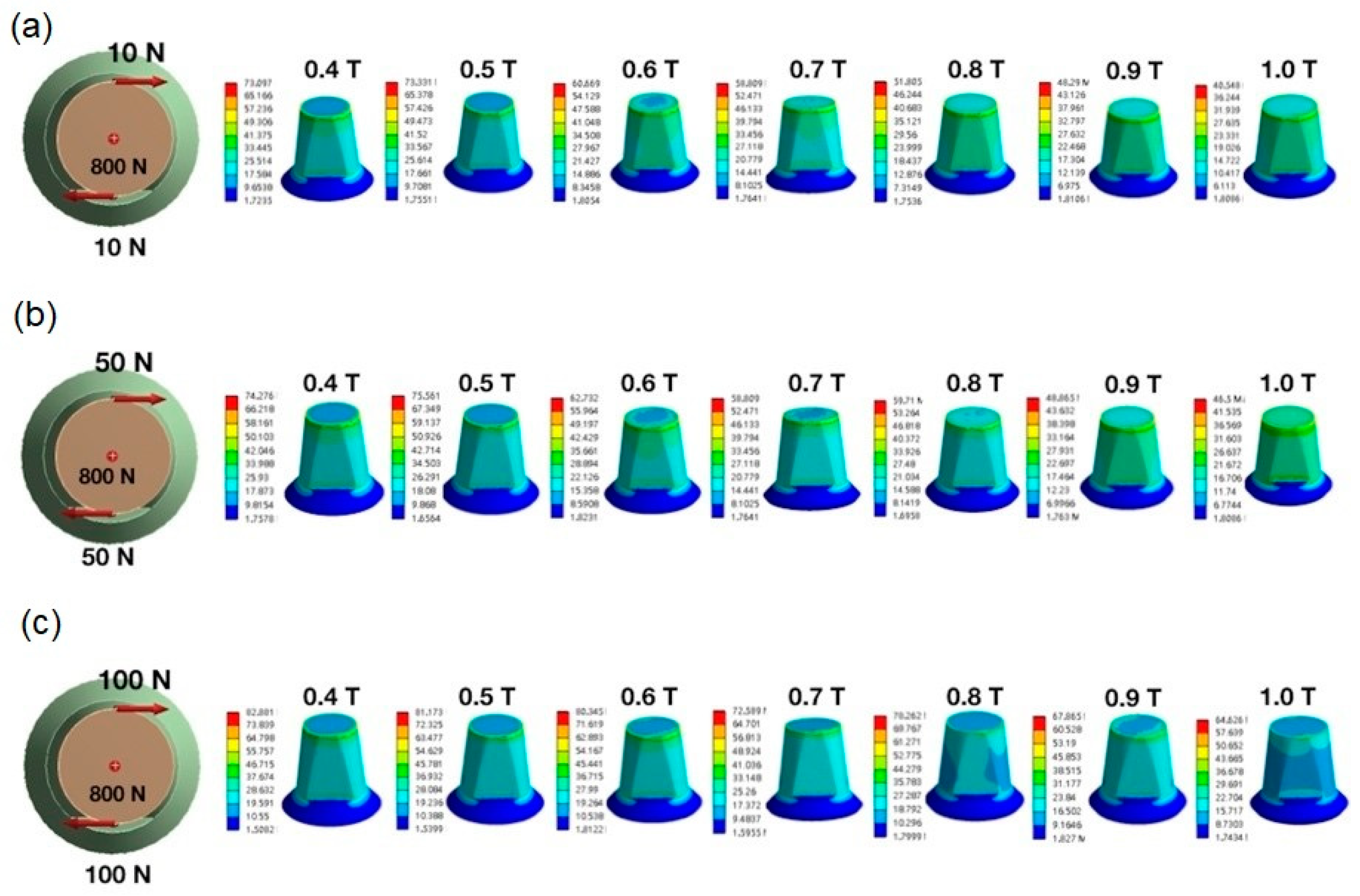
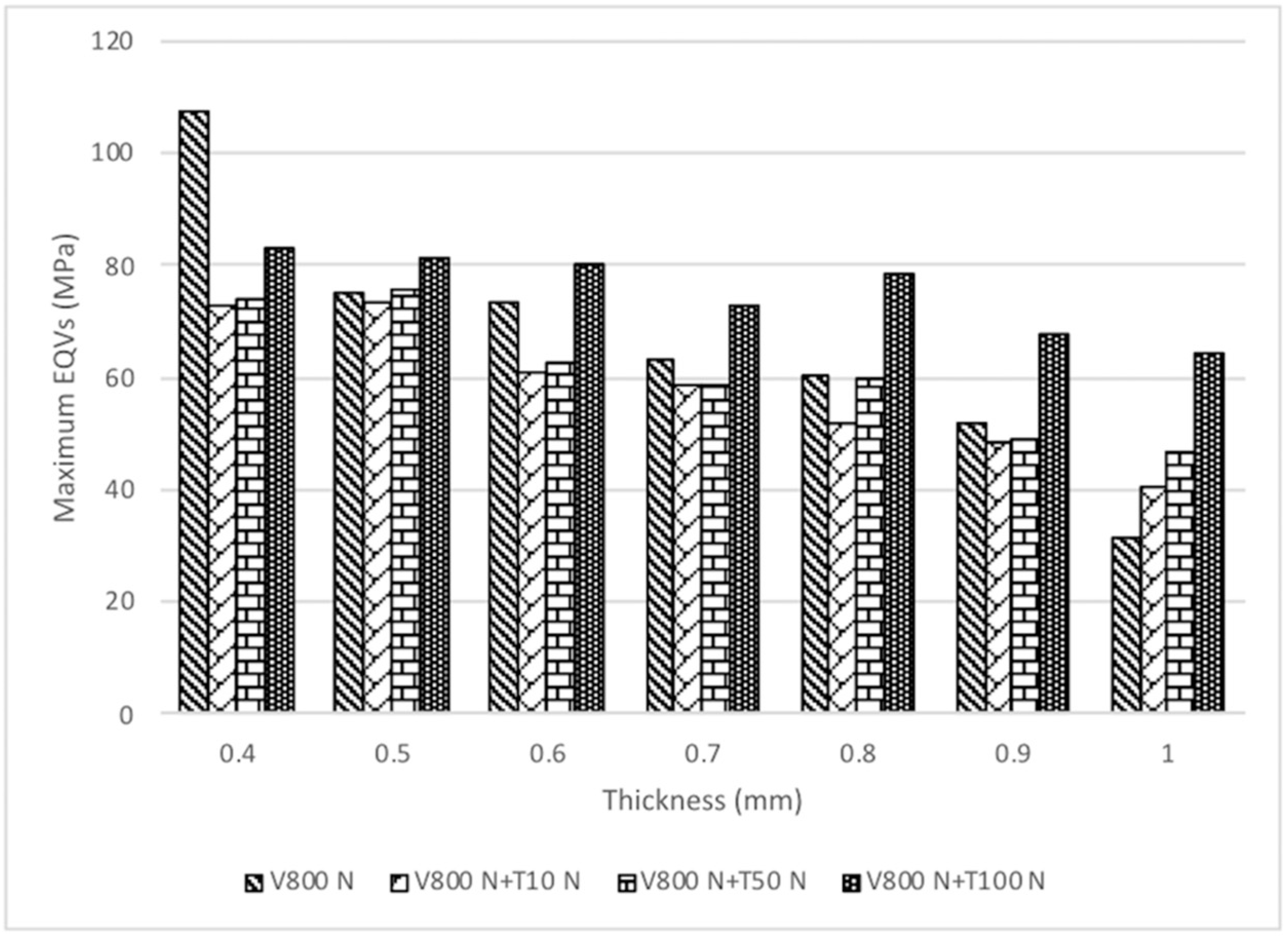
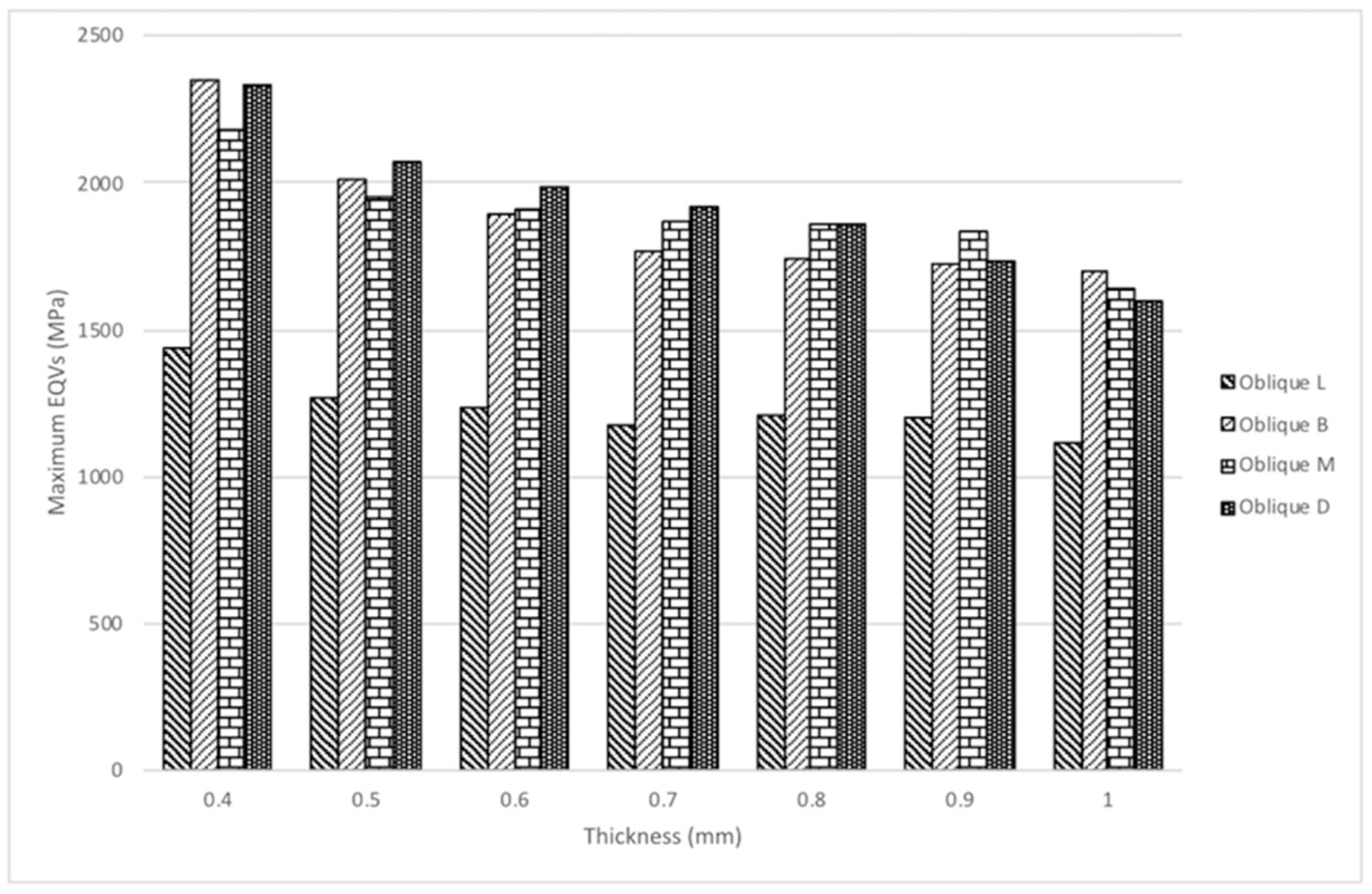
3.2. Finite Element Analysis
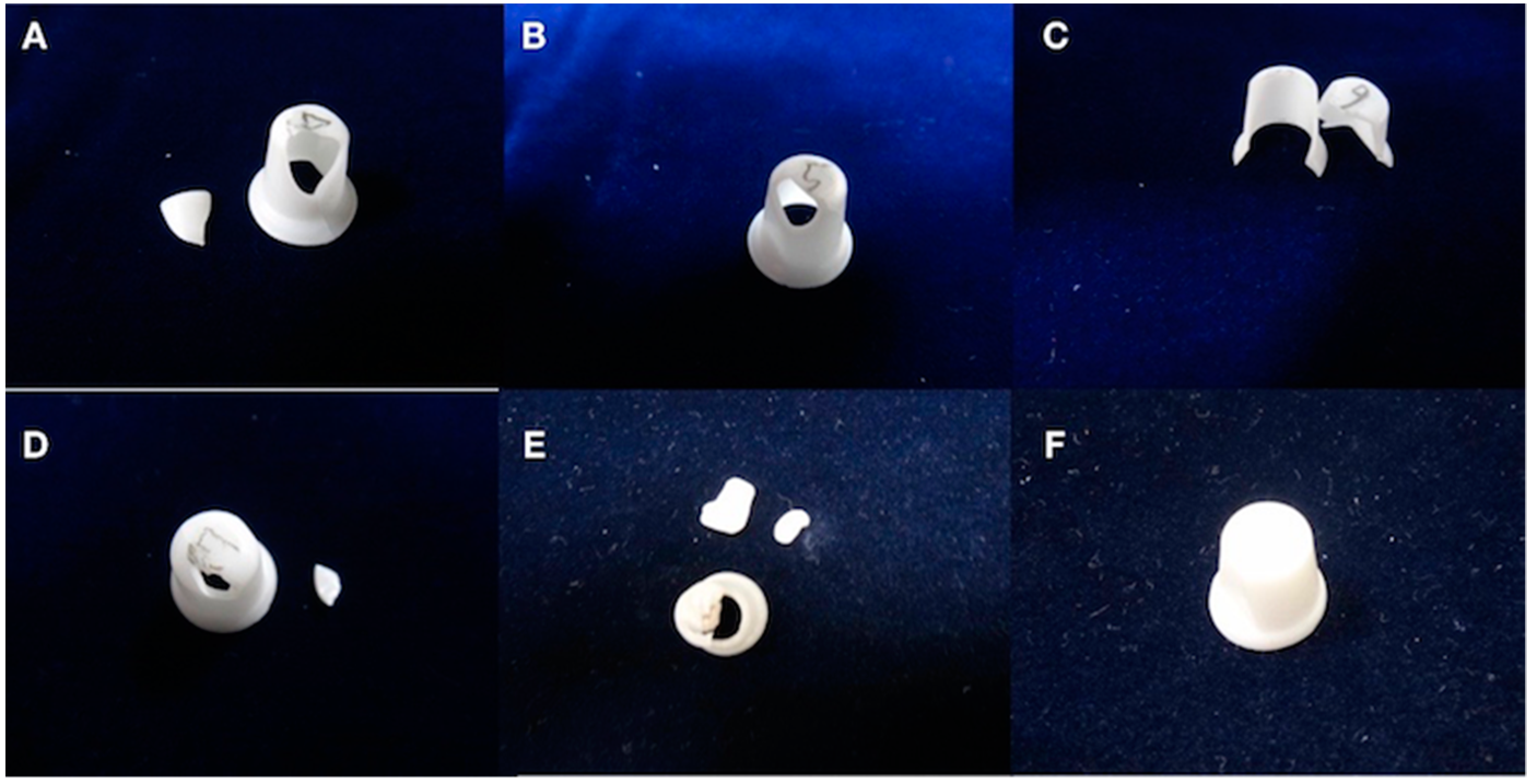
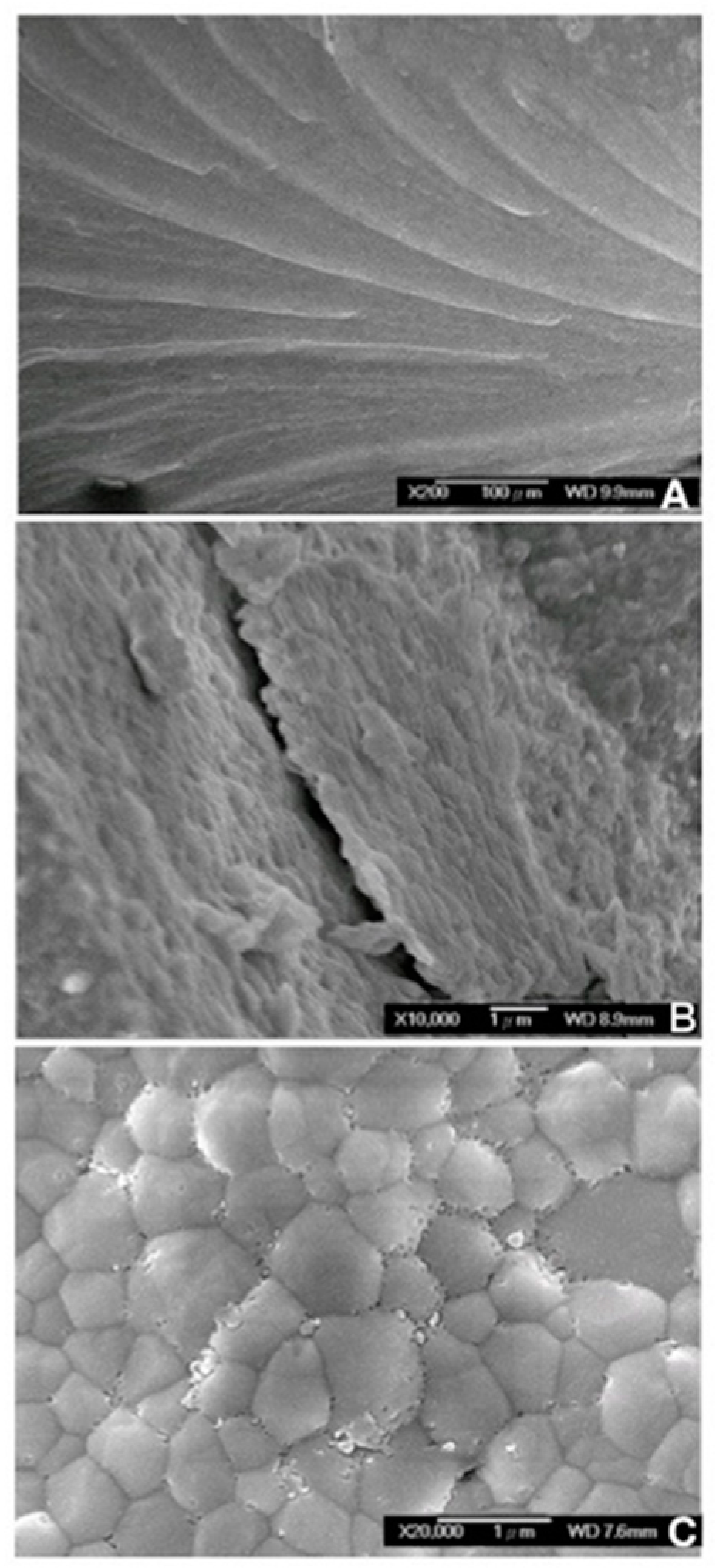
3.3. Microstructure of Zirconia Block after Cyclic Loading Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fang, H.; Tu, S.; Sheng, J.; Shao, A. Depression in sleep disturbance: A review on a bidirectional relationship, mechanisms and treatment. J. Cell. Mol. Med. 2019, 23, 2324–2332. [Google Scholar] [CrossRef] [PubMed]
- Barclay, N.L.; Gregory, A.M. Quantitative genetic research on sleep: A review of normal sleep, sleep disturbances and associated emotional, behavioural, and health-related difficulties. Sleep Med. Rev. 2013, 17, 29–40. [Google Scholar] [CrossRef]
- Murali, R.; Priyadarshni Rangarajan, A.M. Bruxism: Conceptual discussion and review. J. Pharm. Bioallied Sci. 2015, 7, S265–S270. [Google Scholar] [CrossRef] [PubMed]
- Mehta, S.; Banerji, S.; Millar, B.; Suarez-Feito, J.-M. Current concepts on the management of tooth wear: Part 2. Active restorative care 1: The management of localised tooth wear. Br. Dent. J 2012, 212, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Mehta, S.B.; Banerji, S.; Millar, B.J.; Suarez-Feito, J.-M. Current concepts on the management of tooth wear: Part 1. Assessment, treatment planning and strategies for the prevention and the passive management of tooth wear. Br. Dent. J. 2012, 212, 17–27. [Google Scholar] [CrossRef]
- Mehta, S.B.; Banerji, S.; Millar, B.J.; Suarez-Feito, J.-M. Current concepts on the management of tooth wear: Part 3. Active restorative care 2: The management of generalised tooth wear. Br. Dent. J 2012, 212, 121–127. [Google Scholar] [CrossRef][Green Version]
- Mehta, S.B.; Banerji, S.; Millar, B.J.; Suarez-Feito, J.-M. Current concepts on the management of tooth wear: Part 4. An overview of the restorative techniques and dental materials commonly applied for the management of tooth wear. Br. Dent. J. 2012, 212, 169–177. [Google Scholar] [CrossRef]
- Blanco Aguilera, A.; Gonzalez Lopez, L.; Blanco Aguilera, E.; De la Hoz Aizpurua, J.; Rodriguez Torronteras, A.; Segura Saint-Gerons, R.; Blanco Hungría, A. Relationship between self-reported sleep bruxism and pain in patients with temporomandibular disorders. J. Oral Rehabil. 2014, 41, 564–572. [Google Scholar] [CrossRef] [PubMed]
- Dıraçoğlu, D.; Alptekin, K.; Çifter, E.D.; Güçlü, B.; Karan, A.; Aksoy, C. Relationship between maximal bite force and tooth wear in bruxist and non-bruxist individuals. Arch. Oral Biol. 2011, 56, 1569–1575. [Google Scholar] [CrossRef]
- Raadsheer, M.; Van Eijden, T.; Van Ginkel, F.; Prahl-Andersen, B. Contribution of jaw muscle size and craniofacial morphology to human bite force magnitude. J. Dent. Res. 1999, 78, 31–42. [Google Scholar] [CrossRef]
- Naert, I.; Quirynen, M.; van Steenberghe, D.; Darius, P. A study of 589 consecutive implants supporting complete fixed prostheses. Part II: Prosthetic aspects. J. Prosthet. Dent. 1992, 68, 949–956. [Google Scholar] [CrossRef]
- Schwarz, M.S. Mechanical complications of dental implants. Clin. Oral Implants Res. 2000, 11, 156–158. [Google Scholar] [CrossRef]
- Campos, R.E.; Soares, P.V.; Versluis, A.; Júnior, O.B.d.O.; Ambrosano, G.M.; Nunes, I.F. Crown fracture: Failure load, stress distribution, and fractographic analysis. J. Prosthet. Dent. 2015, 114, 447–455. [Google Scholar] [CrossRef]
- Yuan, J.C.C.; Sukotjo, C. Occlusion for implant-supported fixed dental prostheses in partially edentulous patients: A literature review and current concepts. J. Periodontal Implant Sci. 2013, 43, 51–57. [Google Scholar] [CrossRef]
- Sheridan, R.A.; Decker, A.M.; Plonka, A.B.; Wang, H.L. The role of occlusion in implant therapy: A comprehensive updated review. Implant Dent. 2016, 25, 829–838. [Google Scholar] [CrossRef]
- de Souza Melo, G.; Batistella, E.Â.; Bertazzo-Silveira, E.; Gonçalves, T.M.S.V.; de Souza, B.D.M.; Porporatti, A.L.; Flores-Mir, C.; Canto, G.D.L. Association of sleep bruxism with ceramic restoration failure: A systematic review and meta-analysis. J. Prosthet. Dent. 2018, 119, 354–362. [Google Scholar] [CrossRef] [PubMed]
- Piconi, C.; Maccauro, G. Zirconia as a ceramic biomaterial. Biomaterials 1999, 20, 1–25. [Google Scholar] [CrossRef]
- Zhang, Y.; Chai, H.; Lawn, B.R. Graded structures for all-ceramic restorations. J. Dent. Res. 2010, 89, 417–421. [Google Scholar] [CrossRef]
- Hamburger, J.; Opdam, N.; Bronkhorst, E.; Huysmans, M. Indirect restorations for severe tooth wear: Fracture risk and layer thickness. J. Dent. 2014, 42, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Lawn, B.R.; Lloyd, I.K. Characterization of damage modes in dental ceramic bilayer structures. J. Biomed. Mater. Res. 2002, 63, 137–145. [Google Scholar] [CrossRef]
- Denry, I.; Kelly, J.R. State of the art of zirconia for dental applications. Dent. Mater. 2008, 24, 299–307. [Google Scholar] [CrossRef] [PubMed]
- Alghazzawi, T.F.; Lemons, J.; Liu, P.-R.; Essig, M.E.; Janowski, G.M. The failure load of CAD/CAM generated zirconia and glass-ceramic laminate veneers with different preparation designs. J. Prosthet. Dent. 2012, 108, 386–393. [Google Scholar] [CrossRef]
- Lan, T.H.; Liu, P.H.; Chou, M.M.; Lee, H.E. Fracture resistance of monolithic zirconia crowns with different occlusal thicknesses in implant prostheses. J. Prosthet. Dent. 2016, 115, 76–83. [Google Scholar] [CrossRef]
- Kelly, J.R.; Rungruanganunt, P.; Hunter, B.; Vailati, F. Development of a clinically validated bulk failure test for ceramic crowns. J. Prosthet. Dent. 2010, 104, 228–238. [Google Scholar] [CrossRef]
- Hsueh, C.H.; Thompson, G.; Jadaan, O.M.; Wereszczak, A.A.; Becher, P.F. Analyses of layer-thickness effects in bilayered dental ceramics subjected to thermal stresses and ring-on-ring tests. Dent. Mater. 2008, 24, 9–17. [Google Scholar] [CrossRef]
- Nejatidanesh, F.; Moradpoor, H.; Savabi, O. Clinical outcomes of zirconia-based implant-and tooth-supported single crowns. Clin. Oral Investig. 2016, 20, 169–178. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, J.; Luo, L.; Wang, Y. Does Bruxism Contribute to Dental Implant Failure? A Systematic Review and Meta-Analysis. Clin. Implant Dent. Relat. Res. 2016, 18, 410–420. [Google Scholar] [CrossRef] [PubMed]
- Hansen, T.L.; Schriwer, C.; Øilo, M.; Gjengedal, H. Monolithic zirconia crowns in the aesthetic zone in heavy grinders with severe tooth wear–An observational case-series. J. Dent. 2018, 72, 14–20. [Google Scholar] [CrossRef]
- Kim, Y.; Oh, T.J.; Misch, C.E.; Wang, H.L. Occlusal considerations in implant therapy: Clinical guidelines with biomechanical rationale. Clin. Oral Implants Res. 2005, 16, 26–35. [Google Scholar] [CrossRef]
- Hsu, Y.T.; Fu, J.H.; Al-Hezaimi, K.; Wang, H.L. Biomechanical implant treatment complications: A systematic review of clinical studies of implants with at least 1 year of functional loading. Int. J. Oral Maxillofac. Implants 2012, 27, 894–904. [Google Scholar] [PubMed]
- Komiyama, O.; Lobbezoo, F.; De Laat, A.; Iida, T.; Kitagawa, T.; Murakami, H.; Kato, T.; Kawara, M. Clinical management of implant prostheses in patients with bruxism. Int. J. Biomater. 2012, 2012. [Google Scholar] [CrossRef] [PubMed]
- Chai, H.; Lee, J.J.-W.; Mieleszko, A.J.; Chu, S.J.; Zhang, Y. On the interfacial fracture of porcelain/zirconia and graded zirconia dental structures. Acta Biomater. 2014, 10, 3756–3761. [Google Scholar] [CrossRef] [PubMed]
- Bona, A.; Pecho, O.; Alessandretti, R. Zirconia as a dental biomaterial. Materials 2015, 8, 4978–4991. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J. Theory of elasticity, 2nd ed.; McGraw-Hill: New York, NY, USA, 1951; pp. 372–377. [Google Scholar]
- Lawn, B.R. Indentation of ceramics with spheres: A century after Hertz. J. Am. Ceram. Soc. 1998, 81, 1977–1994. [Google Scholar] [CrossRef]
- Hanaor, D.A.; Gan, Y.; Einav, I. Contact mechanics of fractal surfaces by spline assisted discretisation. Int. J. Solids Struct. 2015, 59, 121–131. [Google Scholar] [CrossRef]
- Collings, E. Physical Metallurgy of Titanium Alloys; ASM American Society for Metals: Metals Park, OH, USA, 1984; pp. 201–209. [Google Scholar]
- Green, D.J.; Hannink, R.H.; Swain, M.V. Transformation Toughening of Ceramics; CRC Press: Boca Raton, FL, USA, 1989; pp. 126–138. [Google Scholar]
- Lawn, B.R.; Deng, Y.; Thompson, V.P. Use of contact testing in the characterization and design of all-ceramic crownlike layer structures: A review. J. Prosthet. Dent. 2001, 86, 495–510. [Google Scholar] [CrossRef]
- Lawn, B.R.; Pajares, A.; Zhang, Y.; Deng, Y.; Polack, M.A.; Lloyd, I.K.; Rekow, E.D.; Thompson, V.P. Materials design in the performance of all-ceramic crowns. Biomaterials 2004, 25, 2885–2892. [Google Scholar] [CrossRef]
- McNeill, C. Science and Practice of Occlusion; Quintessence Publishing: Batavia, IL, USA, 1997; pp. 437–456. [Google Scholar]

| Thickness (mm) | Total Cycle Number Mean ± SD | Specimen Number (n) Broken (+) or not (−) |
|---|---|---|
| 0.4 | 5.4 ± 4.6 a | 7 (+) |
| 0.5 | 12.4 ± 5.1 a | 7 (+) |
| 0.6 | 27.1 ± 16.1 a | 7 (+) |
| 0.7 | 1869.3 ± 2227 a | 7 (+) |
| 0.8 | 10,346.9 ± 11,239.3 a | 7 (+) |
| 0.9 | 50,853.4 ± 29,037.0 b | 5 (+)/2 (−) |
| 1.0 | 100,000 c | 7 (−) |
| p value * | <0.01 | <0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, T.-H.; Pan, C.-Y.; Liu, P.-H.; Chou, M.M.C. Fracture Resistance of Monolithic Zirconia Crowns in Implant Prostheses in Patients with Bruxism. Materials 2019, 12, 1623. https://doi.org/10.3390/ma12101623
Lan T-H, Pan C-Y, Liu P-H, Chou MMC. Fracture Resistance of Monolithic Zirconia Crowns in Implant Prostheses in Patients with Bruxism. Materials. 2019; 12(10):1623. https://doi.org/10.3390/ma12101623
Chicago/Turabian StyleLan, Ting-Hsun, Chin-Yun Pan, Pao-Hsin Liu, and Mitch M. C. Chou. 2019. "Fracture Resistance of Monolithic Zirconia Crowns in Implant Prostheses in Patients with Bruxism" Materials 12, no. 10: 1623. https://doi.org/10.3390/ma12101623
APA StyleLan, T.-H., Pan, C.-Y., Liu, P.-H., & Chou, M. M. C. (2019). Fracture Resistance of Monolithic Zirconia Crowns in Implant Prostheses in Patients with Bruxism. Materials, 12(10), 1623. https://doi.org/10.3390/ma12101623






