Interlaminar Shear Behavior of Laminated Carbon Fiber Reinforced Plastic from Microscale Strain Distributions Measured by Sampling Moiré Technique
Abstract
1. Introduction
2. Principle of Strain Measurement
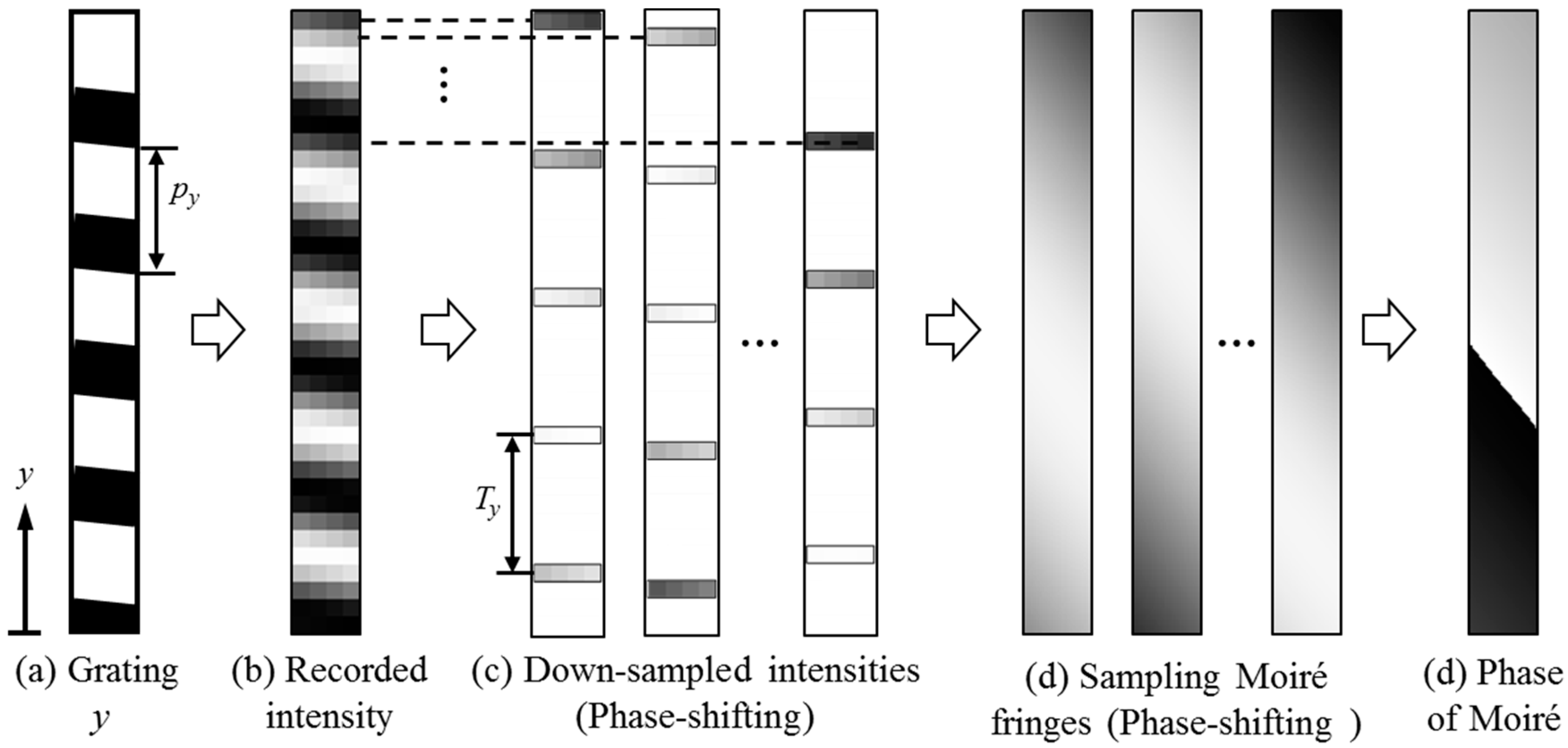
2.1. Phase Extraction from Sampling Moiré Method
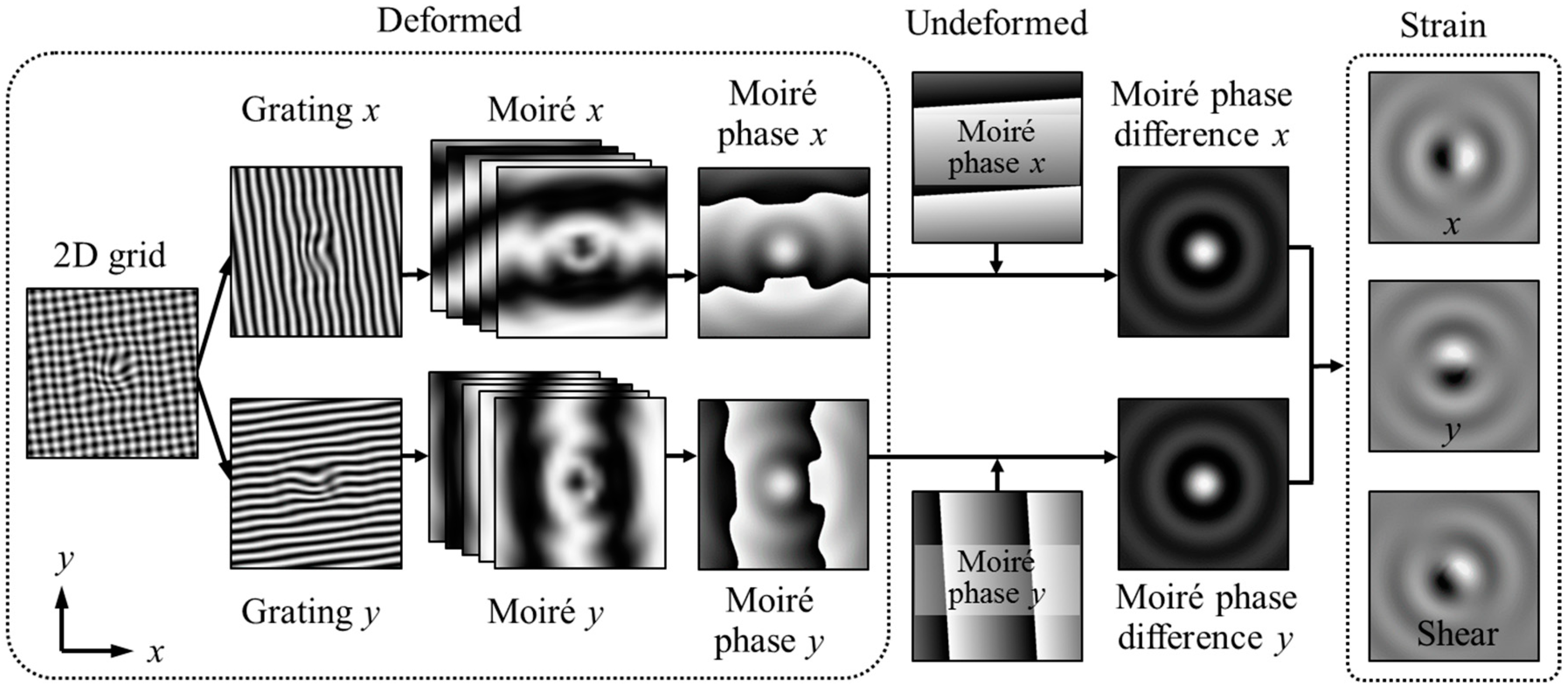
2.2. Strain Measurement Using Local Phase Unwrapping Algorithm
3. Materials and Experiments
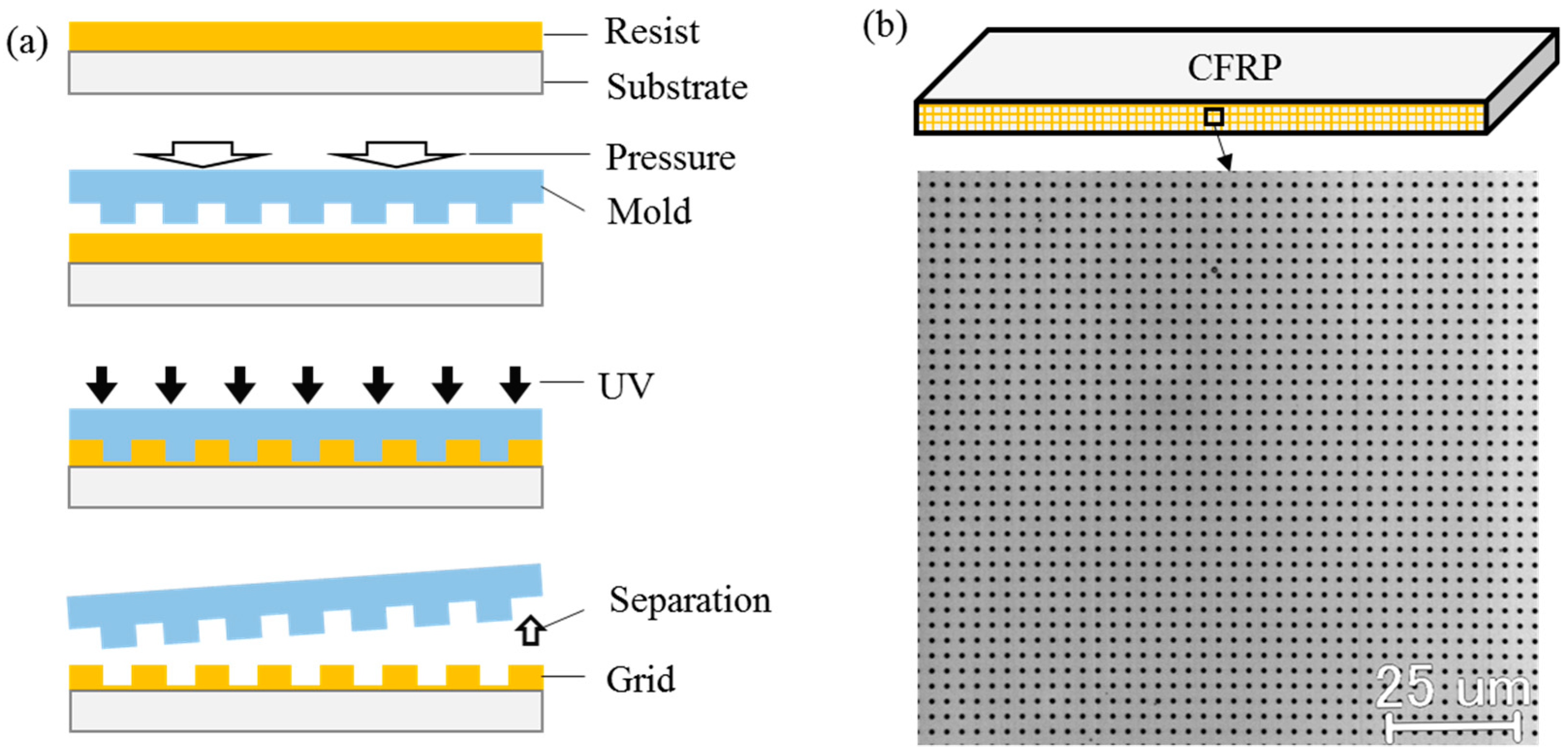
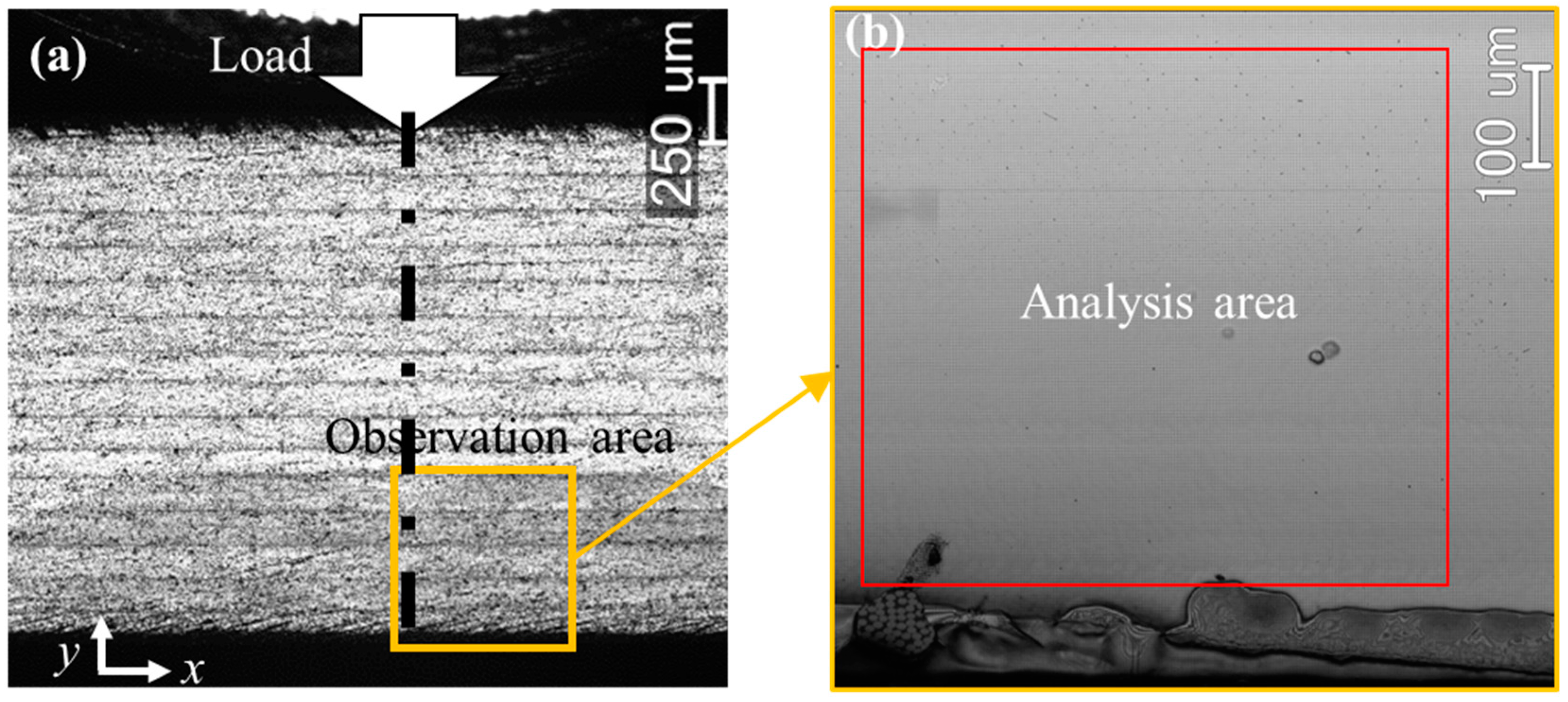
3.1. Specimen Preparation and Grid Fabrication
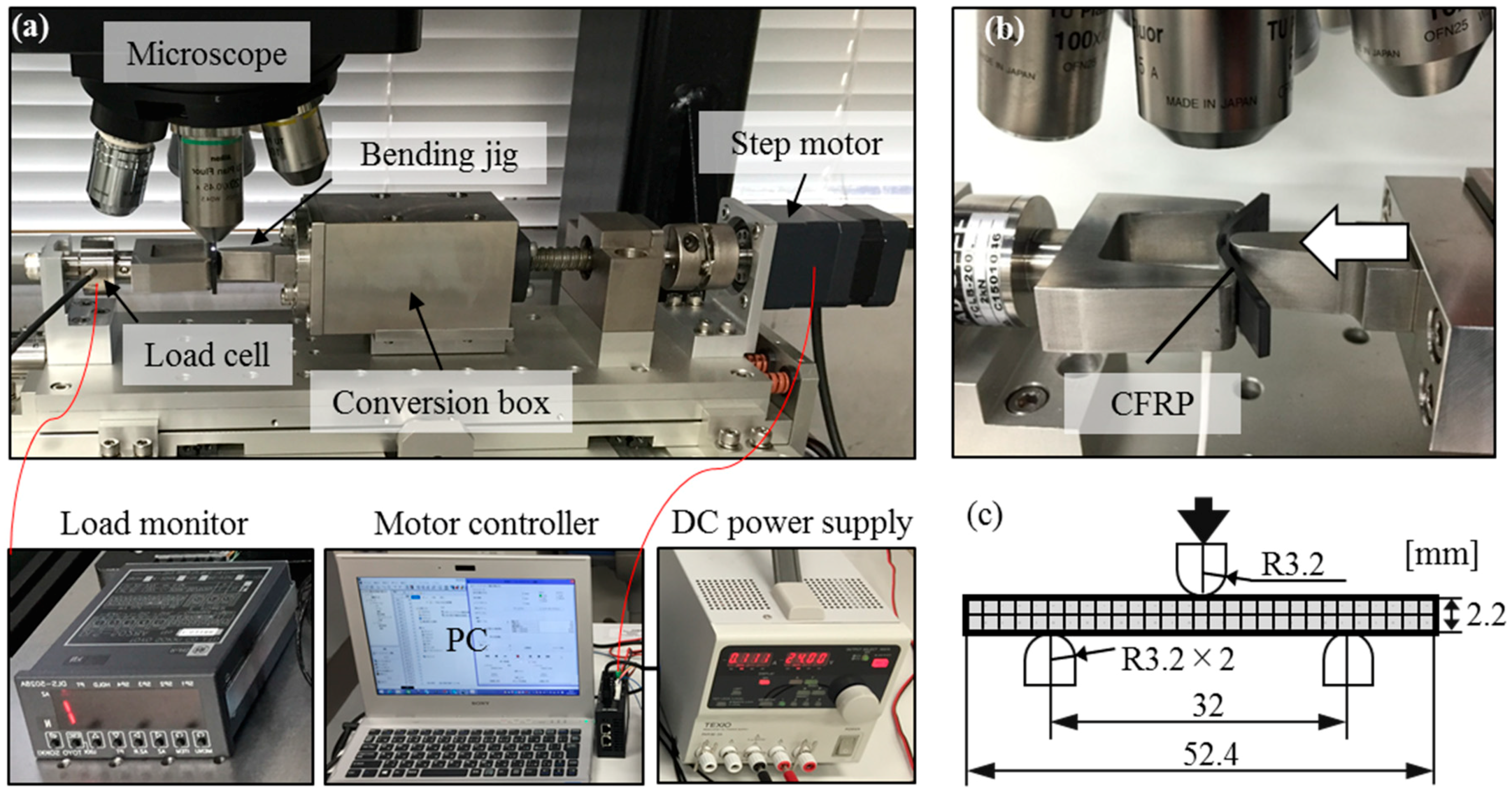
3.2. Three-Point Bending Test
4. Results and Discussion
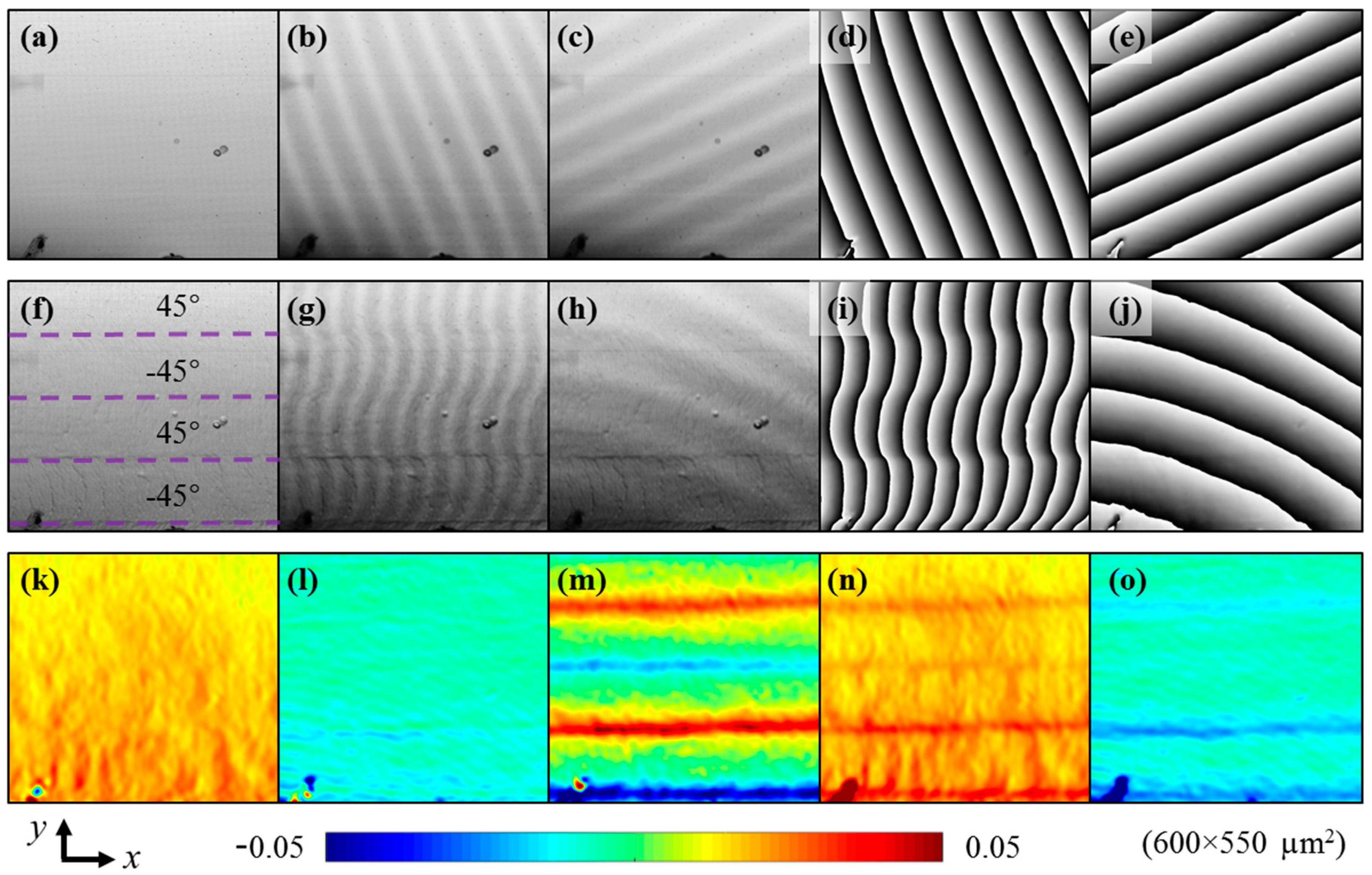
4.1. Normal, Shear and Principal Strain Distributions
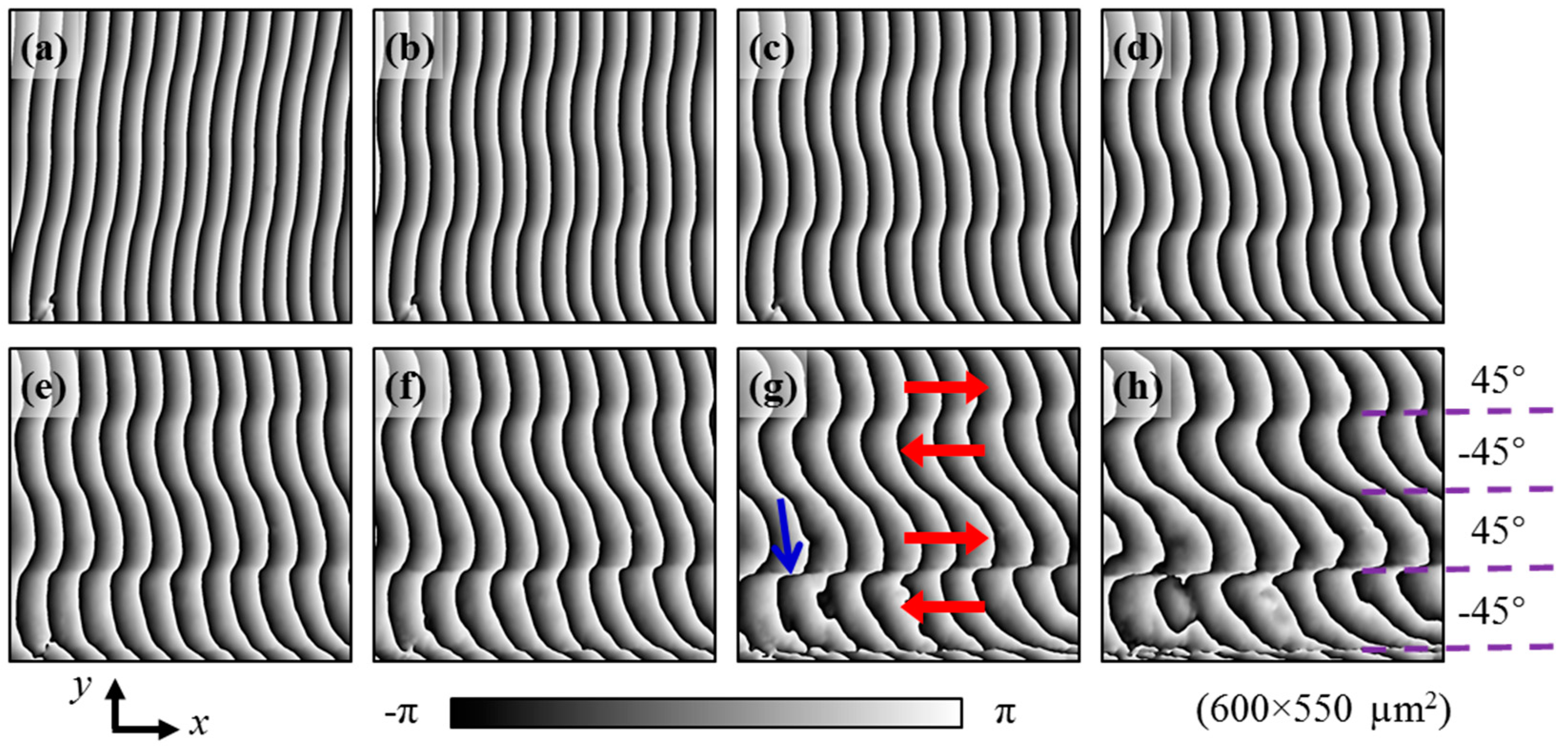
4.2. Visualization of Relative Slip Direction of Different Layers
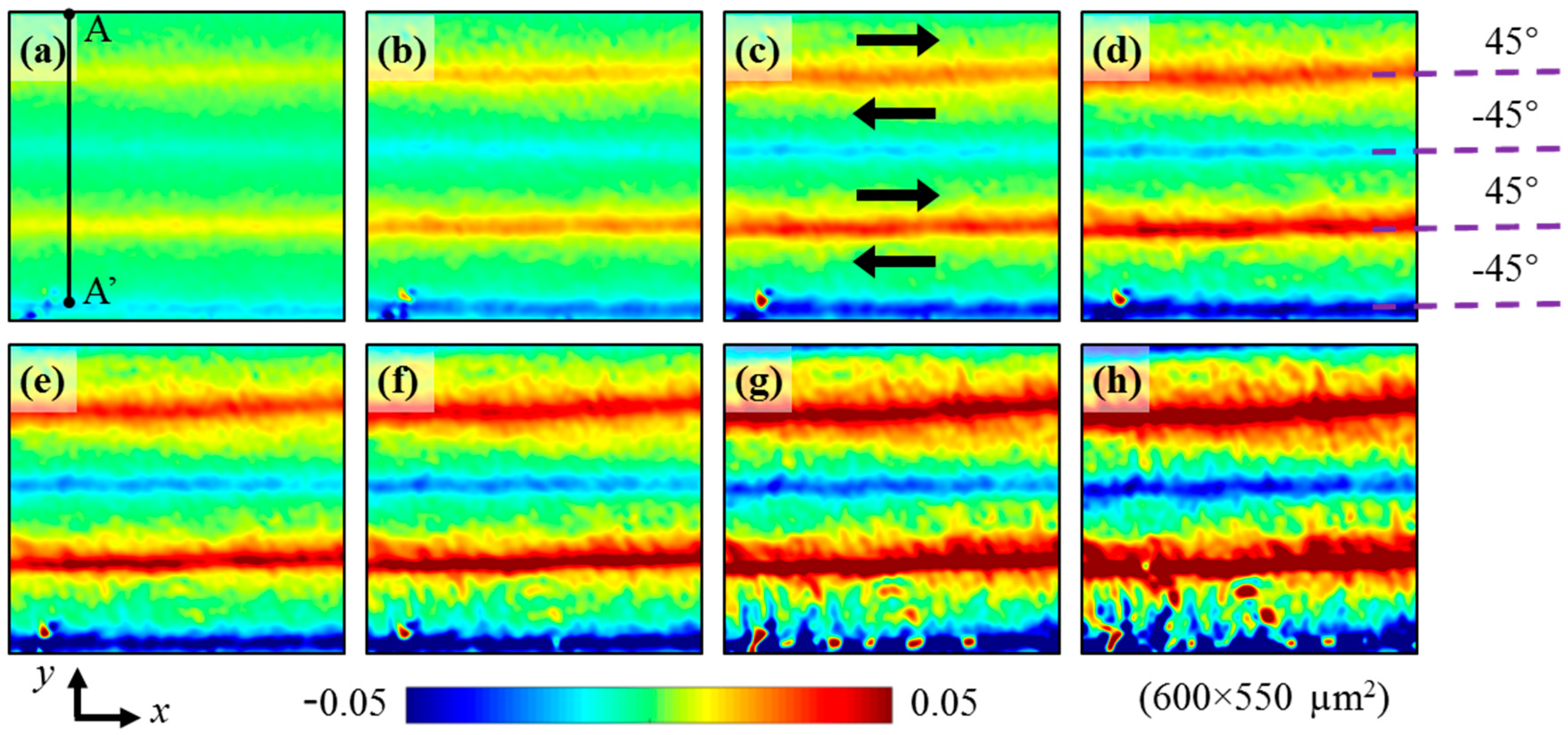
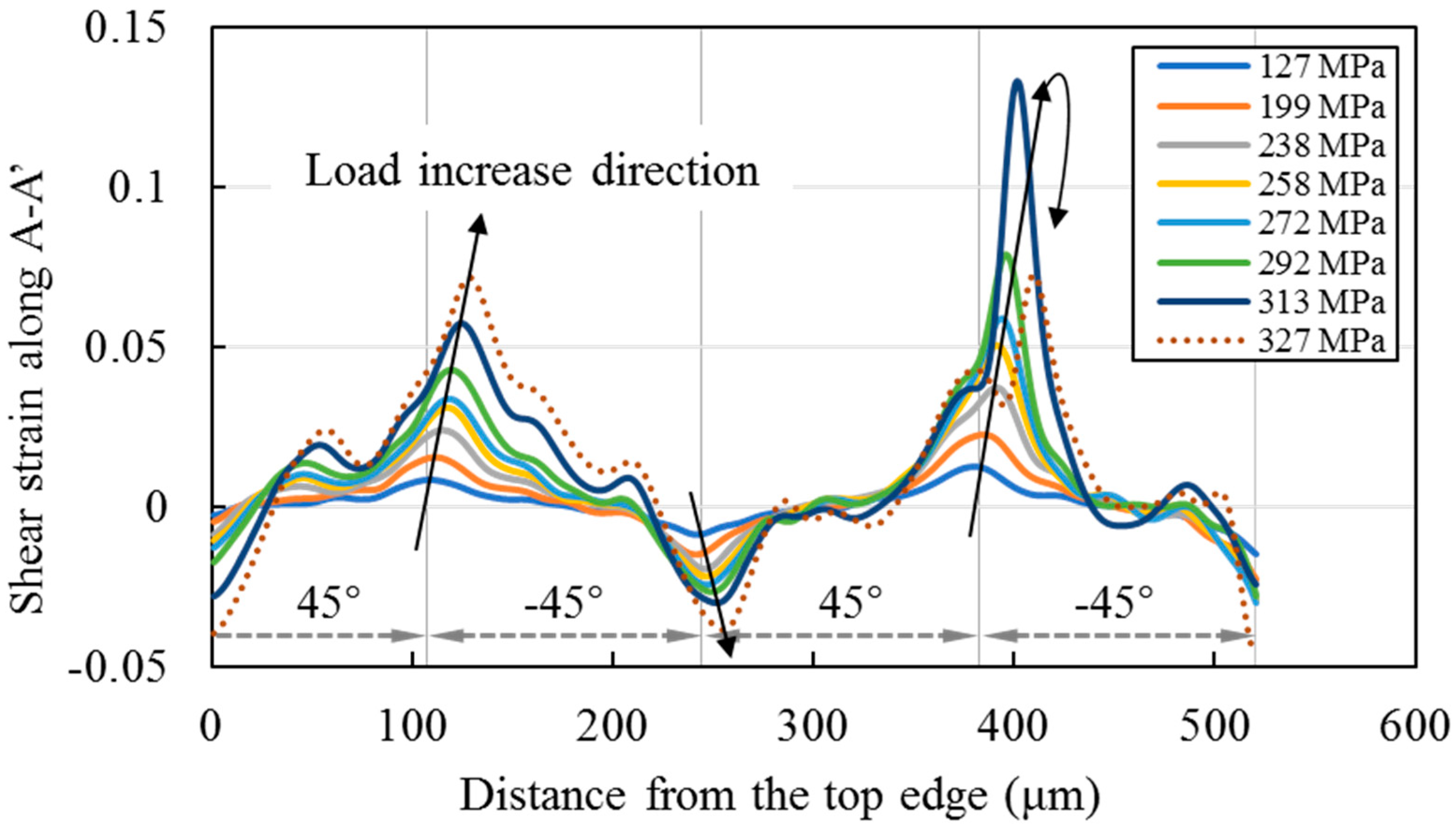
4.3. Evolution of Shear Strain Distribution
4.4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kretsis, G. A review of the tensile, compressive, flexural and shear properties of hybrid fibre-reinforced plastics. Composites 1987, 18, 13–23. [Google Scholar] [CrossRef]
- Ogihara, S.; Takeda, N. Interaction between transverse cracks and delamination during damage progress in CFRP cross-ply laminates. Compos. Sci. Technol. 1995, 54, 395–404. [Google Scholar] [CrossRef]
- Totry, E.; Molina-Aldareguía, J.M.; González, C.; LLorca, J. Effect of fiber, matrix and interface properties on the in-plane shear deformation of carbon-fiber reinforced composites. Compos. Sci. Technol. 2010, 70, 970–980. [Google Scholar] [CrossRef]
- Pham, H.B.; Al-Mahaidi, R.; Saouma, V. Modelling of CFRP–concrete bond using smeared and discrete cracks. Compos. Struct. 2006, 75, 145–150. [Google Scholar] [CrossRef]
- Wang, H.T.; Wu, G. Bond-slip models for CFRP plates externally bonded to steel substrates. Compos. Struct. 2018, 184, 1204–1214. [Google Scholar] [CrossRef]
- Namdari, N.; Dehghan, A. Natural frequencies and mode shapes for vibrations of rectangular and circular membranes: A numerical study. Int. Res. J. Adv. Eng. Sci. 2018, 3, 30–34. [Google Scholar]
- Fuller, J.; Wisnom, M. Pseudo-ductility and damage suppression in thin ply CFRP angle-ply laminates. Compos. Part A Appl. Sci. Manuf. 2015, 69, 64–71. [Google Scholar] [CrossRef]
- Ullah, H.; Harland, A.R.; Blenkinsopp, R.; Lucas, T.; Price, D.; Silberschmidt, V.V. Analysis of nonlinear shear deformations in CFRP and GFRP textile laminates. App. Mech. Mater. 2011, 70, 363–368. [Google Scholar] [CrossRef]
- McDonald, E.E.; Wallace, L.F.; Hickman, G.J.; Hsiao, K.T. Manufacturing and shear response characterization of carbon nanofiber modified CFRP using the out-of-autoclave-vacuum-bag-only cure process. Sci. World J. 2014, 830295. [Google Scholar] [CrossRef] [PubMed]
- Tessema, A.; Ravindran, S.; Wohlford, A.; Kidane, A. In-Situ observation of damage evolution in quasi-isotropic CFRP laminates. In Fracture, Fatigue, Failure and Damage Evolution; Carroll, J., Xia, S.M., Beese, A.M., Berke, R.B., Pataky, G.J., Eds.; Springer: New York, NY, USA, 2018; Volume 7, pp. 67–72. [Google Scholar]
- Mistou, S.; Fazzini, M.; Karama, M. Shear test on CFRP full-field measurement and finite element analysis. Adv. Mater. Res. 2010, 112, 49–62. [Google Scholar] [CrossRef]
- Sciammarella, C.A. The moiré method—A review. Exp. Mech. 1982, 22, 418–433. [Google Scholar] [CrossRef]
- Patorski, K. Handbook of the Moiré Fringe Technique; Elsevier Science: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Anastasi, R.F. An Introduction to Moire Methods with Applications in Composite Materials; U.S. Army Materials Technology Laboratory: Watertown, MA, USA, 1992; p. 60. [Google Scholar]
- Yoneyama, S.; Ifju, P.G.; Rohde, S.E. Identifying through-thickness material properties of carbon-fiber-reinforced plastics using the virtual fields method combined with moiré interferometry. Adv. Compos. Mater. 2018, 27, 1–17. [Google Scholar] [CrossRef]
- Wang, Q.; Ri, S.; Tsuda, H. Micro/nano-scale strain distribution measurement from sampling Moiré fringes. J. Vis. Exp. 2017, 123, e55739. [Google Scholar]
- Walker, C.A. Handbook of Moiré Measurement; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Arakawa, K.; Ishiguma, M.; Takahashi, K. Study of mode I interlaminar fracture in CFRP laminates by moiré interferometry. Int. J. Fract. 1994, 66, 205–212. [Google Scholar] [CrossRef]
- Weller, R.; Shepard, B. Displacement measurement by mechanical interferometry. Proc. Soc. Exp. Stress Anal. 1948, 6, 35–38. [Google Scholar]
- Ifju, P.; Han, B. Recent applications of moiré interferometry. Exp. Mech. 2010, 50, 1129–1147. [Google Scholar] [CrossRef]
- Wang, Q.; Kishimoto, S.; Yamauchi, Y. Three-directional structural characterization of hexagonal packed nanoparticles by hexagonal digital Moiré method. Opt. Lett. 2012, 37, 548–550. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.; Xie, H.; Wang, Q.; Zhu, J. Phase-shifting laser scanning confocal microscopy moiré method and its applications. Meas. Sci. Technol. 2010, 21, 055110. [Google Scholar] [CrossRef]
- Xie, H.; Wang, Q.; Kishimoto, S.; Dai, F. Characterization of planar periodic structure using inverse laser scanning confocal microscopy moiré method and its application in the structure of butterfly wing. J. Appl. Phys. 2007, 101, 103511. [Google Scholar] [CrossRef]
- Kishimoto, S.; Egashira, M.; Shinya, N. Microcreep deformation measurements by a moiré method using electron beam lithography and electron beam scan. Opt. Eng. 1993, 32, 522–526. [Google Scholar] [CrossRef]
- Kishimoto, S.; Wang, Q.; Xie, H.; Zhao, Y. Study of the surface structure of butterfly wings using the scanning electron microscopic moiré method. Appl. Opt. 2007, 46, 7026–7034. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Kishimoto, S.; Asundi, A.; Boay, C.G.; Shinya, N.; Yu, J.; Ngoi, B.K. In-plane deformation measurement using the atomic force microscope moiré method. Nanotechnology 2000, 11, 24–29. [Google Scholar] [CrossRef]
- Ri, S.; Fujigaki, M.; Morimoto, Y. Sampling moiré method for accurate small deformation distribution measurement. Exp. Mech. 2010, 50, 501–508. [Google Scholar] [CrossRef]
- Ri, S.; Muramatsu, T. Theoretical error analysis of the sampling moiré method and phase compensation methodology for single-shot phase analysis. Appl. Opt. 2012, 51, 3214–3223. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Ri, S.; Tsuda, H. Digital sampling Moiré as a substitute for microscope scanning Moiré for high-sensitivity and full-field deformation measurement at micron/nano scales. Appl. Opt. 2016, 55, 6858–6865. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Ri, S.; Tsuda, H.; Koyama, M.; Tsuzaki, K. Two-dimensional Moire phase analysis for accurate strain distribution measurement and application in crack prediction. Opt. Express 2017, 25, 13465–13480. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Ri, S.; Tsuda, H.; Kodera, M.; Suguro, K.; Miyashita, N. Visualization and automatic detection of defect distribution in GaN atomic structure from sampling Moiré phase. Nanotechnology 2017, 28, 455704. [Google Scholar] [CrossRef] [PubMed]
- Kodera, M.; Wang, Q.; Ri, S.; Tsuda, H.; Yoshioka, A.; Sugiyama, T.; Hamamoto, T.; Miyashita, N. Characterization technique for detection of atom-size crystalline defects and strains using two-dimensional fast-Fourier-transform sampling Moiré method. Jpn. J. Appl. Phys. 2018, 57, 04FC04. [Google Scholar] [CrossRef]
- Wang, Q.; Ri, S.; Tsuda, H.; Koyama, M. Optical full-field strain measurement method from wrapped sampling Moiré phase to minimize the influence of defects and its applications. Opt. Laser. Eng. 2018, 110, 155–162. [Google Scholar] [CrossRef]
- Ogihara, S.; Nakatani, H. Effect of ply thickness on mechanical properties in CFRP angle-ply laminates. In Proceedings of the 15th European Conference on Composite Materials, Venice, Italy, 24–28 June 2012. [Google Scholar]
- Fikry, M.M.; Ogihara, S.; Vinogradov, V. The effect of matrix cracking on mechanical properties in FRP laminates. Mech. Adv. Mater. Mod. Process. 2018, 4, 3. [Google Scholar] [CrossRef]
- Aebischer, H.A.; Waldner, S. A simple and effective method for filtering speckle-interferometric phase fringe patterns. Opt. Commun. 1999, 162, 205–210. [Google Scholar] [CrossRef]
- Mittelstedt, C.; Becker, W. Interlaminar stress concentrations in layered structures: Part I-a selective literature survey on the free-edge effect since 1967. J. Compos. Mater. 2004, 38, 1037–1062. [Google Scholar] [CrossRef]
- Wang, Q.; Kishimoto, S.; Tanaka, Y.; Kagawa, Y. Micro/submicro grating fabrication on metals for deformation measurement based on ultraviolet nanoimprint lithography. Opt. Laser. Eng. 2013, 51, 944–948. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Ri, S.; Tsuda, H.; Takashita, Y.; Kitamura, R.; Ogihara, S. Interlaminar Shear Behavior of Laminated Carbon Fiber Reinforced Plastic from Microscale Strain Distributions Measured by Sampling Moiré Technique. Materials 2018, 11, 1684. https://doi.org/10.3390/ma11091684
Wang Q, Ri S, Tsuda H, Takashita Y, Kitamura R, Ogihara S. Interlaminar Shear Behavior of Laminated Carbon Fiber Reinforced Plastic from Microscale Strain Distributions Measured by Sampling Moiré Technique. Materials. 2018; 11(9):1684. https://doi.org/10.3390/ma11091684
Chicago/Turabian StyleWang, Qinghua, Shien Ri, Hiroshi Tsuda, Yosuke Takashita, Ryuta Kitamura, and Shinji Ogihara. 2018. "Interlaminar Shear Behavior of Laminated Carbon Fiber Reinforced Plastic from Microscale Strain Distributions Measured by Sampling Moiré Technique" Materials 11, no. 9: 1684. https://doi.org/10.3390/ma11091684
APA StyleWang, Q., Ri, S., Tsuda, H., Takashita, Y., Kitamura, R., & Ogihara, S. (2018). Interlaminar Shear Behavior of Laminated Carbon Fiber Reinforced Plastic from Microscale Strain Distributions Measured by Sampling Moiré Technique. Materials, 11(9), 1684. https://doi.org/10.3390/ma11091684





