Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study
Abstract
1. Introduction
2. Review on Micromechanics Models
2.1. Numerical Micromechanics Models
2.2. Analytical Micromechanics Models
2.3. Micromechanics Models with Imperfect Interface
3. Comparison on Elastic Theories
3.1. General Framework
3.2. Summary of Elastic Models
3.2.1. Eshelby Model
3.2.2. SCM
3.2.3. Mori–Tanaka Model
3.2.4. GSCM
3.2.5. Rule of Mixture
3.2.6. Chamis Model
3.2.7. Halpin–Tsai Equations
3.2.8. Bridging Model
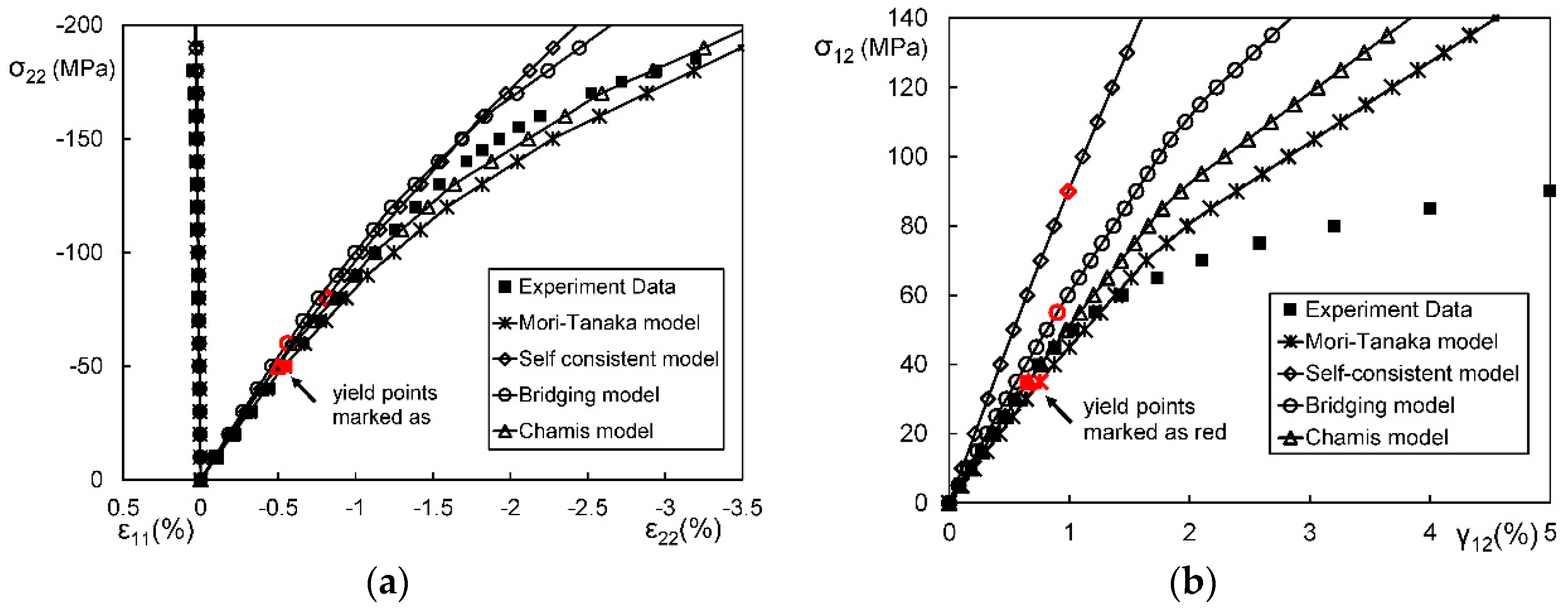
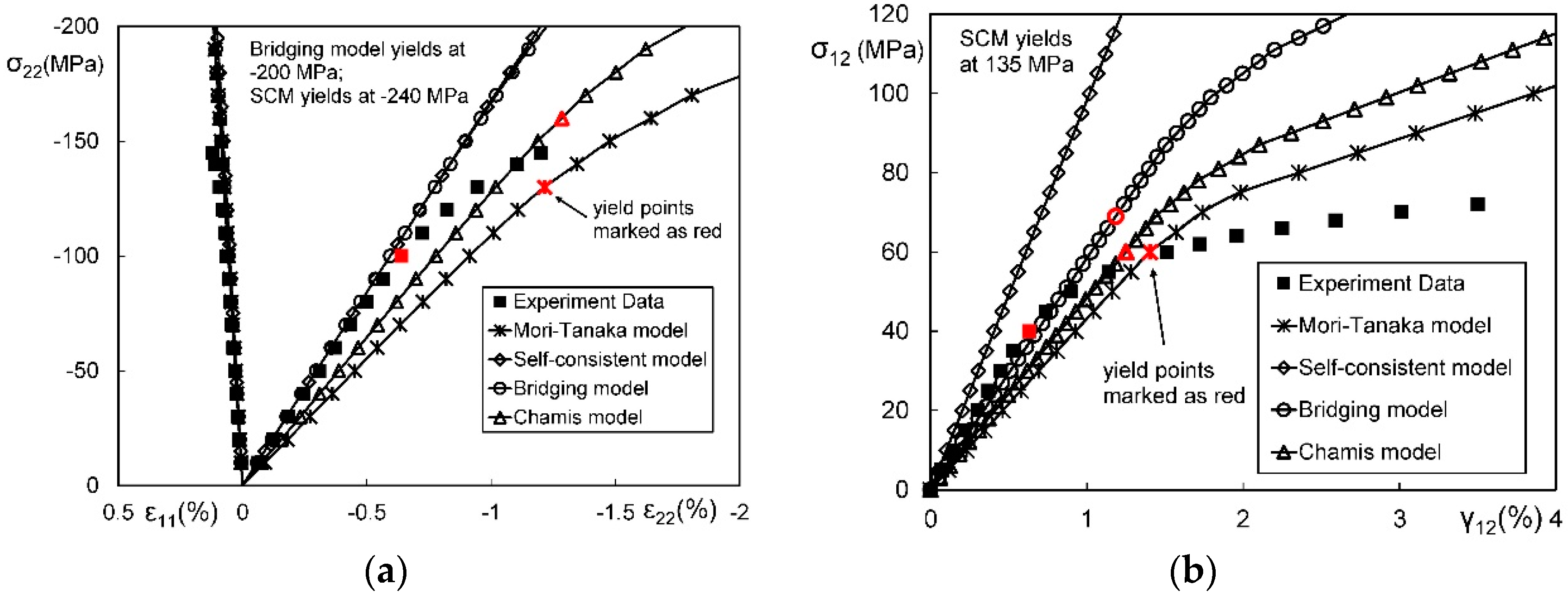
3.3. Quantitative Comparison
4. Comparison on Elastoplastic Behavior
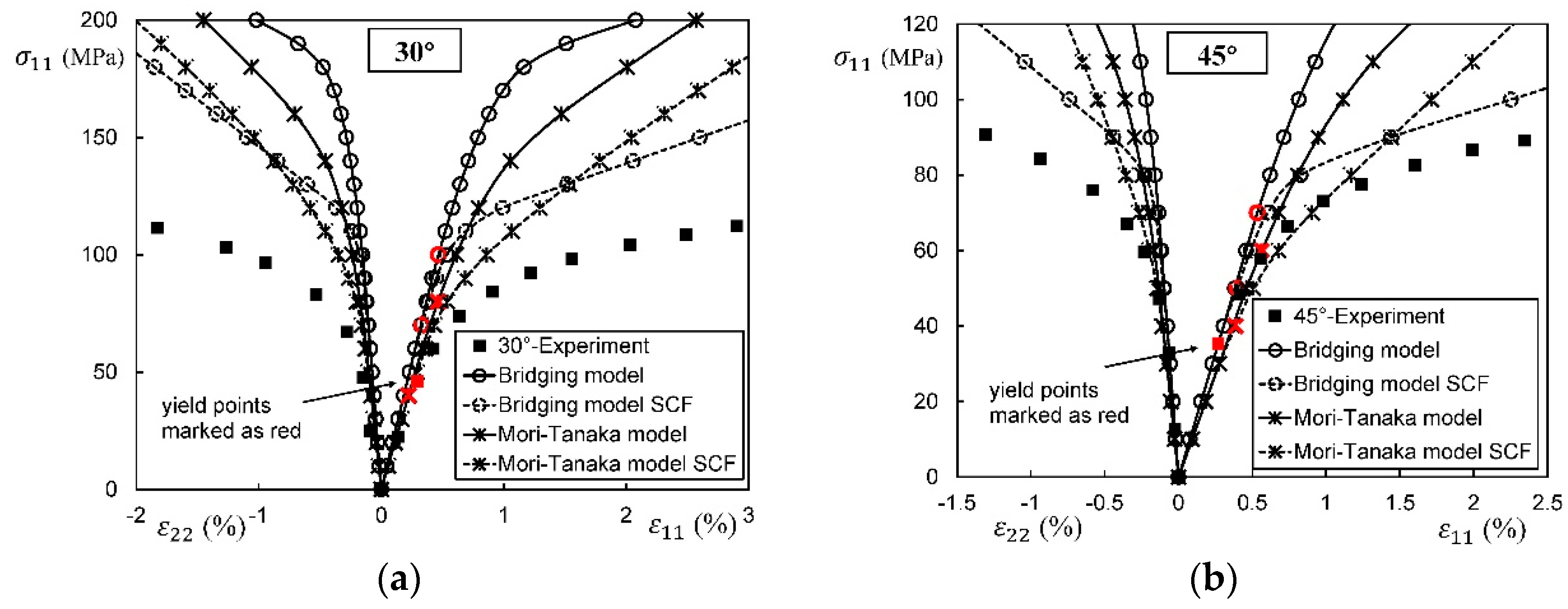
4.1. Comparison on Micromechanics Models
4.2. Comparison on Modifications on Yield Stress
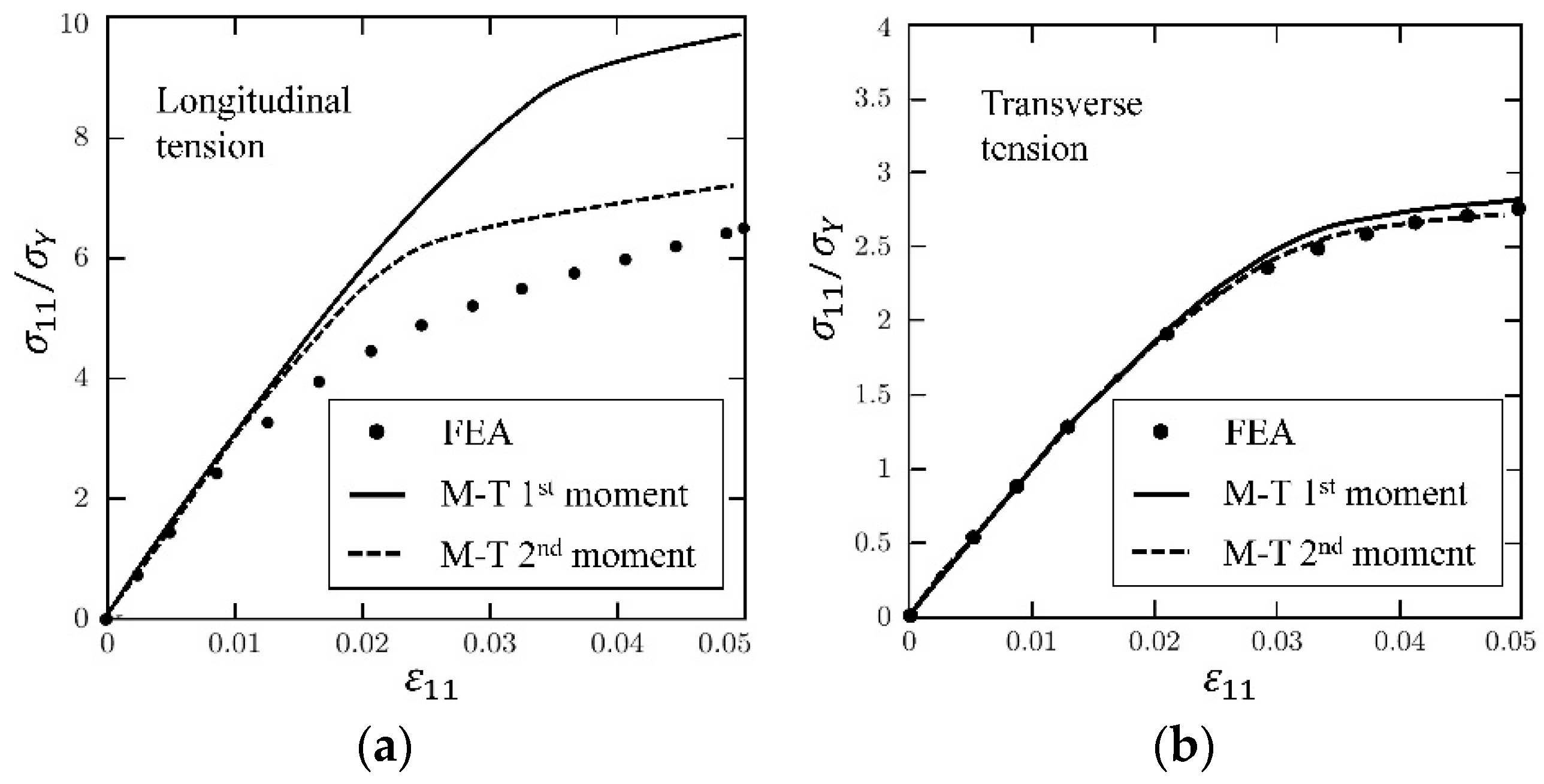
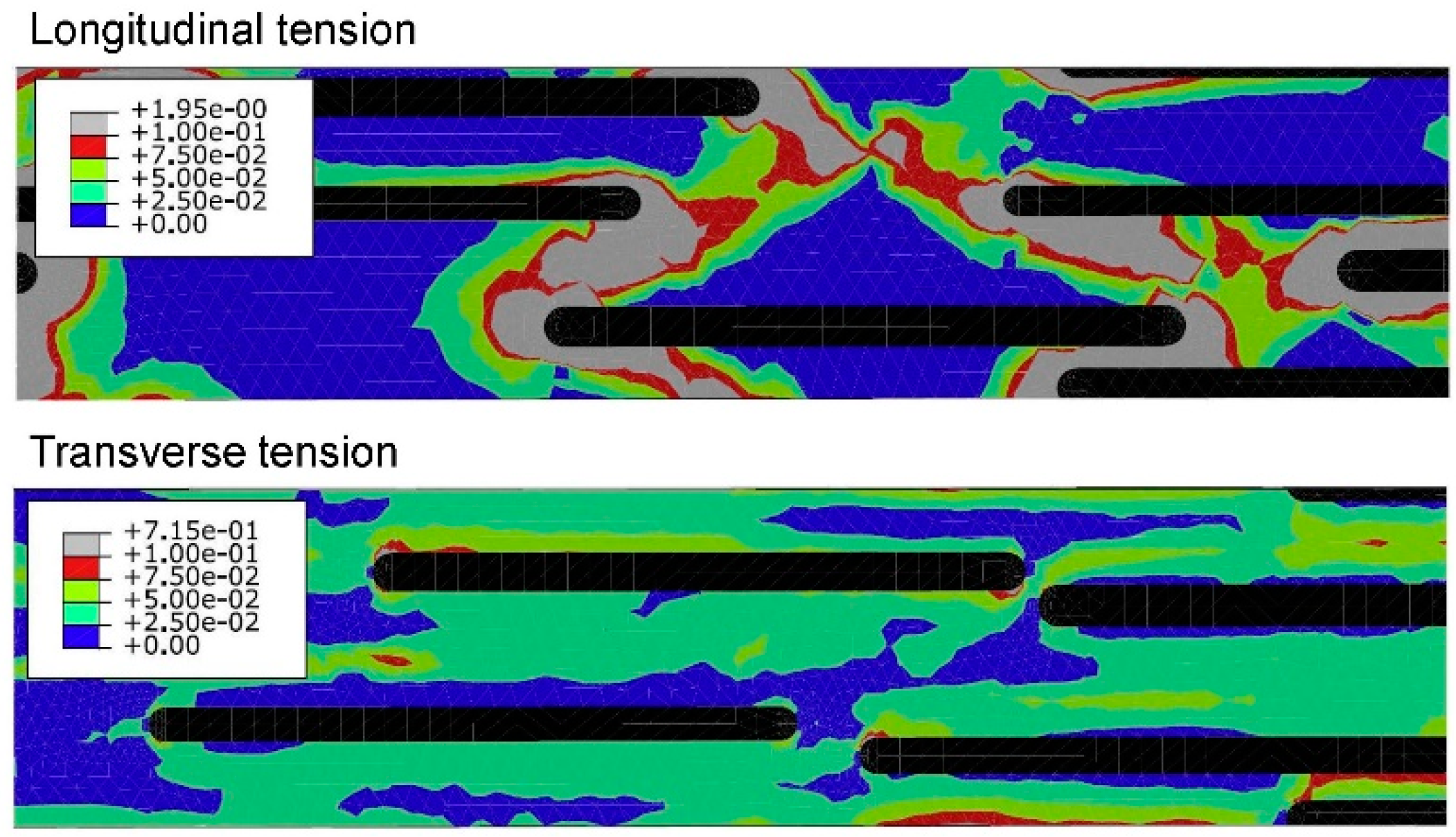
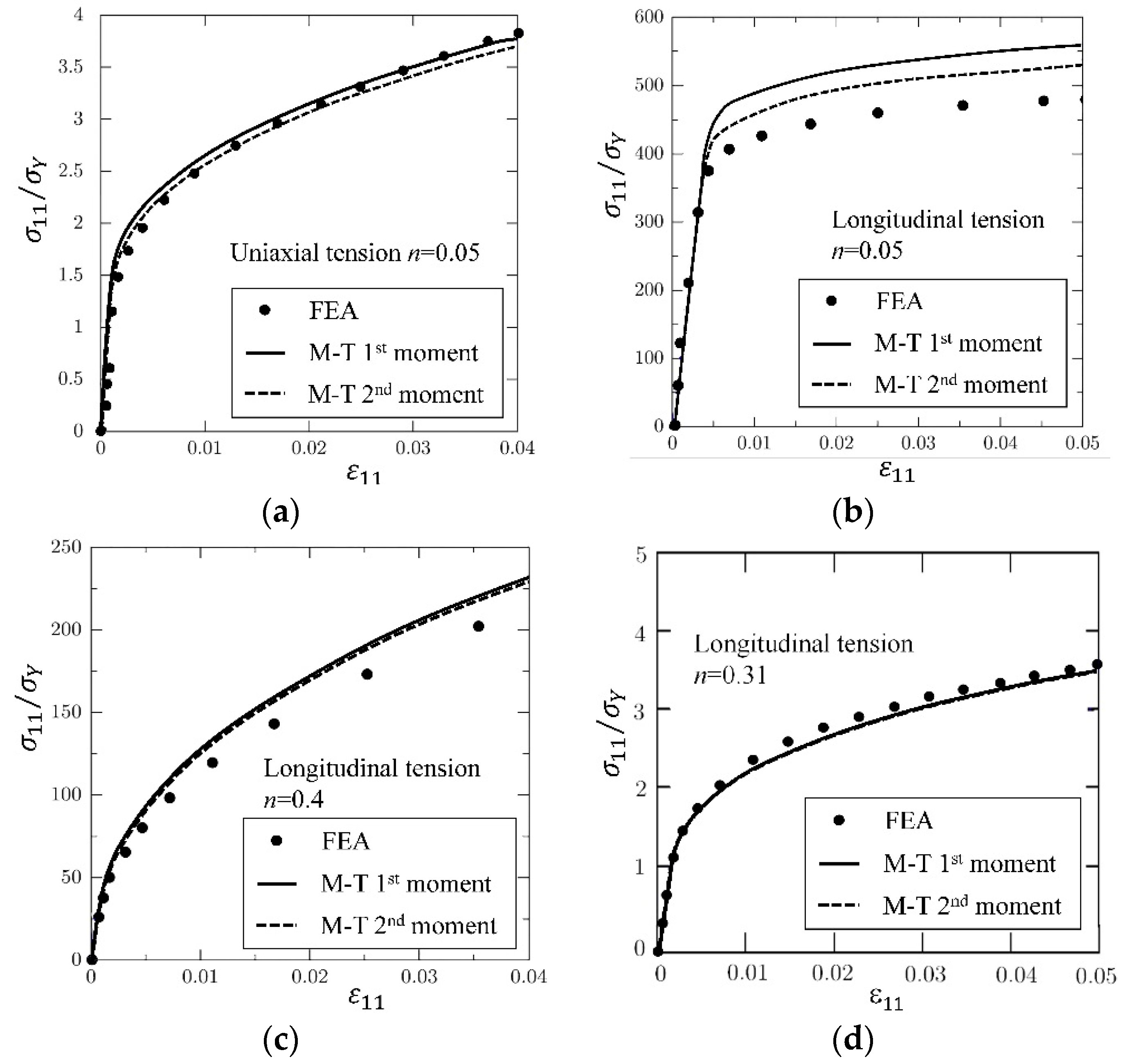
4.2.1. First Moment Approach
4.2.2. Second-Moment Approach
- (a)
- the inclusion aspect ratio is larger than 1,
- (b)
- the elastic stiffness contrast between a fiber and a matrix is high,
- (c)
- work-hardening phenomenon of a matrix is not significant.
4.2.3. SCFs in Matrix
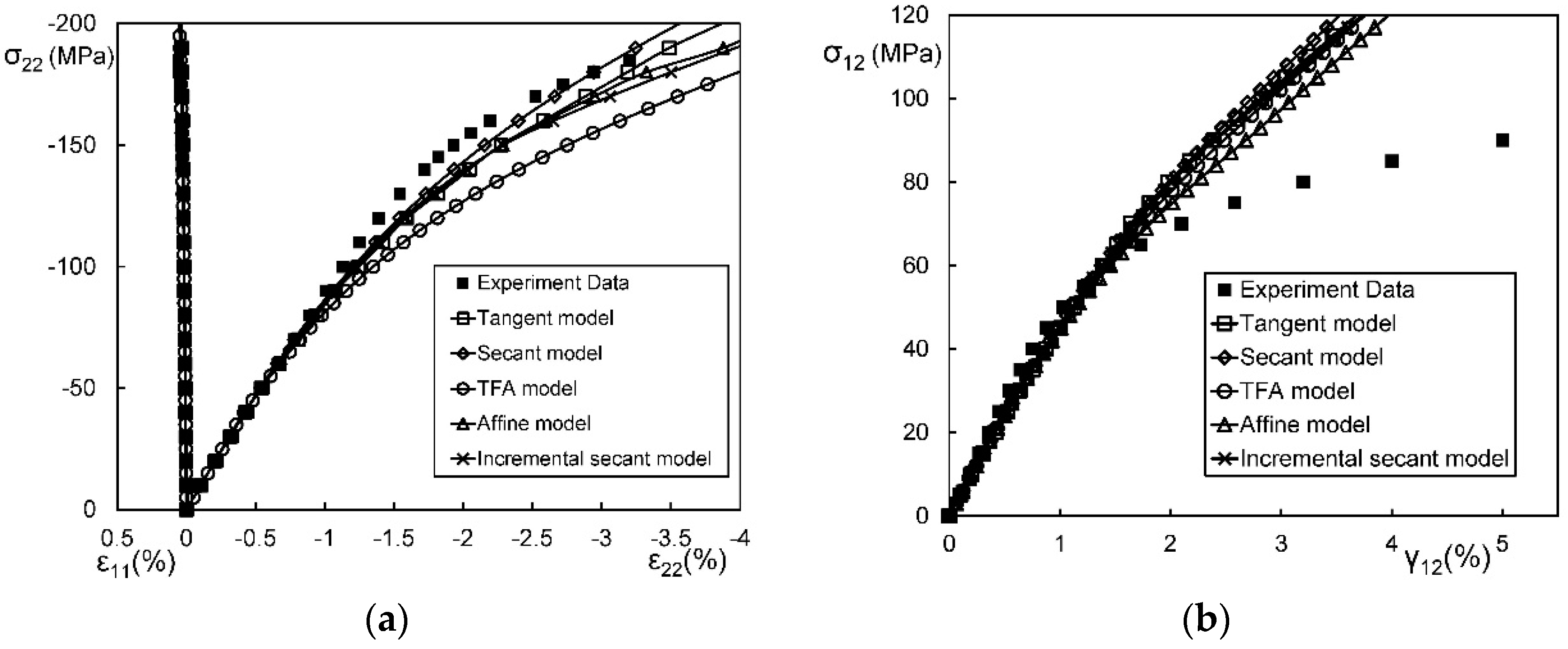
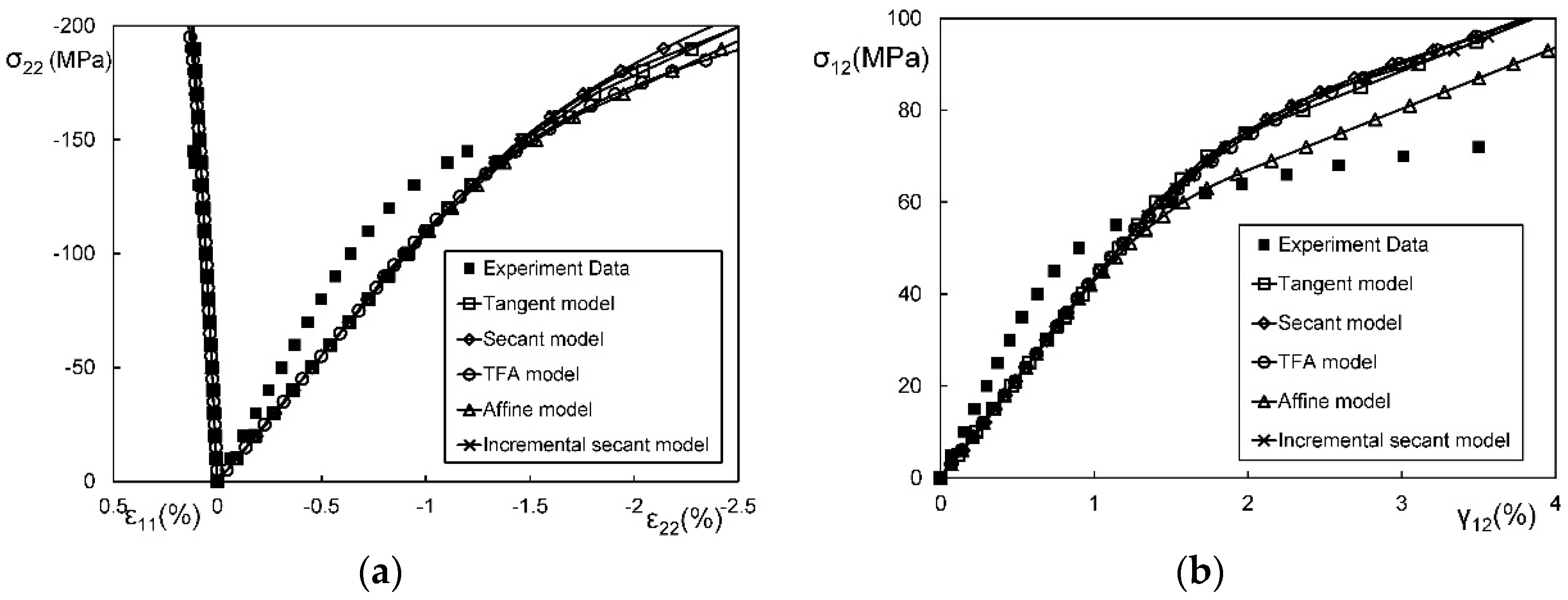
4.3. Comparison on Linearization
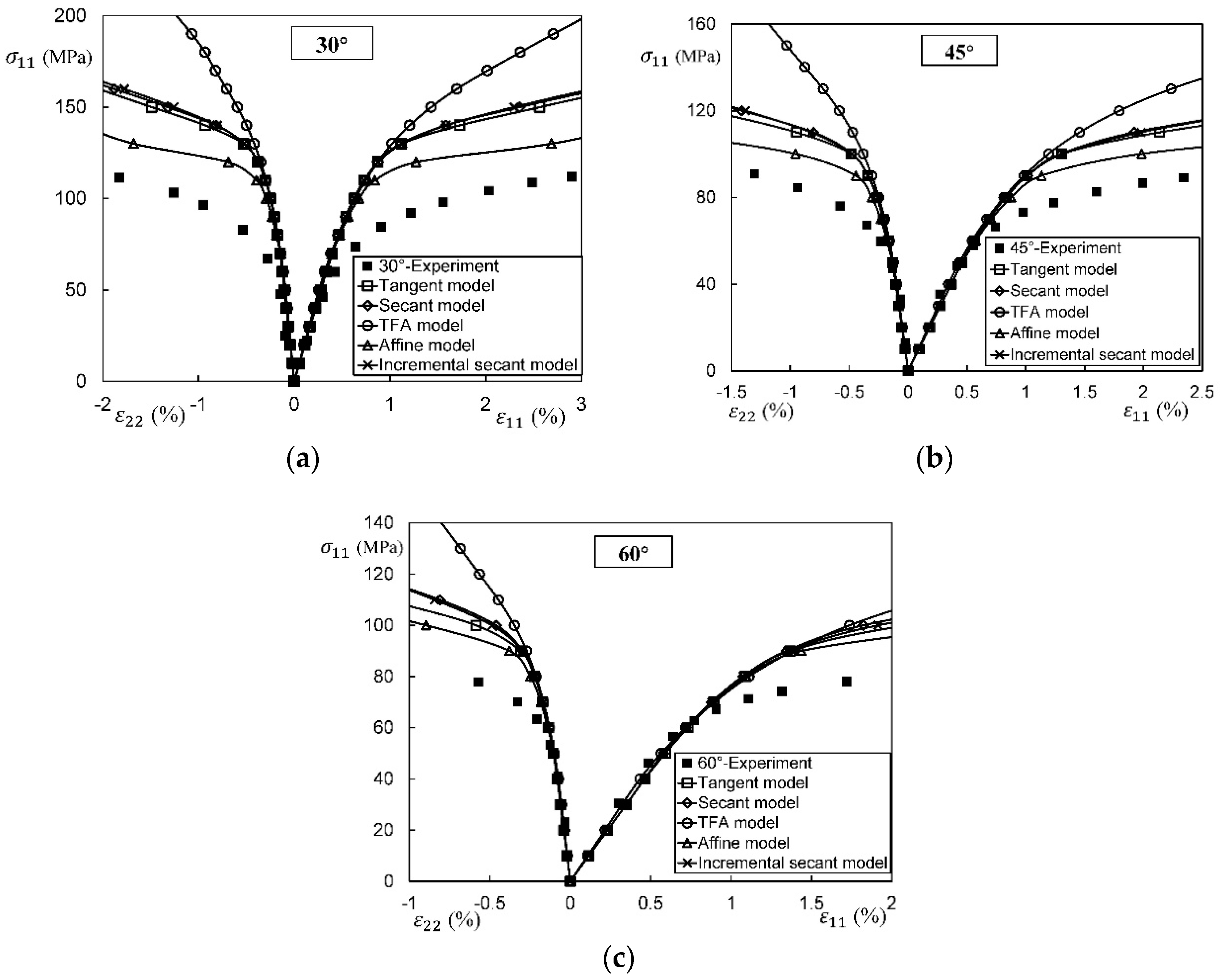
4.3.1. Secant Linearization
4.3.2. Tangent Linearization
4.3.3. Transformation Field Analysis (TFA)
4.3.4. Affine Formulation
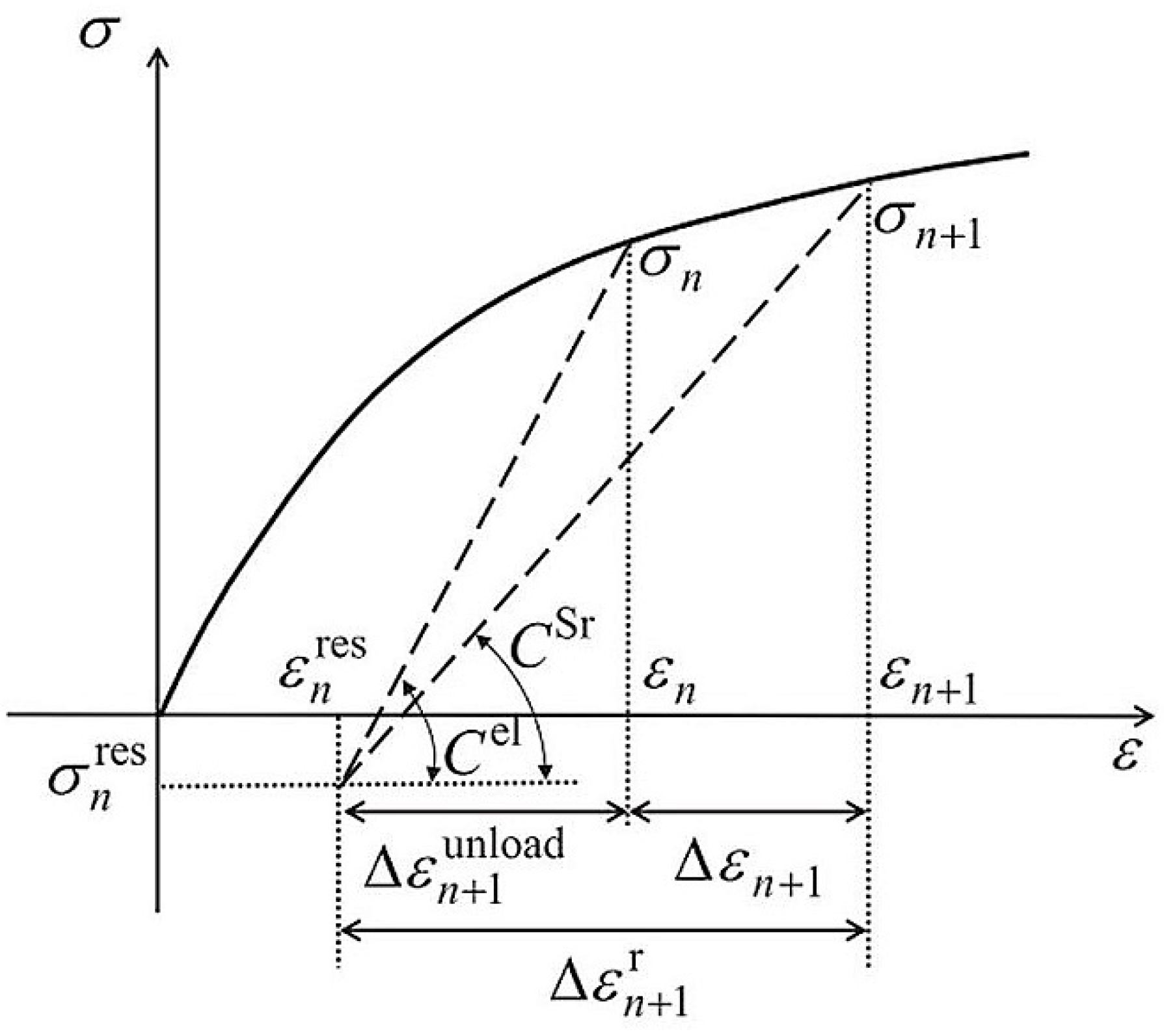
4.3.5. Incremental-Secant Scheme
4.3.6. Quantitative Comparison on the Linearizations
4.4. Comparison on Modifications of a Plastic Eshelby Tensor
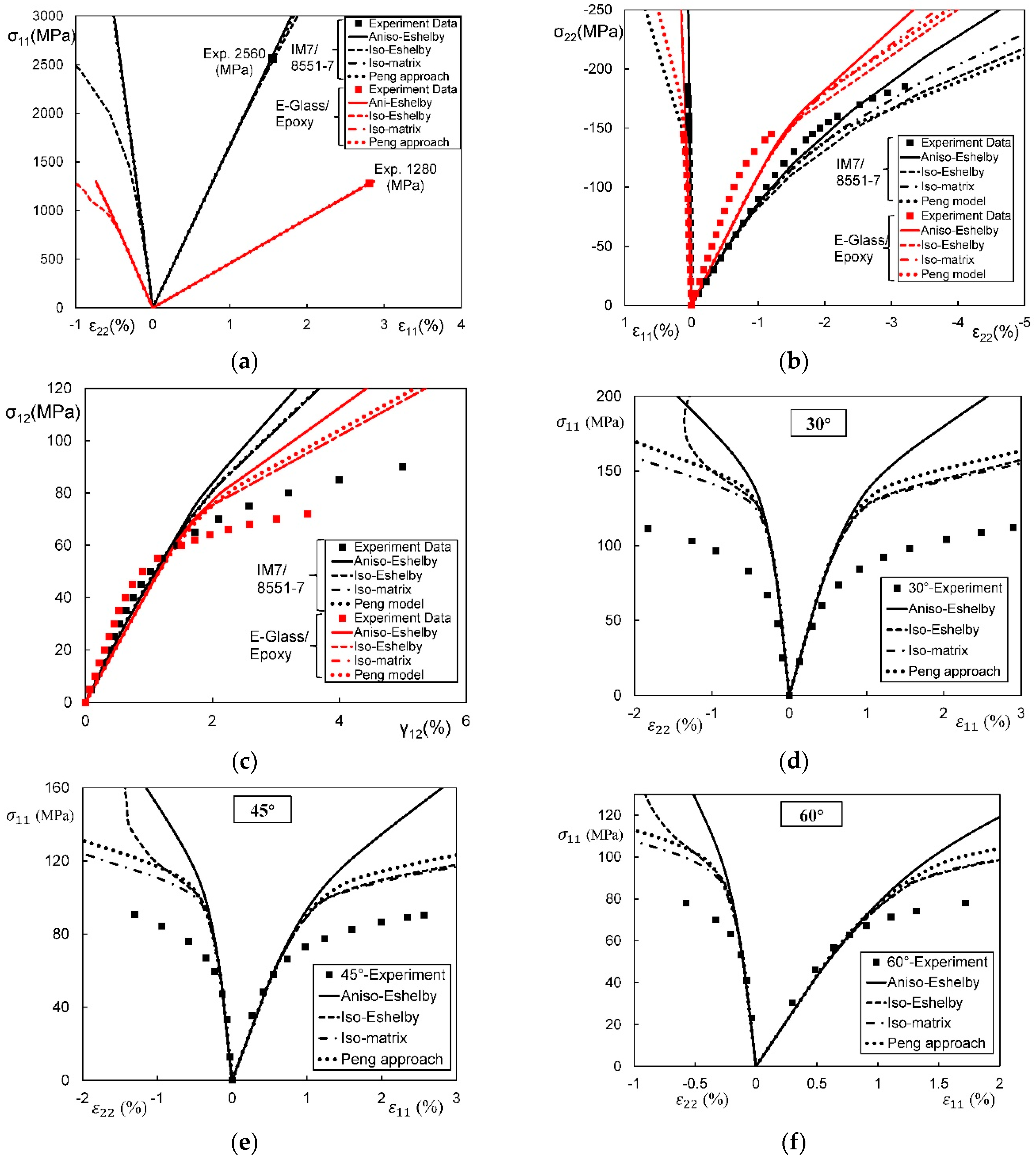
4.4.1. Anisotropic Eshelby Tensor Approach
4.4.2. Isotropic Matrix Method
4.4.3. Isotropic Eshelby Tensor Method
4.4.4. Peng’s Approach
4.4.5. Quantitative Comparison on Modifications of the Eshelby Tensor
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Composites | ||||||
|---|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | Fiber | 80 | 80 | 33.33 | 33.33 | 0.2 |
| Matrix | 3.35 | 3.35 | 1.24 | 1.24 | 0.35 | |
| Composite | 53.5 | 17.7 | 5.83 | 6.32 | 0.28 | |
| E-Glass b/MY750 (Vf = 0.60) | Fiber | 74 | 74 | 30.8 | 30.8 | 0.2 |
| Matrix | 3.35 | 3.35 | 1.24 | 1.24 | 0.35 | |
| Composite | 45.6 | 16.2 | 5.83 | 5.79 | 0.28 | |
| S2-Glass/Epoxy (Vf = 0.60) | Fiber | 87 | 87 | 36.3 | 36.3 | 0.2 |
| Matrix | 3.2 | 3.2 | 1.19 | 1.19 | 0.35 | |
| Composite | 52 | 19 | 6.7 | 6.7 | 0.3 | |
| T300/BSL914C (Vf = 0.60) | Fiber | 230 | 15 | 15 | 7 | 0.2 |
| Matrix | 4 | 4 | 1.48 | 1.48 | 0.35 | |
| Composite | 138 | 11 | 5.5 | 3.93 | 0.28 | |
| T300/PR319 (Vf = 0.60) | Fiber | 230 | 15 | 15 | 7 | 0.2 |
| Matrix | 0.95 | 0.95 | 0.35 | 0.35 | 0.35 | |
| Composite | 129 | 5.6 | 1.33 | 1.86 | 0.32 | |
| AS carbon/Epoxy (Vf = 0.60) | Fiber | 231 | 15 | 15 | 7 | 0.2 |
| Matrix | 3.2 | 3.2 | 1.19 | 1.19 | 0.35 | |
| Composite | 140 | 10 | 6 | 3.35 | 0.3 | |
| AS4/3501-6 (Vf = 0.60) | Fiber | 225 | 15 | 15 | 7 | 0.2 |
| Matrix | 4.2 | 4.2 | 1.57 | 1.57 | 0.34 | |
| Composite | 126 | 11 | 6.6 | 3.93 | 0.28 | |
| IM7/8551-7 (Vf = 0.60) | Fiber | 276 | 19 | 27 | 7 | 0.2 |
| Matrix | 4.08 | 4.08 | 1.48 | 1.48 | 0.38 | |
| Composite | 165 | 8.4 | 5.6 | 2.8 | 0.34 | |
| G40-800/5260 (Vf = 0.60) | Fiber | 290 | 19 | 27 | 7 | 0.2 |
| Matrix | 3.45 | 3.45 | 1.28 | 1.28 | 0.35 | |
| Composite | 173 | 10 | 6.94 | 3.56 | 0.33 | |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.8 | 7.15 | 2.67 | 2.42 | 0.28 |
| E-Glass b/MY750 (Vf = 0.60) | 45.7 | 7.01 | 2.61 | 2.37 | 0.28 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.4 | 6.76 | 2.52 | 2.28 | 0.28 |
| T300/BSL914C (Vf = 0.60) | 139.5 | 7.08 | 2.94 | 2.49 | 0.27 |
| T300/PR319 (Vf = 0.60) | 138.4 | 1.98 | 0.75 | 0.67 | 0.28 |
| AS carbon/Epoxy (Vf = 0.60) | 139.8 | 5.91 | 2.40 | 2.05 | 0.27 |
| AS4/3501-6 (Vf = 0.60) | 136.6 | 7.30 | 3.09 | 2.60 | 0.27 |
| IM7/8551-7 (Vf = 0.60) | 167.1 | 7.73 | 3.07 | 2.50 | 0.29 |
| G40-800/5260 (Vf = 0.60) | 175.3 | 6.52 | 2.67 | 2.19 | 0.28 |
| Average error | 3.1% | 44.3% | 53.5% | 45.5% | 7.3% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 18.91 | 11.34 | 6.96 | 0.23 |
| E-Glass b/MY750 (Vf = 0.60) | 45.8 | 16.80 | 9.80 | 6.15 | 0.24 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.6 | 17.39 | 10.94 | 6.36 | 0.23 |
| T300/BSL914C (Vf = 0.60) | 139.7 | 8.99 | 6.25 | 3.43 | 0.25 |
| T300/PR319 (Vf = 0.60) | 138.4 | 4.19 | 4.18 | 1.55 | 0.24 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 8.06 | 5.82 | 3.06 | 0.25 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 9.14 | 6.37 | 3.53 | 0.25 |
| IM7/8551-7 (Vf = 0.60) | 167.3 | 10.37 | 9.36 | 3.52 | 0.26 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 9.33 | 8.98 | 3.25 | 0.25 |
| Average error | 3.1% | 14.3% | 61.9% | 11.5% | 18.3% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 11.7 | 4.60 | 4.06 | 0.25 |
| E-Glass b/MY750 (Vf = 0.60) | 45.8 | 11.02 | 4.32 | 3.83 | 0.25 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 10.78 | 4.23 | 3.72 | 0.25 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 8.57 | 4.35 | 3.21 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 3.02 | 1.30 | 1.06 | 0.25 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 7.48 | 3.67 | 2.77 | 0.26 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 8.76 | 4.53 | 3.32 | 0.26 |
| IM7/8551-7 (Vf = 0.60) | 167.3 | 9.67 | 4.92 | 3.23 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 8.47 | 4.36 | 2.92 | 0.25 |
| Average error | 3.1% | 28.2% | 25.2% | 26.9% | 14.6% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 12.87 | 4.6 | 4.65 | 0.25 |
| E-Glass b/MY750 (Vf = 0.60) | 45.8 | 12.03 | 4.32 | 4.33 | 0.25 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 11.8 | 4.23 | 4.25 | 0.25 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 8.77 | 4.35 | 3.32 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 3.27 | 1.29 | 1.19 | 0.25 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 7.72 | 3.67 | 2.9 | 0.26 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 8.93 | 4.54 | 3.42 | 0.25 |
| IM7/8551-7 (Vf = 0.60) | 167.3 | 10.1 | 4.92 | 3.42 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 8.85 | 4.35 | 3.09 | 0.25 |
| Average error | 3.1% | 25.1% | 25.2% | 22.4% | 14.9% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 8.252 | 3.076 | 3.076 | 0.26 |
| E-Glass b/MY750 (Vf = 0.60) | 45.7 | 7.84 | 2.92 | 2.92 | 0.26 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 7.58 | 2.82 | 2.82 | 0.26 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 7.14 | 3.225 | 2.811 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 2.169 | 0.85 | 0.82 | 0.26 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 6.1 | 2.65 | 2.36 | 0.26 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 7.39 | 3.39 | 2.93 | 0.26 |
| IM7/8551-7 (Vf = 0.60) | 167.2 | 7.72 | 3.42 | 2.81 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 6.78 | 2.99 | 2.51 | 0.26 |
| Average error | 3.1% | 41.5% | 48.1% | 36.5% | 12.9% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 13.64 | 5.13 | 5.13 | 0.26 |
| E-Glass b/MY750 (Vf = 0.60) | 45.7 | 12.86 | 4.83 | 4.83 | 0.26 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 12.60 | 4.73 | 4.73 | 0.26 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 9.26 | 4.91 | 3.81 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 3.46 | 1.45 | 1.33 | 0.27 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 8.19 | 4.14 | 3.33 | 0.26 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 9.50 | 5.12 | 3.93 | 0.26 |
| IM7/8551-7 (Vf = 0.60) | 167.2 | 10.42 | 5.52 | 3.80 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 9.43 | 4.88 | 3.49 | 0.26 |
| Average error | 3.1% | 21.4% | 18.1% | 15.0% | 12.9% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 11.7 | 4.6 | 4.06 | 0.26 |
| E-Glass b/MY750 (Vf = 0.60) | 45.7 | 11.02 | 4.32 | 3.83 | 0.26 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 10.78 | 4.23 | 3.72 | 0.26 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 8.57 | 4.35 | 3.21 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 3.02 | 1.29 | 1.06 | 0.27 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 7.48 | 3.67 | 2.77 | 0.26 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 8.76 | 4.54 | 3.32 | 0.26 |
| IM7/8551-7 (Vf = 0.60) | 167.2 | 9.67 | 4.92 | 3.23 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 8.47 | 4.35 | 2.92 | 0.26 |
| Average error | 3.1% | 28.2% | 25.2% | 26.9% | 12.9% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 18.1 | 6.28 | 6.24 | 0.26 |
| E-Glass b/MY750 (Vf = 0.60) | 45.7 | 16.8 | 5.84 | 5.8 | 0.26 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 16.9 | 5.81 | 5.77 | 0.26 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 9.6 | 5.35 | 3.66 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 4.41 | 1.82 | 1.55 | 0.27 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 8.7 | 4.64 | 3.29 | 0.26 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 9.7 | 5.54 | 3.76 | 0.26 |
| IM7/8551-7 (Vf = 0.60) | 167.2 | 11.2 | 6.46 | 3.76 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 10.2 | 5.8 | 3.51 | 0.26 |
| Average error | 3.1% | 12.4% | 14.6% | 9.0% | 12.9% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 16.26 | 4.96 | 6.49 | 0.25 |
| E-Glass b/MY750 (Vf = 0.60) | 45.8 | 14.9 | 4.58 | 5.89 | 0.25 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 14.86 | 4.5 | 5.89 | 0.25 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 9.42 | 4.5 | 3.71 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 3.98 | 1.38 | 1.58 | 0.25 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 8.45 | 3.82 | 3.32 | 0.26 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 9.54 | 4.68 | 3.79 | 0.25 |
| IM7/8551-7 (Vf = 0.60) | 167.2 | 10.88 | 5.15 | 3.79 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 9.63 | 4.57 | 3.47 | 0.25 |
| Average error | 3.1% | 15.9% | 22.1% | 8.8% | 15.4% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf =0.62) | 50.9 | 16.26 | 4.95 | 6.49 | 0.25 |
| E-Glass b/MY750 (Vf =0.60) | 45.8 | 14.90 | 4.57 | 5.89 | 0.25 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 14.86 | 4.50 | 5.89 | 0.25 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 9.42 | 4.51 | 3.71 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 3.97 | 1.38 | 1.57 | 0.25 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 8.44 | 3.83 | 3.32 | 0.25 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 9.53 | 4.70 | 3.79 | 0.25 |
| IM7/8551-7 (Vf = 0.60) | 167.2 | 10.87 | 5.18 | 3.78 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 9.62 | 4.60 | 3.47 | 0.25 |
| Average error | 3.1% | 14.9% | 22% | 8.9% | 15.3% |
| Composites | |||||
|---|---|---|---|---|---|
| E-Glass a/LY556 (Vf = 0.62) | 50.9 | 15.40 | 4.57 | 6.02 | 0.25 |
| E-Glass b/MY750 (Vf = 0.60) | 45.8 | 14.16 | 4.21 | 5.49 | 0.25 |
| S2-Glass/Epoxy (Vf = 0.60) | 53.5 | 14.09 | 4.13 | 5.47 | 0.25 |
| T300/BSL914C (Vf = 0.60) | 139.6 | 9.20 | 4.21 | 3.58 | 0.26 |
| T300/PR319 (Vf = 0.60) | 138.4 | 3.78 | 1.27 | 1.47 | 0.25 |
| AS carbon/Epoxy (Vf = 0.60) | 139.9 | 8.21 | 3.56 | 3.19 | 0.26 |
| AS4/3501-6 (Vf = 0.60) | 136.7 | 9.33 | 4.39 | 3.67 | 0.25 |
| IM7/8551-7 (Vf = 0.60) | 167.2 | 10.57 | 4.78 | 3.65 | 0.27 |
| G40-800/5260 (Vf = 0.60) | 175.4 | 9.35 | 4.24 | 3.35 | 0.25 |
| Average error | 3.1% | 18.4% | 27.0% | 11.8% | 15.0% |
References
- Dvorak, G.J.; Bahei-El-Din, Y. Plasticity analysis of fibrous composites. J. Appl. Mech. 1982, 49, 327–335. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. Stress analysis and strength prediction of mechanically fastened joints in FRP: A review. Compos. Part A Appl. Sci. Manuf. 1997, 28, 529–547. [Google Scholar] [CrossRef]
- Liu, P.F.; Zheng, J.Y. Recent developments on damage modeling and finite element analysis for composite laminates: A review. Mater. Des. 2010, 31, 3825–3834. [Google Scholar] [CrossRef]
- Chandra, R.; Singh, S.P.; Gupta, K. Damping studies in fiber-reinforced composites—A review. Compos. Struct. 1999, 46, 41–51. [Google Scholar] [CrossRef]
- Daniel, I.M.; Ishai, O.; Daniel, I.M.; Daniel, I. Engineering Mechanics of Composite Materials; Oxford University Press: New York, NY, USA, 1994; Volume 3. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Castañeda, P.P.; Telega, J.J.; Gambin, B. Nonlinear Homogenization and its Applications to Composites, Polycrystals and Smart Materials. In Proceedings of the NATO Advanced Research Workshop, Warsaw, Poland, 23–26 June 2003; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 170. [Google Scholar]
- Voyiadjis, G.Z.; Ju, J.-W. Inelasticity and Micromechanics of Metal Matrix Composites; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Adams, D.F. Elastoplastic behavior of composites. Compos. Mater. Mech. Compos. Mater. 2016, 2, 169–208. [Google Scholar]
- Chang, T.Y.; Sawamiphakdi, K. Large deformation analysis of laminated shells by ftnife element method. Comput. Struct. 1981, 13, 331–340. [Google Scholar] [CrossRef]
- Chao, W.; Reddy, J. Analysis of laminated composite shells using a degenerated 3-D element. Int. J. Numer. Methods Eng. 1984, 20, 1991–2007. [Google Scholar] [CrossRef]
- Liao, C.; Reddy, J.; Engelstad, S. A solid-shell transition element for geometrically non-linear analysis of laminated composite structures. Int. J. Numer. Methods Eng. 1988, 26, 1843–1854. [Google Scholar] [CrossRef]
- Tolson, S.; Zabaras, N. Finite element analysis of progressive failure in laminated composite plates. Comput. Struct. 1991, 38, 361–376. [Google Scholar] [CrossRef]
- Han, J.; Hoa, S. A three-dimensional multilayer composite finite element for stress analysis of composite laminates. Int. J. Numer. Methods Eng. 1993, 36, 3903–3914. [Google Scholar] [CrossRef]
- Donadon, M.V.; Iannucci, L.; Falzon, B.G.; Hodgkinson, J.M.; de Almeida, S.F.M. A progressive failure model for composite laminates subjected to low velocity impact damage. Comput. Struct. 2008, 86, 1232–1252. [Google Scholar] [CrossRef]
- Dano, M.-L.; Gendron, G.; Picard, A. Stress and failure analysis of mechanically fastened joints in composite laminates. Compos. Struct. 2000, 50, 287–296. [Google Scholar] [CrossRef]
- Cooper, E.; Warrior, N.A. Elastic–plastic material model for finite element analysis of crashworthy composites. Plast. Rubber Compos. 2002, 31, 262–269. [Google Scholar] [CrossRef]
- Schmidt, R.; Weichert, D. A Refined Theory of Elastic-Plastic Shells at Moderate Rotations. ZAMM J. Appl. Math. Mech. 1989, 69, 11–21. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef]
- Brünig, M. Nonlinear analysis and elastic-plastic behavior of anisotropic structures. Finite Elem. Anal. Des. 1995, 20, 155–177. [Google Scholar] [CrossRef]
- Tsai, S.W.; Wu, E.M. A general theory of strength for anisotropic materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Azzi, V.; Tsai, S. Anisotropic strength of composites. Exp. Mech. 1965, 5, 283–288. [Google Scholar] [CrossRef]
- Aykul, H.L.; Sarper Yilmaz, S.M. An elastic–plastic stress analysis steel-reinforced thermoplastic composite cantilever beam. Int. J. Mech. Sci. 2008, 50, 380–388. [Google Scholar] [CrossRef]
- Kaw, A.K. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Tomblin, J.S.; Tauriello, J.D.; Doyle, S.P. A Composite Material Qualification Method That Results in Cost, Time and Risk Reduction. J. Adv. Mater. Covina 2002, 34, 41–51. [Google Scholar]
- Voyiadjis, G.; Thiagarajan, G. An anisotropic yield surface model for directionally reinforced metal-matrix composites. Int. J. Plast. 1995, 11, 867–894. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Thiagarajan, G. A cyclic anisotropic-plasticity model for metal matrix composites. Int. J. Plast. 1996, 12, 69–91. [Google Scholar] [CrossRef]
- Car, E.; Oller, S.; Oñate, E. An anisotropic elastoplastic constitutive model for large strain analysis of fiber reinforced composite materials. Comput. Methods Appl. Mech. Eng. 2000, 185, 245–277. [Google Scholar] [CrossRef]
- Car, E.; Oller, S.; Oñate, E. A large strain plasticity model for anisotropic materials—Composite material application. Int. J. Plast. 2001, 17, 1437–1463. [Google Scholar] [CrossRef]
- Reddy, J. A generalization of two-dimensional theories of laminated composite plates. Commun. Appl. Numer. Methods 1987, 3, 173–180. [Google Scholar] [CrossRef]
- Reddy, J.N. An evaluation of equivalent-single-layer and layerwise theories of composite laminates. Compos. Struct. 1993, 25, 21–35. [Google Scholar] [CrossRef]
- Robbins, D.; Reddy, J. Modelling of thick composites using a layerwise laminate theory. Int. J. Numer. Methods Eng. 1993, 36, 655–677. [Google Scholar] [CrossRef]
- Carrera, E. Evaluation of layerwise mixed theories for laminated plates analysis. AIAA J. 1998, 36, 830–839. [Google Scholar] [CrossRef]
- Kant, T.; Swaminathan, K. Estimation of transverse/interlaminar stresses in laminated composites—A selective review and survey of current developments. Compos. Struct. 2000, 49, 65–75. [Google Scholar] [CrossRef]
- Grujicic, M.; He, T.; Marvi, H.; Cheeseman, B.A.; Yen, C.F. A comparative investigation of the use of laminate-level meso-scale and fracture-mechanics-enriched meso-scale composite-material models in ballistic-resistance analyses. J. Mater. Sci. 2010, 45, 3136–3150. [Google Scholar] [CrossRef]
- Rotem, A. Predicton of laminate failure with the rotem failure criterion. Compos. Sci. Technol. 1998, 58, 1083–1094. [Google Scholar] [CrossRef]
- Rotem, A. The rotem failure criterion: Theory and practice. Compos. Sci. Technol. 2002, 62, 1663–1671. [Google Scholar] [CrossRef]
- Pinho, S.; Darvizeh, R.; Robinson, P.; Schuecker, C.; Camanho, P. Material and structural response of polymer-matrix fibre-reinforced composites. J. Compos. Mater. 2012, 46, 2313–2341. [Google Scholar] [CrossRef]
- Wolfe, W.E.; Butalia, T.S. A strain-energy based failure criterion for non-linear analysis of composite laminates subjected to biaxial loading. Compos. Sci. Technol. 1998, 58, 1107–1124. [Google Scholar] [CrossRef]
- Puck, A.; Mannigel, M. Physically based non-linear stress–strain relations for the inter-fibre fracture analysis of FRP laminates. Compos. Sci. Technol. 2007, 67, 1955–1964. [Google Scholar] [CrossRef]
- Kress, G. Examination of Hashin’s failure criteria for the second world-wide failure exercise. J. Compos. Mater. 2012, 46, 2539–2561. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Hoffman, O. The brittle strength of orthotropic materials. J. Compos. Mater. 1967, 1, 200–206. [Google Scholar] [CrossRef]
- Bektaş, N.B.; Sayman, O. Elasto-plastic stress analysis in simply supported thermoplastic laminated plates under thermal loads. Compos. Sci. Technol. 2001, 61, 1695–1701. [Google Scholar] [CrossRef]
- Pisano, A.A.; Fuschi, P.; De Domenico, D. A layered limit analysis of pinned-joints composite laminates: Numerical versus experimental findings. Compos. Part B Eng. 2012, 43, 940–952. [Google Scholar] [CrossRef]
- Wolfram, U.; Gross, T.; Pahr, D.H.; Schwiedrzik, J.; Wilke, H.J.; Zysset, P.K. Fabric-based Tsai-Wu yield criteria for vertebral trabecular bone in stress and strain space. J. Mech. Behav. Biomed. Mater. 2012, 15, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Besson, J.; Forest, S.; Tanguy, B.; Bugat, S. A yield function for single crystals containing voids. Int. J. Solids Struct. 2013, 50, 2115–2131. [Google Scholar] [CrossRef]
- Morin, L.; Madou, K.; Leblond, J.-B.; Kondo, D. A new technique for finite element limit-analysis of Hill materials, with an application to the assessment of criteria for anisotropic plastic porous solids. Int. J. Eng. Sci. 2014, 74, 65–79. [Google Scholar] [CrossRef]
- Talreja, R. Assessment of the fundamentals of failure theories for composite materials. Compos. Sci. Technol. 2014, 105, 190–201. [Google Scholar] [CrossRef]
- Zahr Viñuela, J.; Pérez-Castellanos, J.L. The anisotropic criterion of von Mises (1928) as a yield condition for PMMCs. A calibration procedure based on numerical cell-analysis. Compos. Struct. 2015, 134, 613–632. [Google Scholar] [CrossRef]
- Sun, C.T.; Chen, J.L. A micromechanical model for plastic behavior of fibrous composites. Compos. Sci. Technol. 1991, 40, 115–129. [Google Scholar] [CrossRef]
- Ochoa, O.O.; Reddy, J.N. Finite Element Analysis of Composite Laminates; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 7. [Google Scholar]
- Oller, S. Numerical Simulation of Mechanical Behavior of Composite Materials; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Drago, A.; Pindera, M.-J. Micro-macromechanical analysis of heterogeneous materials: Macroscopically homogeneous vs periodic microstructures. Compos. Sci. Technol. 2007, 67, 1243–1263. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Chaboche, J. Towards a micromechanics based inelastic and damage modeling of composites. Int. J. Plast. 2001, 17, 411–439. [Google Scholar] [CrossRef]
- Pindera, M.-J.; Khatam, H.; Drago, A.S.; Bansal, Y. Micromechanics of spatially uniform heterogeneous media: A critical review and emerging approaches. Compos. Part B Eng. 2009, 40, 349–378. [Google Scholar] [CrossRef]
- Charalambakis, N. Homogenization techniques and micromechanics. A survey and perspectives. Appl. Mech. Rev. 2010, 63, 030803. [Google Scholar] [CrossRef]
- Ashouri Vajari, D.; González, C.; Llorca, J.; Legarth, B.N. A numerical study of the influence of microvoids in the transverse mechanical response of unidirectional composites. Compos. Sci. Technol. 2014, 97, 46–54. [Google Scholar] [CrossRef]
- Tosun-Felekoğlu, K.; Felekoğlu, B.; Ranade, R.; Lee, B.Y.; Li, V.C. The role of flaw size and fiber distribution on tensile ductility of PVA-ECC. Compos. Part B Eng. 2014, 56, 536–545. [Google Scholar] [CrossRef]
- Brito-Santana, H.; de Medeiros, R.; Rodriguez-Ramos, R.; Tita, V. Different interface models for calculating the effective properties in piezoelectric composite materials with imperfect fiber–matrix adhesion. Compos. Struct. 2016, 151, 70–80. [Google Scholar] [CrossRef]
- Hörrmann, S.; Adumitroaie, A.; Viechtbauer, C.; Schagerl, M. The effect of fiber waviness on the fatigue life of CFRP materials. Int. J. Fatigue 2016, 90, 139–147. [Google Scholar] [CrossRef]
- Espinosa-Almeyda, Y.; Camacho-Montes, H.; Rodríguez-Ramos, R.; Guinovart-Díaz, R.; López-Realpozo, J.C.; Bravo-Castillero, J.; Sabina, F.J. Influence of imperfect interface and fiber distribution on the antiplane effective magneto-electro-elastic properties for fiber reinforced composites. Int. J. Solids Struct. 2017, 112, 155–168. [Google Scholar] [CrossRef]
- Doghri, I.; Ouaar, A. Homogenization of two-phase elasto-plastic composite materials and structures—Study of tangent operators, cyclic plasticity and numerical algorithms. Int. J. Solids Struct. 2003, 40, 1681–1712. [Google Scholar] [CrossRef]
- Rekik, A.; Bornert, M.; Auslender, F. A critical evaluation of local field statistics predicted by various linearization schemes in nonlinear mean-field homogenization. Mech. Mater. 2012, 54, 1–17. [Google Scholar] [CrossRef]
- Kanaun, S. An efficient homogenization method for composite materials with elasto-plastic components. Int. J. Eng. Sci. 2012, 57, 36–49. [Google Scholar] [CrossRef]
- Hou, T.Y.; Wu, X.-H. A Multiscale Finite Element Method for Elliptic Problems in Composite Materials and Porous Media. J. Comput. Phys. 1997, 134, 169–189. [Google Scholar] [CrossRef]
- Ghosh, S.; Lee, K.; Raghavan, P. A multi-level computational model for multi-scale damage analysis in composite and porous materials. Int. J. Solids Struct. 2001, 38, 2335–2385. [Google Scholar] [CrossRef]
- Kanouté, P.; Boso, D.P.; Chaboche, J.L.; Schrefler, B.A. Multiscale Methods for Composites: A Review. Arch. Comput. Methods Eng. 2009, 16, 31–75. [Google Scholar] [CrossRef]
- Ye, J.; Qiu, Y.; Chen, X.; Ma, J. Initial and final failure strength analysis of composites based on a micromechanical method. Compos. Struct. 2015, 125, 328–335. [Google Scholar] [CrossRef]
- Ghorbani Moghaddam, M.; Achuthan, A.; Bednarcyk, B.A.; Arnold, S.M.; Pineda, E.J. A Multiscale Computational Model Combining a Single Crystal Plasticity Constitutive Model with the Generalized Method of Cells (GMC) for Metallic Polycrystals. Materials 2016, 9, 335. [Google Scholar] [CrossRef] [PubMed]
- Patel, D.K.; Hasanyan, A.D.; Waas, A.M. N-Layer concentric cylinder model (NCYL): An extended micromechanics-based multiscale model for nonlinear composites. Acta Mech. 2016, 228, 275–306. [Google Scholar] [CrossRef]
- García-Carpintero, A.; Herráez, M.; Xu, J.; Lopes, C.S.; González, C. A Multi Material Shell Model for the Mechanical Analysis of Triaxial Braided Composites. Appl. Compos. Mater. 2017, 24, 1425–1445. [Google Scholar] [CrossRef]
- Hettich, T.; Hund, A.; Ramm, E. Modeling of failure in composites by X-FEM and level sets within a multiscale framework. Comput. Methods Appl. Mech. Eng. 2008, 197, 414–424. [Google Scholar] [CrossRef]
- Ernst, G.; Vogler, M.; Hühne, C.; Rolfes, R. Multiscale progressive failure analysis of textile composites. Compos. Sci. Technol. 2010, 70, 61–72. [Google Scholar] [CrossRef]
- Greco, F.; Leonetti, L.; Lonetti, P. A two-scale failure analysis of composite materials in presence of fiber/matrix crack initiation and propagation. Compos. Struct. 2013, 95, 582–597. [Google Scholar] [CrossRef]
- Talebi, H.; Silani, M.; Bordas, S.P.A.; Kerfriden, P.; Rabczuk, T. A computational library for multiscale modeling of material failure. Comput. Mech. 2013, 53, 1047–1071. [Google Scholar] [CrossRef]
- Spahn, J.; Andrä, H.; Kabel, M.; Müller, R. A multiscale approach for modeling progressive damage of composite materials using fast Fourier transforms. Comput. Methods Appl. Mech. Eng. 2014, 268, 871–883. [Google Scholar] [CrossRef]
- DorMohammdi, S.; Godines, C.; Abdi, F.; Huang, D.; Repupilli, M.; Minnetyan, L. Damage-tolerant composite design principles for aircraft components under fatigue service loading using multi-scale progressive failure analysis. J. Compos. Mater. 2017, 51, 2181–2202. [Google Scholar] [CrossRef]
- Zhai, J.; Zeng, T.; Xu, G.-D.; Wang, Z.-H.; Cheng, S.; Fang, D.-N. A multi-scale finite element method for failure analysis of three-dimensional braided composite structures. Compos. Part B Eng. 2017, 110, 476–486. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.-L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland Publishing Company: Amsterdam, The Netherlands, 1978; Volume 5. [Google Scholar]
- Guedes, J.; Kikuchi, N. Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods. Comput. Methods Appl. Mech. Eng. 1990, 83, 143–198. [Google Scholar] [CrossRef]
- Fish, J.; Belsky, V. Multi-grid method for periodic heterogeneous media part 2: Multiscale modeling and quality control in multidimensional case. Comput. Methods Appl. Mech. Eng. 1995, 126, 17–38. [Google Scholar] [CrossRef]
- Fish, J.; Shek, K. Finite deformation plasticity for composite structures: Computational models and adaptive strategies. Comput. Methods Appl. Mech. Eng. 1999, 172, 145–174. [Google Scholar] [CrossRef]
- Yu, W.; Tang, T. Variational asymptotic method for unit cell homogenization of periodically heterogeneous materials. Int. J. Solids Struct. 2007, 44, 3738–3755. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, W. Variational asymptotic homogenization of elastoplastic composites. Compos. Struct. 2015, 133, 947–958. [Google Scholar] [CrossRef]
- Zhong, Y.; Qin, W.; Yu, W.; Zhou, X.; Jiao, L. Variational asymptotic homogenization of magneto-electro-elastic materials with coated fibers. Compos. Struct. 2015, 133, 300–311. [Google Scholar] [CrossRef]
- Suquet, P. Elements of homogenization for inelastic solid mechanics. In Homogenization Techniques for Composite Media; Springer: Berlin/Heidelberg, Germany, 1987; Volume 272, pp. 193–278. [Google Scholar]
- Fish, J.; Belsky, V. Multigrid method for periodic heterogeneous media Part 1: Convergence studies for one-dimensional case. Comput. Methods Appl. Mech. Eng. 1995, 126, 1–16. [Google Scholar] [CrossRef]
- Kalamkarov, A.L.; Andrianov, I.V.; Danishevsâ, V.V. Asymptotic homogenization of composite materials and structures. Appl. Mech. Rev. 2009, 62, 030802. [Google Scholar] [CrossRef]
- Yang, Y.; Lei, C.; Gao, C.-F.; Li, J. Asymptotic homogenization of three-dimensional thermoelectric composites. J. Mech. Phys. Solids 2015, 76, 98–126. [Google Scholar] [CrossRef]
- Zhao, J.; Li, H.; Cheng, G.; Cai, Y. On predicting the effective elastic properties of polymer nanocomposites by novel numerical implementation of asymptotic homogenization method. Compos. Struct. 2016, 135, 297–305. [Google Scholar] [CrossRef]
- Zhang, Y.; Shang, S.; Liu, S. A novel implementation algorithm of asymptotic homogenization for predicting the effective coefficient of thermal expansion of periodic composite materials. Acta Mech. Sin. 2017, 33, 368–381. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Kanoute, P.; Roos, A. On the capabilities of mean-field approaches for the description of plasticity in metal matrix composites. Int. J. Plast. 2005, 21, 1409–1434. [Google Scholar] [CrossRef]
- Klusemann, B.; Svendsen, B. Homogenization methods for multi-phase elastic composites: Comparisons and benchmarks. Tech. Mech. 2010, 30, 374–386. [Google Scholar]
- Klusemann, B.; Böhm, H.J.; Svendsen, B. Homogenization methods for multi-phase elastic composites with non-elliptical reinforcements: Comparisons and benchmarks. Eur. J. Mech. A Solids 2012, 34, 21–37. [Google Scholar] [CrossRef]
- Saeb, S.; Steinmann, P.; Javili, A. Aspects of Computational Homogenization at Finite Deformations: A Unifying Review From Reuss’ to Voigt’s Bound. Appl. Mech. Rev. 2016, 68, 050801. [Google Scholar] [CrossRef]
- Matouš, K.; Geers, M.G.D.; Kouznetsova, V.G.; Gillman, A. A review of predictive nonlinear theories for multiscale modeling of heterogeneous materials. J. Comput. Phys. 2017, 330, 192–220. [Google Scholar] [CrossRef]
- Ghossein, E.; Lévesque, M. A comprehensive validation of analytical homogenization models: The case of ellipsoidal particles reinforced composites. Mech. Mater. 2014, 75, 135–150. [Google Scholar] [CrossRef]
- Liu, L.; Huang, Z.M. Stress concentration factor in matrix of a composite reinforced with transversely isotropic fibers. J. Compos. Mater. 2012, 48, 81–98. [Google Scholar] [CrossRef]
- Yao, Z.; Huang, Z.M. Stress concentration factor in the matrix reinforced with fiber having an interface layer. J. Reinf. Plast. Compos. 2013, 32, 105–123. [Google Scholar] [CrossRef]
- Huang, Z.-M.; Liu, L. Predicting strength of fibrous laminates under triaxial loads only upon independently measured constituent properties. Int. J. Mech. Sci. 2014, 79, 105–129. [Google Scholar] [CrossRef]
- Huang, Z.-M.; Liu, L. Assessment of composite failure and ultimate strength without experiment on composite. Acta Mech. Sin. 2014, 30, 569–588. [Google Scholar] [CrossRef]
- Huang, Z.-M.; Xin, L.-M. Stress concentration factors of matrix in a composite. Subjected to transverse loads. In Proceedings of the ICCM2014, Cambridge, UK, 28–30 July 2014. [Google Scholar]
- Yao, Z.; Huang, Z.-M. Stress concentration factors in the matrix with different imperfect interfaces. Int. J. Damage Mech. 2014, 23, 745–771. [Google Scholar] [CrossRef]
- Huang, Z.M.; Xin, L.M. Strength Prediction of Laminated Composites upon Independent Constituent Properties. In Key Engineering Materials; Trans Tech Publications: Zürich, Switzerland, 2016; pp. 153–156. [Google Scholar]
- Huang, Z.-M.; Xin, L.-M. Stress Concentration Factor in Matrix of a Composite Subjected to Transverse Compression. Int. J. Appl. Mech. 2016, 8, 1650034. [Google Scholar] [CrossRef]
- Huang, Z.-M.; Xin, L.-M. In situ strengths of matrix in a composite. Acta Mech. Sin. 2016, 33, 120–131. [Google Scholar] [CrossRef]
- Pierard, O.; Doghri, I. An enhanced affine formulation and the corresponding numerical algorithms for the mean-field homogenization of elasto-viscoplastic composites. Int. J. Plast. 2006, 22, 131–157. [Google Scholar] [CrossRef]
- Azoti, W.L.; Koutsawa, Y.; Tchalla, A.; Makradi, A.; Belouettar, S. Micromechanics-based multi-site modeling of elastoplastic behavior of composite materials. Int. J. Solids Struct. 2015, 59, 198–207. [Google Scholar] [CrossRef]
- Wu, L.; Noels, L.; Adam, L.; Doghri, I. A combined incremental-secant mean-field homogenization scheme with per-phase residual strains for elasto-plastic composites. Int. J. Plast. 2013, 51, 80–102. [Google Scholar] [CrossRef]
- Wu, L.; Noels, L.; Adam, L.; Doghri, I. An implicit-gradient-enhanced incremental-secant mean-field homogenization scheme for elasto-plastic composites with damage. Int. J. Solids Struct. 2013, 50, 3843–3860. [Google Scholar] [CrossRef]
- Wu, L.; Doghri, I.; Noels, L. An incremental-secant mean-field homogenization method with second statistical moments for elasto-plastic composite materials. Philos. Mag. 2015, 95, 3348–3384. [Google Scholar] [CrossRef]
- Wu, L.; Adam, L.; Doghri, I.; Noels, L. An incremental-secant mean-field homogenization method with second statistical moments for elasto-visco-plastic composite materials. Mech. Mater. 2017, 114, 180–200. [Google Scholar] [CrossRef]
- Peng, X.; Tang, S.; Hu, N.; Han, J. Determination of the Eshelby tensor in mean-field schemes for evaluation of mechanical properties of elastoplastic composites. Int. J. Plast. 2016, 76, 147–165. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Hori, M. Micromechanics: Overall Properties of Heterogeneous Materials; Elsevier: Amsterdam, The Netherlands, 2013; Volume 37. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Bohm, H.J.; Eckschlager, A.; Han, W. Multi inclusion unit cell models for metal matrix composites with randomly oriented discontinuous reinforcedments. Comput. Mater. Sci. 2002, 25, 42–53. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Heinrich, C.; Aldridge, M.; Wineman, A.S.; Kieffer, J.; Waas, A.M.; Shahwan, K. The influence of the representative volume element (RVE) size on the homogenized response of cured fiber composites. Model. Simul. Mater. Sci. Eng. 2012, 20, 075007. [Google Scholar] [CrossRef]
- Monetto, I.; Drugan, W.J. A micromechanics-based nonlocal constitutive equation and minimum RVE size estimates for random elastic composites containing aligned spheroidal heterogeneities. J. Mech. Phys. Solids 2009, 57, 1578–1595. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Béchet, E.; Geuzaine, C.; Noels, L. Imposing periodic boundary condition on arbitrary meshes by polynomial interpolation. Comput. Mater. Sci. 2012, 55, 390–406. [Google Scholar] [CrossRef]
- Hoang, T.H.; Guerich, M.; Yvonnet, J. Determining the Size of RVE for Nonlinear Random Composites in an Incremental Computational Homogenization Framework. J. Eng. Mech. 2016, 142, 04016018. [Google Scholar] [CrossRef]
- Siddiqui, M.; Arif, A.F.M. A Computational Approach for the Constitutive Modeling of Elastoplastic Behavior of Metal Matrix Composites. Int. J. Comput. Methods 2016, 14, 1750058. [Google Scholar] [CrossRef]
- Fish, J.; Shek, K.; Pandheeradi, M.; Shephard, M.S. Computational plasticity for composite structures based on mathematical homogenization: Theory and practice. Comput. Methods Appl. Mech. Eng. 1997, 148, 53–73. [Google Scholar] [CrossRef]
- Pettermann, H.E.; Suresh, S. A comprehesive unit cell model a study of coupled effects in piezoelectric 1–3 composites. Int. J. Solids Struct. 2000, 37, 5447–5464. [Google Scholar] [CrossRef]
- Sun, W.; Lin, F.; Hu, X. Computer-aided design and modeling of composite unit cells. Compos. Sci. Technol. 2001, 61, 289–299. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Materials Science Engineering An Introduction; Wiley: New York, NY, USA, 2007; Volume 7. [Google Scholar]
- Brockenbrough, J.R.; Suresh, S.; Wienecke, H.A. Deformation of metal-matrix composites with continuous fibers: Geometrical effects of fiber distribution and shape. Acta Metall. Mater. 1991, 39, 735–752. [Google Scholar] [CrossRef]
- Aboudi, J. Mechanics of Composite Materials: A Unified Micromechanical Approach; Elsevier: Amsterdam, The Netherlands, 2013; Volume 29. [Google Scholar]
- Aghdam, M.M.; Smith, D.J.; Pavier, M.J. Finite element micromechanical modelling of yield and collapse behaviour of metal matrix composites. J. Mech. Phys. Solids 2000, 48, 499–528. [Google Scholar] [CrossRef]
- Würkner, M.; Berger, H.; Gabbert, U. Numerical investigations of effective properties of fiber reinforced composites with parallelogram arrangements and imperfect interface. Compos. Struct. 2014, 116, 388–394. [Google Scholar] [CrossRef]
- Xia, Z.; Zhang, Y.; Ellyin, F. A unified periodical boundary conditions for representative volume elements of composites and applications. Int. J. Solids Struct. 2003, 40, 1907–1921. [Google Scholar] [CrossRef]
- Xia, Z.; Zhou, C.; Yong, Q.; Wang, X. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites. Int. J. Solids Struct. 2006, 43, 266–278. [Google Scholar] [CrossRef]
- Qi, L.; Tian, W.; Zhou, J. Numerical evaluation of effective elastic properties of composites reinforced by spatially randomly distributed short fibers with certain aspect ratio. Compos. Struct. 2015, 131, 843–851. [Google Scholar] [CrossRef]
- Song, W.; Krishnaswamy, V.; Pucha, R.V. Computational homogenization in RVE models with material periodic conditions for CNT polymer composites. Compos. Struct. 2016, 137, 9–17. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, L.; Hu, D.; Liu, C.; Shen, X.; Cho, C.; Li, B. A novel approach to impose periodic boundary condition on braided composite RVE model based on RPIM. Compos. Struct. 2017, 163, 77–88. [Google Scholar] [CrossRef]
- Tyrus, J.M.; Gosz, M.; DeSantiago, E. A local finite element implementation for imposing periodic boundary conditions on composite micromechanical models. Int. J. Solids Struct. 2007, 44, 2972–2989. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, Z.; Ellyin, F. Two-scale analysis of a filament-wound cylindrical structure and application of periodic boundary conditions. Int. J. Solids Struct. 2008, 45, 5322–5336. [Google Scholar] [CrossRef]
- Jacques, S.; De Baere, I.; Van Paepegem, W. Application of periodic boundary conditions on multiple part finite element meshes for the meso-scale homogenization of textile fabric composites. Compos. Sci. Technol. 2014, 92, 41–54. [Google Scholar] [CrossRef]
- Kamarudin, K.-A.; Ismail, A.E. Prediction of elastic properties for unidirectional carbon composites: Periodic boundary condition approach. In Proceedings of the International Integrated Engineering Summit (IIES 2014), Batu Pahat, Malaysia, 1–4 December 2014. [Google Scholar]
- Espadas-Escalante, J.J.; van Dijk, N.P.; Isaksson, P. A study on the influence of boundary conditions in computational homogenization of periodic structures with application to woven composites. Compos. Struct. 2017, 160, 529–537. [Google Scholar] [CrossRef]
- Yuan, Z.; Lu, Z. Numerical analysis of elastic–plastic properties of polymer composite reinforced by wavy and random CNTs. Comput. Mater. Sci. 2014, 95, 610–619. [Google Scholar] [CrossRef]
- Wan, Y.; Wang, Y.; Gu, B. Finite element prediction of the impact compressive properties of three-dimensional braided composites using multi-scale model. Compos. Struct. 2015, 128, 381–394. [Google Scholar] [CrossRef]
- Rekik, A.; Auslender, F.; Bornert, M.; Zaoui, A. Objective evaluation of linearization procedures in nonlinear homogenization: A methodology and some implications on the accuracy of micromechanical schemes. Int. J. Solids Struct. 2007, 44, 3468–3496. [Google Scholar] [CrossRef]
- Ghosh, S.; Lee, K.; Moorthy, S. Multiple scale analysis of heterogeneous elastic structures using homogenization theory and voronoi cell finite element method. Int. J. Solids Struct. 1995, 32, 27–62. [Google Scholar] [CrossRef]
- Ghosh, S.; Moorthy, S. Elastic-plastic analysis of arbitrary heterogeneous materials with the Voronoi Cell finite element method. Comput. Methods Appl. Mech. Eng. 1995, 121, 373–409. [Google Scholar] [CrossRef]
- Ghosh, S.; Lee, K.; Moorthy, S. Two scale analysis of heterogeneous elastic-plastic materials with asymptotic homogenization and Voronoi cell finite element model. Comput. Methods Appl. Mech. Eng. 1996, 132, 63–116. [Google Scholar] [CrossRef]
- Pineda, E.J.; Bednarcyk, B.A.; Waas, A.M.; Arnold, S.M. Progressive failure of a unidirectional fiber-reinforced composite using the method of cells: Discretization objective computational results. Int. J. Solids Struct. 2013, 50, 1203–1216. [Google Scholar] [CrossRef]
- Ghorbani Moghaddam, M.; Achuthan, A.; Bednarcyk, B.A.; Arnold, S.M.; Pineda, E.J. A multi-scale computational model using Generalized Method of Cells (GMC) homogenization for multi-phase single crystal metals. Comput. Mater. Sci. 2015, 96, 44–55. [Google Scholar] [CrossRef]
- Ghorbani Moghaddam, M.; Achuthan, A.; Bednarcyk, B.A.; Arnold, S.M.; Pineda, E.J. Development of a precipitate size-dependent crystal plasticity constitutive model for two-phase materials and its implementation on a multi-scale computational framework. Mater. Sci. Eng. A 2016, 651, 893–903. [Google Scholar] [CrossRef]
- Cavalcante, M.A.A.; Khatam, H.; Pindera, M.-J. Homogenization of elastic–plastic periodic materials by FVDAM and FEM approaches—An assessment. Compos. Part B Eng. 2011, 42, 1713–1730. [Google Scholar] [CrossRef]
- Cavalcante, M.A.A.; Pindera, M.-J. Generalized Finite-Volume Theory for Elastic Stress Analysis in Solid Mechanics—Part I: Framework. J. Appl. Mech. 2012, 79, 051006. [Google Scholar] [CrossRef]
- Cavalcante, M.A.A.; Pindera, M.-J. Generalized Finite-Volume Theory for Elastic Stress Analysis in Solid Mechanics—Part II: Results. J. Appl. Mech. 2012, 79, 051007. [Google Scholar] [CrossRef]
- Cavalcante, M.A.A.; Pindera, M.-J.; Khatam, H. Finite-volume micromechanics of periodic materials: Past, present and future. Compos. Part B Eng. 2012, 43, 2521–2543. [Google Scholar] [CrossRef]
- Beveridge, A.J.; Wheel, M.A.; Nash, D.H. A higher order control volume based finite element method to predict the deformation of heterogeneous materials. Comput. Struct. 2013, 129, 54–62. [Google Scholar] [CrossRef]
- Cavalcante, M.A.A.; Pindera, M.-J. Finite-volume enabled transformation field analysis of periodic materials. Int. J. Mech. Mater. Des. 2013, 9, 153–179. [Google Scholar] [CrossRef]
- Tuković, Ž.; Ivanković, A.; Karač, A. Finite-volume stress analysis in multi-material linear elastic body. Int. J. Numer. Methods Eng. 2013, 93, 400–419. [Google Scholar] [CrossRef]
- Cavalcante, M.A.A.; Pindera, M.-J. Generalized FVDAM theory for elastic–plastic periodic materials. Int. J. Plast. 2016, 77, 90–117. [Google Scholar] [CrossRef]
- Demirdžić, I. A fourth-order finite volume method for structural analysis. Appl. Math. Model. 2016, 40, 3104–3114. [Google Scholar] [CrossRef]
- Yu, W.; Tang, T. A variational asymptotic micromechanics model for predicting thermoelastic properties of heterogeneous materials. Int. J. Solids Struct. 2007, 44, 7510–7525. [Google Scholar] [CrossRef]
- Tang, T.; Yu, W. Variational asymptotic micromechanics modeling of heterogeneous piezoelectric materials. Mech. Mater. 2008, 40, 812–824. [Google Scholar] [CrossRef]
- Neto, M.A.; Yu, W.; Tang, T.; leal, R. Analysis and optimization of heterogeneous materials using the variational asymptotic method for unit cell homogenization. Compos. Struct. 2010, 92, 2946–2954. [Google Scholar] [CrossRef]
- Tang, T.; Yu, W. Asymptotical Approach to Initial Yielding Surface and Elastoplasticity of Heterogeneous Materials. Mech. Adv. Mater. Struct. 2011, 18, 244–254. [Google Scholar] [CrossRef]
- Tang, T.; Horstemeyer, M.F.; Wang, P. Micromechanical analysis of thermoelastoplastic behavior of metal matrix composites. Int. J. Eng. Sci. 2012, 51, 161–167. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Qu, J.; Cherkaoui, M. Fundamentals of Micromechanics of Solids; Wiley Online Library: New York, NY, USA, 2006. [Google Scholar]
- Kerner, E. The elastic and thermo-elastic properties of composite media. Proc. Phys. Soc. Sect. B 1956, 69, 808. [Google Scholar] [CrossRef]
- Hashin, Z.; Rosen, B.W. The elastic moduli of fiber-reinforced materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Christensen, R.M.; Lo, K.H. Solutions for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
- Hashin, Z. Analysis of properties of fiber composites with anisotropic constituents. J. Appl. Mech. 1979, 46, 543–550. [Google Scholar] [CrossRef]
- Hashin, Z. Analysis of composite materials—A survey. J. Appl. Mech. 1983, 50, 481–505. [Google Scholar] [CrossRef]
- Hashin, Z. Thin interphase/imperfect interface in elasticity with application to coated fiber composites. J. Mech. Phys. Solids 2002, 50, 2509–2537. [Google Scholar] [CrossRef]
- Benveniste, Y.; Dvorak, G.J.; Chen, T. Stress fields in composites with coated inclusions. Mech. Mater. 1989, 7, 305–317. [Google Scholar] [CrossRef]
- Chen, T.; Dvorak, G.J.; Benveniste, Y. Stress fields in composites reinforced by coated cylindrically orthotropic fibers. Mech. Mater. 1990, 9, 17–32. [Google Scholar] [CrossRef]
- Benveniste, Y. Models of thin interphases and the effective medium approximation in composite media with curvilinearly anisotropic coated inclusions. Int. J. Eng. Sci. 2013, 72, 140–154. [Google Scholar] [CrossRef]
- Benveniste, Y. Exact results for the local fields and the effective moduli of fibrous composites with thickly coated fibers. J. Mech. Phys. Solids 2014, 71, 219–238. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Huang, Z.-M. A new approach to a bridging tensor. Polym. Compos. 2015, 36, 1417–1431. [Google Scholar] [CrossRef]
- Hori, M.; Nemat-Nasser, S. Double Inclusion model and ovrall moduli of multi phase composites. J. Eng. Mater. Technol. 1994, 116, 305–309. [Google Scholar] [CrossRef]
- Hu, G.K.; Weng, G.J. The connections between the double inclusion model and the Ponte Castaneda-Wills, Mori-Tanaka, and Kuster-Toksoz models. Mech. Mater. 2000, 32, 495–503. [Google Scholar] [CrossRef]
- Aboutajeddine, A.; Neale, K.W. The double inclusion model a new formulation and new estimates. Mech. Mater. 2005, 37, 331–341. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Annalen der Physik 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Chamis, C.C. Simplified composite micromechanics equations for hygral, thermal and mechanical properties. In Proceedings of the 38th Annual Conference of the Society of the Plastics Industry (SPI) Reinforced Plastics/Composites, Institute, Houston, TX, USA, 7–11 February 1983. [Google Scholar]
- Murthy, P.L.; Chamis, C.C. Integrated Composite Analyzer (ICAN)-Users and Programmers Manual; (No.NASA-E-2035); National Aeronautics and Space Administration Cleveland Oh Lewis Research Center: Washington, DC, USA, 1986. [Google Scholar]
- Affdl, J.; Kardos, J. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Huang, Z.-M. Simulation of the mechanical properties of fibrous composites by the bridging micromechanics model. Compos. Part A Appl. Sci. Manuf. 2001, 32, 143–172. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Huang, Z.-M. Bridging tensor with an imperfect interface. Eur. J. Mech. A Solids 2016, 56, 73–91. [Google Scholar] [CrossRef]
- Kaddour, A.S.; Hinton, M.J.; Soden, P.D. A comparison of the predictive capabilities of current failure theories for composite laminates: Additional contributions. Compos. Sci. Technol. 2004, 64, 449–476. [Google Scholar] [CrossRef]
- Ryan, S.; Wicklein, M.; Mouritz, A.; Riedel, W.; Schäfer, F.; Thoma, K. Theoretical prediction of dynamic composite material properties for hypervelocity impact simulations. Int. J. Impact Eng. 2009, 36, 899–912. [Google Scholar] [CrossRef]
- Younes, R.; Hallal, A.; Chehade, F.H.; Fardoun, F. Comparative Review Study on Elastic Properties Modeling for Unidirectional Composite Materials. Composites and Their Properties; INTECH Open Access Publisher: London, UK, 2012. [Google Scholar]
- Medikonda, S.; Tabiei, A.; Hamm, R. A comparative study of the effect of representative volume cell (RVC) boundary conditions on the elastic properties of a micromechanics based unidirectional composite material model. Int. J. Compos. Mater. 2017, 7, 51–71. [Google Scholar]
- Hill, R. Continuum micro-mechanics of elastoplastic polycrystals. J. Mech. Phys. Solids 1965, 13, 89–101. [Google Scholar] [CrossRef]
- Doghri, I.; El Ghezal, M.I.; Adam, L. Finite strain mean-field homogenization of composite materials with hyperelastic-plastic constituents. Int. J. Plast. 2016, 81, 40–62. [Google Scholar] [CrossRef]
- Teng, H. A New Incremental Formulation of Elastic–Plastic Deformation of Two-Phase Particulate Composite Materials. J. Appl. Mech. 2014, 81, 061006. [Google Scholar] [CrossRef]
- Tchalla, A.; Azoti, W.L.; Koutsawa, Y.; Makradi, A.; Belouettar, S.; Zahrouni, H. Incremental mean-fields micromechanics scheme for non-linear response of ductile damaged composite materials. Compos. Part B Eng. 2015, 69, 169–180. [Google Scholar] [CrossRef]
- Berveiller, M.; Zaoui, A. An extension of the self-consistent scheme to plastically-flowing polycrystals. J. Mech. Phys. Solids 1978, 26, 325–344. [Google Scholar] [CrossRef]
- Tandon, G.; Weng, G. A theory of particle-reinforced plasticity. J. Appl. Mech. 1988, 55, 126–135. [Google Scholar] [CrossRef]
- Puck, A.; Schurmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 1998, 58, 1045–1067. [Google Scholar] [CrossRef]
- Li, J.; Weng, G. A secant-viscosity composite model for the strain-rate sensitivity of nanocrystalline materials. Int. J. Plast. 2007, 23, 2115–2133. [Google Scholar] [CrossRef]
- Zahr Viñuela, J.; Pérez-Castellanos, J.L. A particular implementation of the Modified Secant Homogenization Method for particle reinforced metal matrix composites. Compos. Struct. 2014, 109, 260–267. [Google Scholar] [CrossRef]
- Rekik, A.; Allaoui, S.; Gasser, A.; Blond, E.; Andreev, K.; Sinnema, S. Experiments and nonlinear homogenization sustaining mean-field theories for refractory mortarless masonry: The classical secant procedure and its improved variants. Eur. J. Mech. A Solids 2015, 49, 67–81. [Google Scholar] [CrossRef]
- Zhao, Y.; Weng, G. Theory of plasticity for a class of inclusion and fiber-reinforced composites. In Micromechanics and Inhomogeneity; Springer: Berlin/Heidelberg, Germany, 1990; pp. 599–622. [Google Scholar]
- Qiu, Y.P.; Weng, G.J. A Theory of Plasticity for Porous Materials and Particle-Reinforced Composites. J. Appl. Mech. 1992, 59, 261–268. [Google Scholar] [CrossRef]
- Dunn, M.L.; Ledbetter, H. Elastic-plastic behavior of textured short-fiber composites. Acta Mater. 1997, 45, 3327–3340. [Google Scholar] [CrossRef]
- Ramazani, A.S.A.; Najafi, N.C. A nonlinear theoretical model for prediction of mechanical behavior of particulate composites and experimental verification of the model predictions. Polym. Compos. 2010, 31, 1150–1155. [Google Scholar] [CrossRef]
- Dvorak, G.J. Transformation field analysis of inelastic composite materials. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1900, 437, 311–327. [Google Scholar] [CrossRef]
- Dvorak, G.; Wafa, A.; Bahei-El-Din, Y. Implementation of the transformation field analysis for inelastic composite materials. Comput. Mech. 1994, 14, 201–228. [Google Scholar] [CrossRef]
- Nebozhyn, M.V.; Castañeda, P.P. Exact second-order estimate of the self consistent type for nonlnear composite materials. Mech. Mater. 1998, 28, 9–22. [Google Scholar] [CrossRef]
- Suquet, P. Overall properties of nonlinear composites. In Proceedings of the IUTAM Symposium on Micromechanics of Plasticity and Damage of Multiphase Materials, Paris, France, 29 August–1 September 1996; pp. 149–156. [Google Scholar]
- González, C.; LLorca, J. A self-consistent approach to the elasto-plastic behaviour of two-phase materials including damage. J. Mech. Phys. Solids 2000, 48, 675–692. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z. A Review of Analytical Micromechanics Models on Composite Elastoplastic Behaviour. Procedia Eng. 2017, 173, 1283–1290. [Google Scholar] [CrossRef]
- Molinari, A. On the self consistent modeling of elastic plastic behavior of polycrystals. Mech. Mater. 1997, 26, 43–62. [Google Scholar] [CrossRef]
- Molinari, A.; El Houdaigui, F.; Tóth, L.S. Validation of the tangent formulation for the solution of the non-linear Eshelby inclusion problem. Int. J. Plast. 2004, 20, 291–307. [Google Scholar] [CrossRef]
- Mercier, S.; Jacques, N.; Molinari, A. Validation of an interaction law for the Eshelby inclusion problem in elasto-viscoplasticity. Int. J. Solids Struct. 2005, 42, 1923–1941. [Google Scholar] [CrossRef]
- Molinari, A. Self-Consistent Modelling of Plastic and Viscoplastic Polycrystalline Materials; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Masson, R.; Bornert, M.; Suquet, P.; Zaoui, A. An affine formulation for the prediction of the effective properties of nonlinear composites and polycrystals. J. Mech. Phys. Solids 2000, 48, 1203–1227. [Google Scholar] [CrossRef]
- Zaoui, A.; Masson, R. Micromechanics-based modeling of plastic polycrystals: An affine formulation. Mater. Sci. Eng. A 2000, 285, 418–424. [Google Scholar] [CrossRef]
- Pierard, O.; Llorca, J.; Segurado, J.; Doghri, I. Micromechanics of particle-reinforced elasto-viscoplastic composites: Finite element simulations versus affine homogenization. Int. J. Plast. 2007, 23, 1041–1060. [Google Scholar] [CrossRef]
- Doghri, I.; Adam, L.; Bilger, N. Mean-field homogenization of elasto-viscoplastic composites based on a general incrementally affine linearization method. Int. J. Plast. 2010, 26, 219–238. [Google Scholar] [CrossRef]
- Hu, G. A method of plasticity for general aligned spheroidal void or fiber-reinforced composites. Int. J. Plast. 1996, 12, 439–449. [Google Scholar]
- Suquet, P. Overall properties of nonlinear composites: A modified secant moduli theory and its link with Ponte Castañeda’s nonlinear variational procedure. Comptes Rendus de l’Académie des Sciences. Série II, Mécanique, Physique, Chimie, Astronomie 1995, 320, 563–571. [Google Scholar]
- Talbot, D.; Willis, J. Variational principles for inhomogeneous non-linear media. IMA J. Appl. Math. 1985, 35, 39–54. [Google Scholar] [CrossRef]
- Castañeda, P.P. The effective mechanical properties of nonlinear isotropic composites. J. Mech. Phys. Solids 1991, 39, 45–71. [Google Scholar] [CrossRef]
- Castaneda, P.P. New variational principles in plasticity and their application to composite materials. J. Mech. Phys. Solids 1992, 40, 1757–1788. [Google Scholar] [CrossRef]
- Castañeda, P.P. Elastoplastic constitutive relations for fiber-reinforced solids. Int. J. Solids Struct. 1993, 30, 1865–1890. [Google Scholar]
- Castaneda, P.P.; Suquet, P. Nonlinear composites. Adv. Appl. Mech. 1997, 34, 171–302. [Google Scholar]
- Pettermann, H.; Plankensteiner, A.F.; Böhm, H.J.; Rammerstorfer, F.G. A thermo-elasto-plastic constitutive law for inhomogeneous materials based on an incremental Mori–Tanaka approach. Comput. Struct. 1999, 71, 197–214. [Google Scholar] [CrossRef]
- Gavazzi, A.C.; Lagoudas, D.C. On the numerical evaluation of Eshelby’s tensor and its application to elastoplastic fibrous composites. Comput. Mech. 1990, 7, 13–19. [Google Scholar] [CrossRef]
- Lagoudas, D.; Gavazzi, A.; Nigam, H. Elastoplastic behavior of metal matrix composites based on incremental plasticity and the Mori-Tanaka averaging scheme. Comput. Mech. 1991, 8, 193–203. [Google Scholar] [CrossRef]
- He, Z.; Caratini, G.; Dormieux, L.; Kondo, D. Homogenization of anisotropic elastoplastic behaviors of a porous polycrystal with interface effects. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 3213–3236. [Google Scholar] [CrossRef]
- Guéry, A.A.-C.; Cormery, F.; Shao, J.F.; Kondo, D. A micromechanical model of elastoplastic and damage behavior of a cohesive geomaterial. Int. J. Solids Struct. 2008, 45, 1406–1429. [Google Scholar] [CrossRef]
- Jiang, T.; Shao, J.F. On the incremental approach for nonlinear homogenization of composite and influence of isotropization. Comput. Mater. Sci. 2009, 46, 447–451. [Google Scholar] [CrossRef]
- Chen, D.; Shen, W.Q.; Shao, J.F.; Yurtdas, I. Micromechanical modeling of mortar as a matrix-inclusion composite with drying effects. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1034–1047. [Google Scholar] [CrossRef]
- Czarnota, C.; Kowalczyk-Gajewska, K.; Salahouelhadj, A.; Martiny, M.; Mercier, S. Modeling of the cyclic behavior of elastic-viscoplastic composites by the additive tangent Mori-Tanaka approach and validation by finite element calculations. Int. J. Solids Struct. 2015, 56–57, 96–117. [Google Scholar] [CrossRef]
- Lavergne, F.; Sab, K.; Sanahuja, J.; Bornert, M.; Toulemonde, C. Homogenization schemes for aging linear viscoelastic matrix-inclusion composite materials with elongated inclusions. Int. J. Solids Struct. 2016, 80, 545–560. [Google Scholar] [CrossRef]
- Shen, W.Q.; Shao, J.F. An incremental micro-macro model for porous geomaterials with double porosity and inclusion. Int. J. Plast. 2016, 83, 37–54. [Google Scholar] [CrossRef]
- Azoti, W.; Elmarakbi, A. Constitutive modelling of ductile damage matrix reinforced by platelets-like particles with imperfect interfaces: Application to graphene polymer nanocomposite materials. Compos. Part B Eng. 2017, 113, 55–64. [Google Scholar] [CrossRef]
- Huang, Y.; Abou-Chakra Guéry, A.; Shao, J.F. Incremental variational approach for time dependent deformation in clayey rock. Int. J. Plast. 2015, 64, 88–103. [Google Scholar] [CrossRef]
- Huang, Z.M. Latest Advancements of the Bridging Model Theory. Appl. Math. Mech. 2015, 36, 563–581. [Google Scholar]
- Zhu, S.; Mizuno, M.; Kagawa, Y.; Mutoh, Y. Monotonic tension, fatigue and creep behavior of SiC-fiber-reinforced SiC-matrix composites: A review. Compos. Sci. Technol. 1999, 59, 833–851. [Google Scholar] [CrossRef]
- Guo, Z.X.; Derby, B. Fibre uniformity and cavitation during the consolidation of metal-matrix composite via fibre-mat and matrix-foil diffusion bonding. Acta Metall. Mater. 1993, 41, 3257–3266. [Google Scholar] [CrossRef]
- Huang, B.; Yang, Y.; Luo, H.; Yuan, M.; Chen, Y. Effect of the interfacial reaction layer thickness on the thermal residual stresses in SiCf/Ti–6Al–4V composites. Mater. Sci. Eng. A 2008, 489, 178–186. [Google Scholar] [CrossRef]
- Li, J.-S.; Zhang, C.-R.; Li, B. Preparation and characterization of boron nitride coatings on carbon fibers from borazine by chemical vapor deposition. Appl. Surf. Sci. 2011, 257, 7752–7757. [Google Scholar] [CrossRef]
- Hughes, J.D.H. The carbon fibre/epoxy interface—A review. Compos. Sci. Technol. 1991, 41, 13–45. [Google Scholar] [CrossRef]
- Gutowski, W.S. Interface/Interphase engineering of polymers for adhesion enhancement: Part I. Review of micromechanical aspects of polymer interface reinforcement through surface grafted molecular brushes. J. Adhes. 2010, 79, 445–482. [Google Scholar] [CrossRef]
- Jones, F.R. A Review of Interphase Formation and Design in Fibre-Reinforced Composites. J. Adhes. Sci. Technol. 2010, 24, 171–202. [Google Scholar] [CrossRef]
- Duan, H.L.; Yi, X.; Huang, Z.P.; Wang, J. A unified scheme for prediction of effective moduli of multiphase composites with interface effects. Part I: Theoretical framework. Mech. Mater. 2007, 39, 81–93. [Google Scholar] [CrossRef]
- Hashin, Z. Thermoelastic properties of particulate composites with imperfect interface. J. Mech. Phys. Solids 1991, 39, 745–762. [Google Scholar] [CrossRef]
- Tan, H.; Huang, Y.; Liu, C.; Geubelle, P.H. The Mori–Tanaka method for composite materials with nonlinear interface debonding. Int. J. Plast. 2005, 21, 1890–1918. [Google Scholar] [CrossRef]
- Shuttleworth, R. The Surface Tension of Solids. Proc. Phys. Soc. Sect. A 1950, 63, 444. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Ian Murdoch, A. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Yu, H. A new dislocation-like model for imperfect interfaces and their effect on load transfer. Compos. Part A Appl. Sci. Manuf. 1998, 29, 1057–1062. [Google Scholar] [CrossRef]
- Mura, T.; Jasiuk, I.; Tsuchida, B. The stress field of a sliding inclusion. Int. J. Solids Struct. 1985, 21, 1165–1179. [Google Scholar] [CrossRef]
- Huang, J.H.; Furuhashi, R.; Mura, T. Frictional sliding inclusions. J. Mech. Phys. Solids 1993, 41, 247–265. [Google Scholar] [CrossRef]
- Wang, J.; Duan, H.L.; Zhang, Z.; Huang, Z.P. An anti-interpenetration model and connections between interphase and interface models in particle-reinforced composites. Int. J. Mech. Sci. 2005, 47, 701–718. [Google Scholar] [CrossRef]
- Benveniste, Y.; Miloh, T. Imperfect soft and stiff interfaces in two-dimensional elasticity. Mech. Mater. 2001, 33, 309–323. [Google Scholar] [CrossRef]
- Benveniste, Y. A general interface model for a three-dimensional curved thin anisotropic interphase between two anisotropic media. J. Mech. Phys. Solids 2006, 54, 708–734. [Google Scholar] [CrossRef]
- Wang, Y.C.; Huang, Z.M. A bridging tensor containing an interphase. Chin. J. Solid Mech. 2015, 36, 95–104. [Google Scholar]
- Chang, F.-K.; Chang, K.-Y. A Progressive Damage Model for Laminated Composites Containing Stress Concentrations. J. Compos. Mater. 1987, 21, 834–855. [Google Scholar] [CrossRef]
- Ju, J.W.; Lee, H.K. A micromechanical damage model for effective elastoplastic behavior of partially debonded ductile matrix composites. Int. J. Solids Struct. 2001, 38, 6307–6332. [Google Scholar] [CrossRef]
- Shi, Y.; Pinna, C.; Soutis, C. Interface Cohesive Elements to Model Matrix Crack Evolution in Composite Laminates. Appl. Compos. Mater. 2013, 21, 57–70. [Google Scholar] [CrossRef]
- Hill, R. Theory of mechanical properties of fibre-strengthened materials: I. Elastic behaviour. J. Mech. Phys. Solids 1964, 12, 199–212. [Google Scholar] [CrossRef]
- Luo, H.A.; Weng, G.J. On eshelby’s s-tensor in a three-phase cylindrically concentric solid, and the elastic moduli of fiber-reinforced composites. Mech. Mater. 1989, 8, 77–88. [Google Scholar] [CrossRef]
- Hangen, U.; Raabe, D. Modelling of the yield strength of a heavily wire drawn Cu-20%Nb composite by use of a modified linear rule of mixtures. Acta Metall. Mater. 1995, 43, 4075–4082. [Google Scholar] [CrossRef]
- Jacquet, E.; Trivaudey, F.; Varchon, D. Calculation of the transverse modulus of a unidirectional composite material and of the modulus of an aggregate. Application of the rule of mixtures. Compos. Sci. Technol. 2000, 60, 345–350. [Google Scholar] [CrossRef]
- Kim, H.S.; Hong, S.I.; Kim, S.J. On the rule of mixtures for predicting the mechanical properties of composites with homogeneously distributed soft and hard particles. J. Mater. Process. Technol. 2001, 112, 109–113. [Google Scholar] [CrossRef]
- Ji, S. A generalized mixture rule for estimating the viscosity of solid-liquid suspensions and mechanical properties of polyphase rocks and composite materials. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Zhang, L.W.; Lei, Z.X.; Liew, K.M. An element-free IMLS-Ritz framework for buckling analysis of FG–CNT reinforced composite thick plates resting on Winkler foundations. Eng. Anal. Bound. Elem. 2015, 58, 7–17. [Google Scholar] [CrossRef]
- Chamis, C.C.; Abdi, F.; Garg, M.; Minnetyan, L.; Baid, H.; Huang, D.; Housner, J.; Talagani, F. Micromechanics-based progressive failure analysis prediction for WWFE-III composite coupon test cases. J. Compos. Mater. 2013, 47, 2695–2712. [Google Scholar] [CrossRef]
- Soden, P.D.; Hinton, M.J.; Kaddour, A.S. Lamina properties, lay-up configurations and loading conditions for a range of fibre-reinforced composite laminates. Compos. Sci. Technol. 1998, 58, 1011–1022. [Google Scholar] [CrossRef]
- Kaddour, A.; Hinton, M. Input data for test cases used in benchmarking triaxial failure theories of composites. J. Compos. Mater. 2012, 46, 2295–2312. [Google Scholar] [CrossRef]
- Kaddour, A.; Hinton, M.; Smith, P.; Li, S. Mechanical properties and details of composite laminates for the test cases used in the third world-wide failure exercise. J. Compos. Mater. 2013, 47, 2427–2442. [Google Scholar] [CrossRef]
- Huang, Z.-M. Inelastic and Failure Analysis of Laminate Structures by ABAQUS Incorporated with a General Constitutive Relationship. J. Reinf. Plast. Compos. 2007, 26, 1135–1181. [Google Scholar] [CrossRef]
- Aboudi, J. The Generalized Method of Cells and High-Fidelity Generalized Method of Cells Micromechanical Models—A Review. Mech. Adv. Mater. Struct. 2004, 11, 329–366. [Google Scholar] [CrossRef]
- Pettermann, H.E.; Huber, C.O.; Luxner, M.H.; Nogales, S.; Böhm, H.J. An Incremental Mori-Tanaka Homogenization Scheme for Finite Strain Thermoelastoplasticity of MMCs. Materials 2010, 3, 434–451. [Google Scholar] [CrossRef]
- Huang, Z.-M.; Zhou, Y.-X. Bridging Micromechanics Model. In Strength of Fibrous Composites; Springer: Berlin/Heidelberg, Germany, 2012; pp. 53–98. [Google Scholar]
- Kawai, M.; Masuko, Y.; Kawase, Y.; Negishi, R. Micromechanical analysis of the off-axis rate-dependent inelastic behavior of unidirectional AS4/PEEK at high temperature. Int. J. Mech. Sci. 2001, 43, 2069–2090. [Google Scholar] [CrossRef]
- Doghri, I.; Brassart, L.; Adam, L.; Gérard, J.S. A second-moment incremental formulation for the mean-field homogenization of elasto-plastic composites. Int. J. Plast. 2011, 27, 352–371. [Google Scholar] [CrossRef]
- Dvorak, G.J.; Benveniste, Y. On transformation strains and uniform fields in multiphase elastic media. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1992, 437, 291–310. [Google Scholar] [CrossRef]
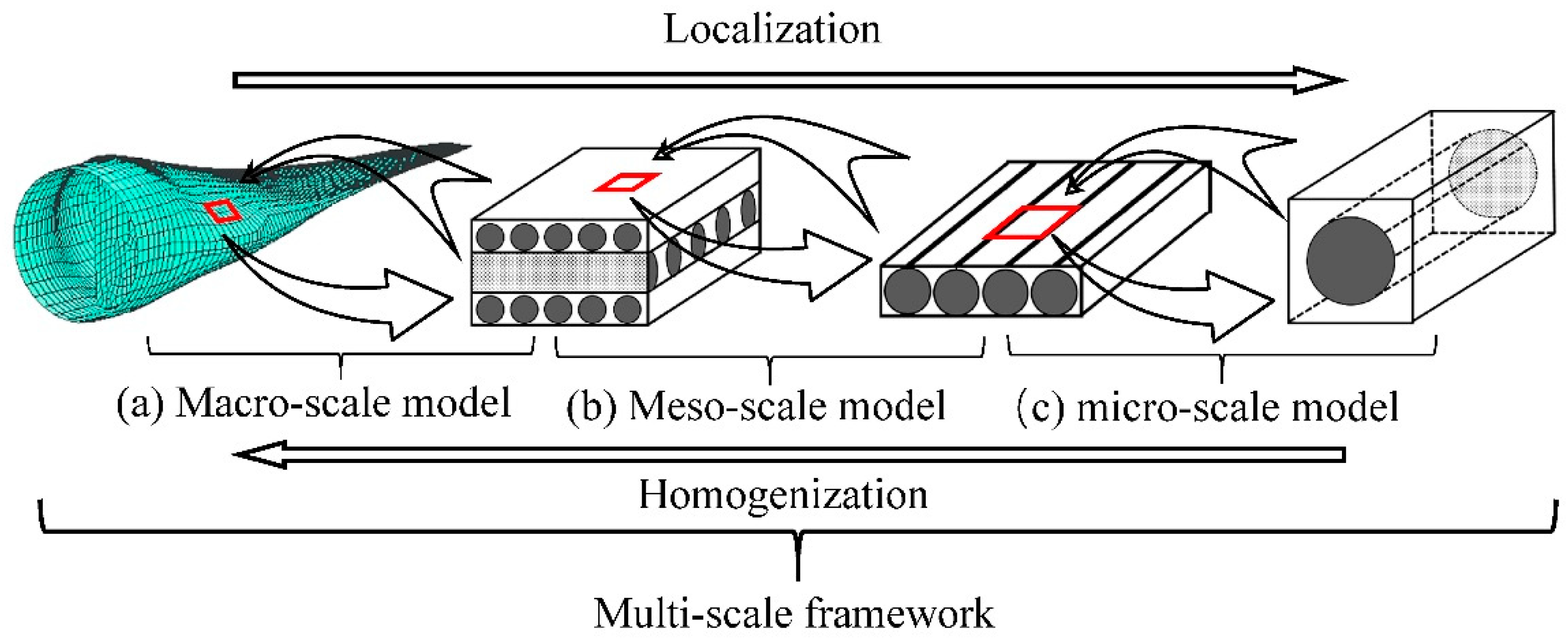
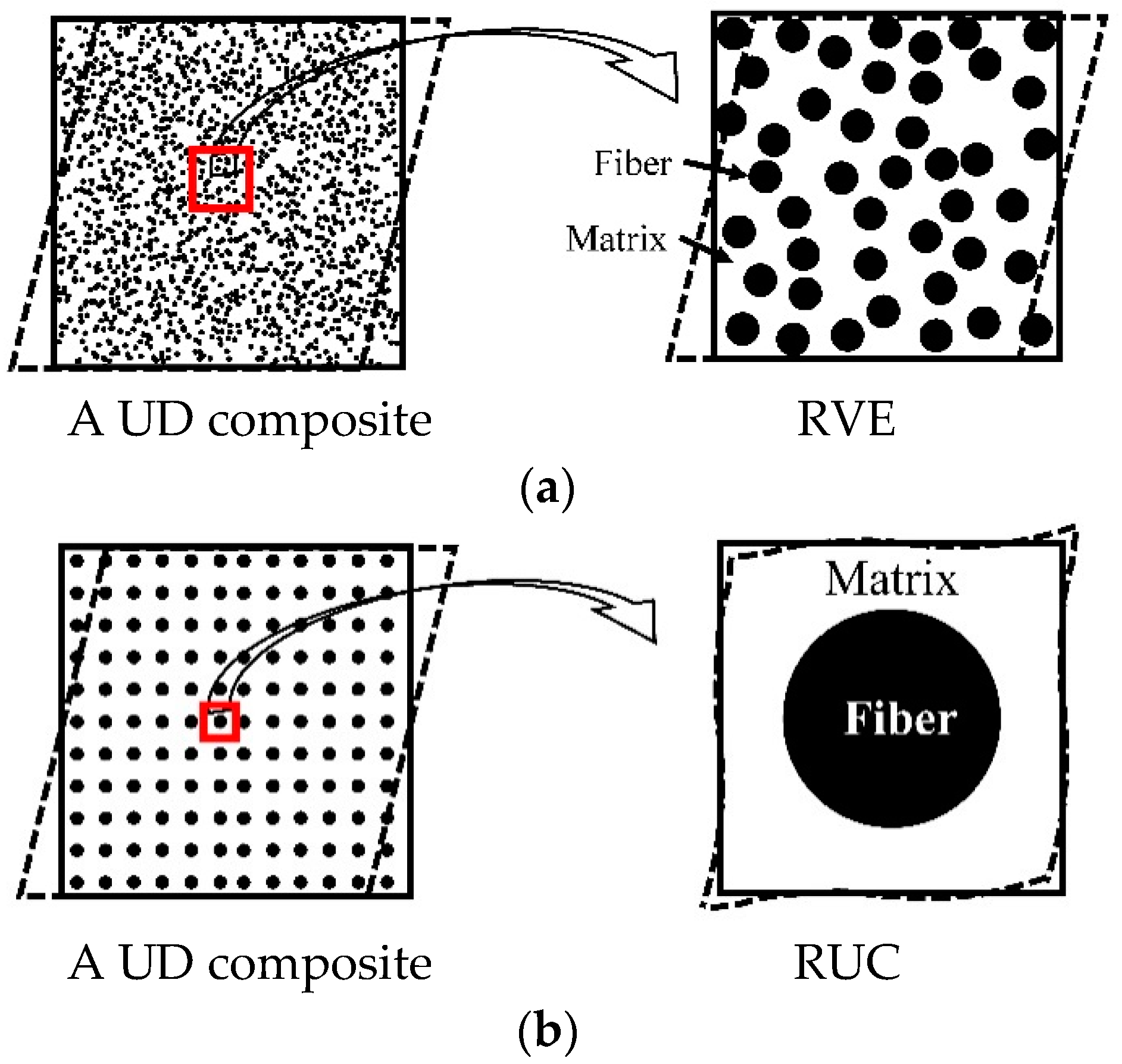
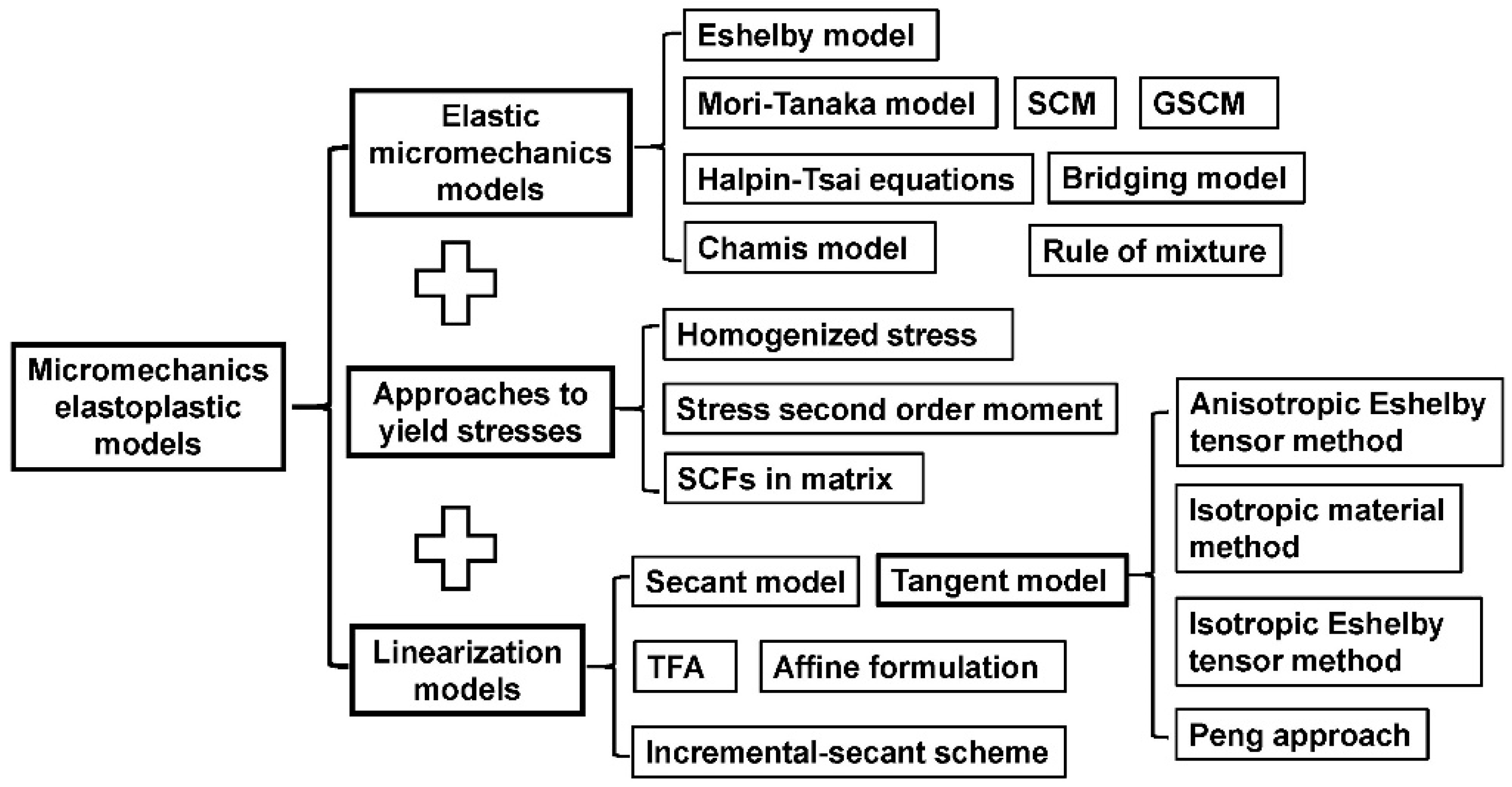

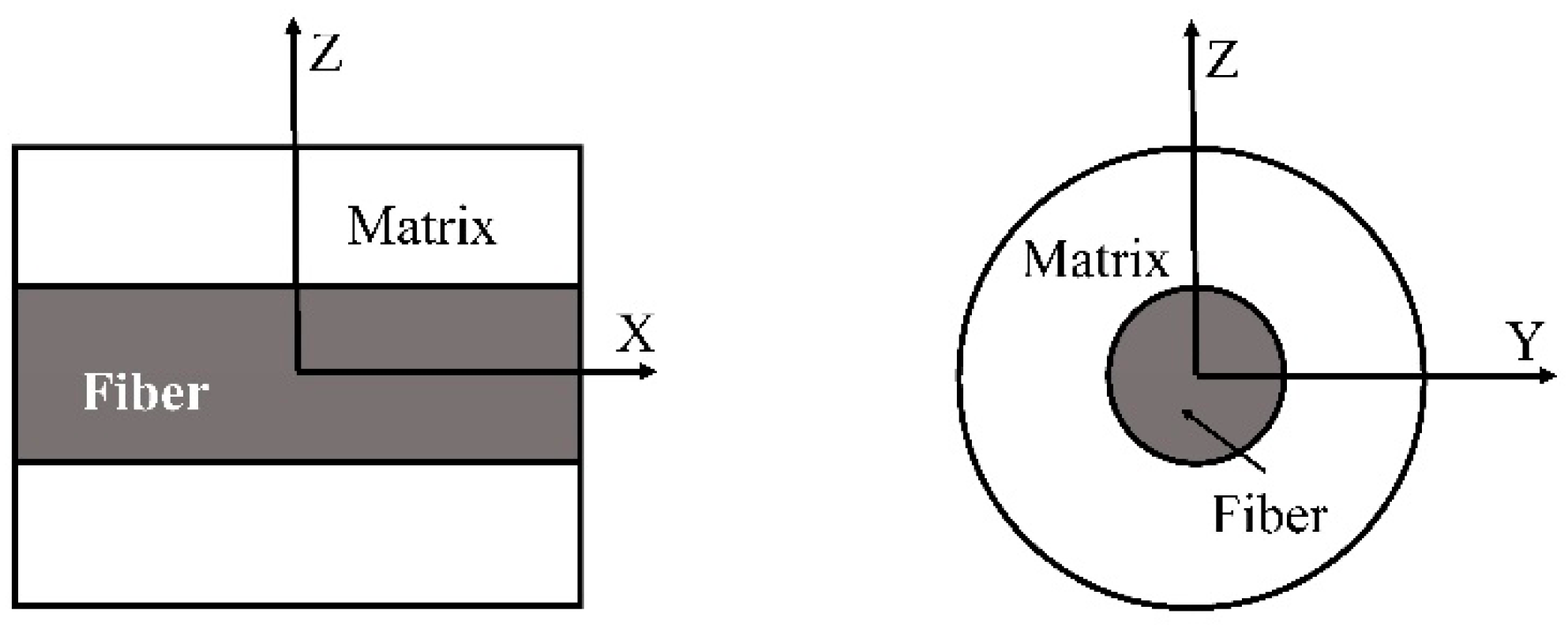
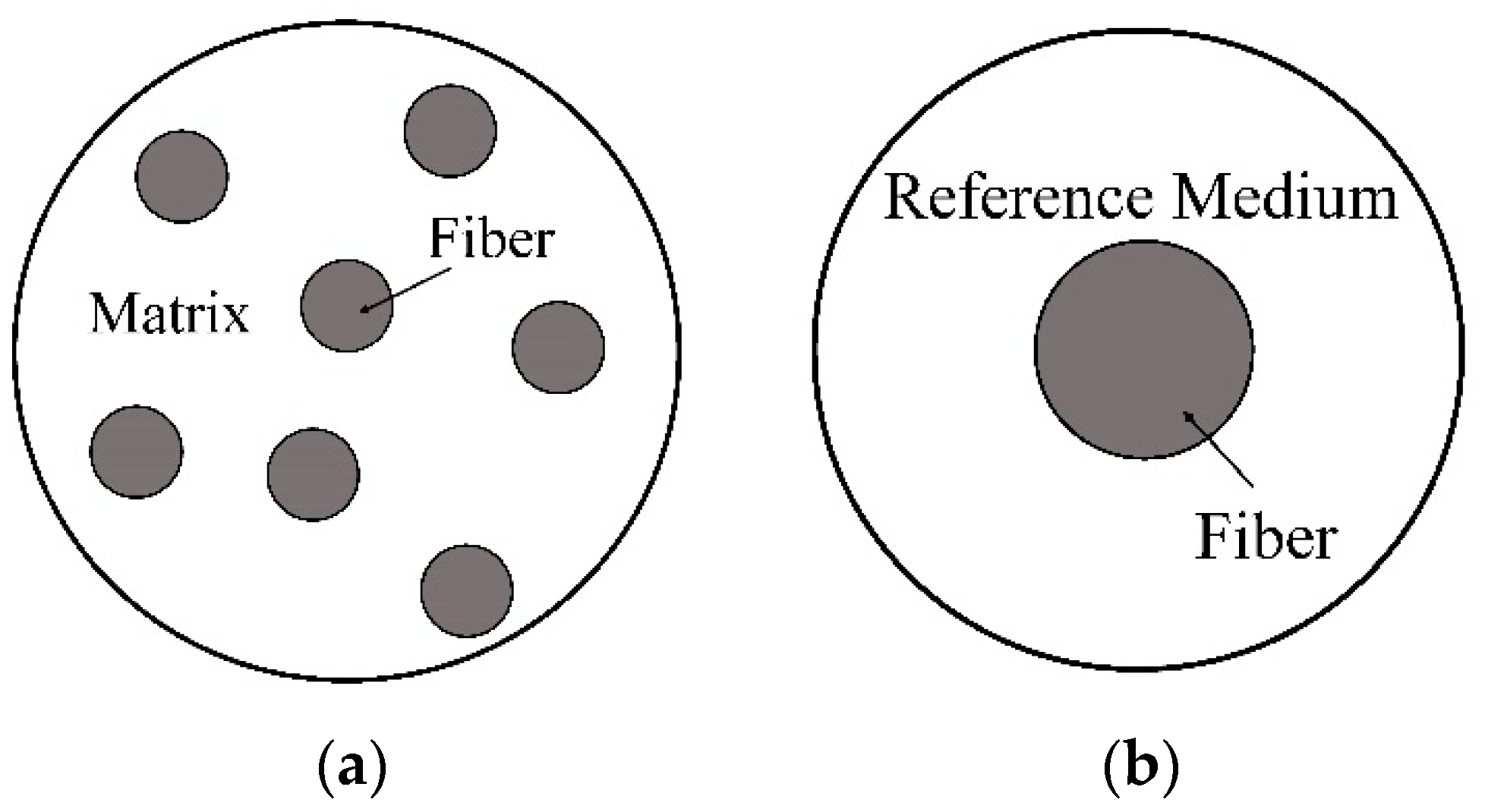
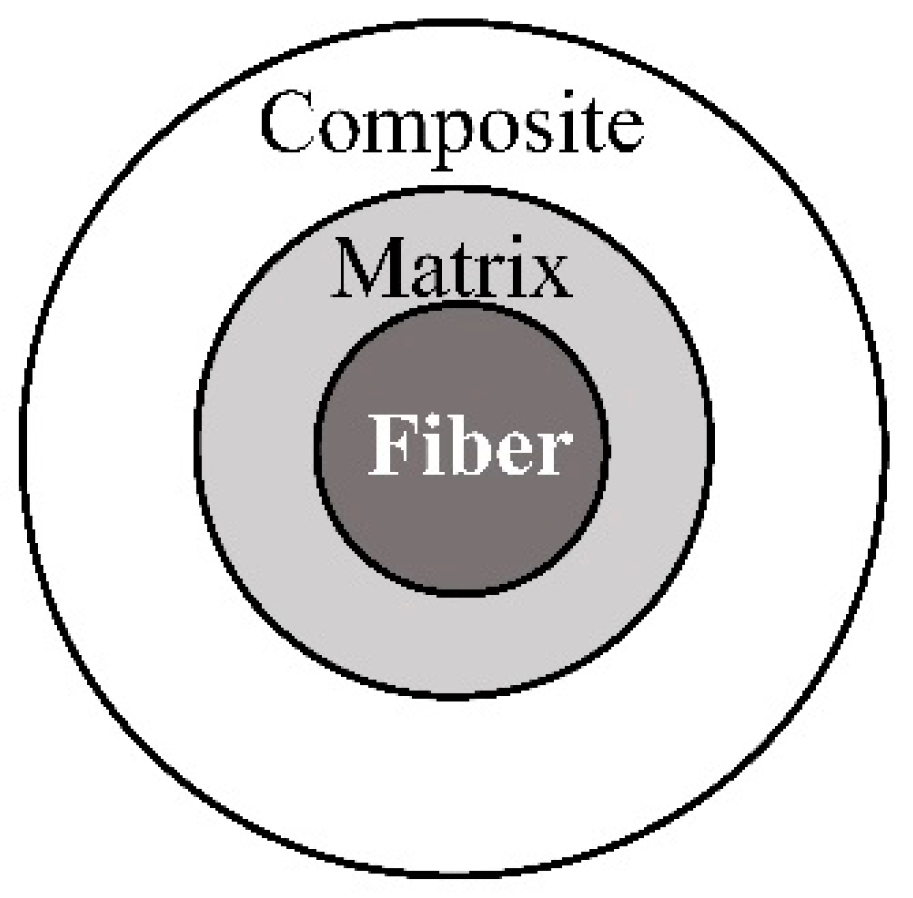
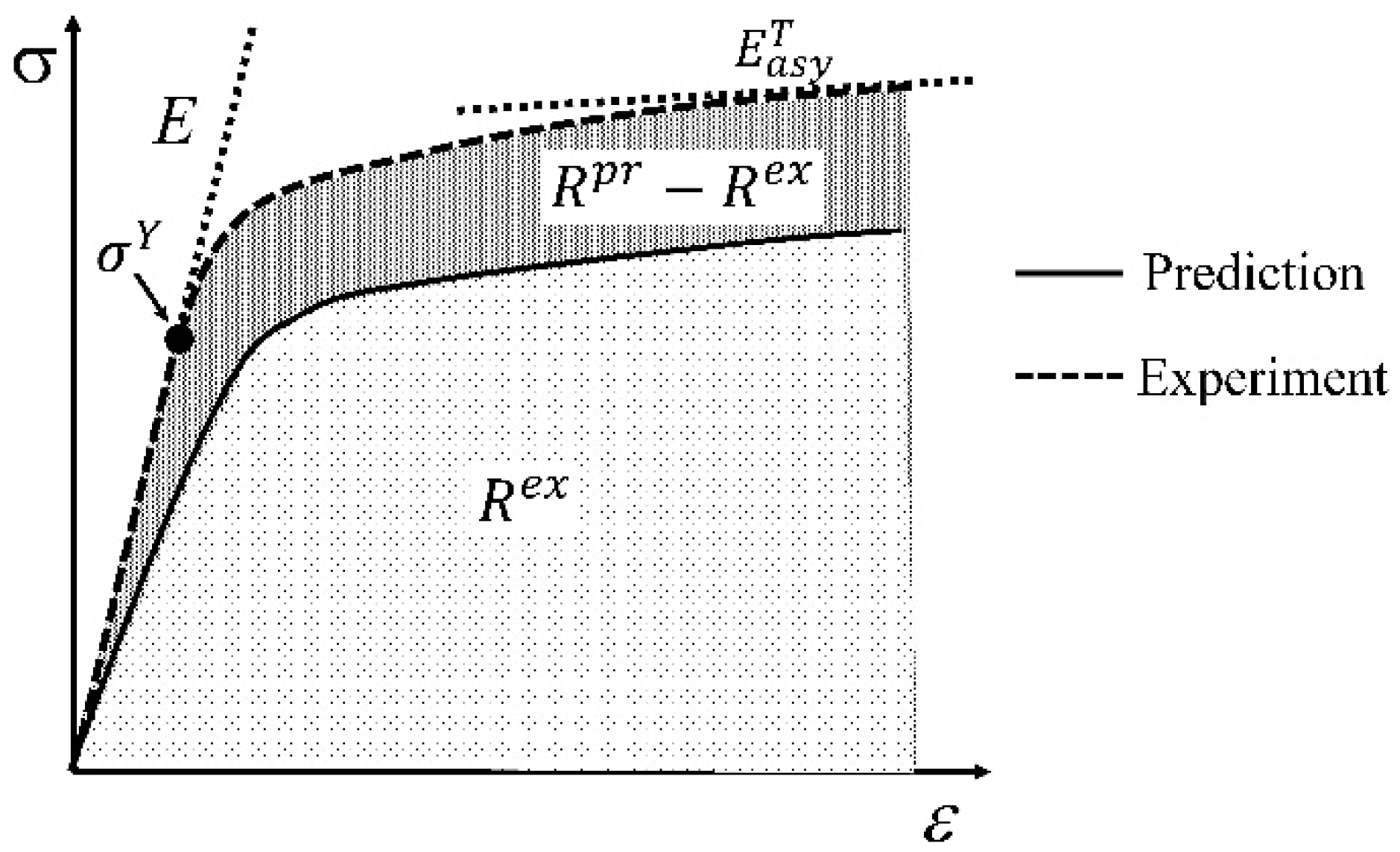





| Complexity | Macro-Scale Model | Meso-Scale Model | Micro-Scale Model |
|---|---|---|---|
| Complexity of plasticity | *** | ** | * |
| Complexity of computation | * | ** | *** |
| Complexity of experiments | *** | ** | * |
| Complexity of modeling | * | ** | *** |
| 1 | |||
| Models | Average Error | Rank | Models | Average Error | Rank |
|---|---|---|---|---|---|
| Bridging Model | 12.4% | 1 | GSCM | 25.1% | 7 |
| SCM | 14.3% | 2 | Halpin–Tsai Equations | 28.2% | 8 |
| FVDAM | 14.9% | 3 | Mori–Tanaka Model | 28.2% | 8 |
| FEM | 15.9% | 4 | Rule of Mixture | 43.5% | 10 |
| GMC | 18.4% | 5 | Eshelby model | 44.3% | 11 |
| Chamis Model | 21.4% | 6 | - | - | - |
| Models | Average Error | Rank | Models | Average Error | Rank |
|---|---|---|---|---|---|
| Bridging Model | 14.6% | 1 | GSCM | 25.2% | 5 |
| Chamis Model | 18.1% | 2 | GMC | 27.0% | 8 |
| FVDAM | 22% | 3 | Rule of Mixture | 48.1% | 9 |
| FEM | 22.1% | 4 | Eshelby model | 53.5% | 10 |
| Halpin–Tsai Equations | 25.2% | 5 | SCM | 62% | 11 |
| Mori–Tanaka Model | 25.2% | 5 | - | - | - |
| Models | Average Error | Rank | Models | Average Error | Rank |
|---|---|---|---|---|---|
| FEM | 8.8% | 1 | GSCM | 22.4% | 7 |
| FVDAM | 8.9% | 2 | Halpin–Tsai Equations | 26.9% | 8 |
| Bridging Model | 9% | 3 | Mori–Tanaka Model | 26.9% | 8 |
| SCM | 11.5% | 4 | Rule of Mixture | 39.1% | 10 |
| GMC | 11.8% | 5 | Eshelby model | 45.5% | 11 |
| Chamis Model | 15% | 6 | - | - | - |
| Models | Average Error | Rank | Models | Average Error | Rank |
|---|---|---|---|---|---|
| Eshelby Model | 7.3% | 1 | GSCM | 14.9% | 7 |
| Rule of Mixture | 12.9% | 2 | GMC | 15% | 8 |
| Bridging Model | 12.9% | 2 | FVDAM | 15.3% | 9 |
| Chamis Model | 12.9% | 2 | FEM | 15.4% | 10 |
| Halpin–Tsai Equations | 12.9% | 2 | SCM | 18.3% | 11 |
| Mori–Tanaka Model | 14.6% | 6 | - | - | - |
| Models | Average Error | Rank | Models | Average Error | Rank |
|---|---|---|---|---|---|
| Bridging model | 10.38% | 1 | Halpin–Tsai equations | 19.24% | 7 |
| FVDAM | 12.83% | 2 | Mori–Tanaka model | 19.59% | 8 |
| FEM | 13.08% | 3 | SCM | 21.82% | 9 |
| Chamis model | 14.09% | 4 | Rule of mixture | 28.4% | 10 |
| GMC | 15.07% | 5 | Eshelby model | 30.72% | 11 |
| GSCM | 18.14% | 6 | - | - | - |
| Approaches | Tension-Shear Coupling | Error of or | Error of σY | Error of | |
|---|---|---|---|---|---|
| Mori–Tanaka Model | Yes | 18.5% | 38.6% | 134.8% | 22.7% |
| Chamis model | No | 14.2% | 61.3% | 154.8% | 29.1% |
| Bridging model | Yes | 12.6% | 90.2% | 206.1% | 53.3% |
| Self-consistent model | Yes | 28.0% | 126.2% | 845.8% | 116.2% |
| Approaches | Non-Monotonic and Non-Proportional Load | Tension-Shear Coupling | Numerical Integration on ESHELBY TENSOR |
|---|---|---|---|
| Tangent model | Yes | Yes | Yes |
| Secant model | No | No | No |
| TFA model | Yes | No | No |
| Affine formulations | No | Yes | Yes |
| Incremental-secant scheme | Yes | No | No |
| Approaches | Non-Monotonic and Non-Proportional Load | Tension-Shear Coupling | Numerical Integration on Eshelby Tensor |
|---|---|---|---|
| Anisotropic Eshelby tensor | Yes | Yes | Yes |
| Isotropic matrix | No | No | No |
| Isotropic Eshelby tensor | Yes | Yes | No |
| Peng approach | Yes | Yes | No |
| Longitudinal Tension | |||||||
|---|---|---|---|---|---|---|---|
| IM7/8551-7 (2500 MPa) | Anisotropic Eshelby tensor | 4132 | −3 | −3 | 51.7 | 4.6 | 4.6 |
| Isotropic Eshelby tensor | 4303 | 191 | 191 | −204 | −286 | −286 | |
| Isotropic Matrix | 4133 | −2.4 | −2.4 | 50.8 | 3.5 | 3.5 | |
| Peng’s approach | 4131 | −3 | −3 | 53.5 | 4.5 | 4.5 | |
| E-Glass/Epoxy (1300 MPa) | Anisotropic Eshelby tensor | 2107 | −4 | −4 | 89 | 6 | 6 |
| Isotropic Eshelby tensor | 2140 | 36 | 36 | 41 | −53 | −53 | |
| Isotropic Matrix | 2109 | −3.4 | −3.4 | 86 | 5.1 | 5.1 | |
| Peng’s approach | 2107 | −4 | −4 | 89 | 6 | 6 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Huang, Z. Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study. Materials 2018, 11, 1919. https://doi.org/10.3390/ma11101919
Wang Y, Huang Z. Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study. Materials. 2018; 11(10):1919. https://doi.org/10.3390/ma11101919
Chicago/Turabian StyleWang, Yanchao, and ZhengMing Huang. 2018. "Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study" Materials 11, no. 10: 1919. https://doi.org/10.3390/ma11101919
APA StyleWang, Y., & Huang, Z. (2018). Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study. Materials, 11(10), 1919. https://doi.org/10.3390/ma11101919





