A Review on Low-Grade Thermal Energy Harvesting: Materials, Methods and Devices
Abstract
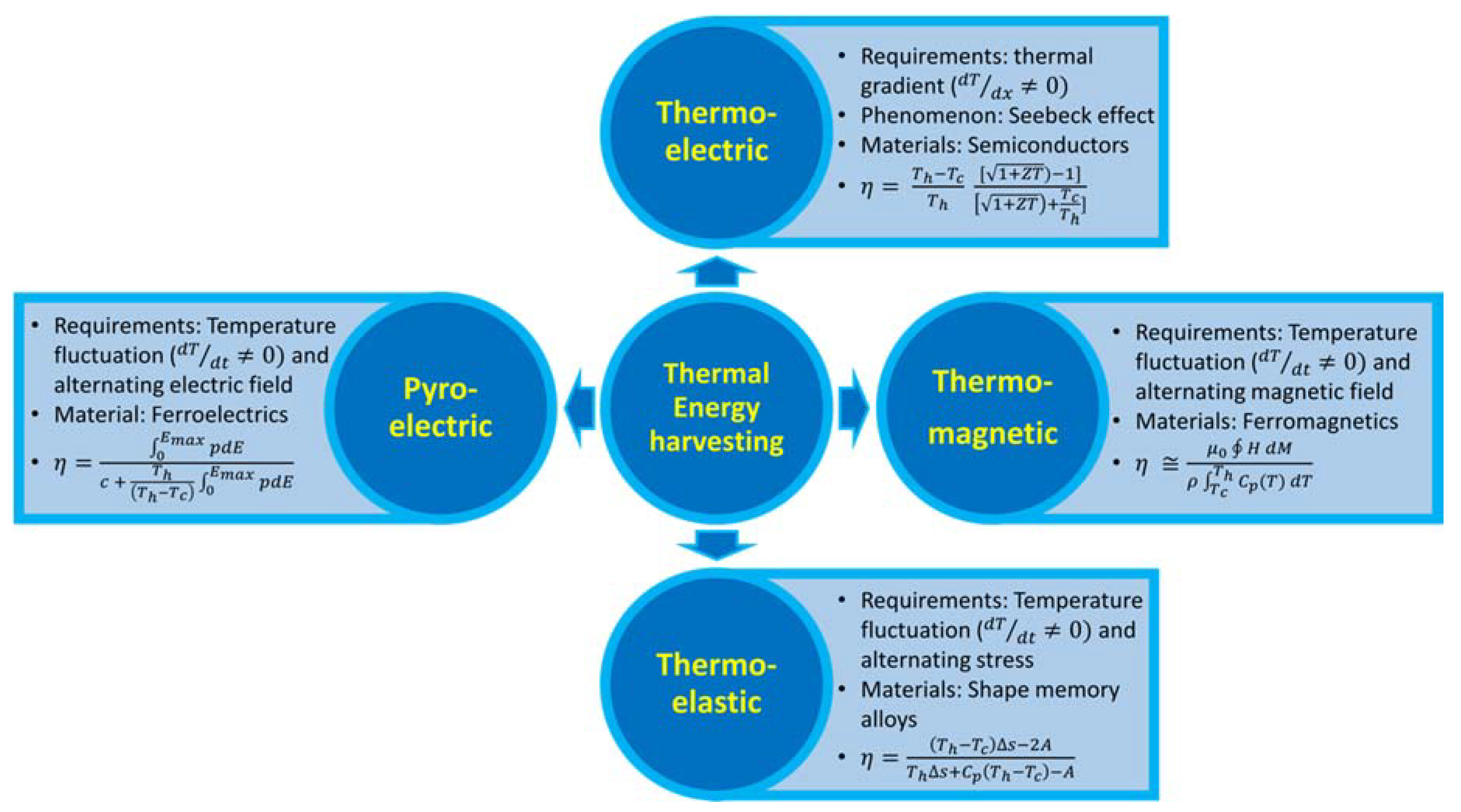
1. Introduction
2. Thermoelectric Energy Harvesting
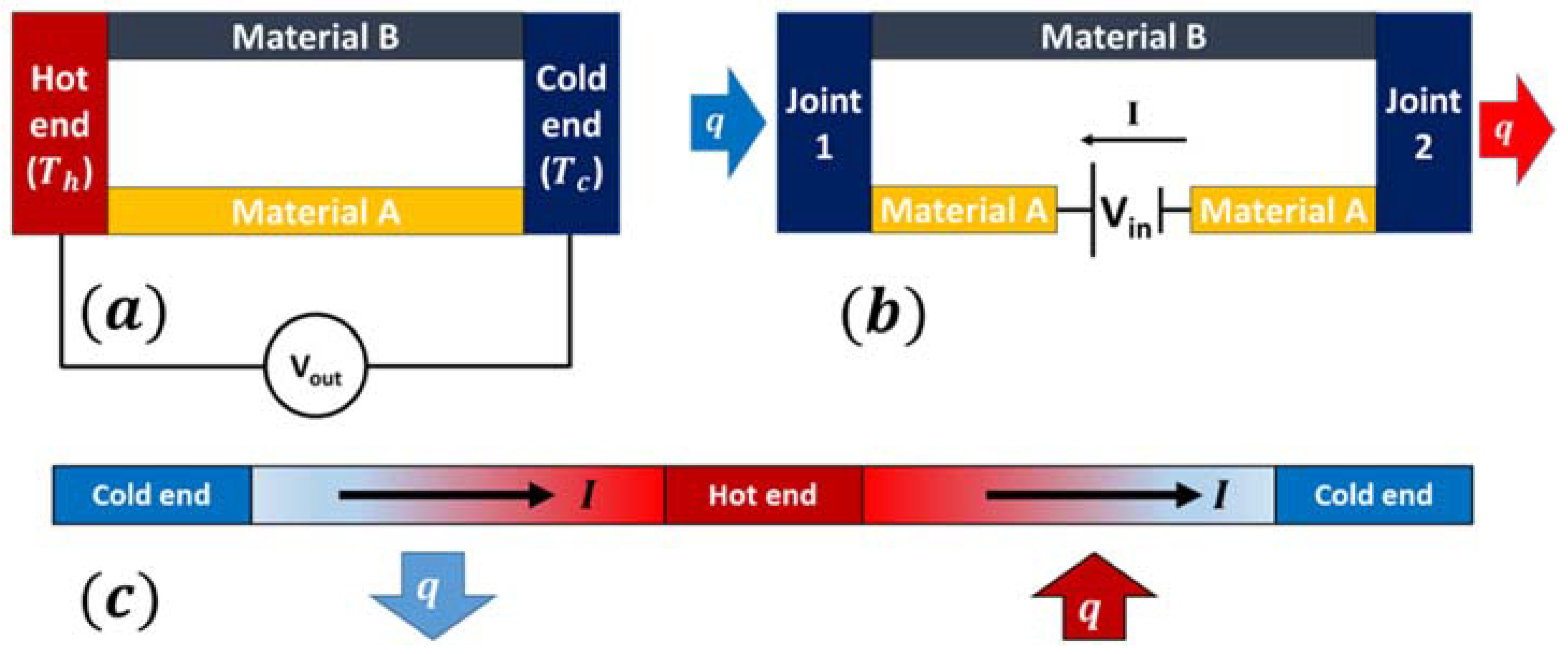
2.1. Seebeck Effect
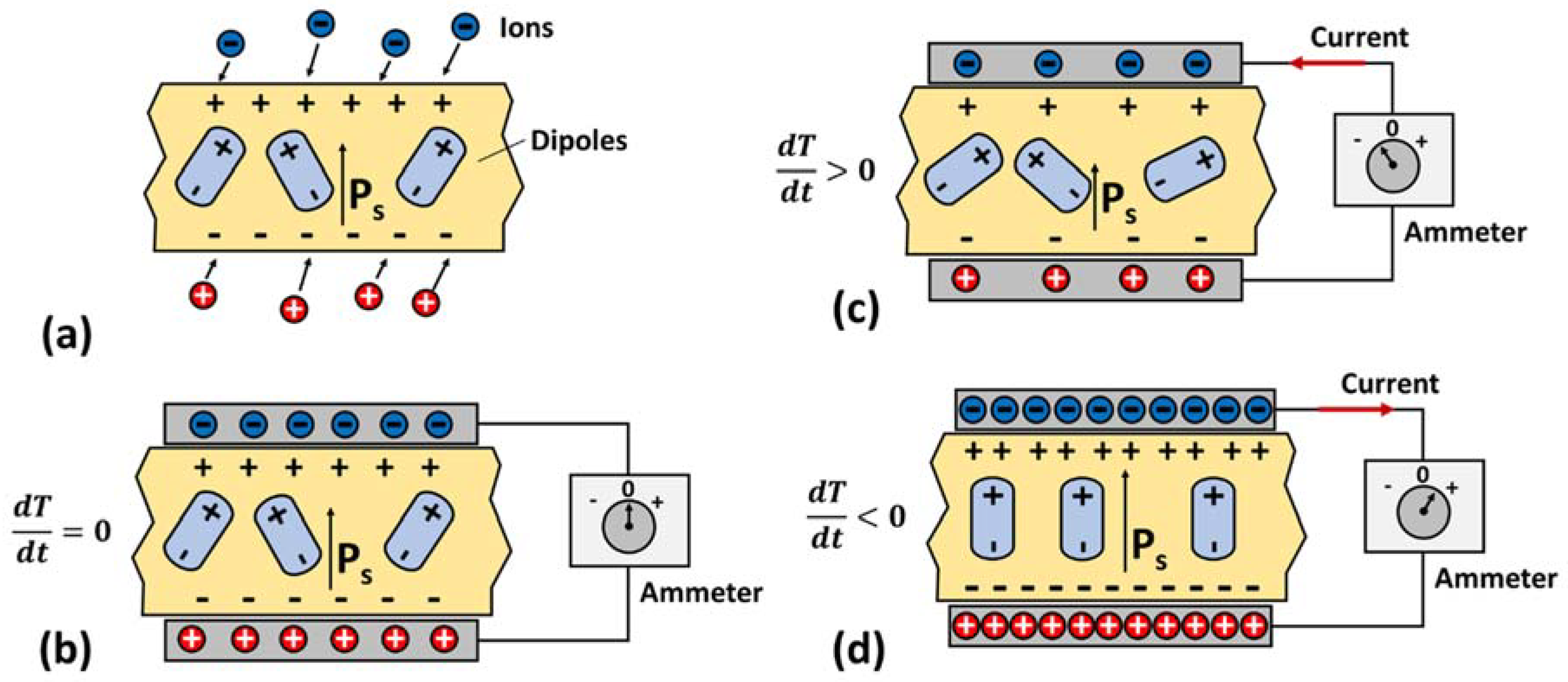
2.2. Peltier Effect
2.3. Thomson Effect
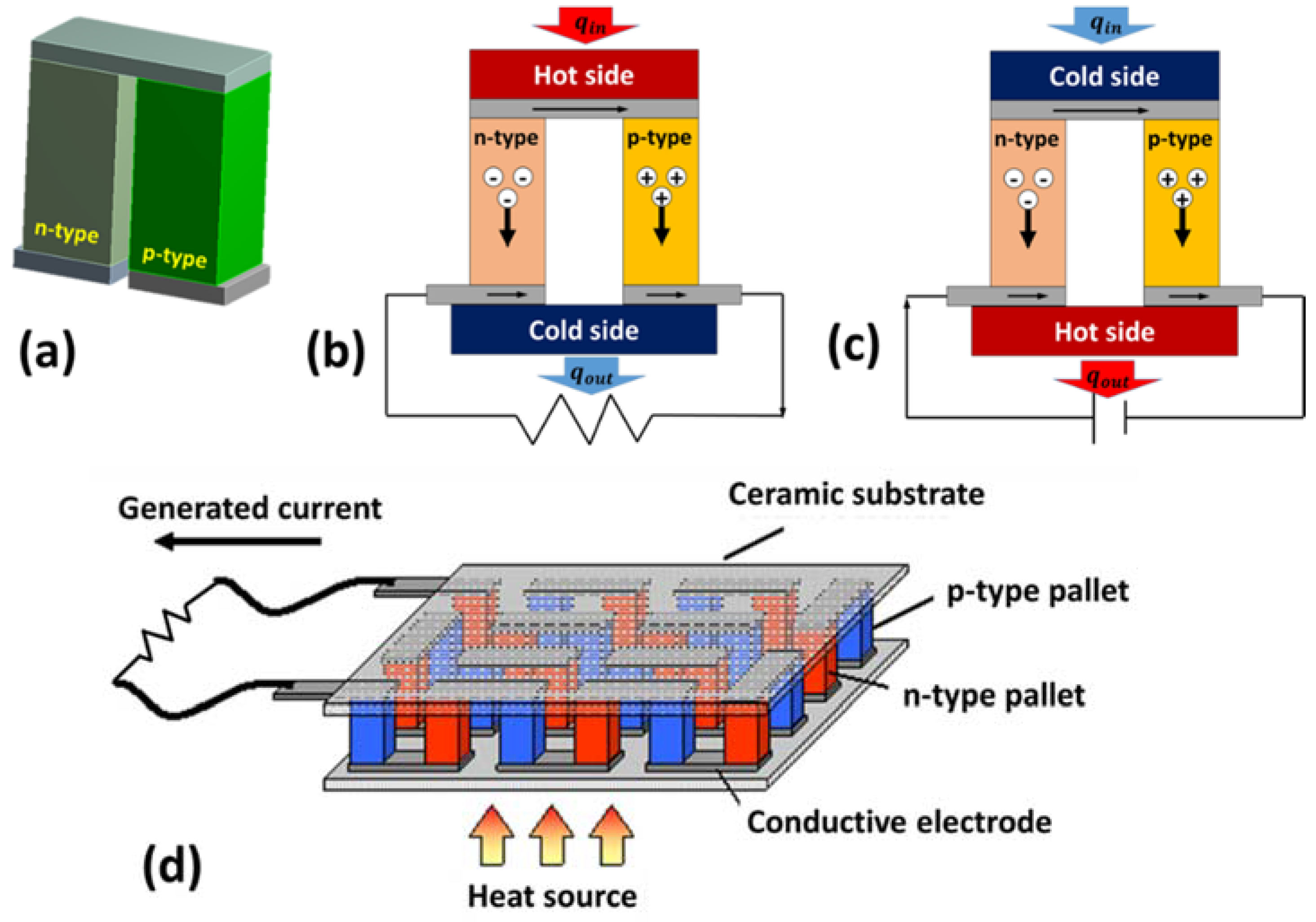
2.4. Working Principle
2.5. Thermoelectric Properties
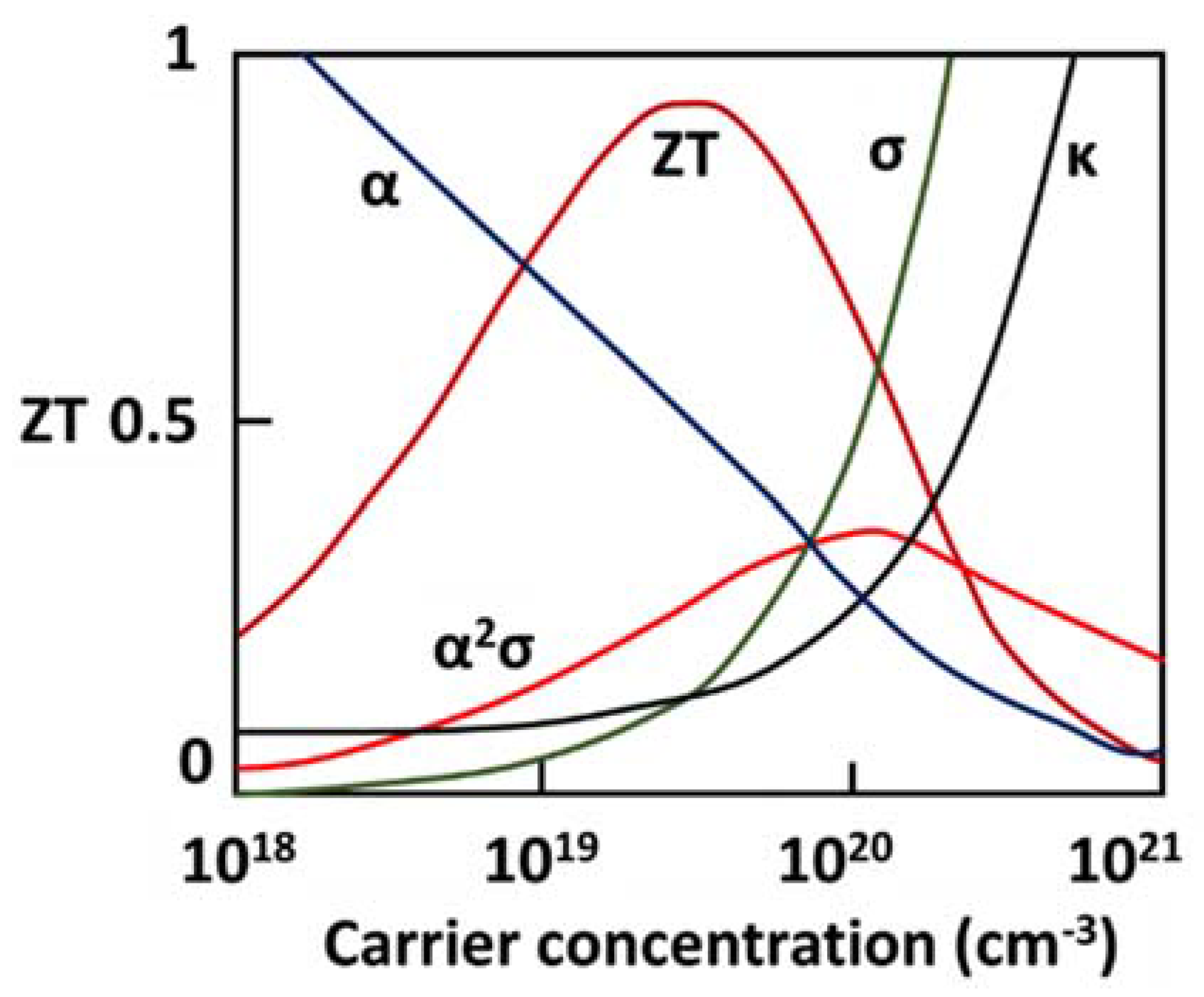
2.5.1. Figure of Merit
2.5.2. Power Factor
2.5.3. Thermal Conductivity
2.5.4. Improving ZT Value
- (1)
- Phonon scattering: Any mechanism that scatters phonons more effectively than the electrons or holes reduces the phonons’ mean free path, and thus enhances the electrical to thermal conductivity ratio of a TE material. Some of the main scattering mechanisms are scattering of phonons by phonons, scattering of phonons by grain boundaries, scattering of phonons by lattice defects/impurity, and scattering of phonons by electrons and holes. Detailed information on this can be found in reference [43].
- (2)
- Complex crystal structures: Complex crystal structures are used to separate the electron-crystal region from the phonon-glass region, so that the region responsible for electron transport should be an electron crystal of a high-mobility semiconductor, whereas the phonon glass should contain the disordered structures and dopants. In 1995, Slack [43] proposed the concept of phonon-glass electron-crystal (PGEC) that would possess electronic conductivity similar to that of a single crystal semiconductor but would have thermal conductivity similar to that of an amorphous material. Later, this concept culminated in discovery of two distinct families of TE materials: filled skutterudites [44,45,46] and intermetallic clathrates [47,48,49].
- (3)
- Nanostructuring: Most of the recent advancements in enhancing ZT is associated with nanostructuring. Because of the quantum size effects on energy carriers, it has been observed that the thermal conductivity of nanostructures such as superlattices are significantly lower than that of the bulk constituent materials [50]. This results in considerable improvement in figure-of-merit in superlattice systems. The concept of superlattices was first introduced by Dresselhaus, Harman, and Venkatasubramanian [51], and since then it has been extensively studied to understand the mechanism for improvement of electron performance, such as electron energy filtering [52], thermionic emission [53], and reduction of phonon thermal conductivity through interface scattering [54]. As shown in Figure 6, Bi2Te3/Sb2Te3 based superlattices [41] and PbTe-based quantum dot super-lattices [55] are currently the state-of-art TE materials.
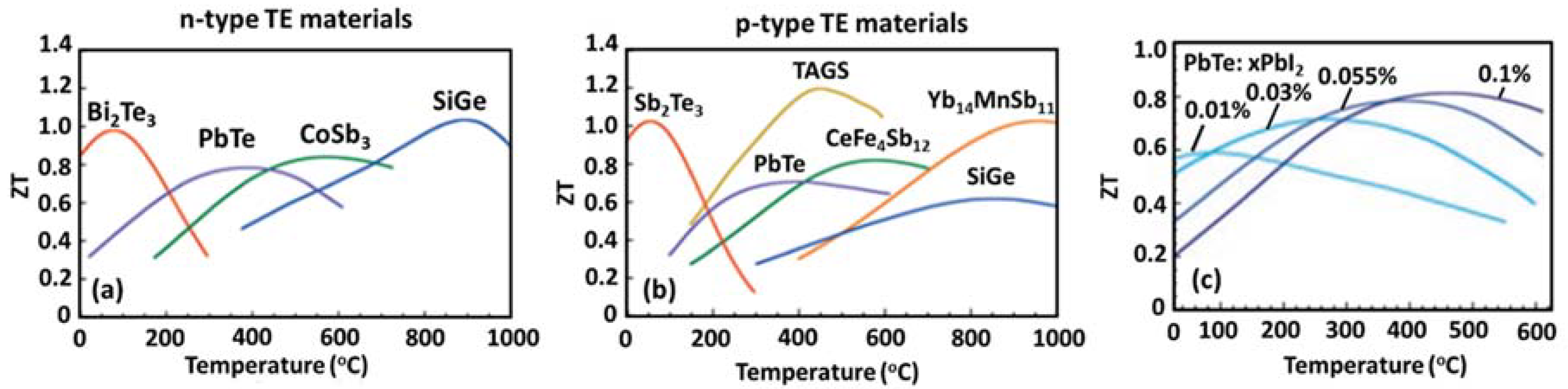
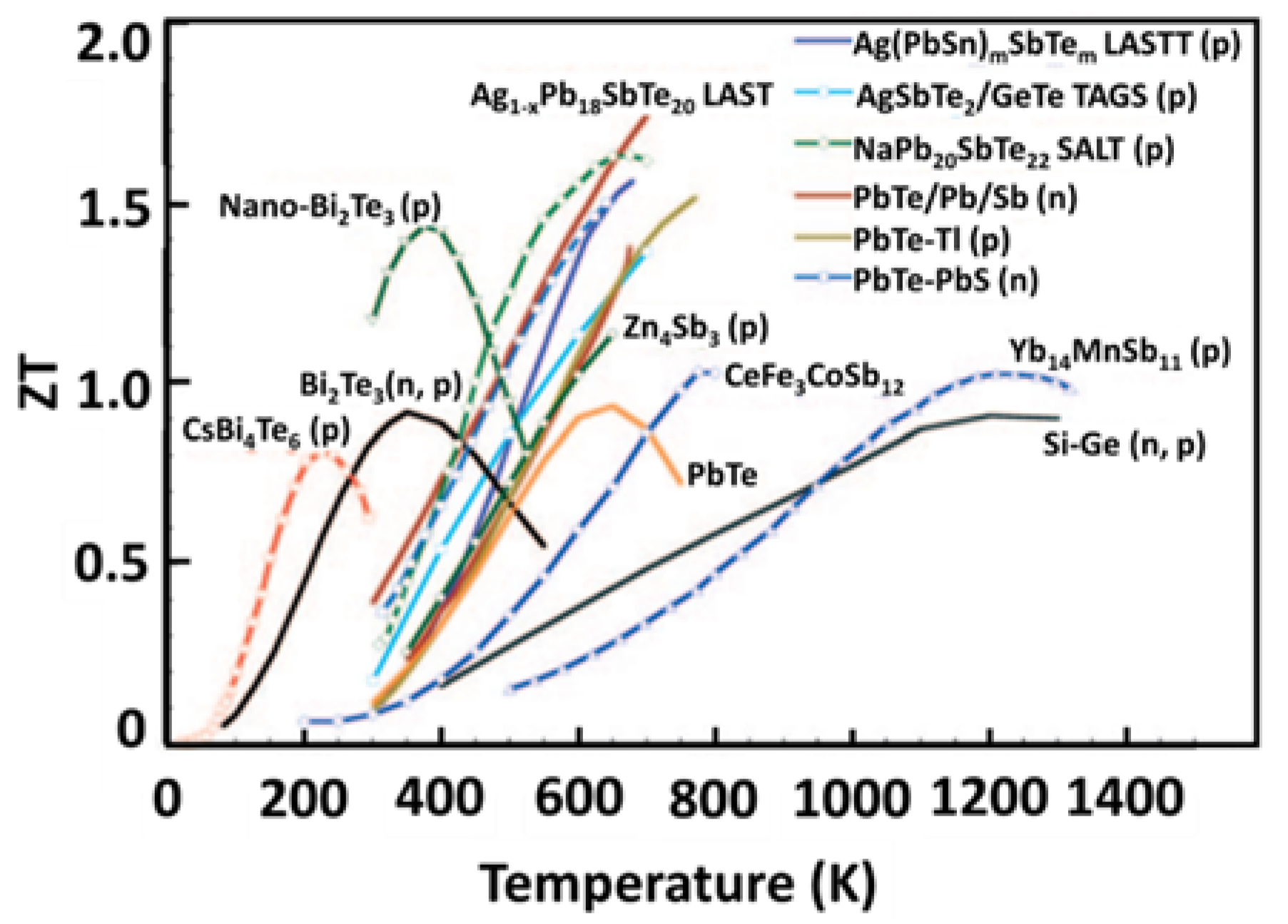
2.6. Thermoelectric Materials
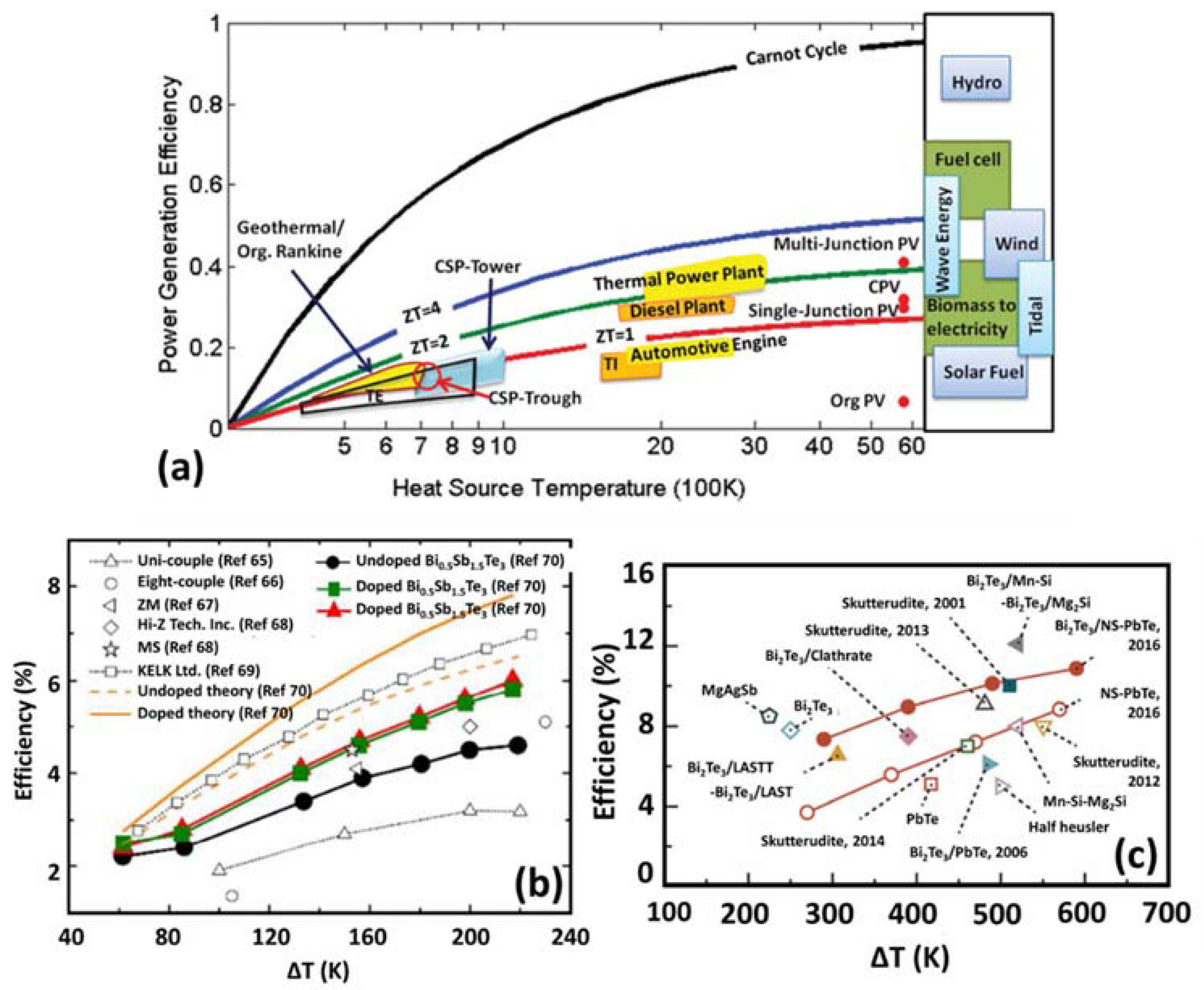
2.7. Thermoelectric Efficiency
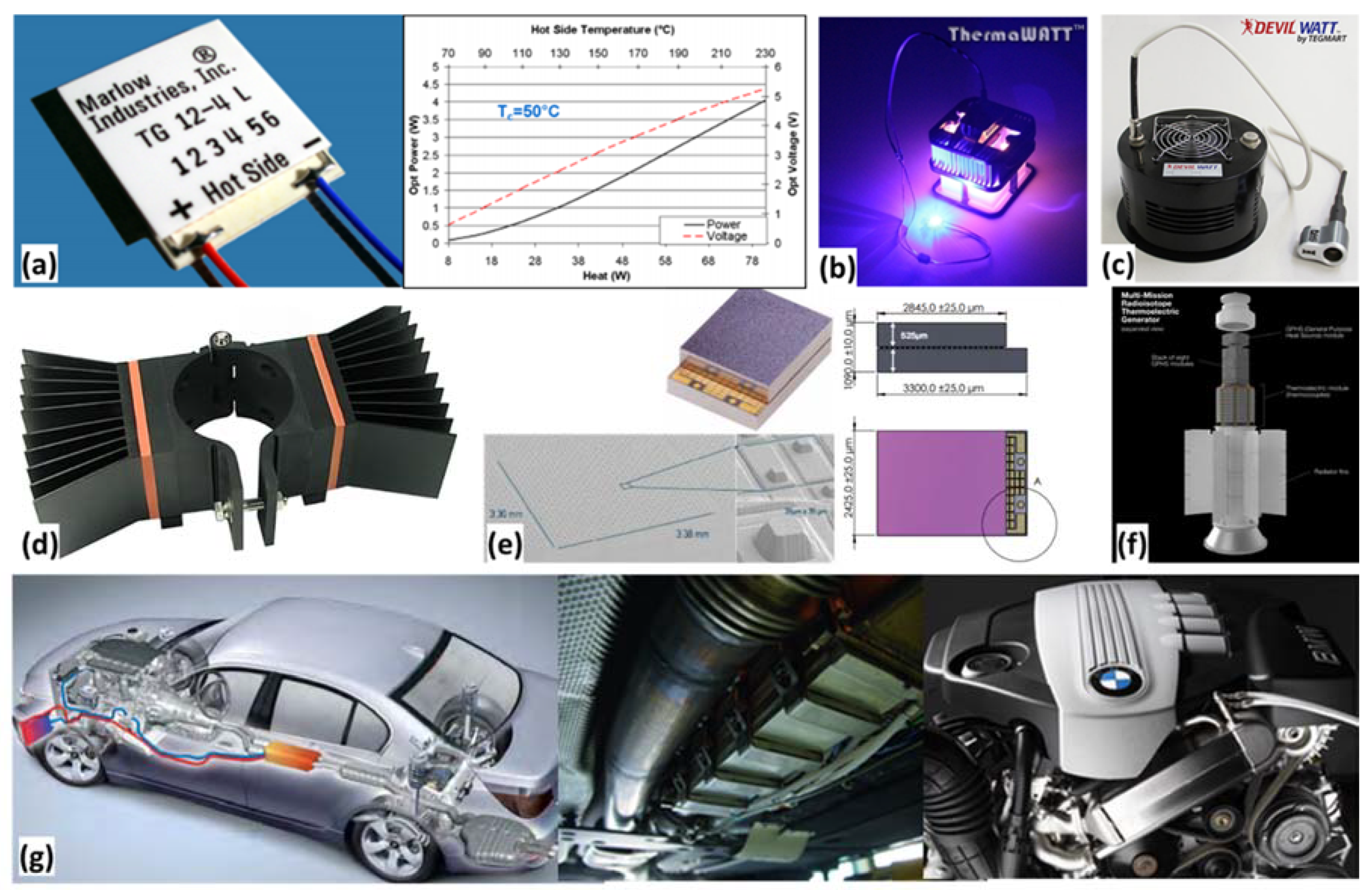
2.8. Thermoelectric Generators
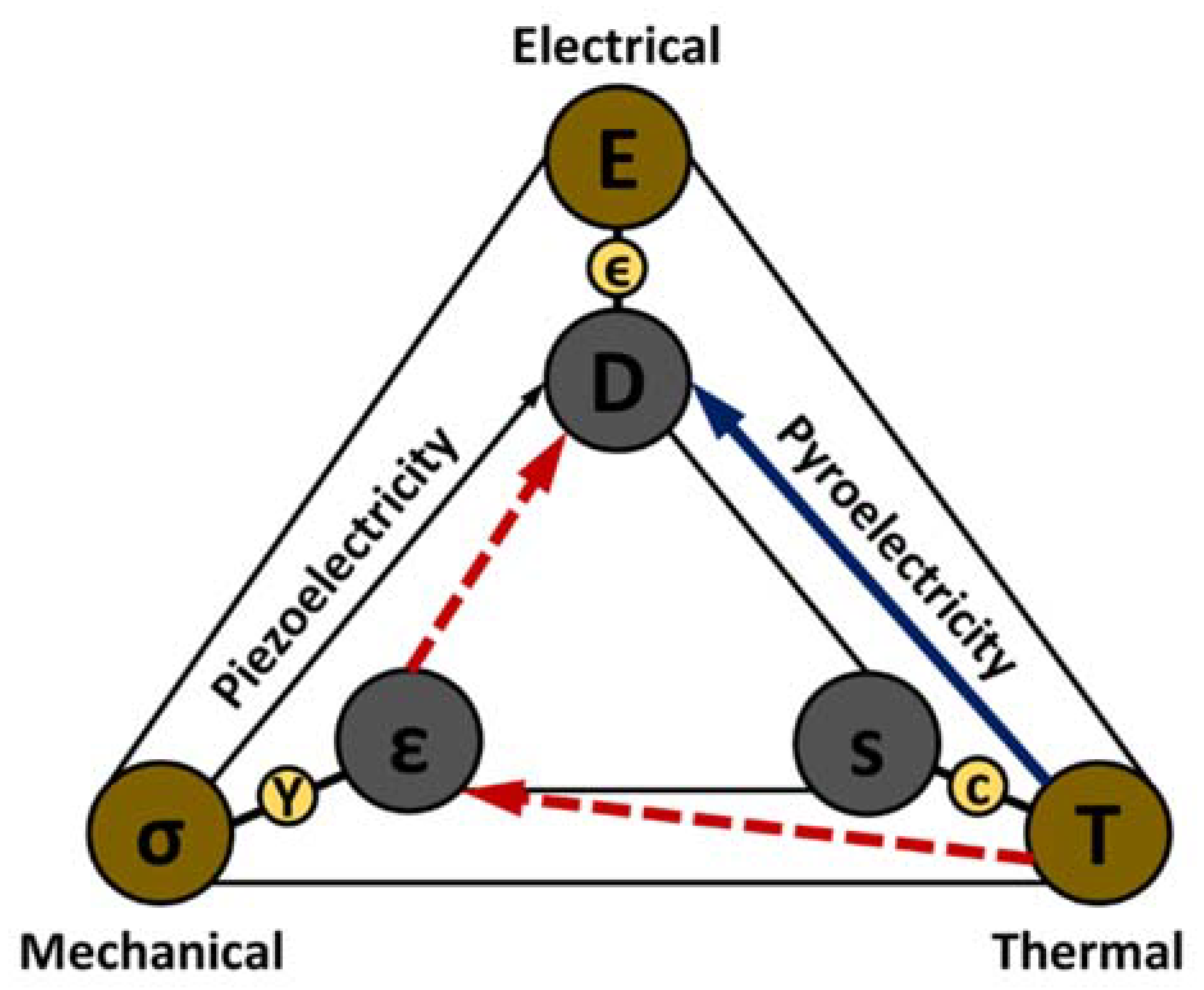
3. Pyroelectric Energy Harvesting
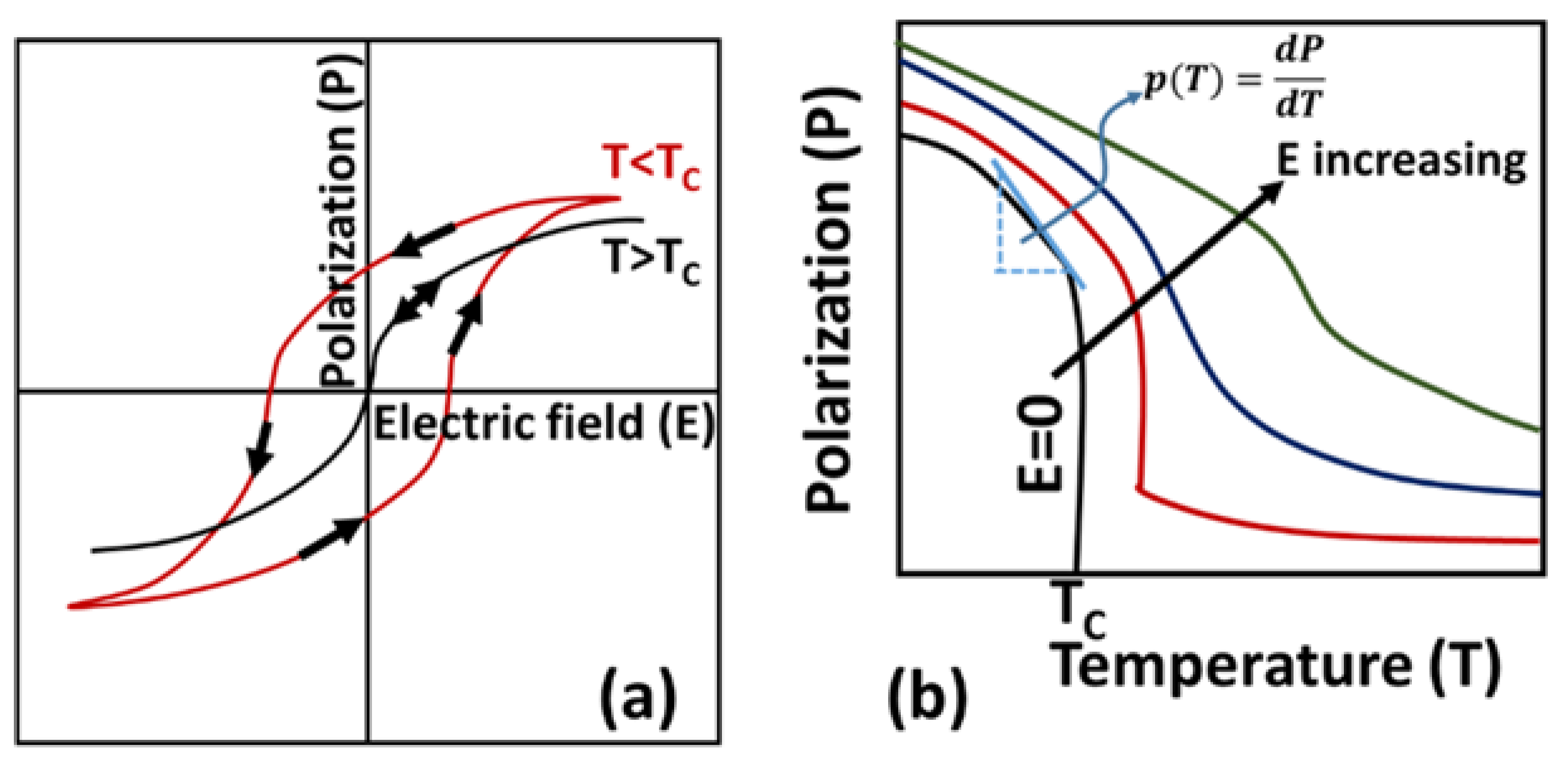
3.1. Working Principle
3.2. Pyroelectric Coefficient
3.3. Figure of Merit
3.4. Pyroelectric Materials
- (1)
- The molecular structure must have a nonzero dipole moment.
- (2)
- The material possesses no center of symmetry.
- (3)
- The material must have either no axis of rotational symmetry or a unique axis of rotational symmetry, not included in an inversion axis.
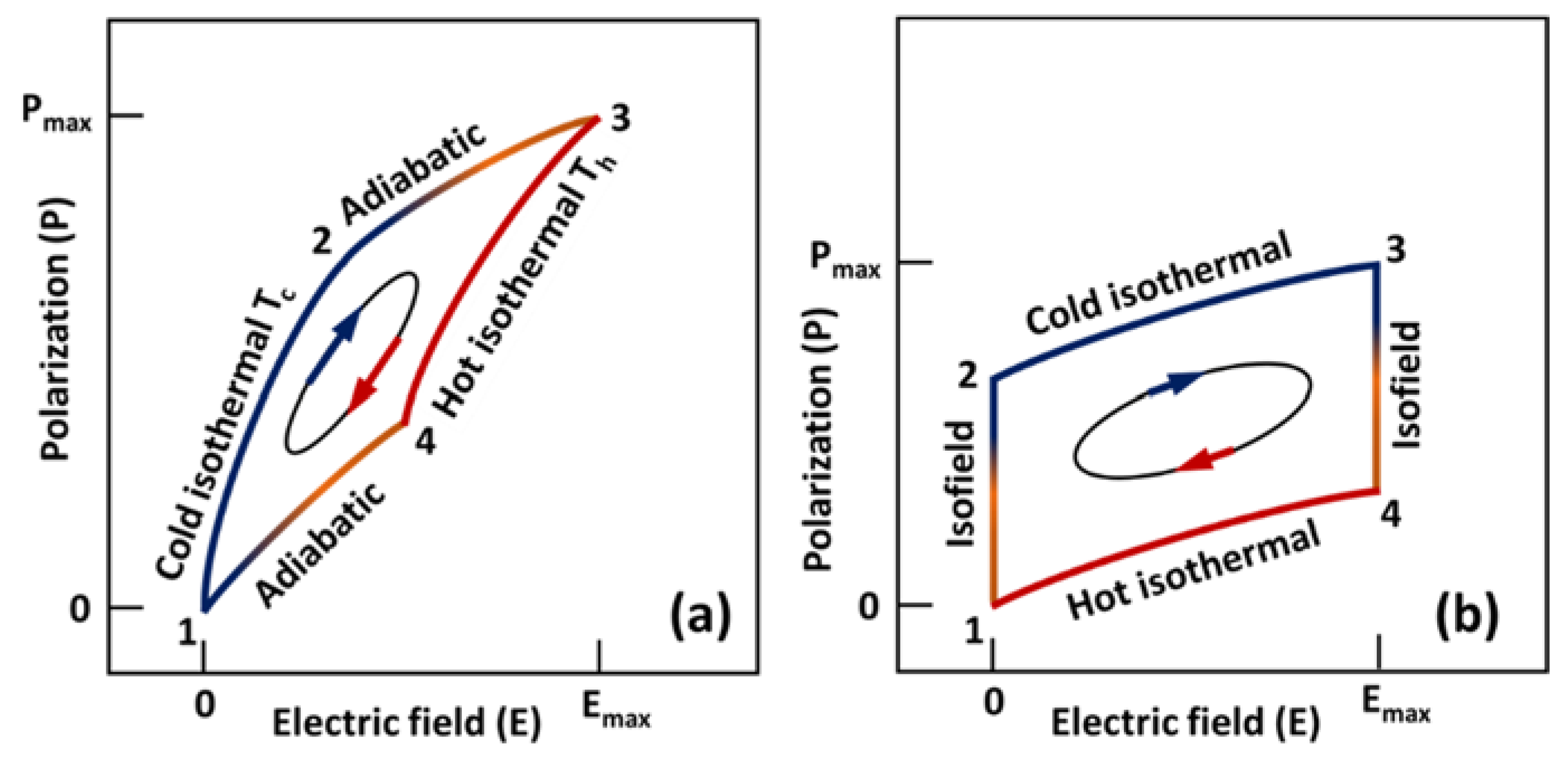
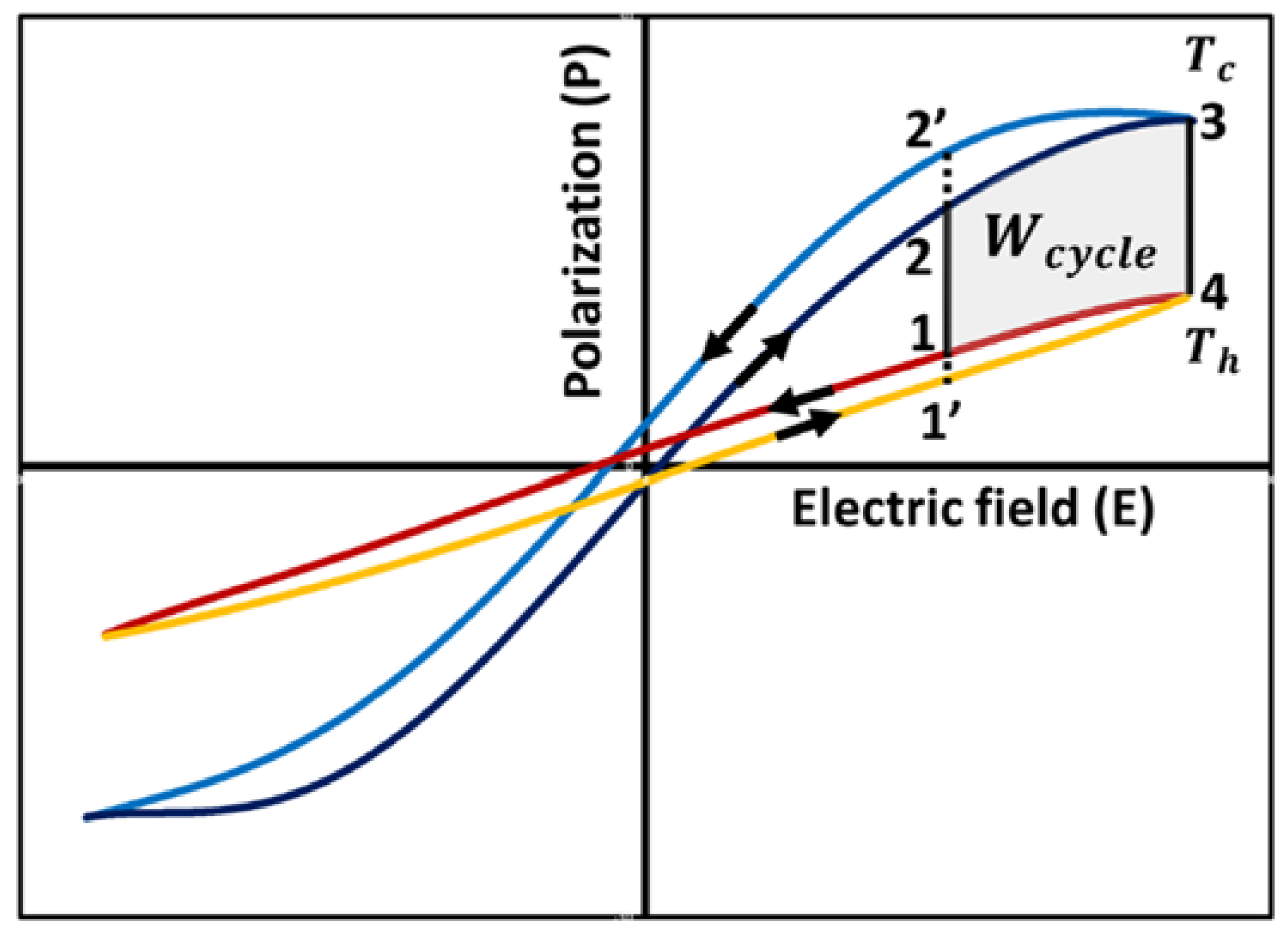
3.5. Thermodynamic Cycles
3.5.1. Pyroelectric Carnot Cycle
3.5.2. Pyroelectric Ericsson Cycle
3.5.3. Modified Ericsson Cycle or Olsen Cycle
3.6. Pyroelectric Generators
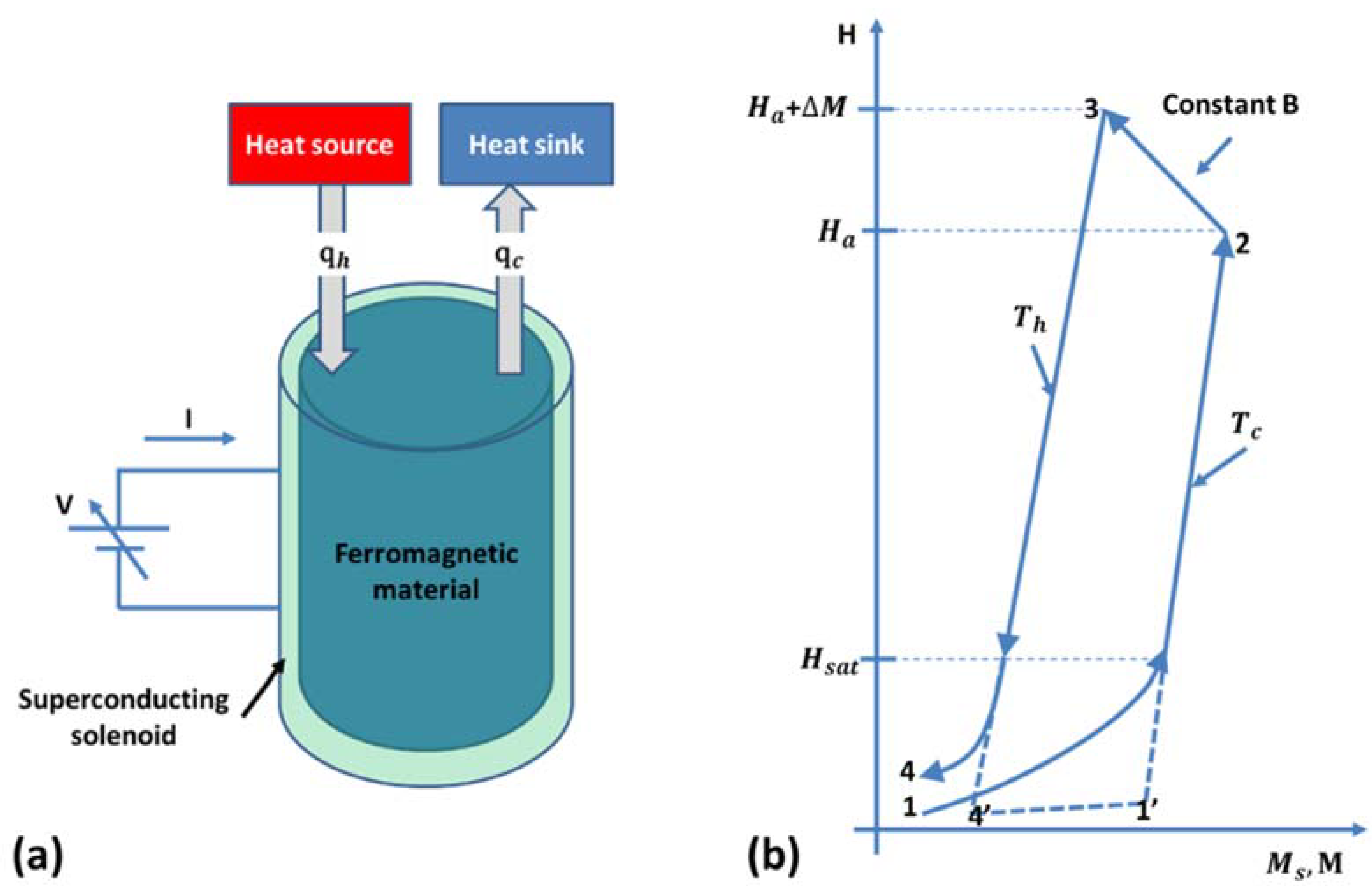
4. Thermomagnetic Energy Harvesting
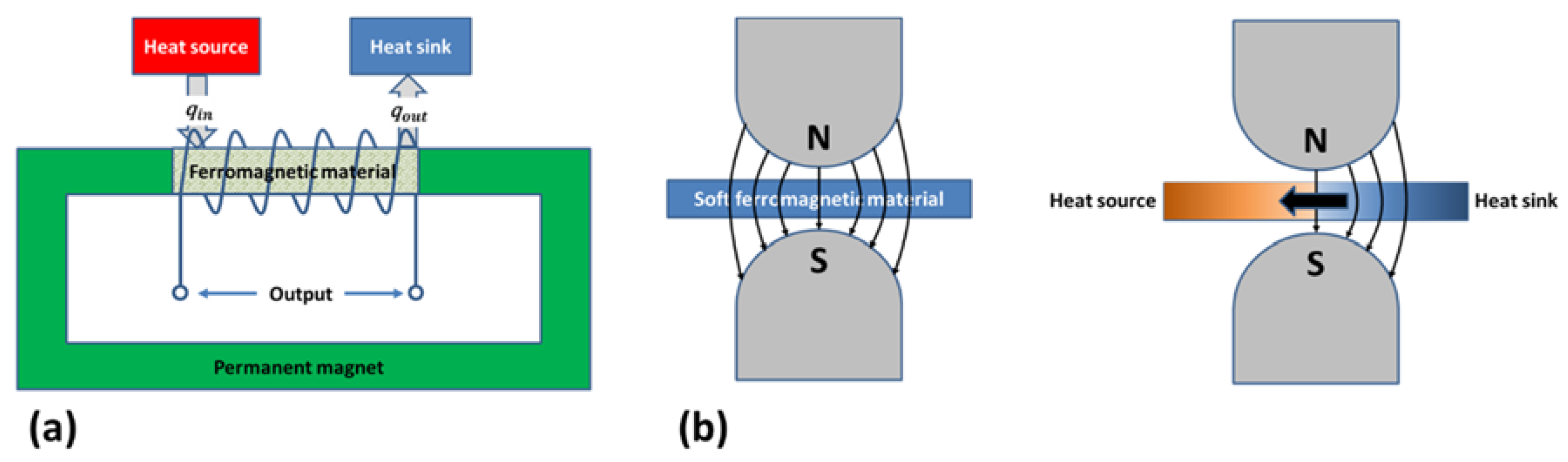
4.1. Working Principle
4.2. Thermomagnetic Cycle
4.3. Thermomagnetic Materials
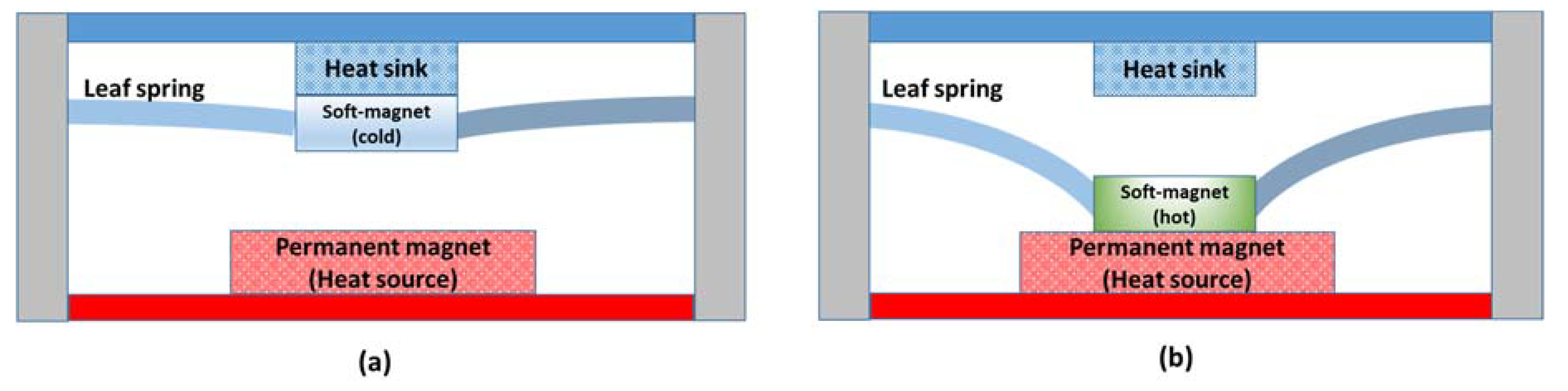
4.4. Thermomagnetic Devices
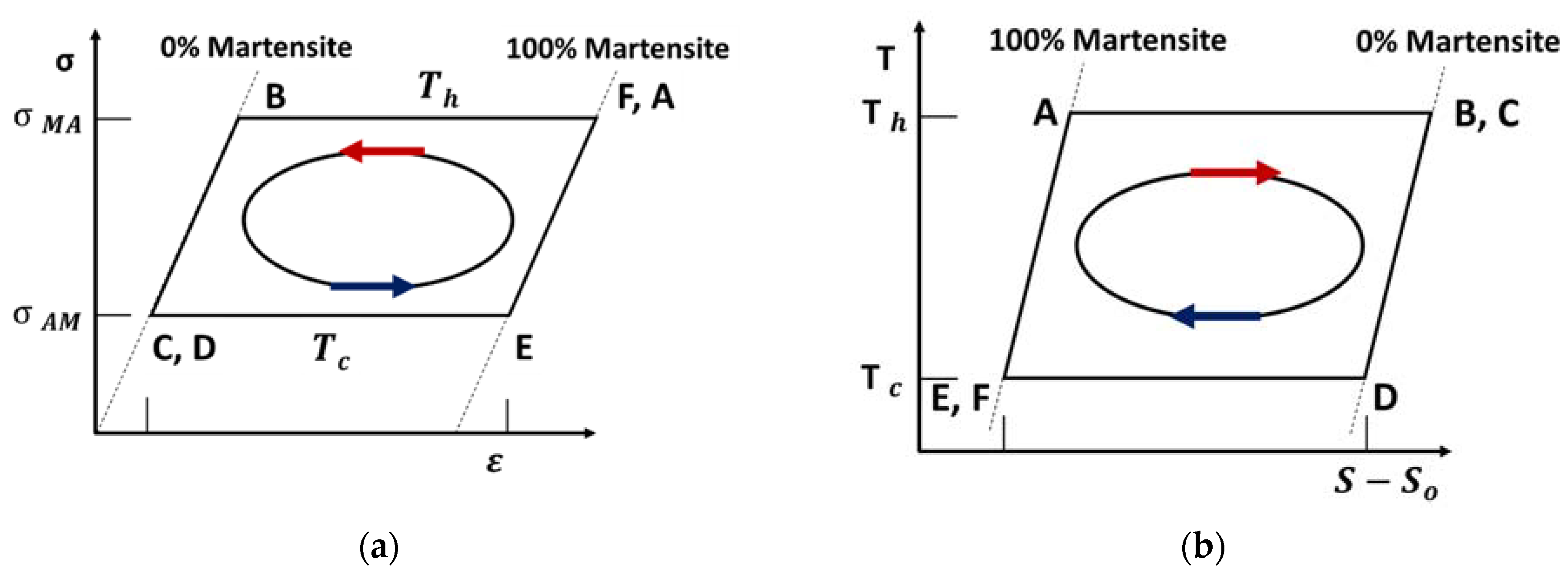
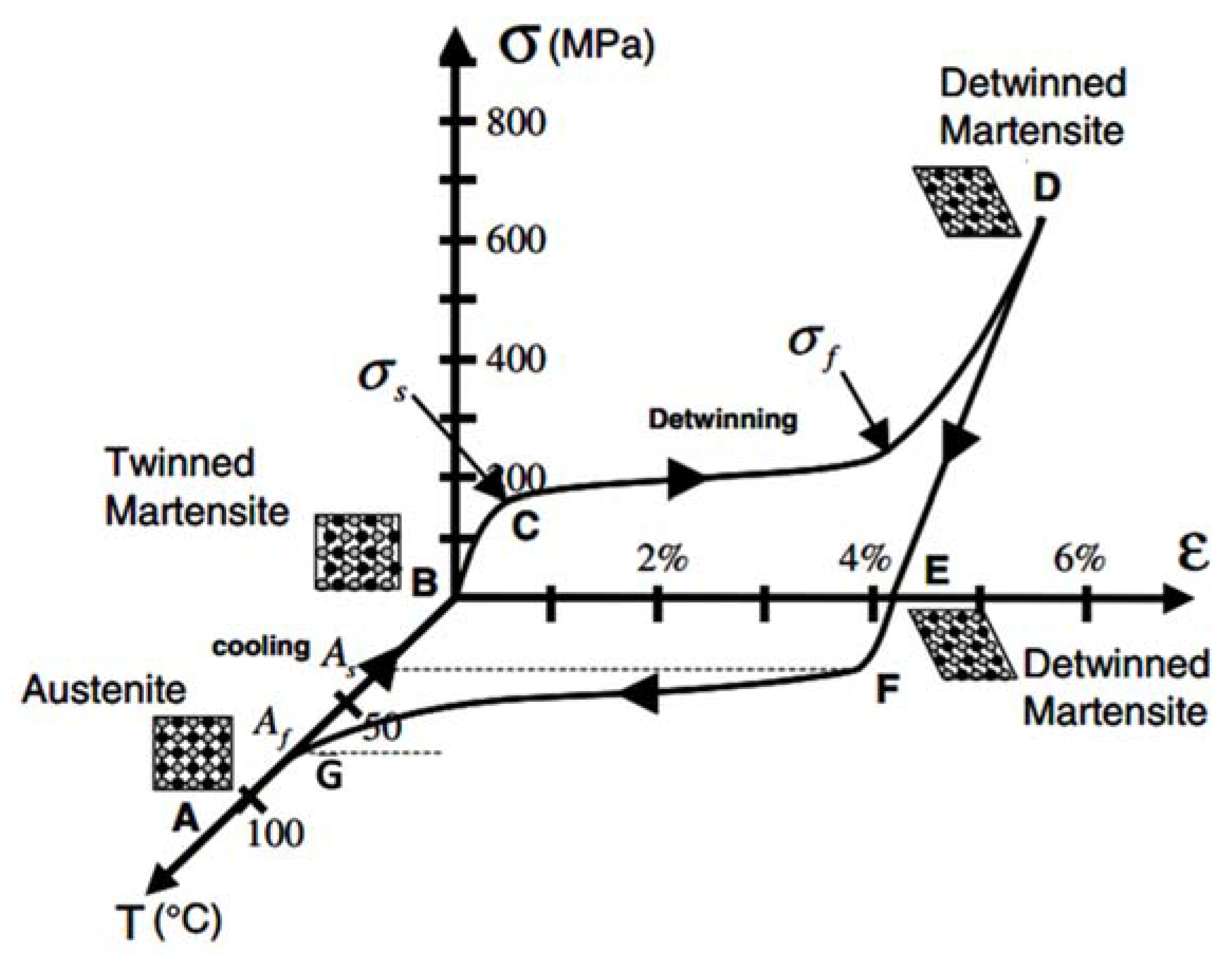
5. Thermoelastic Energy Harvesting
5.1. Working Principle
5.2. Thermoelastic Cycle
5.3. Thermoelastic Efficiency
5.4. Thermoelastic Materials
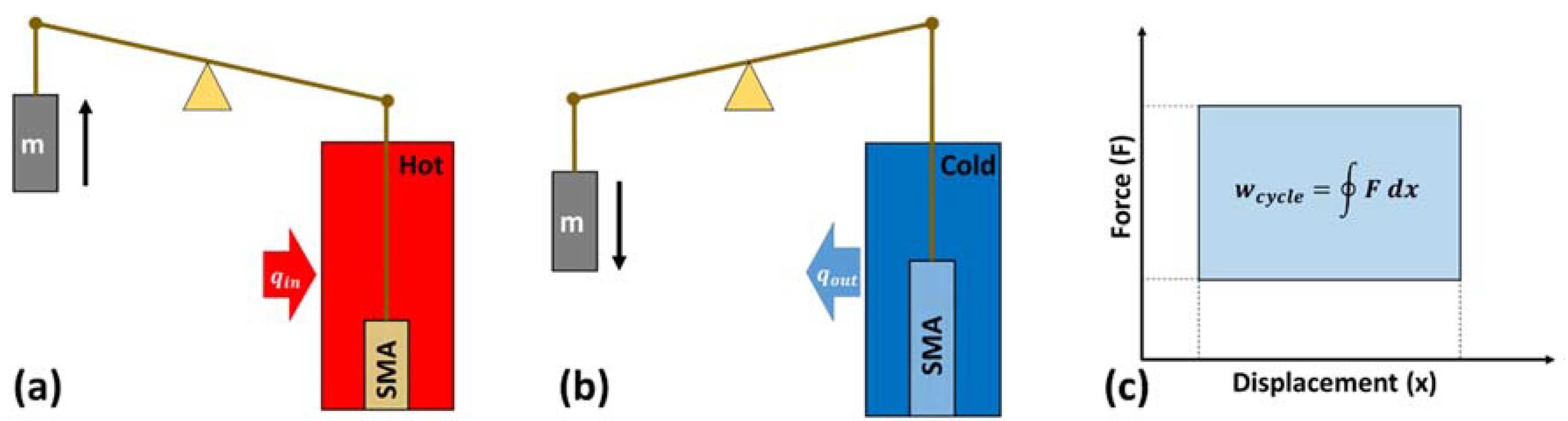
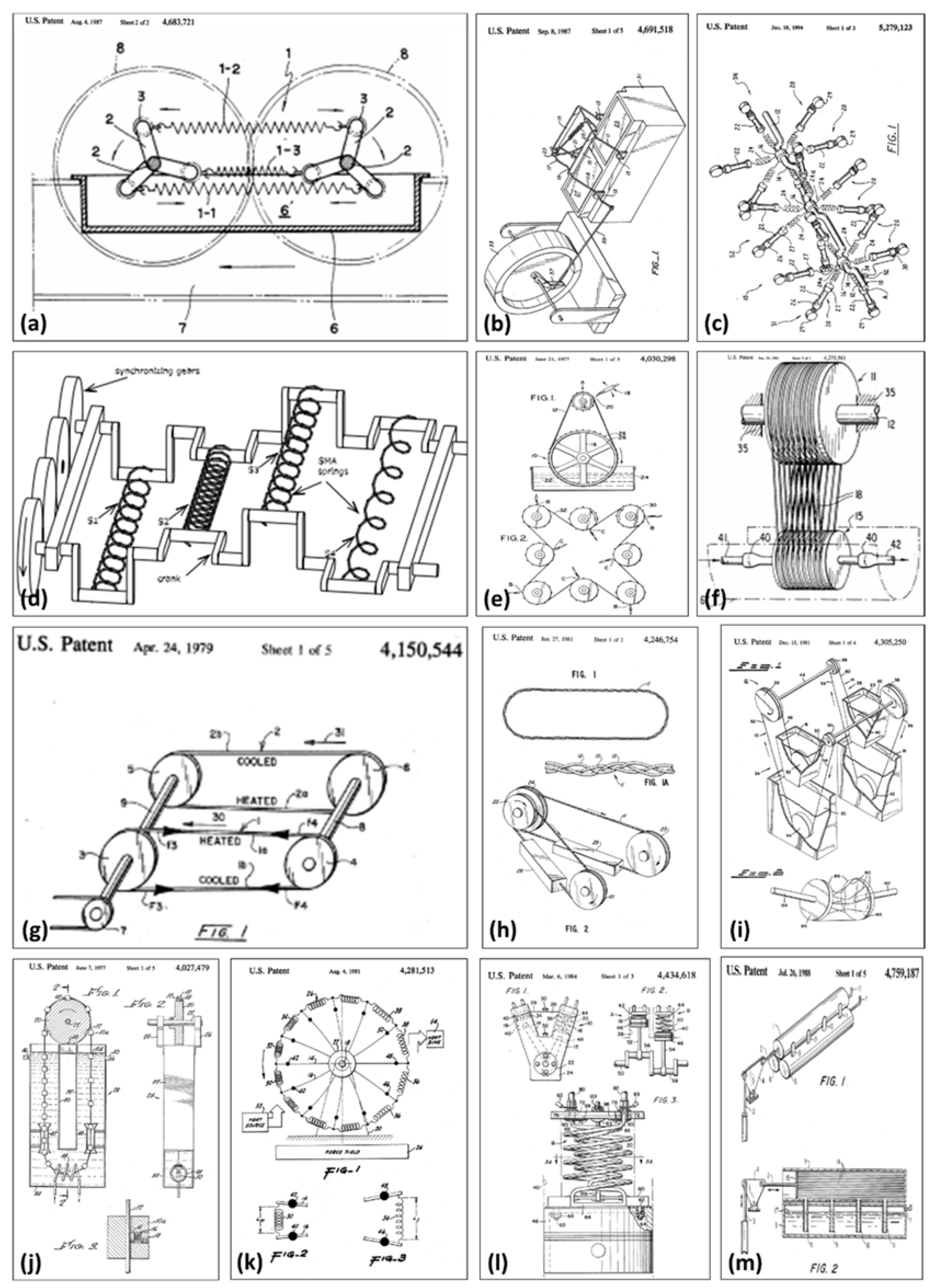
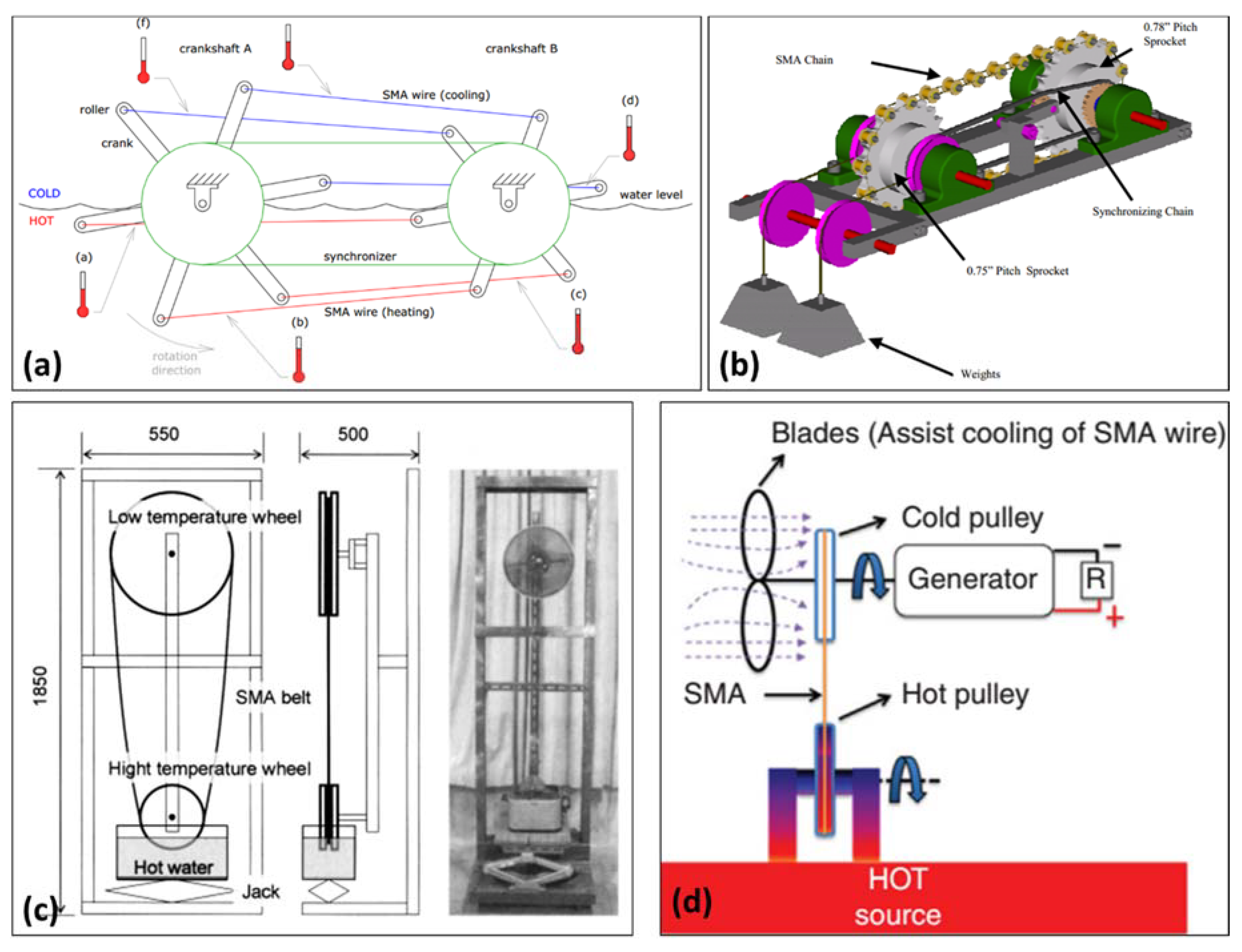
5.5. Thermoelastic Devices (SMA Heat Engines)
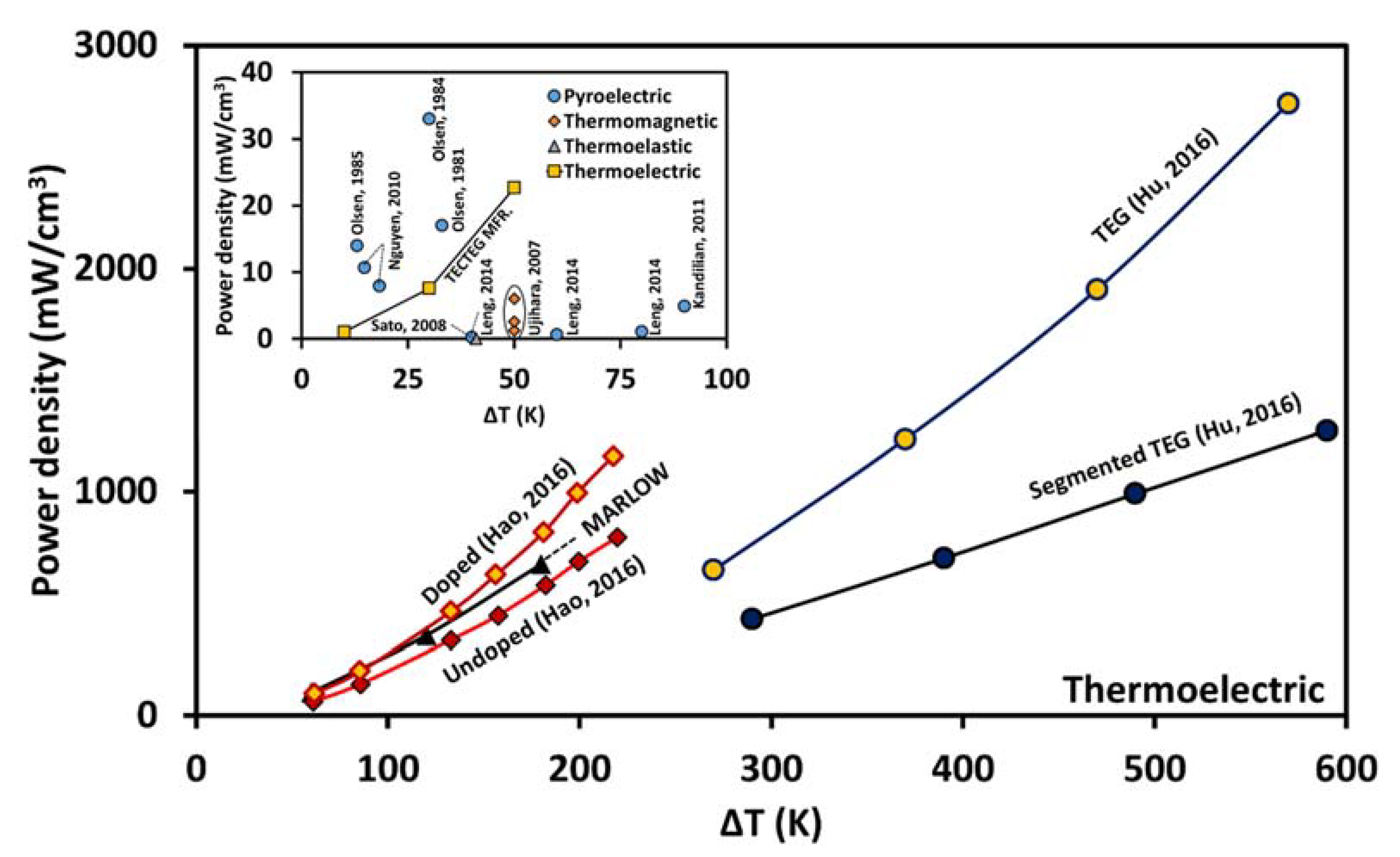
6. Comparative Analysis of the Power Density
7. Cost Considerations
8. Policy Recommendations
- Fund and promote university-based fundamental research projects related to thermal energy harvesting and waste heat recovery.
- Invest in university–industry partnerships to transition the laboratory-based technologies into practice.
- Educate consumers through online and published literature to enhance their awareness about the heat recovery opportunities and its environmental benefits.
- Provide direct financial incentives for each kW of waste heat recovery.
- Offer an investment tax credit on the capital investment related to thermal energy harvesting and heat recovery.
- Offer property tax abatement for facilities that incorporate waste heat recovery.
- Provide low-cost financing to the entities willing to start thermal energy harvesting projects.
9. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- The Energy Flow Chart Released by Lawrence Livermore National Laboratory. Available online: https://flowcharts.llnl.gov/content/assets/images/charts/energy/energy_2011_world.png (accessed on 21 January 2018).
- Geothermal Map of the United States. Available online: https://www.Nrel.Gov/gis/geothermal.Html (accessed on 21 January 2018).
- Johnson, I.; Choate, W.T.; Davidson, A. Waste Heat Recovery. Technology and Opportunities in Us Industry; BCS, Inc.: Laurel, MD, USA, 2008. [Google Scholar]
- Thekdi, A.; Nimbalkar, S.U. Industrial Waste Heat Recovery-Potential Applications, Available Technologies and Crosscutting R&D Opportunities; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2015.
- Erickson, D.C.; Anand, G.; Kyung, I. Heat-activated dual-function absorption cycle. ASHRAE Trans. 2004, 110, 515. [Google Scholar]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Shi, L.; Shu, G.; Tian, H.; Deng, S. A review of modified organic rankine cycles (ORCs) for internal combustion engine waste heat recovery (ICE-WHR). Renew. Sustain. Energy Rev. 2018, 92, 95–110. [Google Scholar] [CrossRef]
- Barse, K.A.; Mann, M.D. Maximizing orc performance with optimal match of working fluid with system design. Appl. Therm. Eng. 2016, 100, 11–19. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.-S.; Kim, H.-J.; Lee, D.-H. Multi-objective optimization of evaporator of organic rankine cycle (ORC) for low temperature geothermal heat source. Appl. Therm. Eng. 2015, 80, 1–9. [Google Scholar] [CrossRef]
- Boyaghchi, F.A.; Heidarnejad, P. Thermoeconomic assessment and multi objective optimization of a solar micro cchp based on organic rankine cycle for domestic application. Energy Convers. Manag. 2015, 97, 224–234. [Google Scholar] [CrossRef]
- Hajabdollahi, H.; Ganjehkaviri, A.; Jaafar, M.N.M. Thermo-economic optimization of rsorc (regenerative solar organic rankine cycle) considering hourly analysis. Energy 2015, 87, 369–380. [Google Scholar] [CrossRef]
- Nazari, N.; Heidarnejad, P.; Porkhial, S. Multi-objective optimization of a combined steam-organic rankine cycle based on exergy and exergo-economic analysis for waste heat recovery application. Energy Convers. Manag. 2016, 127, 366–379. [Google Scholar] [CrossRef]
- Baldi, F.; Larsen, U.; Gabrielii, C. Comparison of different procedures for the optimisation of a combined diesel engine and organic rankine cycle system based on ship operational profile. Ocean Eng. 2015, 110, 85–93. [Google Scholar] [CrossRef]
- Yang, M.-H. Optimizations of the waste heat recovery system for a large marine diesel engine based on transcritical rankine cycle. Energy 2016, 113, 1109–1124. [Google Scholar] [CrossRef]
- Tocci, L.; Pal, T.; Pesmazoglou, I.; Franchetti, B. Small scale organic rankine cycle (ORC): A techno-economic review. Energies 2017, 10, 413. [Google Scholar] [CrossRef]
- Knudsen, T.; Clausen, L.R.; Haglind, F.; Modi, A. Energy and exergy analysis of the kalina cycle for use in concentrated solar power plants with direct steam generation. Energy Procedia 2014, 57, 361–370. [Google Scholar] [CrossRef]
- Haddad, C.; Périlhon, C.; Danlos, A.; François, M.-X.; Descombes, G. Some efficient solutions to recover low and medium waste heat: Competitiveness of the thermoacoustic technology. Energy Procedia 2014, 50, 1056–1069. [Google Scholar] [CrossRef]
- Paanu, T.; Niemi, S.; Rantanen, P. Waste Heat Recovery–Bottoming Cycle Alternatives; Proceedings of the University of Vaasa, Reports; University of Vaasa: Vaasa, Finland, 2012. [Google Scholar]
- Global Geothermal Ltd. Available online: estl.com.au/ (accessed on 21 January 2018).
- Kalex LLC. Available online: http://kalexsystems.com (accessed on 21 January 2018).
- Bombarda, P.; Invernizzi, C.M.; Pietra, C. Heat recovery from diesel engines: A thermodynamic comparison between kalina and orc cycles. Appl. Therm. Eng. 2010, 30, 212–219. [Google Scholar] [CrossRef]
- Radioisotope Thermoelectric Generator (RTG). Available online: https://solarsystem.Nasa.Gov/rps/rtg.Cfm (accessed on 21 January 2018).
- SAS, I. Ansys Mechanical Apdl Theory Reference; ANSYS, Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Hsu, C.-T.; Huang, G.-Y.; Chu, H.-S.; Yu, B.; Yao, D.-J. An effective seebeck coefficient obtained by experimental results of a thermoelectric generator module. Appl. Energy 2011, 88, 5173–5179. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Physics of Thermoelectric Energy Conversion; Morgan & Claypool Publishers: San Rafael, CA, USA, 2017. [Google Scholar]
- Nolas, G.S.; Sharp, J.; Goldsmid, J. Thermoelectrics: Basic Principles and New Materials Developments; Springer: Berlin, Germany, 2013; Volume 45. [Google Scholar]
- Choi, S.-M.; Kim, K.-H.; Jeong, S.-M.; Choi, H.-S.; Lim, Y.S.; Seo, W.-S.; Kim, I.-H. A resistance ratio analysis for cosb 3-based thermoelectric unicouples. J. Electron. Microsc. 2012, 41, 1004–1010. [Google Scholar]
- Wojciechowski, K.T.; Zybala, R.; Mania, R. High temperature CoSb3-Cu junctions. Microelectron. Reliab. 2011, 51, 1198–1202. [Google Scholar] [CrossRef]
- Lee, J.-K.; Choi, S.-M.; Seo, W.-S.; Lee, H.-L.; Kim, I.-H. Thermoelectric properties of the co-doped n-type CoSb3 compound. J. Korean Phys. Soc. 2010, 57, 1010–1014. [Google Scholar]
- Song, B.; Lee, S.; Cho, S.; Song, M.-J.; Choi, S.-M.; Seo, W.-S.; Yoon, Y.; Lee, W. The effects of diffusion barrier layers on the microstructural and electrical properties in cosb 3 thermoelectric modules. J. Alloys Compd. 2014, 617, 160–162. [Google Scholar] [CrossRef]
- Key Components of a Thermoelectric Generator (TEG) Module. Available online: https://www.Digikey.Co.Nz/en/articles/techzone/2014/apr/thermoelectric-energy-generation-takes-flight-for-aircraft-and-spacecraft-monitoring (accessed on 21 January 2018).
- Anant Kishore, R.; Kumar, P.; Sanghadasa, M.; Priya, S. Taguchi optimization of bismuth-telluride based thermoelectric cooler. J. Appl. Phys. 2017, 122, 025109. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Elsheikh, M.H.; Shnawah, D.A.; Sabri, M.F.M.; Said, S.B.M.; Hassan, M.H.; Bashir, M.B.A.; Mohamad, M. A review on thermoelectric renewable energy: Principle parameters that affect their performance. Renew. Sustain. Energy Rev. 2014, 30, 337–355. [Google Scholar] [CrossRef]
- Nolas, G.; Morelli, D.; Tritt, T.M. Skutterudites: A phonon-glass-electron crystal approach to advanced thermoelectric energy conversion applications. Annu. Rev. Mater. Sci. 1999, 29, 89–116. [Google Scholar]
- Dmitriev, A.V.; Zvyagin, I.P. Current trends in the physics of thermoelectric materials. Physics-Uspekhi 2010, 53, 789–803. [Google Scholar] [CrossRef]
- Zheng, J.-C. Recent advances on thermoelectric materials. Front. Phys. China 2008, 3, 269–279. [Google Scholar] [CrossRef]
- Yang, J.; Center, G. Designing advanced thermoelectric materials for automotive applications. In Proceedings of the DOE/EPRI High Efficiency Thermoelectrics Workshop, San Diego, CA, USA, 17–20 February 2004; pp. 16–20. [Google Scholar]
- Stabler, F.R. Commercialization of thermoelectric technology. MRS Online Proc. Libr. Arch. 2005, 886. [Google Scholar] [CrossRef]
- Harman, T.; Walsh, M.; Turner, G. Nanostructured thermoelectric materials. J. Electron Microsc. 2005, 34, 19–22. [Google Scholar] [CrossRef]
- Venkatasubramanian, R.; Siivola, E.; Colpitts, T.; O’quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar] [CrossRef] [PubMed]
- Hsu, K.F.; Loo, S.; Guo, F.; Chen, W.; Dyck, J.S.; Uher, C.; Hogan, T.; Polychroniadis, E.; Kanatzidis, M.G. Cubic AgPbmSbTe2+m: Bulk thermoelectric materials with high figure of merit. Science 2004, 303, 818–821. [Google Scholar] [CrossRef] [PubMed]
- Rowe, D.M. CRC Handbook of Thermoelectrics; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Morelli, D.T.; Meisner, G.P. Low temperature properties of the filled skutterudite CeFe4Sb12. J. Appl. Phys. 1995, 77, 3777–3781. [Google Scholar]
- Sales, B.; Mandrus, D.; Williams, R.K. Filled skutterudite antimonides: A new class of thermoelectric materials. Science 1996, 272, 1325. [Google Scholar] [CrossRef] [PubMed]
- Nolas, G.; Slack, G.; Morelli, D.; Tritt, T.; Ehrlich, A. The effect of rare-earth filling on the lattice thermal conductivity of skutterudites. J. Appl. Phys. 1996, 79, 4002–4008. [Google Scholar] [CrossRef]
- Nolas, G.; Cohn, J.; Slack, G.; Schujman, S. Semiconducting Ge clathrates: Promising candidates for thermoelectric applications. Appl. Phys. Lett. 1998, 73, 178–180. [Google Scholar] [CrossRef]
- Cohn, J.; Nolas, G.; Fessatidis, V.; Metcalf, T.; Slack, G. Glasslike heat conduction in high-mobility crystalline semiconductors. Phys. Rev. Lett. 1999, 82, 779. [Google Scholar] [CrossRef]
- Nolas, G.S. The Physics and Chemistry of Inorganic Clathrates; Springer: Berlin, Germany, 2014; Volume 199. [Google Scholar]
- Yang, R.; Chen, G. Nanostructured thermoelectric materials: From superlattices to nanocomposites. Mater. Integr. 2005, 18, 31–36. [Google Scholar]
- Zheng, X.; Liu, C.; Yan, Y.; Wang, Q. A review of thermoelectrics research—Recent developments and potentials for sustainable and renewable energy applications. Renew. Sustain. Energy Rev. 2014, 32, 486–503. [Google Scholar] [CrossRef]
- Moyzhes, B.; Nemchinsky, V. Thermoelectric figure of merit of metal-semiconductor barrier structure based on energy relaxation length. Appl. Phys. Lett. 1998, 73, 1895–1897. [Google Scholar] [CrossRef]
- Shakouri, A.; Bowers, J.E. Heterostructure integrated thermionic coolers. Appl. Phys. Lett. 1997, 71, 1234–1236. [Google Scholar] [CrossRef]
- Chen, G. Phonon transport in low dimensional. Semicond. Semimet. 2001, 71, 203. [Google Scholar]
- Harman, T.; Taylor, P.; Walsh, M.; LaForge, B. Quantum dot superlattice thermoelectric materials and devices. Science 2002, 297, 2229–2232. [Google Scholar] [CrossRef] [PubMed]
- Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.; Muto, A.; Vashaee, D. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef] [PubMed]
- Yim, W.; Amith, A. Bi-Sb alloys for magneto-thermoelectric and thermomagnetic cooling. Solid-State Electron. 1972, 15. [Google Scholar] [CrossRef]
- Sidorenko, N.; Ivanova, L. Bi-Sb solid solutions: Potential materials for high-efficiency thermoelectric cooling to below 180 k. Inorg. Mater. 2001, 37, 331–335. [Google Scholar] [CrossRef]
- Gelbstein, Y.; Dashevsky, Z.; Dariel, M. High performance n-type pbte-based materials for thermoelectric applications. Phys. B Condens. Matter 2005, 363, 196–205. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, L.-D.; Hao, S.; Jiang, Q.; Zheng, F.; Doak, J.W.; Wu, H.; Chi, H.; Gelbstein, Y.; Uher, C. Origin of the high performance in gete-based thermoelectric materials upon Bi2Te3 doping. J. Am. Chem. Soc. 2014, 136, 11412–11419. [Google Scholar] [CrossRef] [PubMed]
- Perumal, S.; Roychowdhury, S.; Biswas, K. High performance thermoelectric materials and devices based on gete. J. Mater. Chem. C 2016, 4, 7520–7536. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Lin, S.; Chen, Z.; Pei, Y. Realizing the high thermoelectric performance of GeTe by Sb-doping and Se-alloying. Chem. Mater. 2016, 29, 605–611. [Google Scholar] [CrossRef]
- Zhao, L.-D.; Zhang, X.; Wu, H.; Tan, G.; Pei, Y.; Xiao, Y.; Chang, C.; Wu, D.; Chi, H.; Zheng, L. Enhanced thermoelectric properties in the counter-doped SnTe system with strained endotaxial SrTe. J. Am. Chem. Soc. 2016, 138, 2366–2373. [Google Scholar] [CrossRef] [PubMed]
- Banik, A.; Shenoy, U.S.; Saha, S.; Waghmare, U.V.; Biswas, K. High power factor and enhanced thermoelectric performance of SnTe-AgInTe2: Synergistic effect of resonance level and valence band convergence. J. Am. Chem. Soc. 2016, 138, 13068–13075. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Gibbs, Z.M.; Wang, H.; Han, Y.; Li, L.; Snyder, G.J. Thermoelectric performance of co-doped SnTe with resonant levels. Appl. Phys. Lett. 2016, 109, 042102. [Google Scholar] [CrossRef]
- Heikes, R.R.; Ure, R. Thermoelectricity: Science and Engineering; Interscience Publisher: New York, NY, USA, 1961. [Google Scholar]
- Wood, C. Materials for thermoelectric energy conversion. Rep. Prog. Phys. 1988, 51, 459. [Google Scholar] [CrossRef]
- Ahmad, S.; Mahanti, S.; Hoang, K.; Kanatzidis, M. Ab initio studies of the electronic structure of defects in PbTe. Phys. Rev. B 2006, 74, 155205. [Google Scholar] [CrossRef]
- Jovovic, V.; Thiagarajan, S.; Heremans, J.; Komissarova, T.; Khokhlov, D.; Nicorici, A. Low temperature thermal, thermoelectric, and thermomagnetic transport in indium rich Pb1−xSnxTe alloys. J. Appl. Phys. 2008, 103, 053710. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science 2008, 321, 554–557. [Google Scholar] [CrossRef] [PubMed]
- Snyder, G.J.; Christensen, M.; Nishibori, E.; Caillat, T.; Brummerstedt Iversen, B. Disordered zinc in Zn4Sb3 with phonon-glass and electron-crystal thermoelectric properties. Nat. Mater. 2004, 3, 458–463. [Google Scholar] [CrossRef] [PubMed]
- Androulakis, J.; Hsu, K.F.; Pcionek, R.; Kong, H.; Uher, C.; D’Angelo, J.J.; Downey, A.; Hogan, T.; Kanatzidis, M.G. Nanostructuring and high thermoelectric efficiency in p-Type Ag (Pb1–ySny)mSbTe2+m. Adv. Mater. 2006, 18, 1170–1173. [Google Scholar] [CrossRef]
- Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and old concepts in thermoelectric materials. Angew. Chem. Int. Ed. 2009, 48, 8616–8639. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-D.; Huang, Y.-X.; Cheng, C.-H.; Lin, D.T.-W.; Kang, C.-H. A three-dimensional numerical modeling of thermoelectric device with consideration of coupling of temperature field and electric potential field. Energy 2012, 47, 488–497. [Google Scholar] [CrossRef]
- Pérez-Aparicio, J.; Palma, R.; Taylor, R. Finite element analysis and material sensitivity of peltier thermoelectric cells coolers. Int. J. Heat Mass Transf. 2012, 55, 1363–1374. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Huang, S.-Y.; Cheng, T.-C. A three-dimensional theoretical model for predicting transient thermal behavior of thermoelectric coolers. Int. J. Heat Mass Transf. 2010, 53, 2001–2011. [Google Scholar] [CrossRef]
- Meng, J.-H.; Wang, X.-D.; Zhang, X.-X. Transient modeling and dynamic characteristics of thermoelectric cooler. Appl. Energy 2013, 108, 340–348. [Google Scholar] [CrossRef]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer: Berlin, Germany, 2010; Volume 121. [Google Scholar]
- Ouyang, Z.; Li, D. Modelling of segmented high-performance thermoelectric generators with effects of thermal radiation, electrical and thermal contact resistances. Sci. Rep. 2016, 6, 24123. [Google Scholar] [CrossRef] [PubMed]
- Kishore, R.A.; Sanghadasa, M.; Priya, S. Optimization of segmented thermoelectric generator using taguchi and ANOVA techniques. Sci. Rep. 2017, 7, 16746. [Google Scholar] [CrossRef] [PubMed]
- Kishore, R.A.; Kumar, P.; Priya, S. A comprehensive optimization study on Bi2Te3-based thermoelectric generators using the taguchi method. Sustain. Energy Fuels 2018, 2, 175–190. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Esfarjani, K.; Dresselhaus, M.; Ren, Z.; Chen, G. Perspectives on thermoelectrics: From fundamentals to device applications. Energy Environ. Sci. 2012, 5, 5147–5162. [Google Scholar] [CrossRef]
- Hu, X.; Nagase, K.; Jood, P.; Ohta, M.; Yamamoto, A. Power generation evaluated on a bismuth telluride unicouple module. J. Electron. Mater. 2015, 44, 1785–1790. [Google Scholar] [CrossRef]
- Wang, H.; McCarty, R.; Salvador, J.R.; Yamamoto, A.; König, J. Determination of thermoelectric module efficiency: A survey. J. Electron. Mater. 2014, 43, 2274–2286. [Google Scholar] [CrossRef]
- Wang, S.; Xie, W.; Li, H.; Tang, X. Enhanced performances of melt spun Bi2(Te,Se)3 for n-type thermoelectric legs. Intermetallics 2011, 19, 1024–1031. [Google Scholar] [CrossRef]
- Haidar, J.G.; Ghojel, J.I. Waste heat recovery from the exhaust of low-power diesel engine using thermoelectric generators. In Proceedings of the 20 International Conference on Thermoelectrics, Beijing, China, 8–11 June 2001; pp. 413–418. [Google Scholar]
- Kuroki, T.; Kabeya, K.; Makino, K.; Kajihara, T.; Kaibe, H.; Hachiuma, H.; Matsuno, H.; Fujibayashi, A. Thermoelectric generation using waste heat in steel works. J. Electron. Mater. 2014, 43, 2405–2410. [Google Scholar] [CrossRef]
- Hao, F.; Qiu, P.; Tang, Y.; Bai, S.; Xing, T.; Chu, H.-S.; Zhang, Q.; Lu, P.; Zhang, T.; Ren, D. High efficiency Bi2Te3-based materials and devices for thermoelectric power generation between 100 and 300 °C. Energy Environ. Sci. 2016, 9, 3120–3127. [Google Scholar] [CrossRef]
- Hu, X.; Jood, P.; Ohta, M.; Kunii, M.; Nagase, K.; Nishiate, H.; Kanatzidis, M.G.; Yamamoto, A. Power generation from nanostructured pbte-based thermoelectrics: Comprehensive development from materials to modules. Energy Environ. Sci. 2016, 9, 517–529. [Google Scholar] [CrossRef]
- TG12-4 TEG. Available online: https://www.Marlow.Com (accessed on 21 January 2018).
- ThermaWatt, a Candle Powered TEG. Available online: http://www.Tegmart.Com/diy-teg-kits/diy-candle-powered-teg-with-led-options/ (accessed on 21 January 2018).
- DW-DF-10W Camp Stove TEG. Available online: http://www.Tegpower.Com/pro2.Htm (accessed on 21 January 2018).
- EverGen PowerStrap. Available online: http://www.Marlow.Com/power-generators/evergen-power-strap.Html (accessed on 21 January 2018).
- MPG-D655, Micropelt Thermogenerator Chip. Available online: http://www.Micropelt.Com (accessed on 21 January 2018).
- Green Car Congress. Available online: http://www.Greencarcongress.Com/2011/08/bmwthermal-20110830.Html (accessed on 21 January 2018).
- Lang, S.B. Pyroelectricity: From ancient curiosity to modern imaging tool. Phys. Today 2005, 58, 31. [Google Scholar] [CrossRef]
- Donnay, G. Structural mechanism of pyroelectricity in tourmaline. Acta Crystallogr. Sect. A 1977, 33, 927–932. [Google Scholar] [CrossRef]
- Hawkins, K.D.; Mackinnon, I.D.; Schneeberger, H. Influence of chemistry on the pyroelectric effect in tourmaline. Am. Miner. 1995, 80, 491–501. [Google Scholar] [CrossRef]
- Shur, M.; Bykhovski, A.; Gaska, R. Pyroelectric and piezoelectric properties of gan-based materials. MRS Online Proc. Libr. Arch. 1998, 537. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C. Size-dependent pyroelectric properties of gallium nitride nanowires. J. Appl. Phys. 2016, 119, 145102. [Google Scholar] [CrossRef]
- Hunter, S.R.; Lavrik, N.V.; Mostafa, S.; Rajic, S.; Datskos, P.G. Review of Pyroelectric Thermal Energy Harvesting and New Mems-Based Resonant Energy Conversion Techniques. Proc. SPIE 2012. [Google Scholar] [CrossRef]
- Guyomar, D.; Sebald, G. Pyroelectric/electrocaloric energy scanvenging and cooling capabilities in ferroelectric materials. Int. J. Appl. Electromagn. Mech. 2009, 31, 41–46. [Google Scholar]
- Bowen, C.R.; Taylor, J.; LeBoulbar, E.; Zabek, D.; Chauhan, A.; Vaish, R. Pyroelectric materials and devices for energy harvesting applications. Energy Environ. Sci. 2014, 7, 3836–3856. [Google Scholar] [CrossRef]
- Cuadras, A.; Gasulla, M.; Ferrari, V. Thermal energy harvesting through pyroelectricity. Sensors Actuators A Phys. 2010, 158, 132–139. [Google Scholar] [CrossRef]
- Mane, P.; Xie, J.; Leang, K.K.; Mossi, K. Cyclic energy harvesting from pyroelectric materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 10–17. [Google Scholar] [CrossRef] [PubMed]
- Whatmore, R. Pyroelectric devices and materials. Rep. Prog. Phys. 1986, 49, 1335. [Google Scholar] [CrossRef]
- Whatmore, R.W.; Watton, R. Pyroelectric materials and devices. In Infrared Detectors and Emitters: Materials and Devices; Springer: Berlin, Germany, 2001; pp. 99–147. [Google Scholar]
- Li, X.; Lu, S.-G.; Chen, X.-Z.; Gu, H.; Qian, X.-S.; Zhang, Q. Pyroelectric and electrocaloric materials. J. Mater. Chem. C 2013, 1, 23–37. [Google Scholar] [CrossRef]
- Cooper, J. A fast-response pyroelectric thermal detector. J. Sci. Instrum. 1962, 39, 467. [Google Scholar] [CrossRef]
- Ivill, M.; Ngo, E.; Cole, M.W. Method and Characterization of Pyroelectric Coefficients for Determining Material Figures of Merit for Infrared (IR) Detectors; Army Research Lab Aberdeen Proving Ground Md Weapons and Materials Research Directorate: Aberdeen, MD, USA, 2013. [Google Scholar]
- Noh, J.Y.; Yoon, G.H. Topology optimization of piezoelectric energy harvesting devices considering static and harmonic dynamic loads. Adv. Eng. Softw. 2012, 53, 45–60. [Google Scholar] [CrossRef]
- Alpay, S.P.; Mantese, J.; Trolier-McKinstry, S.; Zhang, Q.; Whatmore, R.W. Next-generation electrocaloric and pyroelectric materials for solid-state electrothermal energy interconversion. MRS Bull. 2014, 39, 1099–1111. [Google Scholar] [CrossRef]
- Childress, J. Application of a ferroelectric material in an energy conversion device. J. Appl. Phys. 1962, 33, 1793–1798. [Google Scholar] [CrossRef]
- Hoh, S. Conversion of thermal to electrical energy with ferroelectric materials. Proc. IEEE 1963, 51, 838–845. [Google Scholar] [CrossRef]
- Clingman, W.; Moore, R., Jr. Application of ferroelectricity to energy conversion processes. J. Appl. Phys. 1961, 32, 675–681. [Google Scholar] [CrossRef]
- Sebald, G.; Lefeuvre, E.; Guyomar, D. Pyroelectric energy conversion: Optimization principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 538–551. [Google Scholar] [CrossRef] [PubMed]
- Olsen, R.B.; Bruno, D.A.; Briscoe, J.M. Pyroelectric conversion cycles. J. Appl. Phys. 1985, 58, 4709–4716. [Google Scholar] [CrossRef]
- Frood, D.G. A note on the use of the titanates as thermoelectric transducers. Can. J. Phys. 1954, 32, 313–317. [Google Scholar] [CrossRef]
- Drummond, J. Dielectric power conversion. In Proceedings of the Annual Intersociety Energy Conversion and Engineering Conference, Newark, DE, USA, 18–22 August 1975; pp. 569–575. [Google Scholar]
- Olsen, R.; Brown, D. High efficieincy direct conversion of heat to electrical energy-related pyroelectric measurements. Ferroelectrics 1982, 40, 17–27. [Google Scholar] [CrossRef]
- Olsen, R.B.; Evans, D. Pyroelectric energy conversion: Hysteresis loss and temperature sensitivity of a ferroelectric material. J. Appl. Phys. 1983, 54, 5941–5944. [Google Scholar] [CrossRef]
- Sebald, G.; Pruvost, S.; Guyomar, D. Energy harvesting based on ericsson pyroelectric cycles in a relaxor ferroelectric ceramic. Smart Mater. Struct. 2007, 17, 015012. [Google Scholar] [CrossRef]
- Lee, F.Y.; Goljahi, S.; McKinley, I.M.; Lynch, C.S.; Pilon, L. Pyroelectric waste heat energy harvesting using relaxor ferroelectric 8/65/35 plzt and the olsen cycle. Smart Mater. Struct. 2012, 21, 025021. [Google Scholar] [CrossRef]
- Vats, G.; Chauhan, A.; Vaish, R. Thermal energy harvesting using bulk lead-free ferroelectric ceramics. Int. J. Appl. Ceram. Technol. 2015, 12. [Google Scholar] [CrossRef]
- Chauhan, A.; Patel, S.; Vats, G.; Vaish, R. Enhanced thermal energy harvesting using Li, K-Doped Bi0.5Na0.5TiO3 lead-free ferroelectric ceramics. Energy Technol. 2014, 2, 205–209. [Google Scholar] [CrossRef]
- Vats, G.; Vaish, R.; Bowen, C.R. An analysis of lead-free (Bi0.5Na0.5)0.915-(Bi0.5K0.5)0.05Ba0.02Sr0.015TiO3 ceramic for efficient refrigeration and thermal energy harvesting. J. Appl. Phys. 2014, 115, 013505. [Google Scholar] [CrossRef]
- Vats, G.; Kushwaha, H.S.; Vaish, R. Enormous energy harvesting and storage potential in multiferroic epitaxial thin film hetrostructures: An unforeseen era. Mater. Res. Express 2014, 1, 015503. [Google Scholar] [CrossRef]
- Olsen, R.; Bruno, D.; Briscoe, J.; Dullea, J. Cascaded pyroelectric energy converter. Ferroelectrics 1984, 59, 205–219. [Google Scholar] [CrossRef]
- Olsen, R.B.; Briscoe, J.M.; Bruno, D.A.; Butler, W.F. A pyroelectric energy converter which employs regeneration. Ferroelectrics 1981, 38, 975–978. [Google Scholar] [CrossRef]
- Khodayari, A.; Pruvost, S.; Sebald, G.; Guyomar, D.; Mohammadi, S. Nonlinear pyroelectric energy harvesting from relaxor single crystals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 693–699. [Google Scholar] [CrossRef] [PubMed]
- Kandilian, R.; Navid, A.; Pilon, L. The pyroelectric energy harvesting capabilities of PMN–PT near the morphotropic phase boundary. Smart Mater. Struct. 2011, 20, 055020. [Google Scholar] [CrossRef]
- Olsen, R.B.; Bruno, D.A.; Briscoe, J.M.; Jacobs, E.W. Pyroelectric conversion cycle of vinylidene fluoride-trifluoroethylene copolymer. J. Appl. Phys. 1985, 57, 5036–5042. [Google Scholar] [CrossRef]
- Ikura, M. Conversion of low-grade heat to electricity using pyroelectric copolymer. Ferroelectrics 2002, 267, 403–408. [Google Scholar] [CrossRef]
- Nguyen, H.; Navid, A.; Pilon, L. Pyroelectric energy converter using co-polymer P (VDF-TrFE) and olsen cycle for waste heat energy harvesting. Appl. Therm. Eng. 2010, 30, 2127–2137. [Google Scholar] [CrossRef]
- Navid, A.; Pilon, L. Pyroelectric energy harvesting using olsen cycles in purified and porous poly (vinylidene fluoride-trifluoroethylene) [P (VDF-TrFE)] thin films. Smart Mater. Struct. 2011, 20, 025012. [Google Scholar] [CrossRef]
- Olsen, R.; Bruno, D. Pyroelectric conversion materials. In Proceedings of the Twenty-First Intersociety Energy Conversion Engineering Conference, San Diego, CA, USA, 25–29 August 1986; pp. 89–93. [Google Scholar]
- Zhu, H.; Pruvost, S.; Cottinet, P.; Guyomar, D. Energy harvesting by nonlinear capacitance variation for a relaxor ferroelectric poly (vinylidene fluoride-trifluoroethylene-chlorofluoroethylene) terpolymer. Appl. Phys. Lett. 2011, 98, 222901. [Google Scholar] [CrossRef]
- Leng, Q.; Chen, L.; Guo, H.; Liu, J.; Liu, G.; Hu, C.; Xi, Y. Harvesting heat energy from hot/cold water with a pyroelectric generator. J. Mater. Chem. A 2014, 2, 11940–11947. [Google Scholar] [CrossRef]
- Olsen, R.B. Ferroelectric conversion of heat to electrical energy—A demonstration. J. Energy 1982, 6, 91–95. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, S.; Zhang, Y.; Wang, Z.L. Pyroelectric nanogenerators for driving wireless sensors. Nano Lett. 2012, 12, 6408–6413. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Lee, K.Y.; Gupta, M.K.; Kim, T.Y.; Lee, D.Y.; Oh, J.; Ryu, C.; Yoo, W.J.; Kang, C.Y.; Yoon, S.J. Highly stretchable piezoelectric-pyroelectric hybrid nanogenerator. Adv. Mater. 2014, 26, 765–769. [Google Scholar] [CrossRef] [PubMed]
- Kishore, R.A.; Priya, S. A review on design and performance of thermomagnetic devices. Renew. Sustain. Energy Rev. 2018, 81, 33–44. [Google Scholar] [CrossRef]
- Solomon, D. Improving the performance of a thermomagnetic generator by cycling the magnetic field. J. Appl. Phys. 1988, 63, 915–921. [Google Scholar] [CrossRef]
- Joshi, K.B.; Priya, S. Multi-physics model of a thermo-magnetic energy harvester. Smart Mater. Struct. 2013, 22, 055005. [Google Scholar] [CrossRef]
- Solomon, D. Design of a thermomagnetic generator. Energy Convers. Manag. 1991, 31, 157–173. [Google Scholar] [CrossRef]
- Kishore, R.A.; Priya, S. Low-grade waste heat recovery using reverse magnetocaloric effect. Sustain. Energy Fuels 2017, 1, 1899–1908. [Google Scholar] [CrossRef]
- Hsu, C.-J.; Sandoval, S.M.; Wetzlar, K.P.; Carman, G.P. Thermomagnetic conversion efficiencies for ferromagnetic materials. J. Appl. Phys. 2011, 110, 123923. [Google Scholar]
- Post, A.; Knight, C.; Kisi, E. Thermomagnetic energy harvesting with first order phase change materials. J. Appl. Phys. 2013, 114, 033915. [Google Scholar] [CrossRef]
- Elliott, J. Thermomagnetic generator. J. Appl. Phys. 1959, 30, 1774–1777. [Google Scholar] [CrossRef]
- Kirol, L.D.; Mills, J.I. Numerical analysis of thermomagnetic generators. J. Appl. Phys. 1984, 56, 824–828. [Google Scholar] [CrossRef]
- Phan, M.-H.; Peng, H.-X.; Yu, S.-C.; Tho, N.D.; Nhat, H.N.; Chau, N. Manganese perovskites for room temperature magnetic refrigeration applications. J. Magn. Magn. Mater. 2007, 316, 562–565. [Google Scholar] [CrossRef]
- Srivastava, V.; Song, Y.; Bhatti, K.; James, R. The direct conversion of heat to electricity using multiferroic alloys. Adv. Energy Mater. 2011, 1, 97–104. [Google Scholar] [CrossRef]
- Song, Y. Performance analysis of energy conversion via caloric effects in first-order ferroic phase transformations. Phys. Chem. Chem. Phys. 2014, 16, 12750–12763. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Bhatti, K.P.; Srivastava, V.; Leighton, C.; James, R.D. Thermodynamics of energy conversion via first order phase transformation in low hysteresis magnetic materials. Energy Environ. Sci. 2013, 6, 1315–1327. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494. [Google Scholar] [CrossRef]
- Klimczak, M.; Talik, E. In Magnetocaloric effect of GdTX (T = Mn, Fe, Ni, Pd, X = Al, In) and GdFe6Al6 ternary compounds. J. Phys. Conf. Ser. 2010, 9, 092009. [Google Scholar] [CrossRef]
- Law, J.; Ramanujan, R.; Franco, V. Tunable Curie temperatures in Gd alloyed Fe–B–Cr magnetocaloric materials. J. Alloy. Compd. 2010, 508, 14–19. [Google Scholar] [CrossRef]
- Canepa, F.; Napoletano, M.; Cirafici, S. Magnetocaloric effect in the intermetallic compound Gd7Pd3. Intermetallics 2002, 10, 731–734. [Google Scholar] [CrossRef]
- Spichkin, Y.; Pecharsky, V.; Gschneidner, K., Jr. Preparation, crystal structure, magnetic and magnetothermal properties of (GdxR5−x)Si4, where R = Pr and Tb, alloys. J. Appl. Phys. 2001, 89, 1738–1745. [Google Scholar] [CrossRef]
- Von Ranke, P.; De Oliveira, N.; Gama, S. Theoretical investigations on giant magnetocaloric effect in MnAs1−xSbx. Phys. Lett. A 2004, 320, 302–306. [Google Scholar] [CrossRef]
- Wada, H.; Morikawa, T.; Taniguchi, K.; Shibata, T.; Yamada, Y.; Akishige, Y. Giant magnetocaloric effect of MnAs1−xSbx in the vicinity of first-order magnetic transition. Phys. B Condens. Matter 2003, 328, 114–116. [Google Scholar] [CrossRef]
- Wada, H.; Taniguchi, K.; Tanabe, Y. Extremely large magnetic entropy change of MnAs1−xSbx near room temperature. Mater. Trans. 2002, 43, 73–77. [Google Scholar] [CrossRef]
- Das, S.; Dey, T. Magnetic entropy change in polycrystalline La1−xKx MnO3 perovskites. J. Alloy. Compd. 2007, 440, 30–35. [Google Scholar] [CrossRef]
- Zhong, W.; Chen, W.; Au, C.; Du, Y. Dependence of the magnetocaloric effect on oxygen stoichiometry in polycrystalline La2/3Ba1/3MnO3–δ. J. Magn. Magn. Mater. 2003, 261, 238–243. [Google Scholar] [CrossRef]
- Hanh, D.; Islam, M.; Khan, F.; Minh, D.; Chau, N. Large magnetocaloric effect around room temperature in La0.7Ca0.3−xPbxMnO3 perovskites. J. Magn. Magn. Mater. 2007, 310, 2826–2828. [Google Scholar] [CrossRef]
- Phan, M.-H.; Tian, S.-B.; Yu, S.-C.; Ulyanov, A. Magnetic and magnetocaloric properties of La0.7Ba0.3−xPbxMnO3 compounds. J. Magn. Magn. Mater. 2003, 256, 306–310. [Google Scholar] [CrossRef]
- Sun, W.; Li, J.; Ao, W.; Tang, J.; Gong, X. Hydrothermal synthesis and magnetocaloric effect of La0.7Ca0.2Sr0.1MnO3. Powder Technol. 2006, 166, 77–80. [Google Scholar] [CrossRef]
- Li, J.; Sun, W.; Ao, W.; Tang, J. Hydrothermal synthesis and magnetocaloric effect of La0.5Ca0.3Sr0.2MnO3. J. Magn. Magn. Mater. 2006, 302, 463–466. [Google Scholar] [CrossRef]
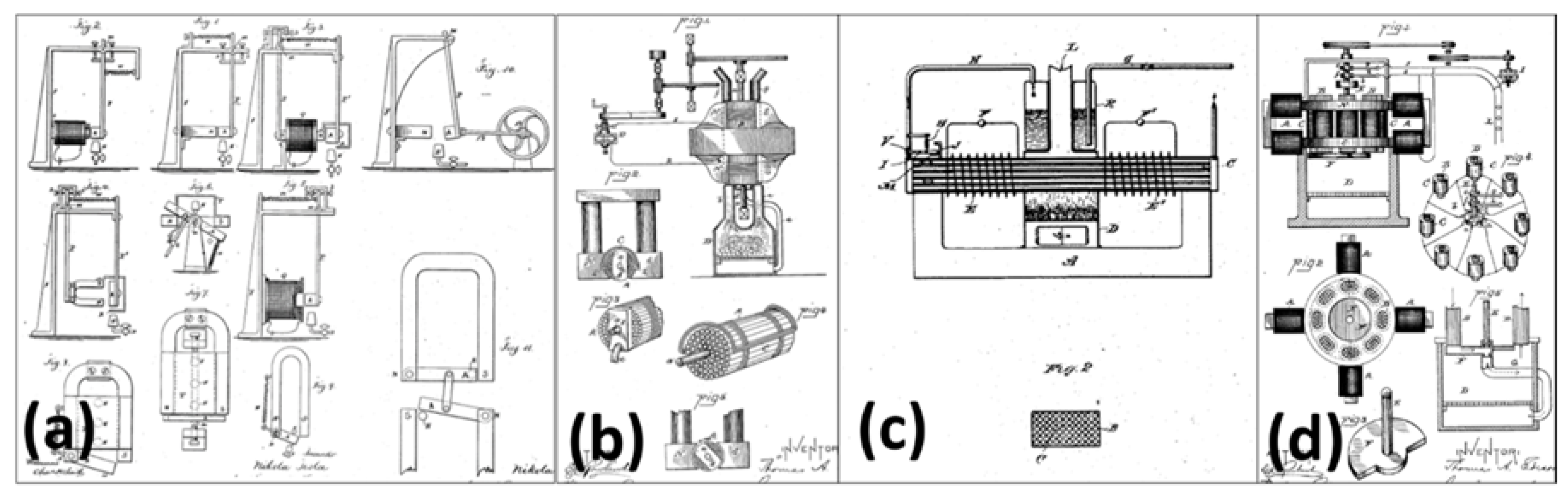
- Tesla, N. Thermo-Magnetic Motor. U.S. Patent 396121, 15 January 1889. [Google Scholar]
- Edison, T.A. Pyromagnetic Motor. U.S. Patent 380100, 27 March 1888. [Google Scholar]
- Tesla, N. Pyromagneto-Electric Generator. U.S. Patent 428057, 13 May 1890. [Google Scholar]
- Edison, T.A. Pyromagnetic Generator. U.S. Patent 476983, 14 June 1892. [Google Scholar]
- Van der Maas, G.J.; Purvis, W.J. “Curie point” motor. Am. J. Phys. 1956, 24, 176–177. [Google Scholar] [CrossRef]
- Murakami, K.; Nemoto, M. Some experiments and considerations on the behavior of thermomagnetic motors. IEEE Trans. Magn. 1972, 8, 387–389. [Google Scholar] [CrossRef]
- Takahashi, Y.; Matsuzawa, T.; Nishikawa, M. Fundamental performance of the disc-type thermomagnetic engine. Electr. Eng. Jpn. 2004, 148, 26–33. [Google Scholar] [CrossRef]
- Takahashi, Y.; Yamamoto, K.; Nishikawa, M. Fundamental performance of triple magnetic circuit type cylindrical thermomagnetic engine. Electr. Eng. Jpn. 2006, 154, 68–74. [Google Scholar] [CrossRef]
- Palmy, C. A new thermo-magnetic wheel. Eur. J. Phys. 2006, 27, 1289. [Google Scholar] [CrossRef]
- Palmy, C. A thermo-magnetic wheel. Eur. News 2007, 38, 32–34. [Google Scholar] [CrossRef]
- Ujihara, M.; Carman, G.; Lee, D. Thermal energy harvesting device using ferromagnetic materials. Appl. Phys. Lett. 2007, 91, 093508. [Google Scholar] [CrossRef]
- Chun, J.; Song, H.-C.; Kang, M.-G.; Kang, H.B.; Kishore, R.A.; Priya, S. Thermo-magneto-electric generator arrays for active heat recovery system. Sci. Rep. 2017, 7, 41383. [Google Scholar] [CrossRef] [PubMed]
- Massad, J.E.; Smith, R.C. A homogenized free energy model for hysteresis in thin-film shape memory alloys. Thin Solid Films 2005, 489, 266–290. [Google Scholar] [CrossRef]
- Müller, I.; Xu, H. On the pseudo-elastic hysteresis. Acta Met. Mater. 1991, 39, 263–271. [Google Scholar] [CrossRef]
- Fedelich, B.; Zanzotto, G. One-dimensional quasistatic nonisothermal evolution of shape-memory material inside the hysteresis loop. Contin. Mech. Thermodyn. 1991, 3, 251–276. [Google Scholar] [CrossRef]
- Raniecki, B.; Lexcellent, C.; Tanaka, K. Thermodynamic models of pseudoelastic behaviour of shape memory alloys. Arch. Mech. 1992, 44, 261–284. [Google Scholar]
- Tanaka, K.; Hayashi, T.; Itoh, Y.; Tobushi, H. Analysis of thermomechanical behavior of shape memory alloys. Mech. Mater. 1992, 13, 207–215. [Google Scholar] [CrossRef]
- Ziótkowski, A. Theoretical analysis of efficiency of shape memory alloy heat engines (based on constitutive models of pseudoelasticity). Mech. Mater. 1993, 16, 365–377. [Google Scholar] [CrossRef]
- Qian, S.; Ling, J.; Hwang, Y.; Radermacher, R.; Takeuchi, I. Thermodynamics cycle analysis and numerical modeling of thermoelastic cooling systems. Int. J. Refrig. 2015, 56, 65–80. [Google Scholar] [CrossRef]
- Lagoudas, D.C. Shape Memory Alloys: Modeling and Engineering Applications; Springer: Berlin, Germany, 2008. [Google Scholar]
- Kurdjumov, G.; Khandros, L. First reports of the thermoelastic behaviour of the martensitic phase of Au-Cd alloys. Dokl. Akad. Nauk SSSR 1949, 66, 211–213. [Google Scholar]
- Buehler, W.J.; Gilfrich, J.; Wiley, R. Effect of low-temperature phase changes on the mechanical properties of alloys near composition tini. J. Appl. Phys. 1963, 34, 1475–1477. [Google Scholar] [CrossRef]
- Stöckel, D. The shape memory effect-phenomenon, alloys and applications. California 1995, 94539, 1–13. [Google Scholar]
- Elahinia, M.H.; Hashemi, M.; Tabesh, M.; Bhaduri, S.B. Manufacturing and processing of niti implants: A review. Prog. Mater. Sci. 2012, 57, 911–946. [Google Scholar] [CrossRef]
- Melton, K.; Mercier, O. Deformation behavior of NiTi-based alloys. Met. Trans. A 1978, 9, 1487–1488. [Google Scholar] [CrossRef]
- Miyazaki, S.; Mizukoshi, K.; Ueki, T.; Sakuma, T.; Liu, Y. Fatigue life of Ti–50 at.% Ni and Ti–40Ni–10Cu (at.%) shape memory alloy wires. Mater. Sci. Eng. A 1999, 273, 658–663. [Google Scholar] [CrossRef]
- Doonkersloot, H.; Vucht, V. Martensitic transformations in Au-Ti, Pd-Ti and Pt-Ti alloys. J. Less-Common Met. 1970, 20, 83–91. [Google Scholar]
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Zhu, J.; Liang, N.; Liew, K.; Huang, W. Energy conversion in shape memory alloy heat engine part i: Theory. J. Intell. Mater. Syst. Struct. 2001, 12, 127–132. [Google Scholar] [CrossRef]
- Funakubo, H.; Kennedy, J. Shape Memory Alloys; Gordon and Breach: New York, NY, USA, 1987. [Google Scholar]
- Shin, M.C.; Kim, C.S.; Chung, Y.H.; Jee, K.K. Twin-Crank Type Heat Engine. U.S. Patent US4683721A, 4 August 1987. [Google Scholar]
- Banks, R. Vertically Oscillating Heat Engine. U.S. Patent # US4691518A, 12 November 1986. [Google Scholar]
- Wechsler, M.S.; Van Gerpen, J.H. Apparatus for Recovery and Use of Waste Thermal Energy. U.S. Patent 5279123A, 18 January 1994. [Google Scholar]
- Iwanaga, H.; Tobushi, H.; Ito, H. Basic research on output power characteristics of a shape memory alloy heat engine:(twin crank heat engine). JSME 1988, 31, 634–637. [Google Scholar] [CrossRef]
- Sandoval, D.J. Thermal Motor. U.S. Patent 4030298A, 8 March 1977. [Google Scholar]
- Wang, F.E. Energy Conversion System. U.S. Patent 4275561A, 30 June 1981. [Google Scholar]
- Pachter, J.J. Engine. U.S. Patent 4150544, 24 April 1979. [Google Scholar]
- Wayman, C.M. Solid State Thermal Engine. U.S. Patent 4246754A, 27 January 1981. [Google Scholar]
- Cory, J.S. Solid State Heat Engine. U.S. Patent 4305250A, 15 December 1981. [Google Scholar]
- Cory, J.S. Variable Density Heat Engine. U.S. Patent 4027479A, 7 June 1977. [Google Scholar]
- Johnson, A.D.; Kirkpatrick, P.F. Field Effect Memory Alloy Heat Engine. U.S. Patent 4281513, 4 August 1981. [Google Scholar]
- Dillon, C.L. Engine Construction. U.S. Patent 4434618, 6 March 1984. [Google Scholar]
- O’hare, L.R. Wire Engine. U.S. Patent 4646523A, 3 March 1987. [Google Scholar]
- Ahlers, M. On the usefulness of martensitic transformations for energy conversion. Scr. Met. 1975, 9, 71–74. [Google Scholar] [CrossRef]
- Golestaneh, A. Efficiency of the solid-state engine made with nitinol memory material. J. Appl. Phys. 1978, 49, 1241–1244. [Google Scholar] [CrossRef]
- Mogutnov, B. The efficiency of heat engines having a solid working body based on alloys with a shape’memory’ effect. Fiz. Met. Met. 1978, 45, 428–430. [Google Scholar]
- Wu, W.-F.; Long, X.-P.; Yu, X.-L.; Feng, Q.-K. A new power generation method utilizing a low grade heat source. J. Zhejiang Univ. Sci. A 2012, 13, 140–145. [Google Scholar] [CrossRef]
- Salzbrenner, R. Shape memory heat engines. J. Mater. Sci. 1984, 19, 1827–1835. [Google Scholar] [CrossRef]
- Schiller, E.H. Heat Engine Driven by Shape Memory Alloys: Prototyping and Design. Master’s Thesis, Virginia Tech, Blacksburg, VA, USA, 2002. [Google Scholar]
- Wakjira, J.F. The vt1 Shape Memory Alloy Heat Engine Design. Master’s Thesis, Virginia Tech, Blacksburg, VA, USA, 2001. [Google Scholar]
- Avirovik, D.; Kumar, A.; Bodnar, R.J.; Priya, S. Remote light energy harvesting and actuation using shape memory alloy-Piezoelectric hybrid transducer. Smart Mater. Struct. 2013, 22, 052001. [Google Scholar] [CrossRef]
- Sato, Y.; Yoshida, N.; Tanabe, Y.; Fujita, H.; Ooiwa, N. Characteristics of a new power generation system with application of a shape memory alloy engine. Electr. Eng. Jpn. 2008, 165, 8–15. [Google Scholar]
- Avirovik, D.; Kishore, R.A.; Vuckovic, D.; Priya, S. Miniature shape memory alloy heat engine for powering wireless sensor nodes. Energy Harvest. Syst. 2014, 1, 13–18. [Google Scholar] [CrossRef]
- Gentherm Global Power Technologies. Available online: http://www.Genthermglobalpower.Com/products/thermoelectric-generators-tegs (accessed on 20 January 2018).
- Hendricks, T.; Choate, W.T. Engineering Scoping Study of Thermoelectric Generator Systems for Industrial Waste Heat Recovery; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2006.


| Temp Range | Source | Temp (°C) | Advantages | Disadvantages/Barriers |
|---|---|---|---|---|
| High >1200 °F (>650 °C) | Nickel refining furnace | 1370–1650 |
|
|
| Steel electric arc furnace | 1370–1650 | |||
| Basic oxygen furnace | 1200 | |||
| Aluminum reverberatory furnace | 1100–1200 | |||
| Copper refining furnace | 760–820 | |||
| Steel heating furnace | 930–1040 | |||
| Copper reverberatory furnace | 900–1090 | |||
| Hydrogen plants | 650–980 | |||
| Fume incinerators | 650–1430 | |||
| Glass melting furnace | 1300–1540 | |||
| Coke oven | 650–1000 | |||
| Iron cupola | 820–980 | |||
| Medium 450–1200 °F (230–650 °C) | Steam boiler exhaust | 230–480 |
| - |
| Gas turbine exhaust | 370–540 | |||
| Reciprocating engine exhaust | 320–590 | |||
| Heat treating furnace | 430–650 | |||
| Drying & baking ovens | 230–590 | |||
| Cement kiln | 450–620 | |||
| Low <450 °C (<230 °C) | Exhaust gases exiting recovery devices in gasfired boilers, ethylene furnaces, etc. | 70–230 |
|
|
| Process steam condensate | 50–90 | |||
| Cooling water from: | - | |||
| furnace doors | 30–50 | |||
| annealing furnaces | 70–230 | |||
| air compressors | 30–50 | |||
| internal combustion | 70–120 | |||
| engines: air conditioning and air conditioning and | 30–40 | |||
| Drying, baking, and curing ovens | 90–230 | |||
| Hot processed liquids/solids | 30–230 |
| Pyroelectric Materials | |||||
|---|---|---|---|---|---|
| PNZST ceramic | 158 | 170 | 0.4 | 2.8 | 95 |
| PNZST ceramic | 145 | 175 | 0.8 | 3.2 | 300 |
| PMN-PT 90/10 ceramic | 35 | 85 | 0.5 | 3.5 | 186 |
| PLZT 8/65/35 ceramic | 25 | 160 | 0.2 | 7.5 | 888 |
| KNTM ceramic | 140 | 160 | 0.1 | 5 | 629 |
| BNLT ceramic | 25 | 120 | 0.1 | 11.2 | 1146 |
| BNKT ceramic | 25 | 110 | 0.1 | 5.2 | 1986 |
| BNK-BST ceramic | 20 | 160 | 0.1 | 4 | 1523 |
| YBFO thin | −258 | 27 | 0.1 | 4 | 7570 |
| PZST | 157 | 177 | 0.4 | 3.2 | 131 |
| PZST | 145 | 178 | 1.2 | 3.2 | 130 |
| PZST | 146 | 159 | 0 | 2.9 | 100 |
| PZST | 110 | 170 | 0 | 2.8 | 0.4 |
| PZN-4.5PT | 100 | 160 | 0 | 2 | 217 |
| PZN-5.5PT | 100 | 190 | 0 | 1.2 | 150 |
| PMN-10PT | 30 | 80 | 0 | 3.5 | 186 |
| PMN-32PT | 80 | 170 | 0 | 0.9 | 100 |
| P(VDF-TrFE) 73/27 | 23 | 67 | 23 | 53 | 30 |
| P(VDF-TrFE) 60/40 | 58 | 77 | 4.1 | 47.2 | 52 |
| P(VDF-TrFE) 60/40 | 67 | 81 | 20.3 | 37.9 | 130 |
| P(VDF-TrFE) 60/40 | 25 | 110 | 20 | 50 | 521 |
| P(VDF-TrFE) 60/40 | 25 | 120 | 20 | 60 | 900 |
| P(VDF-TrFE-CFE) 61.3/29.7/9 | 0 | 25 | 0 | 25 | 50 |
| Material | ΔT (K) | |||
|---|---|---|---|---|
| CuZnAl | 293 | 50 | 13.5 | 92.5 |
| CuZnAl | 293 | 80 | 20.5 | 95.5 |
| TiNi | 323 | 50 | 8.6 | 63.9 |
| TiNi | 323 | 80 | 15.5 | 78.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kishore, R.A.; Priya, S. A Review on Low-Grade Thermal Energy Harvesting: Materials, Methods and Devices. Materials 2018, 11, 1433. https://doi.org/10.3390/ma11081433
Kishore RA, Priya S. A Review on Low-Grade Thermal Energy Harvesting: Materials, Methods and Devices. Materials. 2018; 11(8):1433. https://doi.org/10.3390/ma11081433
Chicago/Turabian StyleKishore, Ravi Anant, and Shashank Priya. 2018. "A Review on Low-Grade Thermal Energy Harvesting: Materials, Methods and Devices" Materials 11, no. 8: 1433. https://doi.org/10.3390/ma11081433
APA StyleKishore, R. A., & Priya, S. (2018). A Review on Low-Grade Thermal Energy Harvesting: Materials, Methods and Devices. Materials, 11(8), 1433. https://doi.org/10.3390/ma11081433






