Influence of the Non-Schmid Effects on the Ductility Limit of Polycrystalline Sheet Metals
Abstract
1. Introduction
- ▪
- First, second, or fourth-order tensors are represented by bold-face letters and symbols (the order of which is indicated by the context).
- ▪
- Scalar parameters and variables are designated by thin letters and symbols.
- ▪
- Macroscopic (resp. microscopic) fields are designated by capital (resp. small) letters and symbols.
- time derivative of .
- co-rotational derivative of .
- transpose of .
- inner product.
- double contraction product ( for the product between two second-order tensors, and
- for the product between a fourth-order tensor and a second-order tensor).
- vector product.
- determinant of tensor .
- sign of .
2. Theoretical Framework
- ▪
- is the total number of slip systems.
- ▪
- is the absolute value of the slip rate of the αth slip system.
- ▪
- and are respectively the symmetric and skew-symmetric part of the Schmid orientation tensor, which is defined as the tensor product . Vectors and , corresponding to BCC single crystals that we have used in the current work are listed in Appendix A.
- ▪
- is the resolved shear stress of the αth slip system, which is equal to .
- ■
- is the critical shear stress of the αth slip system.
- ■
- is an additional term (compared to the classical Schmid law) used to capture the non-Schmid effects. Here, and denote the non-Schmid shear stresses and their number, respectively. As to , they represent material parameters, which can be determined by experimental tests or atomistic simulations [28]. For simplicity, we assume in the current contribution that are the same for all of the slip systems, and we choose the following expansion for the term [28]:where vectors are enumerated in Appendix A (for the case of BCC single crystals).
3. Algorithmic Aspects
- For each strain-path ratio comprised between and (with typical intervals of ).
- ■
- For each time increment :
- ✓
- Compute the plane-stress tangent modulus from the 3D tangent modulus by using an iterative procedure similar to the one developed in [16]. On the other hand, is determined from the microscopic tangent moduli of the different single crystals by Equation (7). Some indications on the method used to compute are given after this algorithm.
- ✓
- For to , at user-defined intervals (with typical increments of ):
- -
- compute the determinant of the acoustic tensor . We recall that the components of are equal to .
- ✓
- Search for the orientation that minimizes over the different values of θ. If , then localized necking is reached. The corresponding angle θ is the orientation of the localization band, while the corresponding limit strain is equal to (as is equal to 1). The computation is then stopped. Otherwise, the integration is continued for the next time increment.
4. Numerical Results
4.1. Material Data
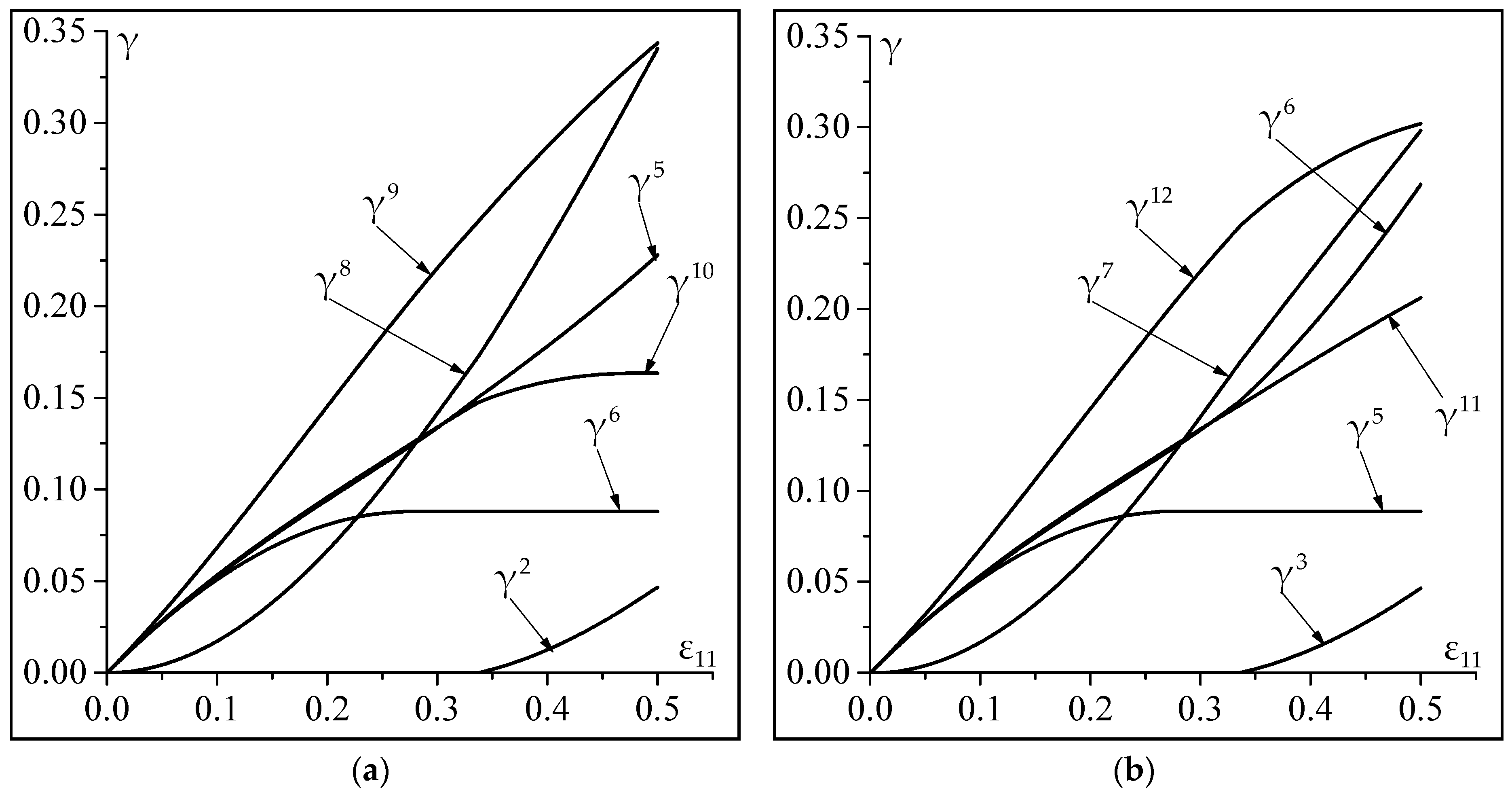
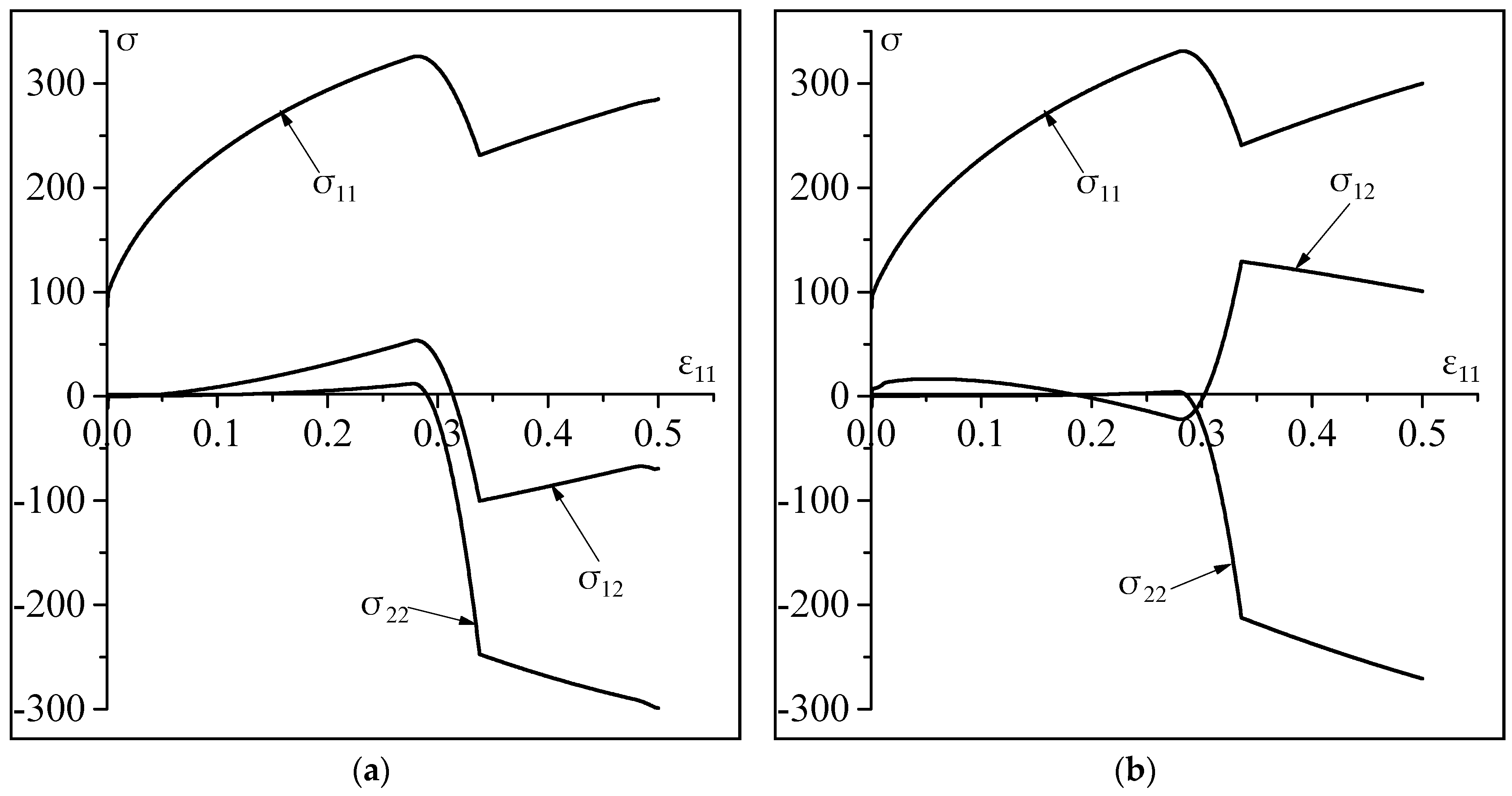
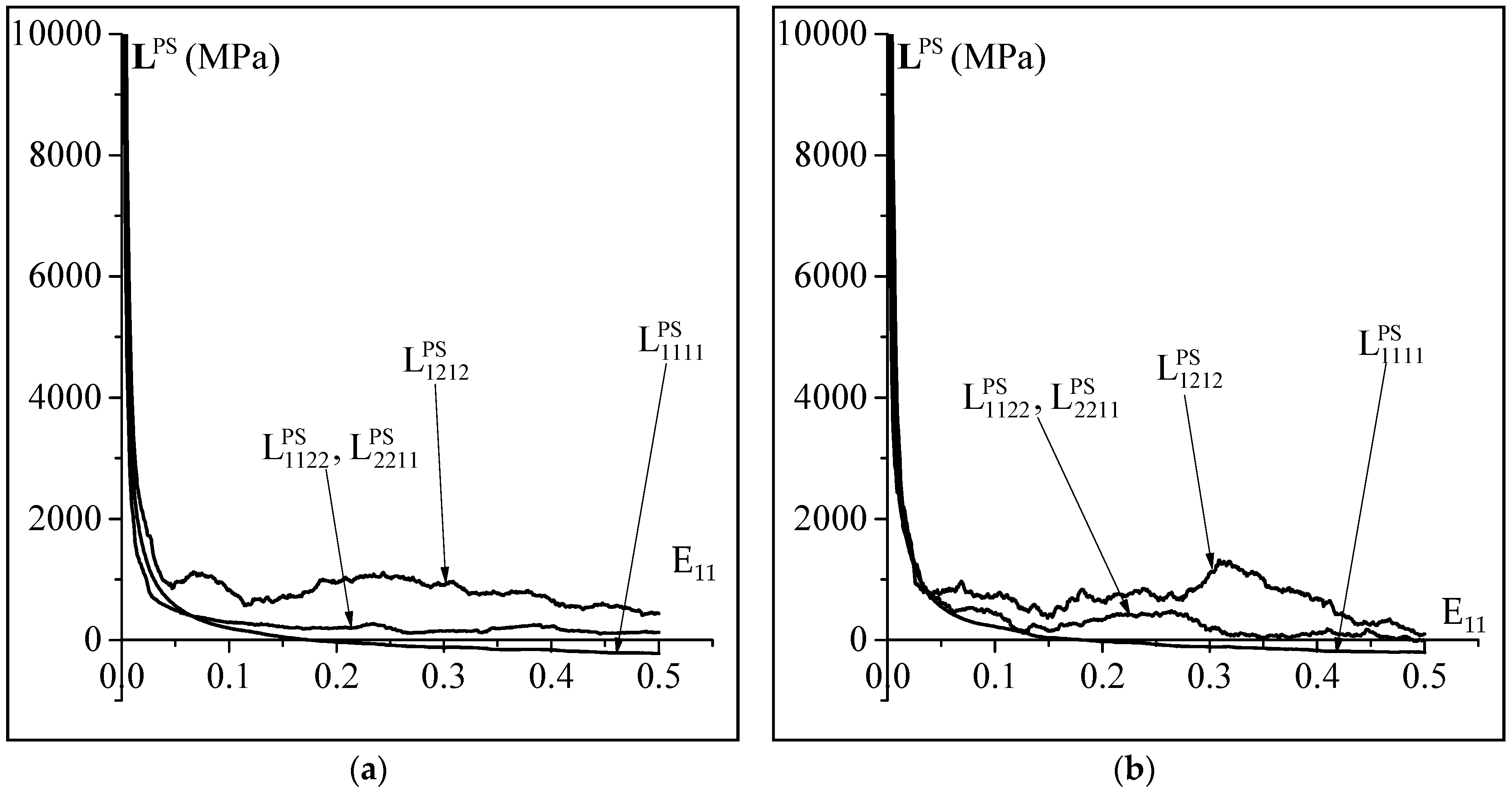
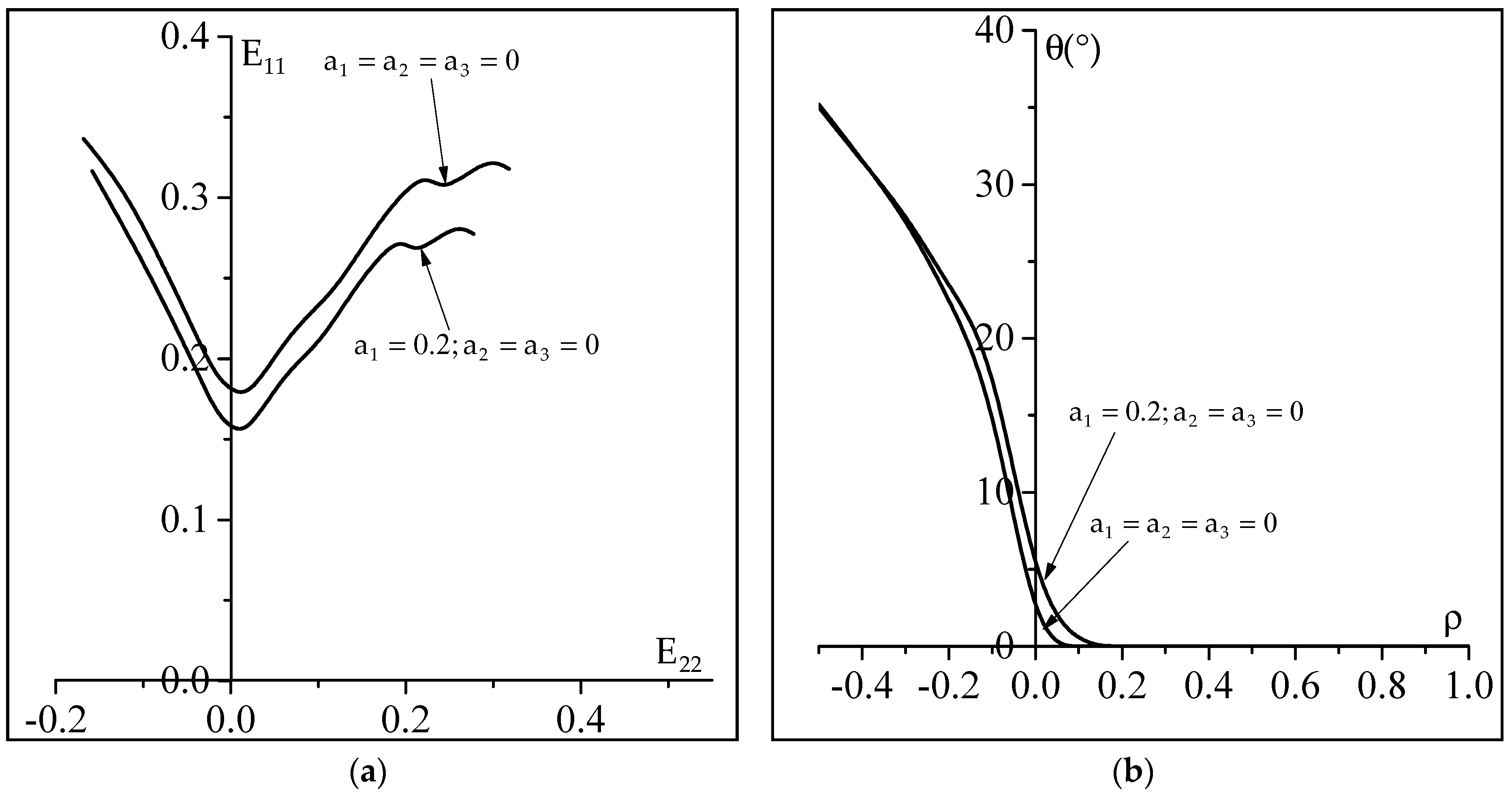
4.2. Significance of the Non-Schmid Effects on the Microscale Constitutive Response
4.3. Influence of the Non-Schmid Effects on Localized Necking
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A
Slip Systems for the BCC Single Crystals Used in the Non-Schmid Crystal Plasticity Model
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | |
References
- Keeler, S.P.; Backofen, W.A. Plastic instability and fracture in sheets stretched over rigid punches. Trans. ASM 1963, 56, 25–48. [Google Scholar]
- Goodwin, G.M. Application of strain analysis to sheet metal forming problems in press shop. Metall. Ital. 1968, 60, 767–774. [Google Scholar]
- Marciniak, Z.; Kuczynski, K. Limit strains in processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Stören, S.; Rice, J.R. Localized necking in thin sheets. J. Mech. Phys. Solids 1975, 23, 421–441. [Google Scholar] [CrossRef]
- Rice, J.R. The localization of plastic deformation. In Proceedings of the 14th International Congress of Theoretical and Applied Mechanics, Delft, The Netherlands, 30 August–4 September 1976; pp. 207–220. [Google Scholar]
- Petryk, H. On energy criteria of plastic instability. In Plastic Instability, Proc. Considere Memorial; Ecole Nationale des Ponts et Chaussees: Paris, France, 1985; pp. 215–226. [Google Scholar]
- Petryk, H.; Thermann, K. Post-critical plastic deformation of biaxially stretched sheets. Int. J. Solids Struct. 1996, 33, 689–705. [Google Scholar] [CrossRef]
- Petryk, H.; Thermann, K. Post-critical plastic deformation in incrementally nonlinear materials. J. Mech. Phys. Solids 2002, 50, 925–954. [Google Scholar] [CrossRef]
- Haddag, B.; Abed-Meraim, F.; Balan, T. Strain localization analysis using a large deformation anisotropic elastic–plastic model coupled with damage. Int. J. Plasticity 2009, 25, 1970–1996. [Google Scholar] [CrossRef]
- Mansouri, L.Z.; Chalal, H.; Abed-Meraim, F. Ductility limit prediction using a GTN damage model coupled with localization bifurcation analysis. Mech. Mater. 2014, 76, 64–92. [Google Scholar] [CrossRef]
- Kuroda, M.; Tvergaard, V. A phenomenological plasticity model with non-normality effects representing observations in crystal plasticity. J. Mech. Phys. Solids 2004, 49, 1239–1263. [Google Scholar] [CrossRef]
- Ben Bettaieb, M.; Abed-Meraim, F. Investigation of localized necking in substrate-supported metal layers: Comparison of bifurcation and imperfection analyses. Int. J. Plasticity 2016, 65, 168–190. [Google Scholar] [CrossRef]
- Signorelli, J.W.; Bertinetti, M.A.; Turner, P.A. Predictions of forming limit diagrams using a rate-dependent polycrystal self-consistent plasticity model. Int. J. Plasticity 2009, 25, 1–25. [Google Scholar] [CrossRef]
- Schwindt, C.; Schlosser, F.; Bertinetti, M.A.; Signorelli, J.W. Experimental and Visco-Plastic Self-consistent evaluation of forming limit diagrams for anisotropic sheet metals: An efficient and robust implementation of the M-K model. Int. J. Plasticity 2015, 73, 62–99. [Google Scholar] [CrossRef]
- Franz, G.; Abed-Meraim, F.; Berveiller, M. Strain localization analysis for single crystals and polycrystals: Towards microstructure-ductility linkage. Int. J. Plasticity 2013, 48, 1–33. [Google Scholar] [CrossRef]
- Akpama, H.K.; Ben Bettaieb, M.; Abed-Meraim, F. Localized necking predictions based on rate-independent self-consistent polycrystal plasticity: Bifurcation analysis versus imperfection approach. Int. J. Plasticity 2017, 91, 205–237. [Google Scholar] [CrossRef]
- Miehe, C.; Schröder, J.; Schotte, J. Computational homogenization analysis in finite plasticity Simulation of texture development in polycrystalline materials. Comput. Method Appl. Mech. Eng. 1999, 171, 387–418. [Google Scholar] [CrossRef]
- Watanabe, I.; Setoyama, D.; Nagasako, N.; Iwata, N.; Nakanishi, K. Multiscale prediction of mechanical behavior of Ferrite-Pearlite steel with Numerical Material Testing. Int. J. Numer. Meth. Eng. 2012, 89, 829–845. [Google Scholar] [CrossRef]
- Schmid, E.; Boas, W. Plasticity of Crystals; Chapman and Hall: London, UK, 1935. [Google Scholar]
- Akpama, H.K.; Ben Bettaieb, M.; Abed-Meraim, F. Influence of the yield surface curvature on the forming limit diagrams predicted by crystal plasticity theory. Lat. Am. J. Solids Struct. 2016, 13, 1250–1269. [Google Scholar] [CrossRef]
- Bassani, J.; Ito, K.; Vitek, V. Complex macroscopic plastic flow arising from non-planar dislocation core structures. Mater. Sci. Eng. A 2001, 319–321, 97–101. [Google Scholar] [CrossRef]
- Gröger, R.; Vitek, V. Multiscale modeling of plastic deformation of molybdenum and tungsten. III. Effects of temperature and plastic strain rate. Acta Mater. 2008, 56, 5426–5439. [Google Scholar] [CrossRef]
- Wang, Z.; Beyerlein, I. An atomistically-informed dislocation dynamics model for the plastic anisotropy and tension-compression asymmetry of BCC metals. Int. J. Plasticity 2011, 27, 1471–1484. [Google Scholar] [CrossRef]
- Mapar, A.; Ghassemi-Armaki, H.; Pourboghrat, F.; Kumar, K.S. A differential-exponential hardening law for non-Schmid crystal plasticity finite element modeling of ferrite single crystals. Int. J. Plasticity 2017, 91, 268–299. [Google Scholar] [CrossRef]
- Chen, P.; Ghassemi-Armaki, H.; Kumar, S.; Bower, A.; Bhat, S.; Sadagopan, S. Microscale-calibrated modeling of the deformation response of dual-phase steels. Acta Mater. 2014, 65, 133–149. [Google Scholar] [CrossRef]
- Srivastava, A.; Ghassemi-Armaki, H.; Sung, H.; Chen, P.; Kumar, S.; Bower, A.F. Micromechanics of plastic deformation and phase transformation in a three-phase TRIP-assisted advanced high strength steel: Experiments and modeling. J. Mech. Phys. Solids 2015, 78, 46–69. [Google Scholar] [CrossRef]
- Qin, Q.; Bassani, J.-L. Non-associated plastic flow in single crystals. J. Mech. Phys. Solids 1992, 40, 835–862. [Google Scholar] [CrossRef]
- Gröger, R.; Bailey, A.; Vitek, V. Multiscale modeling of plastic deformation of molybdenum and tungsten: I. Atomistic studies of the core structure and glide of 1/2111 screw dislocations at 0K. Acta Mater. 2008, 56, 5401–5411. [Google Scholar] [CrossRef]
- Qin, Q.; Bassani, J.-L. Non-Schmid yield behavior in single crystals. J. Mech. Phys. Solids 1992, 40, 813–833. [Google Scholar] [CrossRef]
- Koester, A.; Ma, A.; Hartmaier, A. Atomistically informed crystal plasticity model for body-centered cubic iron. Acta Mater. 2012, 60, 3894–3901. [Google Scholar] [CrossRef]
- Kuroda, M. A phenomenological plasticity model accounting for hydrostatic stress-sensitivity and vertex-type of effect. Mech. Mater. 2004, 36, 285–297. [Google Scholar] [CrossRef]
- Akpama, H.K.; Ben Bettaieb, M.; Abed-Meraim, F. Numerical integration of rate-independent BCC single crystal plasticity models: Comparative study of two classes of numerical algorithms. Int. J. Numer. Meth. Eng. 2016, 108, 363–422. [Google Scholar] [CrossRef]
- Chang, Y.W.; Asaro, R.J. An experimental study of shear localization in aluminum-copper single crystals. Acta Metall. 1981, 29, 241–257. [Google Scholar] [CrossRef]
- Barlat, F. Crystallographic texture, anisotropic yield surfaces and forming limits of sheet metals. Mater. Sci. Eng. 1987, 91, 55–72. [Google Scholar] [CrossRef]

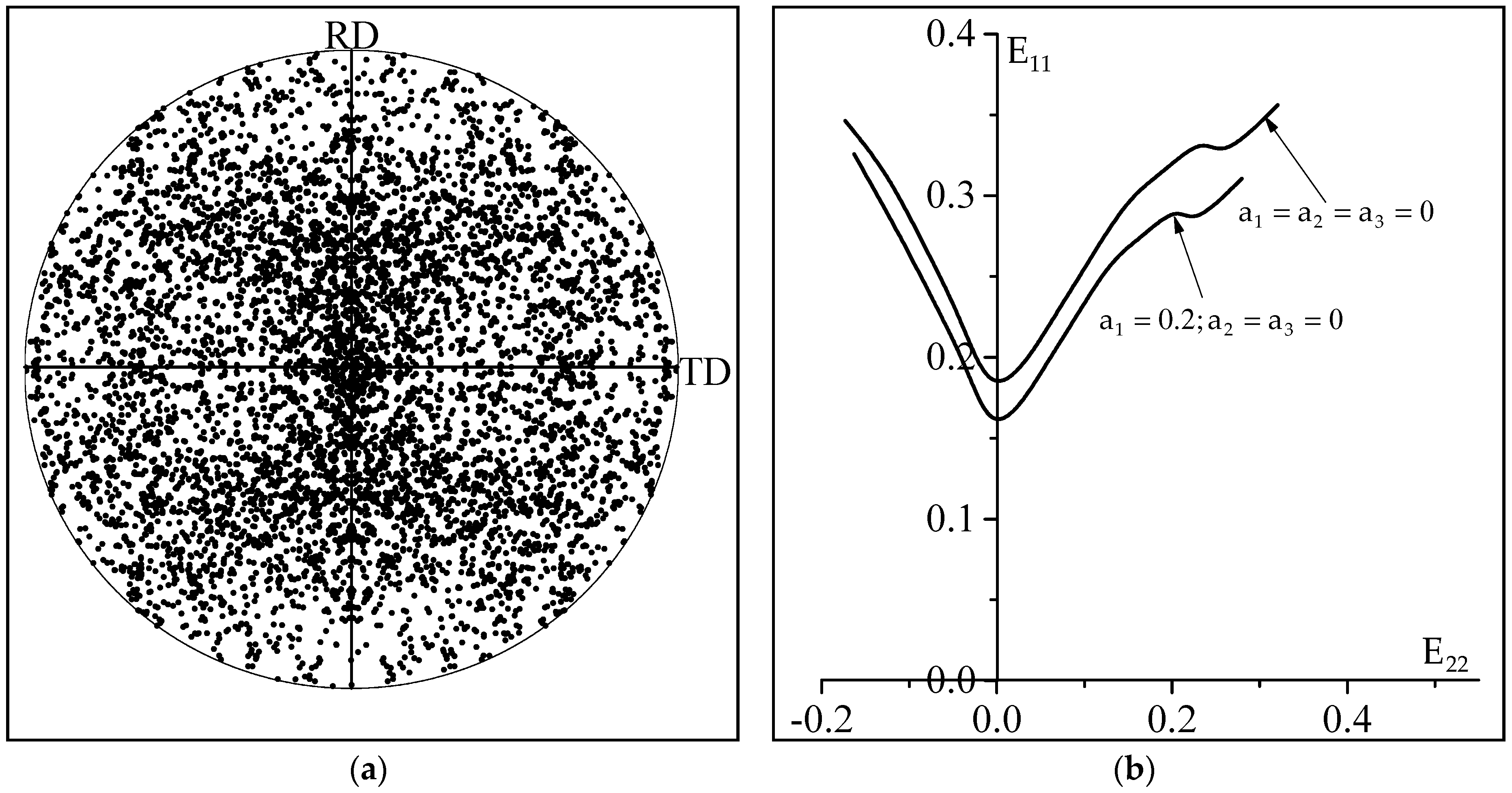
| Elasticity | Hardening | ||||
|---|---|---|---|---|---|
| E | ν | ||||
| 65 GPa | 0.3 | 0.15 | 40 MPa | 1.4 | 390 MPa |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Bettaieb, M.; Abed-Meraim, F. Influence of the Non-Schmid Effects on the Ductility Limit of Polycrystalline Sheet Metals. Materials 2018, 11, 1386. https://doi.org/10.3390/ma11081386
Ben Bettaieb M, Abed-Meraim F. Influence of the Non-Schmid Effects on the Ductility Limit of Polycrystalline Sheet Metals. Materials. 2018; 11(8):1386. https://doi.org/10.3390/ma11081386
Chicago/Turabian StyleBen Bettaieb, Mohamed, and Farid Abed-Meraim. 2018. "Influence of the Non-Schmid Effects on the Ductility Limit of Polycrystalline Sheet Metals" Materials 11, no. 8: 1386. https://doi.org/10.3390/ma11081386
APA StyleBen Bettaieb, M., & Abed-Meraim, F. (2018). Influence of the Non-Schmid Effects on the Ductility Limit of Polycrystalline Sheet Metals. Materials, 11(8), 1386. https://doi.org/10.3390/ma11081386






