Applicability of Mechanical Tests for Biomass Pellet Characterisation for Bioenergy Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Pellet Mechanical Durability
2.3. Biomass Milling Energy
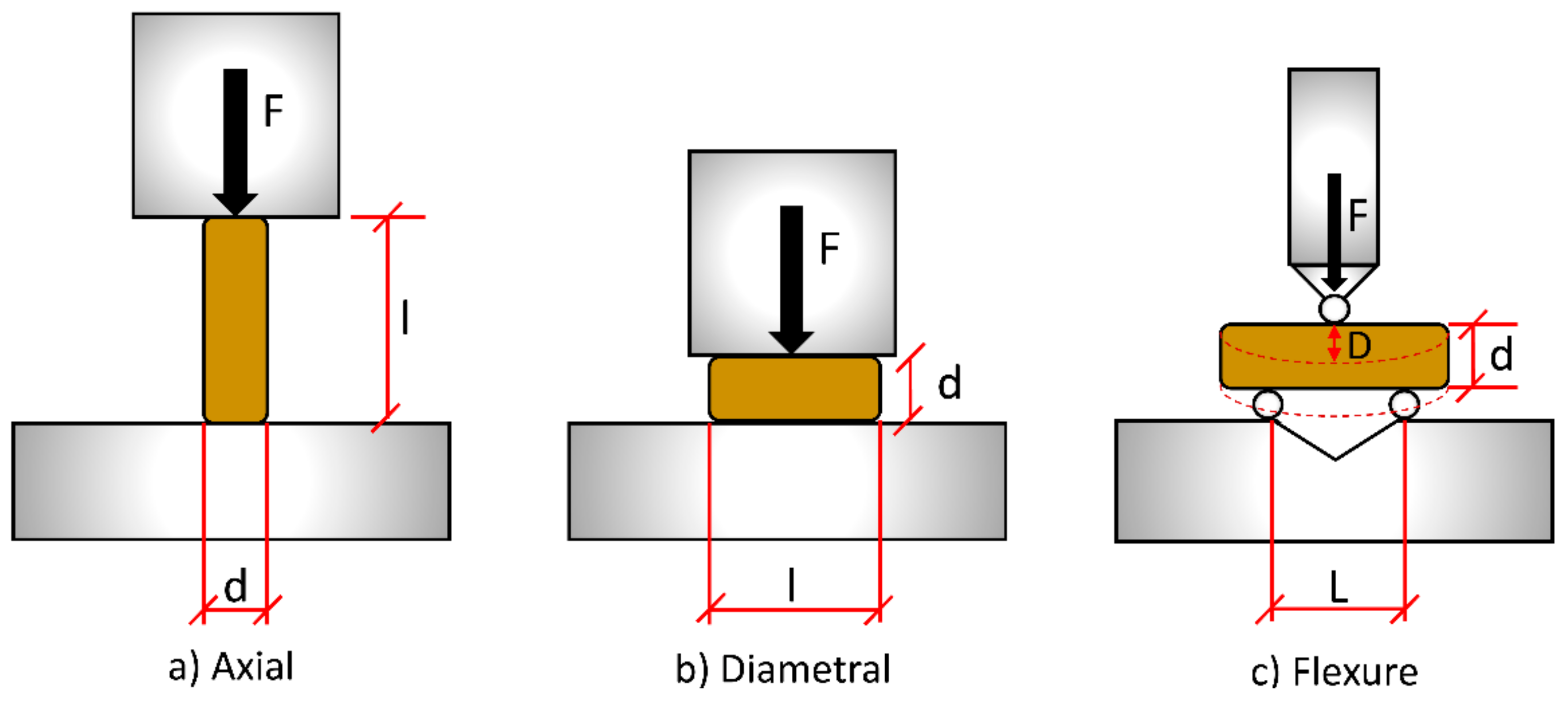
2.4. Quasi-Static Mechanical Strength of Pellets
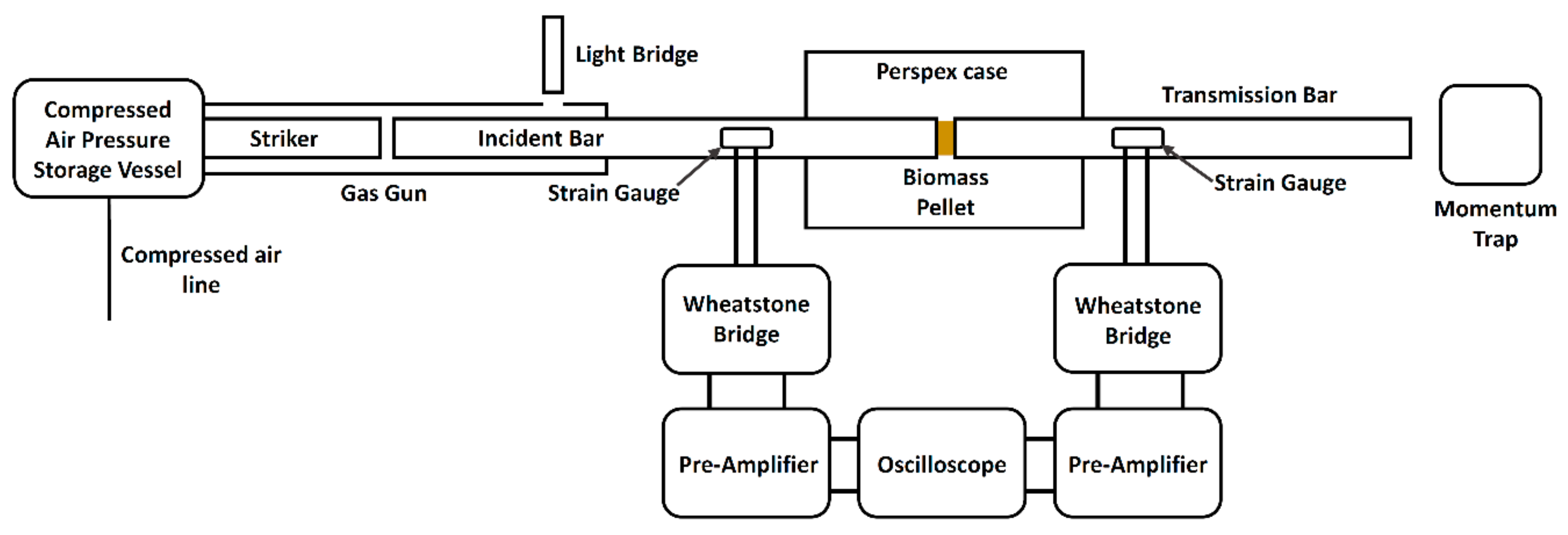
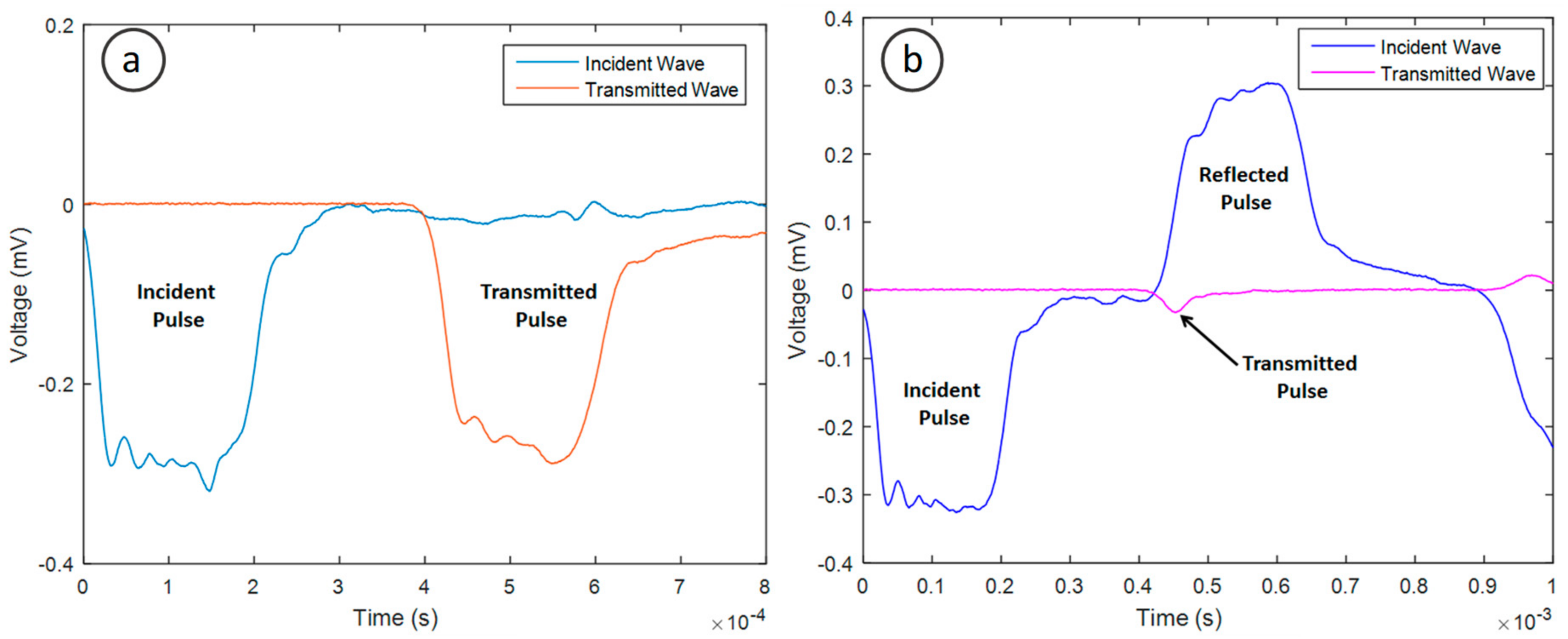
2.5. Dynamic Mechanical Strength of Pellets—Split Hopkinson Bar
3. Results and Discussion
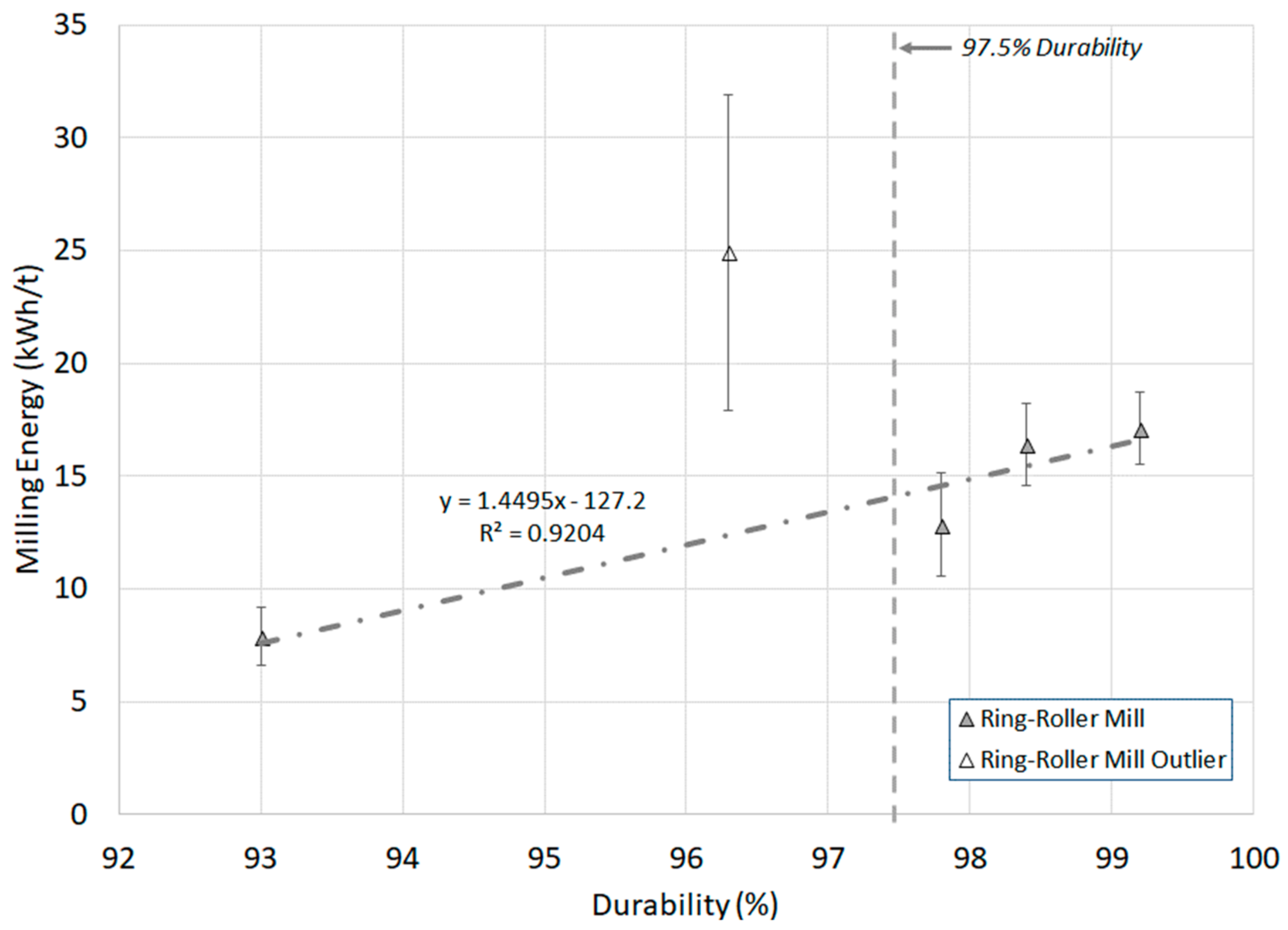
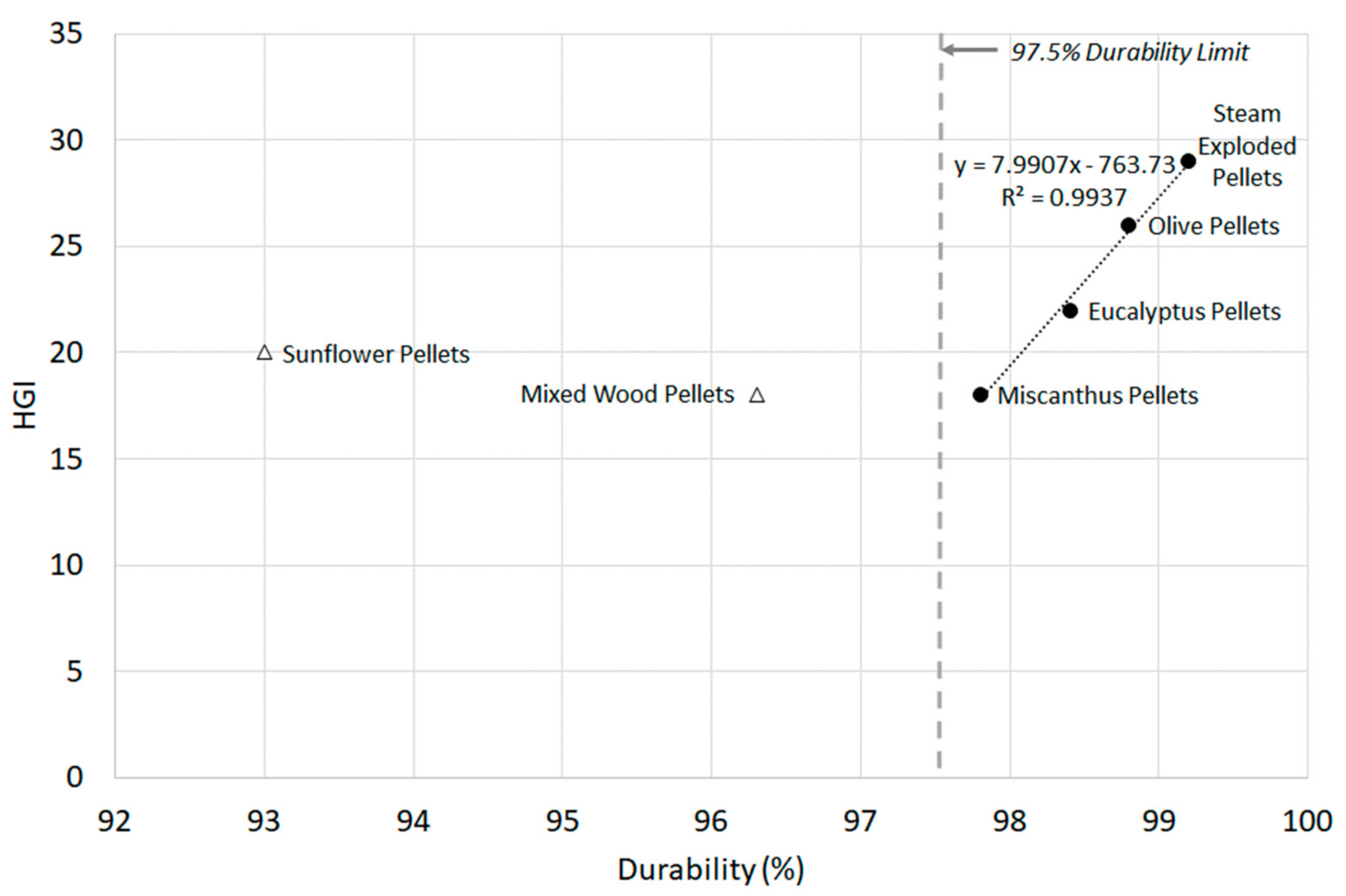
3.1. Pellet Durability
3.2. Quasi-Static Mechanical Strength of Pellet
3.3. Correlations between Quasi-Static Mechanical Strength and Milling Energy
3.4. Dynamic Mechanical Strength of Biomass Pellets
3.5. Correlations between Dynamic Mechanical Strength and Milling Energy
3.6. Comparison of Quasi-Static and Dynamic Mechanical Strength
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tumuluru, J.S.; Wright, C.T.; Hess, J.R.; Kenney, K.L. A review of biomass densification systems to develop uniform feedstock commodities for bioenergy application. Biofuels Bioprod. Biorefin. 2011, 5, 683–707. [Google Scholar] [CrossRef]
- Obernberger, I.; Thek, G. Pellet Production and Logistics. Pellet Handb, 1st ed.; Earthscan Ltd.: London, UK, 2010; pp. 85–129. [Google Scholar]
- Hedlund, F.H.; Astad, J.; Nichols, J. Inherent hazards, poor reporting and limited learning in the solid biomass energy sector: A case study of a wheel loader igniting wood dust, leading to fatal explosion at wood pellet manufacturer. Biomass Bioenergy 2014, 66, 450–459. [Google Scholar] [CrossRef]
- Vassilev, S.V.; Baxter, D.; Andersen, L.K.; Vassileva, C.G. An overview of the chemical composition of biomass. Fuel 2010, 89, 913–933. [Google Scholar] [CrossRef]
- Graham, S.; Ogunfayo, I.; Hall, M.R.; Snape, C.; Quick, W.; Weatherstone, S.; Eastwick, C. Changes in mechanical properties of wood pellets during artificial degradation in a laboratory environment. Fuel Process Technol. 2016, 148, 395–402. [Google Scholar] [CrossRef]
- Graham, S.; Eastwick, C.; Snape, C.; Quick, W. Mechanical degradation of biomass wood pellets during long term stockpile storage. Fuel Process Technol. 2017, 160, 143–151. [Google Scholar] [CrossRef]
- Shang, L.; Nielsen, N.P.K.; Dahl, J.; Stelte, W.; Ahrenfeldt, J.; Holm, J.K.; Thomsen, T.; Henriksen, U.B. Quality effects caused by torrefaction of pellets made from Scots pine. Fuel Process Technol. 2012, 101, 23–28. [Google Scholar] [CrossRef]
- BS EN ISO 17831-1:2015 Solid Biofuels—Determination of Mechanical Durability of Pellets and Briquettes Part 1: Pellets; The British Standards Institution: London, UK, 2015.
- EN ISO 17225-2:2014—Solid Biofuels—Fuel Specifications and Classes Part 2 : Graded Wood Pellets; The British Standards Institution: London, UK, 2014.
- BS EN ISO 17225-6:2014—Solid Biofuels—Fuel Specifications and Classes Part 6 : Graded Non-Woody Pellets; The British Standards Institution: London, UK, 2014.
- Miranda, T.; Montero, I.; Sepúlveda, F.J.; Arranz, J.I.; Rojas, C.V.; Nogales, S. A review of pellets from different sources. Materials 2015, 8, 1413–1427. [Google Scholar] [CrossRef] [PubMed]
- Castellano, J.M.; Gómez, M.; Fernández, M.; Esteban, L.S.; Carrasco, J.E. Study on the effects of raw materials composition and pelletization conditions on the quality and properties of pellets obtained from different woody and non woody biomasses. Fuel 2015, 139, 629–636. [Google Scholar] [CrossRef]
- Gil, M.; Oulego, P.; Casal, M.D.; Pevida, C.; Pis, J.J.; Rubiera, F. Mechanical durability and combustion characteristics of pellets from biomass blends. Bioresour. Technol. 2010, 101, 8859–8867. [Google Scholar] [CrossRef] [PubMed]
- Samuelsson, R.; Thyrel, M.; Sjöström, M.; Lestander, T.A. Effect of biomaterial characteristics on pelletizing properties and biofuel pellet quality. Fuel Process. Technol. 2009, 90, 1129–1134. [Google Scholar] [CrossRef]
- Mani, S.; Tabil, L.G.; Sokhansanj, S. Effects of compressive force, particle size and moisture content on mechanical properties of biomass pellets from grasses. Biomass Bioenergy 2006, 30, 648–654. [Google Scholar] [CrossRef]
- Huang, Y.; Finell, M.; Larsson, S.; Wang, X.; Zhang, J.; Wei, R.; Liu, L. Biofuel pellets made at low moisture content—Influence of water in the binding mechanism of densified biomass. Biomass Bioenergy 2017, 98, 8–14. [Google Scholar] [CrossRef]
- Whittaker, C.; Shield, I. Factors affecting wood, energy grass and straw pellet durability—A review. Renew. Sustain. Energy Rev. 2017, 71, 1–11. [Google Scholar] [CrossRef]
- Holm, J.K.; Henriksen, U.B.; Hustad, J.E.; Sørensen, L.H. Toward an Understanding of Controlling Parameters in Softwood and Hardwood Pellets Production. Energy Fuels 2006, 20, 2686–2694. [Google Scholar] [CrossRef]
- Obernberger, I.; Thek, G. Physical characterisation and chemical composition of densified biomass fuels with regard to their combustion behaviour. Biomass Bioenergy 2004, 27, 653–669. [Google Scholar] [CrossRef]
- Nunes, L.J.R.; Matias, J.C.O.; Catalão, J.P.S. A review on torrefied biomass pellets as a sustainable alternative to coal in power generation. Renew. Sustain. Energy Rev. 2014, 40, 153–160. [Google Scholar] [CrossRef]
- Williams, O.; Lester, E.; Kingman, S.; Giddings, D.; Lormor, S.; Eastwick, C. Benefits of dry comminution of biomass pellets in a knife mill. Biosyst. Eng. 2017, 160, 42–54. [Google Scholar] [CrossRef]
- Mulliken, A.D.; Boyce, M.C. Mechanics of the rate-dependent elastic-plastic deformation of glassy polymers from low to high strain rates. Int. J. Solids Struct. 2006, 43, 1331–1356. [Google Scholar] [CrossRef]
- Kaliyan, N.; Vance Morey, R. Factors affecting strength and durability of densified biomass products. Biomass Bioenergy 2009, 33, 337–359. [Google Scholar] [CrossRef]
- Stelte, W.; Holm, J.K.; Sanadi, A.R.; Barsberg, S.; Ahrenfeldt, J.; Henriksen, U.B. A study of bonding and failure mechanisms in fuel pellets from different biomass resources. Biomass Bioenergy 2011, 35, 910–918. [Google Scholar] [CrossRef]
- Zamorano, M.; Popov, V.; Rodríguez, M.L.; García-Maraver, A. A comparative study of quality properties of pelletized agricultural and forestry lopping residues. Renew. Energy 2011, 36, 3133–3140. [Google Scholar] [CrossRef]
- Carone, M.T.; Pantaleo, A.; Pellerano, A. Influence of process parameters and biomass characteristics on the durability of pellets from the pruning residues of Olea europaea L. Biomass Bioenergy 2011, 35, 402–410. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, K.; Sun, Y. Pelletizing Properties of Wheat Straw Blending with Rice Straw. Energy Fuels 2017, 31, 5126–5134. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H. High-pressure densification of wood residues to form an upgraded fuel. Biomass Bioenergy 2000, 19, 177–186. [Google Scholar] [CrossRef]
- Thomas, M.; van der Poel, A.F.B. Physical quality of pelleted animal feed 1. Criteria for pellet quality. Anim. Feed Sci. Technol. 1996, 61, 89–112. [Google Scholar] [CrossRef]
- Harun, N.Y.; Afzal, M.T. Effect of Particle Size on Mechanical Properties of Pellets Made from Biomass Blends. Procedia Eng. 2016, 148, 93–99. [Google Scholar] [CrossRef]
- Gaitán-Alvarez, J.; Moya, R.; Puente-Urbina, A.; Rodriguez-Zuñiga, A. Physical and Compression Properties of Pellets Manufactured with the Biomass of Five Woody Tropical Species of Costa Rica Torrefied at Different Temperatures and Times. Energies 2017, 10, 1205. [Google Scholar] [CrossRef]
- Pampuro, N.; Bagagiolo, G.; Priarone, P.C.; Cavallo, E. Effects of pelletizing pressure and the addition of woody bulking agents on the physical and mechanical properties of pellets made from composted pig solid fraction. Powder Technol. 2017, 311, 112–119. [Google Scholar] [CrossRef]
- Kirsten, C.; Lenz, V.; Schröder, H.W.; Repke, J.U. Hay pellets–The influence of particle size reduction on their physical-mechanical quality and energy demand during production. Fuel Process. Technol. 2016, 148, 163–174. [Google Scholar] [CrossRef]
- Larsson, S.H.; Samuelsson, R. Prediction of ISO 17831-1:2015 mechanical biofuel pellet durability from single pellet characterization. Fuel Process. Technol. 2017, 163, 8–15. [Google Scholar] [CrossRef]
- Bergman, P.C.A. Combined Torrefaction and Pelletisation. ECN Rep ECN-C--05-073 2005. doi:ECN-C--05-073. Available online: http://www.ecn.nl/docs/library/report/2005/c05073.pdf (accessed on 1 May 2018).
- Chen, W.W.; Song, B. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Springer Science & Business Media: New York, NY, USA, 2010; Volume 1. [Google Scholar]
- Lau, P.C.; Teo, D.C.L.; Mannan, M.A. Characteristics of lightweight aggregate produced from lime-treated sewage sludge and palm oil fuel ash. Constr. Build. Mater. 2017, 152, 558–567. [Google Scholar] [CrossRef]
- Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. B 1949, 62, 676–700. [Google Scholar] [CrossRef]
- Fandrich, R.; Clout, J.M.; Bourgeois, F. The CSIRO Hopkinson Bar Facility for large diameter particle breakage. Miner. Eng. 1998, 11, 861–869. [Google Scholar] [CrossRef]
- Palamidi, E. Hopkinson Bar Testing of Cellular Materials; University of Manchester: Manchester, UK, 2010. [Google Scholar]
- Hiramatsu, Y.; Oka, Y. Determination of the tensile strength of rock by a compression test of an irregular test piece. Int. J. Rock Mech. Min. Sci. 1966, 3, 89–90. [Google Scholar] [CrossRef]
- Rotawave Ltd. The Case for Energy Densification of Biomass & The Advantage of the Rotawave Ties System—Executive Summary 2010:4. Available online: http://www.canadian-biocoal.com/articles/Rotawave TIES system advantage Jun 2010 _final_.pdf (accessed on 1 July 2016).
- BS ISO 3310-2:2013 Test Sieves—Technical Requirements and Testing Part 2 : Test Sieves of Perforated Metal Plate 2013; The British Standards Institution: London, UK, 2013.
- Williams, O.; Newbolt, G.; Eastwick, C.; Kingman, S.; Giddings, D.; Lormor, S.; Lester, E. Influence of mill type on densified biomass comminution. Appl. Energy 2016, 182, 219–231. [Google Scholar] [CrossRef]
- BS EN 16126:2012—Solid Biofuels. Determination of Particle Size Distribution of Disintegrated Pellets; The British Standards Institution: London, UK, 2012.
- BS EN 15149-2:2010: Solid Biofuels. Determination of Particle Size Distribution. Vibrating Screen Method Using Sieve Apertures of 3,15 mm and Below; The British Standards Institution: London, UK, 2010.
- BS EN ISO 17829:2015—Solid Biofuels—Determination of Length and Diameter of Pellets; The British Standards Institution: London, UK, 2015.
- Kretschmann, D.E. Chapter 5—Mechanical Properties of Wood. In Wood Handbook: Wood as an Engineering Material; Forest Products Laboratory: Madison, WI, USA, 2010; pp. 5.1–5.46. Available online: http://charlespetersonflooring.com/wp-content/uploads/2014/04/chapter_05.pdf (accessed on 22 July 2018).
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [PubMed]
- Turner, R. Bottomline in feed processing: Achieving optimum pellet quality. Feed Manag. 1995, 46, 30–33. [Google Scholar]
- Franke, M.; Rey, A. Pelleting quality. World Grain 2006, 24, 78–79. [Google Scholar]
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; Krieger Publishing Company: Malabar, FL, USA, 1993; pp. 280–335. [Google Scholar]
- Pierre, F.; Almeida, G.; Huber, F.; Jacquin, P.; Perré, P. An original impact device for biomass characterisation: Results obtained for spruce and poplar at different moisture contents. Wood Sci. Technol. 2013, 47, 537–555. [Google Scholar] [CrossRef]
- Song, B.; Chen, W. Dynamic Stress Equilibration in Split Hopkinson Pressure Bar Tests on Soft Materials. Exp. Mech. 2004, 44, 300–312. [Google Scholar] [CrossRef]

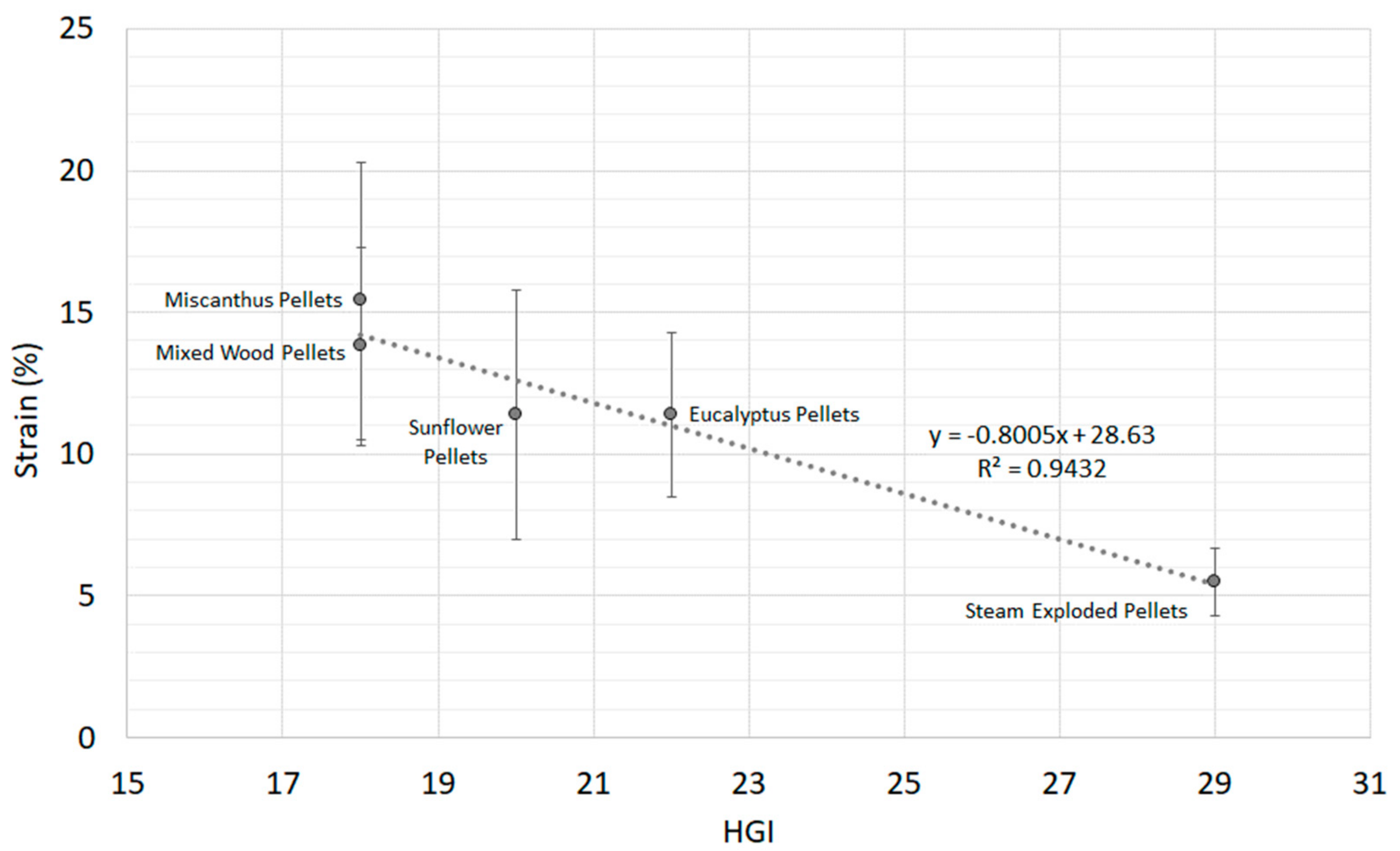
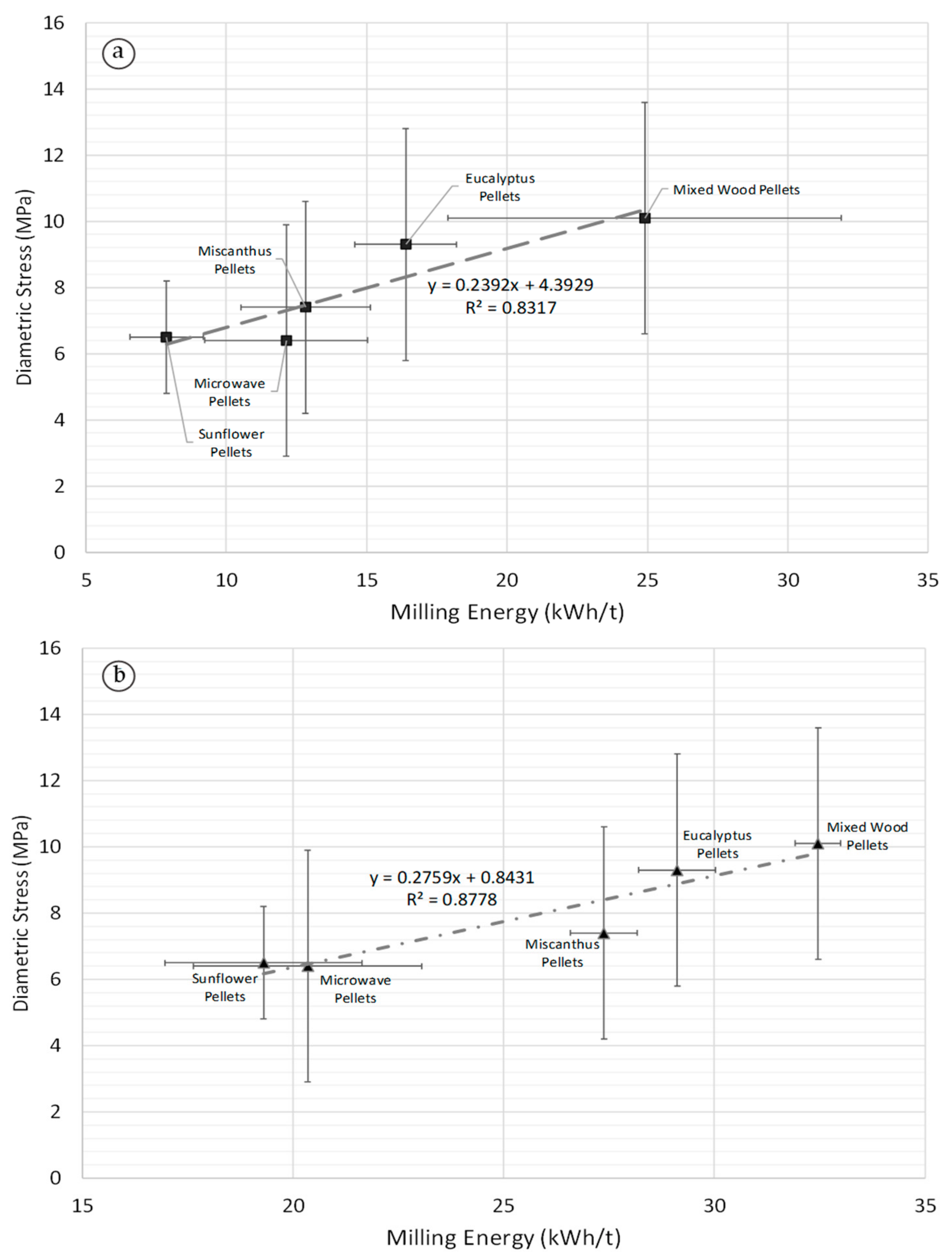


| Sample | Pre-Densified d80 (µm) | Durability (%) | HGI | Ring-Roller Energy (kWh/t) | Ring-Roller d80 (µm) | Knife Mill Energy (kWh/t) | Knife Mill d80 (µm) |
|---|---|---|---|---|---|---|---|
| Eucalyptus Pellets | 1215 | 98 | 22 | 16.4 ± 1.8 | 958 | 29.1 ± 0.9 | 1171 |
| Mixed Wood Pellets | 1373 | 96 | 18 | 24.9 ± 7.0 | 1201 | 32.5 ± 0.5 | 1105 |
| Miscanthus Pellets | 1251 | 98 | 18 | 12.8 ± 2.3 | 1377 | 27.4 ± 0.8 | 1069 |
| Sunflower Pellets | 1744 | 93 | 20 | 7.9 ± 1.3 | 1523 | 19.3 ± 2.3 | 1145 |
| Steam Exploded Pellets | 1196 | 99 | 29 | 17.1 ± 1.6 | 521 | 21.8 ± 1.9 | 1412 |
| Microwave Pellets | – | – | – | 12.1 ± 1.9 | 538 | 20.4 ± 2.7 | 1091 |
| Sample | Proportional Stress Limit σP (MPa) | Elastic Strain εp (%) | Young’s Modulus E (MPa) | Ultimate Strength σS (MPa) | Ductility εs (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| Axial | ||||||||||
| Eucalyptus Pellets | 4.5 | 1.7 | 5.6 | 2.2 | 87 | 39 | 5.5 | 1.8 | 10.3 | 3.0 |
| Mixed Wood Pellets | 3.9 | 0.8 | 3.4 | 0.6 | 115 | 24 | 4.1 | 0.8 | 5.4 | 2.0 |
| Miscanthus Pellets | 6.0 | 1.8 | 5.9 | 1.1 | 106 | 43 | 6.6 | 2.1 | 8.4 | 1.5 |
| Sunflower Pellets | 6.6 | 3.6 | 8.3 | 2.9 | 82 | 38 | 7.5 | 3.5 | 12.9 | 2.5 |
| Microwave Pellets | 3.1 | 0.8 | 2.3 | 0.5 | 140 | 48 | 4.0 | 0.8 | 5.2 | 1.9 |
| Steam Exploded Pellets | 16.7 | 4.4 | 2.1 | 0.6 | 871 | 331 | 19.8 | 3.9 | 3.1 | 0.8 |
| Diametral | ||||||||||
| Eucalyptus Pellets | 7.7 | 3.1 | 5.7 | 1.6 | 133 | 35 | 9.9 | 3.5 | 12.0 | 2.9 |
| Mixed Wood Pellets | 7.9 | 2.9 | 6.5 | 1.5 | 120 | 25 | 9.5 | 3.5 | 13.8 | 3.5 |
| Miscanthus Pellets | 6.6 | 3.0 | 8.5 | 2.5 | 90 | 50 | 7.4 | 3.2 | 15.4 | 4.9 |
| Sunflower Pellets | 5.8 | 1.8 | 6.5 | 1.5 | 96 | 46 | 6.5 | 1.7 | 11.4 | 4.4 |
| Microwave Pellets | 5.5 | 3.1 | 7.3 | 2.7 | 73 | 19 | 6.4 | 3.5 | 11.2 | 4.4 |
| Steam Exploded Pellets | 16.7 | 2.8 | 3.6 | 2.8 | 468 | 71 | 18.4 | 3.2 | 5.5 | 1.2 |
| Flexure | ||||||||||
| Eucalyptus Pellets | 2.2 | 0.9 | 16.6 | 2.9 | 15.4 | 6.8 | 2.4 | 1.0 | 19.2 | 4.4 |
| Mixed Wood Pellets | 2.3 | 1.3 | 16.9 | 3.4 | 15.2 | 7.5 | 2.7 | 1.3 | 26.0 | 10.1 |
| Miscanthus Pellets | 2.6 | 1.0 | 10.5 | 2.9 | 31.6 | 17.8 | 3.0 | 1.1 | 13.4 | 4.0 |
| Sunflower Pellets | 2.5 | 1.4 | 18.0 | 6.4 | 18.0 | 11.7 | 2.9 | 1.8 | 23.9 | 9.4 |
| Microwave Pellets | 3.1 | 1.7 | 7.4 | 2.4 | 40.9 | 15.7 | 3.4 | 1.8 | 8.8 | 3.3 |
| Steam Exploded Pellets | 16.0 | 3.8 | 6.7 | 1.2 | 277.9 | 56.3 | 16.4 | 3.9 | 6.9 | 1.1 |
| Sample | Diametral ss (MPa) | Diametral Ee (MPa) | Axial ss (MPa) | Axial Ee (MPa) | ||
|---|---|---|---|---|---|---|
| Eucalyptus | 1257 | 11 | 129 | 1301 | 5 | 15 |
| Mixed Wood | 1130 | 11 | 124 | 1400 | 7 | 40 |
| Miscanthus | 679 | 12 | 205 | 719 | 7 | 28 |
| Sunflower | 1274 | 12 | 113 | 1283 | 8 | 21 |
| Steam Exploded | 1040 | 19 | 707 | 830 | 15 | 140 |
| Microwave | 1820 | 10 | 57 | 1329 | 3 | 22 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williams, O.; Taylor, S.; Lester, E.; Kingman, S.; Giddings, D.; Eastwick, C. Applicability of Mechanical Tests for Biomass Pellet Characterisation for Bioenergy Applications. Materials 2018, 11, 1329. https://doi.org/10.3390/ma11081329
Williams O, Taylor S, Lester E, Kingman S, Giddings D, Eastwick C. Applicability of Mechanical Tests for Biomass Pellet Characterisation for Bioenergy Applications. Materials. 2018; 11(8):1329. https://doi.org/10.3390/ma11081329
Chicago/Turabian StyleWilliams, Orla, Simon Taylor, Edward Lester, Sam Kingman, Donald Giddings, and Carol Eastwick. 2018. "Applicability of Mechanical Tests for Biomass Pellet Characterisation for Bioenergy Applications" Materials 11, no. 8: 1329. https://doi.org/10.3390/ma11081329
APA StyleWilliams, O., Taylor, S., Lester, E., Kingman, S., Giddings, D., & Eastwick, C. (2018). Applicability of Mechanical Tests for Biomass Pellet Characterisation for Bioenergy Applications. Materials, 11(8), 1329. https://doi.org/10.3390/ma11081329






