Coarse-Grained Simulations Using a Multipolar Force Field Model
Abstract
1. Introduction
2. Materials and Methods
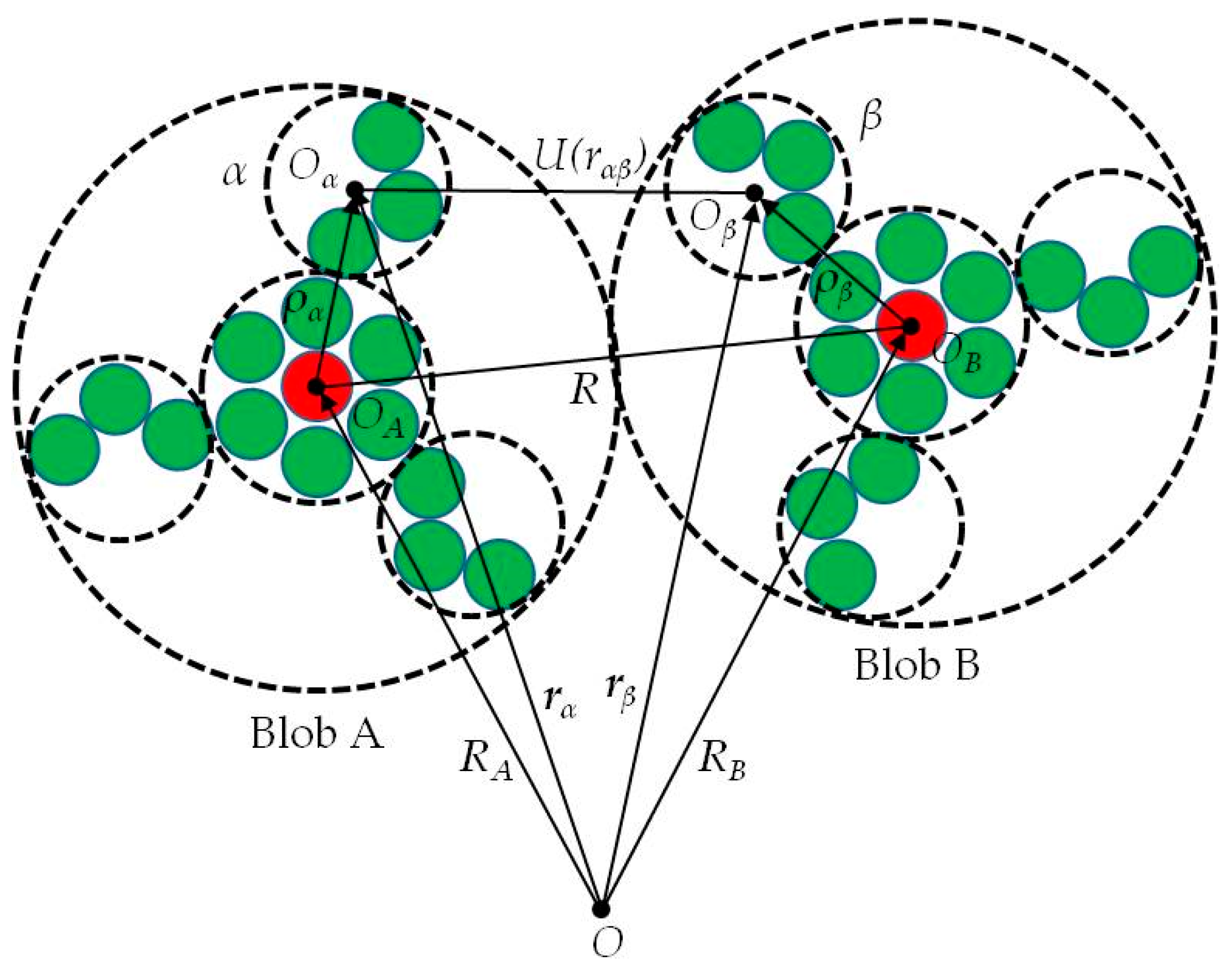
2.1. Interblob Interaction Energy Model
2.2. Interaction Moment Tensors
3. Results and Discussion
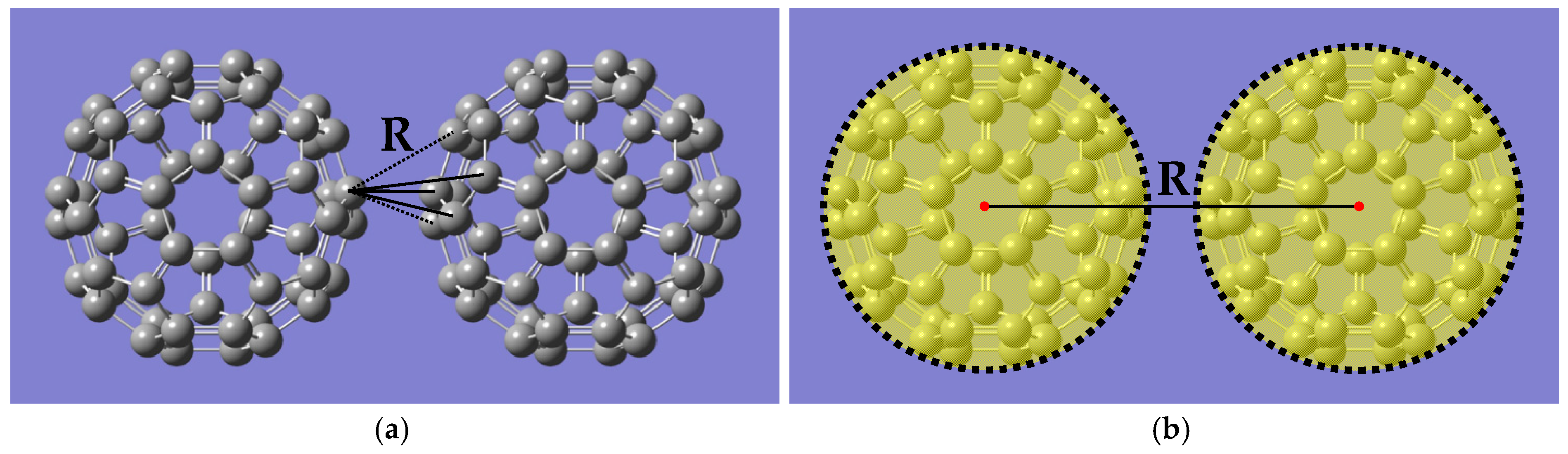
3.1. Structure of C60
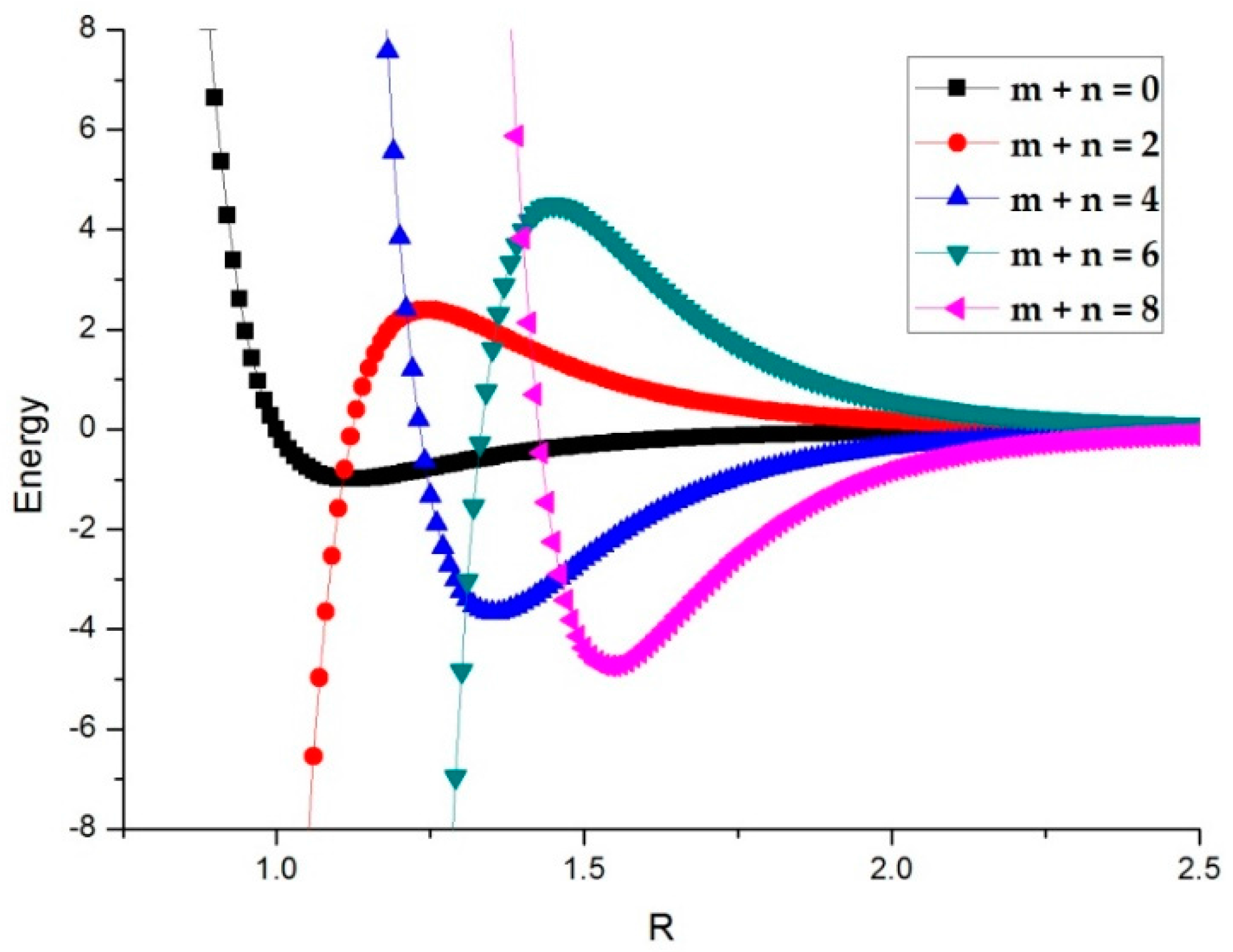
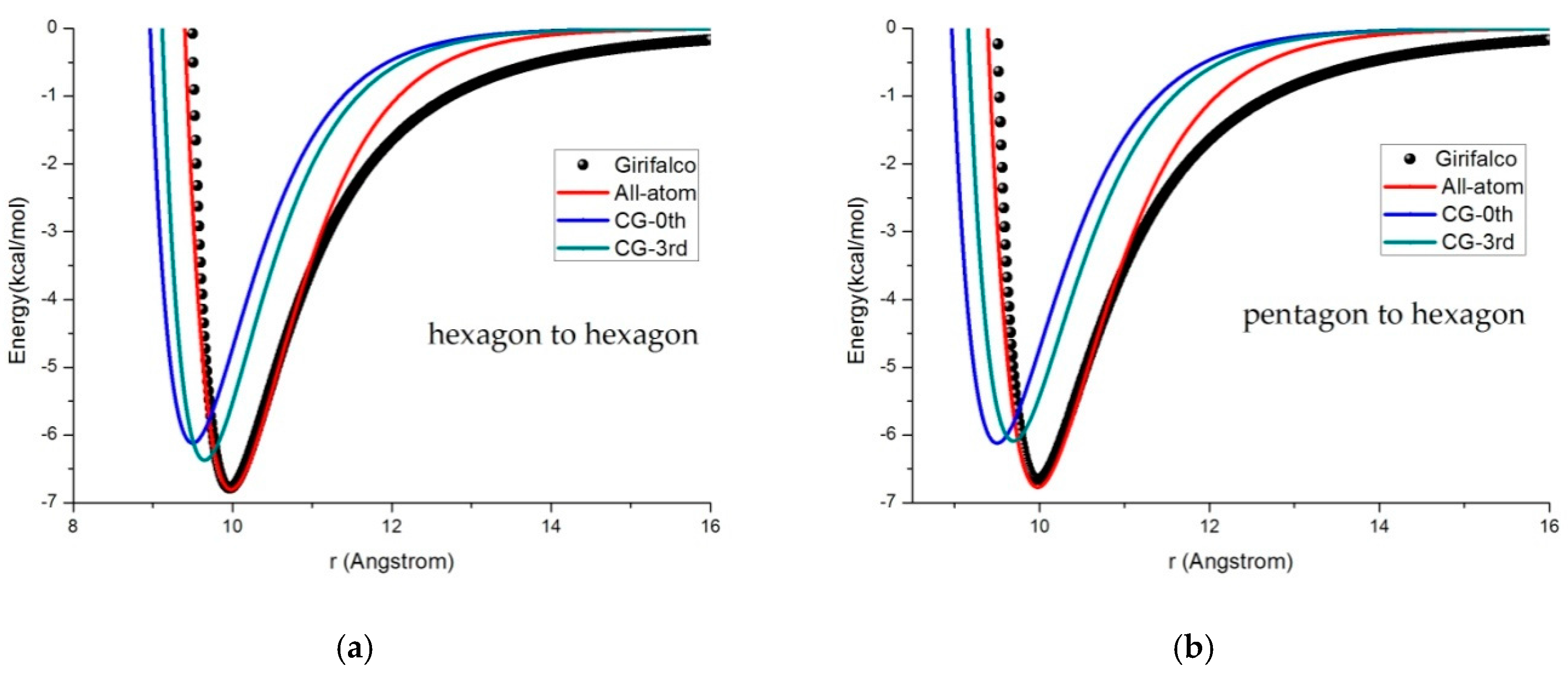
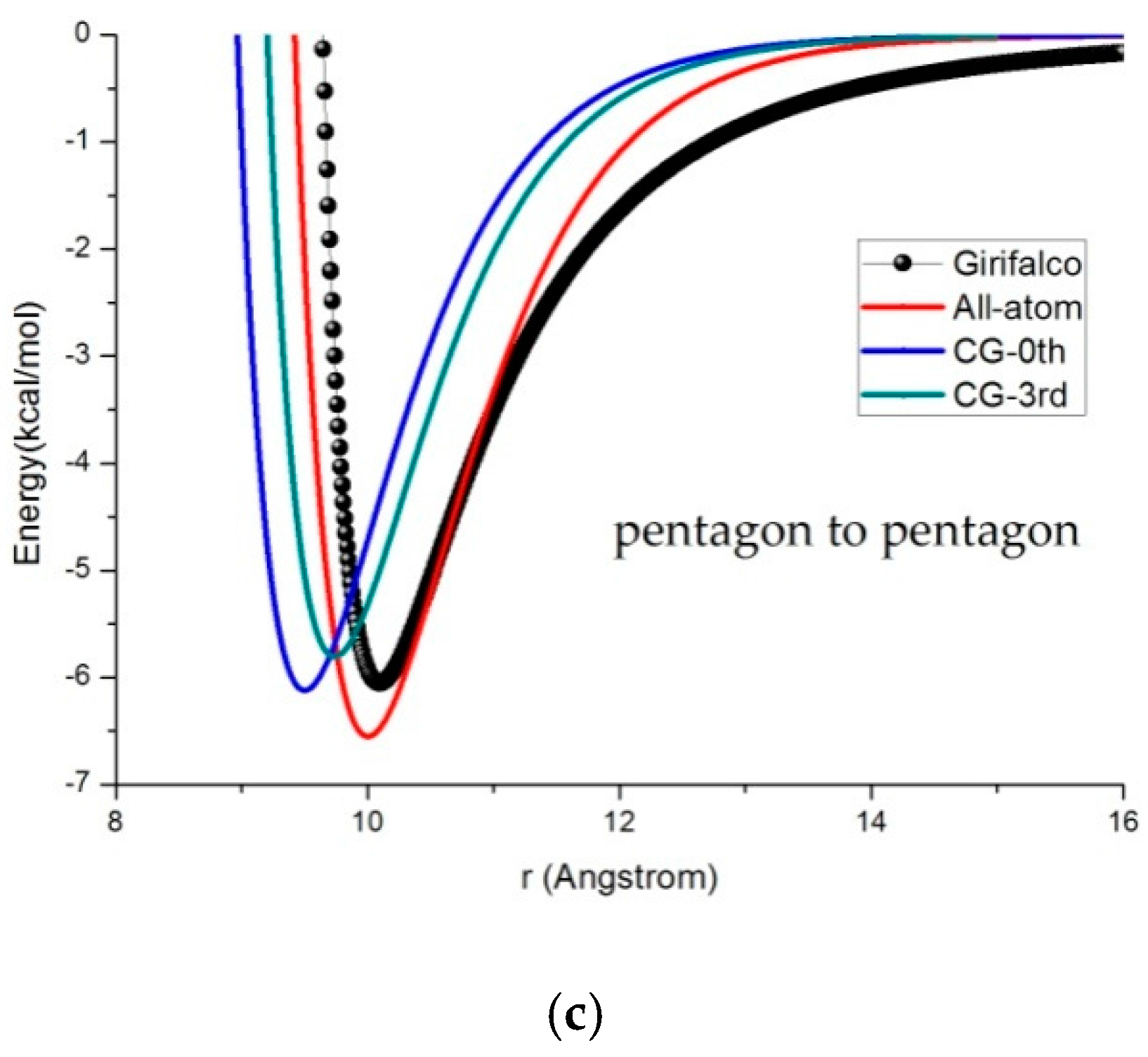
3.2. Potential Curve Fitting
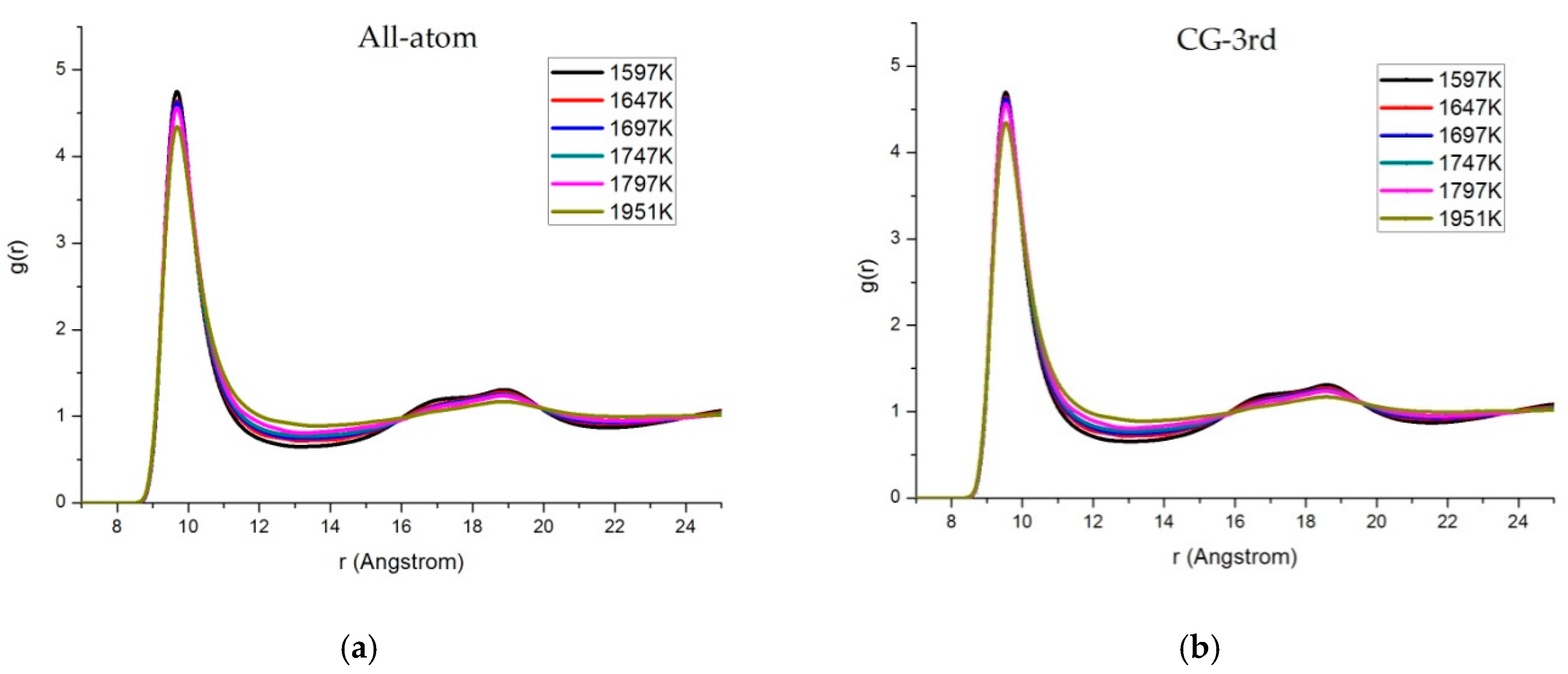
3.3. Radial Distribution Function
3.4. Velocity Autocorrelation Function
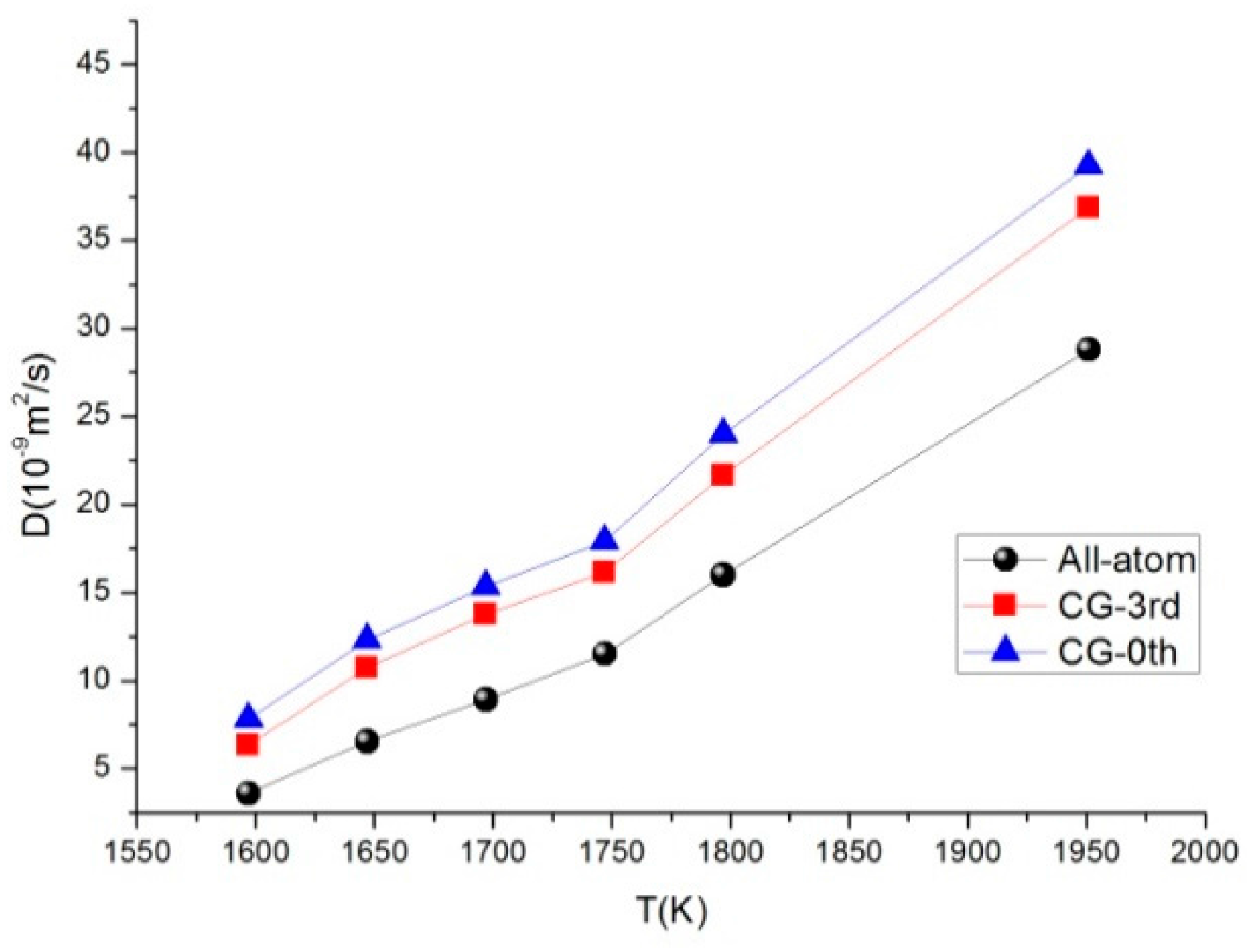
3.5. Self-Diffusion Coefficient
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ho, Y.C.; Wang, Y.S.; Chao, S.D. Molecular dynamics simulations of fluid cyclopropane with MP2/CBS-fitted intermolecular interaction potentials. J. Chem. Phys. 2017, 147, 064507. [Google Scholar] [CrossRef] [PubMed]
- Vranes, M.; Borisev, I.; Tot, S.; Armakovic, S.; Jovic, D.; Gadzuric, S.; Djordjevic, A. Self-assembling, reactivity and molecular dynamics of fullerenol nanoparticles. Phys. Chem. Chem. Phys. 2017, 19, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Rai, B. Molecular dynamics simulation study of translocation of fullerene C60 through skin bilayer: Effect of concentration on barrier properties. Nanoscale 2017, 9, 4114–4127. [Google Scholar] [CrossRef] [PubMed]
- Root, S.E.; Savagatrup, S.; Pais, C.J.; Arya, G.; Lipomi, D.J. Predicting the mechanical properties of organic semiconductors using coarse-grained molecular dynamics simulations. Macromolecules 2016, 49, 2886–2894. [Google Scholar] [CrossRef]
- Edmunds, D.M.; Tangney, P.; Vvedensky, D.; Foulkes, W.M.C. Free-energy coarse-grained potential for C60. J. Chem. Phys. 2015, 143, 164509. [Google Scholar] [CrossRef] [PubMed]
- Monticelli, L. On atomistic and coarse-grained models for C60 fullerene. J. Chem. Theory Comput. 2012, 8, 1370–1378. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, H.; Winkler, R.G. Universal conformational properties of polymers in ionic nanogels. Sci. Rep. 2016, 6, 19836. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.H.; Zhao, X.W.; Liu, Q.H. Interactions between C-60 and vesicles: A coarse-grained molecular dynamics simulation. RSC Adv. 2016, 6, 90388–90396. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-grained protein models and their applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
- Sinitskiy, A.V.; Voth, G.A. Coarse-graining of proteins based on elastic network models. Chem. Phys. 2013, 422, 165–174. [Google Scholar] [CrossRef]
- Liwo, A.; Oldziej, S.; Czaplewski, C.; Kleinerman, D.S.; Blood, P.; Scheraga, H.A. Implementation of molecular dynamics and its extensions with the coarse-grained UNRES force field on massively parallel systems: Toward millisecond-scale simulations of protein structure, dynamics, and thermodynamics. J. Chem. Theory Comput. 2010, 6, 890–909. [Google Scholar] [CrossRef] [PubMed]
- Xiong, L.; Tucker, G.; McDowell, D.L.; Chen, Y. Coarse-grained atomistic simulation of dislocations. J. Mech. Phys. Solids 2011, 59, 160–177. [Google Scholar] [CrossRef]
- Izvekov, S.; Voth, G.A. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B 2005, 109, 2469–2473. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G.; Chu, J.W.; Ayton, G.S.; Krishna, V.; Izvekov, S.; Voth, G.A.; Das, A.; Andersen, H.C. The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. J. Chem. Phys. 2008, 128, 244144. [Google Scholar] [CrossRef] [PubMed]
- Larini, L.; Lu, L.; Voth, G.A. The multiscale coarse-graining method. VI. Implementation of three-body coarse-grained potentials. J. Chem. Phys. 2010, 132, 164107. [Google Scholar] [CrossRef] [PubMed]
- Thorpe, I.F.; Goldenberg, D.P.; Voth, G.A. Exploration of transferability in multiscale coarse-grained peptide models. J. Phys. Chem. B 2011, 115, 11911–11926. [Google Scholar] [CrossRef] [PubMed]
- Yin, C.C.; Li, A.H.T.; Chao, S.D. Liquid chloroform structure from computer simulation with a full ab initio intermolecular interaction potential. J. Chem. Phys. 2013, 139, 194501. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.B.; Li, A.H.T.; Chao, S.D. Liquid properties of dimethyl ether from molecular dynamics simulations using ab initio force fields. J. Comput. Chem. 2012, 33, 998–1003. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.H.; Li, A.H.T.; Chao, S.D. Computer simulation of trifluoromethane properties with ab initio force fields. J. Comput. Chem. 2011, 32, 2414–2421. [Google Scholar] [CrossRef] [PubMed]
- Chao, S.D.; Kress, J.D.; Redondo, A. Coarse-grained rigid blob model for soft matter simulations. J. Chem. Phys. 2005, 122, 234912. [Google Scholar] [CrossRef] [PubMed]
- Chao, S.D.; Kress, J.D.; Redondo, A. An alternative multipolar expansion for intermolecular potential functions. J. Chem. Phys. 2004, 120, 5558–5565. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision A.1; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- David, W.I.F.; Ibberson, R.M.; Matthewman, J.C.; Prassides, K.; Dennis, T.J.S.; Hare, J.P.; Kroto, H.W.; Taylor, R.; Walton, D.R.M. Crystal structure and bonding of ordered C60. Nature 1991, 353, 147–149. [Google Scholar] [CrossRef]
- Girifalco, L.A. Interaction potential for carbon (C60) molecules. J. Phys. Chem. 1991, 95, 5370–5371. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulations, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Rui, P.S.F.; Fernando, M.S.S.F.; Filomena, F.M.F. Monte Carlo simulation of the phase diagram of C60 using two interaction potentials. Enthalpies of sublimation. J. Phys. Chem. B 2002, 106, 10227–10232. [Google Scholar]
- Alder, B.J.; Wainwright, T.E. Decay of the velocity autocorrelation function. Phys. Rev. A 1970, 1, 18–21. [Google Scholar] [CrossRef]
- Green, M.S. Markoff random processes and the statistical mechanics of time-dependent phenomena. J. Chem. Phys. 1952, 20, 1281–1295. [Google Scholar] [CrossRef]
- Green, M.S. Markoff random processes and the statistical mechanics of time-dependent phenomena. II. Irreversible processes in fluids. J. Chem. Phys. 1954, 22, 398–413. [Google Scholar] [CrossRef]
- Cioslowski, J.; Rao, N.; Moncrieff, D. Standard enthalpies of formation of fullerenes and their dependence on structural motifs. J. Am. Chem. Soc. 2000, 122, 8265–8270. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Osawa, E. Information entropy of fullerene. J. Chem. Inf. Model. 2015, 55, 1576–1584. [Google Scholar] [CrossRef] [PubMed]



| Rank-m Tensors | Independent Components | Memory Location |
|---|---|---|
| , , | , , | |
| , , , , , | , , , , , | |
| , , , , , , , , , | , , , , , , , , , | |
| , , , , , , , , , , , , , , | , , , , , , , , , , , , , , |
| Method | C–C (Å) | C=C (Å) | r (Å) |
|---|---|---|---|
| Experiment [23] | 1.455 | 1.391 | 3.545 |
| RHF/STO-3G | 1.453 | 1.367 | 3.524 |
| HF/6-31G(d, p) | 1.449 | 1.373 | 3.523 |
| B3LYP/6-31G(d, p) | 1.453 | 1.395 | 3.550 |
| ωB97XD/6-31G(d)—monomer | 1.450 | 1.386 | 3.535 |
| ωB97XD/6-31G(d)—dimer | 1.452 | 1.388 | 3.538 |
| Rank-m Number | Memory Location | Fitting Parameters |
|---|---|---|
| 0 | 60 | |
| 1 | , , | 0.00000, 0.00002, 0.00002 |
| 2 | , , , | 251.57483, 0.00871, 0.02755, |
| , , | 251.57513, −0.03941, 251.6387 | |
| 3 | , , , | 0.00190, 0.00288, −0.00735, |
| , ,, | −0.00382, −0.00095, 0.00172, | |
| , , , | 0.01110, −0.00650, −0.01328, 0.01462 | |
| 4 | , , , | 1898.65174, −0.08173, 0.23940, |
| , , , | 632.88311, −0.12178, 633.07361, | |
| , , , | −0.07104, 0.07556, 0.02058, | |
| , , , | 0.23205, 1898.67454, −0.34235, | |
| , , | 633.05680, −0.31836, 1899.74600 |
| T (K) | ρ (g/cm3) | D (10−9 m2/s) | ||
|---|---|---|---|---|
| All-Atom Model | CG-3rd Model | CG-0th Model | ||
| 1597 | 1.2195 | 3.598 | 6.330 | 7.818 |
| 1647 | 1.0163 | 6.544 | 10.746 | 12.327 |
| 1697 | 0.9326 | 8.915 | 13.760 | 15.360 |
| 1747 | 0.8728 | 11.514 | 16.163 | 17.914 |
| 1797 | 0.7353 | 16.001 | 21.672 | 23.983 |
| 1951 | 0.5058 | 28.797 | 36.882 | 39.239 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, S.-F.; Chao, S.D. Coarse-Grained Simulations Using a Multipolar Force Field Model. Materials 2018, 11, 1328. https://doi.org/10.3390/ma11081328
Chiu S-F, Chao SD. Coarse-Grained Simulations Using a Multipolar Force Field Model. Materials. 2018; 11(8):1328. https://doi.org/10.3390/ma11081328
Chicago/Turabian StyleChiu, Shuo-Feng, and Sheng D. Chao. 2018. "Coarse-Grained Simulations Using a Multipolar Force Field Model" Materials 11, no. 8: 1328. https://doi.org/10.3390/ma11081328
APA StyleChiu, S.-F., & Chao, S. D. (2018). Coarse-Grained Simulations Using a Multipolar Force Field Model. Materials, 11(8), 1328. https://doi.org/10.3390/ma11081328





