A Consistent Procedure Using Response Surface Methodology to Identify Stiffness Properties of Connections in Machine Tools
Abstract
:1. Introduction
2. Dynamic Characteristics of the Machining Center
2.1. Finite Element Model
2.2. Experimental Modal Analysis
2.3. Comparison between FE and Experimental Modal Data
3. Methods: Design of Experiments, Response Surface Methodology, and Desirability Functions
3.1. Two-Level Designs for Parameter Screening
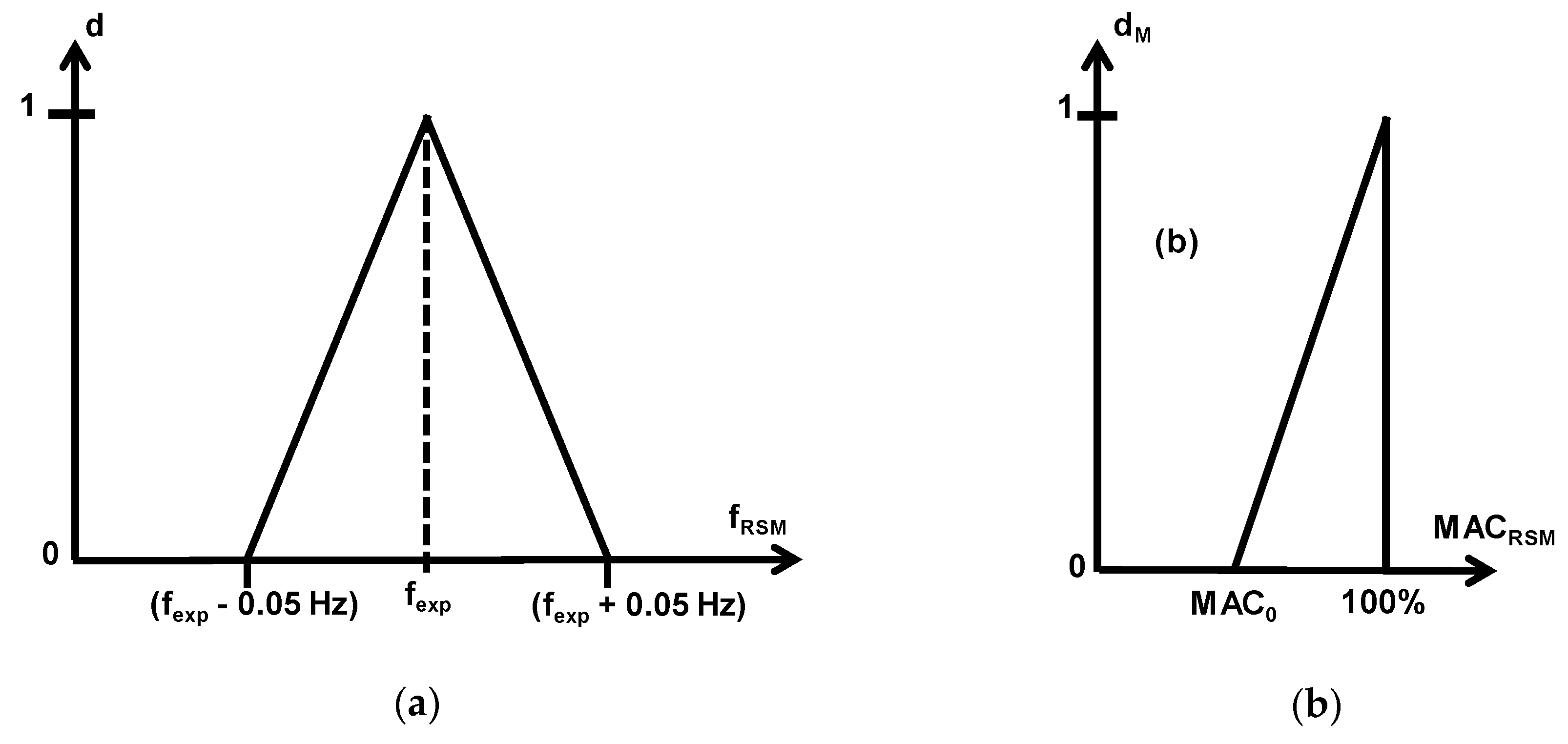
3.2. Response Surface Methodology to Develop an Optimal Mathematical Model
3.3. Identification of Updated Values of the Design Variables using the Optimum RS Model
4. Case Study
4.1. Initial Selection of Candidate Design Variables
- Stiffness values of the connection elements between main components of the machine tool (Figure 4);
- Stiffness values assigned to the elements that attach the machine tool to the foundation (Figure 5); and
- Stiffness value along X direction of the connection element, between the primary and secondary sections of the linear motor.
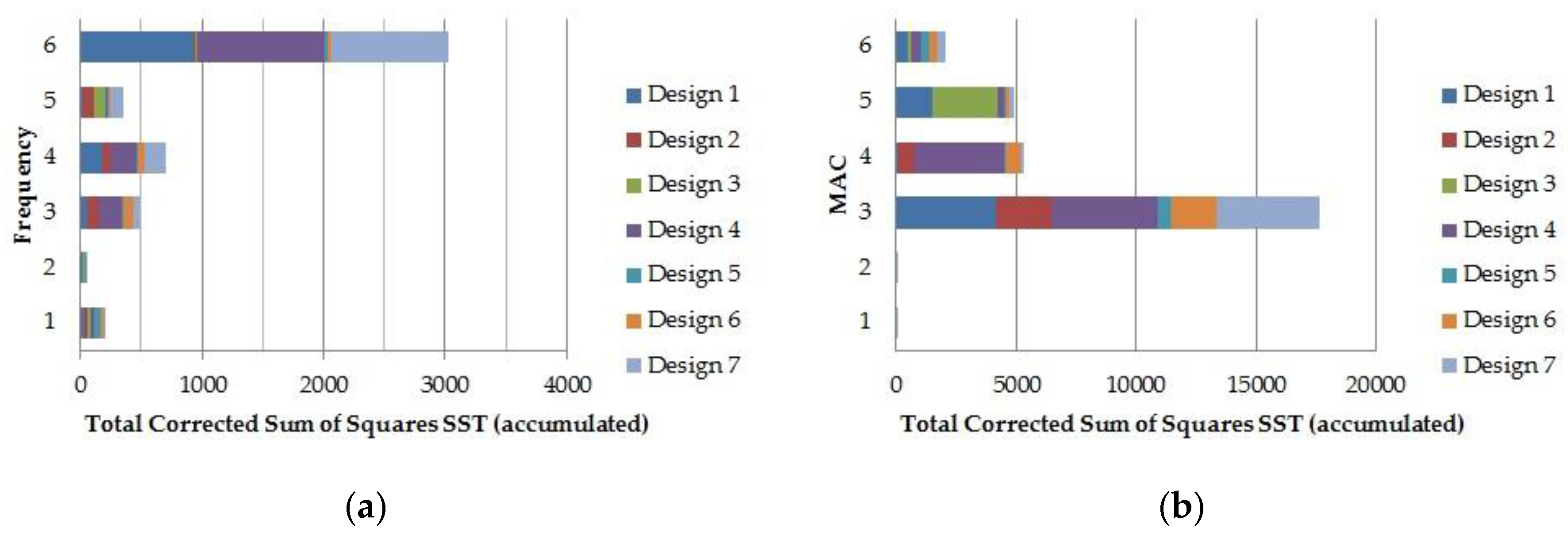
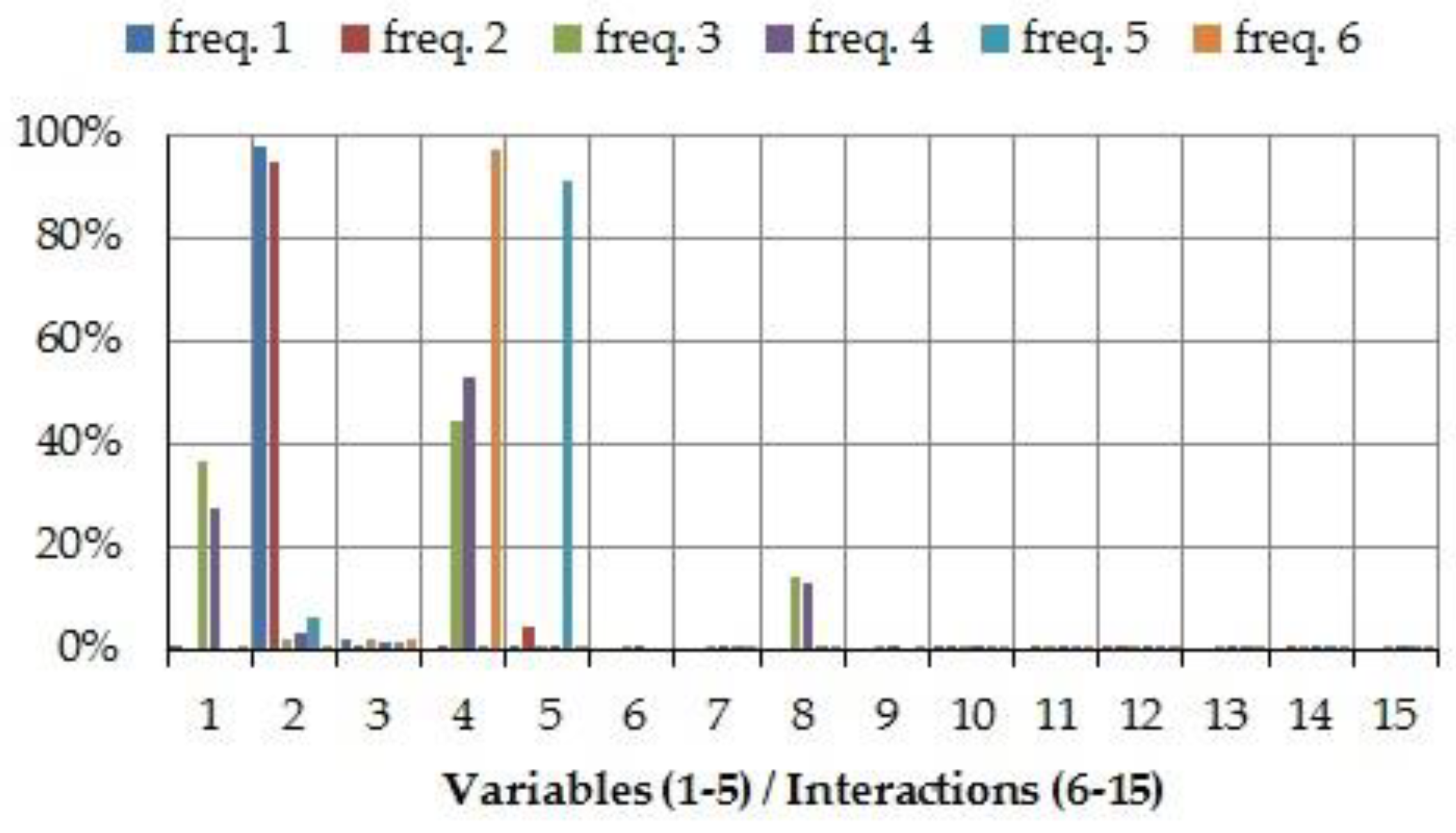
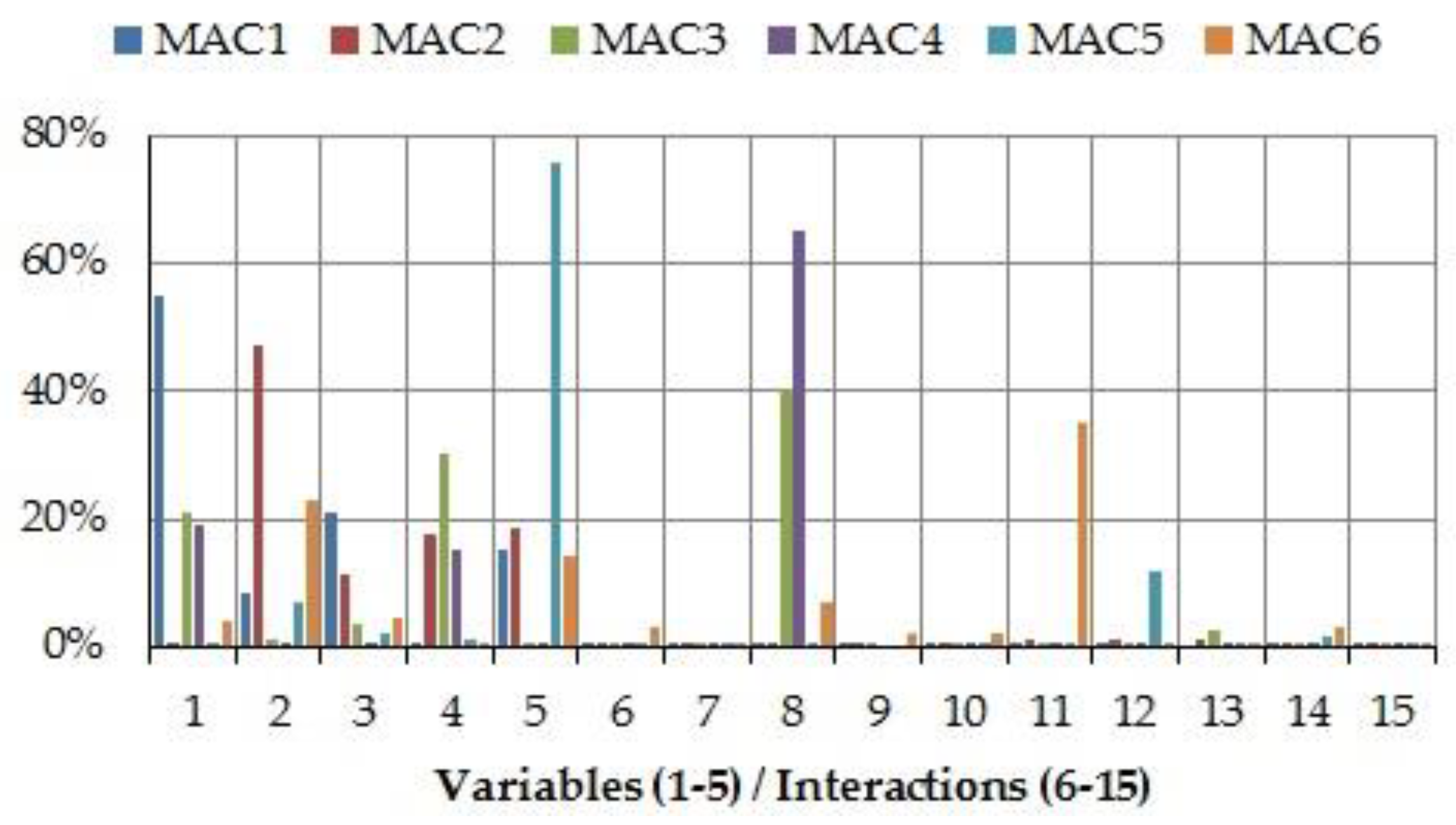
- The fractional factorial experiments have allowed for finding out the design variables and interactions that affect the responses. Therefore, the screening experiment has satisfactorily achieved the initial goal.
- Two design variables do not influence the natural frequencies, namely the stiffness kX11 and horizontal stiffness kX21 of the connections to the foundation.
- Three design variables are only significant for one natural frequency (fFEA5), namely the transverse stiffness kZ63 between the bed frame and foundations, and two stiffnesses between the modules of the machine tool, kZ13 and kY9.
- MAC5 and MAC6 are affected by the largest number of interactions. Furthermore, some of them include design variables that do not influence them individually, for example, interaction kX11-kX21. This situation only appears in these two responses. In addition, the total number of design variables, considered both individually and in interactions, which affect each of these responses is nine (i.e., almost all). Nevertheless, along the complete set of fractional designs, the MAC5 values were always larger than 80% and the MAC6 values ranged from 68% to 73%. Thus, it has been decided not to carry on with the study of these responses, because the number of involved variables would lead to a costly analysis in the next step, while the benefits would be quite poor.
- The natural frequencies fFEA3 and fFEA4 and the corresponding MAC values depend on the same group of design variables, kX210, kY3, kZ4, and kX8. In addition, the natural frequency fFEA6 is dependent on three of these variables, kY3, kZ4, and kX8. Therefore, in the next step of the improvement process, these three natural frequencies will be analyzed together, so as to reduce the number of experiments necessary to define their meta-models. In addition, it is interesting to note that the mode shapes associated to these frequencies take place in plane XZ.
- The natural frequency fFEA5 is affected by four variables that do not have any influence on the frequencies fFEA3, fFEA4, and fFEA6, and, vice versa, the variables that affect these three frequencies do not provide any variability to the natural frequency fFEA5. Moreover, some of the design variables representing stiffness in the X direction, kX8 and kX210, do not affect the 1st and 5th mode shapes, whose principal movement is in plane YZ. Thus, it is concluded that the design variables are working collectively.
4.2. Development of Explicit Relationships between Design Variables and Responses
- Central composite (CC) design 1: including fFEA1 and design variables kY22, kY3, and kZ4. Although it would seem unnecessary to search for this relationship, because fFEA1 is already matched, as it is influenced by the design variables that also influence other frequencies, any change on them would affect this frequency too. So, it is indispensable to know this relationship.
- CC design 2: with the following responses fFEA3, fFEA4, fFEA6, MAC3, and MAC4, and design variables kX210, kY3, kZ4, and kX8.
- CC design 3: including fFEA5 and design variables kY22, kZ63, kZ13, and kY9.
+ 0.0065 · XY3 · XZ4 + 0.0177 · XY22 · XZ4 − 0.4593 · (XY3)2 − 0.5171 · (XY22)2 − 0.0559 · (XZ4)2
+ 0.0177 · XY22 · XZ4 − 0.4593 · (XY3)2 − 0.5171 · (XY22)2 − 0.0559 · (XZ4)2
+ 0.0618 · XY9 · XY22 + 0.1096 · XY9 · XZ63 + 0.0785 · XY22 · XZ63 + 0.0725 · XZ13 · XZ63 −
− 0.2318 · (XY9)2 − 0.1674 · (XY22)2 − 0.8645 · (XZ13)2 − 0.2321 · (XZ63)2
+ 1.3206 · XX8 · XX210 + 0.2019 · XX8 · XY3 − 0.1702 · XX210 · XY3 + 0.1562 · XX210 · XZ4 −
− 2.1869 · (XX8)2 − 0.6804 · (XX210)2
− 1.3133 · XX8 · XX210 + 0.3977 · XX8 · XZ4 −0.1550 · XX210 · XZ4 − 1.2361 · (XX8)2
− 0.2232 · XX8 · XZ4 + 0.1697 · XY3 · XZ4 − 3.2813 · (XX8)2 − 0.2193 · (XY3)2 − 0.3628 · (XZ4)2
+ 10.4715 · XX8 · XX210 + 1.1365 · XX8 · XY3 − 2.6332 · XX8 · XZ4 + 3.0198 · (XZ4)2
− 9.2492 · (XX8)2
4.3. Determination of Updated Values of Design Variables
- The natural frequency fFEA3 approximately matches its experimental pair and, at the same time, the corresponding MAC value is higher than the initial one, only when the design variable kX8 is at its lower boundary. If kX8 takes the central or upper values, it is not possible to adequately accomplish the pairing.
- Also, the natural frequency, fFEA6, needs lower kX8 values to match its experimental pair.
- However, on the other side, at lower kX8 values, it is not viable to adjust the natural frequency fFEA4 while maintaining accurate values of MAC. Intermediate or upper values of kX8 are necessary to improve fFEA4, although they give rise to MAC values slightly poorer than initially.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lopez de Lacalle, L.N.; Lamikiz, A. Machine Tools for Removal Processes: A General View. In Machine Tools for High Performance Machining; Lopez de Lacalle, L.N., Lamikiz, A., Eds.; Springer: London, UK, 2009; pp. 1–45. ISBN 978-1848003798. [Google Scholar]
- Altintas, Y.; Brecher, C.; Weck, M.; Witt, S. Virtual machine tool. CIRP. Ann. Manuf. Technol. 2005, 54, 115–138. [Google Scholar] [CrossRef]
- Quintana, G.; Ciurana, J. Chatter in machining process: A review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Friswell, M.I.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995; ISBN 978-0792334316. [Google Scholar]
- Janter, T. Construction Oriented Updating of Dynamic Finite Element Models Using Experimental Modal Data. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 1989. [Google Scholar]
- Bais, R.S.; Gupta, A.K.; Nakra, B.C.; Kundra, T.K. Studies in dynamic design of drilling machine using updated finite element models. Mech. Mach. Theory 2004, 39, 1307–1320. [Google Scholar] [CrossRef]
- Houming, Z.; Chengyang, W.; Zhenyu, Z. Dynamic characteristics of conjunction of lengthened shrink-fit holder and cutting tool in high-speed milling. J. Mater. Process. Technol. 2008, 207, 154–162. [Google Scholar] [CrossRef]
- Garitaonandia, I.; Fernandes, M.H.; Albizuri, J. Dynamic model of a centerless grinding machine based on an updated FE model. Int. J. Mach. Tools Manuf. 2008, 48, 832–840. [Google Scholar] [CrossRef]
- Garitaonandia, I.; Fernandes, M.H.; Hernandez-Vazquez, J.M.; Ealo, J.A. Prediction of dynamic behavior for different configurations in a drilling-milling machine based on substructuring analysis. J. Sound. Vib. 2016, 365, 70–88. [Google Scholar] [CrossRef]
- Brecher, C.; Esser, M.; Witt, S. Interaction of manufacturing process and machine tool. CIRP Ann. Manuf. Technol. 2009, 58, 588–607. [Google Scholar] [CrossRef]
- Zhou, Y.D.; Chu, L.; Bi, D.S. Structural optimization for hydraulic press frame. China Metal. Equip. Manuf. Technol. 2008, 2, 90–92. [Google Scholar]
- Li, Y.B.; Wu, D.H.; Huang, M.H.; Lu, X.J. Design of Parallel Bearing Structure for 800 MN Forging Press with Consideration of Manufacturing Errors. Appl. Mech. Mater. 2011, 52–54, 2157–2163. [Google Scholar] [CrossRef]
- Markowski, T.; Mucha, J.; Witkowski, W. FEM analysis of clinching joint machine’s C-frame rigidity. Eksploat. Niezawodn. Maint. Reliab. 2013, 15, 51–57. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 6th ed.; John Wiley & Sons: New York, NY, USA, 2005; ISBN 978-0471661597. [Google Scholar]
- Lamikiz, A.; Lopez de Lacalle, L.N.; Sanchez, J.A.; Bravo, U. Calculation of specific cutting coefficients and geometrical aspects in sculptured surface machining. Mach. Sci. Technol. 2005, 9, 411–436. [Google Scholar] [CrossRef]
- Calleja, A.; Bo, P.; Gonzalez, H.; Barton, M.; Lopez de Lacalle, L.N. Highly accurate 5-axis flank CNC machining with conical tools. Int. J. Adv. Manuf. Technol. 2018, 97, 1605–1615. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 4th ed.; John Wiley & Sons: New York, NY, USA, 2016; ISBN 978-1118916018. [Google Scholar]
- Bonte, M.H.A.; van den Boogaard, A.I.; Huétink, J. An optimization strategy for industrial metal forming processes. Struct. Multidiscip. Optim. 2008, 35, 571–586. [Google Scholar] [CrossRef]
- Lü, H.; Yu, D. Brake squeal reduction of vehicle disc brake system with interval parameters by uncertain optimization. J. Sound. Vib. 2014, 333, 7313–7325. [Google Scholar] [CrossRef]
- Wang, R.; Lim, P.; Heng, L.; Mun, S.D. Magnetic Abrasive Machining of Difficult-to-Cut Materials for Ultra-High-Speed Machining of AISI 304 Bars. Materials 2017, 10, 1029:1–1029:11. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, L. Finite element model updating based on Response Surface Methodology. In Proceedings of the 22nd International Modal Analysis Conference, Dearborn, MI, USA, 26–29 January 2004; Society for Experimental Mechanics: Bethel, CT, USA, 2004. Paper No. 93. [Google Scholar]
- Rutherford, A.C.; Inman, D.J.; Park, G.; Hemez, F.M. Use of response surface metamodels for identification of stiffness and damping coefficients in a simple dynamic system. Shock. Vib. 2005, 12, 317–331. [Google Scholar] [CrossRef]
- Ren, W.-X..; Chen, H.-B. Finite element model updating in structural dynamics by using the response surface method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
- Fang, S.-E.; Perera, R. Damage identification by response surface based model updating using D-optimal design. Mech. Syst. Signal Process. 2011, 25, 717–733. [Google Scholar] [CrossRef]
- Sun, W.-Q.; Cheng, W. Finite element model updating of honeycomb sandwich plates using a response surface model and global optimization technique. Struct. Multidiscip. Optim. 2017, 55, 121–139. [Google Scholar] [CrossRef]
- Gallina, A.; Pichler, L.; Uhl, T. Enhanced meta-modelling technique for analysis of mode crossing, mode veering and mode coalescence in structural dynamics. Mech. Syst. Signal Process. 2011, 25, 2297–2312. [Google Scholar] [CrossRef]
- Schaeffler Group. Available online: http://medias.schaeffler.de/medias/en!hp.ec.br.pr/RUE..-E-HL*RUE55-E-HL (accessed on 15 June 2009).
- Van Brussel, H.; Sas, P.; Németh, I.; de Fonseca, P.; van den Braembussche, P. Towards a mechatronic compiler. IEEE/ASME. Trans. Mechatron. 2001, 6, 90–105. [Google Scholar] [CrossRef]
- Law, M.; Altintas, Y.; Phani, A.S. Rapid evaluation and optimization of machine tools with position-dependent stability. Int. J. Mach. Tools Manuf. 2013, 68, 81–90. [Google Scholar] [CrossRef]
- Muñoa, J. Desarrollo de un modelo general para la predicción de la estabilidad del proceso de fresado. Aplicación al fresado periférico, al planeado convencional y a la caracterización de la estabilidad dinámica de fresadoras universales. Ph.D. Thesis, Mondragon University, Arrasate/Mondragón, Spain, 2007. (In Spanish). [Google Scholar]
- Allemang, R.J. Investigation of Some Multiple Input/Output Frequency Response Experimental Modal Analysis Techniques. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 1980. [Google Scholar]
- Link, M.; Hanke, G. Model Quality Assesment and Model Updating. In Modal Analysis and Testing; Maia, N.M.M., Silva, J.M.M., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 305–324. ISBN 978-0-7923-5893-7. [Google Scholar]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Ealo, J.A.; Garitaonandia, I.; Fernandes, M.H.; Hernandez-Vazquez, J.M.; Muñoa, J. A practical study of joints in three-dimensional Inverse Receptance Coupling Substructure Analysis method in a horizontal milling machine. Int. J. Mach. Tools Manuf. 2018, 128, 41–51. [Google Scholar] [CrossRef]
- Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Wang, L.; Li, T.; You, Z. Study on the stiffness of a 5-dof hybrid machine tool with actuation redundancy. Mech. Mach. Theory 2009, 44, 289–305. [Google Scholar] [CrossRef]
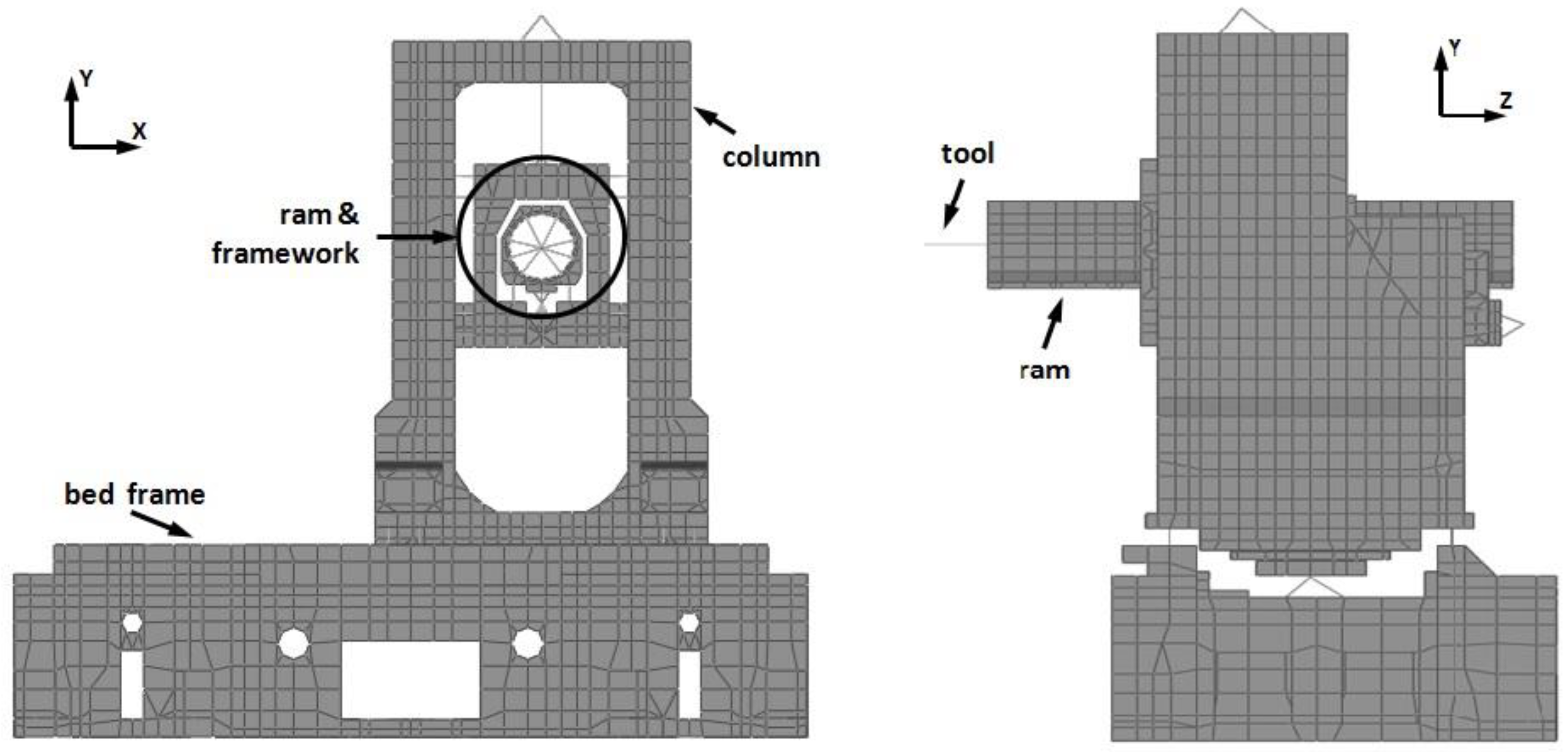
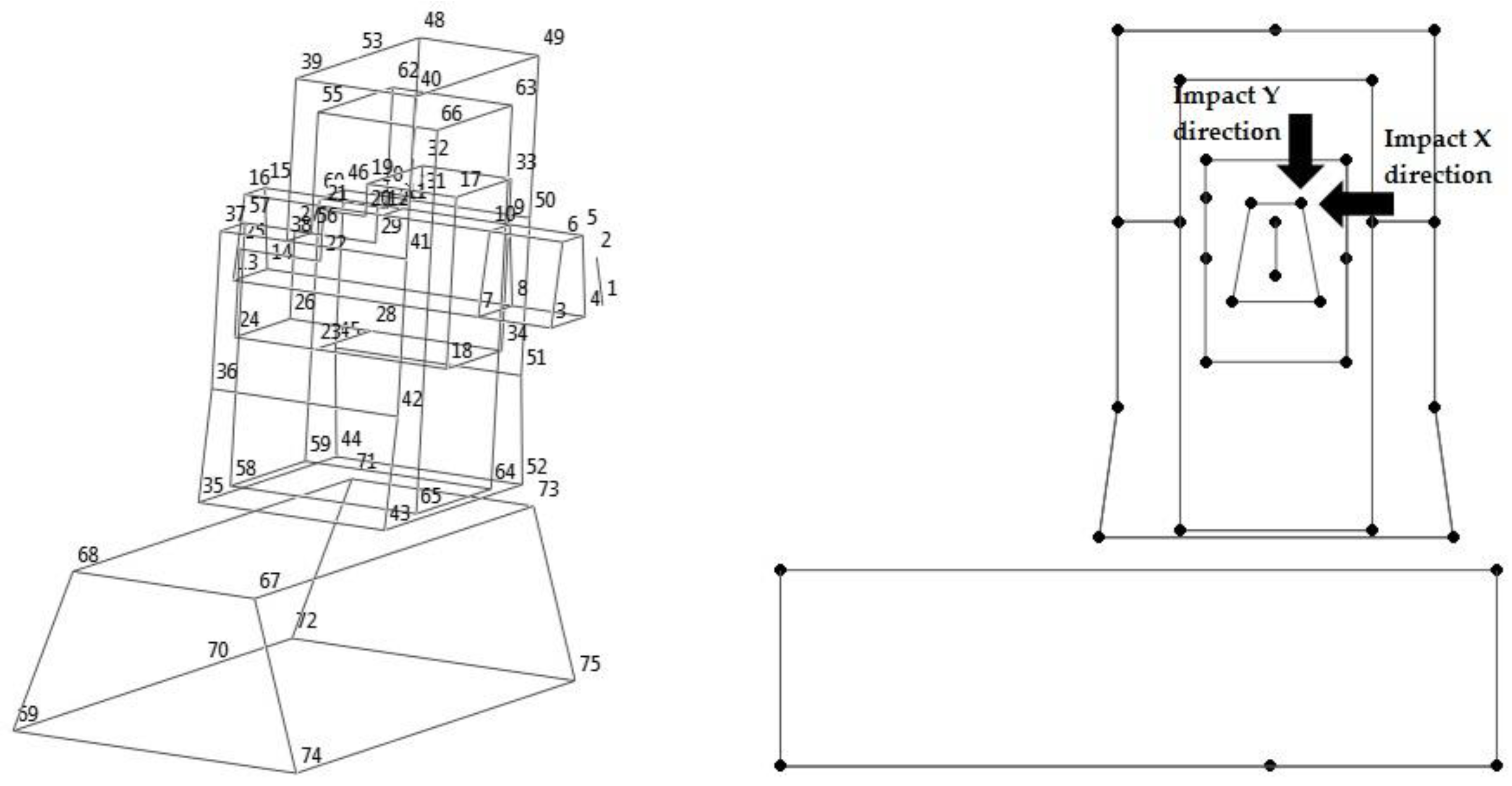

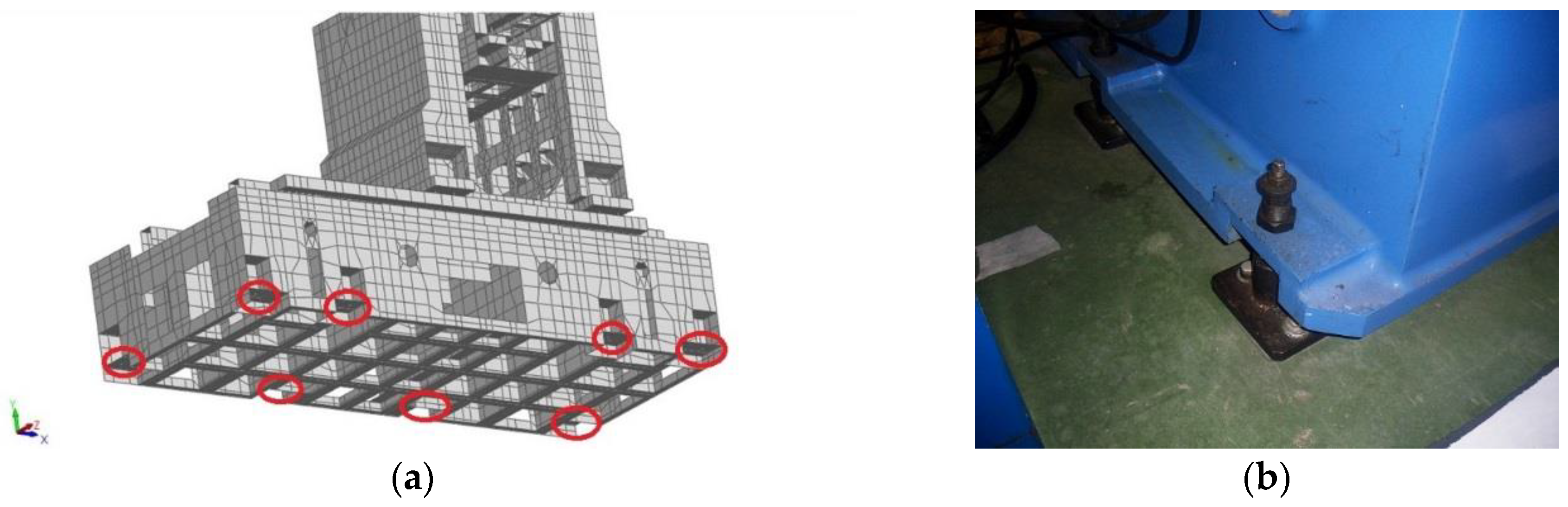

| Parameter | Value(s) | Description |
|---|---|---|
| Stiffness X,Y,Z | 750,750,750 N/μm | Connections foundation-bed frame. |
| Stiffness X,Y,Z | 1,720,750 N/μm | Connections bed frame-column (guideway). |
| Stiffness X,Y,Z | 720,1,750 N/μm | Connections column-framework (guideway). |
| Stiffness X,Y,Z | 560,750,1 N/μm | Connections framework-ram (guideway). |
| Stiffness X | 110 N/μm | Connection between primary and secondary sections of the linear motor. |
| Lumped mass | 120 kg | Spindle. |
| Lumped mass | 1.5 kg | Face milling cutter. |
| Stiffness Y | 176.7 N/μm | Y ball-screw. |
| Lumped mass | 100 kg | Servo motor Y. |
| Stiffness Z | 172.7 N/μm | Z ball-screw. |
| Lumped mass | 100 kg | Servo motor Z. |
| E, ρ | 125 GPa, 7100 kg/m3 | Young’s modulus (E) and mass density (ρ) of the bed frame and column (cast iron). |
| E, ρ | 175 GPa, 7100 kg/m3 | Young’s modulus (E) and mass density (ρ) of the framework and ram (cast iron GGG70). |
| E, ρ | 210 GPa, 7850 kg/m3 | Young’s modulus (E) and mass density (ρ) of specific parts of the machine tool. |
| fFEA1 | fFEA2 | fFEA3 | fFEA4 | fFEA5 | fFEA6 |
|---|---|---|---|---|---|
| 33.7 | 60.4 | 69.7 | 73.9 | 87.5 | 112.3 |
| Mode Order | fexp (Hz) | Damping Ratio (%) | Description of the Mode Shape |
|---|---|---|---|
| 1 | 33.7 | 4.8 | Rotation of the whole structure around the X-axis. |
| 2 | 60.5 | 3.3 | Translation along Y of the framework and ram. |
| 3 | 65.9 | 3.5 | Rotation of the upper part of the machine around the Y-axis. |
| 4 | 77.2 | 5.4 | Rotation of the upper part of the machine around the Y-axis, but now ram is in counter-phase. |
| 5 | 84.0 | 5.1 | Rotation of framework and ram around the X-axis. |
| 6 | 106.5 | 3.3 | Rotation of the whole structure around the Y-axis. Ram is in counter-phase. |
| FEA Order | fFEA (Hz) | fexp1 33.7 | fexp2 60.5 | fexp3 65.9 | fexp4 77.2 | fexp5 84.0 | fexp6 106.5 | Diff. (Hz) | Diff. (%) | Pair Number |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 33.7 | 96.6 | 0.6 | 0.3 | 0.0 | 1.9 | 0.1 | 0.0 | 0.0 | 1 |
| 2 | 60.4 | 1.7 | 98.8 | 1.2 | 0.0 | 1.3 | 0.1 | −0.1 | −0.2 | 2 |
| 3 | 69.7 | 0.0 | 0.0 | 76.3 | 4.3 | 0.0 | 1.5 | 3.8 | 5.8 | 3 |
| 4 | 73.9 | 0.1 | 0.0 | 30.3 | 89.0 | 1.3 | 3.7 | −3.3 | −4.3 | 4 |
| 5 | 87.5 | 1.9 | 0.1 | 1.2 | 0.9 | 91.0 | 0.1 | 3.5 | 4.2 | 5 |
| 6 | 112.3 | 0.0 | 1.0 | 0.1 | 0.0 | 0.1 | 70.3 | 5.8 | 5.4 | 6 |
| Connection | Design Variable | Code | Lower Bound | Nominal Value | Upper Bound | 25–1 Design |
|---|---|---|---|---|---|---|
| Foundation—bed frame | Stiffness X | kX21 | 600 | 750 | 1050 | 1,3,5,6 |
| Foundation—bed frame | Stiffness Y | kY22 | 600 | 750 | 1500 | 1,3,5,6 |
| Foundation—bed frame | Stiffness Z | kZ63 | 600 | 750 | 1050 | 1,3,5,6 |
| Linear motor (inner) | Stiffness X | kX210 | 80 | 110 | 160 | 2,4,6 |
| Bed frame—column | Stiffness Y | kY3 | 450 | 720 | 1125 | 2,4,5,7 |
| Bed frame—column | Stiffness Z | kZ4 | 400 | 750 | 900 | 2,4,5,6 |
| Column—framework | Stiffness X | kX11 | 450 | 720 | 1125 | 2,3,7 |
| Column—framework | Stiffness Z | kZ13 | 400 | 750 | 900 | 2,3,7 |
| Framework—ram | Stiffness X | kX8 | 210 | 560 | 900 | 1,4,7 |
| Framework—ram | Stiffness Y | kY9 | 450 | 750 | 1000 | 1,4,7 |
| Connection | Design Variable | Code | fFEA1 | fFEA3 | fFEA4 | fFEA5 | fFEA6 | MAC3 | MAC4 | MAC5 | MAC6 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Foundation—bed frame | Stiffness X | kX21 | |||||||||
| Foundation—bed frame | Stiffness Y | kY22 | X | X | X | X | |||||
| Foundation—bed frame | Stiffness Z | kZ63 | X | X | X | ||||||
| Linear motor (inner) | Stiffness X | kX210 | X | X | X | X | X | ||||
| Bed frame—column | Stiffness Y | kY3 | X | X | X | X | X | X | X | X | |
| Bed frame—column | Stiffness Z | kZ4 | X | X | X | X | X | X | X | ||
| Column—framework | Stiffness X | kX11 | |||||||||
| Column—framework | Stiffness Z | kZ13 | X | X | X | ||||||
| Framework—ram | Stiffness X | kX8 | X | X | X | X | X | X | |||
| Framework—ram | Stiffness Y | kY9 | X | X | X |
| Responses | Interactions |
|---|---|
| fFEA1 | kY22–kY3 |
| fFEA3 | kX210–kY3, kX210–kZ4, kX210–kX8, kY3–kX8 |
| fFEA4 | kX210–kZ4, kX210–kX8, kZ4–kX8 |
| fFEA5 | kY22–kZ63, kY22–kY9, kZ63–kZ13, kZ63–kY9 |
| fFEA6 | kY3–kZ4, kY3–kX8, kZ4–kX8 |
| MAC3 | kX210–kY3, kX210–kZ4, kX210–kX8, kY3–kZ4, kY3–kX8, kZ4–kX8 |
| MAC4 | kX210–kY3, kX210–kZ4, kX210–kX8, kY3–kX8 |
| MAC5 | kX21–kX11, kX21–kX8, kY22–kZ63, kY22–kZ13, kY22–kY9, kZ63–kZ13, kZ63–kY9, kY3–kY9, kZ13–kY9 |
| MAC6 | kY22–kZ63, kY22–kZ4, kX210–kY3, kX210–kX8, kY3–kZ13, kY3–kX8, kZ4–kY9, kX11–kY9, kZ13–kX8 |
| Coef. | Initial Model | Model 2 | Model 3 |
|---|---|---|---|
| R2 | 0.9997 | 0.9997 | 0.9996 |
| adjR2 | 0.9984 | 0.9986 | 0.9985 |
| predR2 | 0.9974 | 0.9982 | 0.9981 |
| Term | Coef. | Initial Model | Model 2 | Model 3 |
|---|---|---|---|---|
| Constant | b0 | 1410.7606 | 1521.1830 | 1482.9372 |
| kY3 | b1 | 81.6470 | 88.0377 | 85.8242 |
| kY22 | b2 | 94.8073 | 102.2280 | 99.6577 |
| kZ4 | b3 | 12.3961 | 13.3664 | 13.0303 |
| kY3–kY22 | b12 | 9.4043 | 10.1404 | 9.8854 |
| kY3–kZ4 | b13 | 0.4007 | - | - |
| kY22–kZ4 | b23 | 1.0838 | 1.1686 | - |
| (kY3)2 | b11 | −5.9900 | −17.2415 | −16.8080 |
| (kY22)2 | b22 | −18.0039 | −19.4131 | −18.9250 |
| (kZ4)2 | b33 | −1.9461 | −2.0984 | −2.0457 |
| Source | Sum of Squares | Degree of Freedom | Mean Squares | F Value | p Value |
|---|---|---|---|---|---|
| Regression | 36.114 | 8 | 4.514 | 2473.8 | 0.000 |
| Residual | 0.011 | 6 | 0.002 | - | - |
| Total | 36.125 | 14 | 2.580 | - | - |
| Coefficients of Determination | fRSM1 | fRSM3 | fRSM4 | fRSM5 | fRSM6 | MACRSM3 | MACRSM4 |
|---|---|---|---|---|---|---|---|
| R2 | 0.9997 | 0.9910 | 0.9870 | 0.9989 | 0.9995 | 0.9304 | 0.9271 |
| adjR2 | 0.9986 | 0.9845 | 0.9805 | 0.9977 | 0.9993 | 0.8956 | 0.9080 |
| predR2 | 0.9982 | 0.9746 | 0.9750 | 0.9948 | 0.9986 | 0.8692 | 0.8816 |
| Run | fFEA3 | MAC3 | fFEA4 | MAC4 | fFEA6 | kX8 | kX210 | kY3 | kZ4 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 75.2 | 71.8 | 80.0 | 86.8 | 124.3 | 900 | 160 | 1125 | 900 |
| 2 | 73.8 | 84.0 | 78.8 | 88.1 | 121.9 | 900 | 160 | 1125 | 400 |
| 3 | 74.2 | 64.4 | 78.8 | 83.6 | 123.3 | 900 | 160 | 450 | 900 |
| 4 | 73.0 | 81.3 | 77.4 | 87.6 | 122.1 | 900 | 160 | 450 | 400 |
| 5 | 68.3 | 37.5 | 79.1 | 75.0 | 124.2 | 900 | 80 | 1125 | 900 |
| 6 | 67.9 | 47.6 | 76.9 | 78.7 | 121.8 | 900 | 80 | 1125 | 400 |
| 7 | 66.4 | 32.0 | 78.2 | 71.9 | 123.2 | 900 | 80 | 450 | 900 |
| 8 | 66.1 | 40.0 | 75.9 | 74.9 | 122.0 | 900 | 80 | 450 | 400 |
| 9 | 67.5 | 73.0 | 76.8 | 50.2 | 108.5 | 210 | 160 | 1125 | 900 |
| 10 | 66.3 | 72.8 | 76.8 | 51.3 | 105.7 | 210 | 160 | 1125 | 400 |
| 11 | 67.2 | 72.8 | 75.3 | 49.2 | 107.5 | 210 | 160 | 450 | 900 |
| 12 | 66.0 | 72.5 | 75.3 | 50.2 | 104.9 | 210 | 160 | 450 | 400 |
| 13 | 66.1 | 79.1 | 70.5 | 88.3 | 108.3 | 210 | 80 | 1125 | 900 |
| 14 | 65.0 | 80.3 | 70.3 | 86.4 | 105.5 | 210 | 80 | 1125 | 400 |
| 15 | 65.2 | 75.2 | 69.0 | 88.1 | 107.3 | 210 | 80 | 450 | 900 |
| 16 | 64.3 | 79.8 | 68.6 | 89.3 | 104.7 | 210 | 80 | 450 | 400 |
| 17 | 66.7 | 76.4 | 73.0 | 67.7 | 107.2 | 210 | 120 | 787.5 | 650 |
| 18 | 67.5 | 43.9 | 76.3 | 77.7 | 118.5 | 555 | 80 | 787.5 | 650 |
| 19 | 70.4 | 56.8 | 76.0 | 81.8 | 118.0 | 555 | 120 | 450 | 650 |
| 20 | 70.7 | 74.8 | 75.8 | 88.3 | 117.5 | 555 | 120 | 787.5 | 400 |
| 21 | 71.6 | 52.8 | 78.4 | 80.4 | 123.5 | 900 | 120 | 787.5 | 650 |
| 22 | 73.8 | 84.1 | 78.0 | 88.7 | 118.6 | 555 | 160 | 787.5 | 650 |
| 23 | 71.7 | 66.8 | 77.1 | 86.0 | 118.8 | 555 | 120 | 1125 | 650 |
| 24 | 71.5 | 58.3 | 77.3 | 82.8 | 119.0 | 555 | 120 | 787.5 | 900 |
| 25 | 71.3 | 63.8 | 76.8 | 84.7 | 118.5 | 555 | 120 | 787.5 | 650 |
| Initial | 69.7 | 76.3 | 73.9 | 89.0 | 112.3 | ||||
| Obj | 65.9 | 100 | 77.2 | 100 | 106.5 |
| XY22 | XZ63 | XX210 | XY3 | XZ4 | XZ13 | XX8 (1) | XY9 | XX8 (2) |
|---|---|---|---|---|---|---|---|---|
| −0.920 | −0.250 | −0.695 | 1.000 | −0.540 | −0.800 | −1.000 | −0.300 | 0.485 |
| kY22 | kZ63 | kX210 | kY3 | kZ4 | kZ13 | kX8 (1) | kY9 | kX8 (2) |
| 636 | 769 | 92 | 1125 | 515 | 450 | 210 | 642 | 722 |
| FEA Order | fRSM | fFEA | fexp | Diff. (Hz) | Diff. (%) | MAC | MACRSM | kX8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 33.7 | 33.7 | 33.7 | 0.0 | 0.0 | 96.7 | - | (1) |
| 2 | - | 60.5 | 60.5 | 0.0 | 0.0 | 98.7 | - | (1) |
| 3 | 65.9 | 65.8 | 65.9 | −0.1 | −0.2 | 78.9 | 76.5 | (1) |
| 4 | 77.2 | 77.0 | 77.2 | −0.2 | −0.3 | 80.6 | 83.9 | (2) |
| 5 | 84.0 | 84.1 | 84.0 | 0.1 | 0.1 | 80.9 | - | (2) |
| 6 | 106.5 | 106.1 | 106.5 | −0.4 | −0.4 | 70.0 | - | (1) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernandez-Vazquez, J.-M.; Garitaonandia, I.; Fernandes, M.H.; Muñoa, J.; Lacalle, L.N.L.d. A Consistent Procedure Using Response Surface Methodology to Identify Stiffness Properties of Connections in Machine Tools. Materials 2018, 11, 1220. https://doi.org/10.3390/ma11071220
Hernandez-Vazquez J-M, Garitaonandia I, Fernandes MH, Muñoa J, Lacalle LNLd. A Consistent Procedure Using Response Surface Methodology to Identify Stiffness Properties of Connections in Machine Tools. Materials. 2018; 11(7):1220. https://doi.org/10.3390/ma11071220
Chicago/Turabian StyleHernandez-Vazquez, Jesus-Maria, Iker Garitaonandia, María Helena Fernandes, Jokin Muñoa, and Luis Norberto López de Lacalle. 2018. "A Consistent Procedure Using Response Surface Methodology to Identify Stiffness Properties of Connections in Machine Tools" Materials 11, no. 7: 1220. https://doi.org/10.3390/ma11071220
APA StyleHernandez-Vazquez, J.-M., Garitaonandia, I., Fernandes, M. H., Muñoa, J., & Lacalle, L. N. L. d. (2018). A Consistent Procedure Using Response Surface Methodology to Identify Stiffness Properties of Connections in Machine Tools. Materials, 11(7), 1220. https://doi.org/10.3390/ma11071220






