Stress Concentration and Mechanical Strength of Cubic Lattice Architectures
Abstract
1. Introduction
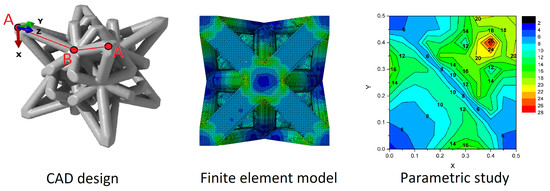
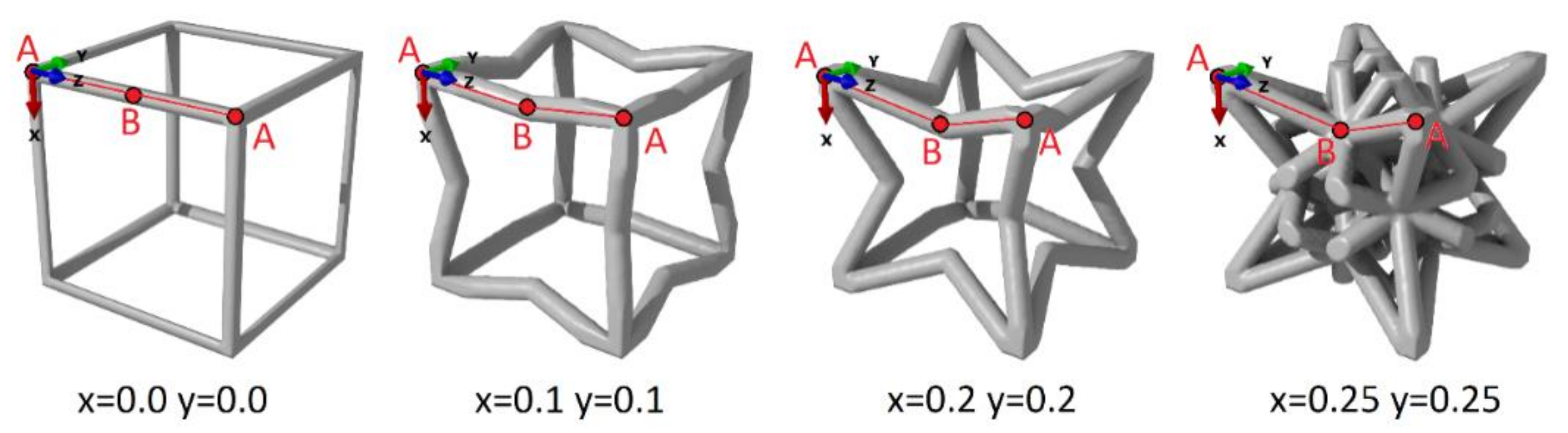
2. Materials and Methods
3. Result
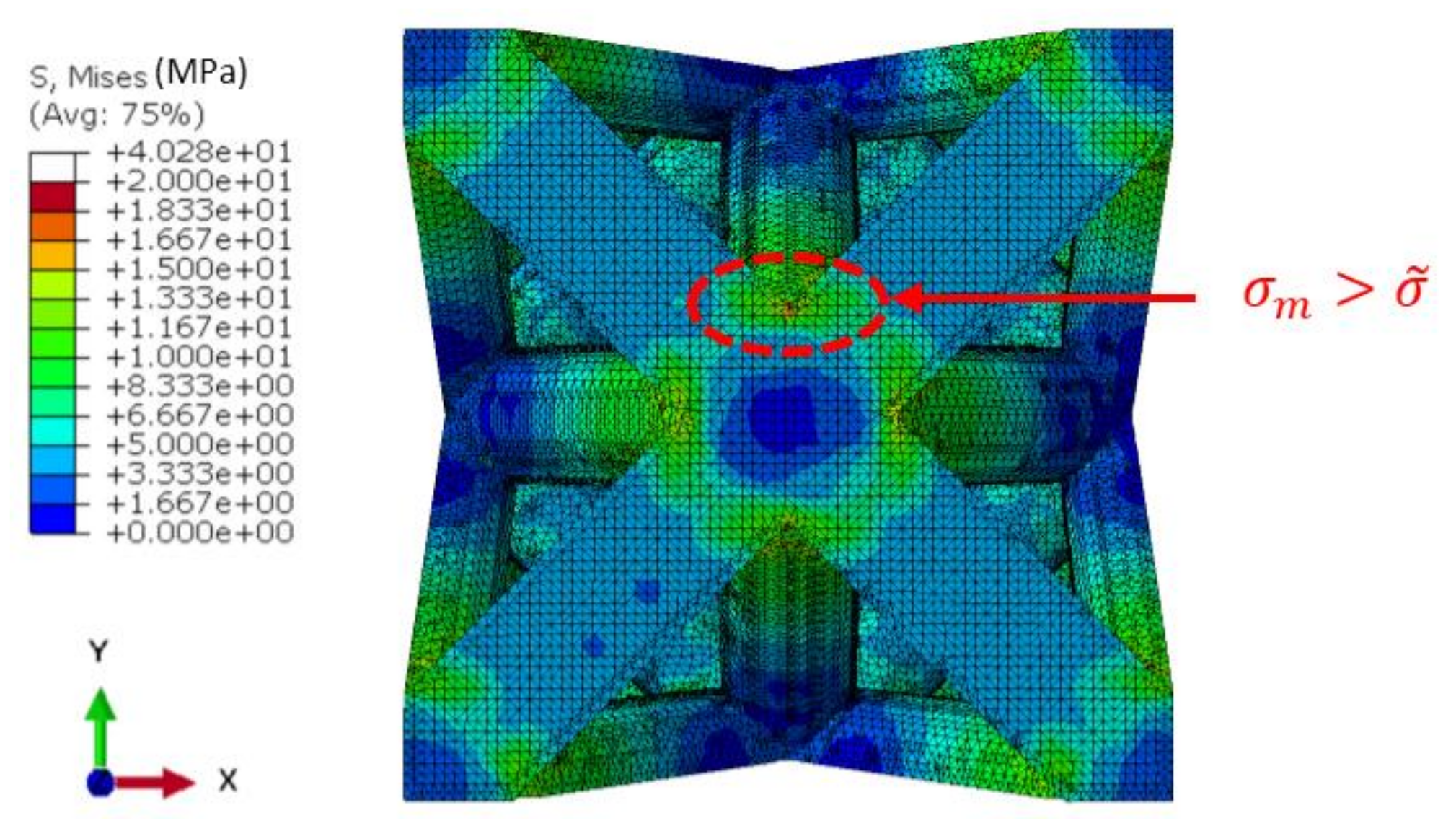
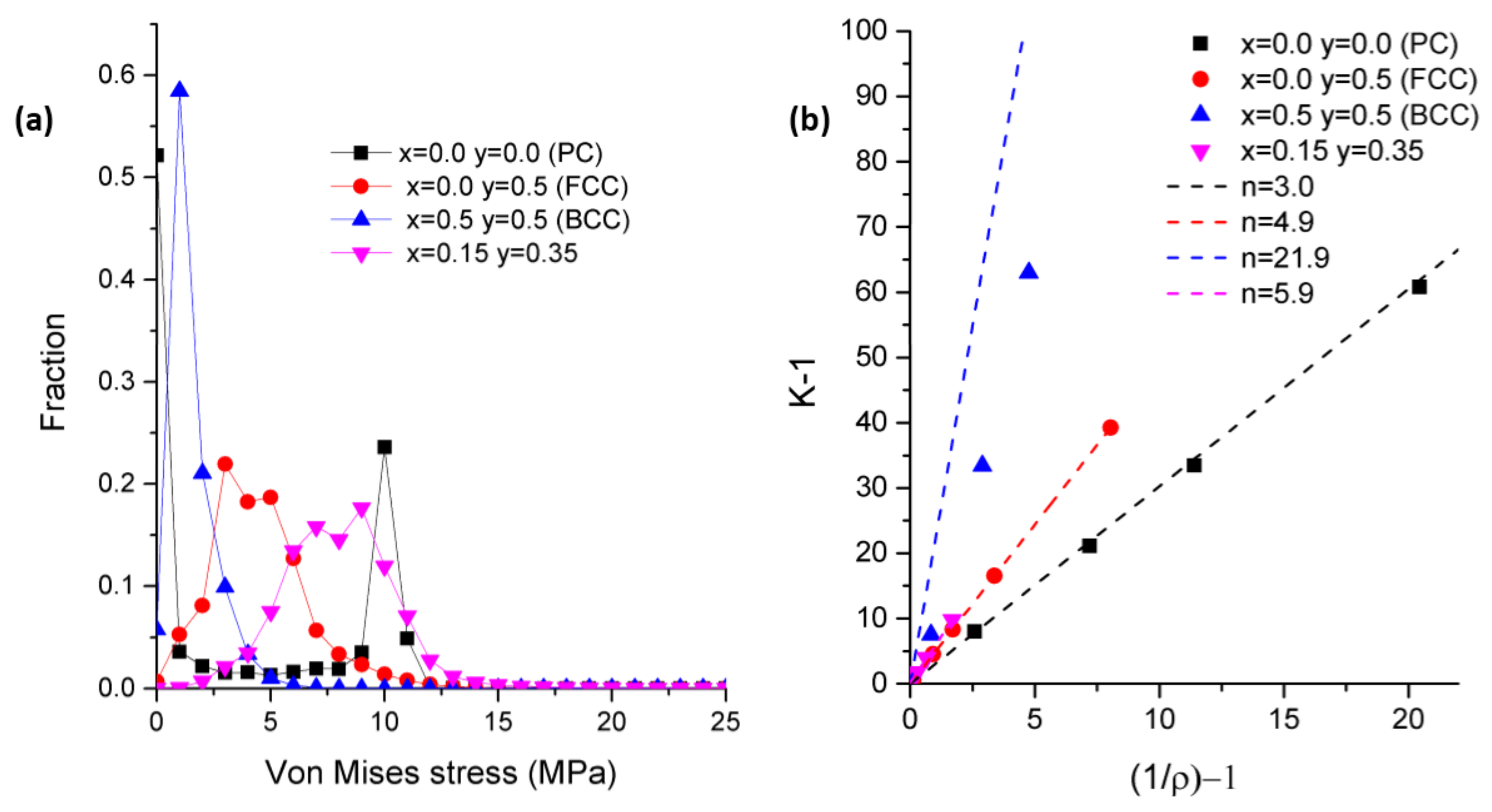
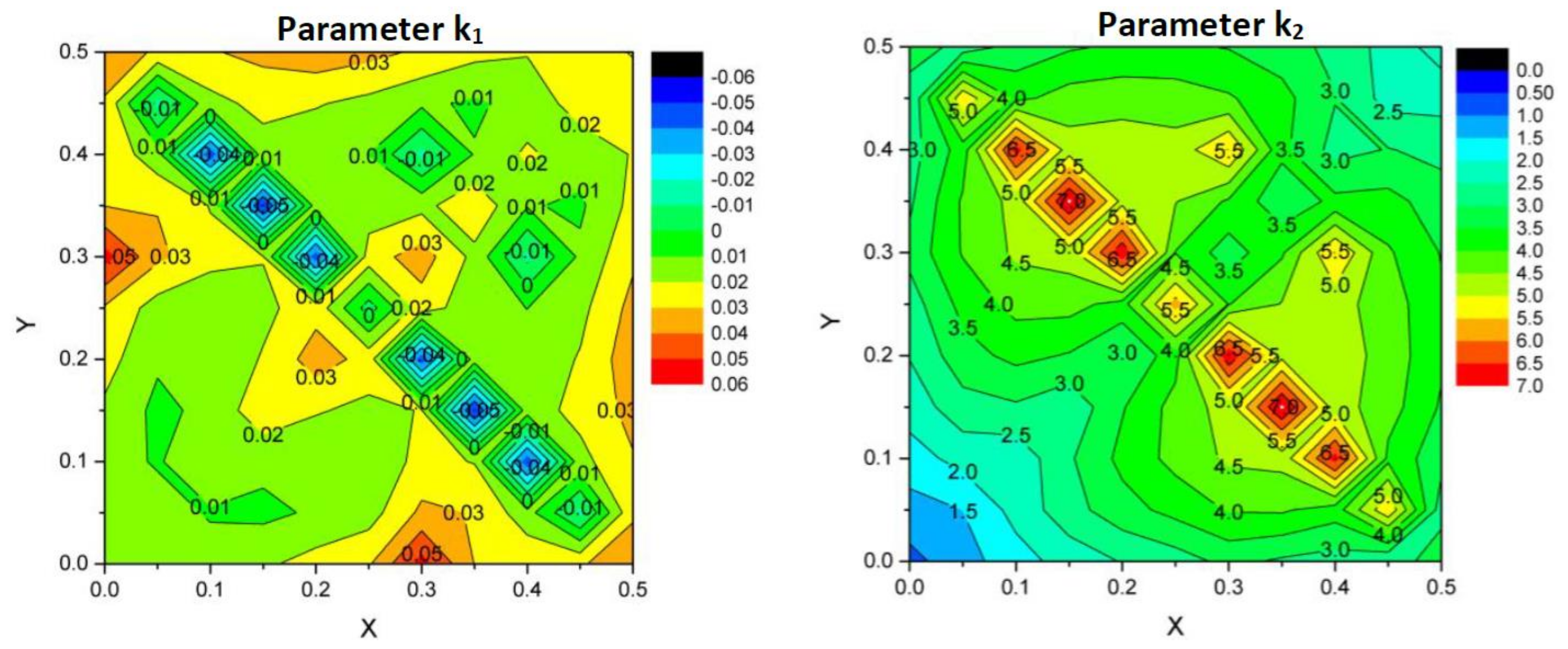
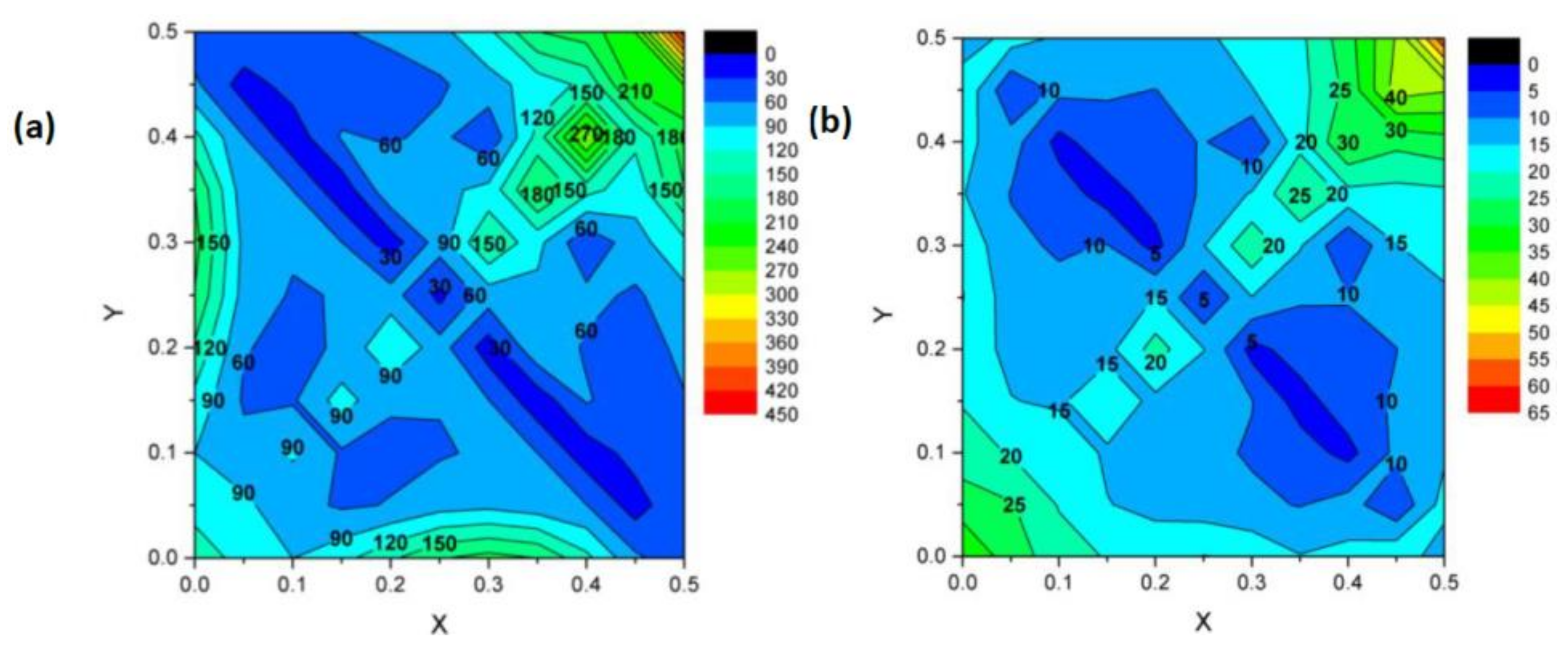
3.1. Stress Field and Maximum
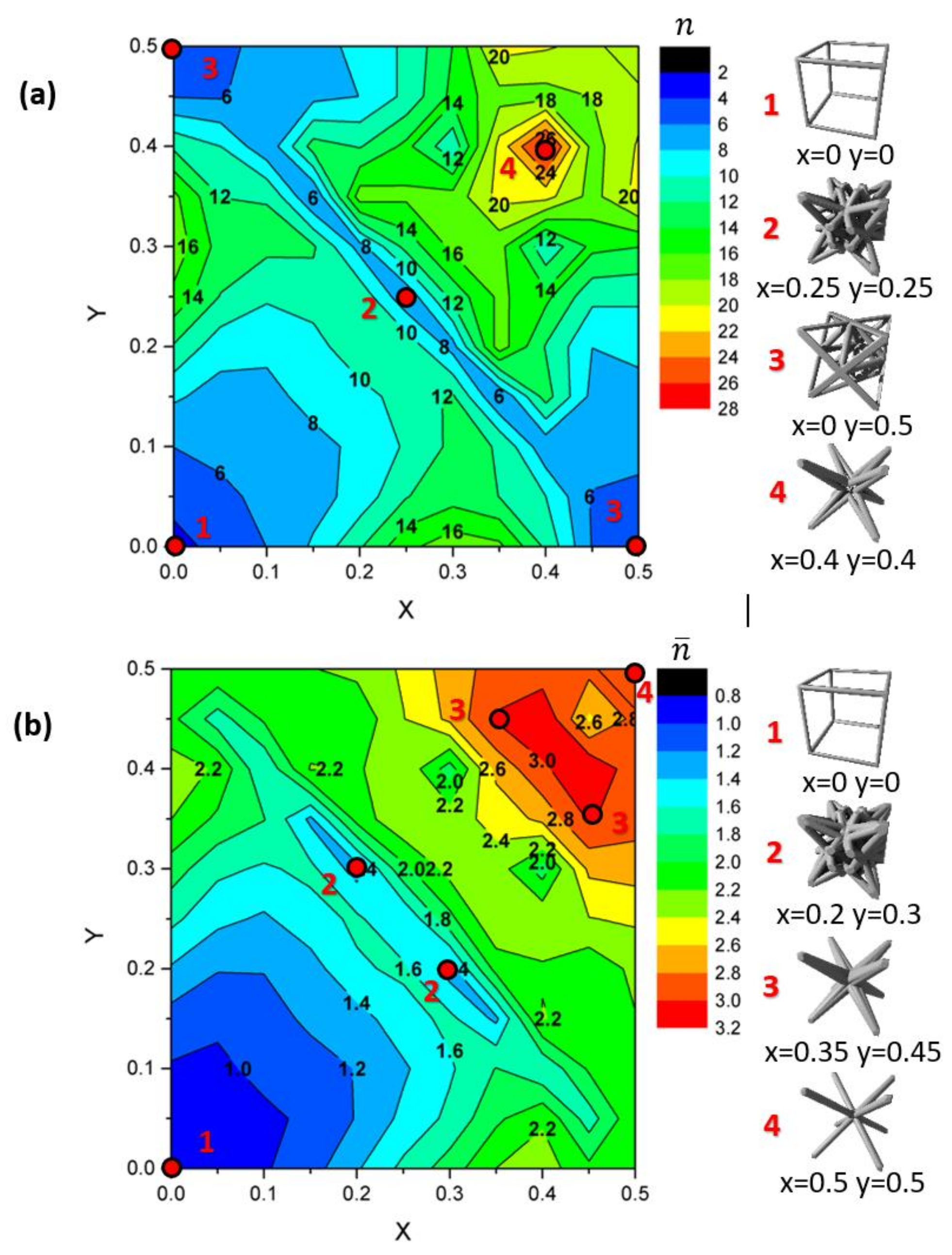
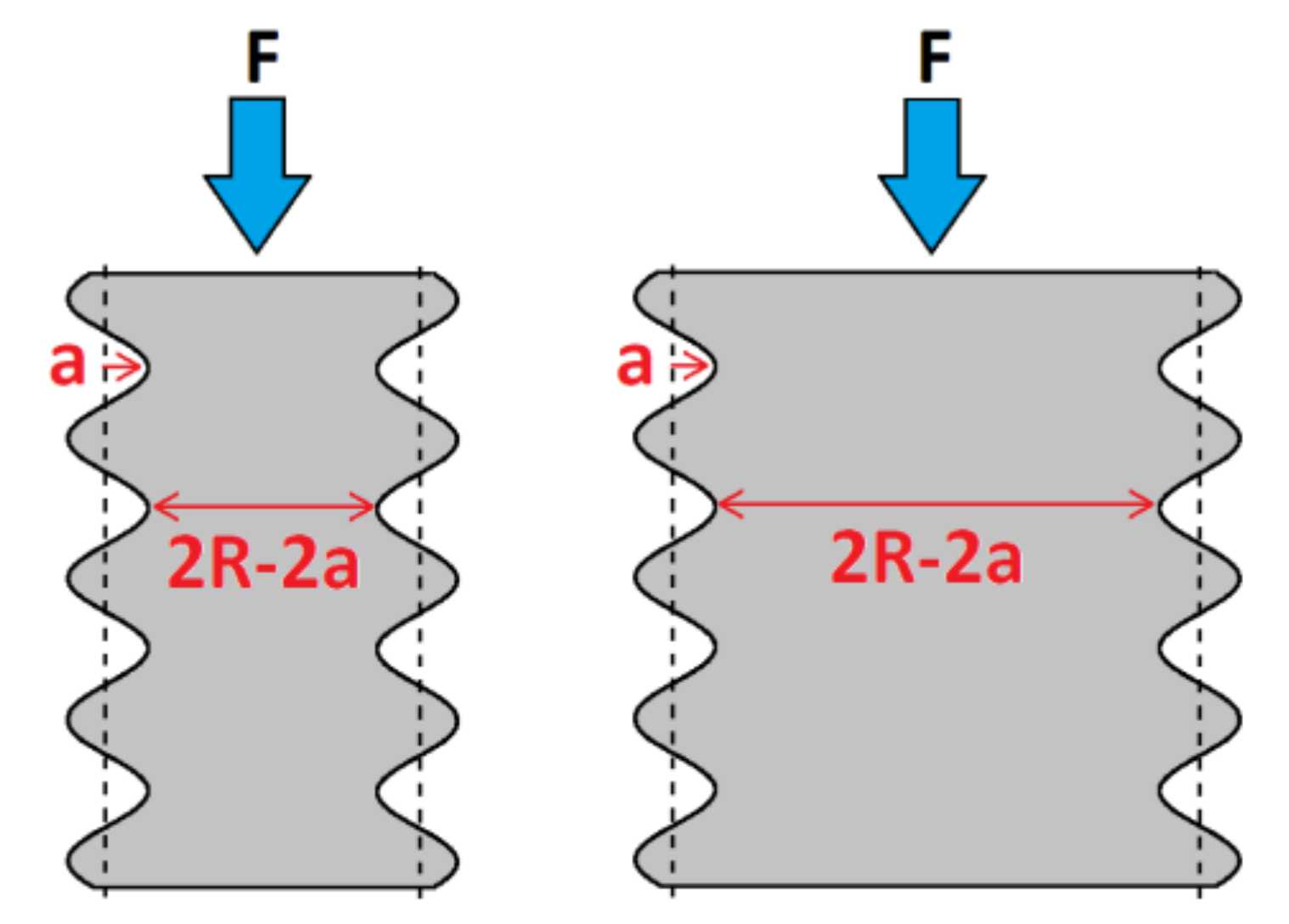
3.2. Stress Concentration Factors
4. Discussion
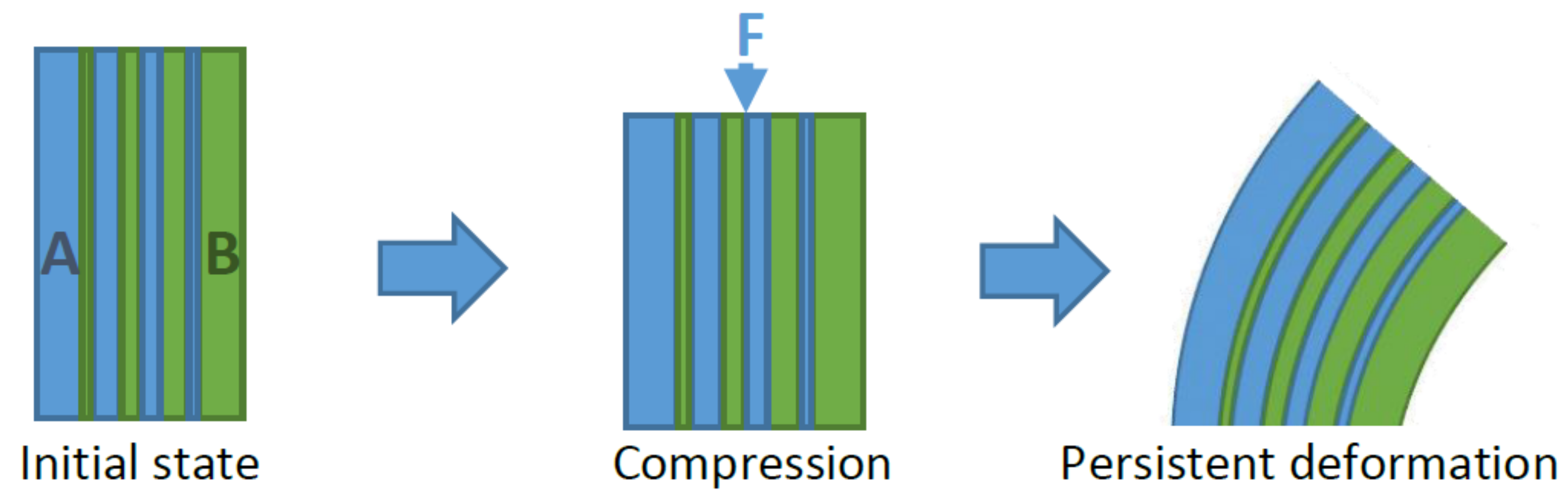
4.1. Case Study and Applications
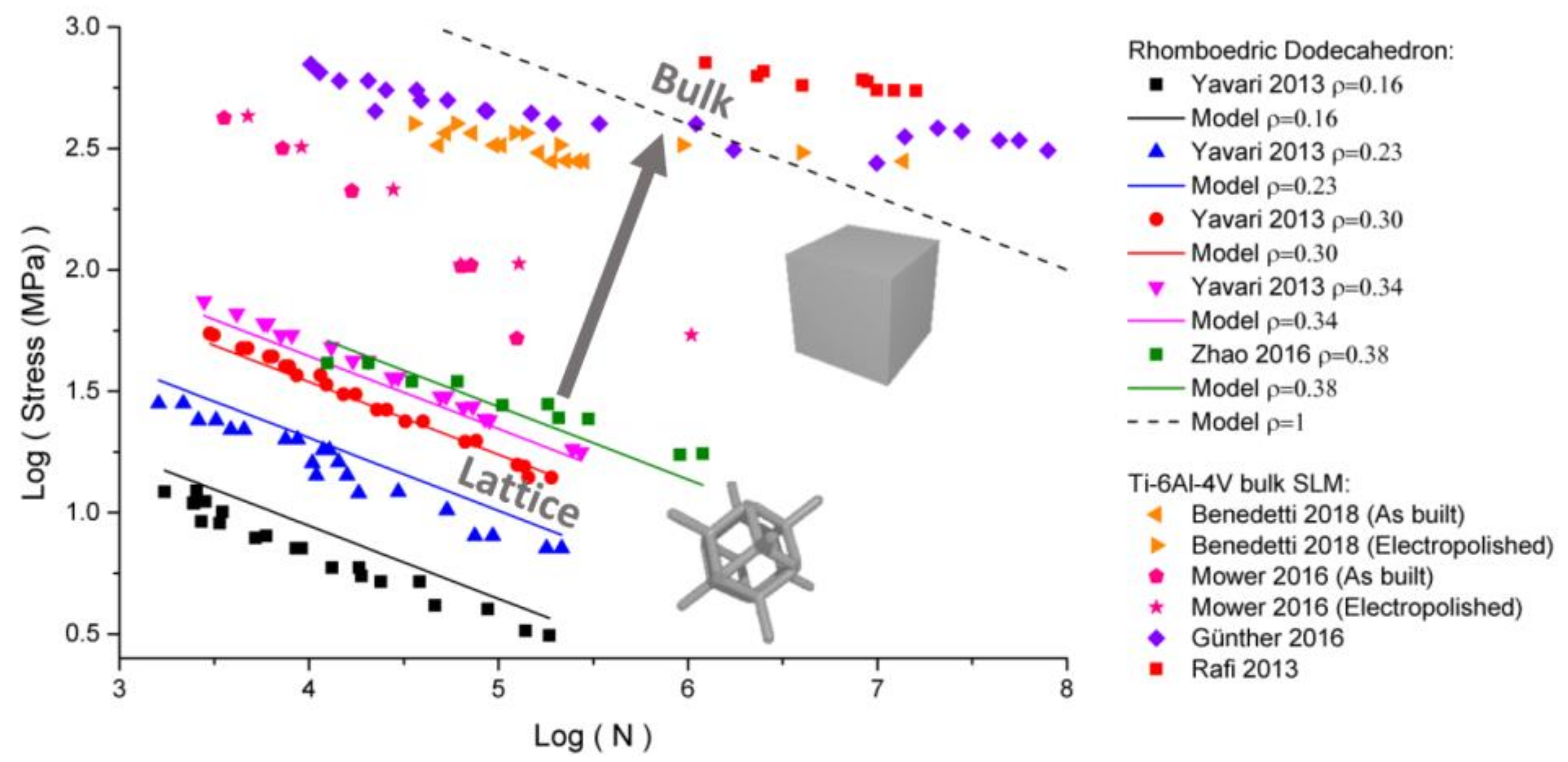
4.2. Fatigue Strength
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yan, C.; Hao, L.; Hussein, A.; Raymont, D. Evaluations of cellular lattice structures manufactured using selective laser melting. Int. J. Mach. Tools Manuf. 2012, 62, 32–38. [Google Scholar] [CrossRef]
- Lhuissier, P.; de Formanoir, C.; Martin, G.; Dendievel, R.; Godet, S. Geometrical control of lattice structures produced by EBM through chemical etching: Investigations at the scale of individual struts. Mater. Des. 2016, 110, 485–493. [Google Scholar] [CrossRef]
- Dong, L.; Deshpande, V.; Wadley, H. Mechanical response of Ti–6Al–4V octet-truss lattice structures. Int. J. Solids Struct. 2015, 60–61, 107–124. [Google Scholar] [CrossRef]
- Ashby, M.; Bréchet, Y. Designing hybrid materials. Acta Mater. 2003, 51, 5801–5821. [Google Scholar] [CrossRef]
- Suard, M.; Martin, G.; Lhuissier, P.; Dendievel, R.; Vignat, F.; Blandin, J.J.; Villeneuve, F. Mechanical equivalent diameter of single struts for the stiffness prediction of lattice structures produced by Electron Beam Melting. Addit. Manuf. 2015, 8, 124–131. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Hefzy, M.S. Continuum Modeling of Three-Dimensional Truss-like Space Structures. AIAA J. 1978, 16, 779–787. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Messner, M.C. Optimal lattice-structured materials. J. Mech. Phys. Solids 2016, 96, 162–183. [Google Scholar] [CrossRef]
- Méjica, G.F.; Lantada, A.D. Comparative study of potential pentamodal metamaterials inspired by Bravais lattices. Smart Mater. Struct. 2013, 22, 115013. [Google Scholar] [CrossRef]
- Favre, J.; Lohmuller, P.; Piotrowski, B.; Kenzari, S.; Laheurte, P.; Meraghni, F. A continuous crystallographic approach to generate cubic lattices and its effect on relative stiffness of architectured materials. Addit. Manuf. 2018, 21, 359–368. [Google Scholar] [CrossRef]
- Salimon, A.; Bréchet, Y.; Ashby, M.F.; Greer, A.L. Potential applications for steel and titanium metal foams. Mech. Behav. Cell. Solids 2005, 40, 5793–5799. [Google Scholar] [CrossRef]
- Reis, F.D.; Ganghoffer, J.F. Equivalent mechanical properties of auxetic lattices from discrete homogenization. Comput. Mater. Sci. 2012, 51, 314–321. [Google Scholar] [CrossRef]
- Evans, K.E. Molecular Network Design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Dallago, M.; Fontanari, V.; Torresani, E.; Leoni, M.; Pederzolli, C.; Potrich, C.; Benedetti, M. Fatigue and biological properties of Ti-6Al-4V ELI cellular structures with variously arranged cubic cells made by selective laser melting. J. Mech. Behav. Biomed. Mater. 2018, 78, 381–394. [Google Scholar] [CrossRef] [PubMed]
- Van Hooreweder, B.; Appers, Y.; Lietaert, K.; Kruth, J.P. Improving the fatigue performance of porous metallic biomaterials produced by Selective Laser Melting. Acta Biomater. 2017, 47, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Zargarian, A.; Esfahanian, M.; Kadkhodapour, J.; Ziaei-Rad, S. Numerical simulation of the fatigue behavior of additive manufactured titanium porous lattice structures. Mater. Sci. Eng. C 2016, 60, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Van Hooreweder, B.; Kruth, J.P. Advanced fatigue analysis of metal lattice structures produced by Selective Laser Melting. CIRP Ann. Manuf. Technol. 2017, 66, 221–224. [Google Scholar] [CrossRef]
- Hrabe, N.W.; Heinl, P.; Flinn, B.; Körner, C.; Bordia, R.K. Compression-compression fatigue of selective electron beam melted cellular titanium (Ti-6Al-4V). J. Biomed. Mater. Res. 2011, 99B, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Hedayati, R.; Hosseini-Toudeshky, H.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A.A. Computational prediction of the fatigue behavior of additively manufactured porous metallic biomaterials. Int. J. Fatigue 2016, 84, 67–79. [Google Scholar] [CrossRef]
- Li, S.J.; Murr, L.E.; Cheng, X.Y.; Zhang, Z.B.; Hao, Y.L.; Yang, R.; Medina, F.; Wicker, R.B. Compression fatigue behavior of Ti–6Al–4V mesh arrays fabricated by electron beam melting. Acta Mater. 2012, 60, 793–802. [Google Scholar] [CrossRef]
- Xiao, L.; Song, W.; Wang, C.; Liu, H.; Tang, H.; Wang, J. Mechanical behavior of open-cell rhombic dodecahedron Ti–6Al–4V lattice structure. Mater. Sci. Eng. A 2015, 640, 375–384. [Google Scholar] [CrossRef]
- Yavari, S.A.; Wauthle, R.; van der Stok, J.; Riemslag, A.C.; Janssen, M.; Mulier, M.; Kruth, J.P.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Fatigue behavior of porous biomaterials manufactured using selective laser melting. Mater. Sci. Eng. C 2013, 33, 4849–4858. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Li, S.J.; Hou, W.T.; Hao, Y.L.; Yang, R.; Misra, R.D.K. The influence of cell morphology on the compressive fatigue behavior of Ti-6Al-4V meshes fabricated by electron beam melting. J. Mech. Behav. Biomed. Mater. 2016, 59, 251–264. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Li, S.J.; Wang, S.G.; Hou, W.T.; Li, Y.; Zhang, L.C.; Hao, Y.L.; Yang, R.; Misra, R.D.K.; Murr, L.E. Compressive and fatigue behavior of functionally graded Ti-6Al-4V meshes fabricated by electron beam melting. Acta Mater. 2018, 150, 1–15. [Google Scholar] [CrossRef]
- Benedetti, M.; Fontanari, V.; Bandini, M.; Zanini, F.; Carmignato, S. Low- and high-cycle fatigue resistance of Ti-6Al-4V ELI additively manufactured via selective laser melting: Mean stress and defect sensitivity. Int. J. Fatigue 2018, 107, 96–109. [Google Scholar] [CrossRef]
- Günther, J.; Krewerth, D.; Lippmann, T.; Leuders, S.; Tröster, T.; Weidner, A.; Niendorf, T.; Biermann, H. Fatigue life of additively manufactured Ti–6Al–4V in the very high cycle fatigue regime. Int. J. Fatigue 2016, 94, 236–245. [Google Scholar] [CrossRef]
- Mower, T.M.; Long, M.J. Mechanical behavior of additive manufactured, powder-bed laser-fused materials. Mater. Sci. Eng. A 2016, 651, 198–213. [Google Scholar] [CrossRef]
- Rafi, H.K.; Karthik, N.V.; Gong, H.; Starr, T.L.; Stucker, B.E. Microstructures and Mechanical Properties of Ti6Al4V Parts Fabricated by Selective Laser Melting and Electron Beam Melting. J. Mater. Eng. Perform. 2013, 22, 3872–3883. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lohmuller, P.; Favre, J.; Piotrowski, B.; Kenzari, S.; Laheurte, P. Stress Concentration and Mechanical Strength of Cubic Lattice Architectures. Materials 2018, 11, 1146. https://doi.org/10.3390/ma11071146
Lohmuller P, Favre J, Piotrowski B, Kenzari S, Laheurte P. Stress Concentration and Mechanical Strength of Cubic Lattice Architectures. Materials. 2018; 11(7):1146. https://doi.org/10.3390/ma11071146
Chicago/Turabian StyleLohmuller, Paul, Julien Favre, Boris Piotrowski, Samuel Kenzari, and Pascal Laheurte. 2018. "Stress Concentration and Mechanical Strength of Cubic Lattice Architectures" Materials 11, no. 7: 1146. https://doi.org/10.3390/ma11071146
APA StyleLohmuller, P., Favre, J., Piotrowski, B., Kenzari, S., & Laheurte, P. (2018). Stress Concentration and Mechanical Strength of Cubic Lattice Architectures. Materials, 11(7), 1146. https://doi.org/10.3390/ma11071146