Optimization of the Iron Ore Direct Reduction Process through Multiscale Process Modeling
Abstract
:1. Introduction
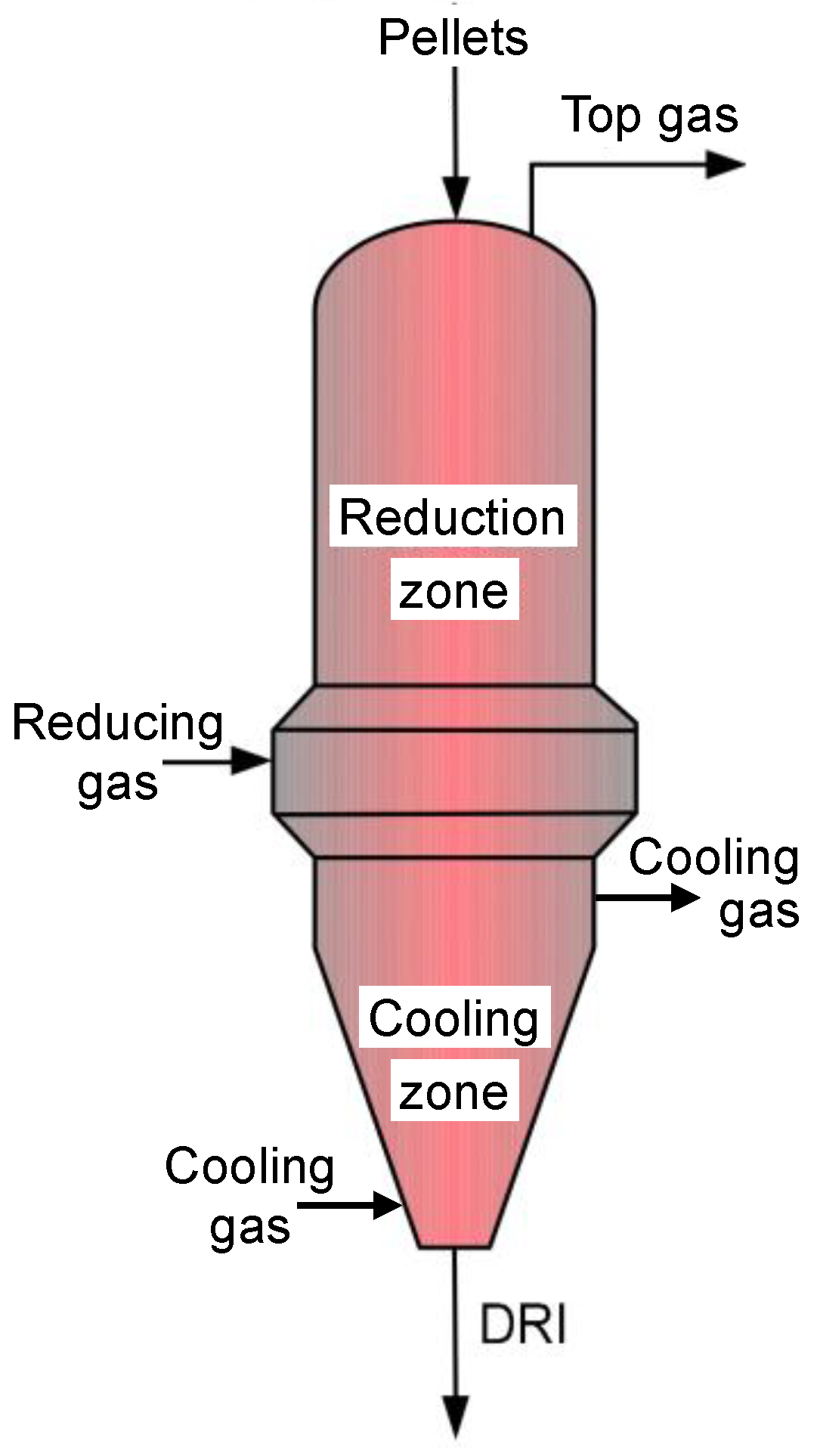
2. Single Pellet Model
3. Shaft Furnace Model
3.1. Previous Works
- The number of reduction steps. This is related to the intermediary iron oxides taken into account. Works with one reduction step consider the direct transformation of hematite to iron, those with two steps consider further the presence of wustite, whereas those with three steps consider also magnetite.
- The description of the pellet transformation: shrinking core or grain models.
- Some models were validated against plant data, others not.
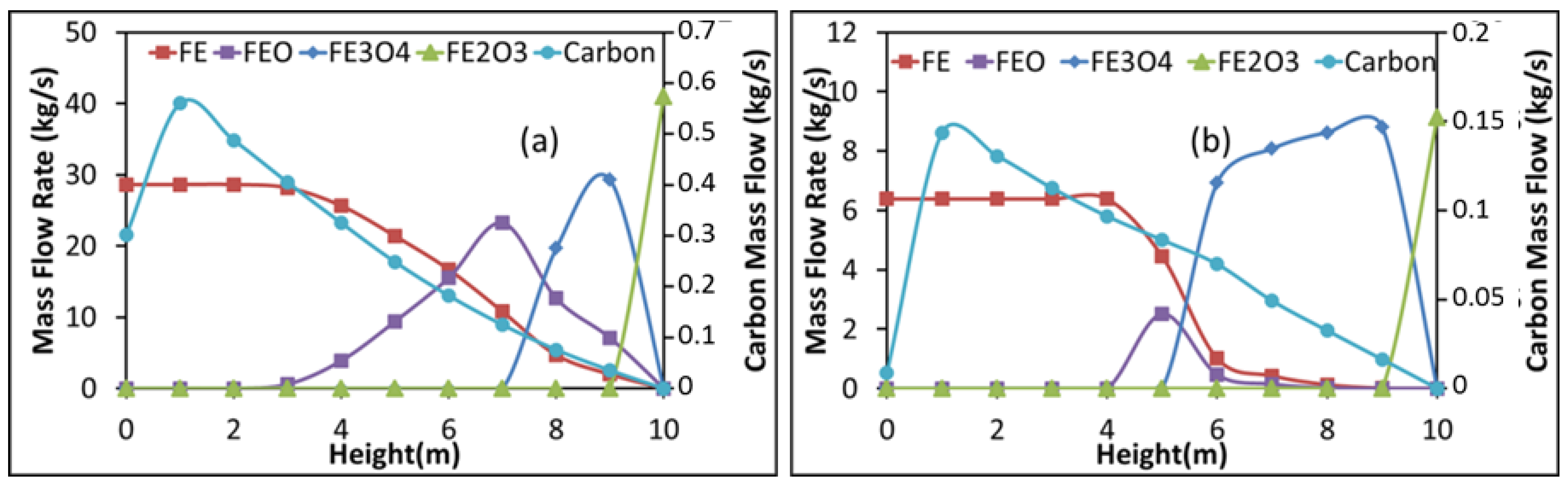
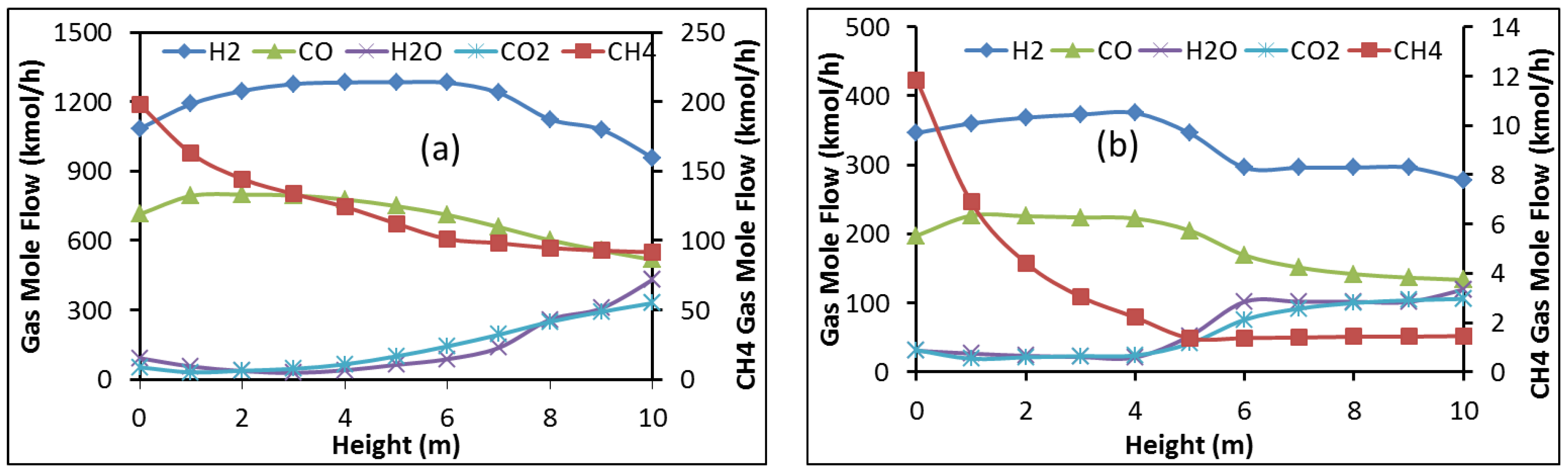
- The molar content of H2 and CO decreases from the reduction zone bottom to its top whereas that of CO2 and H2O increases. Inversely, the content of iron oxides decreases from top to bottom with mainly iron exiting from the shaft bottom.
- The solid and gas temperatures are equal along the shaft except in a thin layer at the top near the solid inlet where a great temperature difference exists, the pellets are charged cold. Moreover, both temperatures increase from the shaft top to its bottom.
- Reaction enthalpy is of great importance, namely, the rather endothermic nature of H2 reduction reactions vs. the exothermic nature of CO reduction reactions, as well as for the models that include it, the endothermic nature of steam methane reforming.
- the inclusion of three reduction steps and the grain model better represent the pellet transformation;
- all the components of the gas mixture (excepting N2 but including CH4) play a role in the transformations;
- two dimensions depict more accurately the reactor internal behavior and the output results; 2D results revealed the presence of two zones: one peripheral where the bustle gas is the reducing gas, and one central where the gas stems from the cooling and transition zones;
- taking supplementary reactions into consideration along with the cooling and transition zones better represents gas phase transformations and can account for carbon deposition.
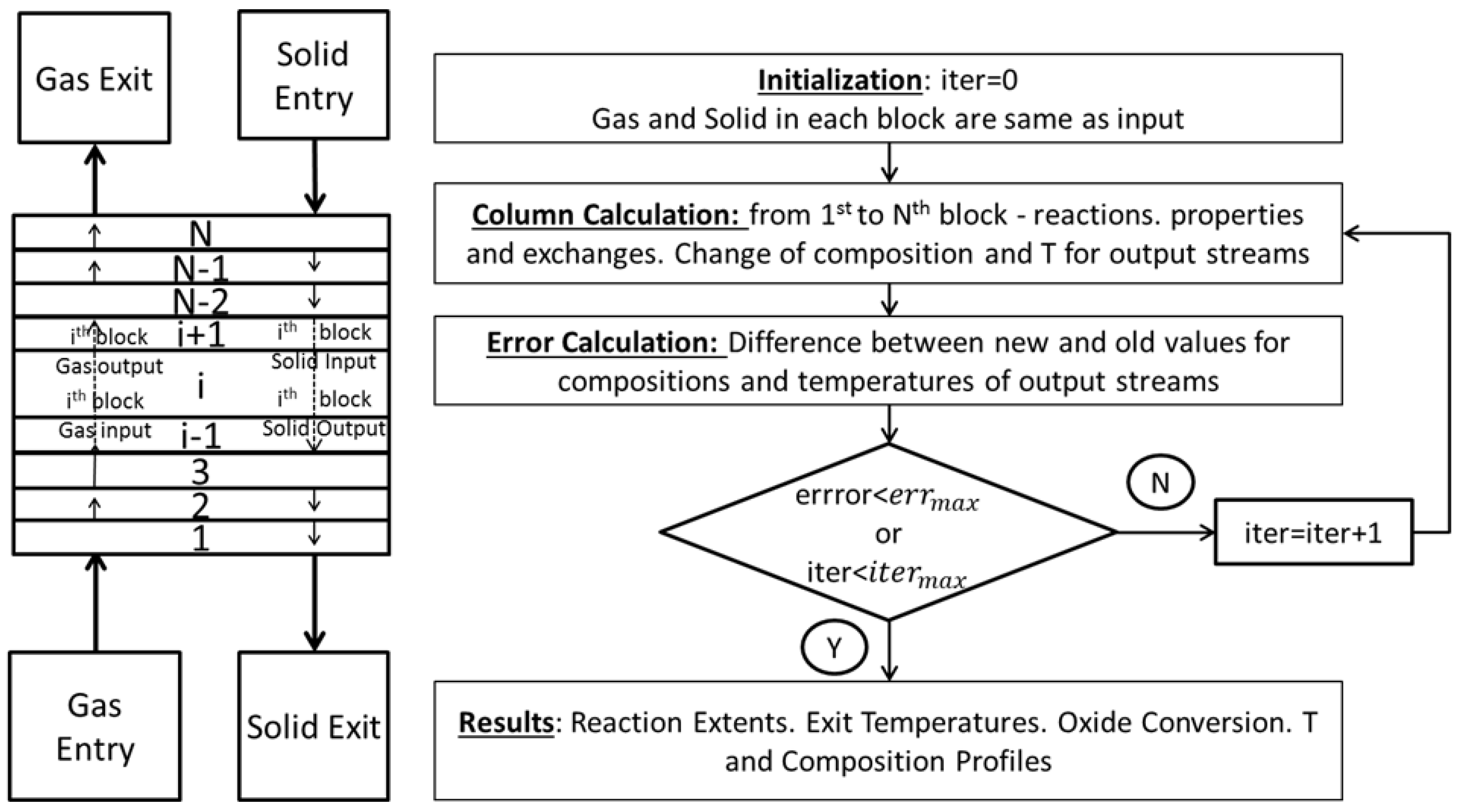
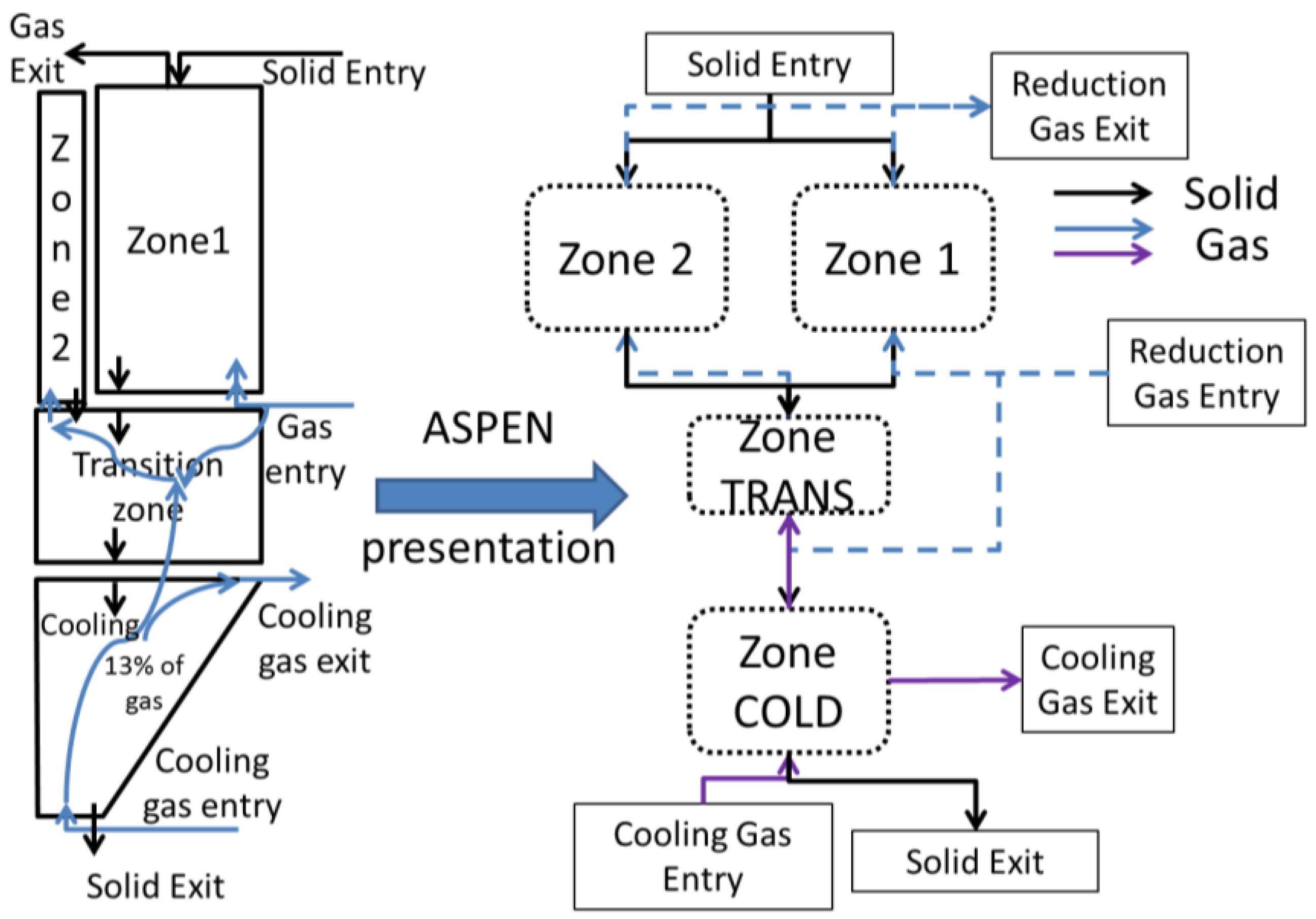
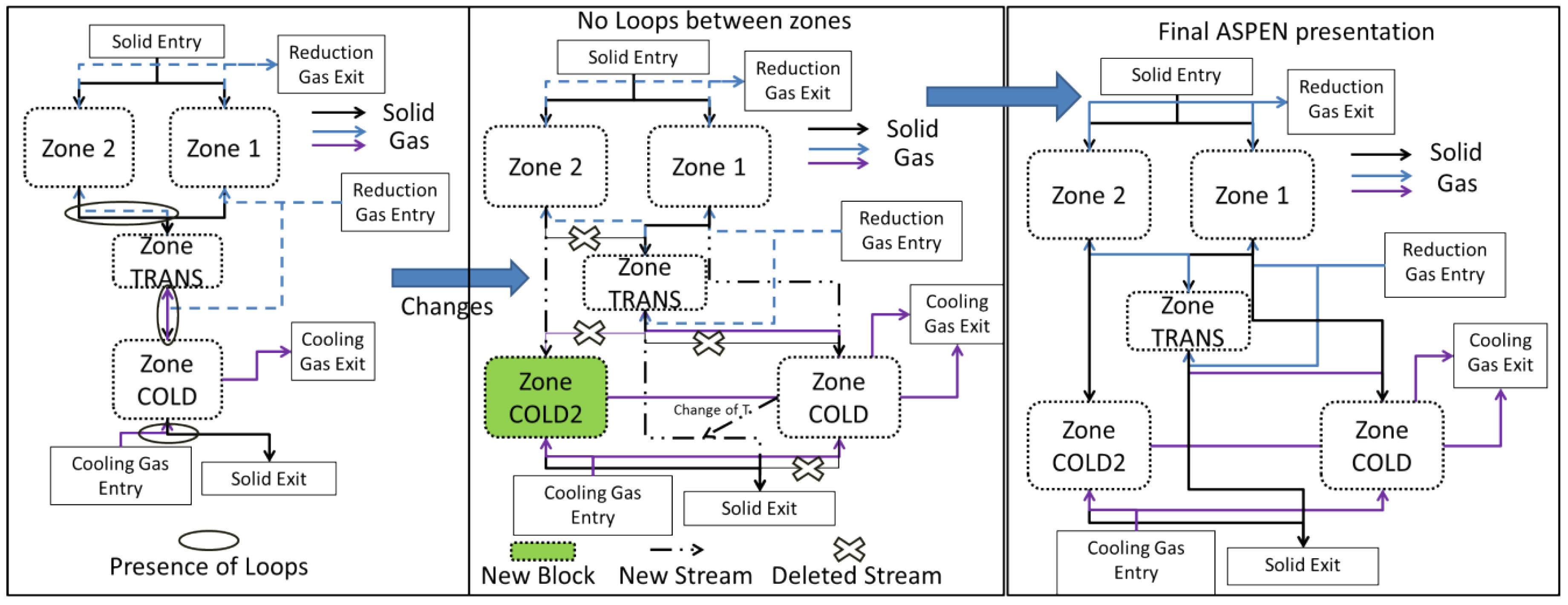
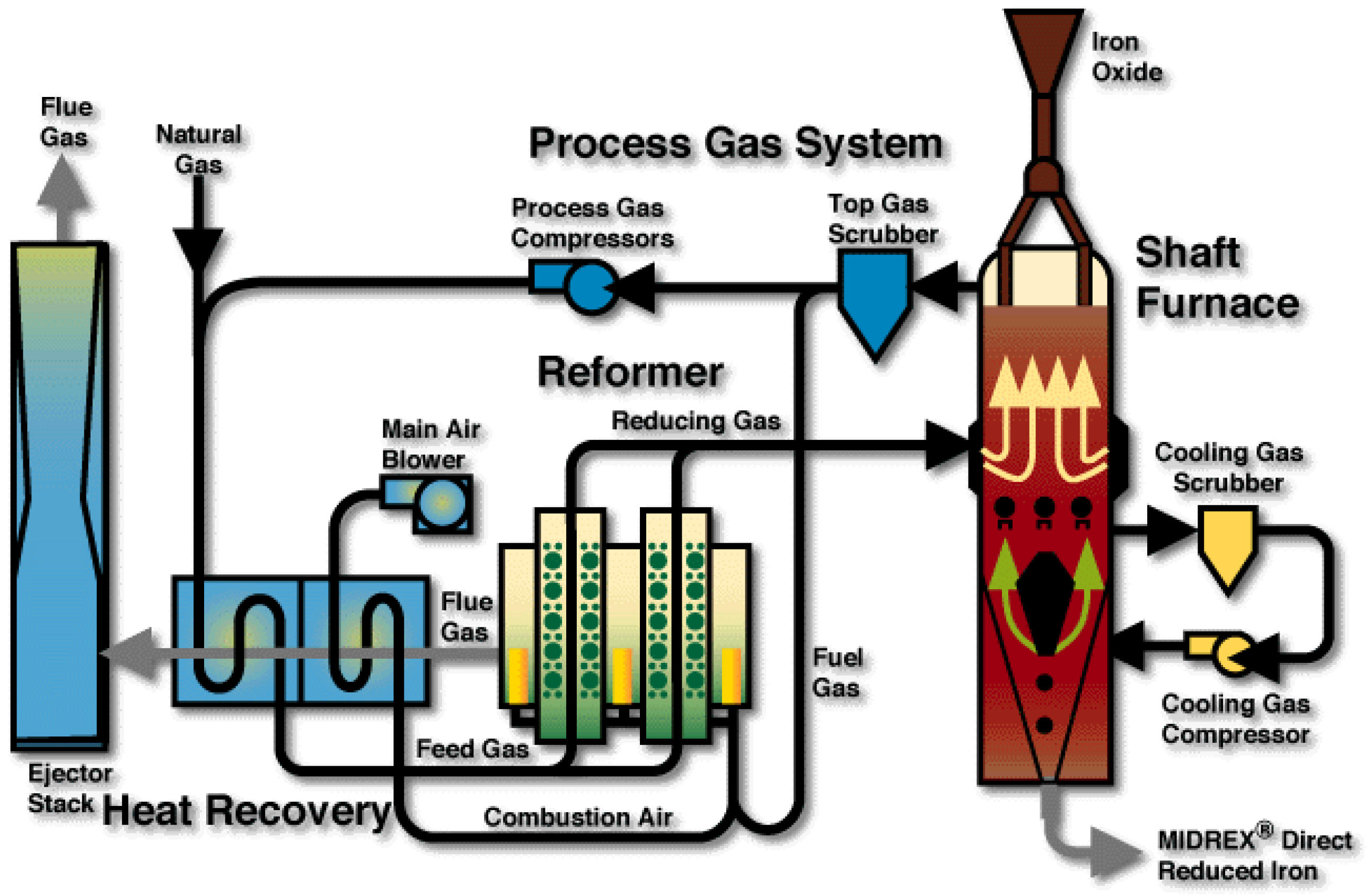
3.2. Aspen Plus Shaft Model
3.3. Results from the Aspen Plus Shaft Model
4. Plant Model
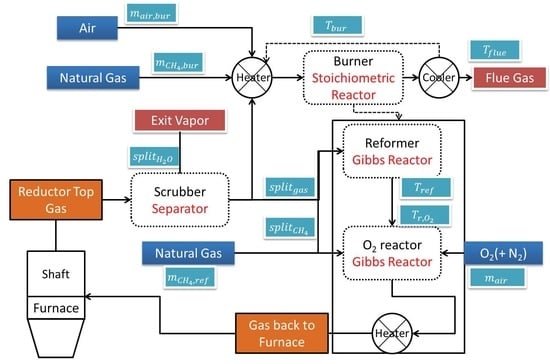
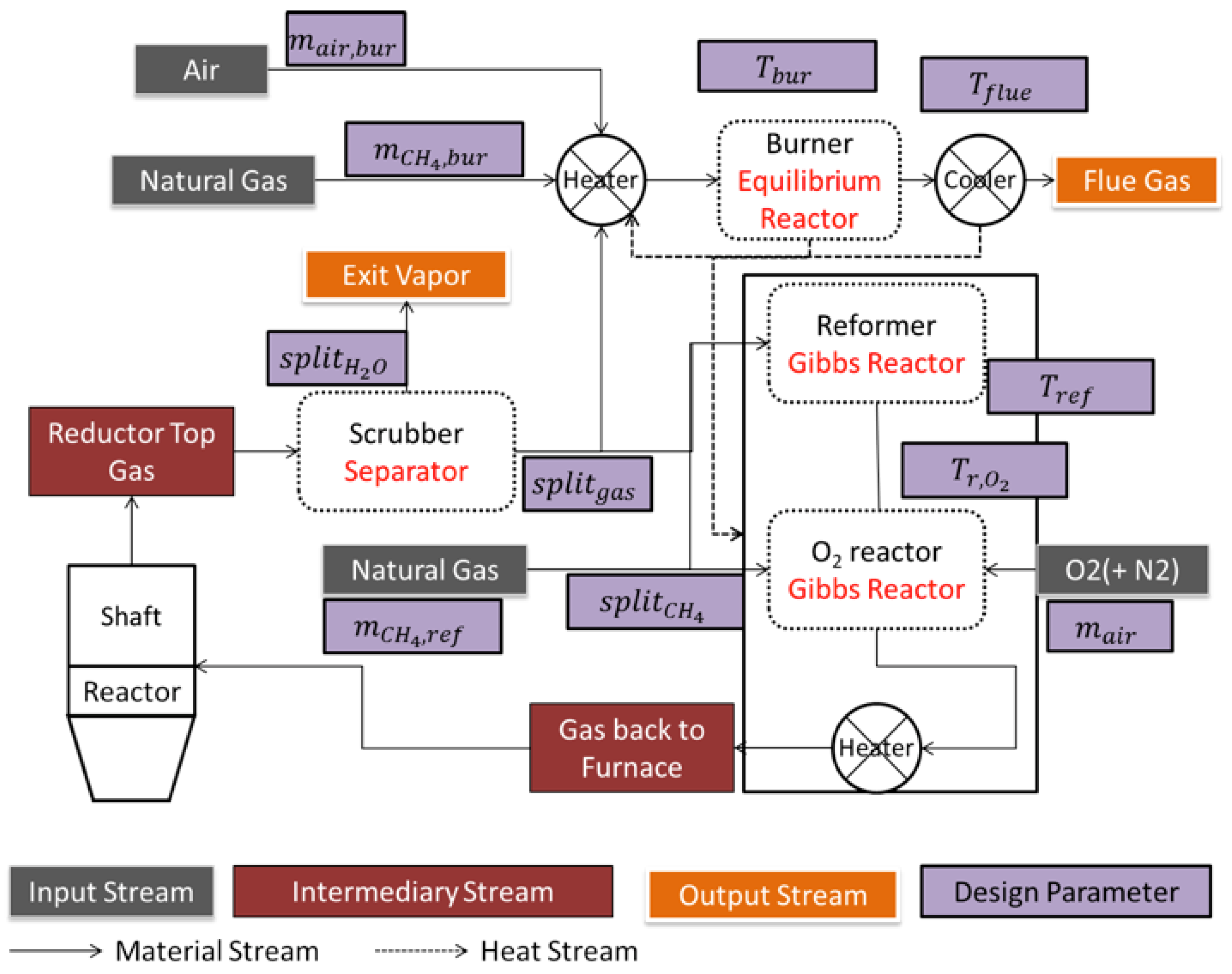
4.1. Aspen Plus Plant Model
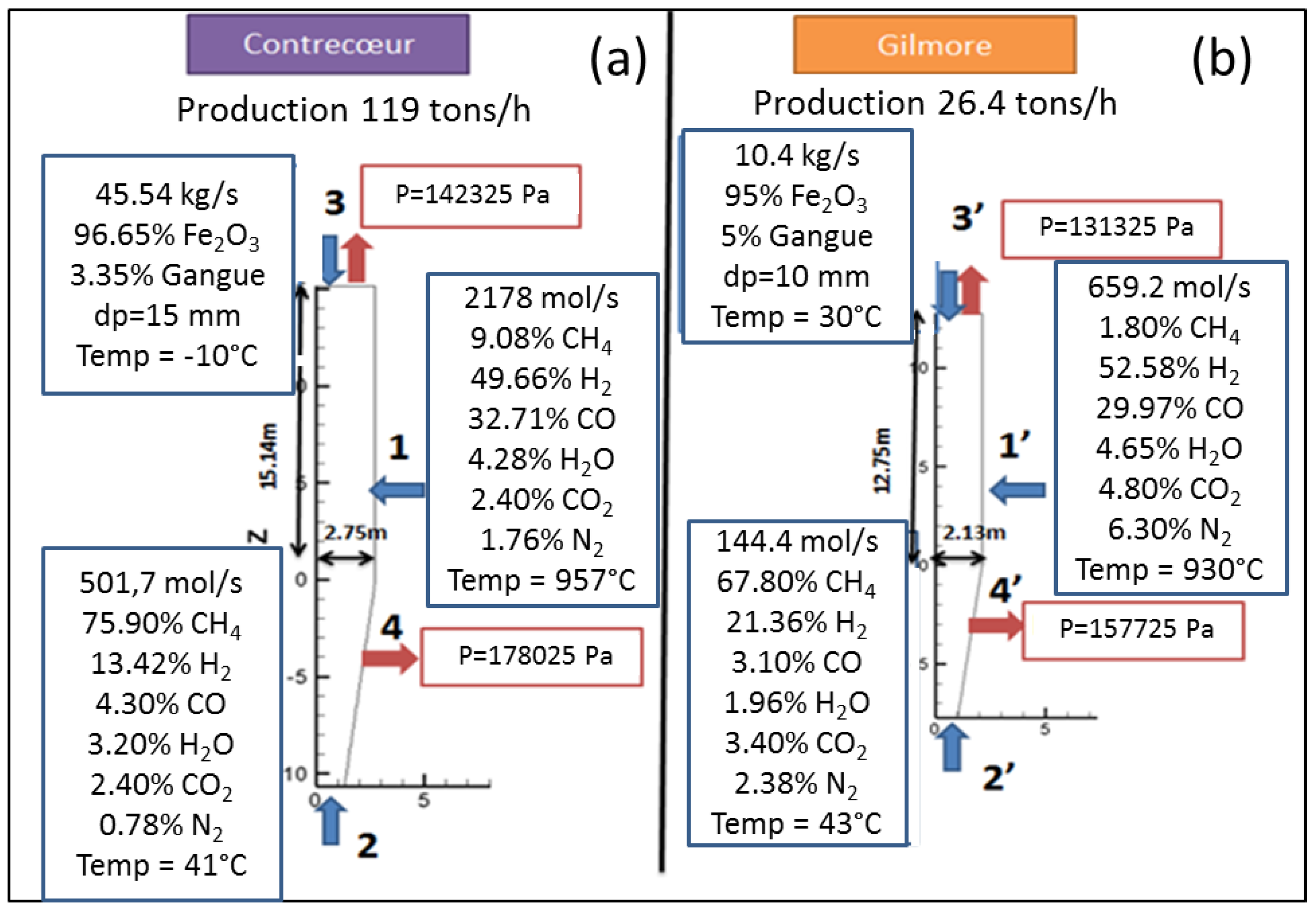
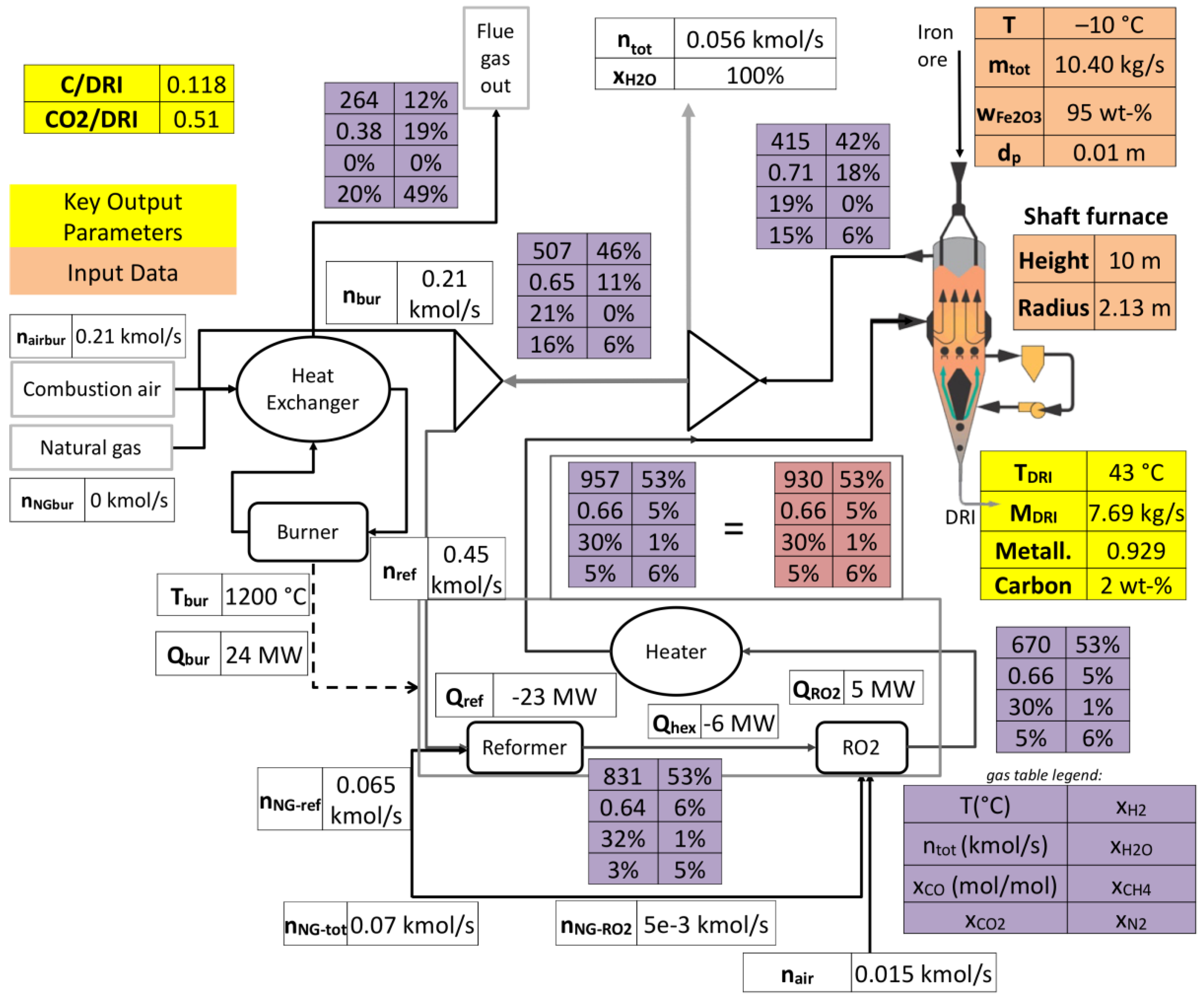
4.2. Results from the Aspen Plus Plant Model
4.3. Process Visualization
4.4. Process Optimization
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Reaction Number | Name | Formula |
|---|---|---|
| Reaction 1 | Hematite reduction | |
| Reaction 2 | Hematite reduction | |
| Reaction 3 | Magnetite reduction | |
| Reaction 4 | Magnetite reduction | |
| Reaction 5 | Wustite reduction | |
| Reaction 6 | Wustite reduction | |
| Reaction 7 | Steam reforming | |
| Reaction 8 | Water gas shift | |
| Reaction 9 | Methane decomposition | |
| Reaction 10 | Boudouard (inverse) |
Appendix B
References
- IEAGHG. Iron and Steel CCS Study (Technoeconomics Integrated Steel Mill). IEAGHG Report. 4 July 2013. Available online: http://ieaghg.org/publications/technical-reports (accessed on 19 May 2018).
- Duarte, P.E.; Becerra, J. Reducing greenhouse gas emissions with Energiron non-selective carbon-free emissions scheme. Stahl Und Eisen 2011, 131, 85. [Google Scholar]
- Chatterjee, A. Sponge Iron Production by Direct Reduction of Iron Oxide; PHI Learning Pvt. Ltd.: Delhi, India, 2010; ISBN 978-81-203-3644-5. [Google Scholar]
- Patisson, F.; Ablitzer, D. Modeling of gas-solid reactions: Kinetics, mass and heat transfer, and evolution of the pore structure. Chem. Eng. Technol. 2000, 23, 75–79. [Google Scholar] [CrossRef]
- Sohn, H.Y. The law of additive reaction times in fluid-solid reactions. Metall. Trans. B 1978, 9, 89–96. [Google Scholar] [CrossRef]
- Hamadeh, H. Modélisation Mathématique Détaillée du Procédé de Réduction Directe du Minerai de fer. Ph.D. Thesis, Université de Lorraine, Nancy, France, 2017. Available online: https://tel.archives-ouvertes.fr/tel-01740462 (accessed on 19 May 2018).
- Ranzani da Costa, A.; Wagner, D.; Patisson, F. Modelling a new, low CO2 emissions, hydrogen steelmaking process. J. Clean. Prod. 2013, 46, 27–35. [Google Scholar] [CrossRef]
- Rahimi, A.; Niksiar, A. A general model for moving-bed reactors with multiple chemical reactions, part I: Model formulation. Int. J. Min. Proc. 2013, 24, 58–66. [Google Scholar] [CrossRef]
- Nouri, S.M.M.; Ebrahim, H.A.; Jamshidi, E. Simulation of direct reduction reactor by the grain model. Chem. Eng. J. 2011, 166, 704–709. [Google Scholar] [CrossRef]
- Shams, A.; Moazeni, F. Modeling and Simulation of the MIDREX Shaft Furnace: Reduction, Transition and Cooling Zones. JOM 2015, 67, 2681–2689. [Google Scholar] [CrossRef]
- Palacios, P.; Toledo, M.; Cabrera, M. Iron ore reduction by methane partial oxidation in a porous media. Int. J. Hydrogen Energy 2015, 40, 9621–9633. [Google Scholar] [CrossRef]
- Alamsari, B.; Torii, S.; Trianto, A.; Bindar, Y. Study of the Effect of Reduced Iron Temperature Rising on Total Carbon Formation in Iron Reactor Isobaric and Cooling Zone. Adv. Mech. Eng. 2010, 2, 192430. [Google Scholar] [CrossRef]
- Alamsari, B.; Torii, S.; Trianto, A.; Bindar, Y. Heat and mass transfer in reduction zone of sponge iron reactor. ISRN Mech. Eng. 2011, 2011, 324659. [Google Scholar] [CrossRef]
- Hamadeh, H.; Patisson, F. Reductor, a 2D Physicochemical Model of the Direct Iron Ore Reduction in a Shaft Furnace. In Proceedings of the AISTech 2017 Conference, Nashville, TN, USA, 8–11 May 2017; pp. 937–946. Available online: http://digital.library.aist.org/pages/PR-372-106.htm (accessed on 19 May 2018).
- Ghadi, A.Z.; Valipour, M.S.; Biglari, M. CFD simulation of two-phase gas-particle flow in the Midrex shaft furnace: The effect of twin gas injection system on the performance of the reactor. Int. J. Hydrogen Energy 2017, 42, 103–118. [Google Scholar] [CrossRef]
- Alhumaizi, K.; Ajbar, A.; Soliman, M. Modelling the complex interactions between reformer and reduction furnace in a midrex-based iron plant. Can. J. Chem. Eng. 2012, 90, 1120–1141. [Google Scholar] [CrossRef]
- KOBELCO Site. Available online: http://www.kobelco.co.jp/english/products/dri/img/flow.gif (accessed on 19 May 2018).
- Ye, G.; Xie, D.; Qiao, W.; Grace, J.R.; Lim, C.J. Modeling of fluidized bed membrane reactors for hydrogen production from steam methane reforming with Aspen Plus. Int. J. Hydrogen Energy 2011, 34, 4755–4762. [Google Scholar] [CrossRef]
- Tripodi, A.; Compagnoni, M.; Ramis, G.; Rossetti, I. Process simulation of hydrogen production by steam reforming of diluted bioethanol solutions: Effect of operating parameters on electrical and thermal cogeneration by using fuel cells. Int. J. Hydrogen Energy 2017, 42, 23776–23783. [Google Scholar] [CrossRef]
- Guo, X.; Wu, S.; Xu, J.; Du, K. Reducing gas composition optimization for COREX® pre-reduction shaft furnace based on CO-H2 mixture. Procedia Eng. 2011, 15, 4702–4706. [Google Scholar] [CrossRef]
- Takahashi, R.; Takahashi, Y.; Yagi, J.I.; Omori, Y. Operation and simulation of pressurized shaft furnace for direct reduction. Trans. Iron Steel Inst. Jpn. 1986, 26, 765–774. [Google Scholar] [CrossRef]
- Byron Smith, R.J.; Loganathan, M.; SHANTHA, M.S. A review of the water gas shift reaction kinetics. Int. J. Chem. React. Eng. 2010, 8. [Google Scholar] [CrossRef]
- Grabke, H.J. Die Kinetik der Entkohlung und Aufkohlung von γ-Eisen in Methan-Wasserstoff-Gemischen. Ber. Bunsenges. Phys. Chem. 1965, 69, 409–414. [Google Scholar] [CrossRef]


| Reference | Reduction Steps | Gas Mixture | Dimen-sions | Geometric Model | Supplementary Reactions |
|---|---|---|---|---|---|
| Rahimi and Niksiar [8] | 3 | H2-CO | 1 | Grain Model | no |
| Nouri et al. [9] | 1 | H2-CO-H2O-CO2-N2-CH4 | 1 | Grain Model | no |
| Shams and Moazeni [10] | 2 | H2-CO-H2O-CO2-N2-CH4 | 1 | Unreacted Shrinking Core Model | methane decomposition + reforming |
| Palacios et al. [11] | 1 | H2-CO | 1 | no, but heat of reaction considered | |
| Bayu and Alamsari [12] Alamsari et al. [13] | 3 | H2-CO-H2O-CO2-N2-CH4 | 1 | methane reforming and water gas shift | |
| Ranzani da Costa et al. [7] | 3 | H2 | 2 | Grain Model (hematite & magnetite), Crystallite Model (Wustite) | no |
| Hamadeh et al. [6,14] | 3 | H2-CO-H2O-CO2-N2-CH4 | 2 | methane decomposition, reforming, water gas shift, Boudouard | |
| Ghadi et al. [15] | 3 | H2-H2O | 2 | Unreacted Shrinking Core Model | no |
| Reference | Heat Contribution | Presence of Cooling & Transition Zones | Pressure Drop | Validation against Industrial Data |
|---|---|---|---|---|
| Rahimi and Niksiar [8] | reaction, convection, diffusion | no | no | no |
| Nouri et al. [9] | reaction, convection | no | no | yes |
| Shams and Moazeni [10] | yes | yes | yes | |
| Palacios et al. [11] | reaction, convection, diffusion | no | no | no |
| Bayu and Alamsari [12] Alamsari et al. [13] | reaction, convection | yes | no | yes |
| Ranzani da Costa et al. [7] | reaction, convection, diffusion | no | no | no |
| Hamadeh et al. [6,14] | yes | yes | yes | |
| Ghadi et al. [15] | no | no | yes |
| Parameter | Contrecoeur | Gilmore | ||||||
|---|---|---|---|---|---|---|---|---|
| Plant Data | Present Model | Reductor Model [14] | Plant Data | Present Model | Reductor Model [14] | Shams Model [10] | ||
| Top gas | CO (vol %) | 19.58 | 18.88 | 19.89 | 18.90 | 19.00 | 20.87 | 19.44 |
| CO2 (vol %) | 17.09 | 15.60 | 14.69 | 14.30 | 14.60 | 13.13 | 17.54 | |
| H2O (vol %) | 19.03 | 19.50 | 19.52 | 21.20 | 17.60 | 20.61 | 18.04 | |
| H2 (vol %) | 40.28 | 40.20 | 40.41 | 37.00 | 42.20 | 37.70 | 37.96 | |
| N2 (vol %) | 1.02 | 1.63 | 1.55 | 7.67 | 6.00 | 8.60 | 7.02 | |
| CH4 (vol %) | 2.95 | 4.19 | 3.91 | - | - | - | - | |
| Temperature (°C) | 285 | 312 | 293 | n.a. | 417 | 285 | 474 | |
| Bottom solid | Fe2O3/Fetot (wt %) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fe3O4/Fetot (wt %) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| FeO/Fetot (wt %) | 6.20 | 6.1 | 6.00 | 7.00 | 7.00 | 4.70 | 10.00 | |
| Fe/Fetot (wt %) | 93.80 | 93.90 | 94.00 | 93.00 | 93.00 | 95.30 | 90.00 | |
| C (wt %) | 2.00 | 2.30 | 2.20 | 2.00 | 1.80 | 0.91 | 1.42 | |
| Average absolute difference with plant data (%) | - | 6.0 | 4.4 | - | 4.0 | 6.9 | 6.5 | |
| Equality to Respect | Controlled Variable | Value (Contrecoeur) | Data (Contrecoeur) | Value (Gilmore) |
|---|---|---|---|---|
| 0.64 | 0.65 | 0.68 | ||
| 0.62 | 0.60 | 0.44 | ||
| 837 °C | - | 830 °C | ||
| 860 °C | - | 670 °C | ||
| 338 mol/s | 380 mol/s | 71 mol/s | ||
| 11.6 mol/s | - | 14.9 mol/s | ||
| 0.434 | 0.92 | 0.92 | ||
| 0 mol/s | - | 8 mol/s | ||
| 295 °C | - | 345 °C | ||
| 871 mol/s | - | 216 mol/s |
| Parameter | Original | Opti-1 | Opti-2 | Opti-3 | Opti-4 | Opti-5 | Opti-6 |
|---|---|---|---|---|---|---|---|
| 1.75 | 1.57 | 1.5 | 1.35 | 1.23 | 1.05 | 1.23 | |
| 8 | 12 | 12 | 12 | 12 | 12 | 16 | |
| (kg/kg) | 0.119 | 0.119 | 0.113 | 0.109 | 0.105 | Diverged | 0.106 |
| Metallization (%) | 93% | 93.3% | 93.3% | 93.3% | 93.3% | 93% | |
| 1.8% | 2% | 2% | 2% | 2% | 2% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Béchara, R.; Hamadeh, H.; Mirgaux, O.; Patisson, F. Optimization of the Iron Ore Direct Reduction Process through Multiscale Process Modeling. Materials 2018, 11, 1094. https://doi.org/10.3390/ma11071094
Béchara R, Hamadeh H, Mirgaux O, Patisson F. Optimization of the Iron Ore Direct Reduction Process through Multiscale Process Modeling. Materials. 2018; 11(7):1094. https://doi.org/10.3390/ma11071094
Chicago/Turabian StyleBéchara, Rami, Hamzeh Hamadeh, Olivier Mirgaux, and Fabrice Patisson. 2018. "Optimization of the Iron Ore Direct Reduction Process through Multiscale Process Modeling" Materials 11, no. 7: 1094. https://doi.org/10.3390/ma11071094
APA StyleBéchara, R., Hamadeh, H., Mirgaux, O., & Patisson, F. (2018). Optimization of the Iron Ore Direct Reduction Process through Multiscale Process Modeling. Materials, 11(7), 1094. https://doi.org/10.3390/ma11071094