The Effect of Particle Shape on Sintering Behavior and Compressive Strength of Porous Alumina
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Analysis of Starting Alumina Powders
2.2. Sintering of Porous Alumina Compacts
2.3. Young’s Modulus and Compressive Strength of Sintered Porous Alumina
3. Results and Discussion
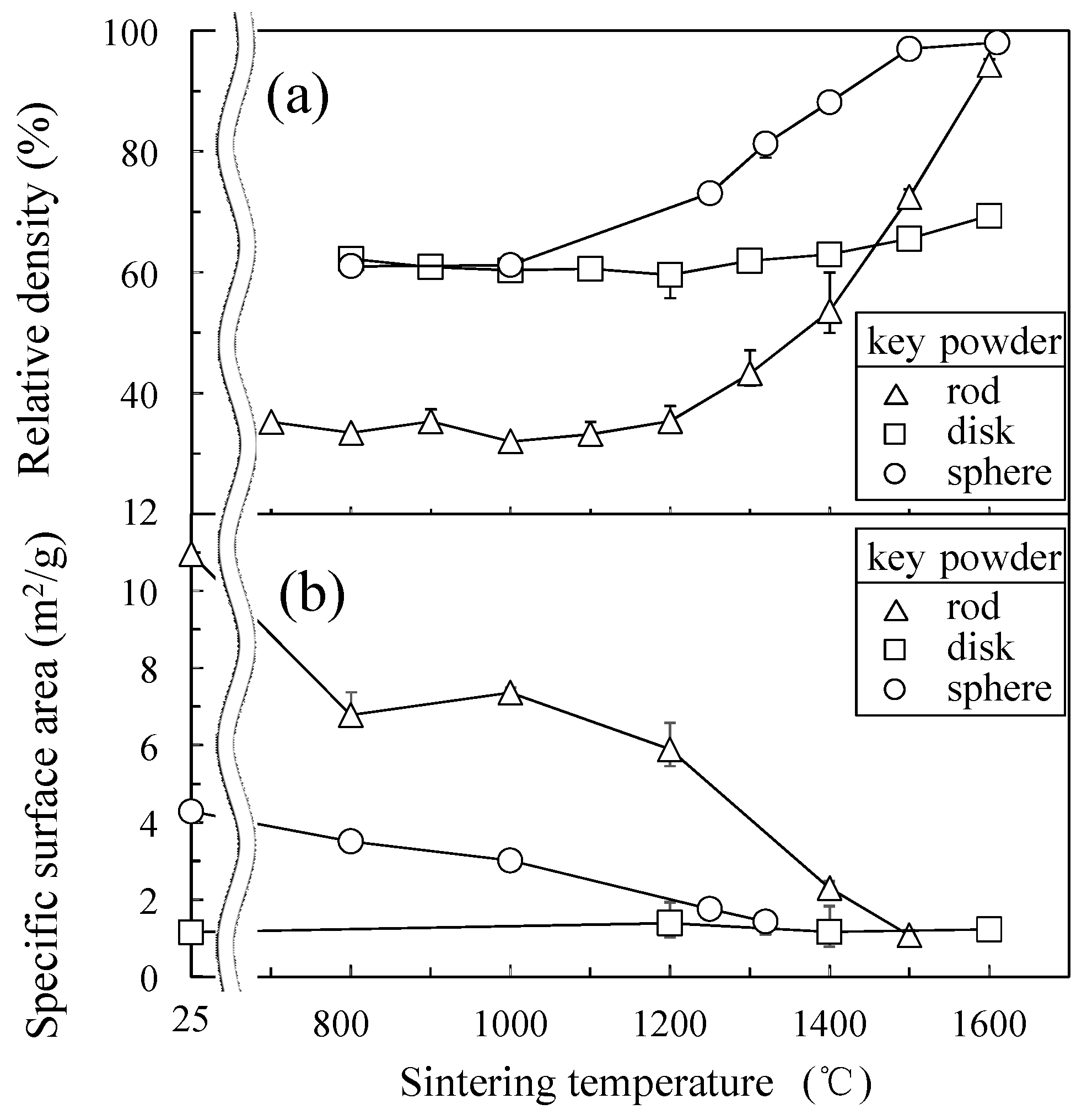
3.1. Sintering Behavior
3.2. Microstructures of the Sintered Alumina Compacts
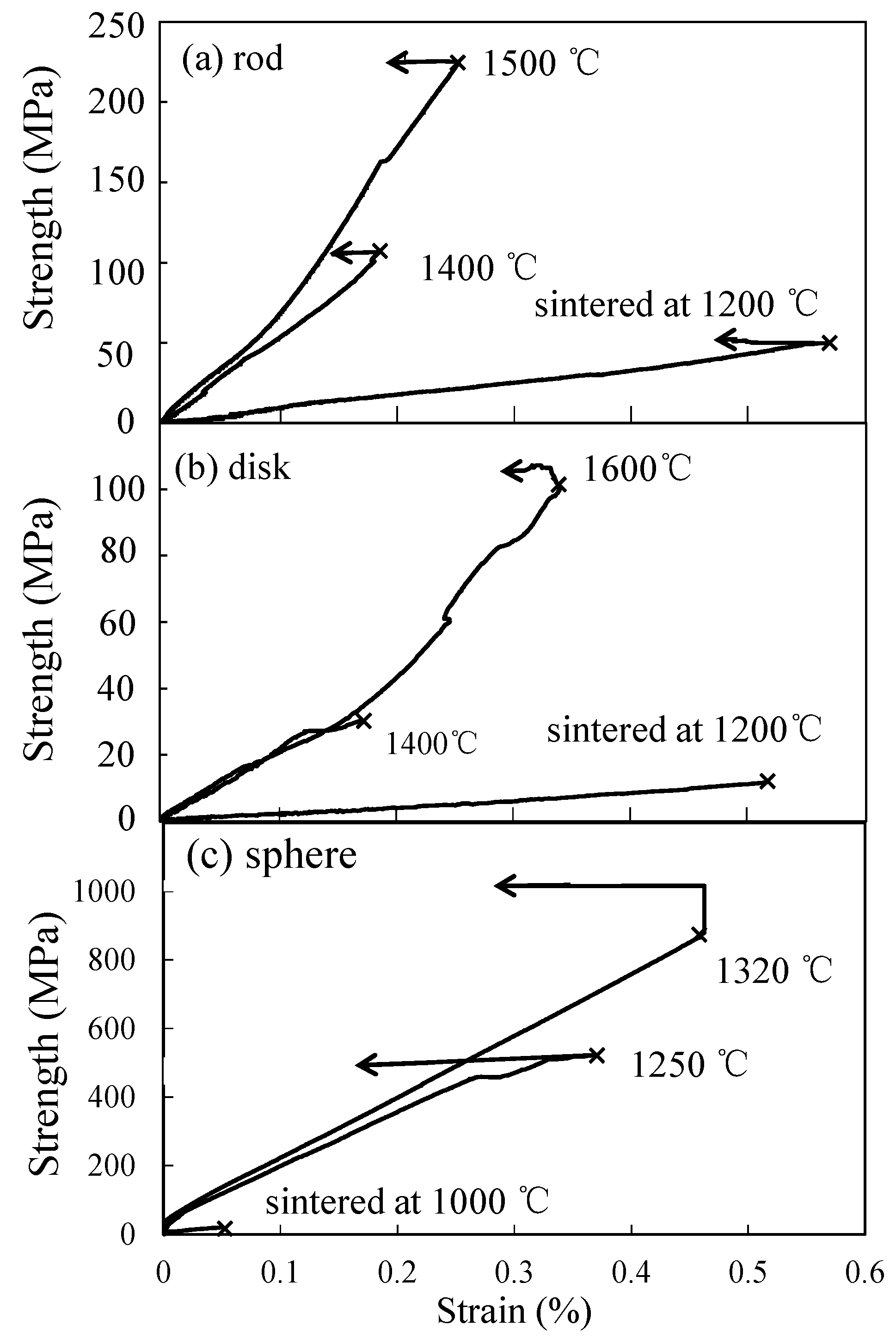
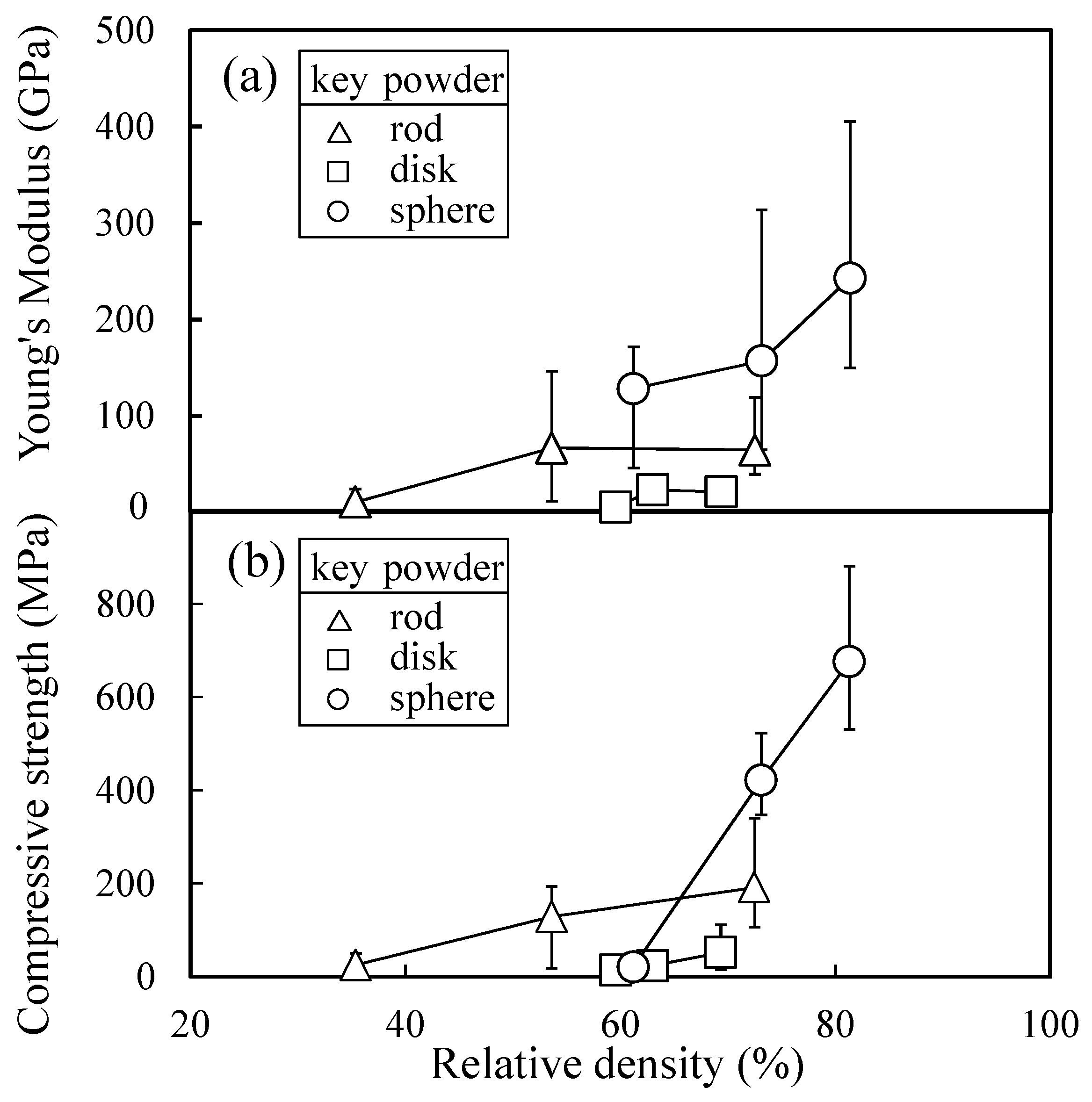
3.3. Compressive Mechanical Properties
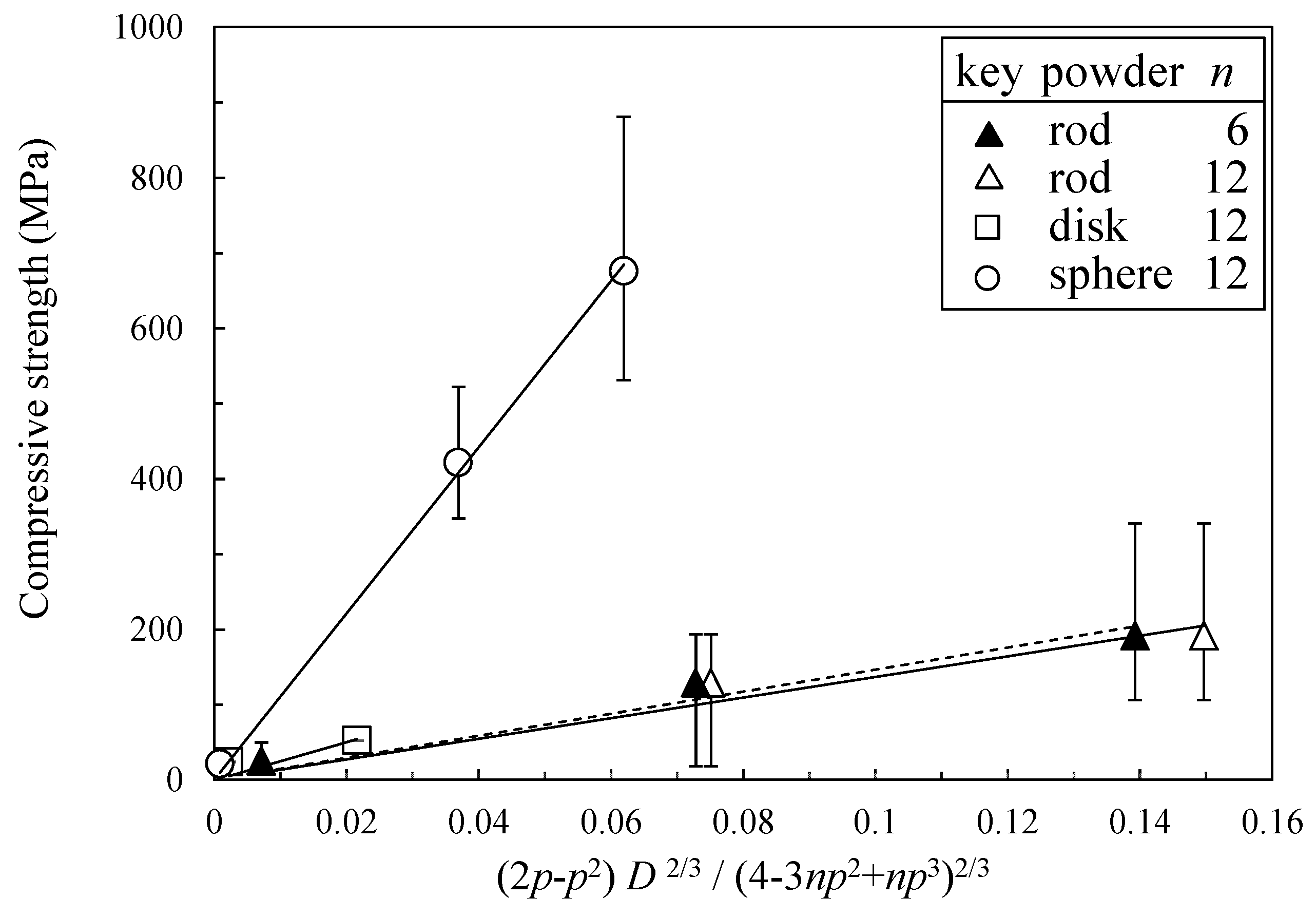
3.4. Analysis of Compressive Strength
3.5. Observation of Fractured Surfaces
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wan, P.; Wang, J. Highly porous nano-SiC with very low thermal conductivity and excellent high temperature behavior. J. Eur. Ceram. Soc. 2018, 38, 463–467. [Google Scholar] [CrossRef]
- Fukushima, M.; Yoshizawa, Y.-I. Fabrication and morphology control of highly porous mullite thermal insulators prepared by gelation freezing route. J. Eur. Ceram. Soc. 2016, 36, 2947–2953. [Google Scholar] [CrossRef]
- Bruzzoniti, M.C.; Appendini, M.; Rivoira, L.; Onida, B.; Bubba, M.D.; Jana, P.; Soraru, G.D. Polymer-derived ceramic aerogels as sorbent materials for the removal of organic dyes from aqueous solutions. J. Am. Ceram. Soc. 2018, 101, 821–830. [Google Scholar] [CrossRef]
- Ma, H.; Hei, Y.; Wei, T.; Li, H. Three-dimensional interconnected porous tablet ceramic: Synthesis and Pb(II) adsorption. Mater. Lett. 2017, 196, 396–399. [Google Scholar] [CrossRef]
- Pechenkin, A.A.; Badmaev, S.D.; Belyaev, V.D.; Sobyanin, V.A. Performance of bifunctional CuO–CeO2/γ-Al2O3 catalyst in dimethoxymethane steam reforming to hydrogen-rich gas for fuel cell feeding. Appl. Catal. B Environ. 2015, 166–167, 535–543. [Google Scholar] [CrossRef]
- Ishiyama, T.; Kurimoto, K.; Kita, M.; Otsuka-Yao-Matsuo, S.; Omata, T. Enhancement by praseodymium addition of catalytic activity of nickel supported on cerium–zirconium oxide in methane steam reforming. J. Ceram. Soc. Jpn. 2014, 122, 537–542. [Google Scholar] [CrossRef]
- Shikazono, N.; Kanno, D.; Matsuzaki, K.; Teshima, H.; Sumino, S.; Kasagi, N. Numerical assessment of SOFC anode polarization based on three dimensional model microstructure reconstructed from FIB-SEM images. J. Electrochem. Soc. 2010, 157, B665–B672. [Google Scholar] [CrossRef]
- Cronin, J.S.; Wilson, J.R.; Barnett, S.A. Impact of pore microstructure evolution on polarization resistance of Ni-yttria-stabilized zirconia fuel cell anodes. J. Power Sources 2011, 196, 2640–2643. [Google Scholar] [CrossRef]
- Abo-Almaged, H.H.; Gaber, A.A. Synthesis and characterization of nano-hydroxyapatite membranes for water desalination. Mater. Today Commun. 2017, 13, 186–191. [Google Scholar] [CrossRef]
- Bukhari, S.Z.A.; Ha, J.-H.; Lee, J.; Song, I.-H. Oxidation-bonded SiC membrane for microfiltration. J. Eur. Ceram. Soc. 2018, 38, 1711–1719. [Google Scholar] [CrossRef]
- Ryshkewitch, E. Compression strength of porous sintered alumina and zirconia. J. Am. Ceram. Soc. 1953, 36, 65–68. [Google Scholar] [CrossRef]
- Rice, R.W. Comparison of stress concentration versus minimum solid area based mechanical property relations. J. Mater. Sci. 1993, 28, 2187–2190. [Google Scholar] [CrossRef]
- Ostrowski, T.; Ziegler, A.; Bordia, R.; Rodel, J. Evolution of Young’s modulus, strength and microstructure during liquid phase sintering. J. Am. Ceram. Soc. 1998, 81, 1852–1860. [Google Scholar] [CrossRef]
- Kim, Y.-W.; Kim, H.-D.; Park, C.B. Processing of microcellular mullite. J. Am. Ceram. Soc. 2005, 88, 3311–3315. [Google Scholar] [CrossRef]
- Hirata, Y.; Shimonosono, T.; Sameshima, T.; Sameshima, S. Compressive mechanical properties of porous alumina compacts. Ceram. Int. 2014, 40, 2315–2322. [Google Scholar] [CrossRef]
- Hirata, Y.; Shimonosono, T.; Sameshima, S.; Tominaga, H. Sintering of alumina powder compacts and their compressive mechanical properties. Ceram. Int. 2015, 41, 11449–11455. [Google Scholar] [CrossRef]
- Hirata, Y.; Takehara, K.; Shimonosono, T. Analyses of Young’s modulus and thermal expansion coefficient of sintered porous alumina compacts. Ceram. Int. 2017, 43, 12321–12327. [Google Scholar] [CrossRef]
- Hirata, Y.; Fujita, H.; Shimonosono, T. Compressive mechanical properties of partially sintered porous alumina of bimodal size system. Ceram. Int. 2017, 43, 1895–1903. [Google Scholar] [CrossRef]
- Dong, X.; Wang, M.; Guo, A.; Zhang, Y.; Ren, S.; Sui, G.; Du, H. Synthesis and properties of porous alumina ceramics with inter-locked plate-like structure through the tert-butyl alcohol-based gel-casting method. J. Alloys Compd. 2017, 694, 1045–1053. [Google Scholar] [CrossRef]
- Faber, K.T.; Evans, A.G. Crack deflection processes—I. Theory. Acta. Metall. 1983, 31, 565–576. [Google Scholar] [CrossRef]
- Dong, W.; Zhu, S.; Bai, T.; Luo, Y. Influence of Al2O3 whisker concentration on mechanical properties of WC–Al2O3 whisker composite. Ceram. Int. 2015, 41, 13685–13691. [Google Scholar] [CrossRef]
- STC Corporation, Alumina (AL998, AL998E). Available online: http://www.ceramics.net/ (accessed on 13 June 2018).
- Accuratus Corporation, Alumina Oxide. Available online: http://accuratus.com/alumox.html (accessed on 28 June 2018).



| Powder No. | L30N2-F1112 | ACLM-27 | AKP20 |
|---|---|---|---|
| Crystal structure | α-alumina | α-alumina | α-alumina |
| Manufacturer | Asahikasei | Sumitomo Chemical | Sumitomo Chemical |
| Particle shape | Rod-like | Disk-like | Spherical |
| Specific surface area (m2/g) | 10.96 | 1.16 | 4.28 |
| Median diameter (μm) | 0.55 | 1.47 | 0.60 |
| True density (g/cm3) | 3.990 | 3.961 | 3.990 |
| Isoelectric point | pH 6.45 | pH 5.28 | pH 5.31 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miyake, K.; Hirata, Y.; Shimonosono, T.; Sameshima, S. The Effect of Particle Shape on Sintering Behavior and Compressive Strength of Porous Alumina. Materials 2018, 11, 1137. https://doi.org/10.3390/ma11071137
Miyake K, Hirata Y, Shimonosono T, Sameshima S. The Effect of Particle Shape on Sintering Behavior and Compressive Strength of Porous Alumina. Materials. 2018; 11(7):1137. https://doi.org/10.3390/ma11071137
Chicago/Turabian StyleMiyake, Kimiya, Yoshihiro Hirata, Taro Shimonosono, and Soichiro Sameshima. 2018. "The Effect of Particle Shape on Sintering Behavior and Compressive Strength of Porous Alumina" Materials 11, no. 7: 1137. https://doi.org/10.3390/ma11071137
APA StyleMiyake, K., Hirata, Y., Shimonosono, T., & Sameshima, S. (2018). The Effect of Particle Shape on Sintering Behavior and Compressive Strength of Porous Alumina. Materials, 11(7), 1137. https://doi.org/10.3390/ma11071137




