Active Enhancement of Slow Light Based on Plasmon-Induced Transparency with Gain Materials
Abstract
1. Introduction
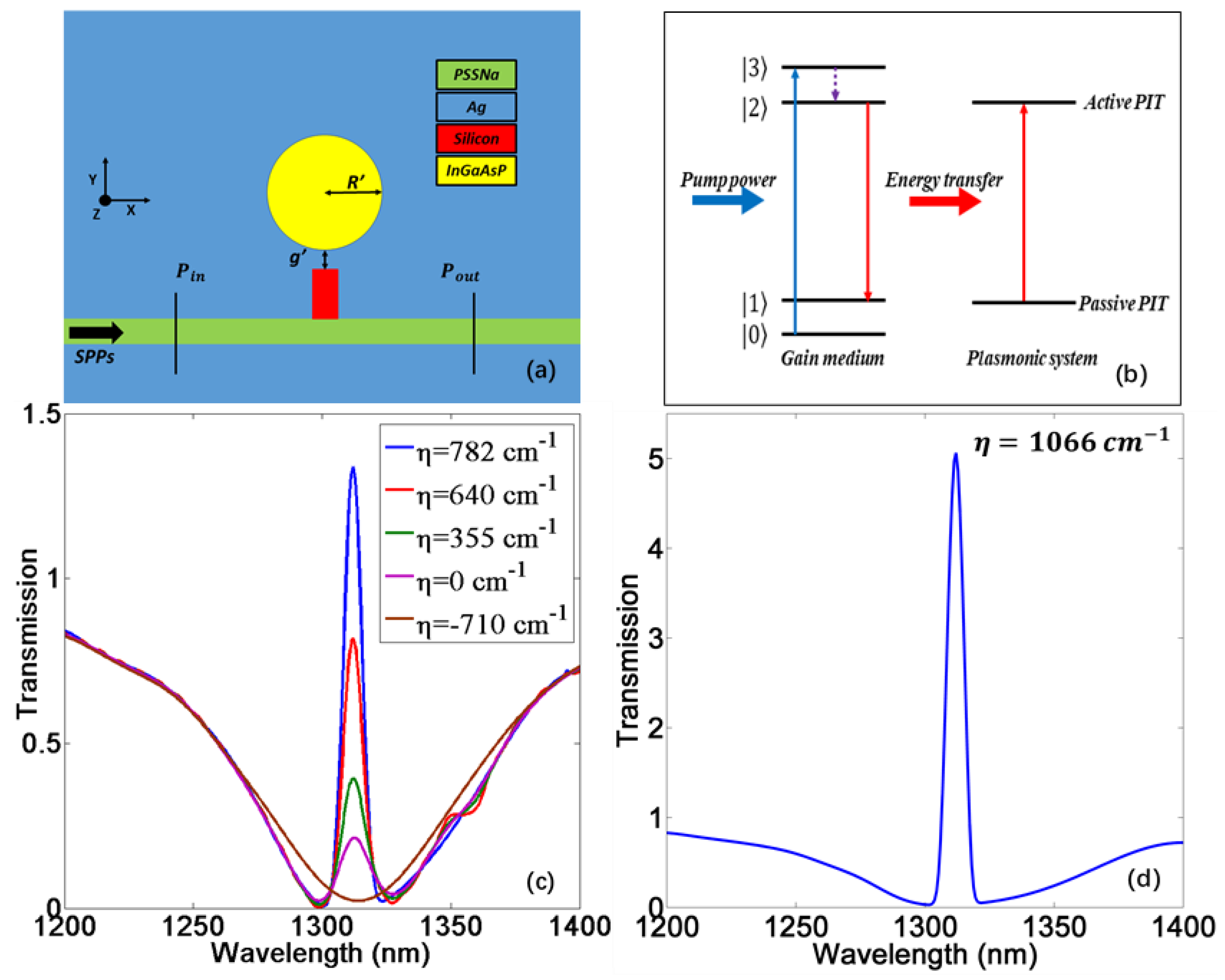
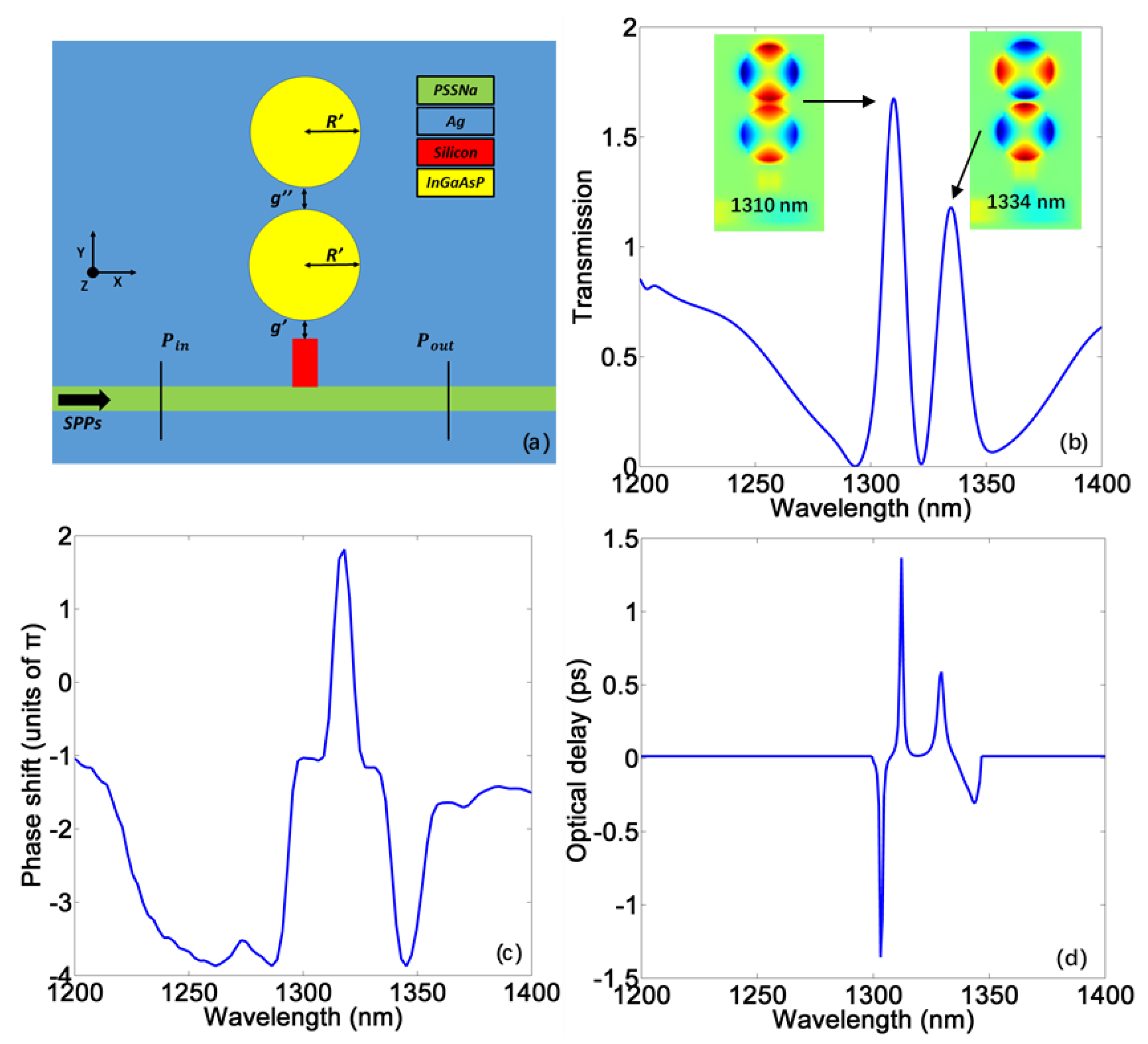
2. Materials and Methods
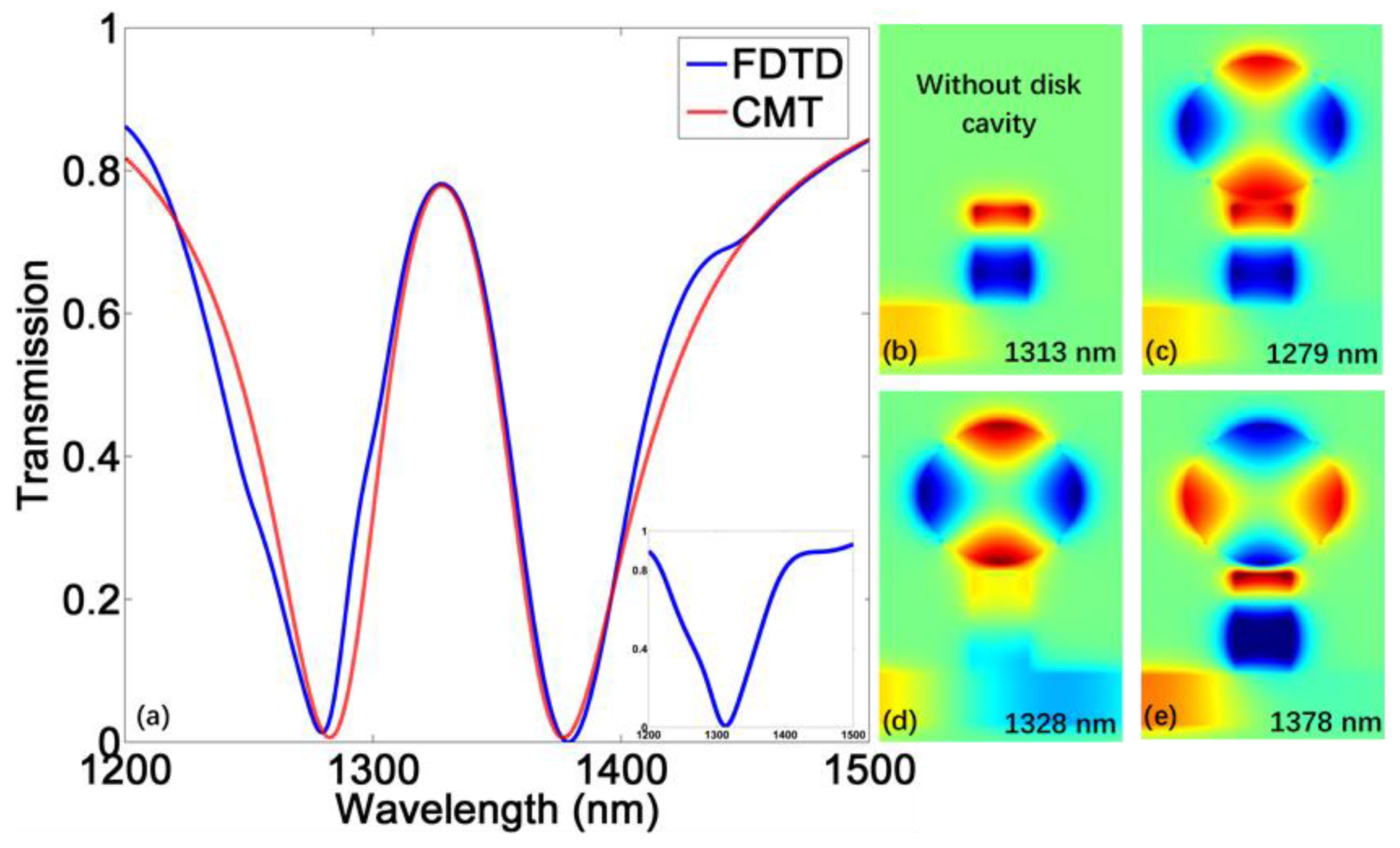
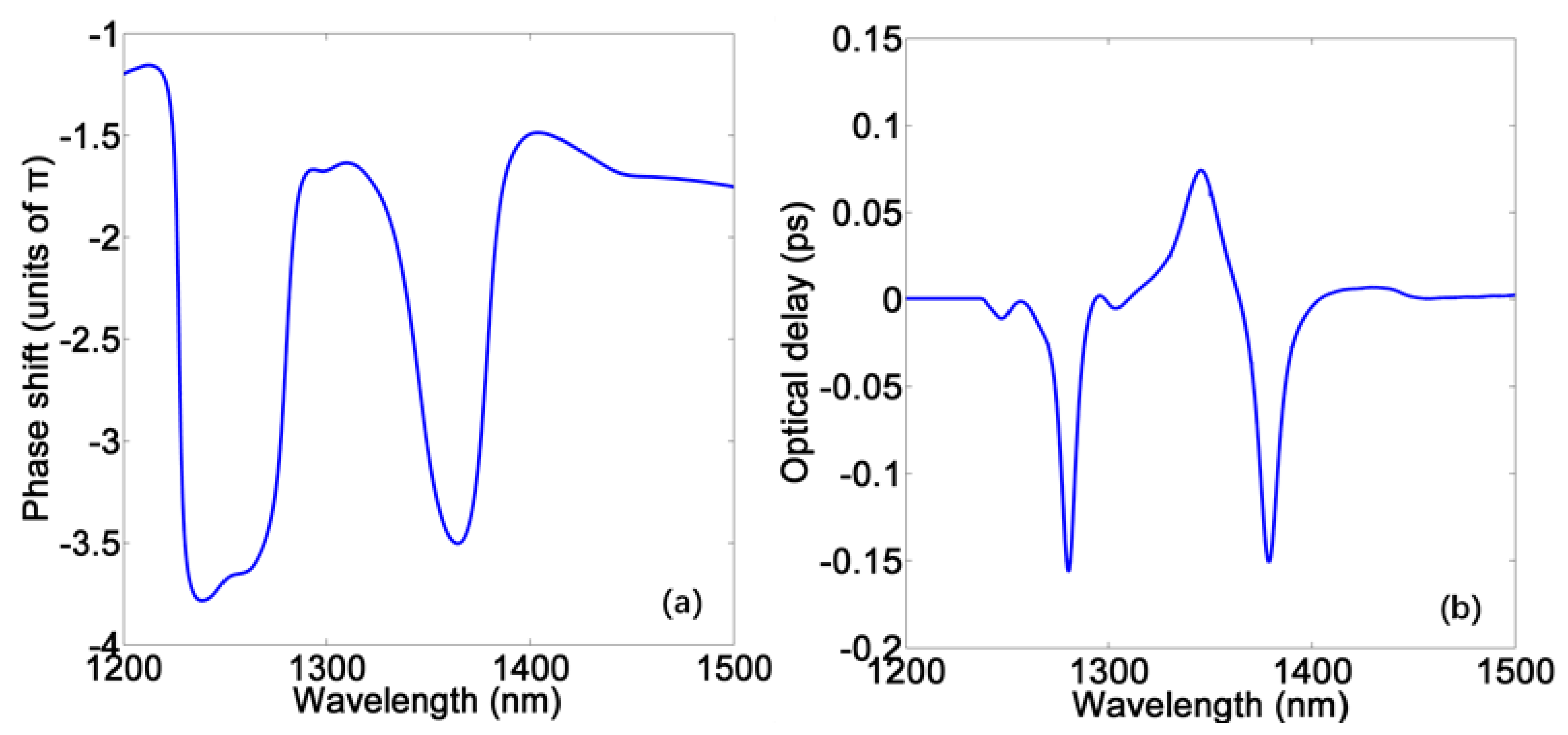
3. The Slow Light Performance
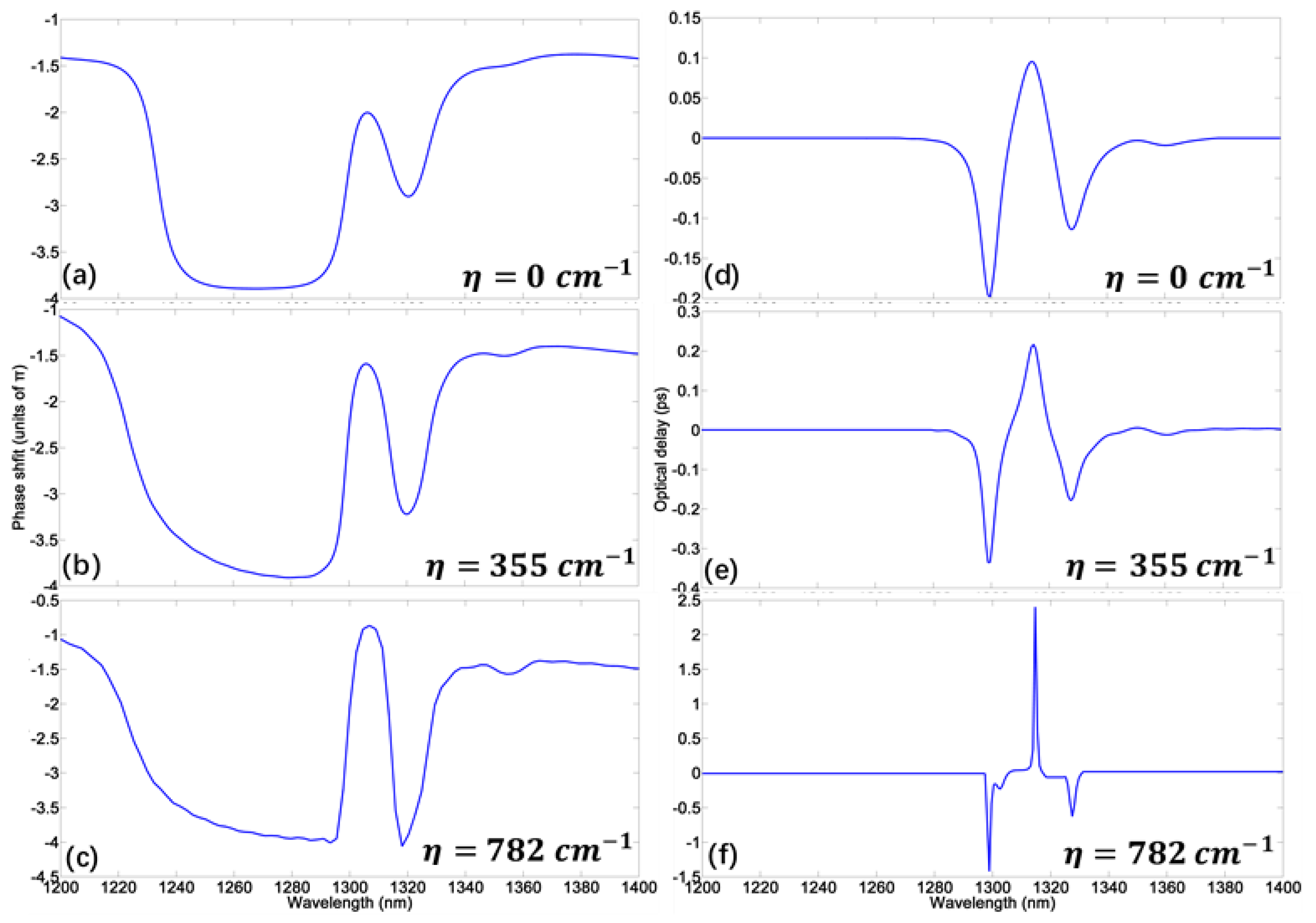
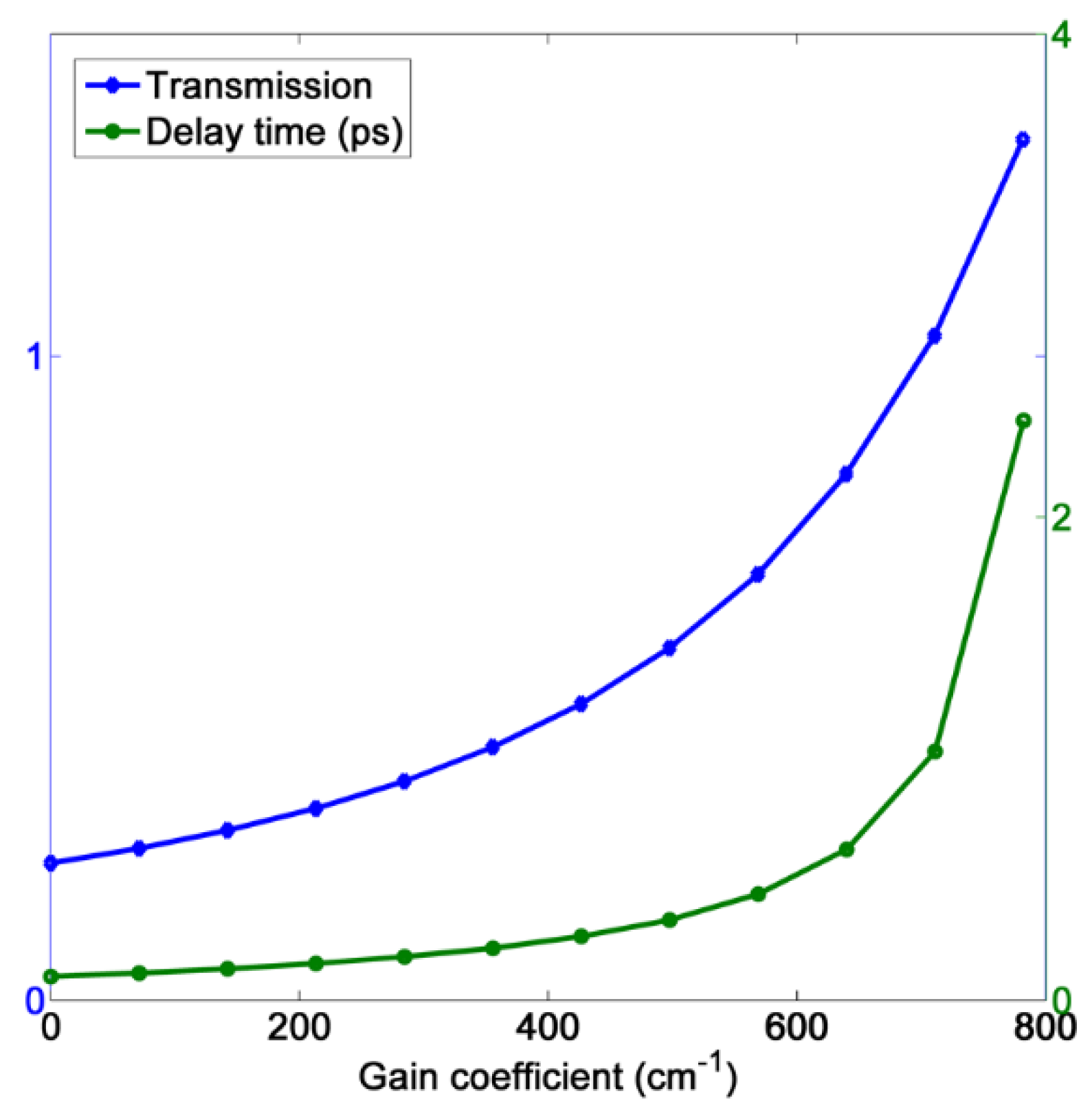
4. Slow Light Enhanced by Gain Material
5. Gain-Assisted Slow Light with Double Channels
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fleischhauer, M.; Physik, F.; Kaiserslautern, D.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 meters per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Schmidt, H.; Imamogdlu, A. Giant Kerr nonlinearities obtained by electromagnetically induced transparency. Opt. Lett. 1996, 21, 1936. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Liu, X.; Mao, D.; Gong, Y.; Wang, G. Induced transparency in nanoscale plasmonic resonator systems. Opt. Lett. 2011, 36, 3233–3235. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Yang, J.; He, X.; Zhang, J.; Huang, J.; Chen, D.; Han, Y. Plasmonic Refractive Index Sensor with High Figure of Merit Based on Concentric-Rings Resonator. Sensors 2018, 18, 116. [Google Scholar] [CrossRef] [PubMed]
- Zhan, S.; Li, H.; He, Z.; Li, B.; Chen, Z.; Xu, H. Sensing analysis based on plasmon induced transparency in nanocavity-coupled waveguide. Opt. Express 2015, 23, 20313–20320. [Google Scholar] [CrossRef] [PubMed]
- Khunsin, W.; Dorfmüller, J.; Esslinger, M.; Vogelgesang, R.; Rockstuhl, C.; Etrich, C.; Kern, K. Quantitative and direct near-field analysis of plasmonic-induced transparency and the observation of a plasmonic breathing mode. ACS Nano 2016, 10, 2214–2224. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Hu, X.; Chai, Z.; Lu, C.; Yang, H.; Gong, Q. Tunable ultracompact chip-integrated multichannel filter based on plasmon-induced transparencies. Appl. Phys. Lett. 2014, 104, 221114. [Google Scholar] [CrossRef]
- Zhan, S.; Li, H.; Cao, G.; He, Z.; Li, B.; Xu, H. Theoretical analysis of plasmon-induced transparency in ring-resonators coupled channel drop filter systems. Plasmonics 2014, 9, 1431–1437. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, B.; Fan, C.; He, J.; Ding, P.; Xue, Q.; Liang, E. A novel planar metamaterial design for electromagnetically induced transparency and slow light. Opt. Express 2013, 21, 25159–25166. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Liu, X.; Mao, D. Plasmonic analog of electromagnetically induced transparency in multi-nanoresonator-coupled waveguide systems. Phys. Rev. A 2012, 85, 53803. [Google Scholar] [CrossRef]
- Han, X.; Wang, T.; Li, X.; Liu, B.; He, Y.; Tang, J. Dynamically tunable slow light based on plasmon induced transparency in disk resonators coupled MDM waveguide system. J. Phys. D Appl. Phys. 2015, 48, 235102. [Google Scholar] [CrossRef]
- Lai, G.; Liang, R.; Zhang, Y.; Bian, Z.; Yi, L.; Zhan, G.; Zhao, R. Double plasmonic nanodisks design for electromagnetically induced transparency and slow light. Opt. Express 2015, 23, 6554–6561. [Google Scholar] [CrossRef] [PubMed]
- Akhavan, A.; Ghafoorifard, H.; Abdolhosseini, S.; Habibiyan, H. Plasmon-induced transparency based on a triangle cavity coupled with an ellipse-ring resonator. Appl. Opt. 2017, 56, 9556–9563. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Wang, Z.; Huang, Q.; Jiang, W.; Wu, Z.; Wang, Y.; Xia, J. Plasmon-induced transparency and high-performance slow light in a plasmonic single-mode and two-mode resonators coupled system. J. Lightwave Technol. 2017, 35, 1710–1717. [Google Scholar] [CrossRef]
- Kurter, C.; Tassin, P.; Zhang, L.; Koschny, T.; Zhuravel, A.P.; Ustinov, A.V.; Anlage, S.M.; Soukoulis, C.M. Classical analogue of electromagnetically induced transparency with a metal-superconductor hybrid metamaterial. Phys. Rev. Lett. 2011, 107, 043901. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Li, H.; Zhan, S.; Li, B.; Chen, Z.; Xu, H. Tunable multi-switching in plasmonic waveguide with Kerr nonlinear resonator. Sci. Rep. 2015, 5, 15837. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Yi, Z.; Xiao, S. Active control of near-field coupling in a terahertz metal-graphene metamaterial. IEEE Photonics Technol. Lett. 2017, 29, 1998–2001. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 2017, 126, 271–278. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Jiang, X.; Yan, X.; Cheng, L.; Wang, B.; Xu, C. Strong interaction between graphene layer and fano resonance in terahertz metamaterials. J. Phys. D Appl. Phys. 2017, 50, 195101. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Prosvirnin, S.L.; Papasimakis, N.; Fedotov, V.A. Lasing spaser. Nat. Photonics 2008, 2, 351–354. [Google Scholar] [CrossRef]
- Deng, Z.L.; Dong, J.W. Lasing in plasmon-induced transparency nanocavity. Opt. Express 2013, 21, 20291–20302. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Ge, C.; Tao, Y.; Zhu, L.; Zheng, K.; Wang, W.; Sun, Y.; Shen, P.; Guo, Z. High-efficiency refractive index sensor based on the metallic nanoslit arrays with gain-assisted materials. Nanophotonics 2016, 5, 548–555. [Google Scholar] [CrossRef]
- Dong, Z.G.; Liu, H.; Cao, J.X.; Li, T.; Wang, S.M.; Zhu, S.N.; Zhang, X. Enhanced sensing performance by the plasmonic analog of electromagnetically induced transparency in active metamaterials. Appl. Phys. Lett. 2010, 97, 114101. [Google Scholar] [CrossRef]
- He, J.; Wang, J.; Ding, P.; Fan, C.; Liang, E. Gain-assisted plasmon induced transparency in t-shaped metamaterials for slow light. J. Opt. 2015, 17, 055002. [Google Scholar] [CrossRef]
- Liu, B.; Zhu, W.; Gunapala, S.D.; Stockman, M.I.; Premaratne, M. Open resonator electric spaser. ACS Nano 2017, 11, 12573–12582. [Google Scholar] [CrossRef] [PubMed]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Baffou, G.; Quidant, R. Thermo-plasmonics: Using metallic nanostructures as nano-sources of heat. Laser Photonics Rev. 2013, 7, 171–187. [Google Scholar] [CrossRef]
- Vyshnevyy, A.A.; Fedyanin, D.Y. Self-heating and cooling of active plasmonic waveguides. ACS Photonics 2016, 3, 51–57. [Google Scholar] [CrossRef]
- Kamada, S.; Okamoto, T.; El-Zohary, S.E.; Haraguchi, M. Design optimization and fabrication of Mach-Zehnder interferometer based on MIM plasmonic waveguides. Opt. Express 2016, 24, 16224–16231. [Google Scholar] [CrossRef] [PubMed]
- Veronis, G.; Fan, S. Modes of subwavelength plasmonic slot waveguides. J. Lightwave Technol. 2007, 25, 2511–2521. [Google Scholar] [CrossRef]
- Yu, Z.; Veronis, G.; Fan, S.; Brongersma, M.L. Gain-induced switching in metal-dielectric-metal plasmonic waveguides. Appl. Phys. Lett. 2008, 92, 041117. [Google Scholar] [CrossRef]
- Bamiedakis, N.; Beals, J.; Penty, R.V.; White, I.H.; Degroot, J.V.; Clapp, T.V. Cost-effective multimode polymer waveguides for high-speed on-board optical interconnects. IEEE J. Quantum Electron. 2009, 45, 415–424. [Google Scholar] [CrossRef]
- Beadie, G.; Brindza, M.; Flynn, R.A.; Rosenberg, A.; Shirk, J.S. Refractive index measurements of poly (methyl methacrylate) (PMMA) from 0.4–1.6 μm. Appl. Opt. 2015, 54, F139–F143. [Google Scholar] [CrossRef] [PubMed]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin, Germany, 2014; Volume 52, pp. 49–74. [Google Scholar]
- Luo, S.; Li, B.; Xiong, D.; Zuo, D.; Wang, X. A high performance plasmonic sensor based on metal-insulator-metal waveguide coupled with a double-cavity structure. Plasmonics 2016, 12, 1–5. [Google Scholar] [CrossRef]
- Ciminelli, C.; Campanella, C.E.; Dell’Olio, F.; Armenise, M.N. Fast light generation through velocity manipulation in two vertically-stacked ring resonators. Opt. Express 2010, 18, 2973–2986. [Google Scholar] [CrossRef] [PubMed]
- Bigelow, M.S.; Lepeshkin, N.N.; Boyd, R.W. Superluminal and slow light propagation in a room-temperature solid. Science 2003, 301, 200–202. [Google Scholar] [CrossRef] [PubMed]
- Ambati, M.; Nam, S.H.; Ulinavila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Observation of stimulated emission of surface plasmon polaritons. Nano Lett. 2008, 8, 3998–4001. [Google Scholar] [CrossRef] [PubMed]
- De, L.A.; Grzelczak, M.P.; Pastorizasantos, I.; Lizmarzán, L.M.; La Deda, M.; Striccoli, M.; Strangi, G. Dispersed and encapsulated gain medium in plasmonic nanoparticles: A multipronged approach to mitigate optical losses. ACS Nano 2011, 5, 5823–5829. [Google Scholar]
- Fujita, M.; Teshima, K.; Baba, T. Low-threshold continuous-wave lasing in photopumped GaInAsP microdisk lasers: Optics and quantum electronics. Jpn. J. Appl. Phys. 2001, 40, L875–L877. [Google Scholar] [CrossRef]
- Watanabe, T.; Saijo, Y.; Hasegawa, Y.; Watanabe, K.; Nishijima, Y.; Baba, T. Ion-sensitive photonic-crystal nanolaser sensors. Opt. Express 2017, 25, 24469–24479. [Google Scholar] [CrossRef] [PubMed]
- Shahamat, Y.; Vahedi, M. Plasmon-induced transparency in a rectangle cavity and an H-shaped structure for sensing and switching applications. J. Nanophotonics 2017, 11, 046012. [Google Scholar] [CrossRef]
- Kirstaedter, N.; Schmidt, O.G.; Ledentsov, N.N.; Bimberg, D.; Ustinov, V.M.; Egorov, A.Y.; Zhukov, A.E.; Maximov, M.V.; Kop’ev, P.S.; Alferov, Z.I. Gain and differential gain of single layer InAs/GaAs quantum dot injection lasers. Appl. Phys. Lett. 1996, 69, 1226–1228. [Google Scholar] [CrossRef]
- Carrere, H.; Marie, X.; Lombez, L.; Amand, T. Optical gain of INGAASN/INP quantum wells for laser applications. Appl. Phys. Lett. 2006, 89, 181115. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Yang, J.; He, X.; Han, Y.; Zhang, J.; Huang, J.; Chen, D.; Xu, S. Active Enhancement of Slow Light Based on Plasmon-Induced Transparency with Gain Materials. Materials 2018, 11, 941. https://doi.org/10.3390/ma11060941
Zhang Z, Yang J, He X, Han Y, Zhang J, Huang J, Chen D, Xu S. Active Enhancement of Slow Light Based on Plasmon-Induced Transparency with Gain Materials. Materials. 2018; 11(6):941. https://doi.org/10.3390/ma11060941
Chicago/Turabian StyleZhang, Zhaojian, Junbo Yang, Xin He, Yunxin Han, Jingjing Zhang, Jie Huang, Dingbo Chen, and Siyu Xu. 2018. "Active Enhancement of Slow Light Based on Plasmon-Induced Transparency with Gain Materials" Materials 11, no. 6: 941. https://doi.org/10.3390/ma11060941
APA StyleZhang, Z., Yang, J., He, X., Han, Y., Zhang, J., Huang, J., Chen, D., & Xu, S. (2018). Active Enhancement of Slow Light Based on Plasmon-Induced Transparency with Gain Materials. Materials, 11(6), 941. https://doi.org/10.3390/ma11060941





