Modulation of Magnetic Properties at the Nanometer Scale in Continuously Graded Ferromagnets
Abstract
1. Introduction to Graded Materials
2. Prior Work on Exchange Graded Layer Structures
3. Epitaxial Graded Structures
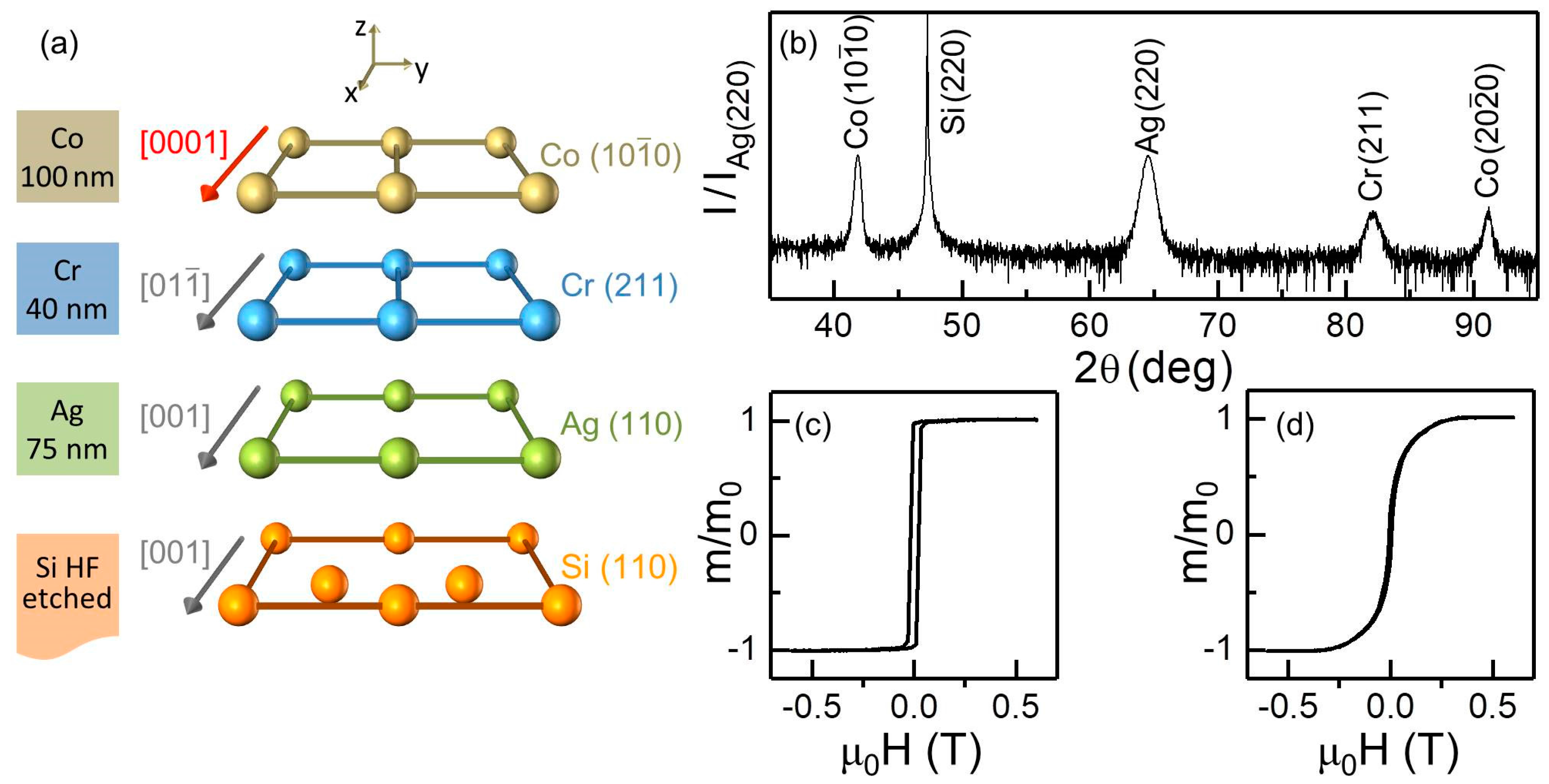
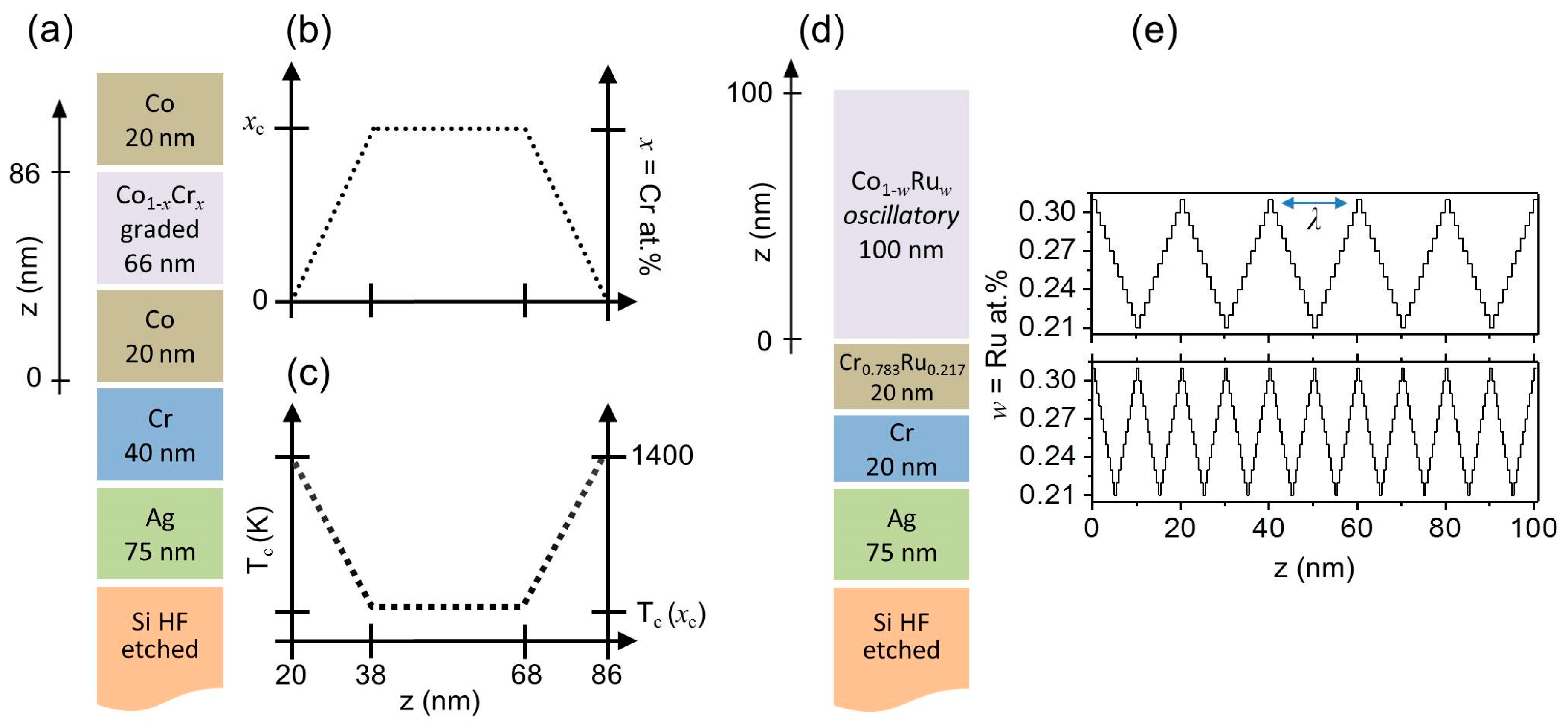
3.1. Test Structures
3.2. Explored Depth Profiles
3.3. Experimental Characterization Methods
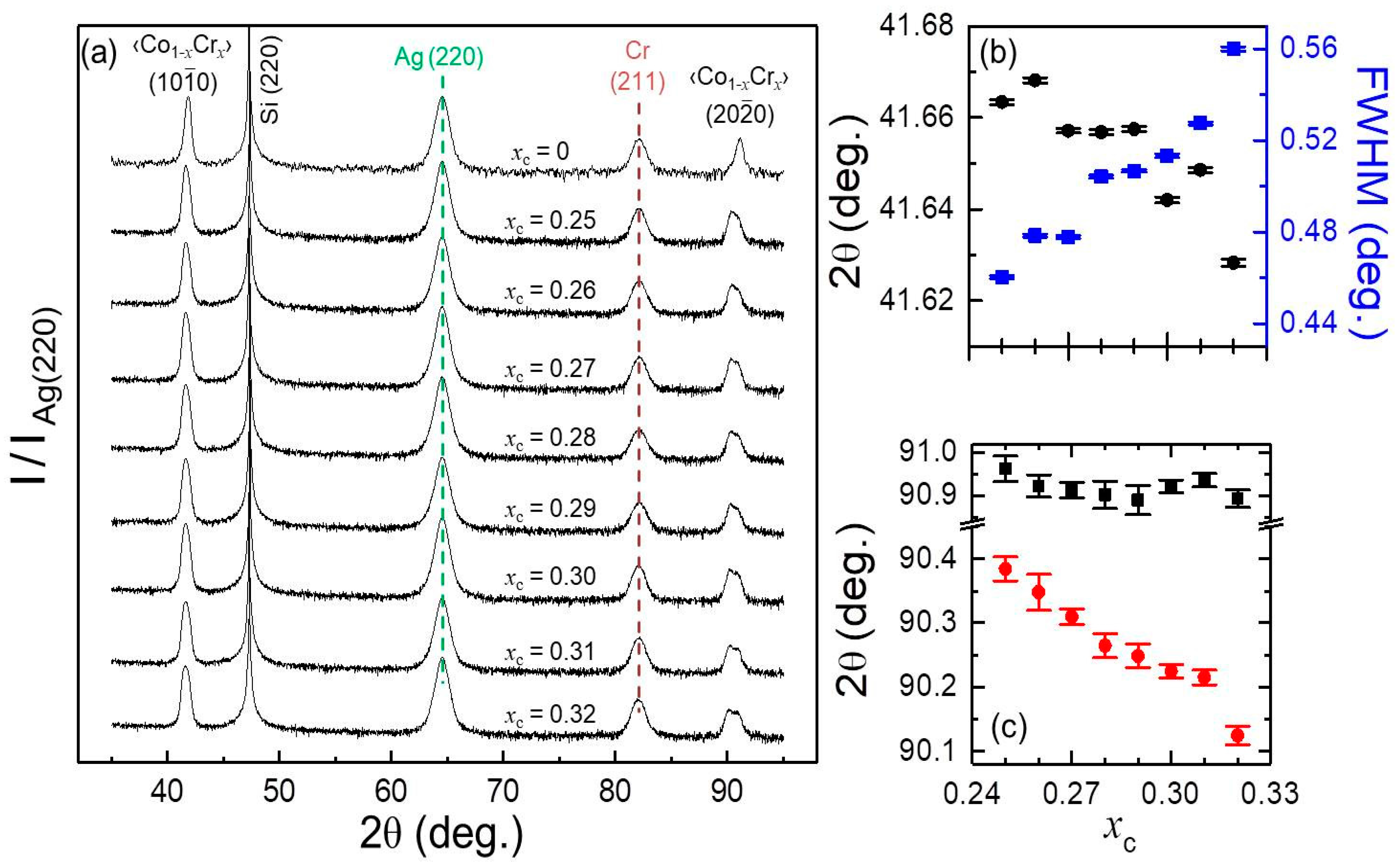
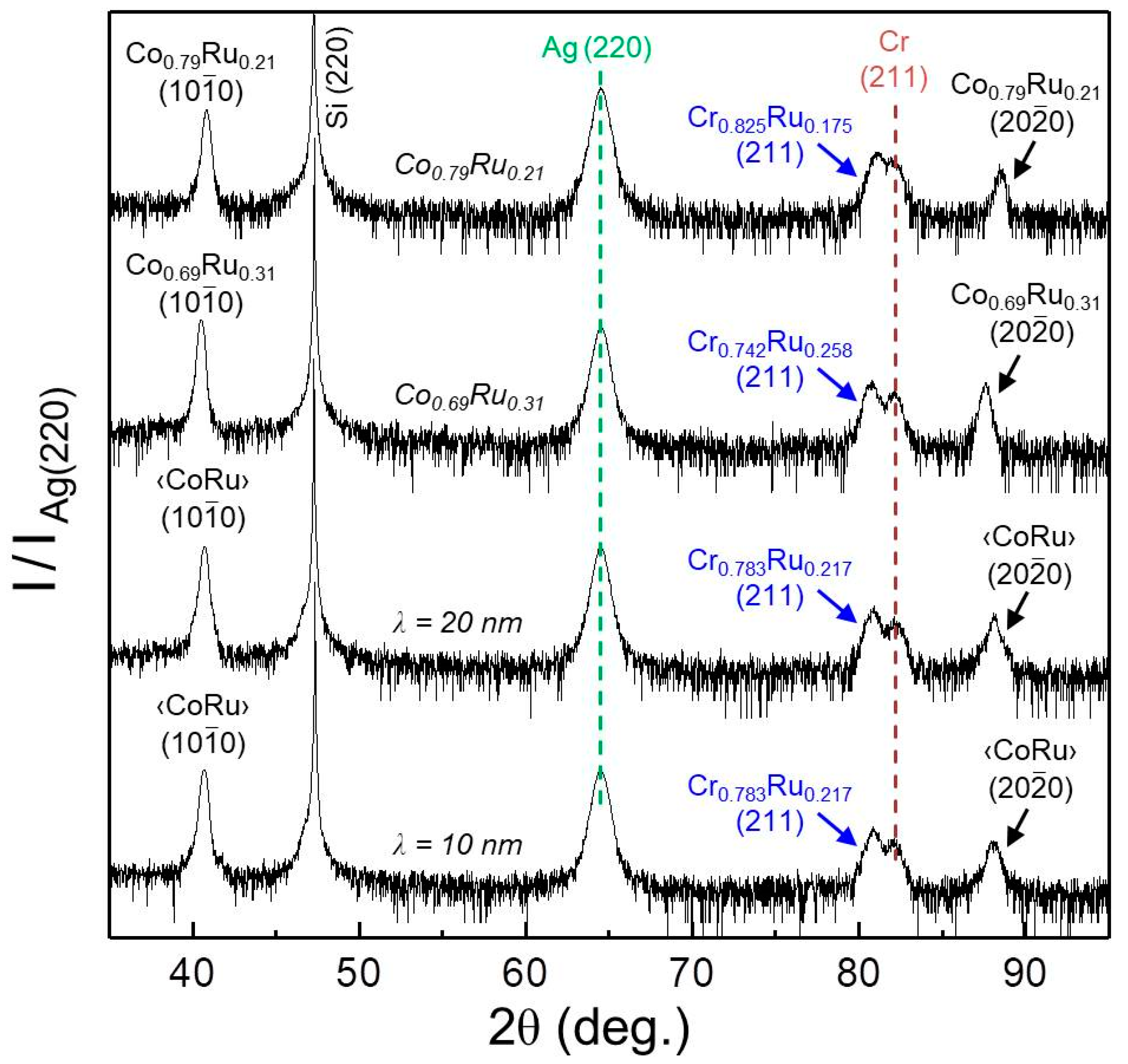
3.4. Fabrication and Epitaxial Properties
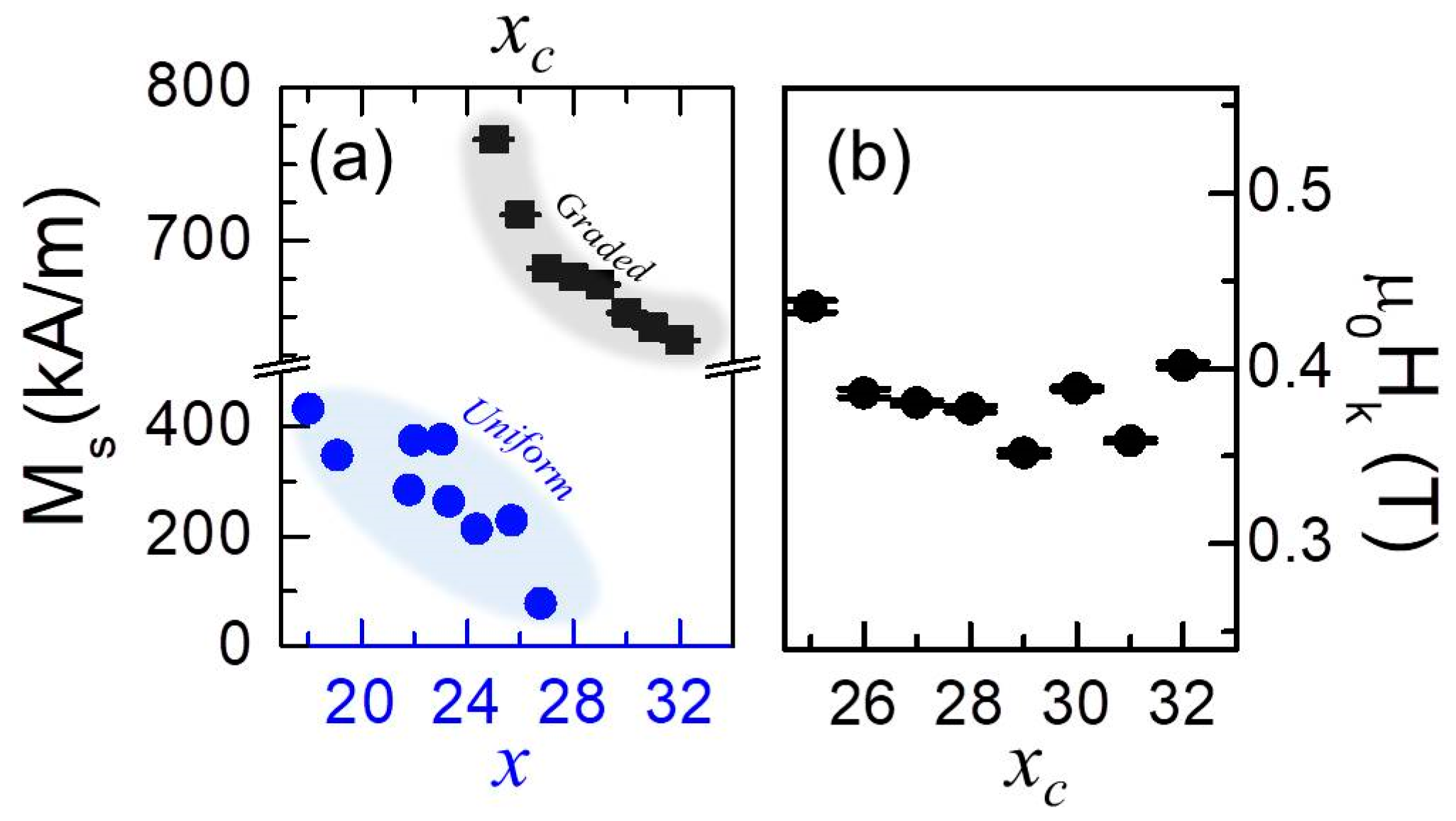
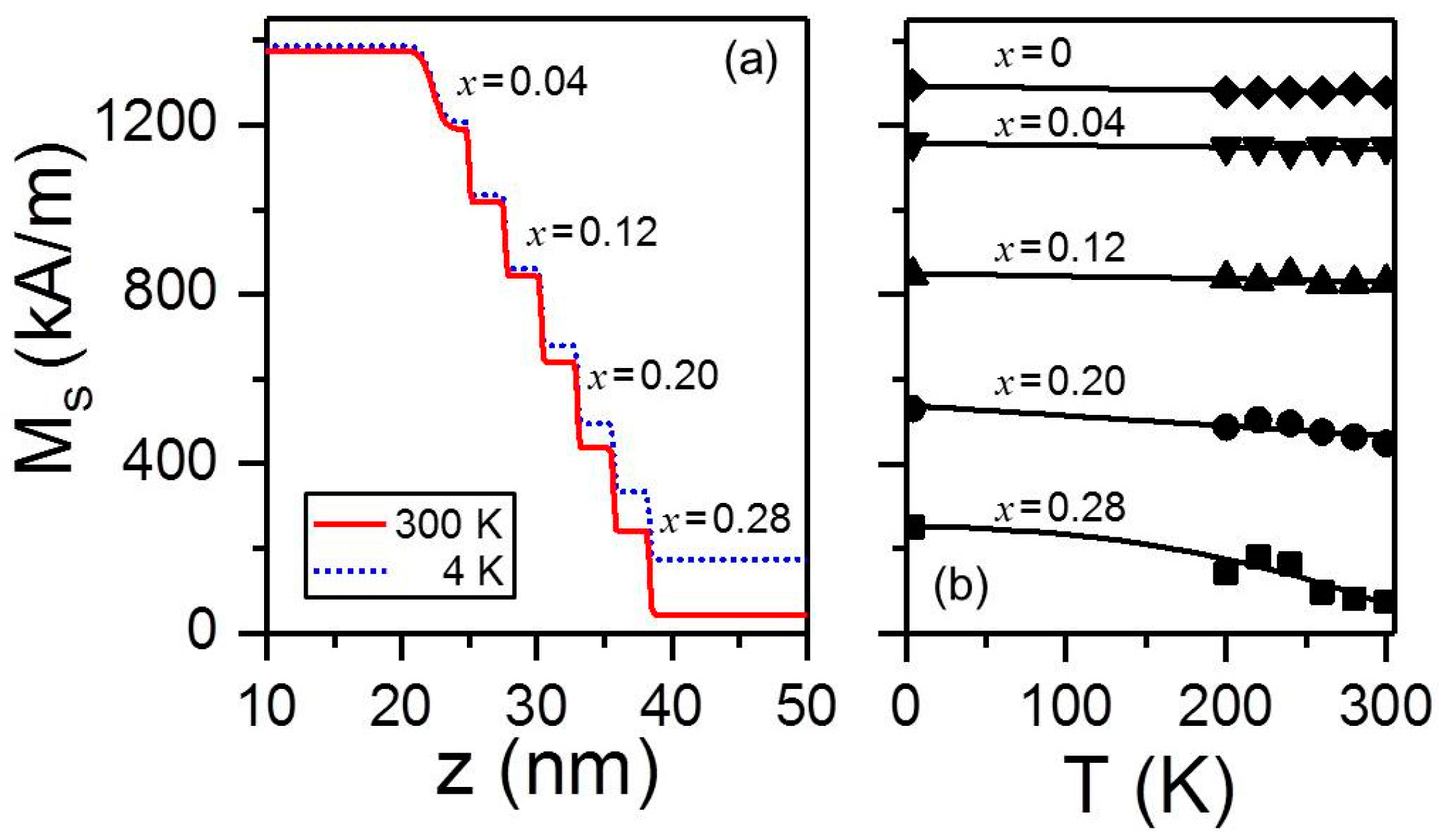
3.5. Macroscopic Magnetic Properties
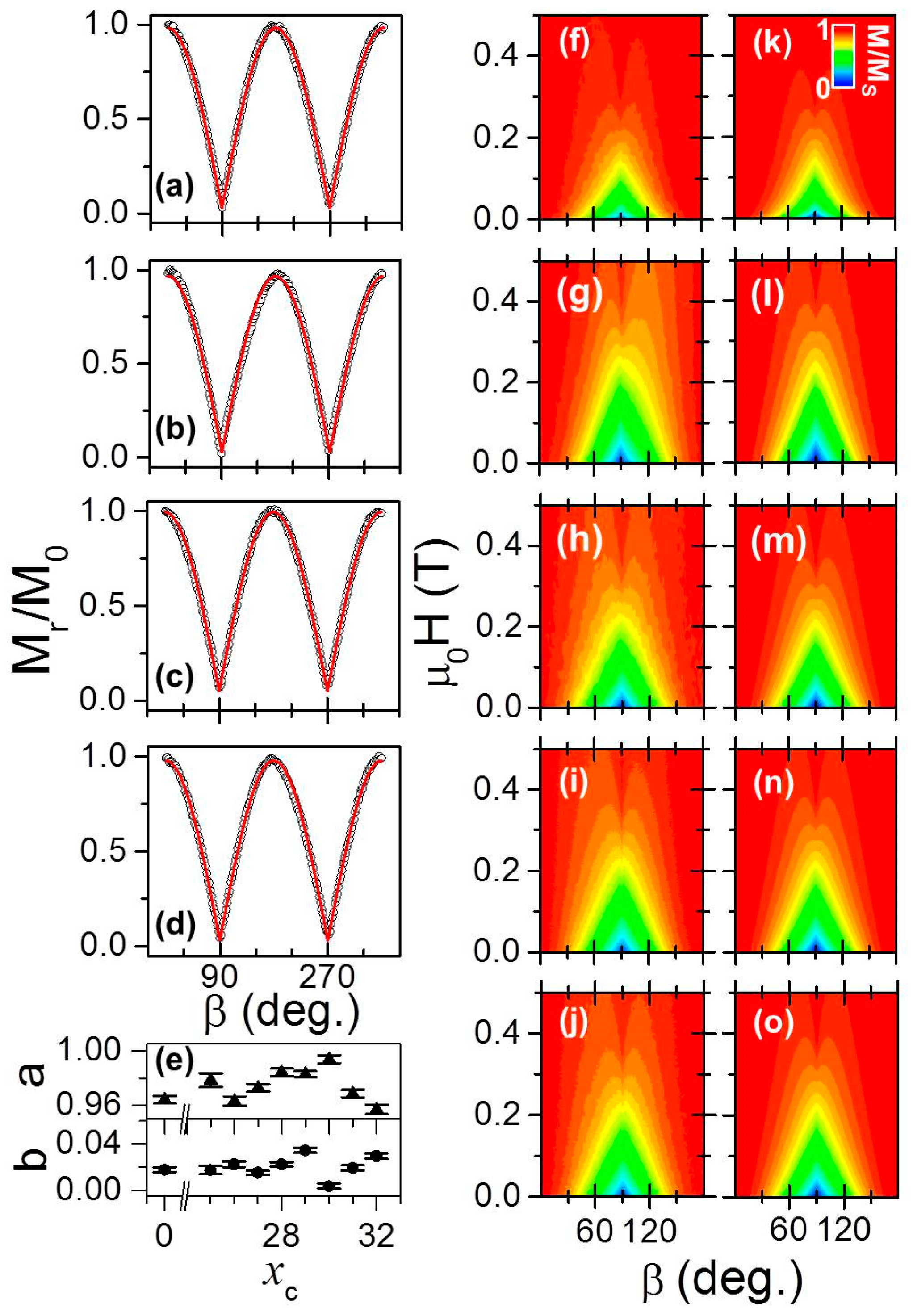
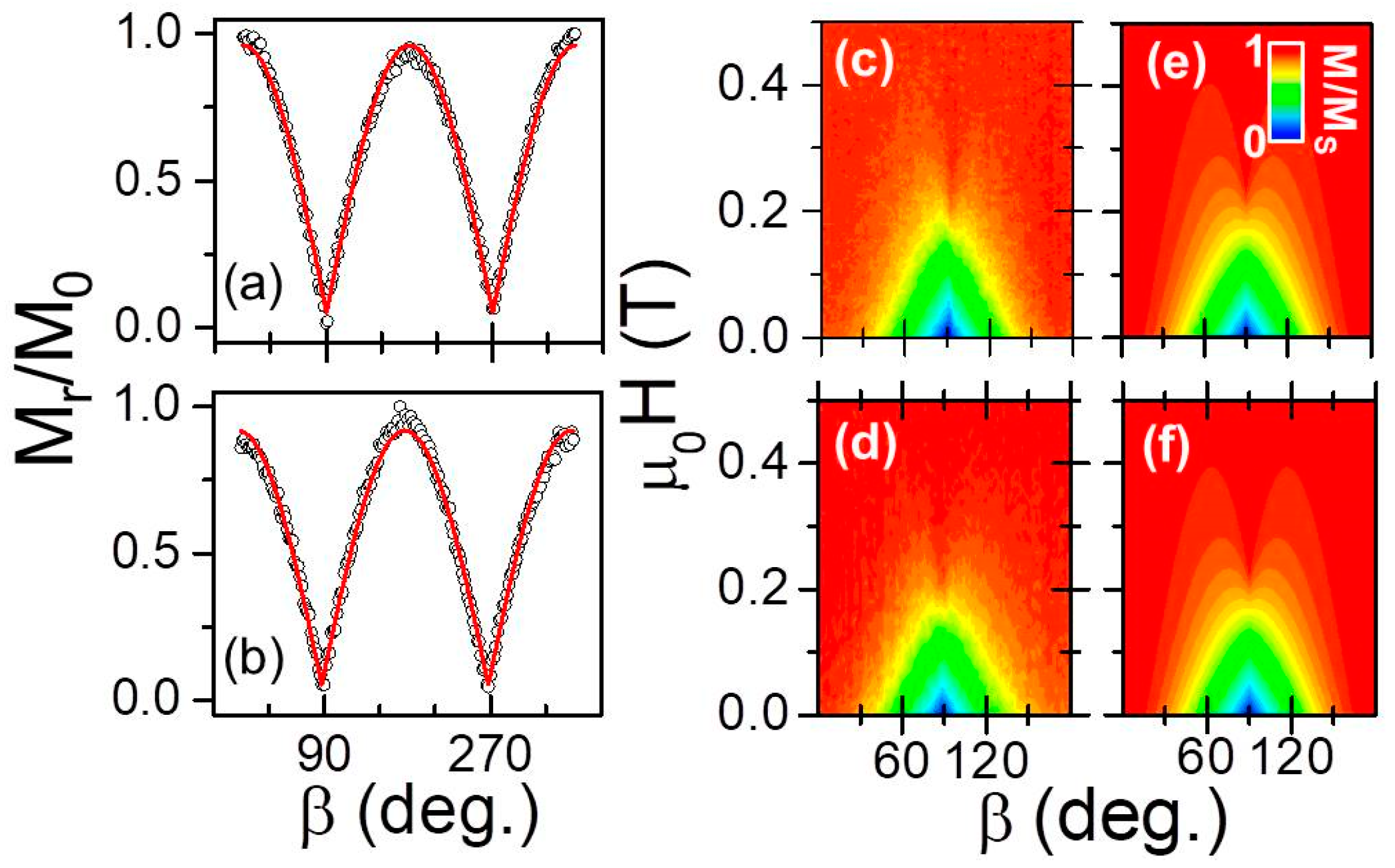
3.5.1. Uniaxial Magnetic Anisotropy
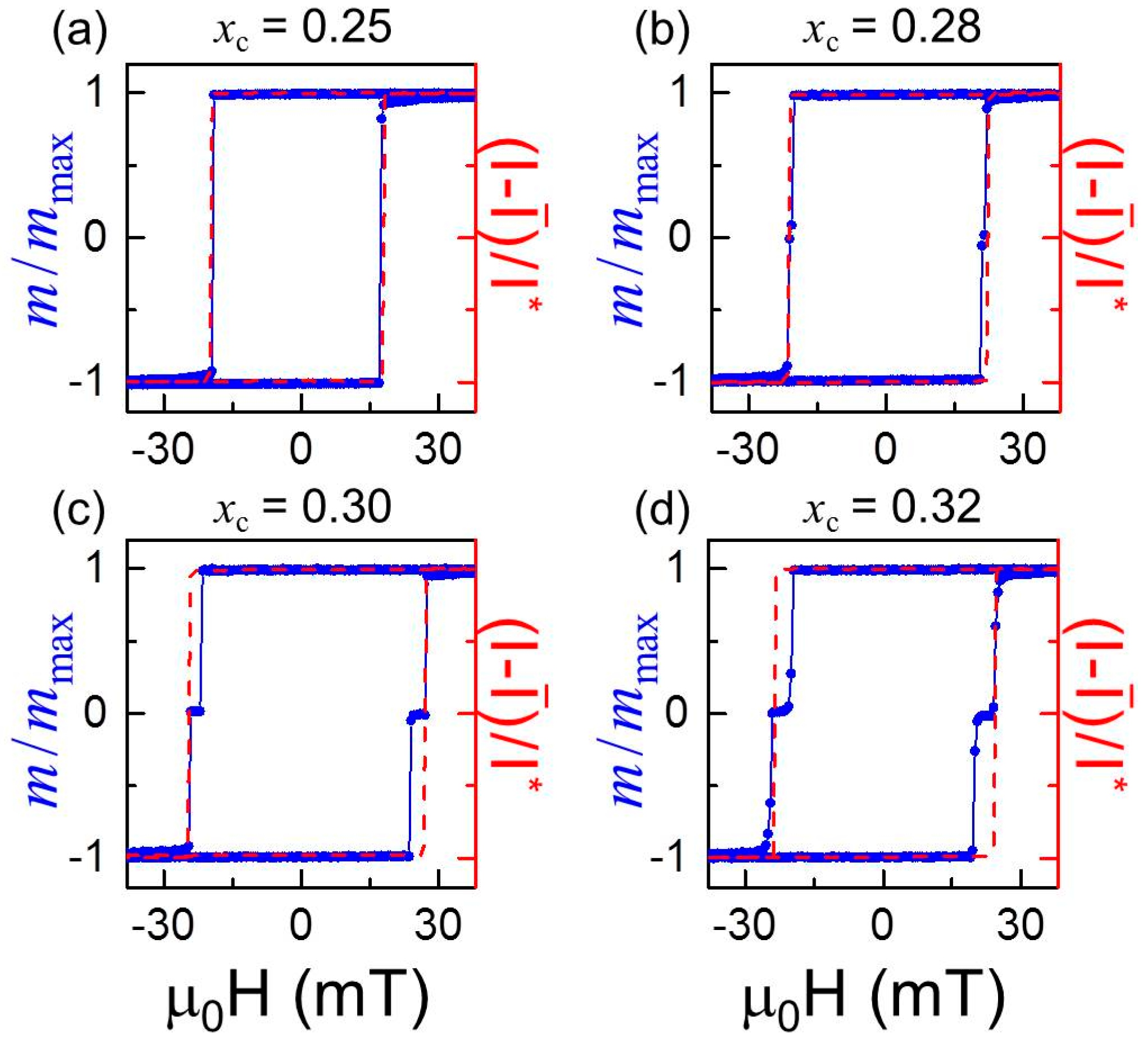
3.5.2. Magnetization Reversal in Symmetric Graded Structures
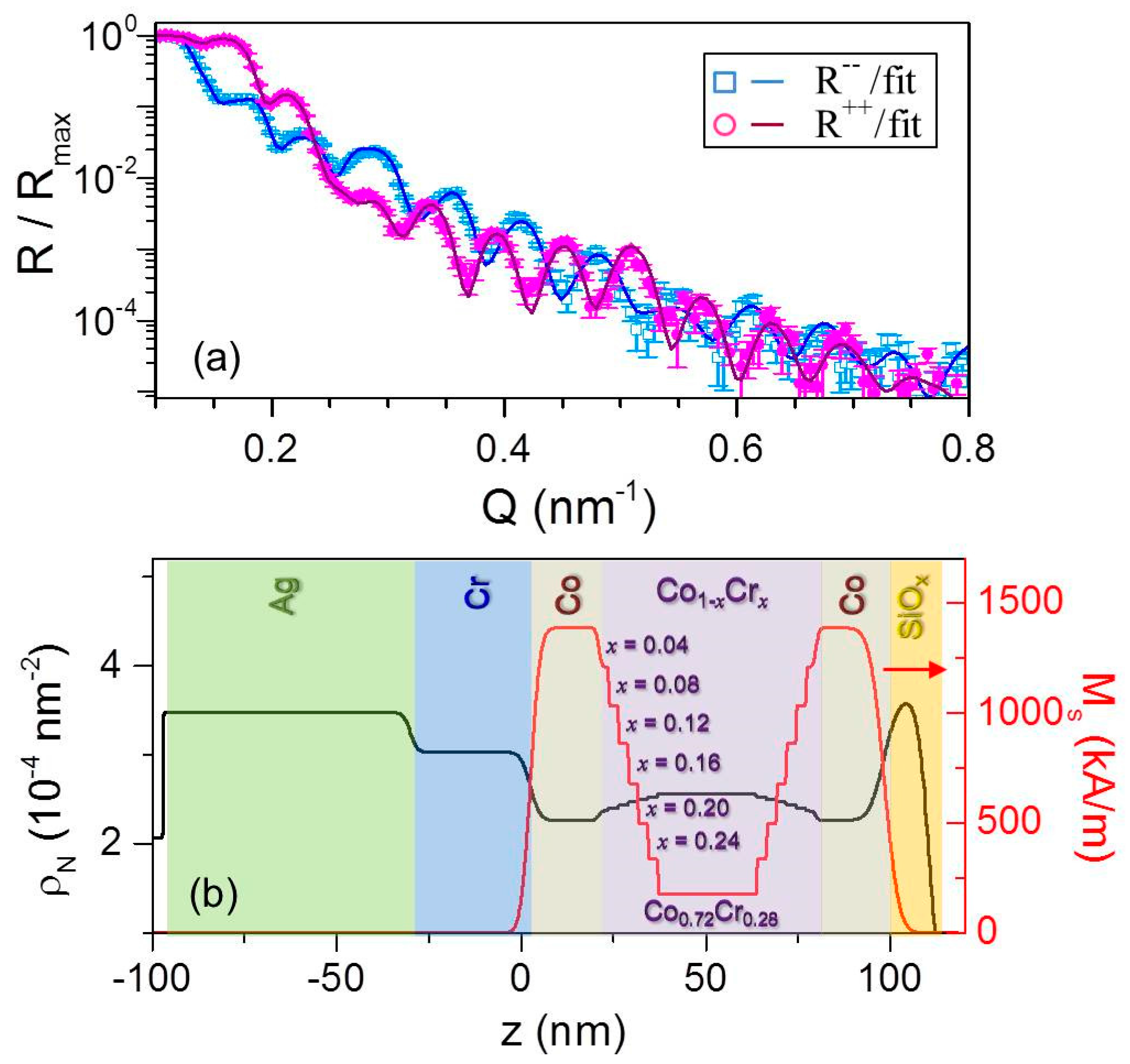
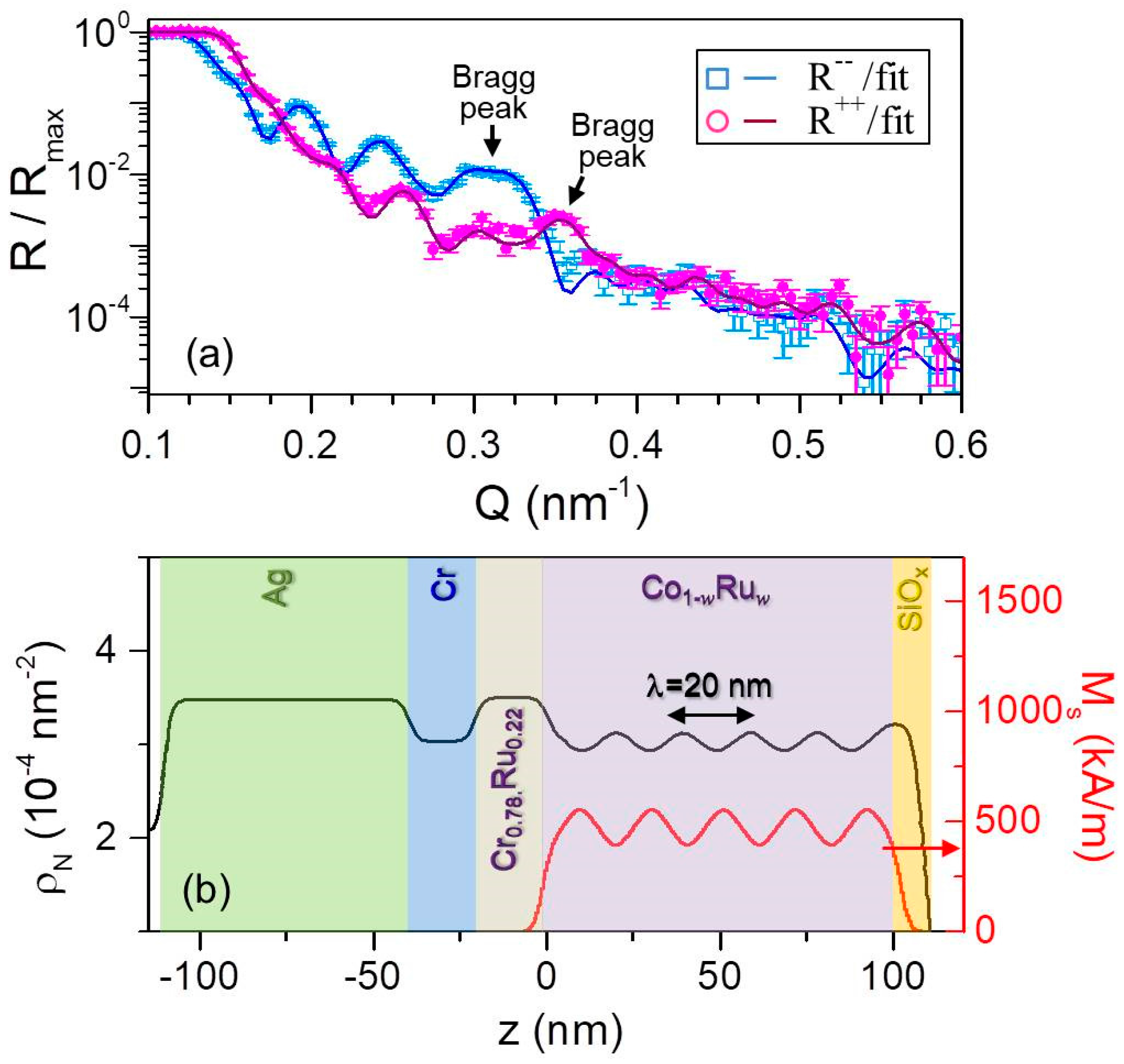
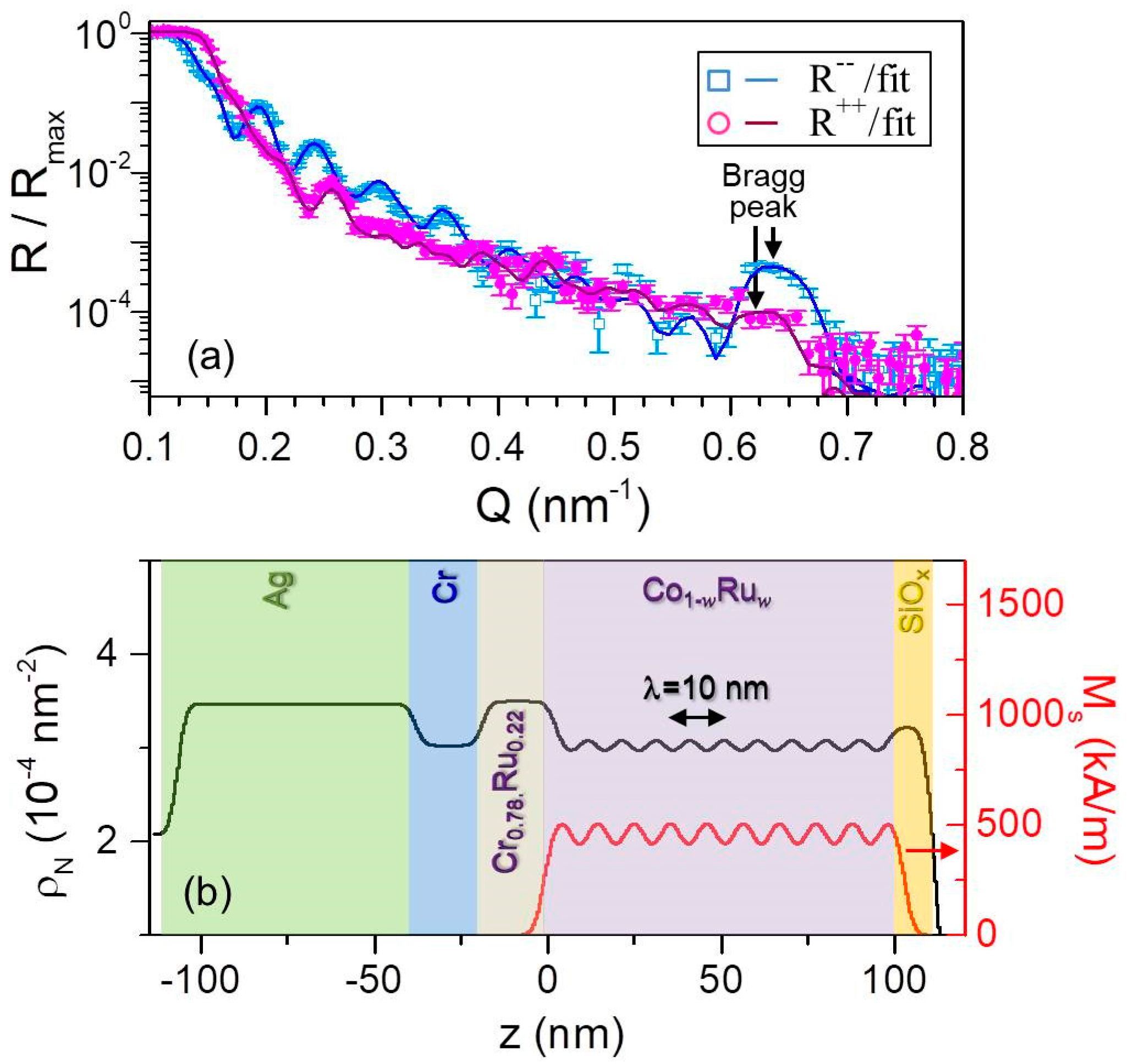
3.6. Polarized Neutron Reflectometry
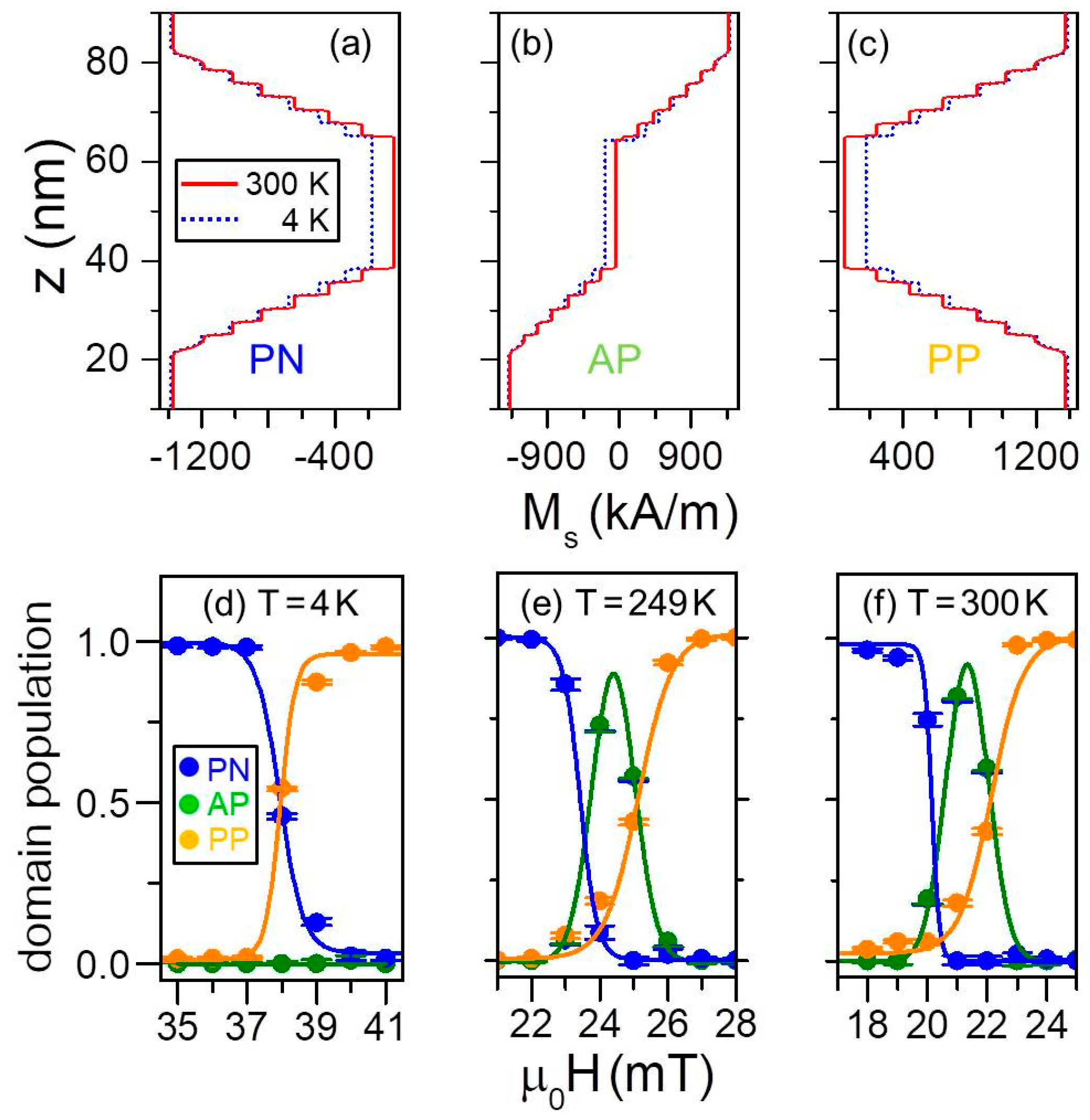
3.6.1. Magnetic Depth Profile
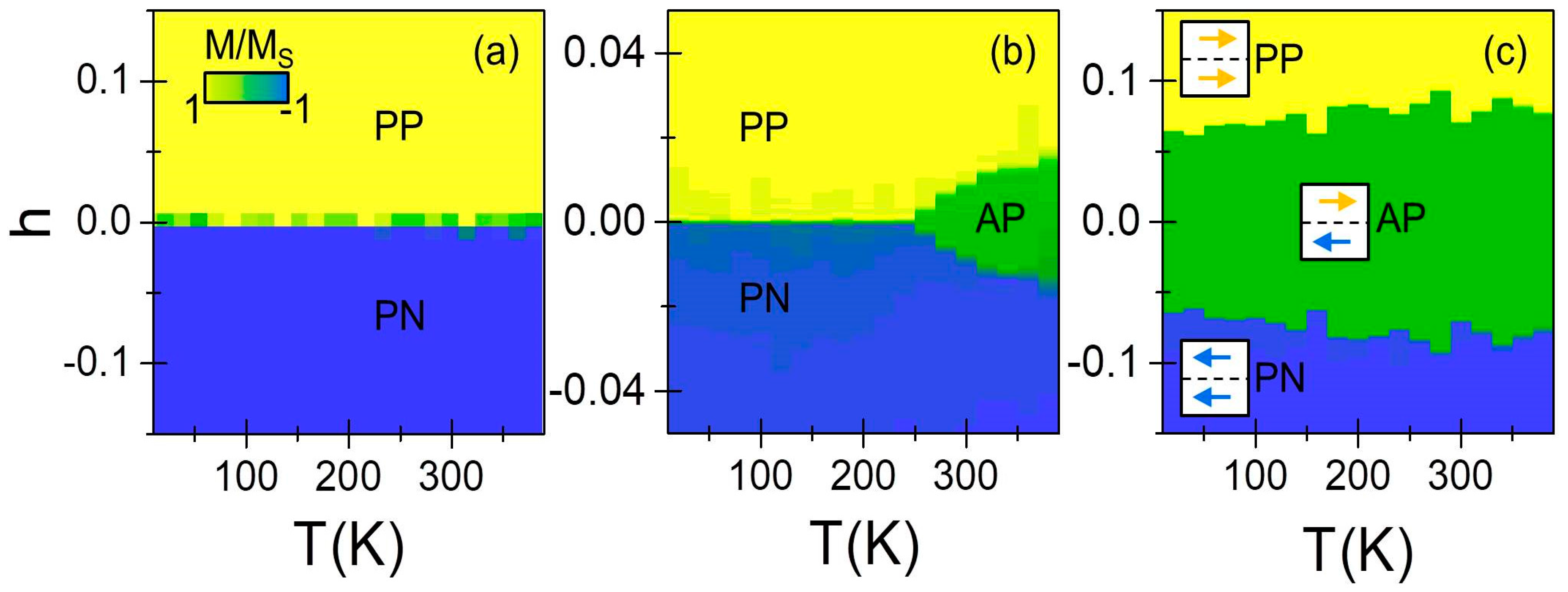
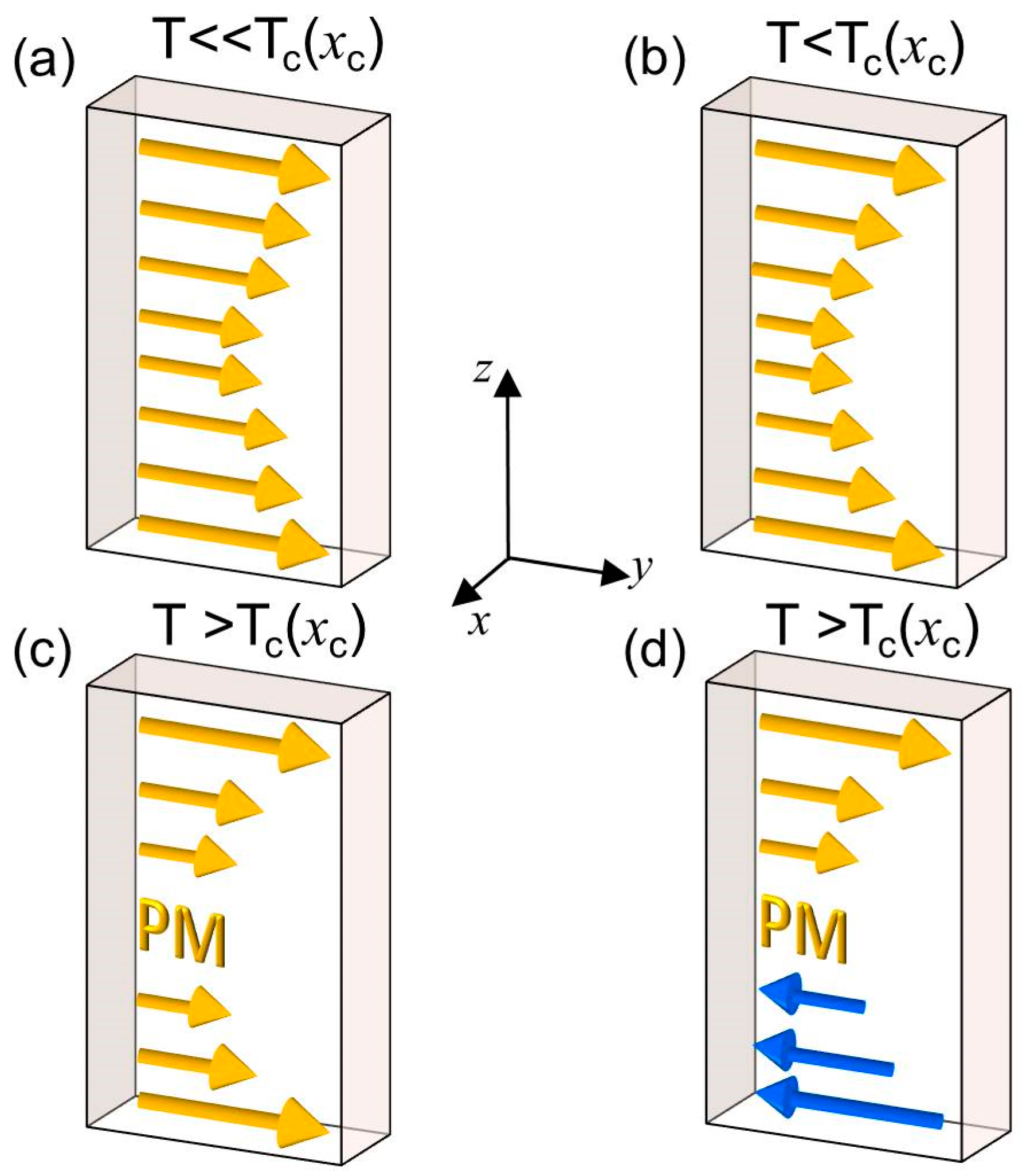
3.6.2. Temperature Dependent Magnetization Reversal
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sander, D.; Valenzuela, S.O.; Makarov, D.; Marrows, C.H.; Fullerton, E.E.; Fischer, P.; McCord, J.; Vavassori, P.; Mangin, S.; Pirro, P.; et al. The 2017 magnetism roadmap. J. Phys. D Appl. Phys. 2017, 50, 363001. [Google Scholar] [CrossRef]
- Kneller, E.; Hawig, R. The exchange-spring magnet: A new material principle for permanent magnets. IEEE Trans. Magn. 1991, 27, 3560–3588. [Google Scholar] [CrossRef]
- Skomski, R.; Coey, J.M.D. Giant energy product in nanostructured two-phase magnets. Phys. Rev. B 1993, 48, 15812. [Google Scholar] [CrossRef]
- Fullerton, E.E.; Jiang, J.S.; Grimsditch, M.; Sowers, C.H.; Bader, S.D. Exchange-spring behavior in epitaxial hard-soft magnetic bilayers. Phys. Rev. B 1998, 83, 6238. [Google Scholar] [CrossRef]
- Fullerton, E.E.; Jiang, J.S.; Bader, S.D. Hard/soft magnetic heterostructures: Model exchange-spring metals. J. Magn. Magn. Mater. 1999, 200, 392–404. [Google Scholar] [CrossRef]
- Fullerton, E.E.; Margulies, D.T.; Supper, N.; Do, H.; Schabes, M.; Berger, A.; Moser, A. Antiferromagnetically coupled magnetic recording media. IEEE Trans. Magn. 2003, 39, 639–644. [Google Scholar] [CrossRef]
- Berger, A.; Supper, N.; Ikeda, Y.; Lengsfield, B.; Moser, A.; Fullerton, E.E. Improved media performance in optimally coupled exchange spring layer media. Appl. Phys. Lett. 2008, 93, 122502. [Google Scholar] [CrossRef]
- Fidler, J.; Schrefl, T.; Hoefinger, S.; Hajduga, M. Recent developments in hard magnetic bulk materials. J. Phys. Condens. Matter 2004, 16, S455. [Google Scholar] [CrossRef]
- Wood, R. The feasibility of magnetic recording at 1 terabit per square inch. IEEE Trans. Magn. 2000, 36, 36–42. [Google Scholar] [CrossRef]
- Berger, A. Magnetization reversal in granular thin films. Physica B 2012, 407, 1322–1329. [Google Scholar] [CrossRef]
- Zhou, T.J.; Lim, B.C.; Liu, B. Anisotropy graded FePt-TiO2 nanocomposite thin films with small grain size. Appl. Phys. Lett. 2009, 94, 152505. [Google Scholar] [CrossRef]
- Kirby, B.J.; Watson, S.M.; Davies, J.E.; Zimanyi, G.T.; Liu, K.; Shull, R.D.; Borchers, J.A. Direct observation of magnetic gradient in Co/Pd pressure-graded media. J. Appl. Phys. 2009, 105, 07C929. [Google Scholar] [CrossRef]
- Marcellini, M.; Pärnaste, M.; Hjörvarsson, B.; Wolff, M. Influence of the distribution of the inherent ordering temperature on the ordering in layered magnets. Phys. Rev. B 2009, 79, 144426. [Google Scholar] [CrossRef]
- Chen, J.S.; Huang, L.S.; Hu, J.F.; Ju, G.; Chow, G.M. FePt-C graded media for ultra-high density magnetic recording. J. Phys. D Appl. Phys. 2010, 43, 185001. [Google Scholar] [CrossRef]
- Kirby, B.J.; Davies, J.E.; Liu, K.; Watson, S.M.; Zimanyi, G.T.; Shull, R.D.; Kienzle, P.A.; Borchers, J.A. Vertically graded anisotropy in Co/Pd multilayers. Phys. Rev. B 2010, 81, 100405. [Google Scholar] [CrossRef]
- Dumas, R.K.; Fang, Y.; Kirby, B.J.; Zha, C.; Bonanni, V.; Nogúes, J.; Akerman, J. Probing vertically graded anisotropy in FePtCu films. Phys. Rev. B 2011, 84, 054434. [Google Scholar] [CrossRef]
- LeGraët, C.; Charlton, T.R.; McLaren, M.; Loving, M.; Morley, S.A.; Kinane, C.J.; Brydson, R.M.D.; Lewis, L.H.; Langridge, S.; Marrows, C.H. Temperature controlled motion of an antiferromagnet-ferromagnet interface within a dopant-graded FeRh epilayer. APL Mater. 2015, 3, 041802. [Google Scholar] [CrossRef]
- Fert, A. Nobel Lecture: Origin, development, and future od spintronics. Rev. Mod. Phys. 2008, 80, 1517. [Google Scholar] [CrossRef]
- Grünberg, P.A. Nobel Lecture: From spin waves to giant magnetoresistance and beyond. Rev. Mod. Phys. 2008, 80, 1531. [Google Scholar] [CrossRef]
- Hellwig, O.; Berger, A.; Kortright, J.B.; Fullerton, E.E. Domain structure and magnetization reversal of antiferromagnetically coupled perpendicular anisotropy films. J. Magn. Magn. Mater. 2007, 319, 13–55. [Google Scholar] [CrossRef]
- Thiele, J.-U.; Maat, S.; Fullerton, E.E. FeRh-FePt exchange spring films for thermally assisted magnetic recording media. Appl. Phys. Lett. 2003, 82, 2859. [Google Scholar] [CrossRef]
- Fallarino, L.; Berger, A.; Binek, C. Giant temperature dependence of the spin reversal field in magnetoelectric chromia. Appl. Phys. Lett. 2014, 104, 022403. [Google Scholar] [CrossRef]
- Fallarino, L.; Binek, C.; Berger, A. Boundary magnetization properties of epitaxial Cr2-xAlxO3 thin films. Phys. Rev. B 2015, 91, 214403. [Google Scholar] [CrossRef]
- Victoria, R.H.; Shen, X. Composite media for perpendicular magnetic recording. IEEE Trans. Magn. 2005, 41, 537–542. [Google Scholar] [CrossRef]
- Suess, D. Multilayer exchange spring media for magnetic recording. Appl. Phys. Lett. 2006, 89, 113105. [Google Scholar] [CrossRef]
- Kirby, B.J.; Belliveau, H.F.; Belyea, D.D.; Kienzle, P.A.; Grutter, A.J.; Riego, P.; Berger, A.; Miller, C.W. Spatial evolution of the ferromagnetic phase transition in an exchange graded film. Phys. Rev. Lett. 2016, 116, 047203. [Google Scholar] [CrossRef] [PubMed]
- Fallarino, L.; Kirby, B.J.; Pancaldi, M.; Riego, P.; Balk, A.L.; Miller, C.W.; Vavassori, P.; Berger, A. Magnetic properties of epitaxial CoCr films with depth-dependent exchange-coupling profiles. Phys. Rev. B 2017, 95, 134445. [Google Scholar] [CrossRef]
- Kirby, B.J.; Fallarino, L.; Riego, P.; Maranville, B.B.; Miller, C.W.; Berger, A. Nanoscale magnetic behavior localization in exchange strength modulated ferromagnets. arXiv 2017, arXiv:1712.04998. [Google Scholar]
- Grimsditch, M.; Fullerton, E.E.; Stamps, R. Exchange and anisotropy effects on spin waves in epitaxial Co films. Phys. Rev. B 1997, 56, 2617. [Google Scholar] [CrossRef]
- Idigoras, O.; Palomares, U.; Suszka, A.K.; Fallarino, L.; Berger, A. Magnetic properties of room temperature grown epitaxial Co1−xRux alloy films. Appl. Phys. Lett. 2013, 103, 102410. [Google Scholar] [CrossRef]
- Inaba, N.; Futamoto, M.; Nakamura, A. Temperature dependence of magnetocrystalline anisotropy energy determined using Co-Cr-Ta single crystal thin films. IEEE Trans. Magn. 1998, 34, 1558–1560. [Google Scholar] [CrossRef]
- Inaba, N.; Uesaka, Y.; Futamoto, M. Compositional and temperature dependence of basic properties of CoCr-alloy thin films. IEEE Trans. Magn. 2000, 36, 54–60. [Google Scholar] [CrossRef]
- Anderson, I.S.; Brown, P.J.; Carpenter, J.M.; der, G.L.; Pynn, R.; Rowe, J.M.; Scharpf, O.; Sears, V.F.; Willish, B.T.M. International Tables for Crystallography; Wiley: Hoboken, NJ, USA; New York, NY, USA, 2006; Chapter 4.4; p. 430. [Google Scholar]
- Qiu, Z.Q.; Bader, S.D. Surface magneto-optic Kerr effect. Rev. Sci. Instrum. 2000, 71, 1243. [Google Scholar] [CrossRef]
- Vavassori, P. Polarization modulation technique for magneto-optical quantitative vector magnetometry. Appl. Phys. Lett. 2000, 77, 1605. [Google Scholar] [CrossRef]
- Felcher, G.P. Polarized neutron reflectometry- a historical perspective. Physica B 1999, 267–268, 154–161. [Google Scholar] [CrossRef]
- Kirby, B.J.; Kienzle, P.A.; Maranville, B.B.; Berk, N.F.; Krycka, J.; Heinrich, F.; Majkrzak, C.F. Phase-sensitive specular neutron reflectometry for imaging the nanometer scale composition depth profile of thin-film materials. Curr. Opin. Colloid Interface Sci. 2012, 17, 44–53. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Braak, C.J.F.T.; Diks, C.G.H.; Higdon, D.; Robinson, B.A.; Hyman, J.M. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Maeda, Y.; Takei, K.; Rogers, D.J. Detection of compositional separation in Co-Ru alloy magnetic films. Jpn. J. Appl. Phys. 1993, 32, 4540. [Google Scholar] [CrossRef]
- Maeda, Y.; Takei, K.; Rogers, D.J. Compositional microstructures in Co-Cr films for magnetic recording. J. Magn. Magn. Mat. 1994, 134, 315–322. [Google Scholar] [CrossRef]
- Ringelstein, V.P.N.; Michel, A.; Boukari, S.; Bouzidi, L.; Persat, N.; Beaurepaire, E.; Hehn, M.; Muller, D.; Cadeville, M.C. Observation of an ordered new compound Co1−xRux prepared by MBE on a Ru buffer layer. J. Magn. Magn. Mater. 1997, 165, 176–179. [Google Scholar]
- Bouzidi, L.; Pierron-Bohnes, V.; Haemmerlé, O.; Bouillet-Ulhaq, C.; Cadeville, M.C. Low range chemical order and induced lattice deformation along the growth direction in epitaxial [0001] Co1−xRux alloys. Thin Solid Films 1998, 318, 215–218. [Google Scholar] [CrossRef]
- Ersen, O.; Bouzid, L.; Pierron-Bohnes, V.; Cadeville, M.C. Chemical ordering along the growth direction in epitaxial [0002] Co1−xRux alloy thin films. Mater. Res. Soc. Symp. Proc. 1998, 528, 11. [Google Scholar] [CrossRef]
- Idigoras, O.; Suszka, A.K.; Vavassori, P.; Obry, B.; Hillebrands, B.; Landeros, P.; Berger, A. Magnetization reversal of in-plane Co films and its dependence on epitaxial alignment. J. Appl. Phys. 2014, 115, 083912. [Google Scholar] [CrossRef]
- Sun, A.-C.; Hsu, J.-H.; Sheng, C.H.; Kuo, P.C.; Huang, H.L. Grain size reduction by doping Cr underlayer with Ru for longitudinal magnetic recording media. IEEE Trans. Magn. 2007, 43, 882–884. [Google Scholar] [CrossRef]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Yuasa, S.; Nagahama, T.; Fukushima, A.; Suzuki, Y.; Ando, K. Giant room-temperature magnetoresistance in single-crystal Fe/MgO/Fe magnetic tunnel junctions. Nat. Mater. 2004, 3, 868–871. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, R. Magneto-optical domain studies in coupled magnetic multilayers. J. Magn. Magn. Mater. 1995, 148, 226–231. [Google Scholar] [CrossRef]
- Bolzoni, F.; Leccabue, L.; Panizzieri, R.; Pareti, L. Magnetic properties and anisotropy of Co-Cr alloy. J. Magn. Magn. Mater. 1983, 31, 845–846. [Google Scholar] [CrossRef]

| λ (nm) | a | b | MS (kAm−1) | µ0Hk (mT) |
|---|---|---|---|---|
| 10 | 0.864 ± 0.008 | 0.053 ± 0.004 | 303 ± 26 | 220 ± 4.3 |
| 20 | 0.909 ± 0.001 | 0.052 ± 0.004 | 294 ± 29 | 231 ± 3.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fallarino, L.; Riego, P.; Kirby, B.J.; Miller, C.W.; Berger, A. Modulation of Magnetic Properties at the Nanometer Scale in Continuously Graded Ferromagnets. Materials 2018, 11, 251. https://doi.org/10.3390/ma11020251
Fallarino L, Riego P, Kirby BJ, Miller CW, Berger A. Modulation of Magnetic Properties at the Nanometer Scale in Continuously Graded Ferromagnets. Materials. 2018; 11(2):251. https://doi.org/10.3390/ma11020251
Chicago/Turabian StyleFallarino, Lorenzo, Patricia Riego, Brian J. Kirby, Casey W. Miller, and Andreas Berger. 2018. "Modulation of Magnetic Properties at the Nanometer Scale in Continuously Graded Ferromagnets" Materials 11, no. 2: 251. https://doi.org/10.3390/ma11020251
APA StyleFallarino, L., Riego, P., Kirby, B. J., Miller, C. W., & Berger, A. (2018). Modulation of Magnetic Properties at the Nanometer Scale in Continuously Graded Ferromagnets. Materials, 11(2), 251. https://doi.org/10.3390/ma11020251





