Vortex Lattice Instabilities in YBa2Cu3O7-x Nanowires
Abstract
:1. Introduction
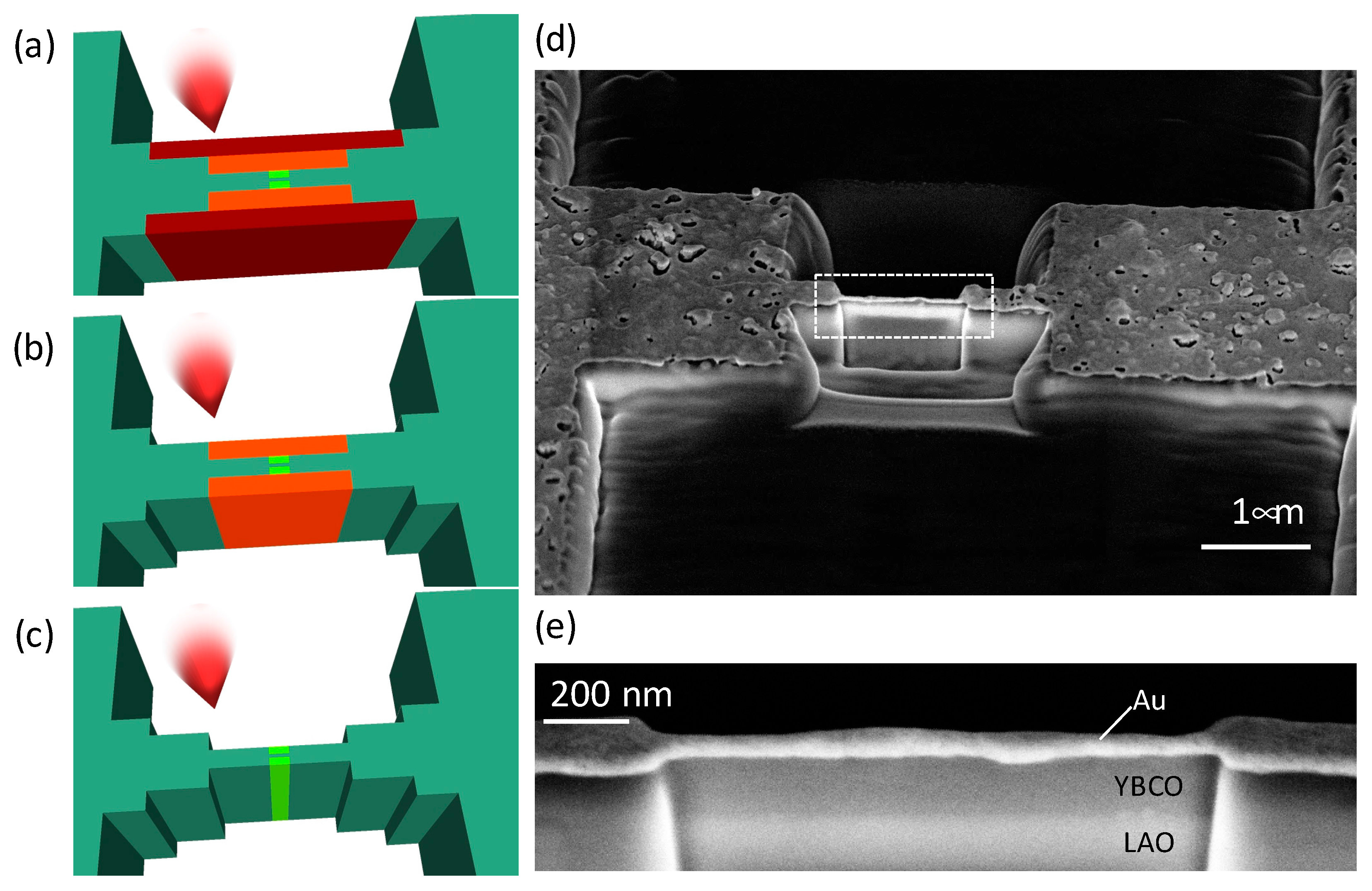
2. Materials and Methods
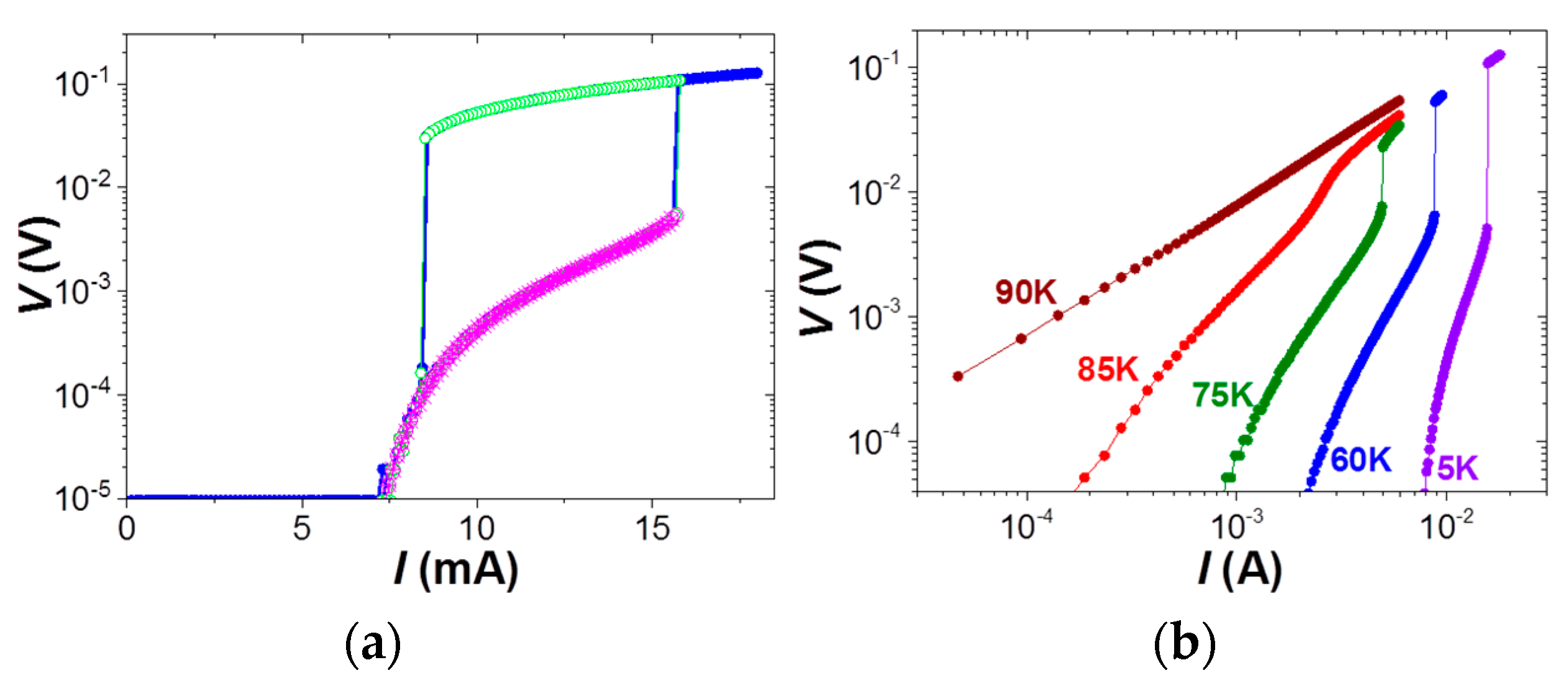
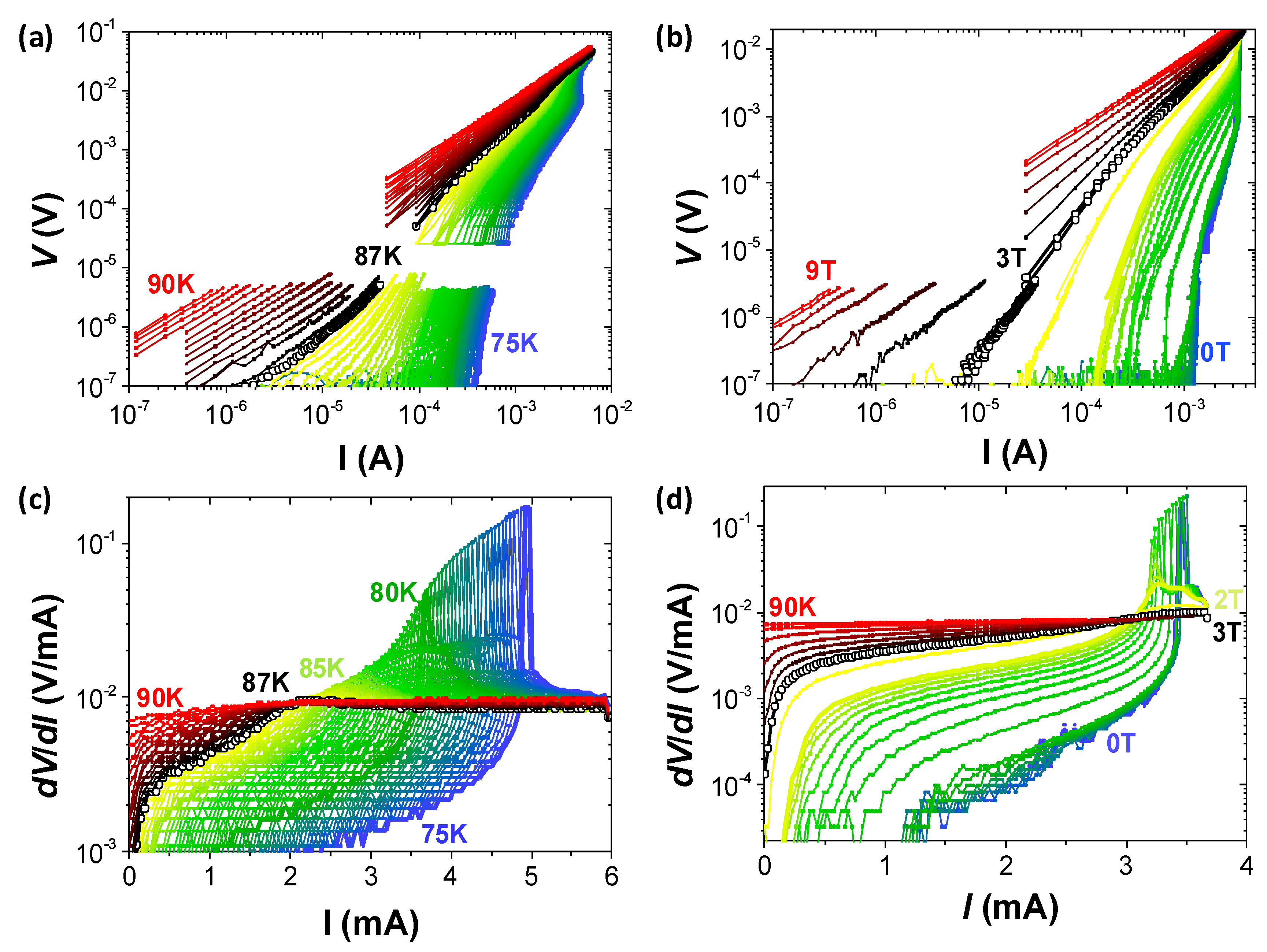
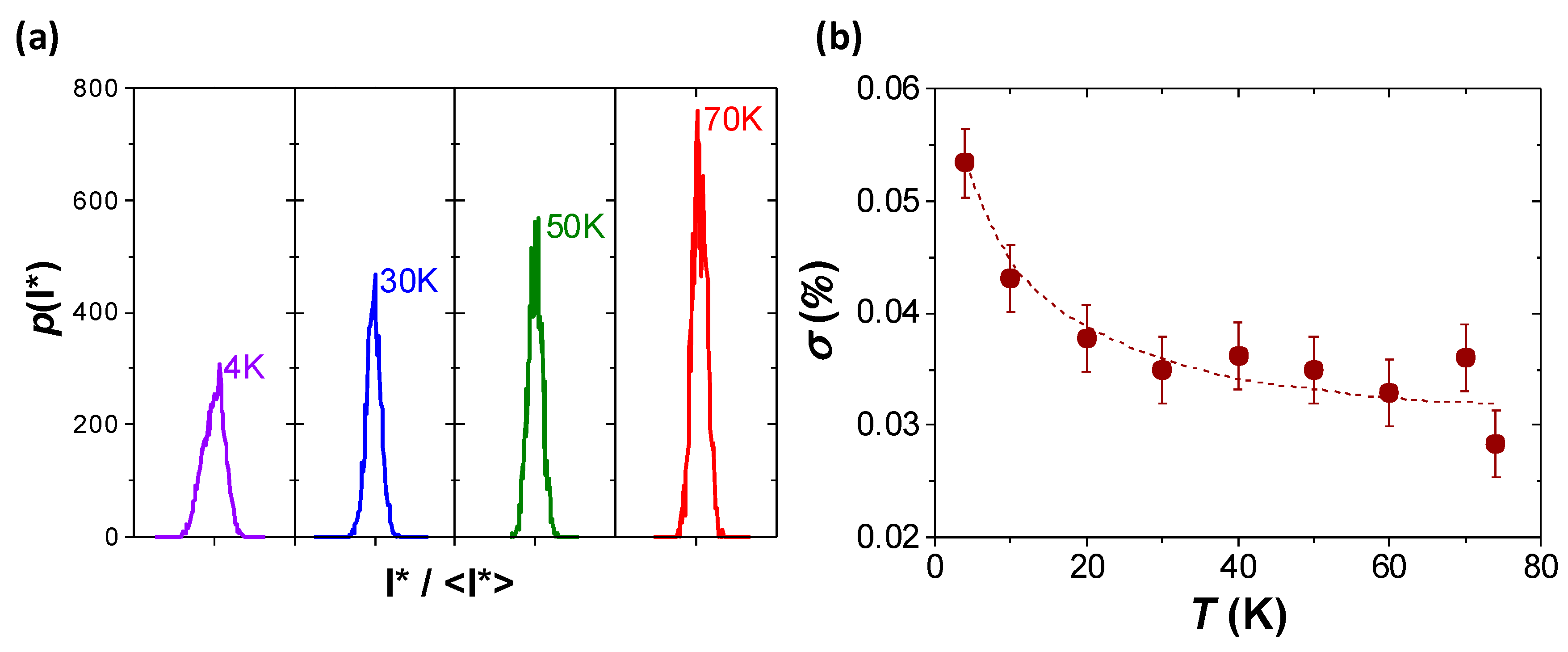
3. Result and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Crabtree, G.W.; Nelson, D.R. Vortex physics in high-temperature superconductors. Phys. Today 1997, 38. [Google Scholar] [CrossRef]
- Langenberg, D.N.; Larkin, A.I. Nonequilibrium Superconductivity Modern Problems in Condensed Matter; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H. Superconducting nanowire single-photon detectors: Physics and applications. Supercond. Sci. Technol. 2012, 25, 63001. [Google Scholar] [CrossRef]
- Attanasio, C.; Cirillo, C. Quasiparticle relaxation mechanisms in superconductor/ferromagnet bilayers. J. Phys. Consens. Matter 2012, 24, 08201. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.Z.; Ayala-Valenzuela, O.; McDonald, R.D.; Bulaevskii, L.N.; Holesinger, T.G.; Ronning, F.; Weisse-Bernstein, N.R.; Williamson, T.L.; Mueller, A.H.; Hoffbauer, M.A.; et al. Characterization of the thin-film NbN superconductor for single-photon detection by transport measurements. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 87, 184507. [Google Scholar] [CrossRef]
- Gol’tsman, G.N.; Okunev, O.; Chulkova, G.; Lipatov, A.; Semenov, A.; Smirnov, K.; Voronov, B.; Dzardanov, A.; Williams, C.; Sobolewski, R. Picosecond superconducting single-photon optical detector. Appl. Phys. Lett. 2001, 79, 705. [Google Scholar] [CrossRef]
- Takesue, H.; Nam, S.W.; Zhang, Q.; Hadfield, R.H.; Honjo, T.; Tamaki, K.; Yamamoto, Y. Quantum key distribution over a 40-dB channel loss using superconducting single-photon detectors. Nat. Photonics 2007, 1, 343. [Google Scholar] [CrossRef]
- Lyatti, M.; Savenko, A.; Poppe, U. Ultra-thin YBCO fims with high critical current density. Supercond. Sci. Technol. 2016, 29, 065017. [Google Scholar] [CrossRef]
- Arpaia, R.; Golubev, D.; Baghdadi, R.; Ciancio, R.; Dražić, G.; Orgiani, P.; Montemurro, D.; Bauch, T.; Lombardi, F. Transport properties of ultrathin YBa2Cu3O7-x nanowires: A route to single photon detection. Phys. Rev. B 2017, 96, 64525. [Google Scholar] [CrossRef]
- Papari, G.; Carillo, F.; Stornaiuolo, D.; Massarotti, D.; Longobardi, L.; Beltram, F.; Tafuri, F. Dynamics of vortex matter in YBCO sub-micron bridges. Phys. C Supercond. Appl. 2014, 506, 188–194. [Google Scholar] [CrossRef]
- Nawaz, S.; Arpaia, R.; Lombardi, F.; Bauch, T. Microwave Response of Superconducting YBCO Nanowire Bridges Sustaining the Critical Depairing Current: Evidence of Josephson-like Behavior. Phys. Rev. Lett. 2013, 110, 167004. [Google Scholar] [CrossRef] [PubMed]
- Larkin, A.I.; Ovchinnikov, Y.N. Nonlinear conductivity of superconductors in the mixed state. J. Exp. Theor. Phys. 1976, 41, 960–965. [Google Scholar]
- Doettinger, S.G.; Huebener, R.P.; Gerdemann, R.; Kühle, A.; Anders, S.; Träuble, T.G.; Villegier, J.C. Electronic Instability at High Flux-Flow Velocities in High-Tc Superconducting Films. Phys. Rev. Lett. 1994, 73, 1691. [Google Scholar] [CrossRef] [PubMed]
- Doettinger, S.G.; Huebener, R.P.; Kühle, A. Electronic instability during vortex motion in cuprate superconductors Regime of low and high magnetic fields. Phys. C Supercond. 1995, 251, 285–289. [Google Scholar] [CrossRef]
- Doettinger, S.G.; Kittelberger, S.; Huebener, R.P. Quasiparticle energy relaxation in the cuprate superconductors. Phys. Rev. B 1997, 56, 14157. [Google Scholar] [CrossRef]
- Grimaldi, G.; Leo, A.; Cirillo, C.; Attanasio, C.; Nigro, A.; Pace, S. Magnetic field and temperature dependence of the critical vortex velocity in type-II superconducting films. J. Phys. Condens. Matter 2009, 21, 254207. [Google Scholar] [CrossRef] [PubMed]
- Kunchur, M.N. Unstable Flux Flow due to Heated Electrons in Superconducting Films. Phys. Rev. Lett. 2002, 89, 137005. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.M.; Kunchur, M.N. Energy relaxation at a hot-electron vortex instability. Phys. Rev. B 2006, 74, 64512. [Google Scholar] [CrossRef]
- Silhanek, A.V.; Leo, A.; Grimaldi, G.; Berdiyorov, G.R.; Milosevic, M.V.; Nigro, A.; Pace, S.; Verellen, N.; Gillijns, W.; et al. V Influence of artificial pinning on vortex lattice instability in superconducting films. New J. Phys. 2012, 14, 53006. [Google Scholar] [CrossRef]
- Shklovskij, V.A.; Nazipova, A.P.; Dobrovolskiy, O.V. Pinning effects on self-heating and flux-flow instability in superconducting films near Tc. Phys. Rev. B 2017, 95, 184517. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Shklovskij, V.A.; Hanefeld, M.; Zörb, M.; Köhs, L.; Huth, M. Pinning effects on flux flow instability in epitaxial Nb thin films. Supercond. Sci. Technol. 2017, 30, 85002. [Google Scholar] [CrossRef]
- Dauler, E.A.; Grein, M.E.; Kerman, A.J.; Marsili, F.; Miki, S.; Nam, S.W.; Shaw, M.D.; Terai, H.; Verma, V.B.; Yamashita, T. Review of superconducting nanowire single-photon detector system design options and demonstrated performance. Opt. Eng. 2014, 53, 081907. [Google Scholar] [CrossRef]
- Bezryadin, A. Superconductivity in Nanowires: Fabrication and Quantum Transport; Wiley–VCH: Weinheim, Germany, 2013. [Google Scholar]
- Schön, G. Quantum engineering: Superconducting nanowires. Nature 2000, 404, 948. [Google Scholar] [CrossRef] [PubMed]
- Lahtinen, V.T.; Pachos, J.K. A short introduction to topological quantum computation. SciPost Phys. 2017, 3. [Google Scholar] [CrossRef]
- Hopkins, D.S.; Pekker, D.; Goldbart, P.M.; Bezryadin, A. Quantum Interference Device Mady by DNA Templating of Superconducting Nanowires. Science 2005, 308, 1762–1765. [Google Scholar] [CrossRef] [PubMed]
- Cirillo, C.; Prischepa, S.L.; Trezza, M.; Bondarenko, V.P.; Attanasio, C. Superconducting nanowire quantum interference device based on Nb ultrathin films deposited on self-assembled porous Si templates. Nanotechnology 2014, 25, 425205. [Google Scholar] [CrossRef] [PubMed]
- Obradors, X.; Puig, T.; Ricart, X.; Coll, M.; Jazquez, J.; Palau, A.; Granados, X. Growth, nanostructure and vortex pinning in superconducting YBa2Cu3O7 thin films based on trifluoroacetate solutions. Supercond. Sci. Technol. 2012, 25, 123001. [Google Scholar] [CrossRef]
- Papari, G.; Carillo, F.; Stornaiuolo, D.; Longobardi, L.; Beltram, F. High critical current density and scaling of phase-slip processes in YBaCuO nanowires. Supercond. Sci. Technol. 2012, 25, 35011. [Google Scholar] [CrossRef]
- Papari, G.P.; Glatz, A.; Carillo, F.; Stornaiuolo, D.; Massarotti, D.; Rouco, V.; Longobardi, L.; Beltram, F.; Vinokur, V.M.; Tafuri, F. Geometrical vortex lattice pinning and melting in YBaCuO submicron bridges. Sci. Rep. 2016, 6, 38677. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, J.; Palau, A.; Durrell, J.H.; Romà, N.; Puig, T.; Obradors, X.; Blamire, M.G. Vortex dynamics in thin films of YBCO with three-dimensional nanoscale patterns. Phys. Rev. B 2009, 79, 064526. [Google Scholar] [CrossRef]
- Palau, A.; Rouco, V.; Luccas, R.F.; Obradors, X.; Puig, T. Vortex dynamics in nanofabricated chemical solution deposition high-temperature superconducting film. In Superconductors at the Nanoscale. From Basic Research to Applications; Wördenweber, R., Moshchalkov, V., Bending, S., Tafuri, F., Eds.; De Gruyter: Berlin, Germany, 2017; Chapter 6; pp. 195–220. [Google Scholar]
- Massarotti, D.; Stornaiuolo, D.; Lucignano, P.; Galletti, L.; Born, D.; Rotoli, G.; Lombardi, F.; Longobardi, L.; Tagliacozzo, A.; Tafuri, F. Breakdown of the escape dynamics in Josephson junctions. Phys. Rev. B 2015, 92, 54501. [Google Scholar] [CrossRef]
- Baumans, X.D.A.; Vyacheslav, S.Z.; Raymenants, E.; Blanco Alvarez, S.; Scheerder, J.E.; Brisbois, J.; Massarotti, D.; Caruso, R.; Tafuri, F.; Janssens, E.; et al. Statistics of Localized phase slips in tunable width planar point contacts. Sci. Rep. 2017, 7, 44569. [Google Scholar] [CrossRef] [PubMed]
- Villegas, J.E.; Vicent, J.L. Vortex-glass transitions in low-Tc superconducting Nb thin films and NbCu superlattices. Phys. Rev. B 2005, 71, 144522. [Google Scholar] [CrossRef]
- Xiao, Z.L.; Voss-de Haan, P.; Jakob, G.; Kluge, T.; Haibach, P.; Adrian, H.; Andrei, E.Y. Flux-flow instability and its anisotropy in Bi2Sr2CaCu2O8 superconducting films. Phys. Rev. B 1999, 59, 1481. [Google Scholar] [CrossRef]
- Vodolazov, D.Y.; Peeters, F.M. Rearrangement of the vortex lattice due to instabilities of vortex flow. Phys. Rev. B 2007, 76, 014521. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rouco, V.; Massarotti, D.; Stornaiuolo, D.; Papari, G.P.; Obradors, X.; Puig, T.; Tafuri, F.; Palau, A. Vortex Lattice Instabilities in YBa2Cu3O7-x Nanowires. Materials 2018, 11, 211. https://doi.org/10.3390/ma11020211
Rouco V, Massarotti D, Stornaiuolo D, Papari GP, Obradors X, Puig T, Tafuri F, Palau A. Vortex Lattice Instabilities in YBa2Cu3O7-x Nanowires. Materials. 2018; 11(2):211. https://doi.org/10.3390/ma11020211
Chicago/Turabian StyleRouco, Víctor, Davide Massarotti, Daniela Stornaiuolo, Gian Paolo Papari, Xavier Obradors, Teresa Puig, Francesco Tafuri, and Anna Palau. 2018. "Vortex Lattice Instabilities in YBa2Cu3O7-x Nanowires" Materials 11, no. 2: 211. https://doi.org/10.3390/ma11020211
APA StyleRouco, V., Massarotti, D., Stornaiuolo, D., Papari, G. P., Obradors, X., Puig, T., Tafuri, F., & Palau, A. (2018). Vortex Lattice Instabilities in YBa2Cu3O7-x Nanowires. Materials, 11(2), 211. https://doi.org/10.3390/ma11020211






