Magnetic Characterization of Direct-Write Free-Form Building Blocks for Artificial Magnetic 3D Lattices
Abstract
1. Introduction
2. Results
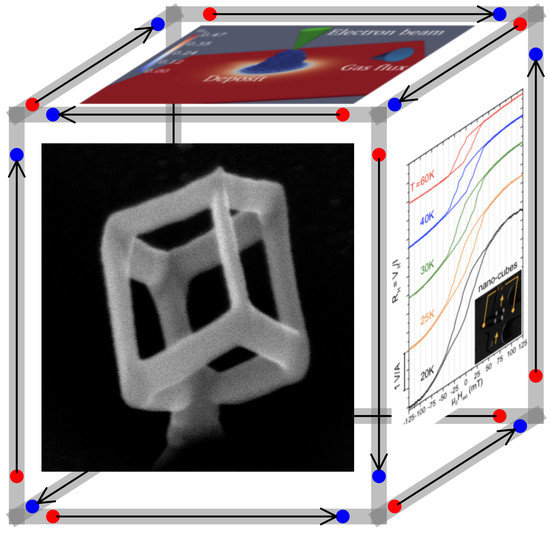
2.1. Geometry of Nano-Cubes and Nano-Trees
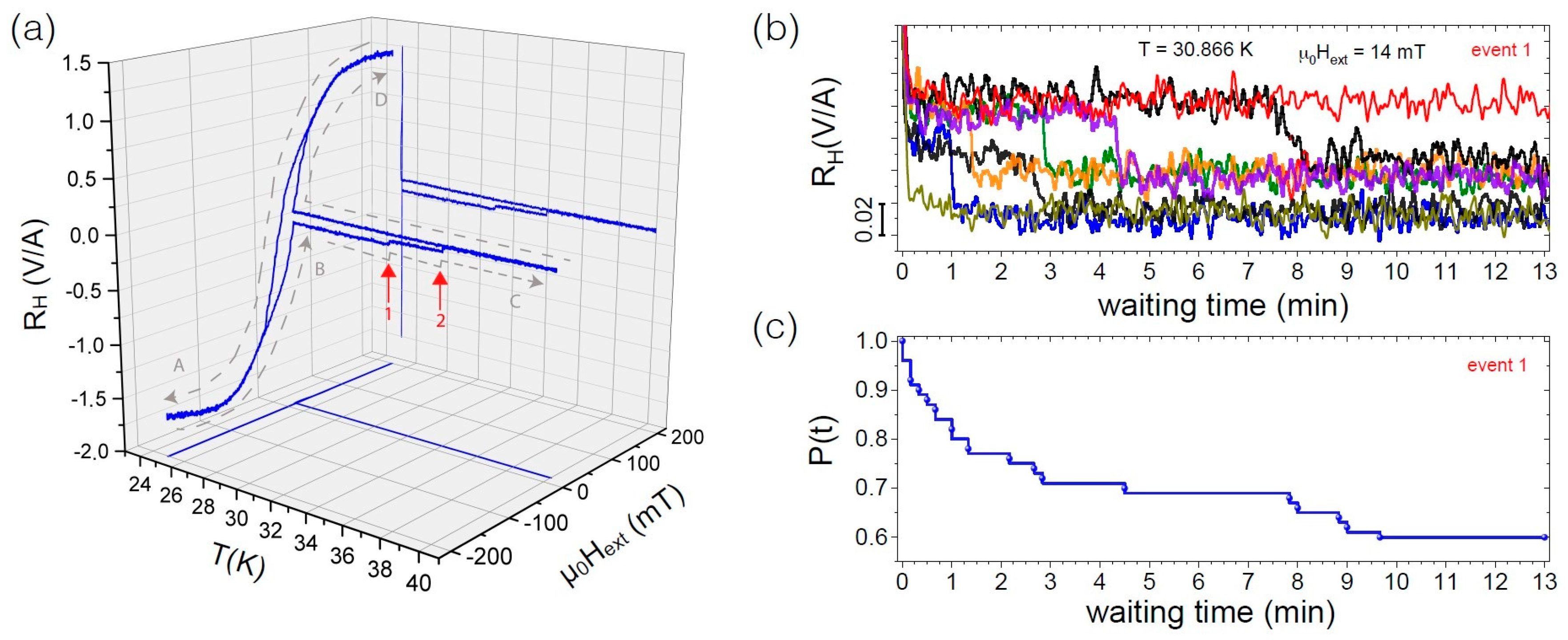
2.2. Temperature-Dependent Magnetization Switching
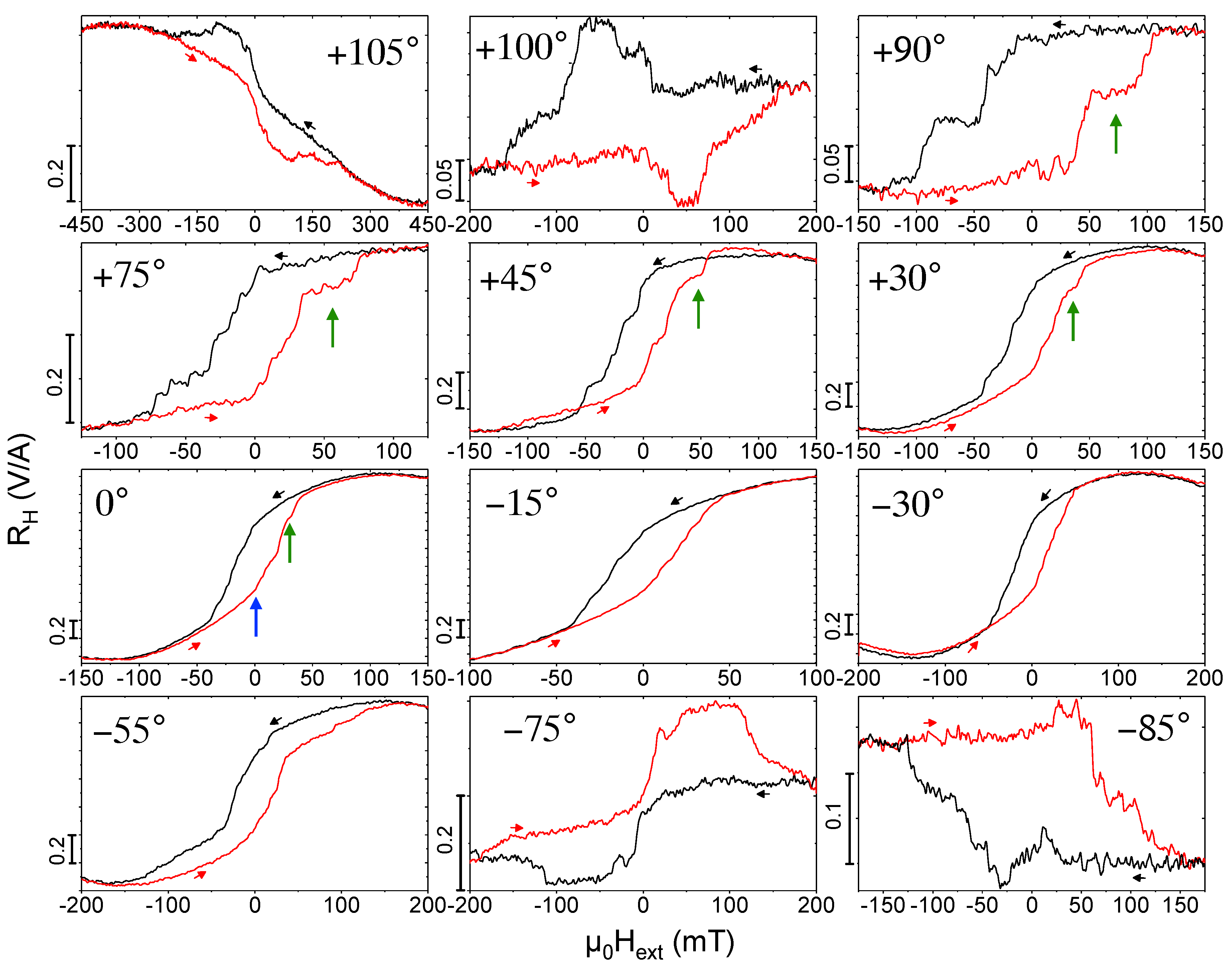
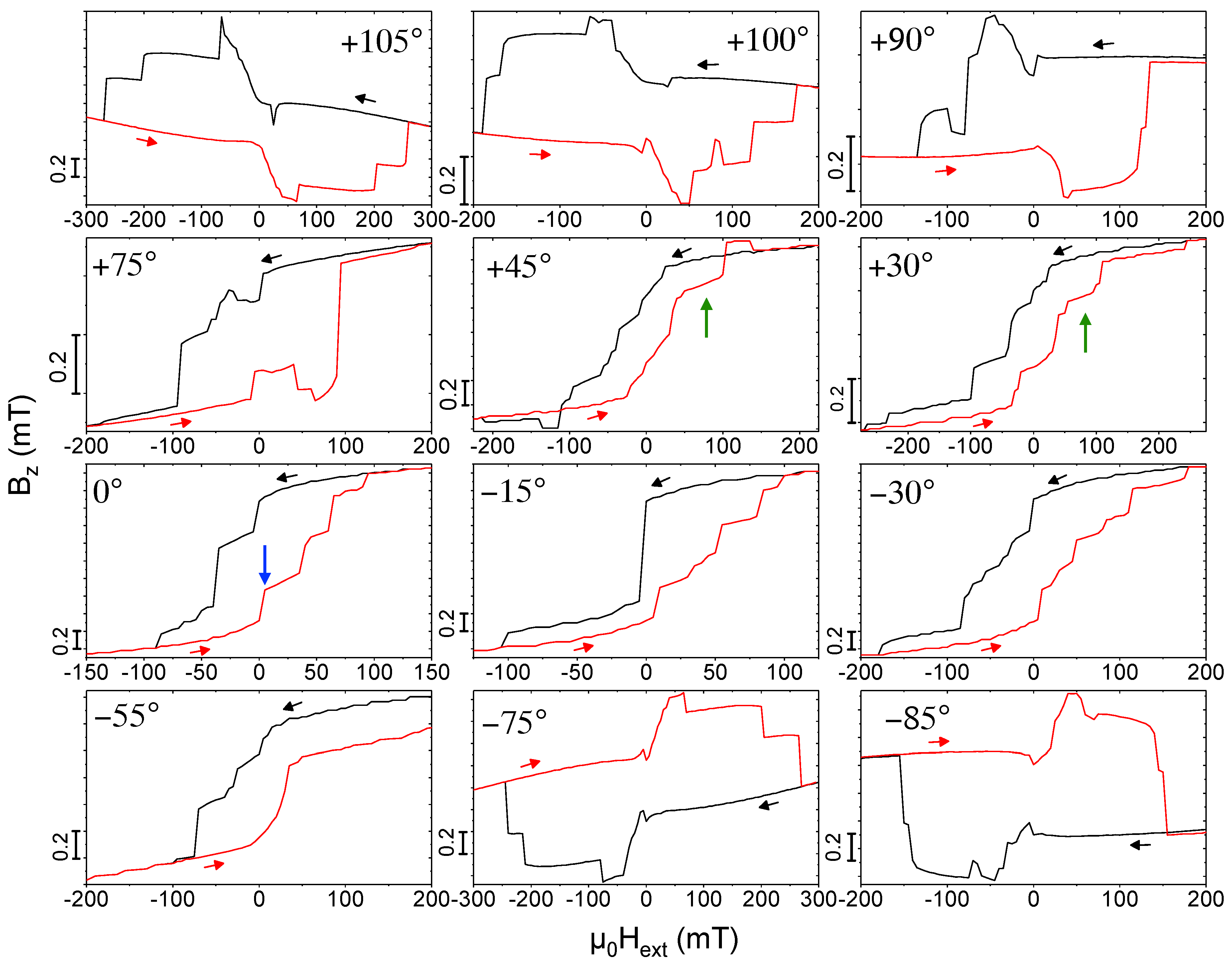
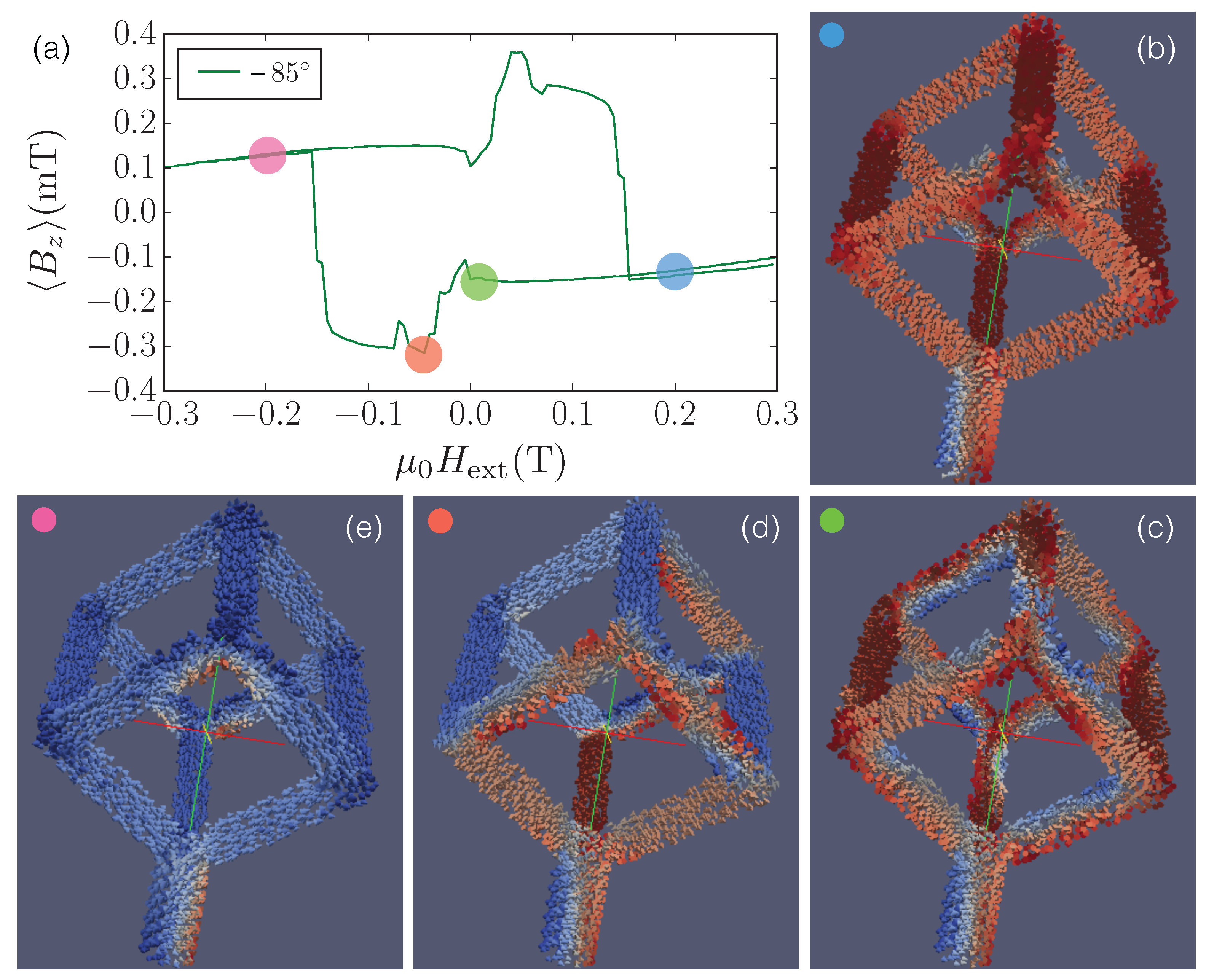
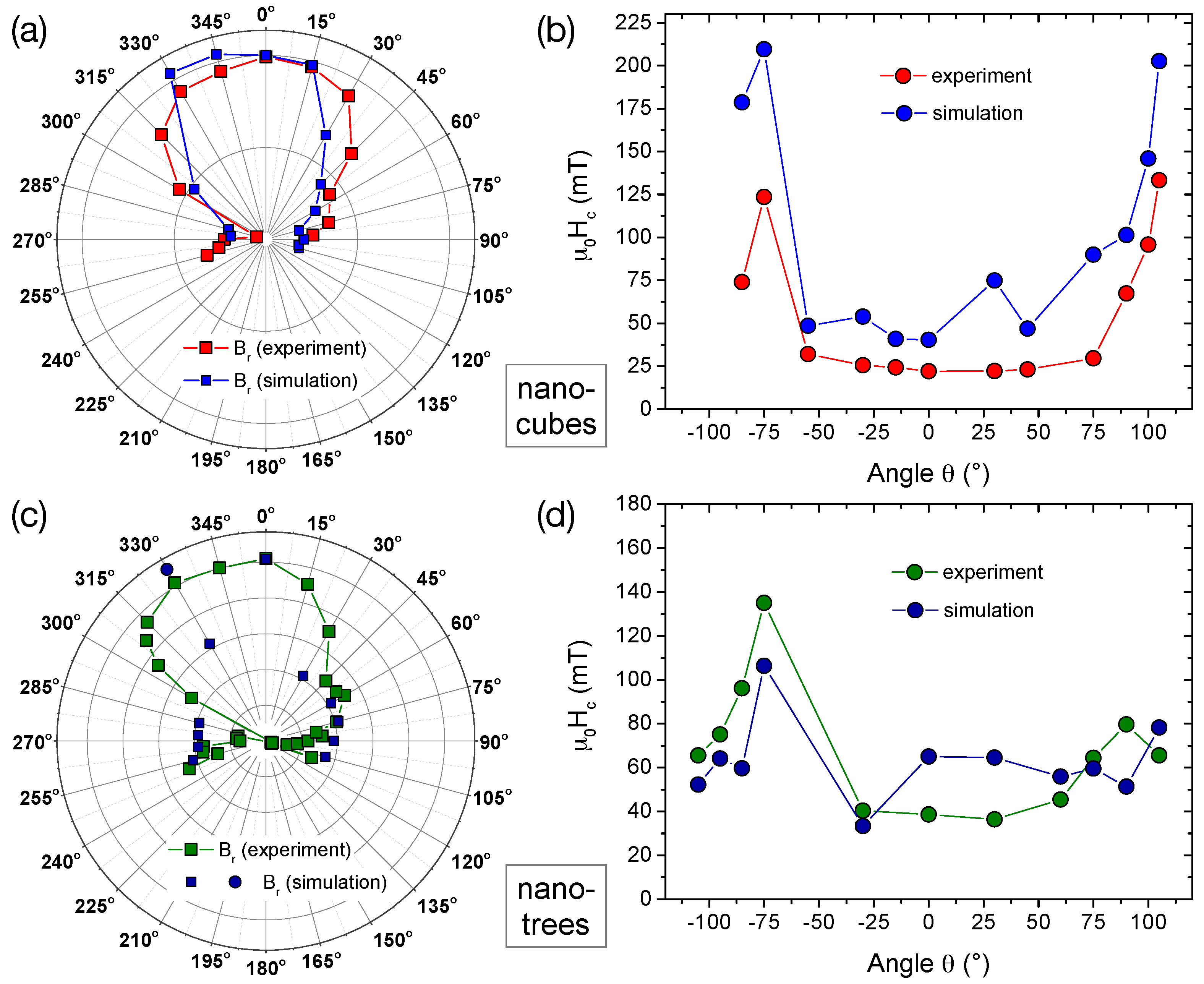
2.3. Angular-Dependent Magnetization Switching—Experiment and Micromagnetic Simulation
3. Discussion
4. Materials and Methods
4.1. Focused Electron Beam Induced Deposition
4.2. Micro-Hall Magnetometry
4.3. Micromagnetic Simulations
- Nano-tree
- Geometrical dimensions: stem diameter nm (cylindrical) and length nm, edge diameters nm and nm (elliptical) at a length of nm. The longer semi-axis with diameter is roughly in the beam direction (see [19] for details). Material parameters: saturation magnetization A/m and exchange constant J/m by averaging the respective value for Fe and Co [36,38].
- Nano-cube
- Geometrical dimensions: stem diameter nm (cylindrical) and length nm, edge diameter nm (cylindrical) at a length of nm. Material parameters: see material parameters for nano-tree.
- The positions of the four nano-trees and nano-cubes on the Hall sensor area were determined from SEM images.
- For each voxel element of the nano-tree/cube, the associated simulated magnetic moment was used to calculate the corresponding dipolar stray field. The stray field contributions of all moments of the nano-tree/cube set to one of the four positions were averaged over positions of the sensor array area (roughly m) in the -plane at the z-position of the 2DEG sensor nm below the substrate surface.
- The resulting four averaged stray fields were added to obtain the full averaged stray field of the four nano-trees/cubes.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| 3D (2D) | Three (Two)-Dimensional |
| FEBID | Focused Electron Beam Induced Deposition |
| SEM | Scanning Electron Microscopy |
| TEM | Transmission Electron Microscopy |
| EELS | Electron Energy Loss Spectroscopy |
References
- Kruglyak, V.V.; Demokritov, S.O.; Grundler, D. Magnonics. J. Phys. D Appl. Phys. 2010, 43, 264001. [Google Scholar] [CrossRef]
- Pulizzi, F. Spintronics. Nat. Mater. 2012, 11, 367. [Google Scholar] [CrossRef] [PubMed]
- Demokritov, S.O.; Slavin, A.N. (Eds.) Magnonics: From Fundamentals to Applications; Springer: Berlin, Germany, 2013. [Google Scholar]
- Fernández-Pacheco, A.; Streubel, R.; Fruchart, O.; Hertel, R.; Fischer, P.; Cowburn, R.P. Three-dimensional nanomagnetism. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Piraux, L.; Renard, K.; Guillemet, R.; Mátéfi-Tempfli, S.; Mátéfi-Tempfli, M.; Antohe, V.A.; Fusil, S.; Bouzehouane, K.; Cros, V. Template-Grown NiFe/Cu/NiFe Nanowires for Spin Transfer Devices. Nano Lett. 2007, 7, 2563–2567. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, C.; Guizar-Sicairos, M.; Scagnoli, V.; Holler, M.; Huthwelker, T.; Menzel, A.; Vartiainen, I.; Müller, E.; Kirk, E.; Gliga, S.; et al. Element-Specific X-Ray Phase Tomography of 3D Structures at the Nanoscale. Phys. Rev. Lett. 2015, 114. [Google Scholar] [CrossRef] [PubMed]
- Bedanta, S.; Barman, A.; Kleemann, W.; Petracic, O.; Seki, T. Magnetic Nanoparticles: A Subject for Both Fundamental Research and Applications. J. Nanomater. 2013, 2013, 22. [Google Scholar] [CrossRef]
- Williams, G.; Hunt, M.; Boehm, B.; May, A.; Taverne, M.; Ho, D.; Giblin, S.; Read, D.; Rarity, J.; Allenspach, R.; et al. Two-photon lithography for 3D magnetic nanostructure fabrication. Nano Res. 2018, 11, 845–854. [Google Scholar] [CrossRef]
- Chern, G.W.; Reichhardt, C.; Nisoli, C. Realizing three-dimensional artificial spin ice by stacking planar nano-arrays. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Perrin, Y.; Canals, B.; Rougemaille, N. Extensive degeneracy, Coulomb phase and magnetic monopoles in artificial square ice. Nature 2016, 540, 410–413. [Google Scholar] [CrossRef] [PubMed]
- Fowlkes, J.D.; Winkler, R.; Lewis, B.B.; Stanford, M.G.; Plank, H.; Rack, P.D. Simulation-Guided 3D Nanomanufacturing via Focused Electron Beam Induced Deposition. ACS Nano 2016, 10, 6163–6172. [Google Scholar] [CrossRef] [PubMed]
- Teresa, J.M.D.; Fernández-Pacheco, A.; Córdoba, R.; Serrano-Ramón, L.; Sangiao, S.; Ibarra, M.R. Review of magnetic nanostructures grown by focused electron beam induced deposition (FEBID). J. Phys. D Appl. Phys. 2016, 49, 1–24. [Google Scholar] [CrossRef]
- Córdoba, R.; Sharma, N.; Kölling, S.; Koenraad, P.M.; Koopmans, B. High-purity 3D nano-objects grown by focused-electron-beam induced deposition. Nanotechnology 2016, 27. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Pacheco, A.; Serrano-Ramón, L.; Michalik, J.M.; Ibarra, M.R.; De Teresa, J.M.; O’Brien, L.; Petit, D.; Lee, J.; Cowburn, R.P. Three dimensional magnetic nanowires grown by focused electron-beam induced deposition. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef] [PubMed]
- Pablo-Navarro, J.; Sanz-Hernández, D.; Magén, C.; Fernández-Pacheco, A.; de Teresa, J.M. Tuning shape, composition and magnetization of 3D cobalt nanowires grown by focused electron beam induced deposition (FEBID). J. Phys. D Appl. Phys. 2017, 50. [Google Scholar] [CrossRef]
- Sanz-Hernández, D.; Hamans, R.F.; Liao, J.W.; Welbourne, A.; Lavrijsen, R.; Fernández-Pacheco, A. Fabrication, Detection, and Operation of a Three-Dimensional Nanomagnetic Conduit. ACS Nano 2017, 11, 11066–11073. [Google Scholar] [PubMed]
- Huth, M.; Porrati, F.; Dobrovolskiy, O. Focused electron beam induced deposition meets materials science. Microelectron. Eng. 2018, 185–186, 9–28. [Google Scholar] [CrossRef]
- García-Cervera, C.J.; Gimbutas, Z.; Weinan, E. Accurate numerical methods for micromagnetics simulations with general geometries. J. Comput. Phys. 2003, 184, 37–52. [Google Scholar] [CrossRef]
- Keller, L.; Mamoori, M.K.I.A.; Pieper, J.; Gspan, C.; Stockem, I.; Schröder, C.; Barth, S.; Winkler, R.; Plank, H.; Pohlit, M.; et al. Direct-write of free-form building blocks for artificial magnetic 3D lattices. Sci. Rep. 2017, arXiv:1709.05847. [Google Scholar]
- Melko, R.G.; den Hertog, B.C.; Gingras, M.J.P. Long-Range Order at Low Temperatures in Dipolar Spin Ice. Phys. Rev. Lett. 2001, 87, 067203. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.F.; Nisoli, C.; Freitas, R.S.; Li, J.; McConville, W.; Cooley, B.J.; Lund, M.S.; Samarth, N.; Leighton, C.; Crespi, V.H.; et al. Artificial spin ice in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 2006, 439, 303–306. [Google Scholar] [CrossRef] [PubMed]
- Ladak, S.; Read, D.E.; Perkins, G.K.; Cohen, L.F.; Branford, W.R. Direct observation of magnetic monopole defects in an artificial spin-ice system. Nat. Phys. 2010, 6, 359–363. [Google Scholar] [CrossRef]
- Mengotti, E.; Heyderman, L.J.; Rodriguez, A.F.; Nolting, F.; Hugli, R.V.; Braun, H.B. Real-space observation of emergent magnetic monopoles and associated Dirac strings in artificial kagome spin ice. Nat. Phys. 2011, 7, 68–74. [Google Scholar] [CrossRef]
- Zhang, S.; Gilbert, I.; Nisoli, C.; Chern, G.W.; Erickson, M.J.; O’Brien, L.; Leighton, C.; Lammert, P.E.; Crespi, V.H.; Schiffer, P. Crystallites of magnetic charges in artificial spin ice. Nature 2013, 500, 553–557. [Google Scholar] [CrossRef] [PubMed]
- Nisoli, C.; Moessner, R.; Schiffer, P. Artificial spin ice: Designing and imaging magnetic frustration. Rev. Mod. Phys. 2013, 85, 1473–1490. [Google Scholar] [CrossRef]
- Gilbert, I.; Lao, Y.; Carrasquillo, I.; O’Brien, L.; Watts, J.D.; Manno, M.; Leighton, C.; Scholl, A.; Nisoli, C.; Schiffer, P. Emergent reduced dimensionality by vertex frustration in artificial spin ice. Nat. Phys. 2016, 12, 162–165. [Google Scholar] [CrossRef]
- Drisko, J.; Marsh, T.; Cumings, J. Topological frustration of artificial spin ice. Nat. Commun. 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.; Schmidt, F.P.; Haselmann, U.; Fowlkes, J.D.; Lewis, B.B.; Kothleitner, G.; Rack, P.D.; Plank, H. Direct-Write 3D Nanoprinting of Plasmonic Structures. ACS Appl. Mater. Interfaces 2017, 9, 8233–8240. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.; Lewis, B.B.; Fowlkes, J.D.; Rack, P.D.; Plank, H. High-Fidelity 3D-Nanoprinting using a Focused Electron Beam: Growth characteristics. ACS Appl. Nano Mater. 2018. under review. [Google Scholar]
- Wirth, S.; Anane, A.; von Molnár, S. Thermally activated magnetization reversal in nanometer-size iron particles. Phys. Rev. B 2000, 63. [Google Scholar] [CrossRef]
- Pohlit, M.; Porrati, F.; Huth, M.; Ohno, Y.; Ohno, H.; Müller, J. Magnetic stray-field studies of a single Cobalt nanoelement as a component of the building blocks of artificial square spin ice. J. Magn. Magn. Mater. 2016, 400, 206–212. [Google Scholar] [CrossRef]
- Pohlit, M.; Porrati, F.; Huth, M.; Ohno, Y.; Ohno, H.; Müller, J. Nanocluster building blocks of artificial square spin ice: Stray-field studies of thermal dynamics. J. Appl. Phys. 2015, 117. [Google Scholar] [CrossRef]
- Wernsdorfer, W.; Orozco, E.B.; Hasselbach, K.; Benoit, A.; Barbara, B.; Demoncy, N.; Loiseau, A.; Pascard, H.; Mailly, D. Experimental Evidence of the Néel-Brown Model of Magnetization Reversal. Phys. Rev. Lett. 1997, 78, 1791–1794. [Google Scholar] [CrossRef]
- Wernsdorfer, W.; Doudin, B.; Mailly, D.; Hasselbach, K.; Benoit, A.; Meier, J.; Ansermet, J.P.; Barbara, B. Nucleation of Magnetization Reversal in Individual Nanosized Nickel Wires. Phys. Rev. Lett. 1996, 77, 1873–1876. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xiong, P.; von Molnár, S.; Ohno, Y.; Ohno, H. Magnetization reversal in elongated Fe nanoparticles. Phys. Rev. B 2005, 71. [Google Scholar] [CrossRef]
- Porrati, F.; Huth, M. Diagram of the states in arrays of iron nanocylinders. Appl. Phys. Lett. 2004, 85, 3157–3159. [Google Scholar] [CrossRef]
- Porrati, F.; Pohlit, M.; Müller, J.; Barth, S.; Biegger, F.; Gspan, C.; Plank, H.; Huth, M. Direct writing of CoFe alloy nanostructures by focused electron beam induced deposition from a heteronuclear precursor. Nanotechnology 2015, 26. [Google Scholar] [CrossRef] [PubMed]
- Pohlit, M.; Stockem, I.; Porrati, F.; Huth, M.; Schröder, C.; Müller, J. Experimental and theoretical investigation of the magnetization dynamics of an artificial square spin ice cluster. J. Appl. Phys. 2016, 120. [Google Scholar] [CrossRef]
- Müller, J.; Körbitzer, B.; Amyan, A.; Pohlit, M.; Ohno, Y.; Ohno, H. Noise spectroscopy studies of GaAs/AlGaAs Hall devices for optimizing micro- and nano-scale magnetic measurements. In Proceedings of the 2015 International Conference on Noise and Fluctuations (ICNF), Xi’an, China, 2–6 June 2015; pp. 1–4. [Google Scholar]
- Müller, J.; Li, Y.; von Molnár, S.; Ohno, Y.; Ohno, H. Single-electron switching in AlxGa1−xAs/GaAs Hall devices. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Cornelissens, Y.G.; Peeters, F.M. Response function of a Hall magnetosensor in the diffusive regime. J. Appl. Phys. 2002, 92. [Google Scholar] [CrossRef]
- Cerchez, M.; Heinzel, T. Correction factor in nondiffusive Hall magnetometry. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Waeyenberge, B.V. The design and verification of MuMax3. AIP Adv. 2014, 4. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Mamoori, M.K.I.; Keller, L.; Pieper, J.; Barth, S.; Winkler, R.; Plank, H.; Müller, J.; Huth, M. Magnetic Characterization of Direct-Write Free-Form Building Blocks for Artificial Magnetic 3D Lattices. Materials 2018, 11, 289. https://doi.org/10.3390/ma11020289
Al Mamoori MKI, Keller L, Pieper J, Barth S, Winkler R, Plank H, Müller J, Huth M. Magnetic Characterization of Direct-Write Free-Form Building Blocks for Artificial Magnetic 3D Lattices. Materials. 2018; 11(2):289. https://doi.org/10.3390/ma11020289
Chicago/Turabian StyleAl Mamoori, Mohanad K. I., Lukas Keller, Jonathan Pieper, Sven Barth, Robert Winkler, Harald Plank, Jens Müller, and Michael Huth. 2018. "Magnetic Characterization of Direct-Write Free-Form Building Blocks for Artificial Magnetic 3D Lattices" Materials 11, no. 2: 289. https://doi.org/10.3390/ma11020289
APA StyleAl Mamoori, M. K. I., Keller, L., Pieper, J., Barth, S., Winkler, R., Plank, H., Müller, J., & Huth, M. (2018). Magnetic Characterization of Direct-Write Free-Form Building Blocks for Artificial Magnetic 3D Lattices. Materials, 11(2), 289. https://doi.org/10.3390/ma11020289