Influence of Polymethylsilsesquioxane Content to the Thermal Stability of Meta-Aramid Fiber Insulation Paper
Abstract
:1. Introduction
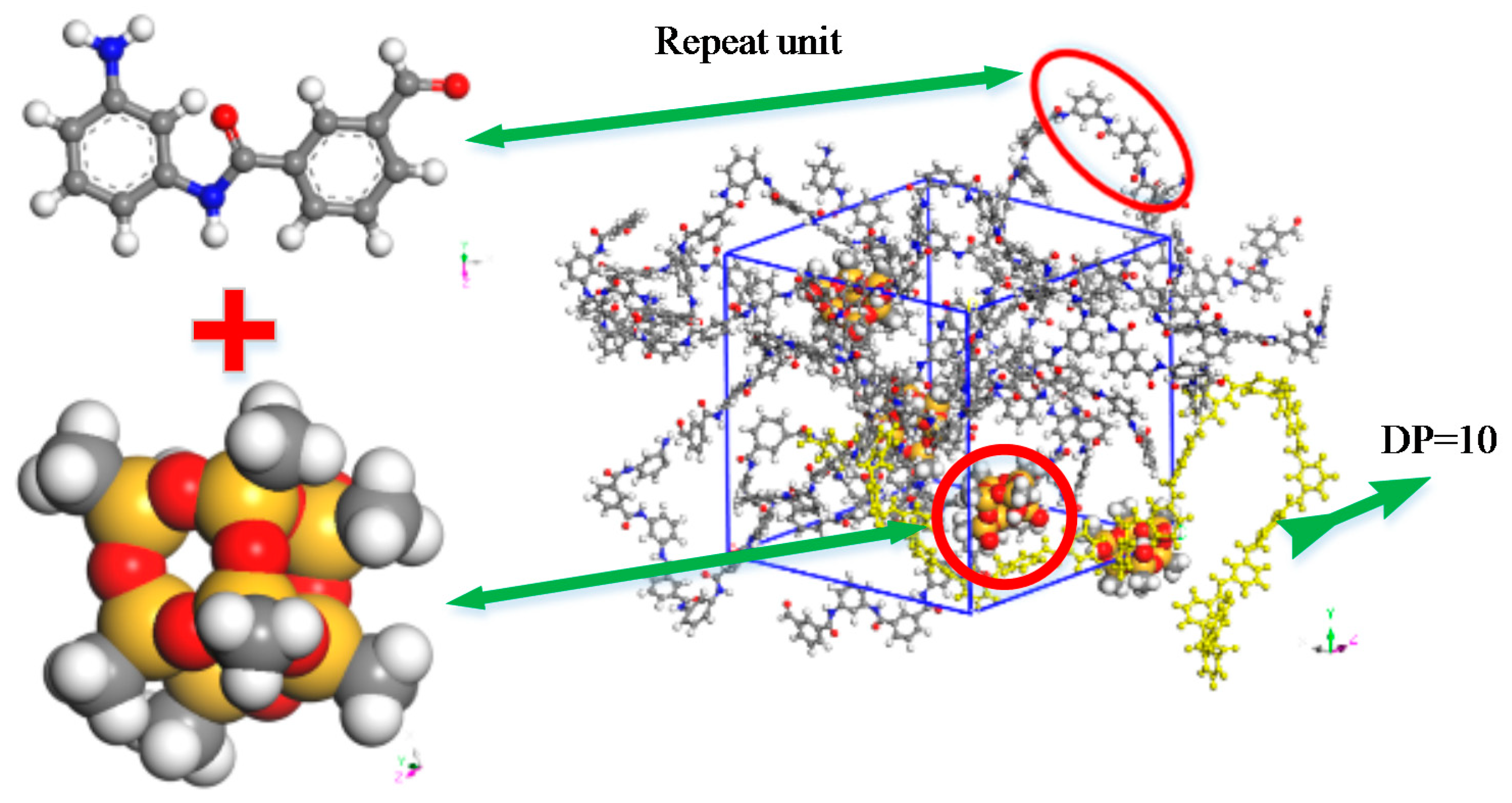
2. Model Construction
3. Parameter Calculation and Result Analysis
3.1. Mechanical Property
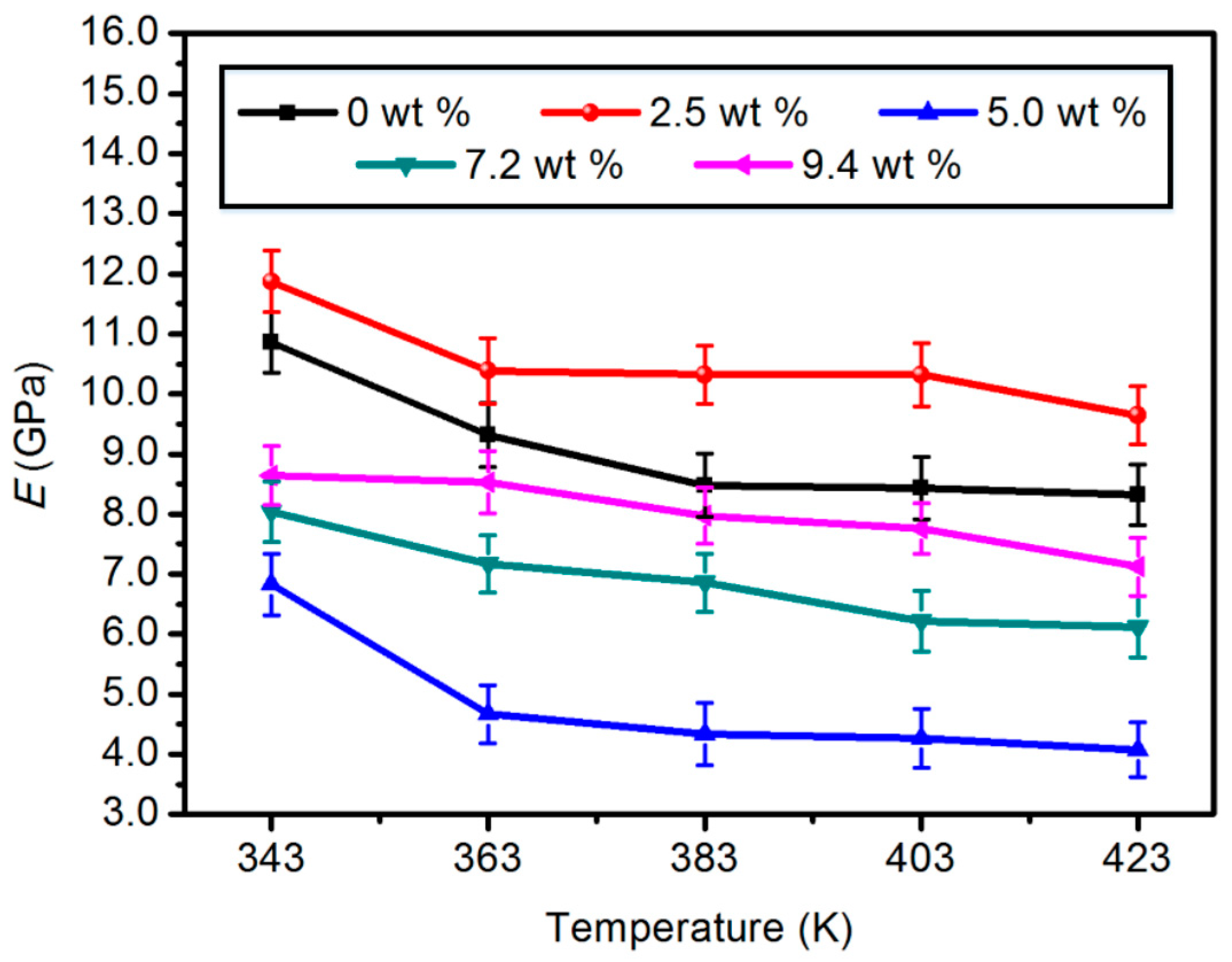
3.1.1. Elastic Modulus (E)
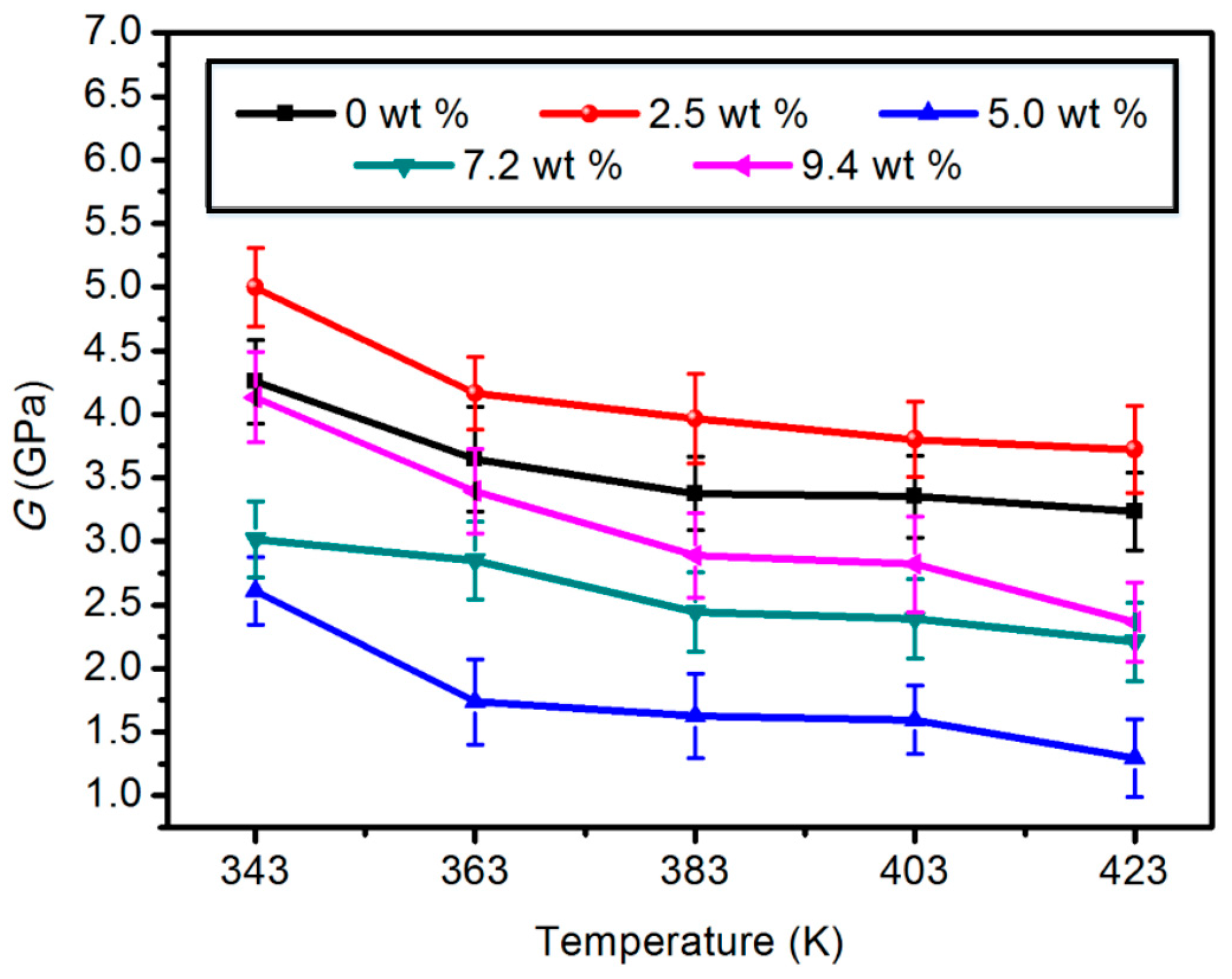
3.1.2. Shear Modulus (G)
3.1.3. Bulk Modulus (K)
3.1.4. Poisson’s Ratio (V) and Cauchy Pressure (C12–C44)
3.2. Interaction Energy
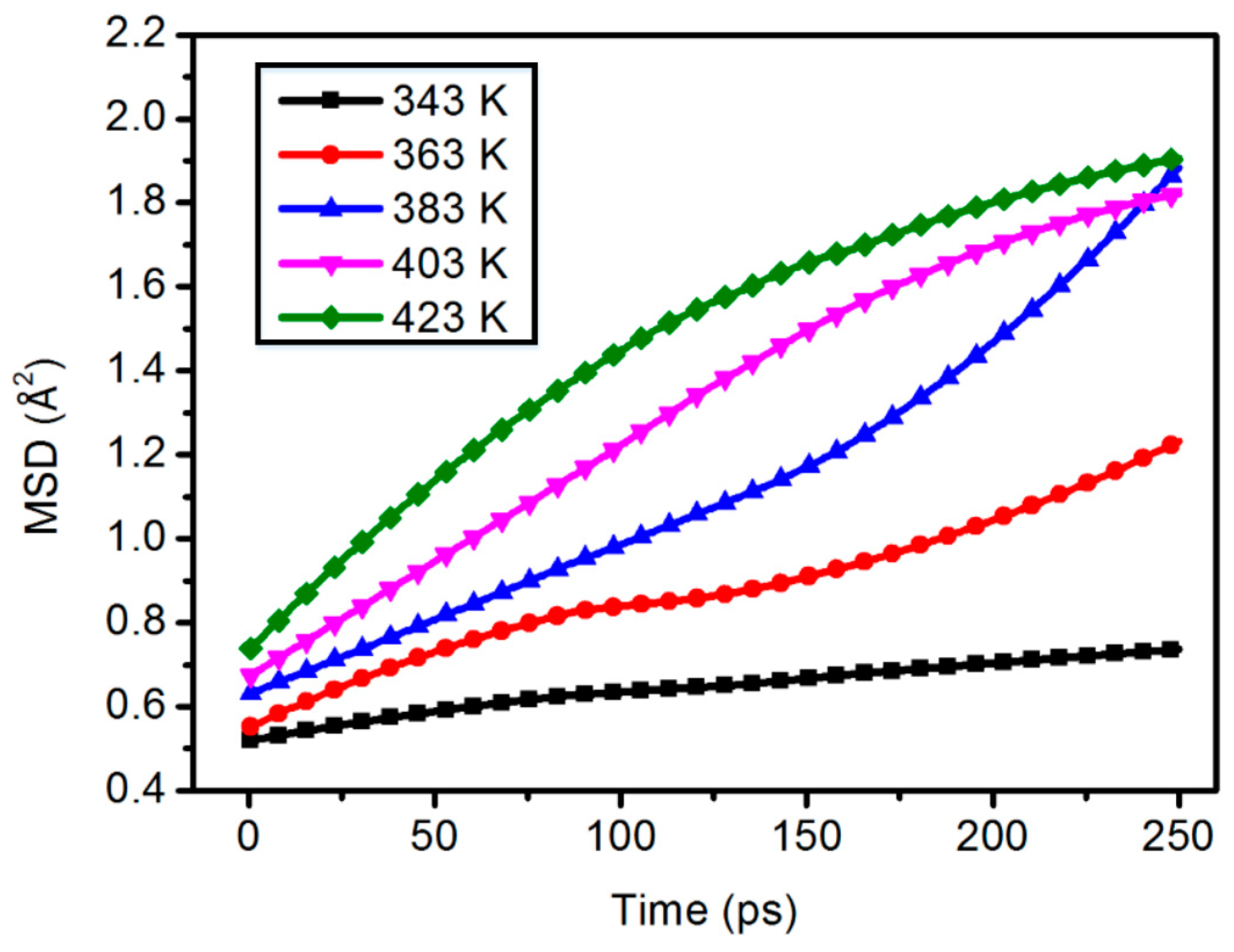
3.3. Mean Square Displacement
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Prevost, T.A.; Oommen, T.V. Cellulose insulation in oil-filled power transformers: Part I-history and development. IEEE Electr. Insul. Mag. 2006, 22, 28–35. [Google Scholar] [CrossRef]
- Oommen, T.V.; Prevost, T.A. Cellulose insulation in oil-filled power transformers: Part II-maintaining insulation integrity and life. IEEE Electr. Insul. Mag. 2006, 22, 5–14. [Google Scholar] [CrossRef]
- Frye, C.L.; Collins, W.T. Oligomeric silsesquioxanes, (HSiO3/2)n. J. Am. Chem. Soc. 1970, 92, 5586–5588. [Google Scholar] [CrossRef]
- Baney, R.H.; Itoh, M.; Sakakibara, A.; Suzuki, T. Silsesquioxanes. Chem. Rev. 1995, 94, 1409–1430. [Google Scholar] [CrossRef]
- Zheng, L.; Kasi, R.M.; Farris, R.J.; Coughlin, E.B. Synthesis and thermal properties of hybrid copolymers of syndiotactic polystyrene and polyhedral oligomeric silsesquioxane. J. Polym. Sci. Polym. Chem. 2002, 40, 885–891. [Google Scholar] [CrossRef]
- Cordes, D.B.; Lickiss, P.D.; Rataboul, F. Recent developments in the chemistry of cubic polyhedral oligosilsesquioxanes. Chem. Rev. 2010, 110, 2081–2173. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.L.; Yan, S.K.; Han, C.C.; Zhang, R.B. Promising Functional Materials Based on Ladder Polysiloxanes. Adv. Mater. 2008, 20, 2970–2976. [Google Scholar] [CrossRef]
- Park, E.S.; Ro, H.W.; Nguyen, C.V. Infrared Spectroscopy Study of Microstructures of Poly(silsesquioxane)s. Chem. Mater. 2008, 20, 1548–1554. [Google Scholar] [CrossRef]
- Xu, H.Y.; Yang, B.H.; Wang, J.F.; Li, C. Preparation, Tg improvement, and thermal stability enhancement mechanism of soluble poly(methyl methacrylate) nanocomposites by incorporating octavinyl polyhedral oligomeric silsesquioxanes. J. Polym. Sci. Polym. Chem. 2010, 45, 5308–5317. [Google Scholar] [CrossRef]
- Gnanasekaran, D.; Ajit, W.P.; Reddy, B.S.R. Influence of moieties on morphology, thermal, and dielectric properties in polyamide-polyhedral oligomeric silsequioxanes nanocomposites. Polym. Eng. Sci. 2013, 53, 1637–1644. [Google Scholar] [CrossRef]
- Ma, W.S.; Zhang, D.Q.; Duan, Y.; Wang, H. Highly monodisperse polysilsesquioxane spheres: Synthesis and application in cotton fabrics. J. Colloid Interf. Sci. 2013, 392, 194–200. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.Q.; Schiraldi, D.A. Thermal and mechanical properties of polyhedral oligomeric silsesquioxane (POSS)/polycarbonate composites. Polymer 2005, 46, 11640–11647. [Google Scholar] [CrossRef]
- Jian, W.; Ge, Q.; Mather, P.T. PEG-POSS Multiblock Polyurethanes: Synthesis, Characterization, and Hydrogel Formation. Macromolecules 2010, 43, 7637–7649. [Google Scholar] [CrossRef]
- Lefèvre, N.; Daoulas, K.C.; Müller, M.; Gohy, J.F.; Fustin, C.A. Self-Assembly in Thin Films of Mixtures of Block Copolymers and Homopolymers Interacting by Hydrogen Bonds. Macromolecules 2010, 43, 7734–7743. [Google Scholar] [CrossRef]
- Kavale, M.S.; Mahadik, D.B.; Parale, V.G.; Wagh, P.B.; Gupta, S.C.; Raoa, A.V.; Barshilia, H.C. Optically transparent, superhydrophobic methyltrimethoxysilane based silica coatings without silylating reagent. Appl. Surf. Sci. 2011, 258, 158–162. [Google Scholar] [CrossRef]
- Shirgholami, M.A.; Shateri-Khalilabad, M.; Yazdanshenas, M.E. Effect of reaction duration in the formation of superhydrophobic polymethylsilsesquioxane nanostructures on cotton fabric. Text. Res. J. 2013, 83, 100–110. [Google Scholar] [CrossRef]
- Lei, C.S.; Li, J.N.; Sun, C.C.; Yang, H.L.; Xia, T.; Hu, Z.J.; Zhuang, Y. A Co-Precursor Approach Coupled with a Supercritical Modification Method for Constructing Highly Transparent and Superhydrophobic Polymethylsilsesquioxane Aerogels. Molecules 2018, 23, 797. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xu, R.W.; Yu, D.W. A novel poly-benzoxazinyl functionalized polyhedral oligomeric silsesquioxane and its nanocomposite with polybenzoxazine. Eur. Polym. J. 2007, 43, 743–752. [Google Scholar] [CrossRef]
- Bourbigot, S.; Turf, T.; Bellayer, S.; Duquesne, S. Polyhedral oligomeric silsesquioxane as flame retardant for thermoplastic polyurethane. Polym. Degrad. Stabil. 2009, 94, 1230–1237. [Google Scholar] [CrossRef]
- Musto, P.; Abbate, M.; Pannico, M.; Scarinzi, G.; Ragosta, G. Improving the photo-oxidative stability of epoxy resins by use of functional POSS additives: A spectroscopic, mechanical and morphological study. Polymer 2012, 53, 5016–5036. [Google Scholar] [CrossRef]
- Leu, C.M.; Yaote, C.A.; Wei, K.H. Polyimide-Side-Chain Tethered Polyhedral Oligomeric Silsesquioxane Nanocomposites for Low-Dielectric Film Applications. Chem. Mater. 2003, 15, 3721–3727. [Google Scholar] [CrossRef]
- Wahab, M.A.; Mya, K.Y.; He, C. Synthesis, morphology, and properties of hydroxyl terminated-POSS/polyimide low-k, nanocomposite films. J. Polym. Sci. Polym. Chem. 2010, 46, 5887–5896. [Google Scholar] [CrossRef]
- Liu, W.C.; Yu, Y.Y.; Chen, W.C. Structural control and properties of low-dielectric-constant poly(hydrogen silsesquioxane) precursors and their thin films. J. Appl. Polym. Sci. 2004, 91, 2653–2660. [Google Scholar] [CrossRef]
- Liu, T.T.; Lu, D.; Zhang, H.; Zheng, M.Y.; Yang, H.Y.; Xu, Y.C.; Luo, C.; Zhu, W.L.; Yu, K.Q.; Jiang, H.L. Applying high-performance computing in drug discovery and molecular simulation. Natl. Sci. Rev. 2016, 3, 49–63. [Google Scholar] [CrossRef] [Green Version]
- Valiyaveettil, S.; Gans, C.; Klapper, M.; Gereke, R.; Müllen, K. Synthesis and structural study of poly(isophthalamide)s. Polym. Bull. 1995, 34, 13–19. [Google Scholar] [CrossRef]
- Mazeau, K.; Heux, L. Molecular dynamics simulations of bulk native crystalline and amorphous structures of cellulose. J. Phys. Chem. B 2003, 107, 2394–2403. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, S.; Wang, X.B.; Hao, J. Enhanced mechanical properties and thermal stability of cellulose insulation paper achieved by doping with melamine-grafted nano-SiO2. Cellulose 2018, 25, 1–15. [Google Scholar] [CrossRef]
- Wang, X.B.; Tang, C.; Wang, Q.; Li, X.P.; Hao, J. Selection of optimal polymerization degree and force field in the molecular dynamics simulation of insulating paper cellulose. Energies 2017, 10, 1377. [Google Scholar] [CrossRef]
- Li, X.; Tang, C.; Wang, Q.; Li, X.P.; Hao, J. Molecular simulation research on the micro effect mechanism of interfacial properties of nano SiO2/meta-aramid fiber. Int. J. Heat Technol. 2017, 35, 123–129. [Google Scholar] [CrossRef]
- Bhargava, B.L.; Balasubramanian, S. Ab initio molecular dynamics simulation of a 1-ethyl-3-methylimidazolium fluoride-hydrogen fluoride mixture. J. Phys. Chem. B 2008, 112, 7566–7573. [Google Scholar] [CrossRef] [PubMed]
- Jeyranpour, F.; Alahyarizadeh, G.; Minuchehr, A. The thermo-mechanical properties estimation of fullerene-reinforced resin epoxy composites bimolecular dynamics simulation—A comparative study. Polymer 2016, 88, 9–18. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applications overview with details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Nishino, T.; Takano, K.; Nakamae, K.J. Elastic modulus of the crystalline regions of cellulose polymorphs. J. Polym. Sci. Polym. Phys. 1995, 33, 1647–1651. [Google Scholar] [CrossRef]
- Lundgaard, L.E.; Hansen, W.; Ingebrigtsen, S. Ageing of Mineral Oil Impregnated Cellulose by Acid Catalysis. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 540–546. [Google Scholar] [CrossRef]
- Wu, J.L. Elasticity; Higher Education Press: Beijing, China, 2001. [Google Scholar]
- Piyarat, N.; Kohji, T.; Yasuhiko, M.A.; Rangsiman, O. Factors Governing the Three-Dimensional Hydrogen Bond Network Structure of Poly(m-phenylene isophthalamide) and a Series of Its Model Compounds: (1) Systematic Classification of Structures Analyzed by the X-ray Diffraction Method. J. Phys. Chem. B 2002, 106, 6842–6848. [Google Scholar] [CrossRef]
- Villarrodil, S.; Paredes, J.I.A.; Martínezalonso, A.; Tascón, J.M.D. Atomic force microscopy and infrared spectroscopy studies of the thermal degradation of nomex aramid fibers. Chem. Mater. 2012, 13, 4297–4304. [Google Scholar] [CrossRef]
- Li, G.L. Organic Silicon Polymer Chemistry, 1st ed.; Science Press: Beijing, China, 1998; p. 103. [Google Scholar]
- Yang, Z.; Feng, L.; Shen, D.; Feng, S.; Zhang, C. Study on the synthesis and thermal degradation of silicone resin containing silphenylene units. Thermochim. Acta 2011, 521, 170–175. [Google Scholar] [CrossRef]
- Deng, M.; Tan, V.B.C.; Tay, T.E. Atomistic modeling: Interfacial diffusion and adhesion of polycarbonate and silanes. Polymer 2004, 45, 6399–6407. [Google Scholar] [CrossRef]
- Xiao, H.M.; Ju, X.H. Intermolecular Interactions in High Energy Systems; Science Press: Beijing, China, 2004. [Google Scholar]
- Zhang, S.G.; Shi, W.Y.; Lei, W.; Xia, M.Z.; Wang, F.Y. Molecular dynamics simulation of interaction between calcite crystal and water-soluble polymers. Acta Phys.-Chim. Sin. 2005, 21, 1198–1204. [Google Scholar] [CrossRef]
- Fu, B.X.; Gelfer, M.Y.; Hsiao, B.S.; Phillips, S.; Viers, B.; Blanski, R.; Ruth, P. Physical gelation in ethylene–propylene copolymer melts induced by polyhedral oligomeric silsesquioxane (POSS) molecules. Polymer 2003, 44, 1499–1506. [Google Scholar] [CrossRef]
- Hofmann, D.; Fritz, L.; Ulbrich, J.; Paul, D. Molecular simulation of small molecule diffusion and solution in dense amorphous polysiloxanes and polyimides. Comput. Theor. Polym. Sci. 2000, 10, 419–436. [Google Scholar] [CrossRef]
- Zhang, Q.G.; Liu, Q.L.; Wu, J.Y.; Chen, Y.; Zhu, A.M. Structure-related diffusion in poly(methylmethacrylate)/polyhedral oligomeric silsesquioxanes composites: A molecular dynamics simulation study. J. Membr. Sci. 2009, 342, 105–112. [Google Scholar] [CrossRef]
- Sheng, Y.P.; Jiang, P.P.; Hua, J.Y.; Zhang, D.Y.; Deng, J.N.; He, J.; Cao, Z.L. Preparation and Characterization of Soybean Oil Based Polyurethane Modified by Polyphenylsilsesquioxane. Acta Polym. Sin. 2015, 3, 290–297. [Google Scholar]
- Han, J.; Gee, R.H.; Boyd, R.H. Glass Transition Temperatures of Polymers from Molecular Dynamics Simulations. Macromolecules 1994, 27, 7781–7784. [Google Scholar] [CrossRef]


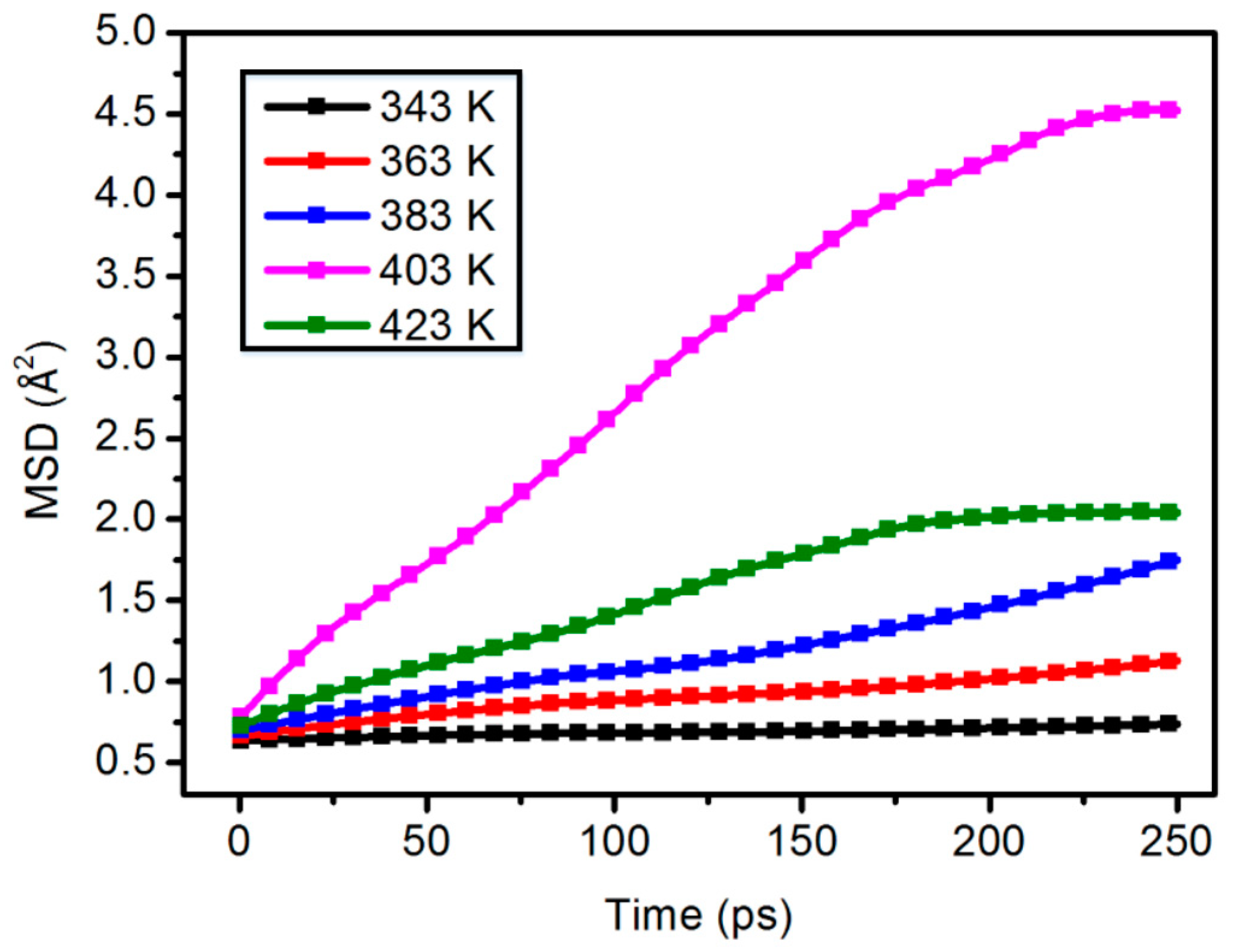
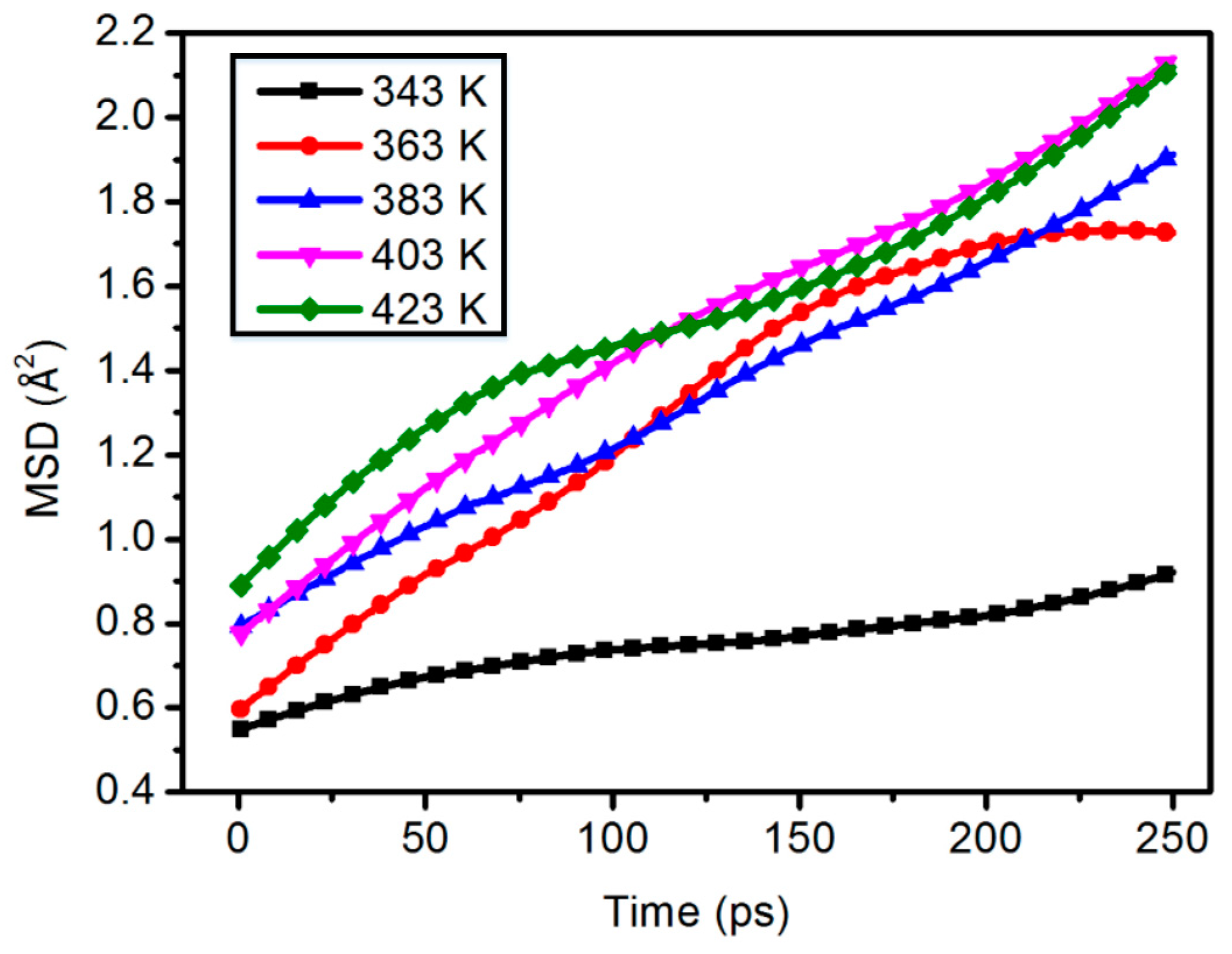
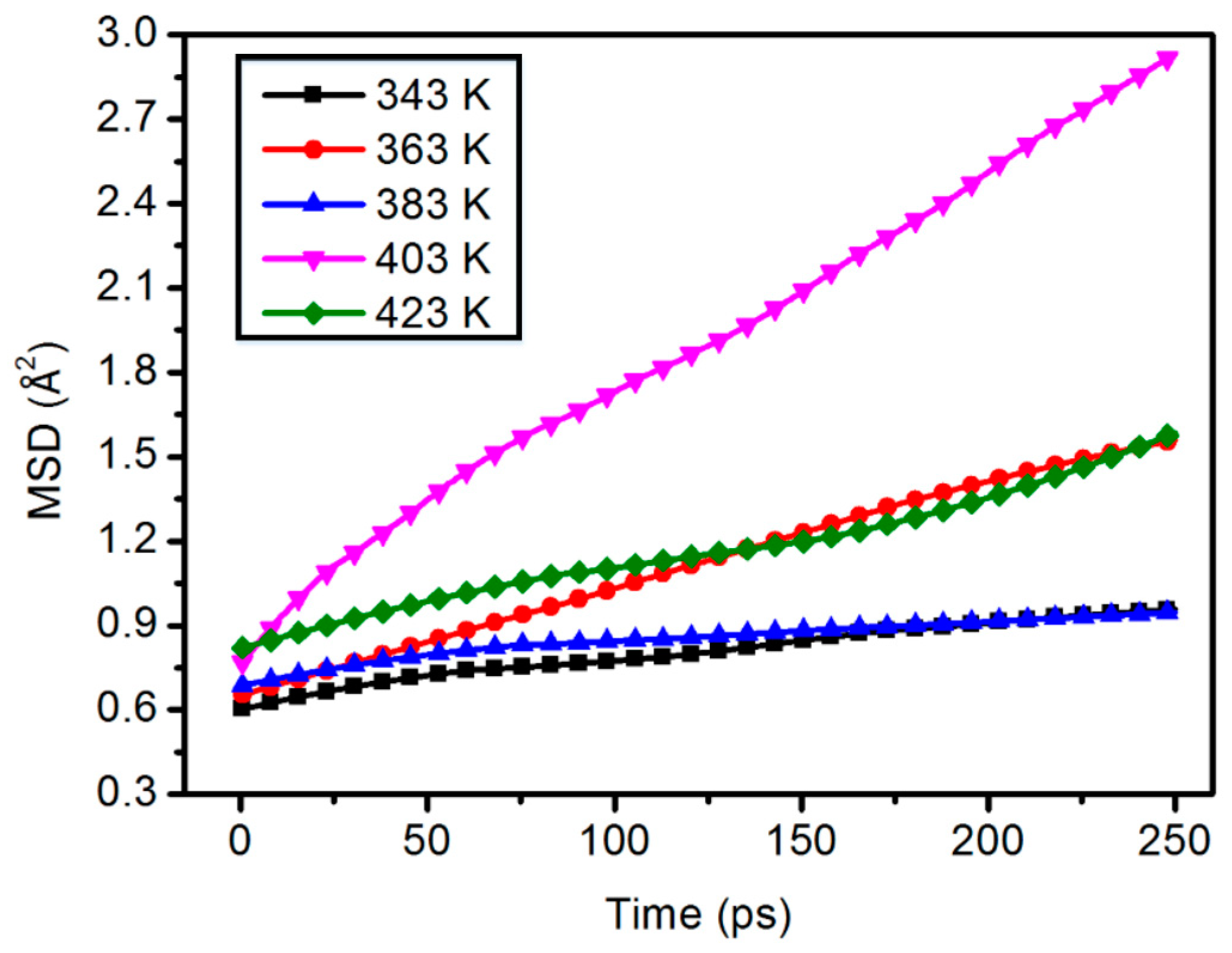
| Mass Percentage (wt %) | Poisson’s Ratio (V) |
|---|---|
| 0 wt % | 0.2701 |
| 2.5 wt % | 0.2567 |
| 5.0 wt % | 0.3300 |
| 7.2 wt % | 0.3103 |
| 9.4 wt % | 0.2945 |
| Mass Percentage (wt %) | Cauchy Pressure (C12–C44) |
|---|---|
| 0 wt % | 0.7934 |
| 2.5 wt % | 1.4826 |
| 5.0 wt % | 1.1685 |
| 7.2 wt % | 1.9970 |
| 9.4 wt % | 1.3886 |
| Temperature (K) | Mass Percentage (wt %) | (kcal/mol) | (kcal/mol) | (kcal/mol) | (kcal/mol) |
|---|---|---|---|---|---|
| 343 | 2.5 wt % | −60.30 | 22,758.54 | −798.98 | 23,617.82 |
| 5.0 wt % | 657.29 | 18,530.88 | −1018.68 | 18,892.27 | |
| 7.2 wt % | 330.34 | 18,925.28 | −2362.19 | 20,957.13 | |
| 9.4 wt % | 301.74 | 244,53.84 | −2962.59 | 27,114.69 | |
| 363 | 2.5 wt % | −57.90 | 228,10.24 | −783.35 | 23,651.50 |
| 5.0 wt % | 695.99 | 18,631.31 | −1028.56 | 18,963.88 | |
| 7.2 wt % | 319.10 | 19,168.66 | −2372.55 | 21,222.11 | |
| 9.4 wt % | 280.73 | 24,646.37 | −2945.34 | 27,310.98 | |
| 383 | 2.5 wt % | −67.12 | 22,971.43 | −774.72 | 23,813.27 |
| 5.0 wt % | 673.10 | 18,780.74 | −999.14 | 19,106.77 | |
| 7.2 wt % | 301.50 | 19,412.03 | −2340.20 | 21,450.73 | |
| 9.4 wt % | 294.69 | 24,683.29 | −2960.78 | 27,349.37 | |
| 403 | 2.5 wt % | −62.94 | 23,014.71 | −779.71 | 23,857.36 |
| 5.0 wt % | 693.37 | 18,896.53 | −1059.95 | 19,263.11 | |
| 7.2 wt % | 278.32 | 19,595.41 | −2368.89 | 21,685.98 | |
| 9.4 wt % | 293.77 | 25,037.45 | −2899.78 | 27,643.45 | |
| 423 | 2.5 wt % | −56.95 | 23,184.02 | −778.17 | 24,019.14 |
| 5.0 wt % | 667.98 | 19,090.43 | −982.06 | 19,404.52 | |
| 7.2 wt % | 275.66 | 19,938.79 | −2342.38 | 22,005.51 | |
| 9.4 wt % | 266.30 | 24,954.38 | −2923.85 | 27,611.94 |
| Temperature (K) | Energy | 0 wt % (kcal/mol) | 2.5 wt % (kcal/mol) |
|---|---|---|---|
| 343 | Valence energy | 11,898.25 | 13,565.77 |
| Nonbond energy | 6050.19 | 6498.12 | |
| 363 | Valence energy | 11,748.40 | 13,534.63 |
| Nonbond energy | 6227.78 | 6635.92 | |
| 383 | Valence energy | 12,126.83 | 13,835.83 |
| Nonbond energy | 6113.74 | 6496.96 | |
| 403 | Valence energy | 12,127.38 | 13,927.94 |
| Nonbond energy | 6403.19 | 6626.21 | |
| 423 | Valence energy | 12,358.77 | 14,136.22 |
| Nonbond energy | 6259.24 | 6399.32 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, W.; Xie, J.; Zhang, J.; Tang, C.; Zhao, Z. Influence of Polymethylsilsesquioxane Content to the Thermal Stability of Meta-Aramid Fiber Insulation Paper. Materials 2018, 11, 2317. https://doi.org/10.3390/ma11112317
Zheng W, Xie J, Zhang J, Tang C, Zhao Z. Influence of Polymethylsilsesquioxane Content to the Thermal Stability of Meta-Aramid Fiber Insulation Paper. Materials. 2018; 11(11):2317. https://doi.org/10.3390/ma11112317
Chicago/Turabian StyleZheng, Wei, Jufang Xie, Jingwen Zhang, Chao Tang, and Zhongyong Zhao. 2018. "Influence of Polymethylsilsesquioxane Content to the Thermal Stability of Meta-Aramid Fiber Insulation Paper" Materials 11, no. 11: 2317. https://doi.org/10.3390/ma11112317
APA StyleZheng, W., Xie, J., Zhang, J., Tang, C., & Zhao, Z. (2018). Influence of Polymethylsilsesquioxane Content to the Thermal Stability of Meta-Aramid Fiber Insulation Paper. Materials, 11(11), 2317. https://doi.org/10.3390/ma11112317





