Simulation of Temperature Distribution and Microstructure Evolution in the Molten Pool of GTAW Ti-6Al-4V Alloy
Abstract
1. Introduction
2. Thermal Modeling of Welding
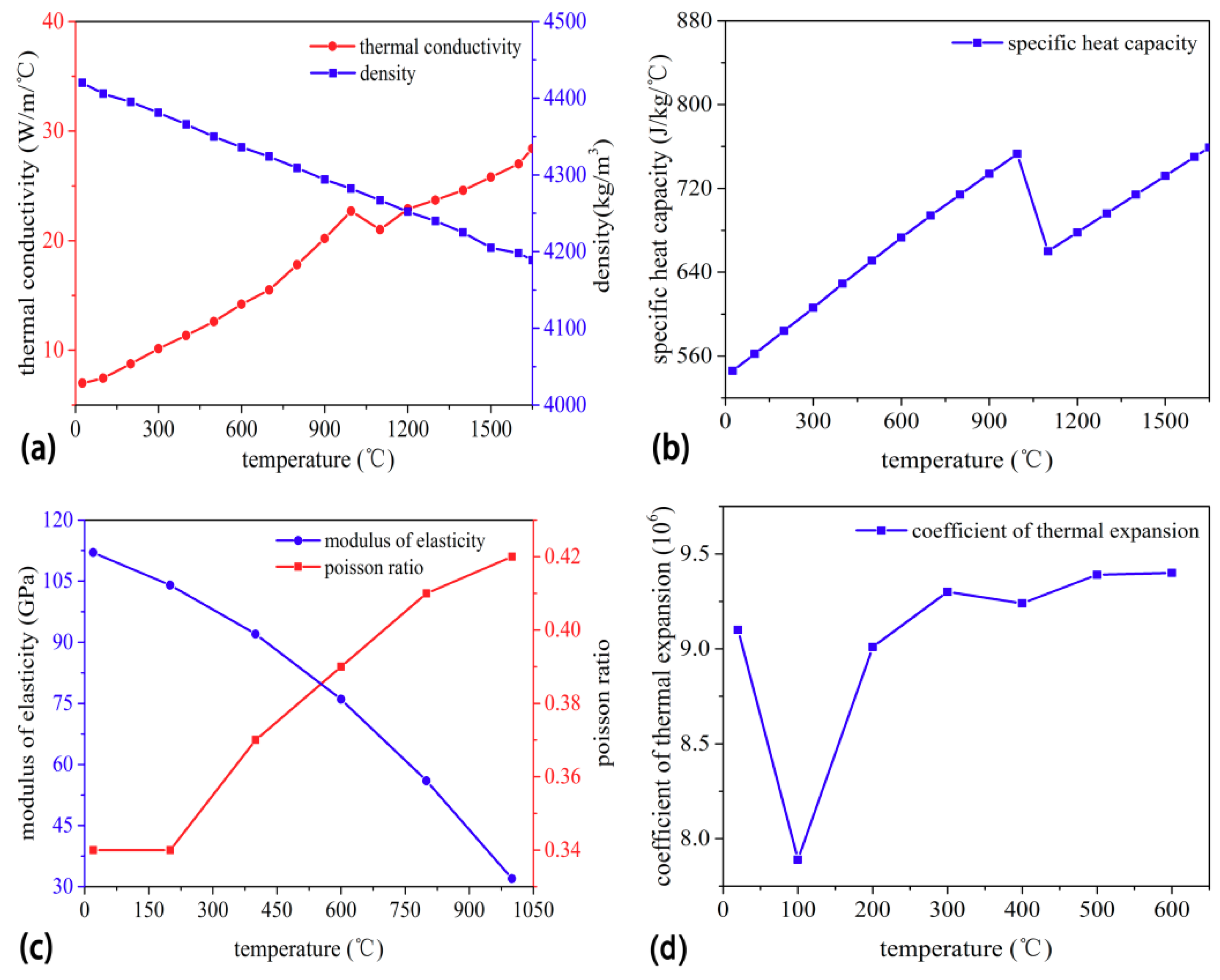
2.1. Meshing and Analysis Settings
2.2. Heat Transfer Equation
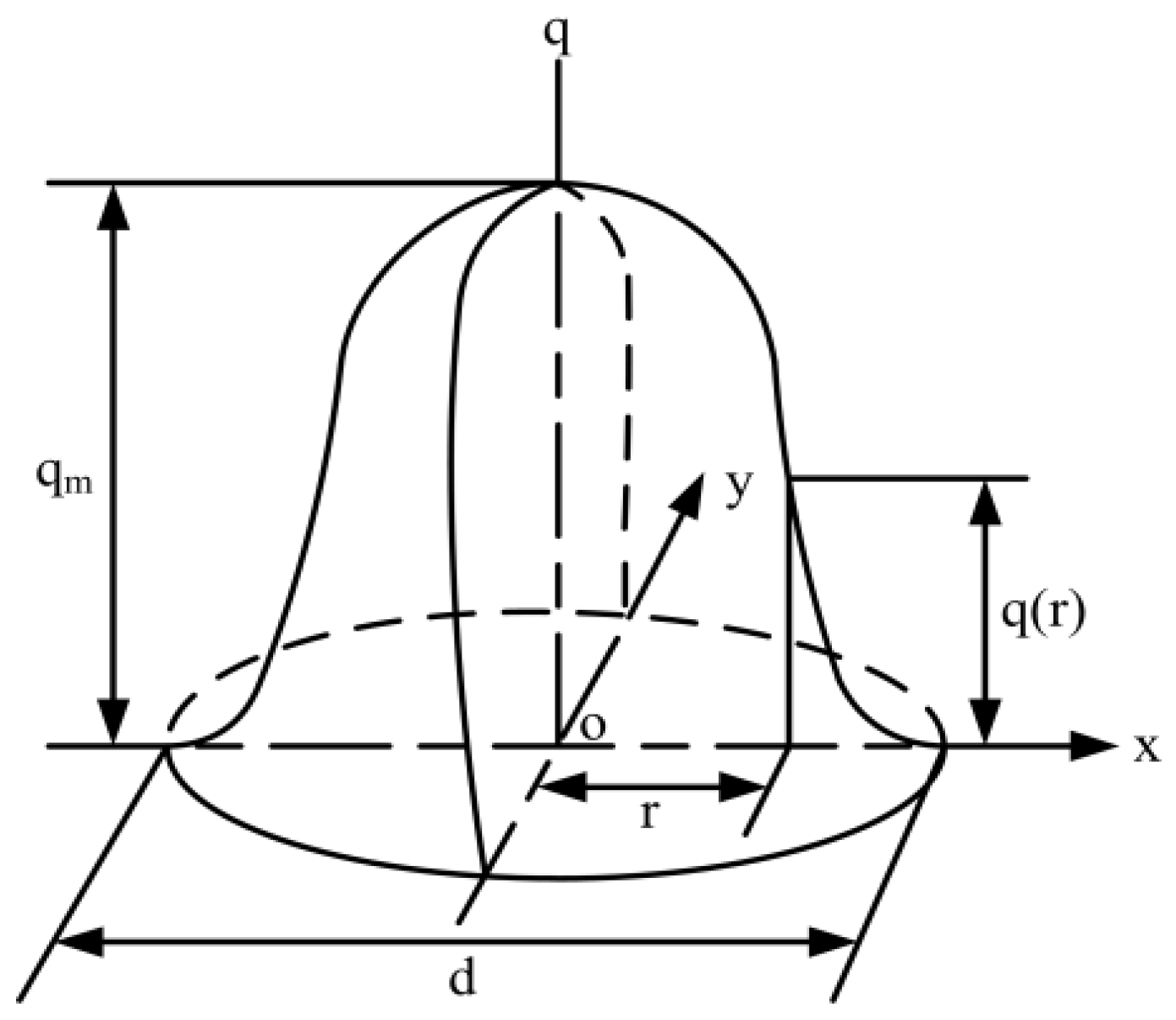
2.3. Heat Source
2.4. Boundary and Initial Conditions
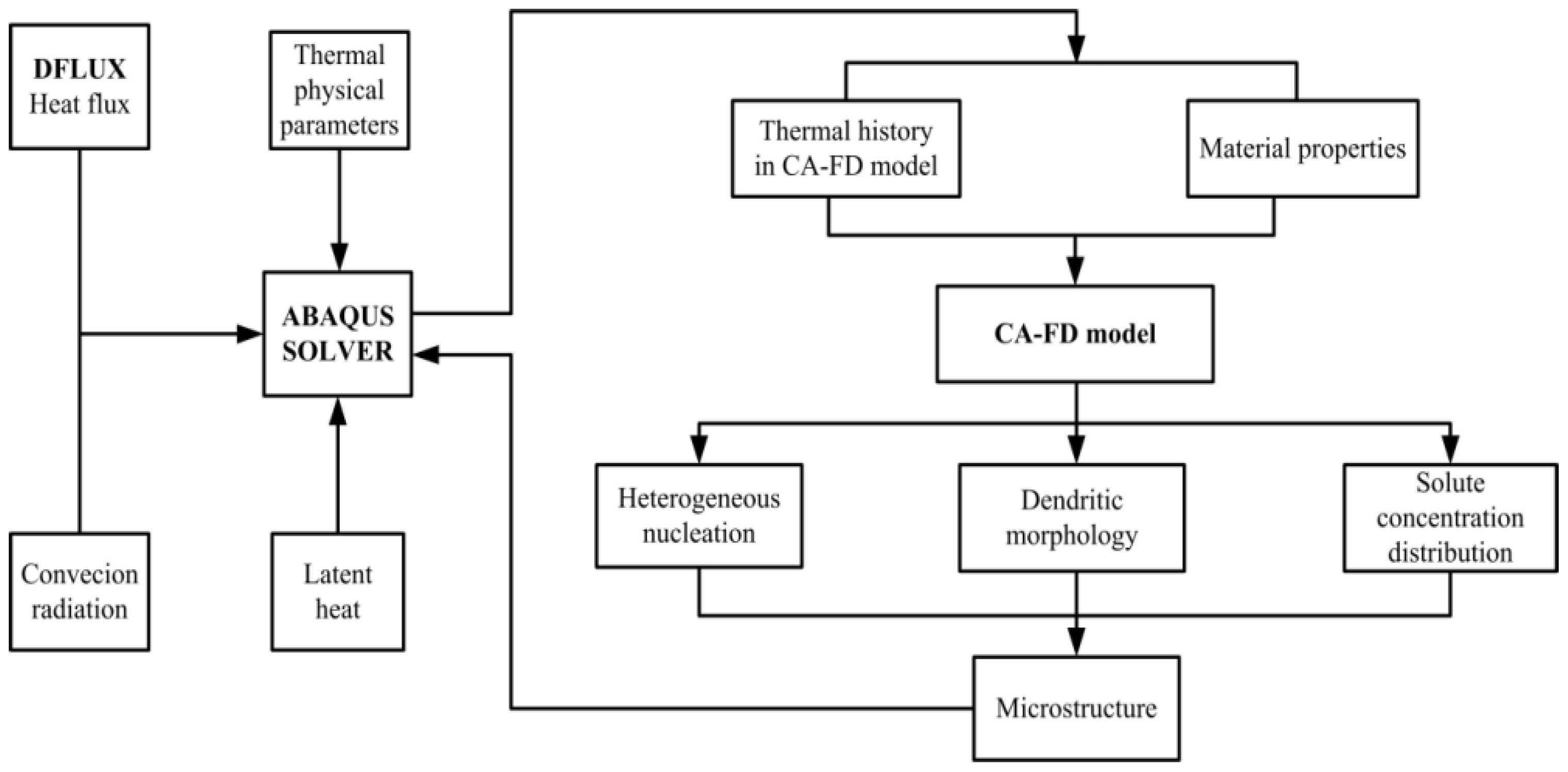
2.5. Macro–Micro Coupling of the Temperature Field
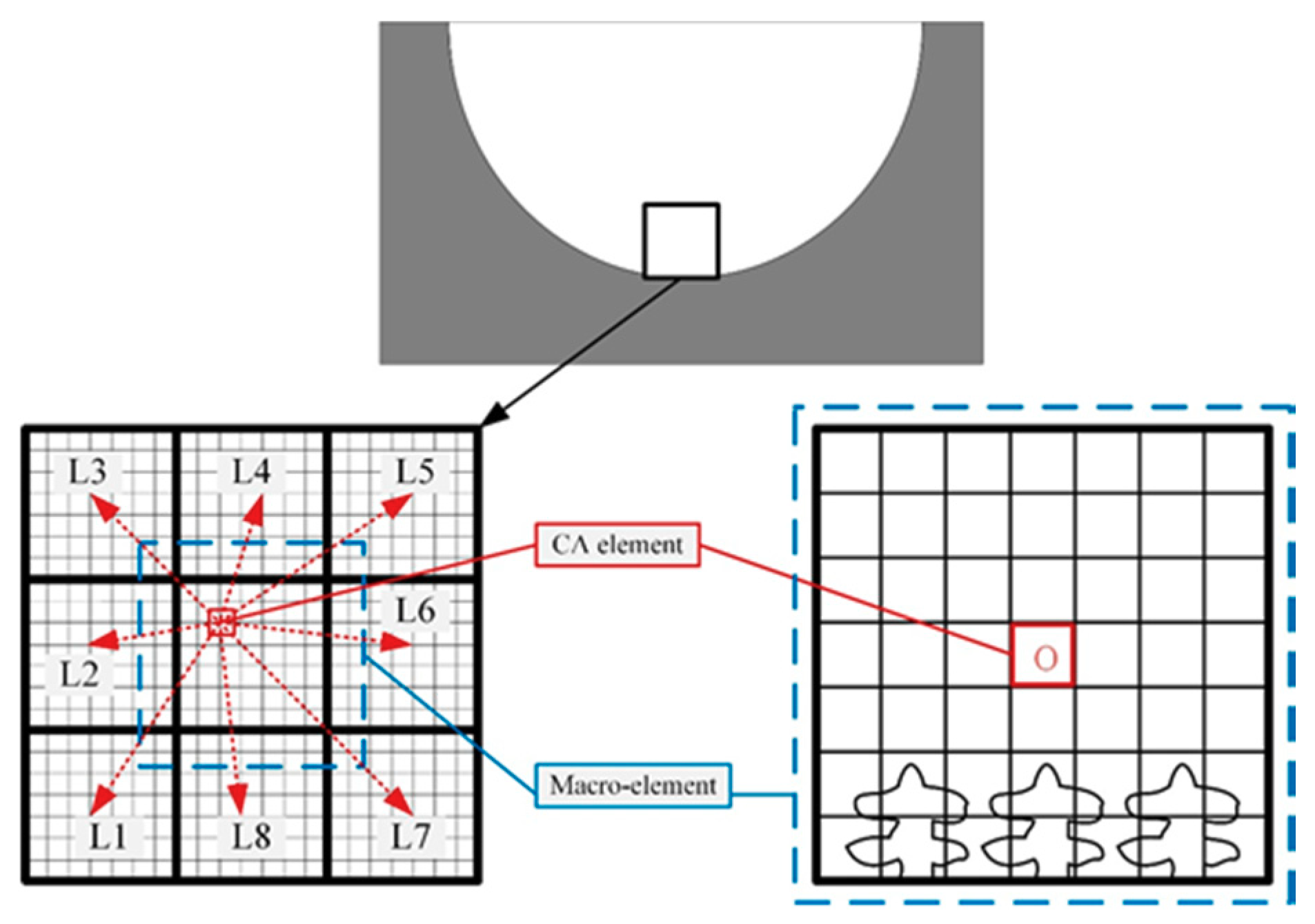
3. Modeling of the Dendritic Growth
3.1. Dendritic Nucleus Model
3.2. Solute Diffusion Model
3.3. Undercooling
3.4. Selection of Time Step
3.5. Experimental Details
4. Results and Discussions
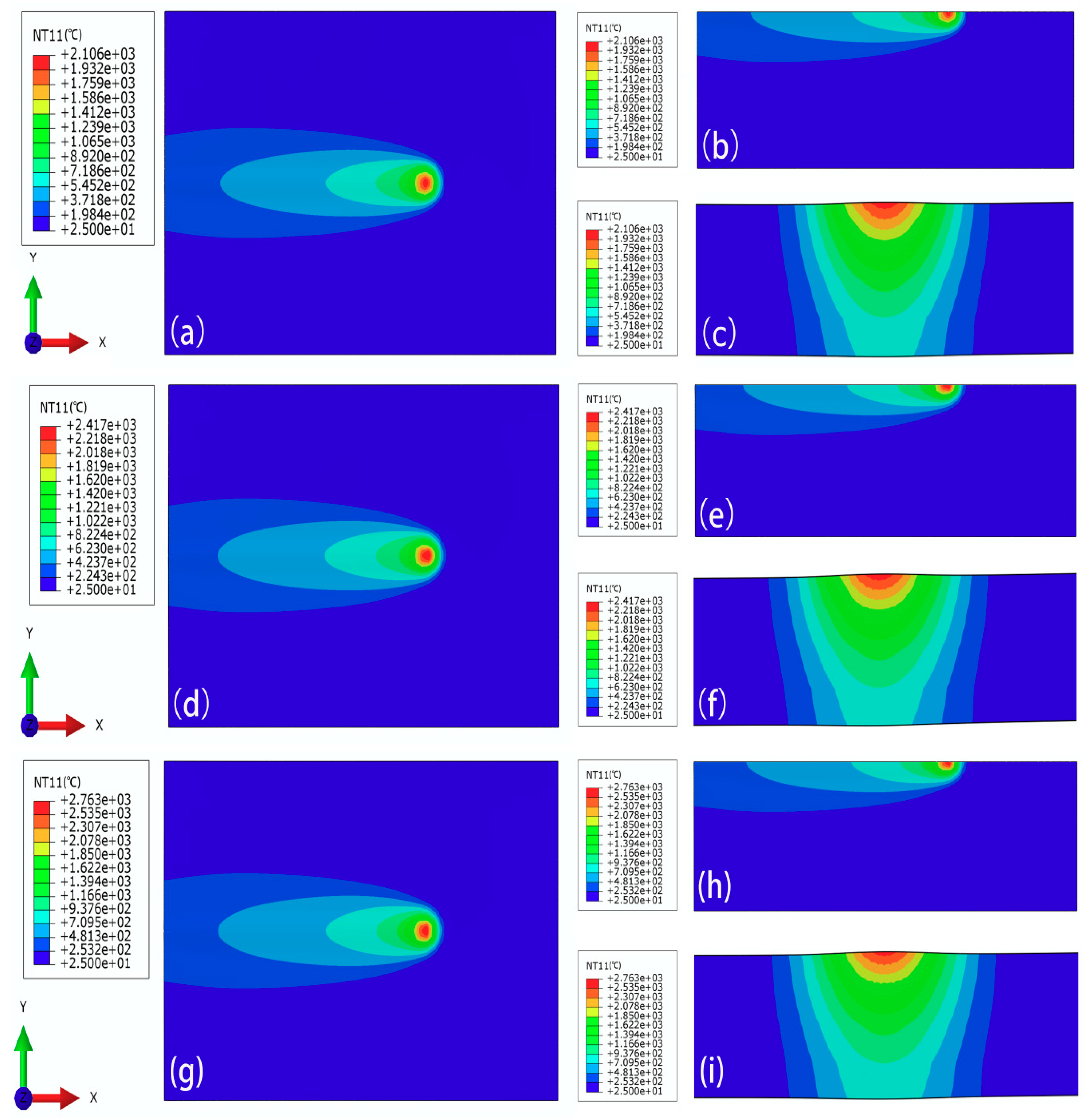
4.1. Temperature Distribution and Weld Bead Geometry
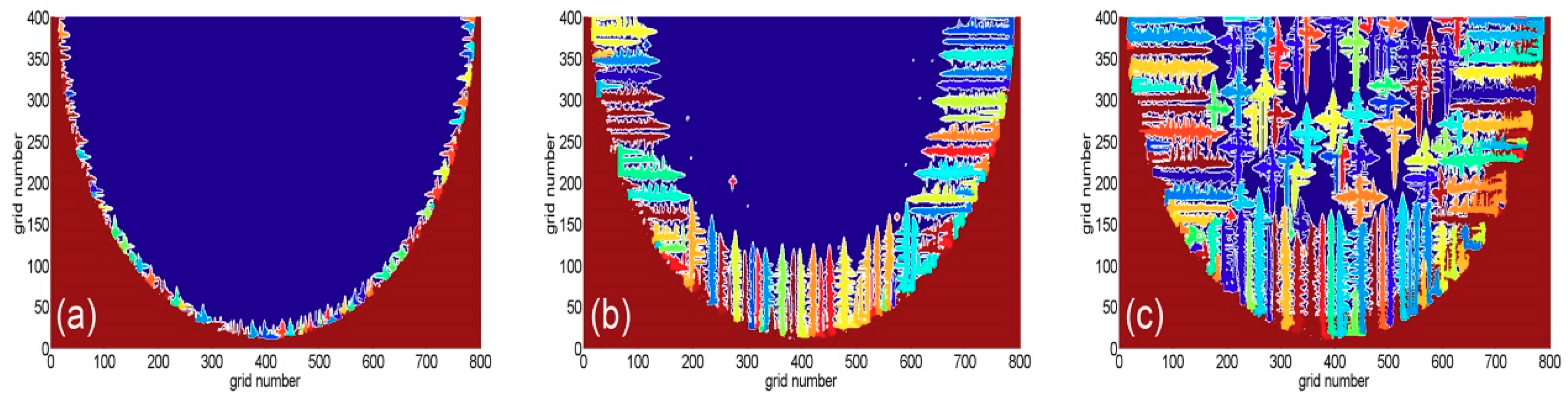
4.2. Calculations and Measurements of the CET
5. Conclusions
- (1)
- In order to ensure the accuracy of the simulated temperature distribution, the developed FE model took nonlinear thermal analysis, the temperature dependency of the thermal materials’ properties, and a moving heat source into consideration. Furthermore, the convection and radiation conditions were also considered in this model.
- (2)
- During the GTAW process, the temperature distribution in a macro region around the molten pool was calculated by the developed FE model under different welding currents. It was found that the transverse cross section of the weld bead was better when the welding current was 75 A. The obtained current parameter acted as the input parameter of the CA-FD coupling model.
- (3)
- Then, the effect of several process conditions on the solidification microstructure was investigated by the CA-FD model, especially solidification time and temperature. It is shown that the coarse columnar crystals are produced with priority in the molten pool and their growth direction is in line with the direction of the negative temperature gradient. With the increase of temperature and solute concentration at the front of the solid-liquid interface, the columnar crystal grains show the trend of transforming to equiaxed crystals.
- (4)
- This work contributes to the understanding of microstructure evolution and temperature characteristics in the molten pool. It can provide a fundamental basis for the selection of welding process parameters for GTAW processing of the TC4 alloy. The present model will be further enhanced to include the effect of fluid flow on dendrite growth in the molten pool.
Author Contributions
Funding
Conflicts of Interest
References
- Lutjering, G.; Williams, J.C. Titanium, 2nd ed.; Springer: Berlin, Germany, 2007; pp. 2–4. ISBN 978-3-540-71397-5. [Google Scholar]
- Wang, D.C. Development and application of high-strength titanium alloys. Chin. J. Nonferr. Met. 2010, 20, 958–963. [Google Scholar]
- Zhao, Y.Q.; Ge, P. Current situation and development of new titanium alloys invented in China. J. Aeronaut. Mater. 2014, 34, 51–61. [Google Scholar]
- Babu, N.K.; Raman, S.G.S.; Mythili, R.; Saroja, S. Correlation of microstructure with mechanical properties of TIG weldments of Ti–6Al–4V made with and without current pulsing. Mater Charact. 2007, 58, 581–587. [Google Scholar] [CrossRef]
- Wang, L.M.; Lin, H.C. The characterization of corrosion resistance in the Ti-6Al-4V alloy fusion zone following a gas tungsten arc welding process. J. Mater. Res. 2009, 24, 3680–3688. [Google Scholar] [CrossRef]
- David, S.A.; Vitek, J.M. Correlation between solidification parameters and weld microstructures. Int. Mater. Rev. 1989, 34, 213–245. [Google Scholar] [CrossRef]
- Kou, S.; Sun, D.K. Fluid flow and weld penetration in stationary arc welds. Metall. Trans. A 1985, 16, 203–213. [Google Scholar] [CrossRef]
- Salimi, S.; Bahemmat, P.; Haghpanahi, M. A 3D transient analytical solution to the temperature field during dissimilar welding processes. Int. J. Mech. Sci. 2014, 79, 66–74. [Google Scholar] [CrossRef]
- Zhang, J.; Liou, F.; Seufzer, W.; Taminger, K. A coupled finite element cellular automaton model to predict thermal history and grain morphology of Ti-6Al-4V during direct metal deposition (DMD). Addit. Manuf. 2016, 11, 32–39. [Google Scholar] [CrossRef]
- Anderson, M.P.; Srolovitz, D.J.; Grest, G.S.; Sahni, P.S. Computer simulation of grain growth—I. kinetics. Acta Metall. 1984, 32, 783–791. [Google Scholar] [CrossRef]
- Wei, H.L.; Elmer, J.W.; DebRoy, T. Crystal growth during keyhole mode laser welding. Acta Mater. 2017, 133, 10–20. [Google Scholar] [CrossRef]
- Qin, R.S.; Wallach, E.R.; Thomson, R.C. A phase-field model for the solidification of multicomponent and multiphase alloys. J. Cryst. Growth 2005, 279, 163–169. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Y.; Zhan, X.; Yu, F. A phase field investigation of dendrite morphology and solute distributions under transient conditions in an Al-Cu welding molten pool. Sci. Technol. Weld. Join. 2016, 21, 446–451. [Google Scholar] [CrossRef]
- Rappaz, M.; Gandin, C.A. Probabilistic modeling of microstructure formation in solidification processes. Acta Metall. Mater. 1993, 41, 345–360. [Google Scholar] [CrossRef]
- Zhan, X.; Wei, Y.; Dong, Z. Cellular automaton simulation of grain growth with different orientation angles during solidification process. J. Mater. Process. Tecnol. 2008, 208, 1–8. [Google Scholar] [CrossRef]
- Zhan, X.; Dong, Z.; Wei, Y.; Ma, R. Simulation of grain morphologies and competitive growth in weld pool of Ni–Cr alloy. J. Cryst. Growth 2009, 311, 4778–4783. [Google Scholar] [CrossRef]
- Wang, Z.J.; Luo, S.; Li, W.Y.; Song, H.W.; Deng, W.D. Simulation of microstructure during laser rapid forming solidification based on cellular automaton. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Chen, S.; Guillemot, G.; Gandin, C.A. Three-dimensional cellular automaton-finite element modeling of solidification grain structures for arc-welding processes. Acta Mater. 2016, 115, 448–467. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Jiang, Y. Numerical simulation of EBCHM for the large-scale TC4 alloy slab ingot during the solidification process. Vacuum 2017, 141, 1–9. [Google Scholar] [CrossRef]
- Ahn, J.; He, E.; Chen, L.; Wimpory, R.C.; Dear, J.P.; Davies, C.W. Prediction and measurement of residual stresses and distortions in fibre laser welded Ti-6Al-4V considering phase transformation. Mater. Des. 2017, 115, 441–457. [Google Scholar] [CrossRef]
- Gandin, C.A.; Rappaz, M. A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes. Acta Metall. Mater. 1994, 42, 2233–2246. [Google Scholar] [CrossRef]
- Nastac, L. Numerical modeling of solidification morphologies and segregation patters in cast dendritic alloys. Acta Mater. 1999, 47, 4253–4262. [Google Scholar] [CrossRef]
- Wang, W.; Lee, P.D.; McLean, M. A model of solidification microstructures in nickel-based superalloys: predicting primary dendrite spacing selection. Acta Mater. 2003, 51, 2971–2987. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 2010, 34, 823–830. [Google Scholar] [CrossRef]
- Tsai, D.C.; Hwang, W.S. Numerical simulation of solidification morphologies of Cu-0.6Cr casting alloy using modified cellular automaton model. Trans. Nonferr. Met. Soc. China 2010, 20, 1072–1077. [Google Scholar] [CrossRef]
- Zhu, M.F.; Stefanescu, D.M. Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys. Acta Mater. 2007, 55, 1741–1755. [Google Scholar] [CrossRef]
- Beltran-Sanchez, L.; Stefanescu, D.M. A quantitative dendrite growth model and analysis of stability concepts. Metll. Mater. Trans. A. 2004, 35, 2471–2485. [Google Scholar] [CrossRef]
- Dal, M.; Masson, P.L.; Carin, M. Estimation of fusion front in 2D axisymmetric welding using inverse method. Int. J. Therm. Sci. 2012, 55, 60–68. [Google Scholar] [CrossRef]

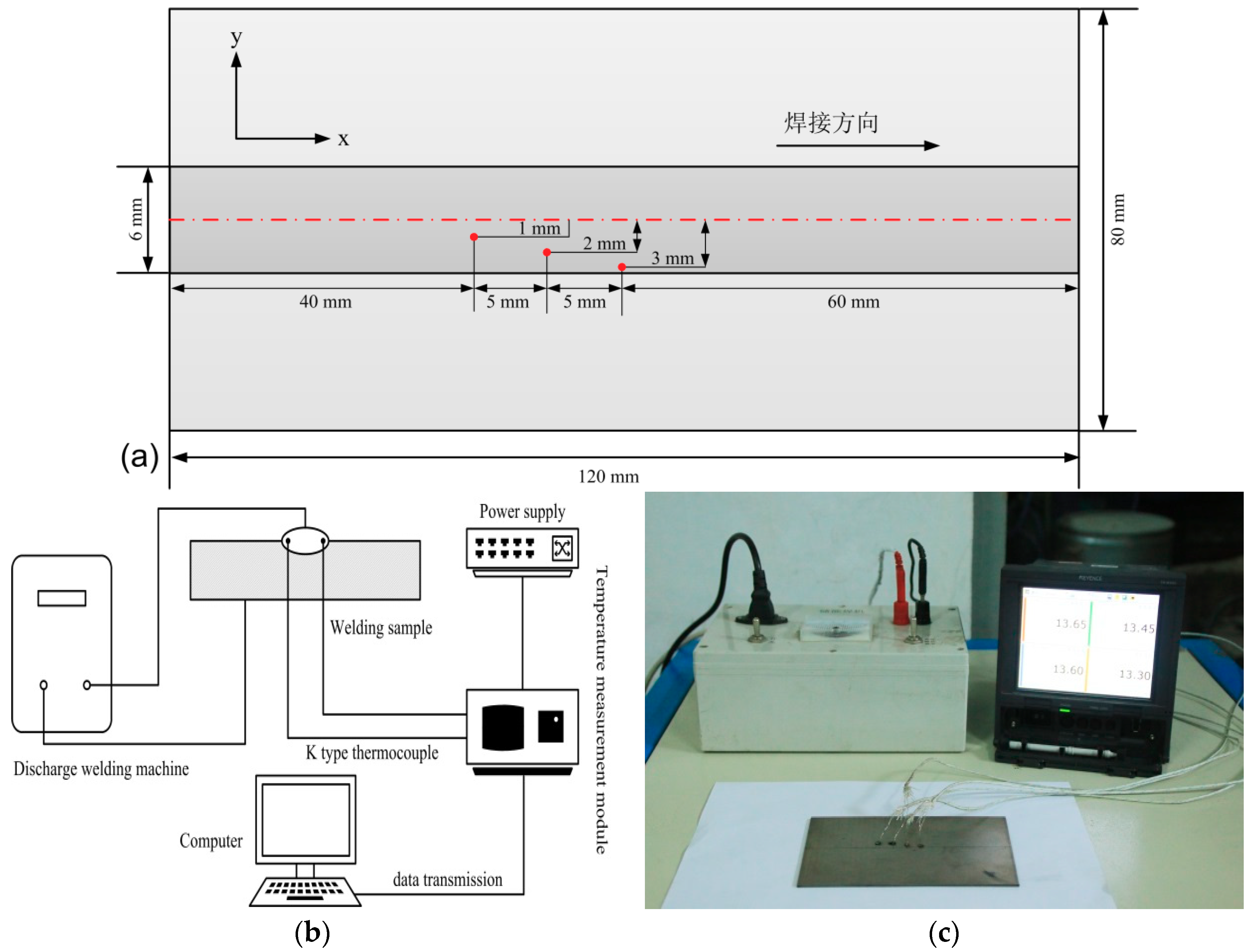





| Element | Ti | Al | V | Fe | O |
|---|---|---|---|---|---|
| wt% | Balance | 5.5–6.76 | 3.5–4.5 | 0.25 | 0.2 |
| Property | Variable | Value |
|---|---|---|
| Liquidus temperature | 1703 °C | |
| Solidus temperature | 1678 °C | |
| Partition coefficient | 0.95 | |
| Diffusion coefficient in liquid | 5 × 10−9 m2/s | |
| Diffusion coefficient in solid | 5 × 10−13 m2/s | |
| Liquidus slope | −1.4 | |
| Maximum nucleation density | 4 × 109/m3 | |
| Standard deviation of undercooling | 0.5 °C | |
| Maximum undercooling | 2 °C | |
| Gibbs–Thomson coefficient | ||
| Initial concentration | 6 at.% |
| Parameters | Welding Speed | Welding Voltage | Welding Current | Welding Efficiency |
|---|---|---|---|---|
| Value | 5 mm/s | 13.8 V | 75 A | 0.8 |
| Parameters | Different Currents | ||
|---|---|---|---|
| Different Distances | I = 60 A | I = 75 A | I = 90 A |
| L = 1 mm | 2013.27 °C | 2394.68 °C | 2681.89 °C |
| L = 2 mm | 1723.94 °C | 2063.25 °C | 2337.25 °C |
| L = 3 mm | 1420.60 °C | 1653.74 °C | 1780.63 °C |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Zhou, Y.; Huang, C.; Chu, Q.; Zhang, W.; Li, J. Simulation of Temperature Distribution and Microstructure Evolution in the Molten Pool of GTAW Ti-6Al-4V Alloy. Materials 2018, 11, 2288. https://doi.org/10.3390/ma11112288
Zhang M, Zhou Y, Huang C, Chu Q, Zhang W, Li J. Simulation of Temperature Distribution and Microstructure Evolution in the Molten Pool of GTAW Ti-6Al-4V Alloy. Materials. 2018; 11(11):2288. https://doi.org/10.3390/ma11112288
Chicago/Turabian StyleZhang, Min, Yulan Zhou, Chao Huang, Qiaoling Chu, Wenhui Zhang, and Jihong Li. 2018. "Simulation of Temperature Distribution and Microstructure Evolution in the Molten Pool of GTAW Ti-6Al-4V Alloy" Materials 11, no. 11: 2288. https://doi.org/10.3390/ma11112288
APA StyleZhang, M., Zhou, Y., Huang, C., Chu, Q., Zhang, W., & Li, J. (2018). Simulation of Temperature Distribution and Microstructure Evolution in the Molten Pool of GTAW Ti-6Al-4V Alloy. Materials, 11(11), 2288. https://doi.org/10.3390/ma11112288




