Electric Current Dependent Fracture in GaN Piezoelectric Semiconductor Ceramics
Abstract
1. Introduction
2. Experiment
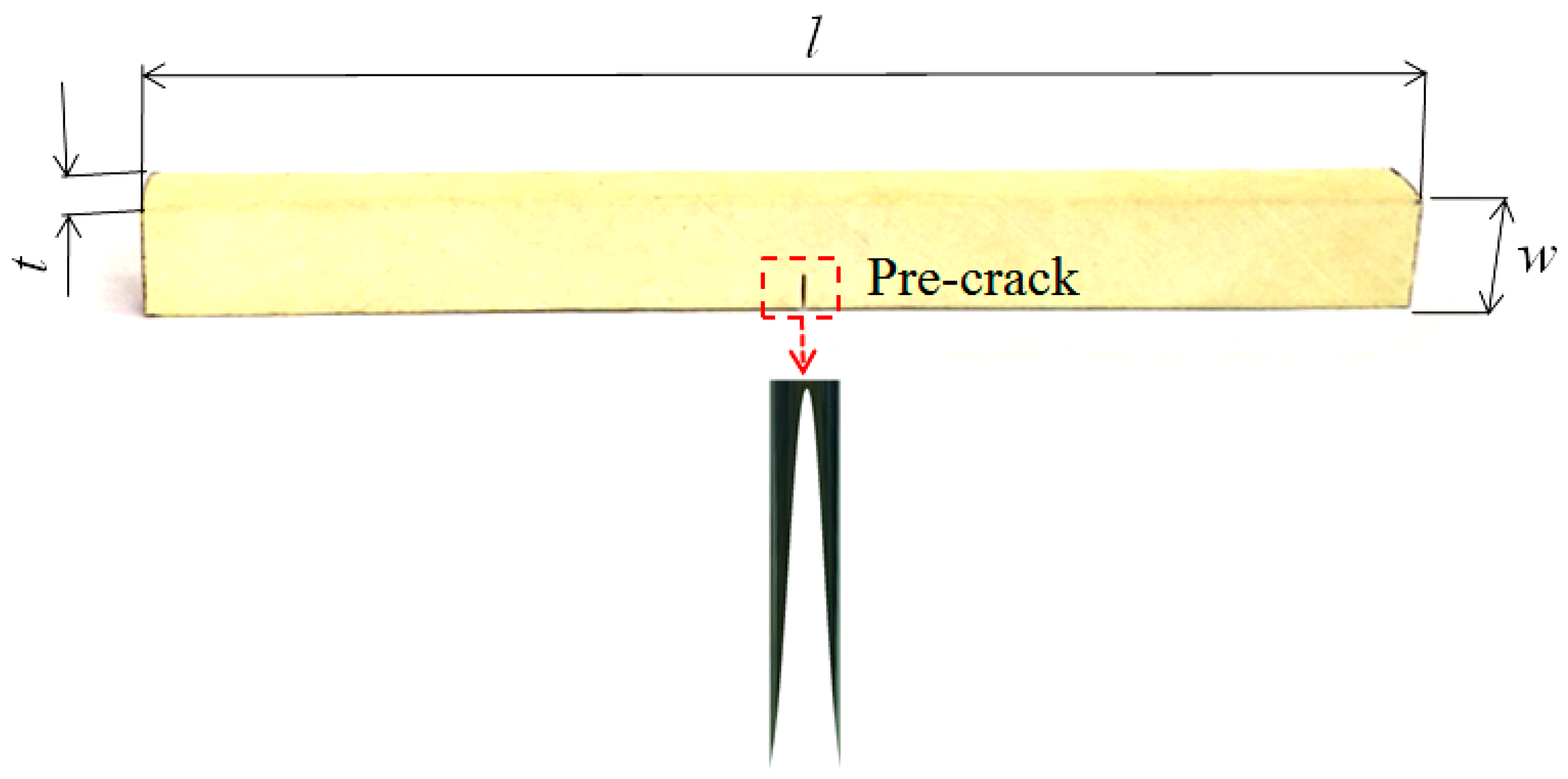
2.1. Material and Specimens
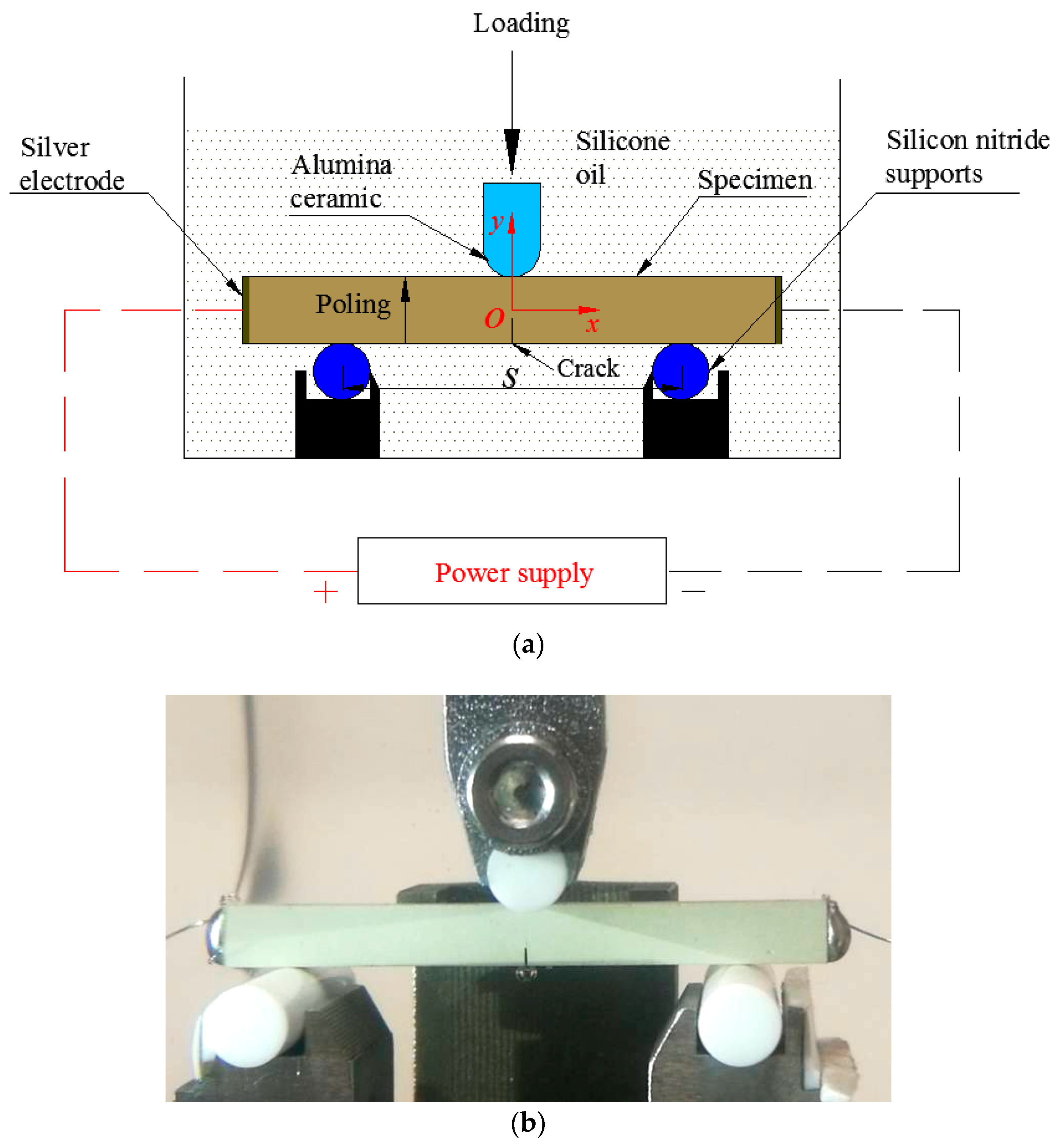
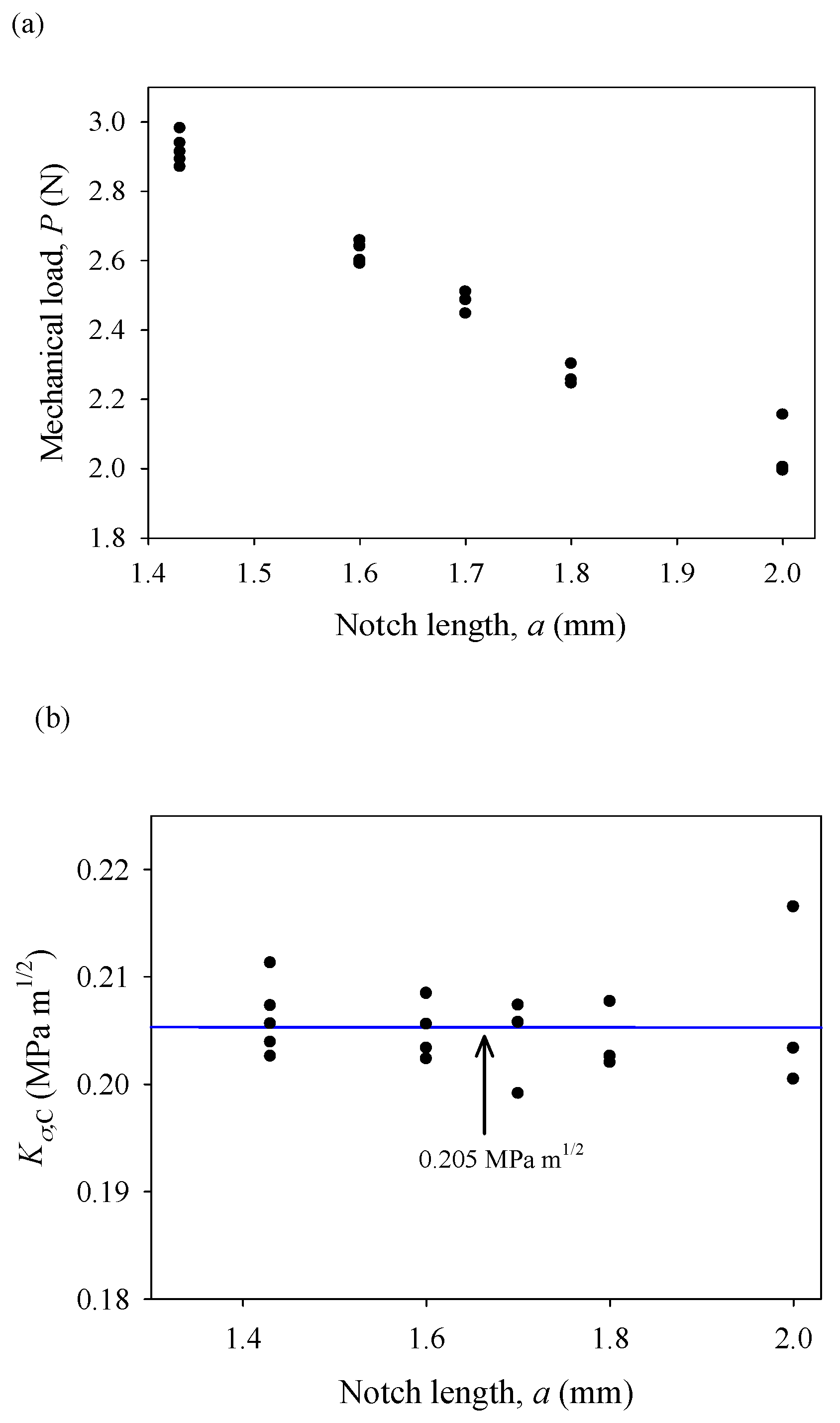
2.2. Experimental Configuration and Fracture Tests
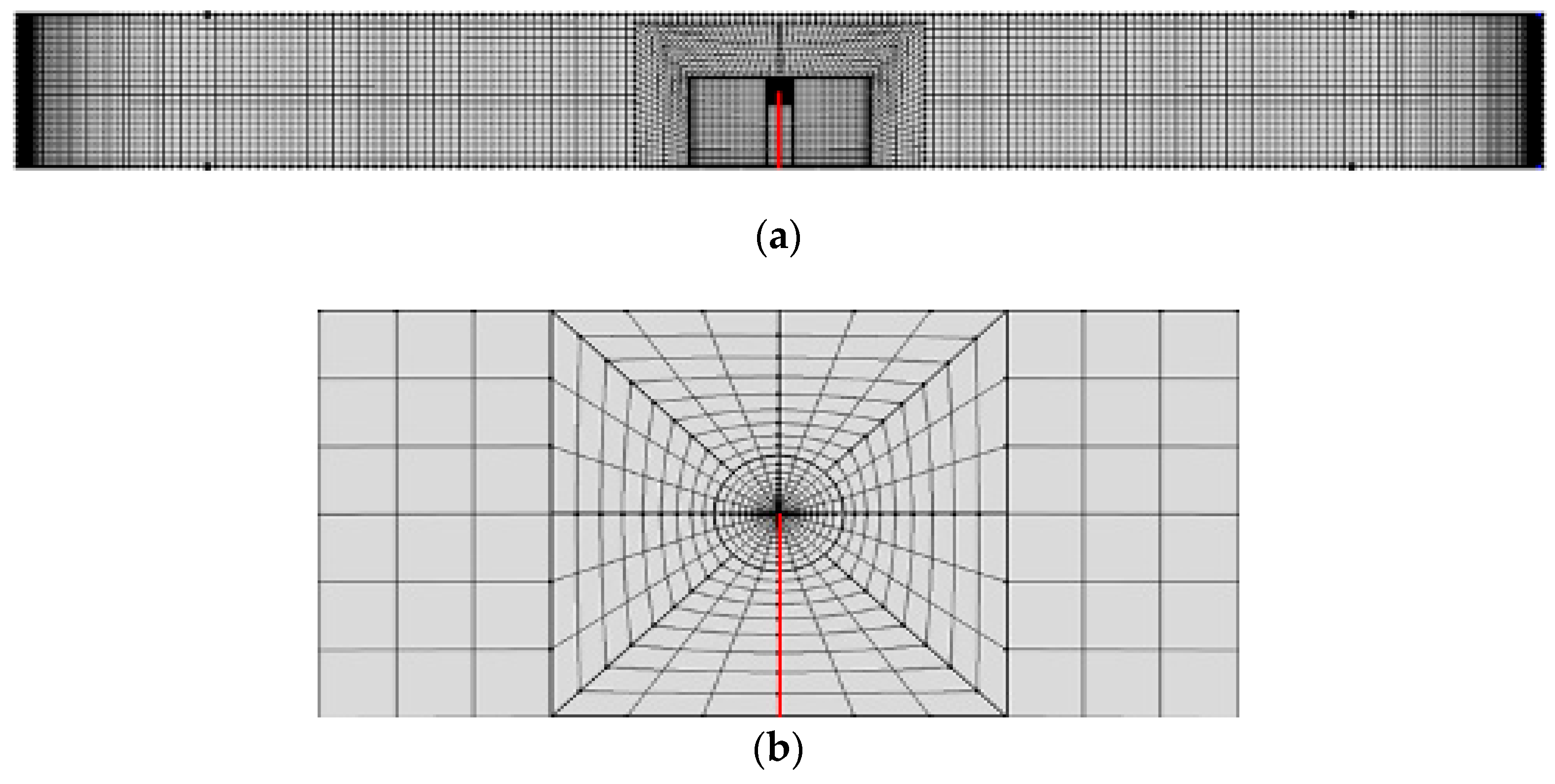
3. Numerical Analysis
3.1. Basic Equations
3.2. Boundary Conditions
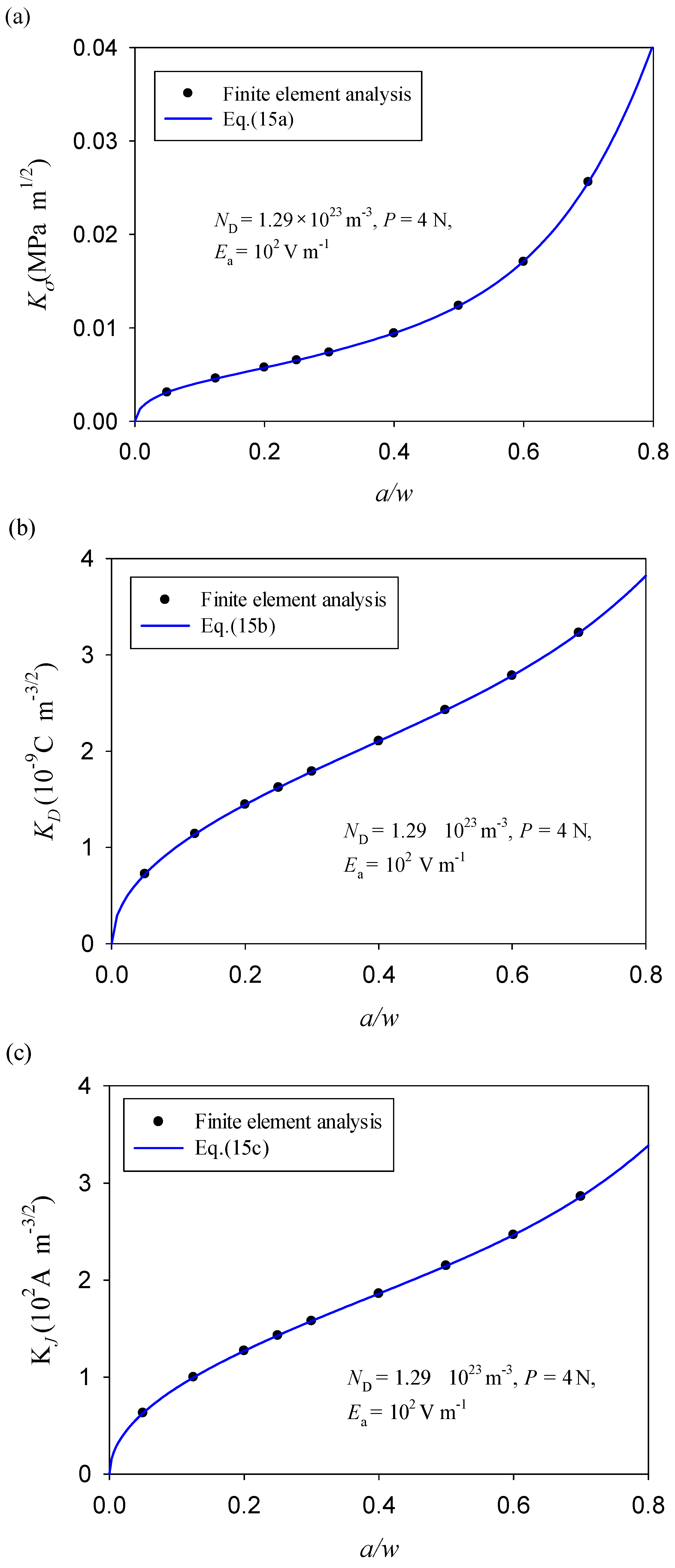
3.3. Intensity Factor
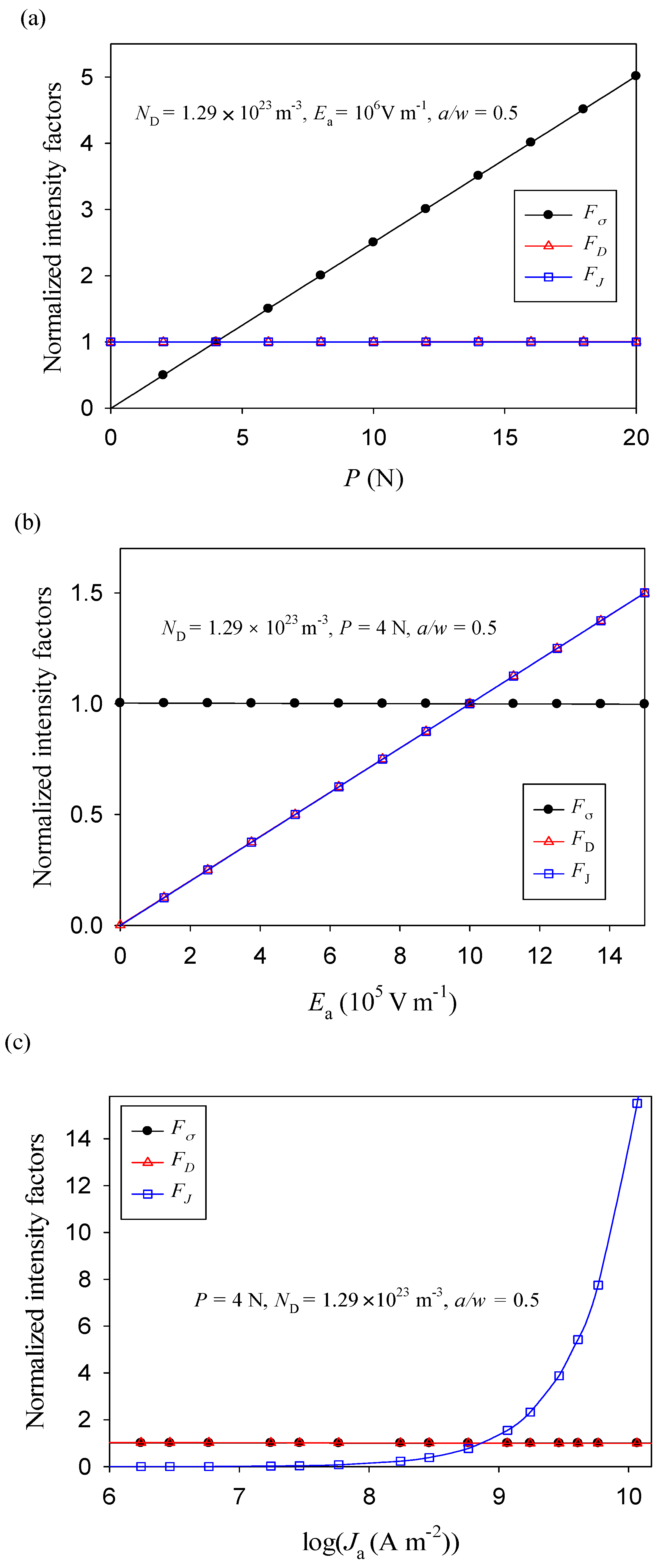
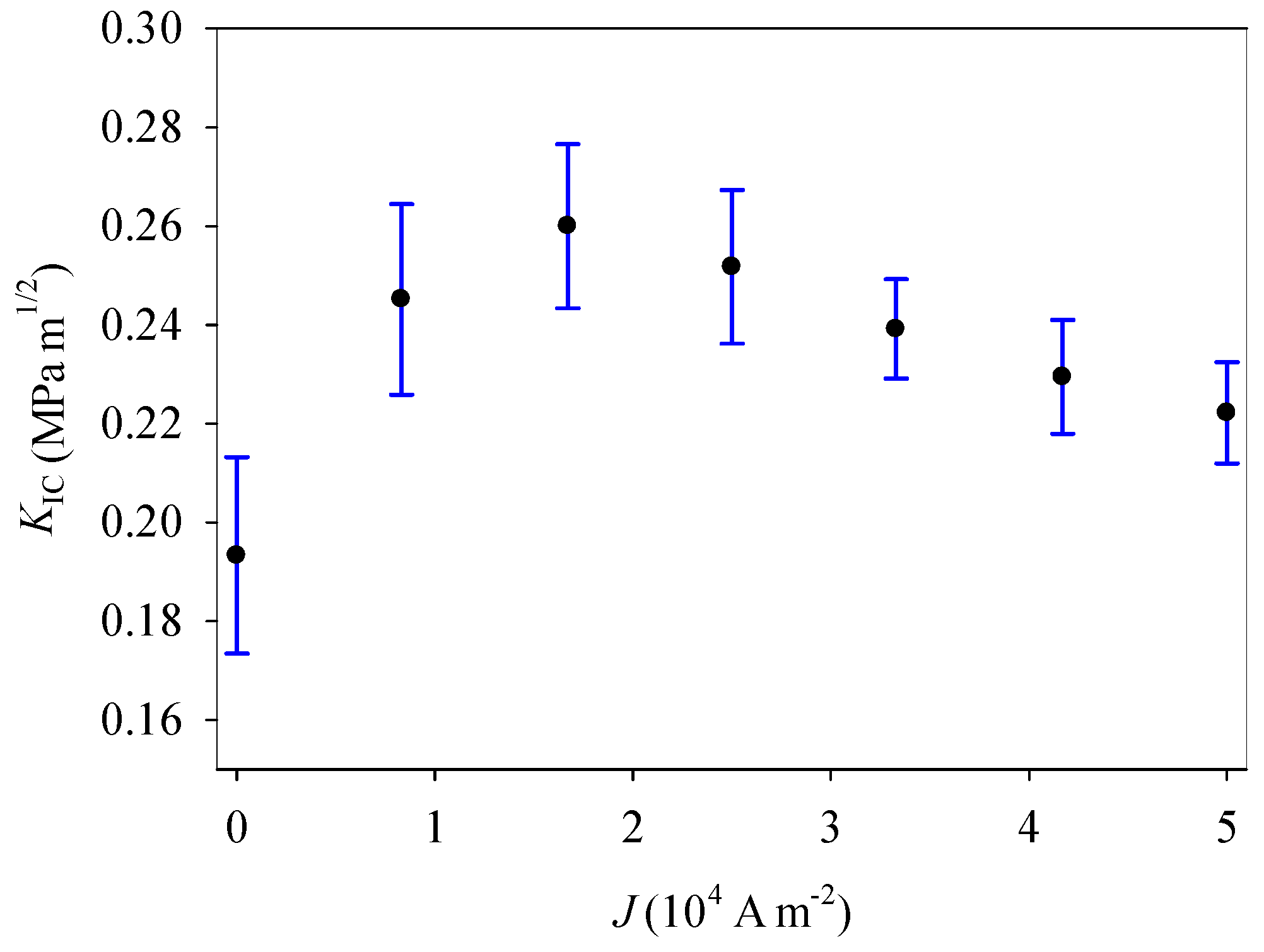
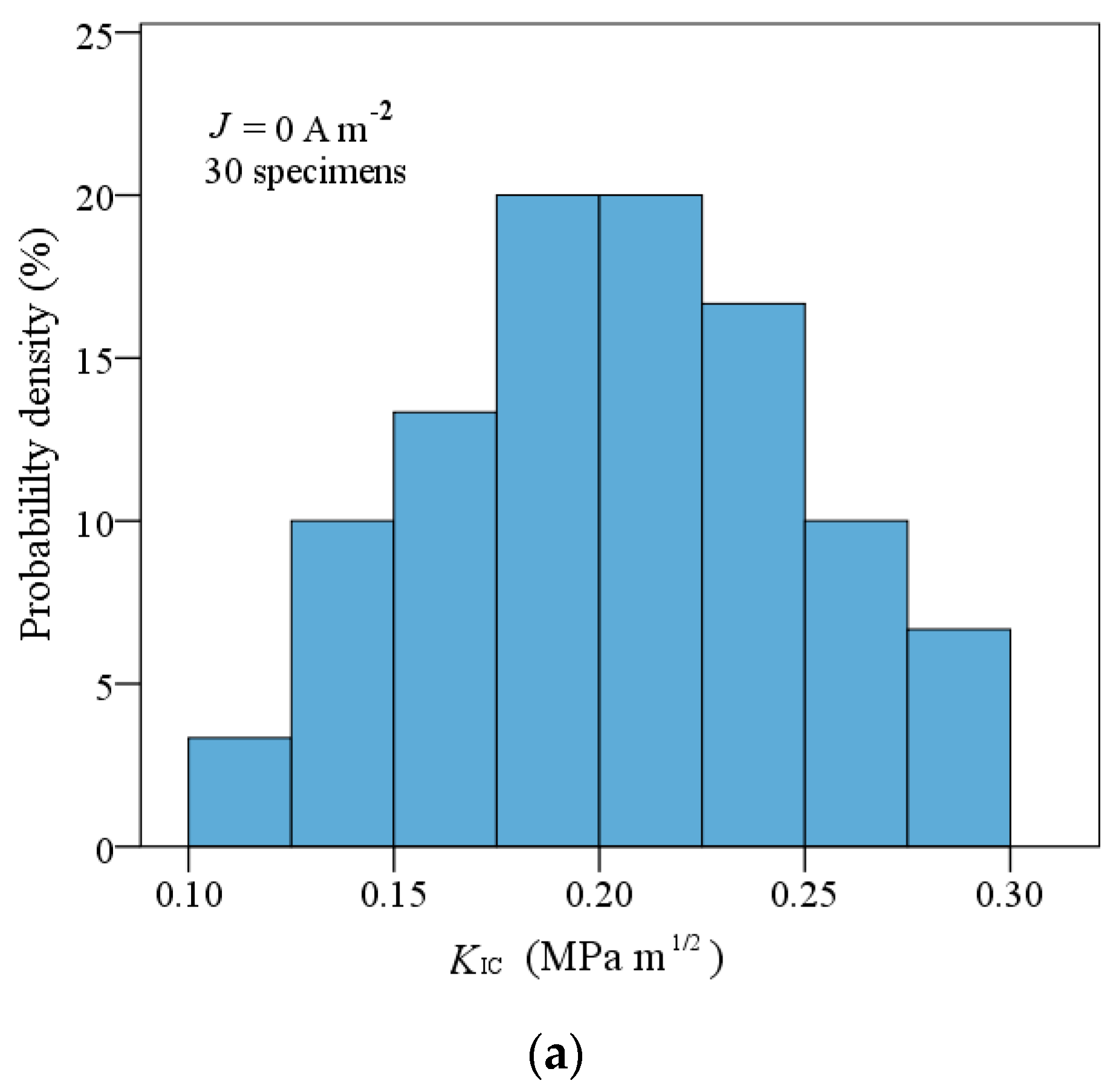
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, G.; Du, J.K.; Wang, J.; Yang, J.S. Electromechanical fields in a nonuniform piezoelectric semiconductor rod. J. Mech. Mater. Struct. 2018, 13, 103–120. [Google Scholar] [CrossRef]
- Qin, G.S.; Zhang, X.; Ma, S.J.; Zhang, Q.Y.; Fan, C.Y.; Zhao, M.H. An accurate computational method for analysis of electromechanical properties of structures with metal-GaN piezoelectric semiconductor contact. Comput. Mater. Sci. 2018, 13, 70–77. [Google Scholar] [CrossRef]
- Fan, S.Q.; Liang, Y.X.; Xie, J.M.; Hu, Y.T. Exact solutions to the electromechanical quantities inside a statically-bent circular ZnO nanowire by taking into account both the piezoelectric property and the semiconducting performance: Part I—Linearized analysis. Nano Energy 2017, 40, 82–87. [Google Scholar] [CrossRef]
- Hutson, A.R. Piezoelectricity and conductivity in ZnO and CdS. Phys. Rev. Lett. 1960, 4, 505–507. [Google Scholar] [CrossRef]
- Heyman, J.S. Phase insensitive acoustoelectric transducer. J. Acoust. Soc. Am. 1978, 64, 243–249. [Google Scholar] [CrossRef]
- Busse, L.J.; Miller, J.G. Response characteristics of a finite aperture, phase insensitive ultrasonic receiver based upon the acoustoelectric effect. J. Acoust. Soc. Am. 1981, 70, 1370–1376. [Google Scholar] [CrossRef]
- Dietz, D.R.; Busse, L.J.; Fife, M.J. Acoustoelectric detection of ultrasound power with composite piezoelectric and semiconductor devices. IEEE Trans. Ultrason. Ferroelectr. 1988, 35, 146–151. [Google Scholar] [CrossRef] [PubMed]
- Hickernell, F.S. The piezoelectric semiconductor and acoustoelectronic device development in the sixties. IEEE Trans. Ultrason. Ferroelectr. 2005, 52, 737–745. [Google Scholar] [CrossRef]
- Jones, K.A.; Chow, T.P.; Wraback, M. AlGaN devices and growth of device structures. J. Mater. Sci. 2015, 50, 3267–3307. [Google Scholar] [CrossRef]
- Wen, X.N.; Wu, W.Z.; Pan, C.F.; Hu, Y.F.; Yang, Q.; Wang, Z.L. Development and progress in piezotronics. Nano Energy 2015, 14, 276–295. [Google Scholar] [CrossRef]
- Trotta, R.; Wildmann, J.S.; Zallo, E.; Schmidt, O.G.; Rastelli, A. Highly entangled photons from hybrid piezoelectric-semiconductor quantum dot devices. Nano Lett. 2014, 14, 3439–3444. [Google Scholar] [CrossRef] [PubMed]
- Alamo, J.A.D.; Joh, J. GaN HEMT reliability. Microelectron. Reliab. 2009, 49, 1200–1206. [Google Scholar] [CrossRef]
- Farrer, J.K.; Carter, C.B. Defect structure in GaN pyramids. J. Mater. Sci. 2006, 41, 779–792. [Google Scholar] [CrossRef]
- Yang, J.S. An anti-plane crack in a piezoelectric semiconductor. Int. J. Fracture 2005, 136, L27–L32. [Google Scholar] [CrossRef]
- Hu, Y.T.; Zeng, Y.; Yang, J.S. A mode III crack in a piezoelectric semiconductor of crystals with 6 mm symmetry. Int. J. Solids Struct. 2007, 44, 3928–3938. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Pan, E. Dynamic anti-plane crack analysis in functional graded piezoelectric semiconductor crystals. Cmes-Comp. Model. Eng. 2014, 99, 273–296. [Google Scholar] [CrossRef]
- Lu, H.H.; Young, D.L.; Sladek, J.; Sladek, V. Three-dimensional analysis for functionally graded piezoelectric semiconductors. J. Intell. Mater. Syst. Strut. 2017, 28, 1391–1406. [Google Scholar] [CrossRef]
- Zhao, M.H.; Li, Y.; Yan, Y.; Fan, C.Y. Singularity analysis of planar cracks in three-dimensional piezoelectric semiconductors via extended displacement discontinuity boundary integral equation method. Eng. Anal. Bound. Elem. 2016, 67, 115–125. [Google Scholar] [CrossRef]
- Fan, C.Y.; Yan, Y.; Xu, G.T.; Zhao, M.H. Piezoelectric-conductor iterative method for analysis of cracks in piezoelectric semiconductors via the finite element method. Eng. Fract. Mech. 2016, 165, 183–196. [Google Scholar] [CrossRef]
- Zhang, Q.Y.; Fan, C.Y.; Xu, G.T.; Zhao, M.H. Iterative boundary element method for crack analysis of two-dimensional piezoelectric semiconductor. Eng. Anal. Bound. Elem. 2017, 83, 87–95. [Google Scholar] [CrossRef]
- Zhao, Y.F.; Zhou, C.G.; Zhao, M.H.; Pan, E.; Fan, C.Y. Penny-shaped cracks in three-dimensional piezoelectric semiconductors via Green’s functions of extended displacement discontinuity. J. Intell. Mater. Syst. Strut. 2017, 28, 1775–1788. [Google Scholar] [CrossRef]
- Danzer, R. On the relationship between ceramic strength and the requirements for mechanical design. J. Eur. Ceram. Soc. 2014, 34, 3435–3460. [Google Scholar] [CrossRef]
- Jelitto, H.; Kessler, H.; Schneider, G.A.; Balke, H. Fracture behavior of poled piezoelectric PZT under mechanical and electrical loads. J. Eur. Ceram. Soc. 2005, 25, 749–757. [Google Scholar] [CrossRef]
- Sato, N.; Takahashi, K. Evaluation of Fracture Strength of Ceramics Containing Small Surface Defects Introduced by Focused Ion Beam. Materials 2018, 11, 457. [Google Scholar] [CrossRef] [PubMed]
- Ancona, M.G.; Binari, S.C.; Meyer, D.J. Fully coupled thermoelectromechanical analysis of GaN high electron mobility transistor degradation. J. Appl. Phys. 2012, 111, 074504. [Google Scholar] [CrossRef]
- De, S.C.; Meneghini, M.; Caria, A.; Dogmus, E.; Zegaoui, M.; Medjdoub, F.; Kalinic, B.; Cesca, T.; Meneghesso, G.; Zanoni, E. GaN-Based Laser Wireless Power Transfer System. Materials 2018, 11, 153. [Google Scholar] [CrossRef]
- Zhang, D.L.; Cheng, X.H.; Zheng, L.; Shen, L.Y.; Wang, Q.; Gu, Z.Y.; Qian, R.; Wu, D.P.; Zhou, W.; Cao, D.; et al. Effects of polycrystalline AlN filmon the dynamic performance of AlGaN/GaN high electron mobility transistors. Mater. Des. 2018, 148, 1–7. [Google Scholar] [CrossRef]
- Latorre-Rey, A.D.; Sabatti, F.F.M.; Albrecht, J.D.; Saraniti, M. Hot electron generation under large-signal radio frequency operation of GaN high-electron-mobility transistors. Appl. Phys. Lett. 2017, 111, 1–5. [Google Scholar] [CrossRef]
- International Organization for Standardization. Fine Ceramics (Advanced Ceramics, Advanced Technical Ceramics)—Test Method for Fracture Toughness of Monolithic Ceramics at Room Temperature by Single Edge Precracked Beam Method; ISO 15732: 2003; International Organization for Standardization: Geneva, Switzerland, 2003. [Google Scholar]
- Carlton, H.D.; Elmer, J.W.; Freeman, D.C.; Schaefferet, R.D.; Derkach, O.; Gallegos, G.F. Laser notching ceramics for reliable fracture toughness testing. J. Eur. Ceram. Soc. 2016, 36, 227–234. [Google Scholar] [CrossRef]
- Araneo, R.; Falconi, C. Lateral bending of tapered piezosemiconductive nanostructures for ultra-sensitive mechanical force to voltage conversion. Nanotechnology 2013, 24, 265707. [Google Scholar] [CrossRef] [PubMed]
- Pierret, R.F. Semiconductor Device Fundamentals, 2nd ed.; Addison Wesley: Boston, MA, USA, 1996; pp. 477–501. ISBN 9780201543933. [Google Scholar]
- Wang, Z.L. Progress in piezotronics and piezo-phototronics. Adv. Mater. 2012, 24, 4632–4646. [Google Scholar] [CrossRef] [PubMed]
- Araneo, R.; Bini, F.; Pea, M.; Notargiacomo, A.; Rinaldi, A.; Lovat, G.; Celozzi, S. Current–voltage characteristics of ZnO nanowires under uniaxial loading. IEEE Trans. Nanotechnol. 2014, 13, 724–735. [Google Scholar] [CrossRef]
- Sze, S.; Ng, K. Physics of Semiconductor Devices, 3rd ed.; Wiley: New York, NY, USA, 2006; pp. 159–160. ISBN 9780471143239. [Google Scholar]
- Khusayfana, N.M.; Qasrawib, A.F.; Khanfar, K.H. Impact of Yb, In, Ag and Au thin film substrates on the crystalline nature, Schottky barrier formation and microwave trapping properties of Bi2O3 films. Mater. Sci. Semicon. Proc. 2017, 64, 63–70. [Google Scholar] [CrossRef]
- Zhou, L. Development and Characterization of Ohmic and Schottky Contacts for GaN and AlGaN Devices. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana and Champaign, IL, USA, 2002. [Google Scholar]
- Yang, J.S. An Introduction to the Theory of Piezoelectricity, 1st ed.; Springer: New York, NY, USA, 2005; pp. 1–29. ISBN 9781441936394. [Google Scholar]
- Zhao, M.H.; Ma, S.J.; Lu, C.; Fan, C.Y.; Qin, G.S. Influence of polarization on the electromechanical properties of GaN piezoelectric semiconductive ceramics. Ceram. Int. 2018, 44, 12648–12654. [Google Scholar] [CrossRef]
- Vasileska, D.; Klimeck, G. Computational Electronics: Semiclassical and Quantum Device Modeling and Simulation, 1st ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 153–154. ISBN 9781420064834. [Google Scholar]
- Fang, F.; Yang, W. Poling-enhanced fracture resistance of lead zirconate titanate ferroelectric ceramics. Mater. Lett. 2000, 46, 131–135. [Google Scholar] [CrossRef]
- Lu, C.; Danzer, R.; Fischer, F.D. Fracture statistics of brittle materials: Weibull or normal distribution. Phys. Rev. E 2002, 65, 067102. [Google Scholar] [CrossRef] [PubMed]
- Fu, R.; Zhang, T.Y. Effects of an electric field on the fracture toughness of poled lead zirconate titanate ceramics. J. Am. Ceram. Soc. 2010, 83, 1215–1218. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Zhao, M.H.; Liu, G.N. Failure behavior and failure criterion of conductive cracks (deep notches) in piezoelectric ceramics I—The charge-free zone model. Acta Mater. 2004, 52, 2013–2024. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Liu, G.N.; Wang, T.H.; Tong, P. Application of the concepts of fracture mechanics to the failure of conductive cracks in piezoelectric ceramic. Eng. Fract. Mech. 2007, 74, 1160–1173. [Google Scholar] [CrossRef]

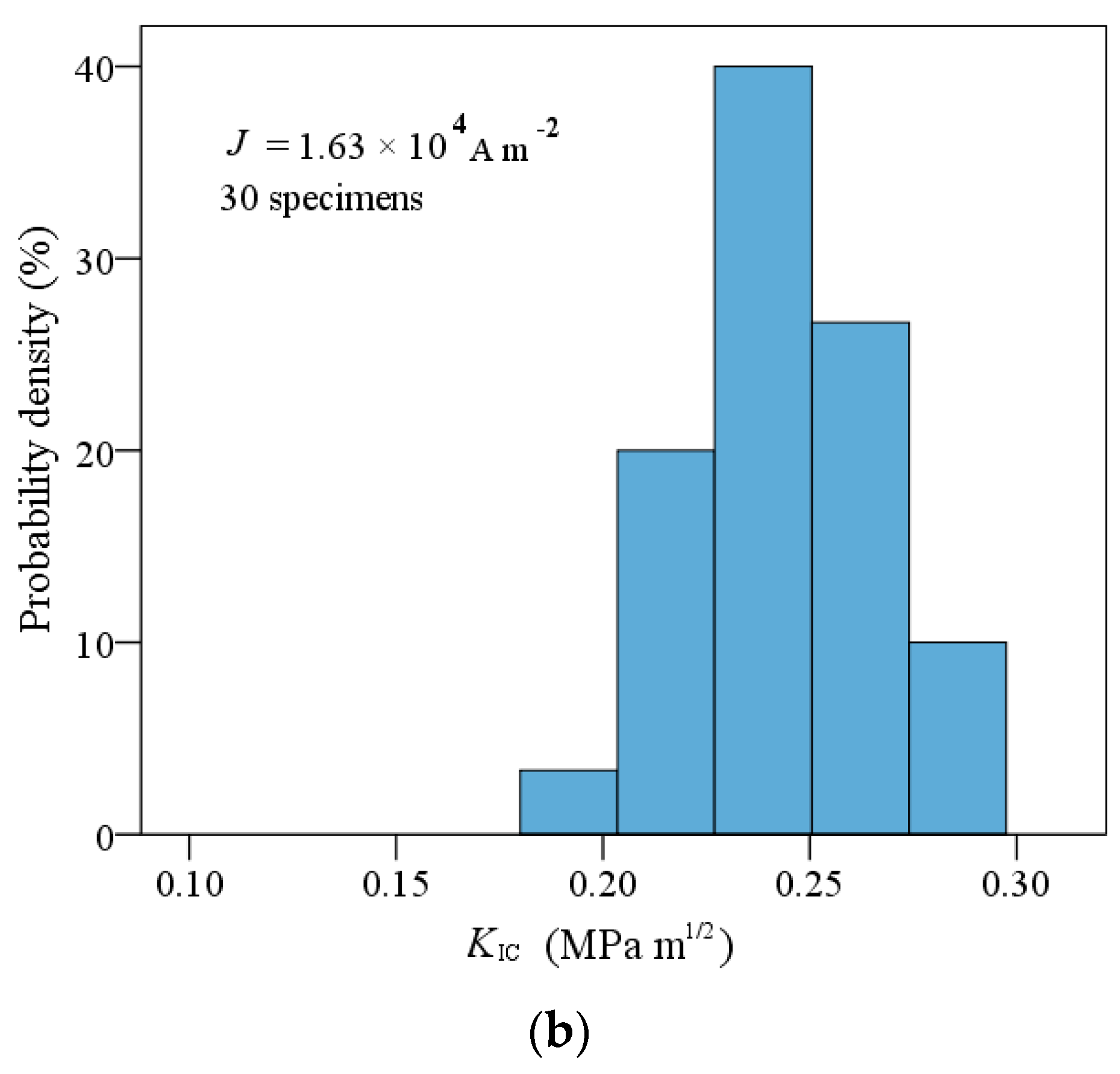



| Elastic Stiffness (109 Nm−2) | Piezoelectric Constant (C m−2) | Relative Dielectric Constant (kij/k0) | Migration Rate (cm2 V−1 s−1) | Diffusion Coefficient (cm2 s−1) |
|---|---|---|---|---|
| C11= 298.4 | e31 = −0.52 | ε11 = 9.5 | μ11 = 653 | d11 = 16.99 |
| C12 = 121.0 | e15 = −0.31 | ε33 = 10.3 | μ33 = 982 | d33 = 25.53 |
| C13 = 142.5 | e33 = 0.61 | |||
| C33 = 289.2 | ||||
| C44 = 23.1 |
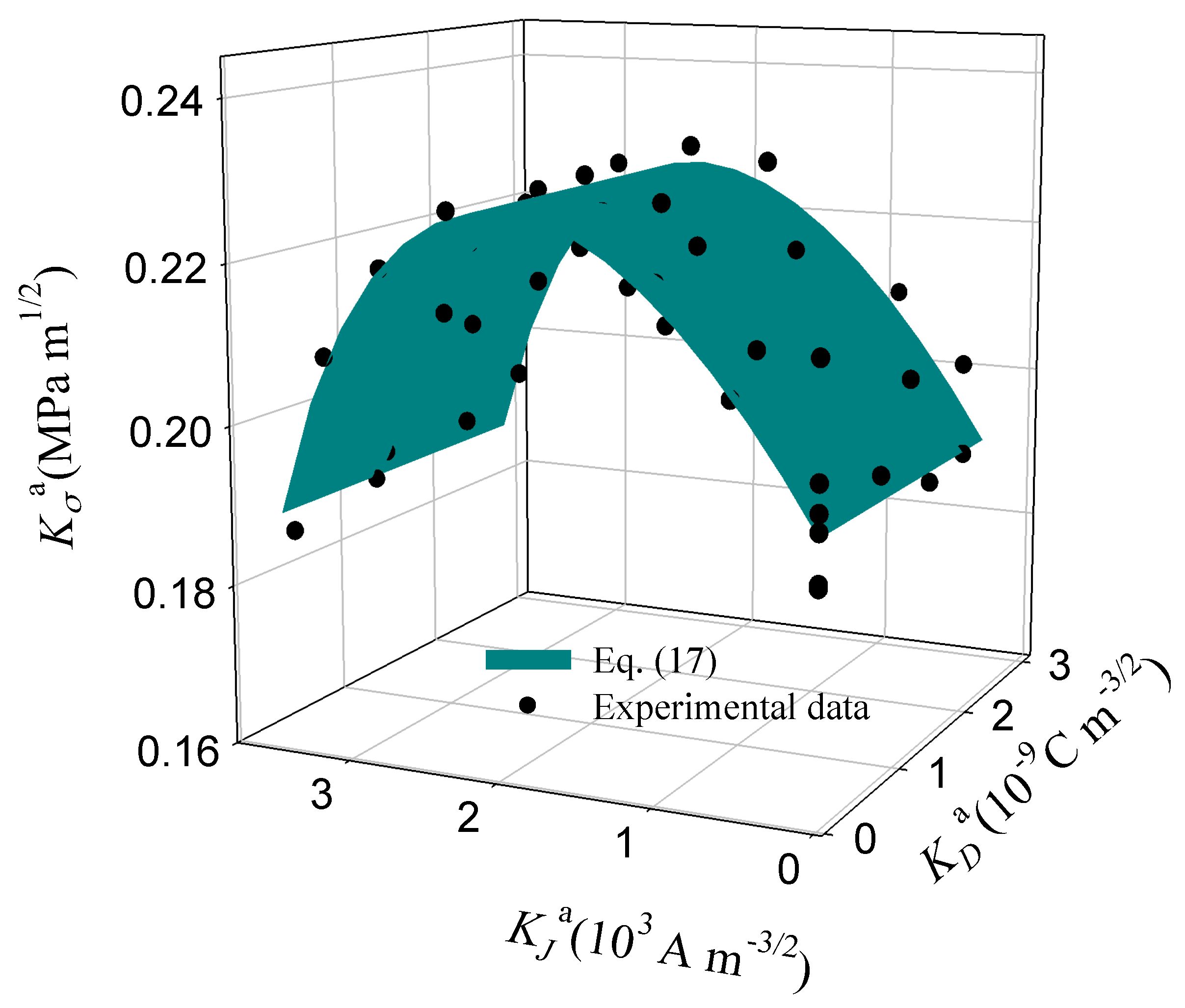
| Intensity Factors | Fitting Coefficients, ej (j = 1, 2, 3, 4, 5) | ||||
|---|---|---|---|---|---|
| Stress intensity factor | 3.055 | −7.141 | 33.479 | −61.360 | 52.909 |
| Electric displacement intensity factor | 1.921 | −0.426 | 2.157 | −3.438 | 3.206 |
| Electric current intensity factor | 1.800 | −0.256 | 2.350 | −4.101 | 4.270 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, G.; Lu, C.; Zhang, X.; Zhao, M. Electric Current Dependent Fracture in GaN Piezoelectric Semiconductor Ceramics. Materials 2018, 11, 2000. https://doi.org/10.3390/ma11102000
Qin G, Lu C, Zhang X, Zhao M. Electric Current Dependent Fracture in GaN Piezoelectric Semiconductor Ceramics. Materials. 2018; 11(10):2000. https://doi.org/10.3390/ma11102000
Chicago/Turabian StyleQin, Guoshuai, Chunsheng Lu, Xin Zhang, and Minghao Zhao. 2018. "Electric Current Dependent Fracture in GaN Piezoelectric Semiconductor Ceramics" Materials 11, no. 10: 2000. https://doi.org/10.3390/ma11102000
APA StyleQin, G., Lu, C., Zhang, X., & Zhao, M. (2018). Electric Current Dependent Fracture in GaN Piezoelectric Semiconductor Ceramics. Materials, 11(10), 2000. https://doi.org/10.3390/ma11102000





