A Continuum Damage Mechanics Model for the Static and Cyclic Fatigue of Cellular Composites
Abstract
:1. Introduction
2. Mechanical Properties and Fatigue Behavior
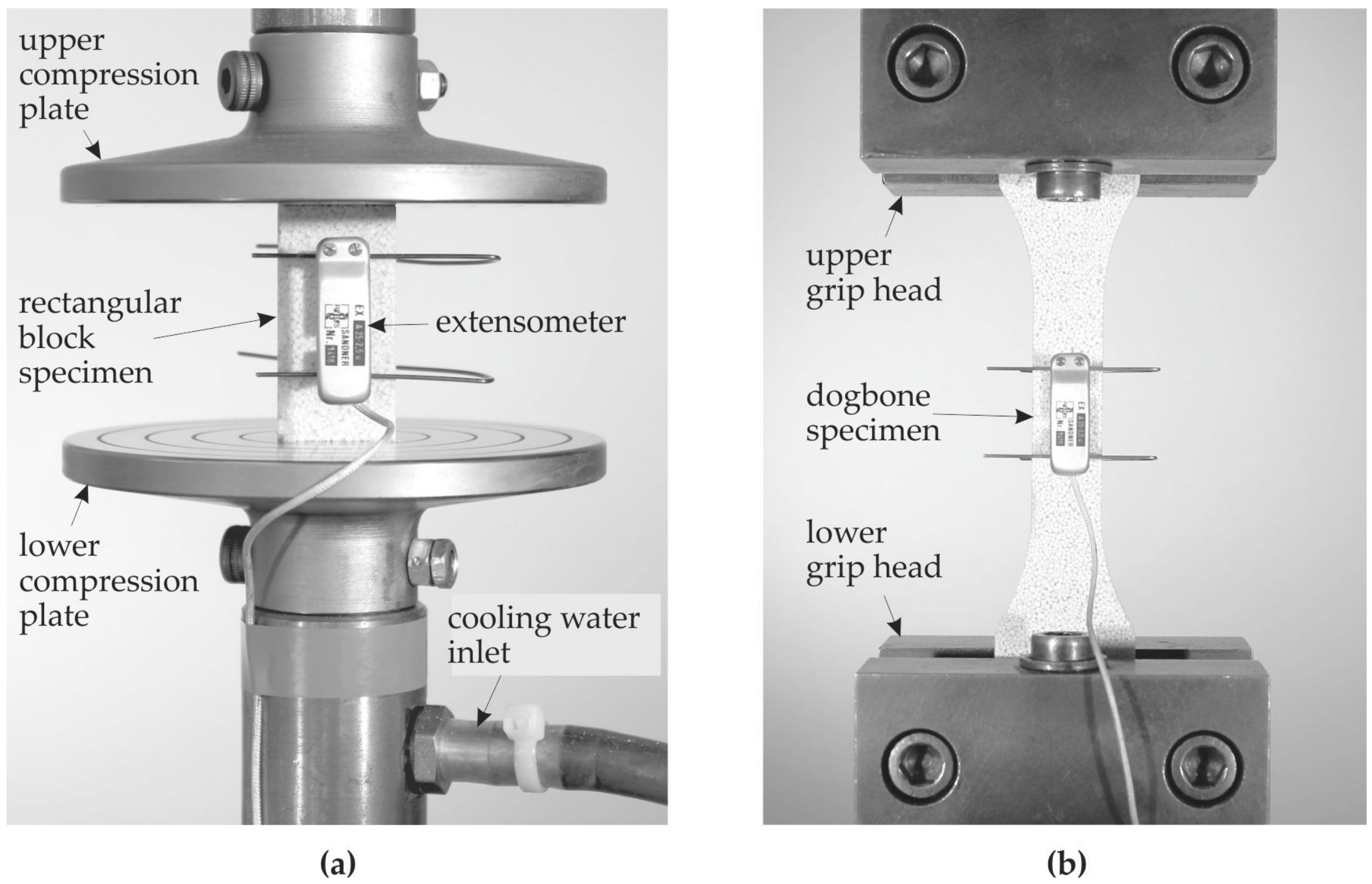
2.1. Constituent Materials
2.2. Quasi-Static Mechanical Properties
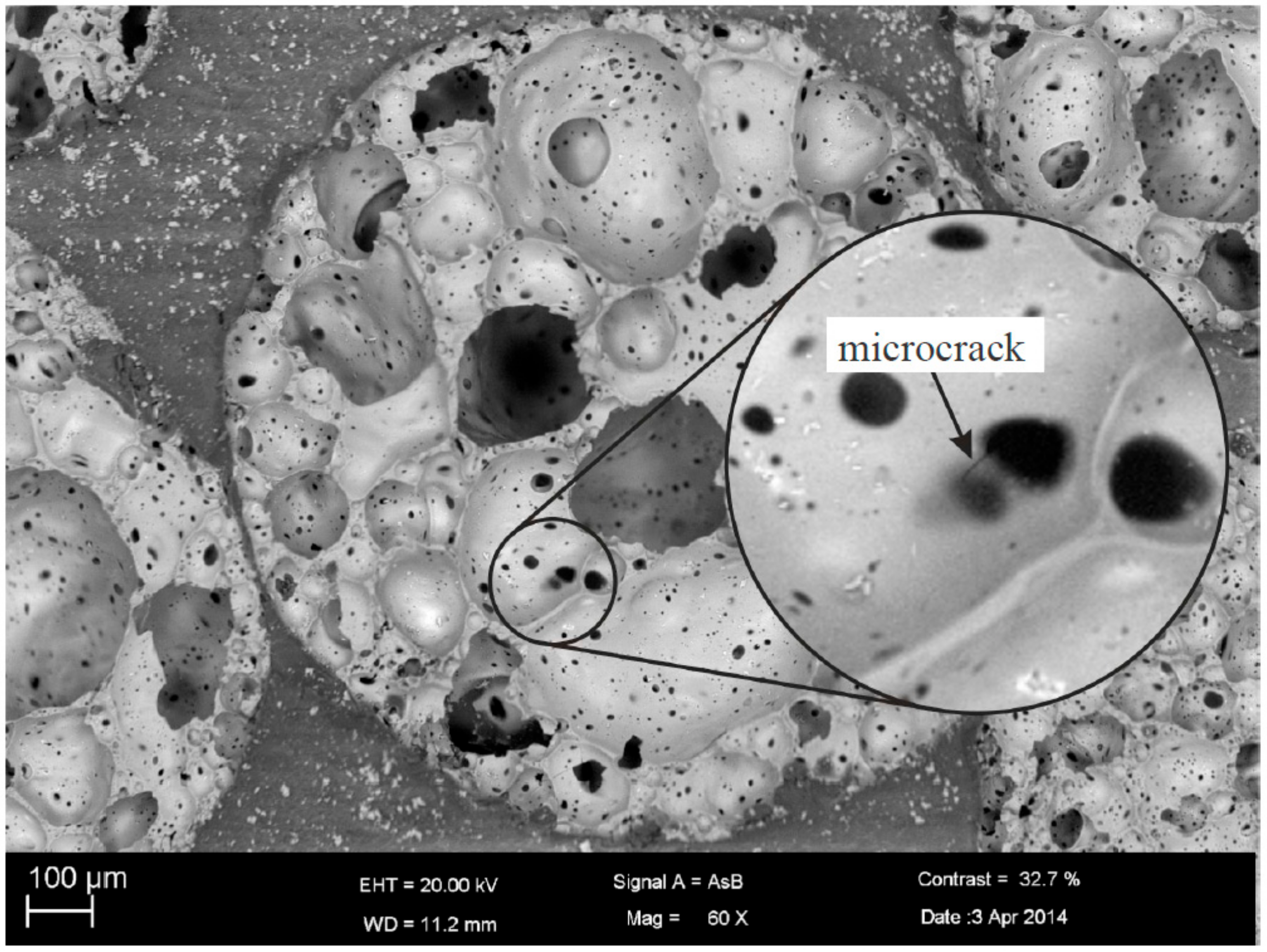
2.3. Static and Cyclic Fatigue Behavior
3. Damage Modeling and Parameter Identification
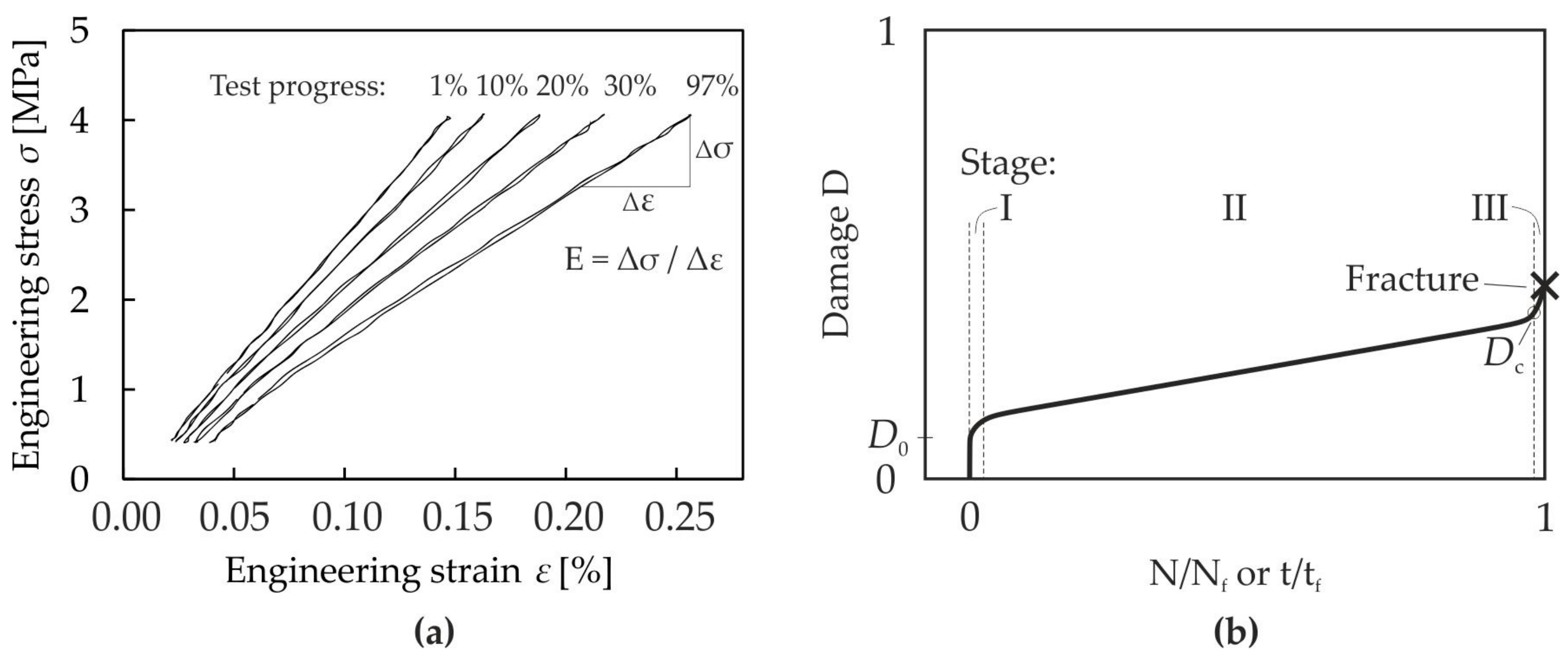
3.1. Static Damage Model
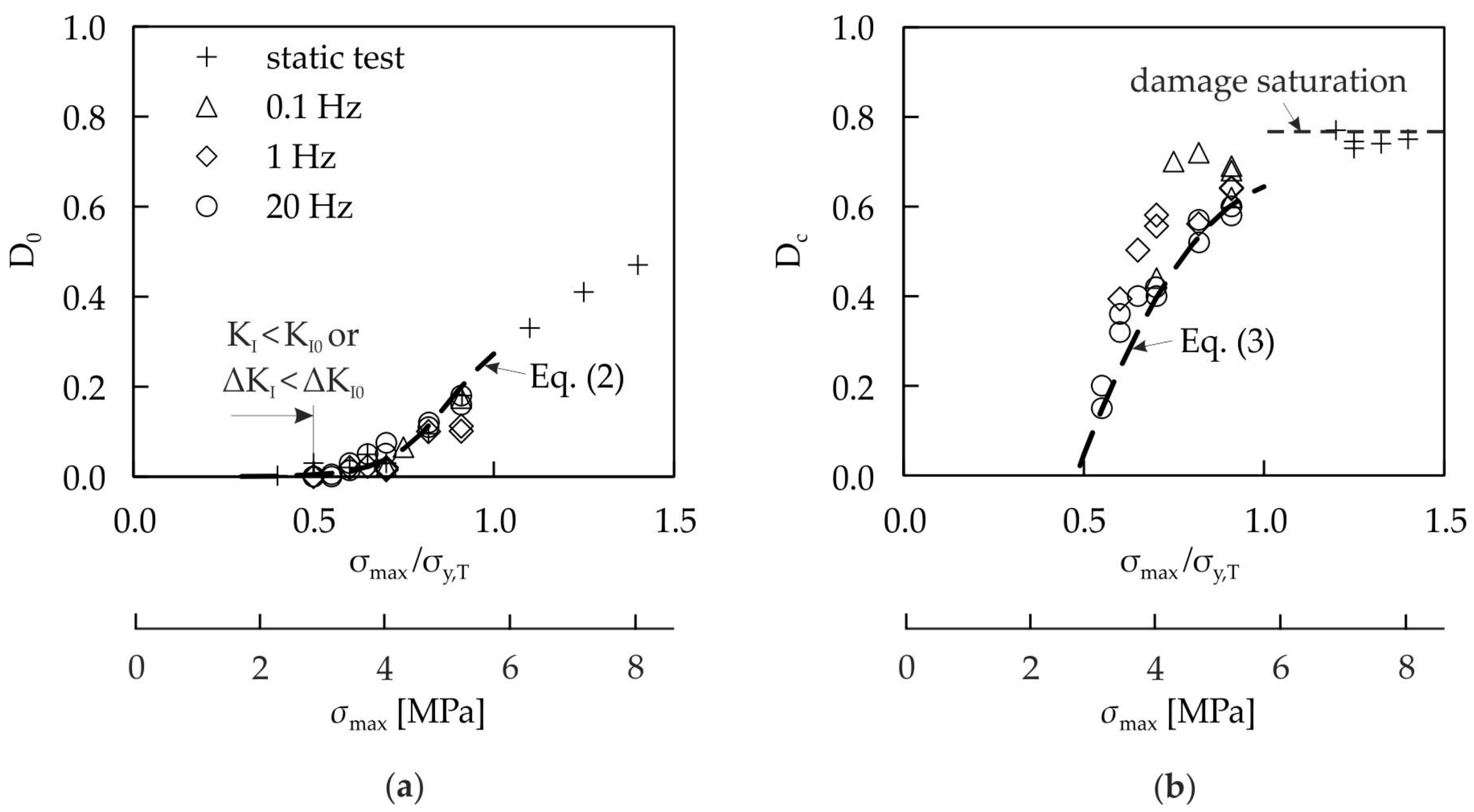
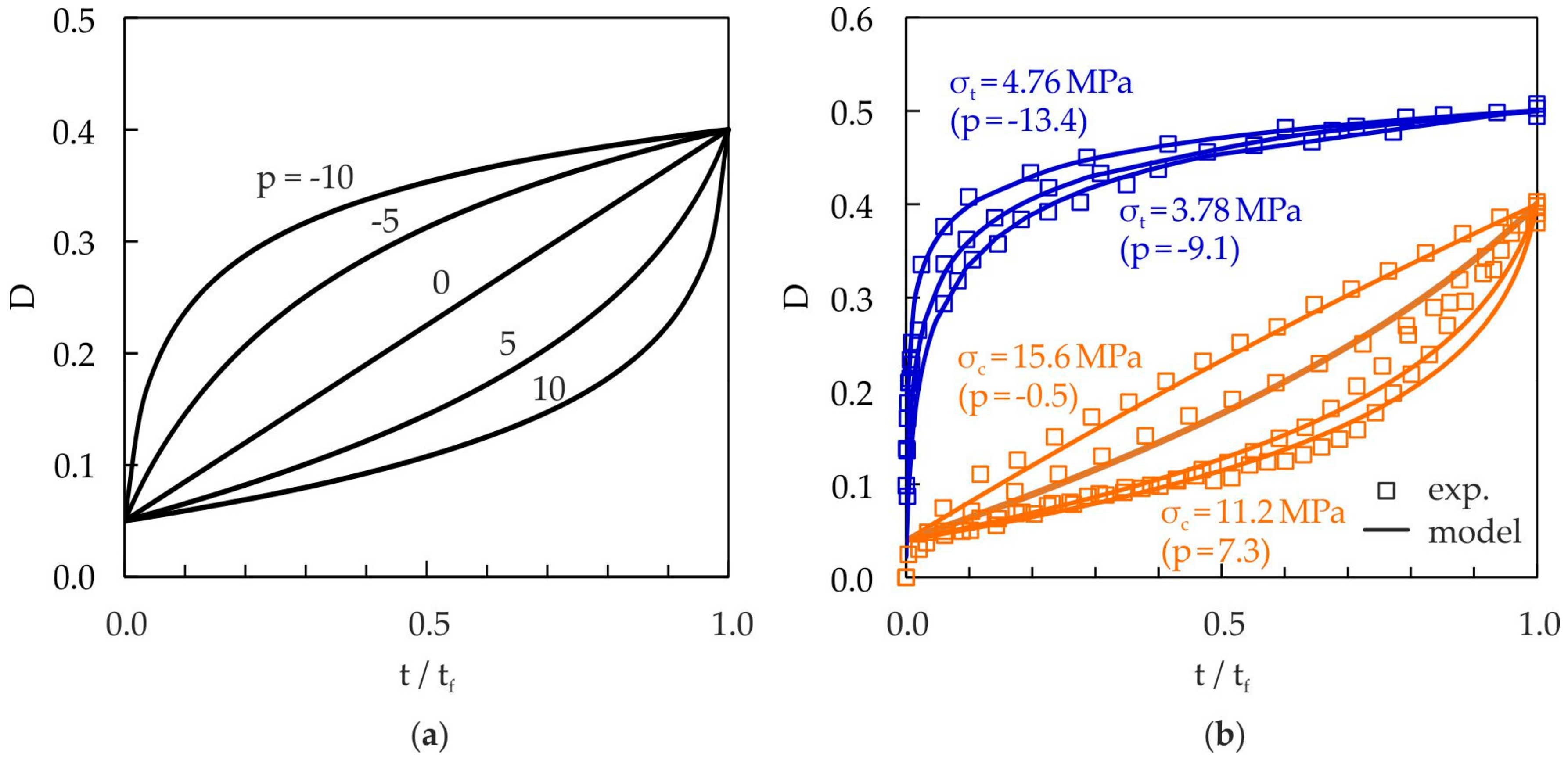
3.1.1. Damage Exponent, p
3.1.2. Stress Exponent, m
3.1.3. Material Parameter, A
3.1.4. Static Damage Model Parameters
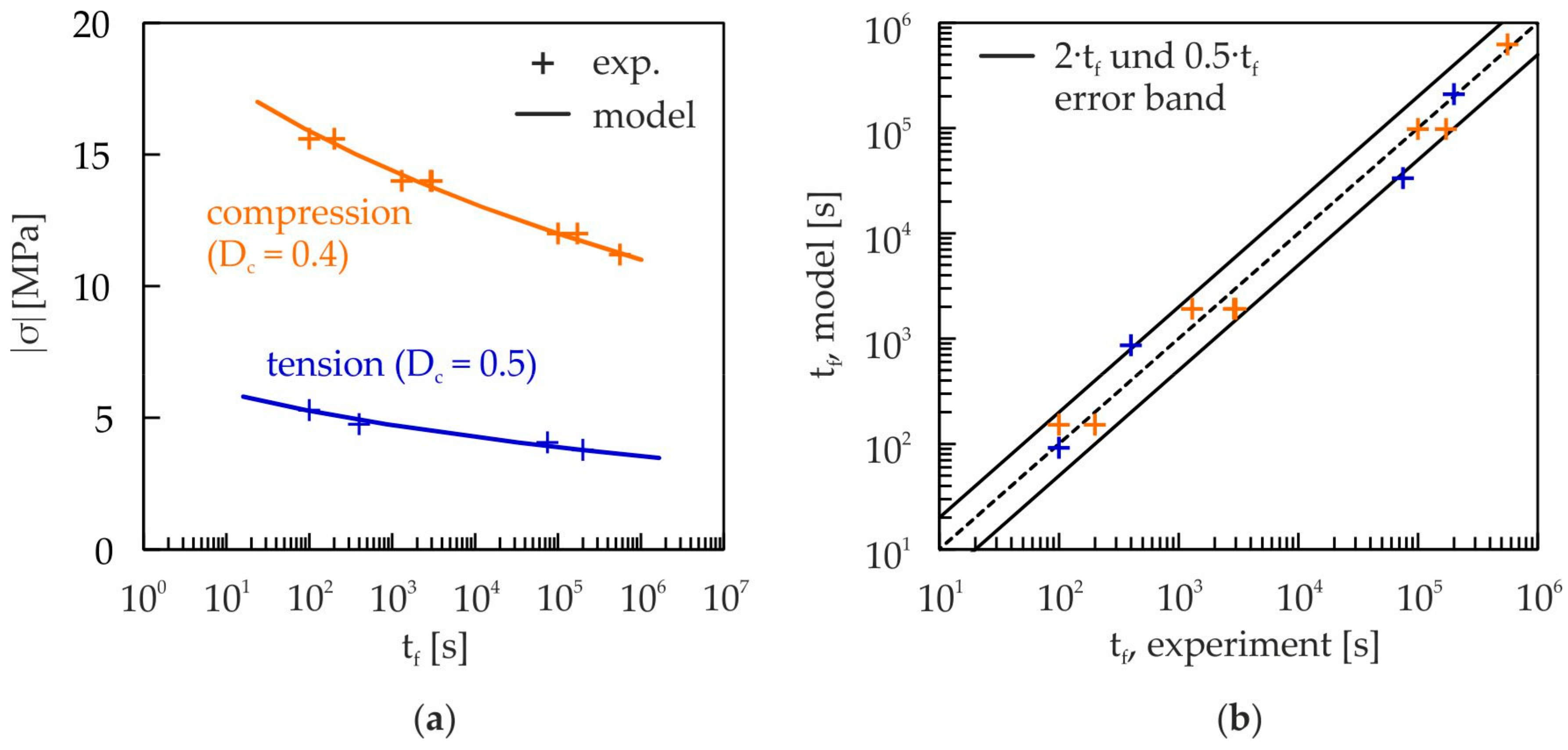
3.1.5. Validation of the Static Damage Model
3.2. Cyclic Damage Model
3.2.1. Damage Exponent, α
3.2.2. Stress Exponent, β
3.2.3. Mean Stress Parameter, M
3.2.4. Cyclic Damage Model Parameters
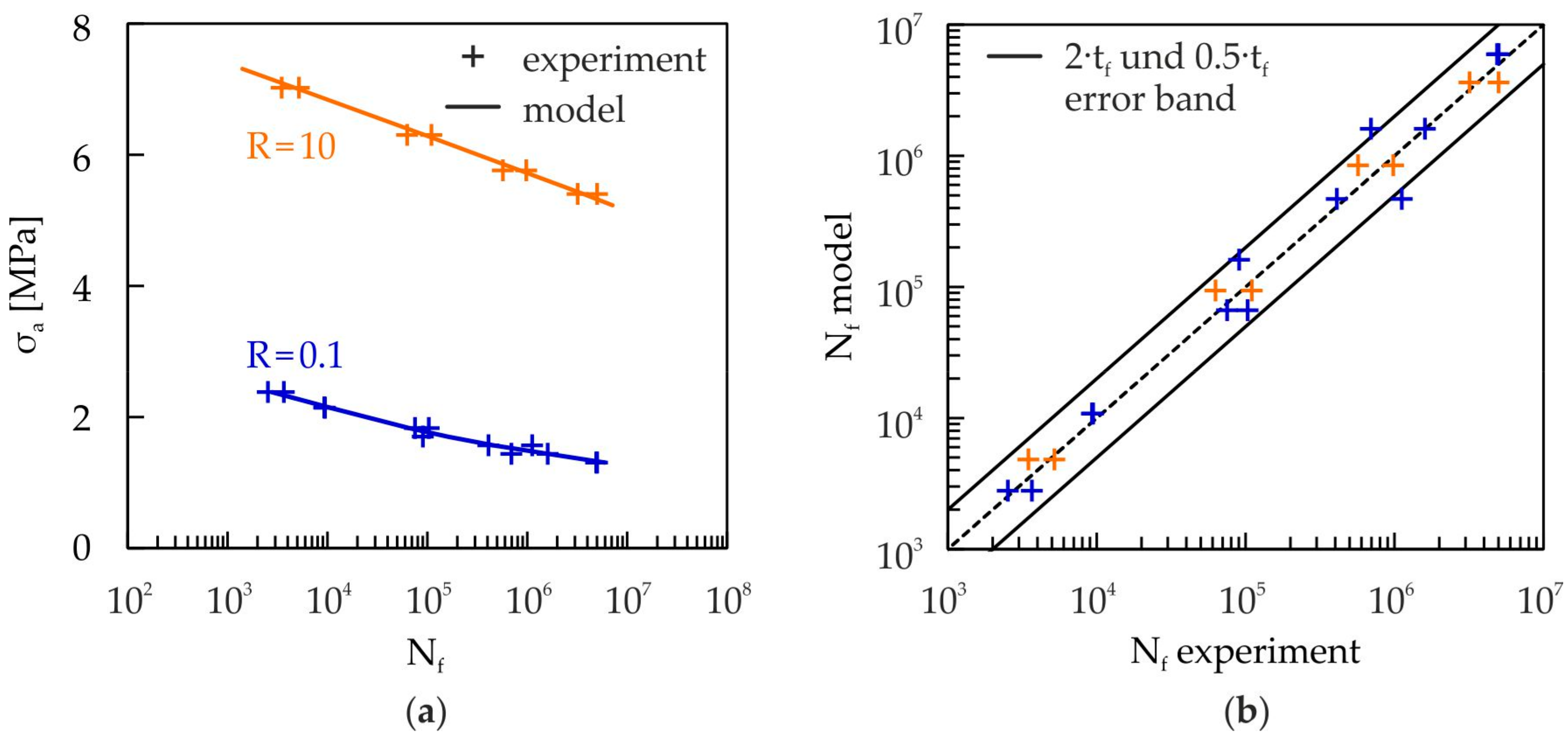
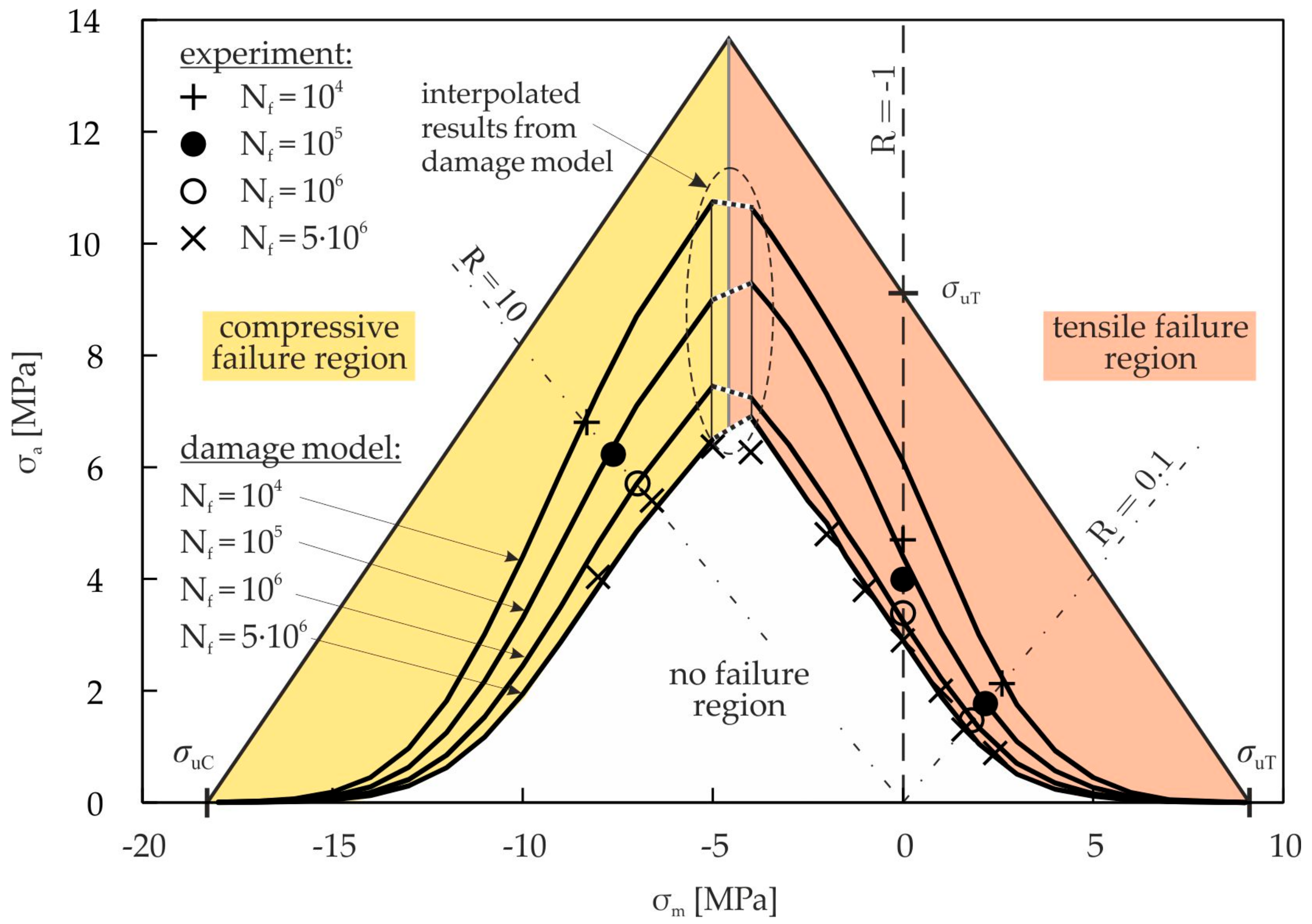
3.2.5. Validation of the Cyclic Damage Model
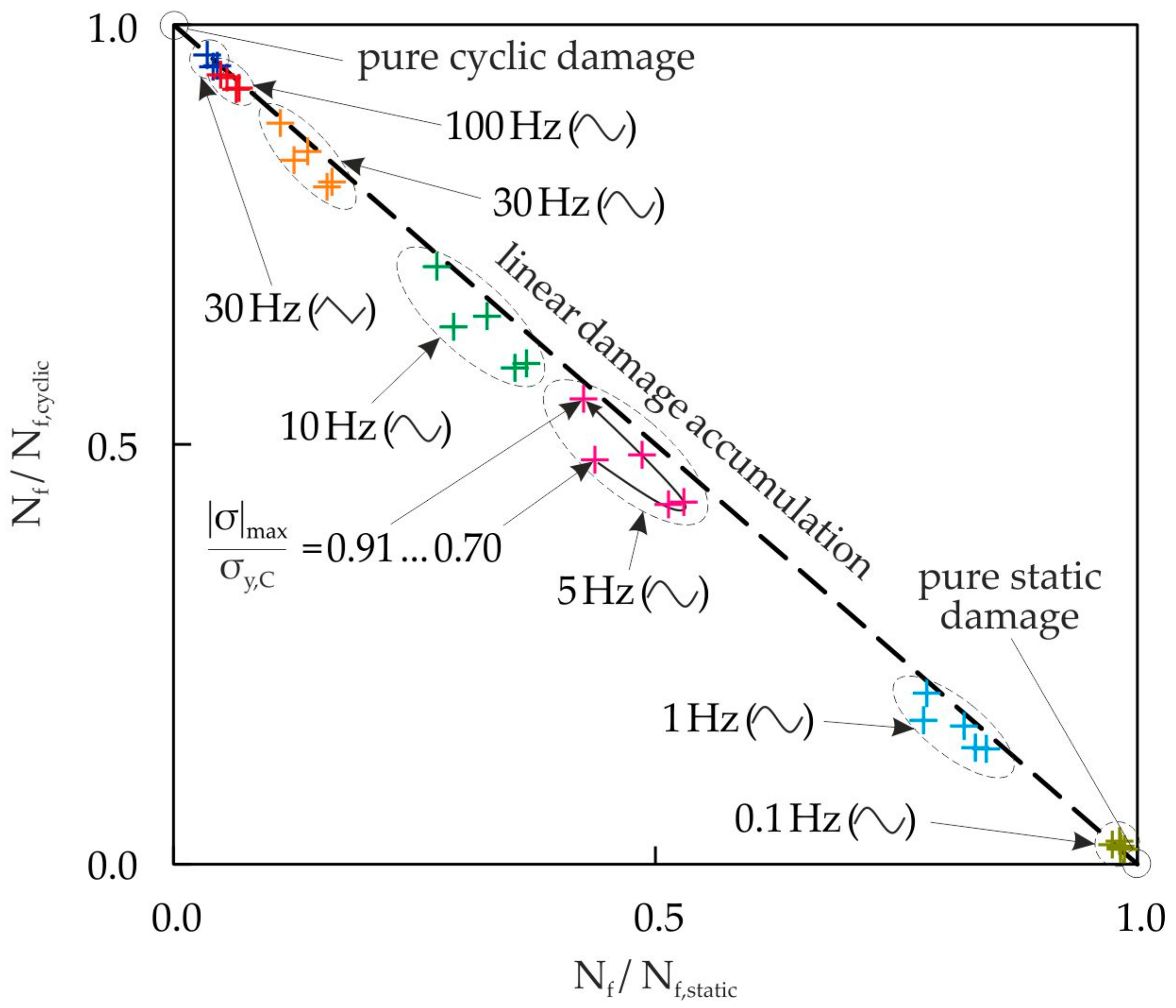
3.3. Damage Interaction Model
3.4. Numerical Integration
4. Damage Model Application
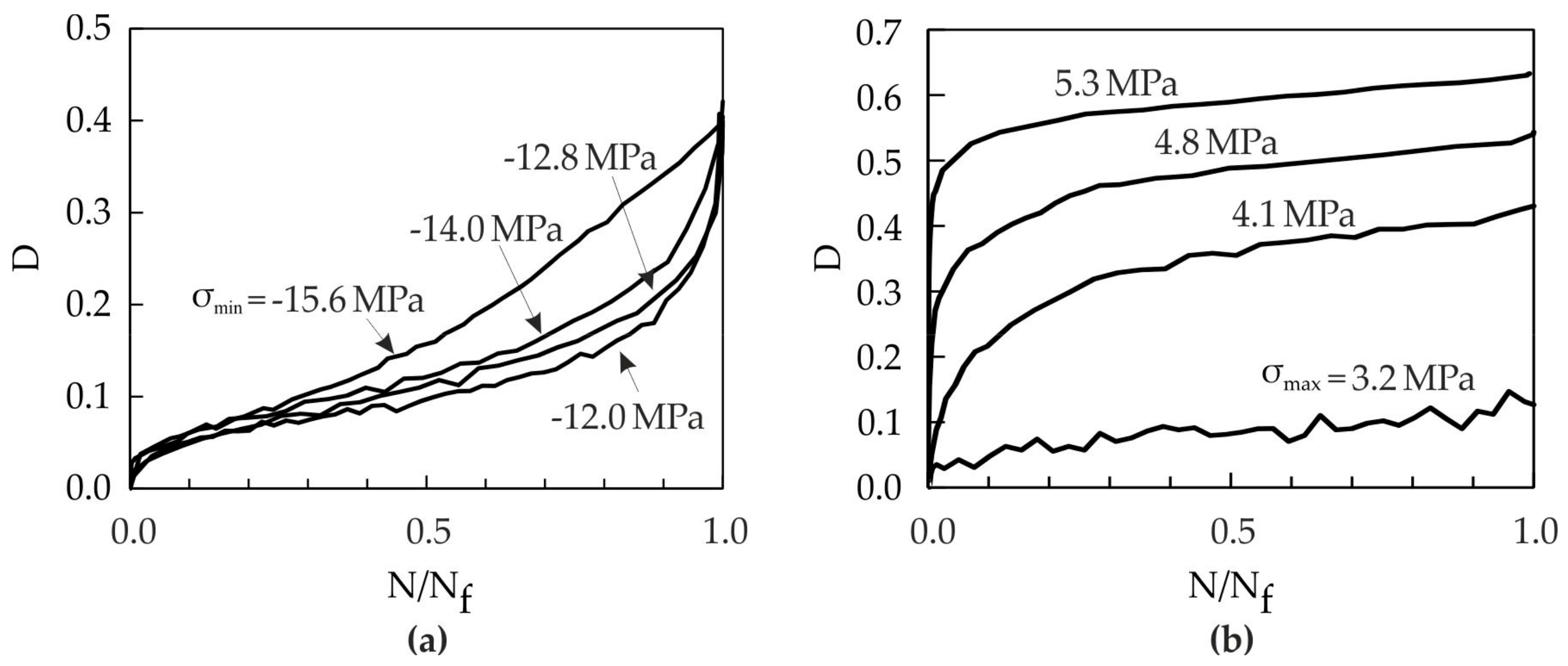
4.1. Mean Stress Effect in Pure Cyclic Damage
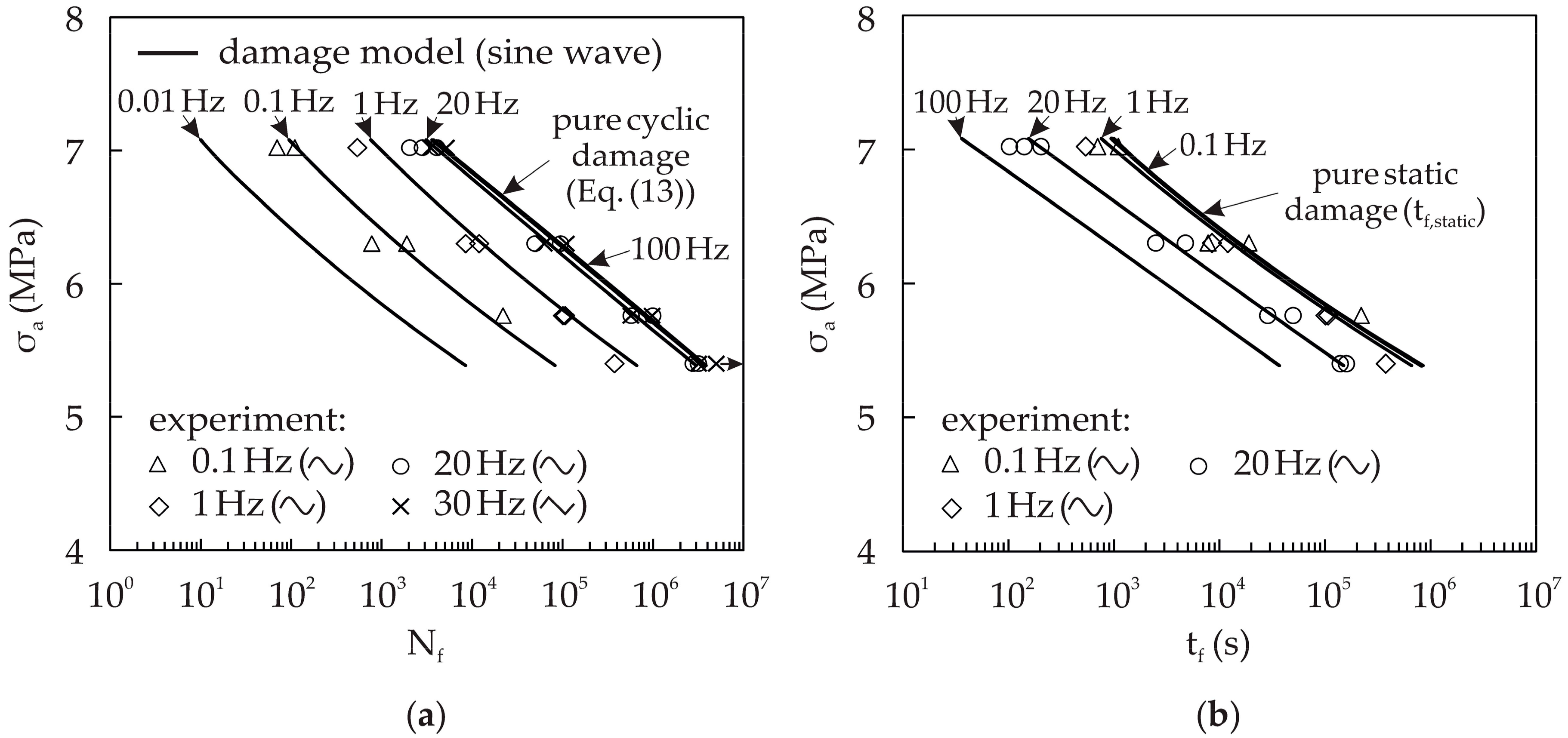
4.2. Frequency Effect in Static and Cyclic Damage Interaction
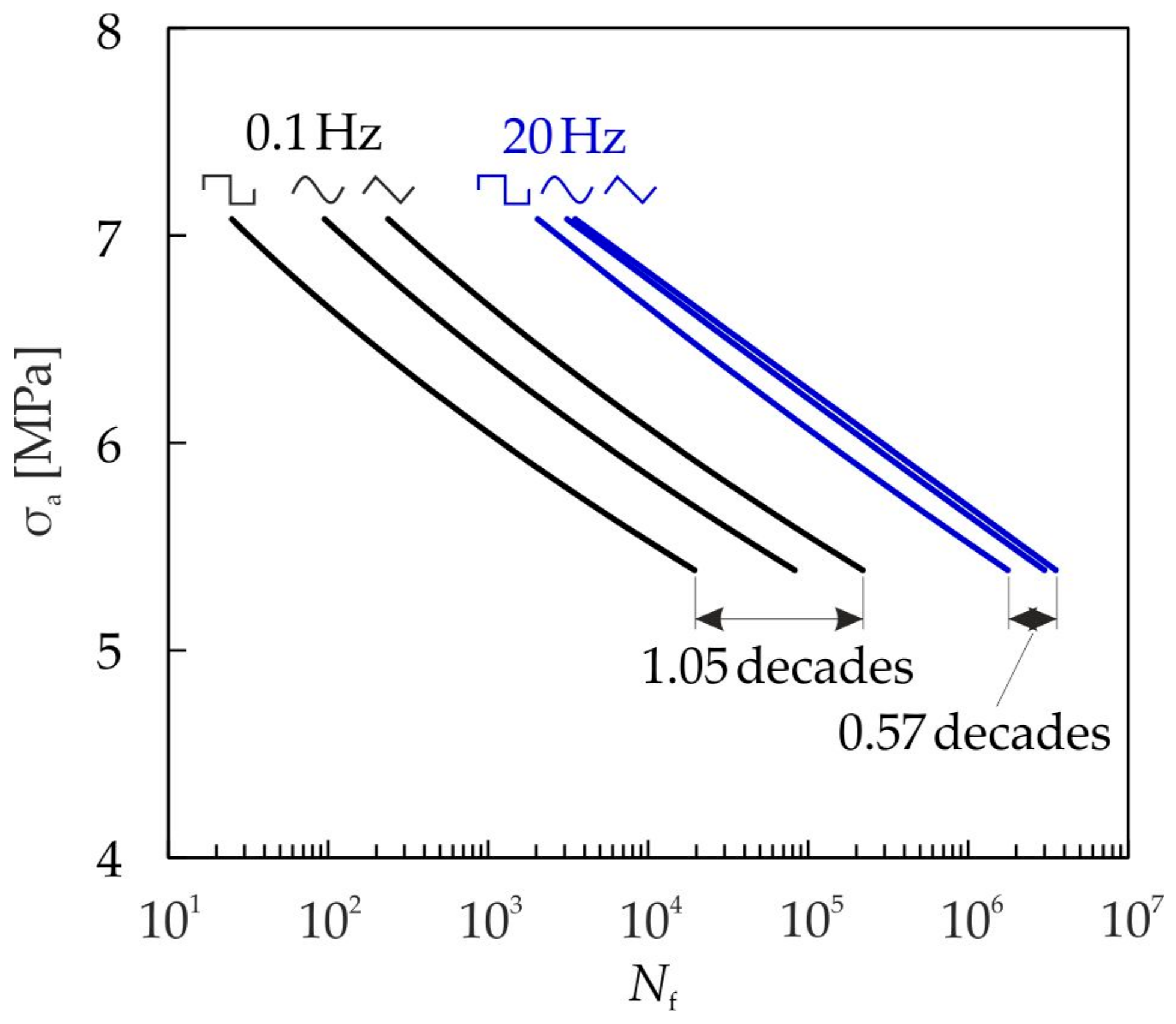
4.3. Influence of the Waveform
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Klaus, H.; Huber, O.; Kuhn, G. Lightweight potential of novel cellular spherical composites. Adv. Eng. Mater. 2005, 7, 1117–1124. [Google Scholar] [CrossRef]
- Huber, O.; Klaus, H.; Dallner, R.; Bartl, F.; Eigenfeld, K.; Kovacs, B.; Godehardt, M. Herstellung und Eigenschaften Syntaktischer Metallschäume mit Unterschiedlichen Matrix- und Füllmaterialien (Part 1–3); Druckguss-Praxis: Berlin, Germany, 2006; pp. 19–24 (Part I), 69–75 (part II), 205–216 (Part III). [Google Scholar]
- Klaus, H. Charakterisierung, Modellierung und Anwendung zellularer Verbundwerkstoffe im elasto-plastischen Bereich. Dissertation, University of Erlangen-Nuremberg, Erlangen, Germany, 2007. [Google Scholar]
- Klaus, H.; Huber, O.; Kuhn, G. Materialverhalten zellularer Kugelverbundwerkstoffe im linear-viskoelastischen Bereich. Tech. Mech. 2006, 26, 71–84. [Google Scholar]
- Huber, O.; Klaus, H. Cellular composites in lightweight sandwich applications. Mater. Lett. 2009, 63, 1117–1120. [Google Scholar] [CrossRef]
- Bartl, F.; Klaus, H.; Dallner, R.; Huber, O. Material behavior of a cellular composite undergoing large deformations. Int. J. Impact Eng. 2009, 36, 667–679. [Google Scholar] [CrossRef]
- Bartl, F. Ein numerisches Werkstoffmodell für Gießtechnisch Hergestellte Verbundwerkstoffe bei hohen Deformationsgeschwindigkeiten. Ph.D. Dissertation, University of Freiberg, Freiberg, Germany, 2009. [Google Scholar]
- Nusholtz, G.; Bilkhu, M.; Founas, M.; Uduma, K.; Du Bois, P. Impact Response of foam: The effect of the state of stress. In Proceedings of the STAPP Conference, Albuquerque, NM, USA, 4–6 November 1996. [Google Scholar]
- Diel, S.; Huber, O.; Saage, H.; Steinmann, P.; Winter, W. Mechanical behavior of a cellular composite under quasi-static, static and cyclic compression loading. J. Mater. Sci. 2012, 47, 5635–5645. [Google Scholar] [CrossRef]
- Diel, S.; Huber, O. Comparison of tensile and compressive creep-fatigue damage behavior of cellular composites. Adv. Mater. Res. 2014, 891–892, 633–638. [Google Scholar] [CrossRef]
- Diel, S.; Huber, O. Cellular composites—Mechanical properties and applications in sandwich structures. In Proceedings of the Conference Cellmat 2012, Dresden, Germany, 7–9 November 2012. [Google Scholar]
- Diel, S.; Huber, O.; Steinmann, P.; Winter, W. Design and validation of a new fixture for the shear testing of cellular solids. Arch. Appl. Mech. 2014, 84, 309–321. [Google Scholar] [CrossRef]
- Diel, S. Charakterisierung und Modellierung des Quasi-Statischen Verhaltens und der Ermüdung eines Zellularen Verbundwerkstoffes. Ph.D. Dissertation, University of Erlangen-Nuremberg, Erlangen, Germany, 2015. [Google Scholar]
- Denk, J.; Diel, S.; Huber, O. Experimental and Numerical Analyses of the Lightweight Potential for Hybrid Thin-Walled Members. Mater. Sci. Forum 2015, 825–826, 732–740. [Google Scholar] [CrossRef]
- Diel, S.; Huber, O. Static and Cyclic Damage Behavior of a Cellular Composite and its Application in a Sandwich Structure. In Proceedings of the ECCM17—17th European Conference on Composite Materials, Munich, Germany, 26–30 June 2016; ISBN 978-3-00-053387-7. [Google Scholar]
- Huber, O.; Klaus, H. Lightweight Moulded Piece and Corresponding Production Method. European Patent EP 2,125,358 B1, 29 January 2014. [Google Scholar]
- Ferreira, J.A.M.; Salviano, K.; Costa, J.D.; Capela, C. Fatigue behaviour in hybrid hollow microsphere/fibre reinforced composites. J. Mater. Sci. 2010, 45, 3547–3553. [Google Scholar] [CrossRef]
- Hossain, M.M.; Shivakumar, K. Compression fatigue performance of a fire resistant syntactic foam. Compos. Struct. 2011, 94, 290–298. [Google Scholar] [CrossRef]
- Hossain, M.M.; Shivakumar, K. Flexural fatigue failures and lifes of Eco-Core sandwich beams. Mater. Des. 2014, 55, 830–836. [Google Scholar] [CrossRef]
- Hossain, M.M.; Shivakumar, K. Shear fatigue characterization of fire resistant syntactic foam core sandwich beam. J. Sandw. Struct. Mater. 2013, 15, 523–540. [Google Scholar] [CrossRef]
- Theocaris, P.S. Viscoelastic properties of epoxy resins derived from creep and relaxation tests at different temperatures. Rheol. Acta 1962, 2, 92–96. [Google Scholar] [CrossRef]
- Melo, J.D.; Medeiros, A.M. Long-term creep-rupture failure envelope of epoxy. Mech. Time Depend. Mater. 2014, 18, 113–121. [Google Scholar] [CrossRef]
- Nagasawa, M.; Kinuhata, H.; Koizuka, H.; Miyamoto, K.; Tanaka, T.; Kishimoto, H.; Koike, T. Mechanical fatigue of epoxy resin. J. Mater. Sci. 1995, 30, 1266–1272. [Google Scholar] [CrossRef]
- Sauer, J.A.; Richardson, G.C. Fatigue of polymers. Int. J. Fract. 1980, 16, 499–532. [Google Scholar] [CrossRef]
- Baker, T.C.; Preston, F.W. Fatigue of glass under static loads. Int. J. Mech. Sci. 1946, 17, 170–178. [Google Scholar] [CrossRef]
- Wiederhorn, S.M. Influence of water vapor on crack propagation in soda-lime glass. J. Am. Ceram. Soc. 1967, 50, 407–414. [Google Scholar] [CrossRef]
- Conley, P.H.; Chandan, H.C.; Bradt, R.C. Dynamic fatigue of foamed glass. In Fracture Mechanics of Ceramics. Volume 4: Crack Growth and Microstructure; Bradt, R.C., Hasselmann, D.P.H., Lange, F.F., Eds.; Plenum Press: New York, NY, USA; London, UK, 1978; pp. 761–772. [Google Scholar]
- Heierli, J.; Gumbsch, P.; Sherman, D. Anticrack-type fracture in brittle foam under compressive stress. Scr. Mater. 2012, 67, 96–99. [Google Scholar] [CrossRef]
- Gurney, C.; Pearson, S. Fatigue of mineral glass under static and cyclic loading. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 192, 537–544. [Google Scholar] [CrossRef]
- Lemaitre, J. A Course on Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Kachanov, L.M. Zeitlicher Ablauf des Bruchprozesses unter Kriechbedingungen. Izvestiya Akademii Nauk UdSSR 1958, 8, 26–31. [Google Scholar]
- Rabotnov, Y.N. Creep Problems in Structural Members; Elsevier: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Lemaitre, J.; Chaboche, J.-L. A nonlinear model of creep-fatigue damage cumulation and interaction. In Proceedings of the IUTAM Symposium on Mechanics of Visco-Elastic Media and Bodies, Gothenburg, Sweden, 2–6 September 1974; Springer: Berlin, Germany, 1975. [Google Scholar]
- Chaboche, J.-L.; Lesne, P.M. A non-linear continuous fatigue damage model. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 1–17. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P. Fatigue Life Prediction of Composites and Composite Structures; Woodhead Publishing: Oxford, UK, 2010. [Google Scholar]
- Lemaitre, J.; Plumtree, A. Application of damage concepts to predict creep-fatigue failure. J. Eng. Mater. Technol. 1979, 101, 284–292. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]



| Density ρ (g/cm3) | Young’s Modulus E (MPa) | Poisson’s Ratio ν (–) | Tensile Yield Strength σy,T (MPa) | Tensile Strength σu,T (MPa) | Compressive Yield Strength σy,C (MPa) | Compressive Strength σu,C (MPa) |
|---|---|---|---|---|---|---|
| 0.72 | 3098 | 0.31 | 5.8 | 9.1 | 17.1 | 18.3 |
| Loading | A | m | p | D0 | Dc |
|---|---|---|---|---|---|
| compression | 4.5 × 10−39 | 30 | −1.8 |σ|/(MPa) + 27.5 | 0.05 | 0.4 |
| tension | 7.0 × 10−29 | 40 | −4.5 σ/(MPa) + 8.0 | Equation (2) | 0.5 |
| Damage in | α | β | M0 | D0 | Dc |
|---|---|---|---|---|---|
| compressive region | −0.43 |σ|max/(MPa) + 7.3 | 4.75 | 12.7 | 0.05 | 0.4 |
| tensile region | −3.2 σmax/(MPa) + 8.8 | 4.5 | 90.9 | Equation (2) | Equation (3) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diel, S.; Huber, O. A Continuum Damage Mechanics Model for the Static and Cyclic Fatigue of Cellular Composites. Materials 2017, 10, 951. https://doi.org/10.3390/ma10080951
Diel S, Huber O. A Continuum Damage Mechanics Model for the Static and Cyclic Fatigue of Cellular Composites. Materials. 2017; 10(8):951. https://doi.org/10.3390/ma10080951
Chicago/Turabian StyleDiel, Sergej, and Otto Huber. 2017. "A Continuum Damage Mechanics Model for the Static and Cyclic Fatigue of Cellular Composites" Materials 10, no. 8: 951. https://doi.org/10.3390/ma10080951
APA StyleDiel, S., & Huber, O. (2017). A Continuum Damage Mechanics Model for the Static and Cyclic Fatigue of Cellular Composites. Materials, 10(8), 951. https://doi.org/10.3390/ma10080951





