Finite Element Modeling of Tensile Deformation Behaviors of Iron Syntactic Foam with Hollow Glass Microspheres
Abstract
:1. Introduction
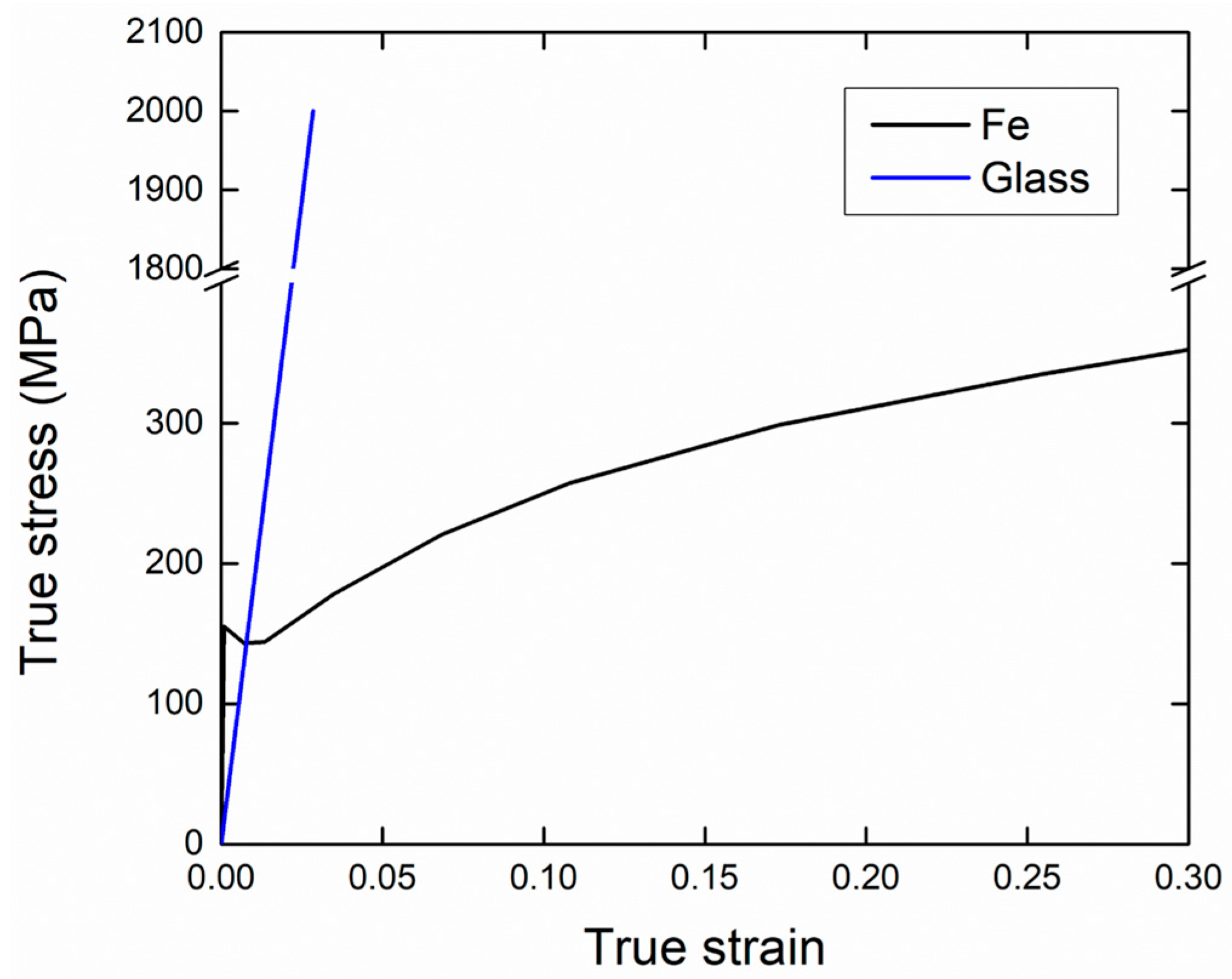
2. Material for Modeling
3. Finite Element Modeling
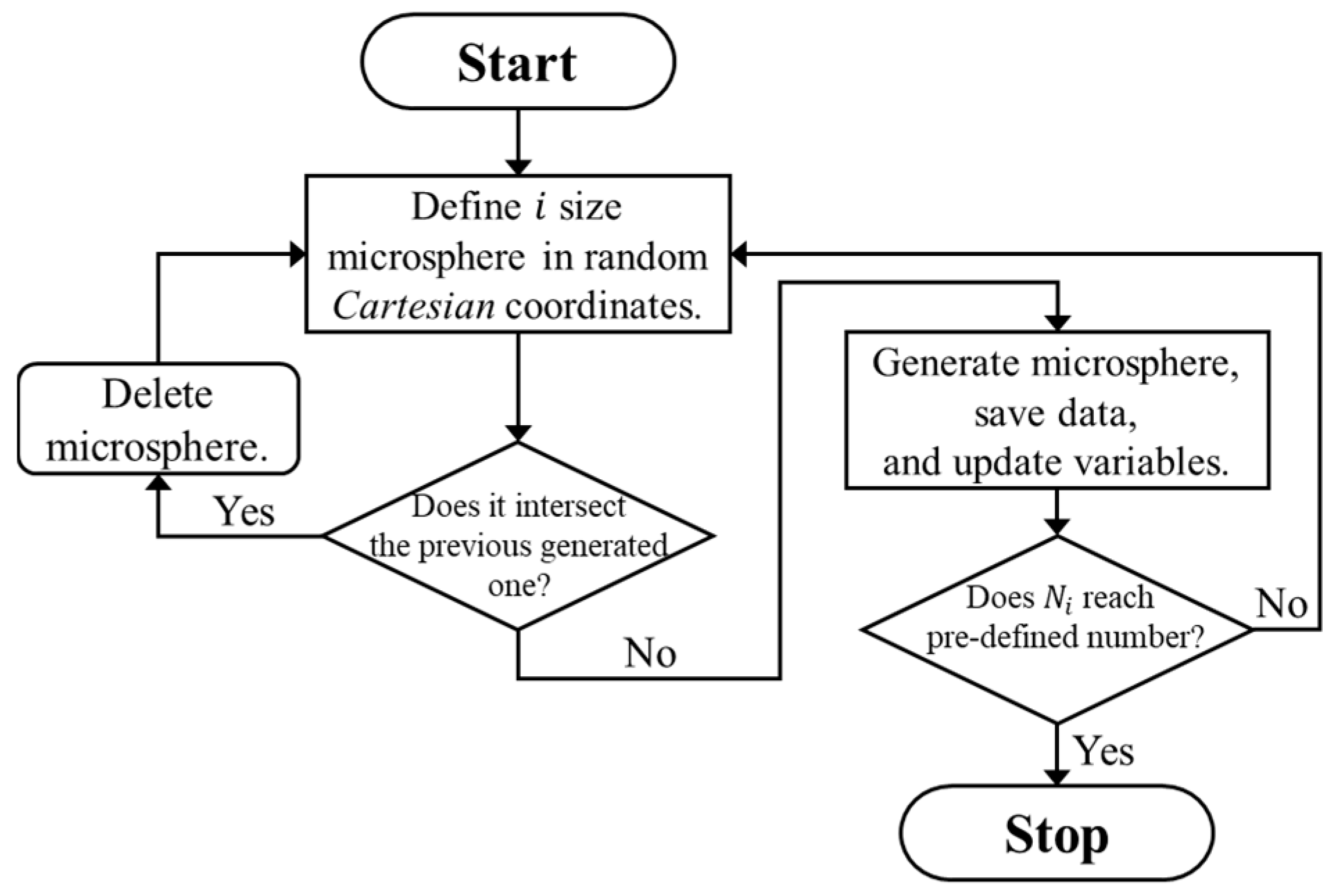
3.1. Modeling Procedures
3.2. Model Implementation
4. Result and Discussion
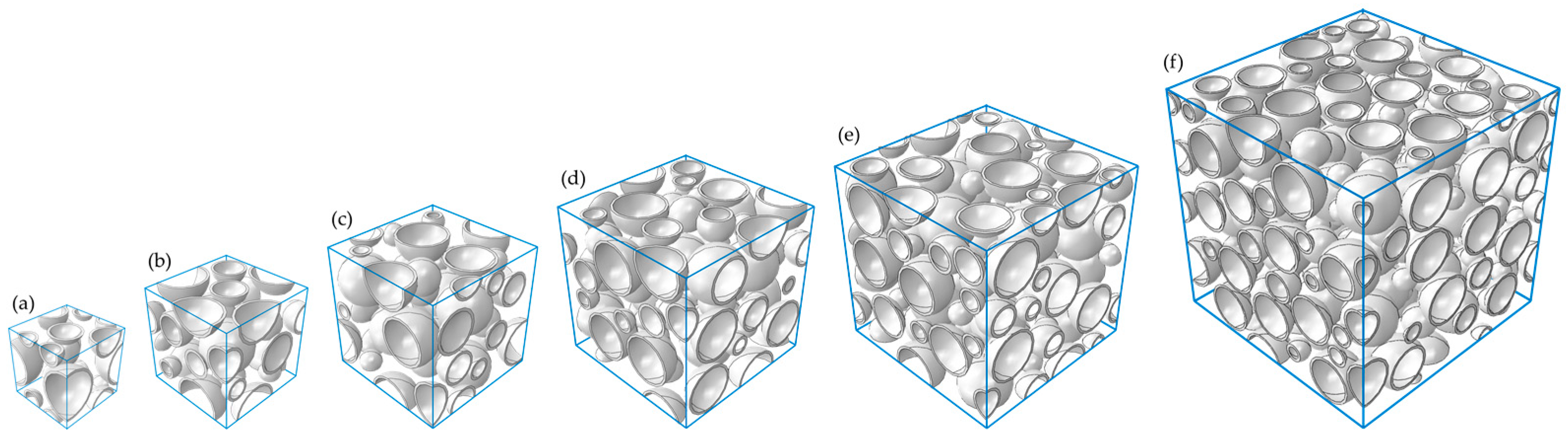
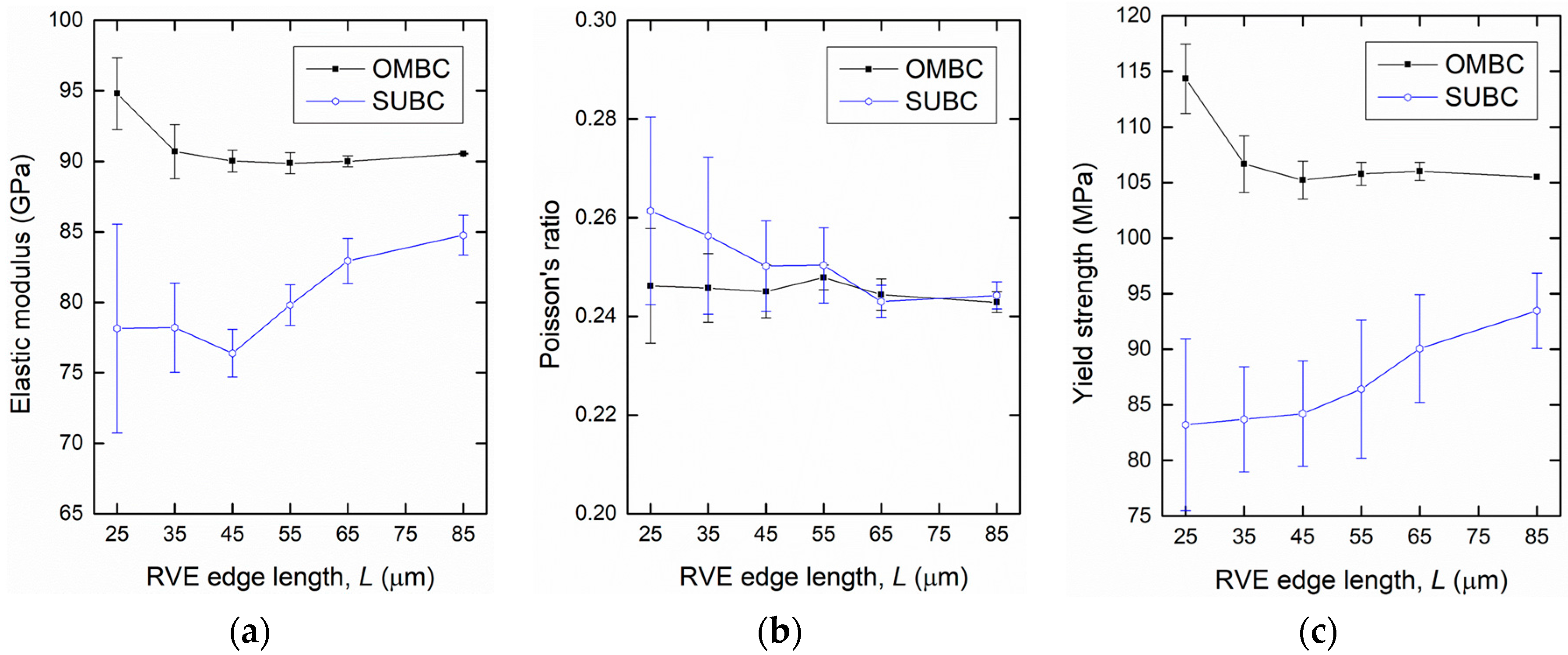
4.1. Determination of RVE
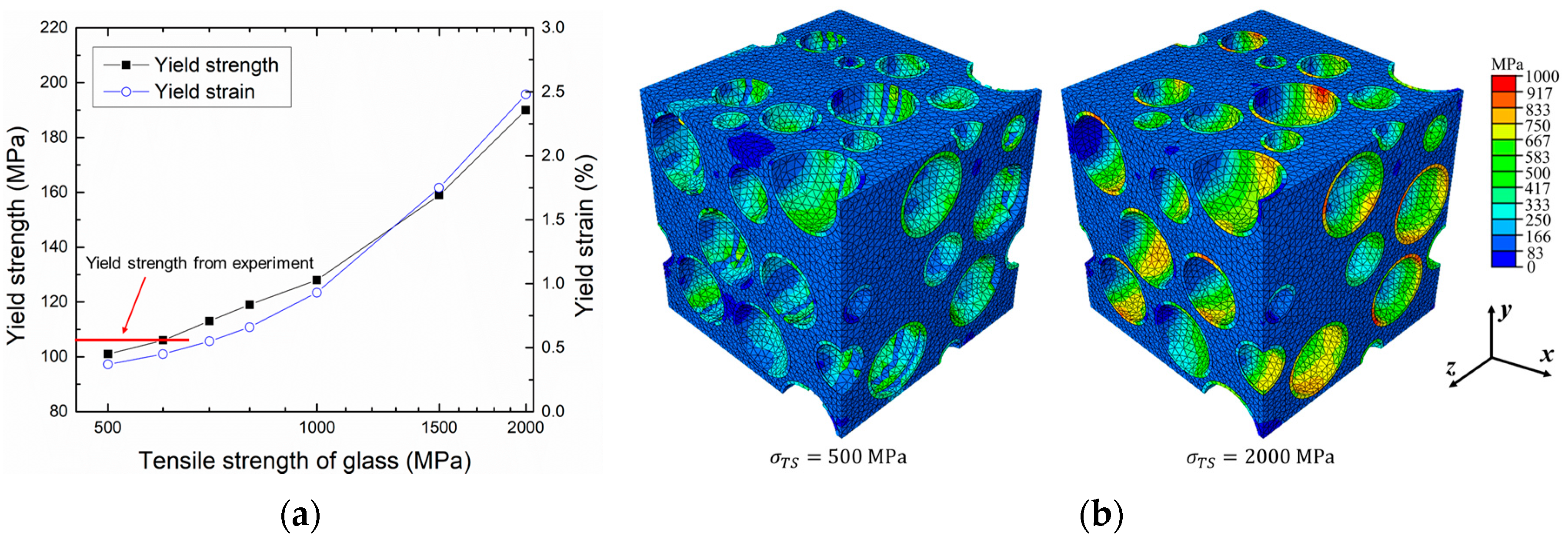
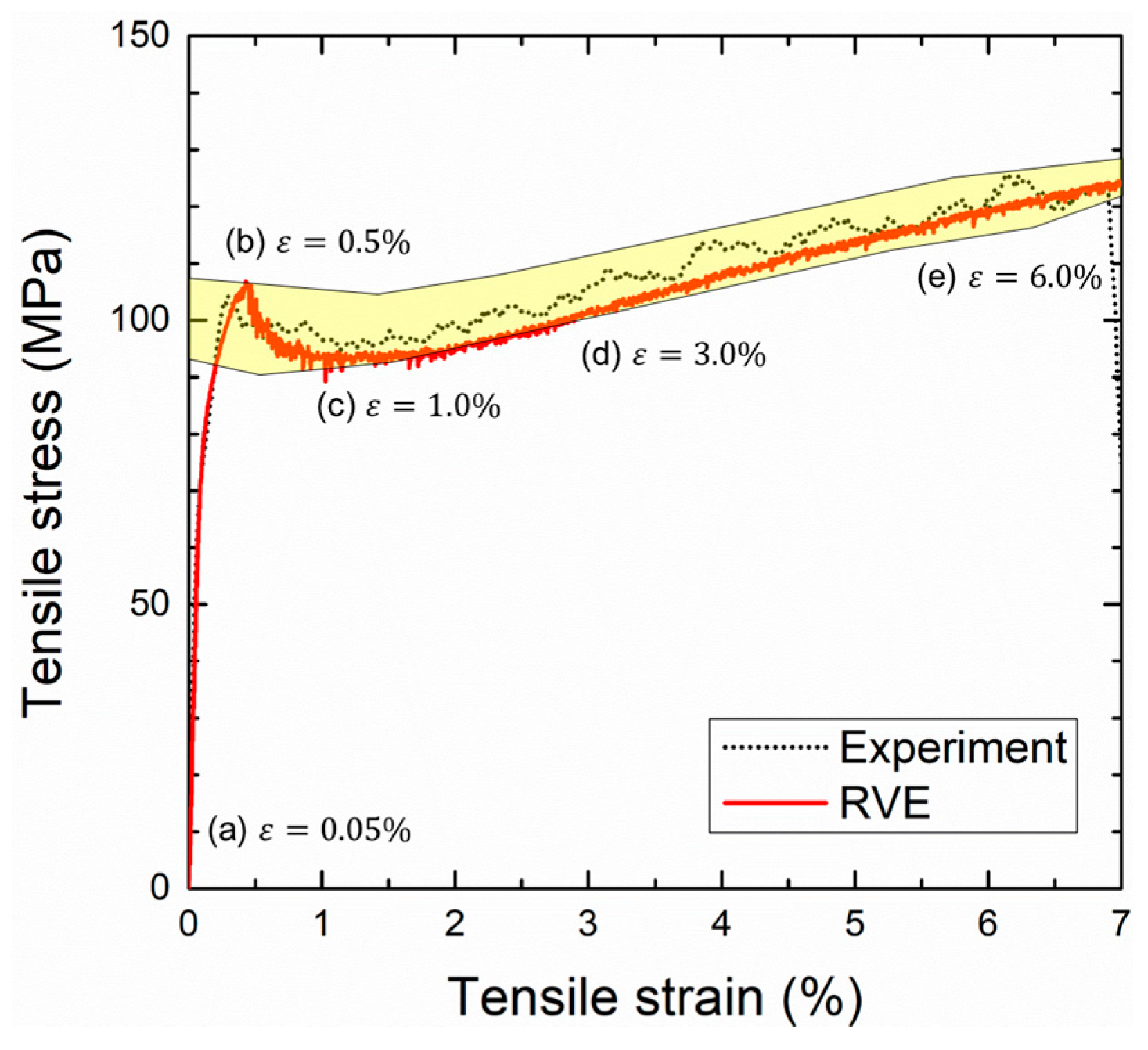
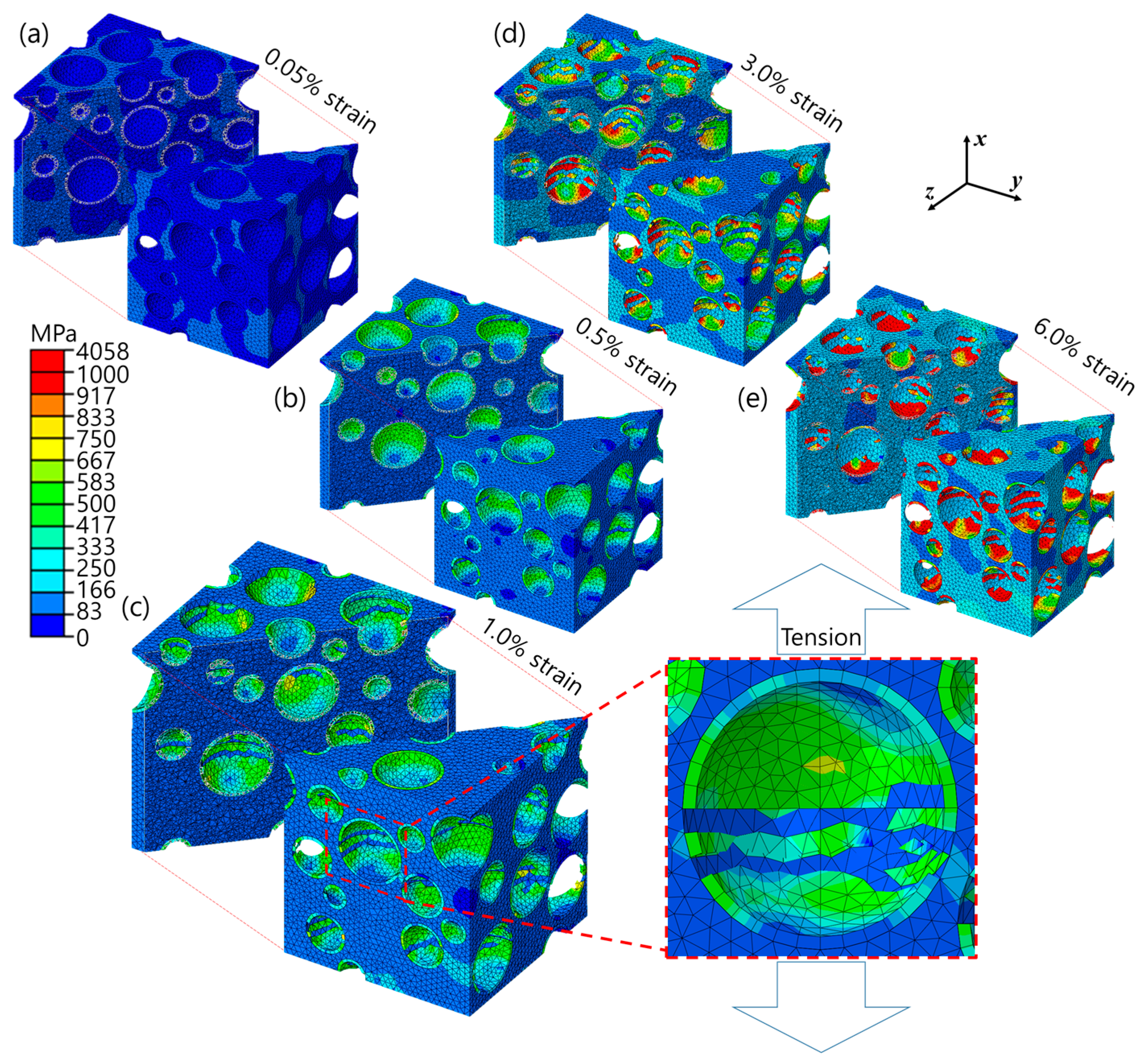
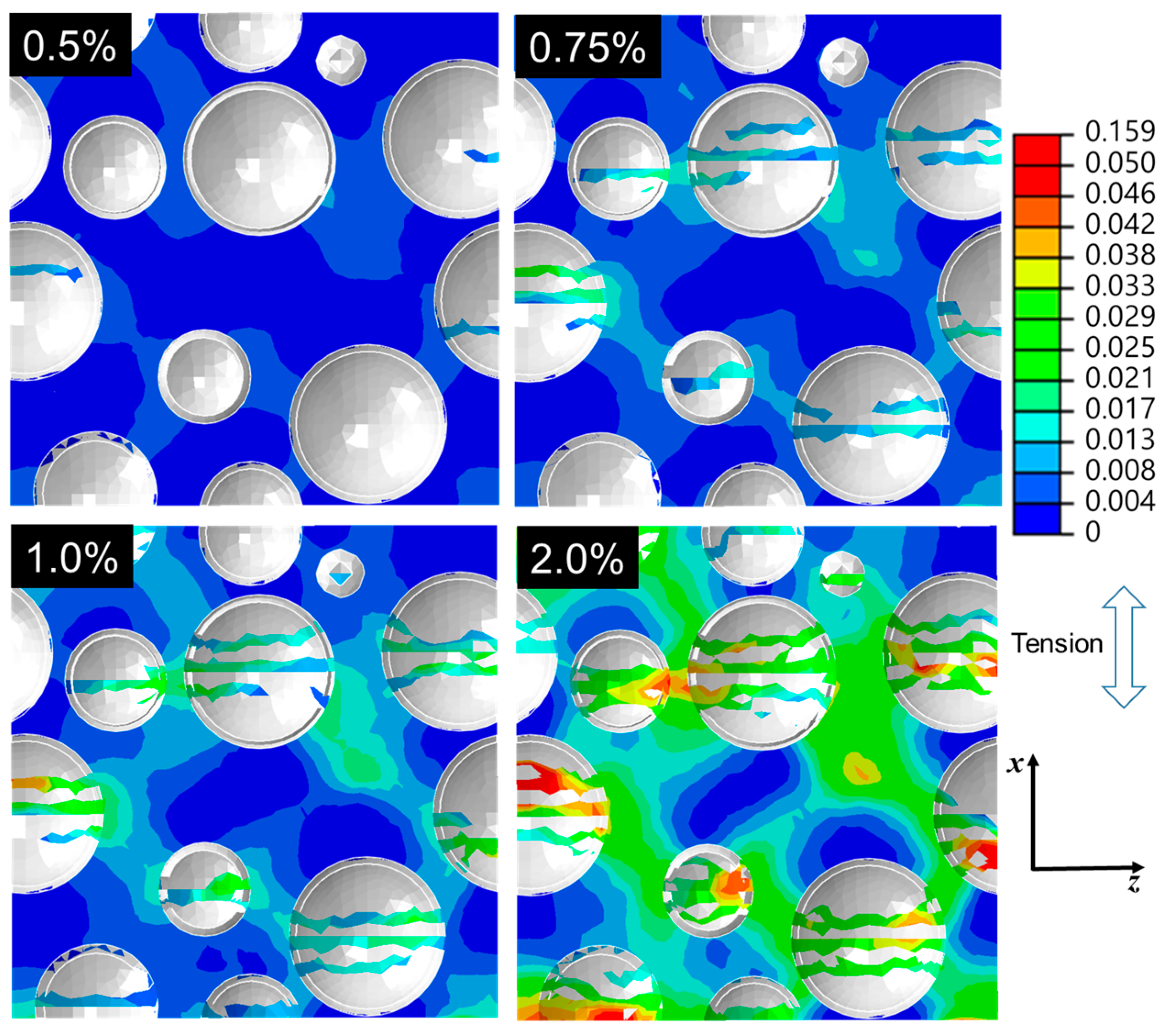
4.2. Tensile Deformation Behaviors
4.3. Discussion
5. Summary and Outlooks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gupta, N.; Rohatgi, P.K. Metal Matrix Syntactic Foams: Processing, Microstructure, Properties and Applications; DEStech Publications Inc.: Lancaster, PA, USA, 2014. [Google Scholar]
- Luong, D.D.; Strbik, O.M., III; Hammond, V.H.; Gupta, N.; Cho, K. Development of high performance lightweight aluminum alloy/SiC hollow sphere syntactic foams and compressive characterization at quasi-static and high strain rates. J. Alloys Compd. 2013, 550, 412–422. [Google Scholar] [CrossRef]
- Mondal, D.P.; Datta Majumder, J.; Jha, N.; Badkul, A.; Das, S.; Patel, A.; Gupta, G. Titanium-cenosphere syntactic foam made through powder metallurgy route. Mater. Des. 2012, 34, 82–89. [Google Scholar] [CrossRef]
- Weise, J.; Salk, N.; Jehring, U.; Baumeister, J.; Lehmhus, D.; Bayoumi, M.A. Influence of Powder Size on Production Parameters and Properties of Syntactic Invar Foams Produced by Means of Metal Powder Injection Moulding. Adv. Eng. Mater. 2013, 15, 118–122. [Google Scholar] [CrossRef]
- Gupta, N.; Luong, D.D.; Cho, K. Magnesium Matrix Composite Foams—Density, Mechanical Properties, and Applications. Metals 2012, 2, 238–252. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Hill, R. A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Bardella, L.; Sfreddo, A.; Ventura, C.; Porfiri, M.; Gupta, N. A critical evaluation of micromechanical models for syntactic foams. Mech. Mater. 2012, 50, 53–69. [Google Scholar] [CrossRef]
- Lee, K.J.; Westmann, R.A. Elastic Properties of Hollow-Sphere-Reinforced Composites. J. Compos. Mater. 1970, 4, 242–252. [Google Scholar] [CrossRef]
- Huang, J.S.; Gibson, L.J. Elastic moduli of a composite of hollow spheres in a matrix. J. Mech. Phys. Solids 1993, 41, 55–75. [Google Scholar] [CrossRef]
- Porfiri, M.; Gupta, N. Effect of volume fraction and wall thickness on the elastic properties of hollow particle filled composites. Compos. Part B Eng. 2009, 40, 166–173. [Google Scholar] [CrossRef]
- Wu, G.H.; Dou, Z.Y.; Sun, D.L.; Jiang, L.T.; Ding, B.S.; He, B.F. Compression behaviors of cenosphere–pure aluminum syntactic foams. Scr. Mater. 2007, 56, 221–224. [Google Scholar] [CrossRef]
- Yu, M.; Zhu, P.; Ma, Y. Effects of particle clustering on the tensile properties and failure mechanisms of hollow spheres filled syntactic foams: A numerical investigation by microstructure based modeling. Mater. Des. 2013, 47, 80–89. [Google Scholar] [CrossRef]
- Weise, J.; Lehmhus, D.; Baumeister, J.; Kun, R.; Bayoumi, M.; Busse, M. Production and Properties of 316L Stainless Steel Cellular Materials and Syntactic Foams. Steel Res. Int. 2014, 85, 486–497. [Google Scholar] [CrossRef]
- Tagliavia, G.; Porfiri, M.; Gupta, N. Analysis of flexural properties of hollow-particle filled composites. Compos. Part B Eng. 2010, 41, 86–93. [Google Scholar] [CrossRef]
- Yu, M.; Zhu, P.; Ma, Y. Experimental study and numerical prediction of tensile strength properties and failure modes of hollow spheres filled syntactic foams. Comput. Mater. Sci. 2012, 63, 232–243. [Google Scholar] [CrossRef]
- Marur, P.R. Numerical estimation of effective elastic moduli of syntactic foams. Finite Elem. Anal. Des. 2010, 46, 1001–1007. [Google Scholar] [CrossRef]
- Bardella, L.; Malanca, F.; Ponzo, P.; Panteghini, A.; Porfiri, M. A micromechanical model for quasi-brittle compressive failure of glass-microballoons/thermoset-matrix syntactic foams. J. Eur. Ceram. Soc. 2014, 34, 2605–2616. [Google Scholar] [CrossRef]
- Huang, R.; Li, P. Elastic behaviour and failure mechanism in epoxy syntactic foams: The effect of glass microballoon volume fractions. Compos. Part B Eng. 2015, 78, 401–408. [Google Scholar] [CrossRef]
- FEE01PAG-01; Kojundo Chemical Laboratory Co., LTD. Available online: http://www.kojundo.jp/msdsjp/FEE01PAG-01.pdf (accessed on 19 October 2017). (In Japanese).
- iM30K 3M™ iM30K Hi-Strength Glass Bubbles; 3M™. Available online: http://multimedia.3m.com/mws/media/491551O/3mtm-im30k-hi-strength-glass-bubbles-tech-info.pdf (accessed on 18 October 2017).
- KSA. Test Pieces for Tensile Test for Metallic Materials; KS B0801; KSA: Seoul, Korea, 26 November 2007. [Google Scholar]
- Widom, B. Random Sequential Addition of Hard Spheres to a Volume. J. Chem. Phys. 1966, 44, 3888–3894. [Google Scholar] [CrossRef]
- Gitman, I.M.; Askes, H.; Sluys, L.J. Representative volume: Existence and size determination. Eng. Fract. Mech. 2007, 74, 2518–2534. [Google Scholar] [CrossRef]
- Bardella, L.; Genna, F. On the elastic behavior of syntactic foams. Int. J. Solids Struct. 2001, 38, 7235–7260. [Google Scholar] [CrossRef]
- Simulia, D.S. ABAQUS. Analysis User’s Manual, version 6.13; Simulia, D.S.: Providence, RI, USA, 2013. [Google Scholar]
- Cho, Y.J.; Lee, W.J.; Park, Y.H. Effect of boundary conditions on plasticity and creep behavior analysis of particle reinforced composites by representative volume element approach. Comput. Mater. Sci. 2015, 100, 67–75. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Hazanov, S.; Amieur, M. On overall properties of elastic heterogeneous bodies smaller than the representative volume. Int. J. Eng. Sci. 1995, 33, 1289–1301. [Google Scholar] [CrossRef]
- Annapragada, S.R.; Sun, D.; Garimella, S.V. Prediction of effective thermo-mechanical properties of particulate composites. Comput. Mater. Sci. 2007, 40, 255–266. [Google Scholar] [CrossRef]
- Huet, C. Application of variational concepts to size effects in elastic heterogeneous bodies. J. Mech. Phys. Solids 1990, 38, 813–841. [Google Scholar] [CrossRef]
- Cho, Y.J.; Lee, W.J.; Park, Y.H. Effect of boundary conditions on the numerical solutions of representative volume element problems for random heterogeneous composite microstructures. Met. Mater. Int. 2014, 20, 1085–1093. [Google Scholar] [CrossRef]
- Yim, S.O.; Lee, W.J.; Cho, D.H.; Park, I.M. Finite element analysis of compressive behavior of hybrid short fiber/particle/mg metal matrix composites using RVE model. Met. Mater. Int. 2015, 21, 408–414. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Wei, D.; Baptiste, D.; Bompard, P.; Francois, D. Cracking and Damage, Strain Localization and Size Effect; Elsevier: New York, NY, USA, 1989. [Google Scholar]
- Bardella, L.; Genna, F. Some Remarks on the Micromechanical Modeling of Glass/Epoxy Syntactic Foams; Ko, F.K., Palmese, G.R., Gogotsi, Y., Wang, A.S.D., Eds.; American Society for Composites: Lancaster, PA, USA, 2005. [Google Scholar]
- Lewandowski, J.J.; Liu, C.; Hunt, W.H., Jr. Effects of matrix microstructure and particle distribution on fracture of an aluminum metal matrix composite. Mater. Sci. Eng. A 1989, 107, 241–255. [Google Scholar] [CrossRef]
- Daoud, A.; Abou El-khair, M.T.; Abdel-Aziz, M.; Rohatgi, P. Fabrication, microstructure and compressive behavior of ZC63 Mg–microballoon foam composites. Compos. Sci. Technol. 2007, 67, 1842–1853. [Google Scholar] [CrossRef]
- Rohatgi, P.K.; Daoud, A.; Schultz, B.F.; Puri, T. Microstructure and mechanical behavior of die casting AZ91D-Fly ash cenosphere composites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 883–896. [Google Scholar] [CrossRef]
- Cho, J.Y.; Kang, Y.; Lee, C.Y.; Park, Y.; Lee, W. Influence of Partially Debonded Interface on Elasticity of Syntactic Foam: A Numerical Study. Materials 2017, 10, 911. [Google Scholar] [CrossRef] [PubMed]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]



| Material | (kg·m−3) | E (GPa) | (MPa) | |
|---|---|---|---|---|
| Iron | 7870 | 198.0 | 0.28 | 155 |
| Glass [24,28] | 2500 | 70.1 | 0.23 | 500–2000 |
| Results | RVE | Experimental | HSupper | VRupper | CS-Based S-C |
|---|---|---|---|---|---|
| E (GPa) | 89.9 | 88.9 | 91.2 | 124.5 | 90.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, Y.J.; Lee, W.; Park, Y.H. Finite Element Modeling of Tensile Deformation Behaviors of Iron Syntactic Foam with Hollow Glass Microspheres. Materials 2017, 10, 1201. https://doi.org/10.3390/ma10101201
Cho YJ, Lee W, Park YH. Finite Element Modeling of Tensile Deformation Behaviors of Iron Syntactic Foam with Hollow Glass Microspheres. Materials. 2017; 10(10):1201. https://doi.org/10.3390/ma10101201
Chicago/Turabian StyleCho, Yi Je, Wookjin Lee, and Yong Ho Park. 2017. "Finite Element Modeling of Tensile Deformation Behaviors of Iron Syntactic Foam with Hollow Glass Microspheres" Materials 10, no. 10: 1201. https://doi.org/10.3390/ma10101201
APA StyleCho, Y. J., Lee, W., & Park, Y. H. (2017). Finite Element Modeling of Tensile Deformation Behaviors of Iron Syntactic Foam with Hollow Glass Microspheres. Materials, 10(10), 1201. https://doi.org/10.3390/ma10101201