Investigation of the Quasi-Brittle Failure of Alashan Granite Viewed from Laboratory Experiments and Grain-Based Discrete Element Modeling
Abstract
1. Introduction
2. Laboratory UCS and BTS Testing
2.1. Sample Preparation and Strength Test Facility
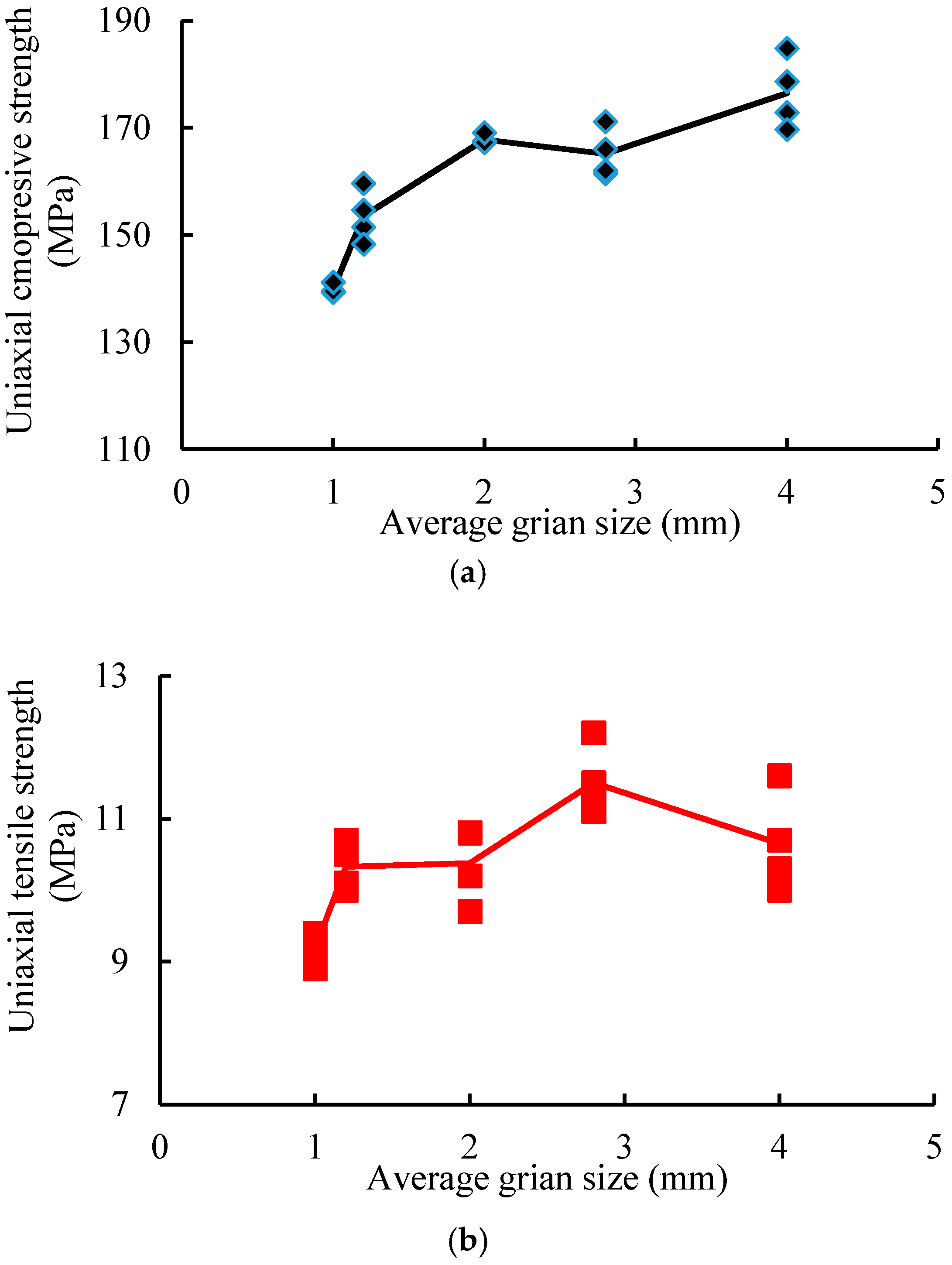
2.2. Experimental Results
3. Numerical Modeling Methodology
3.1. Particle Flow Code
3.2. Grain-Based Model
3.3. Smooth Joint Model
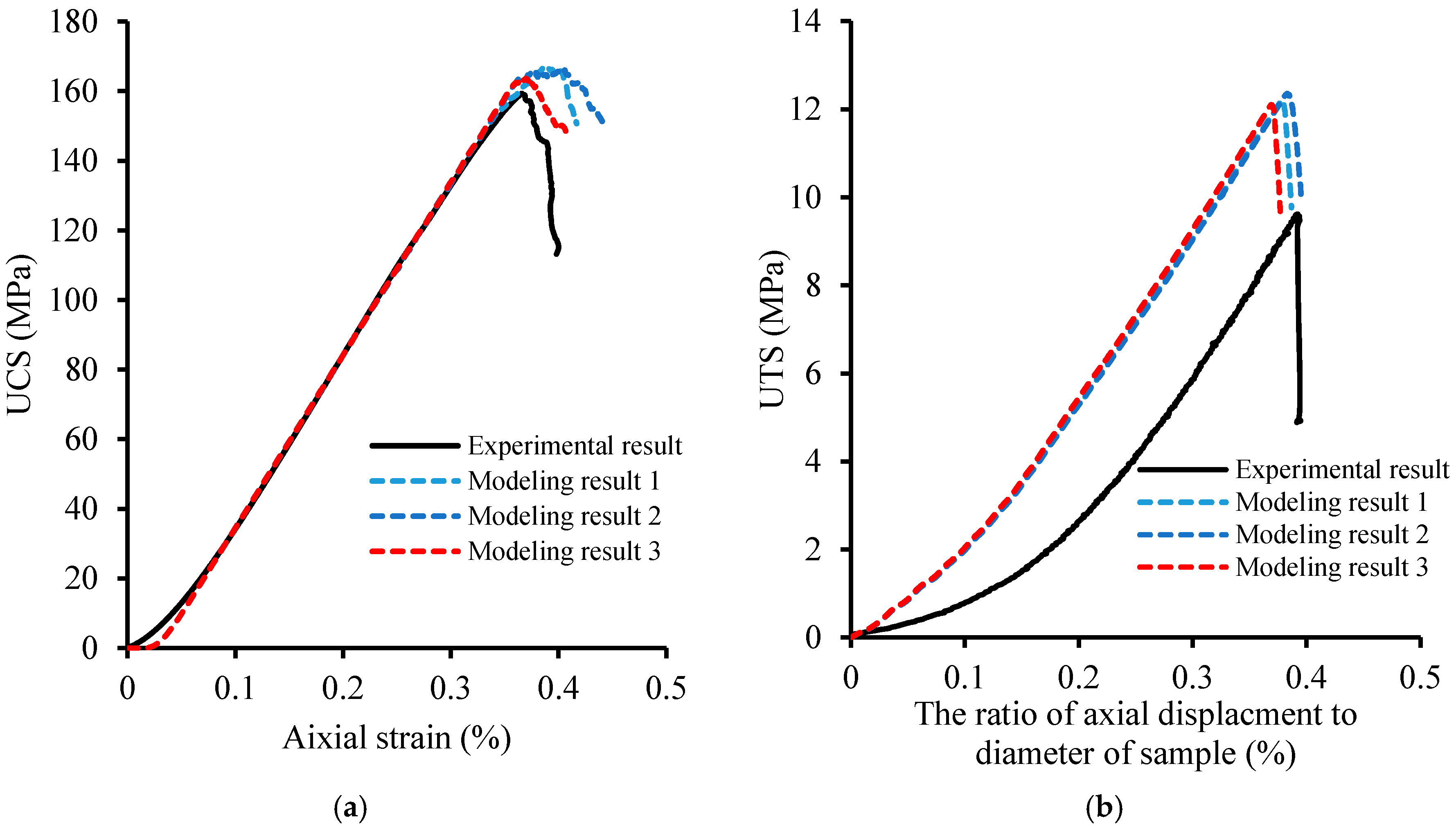
4. Parameter Calibration of Grain-Based Model for Porphyritic Granite
5. Effects of Grain Scale on Granite Strength
5.1. Model Descriptions
5.2. Numerical Strength Testing Results
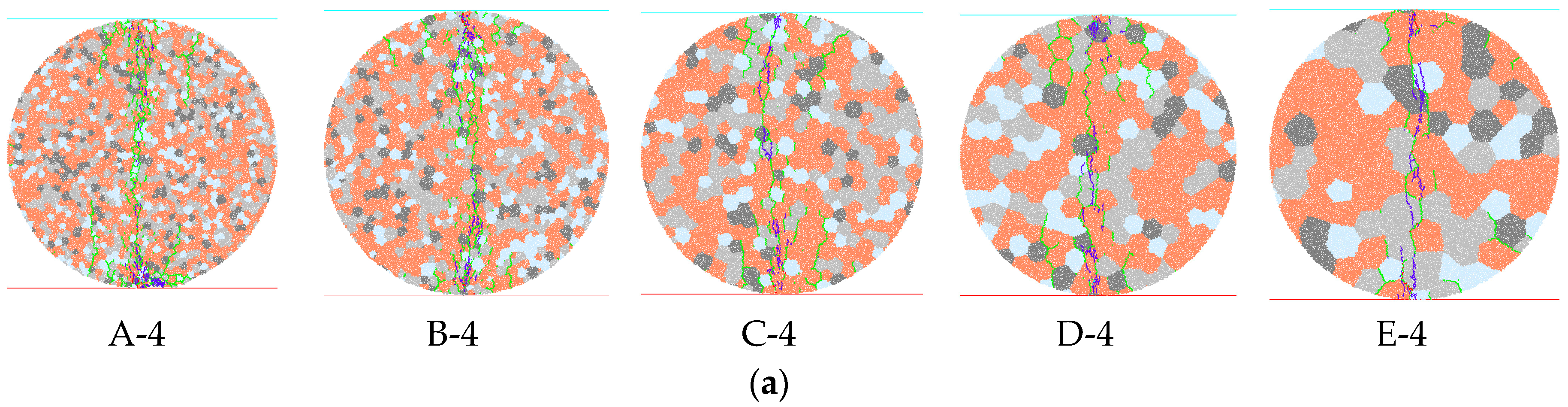
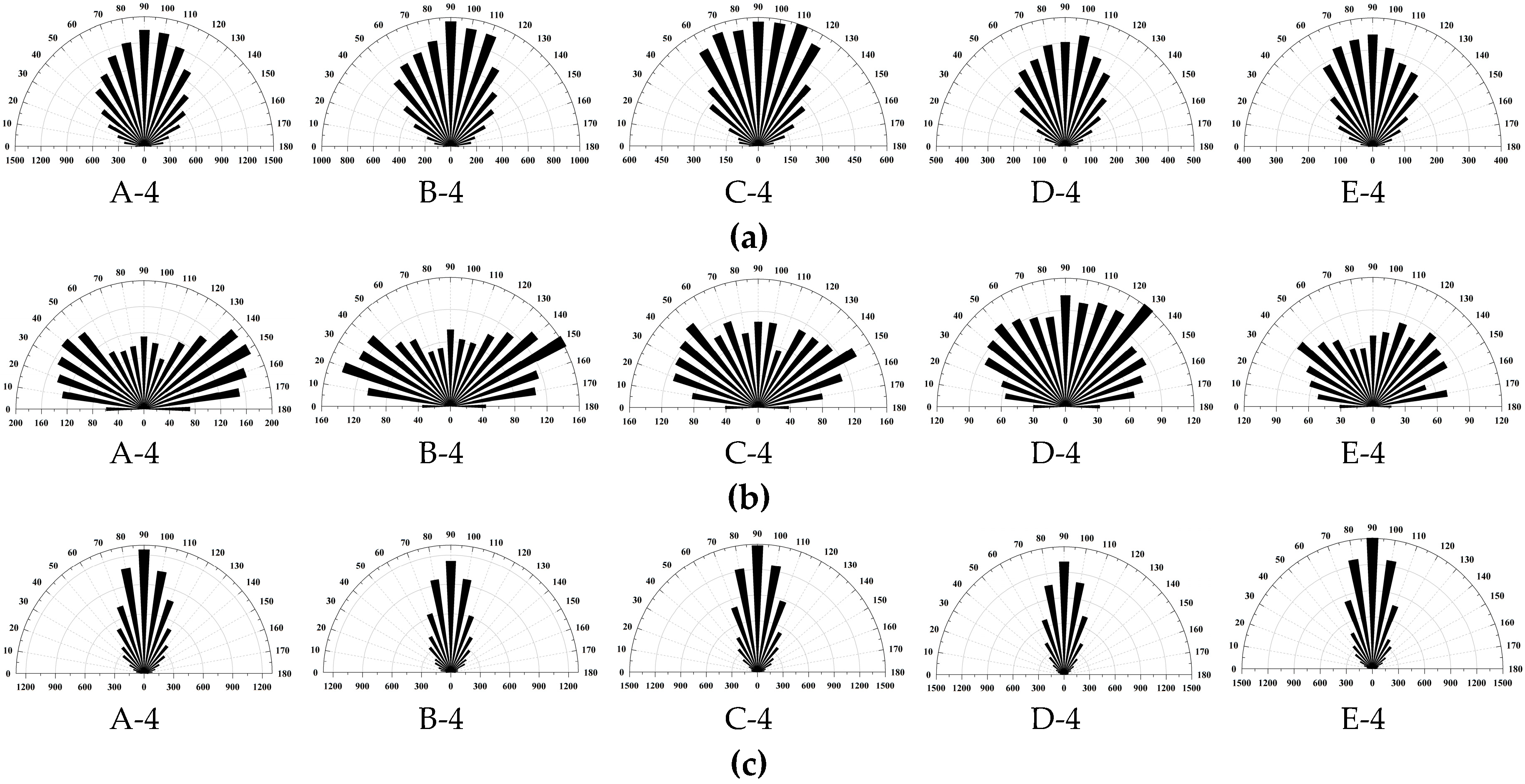
5.3. Patterns of Microcracks
5.4. Discussion
6. Conclusions
- (1)
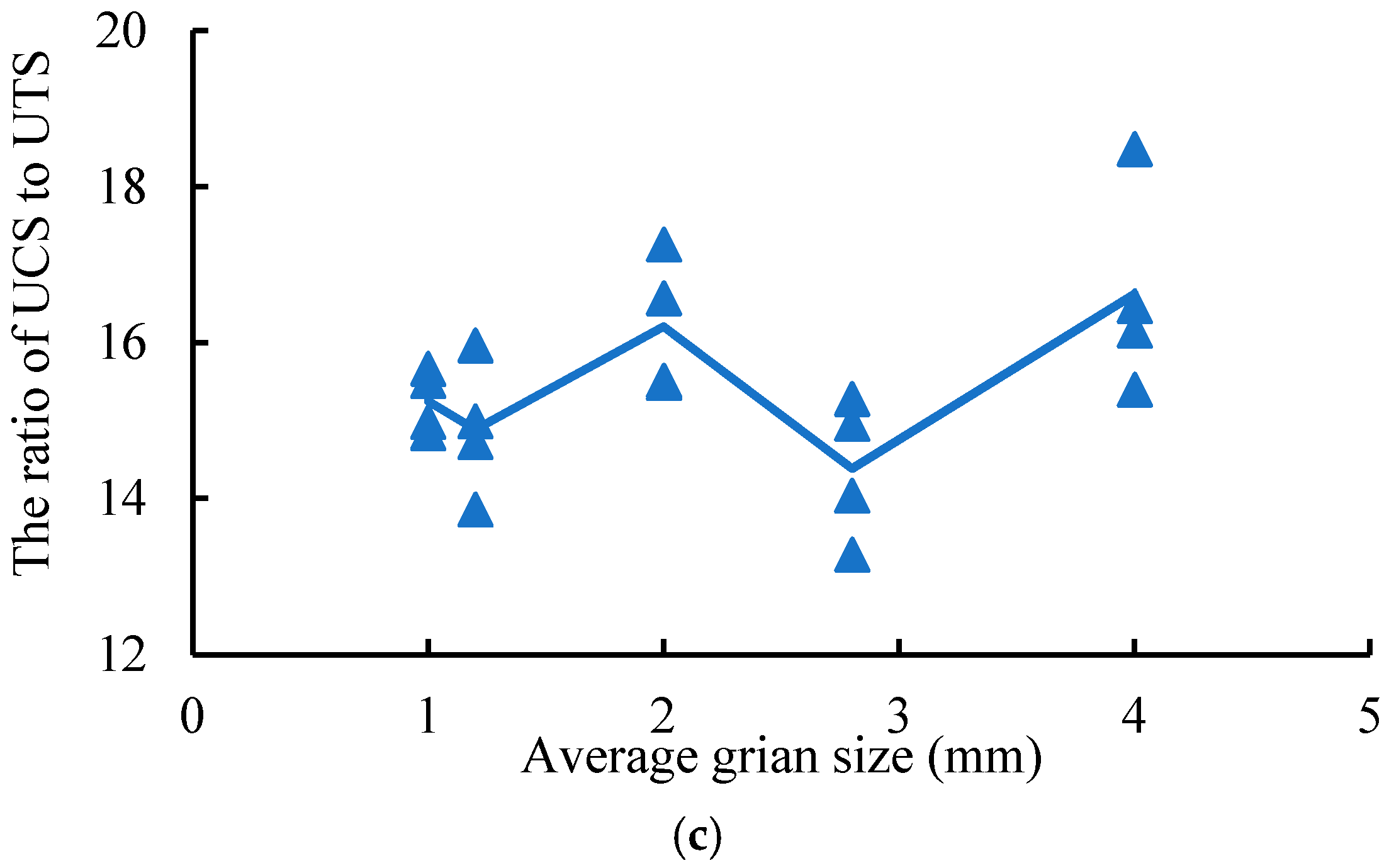
- Using the grain-based approach in PFC2D, it is possible to reproduce the UCS and UTS of Alashan granite. Based on the macroscale mechanical properties of Alashan granite, a successful and valid calibration can be achieved using a model with a height of 8 cm and a width of 4 cm. The modeling results of the ratio of UCS to UTS are in a reasonable range of 10 to 20.
- (2)
- The numerical simulation reveals that the mineral size has a significant influence on the simulated rock strength, and a positive relationship was found between UCS, UTS, and the average mineral diameter in the modeling. This finding may be related to the phenomenon that the direction of fracture propagation is more easily reoriented in the fine grained model than in coarse grained model.
- (3)
- Most of the generated microcracks are tensile cracks both after the UTS and UCS tests. Under the UTS test, with increased average grain size, the number of intragrain microcracks also increases, while the number of intergrain cracks decreases; under uniaxial loading, the ratio of the number of intragrain tensile cracks to the number of intergrain tensile cracks increases as the average grain size increases. The UCS of numerical rock samples is positively related to the ratio of the number of intragrain tensile cracks to the number of intergrain tensile cracks. The variation in grain size distribution has no or minimal influence on the inclination of induced microcracks.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, J.; Chen, W.; Su, R.; Guo, Y.; Jin, Y. Geological disposal of high-level radioactive waste and its key scientific issues. Chin. J. Rock Mech. Eng. 2006, 25, 801–812. [Google Scholar]
- Batchelor, A.S. The stimulation of a hot dry rock geothermal reservoir in the Cornubian Granite, England. In Proceedings of the Eighth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 14 December 1982; pp. 231–248. [Google Scholar]
- Kumari, W.G.P.; Ranjith, P.G.; Perera, M.S.A.; Shao, S.; Chen, B.K.; Lashin, A.; Al Arifi, N.; Rathnaweera, T.D. Mechanical behaviour of Australian Strathbogie granite under in-situ stress and temperature conditions: An application to geothermal energy extraction. Geothermics 2017, 65, 44–59. [Google Scholar] [CrossRef]
- Shao, S.; Wasantha, P.L.P.; Ranjith, P.G.; Chen, B.K. Effect of cooling rate on the mechanical behavior of heated Strathbogie granite with different grain sizes. Int. J. Rock Mech. Min. Sci. 2014, 70, 381–387. [Google Scholar] [CrossRef]
- Willard, R.J.; McWilliams, J.R. Microstructural techniques in the study of physical properties of rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1969, 6, 1–12. [Google Scholar] [CrossRef]
- Irfan, T.Y. Mineralogy, fabric properties and classification of weathered granites in Hong Kong. Q. J. Eng. Geol. Hydrogeol. 1996, 29, 5–35. [Google Scholar] [CrossRef]
- Onodera, T.F.; Asoka Kumara, H.M. Relation between texture and mechanical properties of crystalline rocks. Bull. Int. Assoc. Eng. Geol. 1980, 22, 173–177. [Google Scholar]
- Tuğrul, A.; Zarif, I.H. Correlation of mineralogical and textural characteristics with engineering properties of selected granitic rocks from Turkey. Eng. Geol. 1999, 51, 303–317. [Google Scholar] [CrossRef]
- Lindqvist, J.E.; Åkesson, U.; Malaga, K. Microstructure and functional properties of rock materials. Mater. Charact. 2007, 58, 1183–1188. [Google Scholar] [CrossRef]
- Xia, K.; Nasseri, M.H.B.; Mohanty, B.; Lu, F.; Chen, R.; Luo, S.N. Effects of microstructures on dynamic compression of Barre granite. Int. J. Rock Mech. Min. Sci. 2008, 45, 879–887. [Google Scholar] [CrossRef]
- Yılmaz, N.G.; Goktan, R.M.; Kibici, Y. Relations between some quantitative petrographic characteristics and mechanical strength properties of granitic building stones. Int. J. Rock Mech. Min. Sci. 2011, 48, 506–513. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stimpson, B.; Stead, D. Effects of grain size on the initiation and propagation thresholds of stress-induced brittle fractures. Rock Mech. Rock Eng. 1999, 32, 81–99. [Google Scholar] [CrossRef]
- Merriam, R.; Rieke, H.H.; Kim, Y.C. Tensile strength related to mineralogy and texture of some granitic rocks. Eng. Geol. 1970, 4, 155–160. [Google Scholar] [CrossRef]
- Mendes, F.M.; Aires-Barros, L.; Rodrigues, F.P. The use of modal analysis in the mechanical characterization of rock masses. In Proceedings of the 1st ISRM Congress, Lisbon, Portugal, 25 September–1 October 1966; Volume 1, pp. 217–223. [Google Scholar]
- Brace, W.F.; Paulding, B.W.; Scholz, C.H. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939–3953. [Google Scholar] [CrossRef]
- Sousa, L.M.O. The influence of the characteristics of quartz and mineral deterioration on the strength of granitic dimensional stones. Environ. Earth Sci. 2013, 69, 1333–1346. [Google Scholar] [CrossRef]
- Sajid, M.; Coggan, J.; Arif, M.; Andersen, J.; Rollinson, G. Petrographic features as an effective indicator for the variation in strength of granites. Eng. Geol. 2016, 202, 44–54. [Google Scholar] [CrossRef]
- Yilmaz, N.G.; Karaca, Z.; Goktan, R.M.; Akal, C. Relative brittleness characterization of some selected granitic building stones: Influence of mineral grain size. Constr. Build. Mater. 2009, 23, 370–375. [Google Scholar] [CrossRef]
- Hoek, E.; Bieniawski, Z.T. Fracture propagation mechanism in hard rock. In Proceedings of the First Congress of the International Society for Rock Mechanics, Lisbon, Portugal, 25 September–1 October 1966; Volume 1, pp. 243–249. [Google Scholar]
- Ahrens, T.J.; Rubin, A.M. Impact-induced tensional failure in rock. J. Geophys. Res. E 1993, 98, 1185–1203. [Google Scholar] [CrossRef]
- Li, C.; Prikryl, R.; Nordlund, E. The stress–strain behavior of rock material related to fracture under compression. Eng. Geol. 1998, 49, 293–302. [Google Scholar] [CrossRef]
- Rigopoulos, I.; Tsikouras, B.; Pomonis, P.; Hatzipanagiotou, K. Petrographic investigation of microcrack initiation in mafic ophiolitic rocks under uniaxial compression. Rock Mech. Rock Eng. 2013, 46, 1061–1072. [Google Scholar] [CrossRef]
- Yushi, Z.; Shicheng, Z.; Tong, Z.; Xiang, Z.; Tiankui, G. Experimental investigation into hydraulic fracture network propagation in gas shales using CT scanning technology. Rock Mech. Rock Eng. 2016, 49, 33–45. [Google Scholar] [CrossRef]
- Geraud, Y.; Mazerolle, F.; Raynaud, S.; Lebon, P. Crack location in granitic samples submitted to heating, low confining pressure and axial loading. Geophys. J. Int. 1998, 133, 553–567. [Google Scholar] [CrossRef]
- Sufian, A.; Russell, A.R. Microstructural pore changes and energy dissipation in Gosford sandstone during pre-failure loading using X-ray CT. Int. J. Rock Mech. Min. Sci. 2013, 57, 119–131. [Google Scholar] [CrossRef]
- Akesson, U.; Hansson, J.; Stigh, J. Characterisation of microcracks in the Bohus granite, western Sweden, caused by uniaxial cyclic loading. Eng. Geol. 2004, 72, 131–142. [Google Scholar] [CrossRef]
- Janssen, C.; Wagner, F.; Zang, A.; Dresen, G. Fracture process zone in granite: A microstructural analysis. Int. J. Earth Sci. 2001, 90, 46–59. [Google Scholar] [CrossRef]
- Fujii, Y.; Takemura, T.; Takahashi, M.; Lin, W. Surface features of uniaxial tensile fractures and their relation to rock anisotropy in Inada granite. Int. J. Rock Mech. Min. Sci. 2007, 44, 98–107. [Google Scholar] [CrossRef]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Chen, H.; Lin, E.; Liu, Y. A novel Volume-Compensated Particle method for 2D elasticity and plasticity analysis. Int. J. Solids Struct. 2014, 51, 1819–1833. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, Y.; Liu, Y. Investigating the microstructural effect on elastic and fracture behavior of polycrystals using a nonlocal lattice particle model. Mater. Sci. Eng. A 2015, 631, 173–180. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive, large-scale movements in blocky rock systems. In Proceedings of the International Symposium on Rock Fracture, Nancy, France, 4–6 October 1971. [Google Scholar]
- Lan, H.; Martin, C.D.; Hu, B. Effect of heterogeneity of brittle rock on micromechanical extensile behavior during compression loading. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Nicksiar, M.; Martin, C.D. Factors affecting crack initiation in low porosity crystalline rocks. Rock Mech. Rock Eng. 2014, 47, 1165–1181. [Google Scholar] [CrossRef]
- Potyondy, D.O. A grain-based model for rock: Approaching the true microstructure. In Proceedings of the Rock Mechanics in the Nordic Countries, Kongsberg, Norway, 9–12 June 2010; pp. 225–234. [Google Scholar]
- Bewick, R.P.; Kaiser, P.K.; Bawden, W.F.; Bahrani, N. DEM simulation of direct shear: 1. Rupture under constant normal stress boundary conditions. Rock Mech. Rock Eng. 2014, 47, 1647–1671. [Google Scholar] [CrossRef]
- Bewick, R.P.; Kaiser, P.K.; Bawden, W.F. DEM simulation of direct shear: 2. Grain boundary and mineral grain strength component influence on shear rupture. Rock Mech. Rock Eng. 2014, 47, 1673–1692. [Google Scholar] [CrossRef]
- Hofmann, H.; Babadagli, T.; Yoon, J.S.; Zang, A.; Zimmermann, G. A grain based modeling study of mineralogical factors affecting strength, elastic behavior and micro fracture development during compression tests in granites. Eng. Fract. Mech. 2015, 147, 261–275. [Google Scholar] [CrossRef]
- Hofmann, H.; Babadagli, T.; Zimmermann, G. A grain based modeling study of fracture branching during compression tests in granites. Int. J. Rock Mech. Min. Sci. 2015, 77, 152–162. [Google Scholar] [CrossRef]
- Bahrani, N.; Kaiser, P.K.; Valley, B. Distinct element method simulation of an analogue for a highly interlocked, non-persistently jointed rockmass. Int. J. Rock Mech. Min. Sci. 2014, 71, 117–130. [Google Scholar] [CrossRef]
- Bahrani, N.; Kaiser, P.K. Numerical investigation of the influence of specimen size on the unconfined strength of defected rocks. Comput. Geotech. 2016, 77, 56–67. [Google Scholar] [CrossRef]
- Peng, J.; Wong, L.N.Y.; Teh, C.I. Influence of grain size heterogeneity on strength and microcracking behavior of crystalline rocks. J. Geophys. Res. Solid Earth 2017, 122, 1054–1073. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Han, J.G.; Meng, E.G.; Zhang, Y.K. Features and tectonic significance of Saili super-unit in Bayinnuorigong area of Alashan Banner, Inner Mongolia. Geol. Min. Resour. South China 2003, 2, 36–41. (In Chinese) [Google Scholar]
- Yuan, W.; Yang, Z. The Alashan Terrane was not part of North China by the Late Devonian: Evidence from detrital zircon U–Pb geochronology and Hf isotopes. Gondwana Res. 2015, 27, 1270–1282. [Google Scholar] [CrossRef]
- International Society for Rock Mechanics (ISRM). Suggested methods for determining tensile strength of rock materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 99–103. [Google Scholar]
- Fairhurst, C.E.; Hudson, J.A. Draft ISRM suggested method for the complete stress–strain curve for intact rock in uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 279–289. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.C.; Mitra, R.; Hebblewhite, B.K. Parametric study of smooth joint parameters on the shear behaviour of rock joints. Rock Mech. Rock Eng. 2015, 48, 923–940. [Google Scholar] [CrossRef]
- PFC2D—Particle Flow Code in 2 Dimensions; Version 5.0; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2014.
- Jing, L.; Stephansson, O. Fundamentals of Discrete Element Methods for Rock Engineering: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Asadi, M.S.; Rasouli, V.; Barla, G. A bonded particle model simulation of shear strength and asperity degradation for rough rock fractures. Rock Mech. Rock Eng. 2012, 45, 649–675. [Google Scholar] [CrossRef]
- Park, J.W.; Song, J.J. Numerical method for the determination of contact areas of a rock joint under normal and shear loads. Int. J. Rock Mech. Min. Sci. 2013, 58, 8–22. [Google Scholar] [CrossRef]
- Pierce, M.; Cundall, P.; Potyondy, D.; Ivars, D.M. A synthetic rock mass model for jointed rock. In Proceedings of the 1st Canada-US Rock Mechanics Symposium, Vancouver, BC, Canada, 27–31 May 2007; Volume 1, pp. 341–349. [Google Scholar]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Cai, M. Practical estimates of tensile strength and Hoek–Brown strength parameter mi of brittle rocks. Rock Mech. Rock Eng. 2010, 43, 167–184. [Google Scholar] [CrossRef]



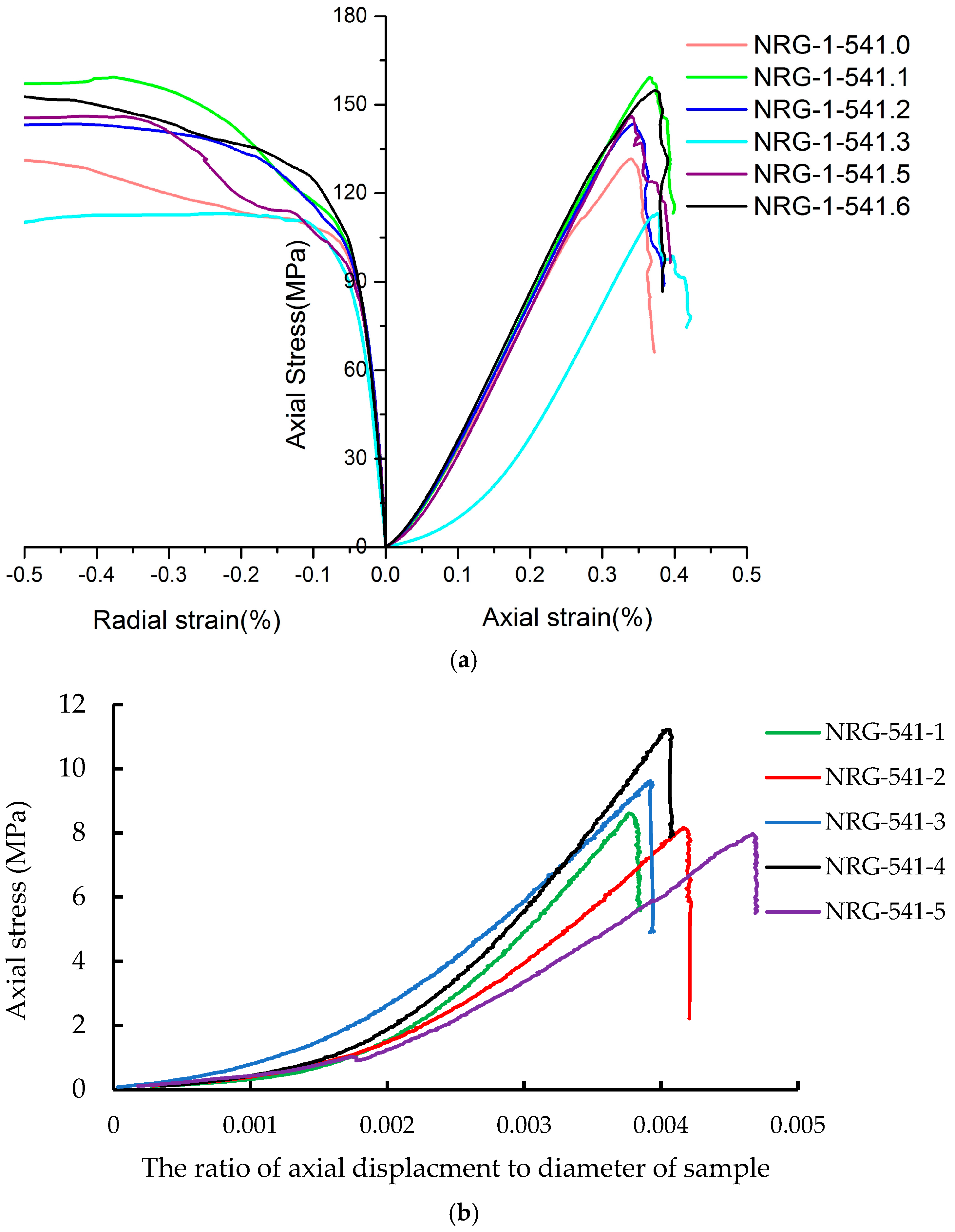


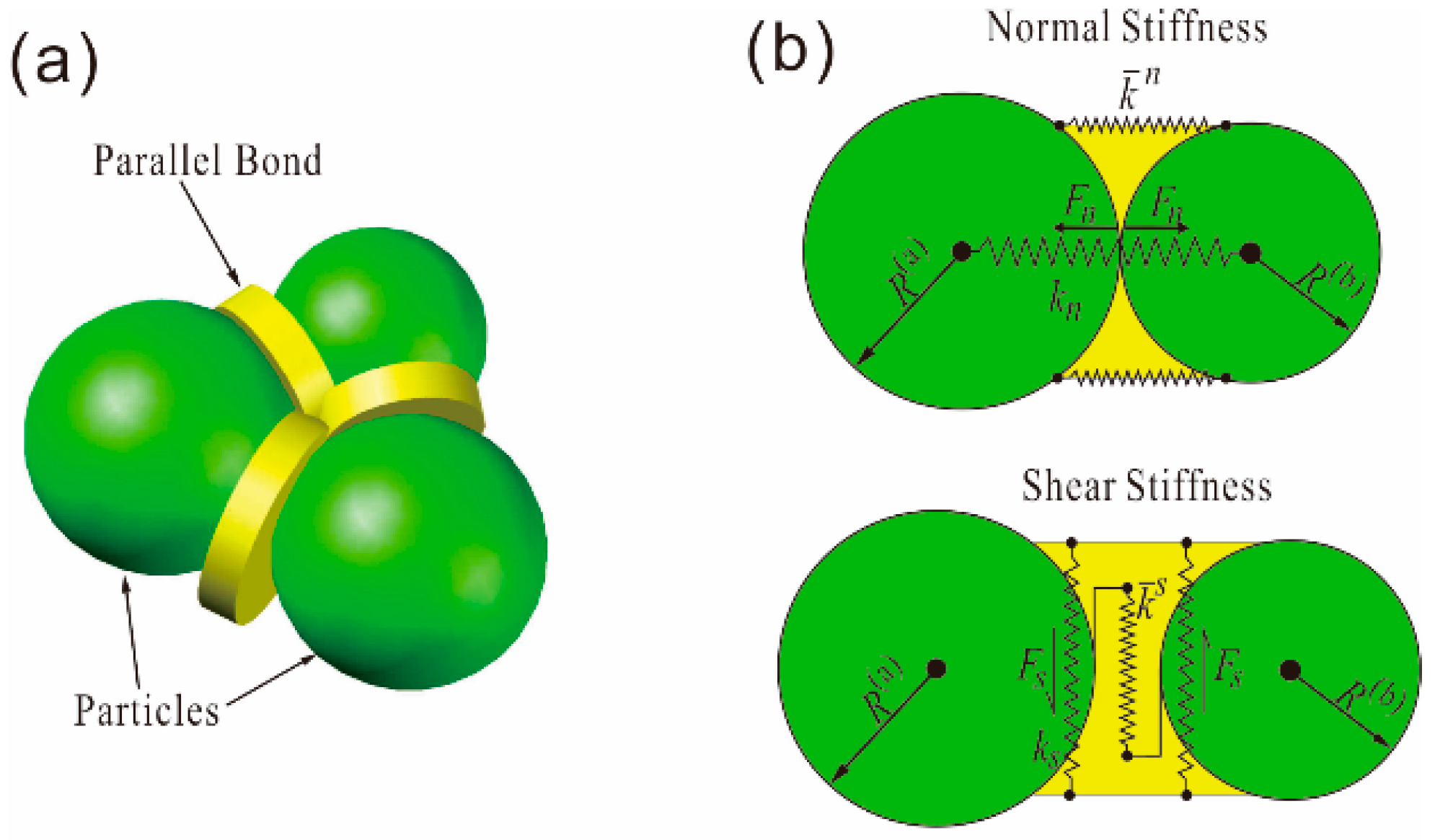
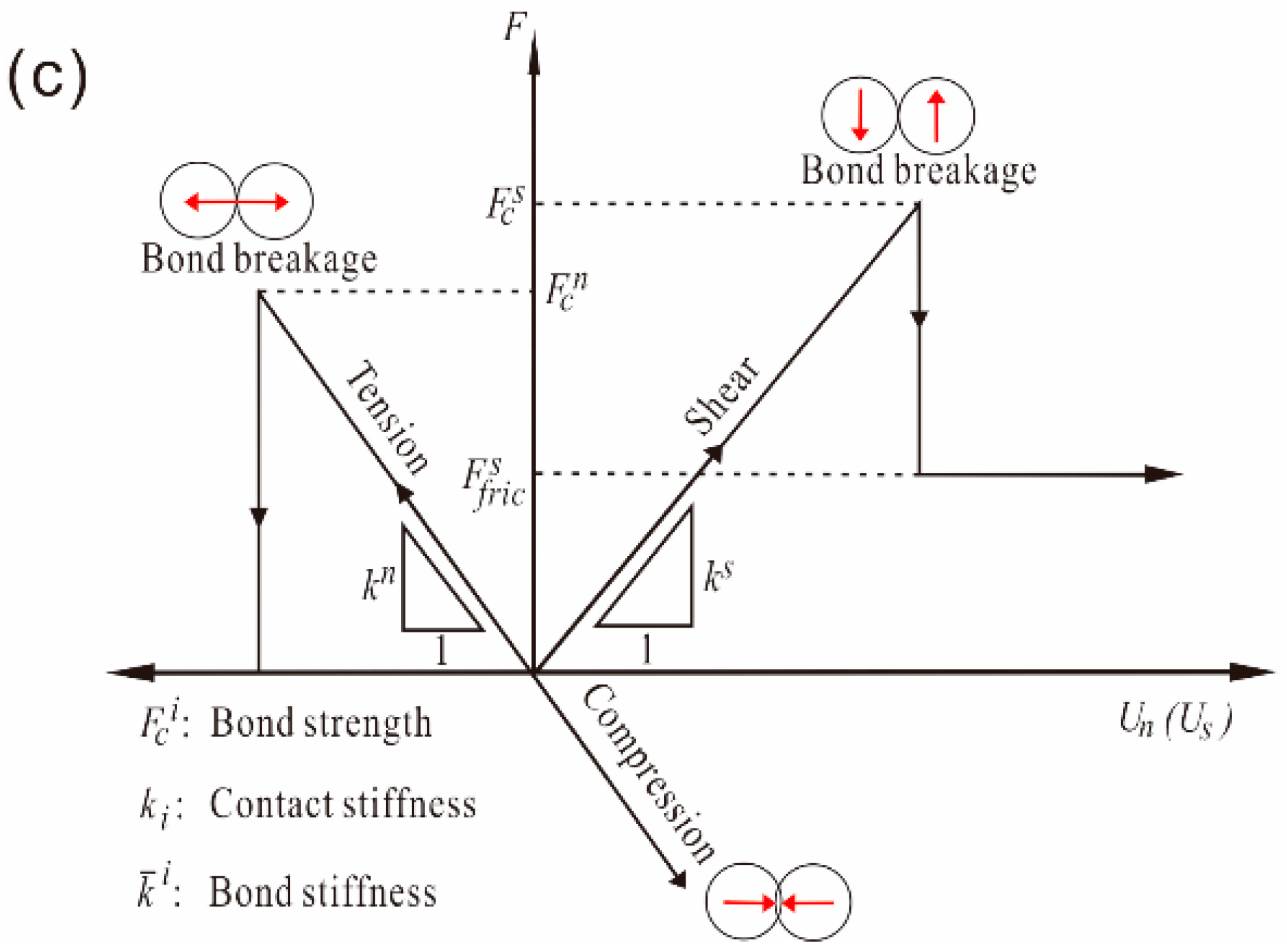
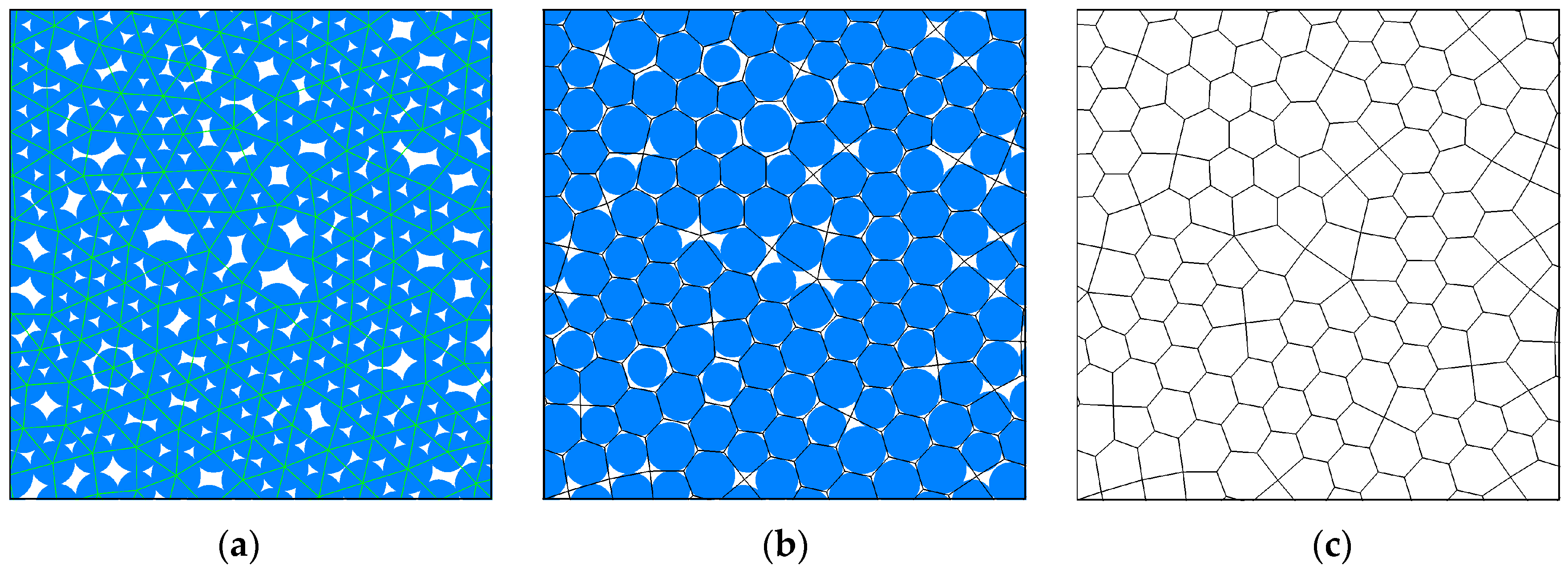
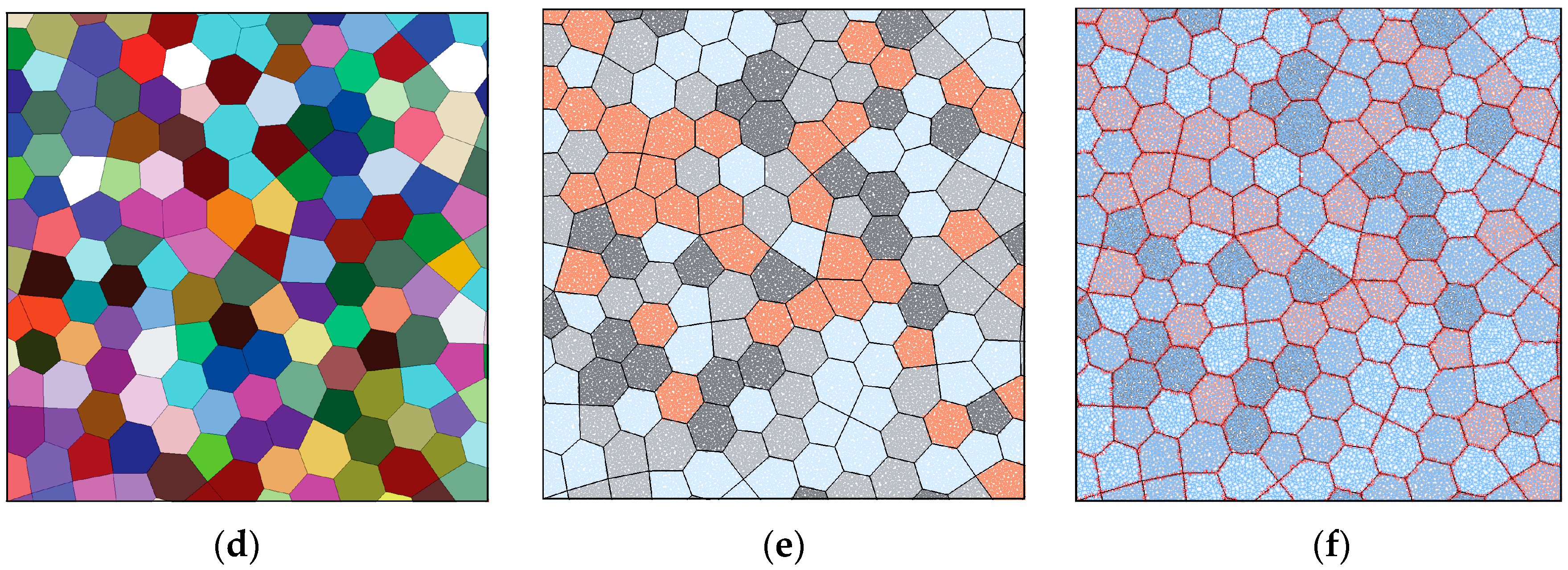
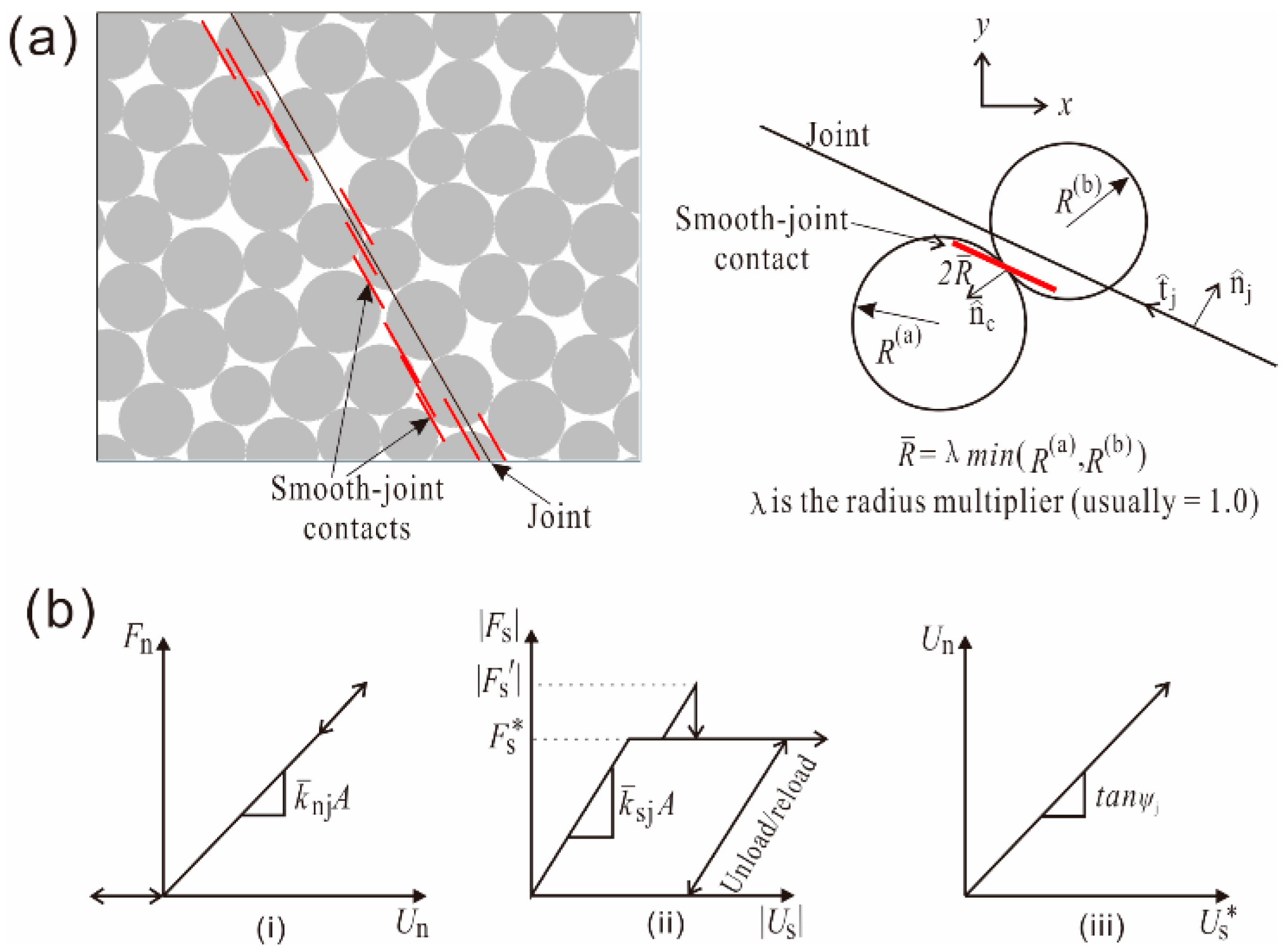
| Input Microparameters | Values | |||
|---|---|---|---|---|
| Quartz | Alkila-Feldspar | Plagioclase | Biotite | |
| Mmicroparameters for minerals | ||||
| Minimum particle radius, Rmin (mm) | 0.1 | 0.1 | 0.1 | 0.1 |
| Ratio of particle radius, Rmax/Rmin | 1.55 | 1.55 | 1.55 | 1.55 |
| Particle density, ρ (kg/m3) | 2600 | 2650 | 2650 | 2850 |
| Modulus of the particle, Ec (GPa) | 60 | 45 | 40 | 23 |
| Contact normal to shear stiffness ratio, kn/ks | 1 | 2 | 2 | 3 |
| Friction coefficient of particle, μ | 0.8 | 0.8 | 0.8 | 0.8 |
| Parallel bond Modulus, (GPa) | 60 | 45 | 40 | 23 |
| Parallel bond normal to shear stiffness ratio, | 1 | 2 | 2 | 3 |
| Parallel bond tensile strength, (MPa) | 50 | 45 | 45 | 40 |
| Parallel bond shear strength, (MPa) | 90 | 113 | 113 | 125 |
| Parallel bond friction angle, (°) | 50 | 48 | 48 | 45 |
| Parallel bond radius multiplier, | 1 | 1 | 1 | 1 |
| Moment contribution factor, | 0.2 | 0.2 | 0.2 | 0.2 |
| Mmicroparameters for mineral boundaries (Smooth joint contact) | ||||
| SJM bond normal stiffness factor | 0.5 | |||
| SJM bond shear stiffness factor | 0.8 | |||
| SJM bond tensile strength, (MPa) | 10 | |||
| SJM bond cohesion, (MPa) | 60 | |||
| SJM bond friction angle, (°) | 40 | |||
| SJM bond friction coefficient, μ’ | 0.8 | |||
| Sample | Average Grainsize (mm) | Uniaxial Compressive Strength (MPa) | Brazilian Tensile Strength (MPa) |
|---|---|---|---|
| A-1 | 1.0 | 139.4 | 8.9 |
| A-2 | 1.0 | 139.3 | 9.3 |
| A-3 | 1.0 | 139.5 | 9.4 |
| A-4 | 1.0 | 141.1 | 9.1 |
| B-1 | 1.2 | 151.4 | 10.1 |
| B-2 | 1.2 | 154.6 | 10.5 |
| B-3 | 1.2 | 159.6 | 10.0 |
| B-4 | 1.2 | 148.3 | 10.7 |
| C-1 | 2.0 | 167.5 | 10.8 |
| C-2 | 2.0 | 167.4 | 9.7 |
| C-3 | 2.0 | 167.2 | 10.8 |
| C-4 | 2.0 | 169.0 | 10.2 |
| D-1 | 2.8 | 161.4 | 11.5 |
| D-2 | 2.8 | 166.0 | 11.1 |
| D-3 | 2.8 | 162.0 | 12.2 |
| D-4 | 2.8 | 171.1 | 11.2 |
| E-1 | 4.0 | 172.8 | 10.7 |
| E-2 | 4.0 | 184.8 | 10.0 |
| E-3 | 4.0 | 178.6 | 11.6 |
| E-4 | 4.0 | 169.6 | 10.3 |
| Sample | Test Modeling | Number of Different Types of Microcracks | |||
|---|---|---|---|---|---|
| Intragrain Shear Cracks | Intragrain Tensile Cracks | Intergrain Shear Cracks | Intergrain Tensile Cracks | ||
| A-4 | BTT | 2 | 315 | 40 | 1503 |
| B-4 | BTT | 1 | 301 | 29 | 1168 |
| C-4 | BTT | 0 | 270 | 21 | 1053 |
| D-4 | BTT | 6 | 331 | 11 | 1011 |
| E-4 | BTT | 3 | 385 | 36 | 620 |
| A-4 | UCT | 51 | 7977 | 2420 | 13,219 |
| B-4 | UCT | 68 | 6994 | 1922 | 9331 |
| C-4 | UCT | 133 | 8485 | 1910 | 5998 |
| D-4 | UCT | 74 | 6993 | 1560 | 4085 |
| E-4 | UCT | 174 | 8252 | 1237 | 3298 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Zhang, L.; Yang, D.; Braun, A.; Han, Z. Investigation of the Quasi-Brittle Failure of Alashan Granite Viewed from Laboratory Experiments and Grain-Based Discrete Element Modeling. Materials 2017, 10, 835. https://doi.org/10.3390/ma10070835
Zhou J, Zhang L, Yang D, Braun A, Han Z. Investigation of the Quasi-Brittle Failure of Alashan Granite Viewed from Laboratory Experiments and Grain-Based Discrete Element Modeling. Materials. 2017; 10(7):835. https://doi.org/10.3390/ma10070835
Chicago/Turabian StyleZhou, Jian, Luqing Zhang, Duoxing Yang, Anika Braun, and Zhenhua Han. 2017. "Investigation of the Quasi-Brittle Failure of Alashan Granite Viewed from Laboratory Experiments and Grain-Based Discrete Element Modeling" Materials 10, no. 7: 835. https://doi.org/10.3390/ma10070835
APA StyleZhou, J., Zhang, L., Yang, D., Braun, A., & Han, Z. (2017). Investigation of the Quasi-Brittle Failure of Alashan Granite Viewed from Laboratory Experiments and Grain-Based Discrete Element Modeling. Materials, 10(7), 835. https://doi.org/10.3390/ma10070835






