Fault Diagnosis for Rolling Bearings under Variable Conditions Based on Visual Cognition
Abstract
:1. Introduction
2. Related Theories
2.1. Recurrence Plot
2.1.1. Recurrence Plot Theory
- (1)
- For the time series , whose sample interval is , we choose the Mutual Information Method and CAO algorithm to calculate the suitable embedding dimensionality and delay time , which could reconstitute the time series. The reconstructed time series is as follows:
- (2)
- Calculate the norm (e.g., the Euclidean norm) of and in reconstructed phase space [33]:
- (3)
- Calculate the recurrence value [34]:where is a predefined cut-off distance and is a Heaviside function:
- (4)
- Utilize a coordinate graph with an abscissa of and ordinate of to draw , where and are the labels of the time series, and the image is an RP.
2.1.2. Comparison between Recurrence Plot and Bi-spectrum
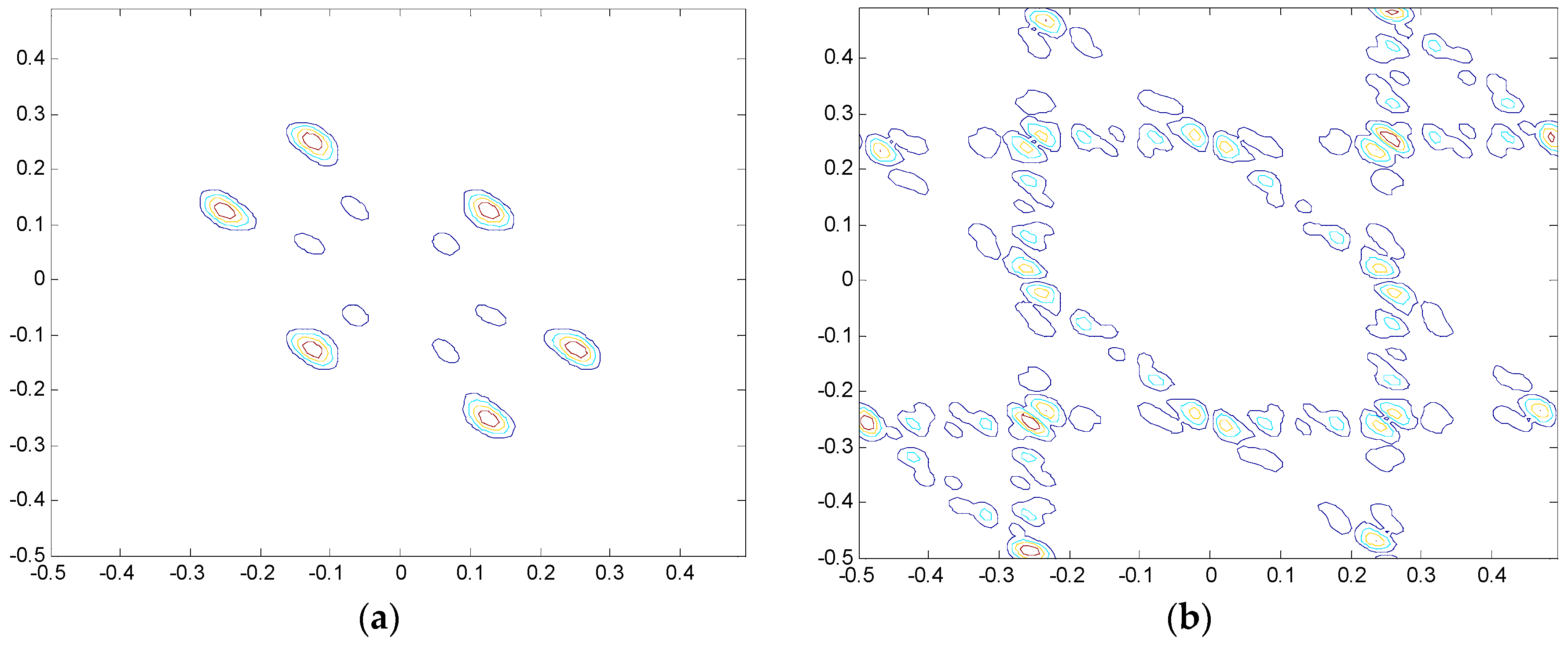
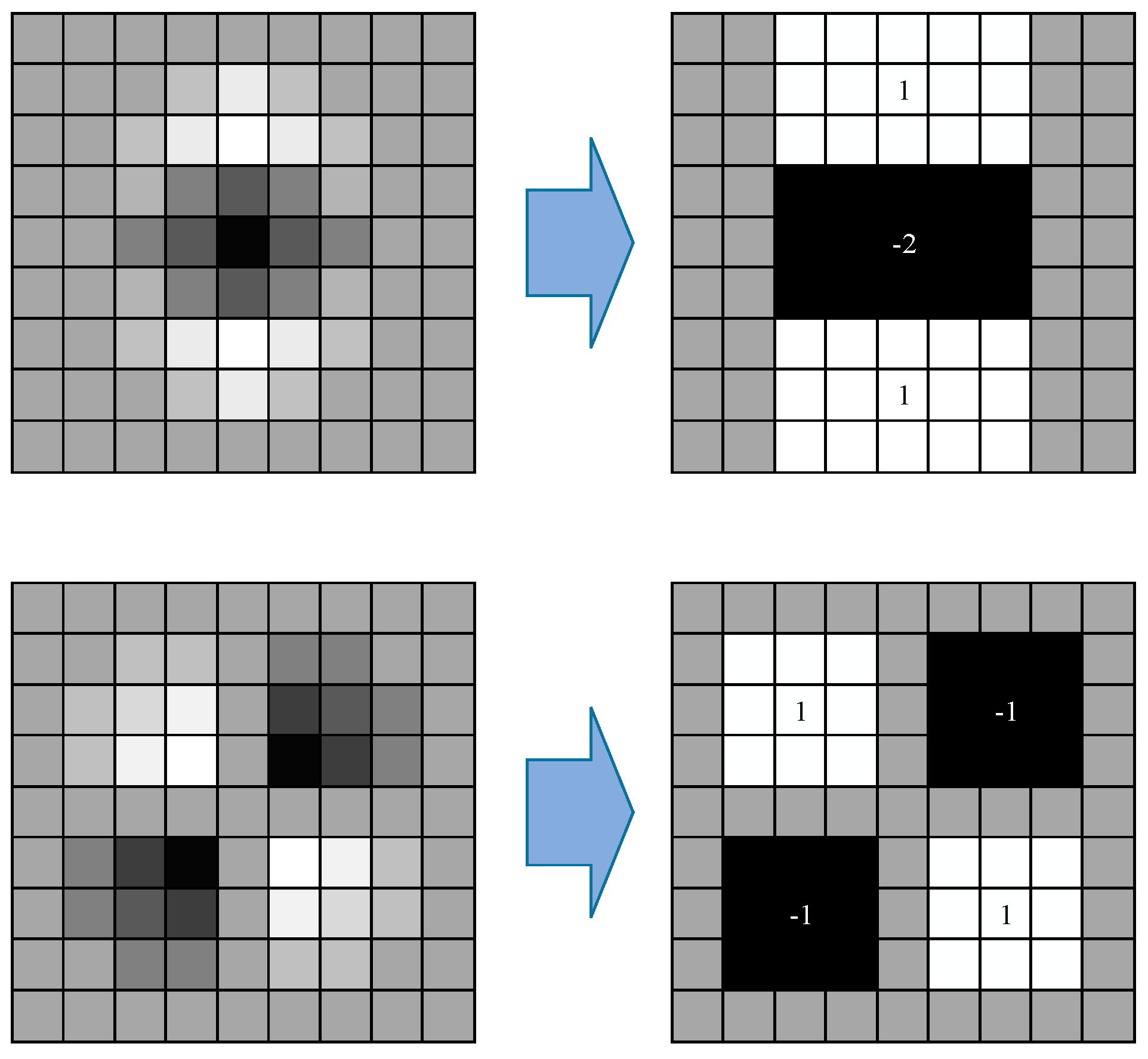
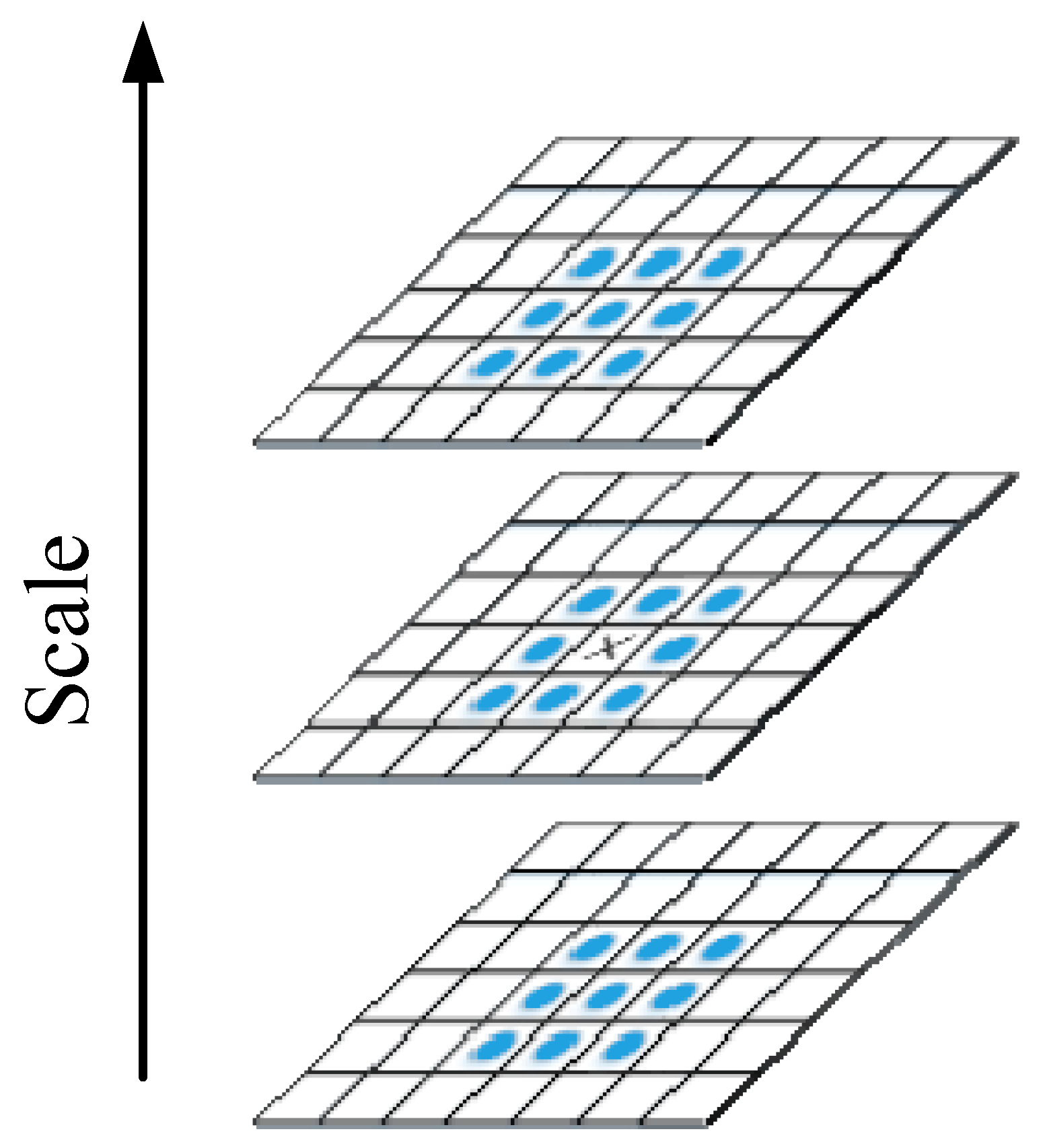
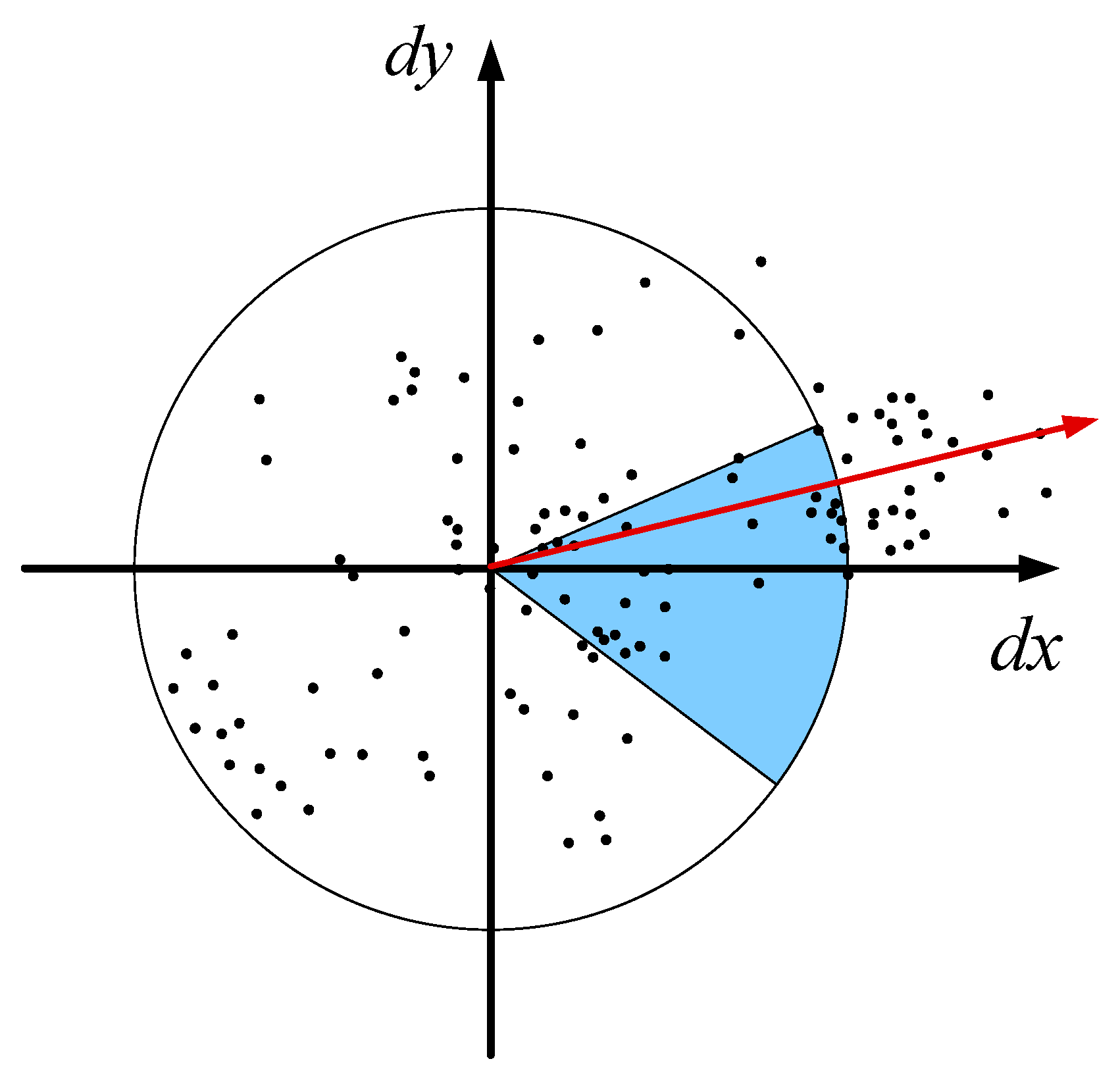
2.2. VIC of the HVS and SURF
2.2.1. VIC Theory
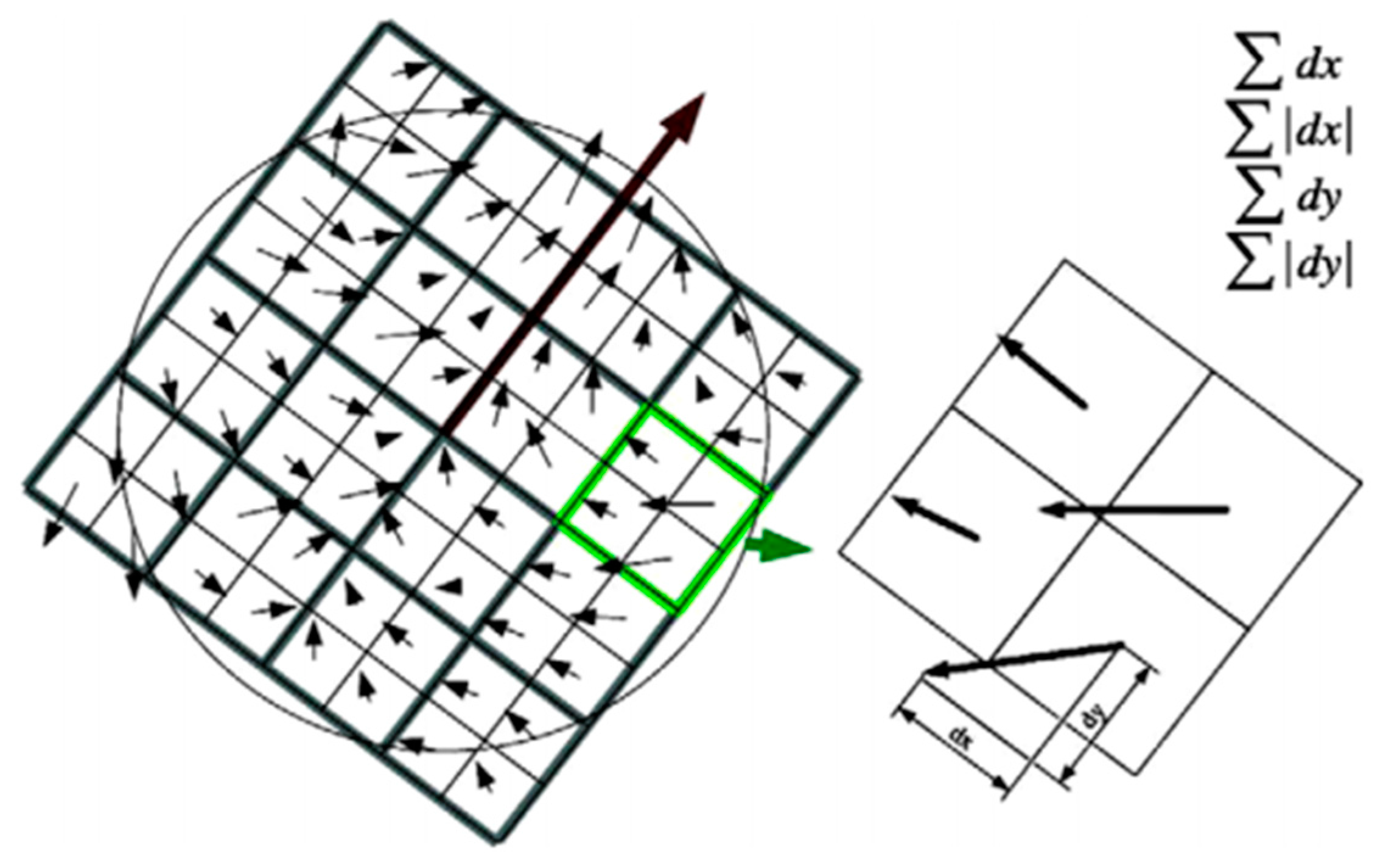
2.2.2. SURF Theory
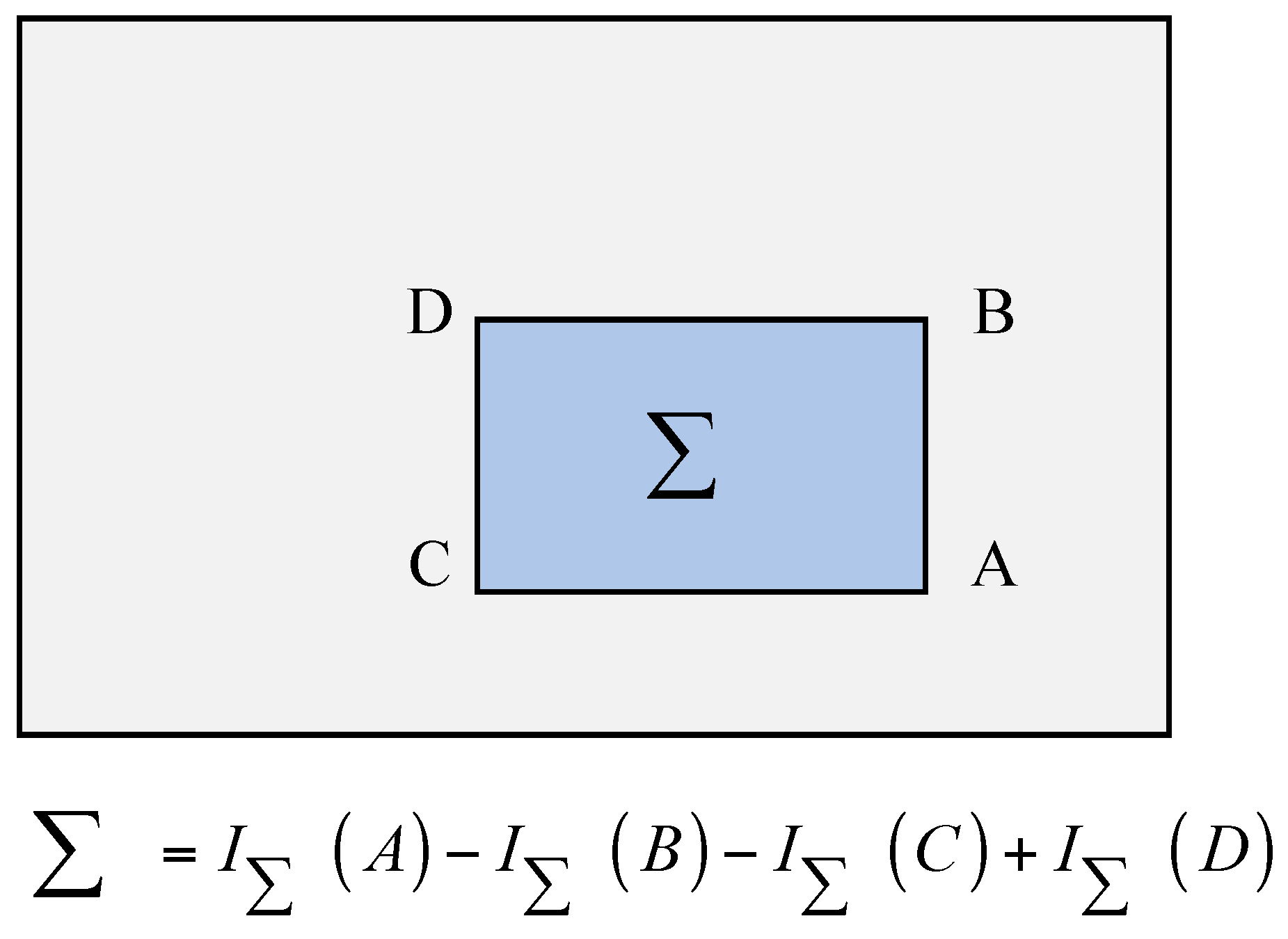
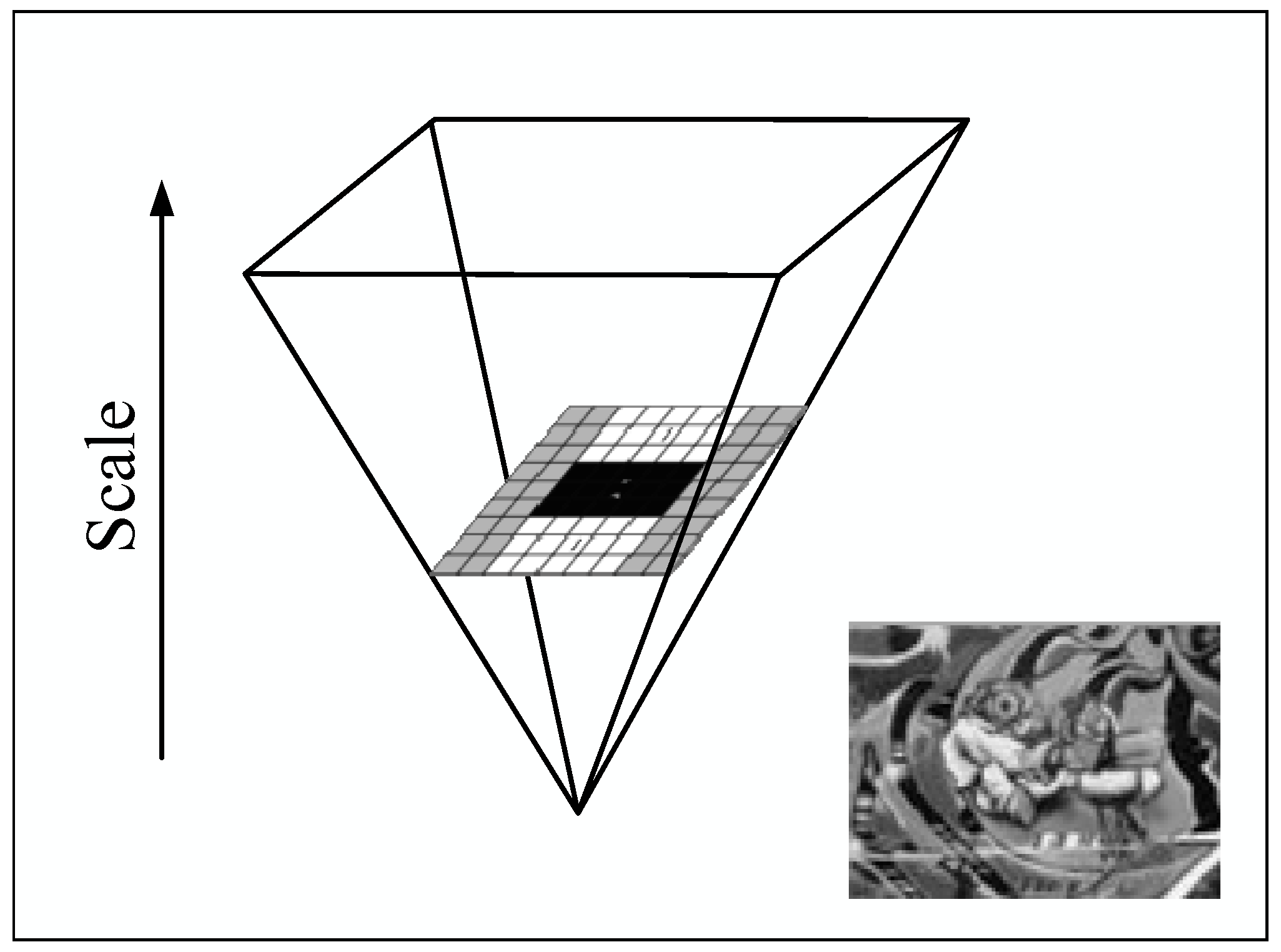
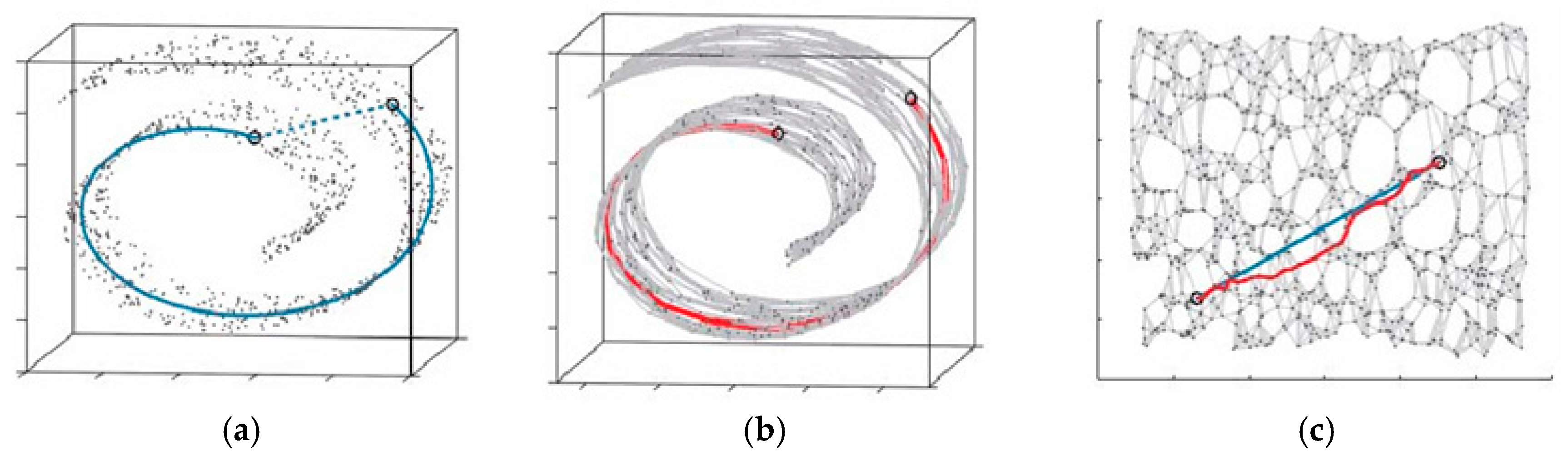
2.3. MPC of the HVS and Isomap
2.3.1. MPC and Manifold Learning
2.3.2. Isomap Theory
2.4. Insprition from Visual Cognition
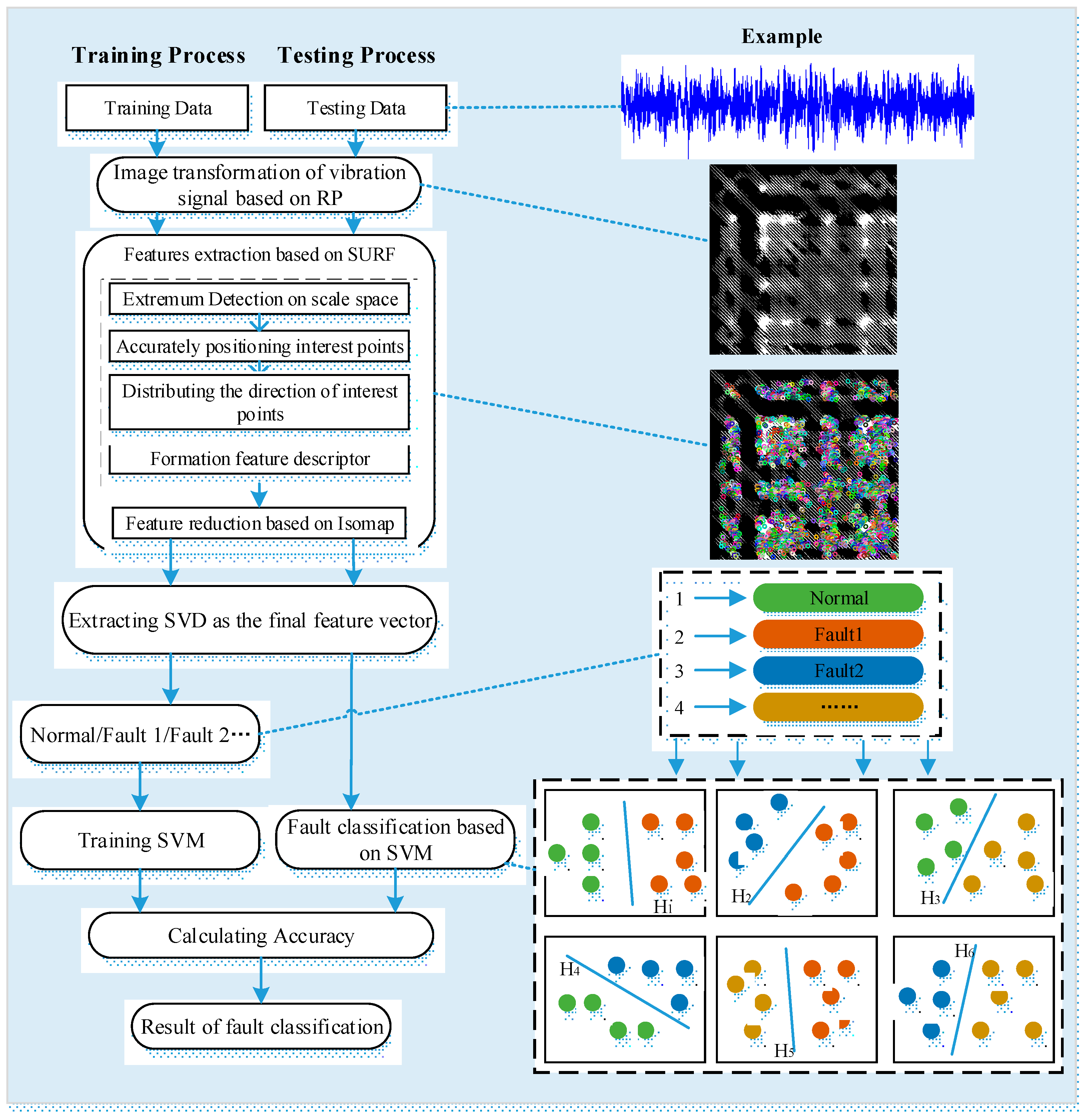
3. Method for Rolling Bearing Fault Diagnosis under Variable Conditions Based on Visual Cognition
3.1. Description of the Rolling Bearing Experimental Data
3.2. Image Transformation of Vibration Signals for Visual Cognition
3.3. Feature Extraction Based on SURF and Isomap
3.4. Fault Classification Based on SVM
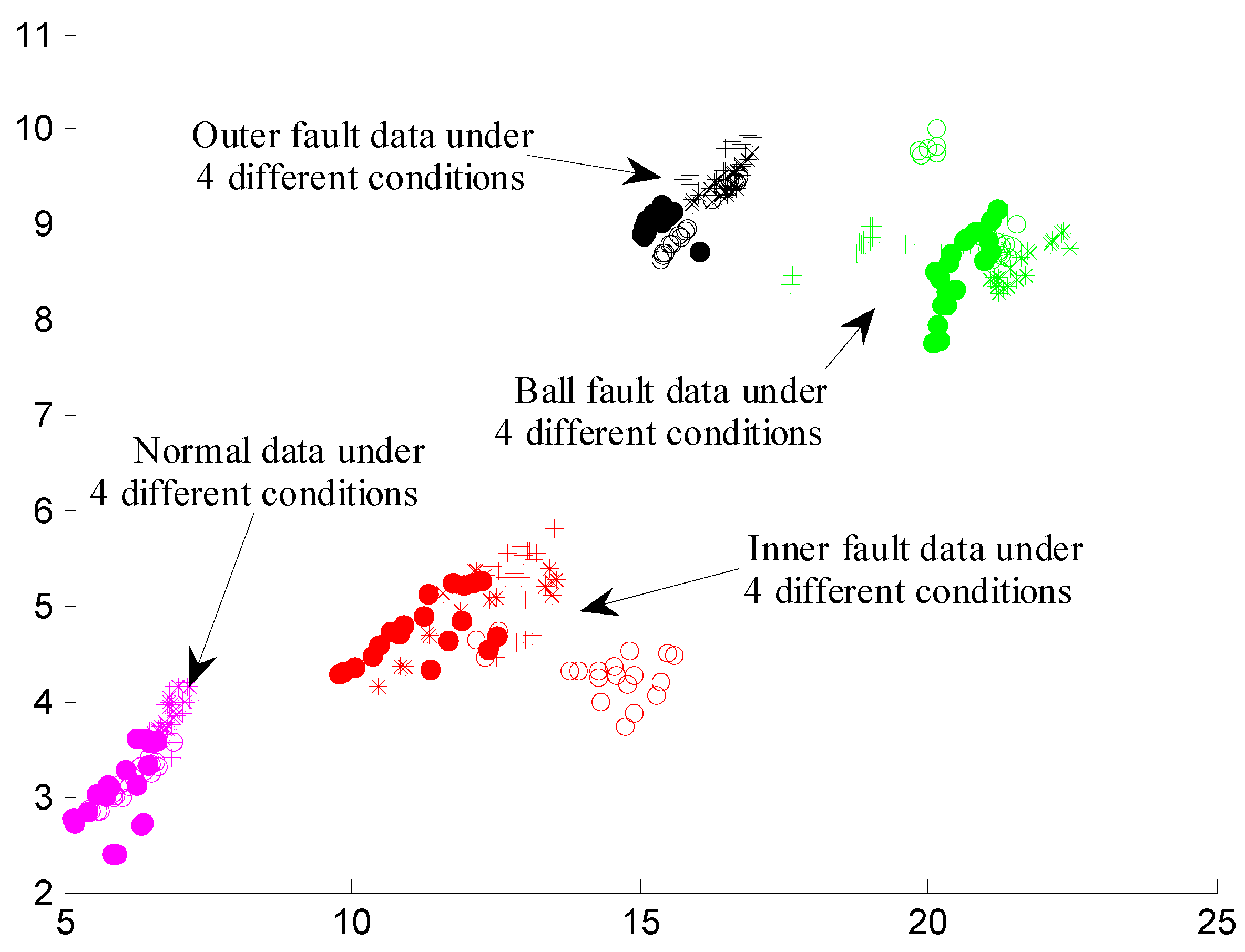
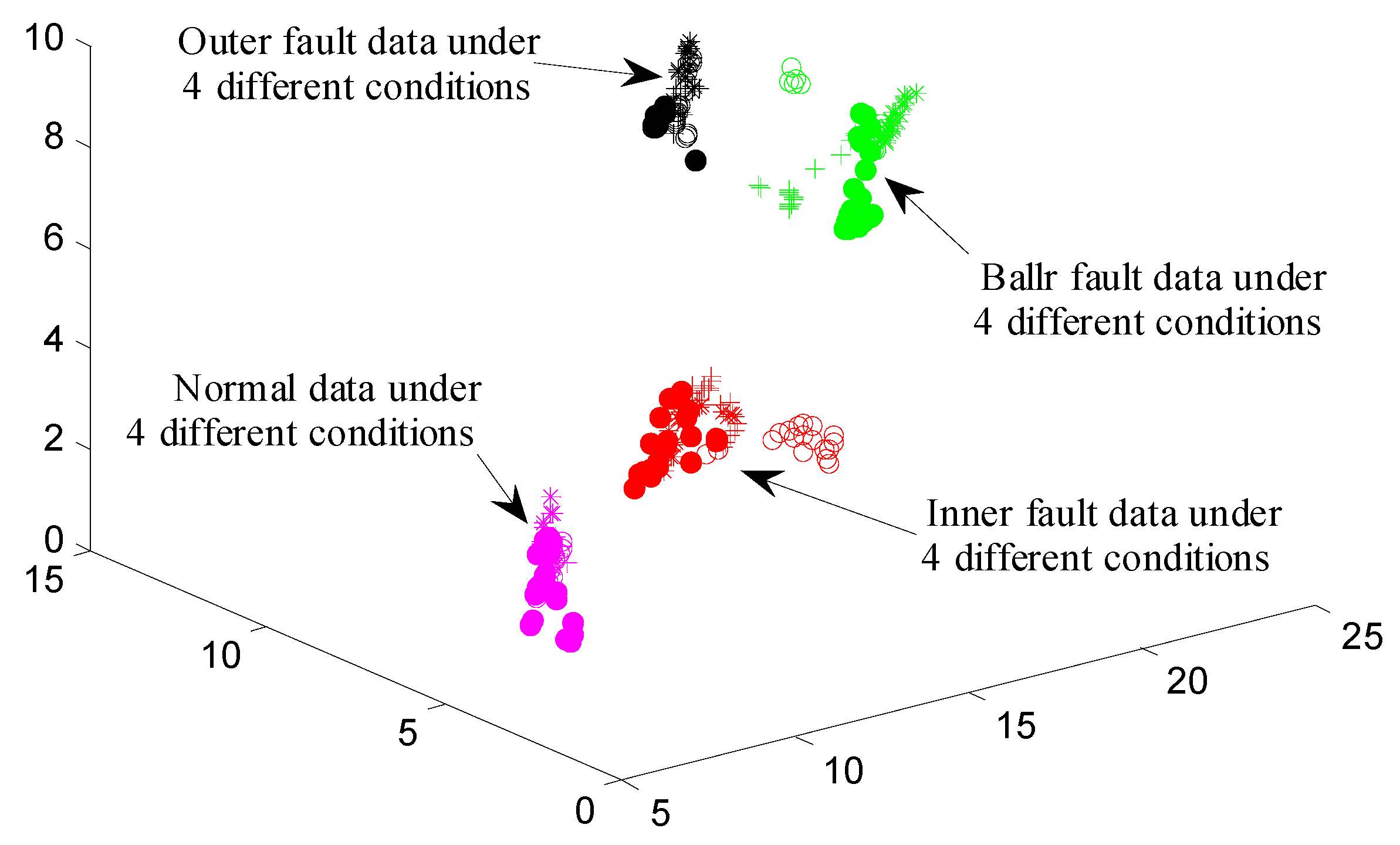
4. Results and Discussion
5. Conclusions
- (1)
- Inspired by VIC of the HVS, stable fault features contained in the vibration signals collected under variable working conditions can be successfully extracted by SURF algorithm.
- (2)
- Inspired by MPC of the HVS, the manifold learning method, Isomap, can successfully excavated meaningful low-dimensional structures hidden within high-dimensional observations.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tao, S.Q.; Zhang, T.; Yang, J.; Wang, X.Q.; Lu, W.N. Bearing Fault Diagnosis Method Based on Stacked Autoencoder and Softmax Regression. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; pp. 6331–6335. [Google Scholar]
- Shakya, P.; Kulkarni, M.S.; Darpe, A.K. Bearing diagnosis based on Mahalanobis-Taguchi-Gram-Schmidt method. J. Sound Vibr. 2015, 337, 342–362. [Google Scholar] [CrossRef]
- Henao, H.; Capolino, G.A.; Fernandez-Cabanas, M.; Filippetti, F.; Bruzzese, C.; Strangas, E.; Pusca, R.; Estima, G.; Riera-Guasp, M.; Hedayati-Kia, S. Trends in Fault Diagnosis for Electrical Machines: A Review of Diagnostic Techniques. IEEE Ind. Electron. Mag. 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Frosini, L.; Harlişca, C.; Szabó, L. Induction Machine Bearing Fault Detection by Means of Statistical Processing of the Stray Flux Measurement. IEEE Trans. Ind. Electron. 2015, 62, 1846–1854. [Google Scholar] [CrossRef]
- Hu, Z.Y.; Wang, C.; Zhu, J.; Liu, X.C.; Kong, F.R. Bearing fault diagnosis based on an improved morphological filter. Measurement 2016, 80, 163–178. [Google Scholar] [CrossRef]
- Al-Bugharbee, H.; Trendafilova, I. A fault diagnosis methodology for rolling element bearings based on advanced signal pretreatment and autoregressive modelling. J. Sound Vibr. 2016, 369, 246–265. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, J.; Lu, C.; Wang, Z.L. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mech. Mach. Theory 2015, 90, 175–186. [Google Scholar] [CrossRef]
- Mishra, C.; Samantaray, A.K.; Chakraborty, G. Rolling element bearing defect diagnosis under variable speed operation through angle synchronous averaging of wavelet de-noised estimate. Mech. Syst. Signal Proc. 2016, 72, 206–222. [Google Scholar] [CrossRef]
- Liu, W.Y.; Han, J.G.; Jiang, J.L. A novel ball bearing fault diagnosis approach based on auto term window method. Measurement 2013, 46, 4032–4037. [Google Scholar] [CrossRef]
- Cheng, J.S.; Yu, D.J.; Yang, Y. A fault diagnosis approach for roller bearings based on EMD method and AR model. Mech. Syst. Signal Proc. 2006, 20, 350–362. [Google Scholar] [CrossRef]
- Liu, X.F.; Bo, L.; Luo, H.L. Bearing faults diagnostics based on hybrid LS-SVM and EMD method. Measurement 2015, 59, 145–166. [Google Scholar] [CrossRef]
- Wu, F.J.; Qu, L.S. Diagnosis of subharmonic faults of large rotating machinery based on EMD. Mech. Syst. Signal Proc. 2009, 23, 467–475. [Google Scholar] [CrossRef]
- Mehala, N.; Dahiya, R. A Comparative Study of FFT, STFT and Wavelet Techniques for Induction Machine Fault Diagnostic Analysis. In Proceedings of the 7th WSEAS International Conference on Computational Intelligence, Man-Machine Systems and Cybernetics, Cairo, Egypt, 29–31 December 2008; pp. 203–208. [Google Scholar]
- Zhou, B.; Lu, C.; Li, L.F.; Chen, Z.H. Health assessment for rolling bearing based on local characteristic-scale decomposition—Approximate entropy and manifold distance. In Proceedings of the 12th World Congress on Intelligent Control and Automation, Guilin, China, 12–15 June 2016; pp. 401–406. [Google Scholar]
- Sha, M.Y.; Liu, L.G. Review on Fault Diagnosis Technology for Bearings Based on Vibration Signal. Bearing 2015, 9, 59–63. [Google Scholar]
- Bei, J.K.; Lu, C.; Wang, Z.L. Performance Assessment and Fault Diagnosis for Hydraulic Pump Based on WPT and SOM. In Proceedings of the International Conference VIBROENGINEERING, Sanya, China, 17–19 September 2013; pp. 23–28. [Google Scholar]
- Miller, G.A. The cognitive revolution: A historical perspective. Trends Cogn. Sci. 2003, 7, 141–144. [Google Scholar] [CrossRef]
- Cavanagh, P. Visual cognition. Vis. Res. 2011, 51, 1538–1551. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.Y.; Zhou, Z.H. Fast l1 -Minimization Algorithms for Robust Face Recognition. IEEE Trans. Image Process. 2010, 22, 3234–3246. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.C.; Jain, A.K.; Li, S.Z. Partial Face Recognition: Alignment-Free Approach. IEEE Trans. Softw. Eng. 2013, 35, 1193–1205. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Yuan, J.S.; Meng, J.J.; Zhang, Z.Y. Robust Part-Based Hand Gesture Recognition Using Kinect Sensor. IEEE Trans. Multimed. 2013, 15, 1110–1120. [Google Scholar] [CrossRef]
- Rautaray, S.S.; Agrawal, A. Vision based hand gesture recognition for human computer interaction: A survey. Artif. Intell. Rev. 2015, 43, 1–54. [Google Scholar] [CrossRef]
- Suarez, J.; Murphy, R.R. Hand Gesture Recognition with Depth Images: A Review. In Proceedings of the 21st IEEE International Symposium on Robot and Human Interactive Communication, Paris, France, 9–13 September 2012; pp. 411–417. [Google Scholar]
- Liu, C.L.; Sako, H. Class-specific feature polynomial classifier for pattern classification and its application to handwritten numeral recognition. Pattern Recognit. 2006, 39, 669–681. [Google Scholar] [CrossRef]
- Shi, M.; Fujisawa, Y.; Wakabayashi, T.; Kimura, F. Handwritten numeral recognition using gradient and curvature of gray scale image. Pattern Recognit. 2002, 35, 2051–2059. [Google Scholar] [CrossRef]
- Han, X.F.; Li, Y. The Application of Convolution Neural Networks in Handwritten Numeral Recognition. Int. J. Database Theory Appl. 2015, 8, 367–376. [Google Scholar] [CrossRef]
- Hollard, V.D.; Delius, H.D. Rotational Invariance in Visual Pattern Recognition by Pigeons and Humans. Science 1982, 218, 804–806. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.Y.; Ng, A.Y.; Yu, K. Unsupervised learning of visual invariance with temporal coherence. In Proceedings of the NIPS Workshop Deep Learning and Unsupervised Feature Learning, Granada, Spain, 16 December 2011. [Google Scholar]
- Seung, H.S.; Lee, D.D. The Manifold Ways of Perception. Science 2000, 290, 2268–2269. [Google Scholar] [CrossRef] [PubMed]
- He, Q.B. Vibration signal classification by wavelet packet energy flow manifold learning. J. Sound Vibr. 2013, 332, 1881–1894. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, Z.S.; Luo, X.; Guo, T.; Qu, J.X.; Li, B. Support vector machine-based Grassmann manifold distance for health monitoring of viscoelastic sandwich structure with material ageing. J. Sound Vibr. 2016, 368, 249–263. [Google Scholar] [CrossRef]
- Yan, J.Q.; Wang, Y.H.; Ouyang, G.X.; Yu, T.; Li, X.L. Using max entropy ratio of recurrence plot to measure electrocorticogram changes in epilepsy patients. Physica A 2016, 443, 109–116. [Google Scholar] [CrossRef]
- Wang, C.H.; Zhong, Z.P.; Jiaqiang, E. Flow regime recognition in spouted bed based on recurrence plot method. Powder Technol. 2012, 219, 20–28. [Google Scholar] [CrossRef]
- Yang, D.; Ren, W.X.; Hu, Y.D.; Li, D. Selection of optimal threshold to construct recurrence plot for structural operational vibration measurements. J. Sound Vibr. 2015, 349, 361–374. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Q.N.; Wu, X.; Na, N. Gear Fault Diagnosis Based on Narrowband Demodulation with Frequency Shift and Spectrum Edit. Int. J. Eng. Technol. Innov. 2016, 6, 243–254. [Google Scholar]
- Liu, J.; Huang, J.Y.; Liu, S.G.; Li, H.L.; Zhou, Q.M.; Liu, J.C. Human visual system consistent quality assessment for remote sensing image fusion. ISPRS J. Photogramm. Remote Sens. 2015, 105, 79–90. [Google Scholar] [CrossRef]
- Liu, J.N. Research on Image Local Invariant Feature and Its Application. Ph.D. Thesis, Shanghai Jiaotong University, Shanghai, China, July 2012. [Google Scholar]
- Nan, G. Research on Visual Invariance and Frequency Effect Based on Dynamic Receptive Fields. Master Thesis, University of Tianjin, Tianjin, China, July 2008. [Google Scholar]
- Tang, T.; Qiao, H. Improving invariance in visual classification with biologically inspired mechanism. Neurocomputing 2014, 133, 328–341. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Cool, L. Speeded-Up Robust Features. Comput. Vis. Image Underst. 2008, 110, 404–417. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, S.C.; Huang, X.M. Real-Time Traffic Sign Detection Using SURF Features on FPGA. In Proceedings of the IEEE High Performance Extreme Computing Conference, Waltham, MA, USA, 10–12 September 2013; pp. 1–6. [Google Scholar]
- Zhou, H. Research on Manifold Perception-Based Image Distance Metric. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, July 2011. [Google Scholar]
- Tian, Y.; Wang, Z.L.; Lu, C. Self-adaptive Bearing Fault Diagnosis Based on Permutation Entropy and Manifold-based Dynamic Time Warping. Mech. Syst. Signal Proc. 2016. [Google Scholar] [CrossRef]
- Hannachi, A.; Turner, A.G. Isomap nonlinear dimensionality reduction and bimodality of Asian monsoon convection. Geophys. Res. Lett. 2013, 40, 1653–1658. [Google Scholar] [CrossRef]
- Data File Download Page of the Rolling Bearings. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 11 May 2017).
- Test-Rig Apparatus of the Rolling Bearing. Available online: http://csegroups.case.edu/bearingdatacenter/pages/apparatus-procedures (accessed on 11 May 2017).







| Fault Diameter | Motor Speed | Inner Race | Rolling Element | Outer Race | ||
|---|---|---|---|---|---|---|
| (inch) | (rpm) | 3 o’clock | 6 o’clock | 12 o’clock | ||
| 0.021 | 1797 | 213.mat | 226.mat | 238.mat | ||
| 1772 | 214.mat | 227.mat | 239.mat | |||
| 1750 | 215.mat | 228.mat | 240.mat | |||
| 1730 | 217.mat | 229.mat | 241.mat | |||
| Conditions | Parameters | Normal | Inner Race Fault | Rolling Element Fault | Outer Race Fault |
|---|---|---|---|---|---|
| Condition 1 | 15 | 12 | 13 | 12 | |
| 4 | 5 | 5 | 5 | ||
| Condition 2 | 15 | 12 | 12 | 12 | |
| 4 | 5 | 5 | 5 | ||
| Condition 3 | 15 | 20 | 13 | 12 | |
| 4 | 2 | 5 | 5 | ||
| Condition 4 | 16 | 11 | 13 | 12 | |
| 4 | 5 | 5 | 5 |
| Groups of Cross Validation | Conditions of Training Data | Conditions of Test Data | ||
|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 1 | 3 | 4 |
| 3 | 3 | 1 | 2 | 4 |
| 4 | 4 | 1 | 2 | 3 |
| Groups of Cross Validation | Classification Accuracy | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2-D | 3-D | 5-D | 8-D | 10-D | 12-D | 15-D | 18-D | 20-D | |
| 1 | 99.166 | 99.166 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2 | 99.166 | 99.166 | 99.166 | 100 | 100 | 100 | 100 | 99.583 | 99.166 |
| 3 | 92.083 | 94.588 | 97.083 | 99.166 | 99.166 | 99.166 | 99.166 | 99.166 | 99.166 |
| 4 | 92.5 | 95.416 | 100 | 99.583 | 99.583 | 99.583 | 99.583 | 99.583 | 99.583 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Zhou, B.; Lu, C.; Yang, C. Fault Diagnosis for Rolling Bearings under Variable Conditions Based on Visual Cognition. Materials 2017, 10, 582. https://doi.org/10.3390/ma10060582
Cheng Y, Zhou B, Lu C, Yang C. Fault Diagnosis for Rolling Bearings under Variable Conditions Based on Visual Cognition. Materials. 2017; 10(6):582. https://doi.org/10.3390/ma10060582
Chicago/Turabian StyleCheng, Yujie, Bo Zhou, Chen Lu, and Chao Yang. 2017. "Fault Diagnosis for Rolling Bearings under Variable Conditions Based on Visual Cognition" Materials 10, no. 6: 582. https://doi.org/10.3390/ma10060582
APA StyleCheng, Y., Zhou, B., Lu, C., & Yang, C. (2017). Fault Diagnosis for Rolling Bearings under Variable Conditions Based on Visual Cognition. Materials, 10(6), 582. https://doi.org/10.3390/ma10060582







