Study on Protection Mechanism of 30CrMnMo-UHMWPE Composite Armor
Abstract
:1. Introduction
2. Ballistic Test and Modeling
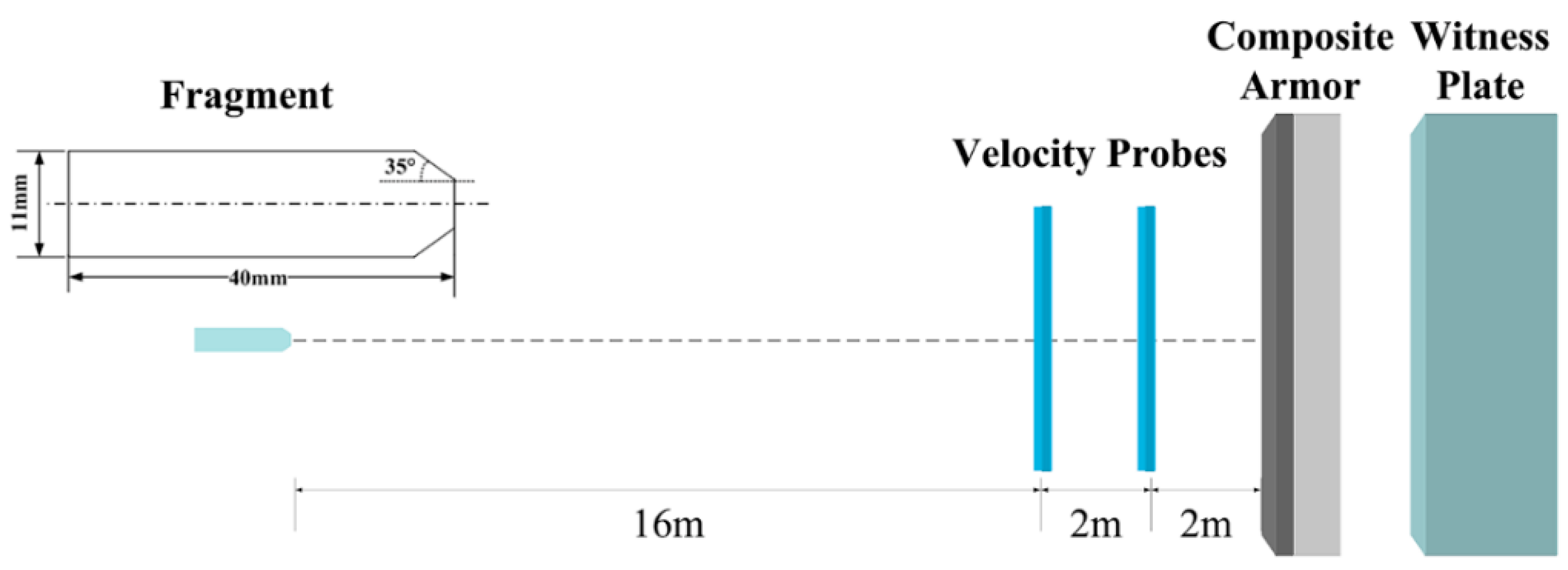
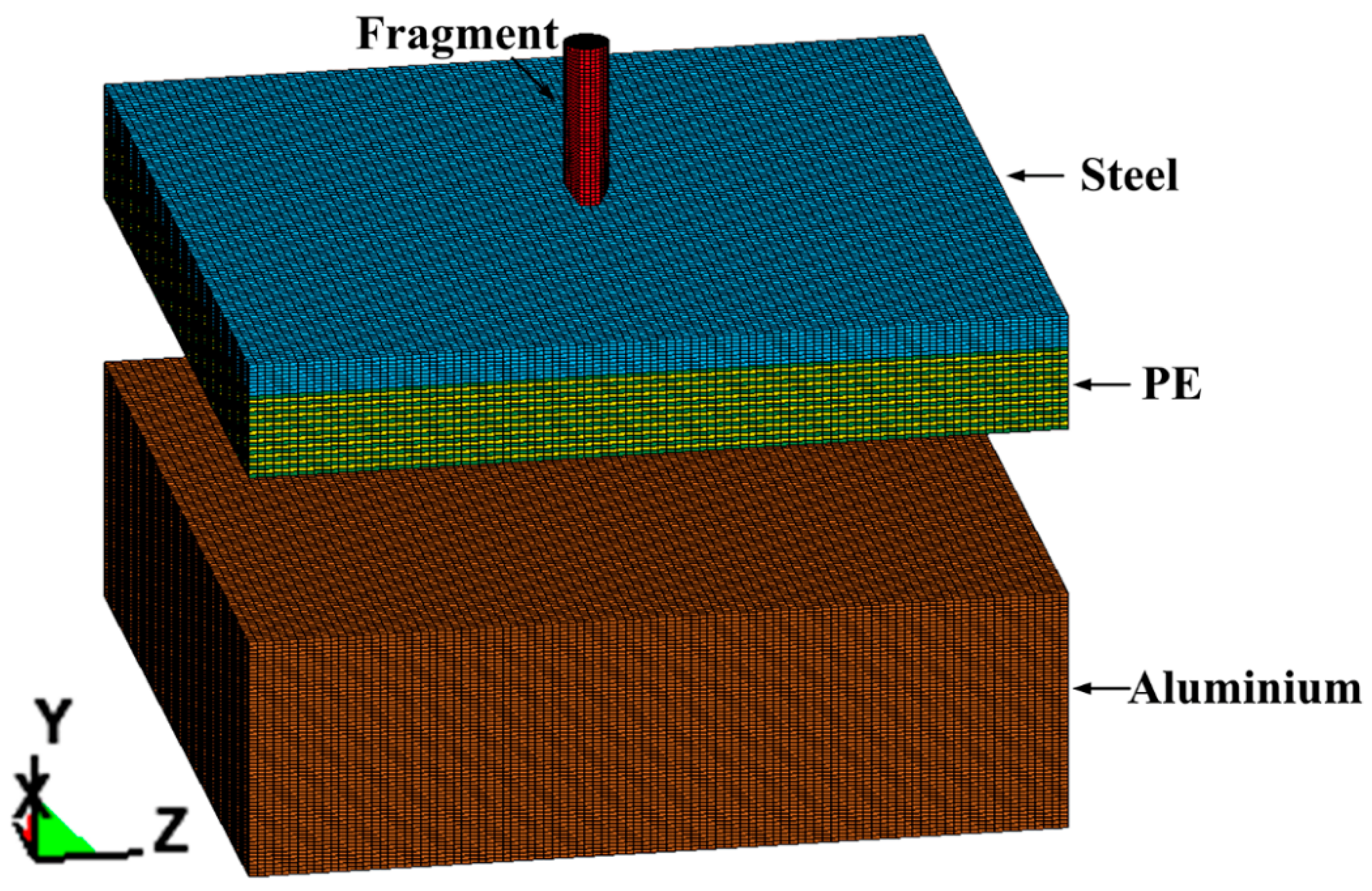
2.1. Experimental Details and Geometrical Models
2.2. Material Models and Parameters
2.3. Other Details
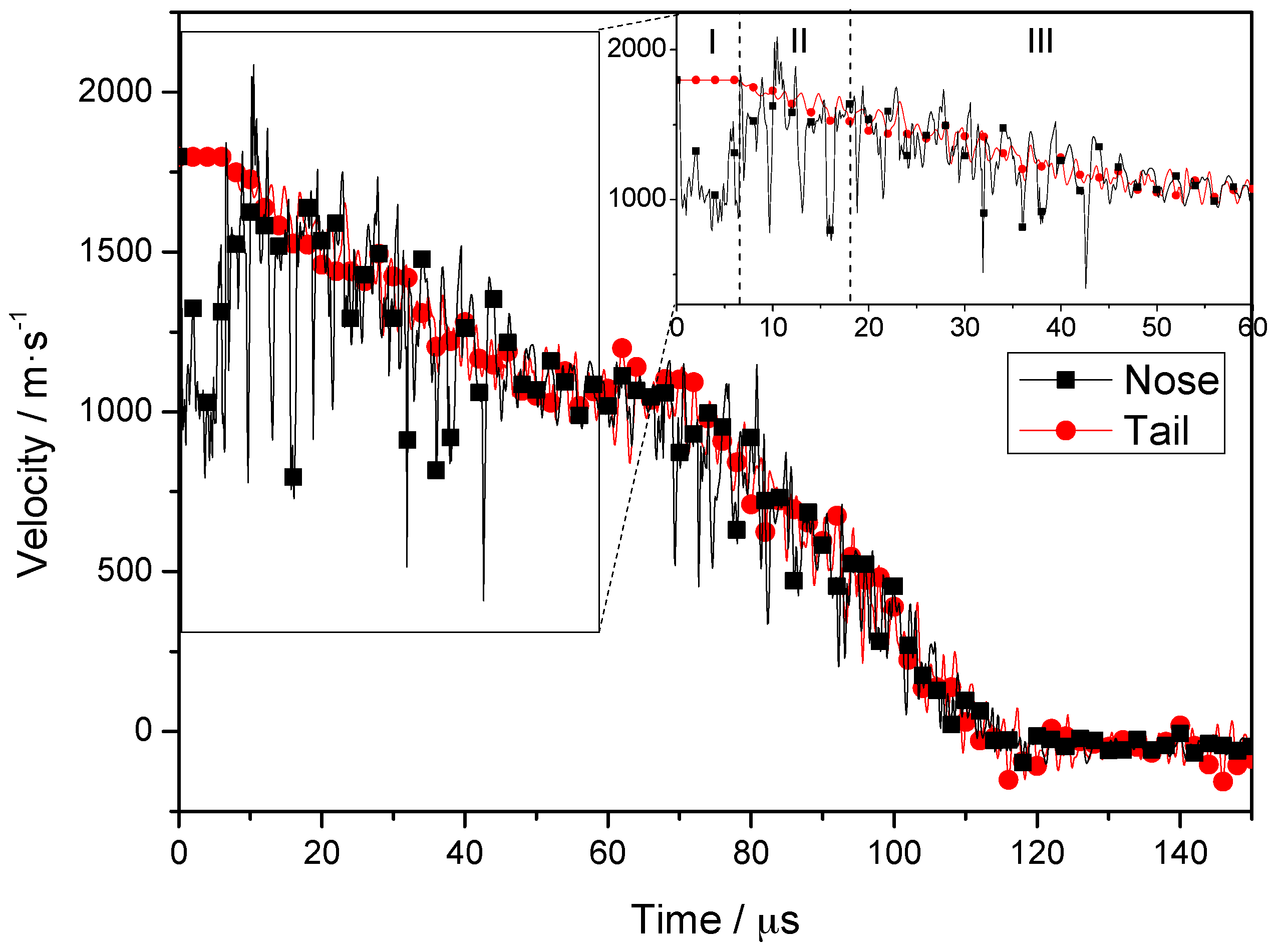
3. Results and Discussion
3.1. Reliability Verification
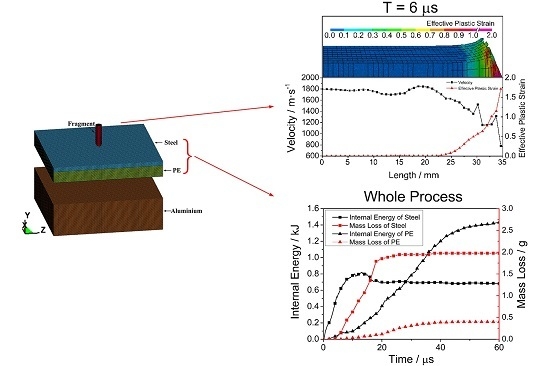
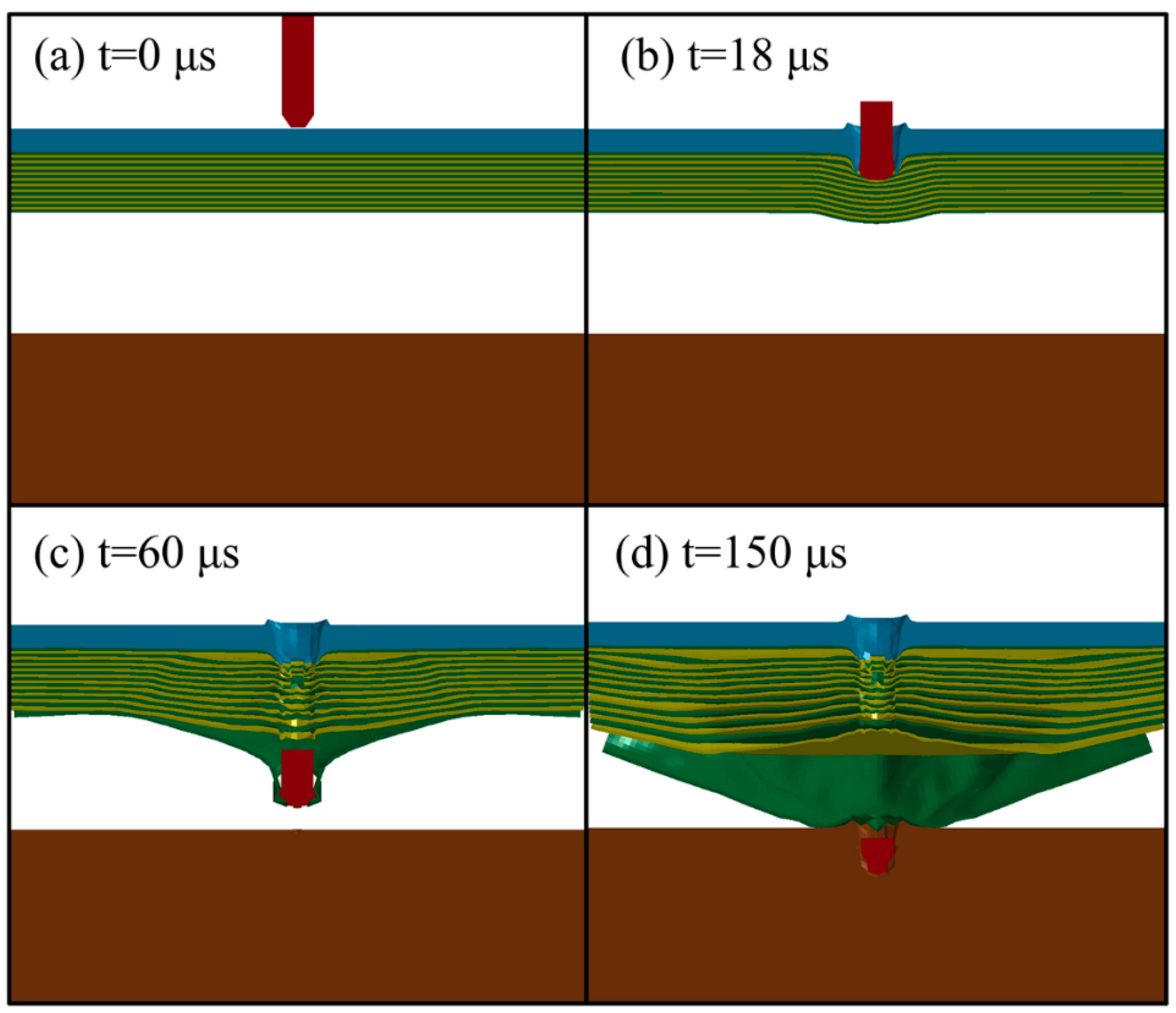
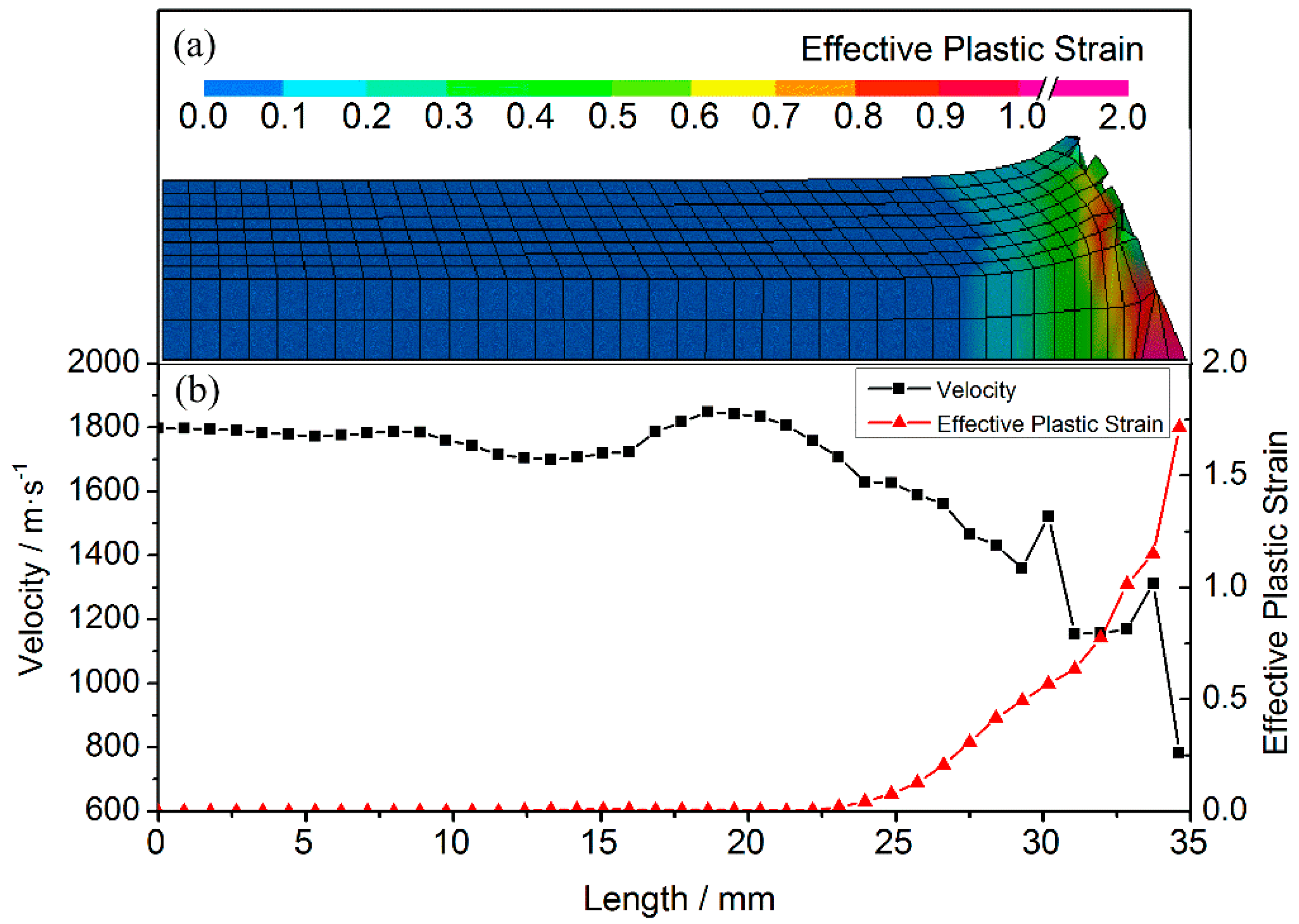
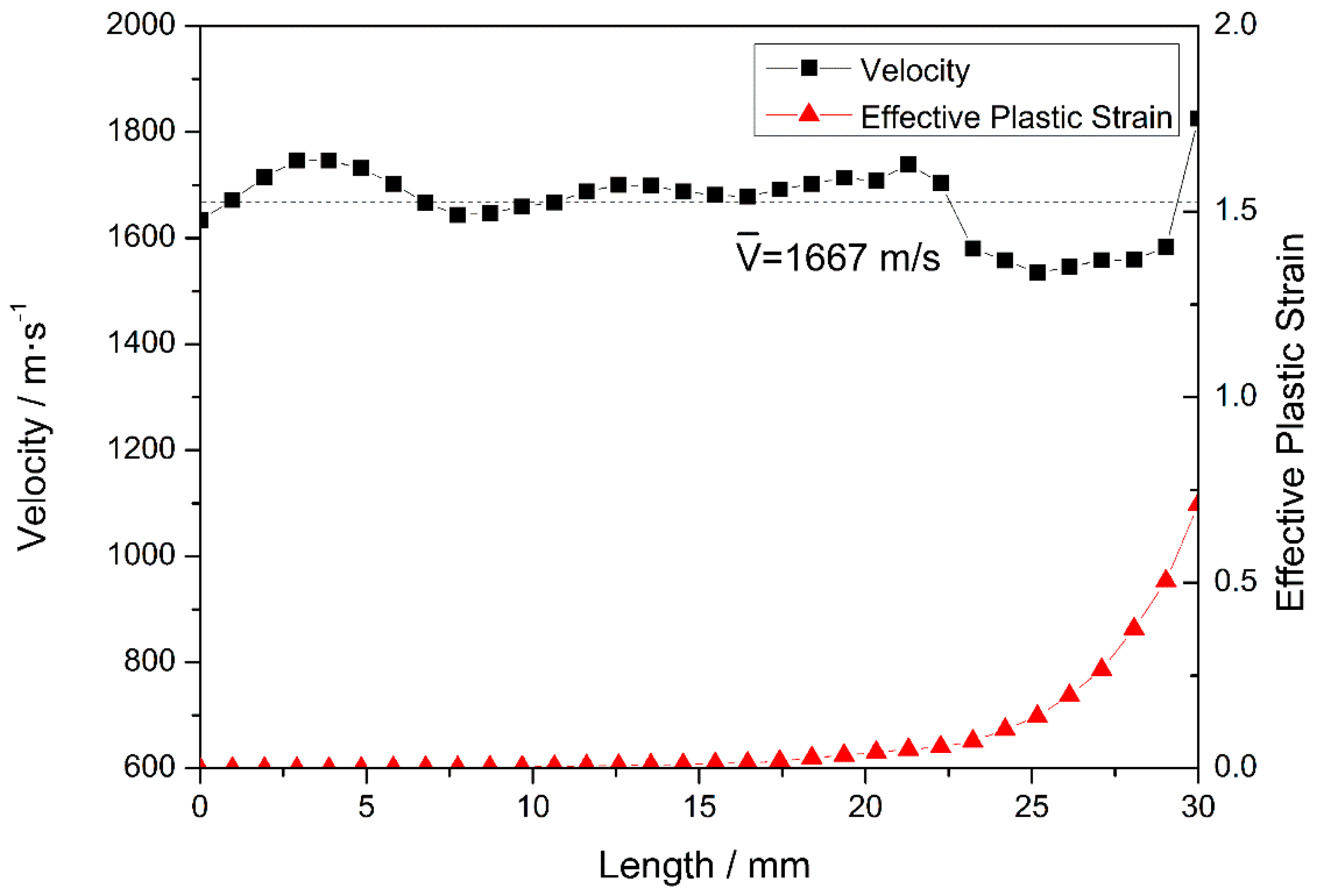
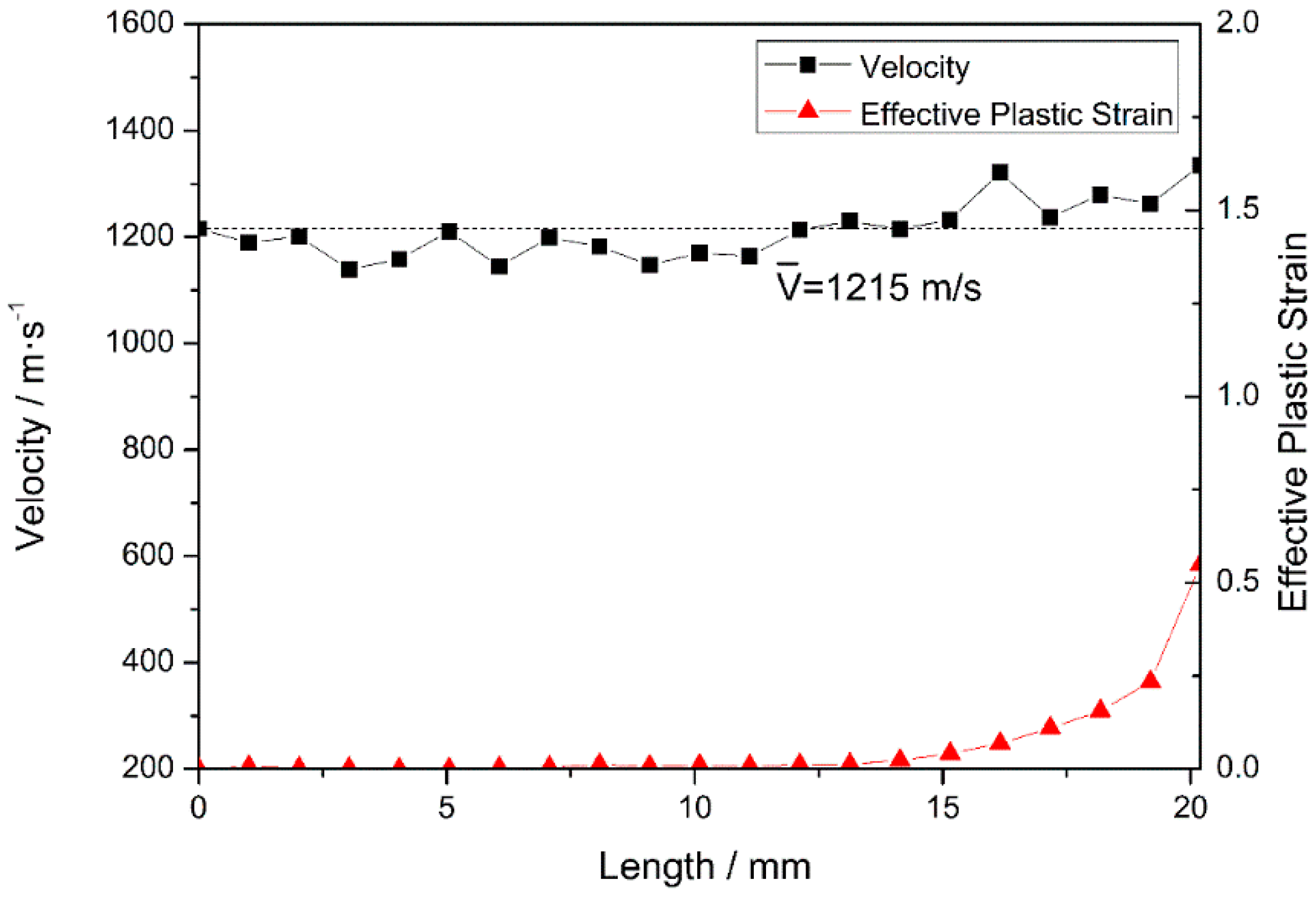
3.2. Penetration Mechanism of the Projectile
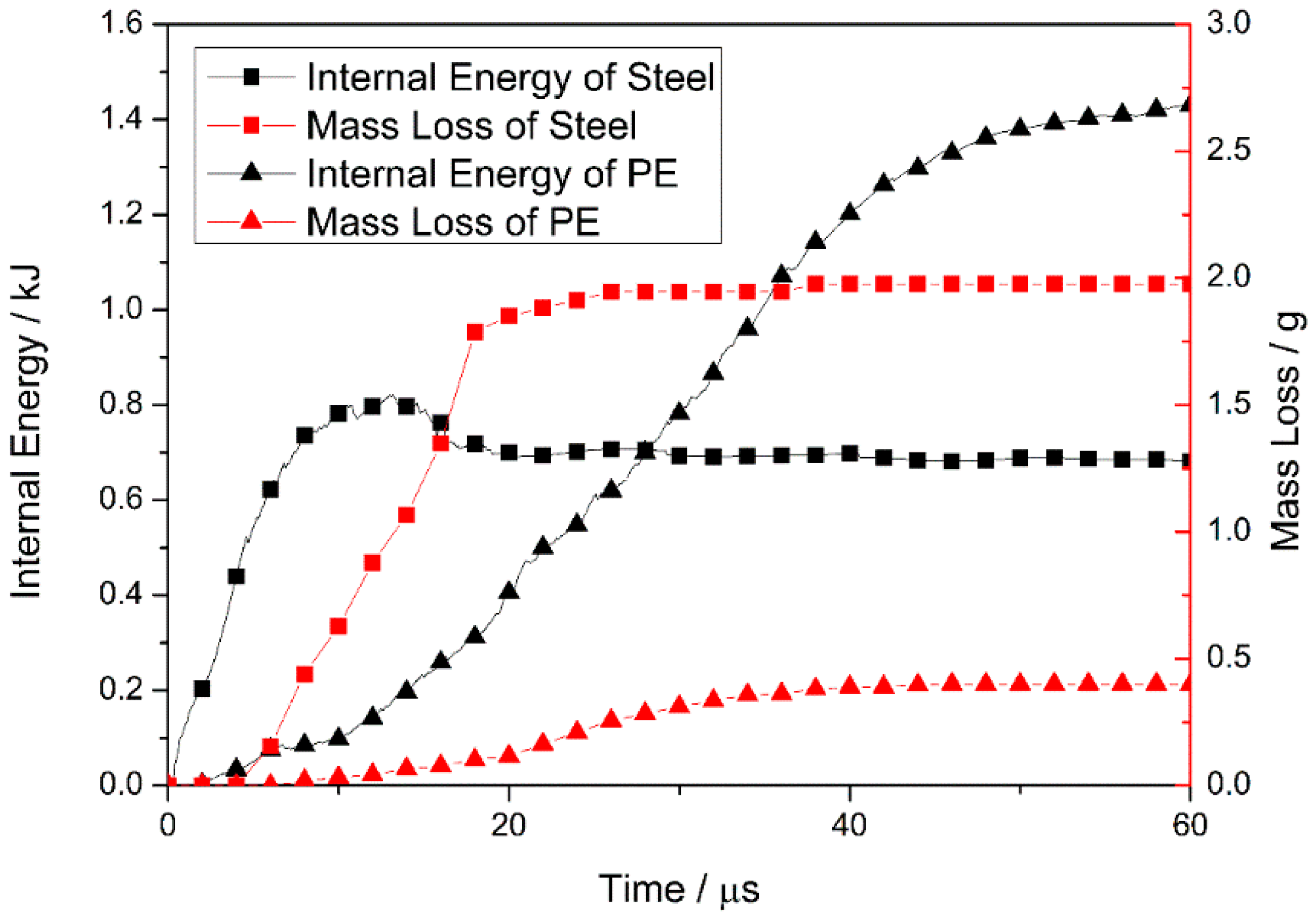
3.3. Analysis of the Internal Energy and Mass Loss of the Armor
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wilkins, M.; Honodel, C.; Sawle, D. Approach to the Study of Light Armor; Lawrence Radiation Laboratory, University of California: Berkeley, CA, USA, 1967. [Google Scholar]
- Reaugh, J.E.; Holt, A.C.; Wilkins, M.L.; Cunningham, B.J.; Hord, B.L.; Kusubov, A.S. Impact Studies of Five Ceramic Materials and Pyrex. Int. J. Impact Eng. 1999, 23, 771–782. [Google Scholar] [CrossRef]
- Madhu, V.; Ramanjaneyulu, K.; Bhat, T.B.; Gupta, N.K. An experimental study of penetration resistance of ceramic armour subjected to projectile impact. Int. J. Impact Eng. 2005, 32, 337–350. [Google Scholar] [CrossRef]
- Sekine, K.; Kumazawa, T.; Tanabe, Y. Influence of joining interlayer on impact damage to laminated boron carbide ceramics. Int. J. Appl. Ceram. Technol. 2015, 12, 1217–1229. [Google Scholar] [CrossRef]
- Greenhalgh, E.S.; Bloodworth, V.M.; Iannucci, L.; Pope, D. Fractographic observations on Dyneema (R) composites under ballistic impact. Compos. Part A 2013, 44, 51–62. [Google Scholar] [CrossRef]
- Sherman, D. Impact failure mechanisms in alumina tiles on finite thickness support and the effect of confinement. Int. J. Impact Eng. 2000, 24, 313–328. [Google Scholar] [CrossRef]
- Krishnan, K.; Sockalingam, S.; Bansal, S.; Rajan, S.D. Numerical simulation of ceramic composite armor subjected to ballistic impact. Compos. Part B 2010, 41, 583–593. [Google Scholar] [CrossRef]
- Matchen, B. Applications of ceramics in armor products. Key Eng. Mater. 1996, 122, 333–342. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Javadpour, G.H. Penetration analysis of a projectile in ceramic composite armor. Compos. Struct. 2008, 82, 269–276. [Google Scholar] [CrossRef]
- Feli, S.; Asgari, M.R. Finite element simulation of ceramic/composite armor under ballistic impact. Compos. Part B 2011, 42, 771–780. [Google Scholar] [CrossRef]
- O'Masta, M.R.; Compton, B.G.; Gamble, E.A.; Zok, F.W.; Deshpande, V.S.; Wadley, H.N.G. Ballistic impact response of an UHMWPE fiber reinforced laminate encasing of an aluminum-alumina hybrid panel. Int. J. Impact Eng. 2015, 86, 131–144. [Google Scholar] [CrossRef]
- Haro, E.E.; Szpunar, J.A.; Odeshi, A.G. Ballistic impact response of laminated hybrid materials made of 5086-H32 aluminum alloy, epoxy and Kevlar® fabrics impregnated with shear thickening fluid. Compos. Part A 2016, 87, 54–65. [Google Scholar] [CrossRef]
- Karagoz, S.; Atapek, S.H.; Yilmaz, A. Microstructural and Fractographical Studies on Quenched and Tempered Armor Steels. Mater. Test. 2010, 52, 316–322. [Google Scholar] [CrossRef]
- Kilic, N.; Ekici, B. Ballistic resistance of high hardness armor steels against 7.62 mm armor piercing ammunition. Mater. Des. 2013, 44, 35–48. [Google Scholar] [CrossRef]
- Duan, Z.Q.; Li, S.X.; Huang, D.W. Microstructures and adiabatic shear bands formed by ballistic impact in steels and tungsten alloy. Fatigue Fract. Eng. Mater. Struc. 2003, 26, 1119–1126. [Google Scholar] [CrossRef]
- Russell, B.P.; Karthikeyan, K.; Deshpande, V.S.; Fleck, N.A. The high strain rate response of ultra high molecular-weight polyethylene: From fibre to laminate. Int. J. Impact Eng. 2013, 60, 1–9. [Google Scholar] [CrossRef]
- Cunniff, P.M. Dimensionless Parameters for Optimization of Textile Based Body Armor Systems; U.S. Army Soldier and Biological Chemical Command Soldier Systems Center: Natick, MA, USA, 1999. [Google Scholar]
- Lee, B.L.; Song, J.W.; Ward, J.E. Failure of spectra polyethylene fiber-reinforced composites under ballistic impact loading. J. Compos. Mater. 1994, 28, 1202–1226. [Google Scholar] [CrossRef]
- Harpell, G.A.; Kavesh, S.; Palley, I.; Prevorsek, D.C. Ballistic-Resistant Article. U.S. Patent No. 4.403.012, 1983. [Google Scholar]
- Ulven, C.; Vaidya, U.K.; Hosur, M.V. Effect of projectile shape during ballistic perforation of VARTM carbon/epoxy composite panels. Compos. Struct. 2003, 61, 143–150. [Google Scholar] [CrossRef]
- MIL-P-46593A (NOTICE 1), Military Specification: Projectile, Calibers .22, .30, .50, and 20 mm Fragment-Simulating. 1996. Available online: http://everyspec.com/MIL-SPECS/MIL-SPECS-MIL-P/MIL-P-46593A_NOTICE-2_38605/ (accessed on 24 January 2017).
- Sasso, M.; Newaz, G.; Amodio, D. Material characterization at high strain rate by Hopkinson bar tests and finite element optimization. Mater. Sci. Eng. A 2008, 487, 289–300. [Google Scholar] [CrossRef]
- Grujicic, M.; Glomski, P.S.; He, T.; Arakere, G.; Bell, W.C.; Cheeseman, B.A. Material Modeling and Ballistic-Resistance Analysis of Armor-Grade Composites Reinforced with High-Performance Fibers. J. Mater. Eng. Perform. 2009, 18, 1169–1182. [Google Scholar] [CrossRef]
- Wen, Y.; Xu, C.; Wang, S.; Batra, R.C. Analysis of behind the armor ballistic trauma. J. Mech. Behav. Biomed. 2015, 45, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Keefe, M.; Bogetti, T.A.; Powers, B. Finite element modeling of transverse impact on a ballistic fabric. Int. J. Mech. Sci. 2006, 48, 33–43. [Google Scholar] [CrossRef]
- Laessig, T.; Bagusat, F.; May, M.; Hiermaier, S. Analysis of the shock response of UHMWPE composites using the inverse planar plate impact test and the shock reverberation technique. Int. J. Impact Eng. 2015, 86, 240–248. [Google Scholar] [CrossRef]
- Nguyen, L.H. The Ballistic Performance of Thick Ultra High Molecular Weight Polyethylene Composite. Ph.D. Thesis, RMIT University, Melbourne, Australia, 2015. [Google Scholar]
- LS-DYNA Keyword User’s Manual, version 971; Livermore Software Technology Corporation: Livermore, CA, USA, 2006.
- Hallquist, J. LS-DYNA Theory Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006. [Google Scholar]
- Hadavinia, H.; Kawashita, L.; Kinloch, A.J.; Moore, D.R.; Williams, J.G. A numerical analysis of the elastic-plastic peel test. Eng. Fract. Mech. 2006, 73, 2324–2335. [Google Scholar] [CrossRef]
- Cho, E.H.; Lee, S.G.; Kim, J.K. Surface modification of UHMWPE with gamma-ray radiation for improving interfacial bonding strength with bone cement (II). Curr. Appl. Phys. 2005, 5, 475–479. [Google Scholar] [CrossRef]
- Oosterom, R.; Ahmed, T.J.; Poulis, J.A.; Bersee, H.E.N. Adhesion performance of UHMWPE after different surface modification techniques. Med. Eng. Phys. 2006, 28, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Hill, R. Acceleration waves in solids. J. Mech. Phys. Solids 1962, 10, 1–16. [Google Scholar] [CrossRef]
- Camacho, G.T.; Ortiz, M. Adaptive Lagrangian modelling of ballistic penetration of metallic targets. Comput. Method Appl. Mech. Eng. 1997, 142, 269–301. [Google Scholar] [CrossRef]
- Chocron, S.; Anderson, C.E.; Walker, J.D.; Ravid, M. A unified model for long-rod penetration in multiple metallic plates. Int. J. Impact Eng. 2003, 28, 391–411. [Google Scholar] [CrossRef]

| Johnson Cook Model | 1045-Steel | 30CrMnMo | Al |
| ρ (g·cm−3) | 7.85 | 7.85 | 2.78 |
| E (Gpa) | 210 | 200 | 69.0 |
| G (Gpa) | 80.8 | 75.9 | 27.0 |
| PR | 0.31 | 0.32 | 0.33 |
| A (GPa) | 0.507 | 1.18 | 0.554 |
| B (GPa) | 0.32 | 0.1625 | 0.351 |
| C | 0.28 | 0.058 | 0.009 |
| n | 0.064 | 0.28 | 0.37 |
| m | 1.06 | 1.15 | 1.09 |
| D1 | 0.15 | 0.123 | 1.5 |
| D2 | 0.72 | 0.0 | 0.0 |
| D3 | 1.66 | 0.0 | 0.0 |
| D4 | 0.005 | 0.694 | 0.0 |
| D5 | -0.84 | 0.501 | 0.0 |
| Orthotropic Elastic Model | UHMWPE | ||
| EA (GPa) | 76.6 | ρ (g·cm−3) | 0.97 |
| EB (GPa) | 0.77 | PRBA | 0.013 |
| EC (GPa) | 76.6 | PRCA | 0.0 |
| GAB (GPa) | 2.0 | PRCB | 0.5 |
| GBC (GPa) | 2.0 | - | - |
| GCA (GPa) | 0.192 | - | - |
| Results | Experiment | Simulation | Relative Error |
|---|---|---|---|
| Penetration depth (mm) | 14.0 | 15.3 | 9.3% |
| Residual mass (g) | 6.2 | 6.6 | 6.5% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Li, G.; Fan, Q.; Wang, Y.; Zheng, H.; Tan, L.; Xu, X. Study on Protection Mechanism of 30CrMnMo-UHMWPE Composite Armor. Materials 2017, 10, 405. https://doi.org/10.3390/ma10040405
Zhou Y, Li G, Fan Q, Wang Y, Zheng H, Tan L, Xu X. Study on Protection Mechanism of 30CrMnMo-UHMWPE Composite Armor. Materials. 2017; 10(4):405. https://doi.org/10.3390/ma10040405
Chicago/Turabian StyleZhou, Yu, Guoju Li, Qunbo Fan, Yangwei Wang, Haiyang Zheng, Lin Tan, and Xuan Xu. 2017. "Study on Protection Mechanism of 30CrMnMo-UHMWPE Composite Armor" Materials 10, no. 4: 405. https://doi.org/10.3390/ma10040405
APA StyleZhou, Y., Li, G., Fan, Q., Wang, Y., Zheng, H., Tan, L., & Xu, X. (2017). Study on Protection Mechanism of 30CrMnMo-UHMWPE Composite Armor. Materials, 10(4), 405. https://doi.org/10.3390/ma10040405