Lattice Modeling of Early-Age Behavior of Structural Concrete
Abstract
:1. Introduction
2. Modeling Framework
2.1. Program Structure
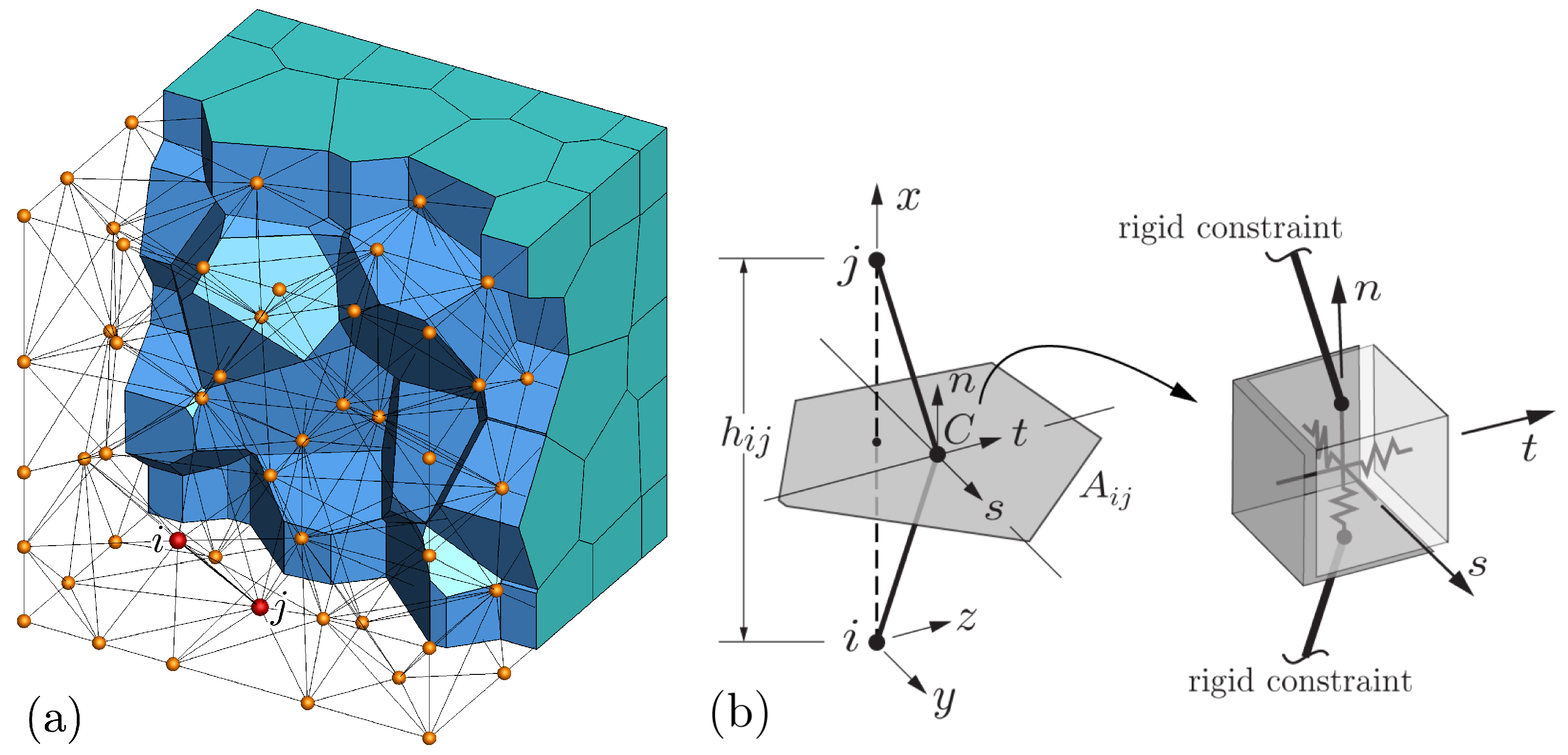
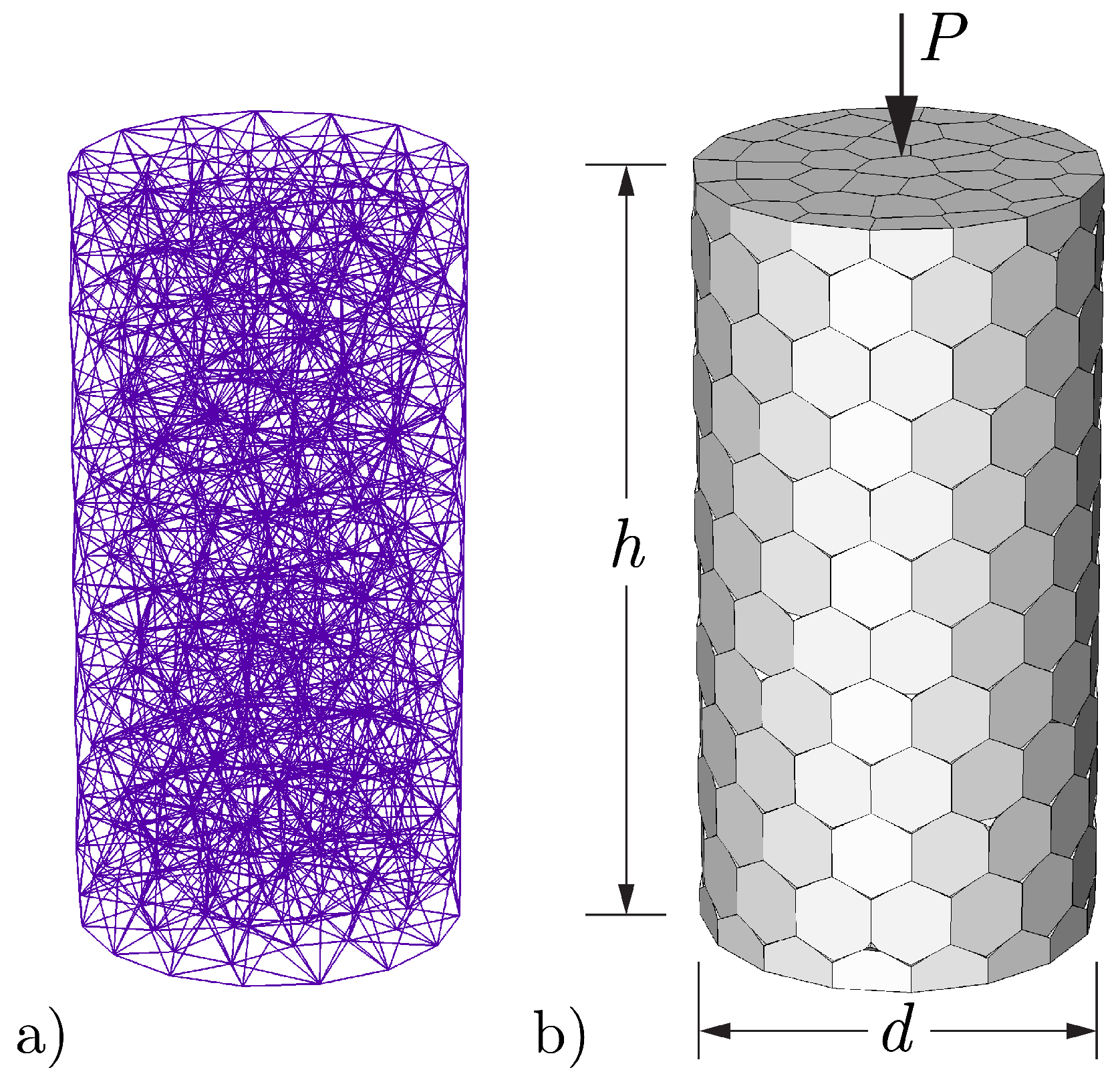
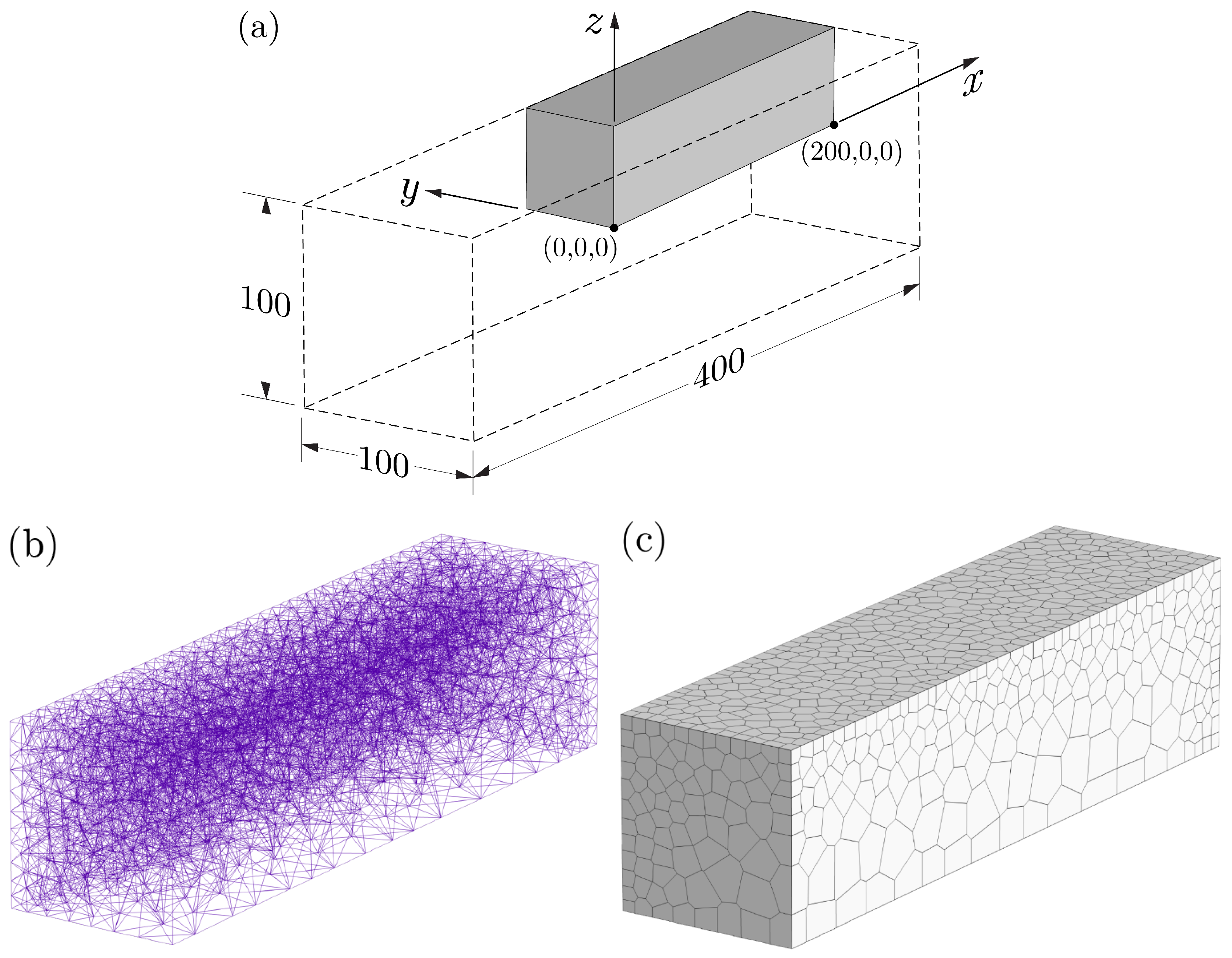
2.2. Domain Discretization
2.3. Cementitious Materials Hydration
2.4. Primary Analysis Modules
2.4.1. Thermal Analysis
- Convection—Convective heat exchange across exposed surfaces depends on the difference between the solid surface temperature and that of the surrounding ambient mediumwhere is the coefficient of convective heat transfer, which depends on wind speed and other factors [34].
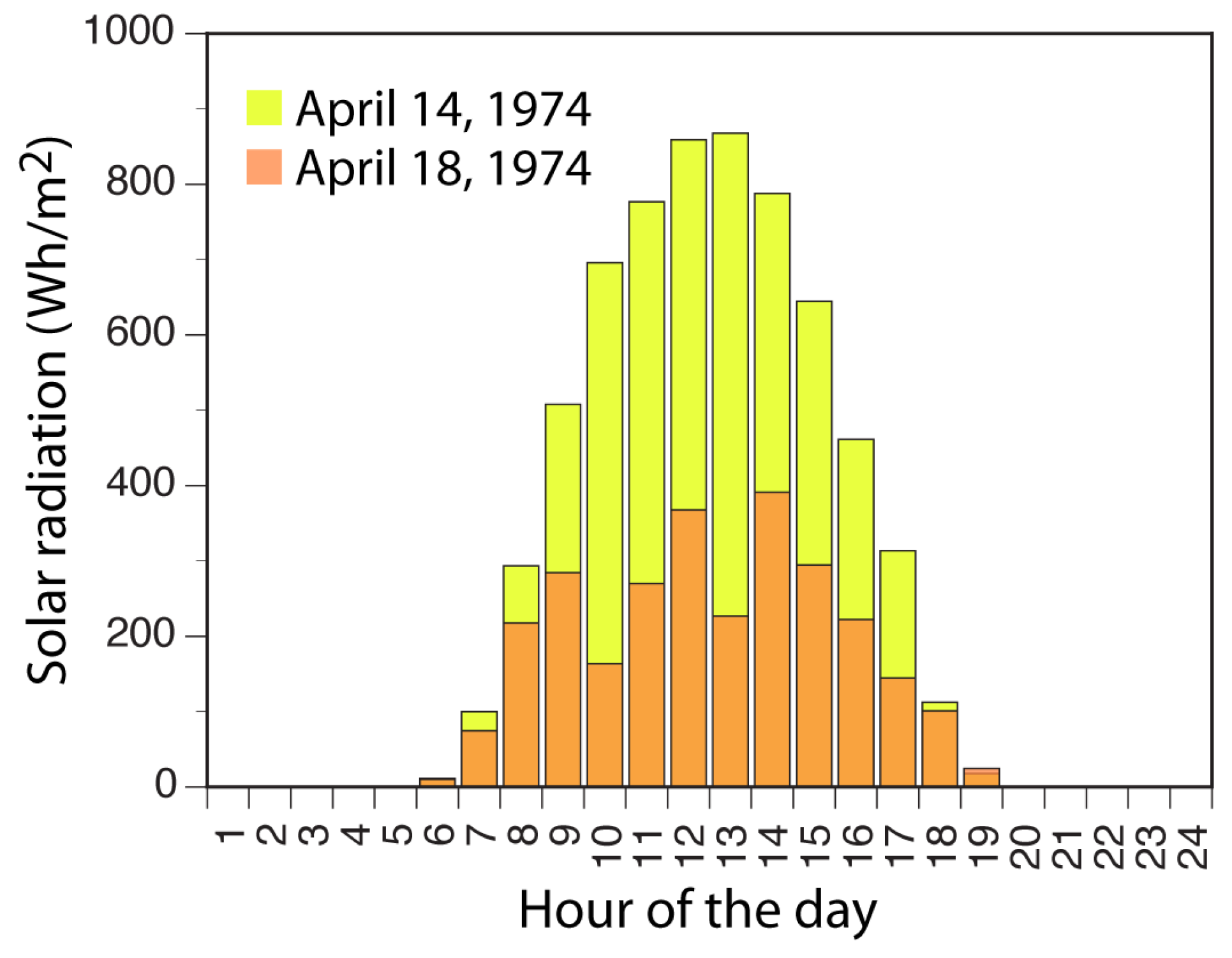
- Solar radiation—The amount of solar radiation reaching the concrete surface depends on several factors including the structure’s location, surface orientation, altitude, atmospheric conditions, time of the day, and day of the year. Incoming heat due to solar radiation isin which is the solar absorptivity of the concrete, which is influenced by the color and texture of the concrete surface, and is the incident solar radiation acting on a horizontal surface (W/m). The latter of the two values can be obtained from recorded weather data for the time period and region of interest.
- Thermal radiation - Heat loss to the surroundings due to grey-body radiation is calculated usingwhere σ is the Stefan-Boltzmann constant ( W/(m · K)), ϵ is the emissivity of the concrete (=0.9, in this study), and is the temperature of the concrete surface (K). is the sky temperature, which depends on the sky emissivity, the dew point temperature, and the cloud conditions [34].
- The heat capacity of the cement paste is estimated using an approach given by Bentz [35], in which heat capacity is a function of degree of reaction of the cement. The heat capacity of the concrete is then determined from the heat capacities of the cement paste and aggregates, according to the mass fractions of each using an ordinary rule of mixtures.
- Thermal conductivity of the concrete is estimated by taking the average of the Hashin-Shtrikman bounds for a two-phase composite formed of paste and aggregates [35].
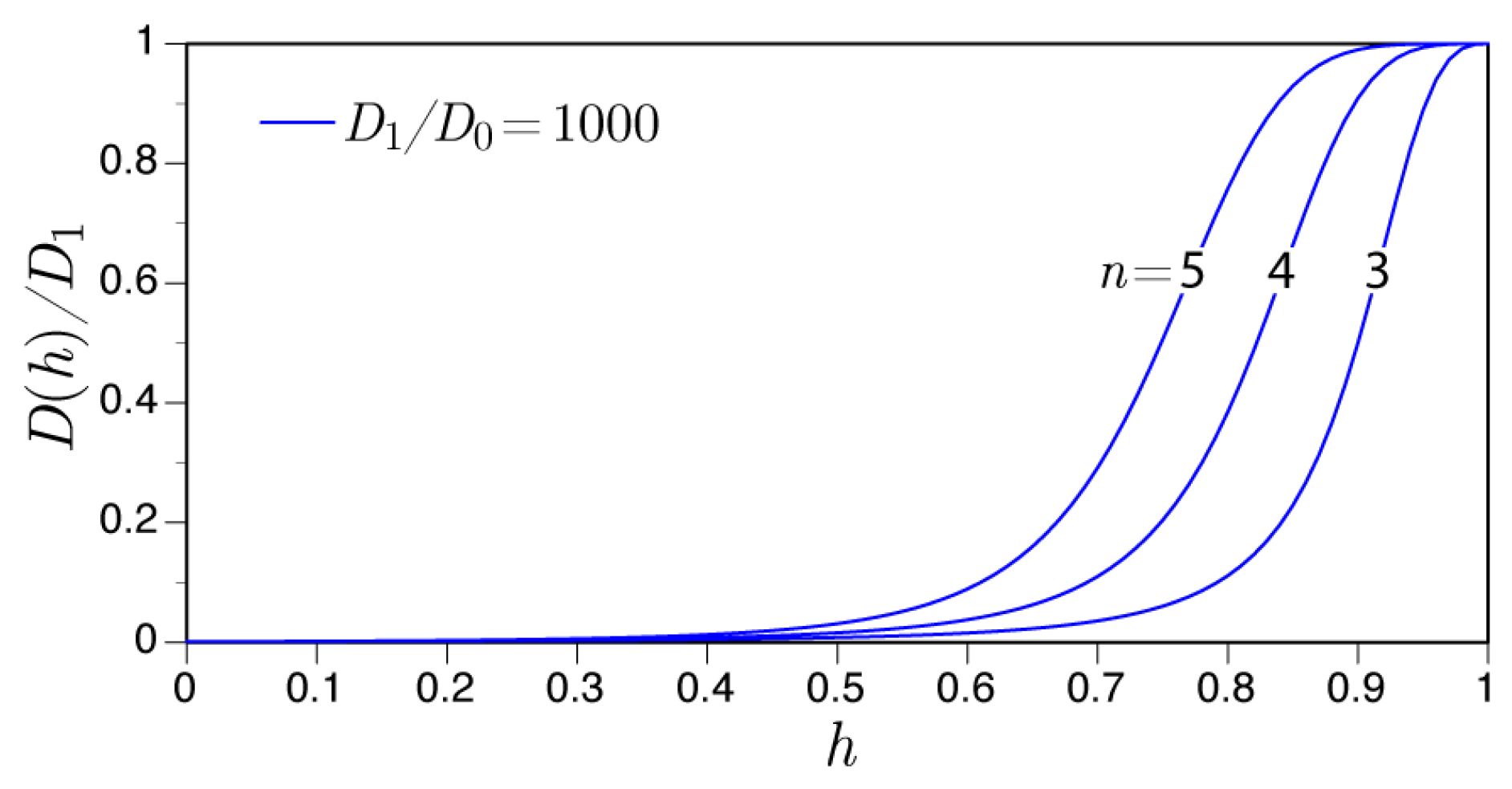
2.4.2. Hygral Analysis
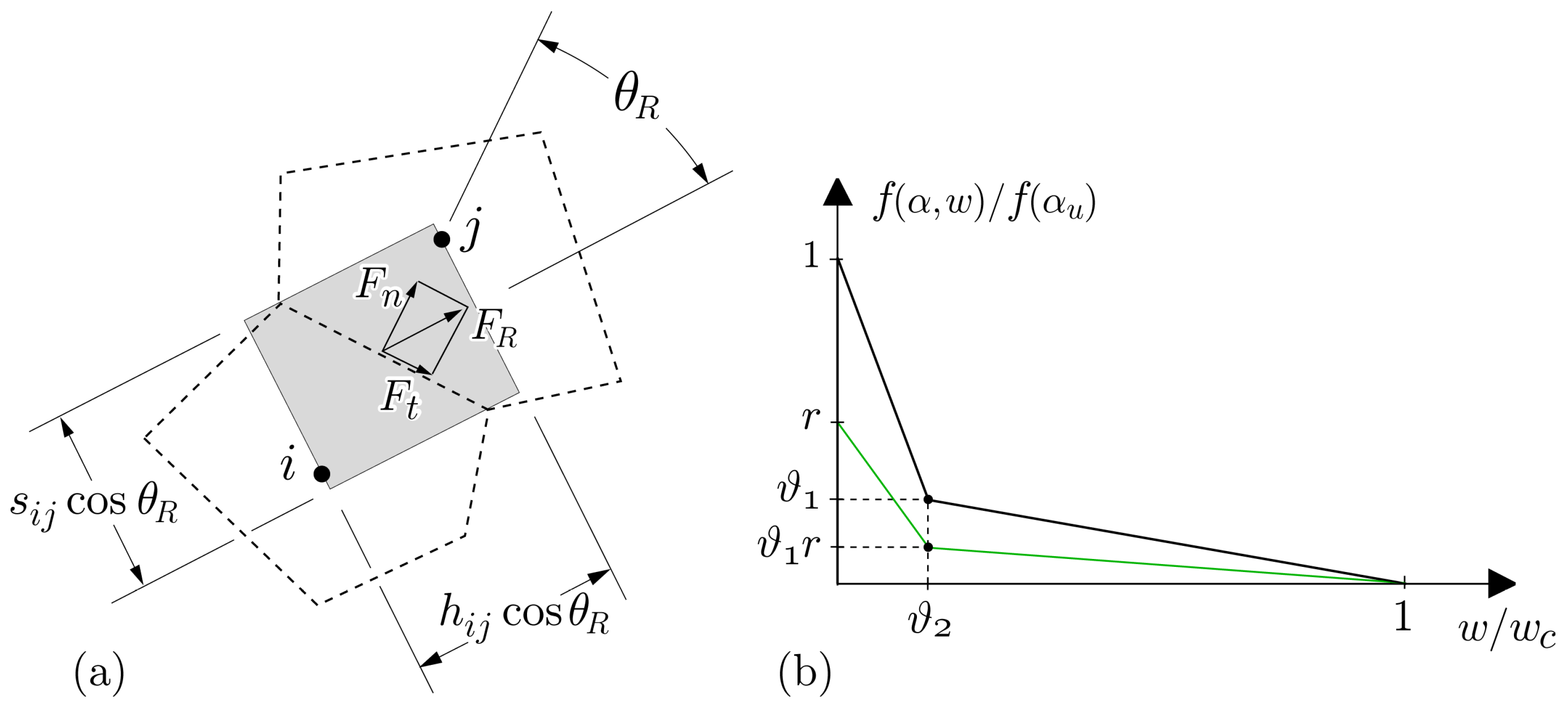
2.4.3. Structural Analysis
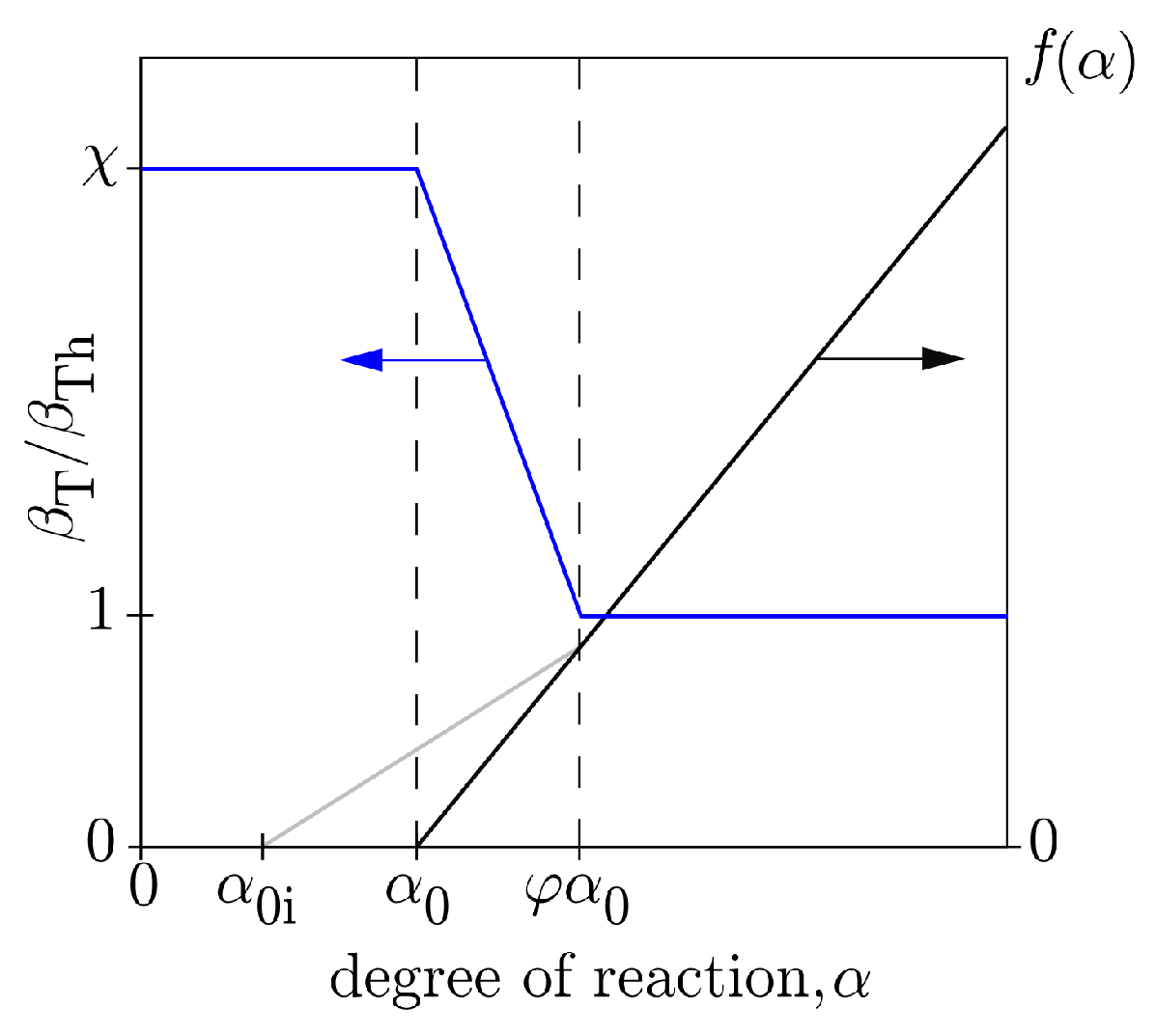
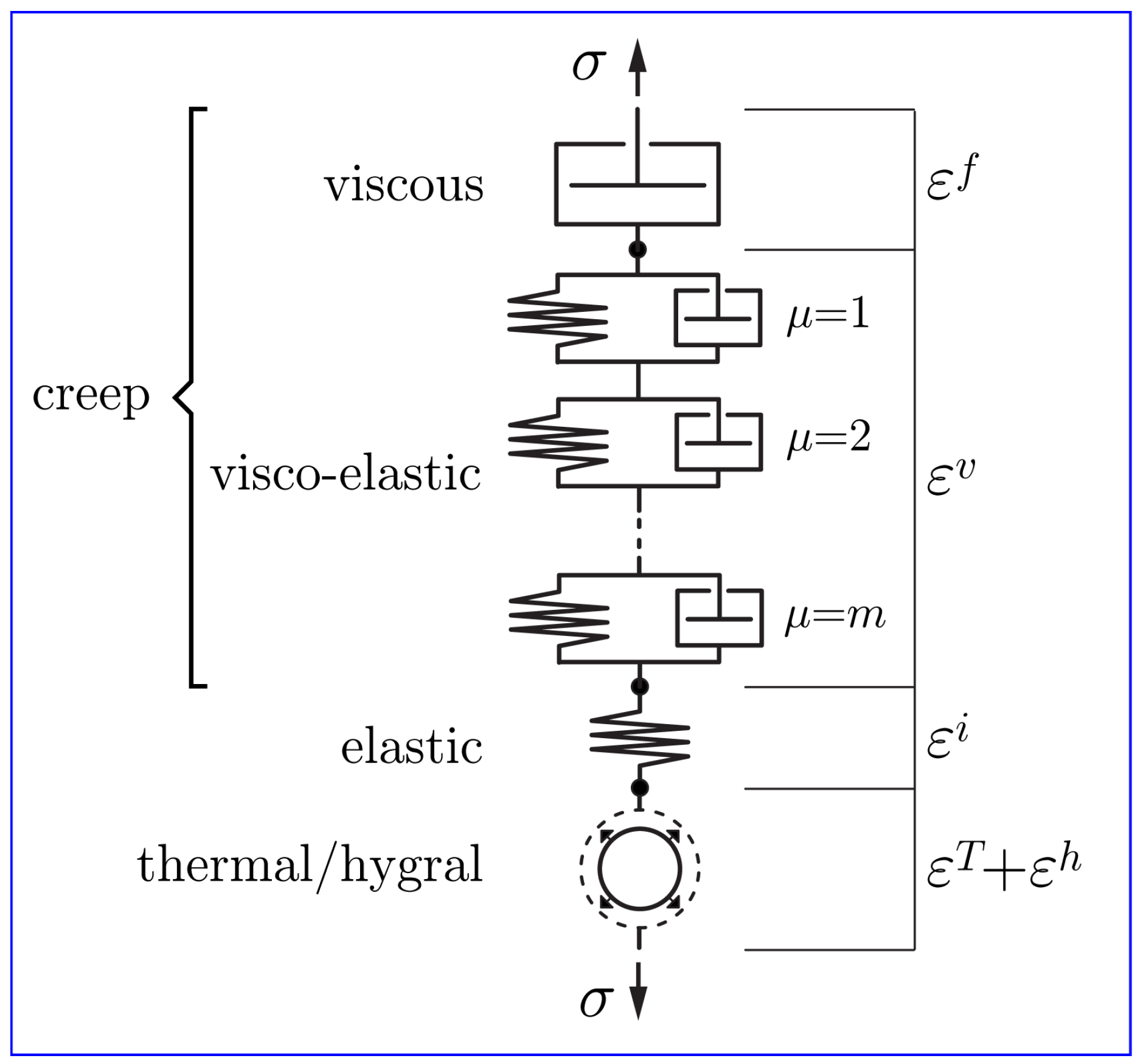
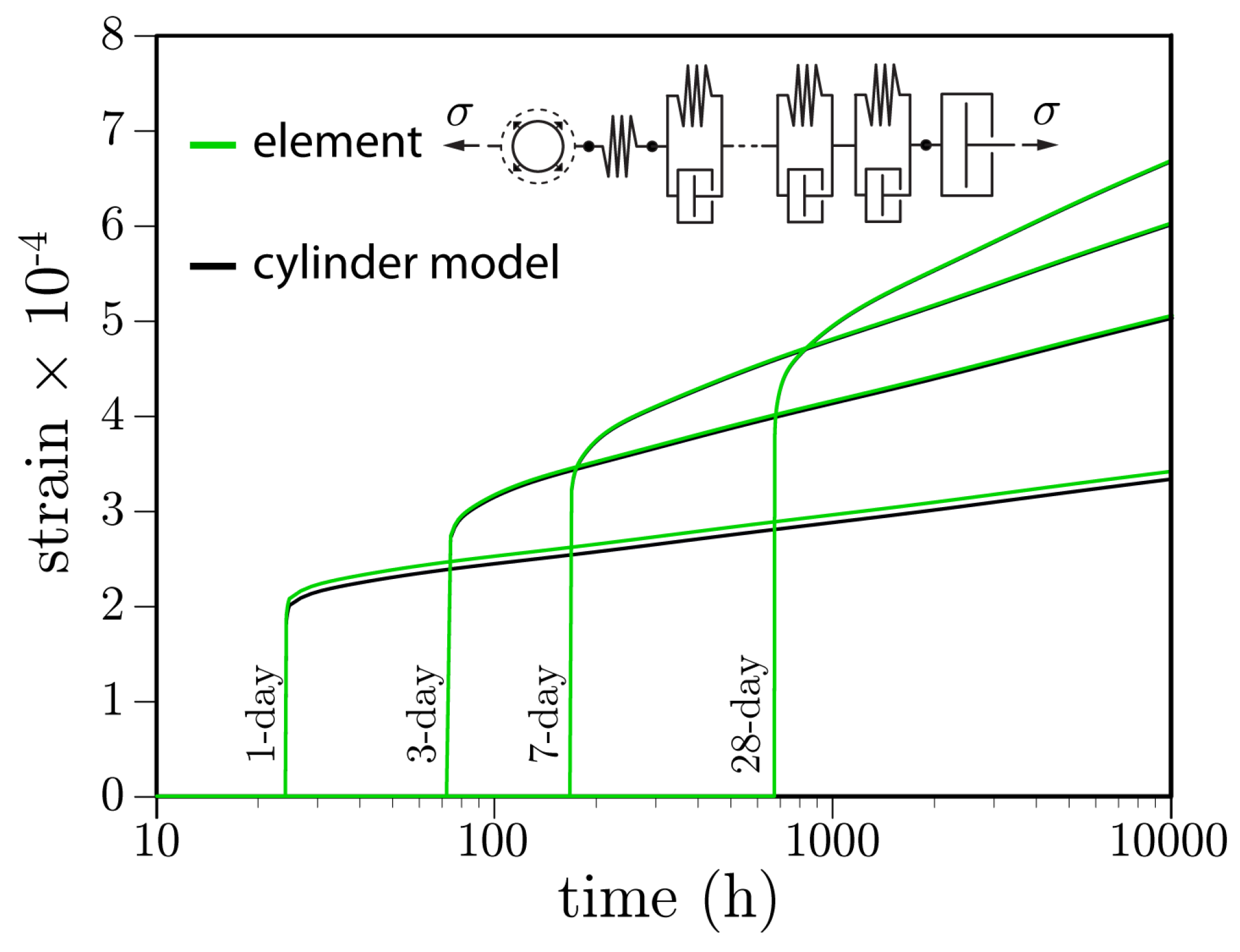
2.5. Stiffness and Creep Representation
3. Validation Exercises
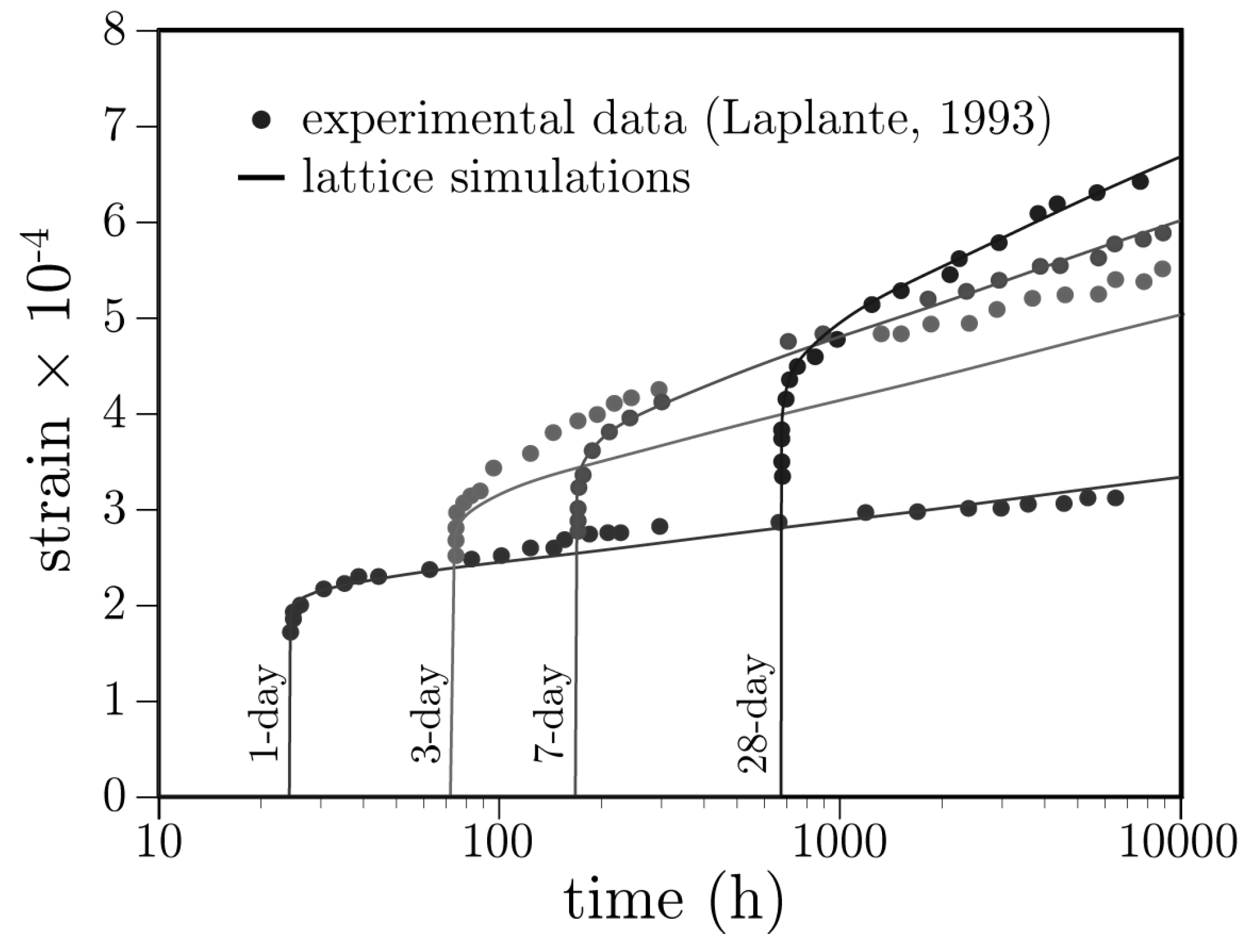
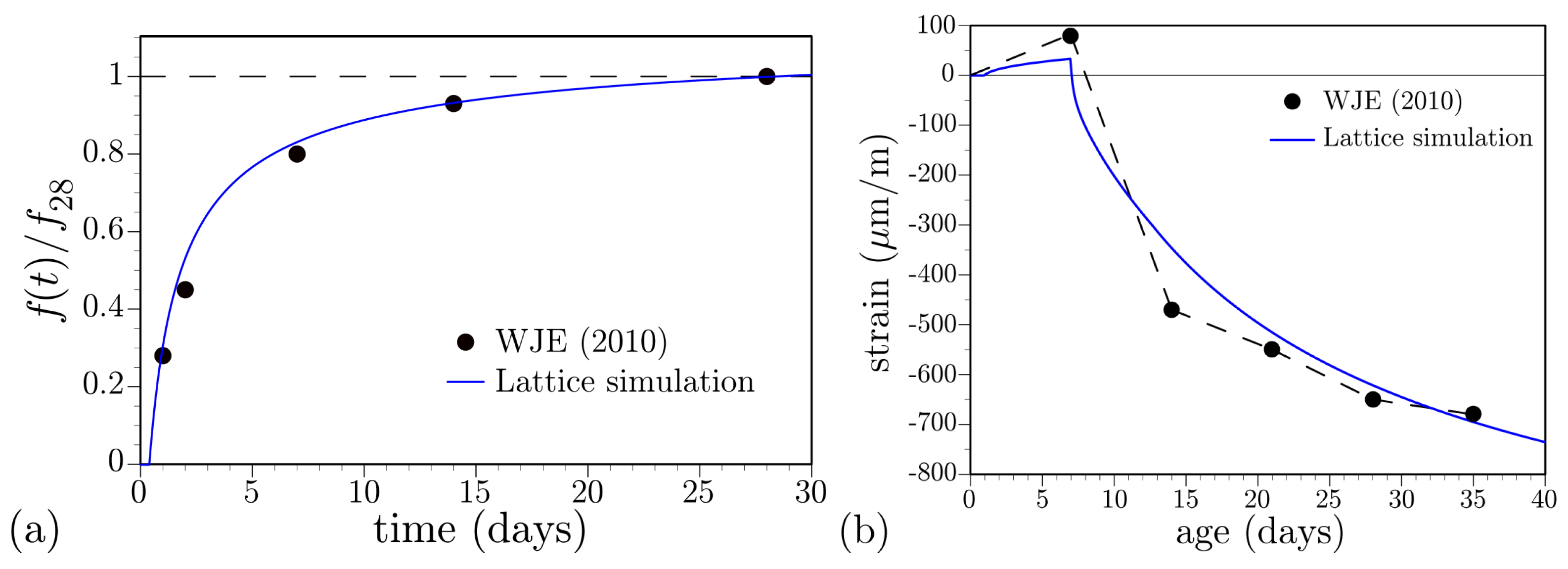
3.1. Stiffness and Basic Creep Development
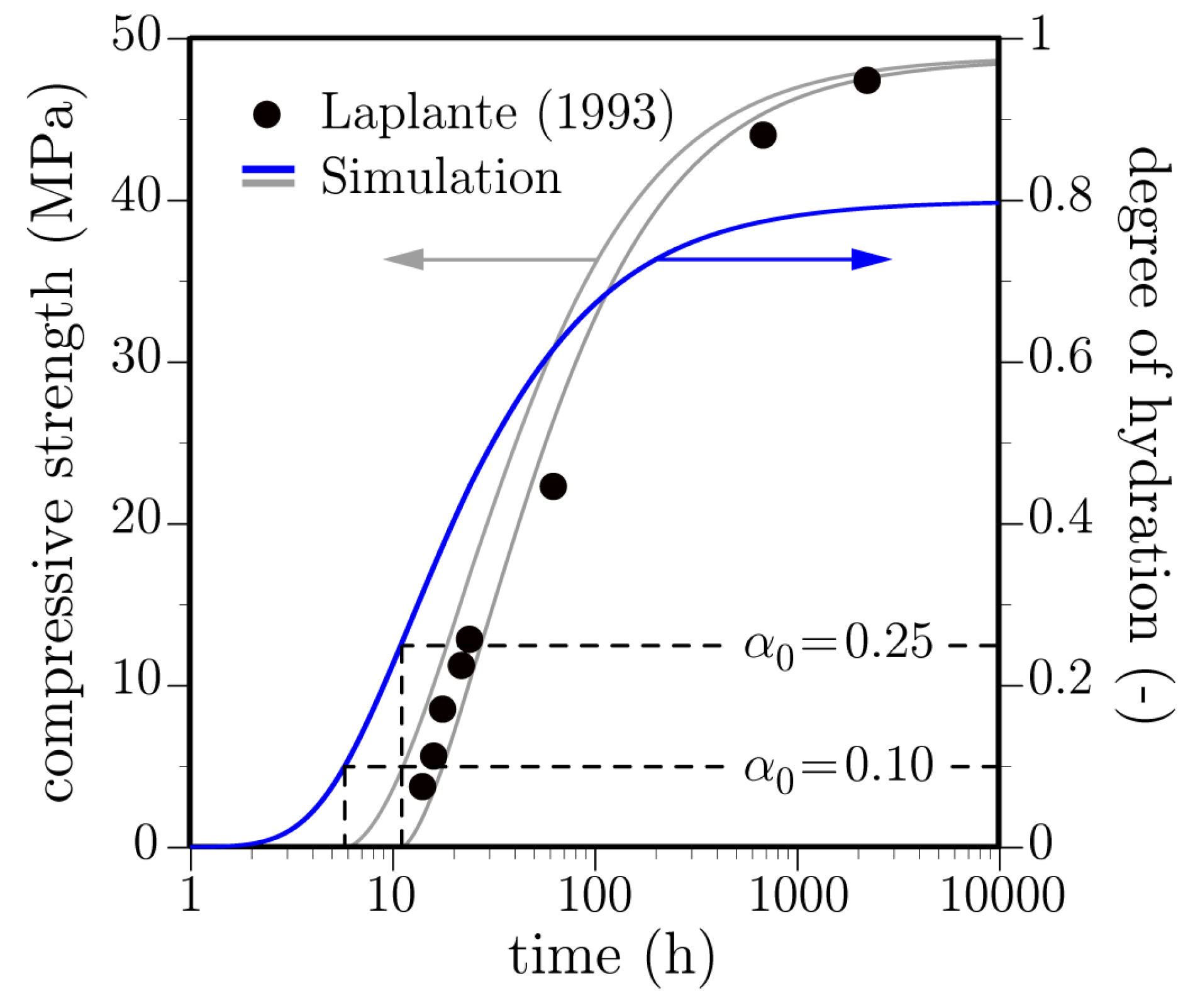
3.2. Strength Development
3.3. Autogenous and Drying Shrinkage Tests
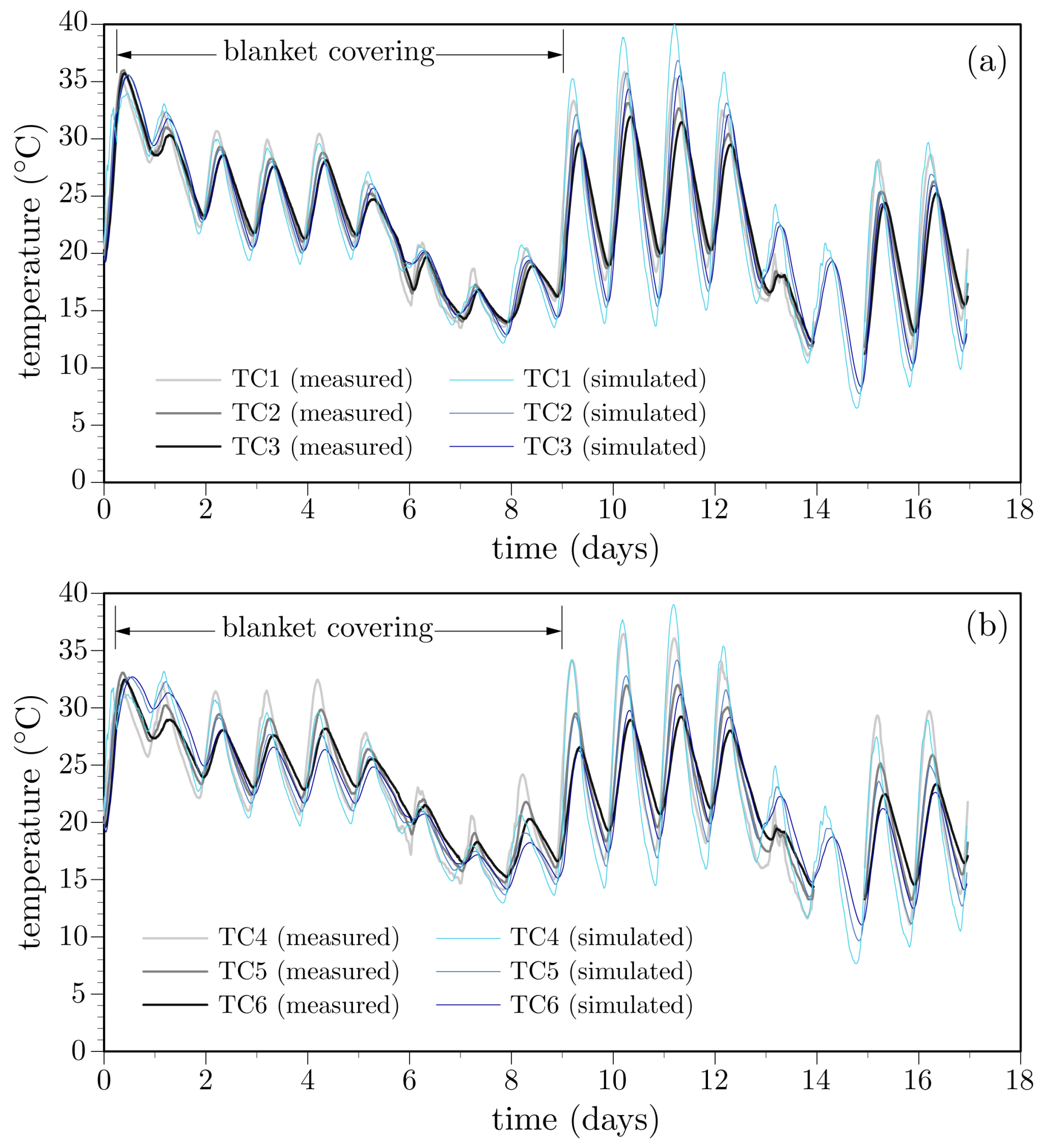
3.4. Analysis of Concrete Bridge Decks
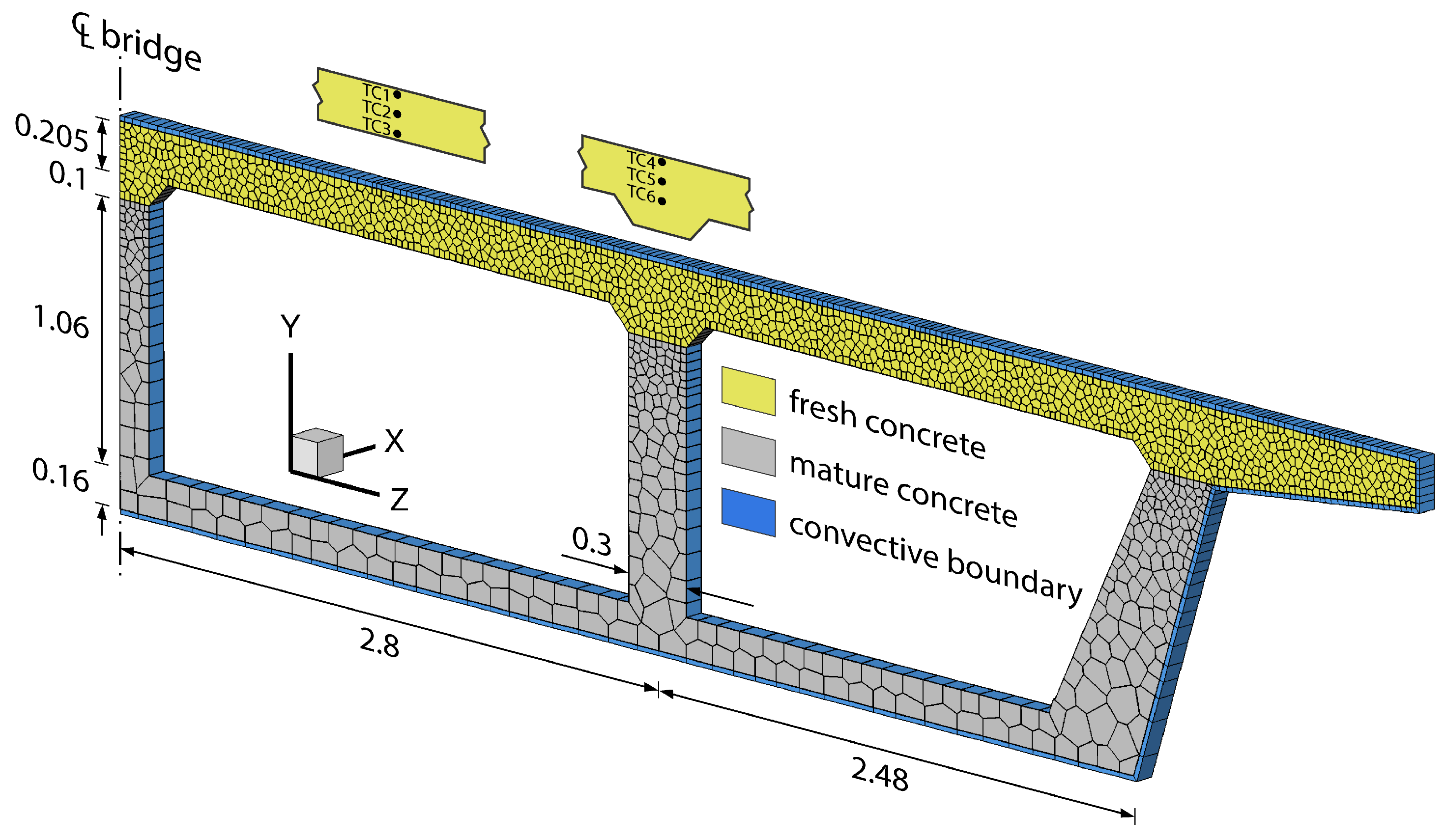
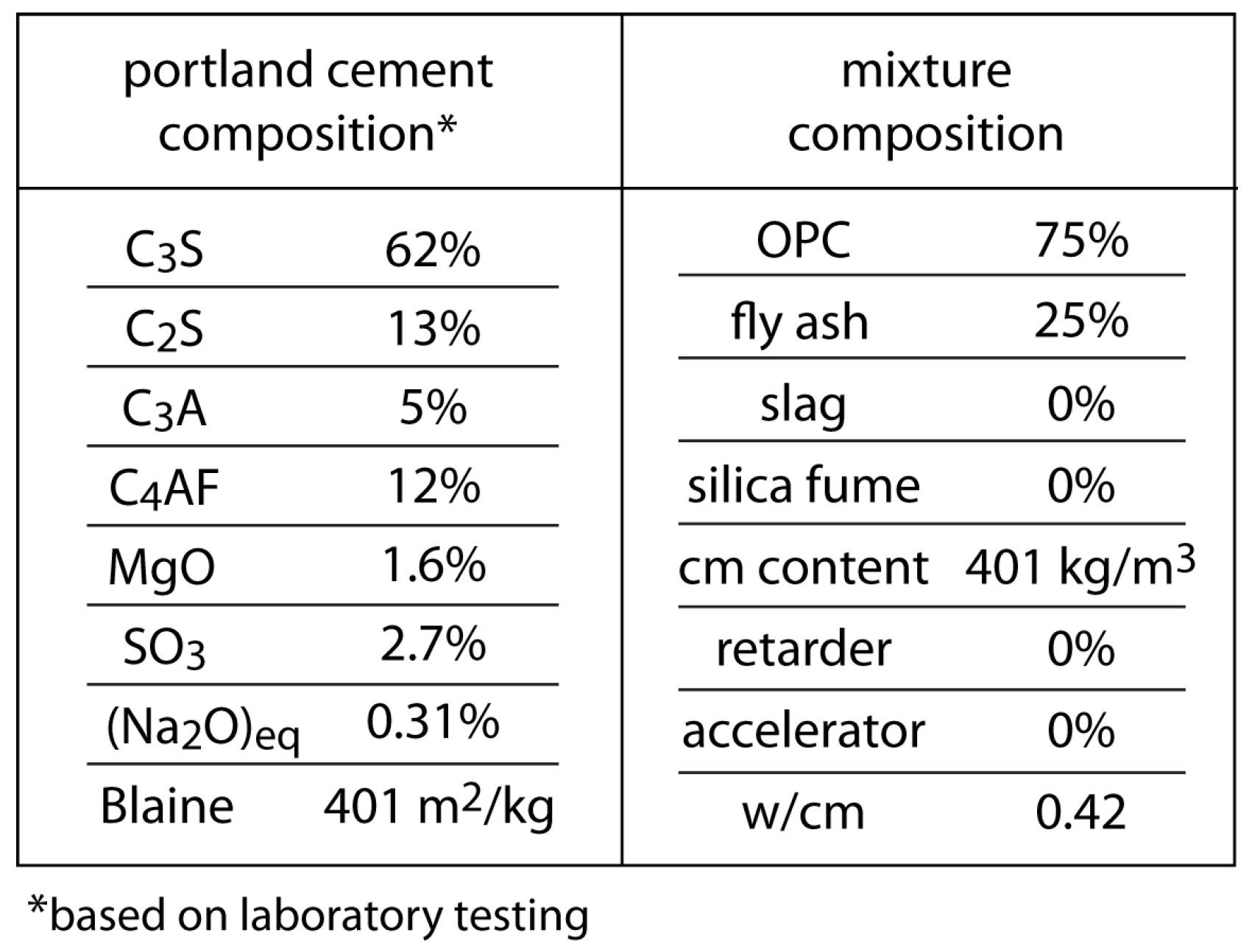
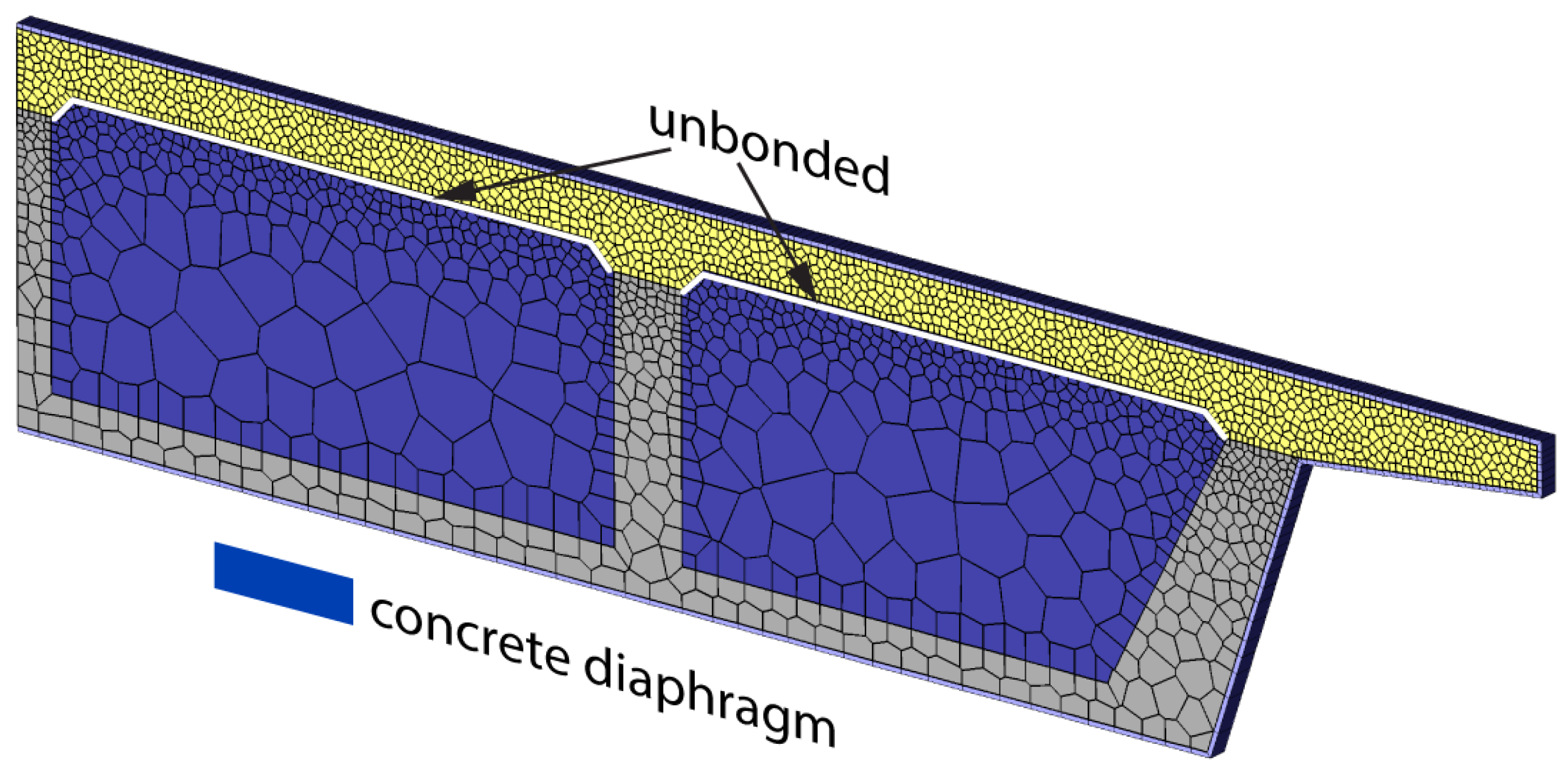
3.4.1. Model Definition
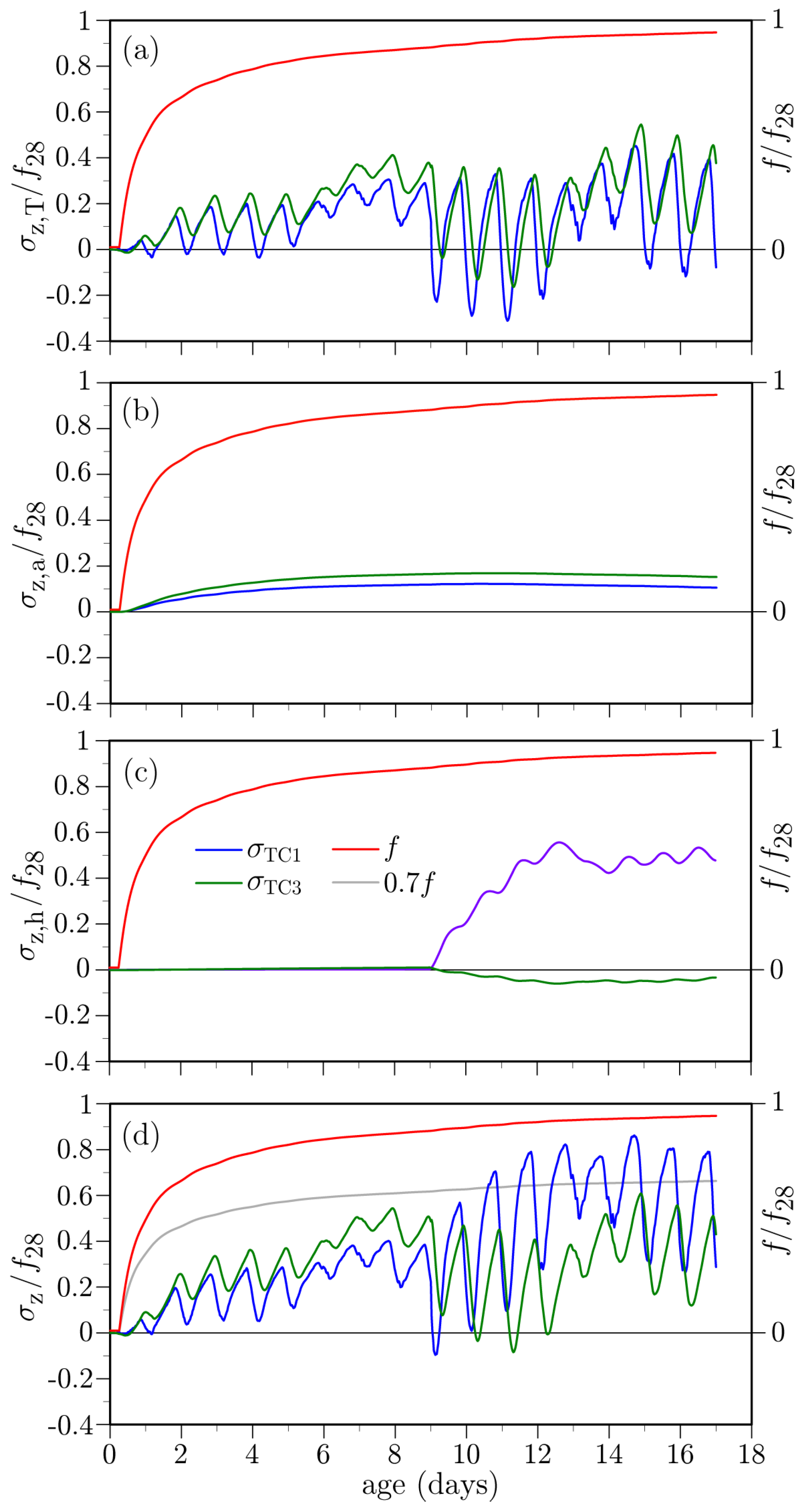
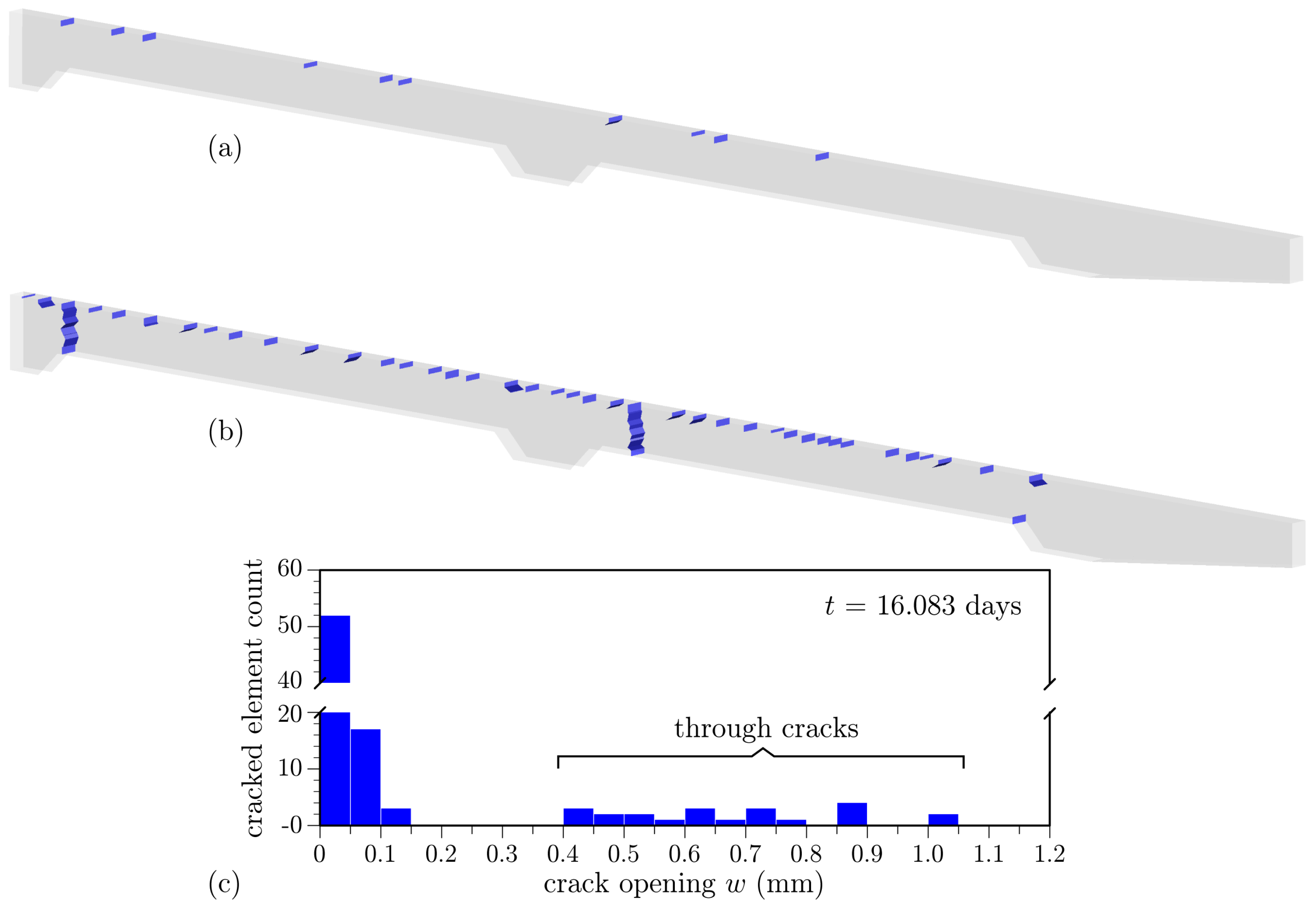
3.4.2. Simulation Results
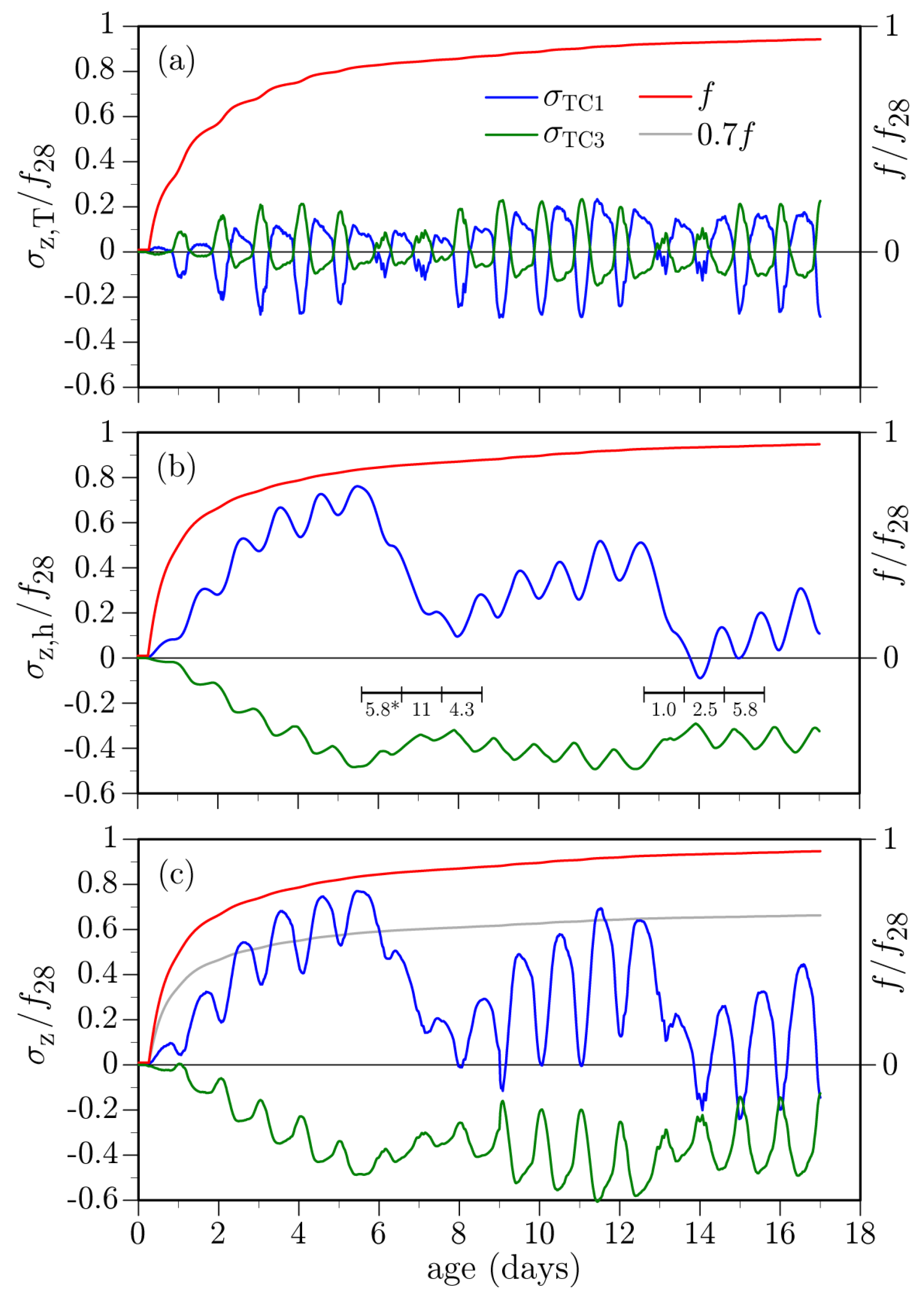
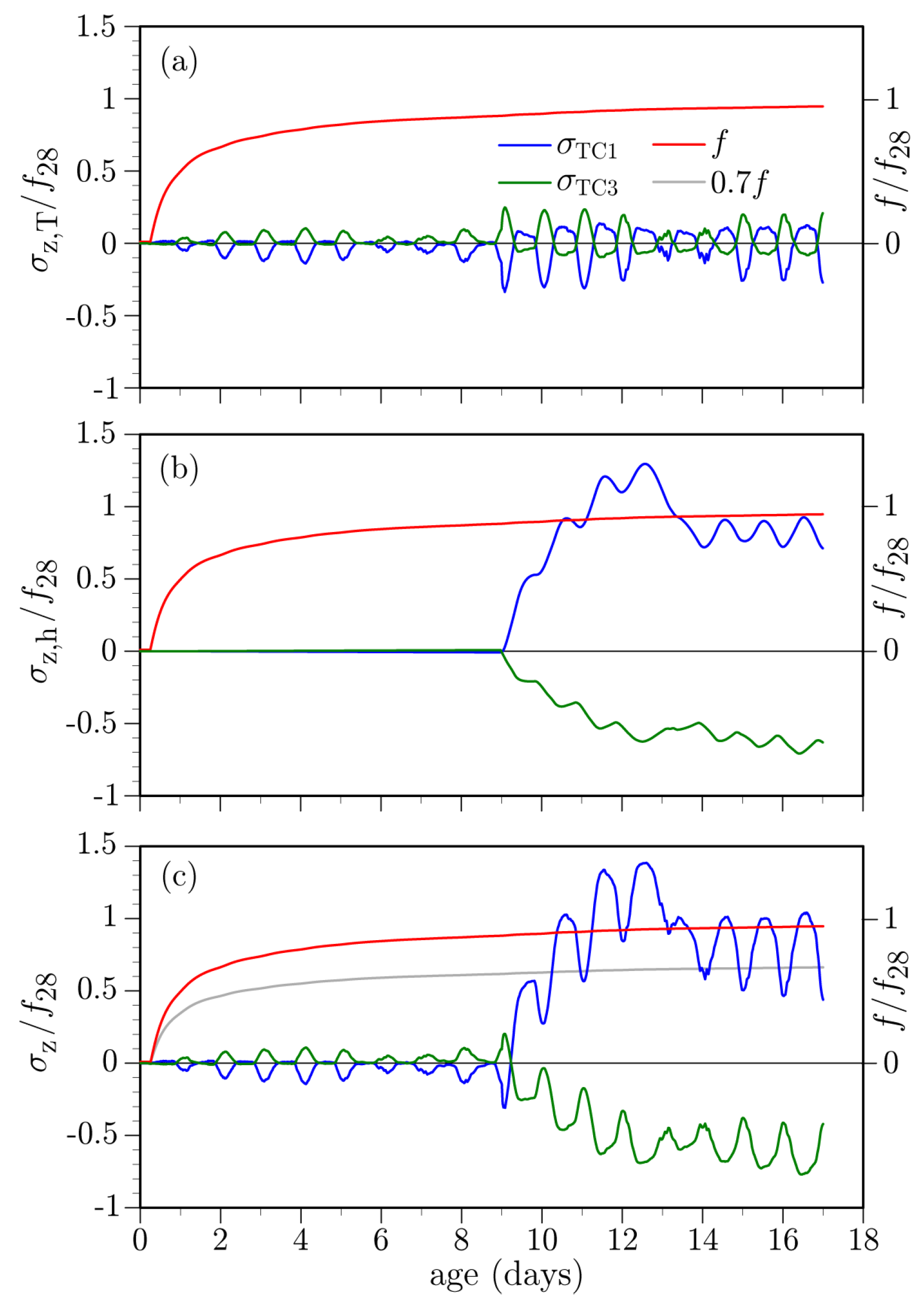
- The influence of environmental factors is evident from the oscillatory behavior of the temperature history recorded by each thermocouple. After the first day, locations closer to the surface exhibit larger temperature swings, whereas deeper locations are less affected by environmental changes. This meets expectations.
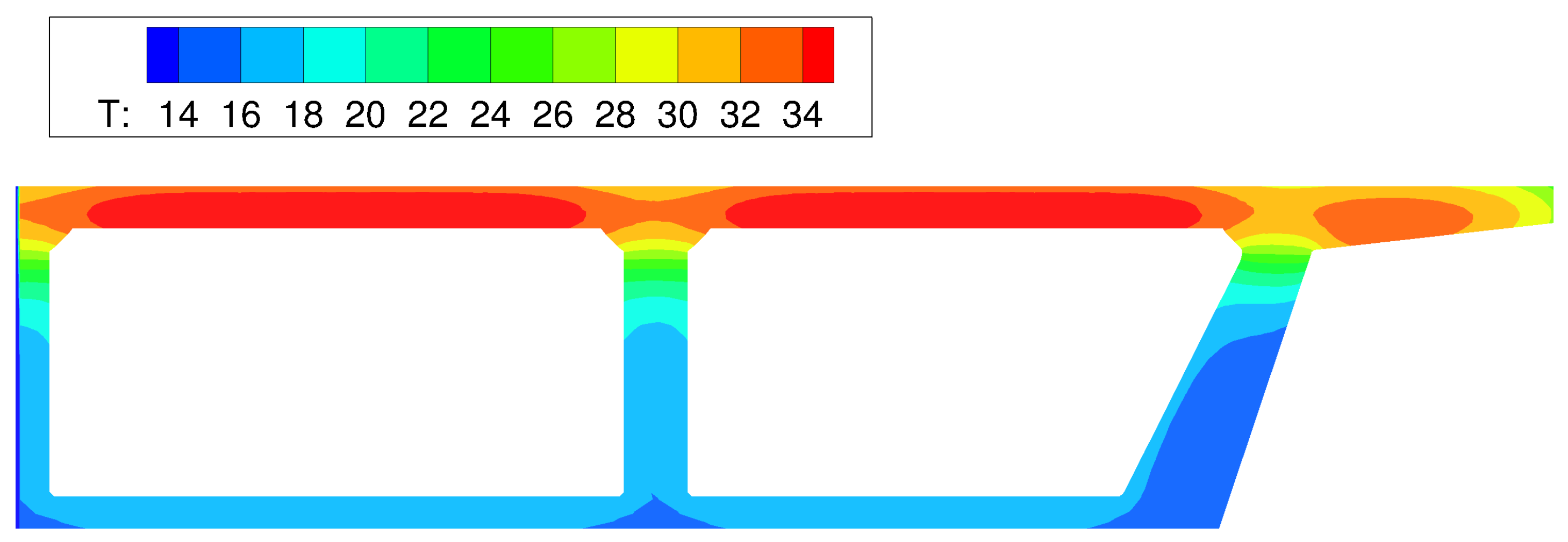
- Peak temperatures occur at about 10 h after concrete casting (Figure 18). The lower temperatures over the supporting girders are due to conduction of heat toward the cooler substrate concrete. Conversely, the insulative properties of the plywood formwork give rise to higher temperatures between the supporting girders. These temperatures are significantly higher than the ambient temperature. The differences between the ambient and measured deck temperatures largely diminish over the first two days after casting, in contrast to mass concrete applications in which large temperature differences can exist for several weeks. Despite the discrete, irregular discretization of the domain, the iso-contours of temperature do not exhibit artifacts associated with mesh bias.
- After removal of the curing sheets, not only do diurnal variations in deck temperature increase, but also the temperature gradient through the deck thickness tends to increase. The implications of the larger thermal gradients are discussed later.
4. Parametric Study
4.1. Curing Protocol
4.2. Structural Configuration
5. Conclusions
- This form of discrete model is capable of simulating the multi-field quantities associated with early-age concrete behavior, despite its discontinuous representation of the problem domain. There are no major disadvantages of this discrete approach with respect to continuum approaches, such as the finite element method. Advantages of this form of discrete model include its simplicity and adeptness at simulating the transition from diffuse damage to localized cracking.
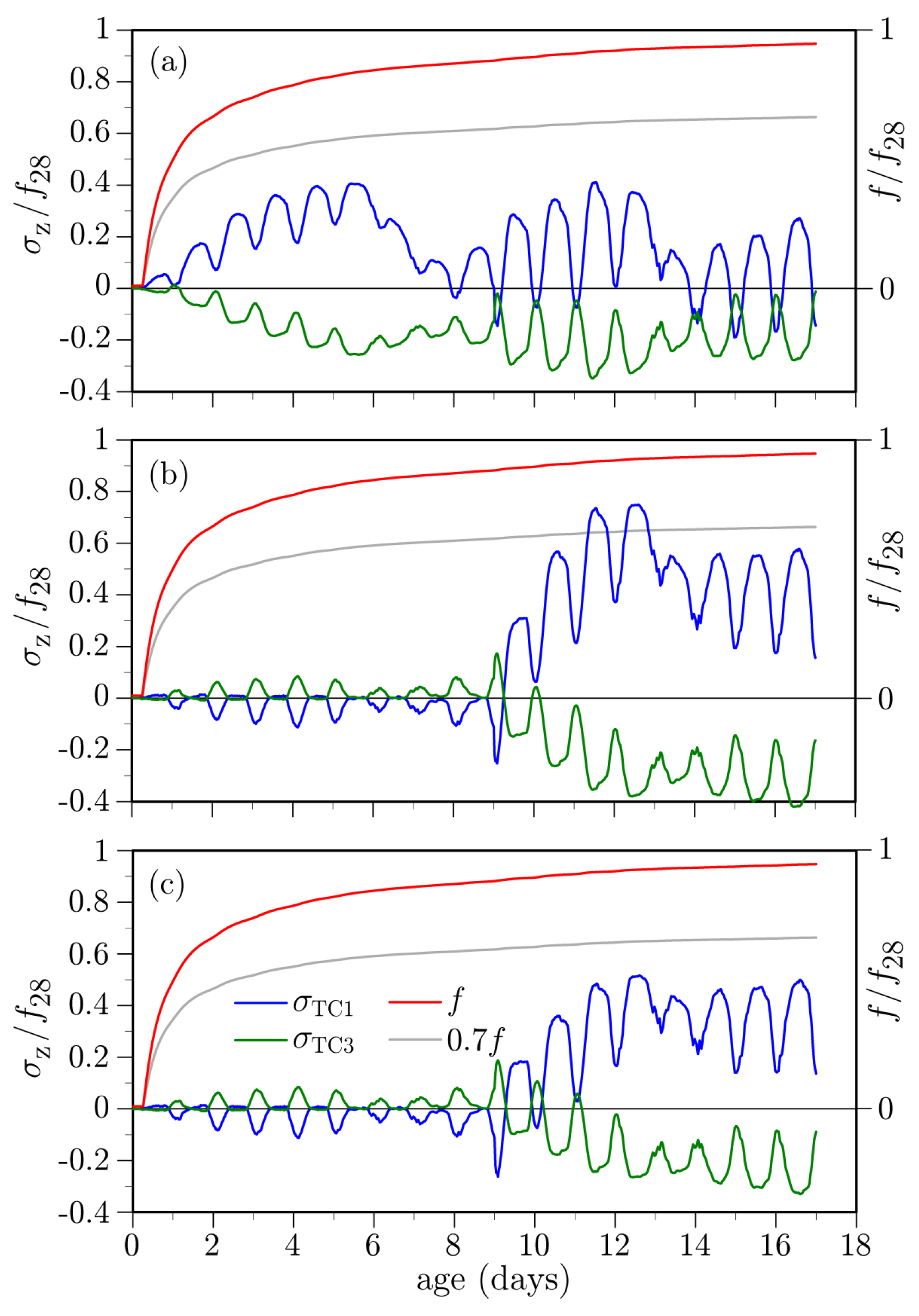
- Stress-to-strength ratio is lacking as a practical measure of cracking potential. Sharp hygral or thermal gradients near exposed surfaces typically cause high stresses, which is indicative of cracking. However, the cracking may only be superficial. Knowledge of the stress conditions through the structural cross-section is also necessary for evaluating the severity and potential consequences of cracking. In this sense, numerical modeling nicely complements knowledge gained by laboratory testing and field observations.
- Structural configuration plays a key role in determining the magnitude and distribution of stresses caused by volume instabilities of the concrete material. Under largely restrained conditions, both thermal and hygral effects were found to be primary contributors to cracking potential, leading to crack propagation through the depth of the deck. Three-dimensional simulations are needed to assess the influence of longitudinal restraints, thermal flexing of the mature concrete girders, and the effects of reinforcing bars.
- Realistic simulations of the early-age behavior of structural concrete require a wealth of information regarding the material constituents, production/curing processes, and structural and environmental boundary conditions. As shown by the parametric studies conducted herein, cracking potential is sensitive to input quantities that are typically not well defined, especially in field applications. Ultimately, the assessment of cracking potential needs to be cast in a probabilistic framework that accounts for uncertainties in the various inputs to the modeling effort.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Symbol | Definition |
| Euclidean distance between nodes i and j [m] | |
| t | time [s, h, d] |
| area of Voronoi facet common to nodes i and j [m] | |
| Thermal analysis | |
| aggregate to cementitious materials ratio [kg/kg] | |
| c | cementitious materials content [kg/m] |
| specific heat capacity [J/(kg · K)] | |
| , | heat flux due to convection and its modified value [W/m] |
| , | heat flux due to solar radiation and its modified value [W/m] |
| , | heat flux due to radiation and its modified value [W/m] |
| concrete equivalent age [h] | |
| water-to-cementitious materials ratio [kg/kg] | |
| D | thermal diffusivity [m/s] |
| apparent activation energy [J/mol] | |
| H | cumulative amount of heat produced by hydration [J/kg] |
| heat of hydration of cement [J/kg] | |
| total heat available for reaction [J/kg] | |
| Q | rate of heat production by cementitious materials hydration [J/(kg · s)] |
| R | universal gas constant [J/(mol · K)] |
| T | temperature [C] |
| , , , | ambient, concrete, reference, and surface temperatures [C] |
| sky temperature [C] | |
| α, | degree of cementitious materials hydration and its ultimate value |
| β, τ | hydration model parameters |
| , | coefficient of thermal expansion and its long-term value [1/C] |
| solar absorptivity of concrete | |
| ϵ | emissivity of concrete |
| , , | heat flux reduction factors |
| λ | thermal conductivity [W/(m · K)] |
| ρ | mass density of concrete [kg/m] |
| σ | Stefan-Boltzmann constant [W/(m · K)] |
| χ | magnifying factor for coefficient of thermal expansion at early-ages |
| coefficient of convective heat transfer [W/(m · K)] | |
| , | elemental and system capacity matrices |
| , | elemental and system conductivity matrices |
| Hygral analysis | |
| h | relative humidity [-] |
| ambient relative humidity [-] | |
| , | relative humidity associated with self-desiccation and its ultimate value [-] |
| n | parameter relating hygral diffusivity and relative humidity |
| , | moisture flux due to convection and its modified value [m/s] |
| s | parameter relating humidity decrease and self-desiccation |
| , | diffusivity values associated with fully dried material [m/s] |
| , | diffusivity values associated with saturated material [m/s] |
| hygral diffusivity [m/s] | |
| hygral shrinkage coefficient | |
| hygral convection coefficient [m/s] | |
| Mechanical analysis | |
| b | element thickness [m] |
| , | compressive strength and its asymptotic limit [MPa] |
| f | tensile strength [MPa] |
| stiffness coefficients of the uniaxial springs [N/m] | |
| stiffness coefficients of the rotational springs [N · m] | |
| parameter relating rate of solidification to degree of hydration | |
| , , | instantaneous elastic, viscoelastic, and viscous strain parameters [1/MPa] |
| age of loading [h] | |
| equivalent age [h] | |
| reduced time representing the thermal-hygral effects on creep [h] | |
| , | times of initial and final concrete setting [h] |
| w | crack opening [m] |
| traction-free crack opening [m] | |
| projected area of element facet [m] | |
| E | elastic modulus of concrete [MPa] |
| , | activation energies for creep and microprestress processes [J/mol] |
| , , | spring-set forces in the normal and two tangential directions [N] |
| , | principal planar and polar second moments of facet area [m] |
| material constitutive matrix | |
| , | elemental and global stiffness matrices |
| , | degrees of hydration at initial and final setting |
| coefficient governing concrete setting behavior | |
| γ | viscoelastic microstrain |
| , | hygral and thermal strains |
| , , | instantaneous elastic, viscoelastic, and viscous flow strains |
| ζ | coefficient governing material property development |
| η | effective microscopic viscosity [MPa/s] |
| κ | stress-to-strength ratio |
| microprestress model parameter [1/(MPa · d)] | |
| microprestress model parameter [MPa/K] | |
| ν | Poisson’s ratio |
| inclination of tensile force resultant relative to the element axis | |
| , | parameters defining the break-point in the tension softening relation |
| σ | axial stress [MPa] |
| stress resultant [MPa] | |
| , | penetration resistance and its value at final setting [MPa] |
| reduced time coefficients for creep and microprestress processes | |
| ξ | factor relating normal and shear spring stiffnesses |
| ω | degree of damage |
| Φ | non-aging micro-compliance function [1/MPa] |
References
- Bentz, D.P. A review of early-age properties of cement-based materials. Cem. Concr. Res. 2008, 38, 196–204. [Google Scholar] [CrossRef]
- Comite Euro-International du Beton (CEB). Durable concrete structures—Design Guide; Thomas Telford Ltd.: London, UK, 1992. [Google Scholar]
- Banthia, N.; Gupta, R. Plastic shrinkage cracking in cementitious repairs and overlays. Mater. Struct. 2009, 42, 567–579. [Google Scholar] [CrossRef]
- Bentz, D.P.; Geiker, M.R.; Hansen, K.K. Shrinkage-reducing admixtures and early age desiccation in cement pastes and mortars. Cem. Concr. Res. 2001, 31, 1075–1085. [Google Scholar] [CrossRef]
- Maggenti, R.; Knapp, C.; Fereira, S. Controlling shrinkage cracking. Concr. Int. 2013, 35, 36–41. [Google Scholar]
- Weiss, W.J.; Yang, W.; Shah, S.P. Shrinkage cracking of restrained concrete slabs. J. Eng. Mech. 1998, 124, 765–774. [Google Scholar] [CrossRef]
- Emborg, M.; Bernander, S. Assessment of risk of thermal cracking in hardening concrete. J. Struct. Eng. 1994, 120, 2893–2912. [Google Scholar] [CrossRef]
- Šavija, B.; Schlangen, E. Use of phase change materials (PCMs) to mitigate early age thermal cracking in concrete: Theoretical considerations. Constr. Build. Mater. 2016, 126, 332–344. [Google Scholar] [CrossRef]
- Subramaniam, K.V.L. Identification of early-age cracking in concrete bridge decks. J. Perform. Constr. Facil. 2016, 30. [Google Scholar] [CrossRef]
- Subramaniam, K.V.L.; Kunin, J.; Curtis, R.; Streeter, D. Influence of early temperature rise and movements and stress development in concrete bridge decks. J. Bridge Eng. 2010, 15, 108–116. [Google Scholar] [CrossRef]
- Zanotti, C.; Meda, A.; Plizzari, G.; Cangiano, S. Evaluation of the risk of cracking in thin concrete walls due to hydration heat. In Concrete under Severe Conditions: Environment and Loading (CONSEC’10); CRC Press: Boca Raton, FL, USA, 2010; pp. 257–264. [Google Scholar]
- Bolander, J.E.; Saito, S. Fracture analyses using spring networks with random geometry. Eng. Fract. Mech. 1998, 61, 569–591. [Google Scholar] [CrossRef]
- Benkemoun, N.; Poullain, P.H.; Al Khazraji, H.; Choinska, M.; Khelidj, A. Meso-scale investigation of failure in the tensile splitting test: Size effect and fracture energy analysis. Eng. Fract. Mech. 2016, 168, 242–259. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice discrete particle model (LDPM) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Eliáš, J.; Vořechovský, M.; Skoček, J.; Bažant, Z.P. Stochastic discrete meso-scale simulations of concrete fracture: Comparison to experimental data. Eng. Fracture Mech. 2015, 135, 1–16. [Google Scholar] [CrossRef]
- Grassl, P.; Jirásek, M. Meso-scale approach to modelling the fracture process zone of concrete subjected to uniaxial tension. Int. J. Solids Struct. 2010, 47, 957–968. [Google Scholar] [CrossRef]
- Kozicki, J.; Tejchman, J. Modelling of fracture process in concrete using a novel lattice model. Granul. Matter 2008, 10, 377–388. [Google Scholar] [CrossRef]
- Nagai, K.; Sato, Y.; Ueda, T. Mesoscopic simulation of failure of mortar and concrete by 3D RBSM. J. Adv. Concr. Technol. 2005, 3, 385–402. [Google Scholar] [CrossRef]
- Schlangen, E.; van Mier, J.G.M. Experimental and numerical analyses of micromechanisms of fracture of cement-based composites. Cem. Concr. Compos. 1992, 14, 105–118. [Google Scholar] [CrossRef]
- Alnaggar, M.; Cusatis, G.; di Luzio, G. Lattice discrete particle modeling (LDPM) of alkali silica reaction (ASR) deterioration of concrete structures. Cem. Concr. Compos. 2013, 41, 45–59. [Google Scholar] [CrossRef]
- Bolander, J.E.; Berton, S. Simulation of shrinkage induced cracking in cement composite overlays. Cem. Concr. Compos. 2004, 26, 861–871. [Google Scholar] [CrossRef]
- Liu, L.; Ye, G.; Schlangen, E.; Chen, H.; Qian, Z.; Sun, W.; van Breugel, K. Modeling of the internal damage of saturated cement paste due to ice crystallization pressure during freezing. Cem. Concr. Compos. 2011, 33, 562–571. [Google Scholar] [CrossRef]
- Šavija, B.; Pacheco, J.; Schlangen, E. Lattice modeling of chloride diffusion in sound and cracked concrete. Cem. Concr. Compos. 2013, 42, 30–40. [Google Scholar] [CrossRef]
- Faria, R.; Anzenha, M.; Figueiras, J.A. Modeling of concrete at early ages: Application to an externally restrained slab. Cem. Concr. Compos. 2006, 28, 572–585. [Google Scholar] [CrossRef]
- Di Luzio, G.; Cusatis, G. Solidification-microprestress-microplane (SMM) theory for concrete at early age: Theory, validation and application. Int. J. Solids Struct. 2013, 50, 957–975. [Google Scholar] [CrossRef]
- Kawai, T. New discrete models and their application to seismic response analysis of structures. Nucl. Eng. Des. 1978, 48, 207–229. [Google Scholar] [CrossRef]
- Asahina, D.; Bolander, J.E. Voronoi-based discretizations for fracture analysis of particulate materials. Powder Technol. 2011, 213, 92–99. [Google Scholar] [CrossRef]
- Schlangen, E.; Garboczi, E.J. New method for simulating fracture using an elastically uniform random geometry lattice. Int. J. Eng. Sci. 1996, 34, 1131–1144. [Google Scholar] [CrossRef]
- Asahina, D.; Landis, E.N.; Bolander, J.E. Modeling of phase interfaces during pre-critical crack growth in concrete. Cem. Concr. Compos. 2011, 33, 966–977. [Google Scholar] [CrossRef]
- Kang, J.; Kim, K.; Lim, Y.M.; Bolander, J.E. Modeling of fiber-reinforced cement composites: Discrete representation of fiber pullout. Int. J. Solids Struct. 2014, 51, 1970–1979. [Google Scholar] [CrossRef]
- Riding, K.A.; Folliard, K.J.; Juenger, M.C.G.; Schindler, A.K. Modeling hydration of cementitious systems. ACI Mater. J. 2012, 109, 225–234. [Google Scholar]
- Schindler, A.K.; Folliard, K.J. Heat of hydration models for cementitious materials. ACI Mater. J. 2005, 102, 24–33. [Google Scholar]
- Poole, J.L. Modeling Temperature Sensitivity and Heat Evolution of Concrete. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2007. [Google Scholar]
- Bentz, D.P. A Computer Model to Predict the Surface Temperature and Time of Wetness of Concrete Pavements and Bridge Decks; Technical Report NISTIR 6551; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2000. [Google Scholar]
- Bentz, D.P. Transient plane source measurements of the thermal properties of hydrating cement pastes. Mater. Struct. 2007, 40, 1073–1080. [Google Scholar] [CrossRef]
- Lewis, R.W.; Morgan, K.; Thomas, H.R.; Seetharamu, K.N. The Finite Element Method in Heat Transfer Analaysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis; PWS Publishers: Boston, MA, USA, 1985; 676p. [Google Scholar]
- Kada, H.; Lachemi, M.; Petrov, N.; Bonneau, O.; Aïtcin, P. Determination of the coefficient of thermal expansion of high performance concrete from initial setting. Mater. Struct. 2002, 35, 35–41. [Google Scholar] [CrossRef]
- Maruyama, I.; Teramoto, A.; Igarashi, G. Strain and thermal expansion coefficients of various cement pastes during hydration at early ages. Mater. Struct. 2014, 47, 27–37. [Google Scholar] [CrossRef]
- Sellevold, E.J.; Bjøntegaard, ∅. Coefficient of thermal expansion of cement paste and concrete: Mechanisms of moisture interaction. Mater. Struct. 2006, 39, 809–815. [Google Scholar] [CrossRef]
- Krauß, M.; Rostásy, F.S. Determination of initial degree of hydration by means of ultrasonic measurements. In Control of Cracking in Early Age Concrete, Proceedings of the International Workshop on Control of Cracking in Early Age Concrete; Mihashi, H., Wittmann, F.H., Eds.; AA Balkema Publishers: Sendai, Japan, 2002; pp. 19–28. [Google Scholar]
- Bažant, Z.P.; Najjar, L.J. Drying of concrete as a non-linear diffusion problem. Cem. Concr. Res. 1971, 1, 461–473. [Google Scholar] [CrossRef]
- Jonasson, J.-E. Moisture Fixation and Moisture Transfer in Concrete; Concrete Structures, SMiRT 8; IASMiR: Brussels, Belgium, 1985; pp. 235–242. [Google Scholar]
- Oh, B.H.; Cha, S.W. Nonlinear analysis of temperature and moisture distributions in early-age concrete structures based on degree of hydration. ACI Mater. J. 2003, 100, 361–370. [Google Scholar]
- Di Luzio, G.; Cusatis, G. Hygro-thermo-chemical modeling of high performance concrete, I: Theory. Cem. Concr. Compos. 2009, 31, 301–308. [Google Scholar] [CrossRef]
- Sadouki, H.; van Mier, J.G.M. Simulation of hygral crack growth in concrete repair system. Mater. Struct. 1997, 203, 518–526. [Google Scholar] [CrossRef]
- Grassl, P. A lattice approach to model flow in cracked concrete. Cem. Concr. Compos. 2009, 31, 454–460. [Google Scholar] [CrossRef]
- Grassl, P.; Bolander, J.E. Three-dimensional network model for coupling of fracture and mass transport in quasi-brittle geomaterials. Materials 2016, 9, 782. [Google Scholar] [CrossRef]
- Nakamura, H.; Srisoros, W.; Yahiro, R.; Kunieda, M. Time-dependent structural analysis considering mass transfer to evaluate deterioration process of RC structures. J. Adv. Concr. Technol. 2006, 4, 147–158. [Google Scholar] [CrossRef]
- Černy, R.; Rovnaniková, P. Transport Processes in Concrete; CRC Press: Boca Raton, FL, USA, 2002; 560p. [Google Scholar]
- Klemczak, B.; Knoppik-Wróbel, A. Reinforced concrete tank walls and bridge abutments: Early-age behaviour, analytic approaches and numerical models. Eng. Struct. 2015, 84, 233–251. [Google Scholar] [CrossRef]
- Bary, B.; Durand, S.; Ranc, G.; Carpentier, O. A coupled thermo-hydro-mechanical model for concrete subjected to moderate temperatures. Int. J. Heat Mass Transfer 2008, 51, 2847–2862. [Google Scholar] [CrossRef]
- Gawin, D.; Pesavento, F.; Schrefler, B.A. Modeling of hygro-thermal behavior of concrete at high temperature with thermo-chemical and mechanical material degradation. Comput. Methods Appl. Mech. Eng. 2003, 192, 1731–1771. [Google Scholar] [CrossRef]
- Eliáš, J. Boundary layer effect on behavior of discrete models. Materials 2017, 10, 157. [Google Scholar] [CrossRef]
- Berton, S.; Bolander, J.E. Crack band model for fracture in irregular lattices. Comput. Methods Appl. Mech. Eng. 2006, 195, 7172–7181. [Google Scholar] [CrossRef]
- Bolander, J.E.; Sukumar, N. Irregular lattice model for quasistatic crack propagation. Phys. Rev. B 2005, 71, 094106. [Google Scholar] [CrossRef]
- Asahina, D.; Aoyagi, K.; Kim, K.; Birkholzer, J.; Bolander, J.E. Elastically-homogeneous lattice models of damage in geomaterials. Comput. Geotech. 2017, 81, 195–206. [Google Scholar] [CrossRef]
- Asahina, D.; Ito, K.; Houseworth, J.; Birkholzer, J.; Bolander, J.E. Simulating the Poisson effect in lattice models of elastic continua. Comput. Geotech. 2016, 70, 60–67. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Mater. Struct. 1983, 16, 155–176. [Google Scholar] [CrossRef]
- Rots, J.G.; Bellitti, B.; Invernizzi, S. Robust modeling of RC structures with an event-by-event strategy. Eng. Fract. Mech. 2008, 75, 590–614. [Google Scholar] [CrossRef]
- De Schutter, G.; Taerwe, L. Degree of hydration-based description of mechanical properties of early age concrete. Mater. Struct. 1996, 29, 335–344. [Google Scholar] [CrossRef]
- Emborg, M. Development of mechanical behaviour at early ages. In Prevention of Thermal Cracking in Concrete at Early Ages; Springenschmid, R., Ed.; RILEM Report 15; E & FN Spon: London, UK, 1998; pp. 76–148. [Google Scholar]
- ∅stergaard, L.; Lange, D.; Stang, H. Early-age stress-crack opening relationships for high performance concrete. Cem. Concr. Compos. 2004, 26, 563–572. [Google Scholar] [CrossRef]
- De Schutter, G.; Taerwe, L. Fracture energy of concrete at early ages. Mater. Struct. 1997, 30, 67–71. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-chemo-mechanical model for concrete. II: Damage and creep. J. Eng. Mech. 1999, 125, 1028–1039. [Google Scholar] [CrossRef]
- Bentz, D.P. Three-dimensional computer simulation of cement hydration and microstructure development. J. Am. Ceramic Soc. 1997, 80, 3–21. [Google Scholar] [CrossRef]
- Van Breugel, K. Numerical simulation of hydration and microstructural development in hardening cement-based materials: (I) Theory. Cem. Concr. Res. 1995, 25, 319–331. [Google Scholar] [CrossRef]
- Torrenti, J.M.; Benboudjema, F. Mechanical threshold of cementitious materials at early age. Mater. Struct. 2005, 38, 299–304. [Google Scholar] [CrossRef]
- Domone, P.L. Uniaxial tensile creep and failure of concrete. Mag. Concr. Res. 1974, 26, 144–152. [Google Scholar] [CrossRef]
- Altoubat, S.A.; Lange, D.A. Creep, shrinkage, and cracking of restrained concrete at early age. ACI Mater. J. 2001, 4, 323–331. [Google Scholar]
- Van Breugel, K.; Lokhorst, S.J. Stress-based crack criterion as a basis for the prevention of through cracks in concrete structures at early-ages. In International RILEM Conference on Early Age Cracking in Cementitious Systems; Kovler, K., Bentur, A., Eds.; RILEM Publications SARL: Paris, France, 2003; pp. 229–236. [Google Scholar]
- Wittmann, F.H.; Roelfstra, P.E.; Mihashi, H.; Huang, Y.-J.; Zhang, X.-H.; Nomura, N. Influence of age at loading, water-cement ratio and rate of loading on fracture energy of concrete. Mater. Struct. 1987, 20, 103–110. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Cusatis, G.; Cedolin, L. Temperature effect on concrete creep modeled by microprestress-solidification theory. J. Eng. Mech. 2004, 130, 691–699. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Prasannan, S. Solidification theory for concrete creep. I: Formulation. J. Eng. Mech. 1989, 115, 1691–1703. [Google Scholar] [CrossRef]
- Laplante, P. Mechanical Properties of Hardening Concrete: A Comparative Analysis of Classical and High Strength Concretes. Ph.D. Thesis, Ecole Nationale des Ponts et Chaussées, Paris, French, 1993. [Google Scholar]
- Mindess, S.; Young, J.F.; Darwin, D. Concrete; Prentice Hall: Upper Saddle River, NJ, USA, 2003; 644p. [Google Scholar]
- Yang, Y.; Sato, R.; Kawai, K. Evaluation of autogenous shrinkage and drying shrinkage based on bound water content of cementitious materials. Proc. JSCE 2001, 53, 193207. [Google Scholar] [CrossRef]
- Wiss, Janney, Elstner Associates, Inc. On-Call Structural Concrete Bridge Deck Cracking Investigation Services; Technical Report WJE No. 2009.2643; Wiss, Janney, Elstner Associates, Inc.: Northbrook, IL, USA, 2011. [Google Scholar]
- Bolander, J.E.; Le, B. Modeling crack development in reinforced concrete structures under service loading. Constr. Build. Mater. 1999, 13, 23–31. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory, National Solar Radiation Database, U.S. Department of Energy. Available online: http://rredc.nrel.gov/solar/old_data/nsrdb/ (accessed on 21 February 2017).
- Lee, Y.; Choi, M.-S.; Yi, S.-T.; Kim, J.-K. Experimental study of the convective heat transfer coefficient of early-age concrete. Cem. Concr. Compos. 2009, 31, 60–71. [Google Scholar] [CrossRef]
- Marceau, M.L.; VanGeem, M.G. Solar reflectance values for concrete. Concr. Int. 2008, 30, 52–58. [Google Scholar]
- Wyrzykowski, M.; Lura, P. Moisture dependence of thermal expansion in cement-based materials at early ages. Cem.Concr. Res. 2013, 53, 25–35. [Google Scholar] [CrossRef]
- Fattuhi, N.I. Curing compounds for fresh or hardened concrete. Build. Environ. 1986, 21, 119–125. [Google Scholar] [CrossRef]
- RILEM Technical Committee TC-242-MDC. RILEM draft recommendation: TC-242-MDC multi-decade creep and shrinkage of concrete: Material model and structural analysis. Mater. Struct. 2015, 48, 753–770. [Google Scholar]
- Forth, J.P. Predicting the tensile creep of concrete. Cem. Concr. Compos. 2015, 55, 70–80. [Google Scholar] [CrossRef]
- ASTM International. ASTM C403-08 Standard Test Method for Time of Setting of Concrete Mixtures by penetration Resistance; Technical Report; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- Hammer, T.A.; Fosså, K.T.; Bjøntegaard, ∅. Cracking tendency of HSC: Tensile strength and self generated stress in the period of setting and early hardening. Mater. Struct. 2007, 40, 319–324. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials; Mc Graw Hill: New York, NY, USA, 2014; 675p. [Google Scholar]
- Roziere, E.; Cortas, R.; Loukili, A. Tensile behaviour of early age concrete: New methods of investigation. Cem. Concr. Compos. 2015, 55, 153–161. [Google Scholar] [CrossRef]
- Baroghel-Bouny, V.; Mounanga, P.; Khelidj, A.; Loukili, A.; Rafai, N. Autogenous deformations of cement pastes, Part II. W/C effects, micro-macro correlations, and threshold values. Cem. Concr. Res. 2006, 36, 123–136. [Google Scholar] [CrossRef]
- Asamoto, S.; Ohtsuka, A.; Kuwahara, Y.; Miura, C. Study on effects of solar radiation and rain on shrinkage, shrinkage cracking and creep of concrete. Cem. Concr. Res. 2011, 41, 590–601. [Google Scholar] [CrossRef]
- Grasley, Z.C.; Lange, D.A.; D’Ambrosia, M.D. Internal relative humidity and drying stress gradients in concrete. Mater. Struct. 2006, 39, 901–909. [Google Scholar] [CrossRef]
- Fu, T.; Deboodt, T.; Ideker, J.H. Development of shrinkage limit specification for high performance concrete used in bridge decks. Cem. Concr. Compos. 2016, 72, 17–26. [Google Scholar] [CrossRef]
- De Sa, C.; Benboudjema, F.; Thiery, M.; Sicard, J. Analysis of microcracking induced by differential drying shrinkage. Cem. Concr. Compos. 2008, 30, 947–956. [Google Scholar] [CrossRef]
- Darwin, D.; Browning, J.; Lindquist, W.D. Control of cracking in bridge decks: Observations from the field. Cem. Concr. Aggreg. 2004, 26. [Google Scholar] [CrossRef]




| Primary Category | Subcategory |
|---|---|
| Materials composition/proportioning | cementitious materials blend |
| admixtures | |
| water content | |
| aggregate | |
| fiber reinforcement | |
| Environmental boundary conditions | heat exchange: conduction, convection, radiation |
| moisture exchange | |
| contaminant exposure | |
| Processing and curing | concrete temperature at placement |
| time of placement | |
| methods of consolidation | |
| curing | |
| Structural boundary conditions | girder spacing and restraint conditions |
| deck depth | |
| reinforcing steel | |
| anticipated loading |
| Hydration Degree Interval | |
|---|---|
| χ | |
| 1 |
| Parameter | = 0.25 | = 0.45 |
|---|---|---|
| 0.017 mm/h | 0.017 mm/h | |
| 9 mm/h | 9 mm/h | |
| n | 6 | 5 |
| 0.76 | 0.88 | |
| s | 1.4 | 3.0 |
| 0.25 mm/h | 0.25 mm/h | |
| 0.0025 | 0.0021 |
| Parameter | Value * |
|---|---|
| 29.0 × 10/MPa | |
| 69.9 × 10/MPa | |
| 5.50 × 10/MPa | |
| 2.2 | |
| 0.01/(MPa · d) | |
| 5 MPa/K |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Prado, A.; Porras, R.; Hafez, O.M.; Bolander, J.E. Lattice Modeling of Early-Age Behavior of Structural Concrete. Materials 2017, 10, 231. https://doi.org/10.3390/ma10030231
Pan Y, Prado A, Porras R, Hafez OM, Bolander JE. Lattice Modeling of Early-Age Behavior of Structural Concrete. Materials. 2017; 10(3):231. https://doi.org/10.3390/ma10030231
Chicago/Turabian StylePan, Yaming, Armando Prado, Rocío Porras, Omar M. Hafez, and John E. Bolander. 2017. "Lattice Modeling of Early-Age Behavior of Structural Concrete" Materials 10, no. 3: 231. https://doi.org/10.3390/ma10030231
APA StylePan, Y., Prado, A., Porras, R., Hafez, O. M., & Bolander, J. E. (2017). Lattice Modeling of Early-Age Behavior of Structural Concrete. Materials, 10(3), 231. https://doi.org/10.3390/ma10030231






