In this section, we present and discuss the results of dielectric relaxation spectroscopy (DRS, TA Instruments, Inc., New Castle, DE, USA) on each of the three systems (PEI2000-PLA5, PEI2000-PLA20, PEI800-PLA5) separately, and then compare the behaviors in order to identify the effects of the different molecular structures (PEI core and PLA arms) and hence obtain information about the molecular relaxation processes.
(1) PEI2000-PLA5
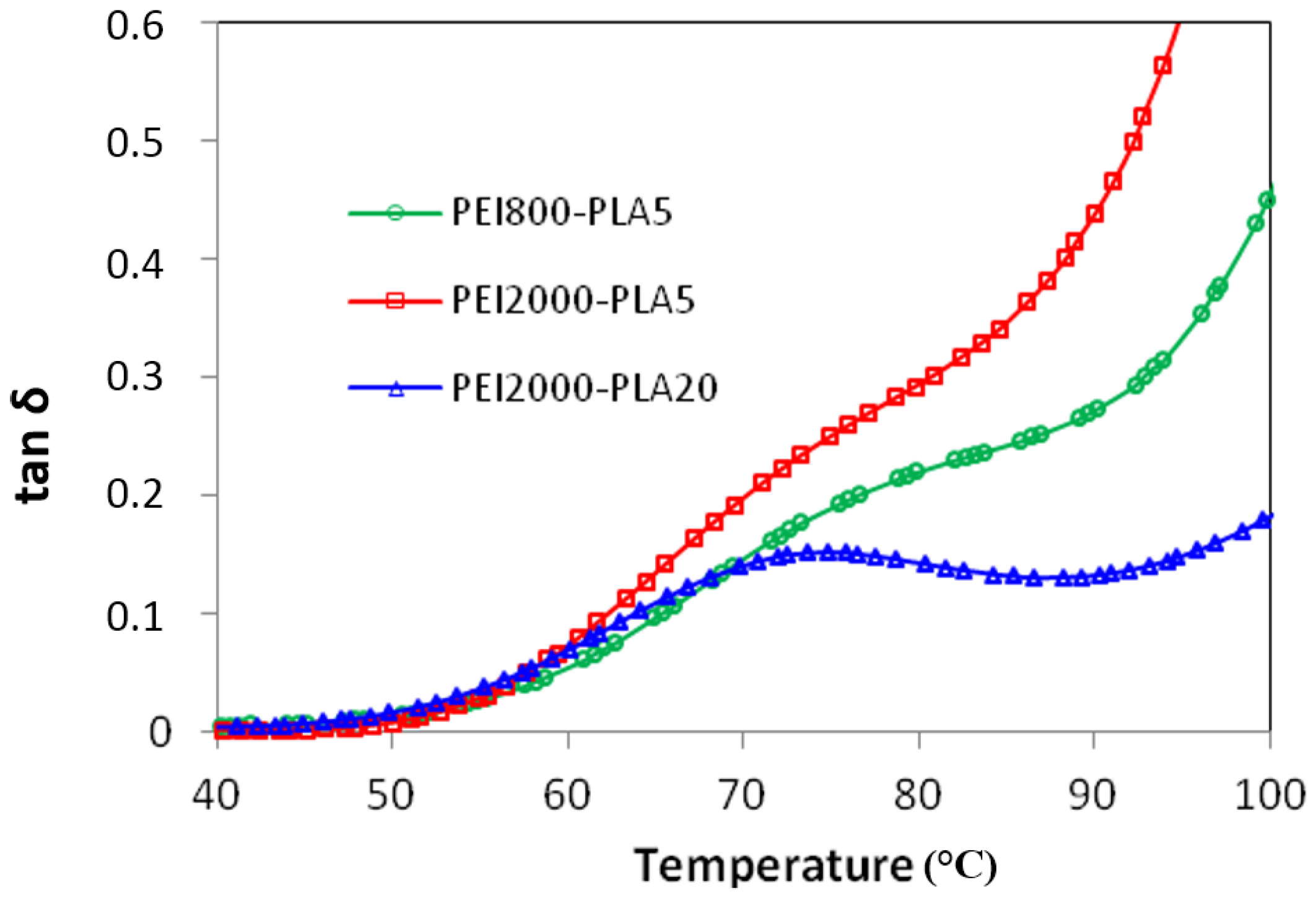
Dielectric relaxation curves for PEI2000-PLA5, PEI2000-PLA20, and PEI800-PLA5 preconditioned samples were obtained at 0.5 and 2 °C/min, over the frequency range from 0.1 Hz to 100 kHz, in order to obtain the dielectric constant ε′, loss factor ε′′, and tan δ signals. As an illustration,
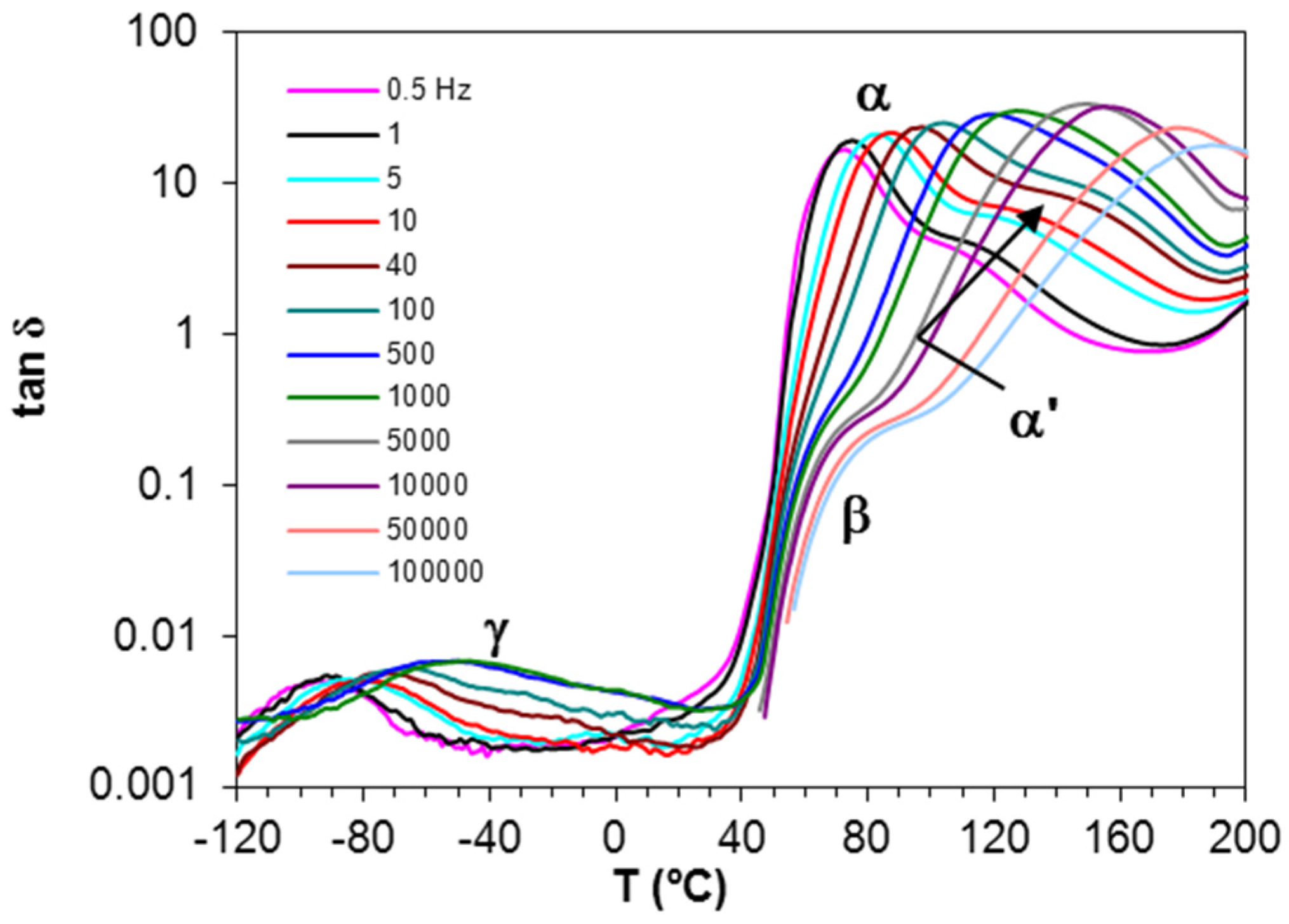
Figure 4 shows the dielectric relaxation curves for the PEI2000-PLA5 sample.
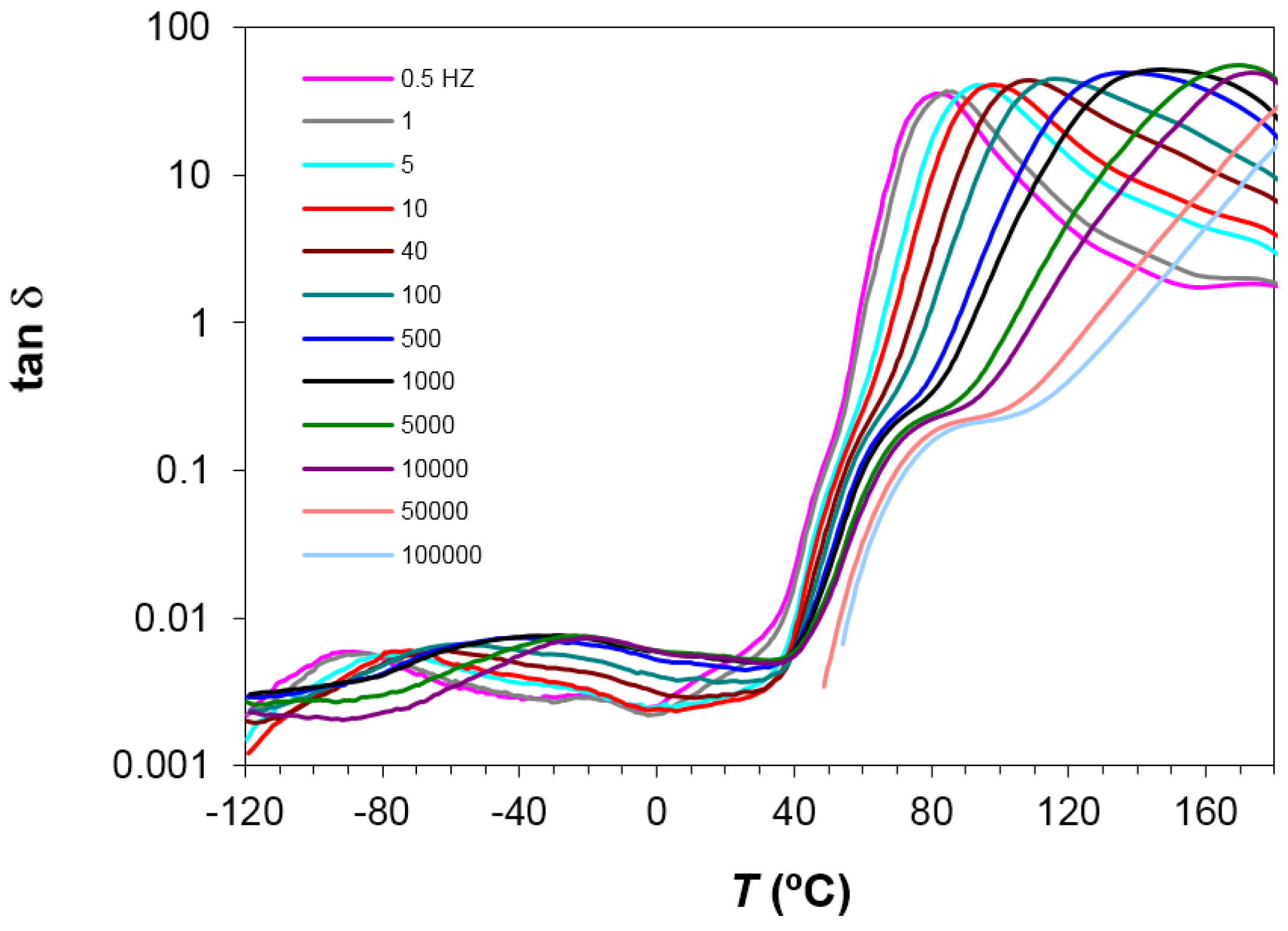
Four dipolar relaxations can be observed in the dielectric relaxation curves of PEI2000-PLA5: these are labelled γ, β, α, and α′, from lowest to highest temperature. The γ-relaxation appears between −90 and −50 °C depending on the measurement frequency, shifting to higher temperature as the frequency increases. The β-relaxation is hidden at low frequencies, but appears as a shoulder at frequencies above 500 Hz, in the temperature interval between 70 °C (0.5 kHz) and 90 °C (100 kHz), increasing in temperature as the frequency increases. In order to determine approximately the frequency dependence of this β-relaxation, an “onset” temperature is found from the intersection of tangents before and after the shoulder, and is used instead of a peak temperature. The α-relaxation is the dominant relaxation, the peak temperature increasing from around 80 °C at the frequency of 1 Hz to 190 °C at 100 kHz. A shoulder, associated with the relaxation labelled α', is observed at temperatures above the α-relaxation. The relaxation map for PEI2000-PLA5 at different heating rates is shown in
Figure 5.
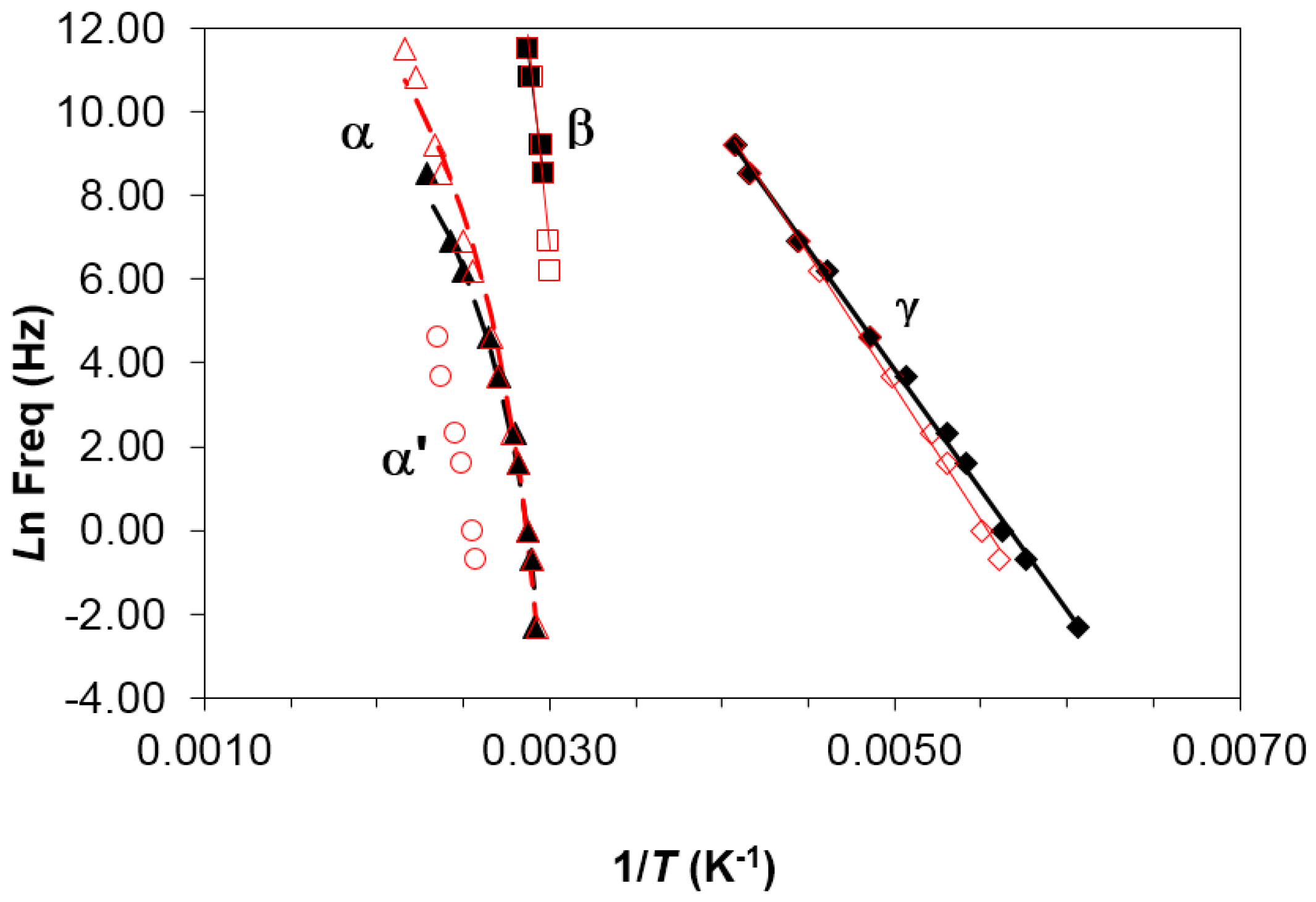
It can be seen that the heating rate has virtually no influence on the relaxation behavior. An Arrhenius dependence on temperature can be seen for the γ- and β-relaxations, from which the activation energy, averaged for the two heating rates used, was found as 50.2 ± 2.3 kJ/mol for the γ-relaxation and 267 ± 15 kJ/mol for the β-relaxation. The activation energy values obtained for each heating rate are shown in
Table 3.
In contrast, the α-relaxation shows a slight curvature which is characteristic of the Vogel–Fulcher–Tammann (VFT) equation:
where
fm is the frequency for which the maximum in tan δ occurs at the temperature
T. The parameters
A,
B, and
T0 of the VFT equation can be determined as follows. Selecting an initial value of
T0 between
Tg − 30 and
Tg − 70, the values of
A and
B are obtained by a least squares fit of the experimental data, together with the degree of fit. This procedure is repeated for successive values of
T0 until the best possible fit is obtained, which thus defines the required values of
T0,
A, and
B. The values obtained for
A,
B, and
T0 in this way for PEI2000-PLA5 are:
A = 18.6 ± 2.0,
B = 1583 ± 314 K, and
T0 = 282.5 ± 7.5 K, being the average of the values obtained for the different heating rates. Given that
Tg for this sample is 321.5 K by DSC (see
Table 2), it can be seen that
T0 is approximately 40 K less than the calorimetric
Tg.
Table 3 lists the results obtained for each heating rate. As well as fitting the VFT equation, an “apparent” activation energy,
Eapp, for the α-relaxation can be determined from the slope of a best fit straight line to the data, which gives values of 264 kJ/mol and 241 kJ/mol for the heating rates of 2 and 0.5 °C/min, respectively (average value 252 ± 12 kJ/mol).
(2) PEI2000
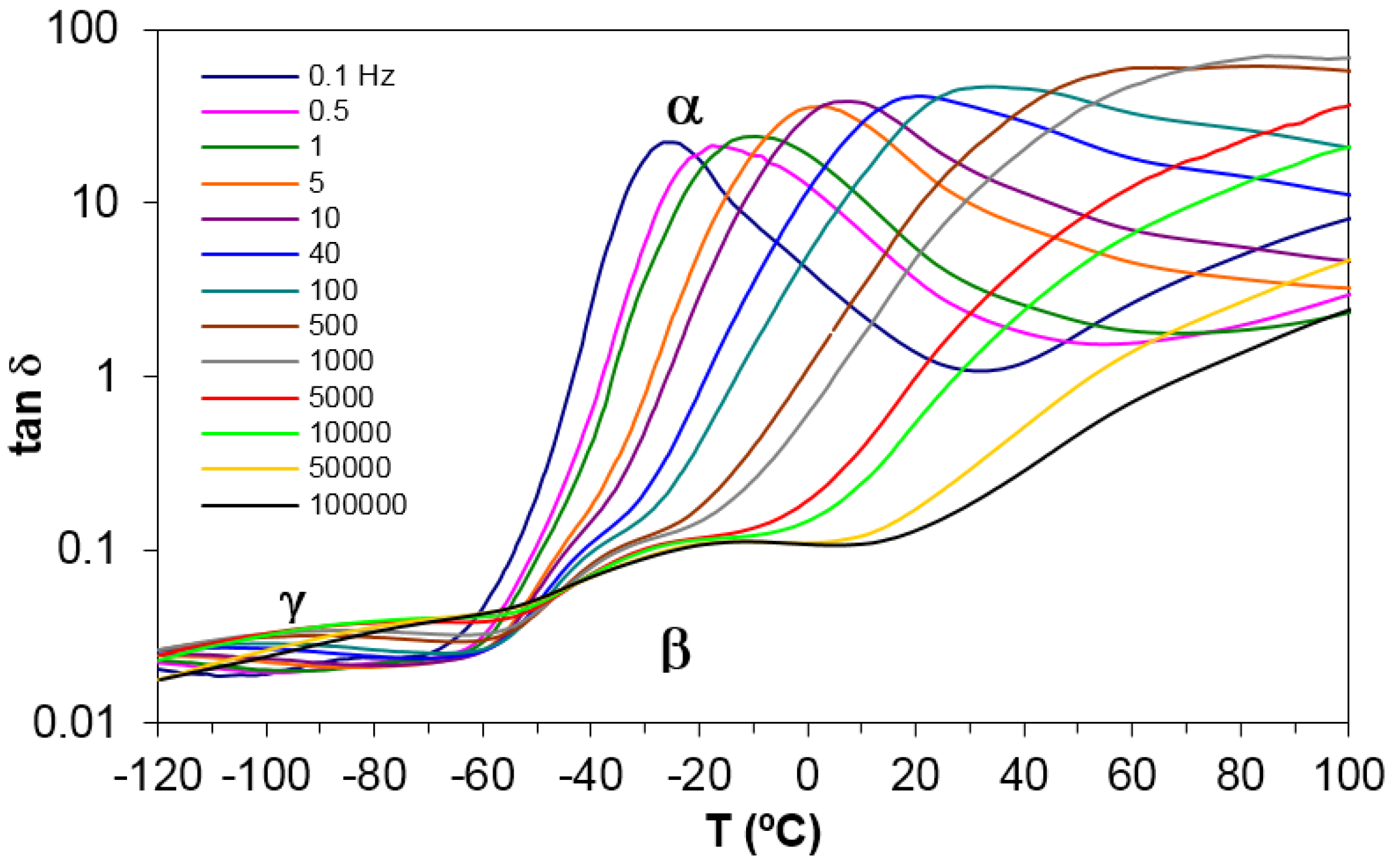
Figure 6 shows the relaxation curves for PEI2000, poly(ethyleneimine), obtained under the same conditions as for PEI2000-PLA5, in order to compare the relaxation peaks of both samples and hence elucidate their possible origins. In these spectra for PEI2000, the γ-relaxation can be seen at around −90 °C at the frequency of 1 Hz, and it moves to higher temperatures with increasing frequency. This relaxation peak is attributed to local motions of the –NH
2 groups of PEI [
19]. The relaxation map for different heating rates is depicted in
Figure 6, where the linear relationship between ln(
fm) and 1/
T indicates an Arrhenius behavior, for which the activation energy associated with this process is found as 41.6 ± 0.4 kJ/mol (see
Table 3), somewhat lower than but of the same order of magnitude as the activation energy for the γ-relaxation of PEI2000-PLA5 (50.2 ± 2.1 kJ/mol).
The β-relaxation of PEI2000, a dipolar relaxation, is observed at temperatures above the γ peak, appearing first as a shoulder at a temperature of about −40 °C at a frequency of 0.1 kHz, and moving to higher temperatures and becoming more pronounced with increasing frequency. This relaxation is associated with motions of the lateral branches of PEI [
19]. The average activation energy, calculated from the slope of the linear representation in
Figure 7, is 92.7 ± 6.3 kJ/mol. In contrast to the comparison of the γ-relaxations, this activation energy for the β-relaxation of PEI2000 is much lower than the average value for the β-relaxation of PEI2000-PLA5 (267.0 ± 14.8 kJ/mol,
Table 3). This indicates that the two relaxations have a different origin: the PLA arms in the PEI
x-PLA
y system do not exist in PEI2000.
The α-relaxation, associated with the glass transition of PEI, is observed at temperatures higher than those of the β-relaxation, and the inverse of the peak temperatures obtained for the different frequencies are plotted in the relaxation map of
Figure 7. In the same way as for the PEI
x-PLA
y systems, a non-linear relationship is observed, though it is less well defined as the frequency range is smaller. If this behavior is fitted by the VFT equation, we obtain the results shown in
Table 3 for the different heating rates used. The average results for the different heating rates are
A = 21.9 ± 3.2,
B = 3709 ± 804 K, and
T0 = 95.5 ± 12.8 K. As can be seen, the value obtained for the parameter
B is very high and
T0 is very low, more than 120 K below
Tg, which does not seem reasonable. This is possibly a consequence of an insufficient range of temperatures and frequencies to obtain reliable values for these parameters. Accordingly, the apparent activation energy,
Eapp, from the average slope of a best fit straight line to the data for the α-relaxation provides a more reliable means of comparing the two systems. For PEI,
Eapp takes values of 78.1 kJ/mol and 63.3 kJ/mol for the heating rates of 0.5 and 2 °C/min, respectively, the average value being 70.7 ± 7.4 kJ/mol. This is noticeably less than that for PEI2000-PLA5, 252 ± 12 kJ/mol, suggesting a much higher degree of co-operativity in the molecular motions associated with the glass transition of the PEI
x-PLA
y systems.
The α-relaxation peak is an asymmetric peak in which the presence of a shoulder on the high temperature side can be clearly observed in
Figure 6. The presence of this shoulder seems to suggest the existence of a relaxation peak, overlapping the dipolar α-relaxation and associated with ionic charge trapped in the PEI, which could be labelled as an α′-relaxation. This is supported by other results, not shown here but to be reported in another paper, where the effect of the molecular weight of the PEI core, up to 25000, on this ionic relaxation is revealed. It is observed there that, with increasing molecular weight of the PEI core, this shoulder corresponding to the ionic α′-relaxation becomes more pronounced and is clearly evident over a wider frequency range.
(3) PLA
Many dielectric studies of amorphous poly(lactide) can be found in the literature, which show that there are three dielectric relaxations, usually designated as α
n, α
s, and β in order of decreasing temperature [
30]. The α
n-relaxation is assigned to the normal mode relaxation due to the component of dipole vector aligned in the direction parallel to the chain contour and the fluctuation of the end-to-end vector, and the α
s-relaxation is assigned to the local segmental modes associated with the glass transition. The β-relaxation is observed at temperatures well below
Tg, and hence is attributed to secondary relaxations in the glassy state, and in particular to twisting motions of the main chains as there are no flexible side groups on which dipoles are attached [
28,
30].
Pluta et al [
27] found that the temperature dependence of the α
s-relaxation follows the VFT Equation (1) with
T0 = 302 K and
B = 800 K, which are stated to be in reasonable agreement with other results [
29,
30]. This value of
T0, though, is only 28 K below the measured
Tg of 330 K, which seems rather low. Accordingly, we converted these values into an apparent activation energy of 354 kJ/mol at an average temperature of 350 K, for comparison with our own results listed in
Table 3. This is a very high value for the activation energy, and it is consistent with the observation that incorporating the PLA arms onto the PEI2000 core molecule results in a much higher activation energy for the PEI2000-PLA5 sample in comparison with that for the PEI2000 alone. Indeed, as is shown below, the activation energy for the glass transition increases significantly relative to the PEI core in all the PEI
x-PLA
y systems studied here.
Pluta et al [
27] also reported a secondary β-relaxation in PLA, with an activation energy of 41.5 kJ/mol, in reasonable agreement with other values in the literature: 39.1 kJ/mol [
28]; 43.9 kJ/mol [
29]; 41.1 kJ/mol [
30]; 36.4 kJ/mol [
31].
The γ-relaxation for PEI2000-PLA5, whose maximum is located between –90 °C at 1 Hz and –50 °C at 1 kHz, corresponds approximately with the temperature of the β-relaxation in PLA (–80 °C) at a frequency of 1 Hz, though the average activation energy, 50.2 ± 2.3 kJ/mol for PEI2000-PLA5, is somewhat higher than that of the β-relaxation of PLA (36.4 to 43.9 kJ/mol, as listed above). Accordingly, the γ-relaxation in PEI2000-PLA5 could be associated with the terminal –OH groups of the PLA arms, with some additional hindrance resulting from the PLA being incorporated as the arms of the star-shaped polymer. The γ-relaxation of the PEI2000, associated with terminal –NH2 groups, is also observed in the same temperature range and its activation energy (41.6 ± 0.4 kJ/mol) is similar to that of PEI2000-PLA5. However, the γ-relaxation of PEI2000-PLA5 cannot be correlated with the γ-relaxation of PEI2000, because the movements of the –NH2 groups should not be seen, as a consequence of their replacement by PLA chains.
The β-relaxation of PEI2000-PLA5 is only observed above 0.5 kHz, and then only as a superimposed shoulder, at about 80 °C, on the low temperature flank of the α-relaxation. The activation energy for the β-relaxation of PEI2000-PLA5 is 267 ± 15 kJ/mol, which is much higher than the β-relaxation of PEI2000 (92.7 ± 6.3 kJ/mol). This suggests that this relaxation could be due to movements of the entire chain of PLA which forms the arms of the multiarm star polymer. The segmental motions associated with the glass transition of PLA have a VFT temperature dependence, from which one can estimate an apparent activation energy of about 114 kJ/mol at 350 K [
24,
30], approximately the same temperature as that at which the β-relaxation of PEI2000-PLA5 is observed. The implication of this would be that these segmental motions of the PLA arms are considerably restricted if they appear as the β-relaxation in the PEI
xPLA
y multiarm star polymers.
On the other hand, the α-relaxation of PEI2000-PLA5, occurring at 70 °C at 1 Hz, is associated with the glass transition of the polymer and could correspond to the α
s-relaxation of the PLA (occurring at about 60 °C at 1 Hz [
27]), but displaced to higher temperatures by the effect of the PEI2000 core. The α′-relaxation of PEI2000-PLA5 (90 °C at 1 Hz) corresponds to the α
N-relaxation of the PLA (85 °C at 1 Hz [
27]), influenced by the PEI core [
27], without excluding the possibility that it could be a Maxwell–Wagner–Sillars type ionic peak because the material may have nano-regions of different conductivity. Above 1 kHz, the α- and α′-relaxations overlap and cause a unique dipolar relaxation. As seen in
Figure 5, the relationship between ln(
fm) and
T−1 is practically linear, from which the apparent average activation energy for the α′-relaxation in the PEI2000-PLA5 is found as 263 ± 38 kJ/mol.
(4) PEI2000-PLA20
The multiarm star polymer PEI2000-PLA20 has the same structure as PEI2000-PLA5, but with the ratio of lactide repeat units to N links now being 20 instead of five. The dielectric relaxation curves for PEI2000-PLA20 are virtually identical to those for PEI2000-PLA5. The relaxation map, shown in
Figure 8, indicates the existence of γ, β, α, and α′ relaxations, very similar to the relaxation map for PEI2000-PLA5 (
Figure 5) but with some small displacements as a consequence of the effect of increasing the number of lactide repeat units.
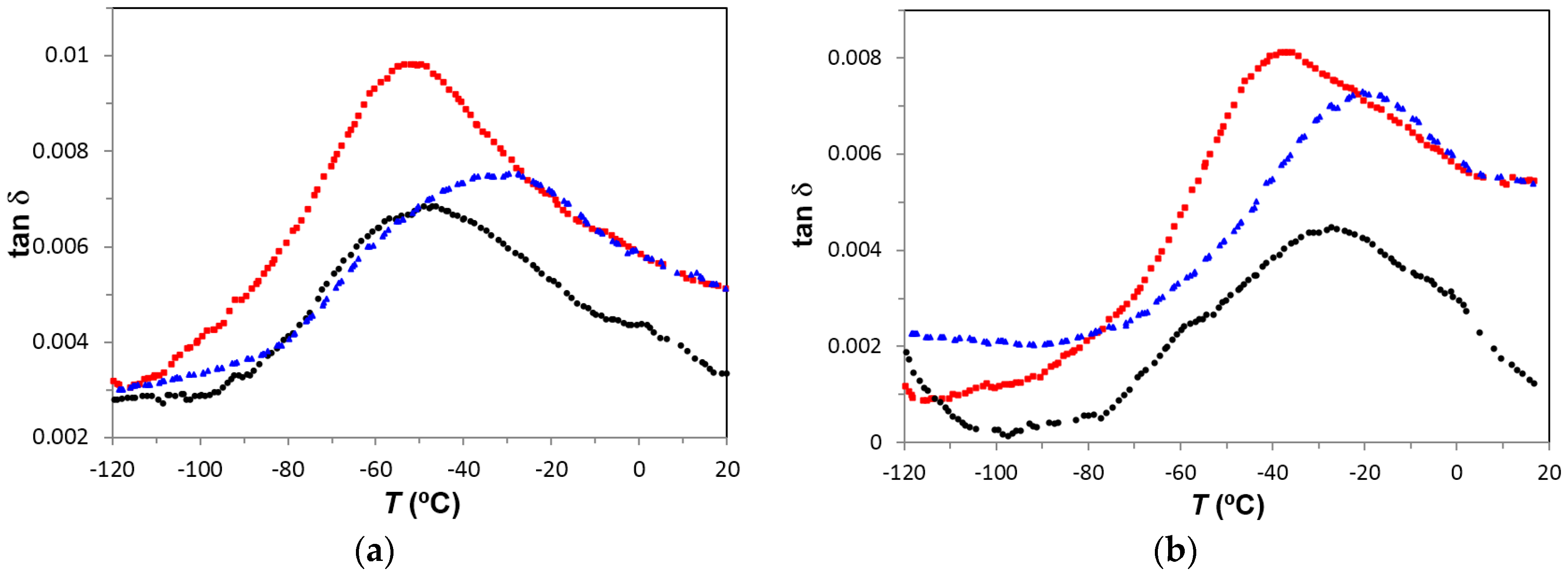
The γ-relaxation (local motions of the –OH groups) is observed in PEI2000-PLA20 at temperatures lower than those for PEI2000-PLA5. Thus, at 1 kHz, γ-relaxation of PEI2000-PLA5 appears at −48 °C while that of PEI2000-PLA20 appears at −53 °C (−27 and −37 °C for 10 kHz, respectively),
Figure 9a,b. The activation energy is similar in both polymers (50.2 ± 2.3 kJ/mol in PEI2000-PLA5 and 54.0 ± 3.2 kJ/mol in PEI2000-PLA 20). Increasing the ratio of lactide repeat units to N links, reduces the temperature at which the γ-relaxation occurs but does not significantly affect the activation energy, which is also relatively unaffected by the heating rate (57.2 kJ/mol at 0.5 °C/min and 50.8 kJ/mol at 2 °C/min for PEI2000-PLA20),
Table 3.
Figure 9a,b also shows that the intensity of the relaxation is greater in PEI2000-PLA20 than in PEI2000-PLA5, regardless of heating rate and frequency, this effect being related to the mobility of a larger number of OH groups present in the PEI2000-PLA20 structure.
The β-relaxation of the PEI2000-PLA20, due to movements of the entire chain of PLA, occurs as a shoulder at low frequencies but develops as a peak as the frequency increases.
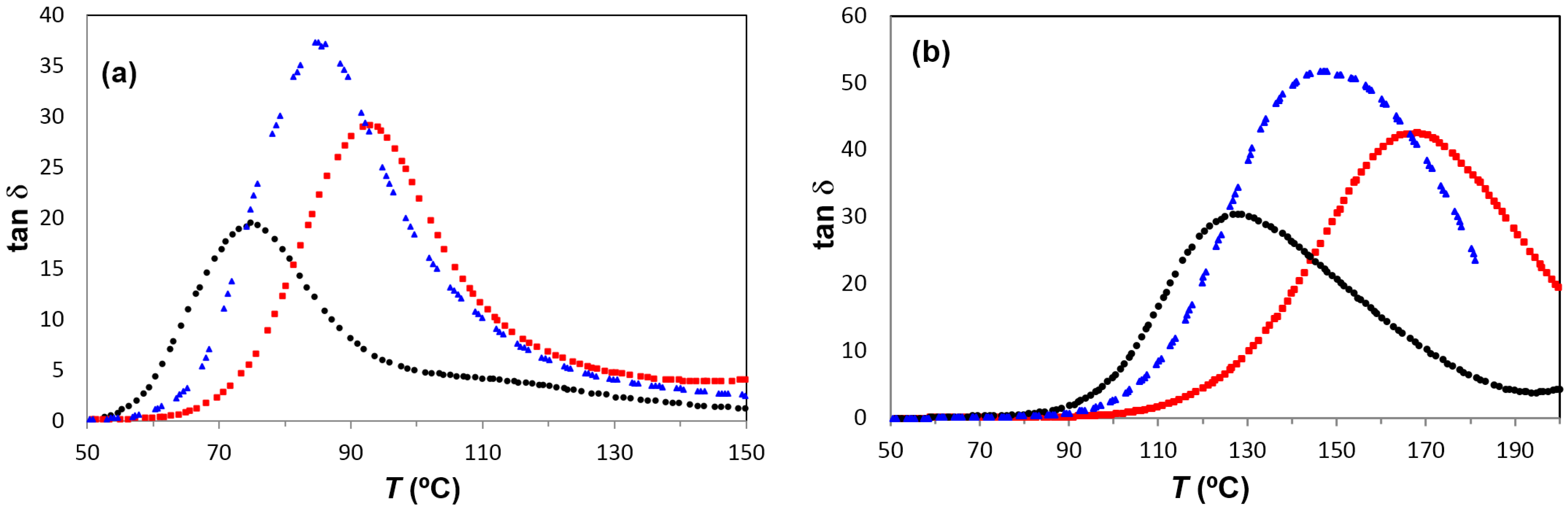
Figure 10 shows the β-relaxation of PEI2000-PLA5 compared with PEI2000-PLA20 at 100 kHz for the heating rate of 0.5 °C/min. For PEI2000-PLA5, a shoulder can be seen between 60 and 85 °C, while for PEI2000-PLA20 there is a clear peak with a maximum around 75 °C. This is because the higher ratio of lactide repeat units to N links in PEI2000-PLA20 results in a higher glass transition temperature, and hence a greater separation of the β- and α-relaxations. The relaxation map,
Figure 8, shows that this β-relaxation is insensitive to the heating rate.
The α-relaxation is observed in PEI2000-PLA20 at higher temperatures than in PEI2000-PLA5, and this difference increases with increasing frequency. For example, as seen in
Figure 11, the α-relaxation is observed at 75 °C in PEI2000-PLA5 and at 93 °C in PEI2000-PLA20 for the frequency of 1 Hz, while for 1 kHz these temperatures are 127 and 169 °C, respectively.
On the relaxation map in
Figure 8, the representation of ln(
fm) vs.
T−1 for PEI2000-PLA20 is non-linear for the α-relaxation, adjusting to the VFT Equation (1). The parameters of this equation are given in
Table 3 for the heating rates studied, the average values being:
A = 15.1 ± 1.1,
B = 1398 ± 173 K, and
T0 = 274.5 ± 6.4 K. Comparing the results for PEI2000-PLA5 and PEI2000-PLA20, it can be seen that, for the same heating rate, the parameters of the VFT equation are lower in the PEI2000-PLA20. The apparent activation energy, calculated from the average slope of a best fit straight to the experimental data, is
Eapp = 170.0 ± 1.2 kJ/mol for the PEI2000-PLA20, and is lower for PEI2000-PLA20 than for PEI2000-PLA5, possibly as a consequence of the greater flexibility of the PLA20 chains.
The dipolar α′-relaxation appears at temperatures higher than the α-relaxation. This relaxation is more visible on decreasing both the frequency and the heating rate. In PEI2000-PLA20, this relaxation peak is better defined than in the PEI2000-PLA5 due to the higher ratio of lactide repeat units to N links, as shown in
Figure 12. The relaxation map in
Figure 8 shows that there is a linear relationship between ln(
fm) and
T−1 over the rather limited frequency range available, from which the activation energy is found as 131.0 kJ/mol, for the heating rate of 0.5 °C/min, significantly less than that obtained for PEI 2000-PLA5 at the same heating rate.
(5) PEI800-PLA5
The multiarm star polymer PEI800-PLA5 has the same ratio (= 5) of lactide repeat units to N links as for PEI2000-PLA5, but a lower molecular weight for the hyperbranched poly(ethyleneimine) core. The dielectric relaxation curves are similar to that for PEI2000-PLA5, and are shown in
Figure 13.
The γ-relaxation for PEI800-PLA5, associated with local movements of the hydroxyl groups, appears at a slightly higher temperature than for PEI2000-PLA5 and PEI2000-PLA20, as shown in
Figure 14: at 1 Hz and 2 °C/min, the γ-relaxation appears a −90 °C for PEI800-PLA5, at −95 °C for PEI2000-PLA5, and at −97 °C for PEI2000-PLA20.
Figure 9 compares the γ-relaxation for all three samples at two selected frequencies: 1 kHz and 10 kHz. It is noted that the magnitude of tan δ for PEI800-PLA5 is intermediate between PEI2000-PLA20 and PEI2000-PLA5, the highest value being for PEI2000-PLA20. This might appear to suggest that the position of the γ-relaxation on the temperature scale is determined principally by the average molecular weight of the PEI core, whereas the intensity of the relaxation peak is dominated by the density of the PLA branches. However, these two effects are inter-related, since a higher molecular weight PEI core will imply a higher density of the arms, and so the individual contributions of each cannot be distinguished by these results. The relaxation map of
Figure 15 shows that this relaxation is practically independent of the heating rate. The average activation energy for PEI800-PLA5 is 53.7±1.4 kJ/mol, very close to those for PEI 2000-PLA5 and PEI2000-PLA20, 50.2±1.3 kJ/mol and 54.2±3.2 kJ/mol, respectively.
As was also observed in the other samples, the β-relaxation becomes more visible at frequencies higher than 100 Hz for PEI800-PLA5, when it appears as a shoulder between 70 and 90 °C, as seen in
Figure 13. Using the same procedure of determining an “onset” temperature for the β-relaxation as was used earlier for PEI2000-PLA5, the frequency of the β-relaxation can be estimated, and the relaxation map,
Figure 15, shows an Arrhenius relationship between ln(
fm) and
T−1 with an average activation energy of 261 ± 4 kJ/mol, independent of the heating rate. This is almost identical to the value for PEI2000-PLA5 (267 ± 15 kJ/mol), but both are smaller than that for PEI2000-PLA20 (354 ± 10 kJ/mol), as can be seen in
Table 3. The results indicate that the β-relaxation is influenced by the content of lactide repeat units/N link, not being sensitive to the effect of the molecular weight of the PEI core.
When comparing the results for the β-relaxation of PEI800-PLA5 with those for PEI2000-PLA5 and PEI2000-PLA20, we observe that the β-relaxation is located in the same temperature range for all samples, as shown in
Figure 10, but occurs as a shoulder on samples with the same content of PLA, PEI2000-PLA5, and PEI800-PLA5, while it appears as a peak in the multiarm star polymer of higher PLA content, PEI2000-PLA20, for which the glass transition is better separated from the β-relaxation.
Figure 11a,b show the α-relaxation for PEI800-PLA5 for frequencies of 1 Hz and 1 kHz and a heating rate of 0.5 °C/min. For the frequency of 1 Hz, the α-relaxation peak is observed at 85 °C. This temperature is intermediate between the peak temperatures obtained for PEI2000-PLA5 and PEI2000-PLA20, 75°C and 93 °C, respectively. This behavior is observed for all the frequencies used, as shown in
Figure 14, the difference being more marked as the frequency increases; however, for the minimum frequency of 0.1 Hz, the values of the temperature of the α-relaxation peak, associated with the glass transition of these multiarm star polymers, are substantially similar, as was observed in the DSC results (see
Table 2). The VFT parameters obtained for the PEI800-PLA5 are
A = 15.1 ± 0.2,
B = 1107.1 ± 298 K, and
T0 = 285.7 ± 11.4 K. These parameters are intermediate between those for PEI2000-PLA5 (
A = 18.6 ± 2.0,
B = 1583.0 ± 314 K, and
T0 = 282.5 ± 7.6 K) and PEI2000-PLA20 (
A = 15.0 ± 1.1,
B = 1398.8 ± 173 K and
T0 = 274.0 ± 6.9 K), as given in
Table 3. The average apparent activation energy,
Eapp, for this relaxation in PEI800-PLA5 is 194 ± 8 kJ/mol, intermediate between those for PEI2000-PLA5 (252 ± 11 kJ/mol) and PEI2000-PLA20 (170 ± 2 kJ/mol) and higher than the PEI800 (68.7 ± 2.6 kJ mol
−1), see
Table 3. To explain the fact that these results for PEI800 PLA5 are intermediate between those for the other two multiarm star polymers, we consider the following.
It has been observed that the α-relaxation associated with the glass transition and the apparent activation energies for PEI800-PLA5 are much higher than for the PEI800 core, which can be explained by the predominant effect of the branches of PLA. The structure of the PEI800-PLA5 is much more complex than that of PEI800 and this translates into greater difficulty of molecular movement and consequently a higher activation energy. Comparing the multiarm star polymers with the same PLA content but with different molecular weights for the core, we observe that the temperature at which the α-relaxation peak appears and the activation energy for PEI800-PLA5 are higher than for PEI2000-PLA5; this can be attributed to the reduction in the molecular weight of the PEI core giving a structure which allows greater proximity and interaction between the branches of the PLA, and therefore the co-operative molecular mobility associated with the branches of PLA and the PEI core is more hindered, and as a consequence the α-relaxation is displaced towards higher temperatures. On the other hand, as was explained in the comparative analysis of PEI2000-PLA5 and PEI2000-PLA20, by increasing the ratio of lactide repeat units to N links, the possibilities for interaction between PLA chains increases, and the temperature of the α-relaxation peak for PEI2000-PLA20 is greater than for the other two multiarm star polymers, PEI800-PLA5 and PEI2000-PLA5.
The α′-relaxation, associated with the normal mode relaxation due to fluctuations of the end-to-end vector in the PLA arms, is more pronounced in PEI2000-PLA20, and appears as a well-defined peak, whereas this relaxation for the other two star-shaped polymers appears as a shoulder, as shown in
Figure 12. The average activation energy for this α′-relaxation has been determined as 254 kJ/mol in PEI800-PLA5, virtually identical to that for PEI2000-PLA5 (263 kJ/mol), and considerably greater than that for PEI2000-PLA20 (131 kJ/mol). This indicates a null effect of the PEI core on this relaxation, as expected, while an increase in the ratio of lactide repeat units to N links causes a sharp decrease in the activation energy and a better definition of the relaxation peak. This possible assignment of this relaxation does not exclude that it could be a Maxwell–Wagner–Sillars type ionic peak because the material may have nano-regions of different conductivity.
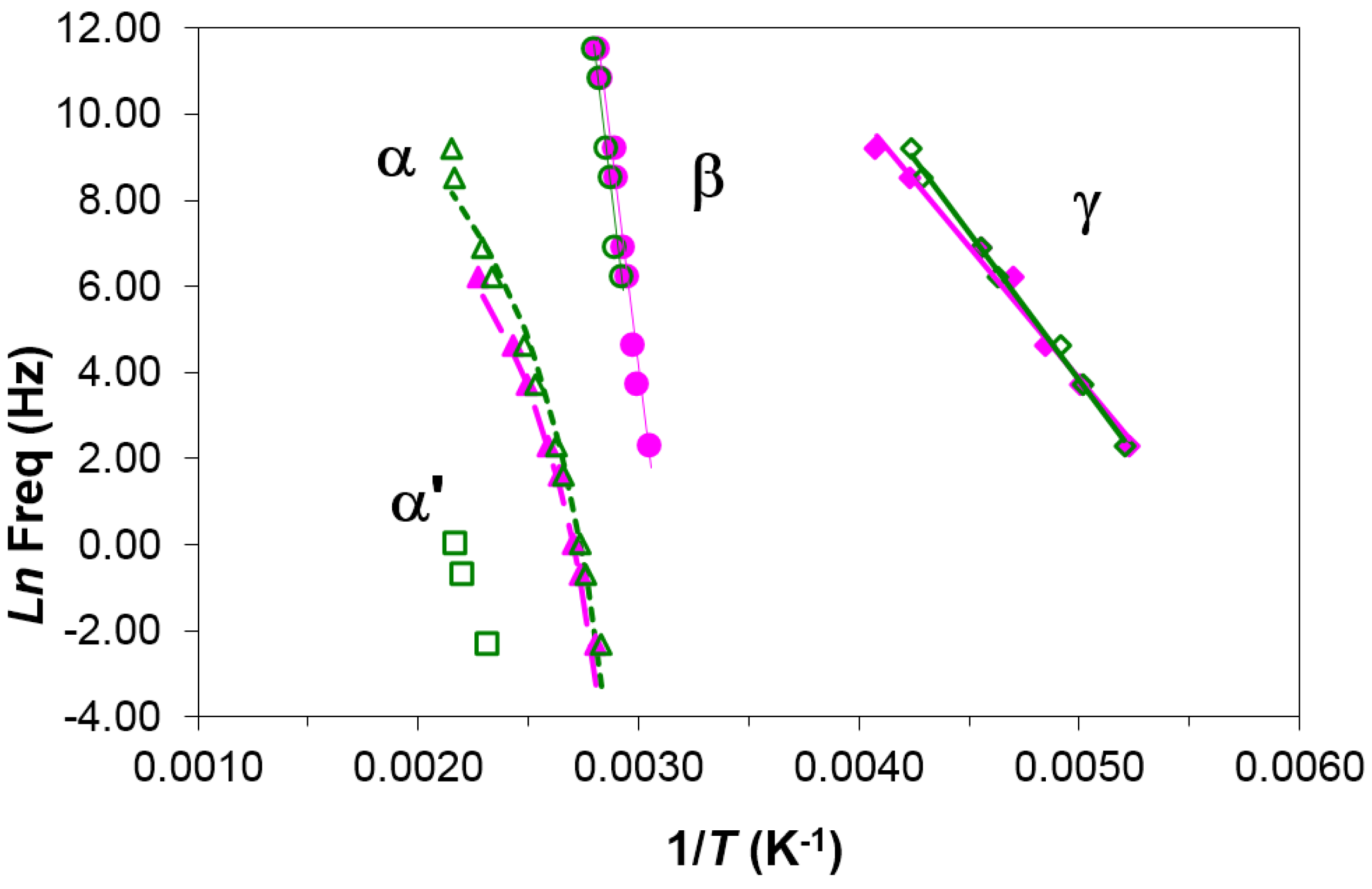
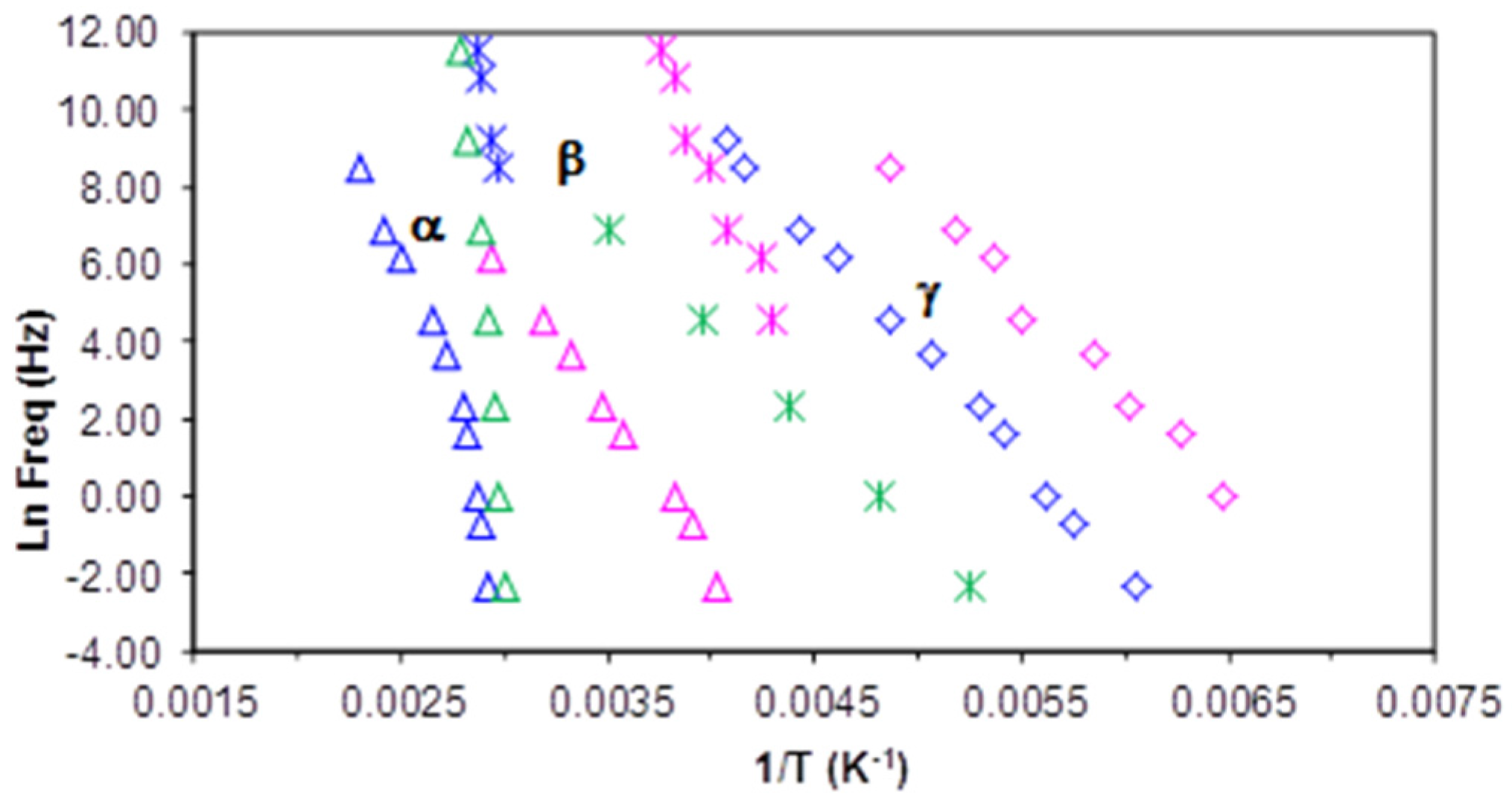
Finally, we compare the multiarm star polymer PEI2000-PLA5 with PEI2000 and PLA on the relaxation map in
Figure 16 in order to further clarify some of the ideas presented above. The data for amorphous PLA have been taken from
Figure 5 of Laredo et al [
32], with their secondary relaxation labelled β
III being taken as the β-relaxation. It is immediately apparent that the α-relaxation for PEI2000 is quite different from that for PEI2000-PLA5 whereas the relaxations for PEI2000-PLA5 and amorphous PLA merge at low frequency, and have approximately the same value of
T0, (as in fact do all the multiarm star polymers, see
Table 3). The α-relaxation of all the multiarm star polymers is associated with the glass transition of the polylactide arms, with a displacement to higher temperatures as the frequency increases as a consequence of the restriction on mobility imposed by the PEI core. Likewise, the β-relaxation for PEI2000 can be seen to be widely separated from that of PEI2000-PLA5, and with a much lower activation energy (see
Table 3), whereas again the relaxation in the multiarm star polymer appears to coincide with an extrapolation of the relaxation in the amorphous PLA. In fact, the β-relaxation in PEI2000-PLA5 closely superposes on the α-relaxation of the PLA in just the region in which the extrapolated β-relaxation of the PLA would intersect with the α-relaxation. This is consistent with the interpretation made in an earlier section that the β-relaxation in PEI2000-PLA5 was associated with the entire PLA chain, and supports the observation by Laredo et al [
32] that the β-relaxation in PEI2000-PLA5 displays Johari-Goldstein characteristics. Lastly,
Figure 16 also shows clearly the wide discrepancy between the γ-relaxations in PEI2000 and PEI2000-PLA5; even though they have similar slopes and hence similar activation energies (see
Table 3), these relaxations are associated with quite different terminal groups.