Material State Awareness for Composites Part II: Precursor Damage Analysis and Quantification of Degraded Material Properties Using Quantitative Ultrasonic Image Correlation (QUIC)
Abstract
:1. Introduction
1.1. Definition of Precursor
1.2. QUIC Using Nonlocal Mechanics for Material State Awareness
1.3. Quantification of Degraded Material Properties
1.4. The Proposed Study
2. Materials and Methods
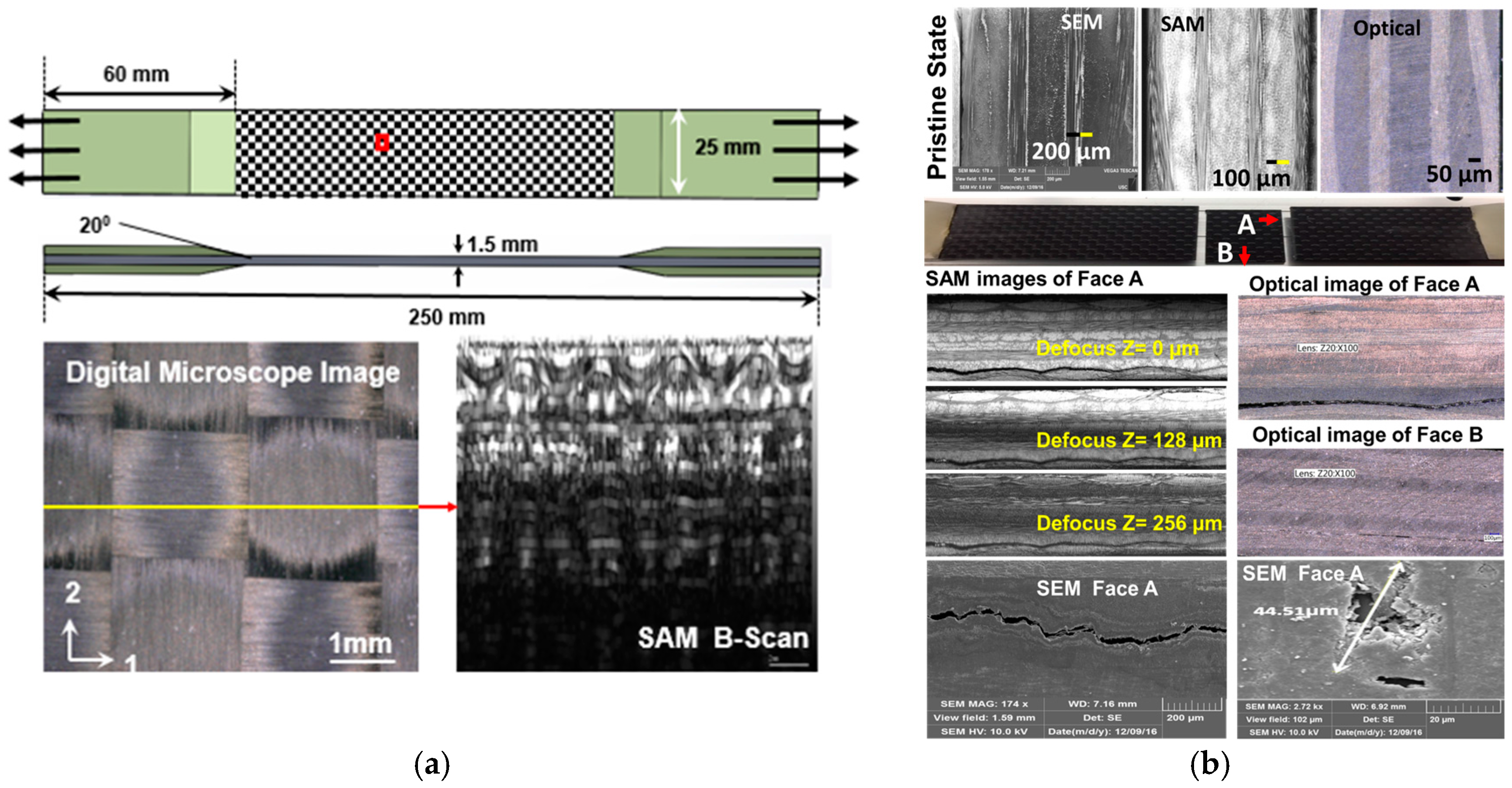
2.1. Composite Fatigue Testing
2.2. Experimental Process for QUIC
2.3. Benchmark Study Using Micro-Optical Imaging
3. Theoretical Development of QUIC
3.1. Damage State Quantification Using Nonlocal Continuum Theory
- (1)
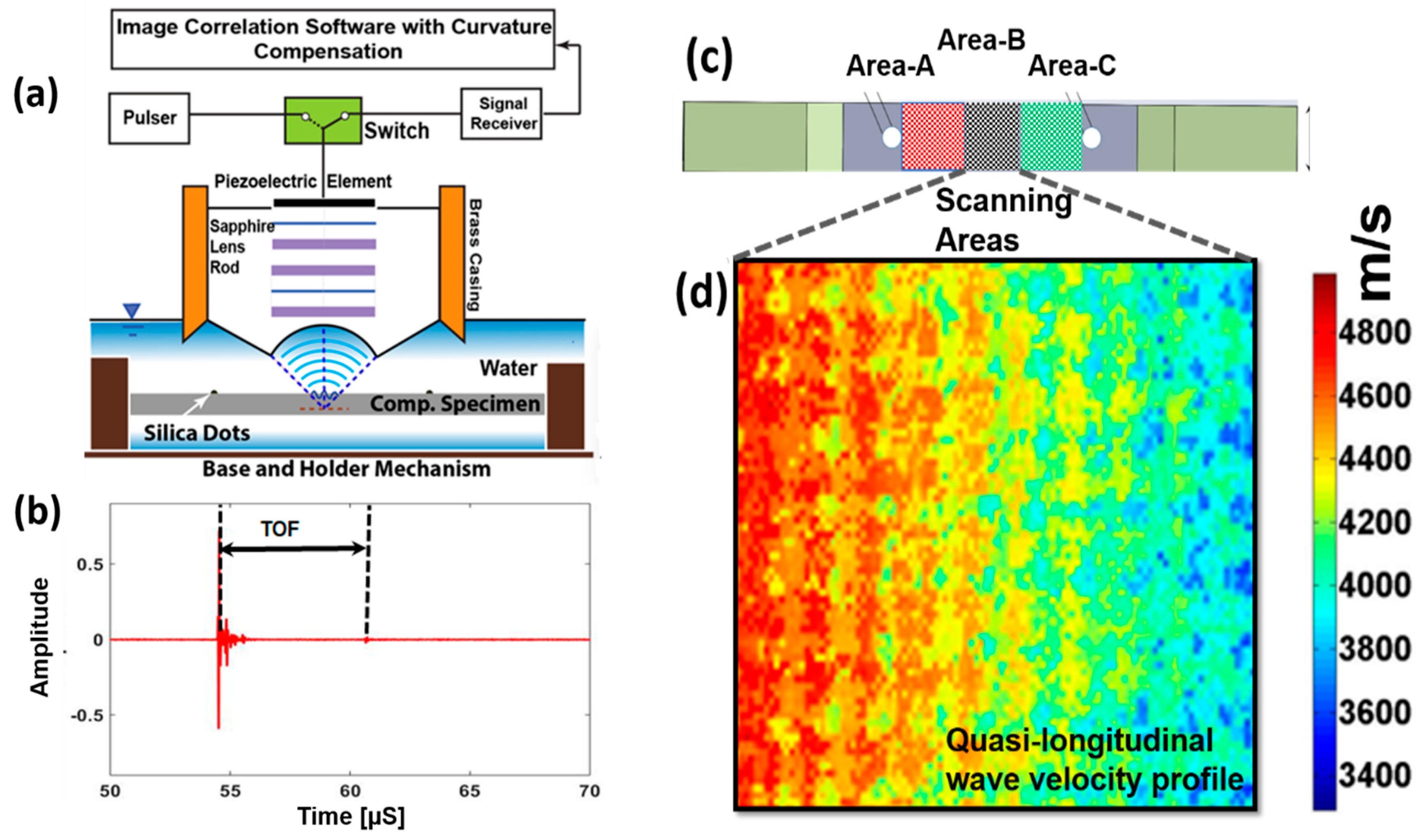
- Z-scans, where SAM scans were performed at different defocus distances across depth using a broadband ~25 MHz transducer manufactured by PVA Tepla AG, Wettenberg, Germany. Scans were performed at three different areas (Area-A, Area-B, and Area-C) on the specimen to cover the whole gage area as shown in the Figure 3c. Each area was discretized into a number of pixels, and the A-scan signal at each pixel point was recorded for further analysis.
- (2)
- A typical A-scan signal at a pixel point is shown in the Figure 3b. The first wave packet in the signal is the normal reflection of the incident wave while the second one is the backside reflection of the transmitted wave.
- (3)
- Time-of-flight (TOF) between the front and backside reflections can be seen as the time taken by the transmitted wave to travel through the specimen. TOF was calculated at each pixel point. By dividing the wave path (twice the thickness) of the specimen by TOF, quasi-longitudinal wave velocity at each pixel point was obtained. Then the 2D distributions of the wave velocities were obtained at three different scanning areas as shown in the Figure 2c.
- (4)
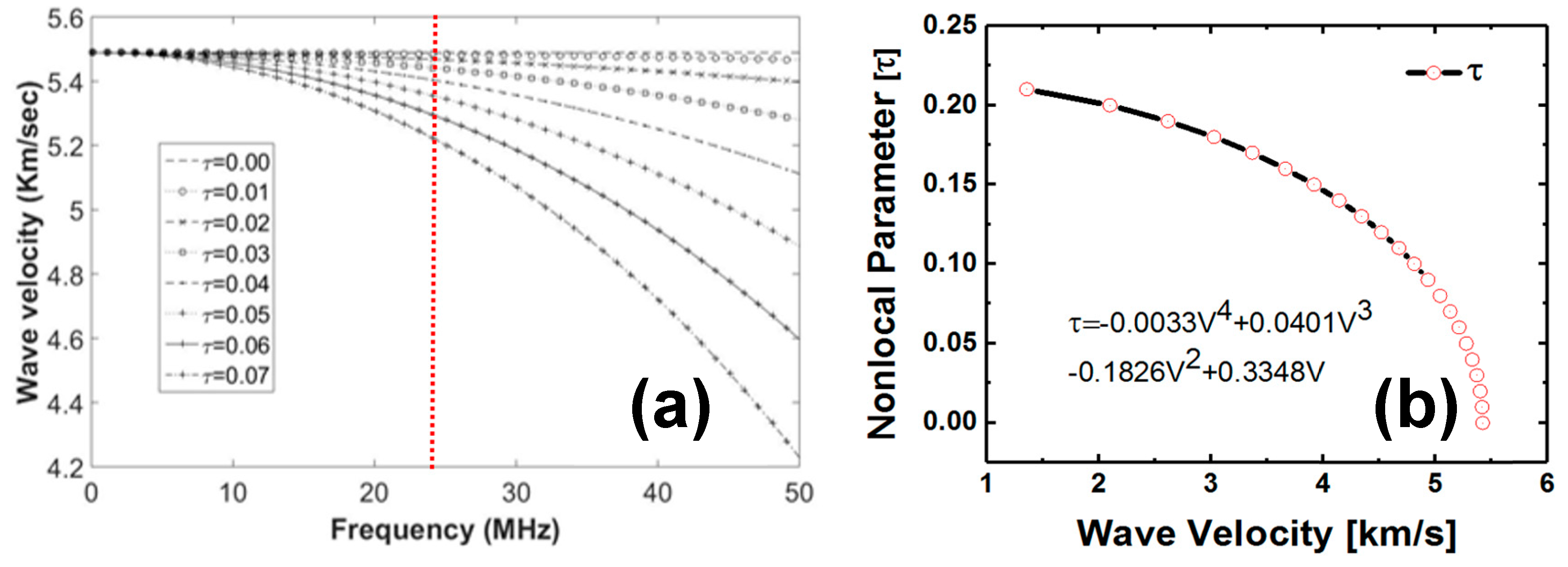
- Next the nonlocal parameter, τ, were obtained from the nonlocal dispersion curve at ~25 MHz as shown in Figure 3b at each pixel.
- (5)
- The nonlocal parameter obtained at the pristine state is called the intrinsic material property adjuster, , while the parameter calculated at different fatigue interval is called the intrinsic material state parameter, . Next, the average and the standard deviation of the intrinsic material state parameters were calculated from the data.
- (6)
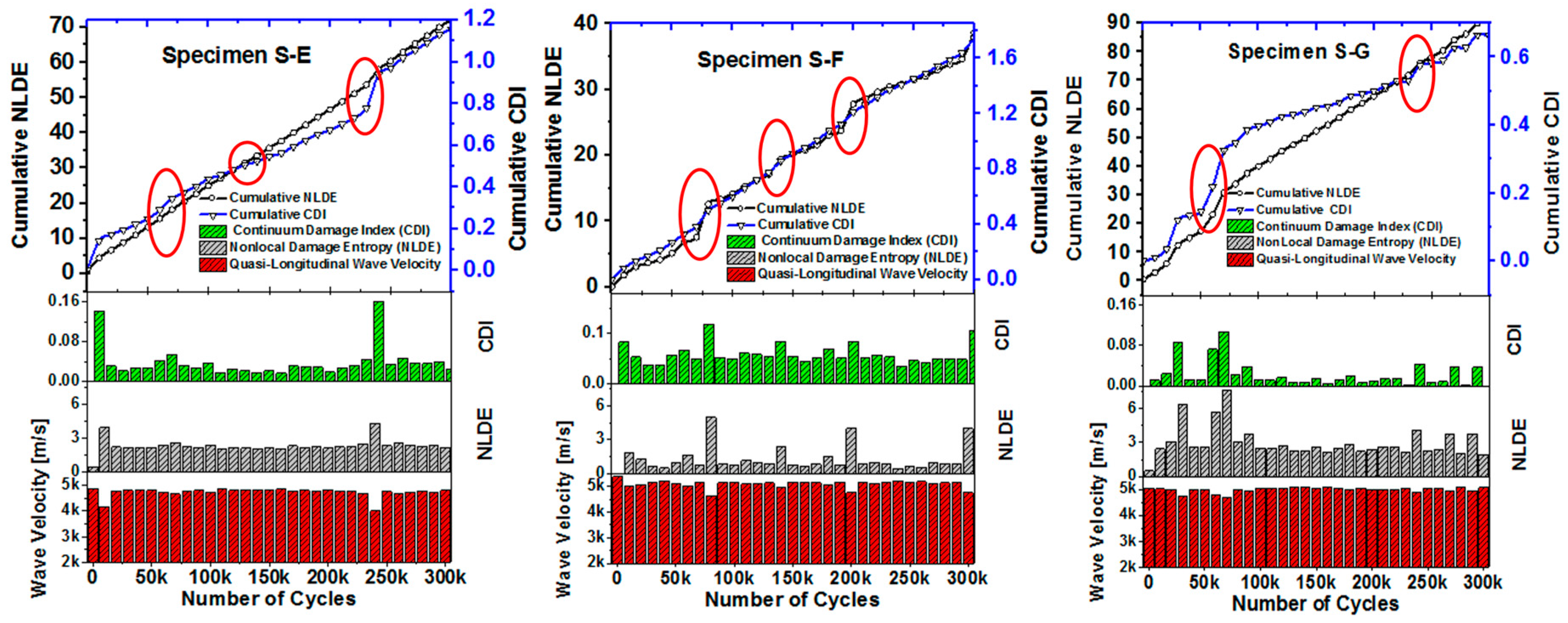
- The overall damage state of the material was quantified by the Nonlocal Damage Entropy (NLDE), using the above mentioned nonlocal parameters calculated at each pixelwhere i denotes the i-th pixel on the specimen, and the NLDE is the summation of the nonlocal parameters (Equation (9)) over all the pixel points.
- (7)
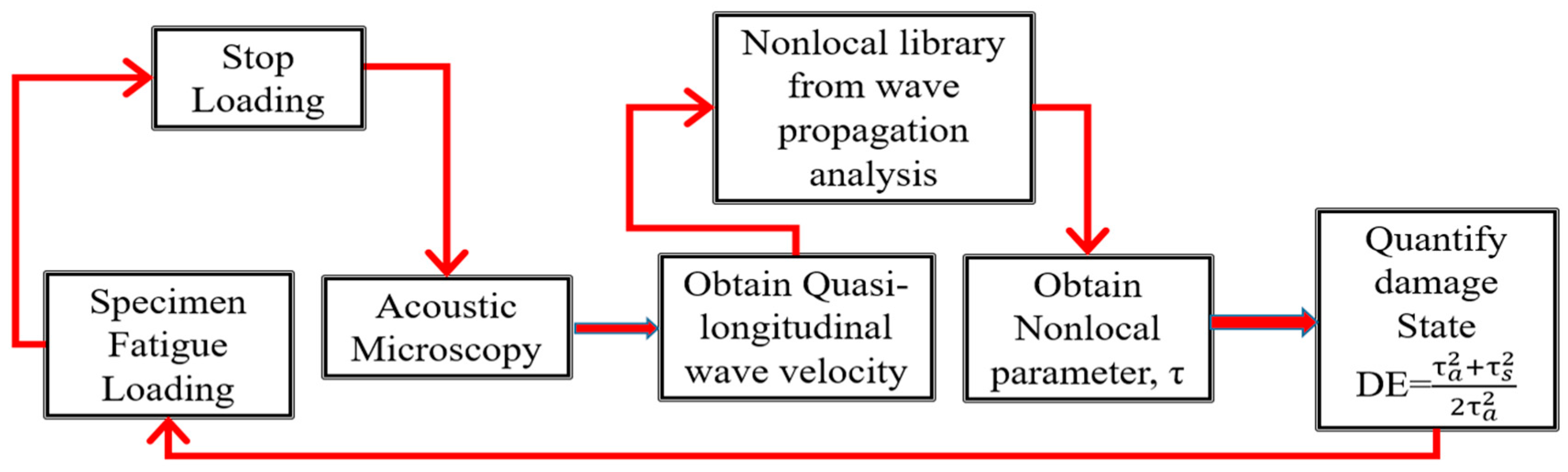
- Cumulative damage growth was then calculated to obtain the damage growth under the fatigue loading. The detailed process is shown in Figure 4.
3.2. Damage State Quantification from the Evaluation of Stiffness Degradation
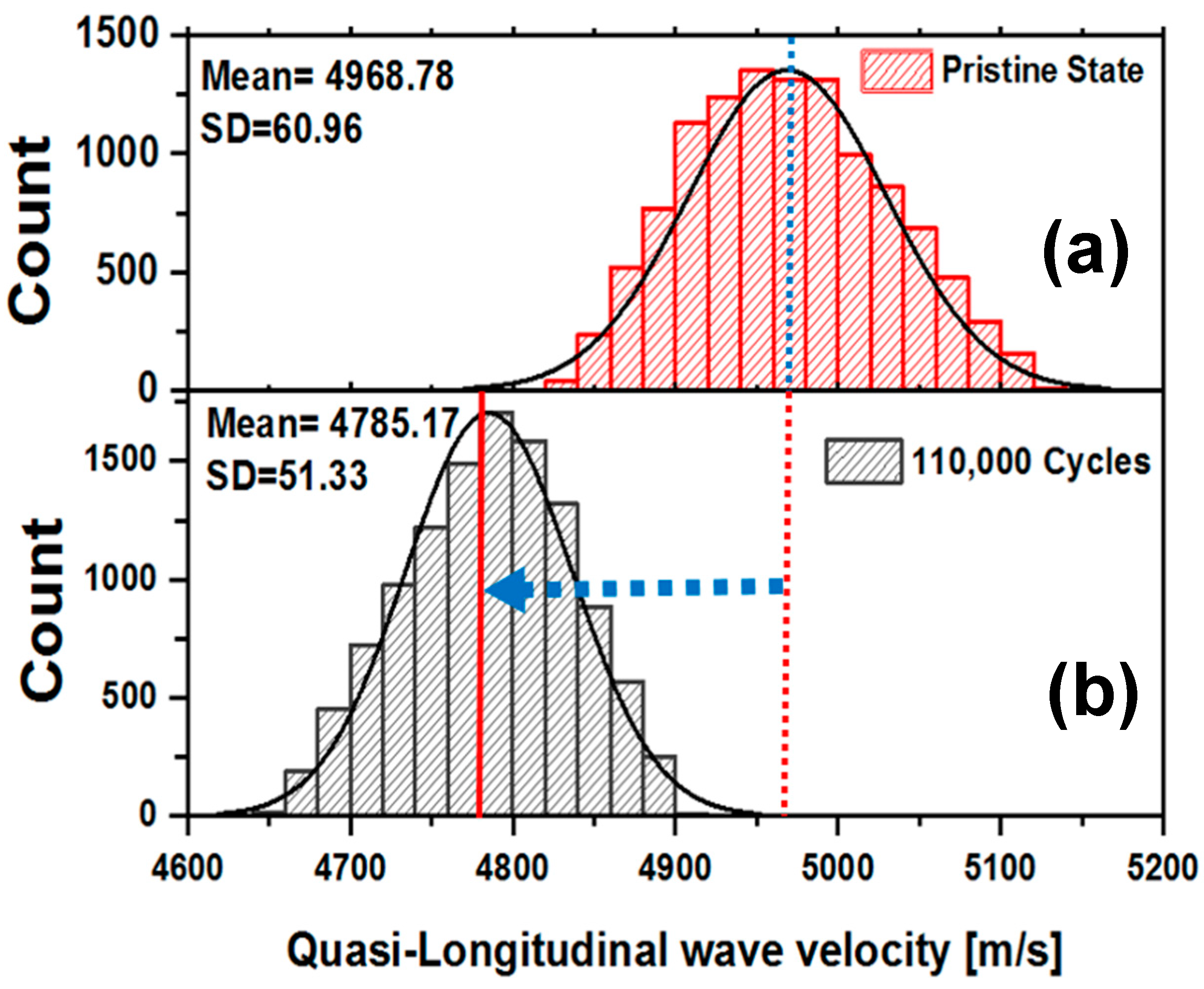
3.3. Probability Distribution of Quasi-Longitudinal Wave Velocity
4. Results and Discussion
4.1. Damage Quantification Using Quantitative Ultrasonic Image Correlation (QUIC)
4.1.1. A Proof of Material Degradation
4.1.2. Damage Quantification Using Nonlocal-Continuum Mechanics
4.1.3. Benchmark Damage Quantification from Stiffness Degradation
4.2. Benchmark Damage Characterization Using Micro-Optical Microscopy
4.3. Damage Characterization Using Scanning Electron Microscopy (SEM)
4.4. Damage Characterization Using Scanning Acoustic Microscopy (SAM)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviation
| Stress Tensor | |
| Strain Tensor | |
| Constitutive Matrix | |
| Nonlocal Stress Tensor | |
| Nonlocal Kernel function | |
| Force | |
| Density | |
| Displacement | |
| Kronecker delta | |
| L | Laplace operator |
| Amplitude Vector | |
| Wave Vector | |
| Frequency | |
| Intrinsic length scale factor | |
| Intrinsic length scale factor | |
| Length Scale | |
| Nonlocal Parameters | |
| Nonlocal Parameters | |
| Intrinsic material property adjuster | |
| Intrinsic material property state | |
| Stiffness tensor | |
| Quasi-longitudinal wave velocity | |
| Damage Tensor |
References
- Allen, D.H. Damage Evolution in Laminates in Damage Mechanics of Composite Materials; Talreja, R., Ed.; Elsevier: Amsterdam, The Netherlands, 1994; pp. 79–114. [Google Scholar]
- Reifsnider, K.L.; Case, S.W. (Eds.) Damage tolerance and durability of material systems. In Damage Tolerance and Durability of Material Systems; Wiley-VCH: Weinheim, Germany, 2002; p. 435. ISBN 0-471-15299-4. [Google Scholar]
- Soutis, C.; Beaumont, P.W. Multi-Scale Modelling of Composite Material Systems: The Art of Predictive Damage Modelling; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Ghosh, S. Adaptive concurrent multi-level model for multiscale analysis of composite materials including damage. In Multiscale Modeling and Simulation of Composite Materials and Structures; Kwon, Y.W., Allen, D.H., Talreja, R., Eds.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Nagy, P.B. Fatigue damage assessment by nonlinear ultrasonic materials characterization. Ultrasonics 1998, 36, 375–381. [Google Scholar] [CrossRef]
- Otto, B. Fatigue Damage and Its Nondestructive Evaluation: An Overview. In Review of Progress in Quantitative Nondestructive Evaluation; Thompson, D.O., Chimenti, D.E., Eds.; Springer: New York, NY, USA, 1998; pp. 1–13. [Google Scholar]
- Deng, M.; Pei, J. Assessment of Accumulated Fatigue Damage in Solid Plates using Nonlinear Lamb Wave Approach. Appl. Phys. Lett. 2007, 90, 121902. [Google Scholar] [CrossRef]
- McCormick, N.; Lord, J. Digital Image Correlation. Mater. Today 2010, 13, 52–54. [Google Scholar] [CrossRef]
- Dayal, V.; Kinra, V.K. Leaky Lamb waves in an anisotropic plate II: Nondestructive evaluation of matrix cracks in fiber-reinforced composites. J. Acoust. Soc. Am. 1991, 89, 1590–1598. [Google Scholar] [CrossRef]
- Banerjee, S. Estimation of intrinsic damage state in materials using non-local perturbation: Application to active health monitoring. J. Intell. Mater. Syst. Struct. 2009, 20, 1221–1232. [Google Scholar] [CrossRef]
- Banerjee, S.; Ahmed, R. Precursor/incubation of multi-scale damage state quantification in composite materials: Using hybrid microcontinuum field theory and high-frequency ultrasonics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
- Briggs, G.A.D.; Kolosov, O.V. Acoustic Microscopy, 2nd ed; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Drescher-Krasicka, E.; Willis, J.R. Mapping Stress with Ultrasound. Nature 1996, 384, 52–55. [Google Scholar]
- Kundu, T. Inversion of acoustic material signature of layered solids. J. Acoust. Soc. Am. 1992, 91, 591–600. [Google Scholar] [CrossRef]
- Nishida, M.; Endo, T.; Adachi, T.; Matsumoto, H. Measurement of local elastic moduli by magnitude and phase acoustic microscope. NDTE Int. 1997, 30, 271–277. [Google Scholar] [CrossRef]
- Zinin, P.; Weise, W. Theory and Applications of Acoustic Microscopy, in Ultrasonic Nondestructive Evaluation. In Engineering and Biological Material Characterization; Kundu, T., Ed.; CRC Press: Boca Raton, FL, USA, 2004; pp. 654–724. [Google Scholar]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Donadon, M.V.; De Almeida, S.F.M.; Arbelo, M.A.; de Faria, A.R. A three-dimensional ply failure model for composite structures. Int. J. Aerosp. Eng. 2009, 2009. [Google Scholar] [CrossRef]
- Ladeveze, P.; LeDantec, E. Damage modeling of the elementary ply for laminated composites. Compos. Sci. Technol. 1992, 43, 257–267. [Google Scholar] [CrossRef]
- Ladevèze, P.; Lubineau, G. On a damage mesomodel for laminates: Micro-meso relationships, possibilities and limits. Compos. Sci. Technol. 2001, 61, 2149–2158. [Google Scholar] [CrossRef]
- Habib, A.; Shelke, A.; Vogel, M.; Brand, S.; Jiang, X.; Pietsch, U.; Banerjee, S.; Kundu, T. Quantitative Ultrasonic Characterization of c-axis oriented polycrystalline AlN thin film for smart device application. Acta Acust. United Acust. 2015, 101, 675–683. [Google Scholar] [CrossRef]
- Astm, D. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM D3039/D 3039M; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- Kundu, T. A Complete Acoustic Microscopical Analysis of Multilayered Specimens. ASME J. Appl. Mech. 1992, 59, 54–60. [Google Scholar] [CrossRef]
- Patra, S.; Banerjee, S.; Terejanu, G.; Chanda, A. Subsurface pressure profiling: A novel mathematical paradigm for computing colony pressures on substrate during fungal infections. Sci. Rep. 2015, 5, 12928. [Google Scholar] [CrossRef] [PubMed]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Shelke, A.; Banerjee, S.; Kundu, T.; Amjad, U.; Grill, W. Multi-scale damage state estimation in composites using nonlocal elastic kernel: An experimental validation. Int. J. Solids Struct. 2011, 48, 1219–1228. [Google Scholar] [CrossRef]
- Lazar, M.; Maugin, G.A.; Aifantis, E.C. On a theory of nonlocal elasticity of bi-Helmholtz type and some applications. Int. J. Solids Struct. 2006, 43, 1404–1421. [Google Scholar] [CrossRef]
- Gresil, M.; Giurgiutiu, V. Prediction of attenuated guided waves propagation in carbon fiber composites using Rayleigh damping model. J. Intell. Mater. Syst. Struct. 2015, 26, 2151–2169. [Google Scholar] [CrossRef]
- Marguères, P.; Meraghni, F. Damage induced anisotropy and stiffness reduction evaluation in composite materials using ultrasonic wave transmission. Compos. Part A Appl. Sci. Manuf. 2013, 45, 134–144. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patra, S.; Banerjee, S. Material State Awareness for Composites Part II: Precursor Damage Analysis and Quantification of Degraded Material Properties Using Quantitative Ultrasonic Image Correlation (QUIC). Materials 2017, 10, 1444. https://doi.org/10.3390/ma10121444
Patra S, Banerjee S. Material State Awareness for Composites Part II: Precursor Damage Analysis and Quantification of Degraded Material Properties Using Quantitative Ultrasonic Image Correlation (QUIC). Materials. 2017; 10(12):1444. https://doi.org/10.3390/ma10121444
Chicago/Turabian StylePatra, Subir, and Sourav Banerjee. 2017. "Material State Awareness for Composites Part II: Precursor Damage Analysis and Quantification of Degraded Material Properties Using Quantitative Ultrasonic Image Correlation (QUIC)" Materials 10, no. 12: 1444. https://doi.org/10.3390/ma10121444
APA StylePatra, S., & Banerjee, S. (2017). Material State Awareness for Composites Part II: Precursor Damage Analysis and Quantification of Degraded Material Properties Using Quantitative Ultrasonic Image Correlation (QUIC). Materials, 10(12), 1444. https://doi.org/10.3390/ma10121444




