Acoustic Anomalies and Fast Relaxation Dynamics of Amorphous Progesterone as Revealed by Brillouin Light Scattering
Abstract
1. Introduction
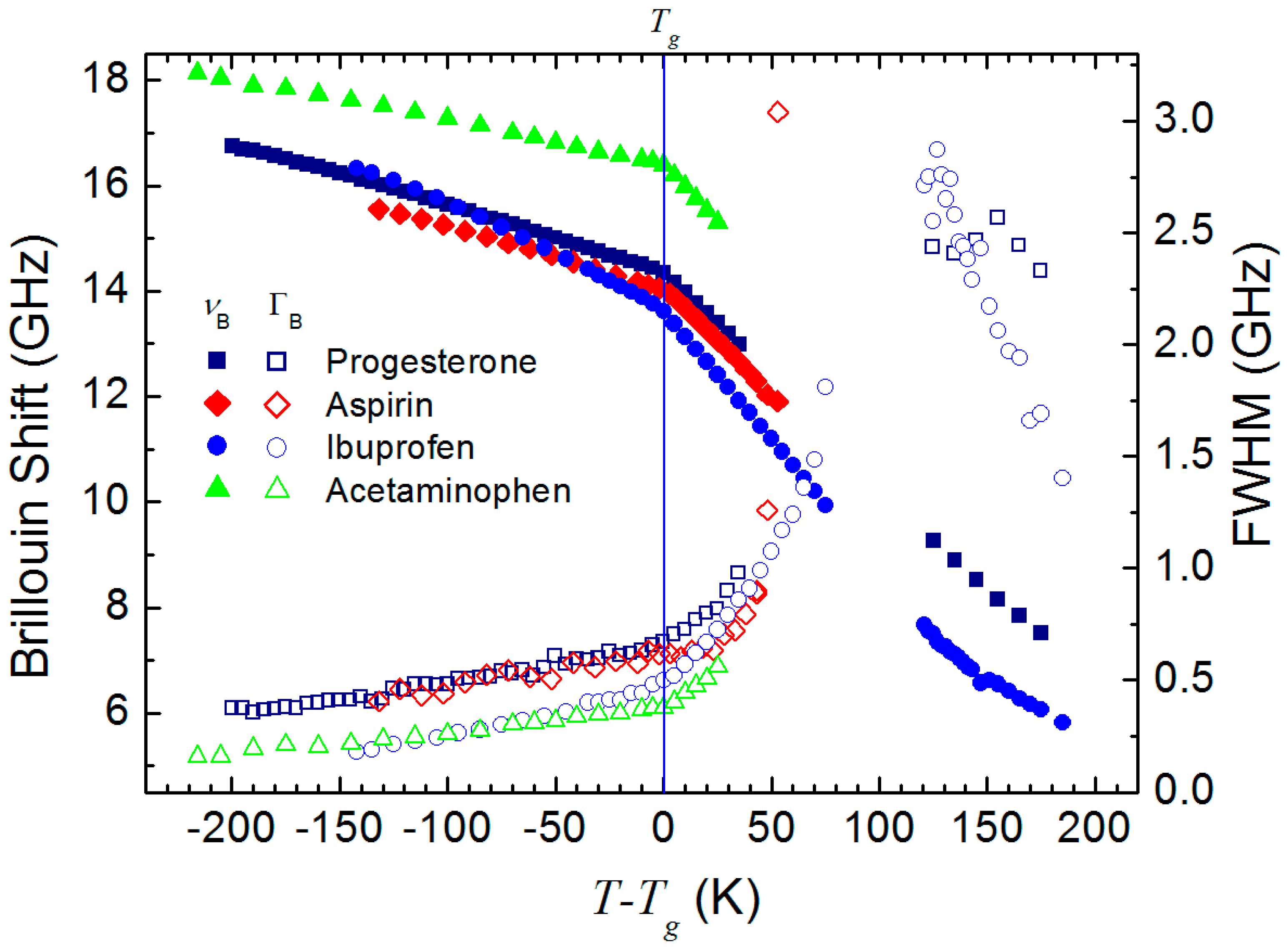
2. Results
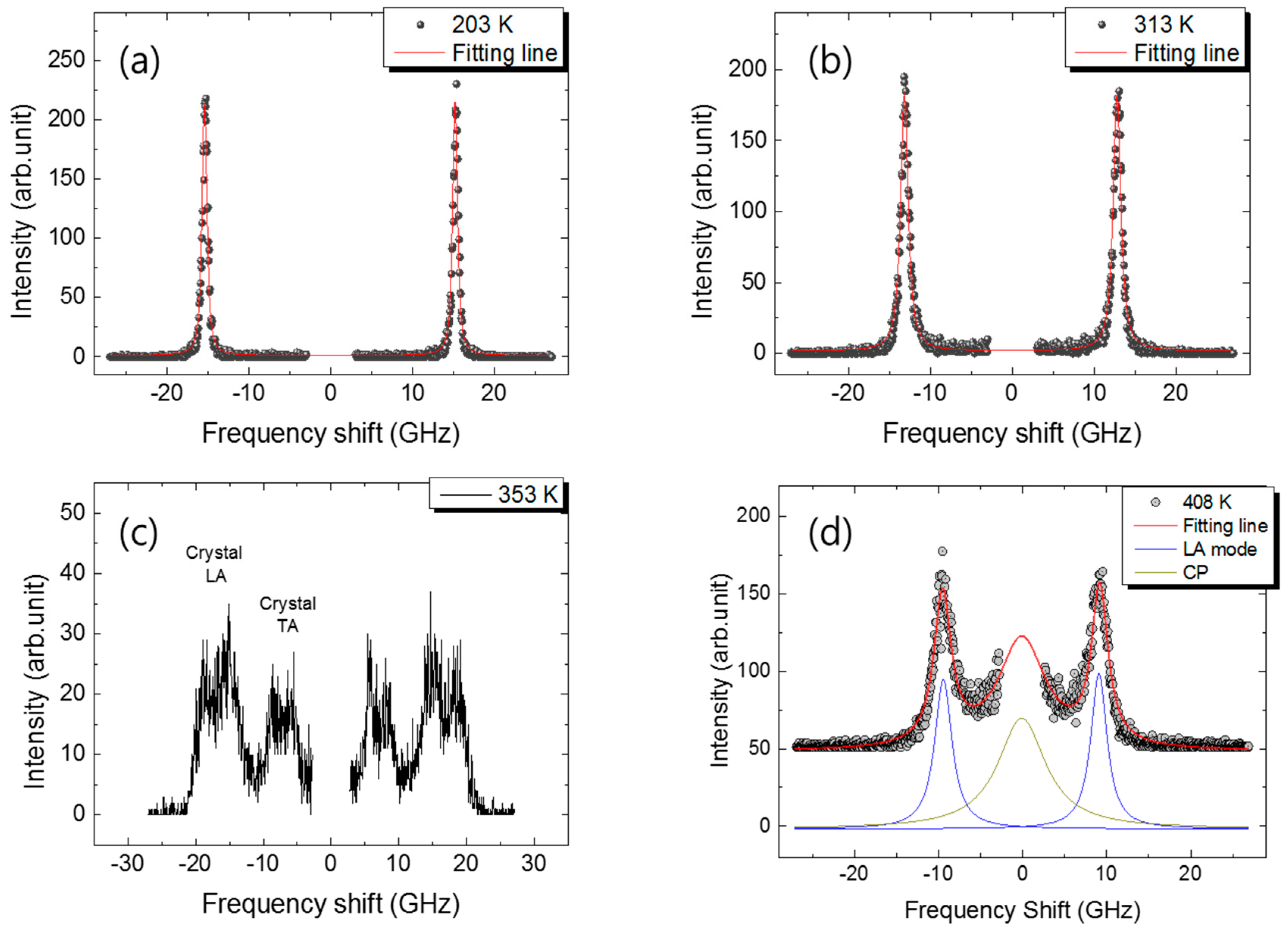
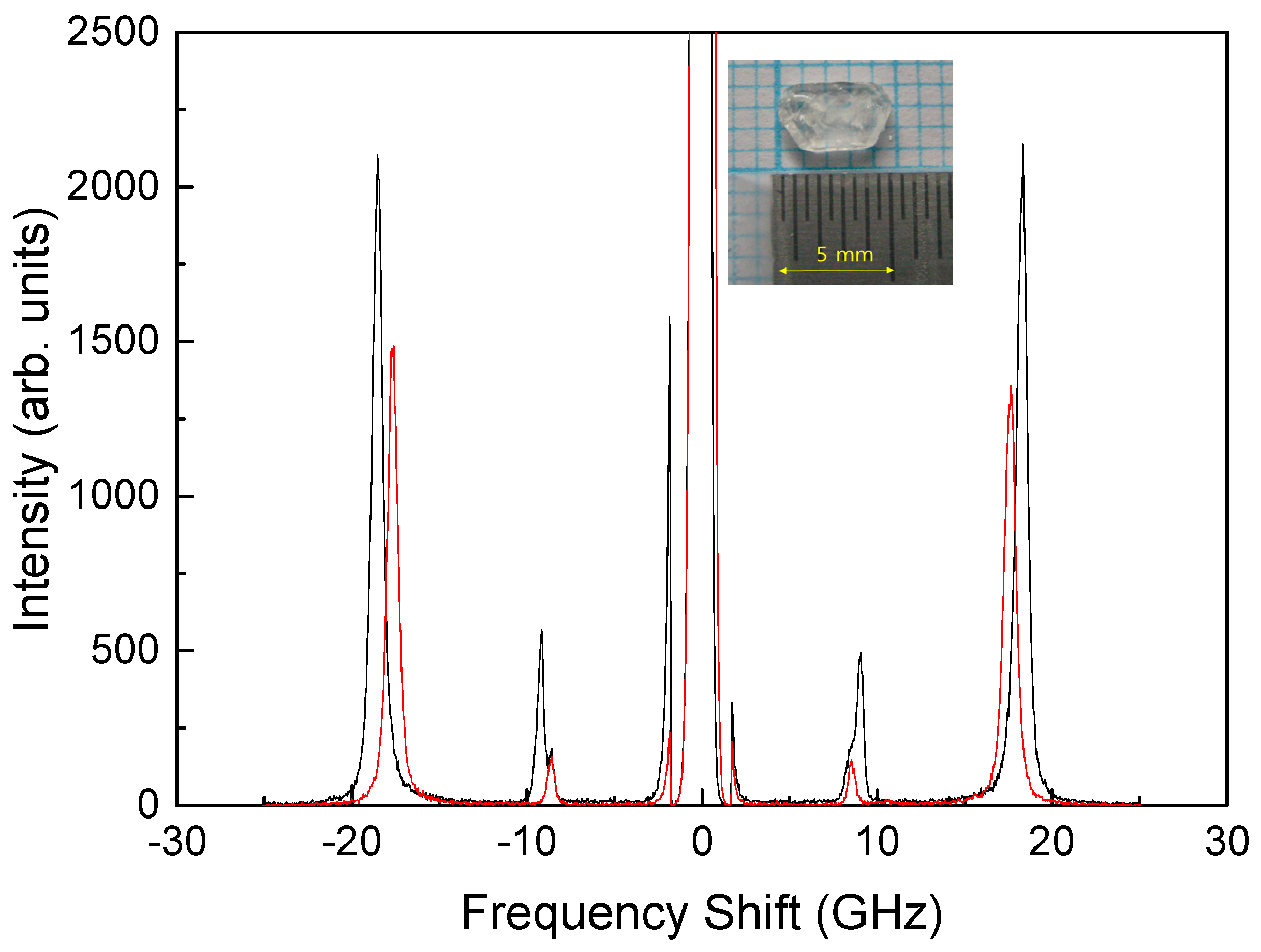
2.1. Brillouin Scattering Spectrum
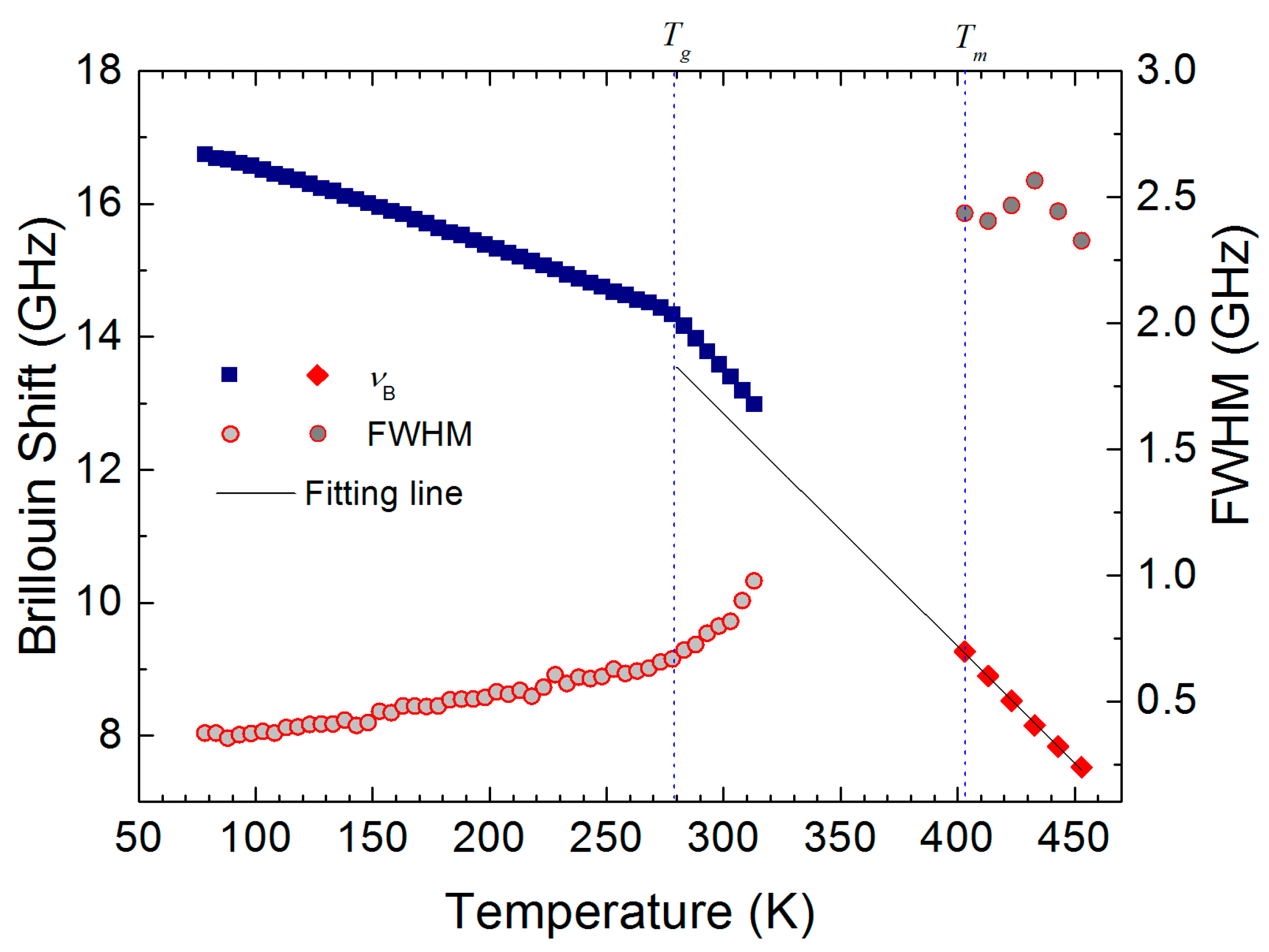
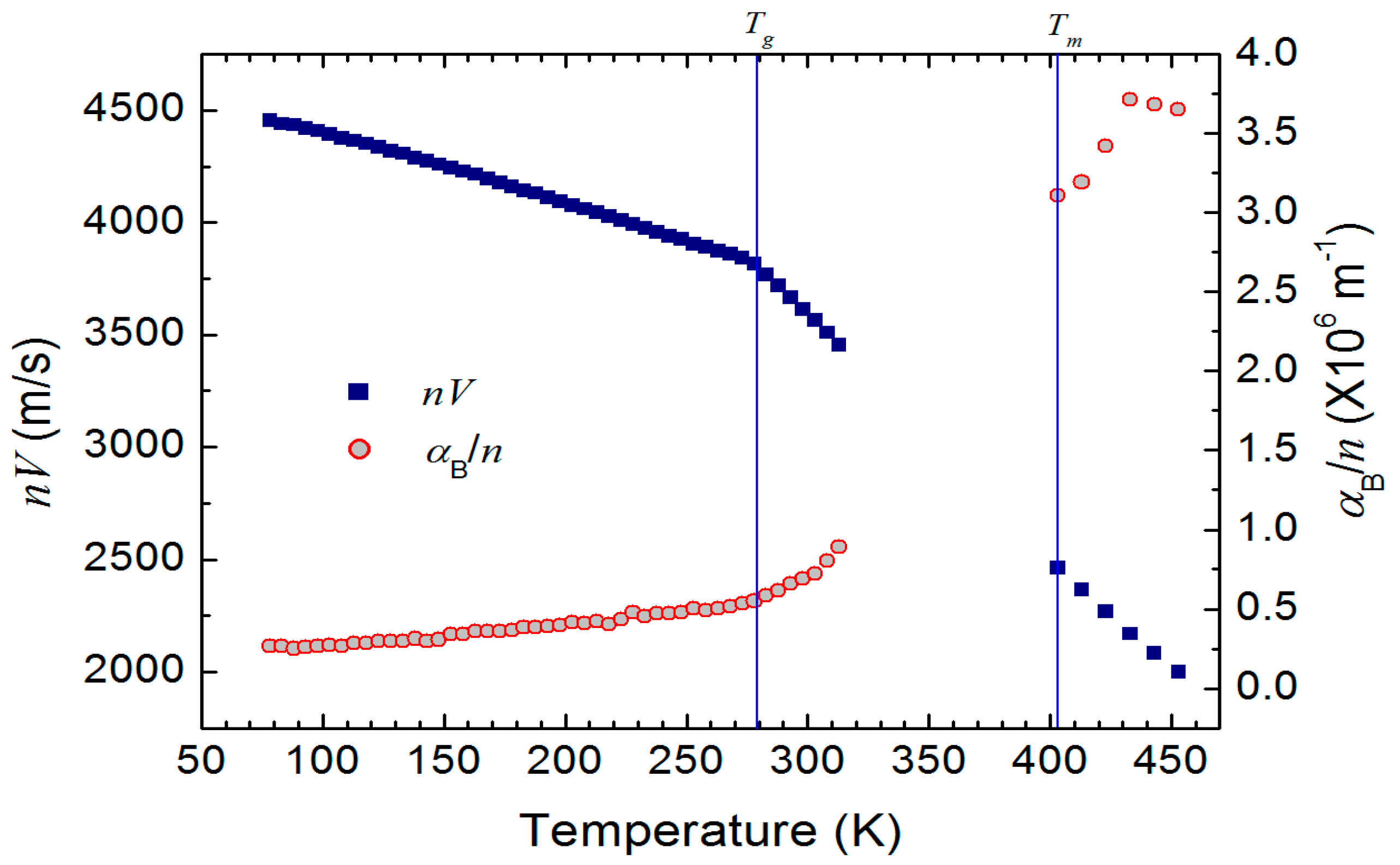
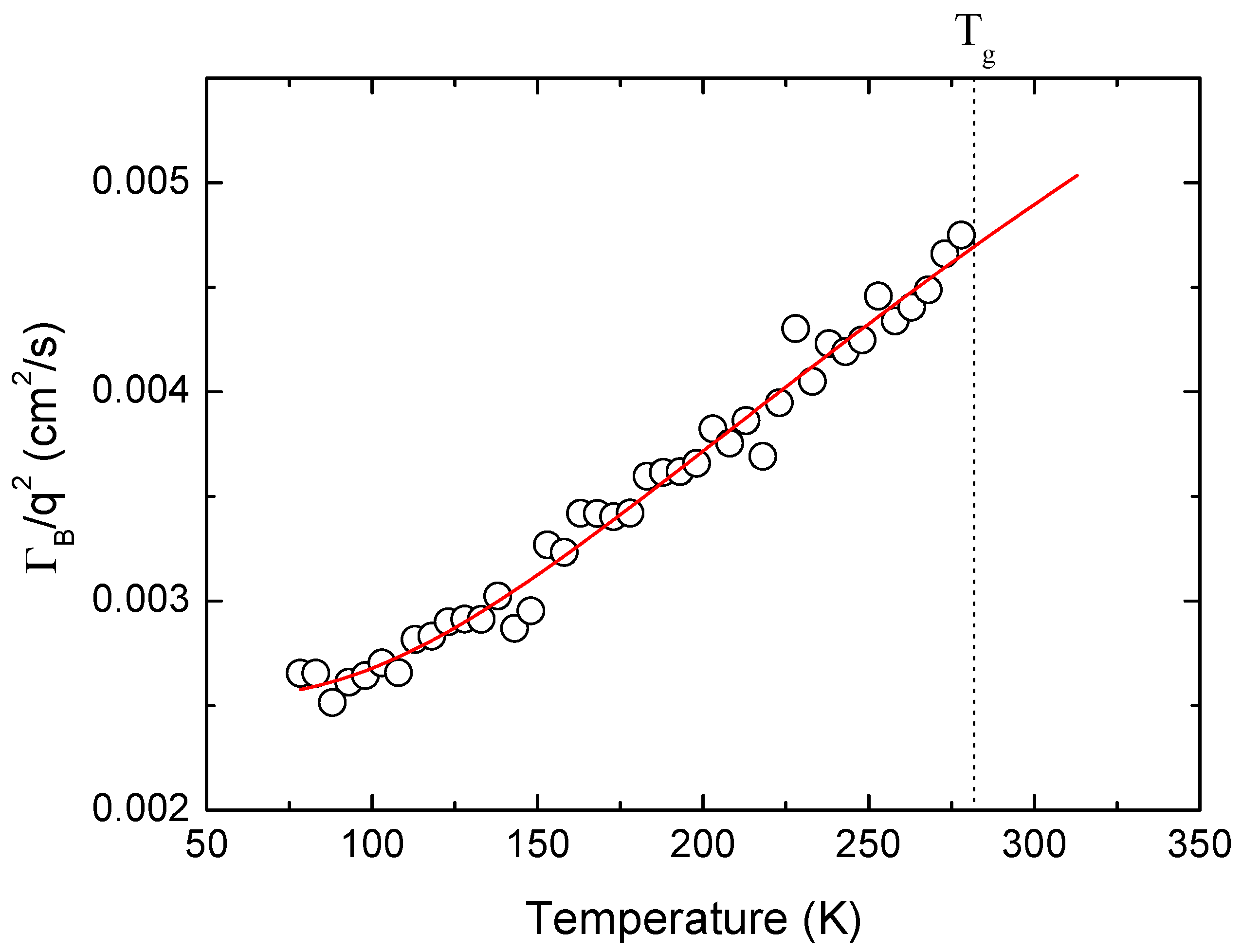
2.2. Analysis and Comparison
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Methods
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hancock, B.C.; Zograf, G. Characteristics and Significance of the Amorphous State in Pharmaceutical Systems. J. Pharm. Sci. 1997, 86, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Descamps, M. Disordered Pharmaceutical Materials, 1st ed.; Wiley-VCH: Weinheim, Germany, 2016; ISBN 978-3-527-33125-3. [Google Scholar]
- Johari, G.P.; Pyke, D. On the glassy and supercooled liquid states of a common medicament: Aspirin. Phys. Chem. Chem. Phys. 2000, 2, 5479–5484. [Google Scholar] [CrossRef]
- Dyre, J.C. The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 2006, 78, 953–972. [Google Scholar] [CrossRef]
- Kothari, K.; Ragoonanan, V.; Suryanarayanan, R. Influence of Molecular Mobility on the Physical Stability of Amorphous Pharmaceuticals in the Supercooled and Glassy States. Mol. Pharm. 2014, 11, 3048–3055. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P.; Kim, S.; Shanker, R.M. Dielectric Relaxation and Crystallization of Ultraviscous Melt and Glassy States of Aspirin, Ibuprofen, Progesterone, and Quinidine. J. Pharm. Sci. 2007, 96, 1159–1175. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P.; Kim, S.; Shanker, R.M. Dielectric Study of Equimolar Acetaminophen–Aspirin, Acetaminophen–Quinidine, and Benzoic Acid–Progesterone Molecular Alloys in the Glass and Ultraviscous States and Their Relevance to Solubility and Stability. J. Pharm. Sci. 2010, 99, 1358–1374. [Google Scholar] [CrossRef] [PubMed]
- Campsteyn, H.; Dupont, L.; Dideberg, O. Structure Cristalline et Moléculaire de la Progestérone, C21H30O2. Acta Crystallogr. Sect. B 1972, 28, 3032–3042. [Google Scholar] [CrossRef]
- Foresti, S.E.; Krajewski, A.; Mongiorgi, R.; Riva de Sanseverino, L.; Cameroni, R. 4-Pregnen-3,20-Dione (Progesterone, Form 2). Cryst. Struct. Commun. 1975, 4, 189–192. [Google Scholar]
- Payne, R.S.; Roberts, R.J.; Rowe, R.C.; Docherty, R. Examples of successful crystal structure prediction: Polymorphs of primidone and progesterone. Int. J. Pharm. 1999, 177, 231–245. [Google Scholar] [CrossRef]
- Narayana Kalkura, S.; Devanarayanan, S. Growth of progesterone crystals in silica gel and their characterization. J. Mater. Sci. Lett. 1988, 7, 827–829. [Google Scholar] [CrossRef]
- Wang, F.; Wachter, J.A.; Antosz, F.J.; Berglund, K.A. An investigation of solvent mediated polymorphic transformation of progesterone using in situ Raman spectroscopy. Org. Process Res. Dev. 2000, 4, 391–395. [Google Scholar] [CrossRef]
- Cendejas-Santana, G.; Hinojosa-Torres, J.; Gastaño, V.M. Progesterone crystallization from a solvent: A new procedure. Mater. Res. Innovat. 2002, 6, 252–255. [Google Scholar] [CrossRef]
- Falcon, J.A.; Berglund, K.A. In situ monitoring of antisolvent addition crystallization with principal components analysis of Raman spectra. Cryst. Growth Des. 2004, 4, 457–463. [Google Scholar] [CrossRef]
- Lancaster, R.W.; Karamertzanis, P.G.; Hulme, A.T.; Tocher, D.A.; Lewis, T.C.; Price, S.L. The polymorphism of progesterone: Stabilization of a ‘disappearing’ polymorph by co-crystallization. J. Pharm. Sci. 2007, 96, 3419–3431. [Google Scholar] [CrossRef] [PubMed]
- Comez, L.; Masciovecchio, C.; Monaco, G.; Fioretto, D. Progress in liquid and glass physics by Brillouin scattering spectroscopy. Solid Stat Phys. 2012, 63, 1–77. [Google Scholar]
- Ko, J.-H.; Lee, K.-S.; Ike, Y.; Kojima, S. Elastic properties of aspirin in its crystalline and glassy phases studied by micro-Brillouin scattering. Chem. Phys. Lett. 2008, 465, 36–39. [Google Scholar] [CrossRef]
- Kim, T.H.; Ko, J.-H.; Lee, K.-S.; Ike, Y.; Kojima, S. Growth of Aspirin Single Crystals and the Temperature Dependence of Its Elastic Constants As Studied by Brillouin Scattering. New Phys. Sae Mulli 2009, 58, 596–601. [Google Scholar]
- Ko, J.-H.; Kim, T.H.; Lee, K.-S.; Kojima, S. Acoustic properties of aspirin in its various phases and transformation stages studied by Brillouin scattering. J. Non-Cryst. Solids 2011, 357, 547–551. [Google Scholar] [CrossRef]
- Ko, J.-H.; Kim, T.H.; Lee, K.-S.; Kojima, S. Brillouin scattering study on crystalline and glassy states of anti-inflammatory racemic S(+)–R(−) ibuprofen. Chem. Phys. Lett. 2011, 515, 221–225. [Google Scholar] [CrossRef]
- Kim, T.H.; Shibata, T.; Kojima, S.; Shin, D.-M.; Hwang, Y.-H.; Ko, J.-H. Comparison of thermal and elastic properties of glassy racemic and enantiomorphic ibuprofen studied by Brillouin light scattering and modulated differential scanning calorimetry. Curr. Appl. Phys. 2014, 14, 965–969. [Google Scholar] [CrossRef]
- Shin, D.-M.; Hwang, Y.-H.; Ko, J.-H.; Kojima, S. Relaxation behaviors of enantiomorphic S-ibuprofen as revealed by dielectric and photon correlation spectroscopies. Curr. Appl. Phys. 2015, 15, 958–963. [Google Scholar] [CrossRef]
- Kwon, H.-J.; Kim, T.H.; Ko, J.-H.; Hwang, Y.-H. Relaxation phenomena in supercooled liquid and glassy acetaminophen studied by dielectric, photon correlation and Brillouin light scattering spectroscopies. Chem. Phys. Lett. 2013, 556, 117–121. [Google Scholar] [CrossRef]
- Kim, T.H.; Ko, J.-H.; Kwon, E.M.; Jun, J.-G. Micro-Brillouin Spectroscopy Applied to the Glass Transition of Anti-inflammatory Egonol. J. Opt. Soc. Korea 2010, 14, 403–408. [Google Scholar] [CrossRef]
- Ko, J.-H.; Kim, T.H.; Jung, S.H.; Jun, J.-G. Study on the Possibility of Vitrification and Phase Transition in Decursinol Studied by Using Brillouin Light Scattering. New Phys. Sae Mulli 2013, 63, 444–448. [Google Scholar]
- Shibata, T.; Takayama, H.; Kim, T.H.; Kojima, S. Acoustic and thermal anomalies in a liquid–glass transition of racemic S(+)–R(−) ketoprofen. Chem. Phys. Lett. 2014, 592, 80–84. [Google Scholar] [CrossRef]
- Vacher, R.; Boyer, L. Brillouin scattering: A tool for the measurement of elastic and photoelastic constants. Phys. Rev. B 1972, 6, 639–673. [Google Scholar] [CrossRef]
- Ko, J.-H.; Kim, D.H.; Kojima, S.; Kim, J.-H.; Choo, W.K. Brillouin Scattering Study on Polycrystalline Relaxor Ferroelectrics. Jpn. J. Appl. Phys. 2003, 42, 3076–3079. [Google Scholar] [CrossRef]
- Watanabe, A. A Trial Production of a Table of the Optical Crystallographic Characteristics of Crystalline Drugs Including Crystal Habits (Study of Crystalline Drugs by Means of a Polarizing Microscope. XIX. Yakugaku Zasshi 2002, 122, 595–606. [Google Scholar] [CrossRef] [PubMed]
- Torell, L.M. Brillouin scattering study of hypersonic relaxation in Ca(NO3)2-KNO3 mixture. J. Chem. Phys. 1982, 76, 3467–3473. [Google Scholar] [CrossRef]
- Kriegs, H.; Meier, G.; Gapinski, J.; Patkowski, A. The effect of intramolecular relaxations on the damping of longitudinal and transverse phonons in polysiloxanes studied by Brillouin spectroscopy. J. Chem. Phys. 2008, 128, 014507. [Google Scholar] [CrossRef] [PubMed]
- Fioretto, D.; Scarponi, F. Dynamics of a glassy polymer studied by Brillouin light scattering. Mater. Sci. Eng. A 2009, 521–522, 243–246. [Google Scholar] [CrossRef]
- Comez, L.; Pietrella, M.; Fioretto, D.; Monaco, G.; Scarponi, F.; Verbeni, R. Brillouin-scattering study of the fast dynamics of m-toluidine. Philos. Mag. 2007, 87, 651–656. [Google Scholar] [CrossRef]
- Schammé, B.; Mignot, M.; Couvrat, N.; Tognetti, V.; Joubert, L.; Dupray, V.; Delbreilh, L.; Dargent, E.; Coquerel, G. Molecular Relaxations in Supercooled Liquid and Glassy States of Amorphous Quinidine: Dielectric Spectroscopy and Density Functional Theory Approaches. J. Phys. Chem. B 2016, 120, 7579–7592. [Google Scholar] [CrossRef] [PubMed]
- Shikii, K.; Sakamoto, S.; Seki, H.; Utsumi, H.; Yamaguchi, K. Narcissistic aggregation of steroid compounds in diluted solution elucidated by CSI-MS, PFG NMR and X-ray analysis. Tetrahedron 2004, 60, 3487–3492. [Google Scholar] [CrossRef]
- Bryk, T.; Ruocco, G.; Scopigno, T.; Seitsonen, A.P. Pressure-induced emergence of unusually high-frequency transverse excitations in a liquid alkali metal: Evidence of two types of collective excitations contributing to the transverse dynamics at high pressures. J. Chem. Phys. 2015, 143, 104502. [Google Scholar] [CrossRef] [PubMed]
- Grzybowska, K.; Capaccioli, S.; Paluch, M. Recent developments in the experimental investigations of relaxations in pharmaceuticals by dielectric techniques at ambient and elevated pressure. Adv. Drug Deliv. Rev. 2016, 100, 158–182. [Google Scholar] [CrossRef] [PubMed]
- Ko, J.-H.; Jeong, M.-S.; Lee, B.W.; Kim, J.H.; Ko, Y.H.; Kim, K.J.; Kim, T.H.; Kojima, S.; Ahart, M. Pressure Dependence of Acoustic Properties of Liquid Ethanol by using High-pressure Brillouin Spectroscopy. Korean J. Opt. Photon. 2013, 24, 279–286. [Google Scholar] [CrossRef]
- Oh, S.H.; Cho, B.J.; Jeong, M.S.; Ko, J.-H. Evaluation of the isothermal curing process of UV-cured resin in terms of elasticity studied through micro-Brillouin light scattering. J. Inf. Disp. 2016, 17, 87–91. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.H.; Yoo, H.; Ko, J.-H. Acoustic Anomalies and Fast Relaxation Dynamics of Amorphous Progesterone as Revealed by Brillouin Light Scattering. Materials 2017, 10, 1426. https://doi.org/10.3390/ma10121426
Kim TH, Yoo H, Ko J-H. Acoustic Anomalies and Fast Relaxation Dynamics of Amorphous Progesterone as Revealed by Brillouin Light Scattering. Materials. 2017; 10(12):1426. https://doi.org/10.3390/ma10121426
Chicago/Turabian StyleKim, Tae Hyun, Hyojong Yoo, and Jae-Hyeon Ko. 2017. "Acoustic Anomalies and Fast Relaxation Dynamics of Amorphous Progesterone as Revealed by Brillouin Light Scattering" Materials 10, no. 12: 1426. https://doi.org/10.3390/ma10121426
APA StyleKim, T. H., Yoo, H., & Ko, J.-H. (2017). Acoustic Anomalies and Fast Relaxation Dynamics of Amorphous Progesterone as Revealed by Brillouin Light Scattering. Materials, 10(12), 1426. https://doi.org/10.3390/ma10121426




