The Structure of Liquid and Amorphous Hafnia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. High Energy X-ray Diffraction
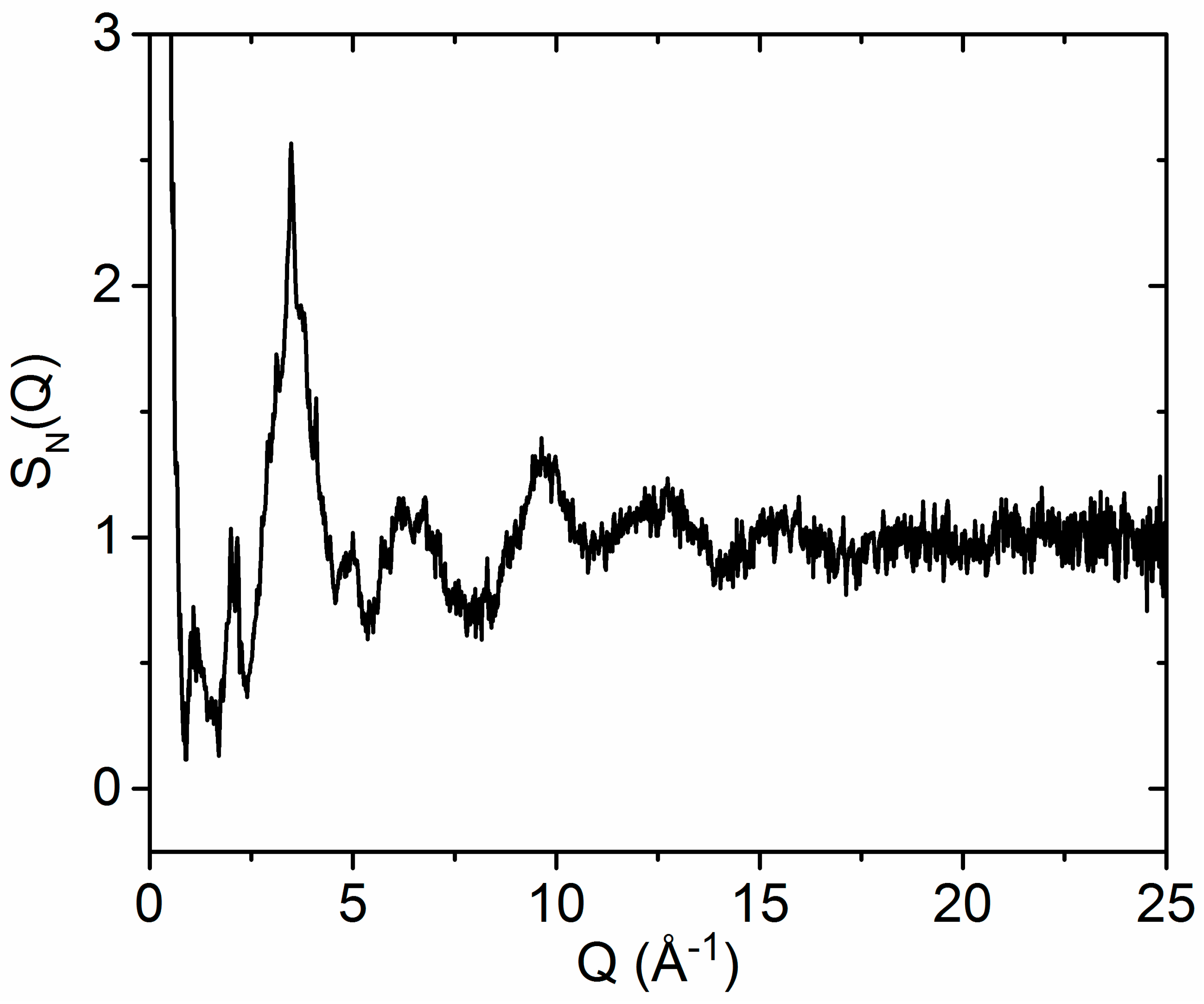
2.3. Neutron Diffraction
2.4. Ab Initio Molecular Dynamics Simulations
2.5. Classical Molecular Dynamics Simulations
3. Results
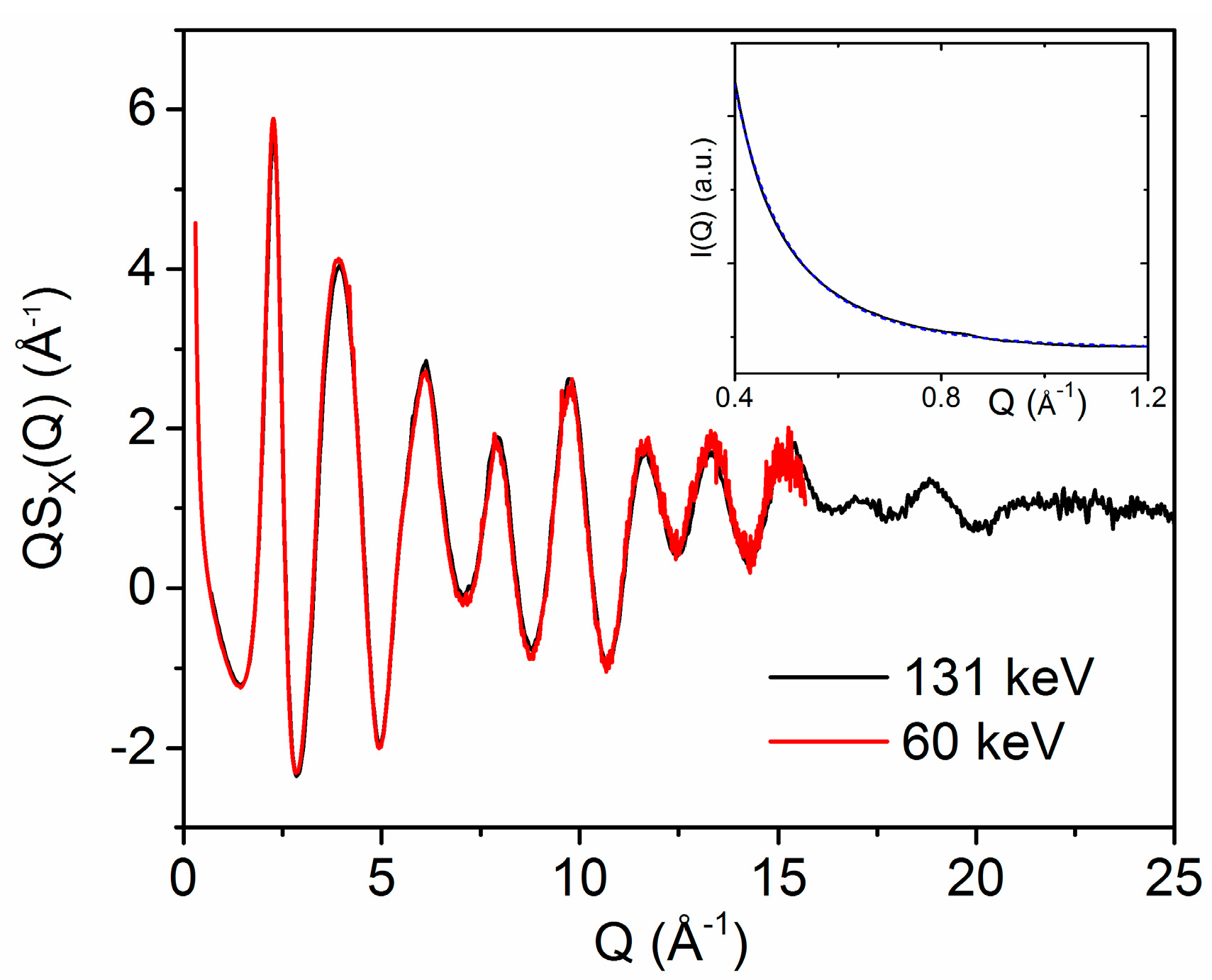
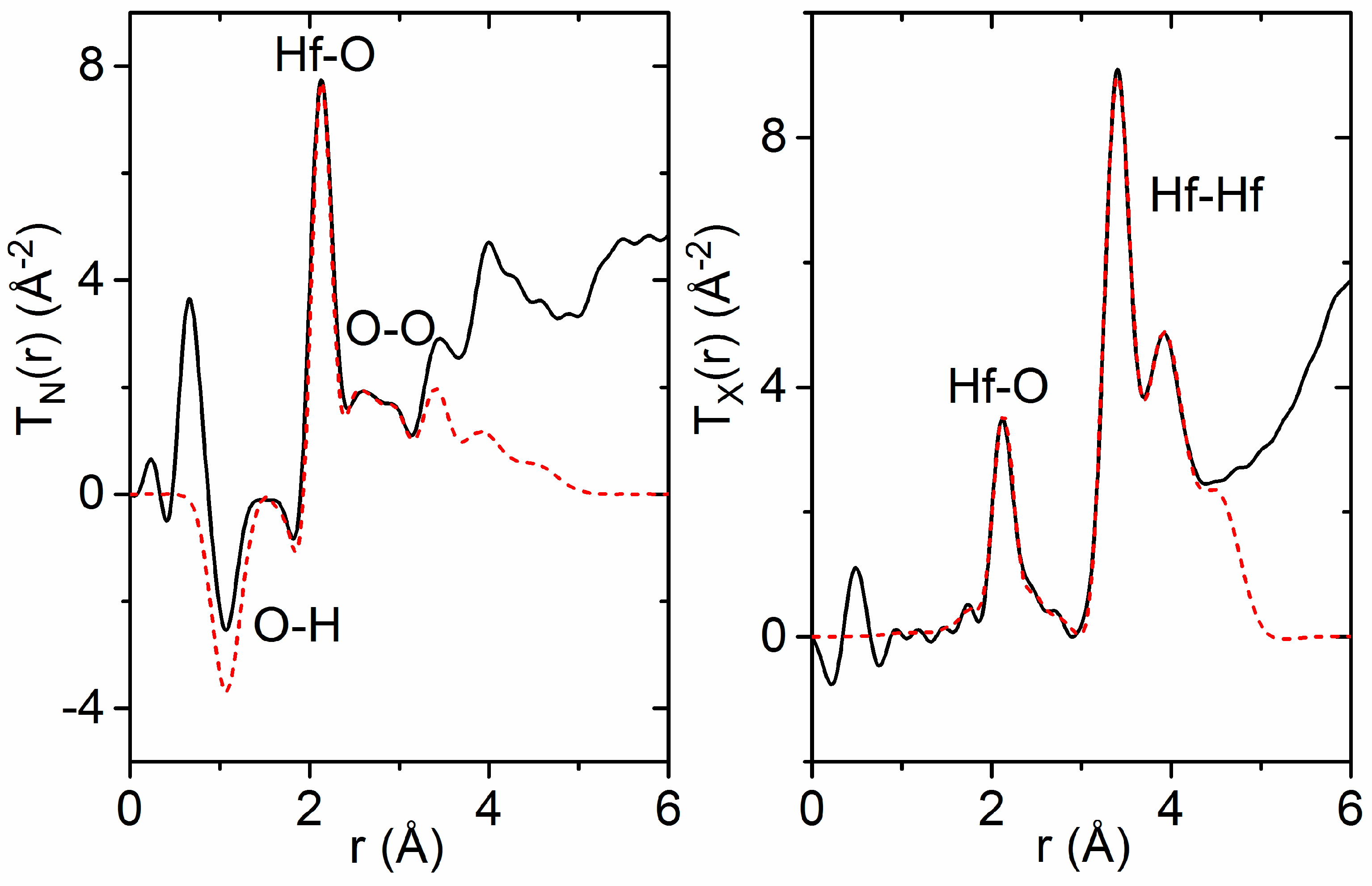
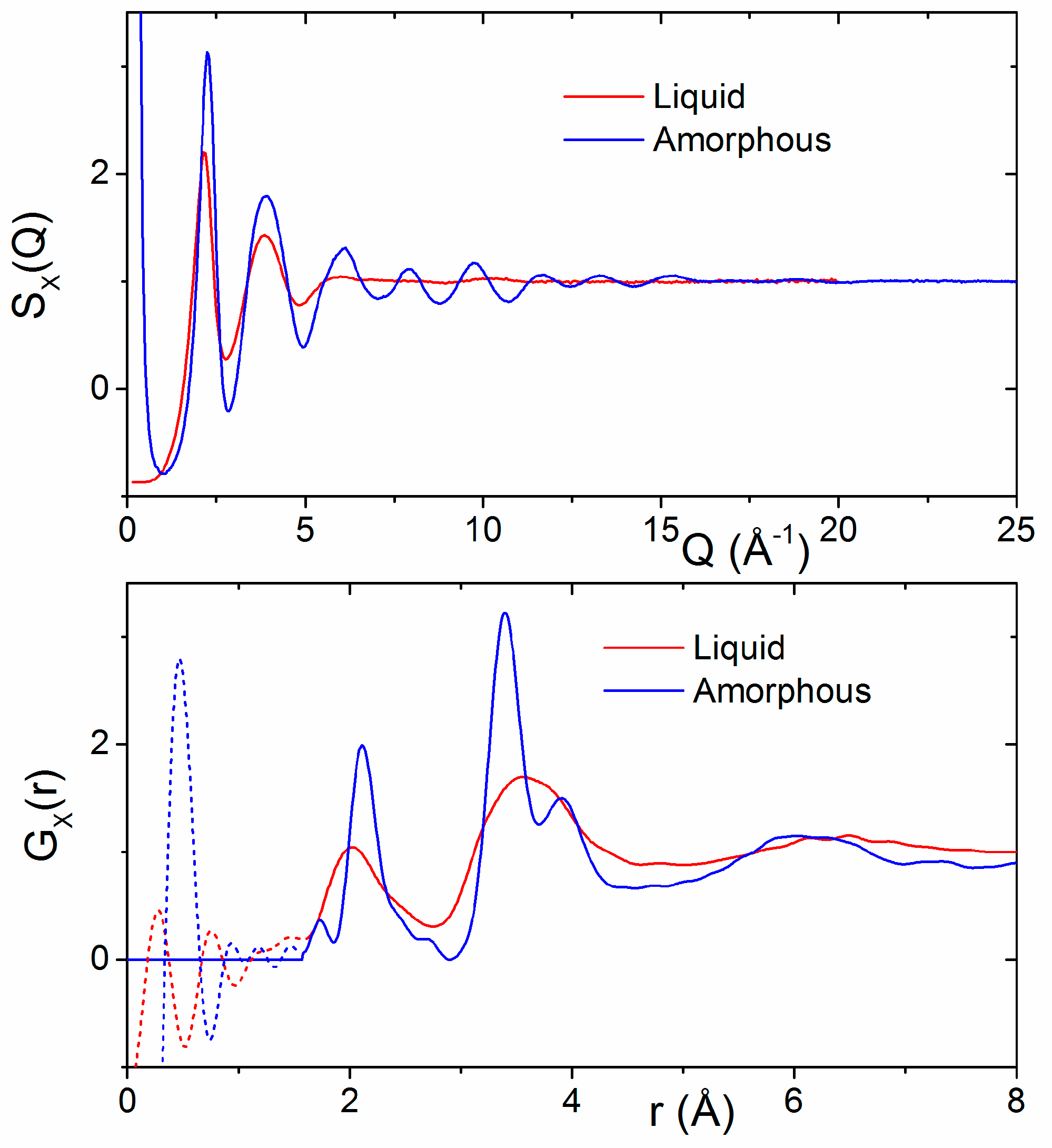
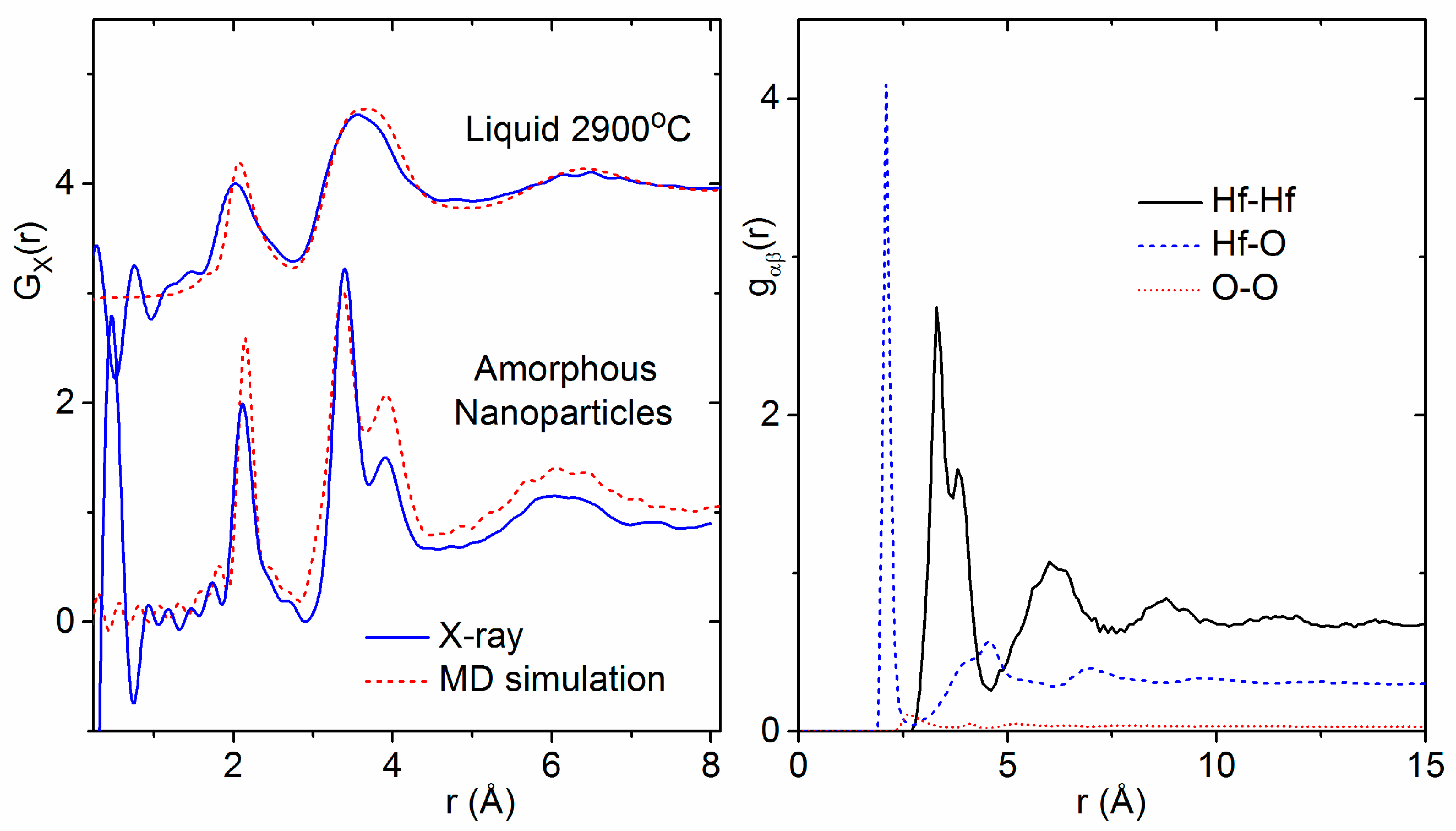
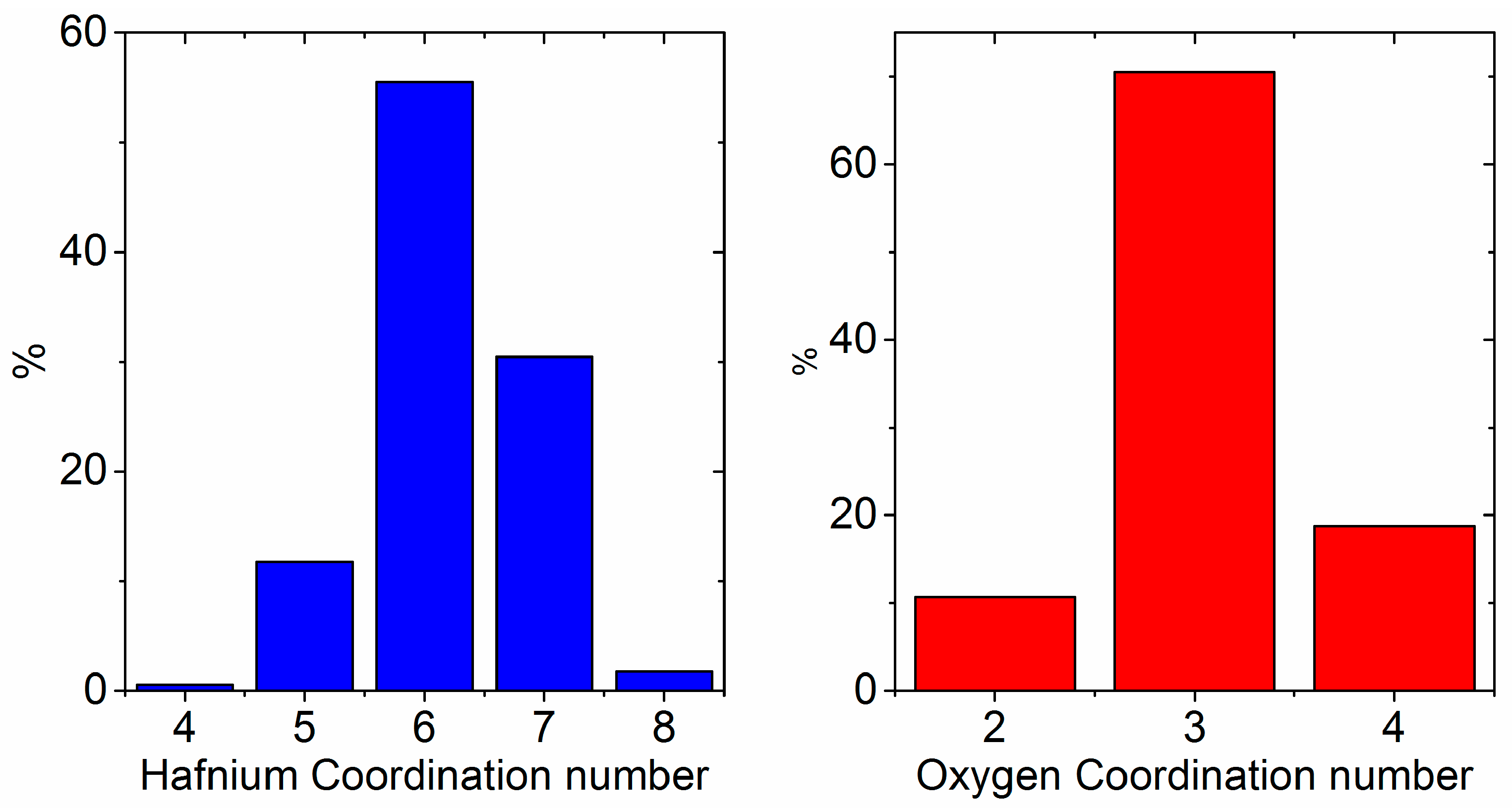
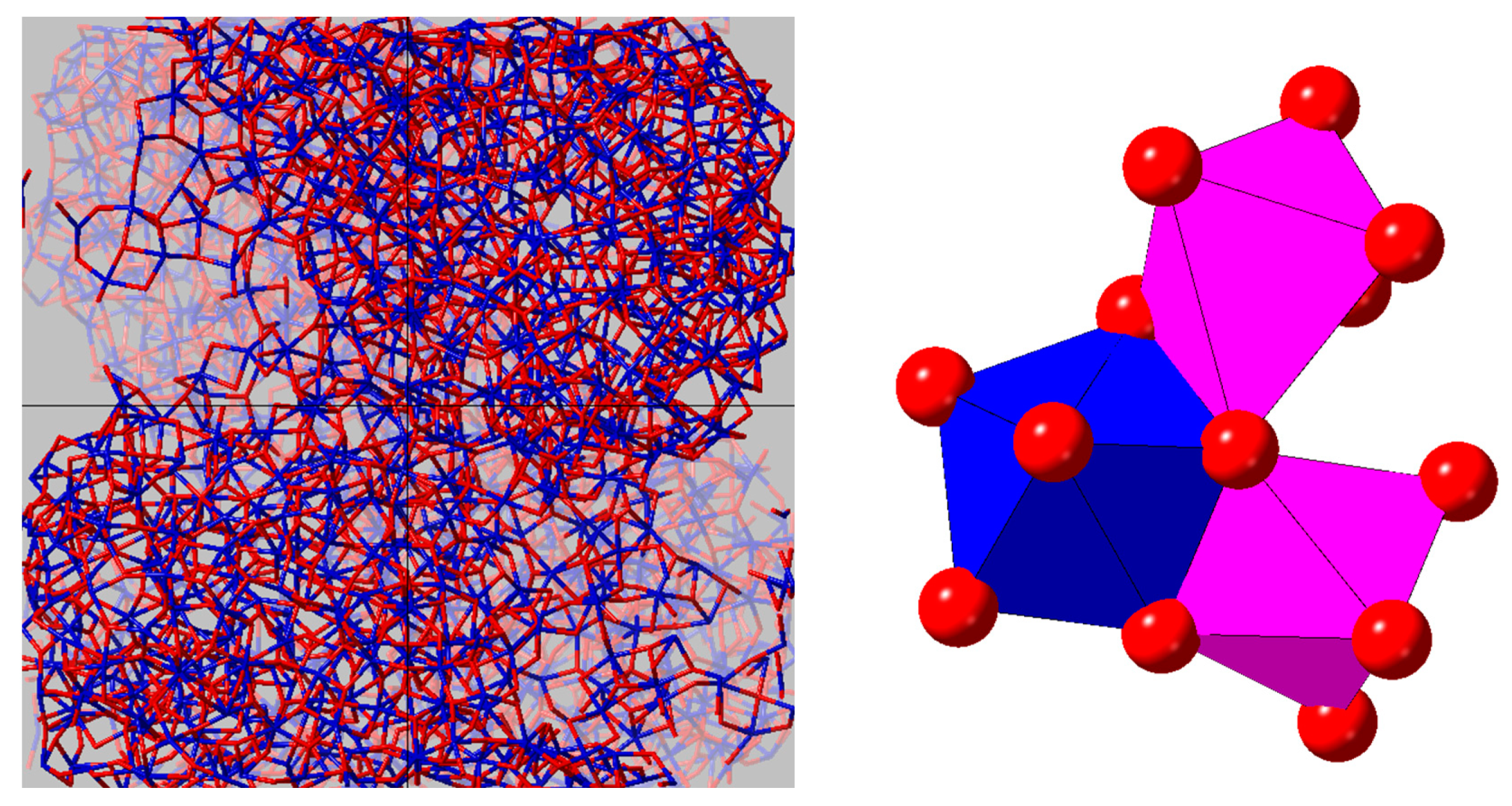
3.1. X-ray and Neutron Diffraction of Amorphous HfO2
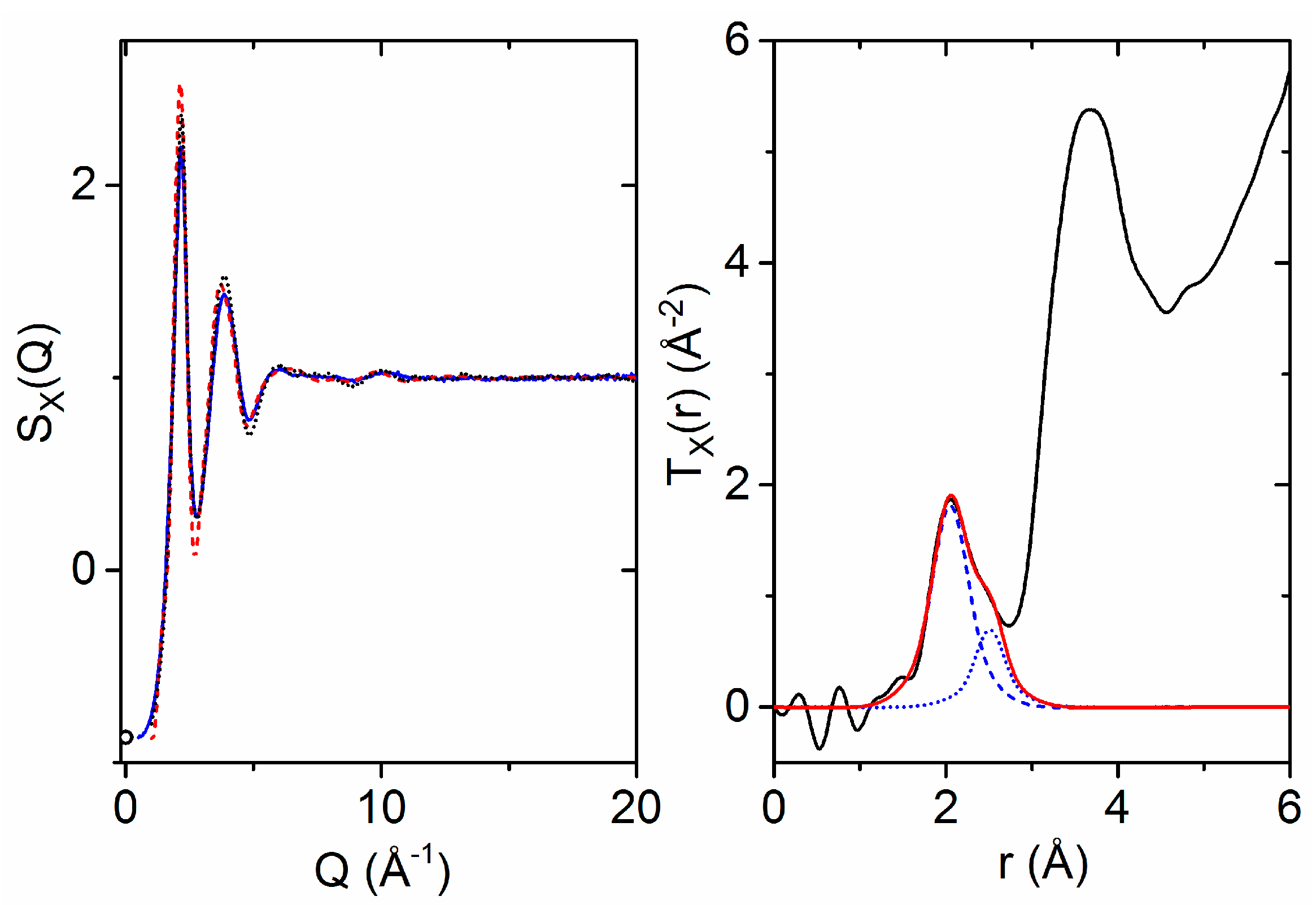
3.2. X-ray Diffraction of Molten HfO2
SNEUTRON(Q = 0) = 16∙SHfHf(Q) + 48∙SHfO(Q) + 36∙SOO(Q).
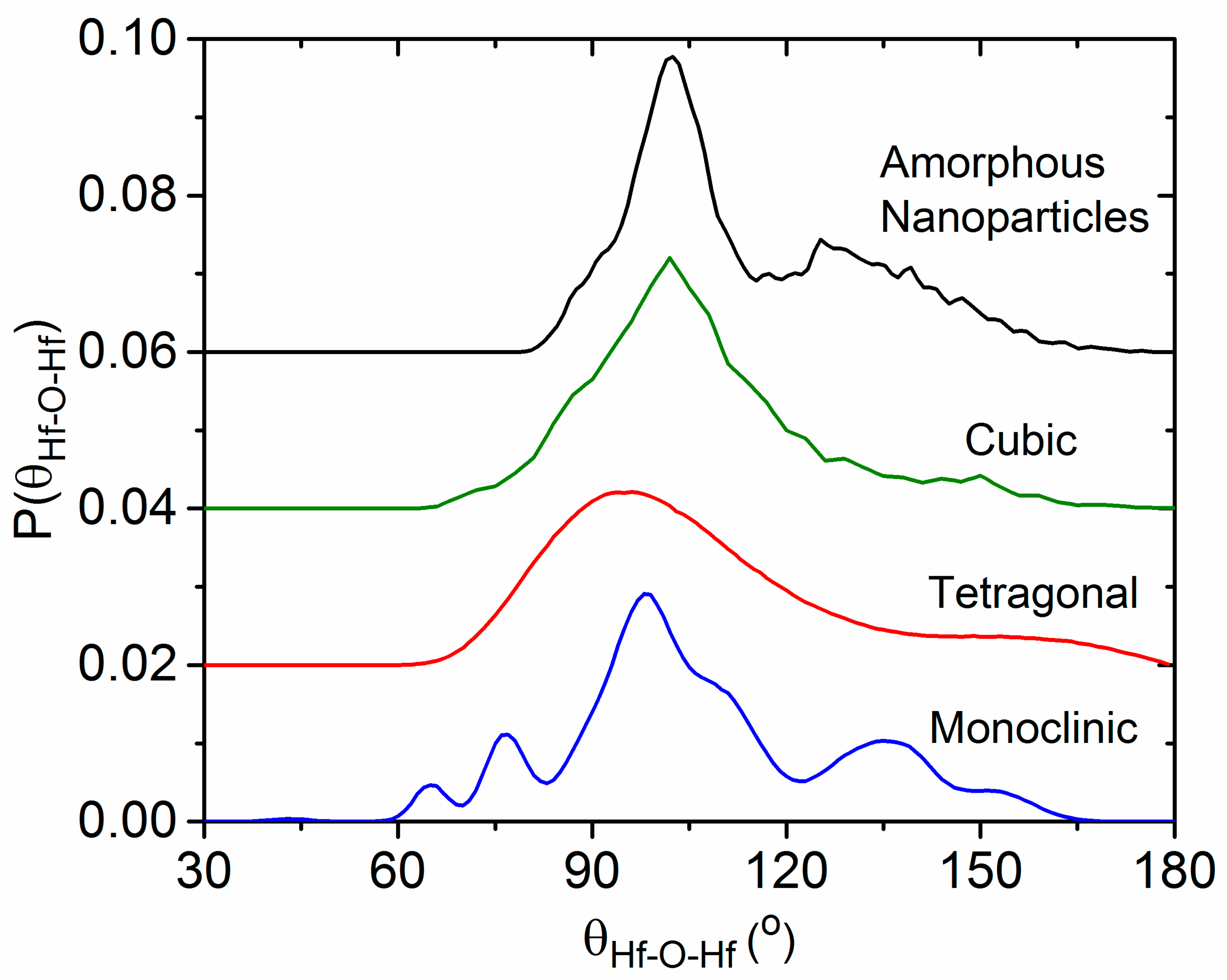
4. Discussion
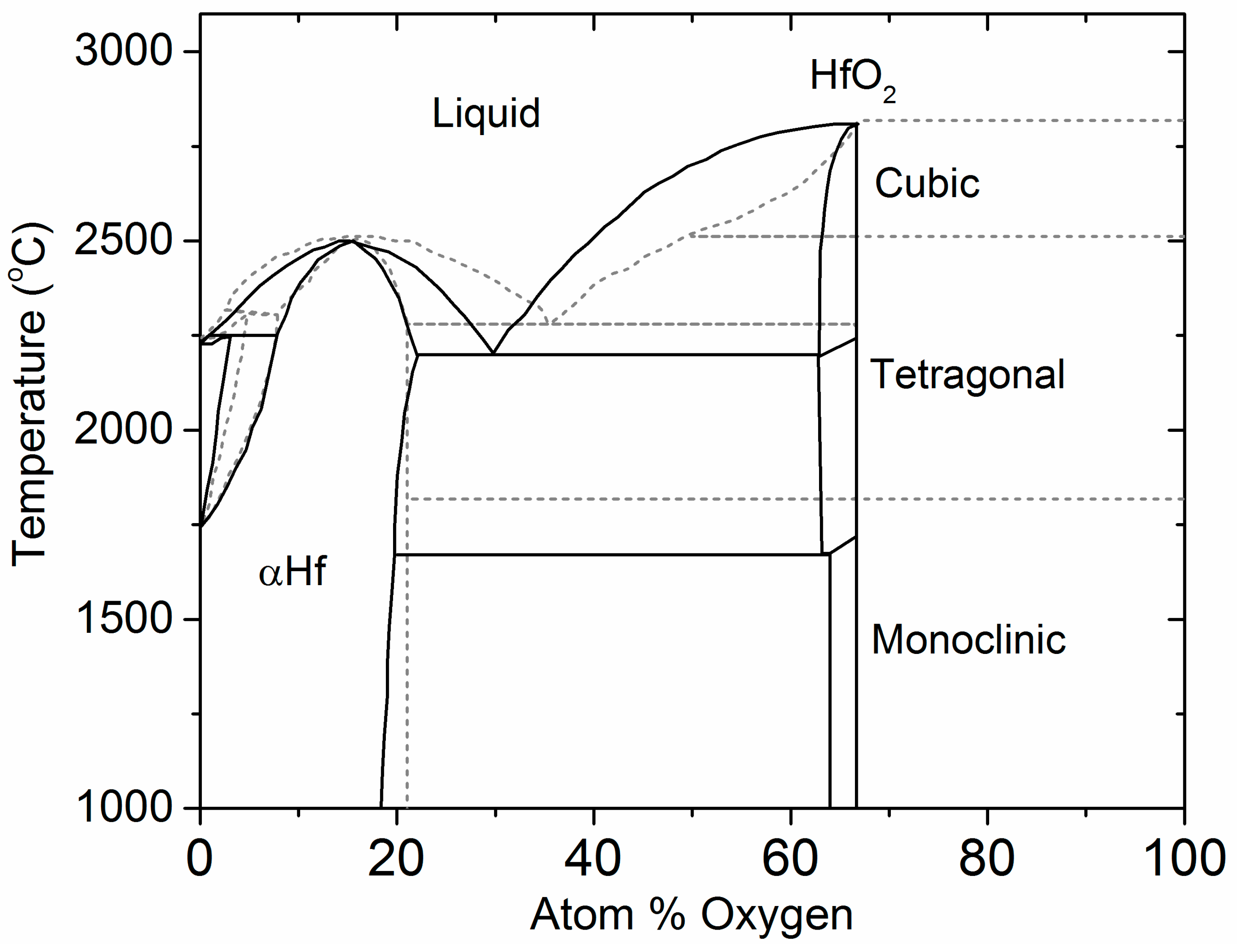
4.1. The Hf–O Phase Diagram
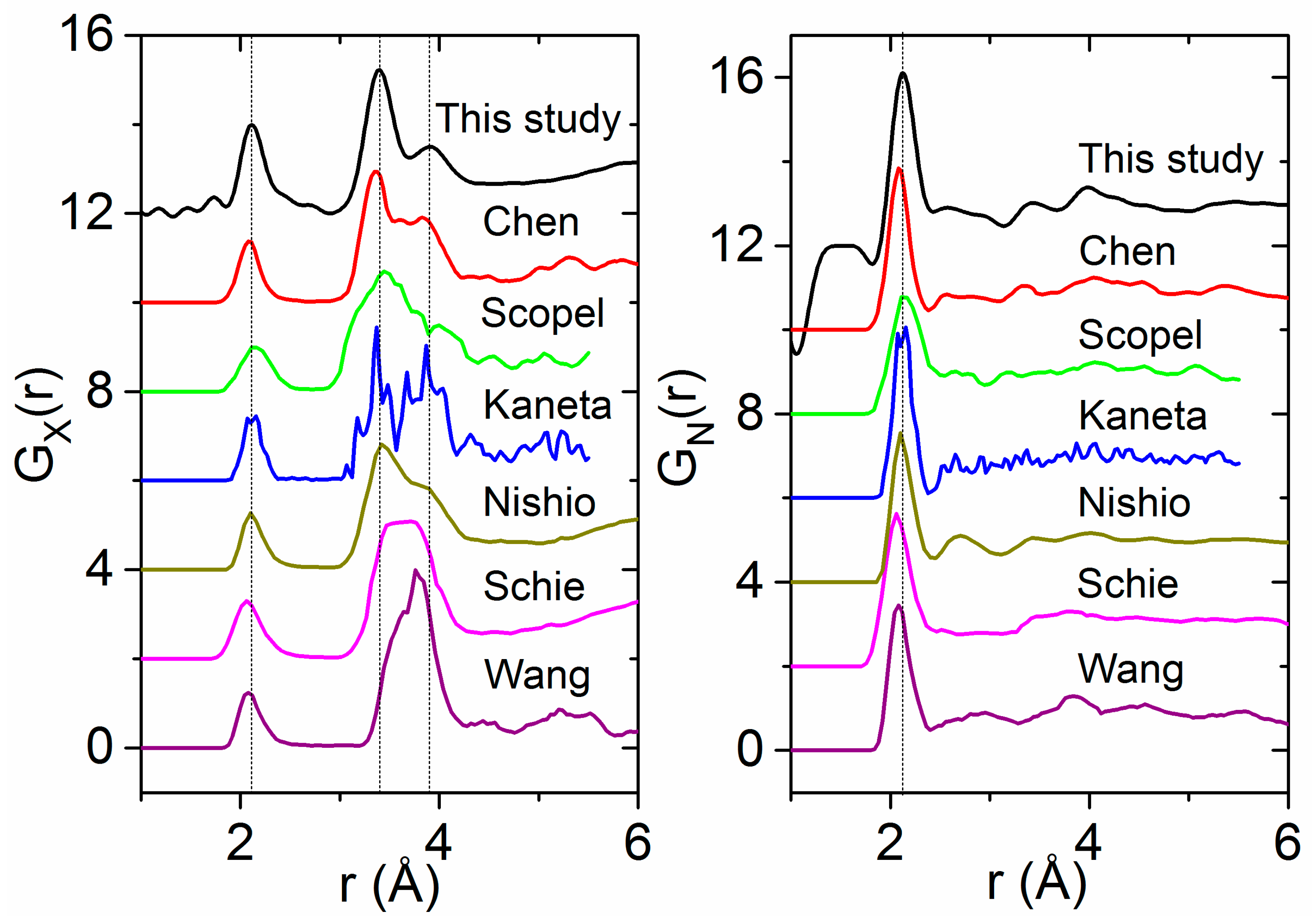
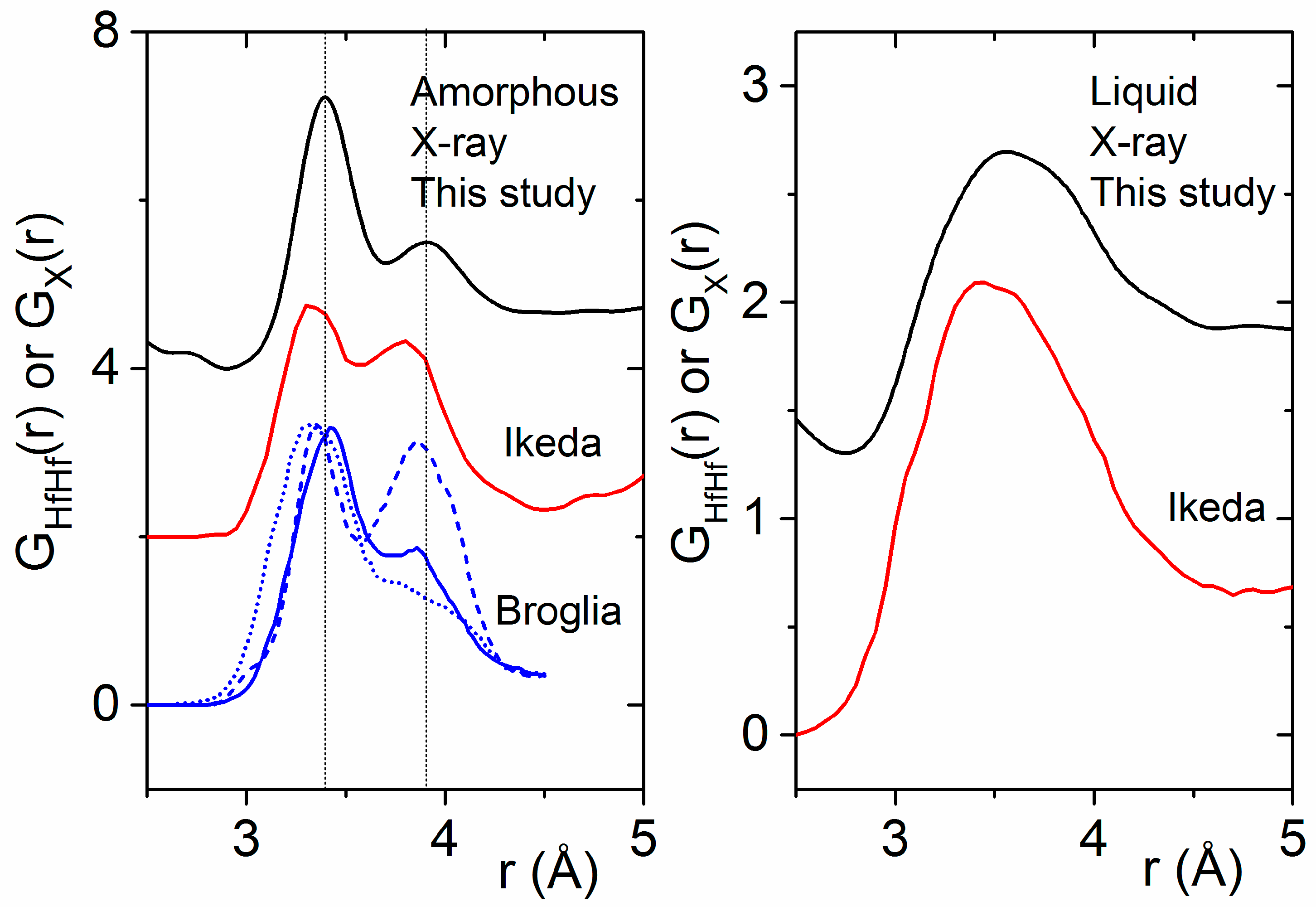
4.2. Previous Experimental Studies on HfO2
4.3. Previous Theoretical Studies of HfO2
4.4. The Effect of Density on Amorphous HfO2 Structure
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Classical MD Simulations
References
- Broglia, G.; Ori, G.; Larcher, L.; Montorsi, M. Molecular dynamics simulation of amorphous HfO2 for resistive RAM applications. Model. Simul. Mater. Sci. Eng. 2014, 22, 065006. [Google Scholar] [CrossRef]
- Schie, M.; Müller, M.P.; Salinga, M.; Waser, R.; Souza, R.A.D. Ion migration in crystalline and amorphous HfOX. J. Chem. Phys. 2017, 146, 094508. [Google Scholar] [CrossRef]
- Scopel, W.L.; da Silva, A.J.R.; Fazzio, A. Amorphous HfO2 and Hf1-xSixO via a melt-and-quench scheme using ab initio molecular dynamics. Phys. Rev. B 2008, 77, 172101. [Google Scholar] [CrossRef]
- Ceresoli, D.; Vanderbilt, D. Structural and dielectric properties of amorphous ZrO2 and HfO2. Phys. Rev. B 2006, 74, 125108. [Google Scholar] [CrossRef]
- Kaneta, C.; Yamasaki, T. Oxygen-related defects in amorphous HfO2 gate dielectrics. Microelectron. Eng. 2007, 84, 2370–2373. [Google Scholar] [CrossRef]
- Chen, T.-J.; Kuo, C.-L. First principles study of the structural, electronic, and dielectric properties of amorphous HfO2. J. Appl. Phys. 2011, 110, 064105. [Google Scholar] [CrossRef]
- Nishio, K.; Miyazaki, T.; Nakamura, H. Universal Medium-Range Order of Amorphous Metal Oxides. Phys. Rev. Lett. 2013, 111, 155502. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, M.; Kresse, G.; Nabatame, T.; Toriumi, A. First principles molecular dynamics simulations for amorphous HfO2 and Hf1-xSixO2 systems. Mater. Sci. 2005, 23, 401. [Google Scholar]
- Skinner, L.B.; Benmore, C.J.; Weber, J.K.R.; Du, J.; Neuefeind, J.; Tumber, S.K.; Parise, J.B. Low Cation Coordination in Oxide Melts. Phys. Rev. Lett. 2014, 112, 157801. [Google Scholar] [CrossRef] [PubMed]
- Eilers, H.; Tissue, B.M. Synthesis of nanophase ZnO, Eu2O3, and ZrO2 by gas-phase condensation with cw-CO2 laser heating. Mater. Lett. 1995, 24, 261–265. [Google Scholar] [CrossRef]
- Tavakoli, A.H.; Maram, P.S.; Widgeon, S.J.; Rufner, J.; van Benthem, K.; Ushakov, S.; Sen, S.; Navrotsky, A. Amorphous Alumina Nanoparticles: Structure, Surface Energy, and Thermodynamic Phase Stability. J. Phys. Chem. C 2013, 117, 17123–17130. [Google Scholar] [CrossRef]
- Sharma, G.; Ushakov, S.V.; Li, H.; Castro, R.H.R.; Navrotsky, A. Calorimetric Measurements of Surface Energy of Amorphous HfO2 Nanoparticles Produced by Gas Phase Condensation. J. Phys. Chem. C 2017, 121, 10392–10397. [Google Scholar] [CrossRef]
- Hammersley, A.P.; Svensson, S.O.; Hanfland, M.; Fitch, A.N.; Hausermann, D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Press. Res. 1996, 14, 235–248. [Google Scholar] [CrossRef]
- Skinner, L.B.; Benmore, C.J.; Parise, J.B. Area detector corrections for high quality synchrotron X-ray structure factor measurements. Nucl. Instrum. Meth. A 2012, 662, 61–70. [Google Scholar] [CrossRef]
- Qiu, X.; Thompson, J.W.; Billinge, S.J.L. PDFgetX2: A GUI-driven program to obtain pair distribution function from X-ray powder diffraction data. J. Appl. Cryst. 2004, 37, 678. [Google Scholar] [CrossRef]
- Keen, D. A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Cryst. 2001, 34, 172–177. [Google Scholar] [CrossRef]
- Neuefeind, J.; Feygenson, M.; Carruth, J.; Hoffmann, R.; Chipley, K.K. The Nanoscale Ordered MAterials Diffractometer NOMAD at the Spallation Neutron Source SNS. Nucl. Instrum. Meth. B 2012, 287, 68–75. [Google Scholar] [CrossRef]
- NOMAD Data Reduction Manual. Available online: https://neutrons.ornl.gov/sites/default/files/How to reduce NOMAD data_01_28_2016.pdf (accessed on 28 January 2016).
- CP2K, Intel Branch. Available online: https://github.com/cp2k/cp2k/tree/intel (accessed on 22 June 2017).
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bussi, G.; Zykova-Timan, T.; Parrinello, M. Isothermal-isobaric molecular dynamics using stochastic velocity rescaling. J. Chem. Phys. 2009, 130, 074101. [Google Scholar] [CrossRef] [PubMed]
- McGibbon, R.T.; Beauchamp, K.A.; Harrigan, M.P.; Klein, C.; Swails, J.M.; Hernández, C.X.; Schwantes, C.R.; Wang, L.-P.; Lane, T.J.; Pande, V.S. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Zhou, X.W.; Wadley, H.N.G. A charge transfer ionic-embedded atom method potential for the O–Al–Ni–Co–Fe system. J. Phys. Condens. Matter 2005, 17, 3619–3635. [Google Scholar] [CrossRef]
- Zhou, X.W.; Wadley, H.N.G.; Filhol, J.S.; Neurock, M.N. Modified charge transfer-embedded atom method potential for metal metal oxide systems. Phys. Rev. B 2004, 69, 035402. [Google Scholar] [CrossRef]
- Sasikumar, K.; Narayanan, B.; Cherukara, M.; Kinaci, A.; Sen, F.G.; Gray, S.K.; Chan, M.K.Y.; Sankaranarayanan, S.K.R.S. Evolutionary Optimization of a Charge Transfer Ionic Potential Model for Ta/Ta-Oxide Heterointerfaces. Chem. Mater. 2017, 29, 3603–3614. [Google Scholar] [CrossRef]
- Jaffe, J.E.; Bachorz, R.A.; Gutowski, M. Low-temperature polymorphs of ZrO2 and HfO2: A density-functional theory study. Phys. Rev. B 2005, 72, 144107. [Google Scholar] [CrossRef]
- Passerini, L. Isoformismo tra ossidi di metallic tetravalenti. I sistemi: CeO2–ThO2, CeO2–ZrO2, CeO2–HfO2. Gazz. Chim. Ital. 1930, 60, 762–776. [Google Scholar]
- Ruh, R.; Corfield, P.W.R. Crystal Structure of Monoclinic Hafnia and Comparison with Monoclinic Zirconia. J. Am. Ceram. Soc. 1970, 53, 126–129. [Google Scholar] [CrossRef]
- Kolafa, J.; Perram, J.W. Cutoff Errors in the Ewald Summation Formulae for Point Charge Systems. Mol. Simul. 1992, 9, 351–368. [Google Scholar] [CrossRef]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Nosé, S.; Klein, M.L. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983, 50, 1055–1076. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Skinner, L.B.; Huang, C.; Schlesinger, D.; Pettersson, L.G.M.; Nilsson, A.; Benmore, C.J. Benchmark oxygen-oxygen pair-distribution function of ambient water from x-ray diffraction measurements with a wide Q-range. J. Chem. Phys. 2013, 138, 074506. [Google Scholar] [CrossRef] [PubMed]
- Pickup, D.; Moss, R.; Newport, R. NXFit: A program for simultaneously fitting X-ray and neutron diffraction pair-distribution functions to provide optimized structural parameters. J. Appl. Cryst. 2014, 47, 1790–1796. [Google Scholar] [CrossRef]
- Skinner, L.B.; Barnes, A.C.; Salmon, P.S.; Hennet, L.; Fischer, H.E.; Benmore, C.J.; Kohara, S.; Weber, J.K.R.; Bytchkov, A.; Wilding, M.C.; et al. Joint diffraction and modeling approach to the structure of liquid alumina. Phys. Rev. B 2013, 87, 024201. [Google Scholar] [CrossRef] [Green Version]
- Soper, A.K.; Barney, E.R. On the use of modification functions when Fourier transforming total scattering data. J. Appl. Cryst. 2012, 45, 1314–1317. [Google Scholar] [CrossRef]
- Domagala, R.F.; Ruh, R. The hafnium-oxygen system. Am. Soc. Met. Trans. Quart. 1965, 58, 164–175. [Google Scholar]
- Okamoto, H. Hf–O (Hafnium-Oxygen). In Binary Alloy Phase Diagrams; Massalski, T.B., Ed.; ASM International: Materials Park, OH, USA, 1990; Volume 2, pp. 2096–2097. [Google Scholar]
- Ruh, R.; Patel, V.A. Proposed Phase Relations in the HfO2-Rich Portion of the System Hf–HfO2. J. Am. Ceram. Soc. 1973, 56, 606–607. [Google Scholar] [CrossRef]
- Massalski, T.B. Binary Alloy Phase Diagrams; ASM International: Materials Park, OH, USA, 1990; Volume 2. [Google Scholar]
- Shin, D.; Arróyave, R.; Liu, Z.-K. Thermodynamic modeling of the Hf–Si–O system. Calphad 2006, 30, 375–386. [Google Scholar] [CrossRef]
- Shin, D.; Liu, Z.-K. Phase stability of hafnium oxide and zirconium oxide on silicon substrate. Scr. Mater. 2007, 57, 201–204. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.P.; Stevens, R. Hafnia and hafnia-toughened ceramics. J. Mater. Sci. 1992, 27, 5397–5430. [Google Scholar] [CrossRef]
- Coutures, J.P.; Coutures, J. The System HfO2-TiO2. J. Am. Ceram. Soc. 1987, 70, 383–387. [Google Scholar] [CrossRef]
- Wolten, G.M. Diffusionless Phase Transformations in Zirconia and Hafnia. J. Am. Ceram. Soc. 1963, 46, 418–422. [Google Scholar] [CrossRef]
- Clausing, P. Über die Schmelzpunkte des Zirkonoxydes und des Hafniumoxydes. Z. Anorg. Allg. Chem. 1932, 204, 33–39. [Google Scholar] [CrossRef]
- Henning, F. Der Schmelzpunkt des Hafniumoxydes. Naturwissenschaften 1925, 13, 661. [Google Scholar] [CrossRef]
- Boganov, A.G.; Rudenko, V.S.; Makarov, L.P. X-ray Investigation of Zirconium and Hafnium Oxides at Temperatures up to 2750 °C. Proc. Acad. Sci. USSR. Chem. Sect. 1965, 160, 146–148. [Google Scholar]
- National Research Council (U.S.). Committee on Chemical Data for Ceramists. In Data on Chemicals for Ceramic Use : Formulas, Molecular Weights, Colors, Crystal Forms, Densities, Refractive Indices, Melting Points, Boiling Points, Transition Points, Decomposition Temperatures; The National Research Council, National Academy of Sciences: Washington, DC, USA, 1949; Volume 118. [Google Scholar]
- Wang, C.; Zinkevich, M.; Aldinger, F. The Zirconia–Hafnia System: DTA Measurements and Thermodynamic Calculations. J. Am. Ceram. Soc. 2006, 89, 3751–3758. [Google Scholar] [CrossRef]
- Hann, R.E.; Suitch, P.R.; Pentecost, J.L. Monoclinic Crystal Structures of ZrO2 and HfO2 Refined from X-ray Powder Diffraction Data. J. Am. Ceram. Soc. 1985, 68, C-285–C-286. [Google Scholar] [CrossRef]
- Gritsenko, V.; Gritsenko, D.; Shaimeev, S.; Aliev, V.; Nasyrov, K.; Erenburg, S.; Tapilin, V.; Wong, H.; Poon, M.C.; Lee, J.H.; et al. Atomic and electronic structures of amorphous ZrO2 and HfO2 films. Microelectron. Eng. 2005, 81, 524–529. [Google Scholar] [CrossRef]
- Perevalov, T.V.; Gritsenko, V.A.; Erenburg, S.B.; Badalyan, A.M.; Wong, H.; Kim, C.W. Atomic and electronic structure of amorphous and crystalline hafnium oxide: X-ray photoelectron spectroscopy and density functional calculations. J. Appl. Phys. 2007, 101, 053704. [Google Scholar] [CrossRef]
- Zhang, F.; Chupas, P.J.; Lui, S.L.A.; Hanson, J.C.; Caliebe, W.A.; Lee, P.L.; Chan, S.W. In situ study of the crystallization from amorphous to cubic zirconium oxide: Rietveld and reverse Monte Carlo analyses. Chem. Mater. 2007, 19, 3118–3126. [Google Scholar] [CrossRef]
- Wang, Y.; Zahid, F.; Wang, J.; Guo, H. Structure and dielectric properties of amorphous high-k oxides: HfO2, ZrO2, and their alloys. Phys. Rev. B 2012, 85, 224110. [Google Scholar] [CrossRef]
- Kohara, S.; Ohara, K.; Tajiri, H.; Song, C.; Sakata, O.; Usuki, T.; Benino, Y.; Mizuno, A.; Masuno, A.; Okada Junpei, T.; et al. Synchrotron X-ray Scattering Measurements of Disordered Materials. Zeitschrift Für Physikalische Chemie 2016, 230, 339. [Google Scholar] [CrossRef]
- Zhao, X.; Ceresoli, D.; Vanderbilt, D. Structural, electronic, and dielectric properties of amorphous ZrO2 from ab initio molecular dynamics. Phys. Rev. B 2005, 71, 085107. [Google Scholar] [CrossRef]
- Streitz, F.H.; Mintmire, J.W. Electrostatic Potentials for Metal-Oxide Surfaces and Interfaces. Phys. Rev. B 1994, 50, 11996–12003. [Google Scholar] [CrossRef]
| Phase | Number of Atoms | Box Dimensions |
|---|---|---|
| Cubic | 1500 | Lx = Ly = Lz = 25.37 |
| Tetragonal | 2058 | Lx = Ly = 25.04 and Lz = 36.40 |
| Monoclinic | 1500 | Lx = Ly = Lz = 25.6419 xy = yz = 0.0 and xz = −4.47 |
| Technique | Hf–O CN | Hf–O Peak (Å) | Hf–Hf Peaks (Å) | Density (g∙cm−3) | Reference |
|---|---|---|---|---|---|
| X/N-PDF a-HfO2 | 6.8(6) | 2.13(1) | 3.38(1), 3.89(1) | 7.69 | This study |
| X-PDF Liquid HfO2 | 7.0(6) | 2.05(1) | 3.67(2) | 8.16 | This study |
| Liquid ZrO2 * | 5.9 | 2.1 | 3.7 | 4.98 | Kohara et al. [62] |
| X-PDF on a-ZrO2* | 6.7 | 2.1 | - | - | Zhang et al. [60] |
| DFT | 6.1 | 2.09(30) | 3.0, 4.3 | 8.63 | Chen et al. [6] |
| DFT | 5.7 | 2.12 | - | 8.6 | Kaneta et al. [5] |
| DFT | 6.0 | - | 3.3, 3.8 | - | Ikeda et al. [8] |
| DFT | 6.44 | - | - | 9.39 | Ceresoli et al. [4] |
| Ab initio MD | 6.76 | 2.2(3) | 3.45, 4.00 | - | Scopel et al. [3] |
| Ab initio MD | 6.57 | 2.08 | 3.5–3.6, 3.8 | 9.39 | Nishio et al. [7] |
| Classical MD | 6.13 6.92 7.63 | 2.112 | 3.35, 3.86 3.41, 3.86 3.32, 3.7–4.2 | 8.6 10.19 11.5 | Broglia et al. [1] |
| MD | 6.2 | 2.15 | 3.37, 3.92 | 7.69 | This study |
| Classical MD | 5.76 | 2.08 | 3.6 | 7.97 | Wang et al. [61] |
| Classical MD | 6.74 | 2.06 | 3.44, 3.72 | 7.85 | Schie et al. [2] |
| Cubic | 8 | 2.21 | 3.62 | 10.45 1 | Passerini et al. [31] |
| Monoclinic | 7 | 2.13 | 3.43, 3.94 | 10.11 | Hann et al. [57] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallington, L.C.; Ghadar, Y.; Skinner, L.B.; Weber, J.K.R.; Ushakov, S.V.; Navrotsky, A.; Vazquez-Mayagoitia, A.; Neuefeind, J.C.; Stan, M.; Low, J.J.; et al. The Structure of Liquid and Amorphous Hafnia. Materials 2017, 10, 1290. https://doi.org/10.3390/ma10111290
Gallington LC, Ghadar Y, Skinner LB, Weber JKR, Ushakov SV, Navrotsky A, Vazquez-Mayagoitia A, Neuefeind JC, Stan M, Low JJ, et al. The Structure of Liquid and Amorphous Hafnia. Materials. 2017; 10(11):1290. https://doi.org/10.3390/ma10111290
Chicago/Turabian StyleGallington, Leighanne C., Yasaman Ghadar, Lawrie B. Skinner, J. K. Richard Weber, Sergey V. Ushakov, Alexandra Navrotsky, Alvaro Vazquez-Mayagoitia, Joerg C. Neuefeind, Marius Stan, John J. Low, and et al. 2017. "The Structure of Liquid and Amorphous Hafnia" Materials 10, no. 11: 1290. https://doi.org/10.3390/ma10111290
APA StyleGallington, L. C., Ghadar, Y., Skinner, L. B., Weber, J. K. R., Ushakov, S. V., Navrotsky, A., Vazquez-Mayagoitia, A., Neuefeind, J. C., Stan, M., Low, J. J., & Benmore, C. J. (2017). The Structure of Liquid and Amorphous Hafnia. Materials, 10(11), 1290. https://doi.org/10.3390/ma10111290






