Ultra-Thin Multi-Band Polarization-Insensitive Microwave Metamaterial Absorber Based on Multiple-Order Responses Using a Single Resonator Structure
Abstract
:1. Introduction
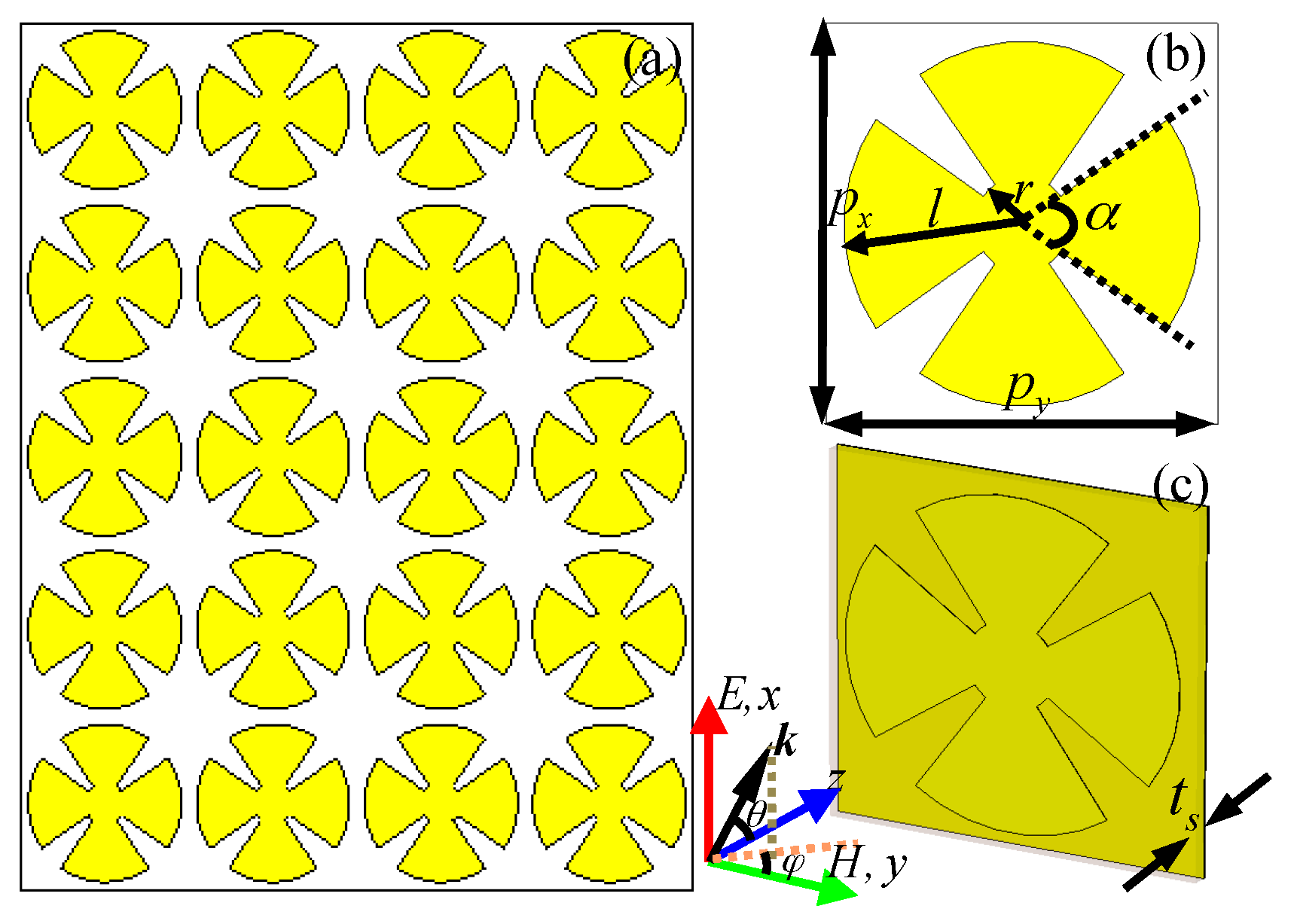
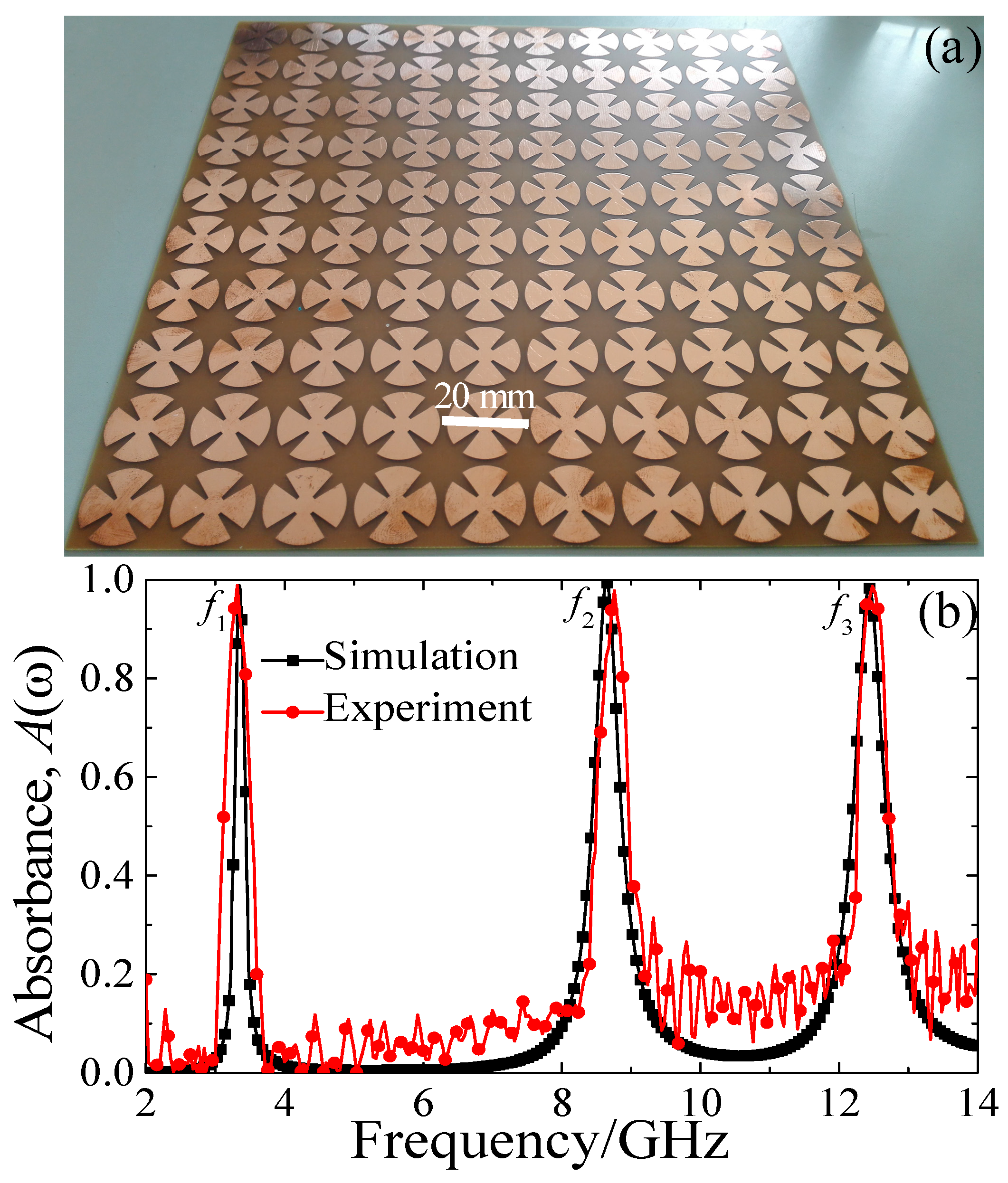
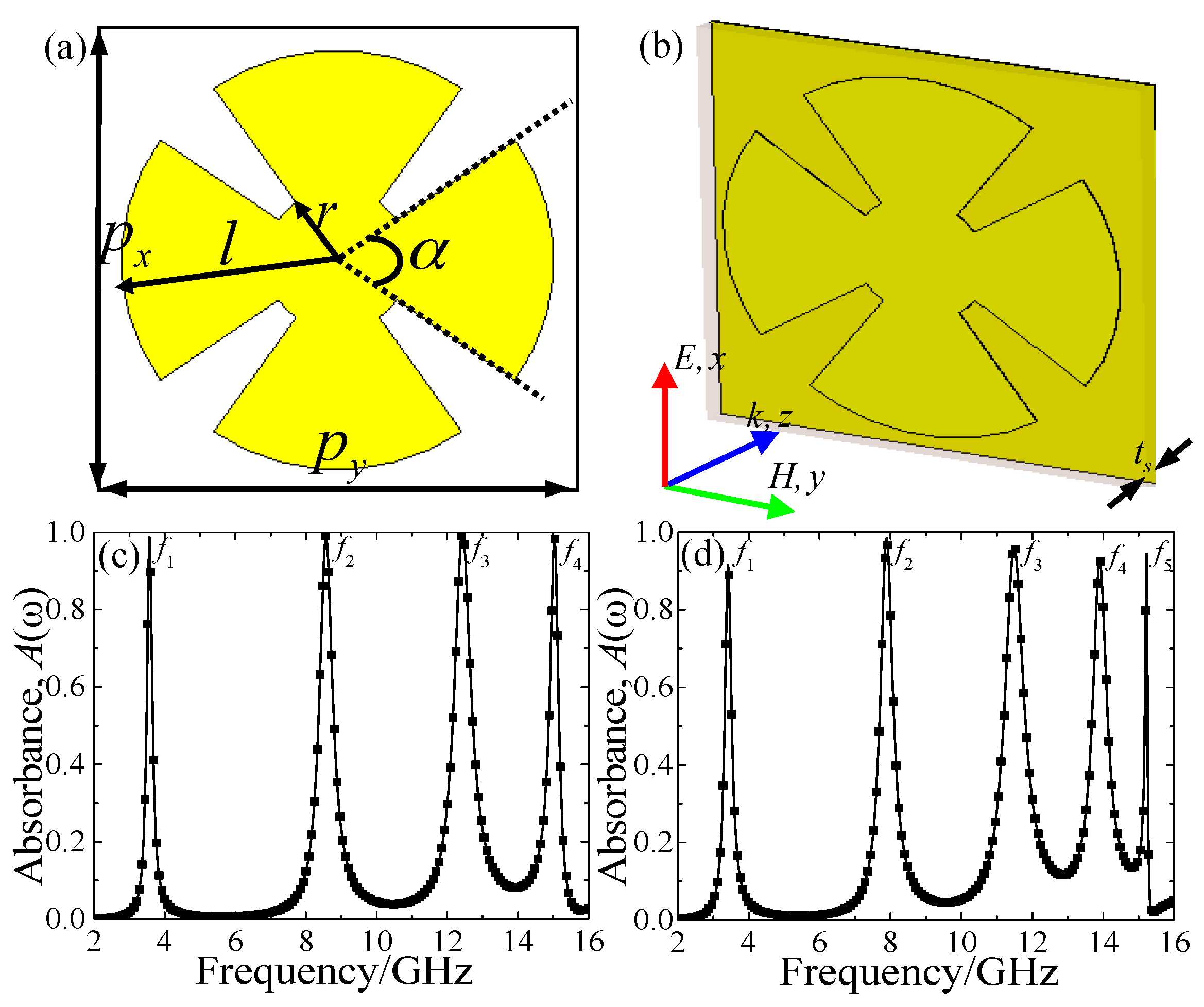
2. Unit-Cell Structure Design, Simulation and Experiment
3. Results and Discussions
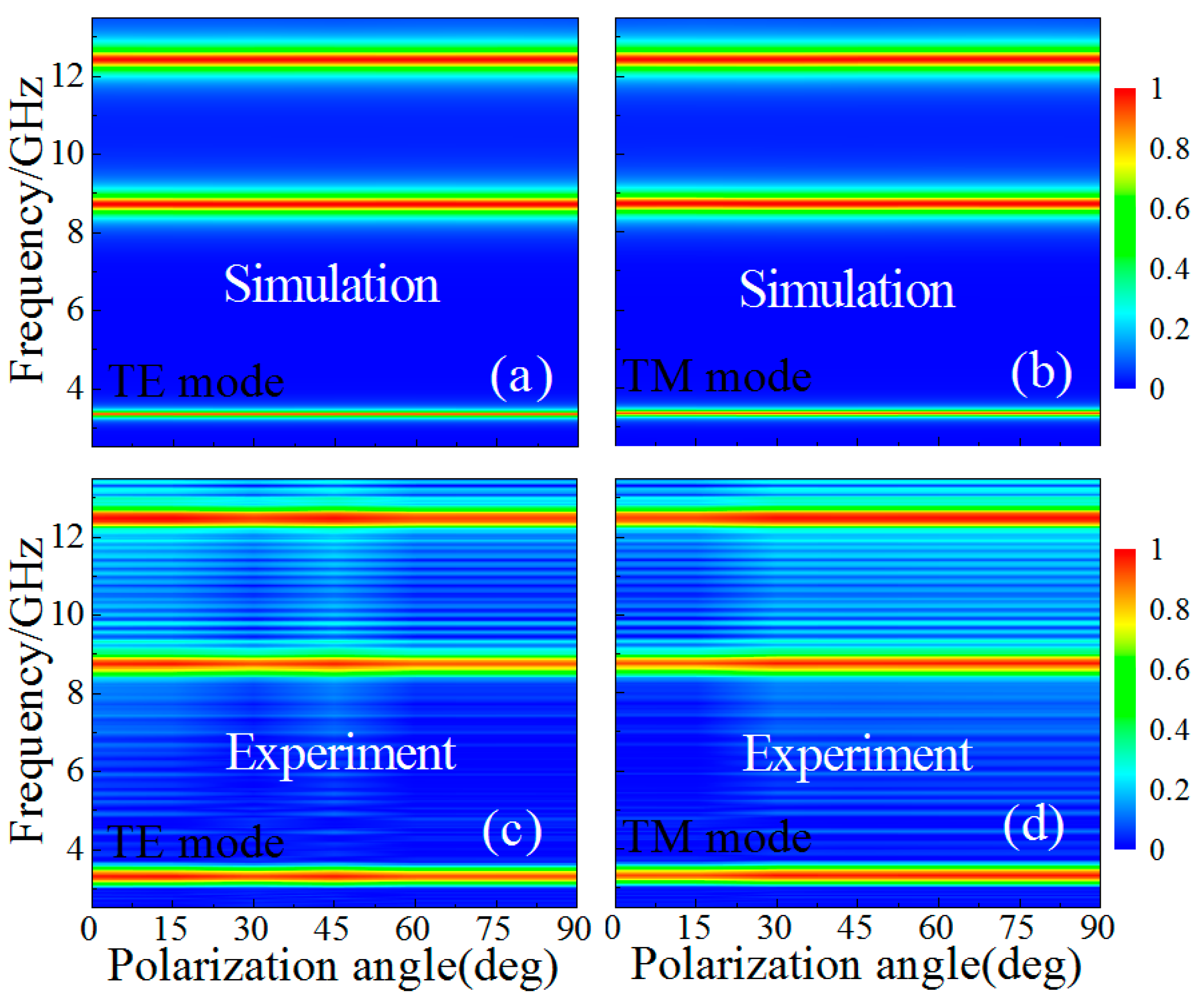
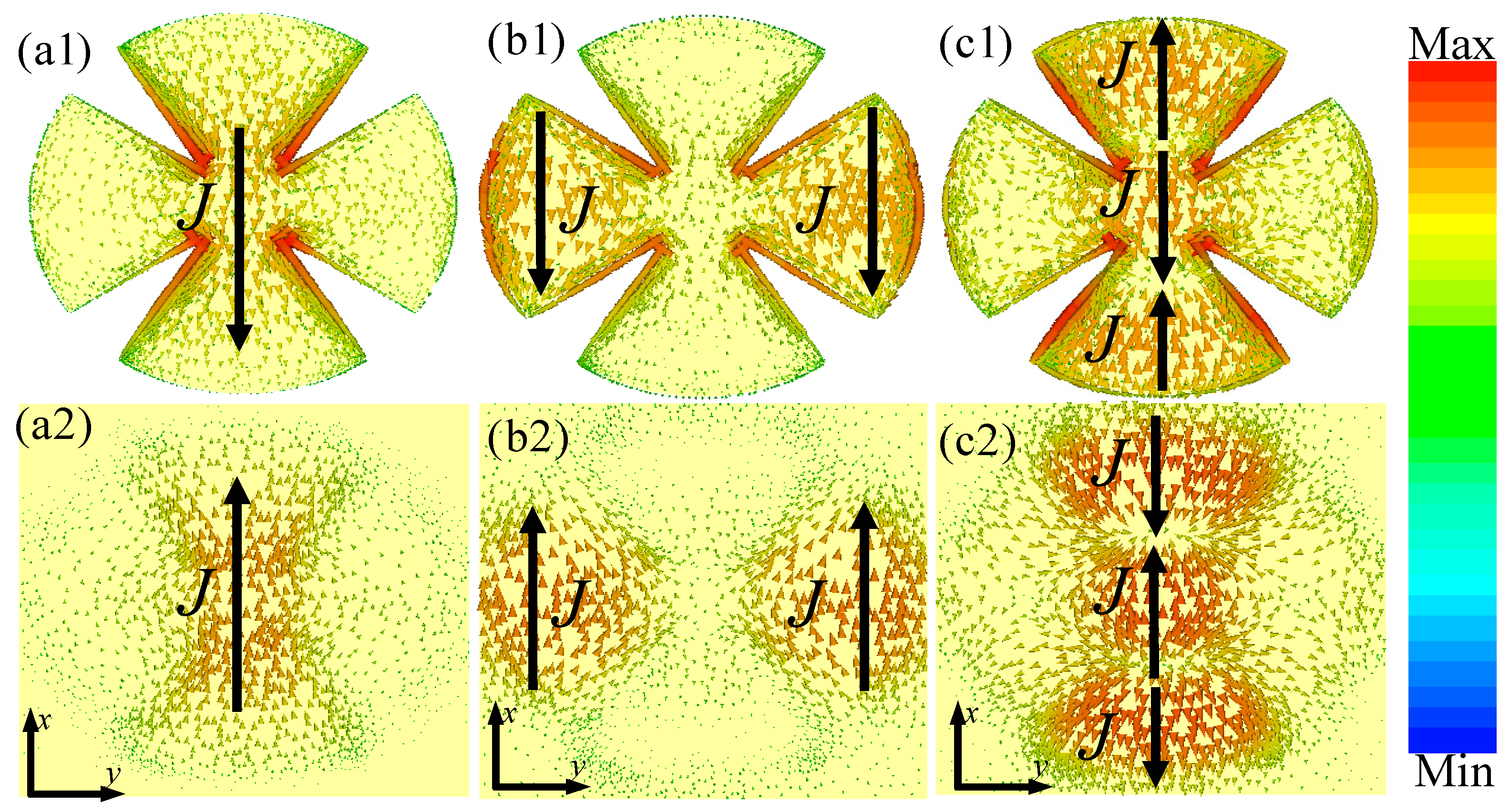
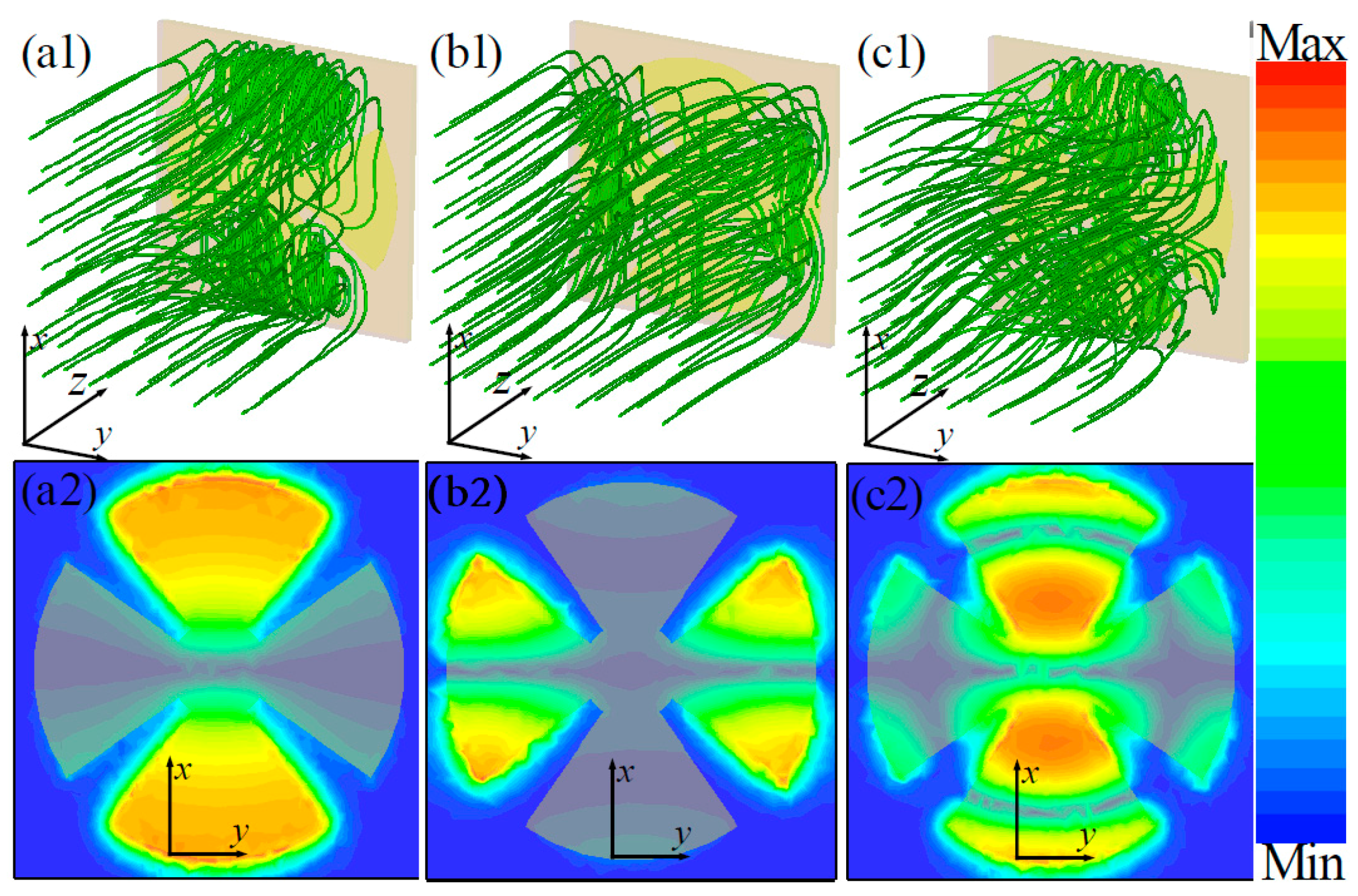
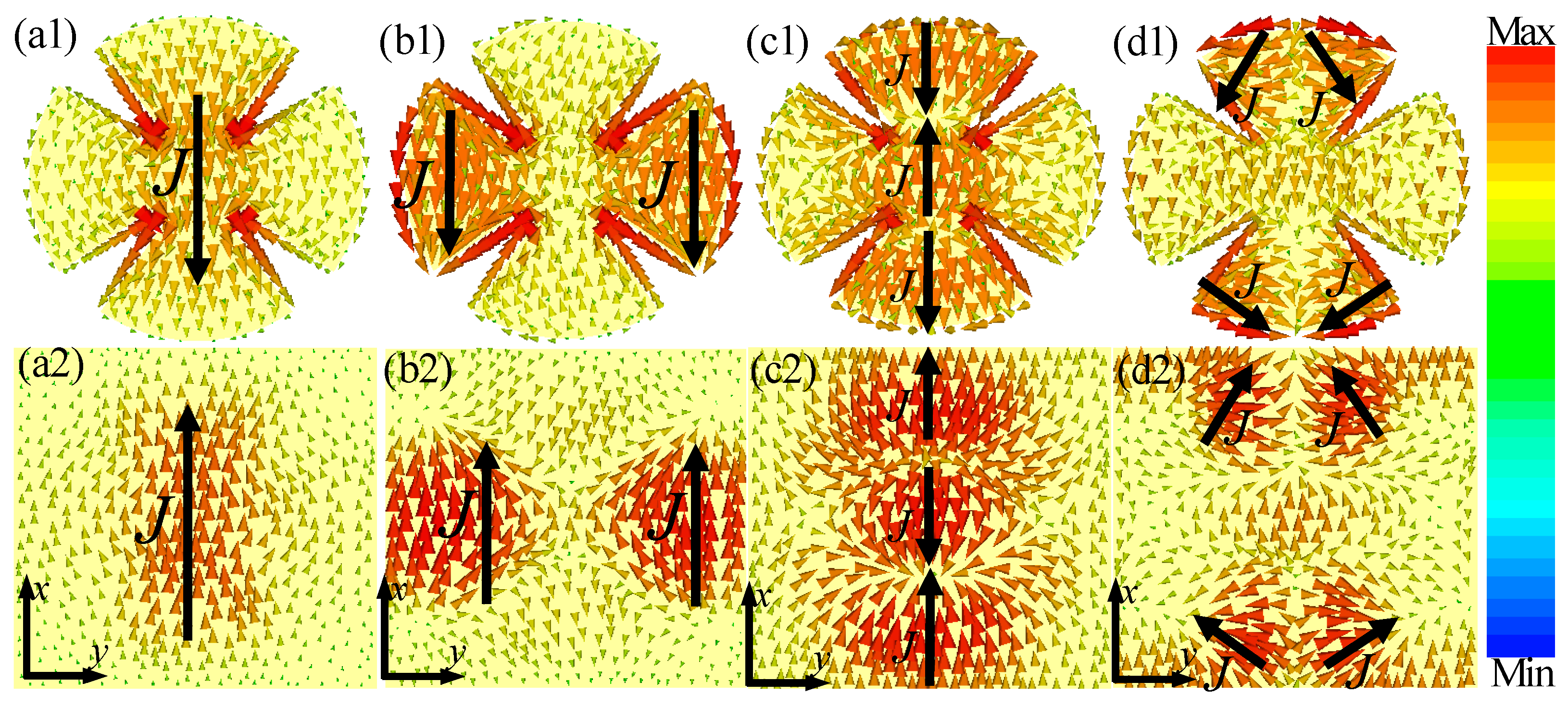
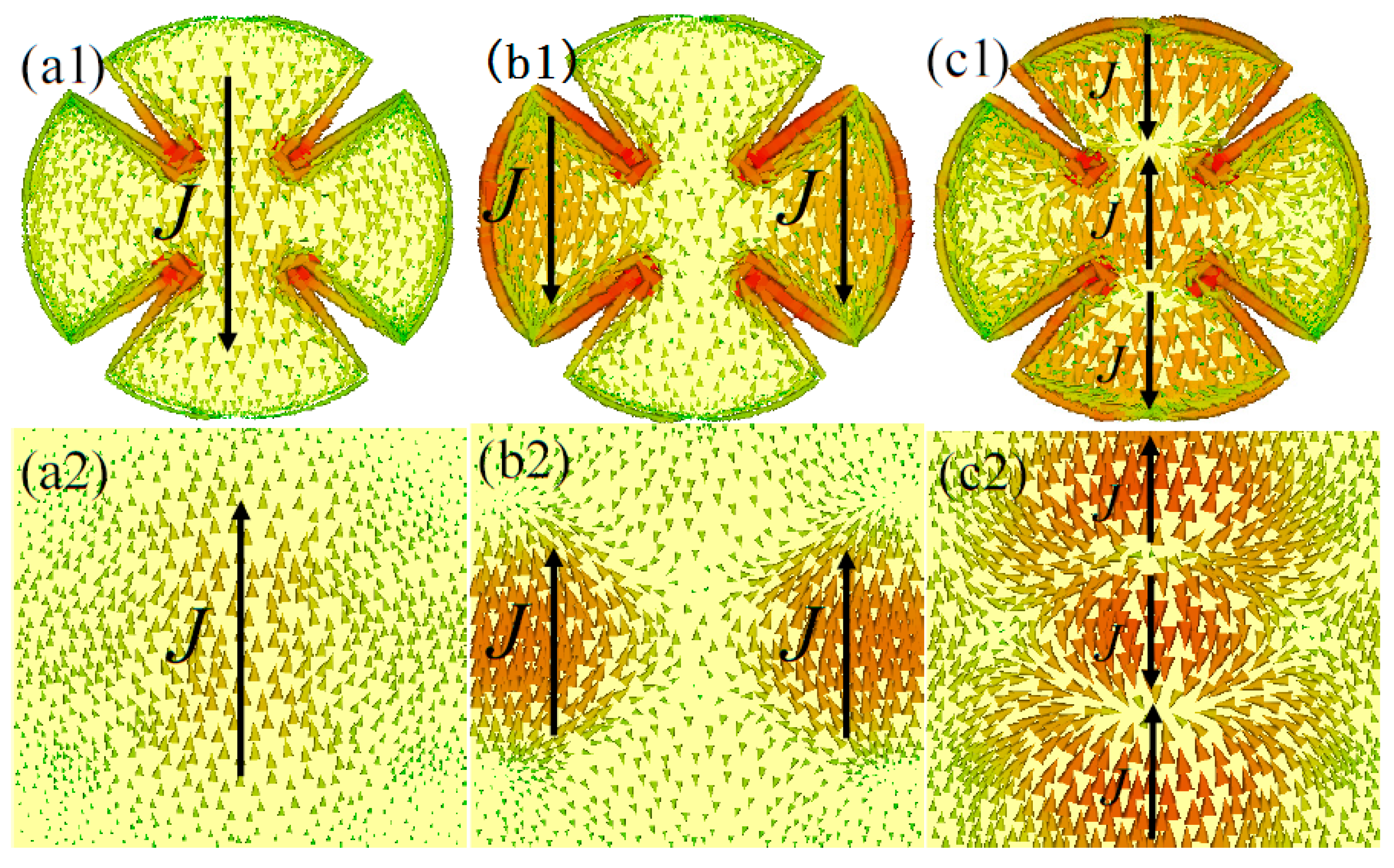
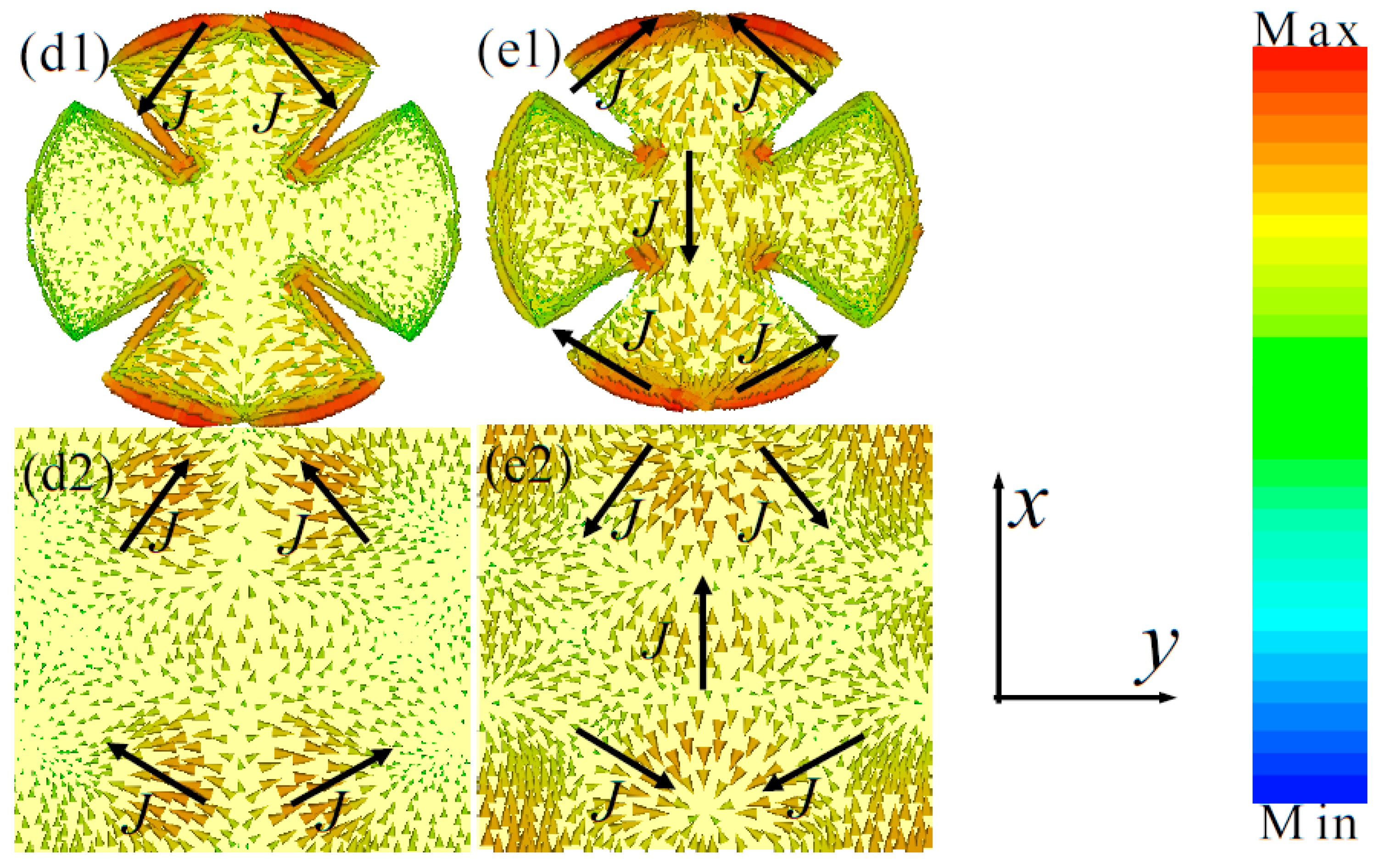
3.1. Triple-Band Metamaterial Absorber (MMA)
3.2. Four-Band and Five-Band MMAs
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cui, T.J.; David, R.S.; Liu, R. Metamaterials: Theory, Design, and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Liu, R.; Ji, C.; Mock, J.J.; Chin, J.Y.; Cui, T.J.; Smith, D.R. Broadband Ground-Plane Cloak. Science 2009, 323, 366–369. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Agrawal, A.; Abashin, M.; Chau, K.J.; Lezec, H.J. All-angle negative refraction and active flat lensing of ultraviolet light. Nature 2013, 497, 470–474. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, M.; Zarrabi, F.B.; Ahmadian, R.; Mansouri, Z.; Keshtkar, A. Miniaturization of antenna for wireless application with difference metamaterial structures. Prog. Electromagn. Res. 2014, 145, 19–29. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial electromagnetic wave absorbers. Adv. Mater. 2012, 24, 98–120. [Google Scholar] [CrossRef] [PubMed]
- Pu, M.B.; Chen, P.; Wang, Y.Q.; Zhao, Z.Y.; Wang, C.T.; Huang, C.; Hu, C.G.; Luo, X.G. Strong enhancement of light absorption and highly directive thermal emission in graphene. Opt. Express 2013, 21, 11618–11627. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.J.; Yan, Z.D.; Wang, Q.G.; Chen, J.; Zhu, M.W.; Liu, B.; Liu, F.X.; Sui, C.H. Ultrathin amorphous silicon thin-film solar cells by magnetic plasmonic metamaterial absorbers. RSC Adv. 2015, 5, 81866–81874. [Google Scholar] [CrossRef]
- Carranza, I.E.; Grant, J.P.; Gough, J.; Cumming, D. Terahertz metamaterial absorbers implemented in CMOS technology for imaging applications: Scaling to large format focal plane Arrays. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 4700508. [Google Scholar]
- Cheng, Y.Z.; Mao, X.S.; Wu, C.J.; Wu, L.; Gong, R.Z. Infrared non-planar plasmonic perfect absorber for enhanced sensitive refractive index sensing. Opt. Mater. 2016, 53, 195–200. [Google Scholar] [CrossRef]
- Dayal, G.; Chin, X.Y.; Soci, C.; Singh, R. High-Q plasmonic fano resonance for multiband surface-enhanced infrared absorption of molecular vibrational sensing. Adv. Opt. Mater. 2017, 5. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Yang, H.L.; Cheng, Z.Z.; Wu, N. Perfect metamaterial absorber based on a split-ring-cross resonator. Appl. Phys. A 2011, 102, 99–103. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Zhou, P.H.; Zhang, H.B.; Chen, L.; Deng, L.J. A wide-angle planar metamaterial absorber based on split ring resonator coupling. J. Appl. Phys. 2011, 110, 044102. [Google Scholar]
- Li, S.; Gao, J.; Cao, X.; Zhang, Z.; Zheng, Y.; Zhang, C. Multiband and broadband polarization-insensitive perfect absorber devices based on a tunable and thin double split-ring metamaterial. Opt. Express 2015, 23, 3523–3533. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.C.; Cheng, Y.Z. Ultrabroadband microwave metamaterial absorber based on electric SRR loaded lumped resistors. J. Electron. Mater. 2016, 44, 4269. [Google Scholar] [CrossRef]
- Hu, C.G.; Li, X.; Feng, Q.; Chen, X.N.; Luo, X.G. Investigation on the role of the dielectric loss in metamaterial absorber. Opt. Express 2010, 18, 6598–6603. [Google Scholar] [CrossRef] [PubMed]
- Yoo, Y.J.; Kim, Y.J.; Hwang, J.S.; Rhee, J.Y.; Kim, K.W. Triple-band perfect metamaterial absorption based on single cut-wire bar. Appl. Phys. Lett. 2015, 106, 071105. [Google Scholar] [CrossRef]
- Shen, X.; Cui, T.J.; Zhao, J.; Ma, H.F.; Jiang, W.X.; Li, H. Polarization-independent wide-angle triple-band metamaterial absorber. Opt. Express 2011, 19, 9401–9407. [Google Scholar] [CrossRef] [PubMed]
- Park, J.W.; Tuong, P.V.; Rhee, J.Y.; Kim, K.W. Multi-band metamaterial absorber based on the arrangement of donut-type resonators. Opt. Express 2013, 21, 9691–9702. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.X.; Zhai, X.; Wang, G.Z.; Huang, W.Q.; Wang, L.L. Design of a four-band and polarization-insensitive terahertz metamaterial absorber. IEEE Photonics J. 2015, 7. [Google Scholar] [CrossRef]
- Liu, X.; Starr, T.; Starr, A.F.; Padilla, W.J. Infrared spatial and frequency selective metamaterial with near-unity absorbance. Phys. Rev. Lett. 2010, 104, 207403. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Z.; Nie, Y.; Gong, R.Z. Metamaterial absorber and extending absorbance bandwidth based on multi-cross resonators. Appl. Phys. B 2013, 111, 483–488. [Google Scholar] [CrossRef]
- Ma, W.; Wen, Y.; Yu, X. Broadband metamaterial absorber at mid-infrared using multiplexed cross resonators. Opt. Express 2013, 21, 30724–30730. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.P.; Yang, Y.; Zang, Y.; Gu, J.; Han, J.; Zhang, W.; Cui, T.J. Triple-band terahertz metamaterial absorber: Design, experiment, and physical interpretation. Appl. Phys. Lett. 2012, 101, 154102. [Google Scholar] [CrossRef]
- Li, H.; Yuan, L.H.; Zhou, B.; Shen, X.P.; Cheng, Q.; Cui, T.J. Ultrathin multiband gigahertz metamaterial absorbers. J. Appl. Phys. 2011, 110, 014909. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Nie, Y.; Gong, R.Z.; Yang, H.L. Multi-band metamaterial absorber using cave-cross resonator. Eur. Phys. J. Appl. Phys. 2011, 56, 31301. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Nie, Y.; Gong, R.Z. A polarization-insensitive and omnidirectional broadband terahertz metamaterial absorber based on coplanar multi-squares films. Opt. Laser Technol. 2013, 8, 415–421. [Google Scholar] [CrossRef]
- Kollatou, T.M.; Dimitriadis, A.I.; Assimonis, S.D.; Kantartzis, N.V.; Antonopoulos, C.S. Multi-band highly absorbing microwave metamaterial structures. Appl. Phys. A 2014, 115, 555–561. [Google Scholar] [CrossRef]
- Ye, Y.Q.; Jin, Y.; He, S.L. Omnidirectional, polarization-insensitive and broadband thin absorber in the terahertz regime. J. Opt. Soc. Am. B 2010, 27, 498–504. [Google Scholar] [CrossRef]
- Ding, F.; Cui, Y.X.; Ge, X.C.; Zhang, F.; Jin, Y.; He, S.L. Ultra-broadband microwave metamaterial absorber. Appl. Phy. Lett. 2012, 100, 103506. [Google Scholar] [CrossRef]
- Liang, Q.Q.; Yu, W.X.; Zhao, W.; Wang, T.; Zhao, J.; Zhang, H.; Tao, S. Numerical study of the meta-nanopyramid array as efficient solar energy absorber. Opt. Express 2013, 3, 1188–1196. [Google Scholar] [CrossRef]
- Zheng, D.H.; Cheng, Y.Z.; Cheng, D.F.; Nie, Y.; Gong, R.Z. Four-band polarization-insensitive metamaterial absorber based on flower-shaped structures. Prog. Electromagn. Res. 2013, 142, 221–229. [Google Scholar] [CrossRef]
- Yin, X.; Chen, L.; Li, X. Ultra-broadband super light absorber based on multi-sized tapered hyperbolic metamaterial waveguide arrays. J. Lightw. Technol. 2015, 33, 3704–3710. [Google Scholar] [CrossRef]
- Yoo, Y.J.; Kim, Y.J.; Pham, V.T.; Rhee, J.Y.; Kim, K.W.; Jang, W.H.; Kim, Y.H.; Cheong, H.; Lee, Y.P. Polarization-independent dual-band perfect absorber utilizing multiple magnetic resonances. Opt. Express 2013, 21, 32484–32490. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.J.; Yoo, Y.J.; Kim, K.W.; Rhee, J.Y.; Kim, Y.H.; Lee, Y.P. Dual broadband metamaterial absorber. Opt. Express 2015, 23, 3861. [Google Scholar] [CrossRef] [PubMed]
- Dung, N.V.; Tuong, P.V.; Yoo, Y.J.; Kim, Y.J.; Tung, B.S.; Lam, V.D.; Rhee, J.Y.; Kim, K.W.; Kim, Y.H.; Chen, L.Y.; et al. Perfect and broad absorption by the active control of electric resonance in metamaterial. J. Opt. 2015, 17, 045105. [Google Scholar] [CrossRef]
- Kim, S.J.; Yoo, Y.J.; Kim, Y.J.; Lee, Y.P. Triple-band metamaterial absorption utilizing single rectangular hole. Opt. Commun. 2017, 382, 151–156. [Google Scholar] [CrossRef]
- Lee, D.J.; Hwang, J.G.; Lim, D.; Hara, T.; Lim, S. Incident angle-and polarization-insensitive metamaterial absorber using circular sectors. Sci. Rep. 2016, 6, 27155. [Google Scholar] [CrossRef] [PubMed]
- Govind, D.; Ramakrishna, S.A. Multipolar localized resonances for multi-band metamaterial perfect absorbers. J. Opt. 2014, 16, 094016. [Google Scholar]
- Cheng, Y.Z.; Huang, M.L.; Chen, H.R.; Guo, Z.Z.; Gong, R.Z.; Mao, X.S. Ultrathin six-band polarization-insensitive perfect metamaterial absorber based on a cross-cave patch resonator for terahertz waves. Materials 2017, 10, 591. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Luo, Y.; Fernández-Domínguez, A.I.; Shen, X.P.; Maier, S.A.; Cui, T.J. High-order localized spoof surface plasmon resonances and experimental verifications. Sci. Rep. 2015, 5, 9590. [Google Scholar] [CrossRef] [PubMed]
- Park, M.S.; Bhattarai, K.; Kim, D.K.; Kang, S.W.; Kim, J.O.; Zhou, J.F.; Jang, W.Y.; Noyola, M.; Urbas, A.; Ku, Z.; et al. Enhanced transmission due to antireflection coating layer at surface plasmon resonance wavelengths. Opt. Express 2014, 22, 30161–30169. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.Z.; Cheng, Z.Z.; Mao, X.S.; Gong, R.Z. Ultra-Thin Multi-Band Polarization-Insensitive Microwave Metamaterial Absorber Based on Multiple-Order Responses Using a Single Resonator Structure. Materials 2017, 10, 1241. https://doi.org/10.3390/ma10111241
Cheng YZ, Cheng ZZ, Mao XS, Gong RZ. Ultra-Thin Multi-Band Polarization-Insensitive Microwave Metamaterial Absorber Based on Multiple-Order Responses Using a Single Resonator Structure. Materials. 2017; 10(11):1241. https://doi.org/10.3390/ma10111241
Chicago/Turabian StyleCheng, Yong Zhi, Zheng Ze Cheng, Xue Song Mao, and Rong Zhou Gong. 2017. "Ultra-Thin Multi-Band Polarization-Insensitive Microwave Metamaterial Absorber Based on Multiple-Order Responses Using a Single Resonator Structure" Materials 10, no. 11: 1241. https://doi.org/10.3390/ma10111241
APA StyleCheng, Y. Z., Cheng, Z. Z., Mao, X. S., & Gong, R. Z. (2017). Ultra-Thin Multi-Band Polarization-Insensitive Microwave Metamaterial Absorber Based on Multiple-Order Responses Using a Single Resonator Structure. Materials, 10(11), 1241. https://doi.org/10.3390/ma10111241




