Simulation and Experimental Studies on Grain Selection and Structure Design of the Spiral Selector for Casting Single Crystal Ni-Based Superalloy
Abstract
:1. Introduction
2. Models and Methods
2.1. Physical and Mathematical Model
2.1.1. Energy Conservation Models
2.1.2. Grain Nucleation and Growth
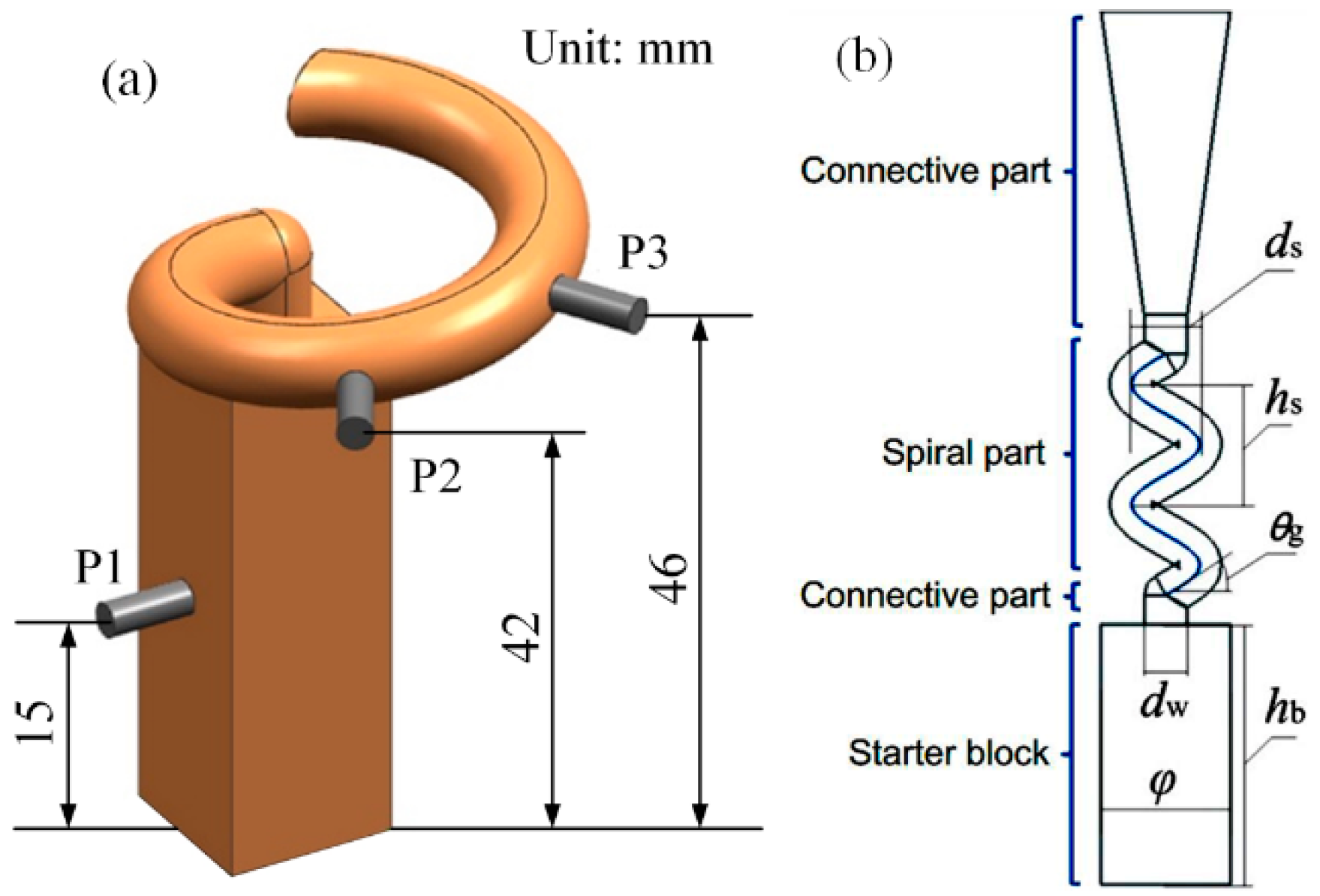
2.2. Materials and Methods
2.2.1. Temperature Measurement Experiment
2.2.2. Microstructure Experiment
2.2.3. Simulation Method
3. Results and Discussion
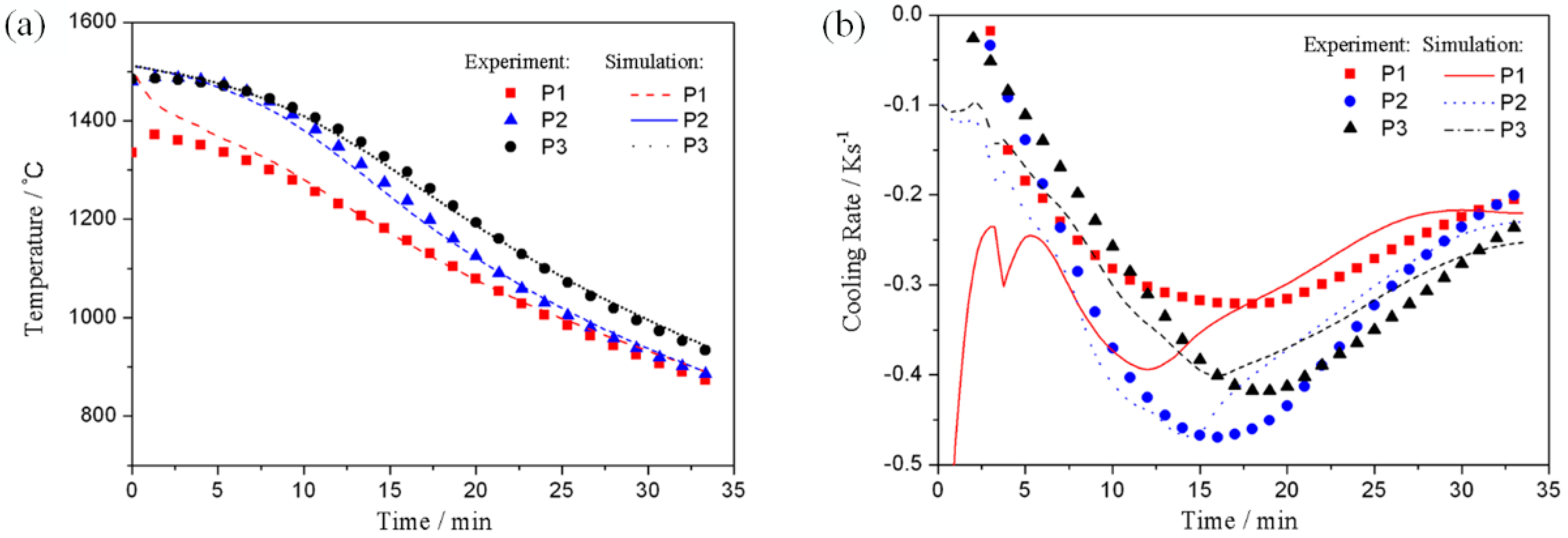
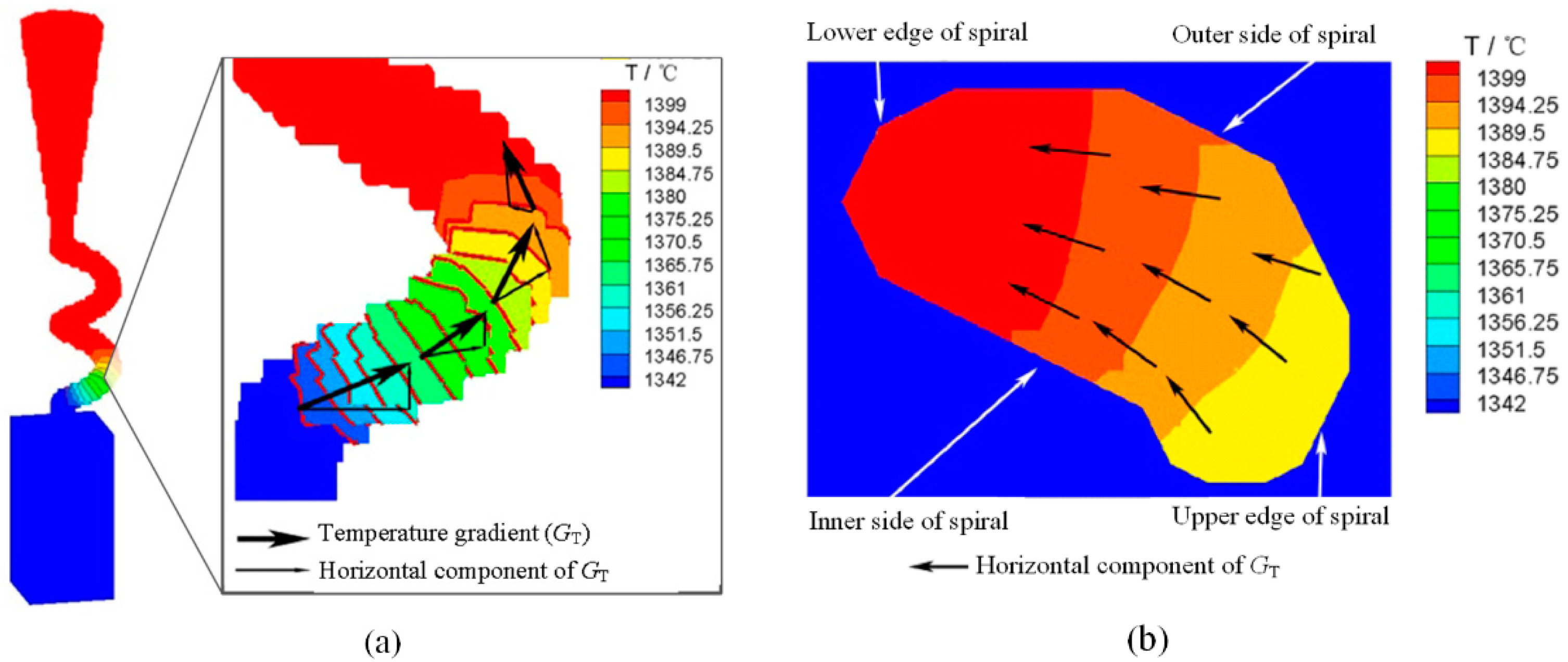
3.1. Temperature Comparison
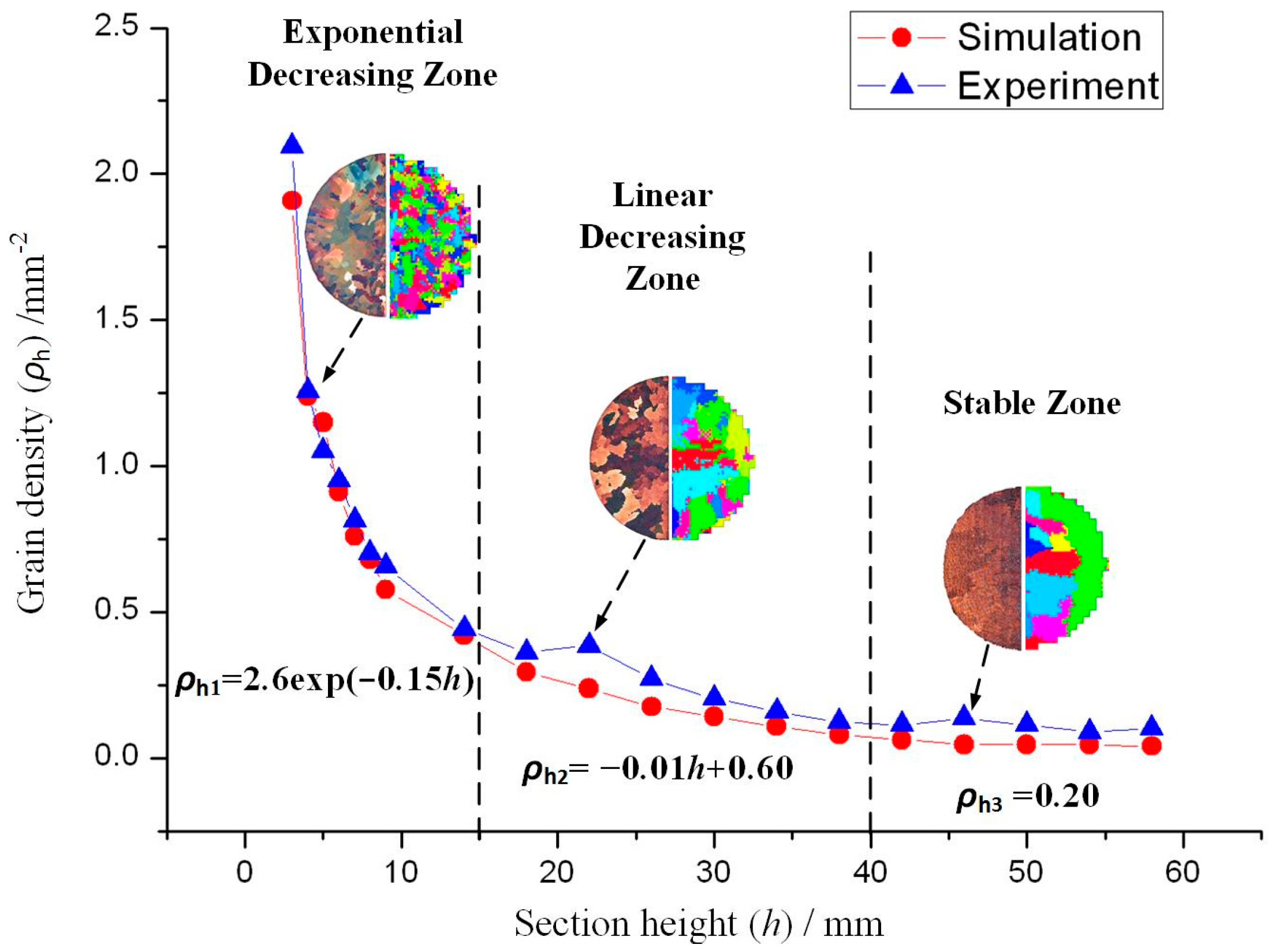
3.2. Microstructure Evolution
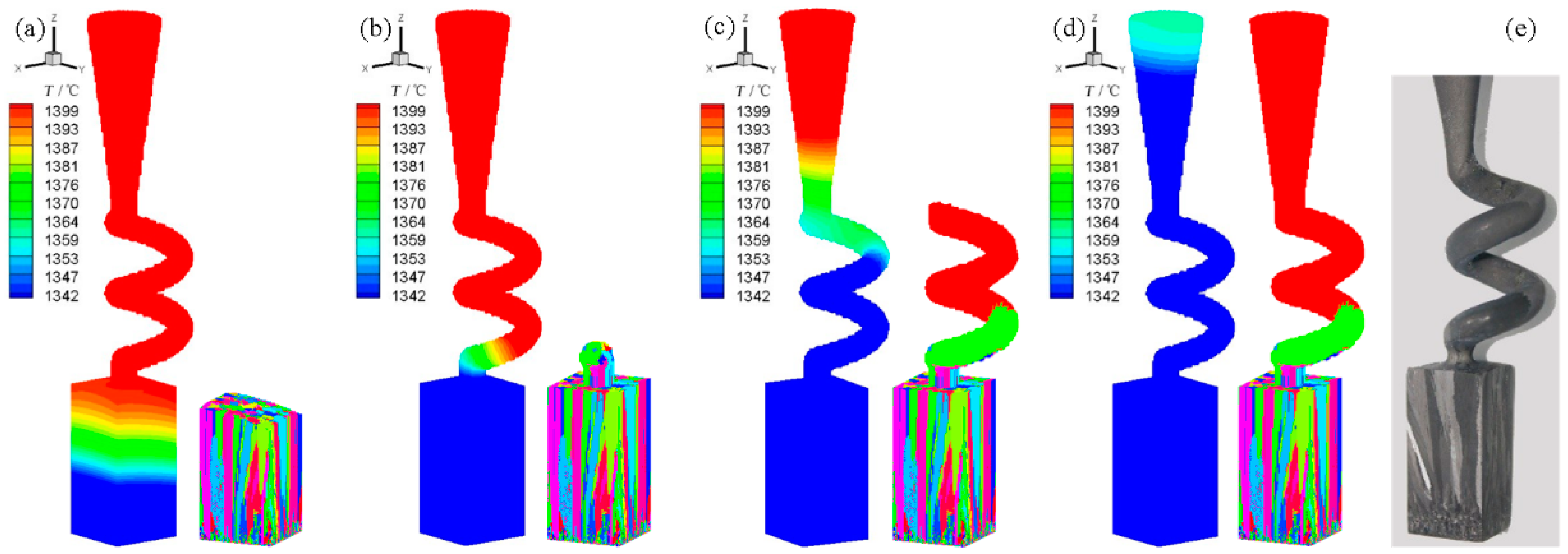
3.2.1. Grain Evolution in Starter Block
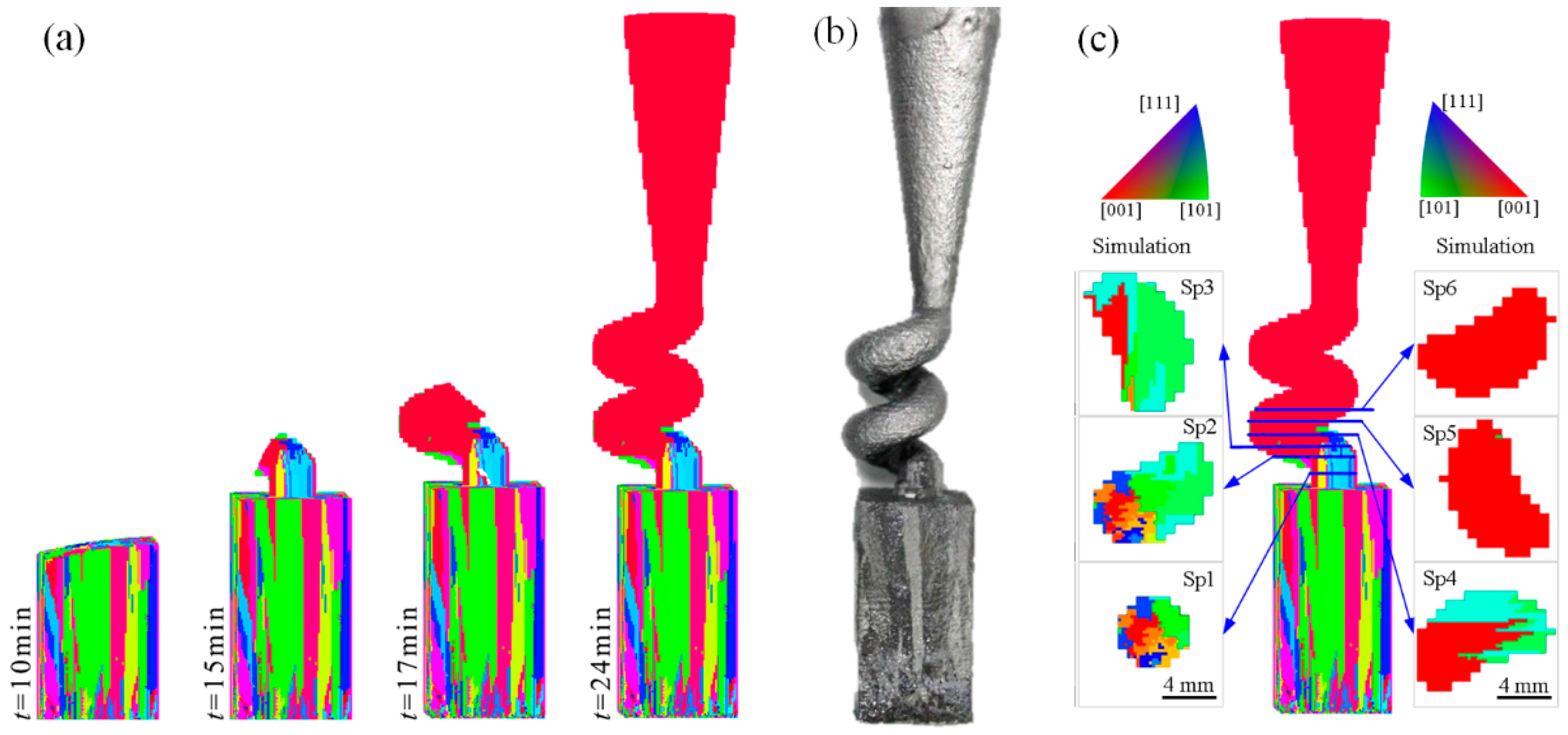
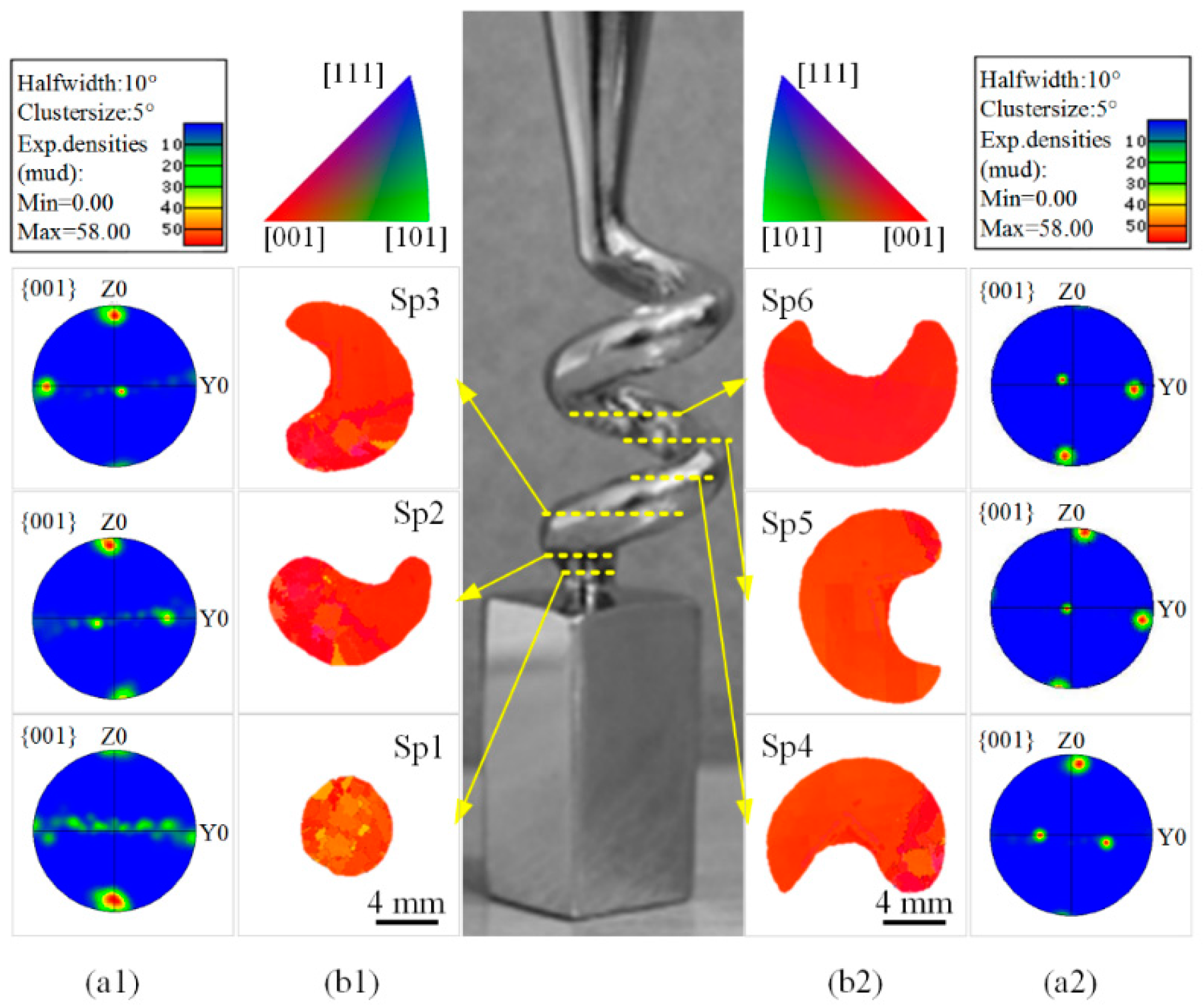
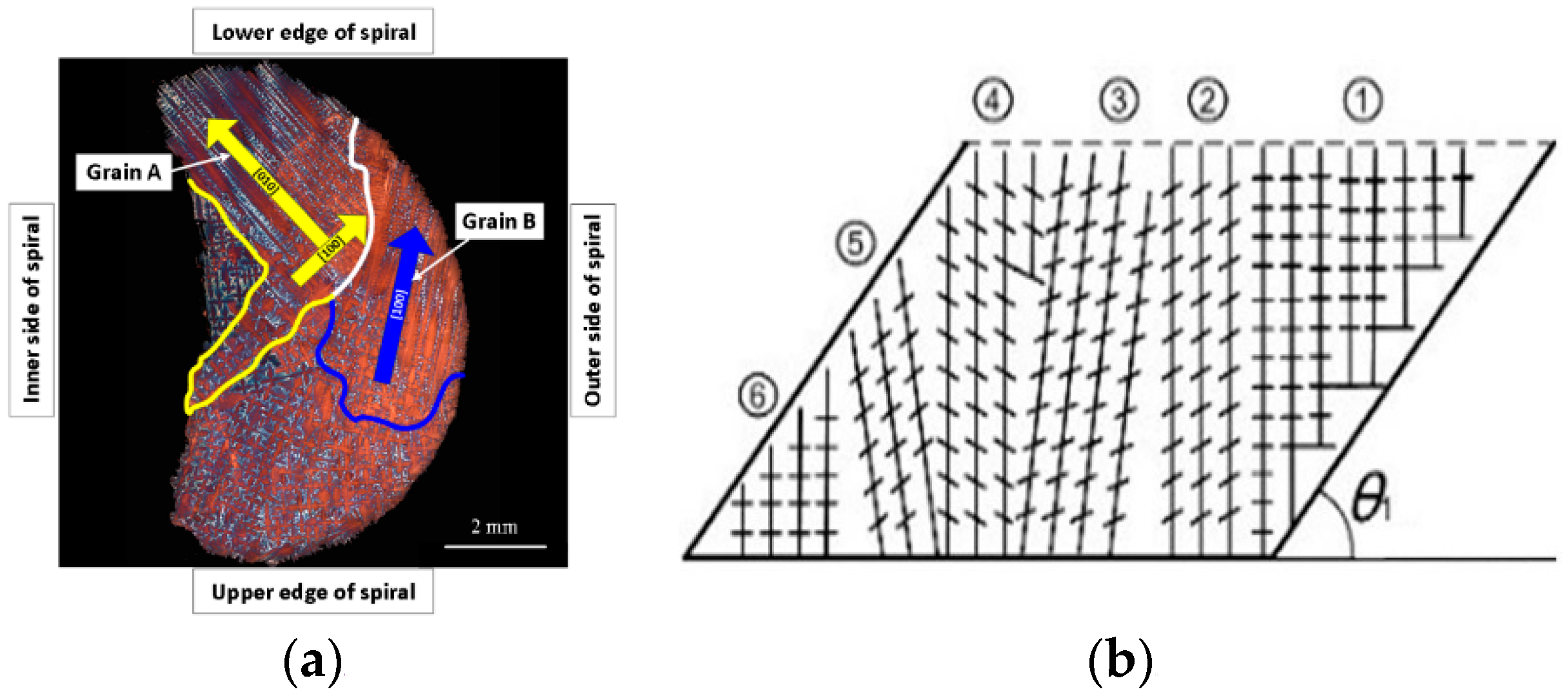
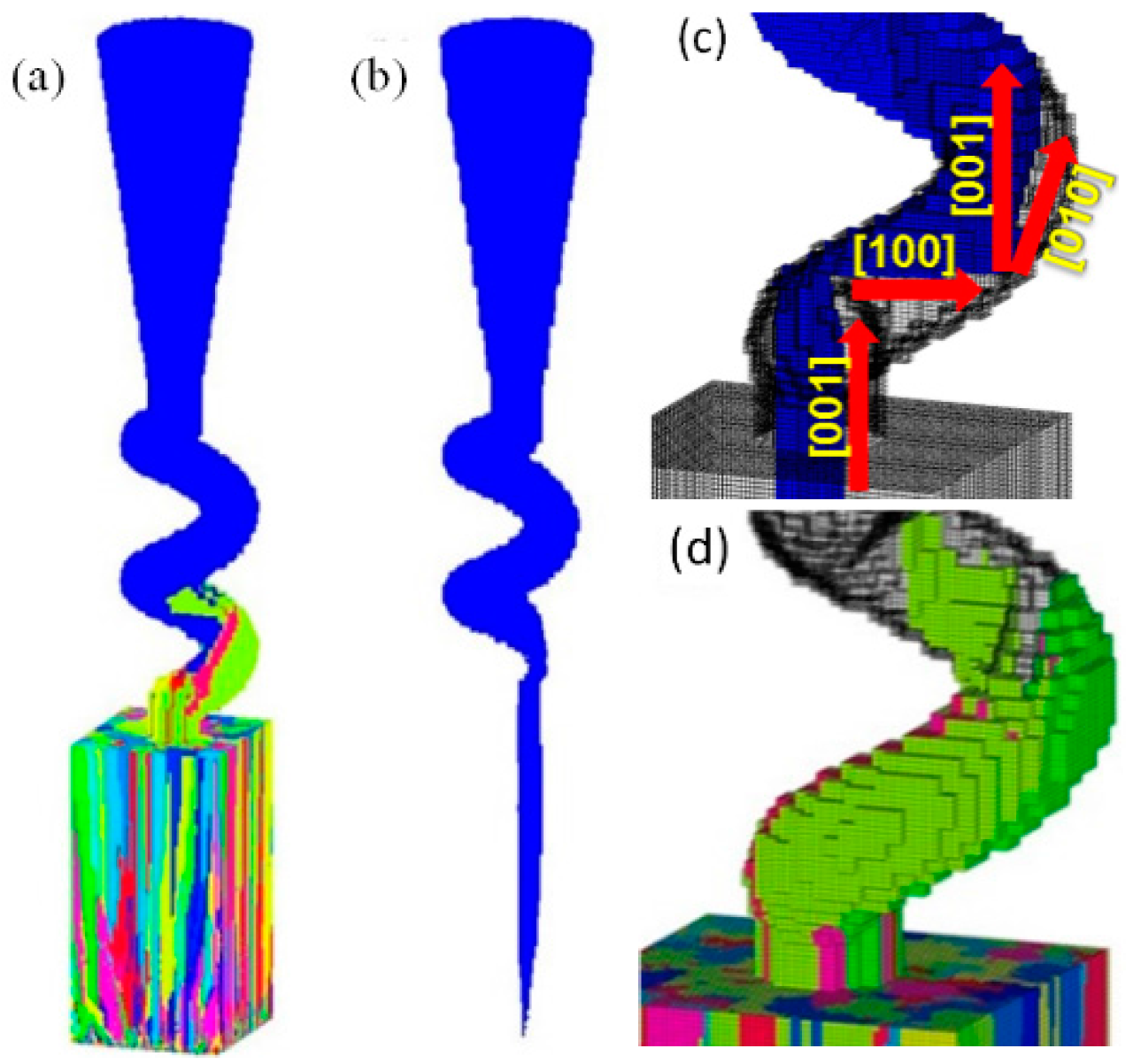
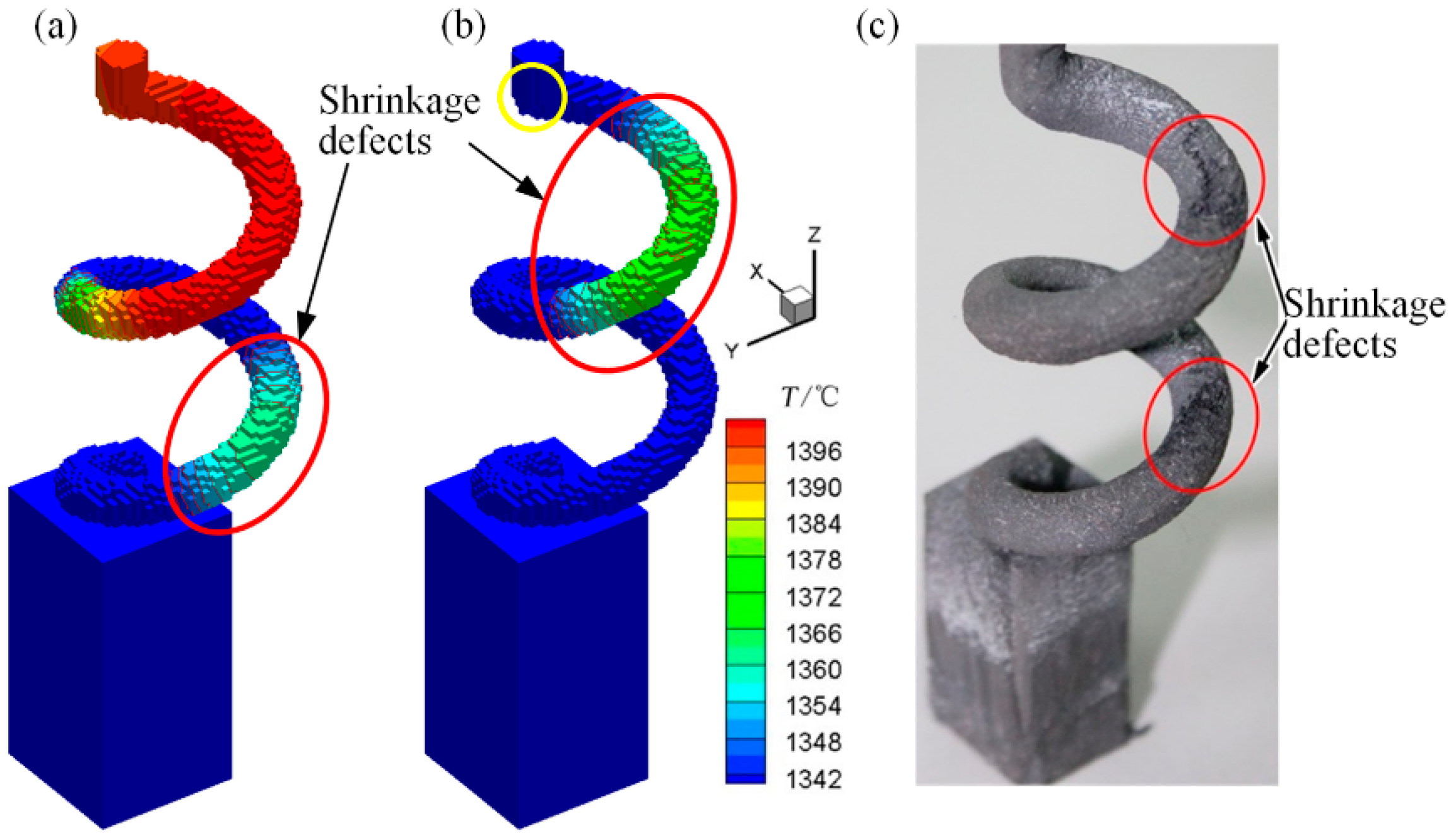
3.2.2. Grain Evolution in Spiral Part
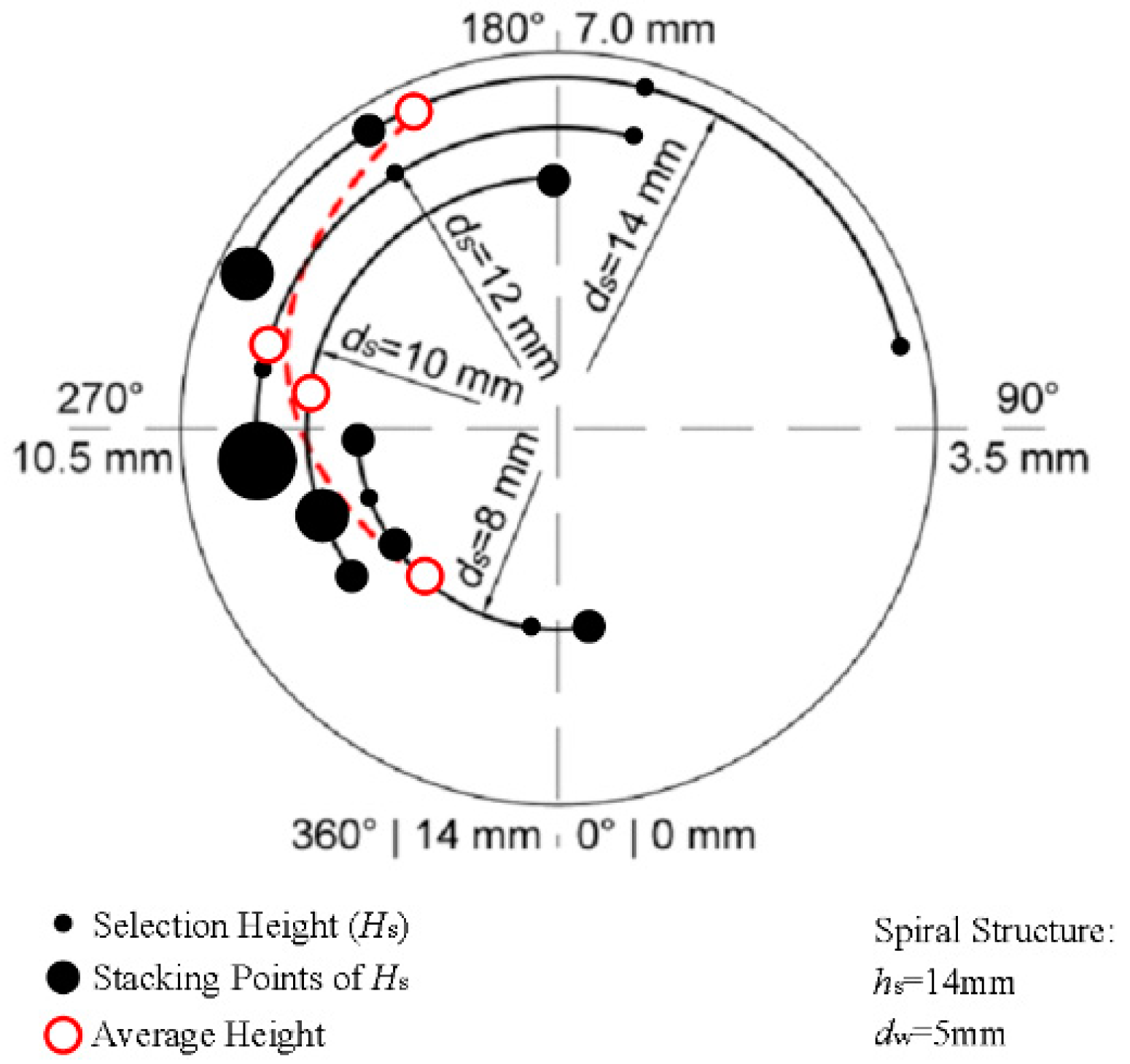
3.3. Simulation Analysis and Validation of Selection Mechanism
4. Selector Structure Design
4.1. Effects of Structural Parameters on Grain Selection
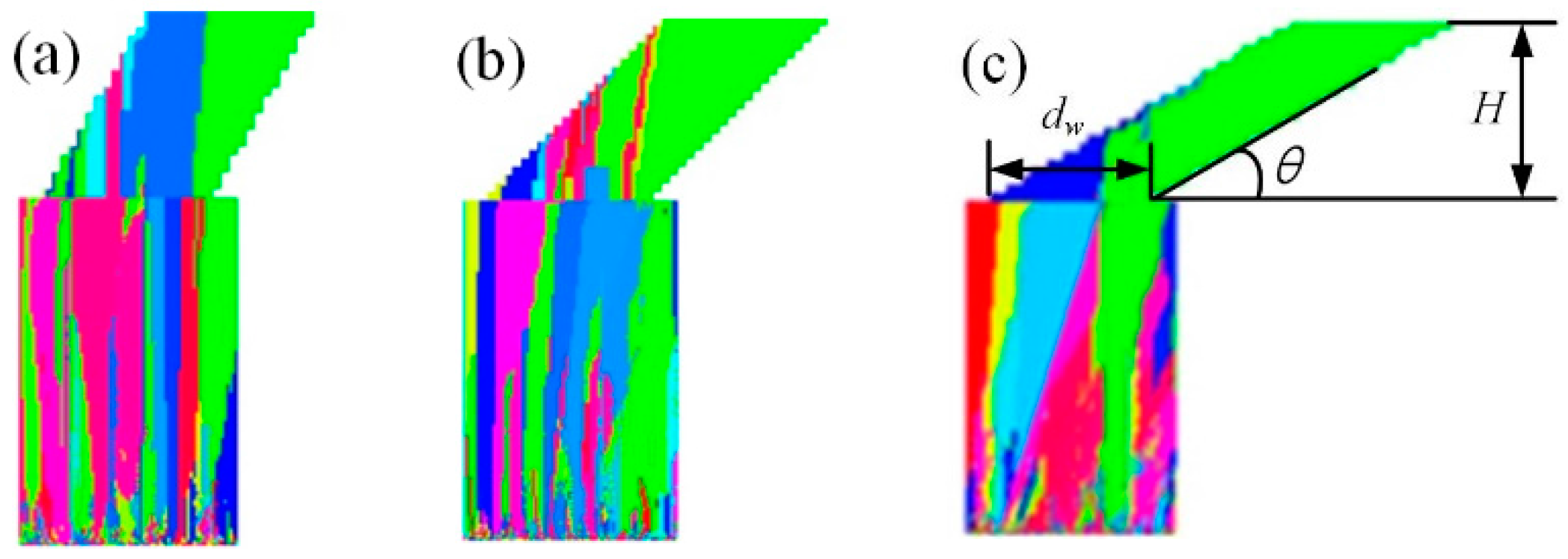
4.1.1. Effects of hb and φ
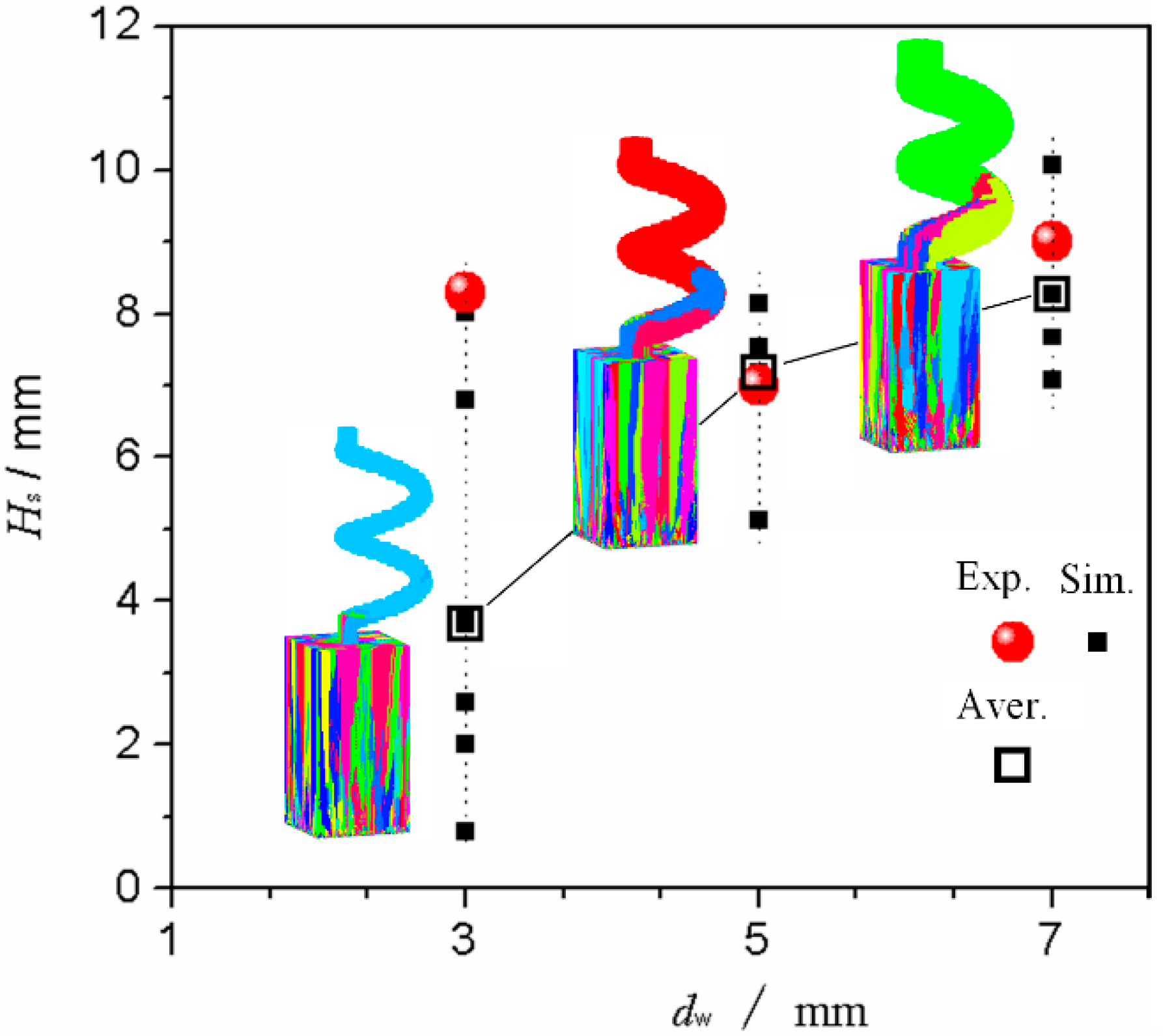
4.1.2. Effects of dw
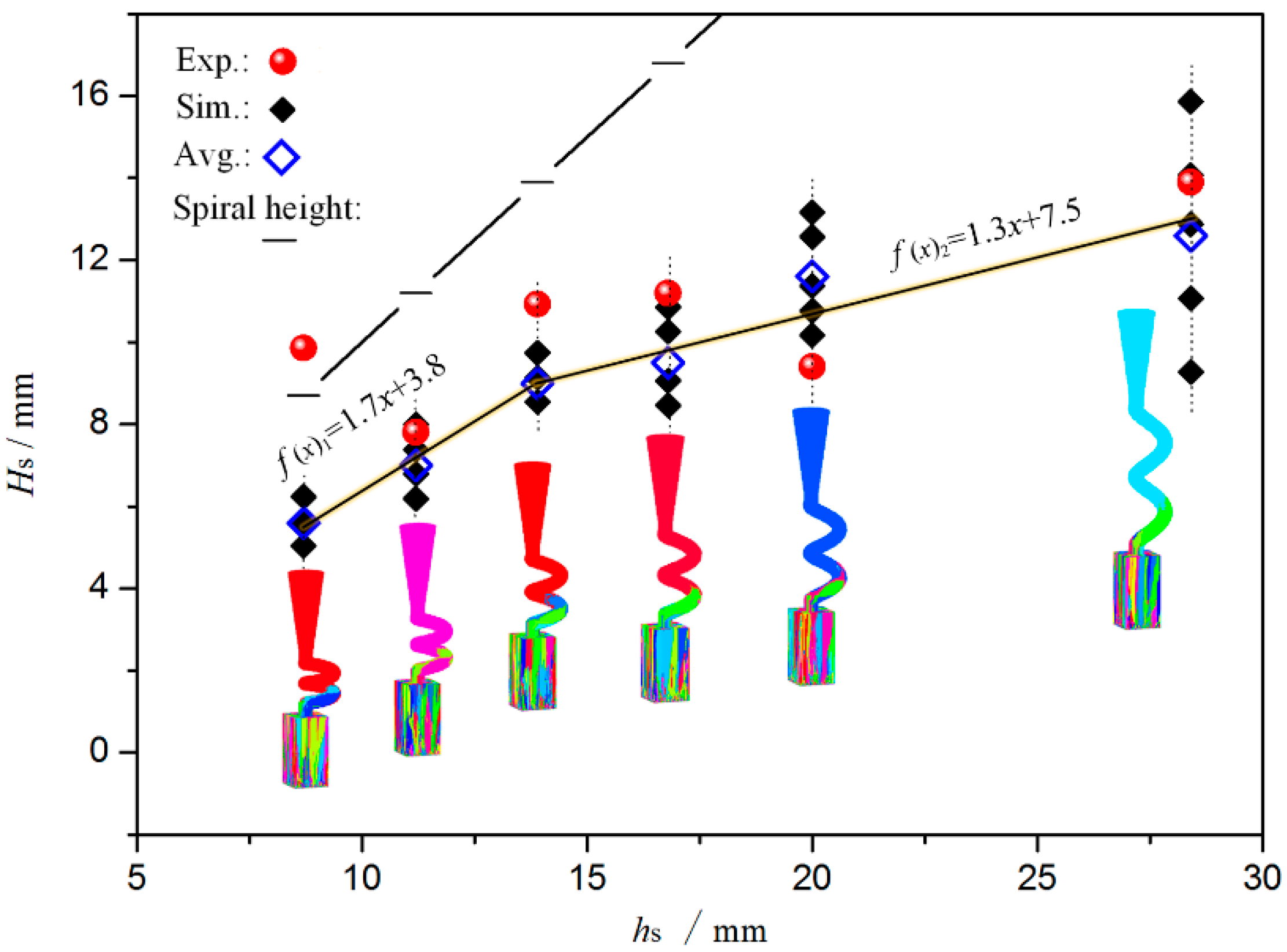
4.1.3. Effects of hs
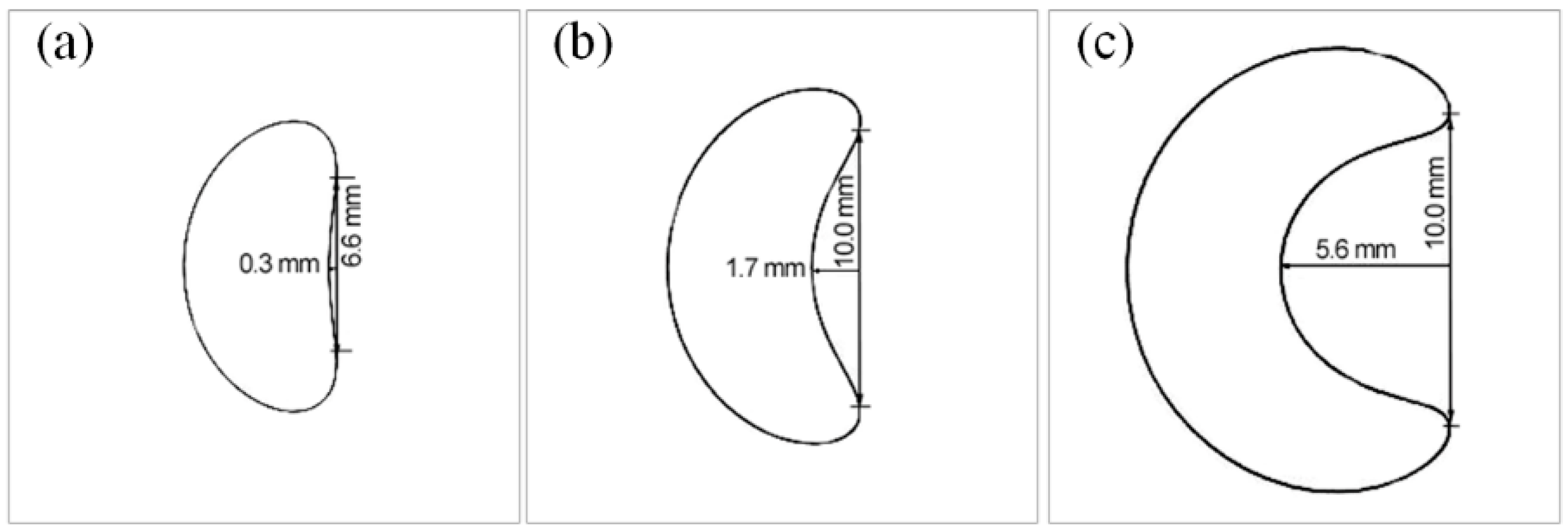
4.1.4. Effects of ds
4.2. Improvement of Spiral Structure
5. Conclusions
- (1)
- Thermal transfer and microstructure models based on CA-FD were built to simulate the temperature variation and microstructure evolution in the spiral selector during the single crystal superalloy casting.
- (2)
- Temperature curves and cooling rates in different points of the selector were compared through experimentation and simulations. The corresponding average errors were below 1.5%. The microstructure evolutions in the selector were investigated through EBSD and simulations and agreed well. The grain selection mechanism was further analyzed and verified with simulations. The design rules of the selector parameters, based on the two selection effects, were proposed.
- (3)
- The effects of the spiral structure parameters on the grain selection were studied through precise casting of different spiral selectors fabricated with 3D printing. The design criteria for these parameters, such as the starter block height (hb), the spiral tunnel diameter (dw), the spiral pitch (hs) and the spiral diameter (ds), were proposed, whereas the spiral selector structure was improved. The results demonstrated that this improved selector could accurately and efficiently select a single crystal.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, Y. Formation of stray grains during directional solidification of a nickel-based superalloy. Scr. Mater. 2011, 65, 281–284. [Google Scholar] [CrossRef]
- Wang, T.; Itsuo, O.; Hideyuki, Y.; Su, Y.; Guo, J. Structure defect prediction of single crystal turbine blade by dendrite envelope tracking model. Trans. Nonferrous Met. Soc. 2006, 16, s582–s585. [Google Scholar] [CrossRef]
- Caron, P.; Khan, T. Evolution of Ni-based superalloys for single crystal gas turbine blade applications. Aerosp. Sci. Technol. 1999, 3, 513–523. [Google Scholar]
- Yang, X.; Ness, D.; Lee, P.D.; D’Souza, N. Simulation of stray grain formation during single crystal seed melt-back and initial withdrawal in the Ni-base superalloy CMSX4. Mater. Sci. Eng. A 2005, 413–414, 571–577. [Google Scholar] [CrossRef]
- Yasuda, H.; Ohnaka, I.; Kawasaki, K.; Sugiyama, A.; Ohmichi, T.; Iwane, J.; Umetani, K. Direct observation of stray crystal formation in unidirectional solidification of Sn–Bi alloy by X-ray imaging. J. Cryst. Growth 2004, 262, 645–652. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Q.Y.; Sun, C.B.; Qi, X.; Tang, N.; Liu, B.C. Simulation and Experimental Studies on Grain Selection Behavior of Single Crystal Superalloy: II. Spiral Part. Acta Metall. Sin. 2013, 49, 1521–1531. [Google Scholar] [CrossRef]
- Esaka, H.; Shinozuka, K.; Tamura, M. Analysis of single crystal casting process taking into account the shape of pigtail. Mater. Sci. Eng. A 2005, 413, 151–155. [Google Scholar] [CrossRef]
- Carter, P.; Cox, D.C.; Gandin, C.A.; Reed, R.C. Process modelling of grain selection during the solidification of single crystal superalloy castings. Mater. Sci. Eng. A 2000, 280, 233–246. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, X. EBSD Studies of Grain Evolution and Grain Selection Behavior during The Preparation of Ni–Based Single Crystal Superalloy DD3. Acta Metall. Sin. 2011, 47, 1251–1256. [Google Scholar]
- Dai, H.J.; D’Souza, N.; Dong, H.B. Grain selection in spiral selectors during investment casting of single-crystal turbine blades: Part 1. Experimental investigation. Metall. Mater. Trans. A 2011, 42A, 3430–3438. [Google Scholar] [CrossRef]
- Zheng, Q.; Hou, G.C.; Tian, W.M.; Jin, T.; Sun, X.F.; Guan, H.R.; Hu, Z.Q. Grain selection behavior of single crystal superalloy. Chin. J. Nonferrous Met. 2001, 11, 176–178. [Google Scholar]
- Epishin, A.I.; Nolze, G. Investigation of the competitive grain growth during solidification of single crystals of nickel-based superalloys. Crystallogr. Rep. 2006, 51, 710–714. [Google Scholar] [CrossRef]
- D’Souza, N.; Ardakani, M.G.; Mclean, M.; Shollock, B.A. Directional and single-crystal solidification of Ni-base superalloys part I. the role of curved isotherms on grain selection. Metall. Mater. Trans. A 2000, 31, 2877–2886. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Volek, A.; Green, N.R. Mechanism of competitive grain growth in directional solidification of a nickel-base superalloy. Acta Mater. 2008, 56, 2631–2637. [Google Scholar] [CrossRef]
- Walton, D.; Chalmers, B. The origin of the preferred orientation in the columnar zone of ingots. Trans. Am. Inst. Min. Metall. Eng. 1959, 215, 447–457. [Google Scholar]
- Jiang, L.; Li, S.; Han, Y. Investigation on selection crystal behavior of a Ni3Al-based single crystal superalloy IC6SX. Procedia Eng. 2012, 27, 1135–1140. [Google Scholar] [CrossRef]
- Meng, X.; Lu, Q.; Li, J.; Jin, T.; Sun, X.; Zhang, J.; Chen, Z.; Wang, Y.; Hu, Z. Modes of grain selection in spiral selector during directional solidification of nickel-base superalloys. J. Mater. Sci. Technol. 2012, 28, 214–220. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Lin, M.; Yu, D.; Zhou, X.W.; Gu, Y.X.; Fu, H.Z. Dependence of competitive grain growth on secondary dendrite orientation during directional solidification of a Ni-based superalloy. Metall. Mater. Trans. A 2013, 44, 1–9. [Google Scholar] [CrossRef]
- Dai, H.J.; Dong, H.B.; D’Souza, N. Grain selection in spiral selectors during investment casting of single-crystal components: Part II. numerical modeling. Metall. Mater. Trans. A 2011, 42A, 3439–3446. [Google Scholar] [CrossRef]
- Seo, S.M.; Kim, I.S.; Lee, J.H.; Jo, C.Y.; Miyahara, H.; Ogi, K. Grain structure and texture evolutions during single crystal casting of the Ni-base superalloy CMSX-4. Met. Mater. Int. 2009, 15, 391–398. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, L.; Li, C.; Wang, N.; Lu, X.; Ren, Z. Influence of spiral crystal selector on crystal orientation of single crystal superalloy. Trans. Nonferrous Met. Soc. 2012, 22, 1092–1095. [Google Scholar] [CrossRef]
- Wang, N.; Liu, L.; Gao, S.; Zhao, X.; Huang, T.; Zhang, J.; Fu, H. Simulation of grain selection during single crystal casting of a Ni-base superalloy. J. Alloy Compd. 2014, 586, 220–229. [Google Scholar] [CrossRef]
- Viardin, A.; Založnik, M.; Souhar, Y.; Apel, M.; Combeau, H. Mesoscopic modeling of spacing and grain selection in columnar dendritic solidification: Envelope versus phase-field model. Acta Mater. 2017, 122, 386–399. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Q.Y.; Sun, C.B.; Qi, X.; Tang, N.; Liu, B.C. Simulation and Experimental Studies on Grain Selection Behavior of Single Crystal Superalloy: I. Starter Block. Acta Metall. Sin. 2013, 49, 1508–1520. [Google Scholar] [CrossRef]
- Cui, K.; Xu, Q.; Yu, J.; Liu, B.; Kimatsuka, A.; Kuroki, Y.; Yokoyama, F. Radiative heat transfer calculation for superalloy turbine blade in directional solidification process. Acta Metall. Sin. 2007, 43, 465. [Google Scholar]
- Nastac, L. Numerical modeling of solidification morphologies and segregation patterns in cast dendritic alloys. Acta Mater. 1999, 47, 4253–4262. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Q. Multi-scale simulation of directional dendrites growth in superalloys. J. Mater. Process. Technol. 2016, 238, 132–141. [Google Scholar] [CrossRef]
- Li, J.R.; Zhong, Z.G.; Tang, D.Z.; Liu, S.Z.; Wei, P.; Wei, P.Y.; Wu, Z.T.; Huang, D.; Han, M. A low-cost second generation single crystal superalloy DD6. In Proceedings of the Superalloys 2000, Warrendale, PA, USA, 17–21 September 2000; pp. 777–783. [Google Scholar]
- Gao, S.F.; Liu, L.; Wang, N.; Zhao, X.B.; Zhang, J.; Fu, H.Z. Grain selection during casting Ni-base, single-crystal superalloys with spiral grain selector. Metall. Mater. Trans. A 2012, 43, 3767–3775. [Google Scholar] [CrossRef]


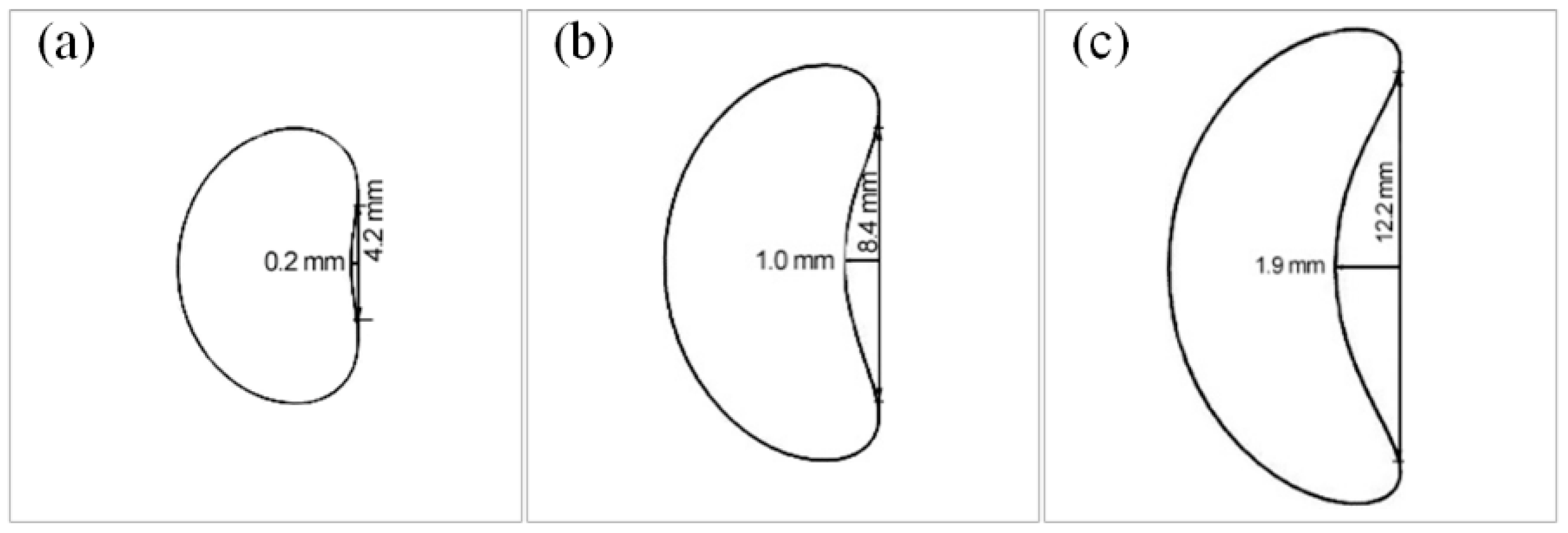
| ES1 Group (ds = 12 mm, dw = 5 mm) | ES2 Group (hs = 14 mm, θ = 30°) | |||
|---|---|---|---|---|
| hs/mm | θ/° | hs/mm | θ/° | dw/mm |
| 8.7 | 13.0 | 16.8 | 24.0 | 3 |
| 11.2 | 16.5 | 20.1 | 28.0 | 5 |
| 14.0 | 20.2 | 27.4 | 37.0 | 7 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Liquidus/K | 1672 | Thermal conductivity of alloy/J·(m·s·K)−1 | 33.2 |
| Solidus/K | 1615 | Specific heat of alloy/kJ·(kg·K) −1 | 0.773 |
| Density of alloy/kg·m−3 | 8780 | Liquidus slope/°C·%−1 | −3.95 |
| Latent heat/kJ·kg−1 | 99 | diffusion coefficient in liquid(DL)/m2·s−1 | 3.6 × 10−9 |
| Concentration/wt % | 39.006 | diffusion coefficient in liquid (DS)/m2·s−1 | 1.0 × 10−12 |
| Density of shell/kg·m−3 | 2500 | Thermal conductivity of shell/J·(m·s·K)−1 | 1.95 |
| Specific heat of shell/kJ·(kg·K)−1 | 1.323 | Cast-shell interface resistance/m2·K·W−1 | 1.8 × 10−2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Xu, Q. Simulation and Experimental Studies on Grain Selection and Structure Design of the Spiral Selector for Casting Single Crystal Ni-Based Superalloy. Materials 2017, 10, 1236. https://doi.org/10.3390/ma10111236
Zhang H, Xu Q. Simulation and Experimental Studies on Grain Selection and Structure Design of the Spiral Selector for Casting Single Crystal Ni-Based Superalloy. Materials. 2017; 10(11):1236. https://doi.org/10.3390/ma10111236
Chicago/Turabian StyleZhang, Hang, and Qingyan Xu. 2017. "Simulation and Experimental Studies on Grain Selection and Structure Design of the Spiral Selector for Casting Single Crystal Ni-Based Superalloy" Materials 10, no. 11: 1236. https://doi.org/10.3390/ma10111236
APA StyleZhang, H., & Xu, Q. (2017). Simulation and Experimental Studies on Grain Selection and Structure Design of the Spiral Selector for Casting Single Crystal Ni-Based Superalloy. Materials, 10(11), 1236. https://doi.org/10.3390/ma10111236




