Effect of Nano-CuO on Engineering and Microstructure Properties of Fibre-Reinforced Mortars Incorporating Metakaolin: Experimental and Numerical Studies
Abstract
:1. Introduction
2. Methodology
2.1. Experimental Program
2.1.1. Materials
2.1.2. Mix Proportions
2.1.3. Production of Specimens
2.1.4. Test Procedures
2.2. Prediction Method
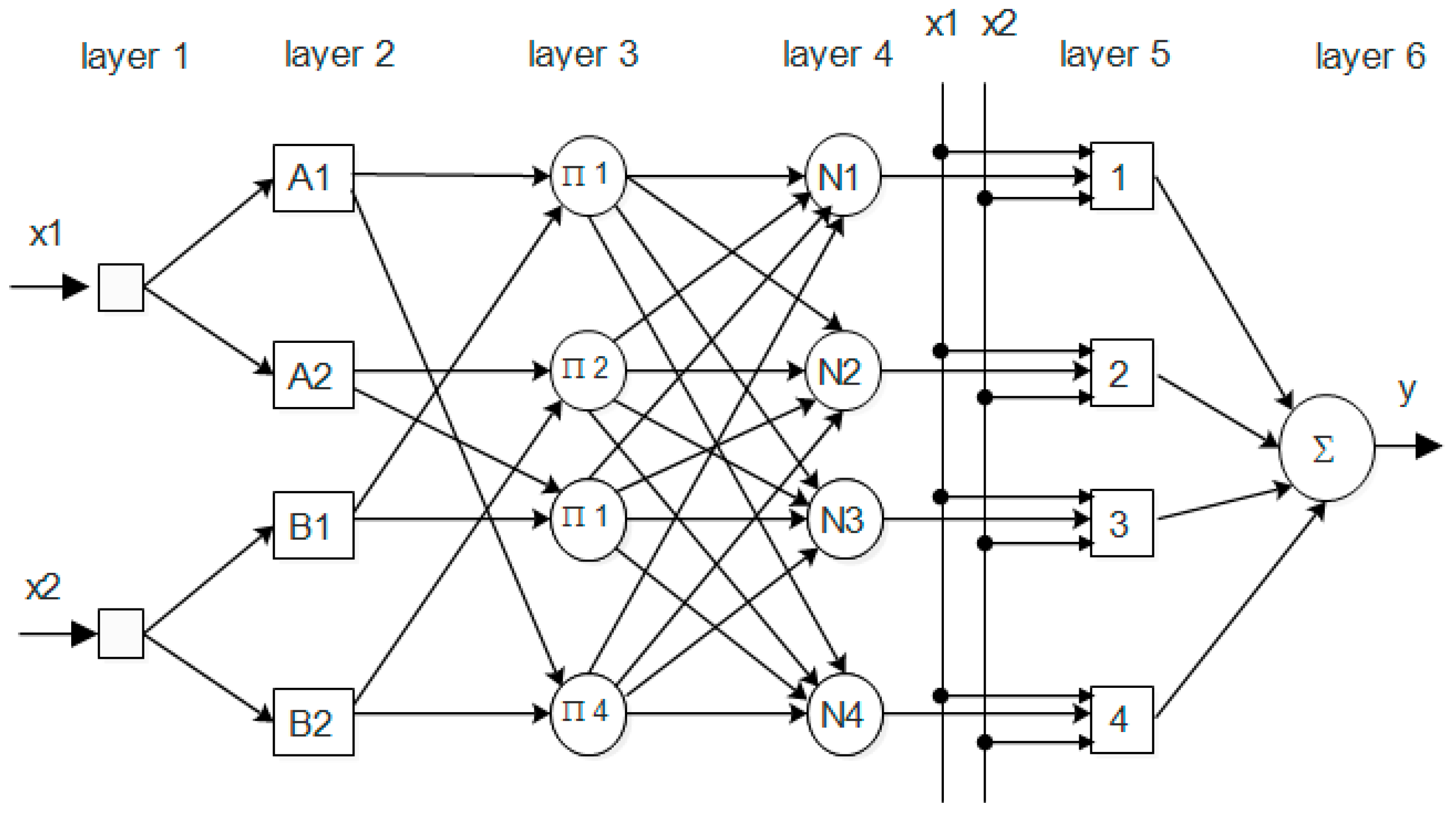
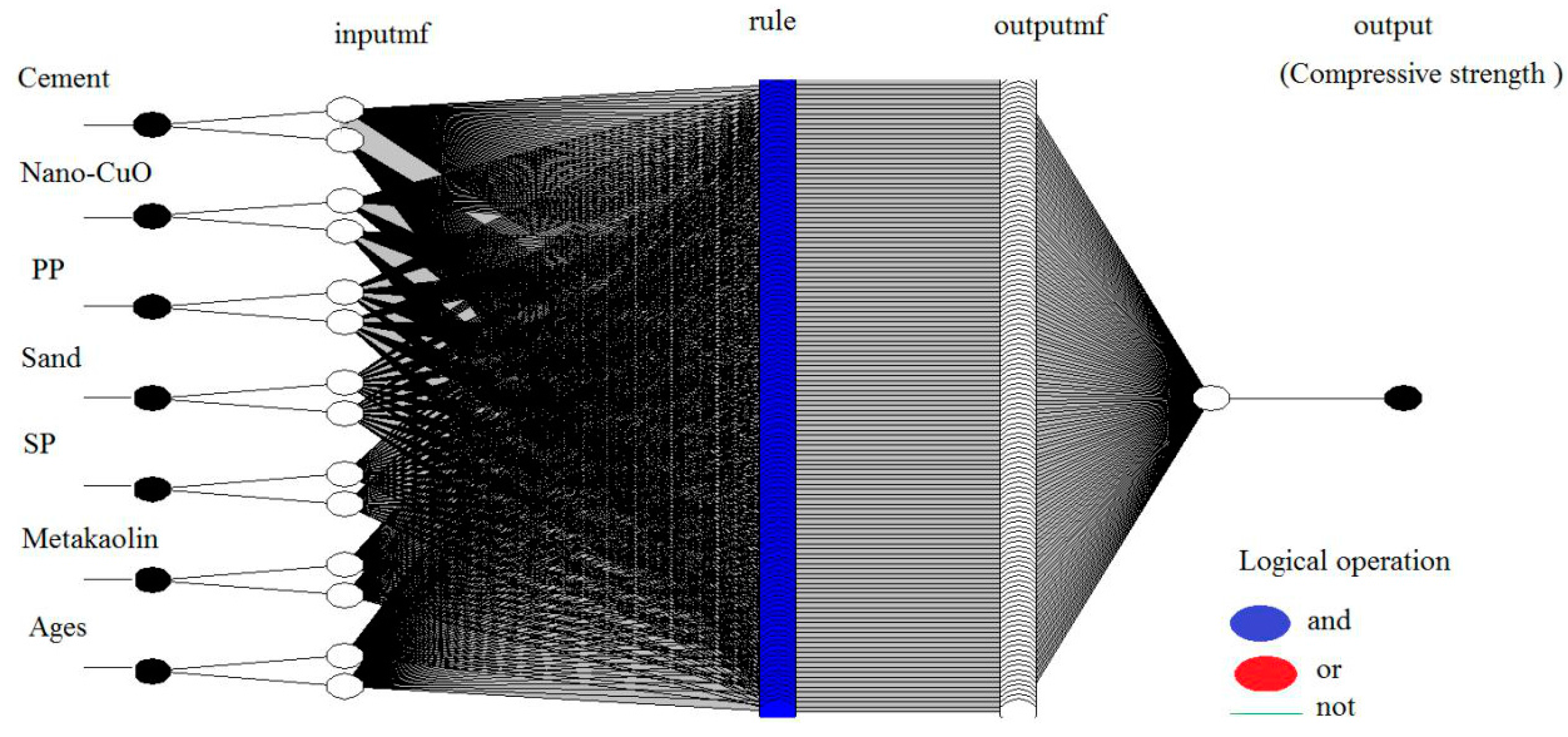
2.2.1. Application of ANFIS to Predict Concrete Properties
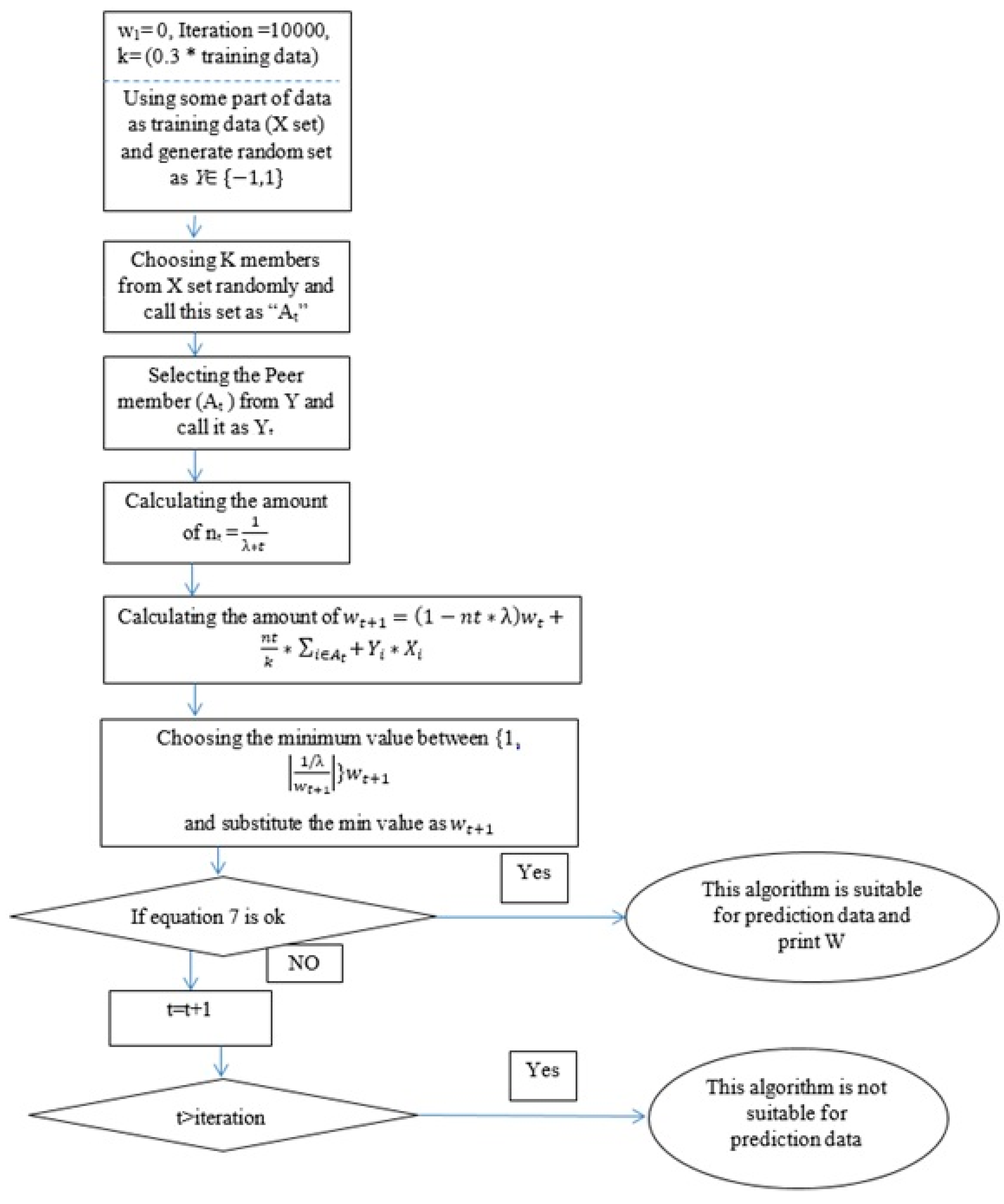
2.2.2. Pegasus (Primal Estimated Sub-Gradient Solver for SVM)
Using Mini-Batch Iterations to Implement Pegasos
3. Results and Discussion
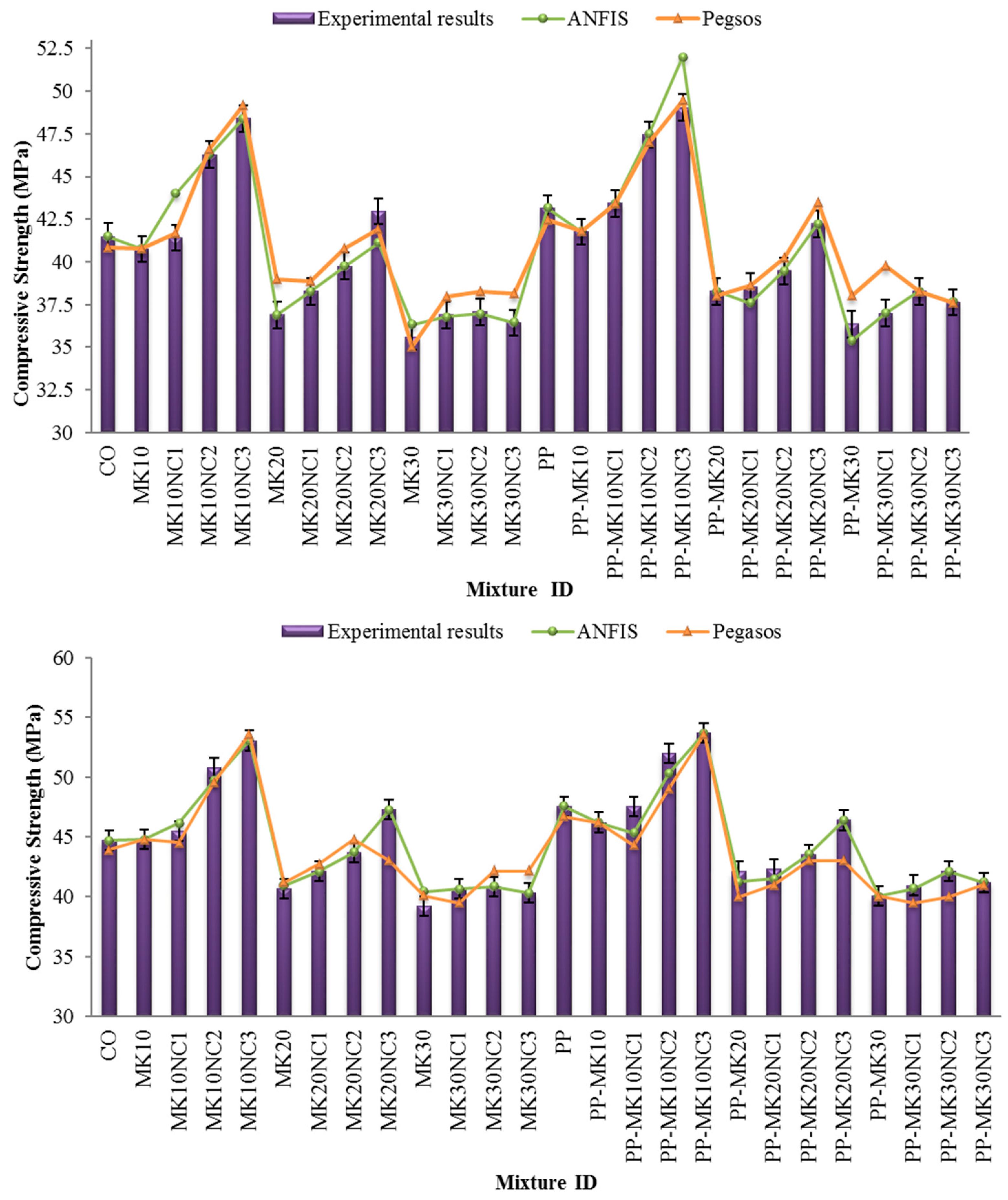
3.1. Compressive Strength
- Filling property: NC can act as a filler to improve the density of mortar resulting in a significant reduction of porosity. Figure 8 shows the SEM micrographs of MK10 and MK10NC3 samples. As shown in Figure 8b, the microstructure of cement matrix containing NC was more compact and the porosity was significantly reduced. The SEM results confirmed that NC, having the filling ability property, can fill the porosity in cement paste and make a denser cement matrix.
- Acting as a nucleus: In the structure of the C-S-H gel, the nanoparticles can act like a nucleus forming an extremely strong bond with C-S-H gel particles [36]. Thus, when nanomaterials are uniformly dispersed in cement, they can promote the cement hydration due to their high reactivity, results in improvement of mechanical properties and durability of mortars.
- Crystal-formation control: If the amount of nanoparticles and their spacing are appropriate, the formation process of Ca(OH)2 crystals in the transition area can be reduced [36]. Therefore, with increase of NC up to 3%, the compressive strength raised except for the samples containing 30% MK. It can be stated that NC can lead to a denser structure with less porosity when an appropriate amount is added.
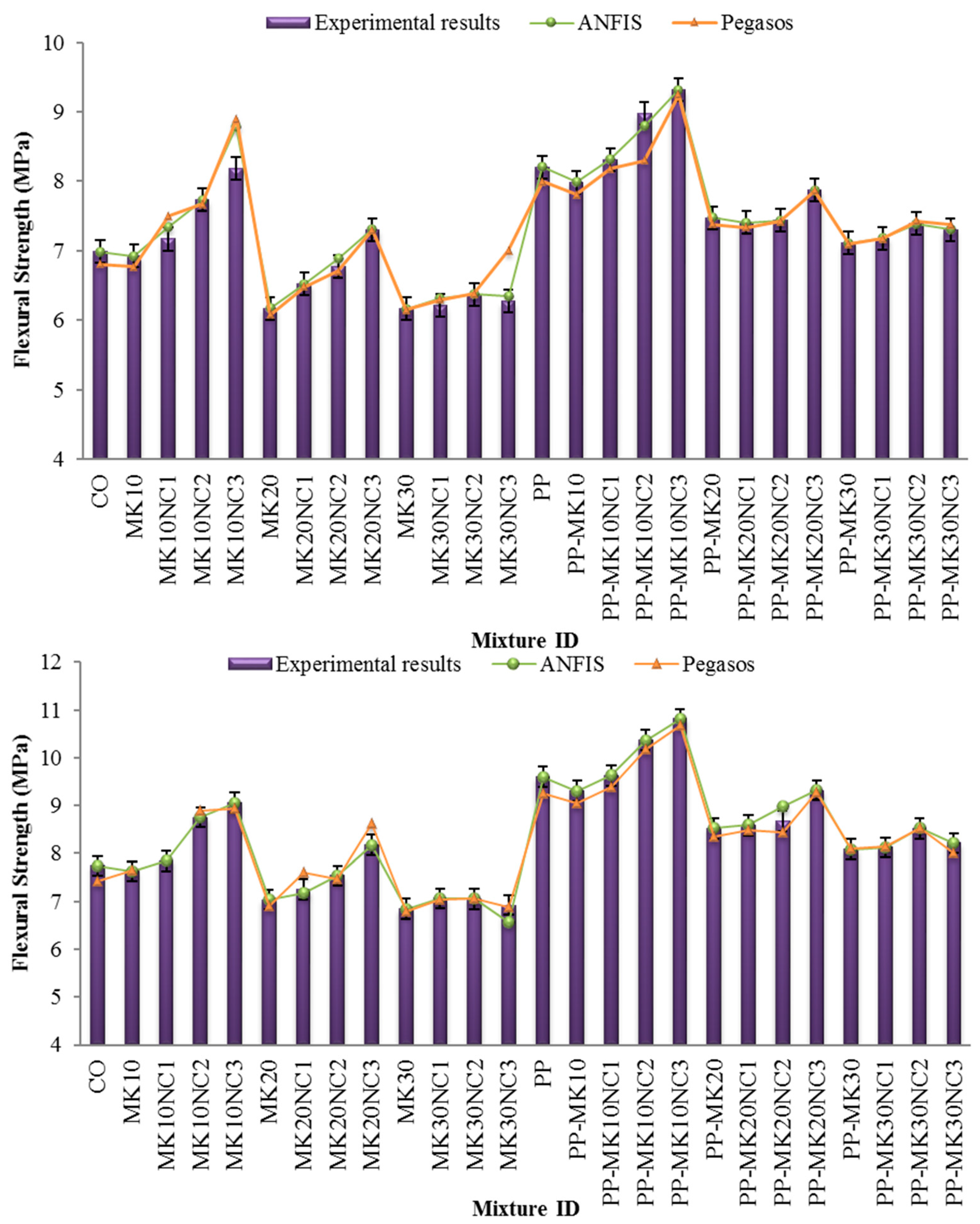
3.2. Flexural Strength
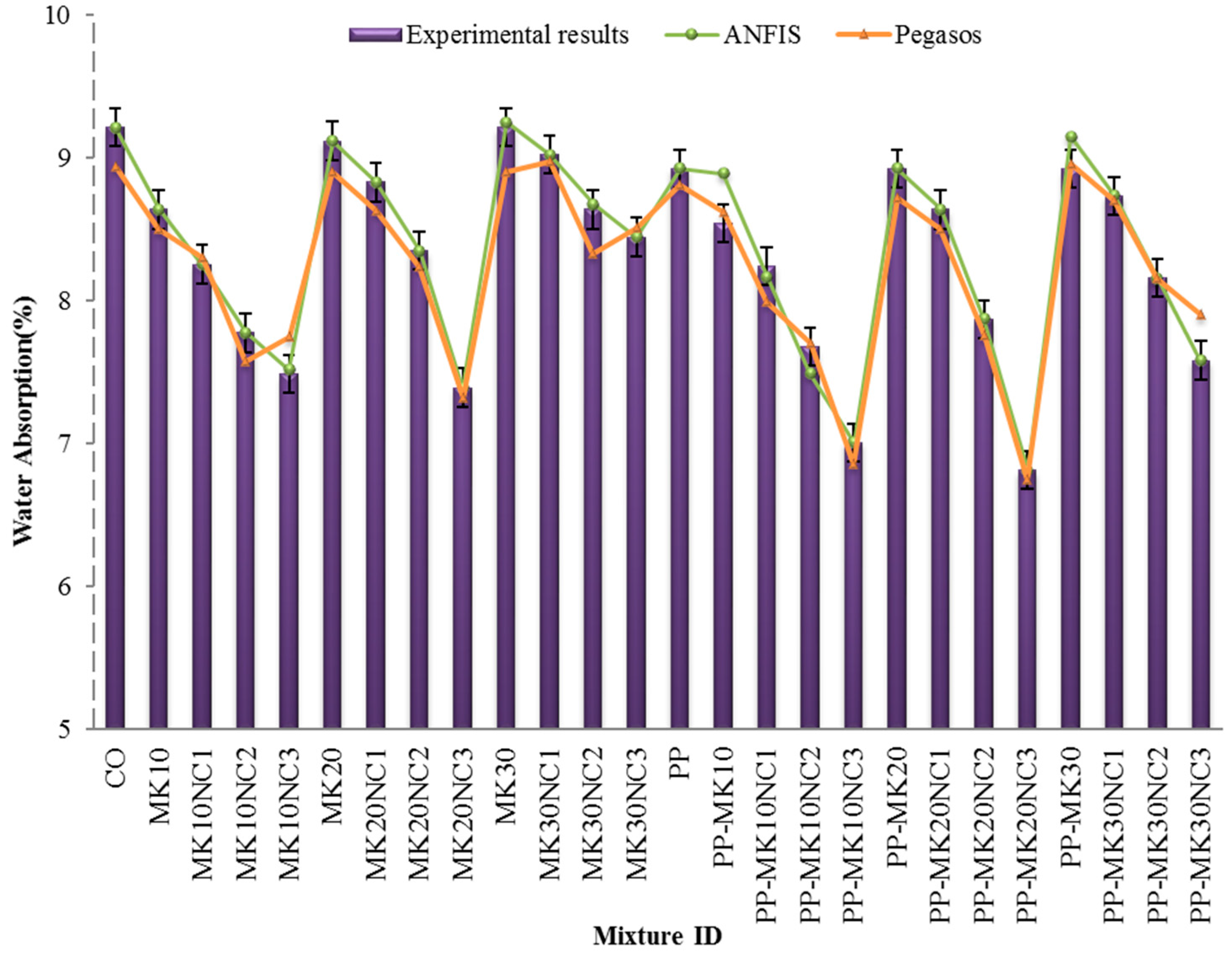
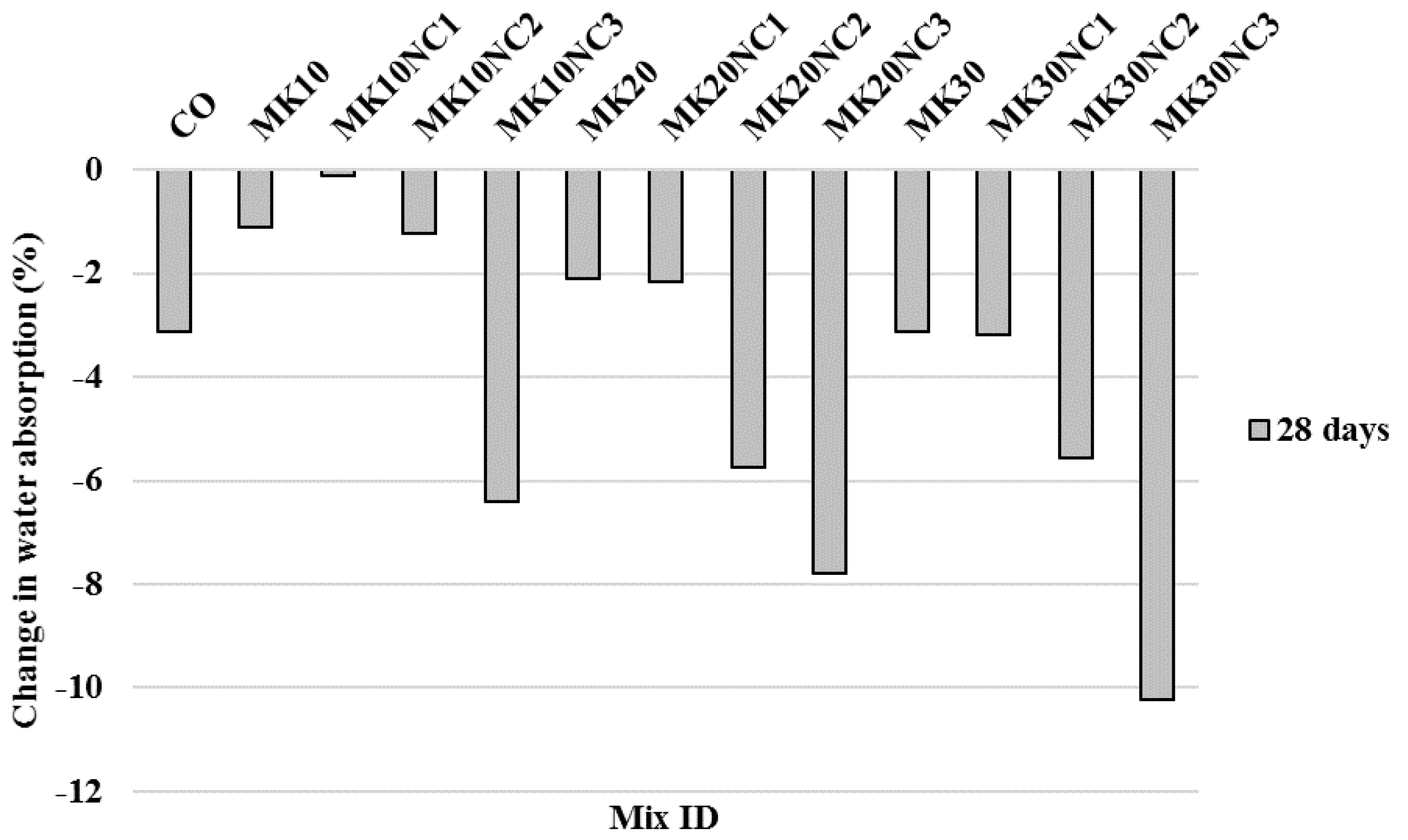
3.3. Water Absorption
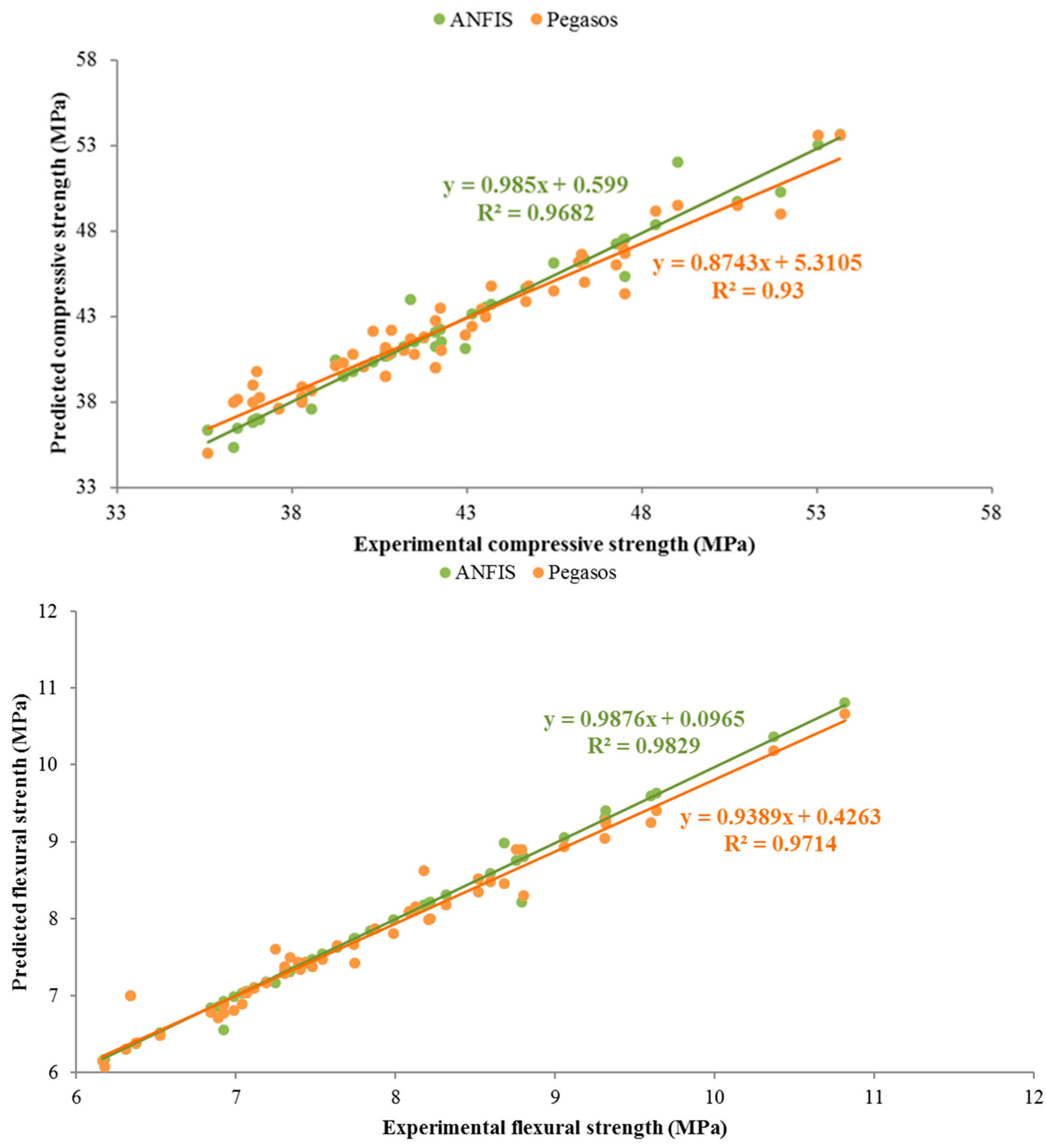
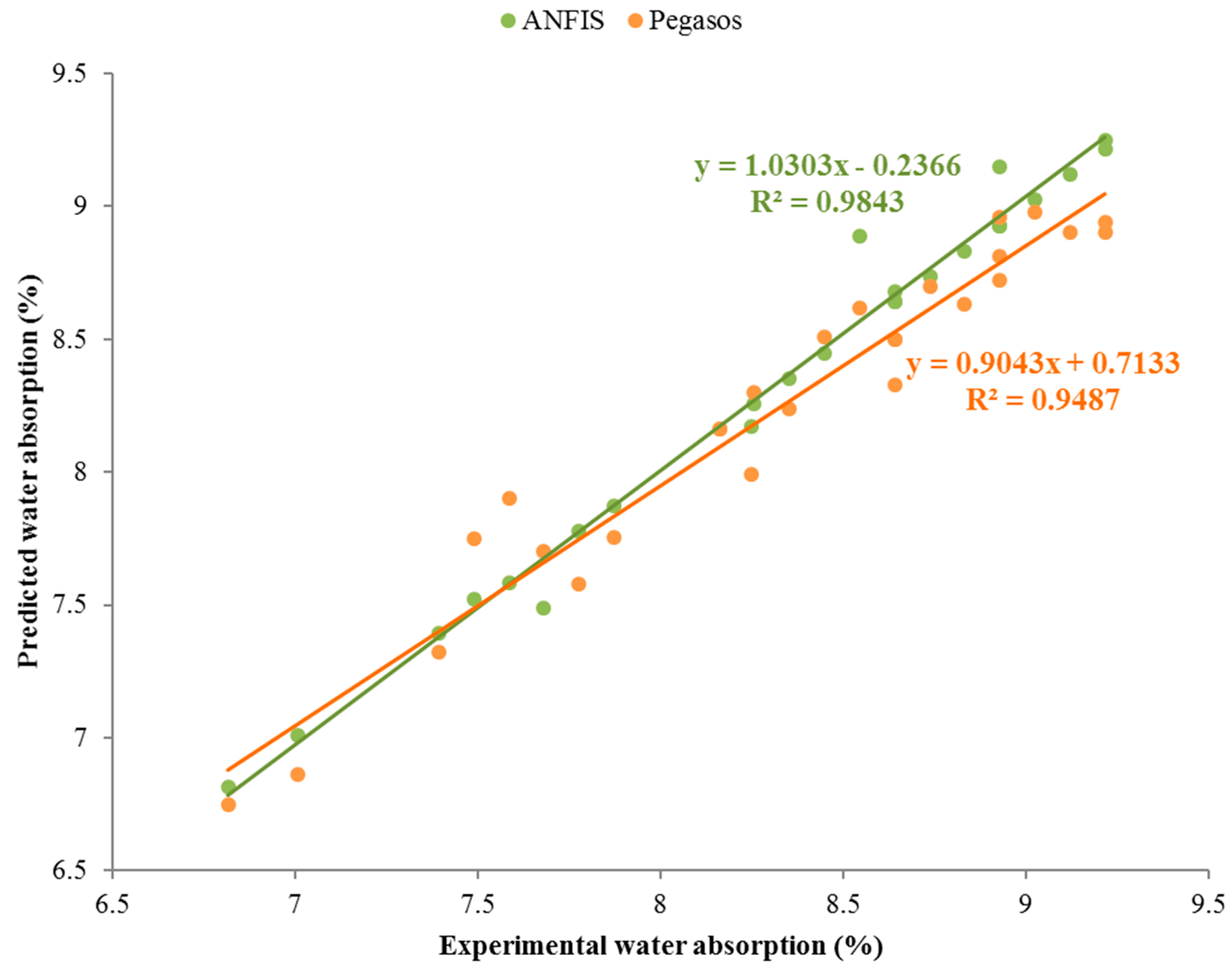
4. Accuracy of Predicted Methods
- Using ANFIS can get estimated results that are closer to the experimental results than Pegasos model.
- Using Pegasos model as an algorithm can obtain upper and lower bounds for each predicted data, while using ANFIS can only lead to one mean value, so user does not have any tolerance to report the data.
- Using ANFIS model requires obtaining the function, number of epoch and hidden layers with trial and error processes, while trial and error is not used in Pegasos algorithm.
- The speed of prediction process decreases with increasing number of data and input layers in ANFIS method and sometimes more time is required to run model when the hidden layers increase, however it is not an issue in Pegasos algorithm.
5. Conclusions
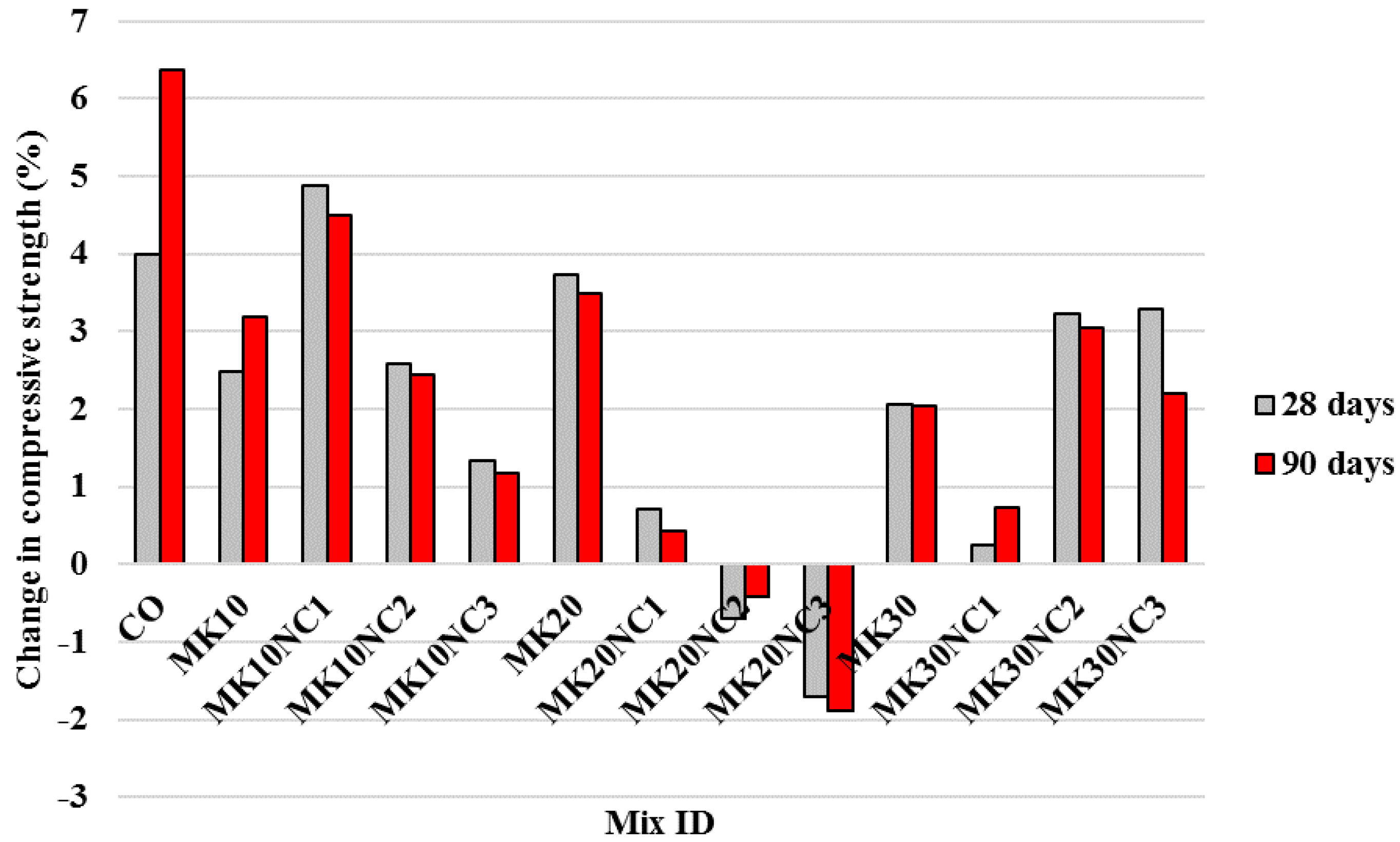
- The compressive and flexural strengths decreased with increasing MK content at both 28 and 90 days.
- Using of 0.3% PP fibres improved the compressive strength slightly. The average compressive strength for all samples increased by 2% at 28 and 90 days which is negligible.
- Compared to the CO sample, the incorporation of 3% NC increased the strength of samples containing 10% MK up to 17% and 19% at 28 and 90 days, respectively.
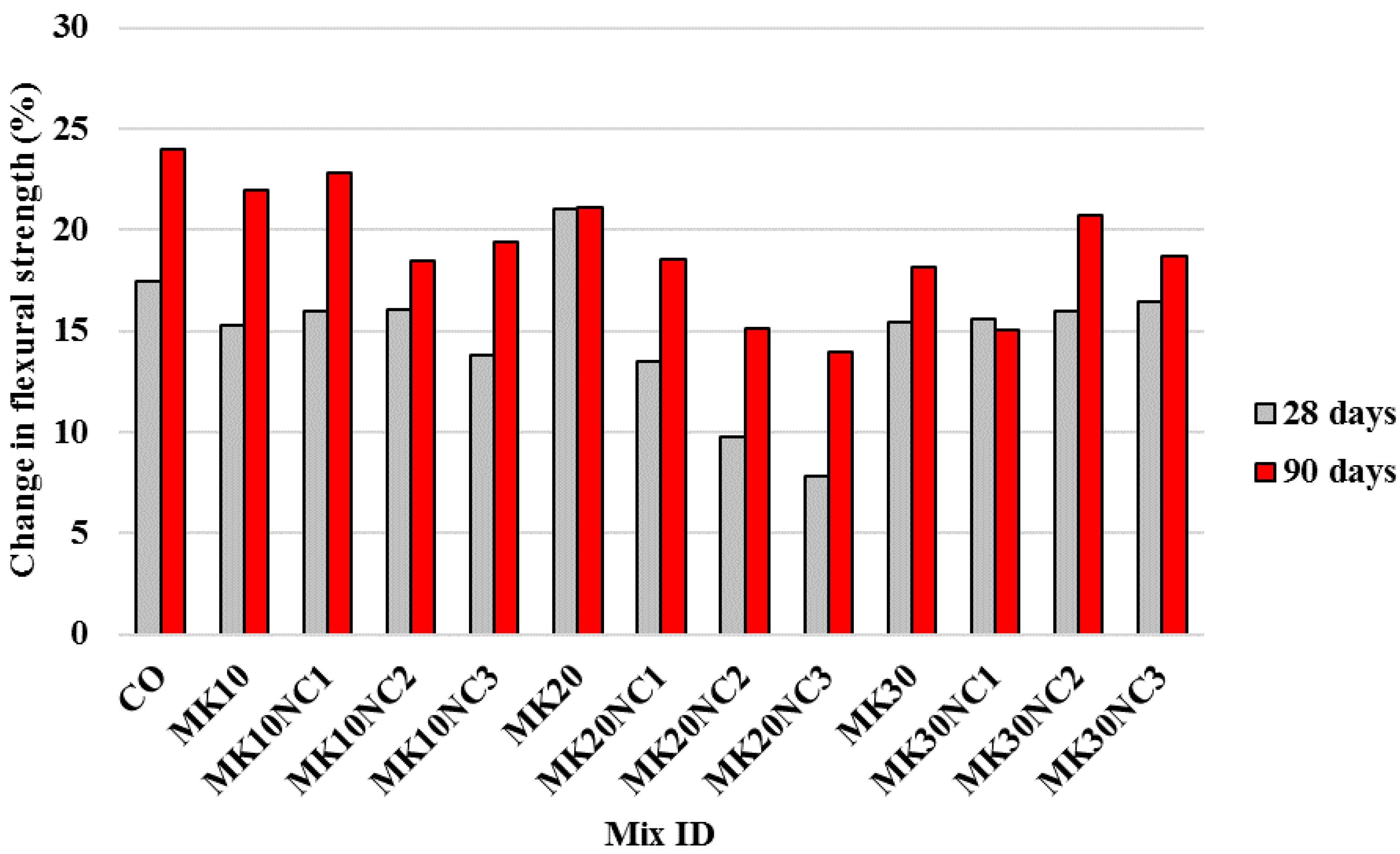
- Significant improvement in flexural strength was seen when PP fibres were used. Compared to the samples without PP, the samples with PP indicated an average increase of flexural strength by 12.7% and 17.4%, at 28 and 90 days, respectively.
- Comparing with other samples tested, mortars containing 3% NC and 10% MK were considered as the most suitable mixtures for mechanical properties.
- It was observed that the water absorption of mortar samples decreased with the increase of MK content up to 10%. However, the addition of more MK (i.e., 20% and 30%) did not have remarkable impact on the water absorption.
- The addition of PP improved water absorption. The water absorption results showed that an addition of 0.3% PP fibres reduced the water absorption of mortar compared to the samples without PP.
- The water absorption results decreased with increasing the contents of nanoparticles and MK.
- SEM images illustrated that the morphology of cement matrix became more porous with increasing MK content, but the porosity reduced with the inclusion of NC. In addition, there were more cement hydration products adhered around the fibres, accompanied with a more compact microstructure due to the filling ability of nanoparticles. This could improve the fibre–matrix interface, and thus enhance the load transfer between the cement matrix and fibres, leading an improvement in flexural strength of mortar.
- Based on the statistical values of MAPE, RRMSE and R2, the ANFIS model showed the best prediction accuracy and can be used to predict the properties of fibre reinforced cement mortar accurately.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Siddique, R.; Klaus, J. Influence of metakaolin on the properties of mortar and concrete: A review. Appl. Clay Sci. 2009, 43, 392–400. [Google Scholar] [CrossRef]
- Khotbehsara, M.M.; Mohseni, E.; Ozbakkaloglu, T.; Ranjbar, M.M. Durability Characteristics of Self-Compacting Concrete Incorporating Pumice and Metakaolin. J. Mater. Civ. Eng. 2017, 29, 04017218. [Google Scholar] [CrossRef]
- Mohseni, E.; Yazdi, A.; Miyandehi, B.M.; Zadshir, M.; Ranjbar, M.M. Combined Effects of Metakaolin, Rice Husk Ash, and Polypropylene Fiber on the Engineering Properties and Microstructure of Mortar. J. Mater. Civ. Eng. 2017, 29, 04017025. [Google Scholar] [CrossRef]
- Nili, M.; Afroughsabet, V. Combined effect of silica fume and steel fibers on the impact resistance and mechanical properties of concrete. Int. J. Impact Eng. 2010, 37, 879–886. [Google Scholar] [CrossRef]
- Richardson, A.E. Compressive strength of concrete with polypropylene fibre additions. Struct. Surv. 2006, 24, 138–153. [Google Scholar] [CrossRef]
- Mohseni, E.; Khotbehsara, M.M.; Naseri, F.; Monazami, M.; Sarker, P. Polypropylene fiber reinforced cement mortars containing rice husk ash and nano-alumina. Constr. Build. Mater. 2016, 111, 429–439. [Google Scholar] [CrossRef]
- Alhozaimy, A.M.; Soroushian, P.; Mirza, F. Mechanical properties of polypropylene fiber reinforced concrete and the effects of pozzolanic materials. Cem. Concr. Compos. 1996, 18, 85–92. [Google Scholar] [CrossRef]
- Mohseni, E.; Ranjbar, M.M.; Yazdi, A.; Hosseiny, S.S.; Roshandel, E. The effects of silicon dioxide, iron (III) oxide and copper oxide nanomaterials on the properties of self-compacting mortar containing fly ash. Mag. Concr. Res. 2015, 67, 1112–1124. [Google Scholar] [CrossRef]
- Du, H.; Du, S.; Liu, X. Effect of nano-silica on the mechanical and transport properties of lightweight concrete. Constr. Build. Mater. 2015, 82, 114–122. [Google Scholar] [CrossRef]
- Sun, J.; Xu, Z.; Li, W.; Shen, X. Effect of Nano-SiO2 on the Early Hydration of Alite-Sulphoaluminate Cement. Nanomaterials 2017, 7, 102. [Google Scholar] [CrossRef] [PubMed]
- Madandoust, R.; Mohseni, E.; Mousavi, S.Y.; Namnevis, M. An experimental investigation on the durability of self-compacting mortar containing nano-SiO2, nano-Fe2O3 and nano-CuO. Constr. Build. Mater. 2015, 86, 44–50. [Google Scholar] [CrossRef]
- Mohseni, E.; Miyandehi, B.M.; Yang, J.; Yazdi, A. Single and combined effects of nano-SiO2, nano-Al2O3 and nano-TiO2 on the mechanical, rheological and durability properties of self-compacting mortar containing fly ash. Constr. Build. Mater. 2015, 84, 331–340. [Google Scholar] [CrossRef]
- Mohseni, E.; Naseri, F.; Amjadi, R.; Khotbehsara, M.M.; Ranjbar, M.M. Microstructure and durability properties of cement mortars containing nano-TiO2 and rice husk ash. Constr. Build. Mater. 2016, 114, 656–664. [Google Scholar] [CrossRef]
- Yang, J.; Mohseni, E.; Behforouz, B.; Khotbehsara, M.M. An experimental investigation into the effects of Cr2O3 and ZnO2 nanoparticles on the mechanical properties and durability of self-compacting mortar. Int. J. Mater. Res. 2015, 106, 886–892. [Google Scholar] [CrossRef]
- Li, W.; Ji, W.; Isfahani, F.T.; Wang, Y.; Li, G.; Xing, F. Nano-Silica Sol-Gel and Carbon Nanotube Coupling Effect on the Performance of Cement-Based Materials. Nanomaterials 2017, 7, 185. [Google Scholar] [CrossRef] [PubMed]
- Mohseni, E.; Tsavdaridis, K. Effect of Nano-Alumina on Pore Structure and Durability of Class F Fly Ash Self-Compacting Mortar. Am. J. Eng. Appl. Sci. 2016, 9, 323–333. [Google Scholar] [CrossRef]
- Rashad, A.M. Effects of ZnO2, ZrO2, Cu2O3, CuO, CaCO3, SF, FA, cement and geothermal silica waste nanoparticles on properties of cementitious materials—A short guide for Civil Engineer. Constr. Build. Mater. 2013, 48, 1120–1133. [Google Scholar] [CrossRef]
- Nazari, A.; Riahi, S. Effects of CuO nanoparticles on compressive strength of self-compacting concrete. Sadhana 2011, 36, 371. [Google Scholar] [CrossRef]
- Khotbehsara, M.M.; Mohseni, E.; Yazdi, A.; Sarker, P.; Ranjbar, M.M. Effect of nano-CuO and fly ash on the properties of self-compacting mortar. Constr. Build. Mater. 2015, 94, 758–766. [Google Scholar] [CrossRef]
- Nazari, A.; Rafieipour, M.H.; Riahi, S. The effects of CuO nanoparticles on properties of self compacting concrete with GGBFS as binder. Mater. Res. 2011, 14, 307–316. [Google Scholar] [CrossRef]
- Nazari, A.; Khalaj, G.; Riahi, S.; Bohlooli, H.; Kaykha, M.M. Prediction total specific pore volume of geopolymers produced from waste ashes by ANFIS. Ceram. Int. 2012, 38, 3111–3120. [Google Scholar] [CrossRef]
- Zapata-Ordúz, L.E.; Portela, G.; Suárez, O.M. Weibull statistical analysis of splitting tensile strength of concretes containing class F fly ash, micro/nano-SiO2. Ceram. Int. 2014, 40, 7373–7388. [Google Scholar] [CrossRef]
- Cüneyt Aydin, A.; Tortum, A.; Yavuz, M. Prediction of concrete elastic modulus using adaptive neuro-fuzzy inference system. Civ. Eng. Environ. Syst. 2006, 23, 295–309. [Google Scholar] [CrossRef]
- Na, U.J.; Park, T.W.; Feng, M.Q.; Chung, L. Neuro-fuzzy application for concrete strength prediction using combined non-destructive tests. Mag. Concr. Res. 2009, 61, 245–256. [Google Scholar] [CrossRef]
- Neshat, M.; Adeli, A.; Masoumi, A.; Sargolzae, M. A comparative study on ANFIS and fuzzy expert system models for concrete mix design. Int. J. Comput. Sci. Issues 2011, 8, 196–210. [Google Scholar]
- Nazari, A.; Riahi, S. Experimental investigations and ANFIS prediction of water absorption of geopolymers produced by waste ashes. J. Non-Cryst. Solids 2012, 358, 40–46. [Google Scholar] [CrossRef]
- Ahmadi-Nedushan, B. Prediction of elastic modulus of normal and high strength concrete using ANFIS and optimal nonlinear regression models. Constr. Build. Mater. 2012, 36, 665–673. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, L.-N.; Ji, X. Prediction of concrete compressive strength: Research on hybrid models genetic based algorithms and ANFIS. Adv. Eng. Softw. 2014, 67, 156–163. [Google Scholar] [CrossRef]
- Vakhshouri, B.; Nejadi, S. Predicition Of Compressive Strength In Light-Weight Self-Compacting Concrete By ANFIS Analytical Model. Arch. Civ. Eng. 2015, 61, 53. [Google Scholar] [CrossRef]
- Çevik, A.; Kuroglu, A.E.; Bilgehan, M.; Gulsan, M.E.; Albegmprli, H.M. Support vector machines in structural engineering: A review. J. Civ. Eng. Manag. 2015, 21, 261–281. [Google Scholar] [CrossRef]
- Naseri, F.; Jafari, F.; Mohseni, E.; Tang, W.C.; Feizbakhsh, S.; Khatibinia, M. Experimental observations and SVM-based prediction of properties of polypropylene fibres reinforced self-compacting composites incorporating nano-CuO. Constr. Build. Mater. 2017, 143, 589–598. [Google Scholar] [CrossRef]
- Khatibinia, M.; Feizbakhsh, A.; Mohseni, E.; Ranjbar, M.M. Modeling mechanical strength of self–compacting mortar containing nanoparticles using wavelet–based support vector machine. Comput. Concr. 2016, 18, 1065–1082. [Google Scholar]
- Shalev-Shwartz, S.; Singer, Y.; Srebro, N.; Cotter, A. Pegasos: Primal estimated sub-gradient solver for SVM. Math. Program. 2011, 127, 3–30. [Google Scholar] [CrossRef]
- Abraham, A. Adaptation of Fuzzy Inference System Using Neural Learning. In Fuzzy Systems Engineering: Theory and Practice; Nedjah, N., Mourelle, L.D.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 53–83. [Google Scholar]
- Jang, J.-S.R. Fuzzy modeling using generalized neural networks and Kalman filter algorithm. In Proceedings of the Ninth National Conference on Artificial Intelligence, Anaheim, CA, USA, 14–19 July 1991; AAAI Press: Anaheim, CA, USA, 1991; Volume 2, pp. 762–767. [Google Scholar]
- Bahadori, H.; Hosseini, P. Reduction of cement consumption by the aid of silica nano-particles (investigation on concrete properties). J. Civ. Eng. Manag. 2012, 18, 416–425. [Google Scholar] [CrossRef]
- Takác, M.; Bijral, A.; Richtarik, P.; Srebro, N. Mini-Batch Primal and Dual Methods for SVMs. Cornell Univ. Libr. 2013, 3, 1022–1030. [Google Scholar]
- Ramezanianpour, A.A. Metakaolin. In Cement Replacement Materials: Properties, Durability, Sustainability; Springer: Berlin/Heidelberg, Germany, 2014; pp. 225–255. [Google Scholar]
- Poon, C.S.; Lam, L.; Kou, S.C.; Wong, Y.L.; Wong, R. Rate of pozzolanic reaction of metakaolin in high-performance cement pastes. Cem. Concr. Res. 2001, 31, 1301–1306. [Google Scholar] [CrossRef]
- Anwar Hossain, K.M. Properties of volcanic pumice based cement and lightweight concrete. Cem. Concr. Res. 2004, 34, 283–291. [Google Scholar] [CrossRef]
- Kabay, N.; Tufekci, M.M.; Kizilkanat, A.B.; Oktay, D. Properties of concrete with pumice powder and fly ash as cement replacement materials. Constr. Build. Mater. 2015, 85, 1–8. [Google Scholar] [CrossRef]
- Mohseni, E.; Tang, W.; Cui, H. Chloride Diffusion and Acid Resistance of Concrete Containing Zeolite and Tuff as Partial Replacements of Cement and Sand. Materials 2017, 10, 372. [Google Scholar] [CrossRef] [PubMed]
- Wild, S.; Khatib, J.M. Portlandite consumption in metakaolin cement pastes and mortars. Cem. Concr. Res. 1997, 27, 137–146. [Google Scholar] [CrossRef]
- Bentz, D.P.; Garboczi, E.J. Simulation Studies of the Effects of Mineral Admixtures on the Cement Paste-Aggregate Interfacial Zone (SP-105). ACI Mater. J. 1991, 88, 518–529. [Google Scholar]
- Karahan, O.; Atiş, C.D. The durability properties of polypropylene fiber reinforced fly ash concrete. Mater. Des. 2011, 32, 1044–1049. [Google Scholar] [CrossRef]
- Tanyildizi, H. Statistical analysis for mechanical properties of polypropylene fiber reinforced lightweight concrete containing silica fume exposed to high temperature. Mater. Des. 2009, 30, 3252–3258. [Google Scholar] [CrossRef]
- Sanchez, F.; Sobolev, K. Nanotechnology in concrete—A review. Constr. Build. Mater. 2010, 24, 2060–2071. [Google Scholar] [CrossRef]
- Mohseni, E.; Saadati, R.; Kordbacheh, N.; Parpinchi, Z.S.; Tang, W.C. Engineering and microstructural assessment of fibre-reinforced self-compacting concrete containing recycled coarse aggregate. J. Clean. Prod. 2017, 168, 605–613. [Google Scholar] [CrossRef]
- Gong, A.-M.; Sun, Y.; Peng, Y.-L. Experimental study of effect of polypropylene fiber on concrete workability. J. Build. Mater. 2007, 10, 488–492. [Google Scholar]
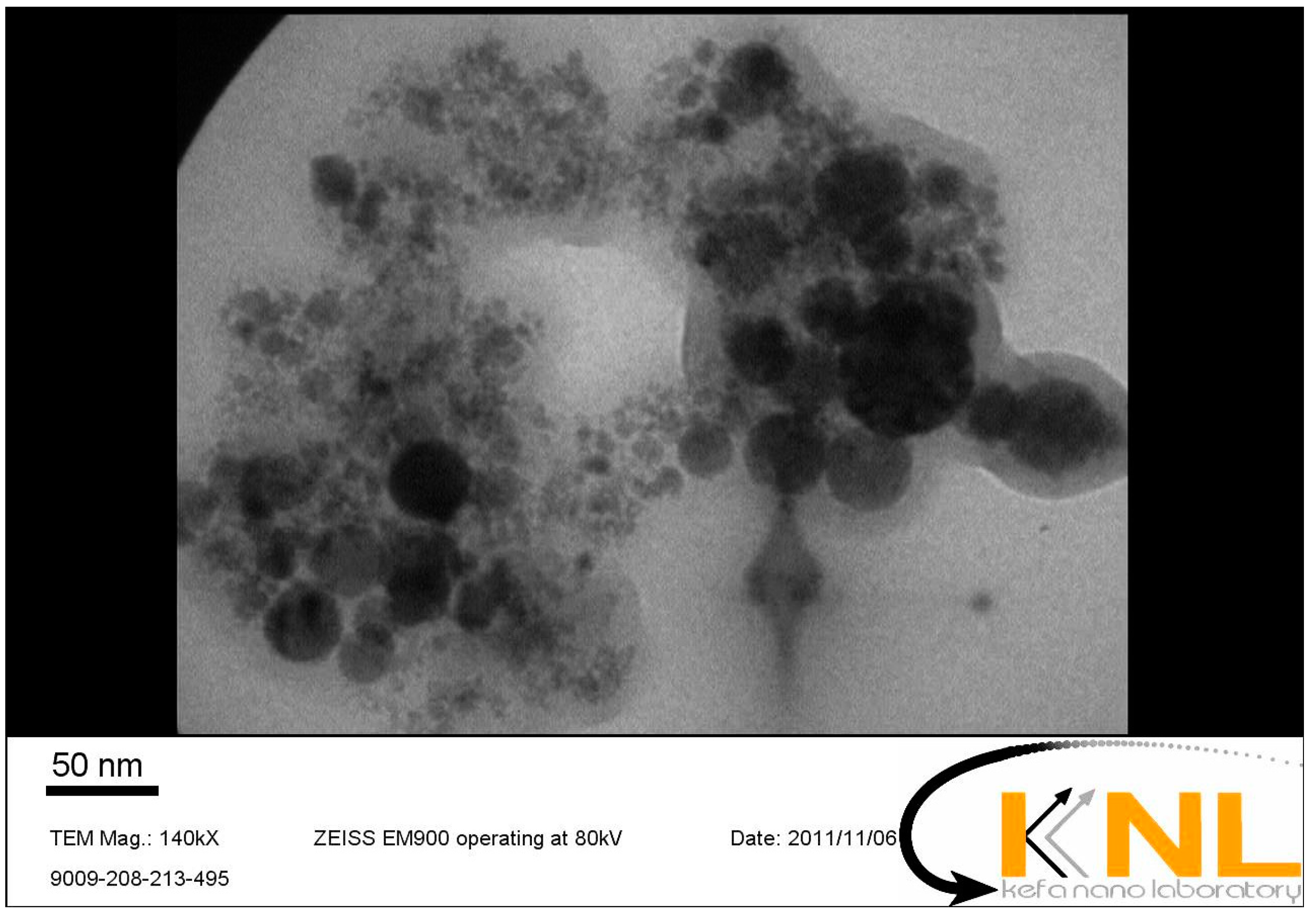



| Chemical Analysis (%) | Cement | MK |
|---|---|---|
| SiO2 | 21.75 | 52.1 |
| Al2O3 | 5.15 | 43.8 |
| Fe2O3 | 3.23 | 2.6 |
| CaO | 63.75 | 0.2 |
| MgO | 1.15 | 0.21 |
| SO3 | 1.95 | 0 |
| K2O | 0.56 | 0.32 |
| Na2O | 0.33 | 0.11 |
| L.O.I | 2.08 | 0.99 |
| Surface area (BET) (m2/g) | 0.31 | 2.54 |
| Specific gravity | 3.15 | 2.6 |
| Nanoparticles | Average Diameter (nm) | Specific Surface Area (m2/g) | Purity (%) |
|---|---|---|---|
| nano-CuO | 20 ± 3 | 200 | >99 |
| Unit weight (g/cm3) | 0.9–0.91 |
| Reaction with water | Hydrophobic |
| Tensile strength (MPa) | 300–400 |
| Elongation at break (%) | 100–600 |
| Melting point (°C) | 175 |
| Thermal conductivity (W/m/K) | 0.12 |
| Length (mm) | 6 |
| Diameter (μm) | 20 |
| Sample ID | Cement (kg/m3) | MK (kg/m3) | NC (kg/m3) | PP (kg/m3) | Water (kg/m3) | Sand (kg/m3) | SP (kg/m3) |
|---|---|---|---|---|---|---|---|
| CO | 450 | 0 | 0 | 0 | 220 | 1430 | 0.9 |
| MK10 | 405 | 45 | 0 | 0 | 220 | 1415 | 1.9 |
| MK10NC1 | 400.5 | 45 | 4.5 | 0 | 220 | 1410 | 1.9 |
| MK10NC2 | 396 | 45 | 9 | 0 | 220 | 1400 | 1.9 |
| MK10NC3 | 391.5 | 45 | 13.5 | 0 | 220 | 1395 | 1.9 |
| MK20 | 360 | 90 | 0 | 0 | 220 | 1400 | 2.5 |
| MK20NC1 | 355.5 | 90 | 4.5 | 0 | 220 | 1390 | 2.5 |
| MK20NC2 | 351 | 90 | 9 | 0 | 220 | 1385 | 2.5 |
| MK20NC3 | 346.5 | 90 | 13.5 | 0 | 220 | 1380 | 2.5 |
| MK30 | 315 | 135 | 0 | 0 | 220 | 1380 | 3.5 |
| MK30NC1 | 310.5 | 135 | 4.5 | 0 | 220 | 1375 | 3.5 |
| MK30NC2 | 306 | 135 | 9 | 0 | 220 | 1370 | 3.5 |
| MK30NC3 | 301.5 | 135 | 13.5 | 0 | 220 | 1360 | 3.5 |
| PP | 450 | 0 | 0 | 1.35 | 220 | 1430 | 1.75 |
| PP-MK10 | 405 | 45 | 0 | 1.35 | 220 | 1415 | 2.75 |
| PP-MK10NC1 | 400.5 | 45 | 4.5 | 1.35 | 220 | 1410 | 2.75 |
| PP-MK10NC2 | 396 | 45 | 9 | 1.35 | 220 | 1400 | 2.75 |
| PP-MK10NC3 | 391.5 | 45 | 13.5 | 1.35 | 220 | 1395 | 2.75 |
| PP-MK20 | 360 | 90 | 0 | 1.35 | 220 | 1400 | 3.75 |
| PP-MK20NC1 | 355.5 | 90 | 4.5 | 1.35 | 220 | 1390 | 3.75 |
| PP-MK20NC2 | 351 | 90 | 9 | 1.35 | 220 | 1385 | 3.75 |
| PP-MK20NC3 | 346.5 | 90 | 13.5 | 1.35 | 220 | 1380 | 3.75 |
| PP-MK30 | 315 | 135 | 0 | 1.35 | 220 | 1380 | 4.25 |
| PP-MK30NC1 | 310.5 | 135 | 4.5 | 1.35 | 220 | 1375 | 4.25 |
| PP-MK30NC2 | 306 | 135 | 9 | 1.35 | 220 | 1370 | 4.25 |
| PP-MK30NC3 | 301.5 | 135 | 13.5 | 1.35 | 220 | 1360 | 4.25 |
| ANFIS | R2 Values for: Training Set, Testing Set, and Validation Set | |||
| Data Set | Training Set | Testing Set | Validation Set | |
| Compressive strength | R2 | 1 | 0.90 | 0.94 |
| RRMSE | 2.96 × 10−6 | 9.48 × 10−4 | 4.8540 × 10−4 | |
| MAPE | 0.046 | 0.41 | 0.08 | |
| Flexural strength | R2 | 1 | 0.96 | 0.94 |
| RRMSE | 6.98 × 10−3 | 0.016 | 0.0068 | |
| MAPE | 2.94 | 0.015 | 0.013 | |
| Water absorption | R2 | 1 | 0.93 | 0.97 |
| RRMSE | 1.18 × 10−5 | 0.0023 | 0.0025 | |
| MAPE | 0.004 | 1.27 | 1.58 | |
| ANFIS | The Relationship Between Predicted Values (y) and Experimental Data (x) | |||
| Data Set | Training Set | Testing Set | Validation Set | |
| Compressive strength | y = 0.99x + 0.01 | y = 0.99x + 0.23 | y = 0.96x + 1.3 | |
| Flexural strength | y = 0.99x + 0.002 | y = 1.04x − 0.37 | y = 0.99x + 0.01 | |
| Water absorption | y = 0.99x + 0.02 | y = 1.009x + 0.07 | y = 1.17x − 1.43 | |
| Pegasos | R2 Values for: Training Set, Testing Set, and Validation Set | |||
| Data Set | Training Set | Testing Set | ||
| Compressive strength | R2 | 0.96 | 0.9 | |
| RRMSE | 2.91 × 10−4 | 0.00052 | ||
| MAPE | 1.85 | 2.47 | ||
| flexural strength | R2 | 0.99 | 0.91 | |
| RRMSE | 0.0017 | 0.005 | ||
| MAPE | 1.07 | 3.31 | ||
| Water absorption | R2 | 0.96 | 0.9 | |
| RRMSE | 2.96 × 10−6 | 2.85 × 10−3 | ||
| MAPE | 0.00305 | 1.66 | ||
| Pegasos | The Relationship between Predicted Values (y) and Experimental Data (x) | |||
| Data Set | Training Set | Testing Set | ||
| Compressive strength | y = 0.91x + 4.23 | y = 0.78x + 10.41 | ||
| Flexural strength | y = 0.97x + 0.12 | y = 0.88x + 1.03 | ||
| Water absorption | y = 0.8x + 1.58 | y = 0.92x + 0.47 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghanei, A.; Jafari, F.; Khotbehsara, M.M.; Mohseni, E.; Tang, W.; Cui, H. Effect of Nano-CuO on Engineering and Microstructure Properties of Fibre-Reinforced Mortars Incorporating Metakaolin: Experimental and Numerical Studies. Materials 2017, 10, 1215. https://doi.org/10.3390/ma10101215
Ghanei A, Jafari F, Khotbehsara MM, Mohseni E, Tang W, Cui H. Effect of Nano-CuO on Engineering and Microstructure Properties of Fibre-Reinforced Mortars Incorporating Metakaolin: Experimental and Numerical Studies. Materials. 2017; 10(10):1215. https://doi.org/10.3390/ma10101215
Chicago/Turabian StyleGhanei, Amir, Faezeh Jafari, Mojdeh Mehrinejad Khotbehsara, Ehsan Mohseni, Waiching Tang, and Hongzhi Cui. 2017. "Effect of Nano-CuO on Engineering and Microstructure Properties of Fibre-Reinforced Mortars Incorporating Metakaolin: Experimental and Numerical Studies" Materials 10, no. 10: 1215. https://doi.org/10.3390/ma10101215







