A New Cluster Analysis-Marker-Controlled Watershed Method for Separating Particles of Granular Soils
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Setup and Image Acquisition
2.3. Image Post-Processing
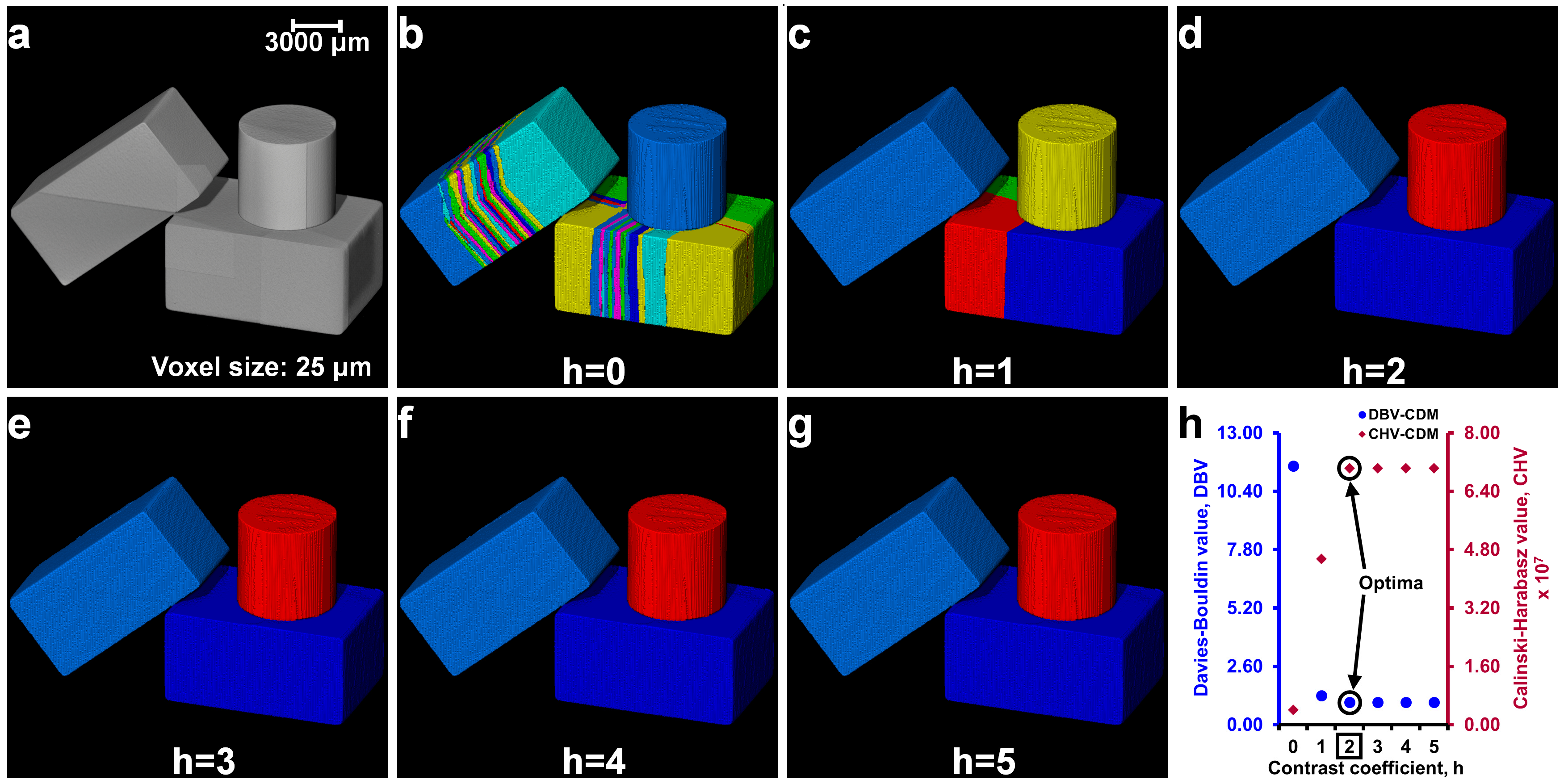
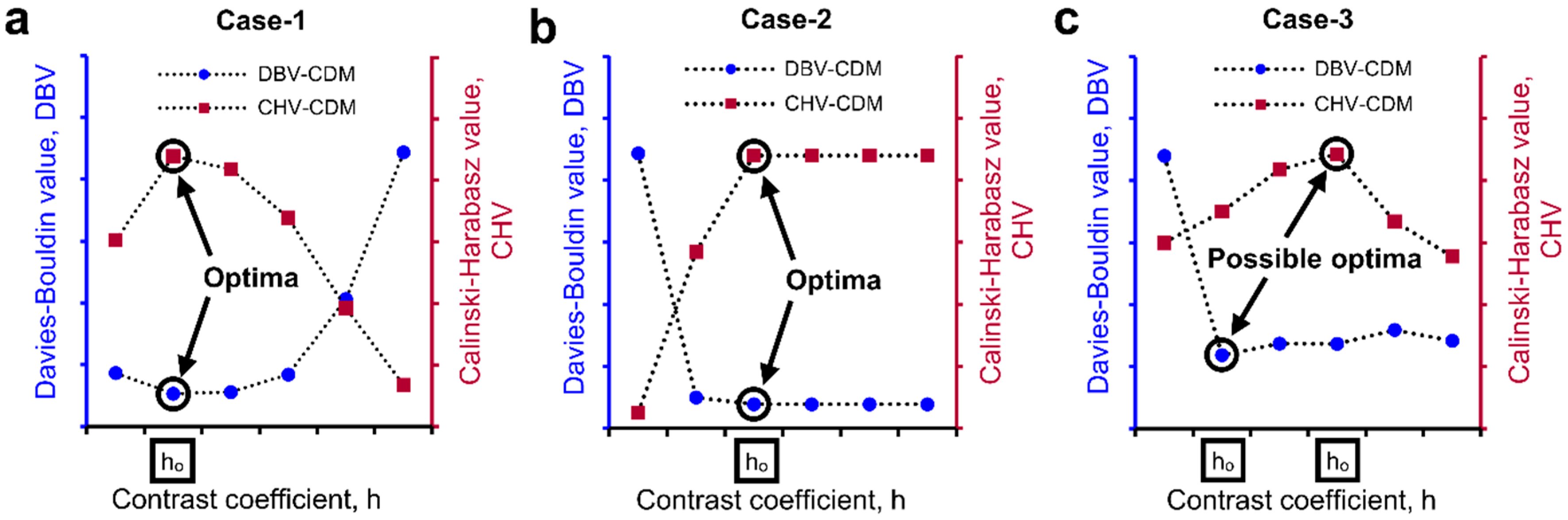
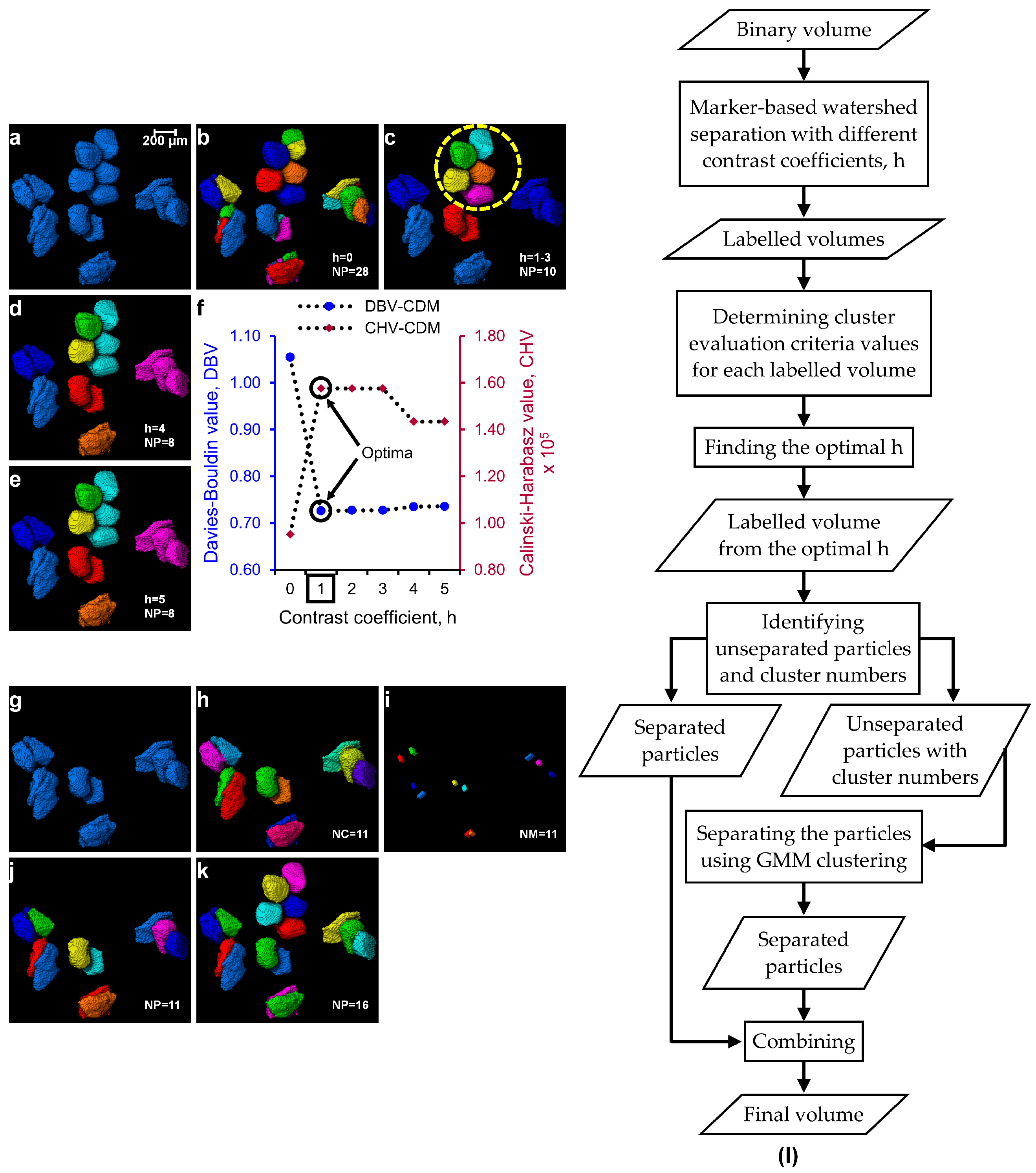
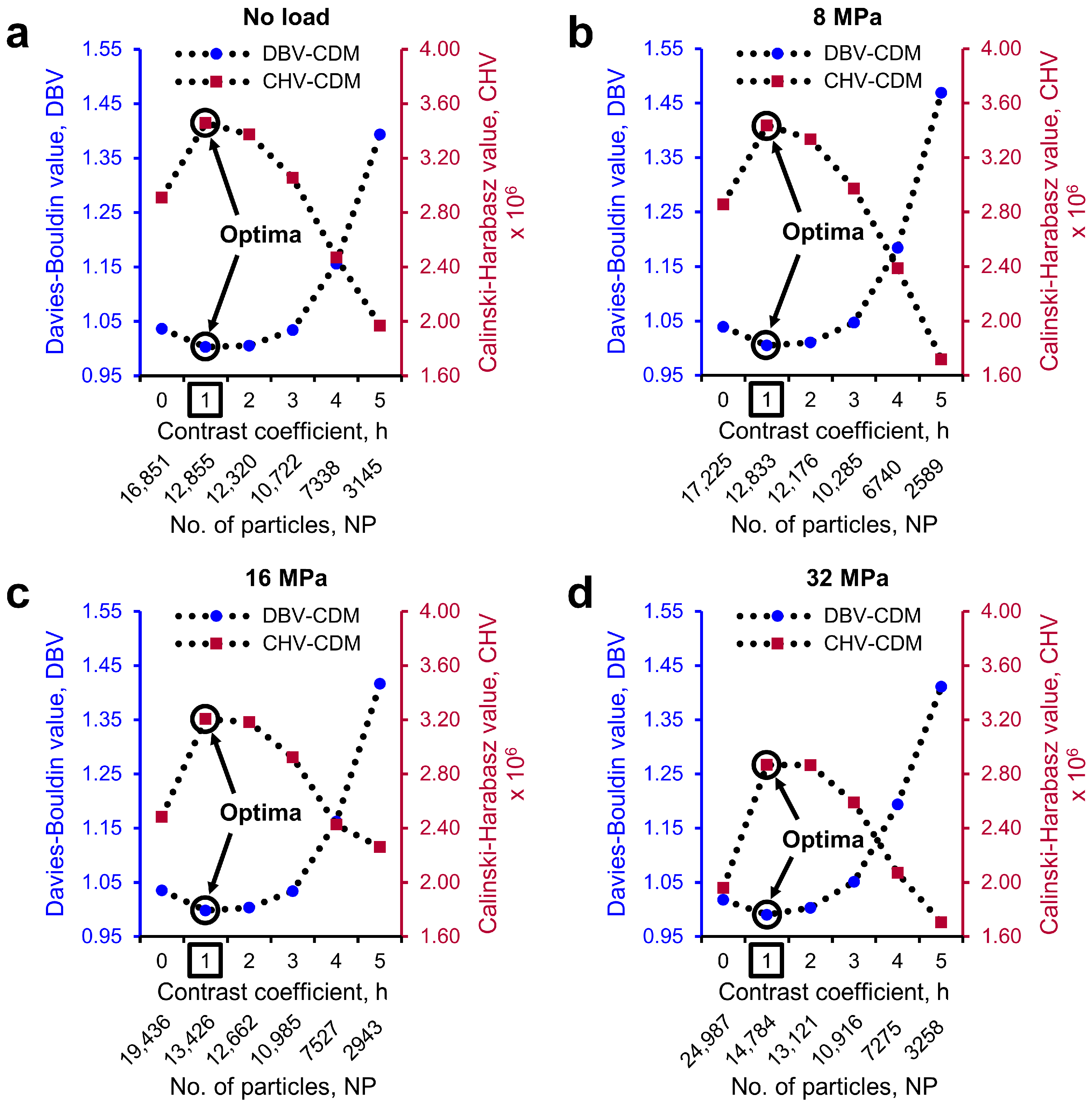
2.4. Determination of Optimal h-Maxima Contrast Value
2.5. Separation of Particles Using Clustering by Gaussian Mixture Models
3. Results and Discussion
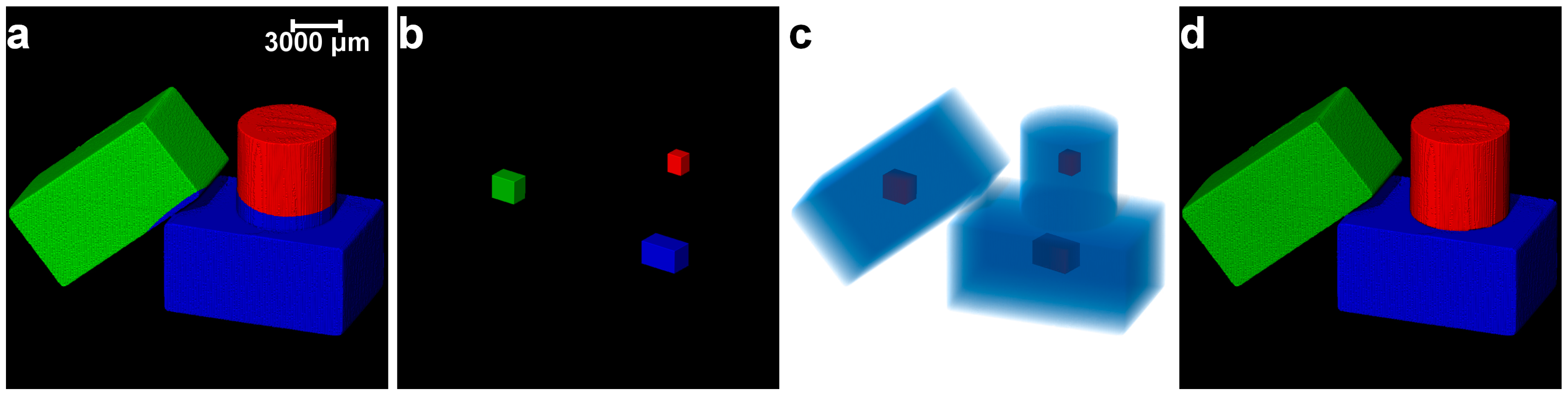
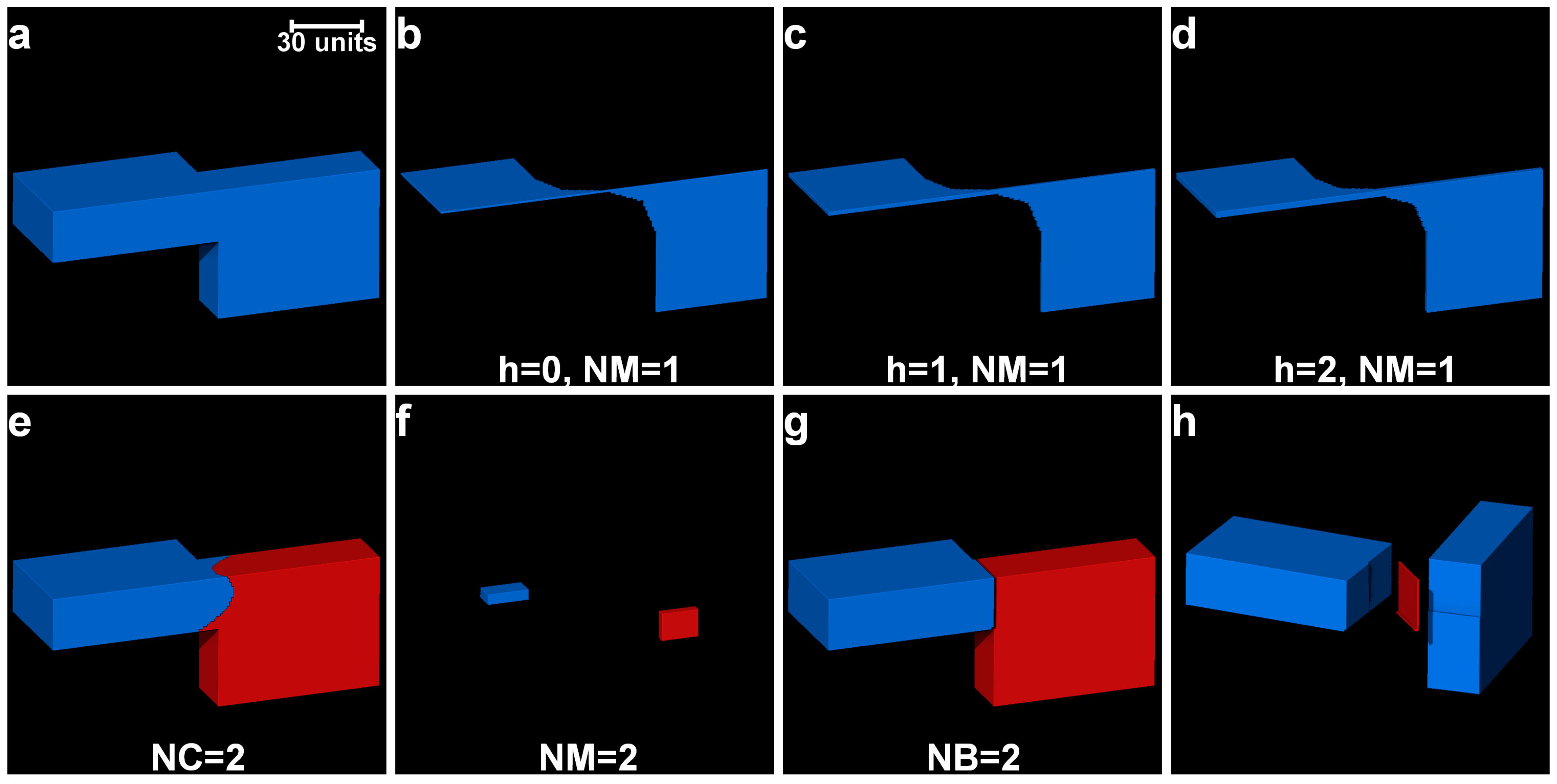
3.1. Separation of Particles Using the Routine Watershed Method
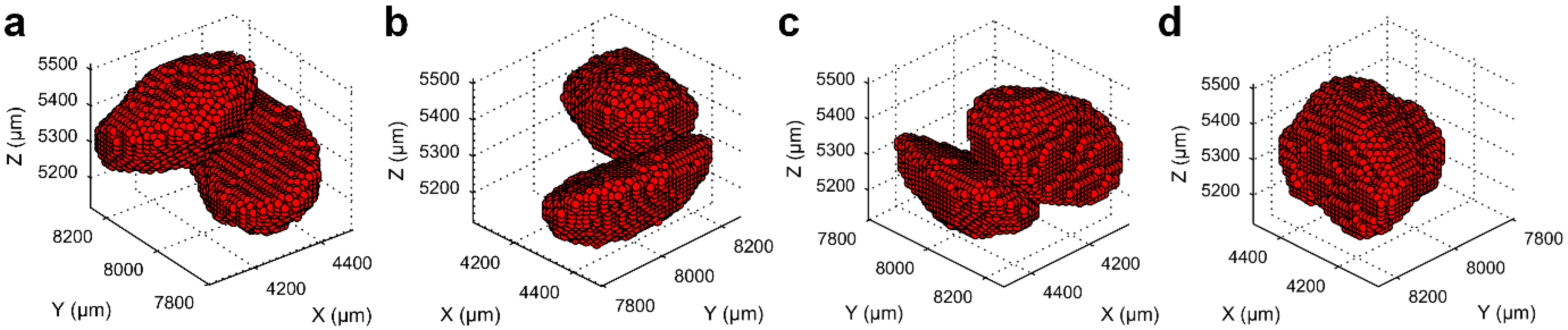
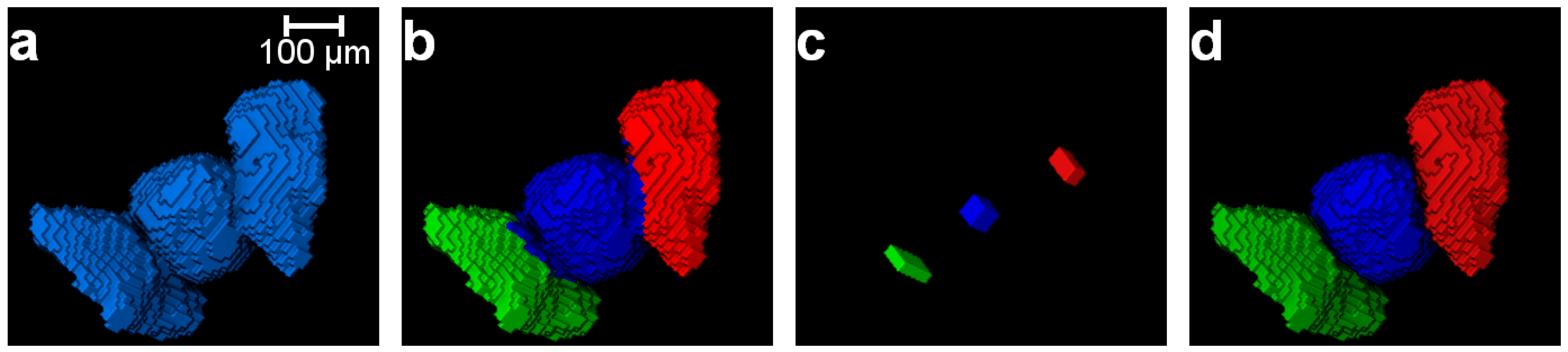
3.2. Separation of Particles Using the MPSM
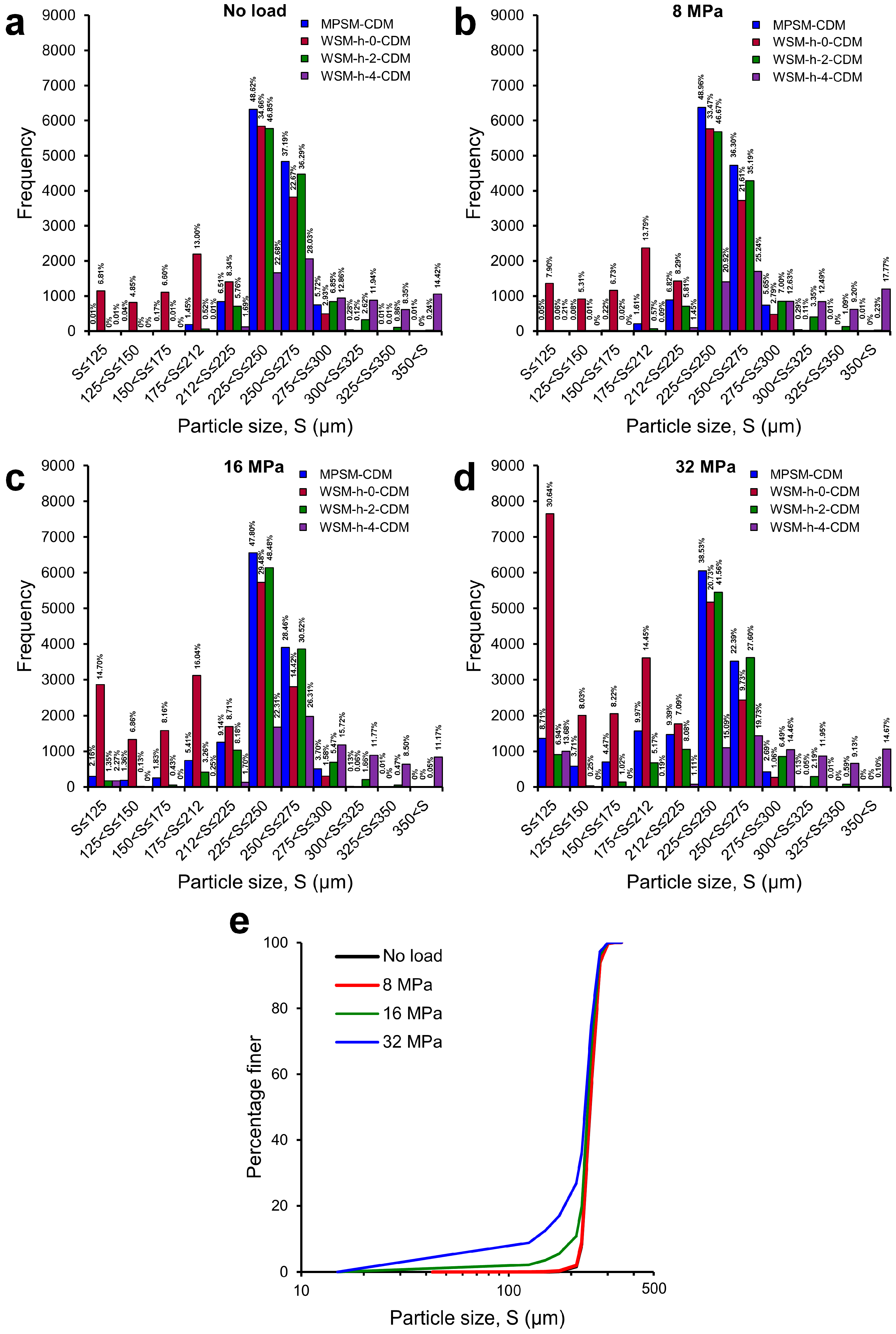
3.3. Particle Size Distributions
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fonseca, J.; O’Sullivan, C.; Coop, M.R.; Lee, P.D. Quantifying the evolution of soil fabric during shearing using scalar parameters. Géotechnique 2013, 63, 818–829. [Google Scholar] [CrossRef]
- Fonseca, J.; O’Sullivan, C.; Coop, M.R.; Lee, P.D. Quantifying the evolution of soil fabric during shearing using directional parameters. Géotechnique 2013, 63, 487–499. [Google Scholar] [CrossRef]
- Alshibli, K.A.; Batiste, S.N.; Sture, S. Strain localization in sand: Plane strain versus triaxial compression. J. Geotech. Geoenviron. Eng. 2003, 129, 483–494. [Google Scholar] [CrossRef]
- Druckrey, A.M.; Alshibli, K.A.; Al-Raoush, R.I. 3D characterization of sand particle-to-particle contact and morphology. Comput. Geotech. 2016, 74, 26–35. [Google Scholar] [CrossRef]
- Desrues, J.; Chambon, R.; Mokni, M.; Mazerolle, F. Void ratio evolution inside shear bands in triaxial sand specimens studied by computed tomography. Géotechnique 1996, 46, 529–546. [Google Scholar] [CrossRef]
- Fonseca, J.; O’Sullivan, C.; Coop, M.R.; Lee, P.D. Non-invasive characterization of particle morphology of natural sands. Soils Found. 2012, 52, 712–722. [Google Scholar] [CrossRef]
- Higo, Y.; Oka, F.; Sato, T.; Matsushima, Y.; Kimoto, S. Investigation of localized deformation in partially saturated sand under triaxial compression using micro focus X-ray CT with digital image correlation. Soils Found. 2013, 53, 181–198. [Google Scholar] [CrossRef]
- Hall, S.A.; Bornert, M.; Desrues, J.; Pannier, Y.; Lenoir, N.; Viggiani, G.; Bésuelle, P. Discrete and continuum analysis of localised deformation in sand using X-ray uCT and volumetric digital image correlation. Géotechnique 2010, 60, 315–322. [Google Scholar] [CrossRef]
- Al Mahbub, A.; Haque, A. X-ray computed tomography imaging of the microstructure of sand particles subjected to high pressure one-dimensional compression. Materials 2016, 9, 890. [Google Scholar] [CrossRef] [PubMed]
- Cil, M.B.; Alshibli, K.A. 3D evolution of sand fracture under 1D compression. Géotechnique 2014, 64, 351–364. [Google Scholar] [CrossRef]
- Alshibli, K.A.; Hasan, A. Spatial variation of void ratio and shear band thickness in sand using X-ray computed tomography. Géotechnique 2008, 58, 249–257. [Google Scholar] [CrossRef]
- Hasan, A.; Alshibli, K.A. Experimental assessment of 3D particle-to-particle interaction within sheared sand using synchrotron microtomography. Géotechnique 2010, 60, 369–379. [Google Scholar] [CrossRef]
- Beucher, S.; Lantuéjoul, C. Use of watersheds in contour detection. In Proceedings of the International Workshop on Image Processing, Real-Time Edge and Motion Detection/Estimation, Rennes, France, 17–21 September 1979. [Google Scholar]
- Faessel, M.; Jeulin, D. Segmentation of 3D microtomographic images of granular materials with the stochastic watershed. J. Microsc. 2010, 239, 17–31. [Google Scholar] [CrossRef] [PubMed]
- Meyer, F.; Beucher, S. Morphological segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis: Principles and Applications, 2nd ed.; Corrected 2nd printing; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-642-07696-1. [Google Scholar] [CrossRef]
- Pal, N.R.; Pal, S.K. A review on image segmentation techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
- Wang, L.B.; Frost, J.D.; Lai, J.S. Three-dimensional digital representation of granular material microstructure from X-ray tomography imaging. J. Comput. Civ. Eng. 2004, 18, 28–35. [Google Scholar] [CrossRef]
- Alshibli, K.A.; Druckrey, A.M.; Al-Raoush, R.I.; Weiskittel, T.; Lavrik, N.V. Quantifying morphology of sands using 3D imaging. J. Mater. Civ. Eng. 2015, 27. [Google Scholar] [CrossRef]
- Otsu, N. A thresholding selection method from grayscale histogram. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- FEI Visualizations Sciences Group. Avizo 9.1.1, FEI Visualizations Sciences Group: Hillsboro, OR, USA, 2016.
- MathWorks. MATLAB 2016a,b, MathWorks: Natick, MA, USA, 2016.
- McLachlan, G.; Peel, D. Finite Mixture Models; John Wiley & Sons, Inc.: New York, NY, USA, 2000; ISBN 0-471-00626-2. [Google Scholar]
- Kanatani, K.-I. Distribution of directional data and fabric tensors. Int. J. Eng. Sci. 1984, 22, 149–164. [Google Scholar] [CrossRef]
- Kenley, P.R. Brighton Group-Geology. In Engineering Geology of Melbourne, Proceedings of the Seminar on Engineering Geology of Melbourne, Melbourne, Victoria, Australia, 16 September 1992; Peck, W.A., Neilson, J.L., Olds, R.J., Seddon, K.D., Eds.; Balkema: Rotterdam, The Netherlands; pp. 191–196. ISBN 90-5410-0834.
- AS 1152-1993. Specification for Test Sieves; Standards Australia. 1993. Available online: https://www-saiglobal-com.ezproxy.lib.monash.edu.au/online/autologin.asp (accessed on 30 March 2016).
- AS 1289.6.6.1-1998. Methods of Testing Soils for Engineering Purposes: Method 6.6.1- Soil Strength and Consolidation Tests- Determination of the One-Dimensional Consolidation Properties of a Soil- Standard Method; Standards Australia. 1998. Available online: https://www-saiglobal-com.ezproxy.lib.monash.edu.au/online/Script/OpenDoc.asp?name=AS+1289%2E6%2E6%2E1%2D1998&path=https%3A%2F%2Fwww%2Esaiglobal%2Ecom%2FPDFTemp%2Fosu%2D2017%2D03%2D01%2F9773910904%2Fs661%2Epdf&docn=stds000021517 (accessed on 1 March 2016).
- ASTM D2435/D2435M-11. Standard Test Methods for One-Dimensional Consolidation Properties of Soils Using Incremental Loading; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Deben UK Ltd. CT5000, Deben UK Ltd.: Woolpit, UK, 2013.
- Deben UK Ltd. MICROTEST (V6.13), Deben UK Ltd.: Woolpit, UK, 2013.
- Xradia. XMReconstructor-Cone Beam-10, Xradia: Pleasanton, CA, USA, 2011.
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Pun, T. Entropic thresholding, a new approach. Comput. Graph. Image Process. 1981, 16, 210–239. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Tsai, W.H. Moment-preserving thresholding: A new approach. Comput. Vis. Graph. Image Process 1985, 29, 377–393. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95442-2. [Google Scholar] [CrossRef]







| Percentage of Length | No. of Markers | No. of Separated Particles (No. of Wrong Separations) | Percentage of Length | No. of Markers | No. of Separated Particles (No. of Wrong Separations) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 15 | 3 | 3 |
| 2 | 0 | 0 | 17.5 | 3 | 3 |
| 3 | 2 | 2 | 20 | 3 | 3 |
| 4 | 3 | 3 (1) | 25 | 3 | 3 |
| 5 | 3 | 3 (1) | 30 | 3 | 3 |
| 6 | 3 | 3 (1) | 35 | 3 | 3 |
| 7 | 3 | 3 (1) | 40 | 3 | 3 |
| 8 | 3 | 3 | 50 | 3 | 3 |
| 9 | 3 | 3 | 60 | 3 | 3 |
| 10 | 3 | 3 | 70 | 3 | 3 |
| 12.5 | 3 | 3 | 80 | 1 | 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.F.; Haque, A. A New Cluster Analysis-Marker-Controlled Watershed Method for Separating Particles of Granular Soils. Materials 2017, 10, 1195. https://doi.org/10.3390/ma10101195
Alam MF, Haque A. A New Cluster Analysis-Marker-Controlled Watershed Method for Separating Particles of Granular Soils. Materials. 2017; 10(10):1195. https://doi.org/10.3390/ma10101195
Chicago/Turabian StyleAlam, Md Ferdous, and Asadul Haque. 2017. "A New Cluster Analysis-Marker-Controlled Watershed Method for Separating Particles of Granular Soils" Materials 10, no. 10: 1195. https://doi.org/10.3390/ma10101195
APA StyleAlam, M. F., & Haque, A. (2017). A New Cluster Analysis-Marker-Controlled Watershed Method for Separating Particles of Granular Soils. Materials, 10(10), 1195. https://doi.org/10.3390/ma10101195





