The Dynamic Response and Vibration of Functionally Graded Carbon Nanotube-Reinforced Composite (FG-CNTRC) Truncated Conical Shells Resting on Elastic Foundations
Abstract
1. Introduction
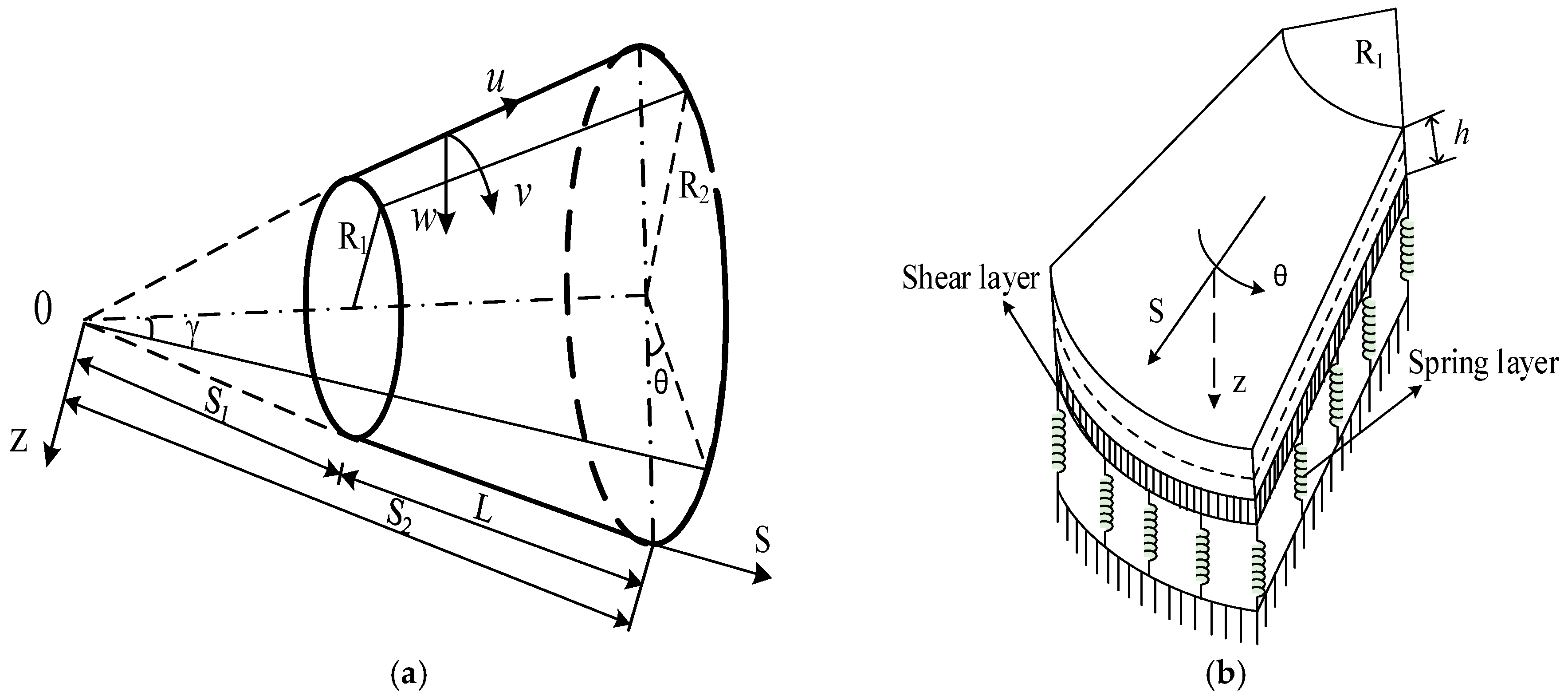
2. Formulation of the Problem
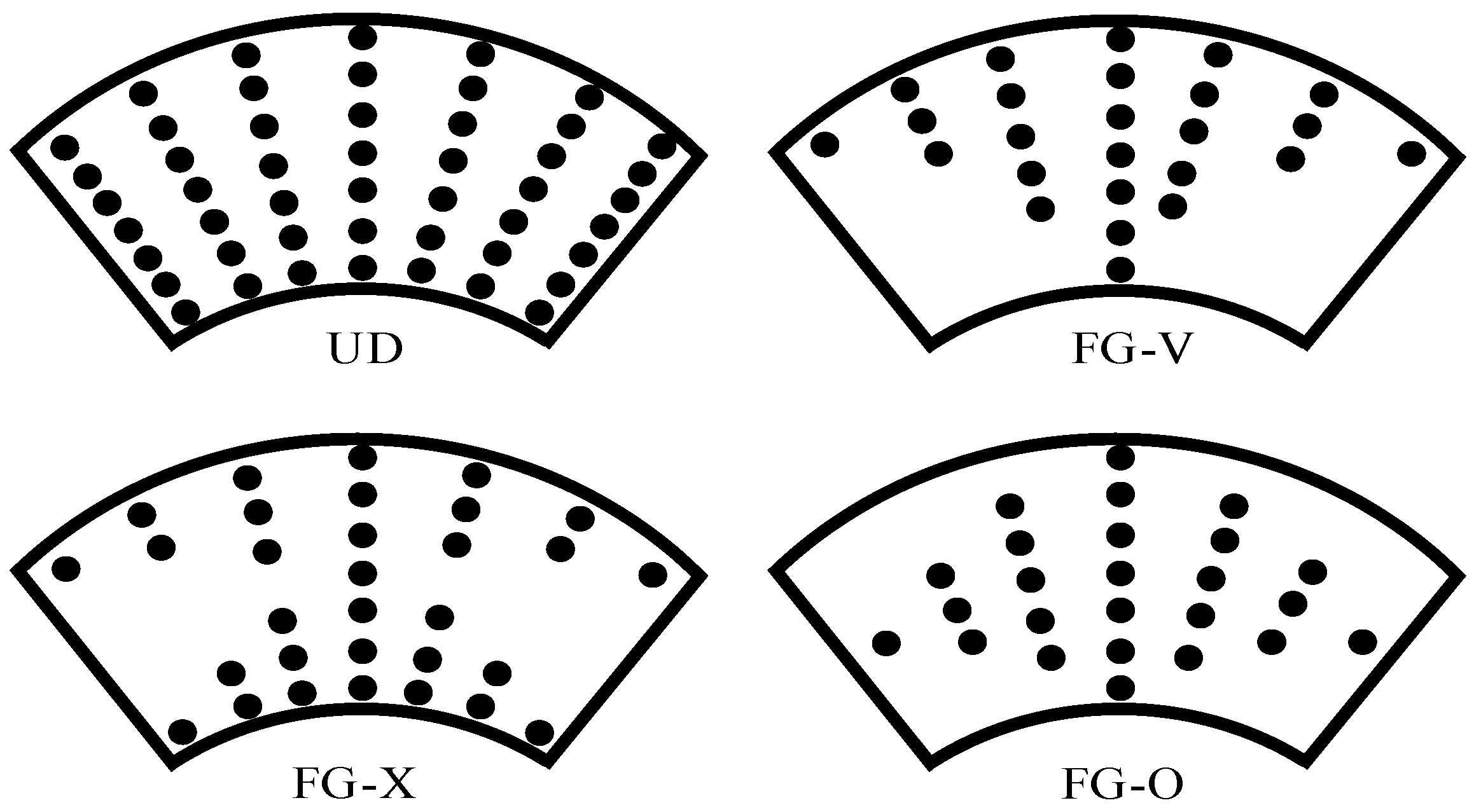
2.1. Determination of the Elastic Modules of CNTRCs and FG-CNTRC
2.2. Analytical Modeling of Elastic Medium
2.3. Basic Formulation of the FG-CNTRC Truncated Conical Shells Surrounded by Elastic Foundations
2.4. The Solution of Basic Equations
2.5. Vibration Analysis
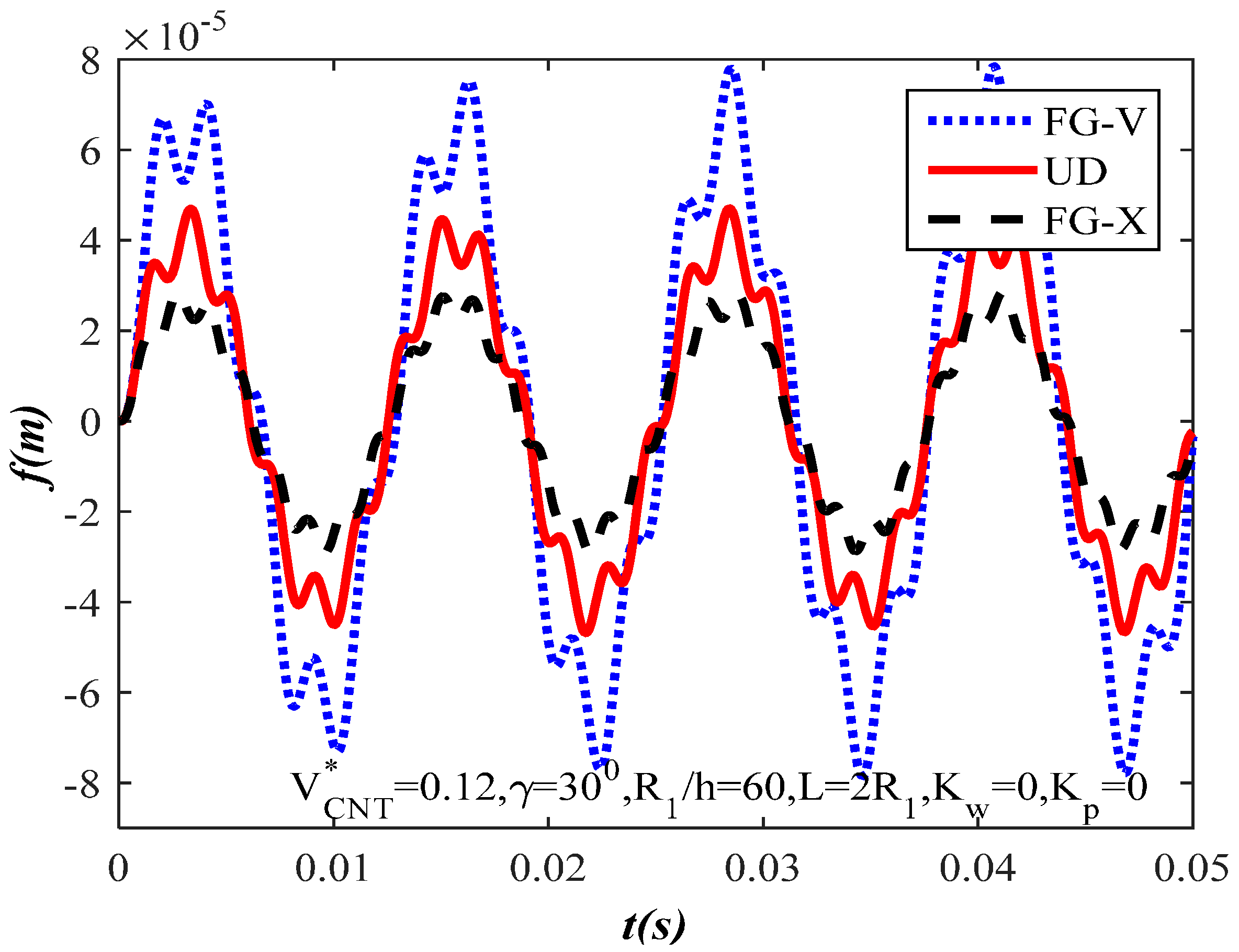
3. Numerical Results and Discussion
3.1. Validation
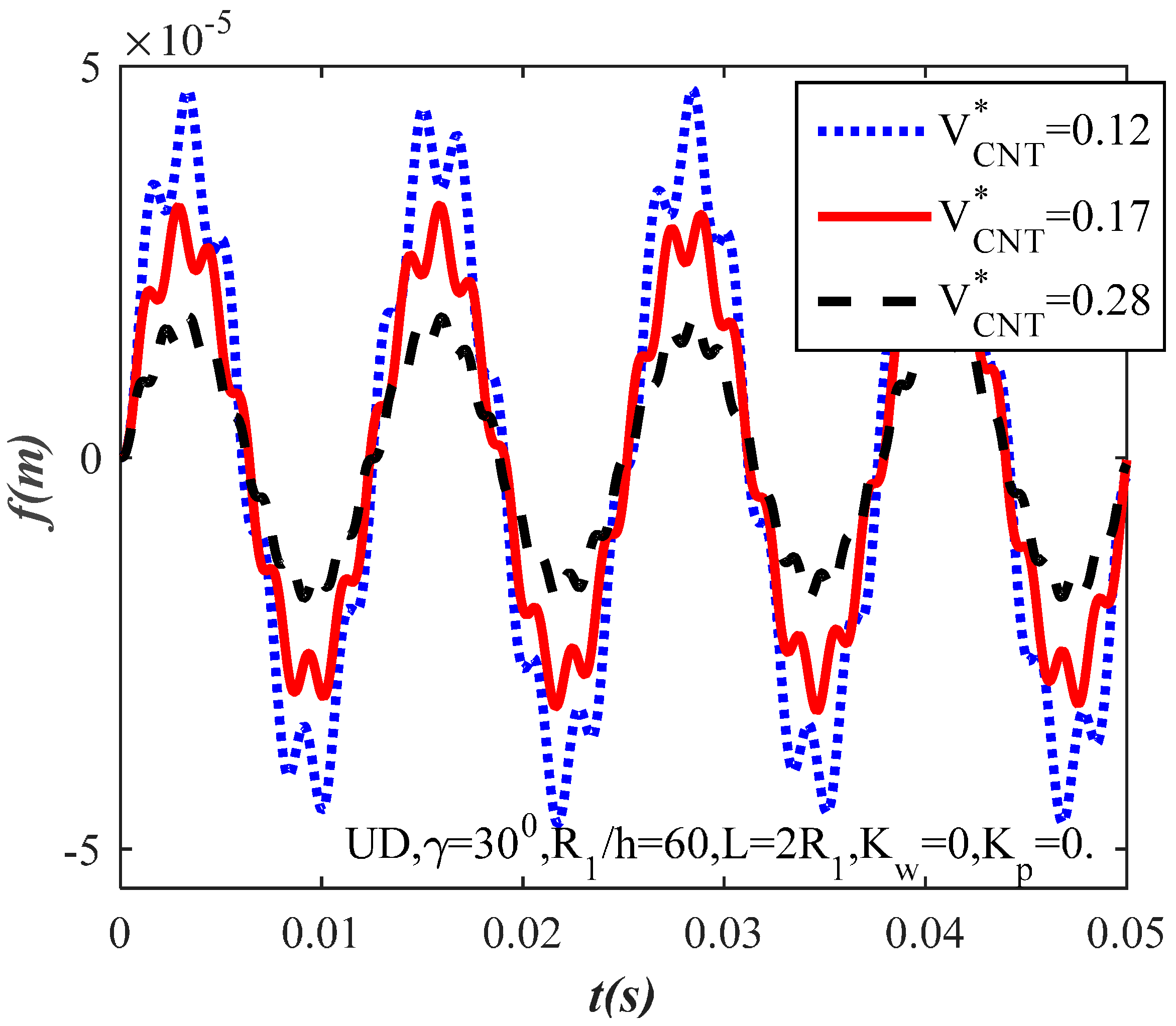
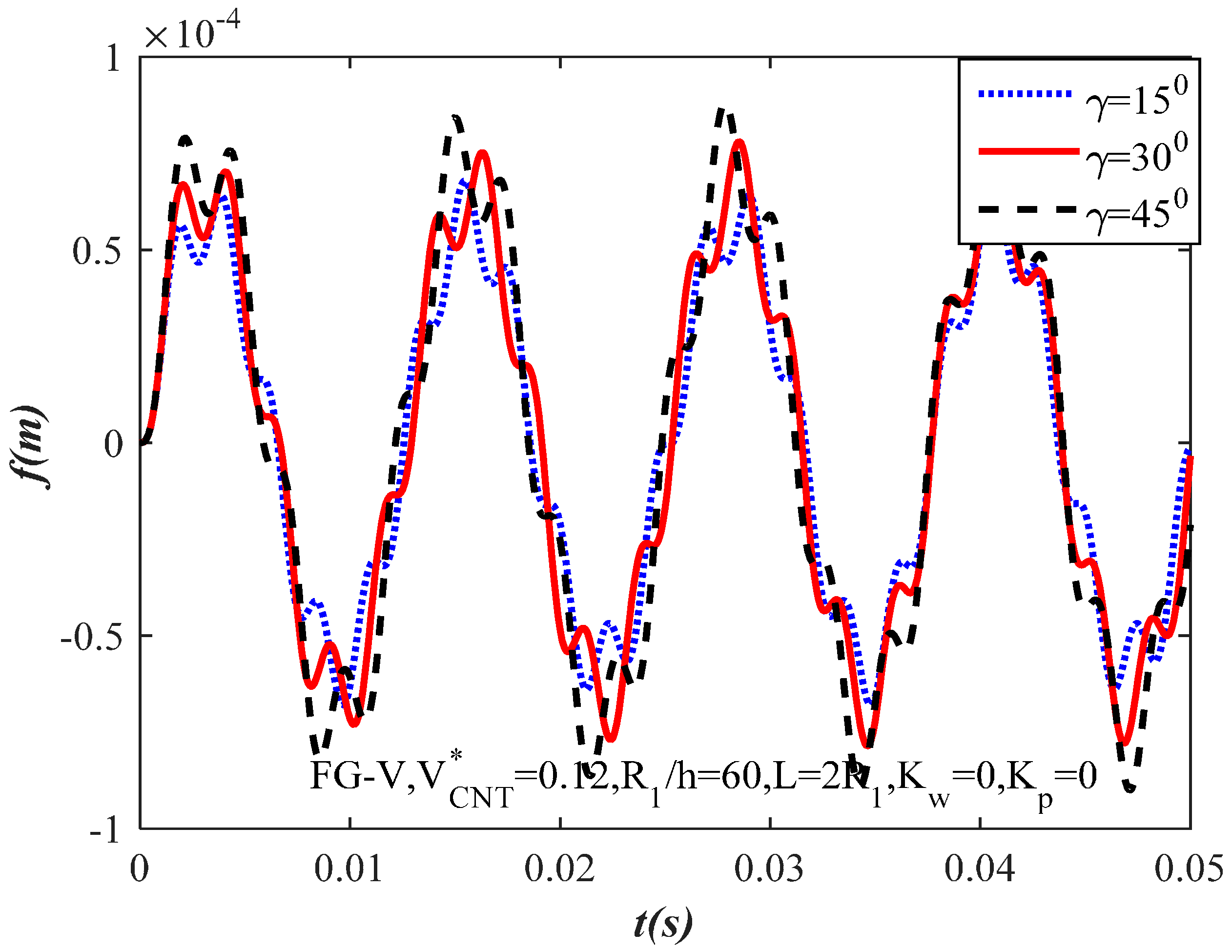
3.2. The Natural Frequency and Dynamic Response
4. Conclusions
- The value of the non-dimensional frequency negligible decreases when the values of semi-vertex angle increase.
- The value of the amplitude and non-dimensional frequency of the shells are significantly affected by various types of CNT distributions. In the case of the FG-X type of CNT distribution, the amplitude value is the smallest and the non-dimensional frequency is the highest.
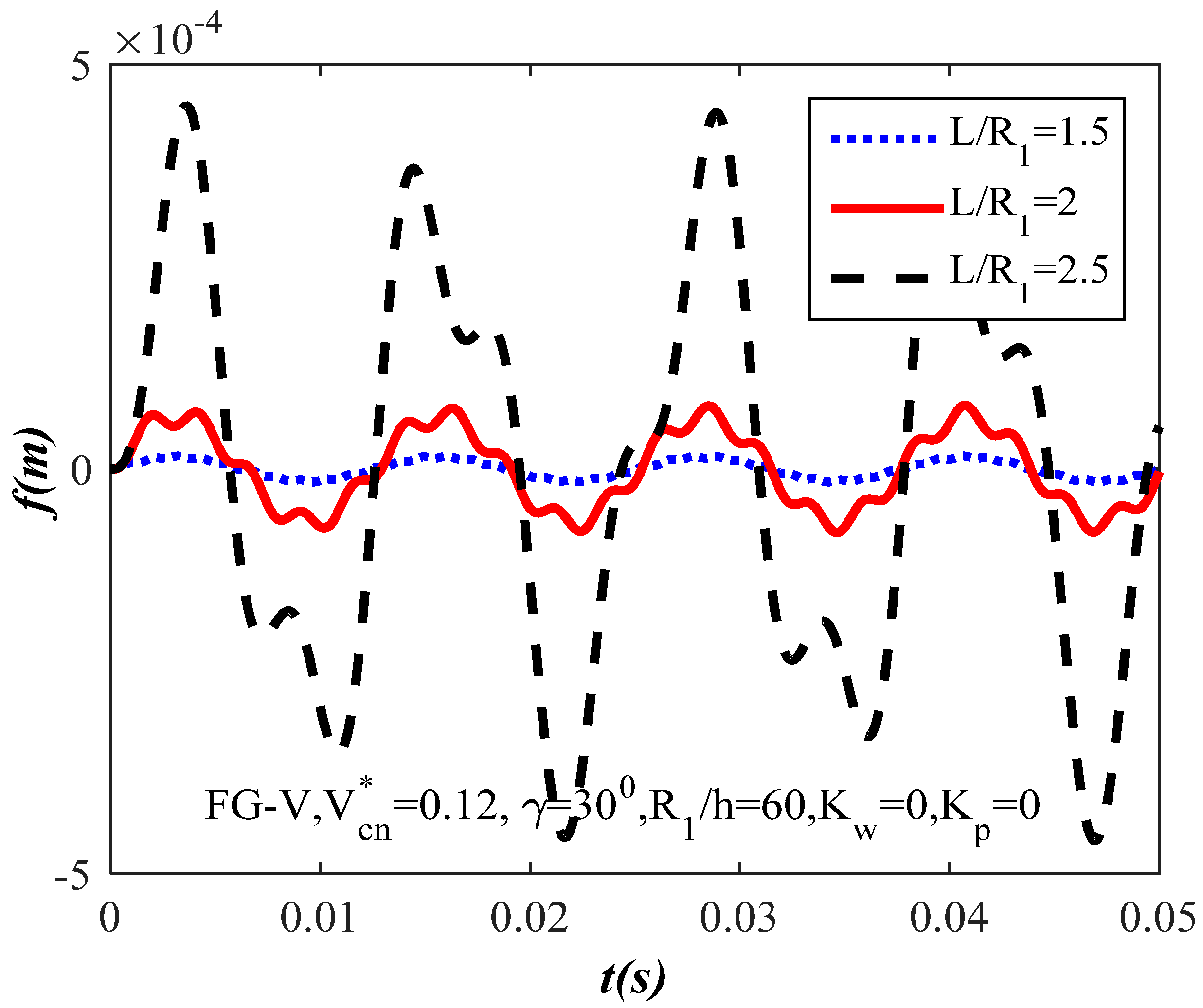
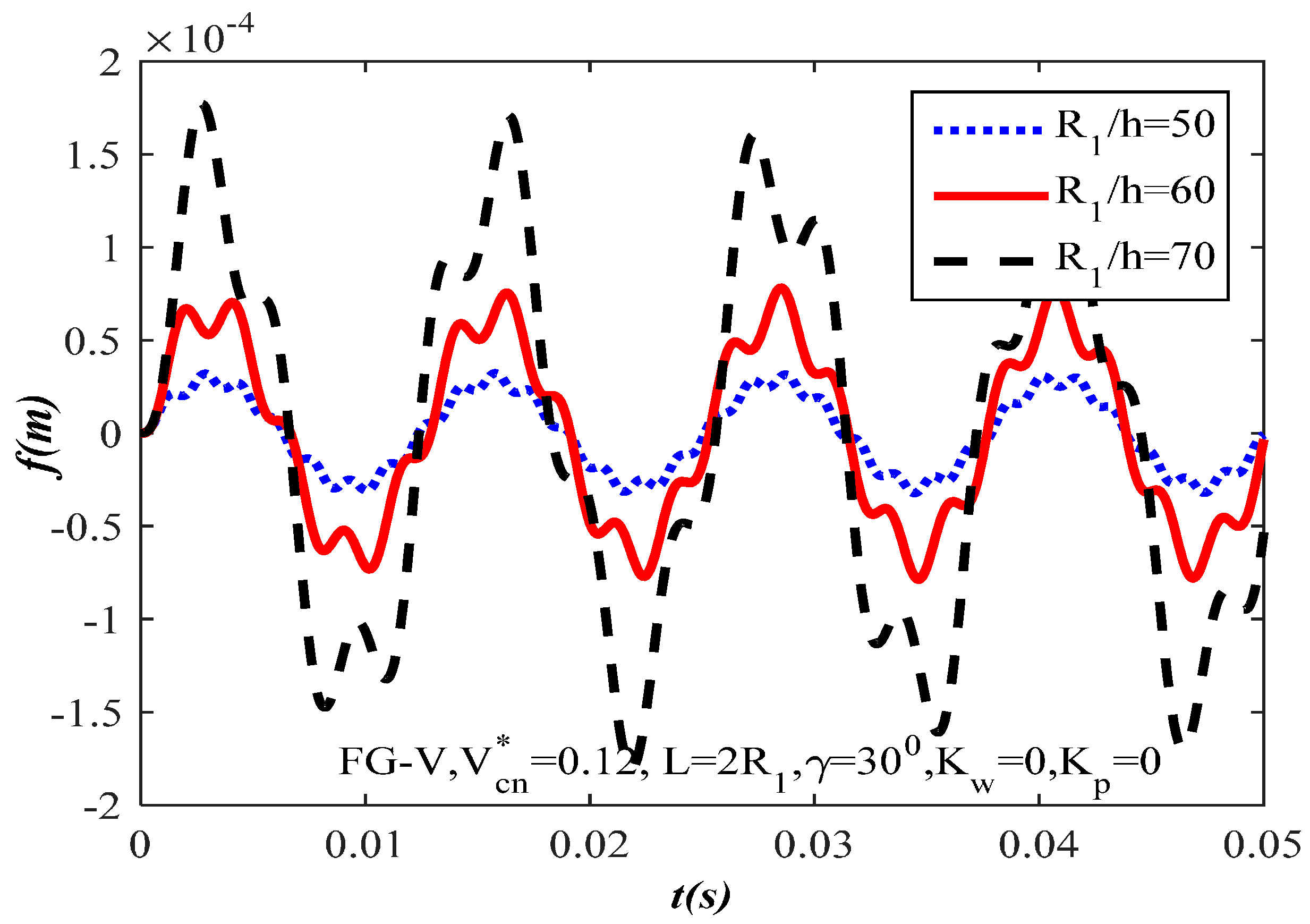
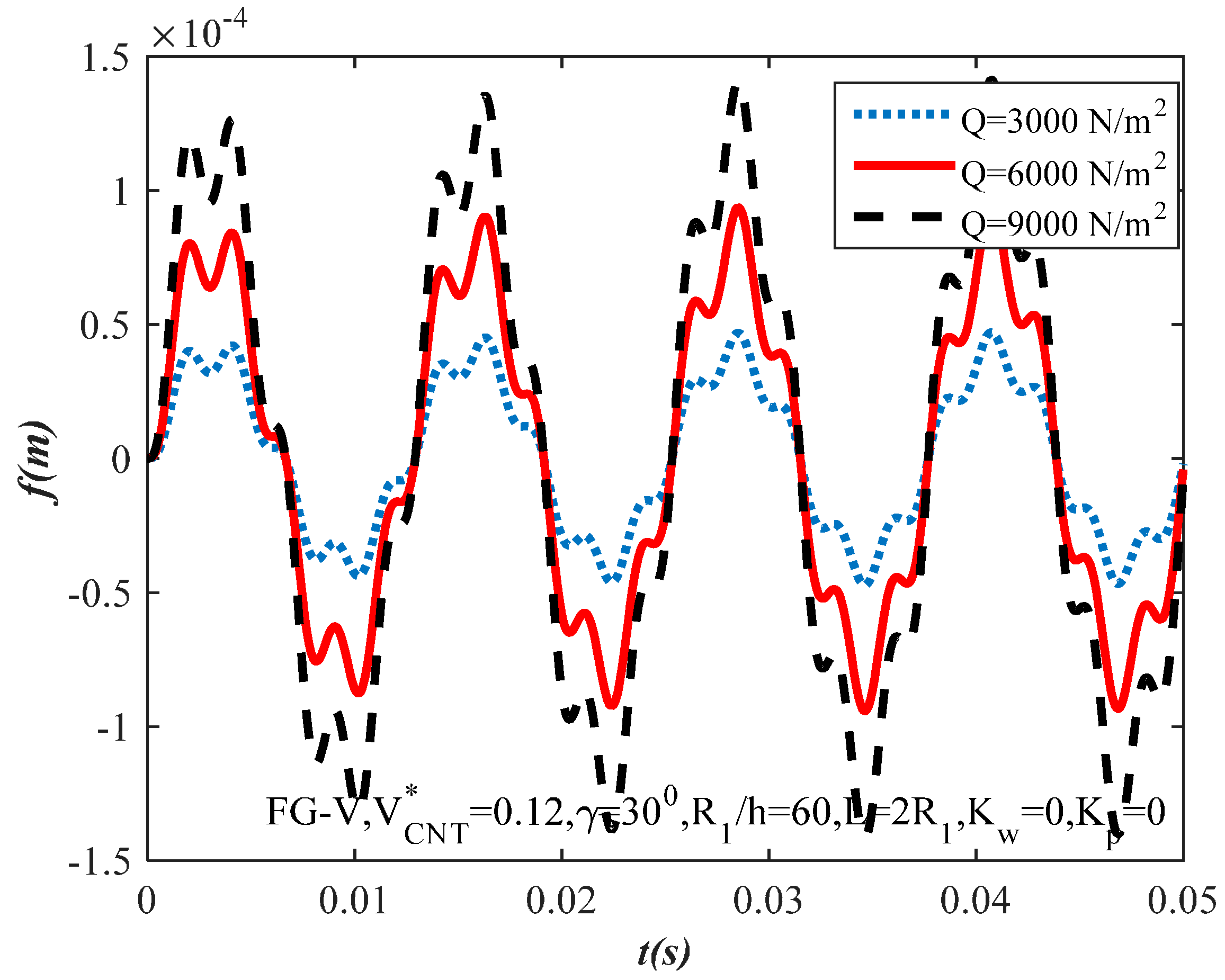
- The results obtained also demonstrate that the time–deflection curves are affected greatly by variations in parameters such as ratio , length-to-radius ratio , and amplitude .
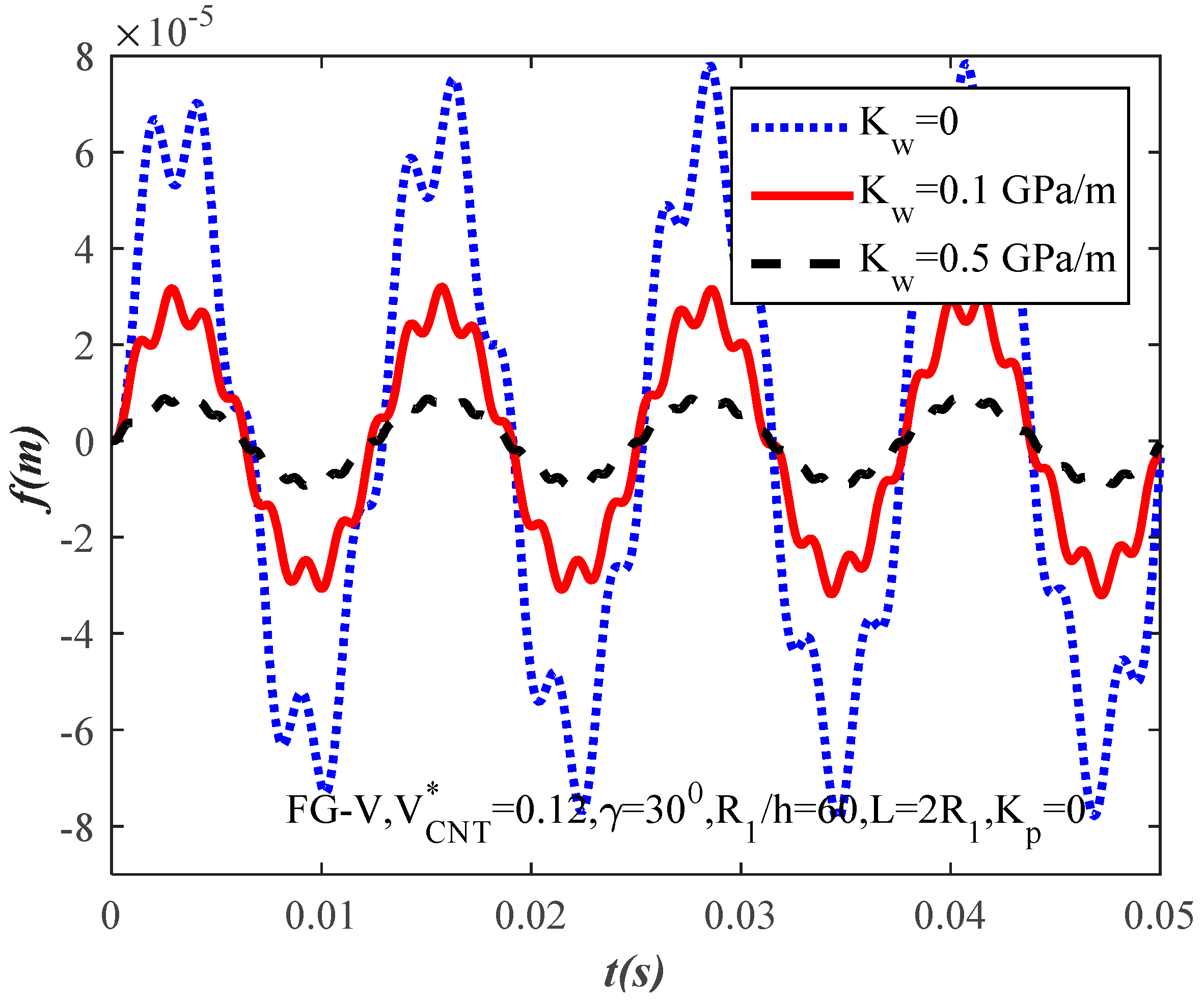
- The elastic foundations strongly affect the dynamic response of FG-CNTRC truncated conical shells. The elastic foundations have positive effects on the amplitudes of FG-CNTRC truncated conical shells.
- The stress function, Galerkin method, Runge–Kutta method, and analytical approach are used to assess the dynamic responses of FG-CNTRC truncated conical shells resting on elastic foundations.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Wang, X.; Li, Q.; Xie, J.; Jin, Z.; Wang, J.; Li, Y.; Jiang, K.; Fan, S. Fabrication of Ultra long and Electrically Uniform Single-Walled Carbon Nanotubes on Clean Substrates. Nano Lett. 2009, 9, 3137–3141. [Google Scholar] [CrossRef] [PubMed]
- Liew, K.M.; Lei, Z.X.; Zhang, L.W. Mechanical analysis of functionally graded carbon nanotube reinforced composites. A review. Compos. Struct. 2015, 12, 90–97. [Google Scholar] [CrossRef]
- Yu, M.F.; Lourie, O.; Dyer, M.J.; Moloni, K.; Kelly, T.F.; Ruoff, R.S. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load. Science 2000, 287, 637–640. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Locascio, M.; Zapol, P.; Li, S.; Mielke, S.L.; Schatz, G.C.; Espinosa, H.D. Measurements of near-ultimate strength for multiwalled carbon nanotubes and irradiation-induced crosslinking improvements. Nat. Nano 2008, 3, 626–631. [Google Scholar] [CrossRef] [PubMed]
- Collins, P.G. Nanotubes for Electronics. Sci. Am. 2000, 283, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Charlier, J.C.; Roche, S. Electronic and transport properties of nanotubes. Rev. Mod. Phys. 2007, 79, 677–732. [Google Scholar] [CrossRef]
- Thostenson, E.; Li, C.; Chou, T. Nanocomposites in context. Compos. Sci. Technol. 2005, 65, 491–516. [Google Scholar]
- Aliahmad, N.; Shrestha, S.; Varahramyan, K.; Agarwal, M. Poly(vinylidene fluoride-hexafluoropropylene) polymer electrolyte for paper-based and flexible battery applications. AIP Adv. 2016, 6, 065206. [Google Scholar] [CrossRef]
- Aliahmad, N.; Agarwal, M.; Shrestha, S.; Varahramyan, K. Paper-based lithium-ion batteries using carbon nanotube-coated wood microfibers. IEEE Trans. Nanotechnol. 2013, 12, 408–412. [Google Scholar] [CrossRef]
- Agarwal, M.; Xing, Q.; Shim, B.; Kotov, N.; Varahramyan, K.; Lvov, Y. Conductive paper from lignocellulose wood microfibers coated with nanocomposite of carbon nanotubes and conductive polymers. Nanotechnol. J. 2009, 20, 215602. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.S. Nonlinear bending of functionally graded carbon nanotube reinforced composite plates in thermal environments. Compos. Struct. 2009, 91, 9–19. [Google Scholar] [CrossRef]
- Amin, G.S.; Parviz, M.; Sima, Z. Vibration analysis of pre-twisted functionally graded carbon nanotube reinforced composite beams in thermal environment. Compos. Struct. 2017, 162, 325–340. [Google Scholar]
- Wu, H.L.; Kitipornchai, S.; Jie, Y. Imperfection sensitivity of thermal post-buckling behavior of functionally graded carbon nanotube-reinforced composite beams. Appl. Math. Model. 2017, 42, 735–752. [Google Scholar] [CrossRef]
- Wu, H.L.; Yang, J.; Kitipornchai, S. Imperfection sensitivity of post-buckling behaviour of functionally graded carbon nanotube-reinforced composite beams. Thin-Wall. Struct. 2016, 108, 225–233. [Google Scholar] [CrossRef]
- Mirzaei, M.; Kiani, Y. Free vibration of functionally graded carbon nanotube reinforced composite cylindrical panels. Compos. Struct. 2016, 142, 45–56. [Google Scholar] [CrossRef]
- Enrique, G.M.; Luis, R.T.; Rafael, C.T.; Andrés, S. Buckling analysis of functionally graded carbon nanotube-reinforced curved panels under axial compression and shear. Compos. Part B 2017, 108, 243–256. [Google Scholar]
- Zhang, L.W.; Lei, Z.X.; Liew, K.M.; Yu, J.L. Static and dynamic of carbon nanotube reinforced functionally graded cylindrical panels. Compos. Struct. 2014, 111, 205–212. [Google Scholar] [CrossRef]
- Phung, V.P.; Qui, X.L.; Nguyen, X.H.; Abdel, W.M. Size-dependent isogeometric analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Compos. Struct. 2017, 166, 120–135. [Google Scholar] [CrossRef]
- Lei, Z.X.; Zhang, L.W.; Liew, K.M. Meshless modeling of geometrically nonlinear behavior of CNT-reinforced functionally graded composite laminated plates. Appl. Math. Comput. 2017, 295, 24–46. [Google Scholar] [CrossRef]
- Kiani, Y. Free vibration of functionally graded carbon nanotube reinforced composite plates integrated with piezoelectric layers. Appl. Math. Comput. 2016, 72, 2433–2449. [Google Scholar] [CrossRef]
- Lei, Z.X.; Zhang, L.W.; Liew, K.M. Buckling analysis of CNT reinforced functionally graded laminated composite plates. Compos. Struct. 2016, 152, 62–73. [Google Scholar] [CrossRef]
- Duc, N.D.; Lee, J.H.; Nguyen-Thoi, T.; Thang, P.T. Static response and free vibration of functionally graded carbon nanotube-reinforced composite rectangular plates resting on Winkler-Pasternak elastic foundations. Aerosp. Sci. Technol. 2017, 68, 391–402. [Google Scholar] [CrossRef]
- Thanh, N.V.; Khoa, N.D.; Tuan, N.D.; Phuong, T.; Duc, N.D. Nonlinear dynamic response and vibration of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) shear deformable plates with temperature-dependent material properties and surrounded on elastic foundations. J. Therm. Stress 2017, 40, 1254–1274. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J.; Faghih, M.S. Vibrational analysis of functionally graded carbon nanotube-reinforced composite spherical shells resting on elastic foundation using the variational differential quadrature method. Eur. J. Mech. A Solid 2016, 60, 166–182. [Google Scholar] [CrossRef]
- Ansari, R.; Pourashraf, T.; Gholami, R.; Shahabodini, A. Analytical solution for nonlinear post-buckling of functionally graded carbon nanotube-reinforced composite shells with piezoelectric layers. Compos. Part B 2016, 90, 267–277. [Google Scholar] [CrossRef]
- Alibeigloo, A.; Pasha, A.A.Z. Thermo-electro-elasticity solution of functionally graded carbon nanotube reinforced composite cylindrical shell embedded in piezoelectric layers. Compos. Struct. 2017, 173, 268–280. [Google Scholar] [CrossRef]
- Jam, J.E.; Kiani, Y. Buckling of pressurized functionally graded carbon nanotube reinforced conical shells. Compos. Struct. 2015, 125, 586–595. [Google Scholar] [CrossRef]
- Duc, N.D.; Cong, P.H.; Tuan, N.D.; Phuong, T.; Thanh, N.V. Thermal and mechanical stability of functionally graded carbon nanotubes (FG CNT)-reinforced composite truncated conical shells surrounded by the elastic foundations. Thin-Wall. Struct. 2017, 115, 300–310. [Google Scholar] [CrossRef]
- Mirzaei, M.; Kiani, Y. Thermal buckling of temperature dependent FG-CNT reinforced composite conical shells. Aerosp. Sci. Technol. 2015, 47, 42–53. [Google Scholar] [CrossRef]
- Heydarpour, Y.; Aghdam, M.M.; Malekzadeh, P. Free vibration analysis of rotating functionally gradedcarbon nanotube-reinforced composite truncated conical shells. Compos. Struct. 2014, 117, 187–200. [Google Scholar] [CrossRef]
- Reza, A.; Jalal, T. Numerical study on the buckling and vibration of functionally graded carbon nanotube-reinforced composite conical shells under axial loading. Compos. Part B 2016, 95, 196–208. [Google Scholar]
- Mehri, M.; Asadi, H.; Wang, Q. Buckling and vibration analysis of a pressurized CNT reinforced functionally graded truncated conical shell under an axial compression using HDQ method. Comput. Methods Appl. Mech. Eng. 2016, 303, 75–100. [Google Scholar] [CrossRef]
- Mehri, M.; Asadi, H.; Wang, Q. On dynamic instability of a pressurized functionally grated carbon nanotube reinforced truncated conical shell subjected to yawed supersonic airflow. Compos. Struct. 2016, 153, 938–951. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Postbuckling of axially compressed nanotube-reinforced composite cylindrical panels resting on elastic foundations in thermal environments. Compos. Part B 2014, 67, 50–61. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Thermal postbuckling of nanotube-reinforced composite cylindrical panels resting on elastic foundations in thermal environments. Compos. Struct. 2015, 123, 383–392. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Nonlinear response of nanotube-reinforced composite cylindrical panels subjected to combined loadings and resting on elastic foundations. Compos. Struct. 2015, 131, 939–950. [Google Scholar] [CrossRef]
- Shen, H.S. Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite cylindrical shells. Compos. Part B 2012, 43, 1030–1038. [Google Scholar] [CrossRef]
- Shen, H.S. Torsional postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments. Compos. Struct. 2014, 116, 477–488. [Google Scholar] [CrossRef]
- Zhang, L.W.; Lei, Z.X.; Liew, K.M.; Yu, J.L. Large deflection geometrically nonlinear analysis of carbon nanotube reinforced functionally graded cylindrical panels. J. Comput. Methods Appl. Mech. Eng. 2014, 273, 1–18. [Google Scholar] [CrossRef]
- Zhang, L.W.; Lei, Z.X.; Liew, K.M. Vibration characteristic of moderately thick functionally graded carbon nanotube reinforced composite skew plates. Compos. Struct. 2015, 122, 172–183. [Google Scholar] [CrossRef]
- Zhang, L.W.; Lei, Z.X.; Liew, K.M. Free vibration analysis of functionally graded carbon nanotube reinforced composite triangular plates using the FSDT and element-free IMLS-Ritz method. Compos. Struct. 2015, 120, 189–199. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments. Part I: Axially loaded shells. Compos. Struct. 2011, 93, 2096–2108. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments. Part II: Pressure loaded shells. Compos. Struct. 2011, 93, 2496–2503. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Osmancelebioglu, E. The free vibration of sandwich truncated conical shells containing functionally graded layers within the shear deformation theory. Compos. Part B 2017, 120, 197–211. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Buckling analysis of freely-supported functionally graded truncated conical shells under external pressures. Compos. Struct. 2015, 132, 746–758. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Pancar, E.B. The effect of heterogeneity on the parametric instability of axially excited orthotropic conical shells. Thin-Wall. Struct. 2017, 115, 240–246. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Kuruoglu, N. On the solution of the buckling problem of functionally graded truncated conical shells with mixed boundary conditions. Compos. Struct. 2015, 123, 282–291. [Google Scholar] [CrossRef]
- Najafov, A.M.; Sofiyev, A.H. The non-linear dynamics of FGM truncated conical shells surrounded by an elastic medium. Int. J. Mech. Sci. 2013, 66, 33–44. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Kuruoglu, N. Buckling analysis of nonhomogeneous orthotropic thin-walled truncated conical shells in large deformation. Thin-Wall. Struct. 2013, 62, 131–141. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Kuruoğlu, N. The stability of FGM truncated conical shells under combined axial and external mechanical loads in the framework of the shear deformation theory. Compos. Part B 2016, 92, 463–476. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Influence of the initial imperfection on the non-linear buckling response of FGM truncated conical shells. Int. J. Mech. Sci. 2011, 53, 753–761. [Google Scholar] [CrossRef]
- Sofiyev, A.H. On the vibration and stability of shear deformable FGM truncated conical shells subjected to an axial load. Compos. Part B 2015, 80, 53–62. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Kuruoglu, N. Non-linear buckling of an FGM truncated conical shell surrounded by an elastic medium. Int. J. Press. Vessel. Pip. 2013, 107, 38–49. [Google Scholar] [CrossRef]
- Agamirov, V.L. Dynamic Problems of Nonlinear Shells heory; Science Edition; Nauka: Moscow, Russia, 1990. [Google Scholar]
- Sofiyev, A.H. The buckling of FGM truncated conical shells subjected to axial compressive load and resting on Winkler-Pasternak foundations. Int. J. Press. Vessels Pip. 2010, 87, 753–761. [Google Scholar] [CrossRef]
- Anh, V.T.T.; Bich, D.H.; Duc, N.D. Nonlinear buckling analysis of thin FGM annular spherical shells on elastic foundations under external pressure and thermal loads. Eur. J. Mech. A Solid 2015, 50, 28–38. [Google Scholar] [CrossRef]
- Duc, N.D. Nonlinear dynamic response of imperfect eccentrically stiffened FGM double curved shallow shells on elastic foundation. Compos. Struct. 2013, 102, 306–314. [Google Scholar] [CrossRef]
- Duc, N.D. Nonlinear Static and Dynamic Stability of Functionally Graded Plates and Shells; Vietnam National University Press: Hanoi, Vietnam, 2014. [Google Scholar]
- Li, F.M.; Kishimoto, K.; Huang, W.H. The calculations of natural frequencies and forced vibration responses of conical shell using the Rayleigh-Ritz method. Mech. Res. Commun. 2009, 36, 595–602. [Google Scholar] [CrossRef]
- Lam, K.Y.; Hua, L. Influence of boundary conditions on the frequency characteristics of a rotating truncated circular conical shell. J. Sound. Vib. 1999, 223, 171–195. [Google Scholar] [CrossRef]


| 2 | 3 | 4 | 5 | 6 | ||
|---|---|---|---|---|---|---|
| Li et al. [59] | 0.8431 | 0.7416 | 0.6419 | 0.5590 | 0.5008 | |
| Lam and Hua [60] | 0.8429 | 0.7376 | 0.6362 | 0.5528 | 0.4950 | |
| Present | 0.8700 | 0.7934 | 0.6831 | 0.5491 | 0.3976 | |
| Li et al. [59] | 0.7642 | 0.7211 | 0.6747 | 0.6336 | 0.6049 | |
| Lam and Hua [60] | 0.7655 | 0.7212 | 0.6739 | 0.6323 | 0.6035 | |
| Present | 0.7205 | 0.7023 | 0.6689 | 0.6149 | 0.5350 |
| FG-O | FG-V | FG-X | FG-O | FG-V | FG-X | FG-O | FG-V | FG-X | |
|---|---|---|---|---|---|---|---|---|---|
| 50 | 1.039 | 1.236 | 1.905 | 1.214 | 1.455 | 2.275 | 1.586 | 1.878 | 2.905 |
| 60 | 0.816 | 0.989 | 1.561 | 0.940 | 1.153 | 1.859 | 1.260 | 1.513 | 2.387 |
| 70 | 0.646 | 0.804 | 1.310 | 0.726 | 0.925 | 1.555 | 1.013 | 1.242 | 2.012 |
| 80 | 0.505 | 0.656 | 1.118 | 0.544 | 0.740 | 1.320 | 0.814 | 1.029 | 1.725 |
| 100 | 0.255 | 0.421 | 0.838 | 0.154 | 0.430 | 0.974 | 0.485 | 0.699 | 1.310 |
| UD | FG-O | FG-V | FG-X | |
|---|---|---|---|---|
| 15° | 1.3672 | 0.8341 | 1.0526 | 1.7414 |
| 30° | 1.2463 | 0.8160 | 0.9889 | 1.5606 |
| 45° | 1.1507 | 0.7866 | 0.9311 | 1.4238 |
| 60° | 1.0898 | 0.7658 | 0.8935 | 1.3371 |
| 75° | 1.0567 | 0.7544 | 0.8731 | 1.2900 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen Dinh, D.; Nguyen, P.D. The Dynamic Response and Vibration of Functionally Graded Carbon Nanotube-Reinforced Composite (FG-CNTRC) Truncated Conical Shells Resting on Elastic Foundations. Materials 2017, 10, 1194. https://doi.org/10.3390/ma10101194
Nguyen Dinh D, Nguyen PD. The Dynamic Response and Vibration of Functionally Graded Carbon Nanotube-Reinforced Composite (FG-CNTRC) Truncated Conical Shells Resting on Elastic Foundations. Materials. 2017; 10(10):1194. https://doi.org/10.3390/ma10101194
Chicago/Turabian StyleNguyen Dinh, Duc, and Pham Dinh Nguyen. 2017. "The Dynamic Response and Vibration of Functionally Graded Carbon Nanotube-Reinforced Composite (FG-CNTRC) Truncated Conical Shells Resting on Elastic Foundations" Materials 10, no. 10: 1194. https://doi.org/10.3390/ma10101194
APA StyleNguyen Dinh, D., & Nguyen, P. D. (2017). The Dynamic Response and Vibration of Functionally Graded Carbon Nanotube-Reinforced Composite (FG-CNTRC) Truncated Conical Shells Resting on Elastic Foundations. Materials, 10(10), 1194. https://doi.org/10.3390/ma10101194





