MMCS: Multi-Module Charging Strategy for Increasing the Lifetime of Wireless Rechargeable Sensor Networks
Abstract
:1. Introduction
2. Related Works
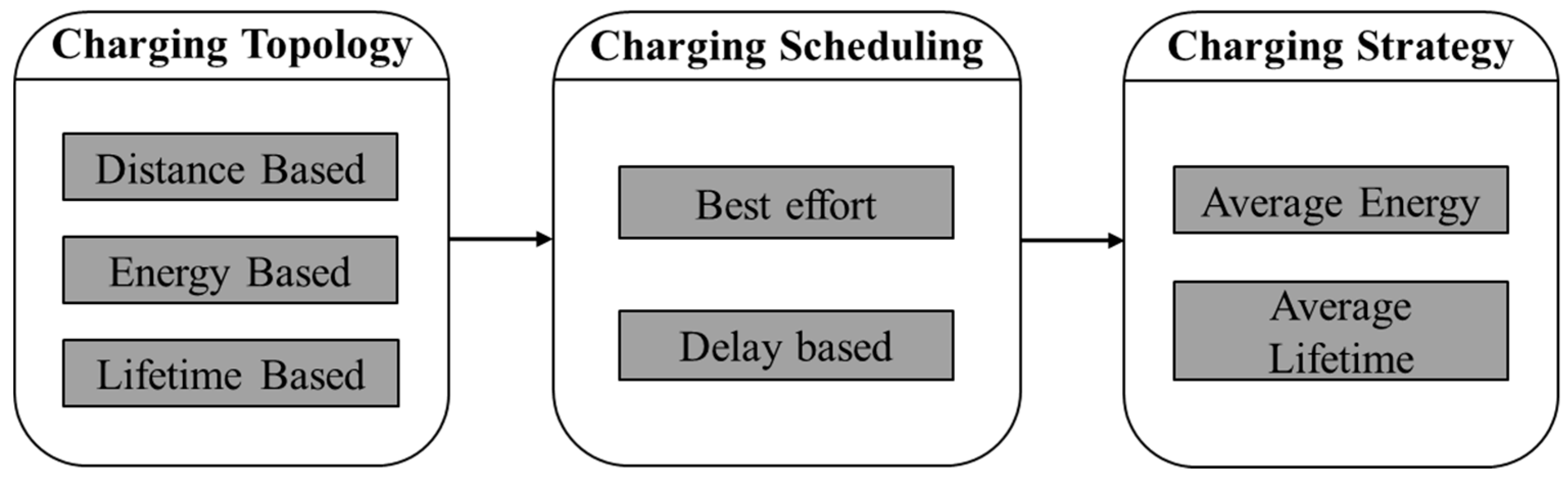
3. Multi-Module Charging Strategy
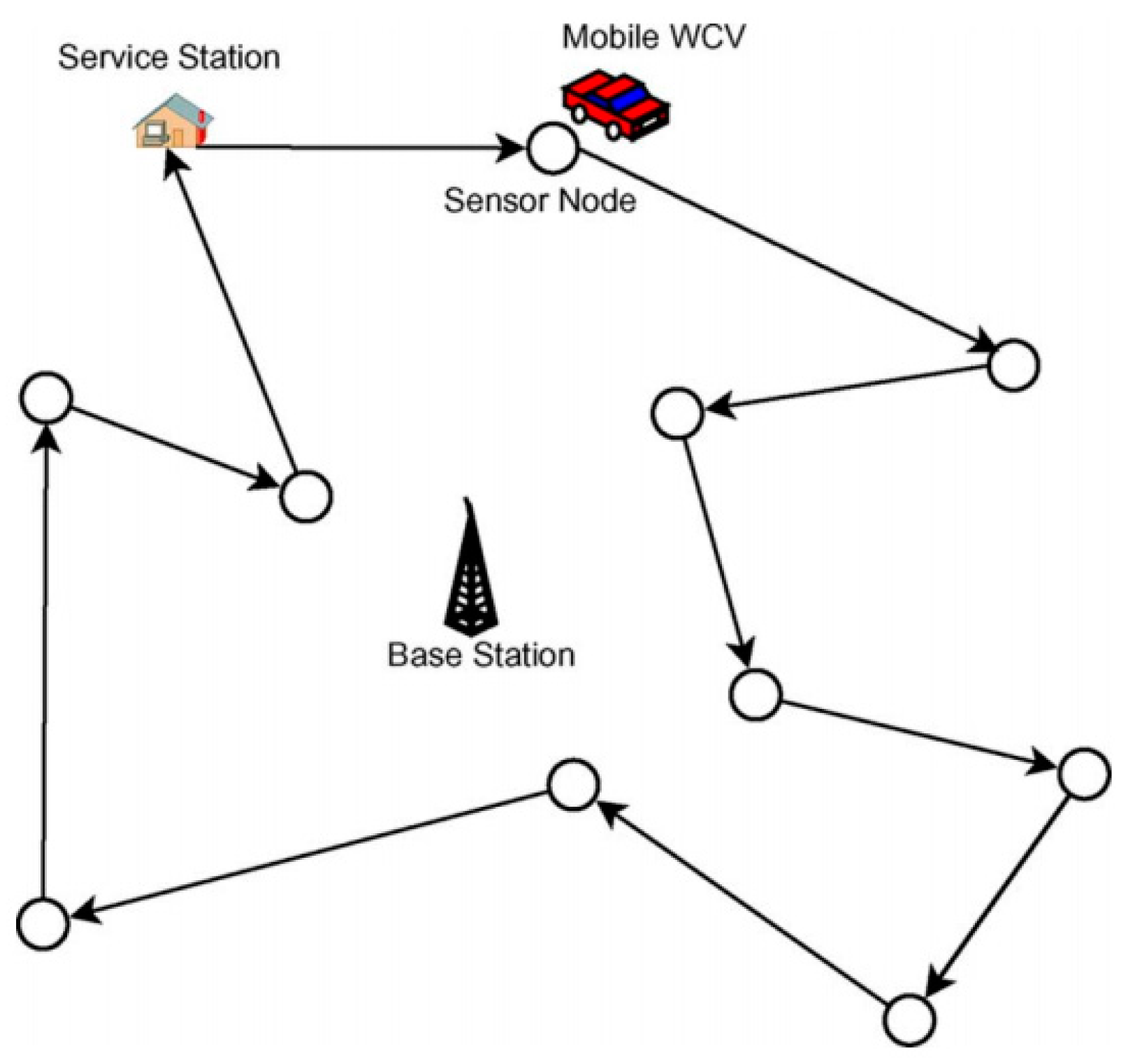
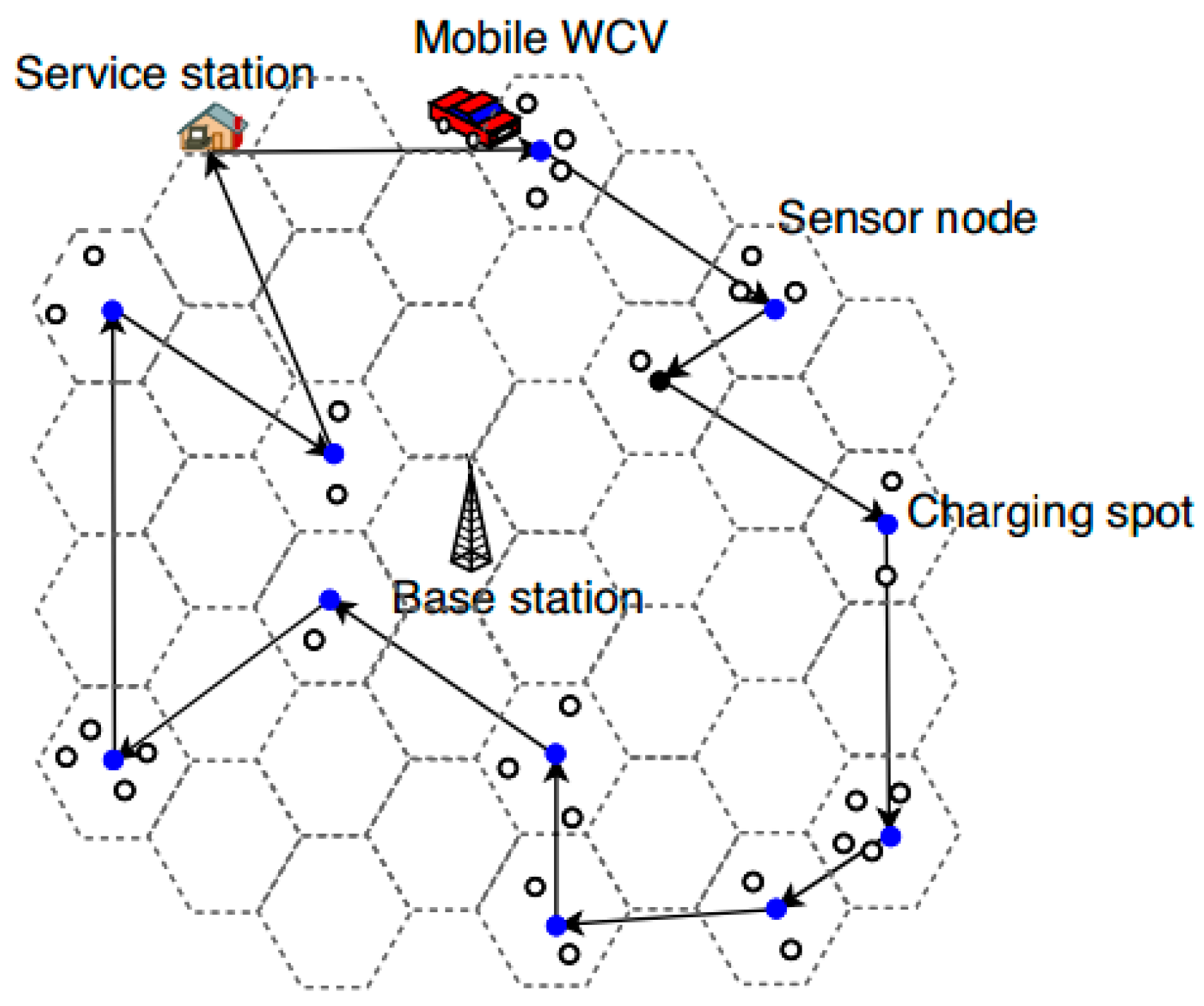
3.1. Problem Definition
3.2. Method Description
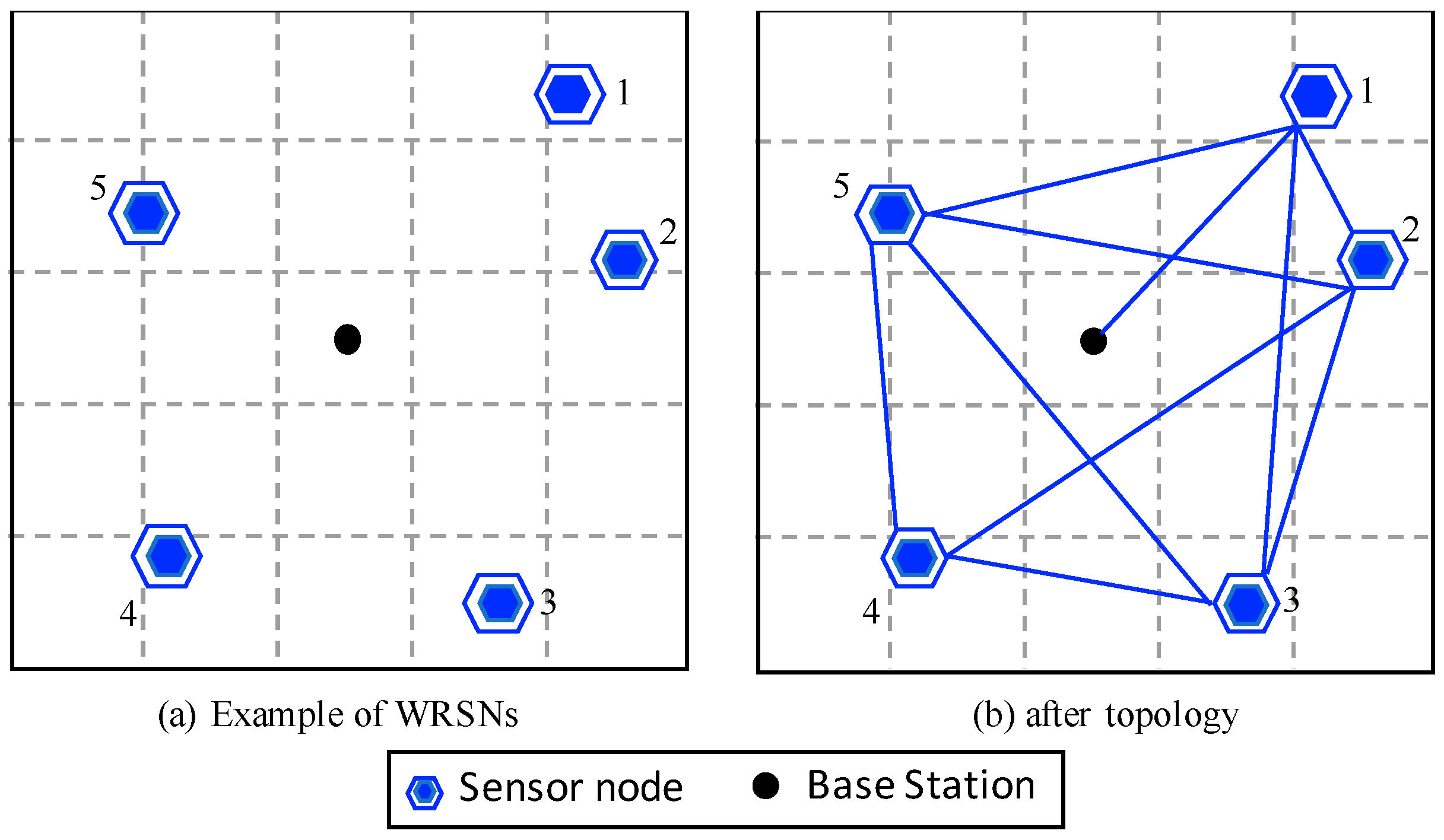
3.2.1. The Stage of Charging Topology
- Distance-based module: The travel distance of a WCV is limited by its battery capacity. In MMCS, a distance-based topology is designed to plan the shortest travel path. The first node S is the with the lowest LTn. Node S then establishes adjacent relations with three with the shortest distance to S. The next node is the with the shortest path to S. Repeat this process until all the CNs are complete.
- Energy/Lifetime-based module: The energy consumption rate of each is different; however, there are different degrees of criticality. Therefore, MMCS utilizes the remainder of energy/lifetime as a basis for establishing the topology. In terms of energy-based topology construction, each is first sorted in the ascending order, then the is sequentially chosen as Node S, which establishes adjacent relations with three with the lowest En. In lifetime-based construction, is selected because of its lifetime.
3.2.2. The Stage of Charging Scheduling
- Best-effort module: Best effort is a concept used for attempting the rescue of which WCV can pass. The best-effort module algorithm is shown in Figure 5. The nodes in are first sorted in an ascending order; then, MMCS is used to define the source (SN) as the present location of WCV and its destination (DN) as the location of with lowest LTn. Next, the Dijkstra algorithm is executed to determine the shortest path. If SN does not directly connect with the DN, check if Bc and Bm are sufficient to charge and move to the first relay between SN and DN, and then from first relay to DN. If energy is sufficient, the first relay is defined as the next node to which WCV will move to charge.
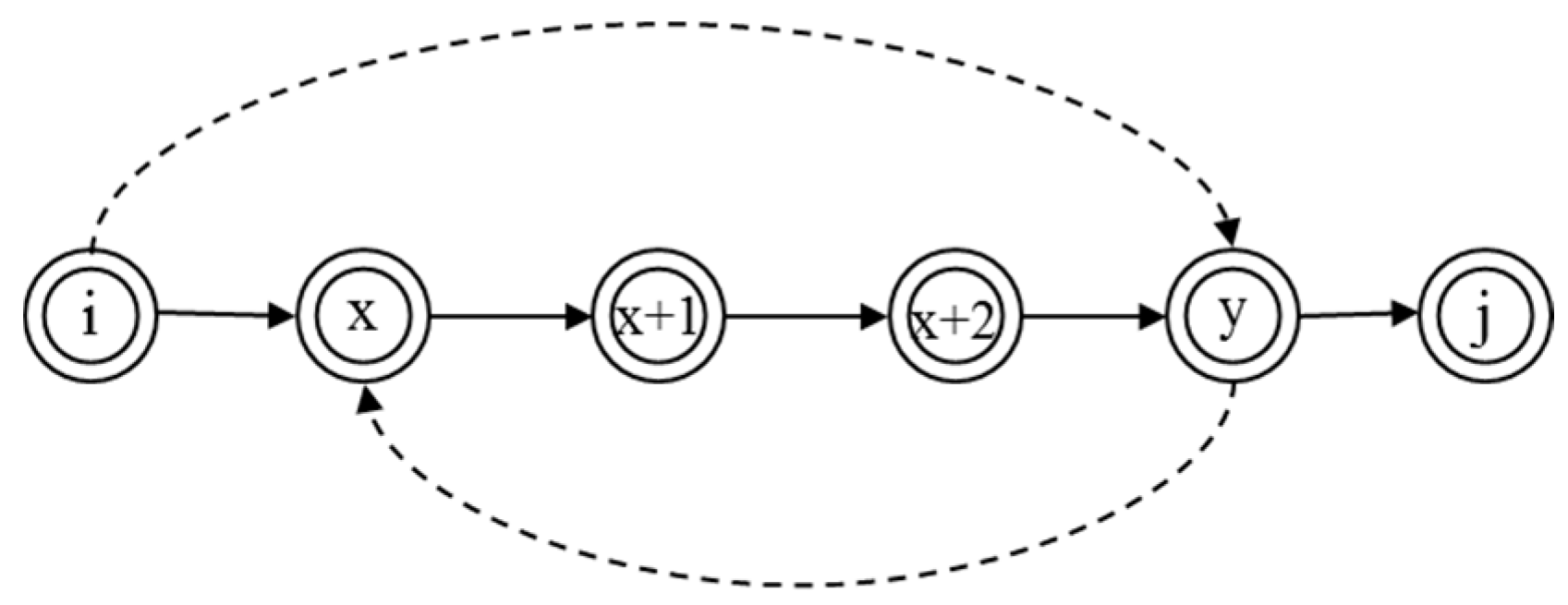
- Delay-based module: The concept of best effort only considers the relay station bringing the result of DN. However, the insert relay not only affect the DN but also other that are subsequent to SN. If a subsequent to SN is more critical than relay , it may lead to node death. Therefore, in the MMCS the delay time is considered instead of the scheduling time, and the delay-based method is proposed. Figure 6 shows the process of delay time.
3.2.3. The Stage of Charging Strategy
- Average energy module: As shown in Equation (12), CNs selected in the charging topology stage are nodes that are more urgent. To enhance CNs to a high-energy level, MMCS uses double CNs (dCNs) as threshold for improving energy. Next, the En of urgent nodes is enhanced by enhancing energy of nodes with the lowest En to next higher energy level.
- Average lifetime module: As shown in Equation (13), to enhance CNs to a high-energy level, MMCS uses dCNs as threshold for improving energy. The LTn of critical nodes is enhanced by enhancing the energy of nodes with the lowest LTn to next higher lifetime level.
3.3. An Example of Multi-Module Charging Strategy
4. Experimental Results and Analysis
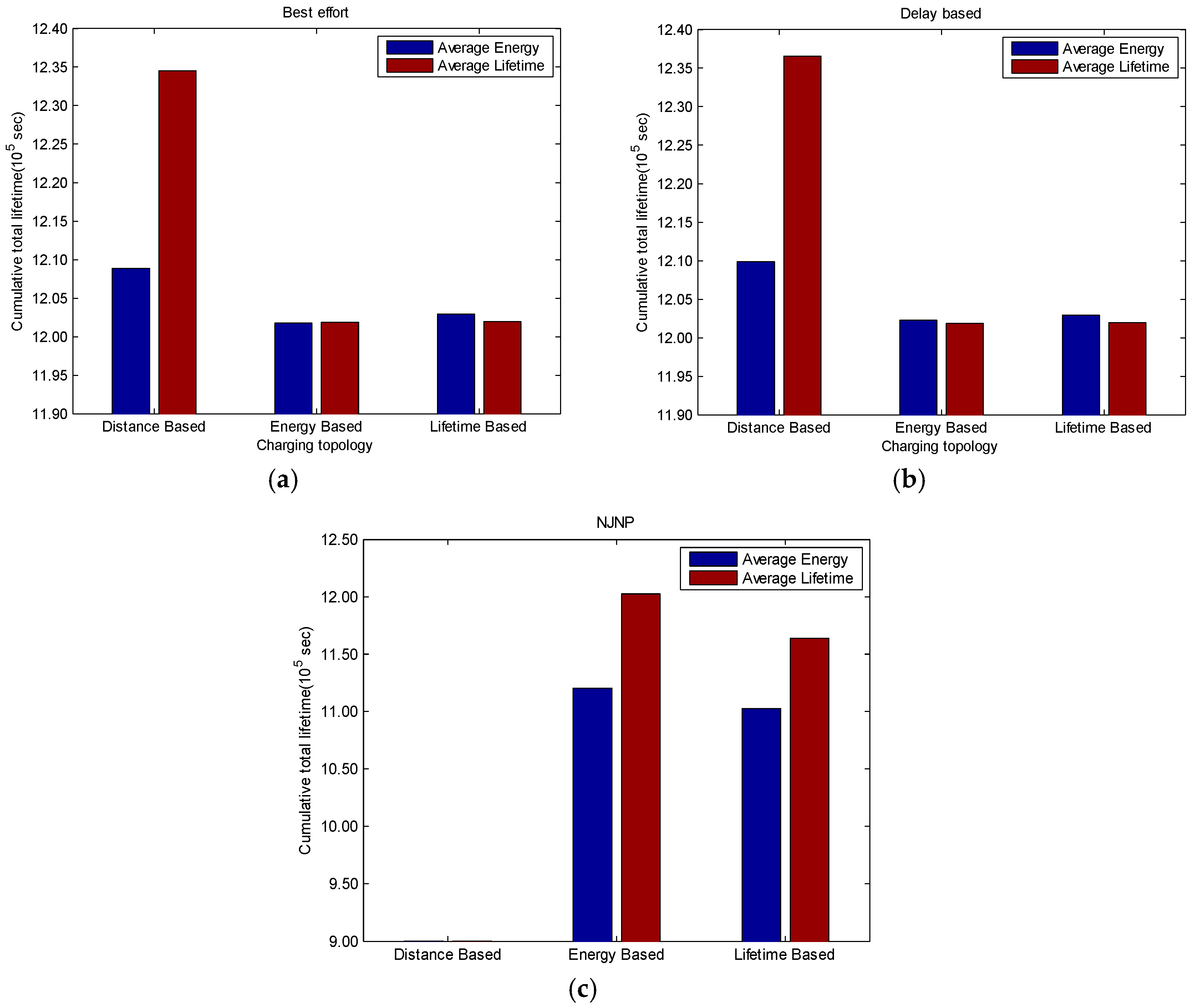
4.1. The Combination Experiment of Multi-Module Charging Strategy
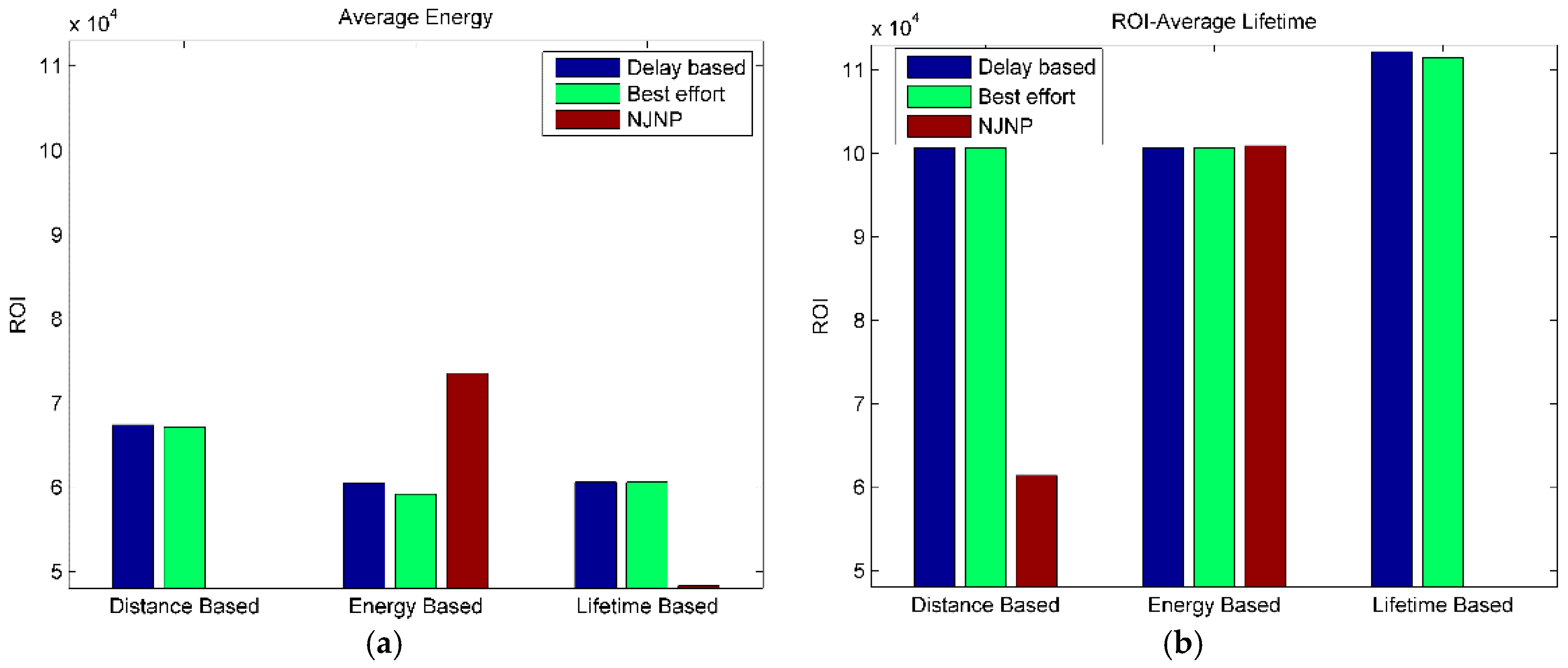
4.2. Result of Return on Investment Analysis of Battery
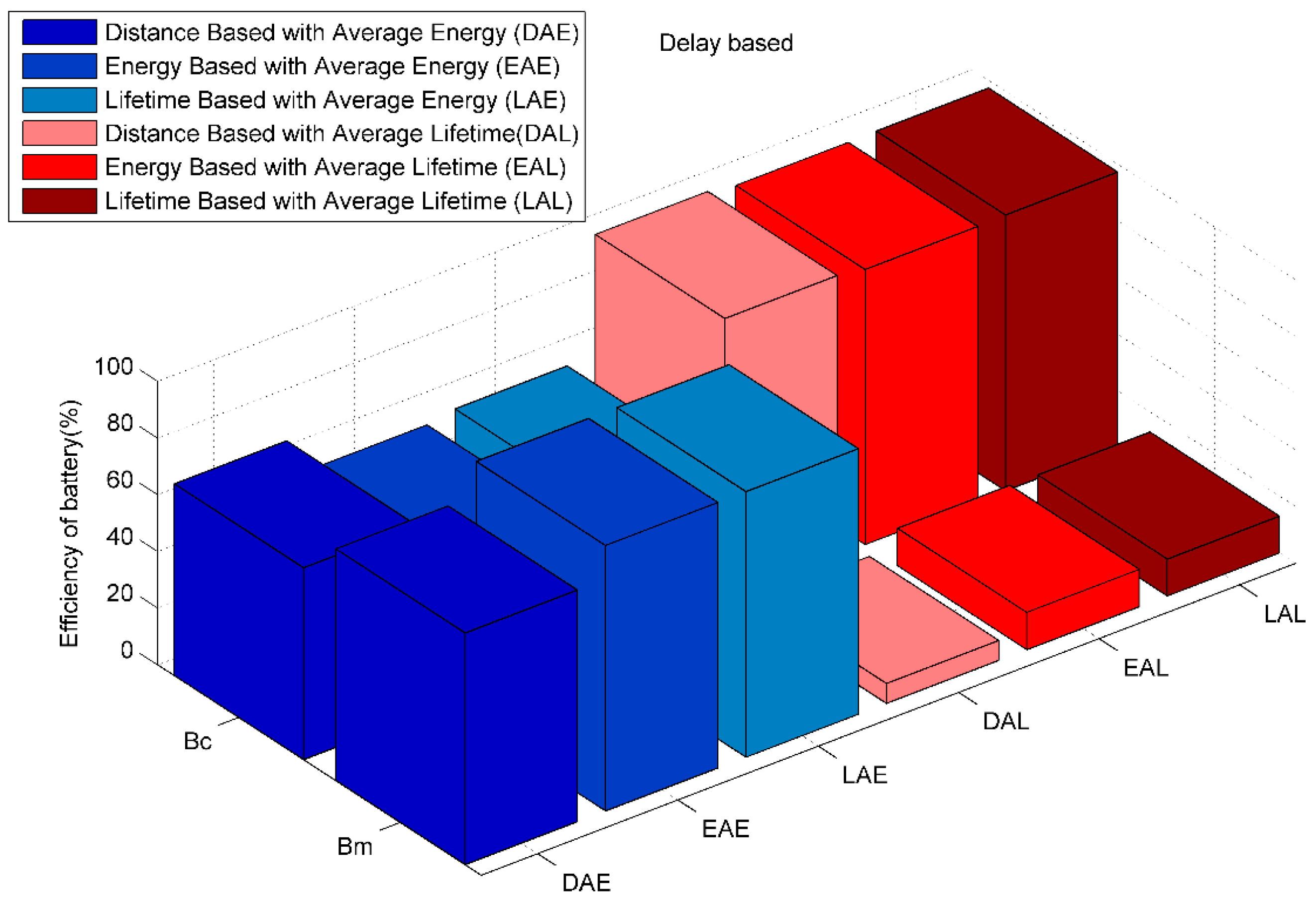
4.3. Efficiency of Battery
4.4. Extended Lifetime of Wireless Rechargeable Sensor Networks
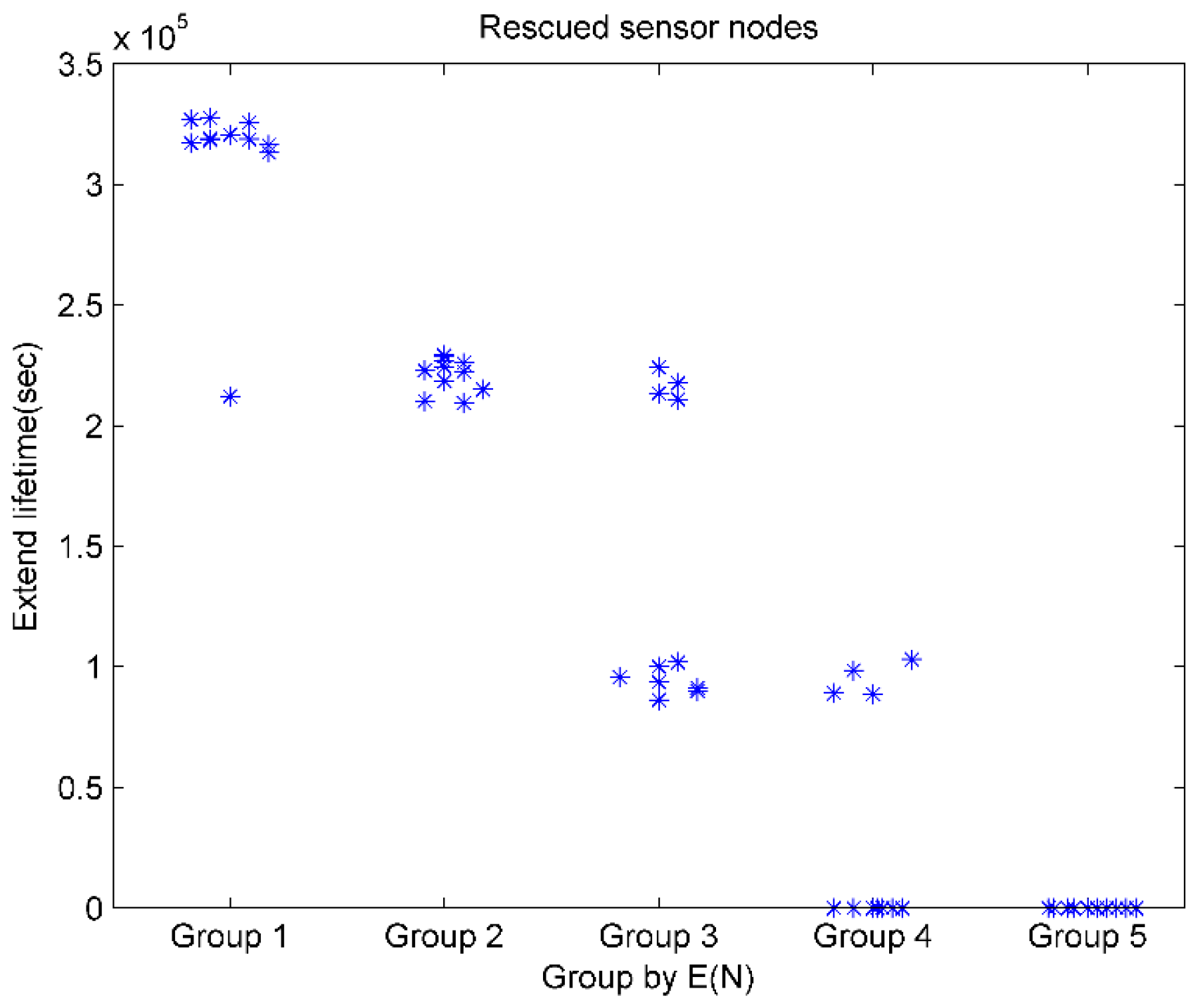
4.5. Distribution of the Rescued Sensor Nodes
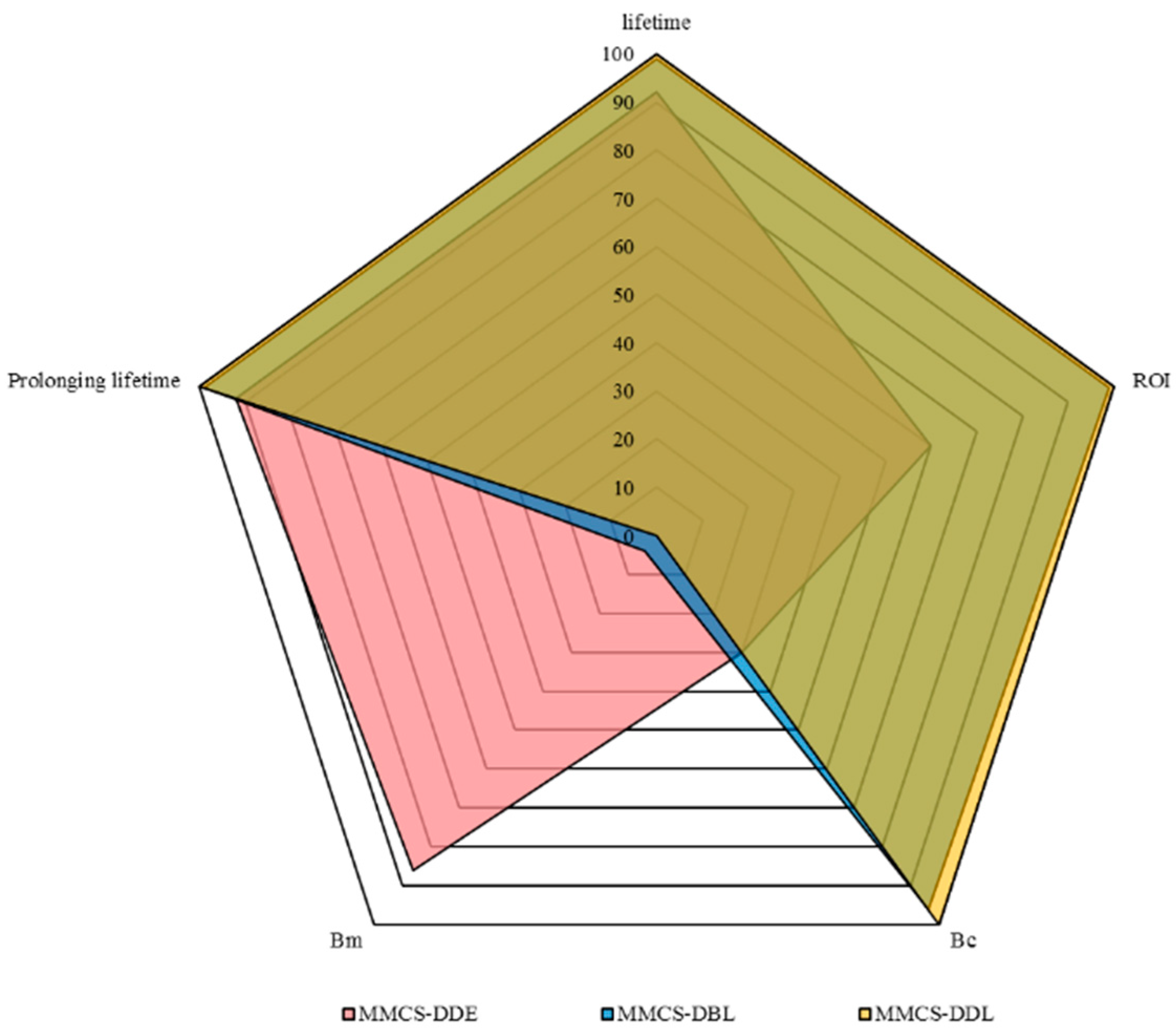
4.6. Comprehensive Comparison
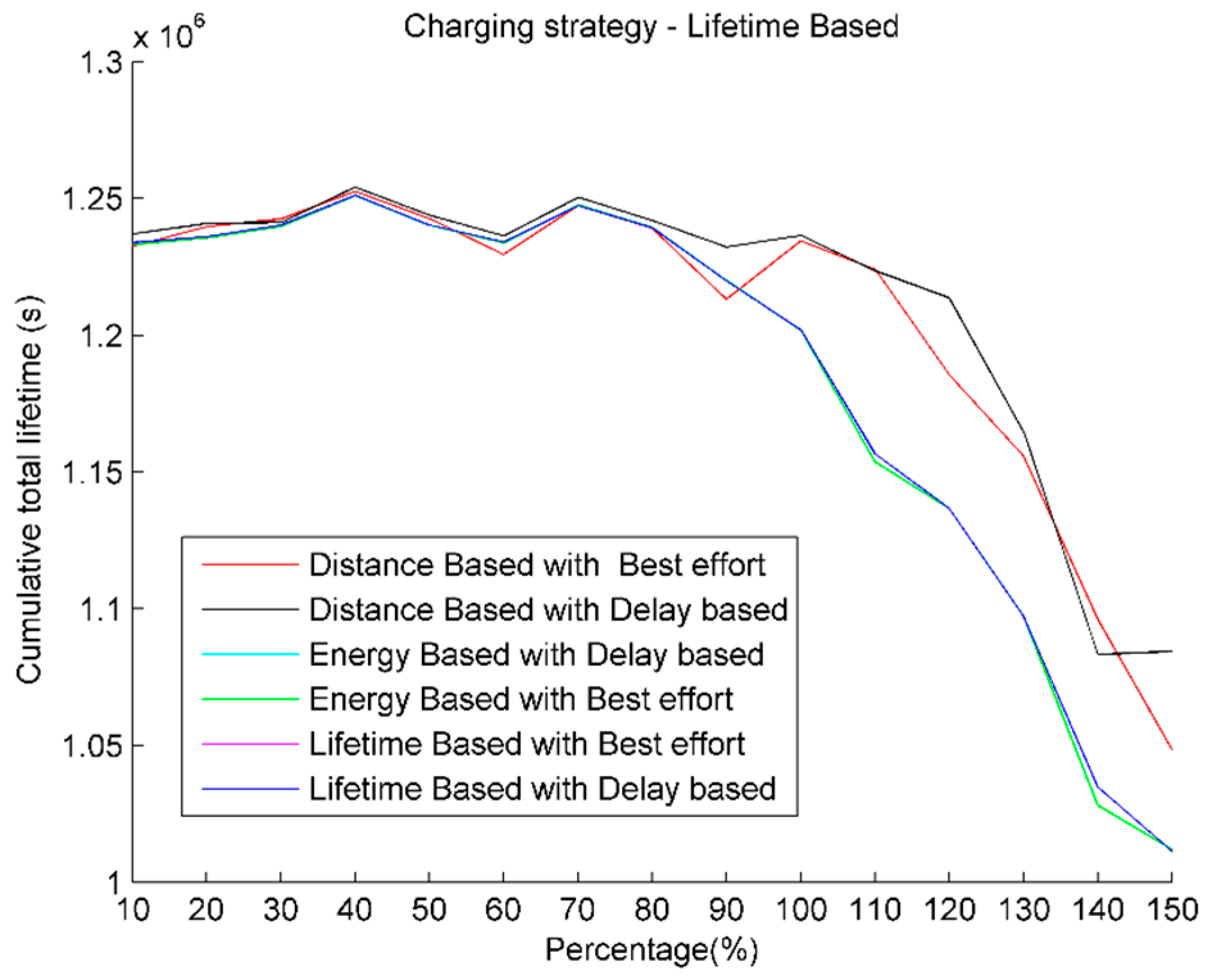
4.7. Effect of Variation of the Amount of Charge
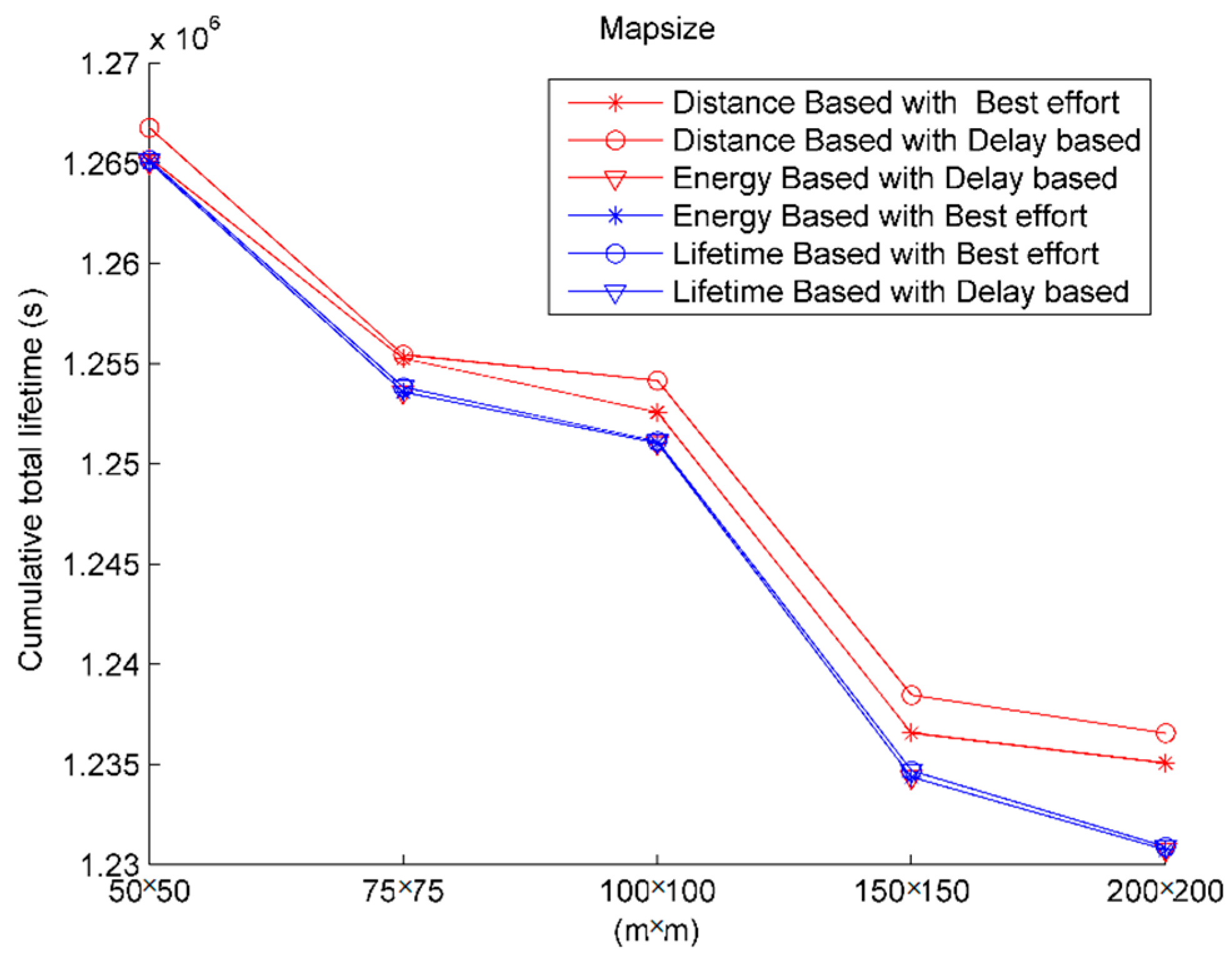
4.8. The Analysis of Density
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shi, Y.; Xie, L.; Thomas Hou, Y.; Sherali, H.D. On renewable sensor networks with wireless energy transfer. In Proceedings of the 2011 IEEE International Conference on Computer Communications (INFOCOM), Shanghai, China, 10–15 April 2011; pp. 1350–1358.
- Xie, L.; Shi, Y.; Thomas Hou, Y.; Sherali, H.D. Making sensor networks immortal: An energy-renewal approach with wireless power transfer. IEEE/ACM Trans. Netw. 2012, 20, 1748–1761. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Shi, Y.; Thomas Hou, Y.; Lou, W.; Sherali, H.D.; Midkiff, S.F. On renewable sensor networks with wireless energy transfer: The multi-node case. In Proceedings of the 2012 9th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Seoul, Korea, 18–21 June 2012; pp. 10–18.
- Xie, L.; Shi, Y.; Thomas Hou, Y.; Lou, A. Wireless power transfer and applications to sensor networks. IEEE Wirel. Commun. 2013, 20, 140–145. [Google Scholar]
- Xie, L.; Shi, Y.; Thomas Hou, Y.; Lou, W.; Sherali, H.D.; Midkiff, S.F. Bundling mobile base station and wireless energy transfer: Modeling and optimization. In Proceedings of the 2013 Proceedings IEEE International Conference on Computer Communications (INFOCOM), Turin, Italy, 14–19 April 2013; pp. 1636–1644.
- Xie, L.; Shi, Y.; Thomas Hou, Y.; Lou, W.; Sherali, H.D.; Zhou, H.; Midkiff, S.F. A mobile platform for wireless charging and data collection in sensor networks. IEEE J. Sel. Areas Commun. 2015, 33, 1521–1533. [Google Scholar] [CrossRef]
- Guo, S.; Wang, C.; Yang, Y. Mobile data gathering with wireless energy replenishment in rechargeable sensor networks. In Proceedings of the 2013 Proceedings IEEE International Conference on Computer Communications (INFOCOM), Turin, Italy, 14–19 April 2013; pp. 1932–1940.
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Minimizing charging delay in wireless rechargeable sensor networks. In Proceedings of the 2013 Proceedings IEEE International Conference on Computer Communications (INFOCOM), Turin, Italy, 14–19 April 2013; pp. 2922–2930.
- Hu, C.; Wang, Y.; Zhou, L. Make Imbalance Useful. In Joint International Conference on Pervasive Computing and the Networked World; Springer International Publishing: Istanbul, Turkey, 2013; pp. 160–171. [Google Scholar]
- Gross, D.; Shortle, J.F.; Thompson, J.M.; Harris, C.M. Fundamentals of Queueing Theory, 4th ed.; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Peng, Y.; Li, Z.; Zhang, W.; Qiao, D. Prolonging sensor network lifetime through wireless charging. In Proceedings of the 2010 IEEE 31st Real-Time Systems Symposium (RTSS), San Diego, CA, USA, 30 November–3 December 2010; pp. 129–139.
- He, L.; Gu, Y.; Pan, J.; Zhu, T. On-demand charging in wireless sensor networks: Theories and applications. In Proceedings of the 2013 IEEE 10th International Conference on Mobile Ad-Hoc and Sensor Systems, Hangzhou, China, 14–16 October 2013; pp. 28–36.
- He, L.; Gu, Y.; Pan, J.; Zhu, T. Evaluating the on-demand mobile charging in wireless sensor networks. IEEE Trans. Mob. Comput. 2015, 14, 1861–1875. [Google Scholar] [CrossRef]




| Reference | Focus on | Energy Constraints of WCV 1 | Traveling Path (Static/Dynamic) |
|---|---|---|---|
| Guo et al. (2013) [8] | Traveling path of WCV | No | Static |
| Fu et al. (2013) [9] | Traveling path of WCV | No | Static |
| Hu et al. (2013) [10] | On-demand mobile charging problem (scheduling) | No | Dynamic |
| Xie et al. (2012–2015) [4,5,6,7] | Traveling path of WCV | No | Static |
| He et al. (2013–2015) [13,14] | On-demand mobile charging problem (scheduling) | No | Dynamic |
| Type | Electromagnetic Induction | Coupling Magnetic Resonance | Micro-Wave Conversion | Laser Light Sensor |
|---|---|---|---|---|
| Theory | Faraday‘s law | Same resonance frequency energy transfer | Electromagnetic wave transfer | Laser and the Solar panels |
| Power transmission | W~hundreds of KW | W~hundreds of KW | >100 mW | hundreds of KW |
| Transmission distance | <10 cm | 5 m | >10 m | >100 m |
| Conversion efficiency | 70% | 50% | 1.6% | 25% |
| Advantage | High conversion efficiency | Multiple charging | Radio wave transmission and automatic charging anywhere | Technology matures over long distances |
| Parameter | The Definition of Parameter |
|---|---|
| BS | Base station |
| N | Set of all sensor nodes |
| CNs | Candidate nodes are the set of nodes selected for charging, |
| En | Energy of sensor node n. |
| Cn | Energy consumption for sensor node n |
| LTn | Rest of the lifetime of sensor node n |
| EDn | Energy demand of sensor node n |
| Bm | Battery for WCV moving |
| Bc | Battery for WCV charging sensor nodes |
| V | Travelling speed of WCV |
| CM | Energy consumption of WCV |
| R | Charging rate of the sensor nodes |
| Di,j | Path distance of Nodei to Nodej |
| Tt | Total travelling time of WCV |
| CG | Consumption grades of sensor nodes |
| CDik | Cumulative total travel time of WCV from Nodei to Nodek |
| CEDik | Cumulative total time of charging the noden from Nodei to Nodek |
| DTik | Delay time of Nodek |
| Parameters | The Value of Parameters | Unit |
|---|---|---|
| Number of sensor nodes | 5 | - |
| Energy consumption for sensor nodes. | 10–20 | J/min |
| Battery capacity of the sensor nodes | 15,000 | J |
| Charging rate of the sensor nodes. | 20 | J/min |
| Parameters | The Value of Parameters | Unit |
|---|---|---|
| Map scale | 100 × 100 | m2 |
| Number of sensor nodes | 100 | - |
| Energy consumption for sensor nodes | 0.2–1 | J/min |
| Battery capacity of the sensor nodes | 15,000 | J |
| Charging rate of the sensor nodes. | 6 | J/min |
| Energy consumption for WCV | 80 | J/min |
| Moving speed of WCV | 1 | m/s |
| Battery capacity of the WCV’s battery for moving | 45,000 | J |
| Battery capacity of the WCV’s battery for charging | 45,000 | J |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.-Y.; Lin, J.-C.; Wu, Y.-F.; Huang, S.-C. MMCS: Multi-Module Charging Strategy for Increasing the Lifetime of Wireless Rechargeable Sensor Networks. Energies 2016, 9, 664. https://doi.org/10.3390/en9090664
Chang H-Y, Lin J-C, Wu Y-F, Huang S-C. MMCS: Multi-Module Charging Strategy for Increasing the Lifetime of Wireless Rechargeable Sensor Networks. Energies. 2016; 9(9):664. https://doi.org/10.3390/en9090664
Chicago/Turabian StyleChang, Hong-Yi, Jia-Chi Lin, Yu-Fong Wu, and Shih-Chang Huang. 2016. "MMCS: Multi-Module Charging Strategy for Increasing the Lifetime of Wireless Rechargeable Sensor Networks" Energies 9, no. 9: 664. https://doi.org/10.3390/en9090664





