A Power Balance Aware Wireless Charger Deployment Method for Complete Coverage in Wireless Rechargeable Sensor Networks
Abstract
:1. Introduction
2. Experimental Section
2.1. Problem Statement
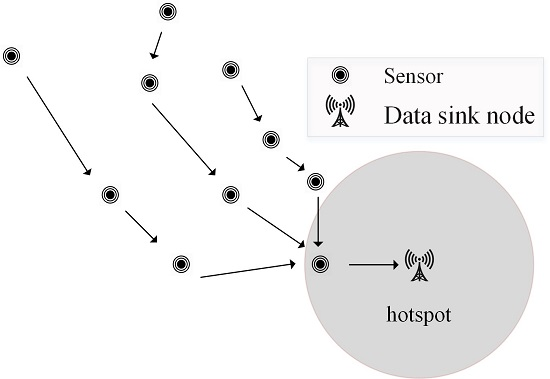
2.1.1. The WRSN Model
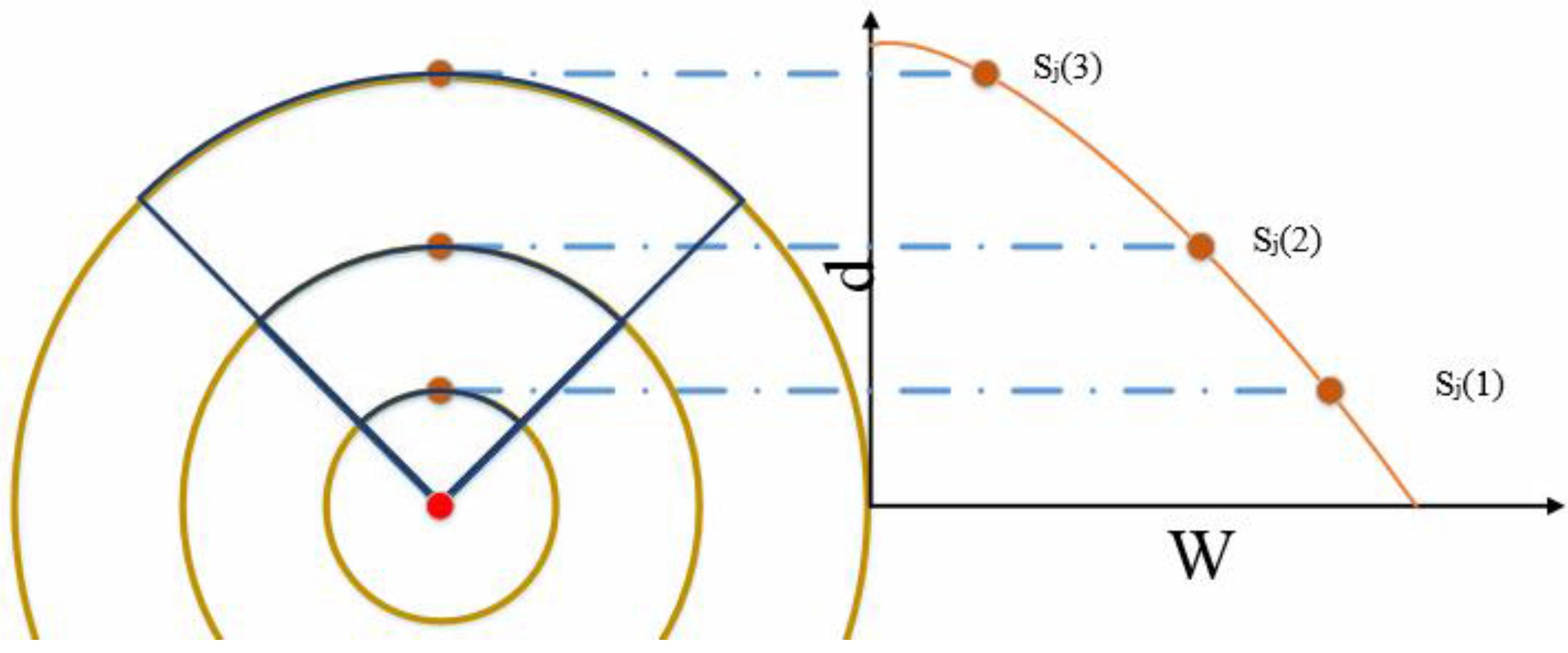
2.1.2. Coverage Area and Charging Power Model
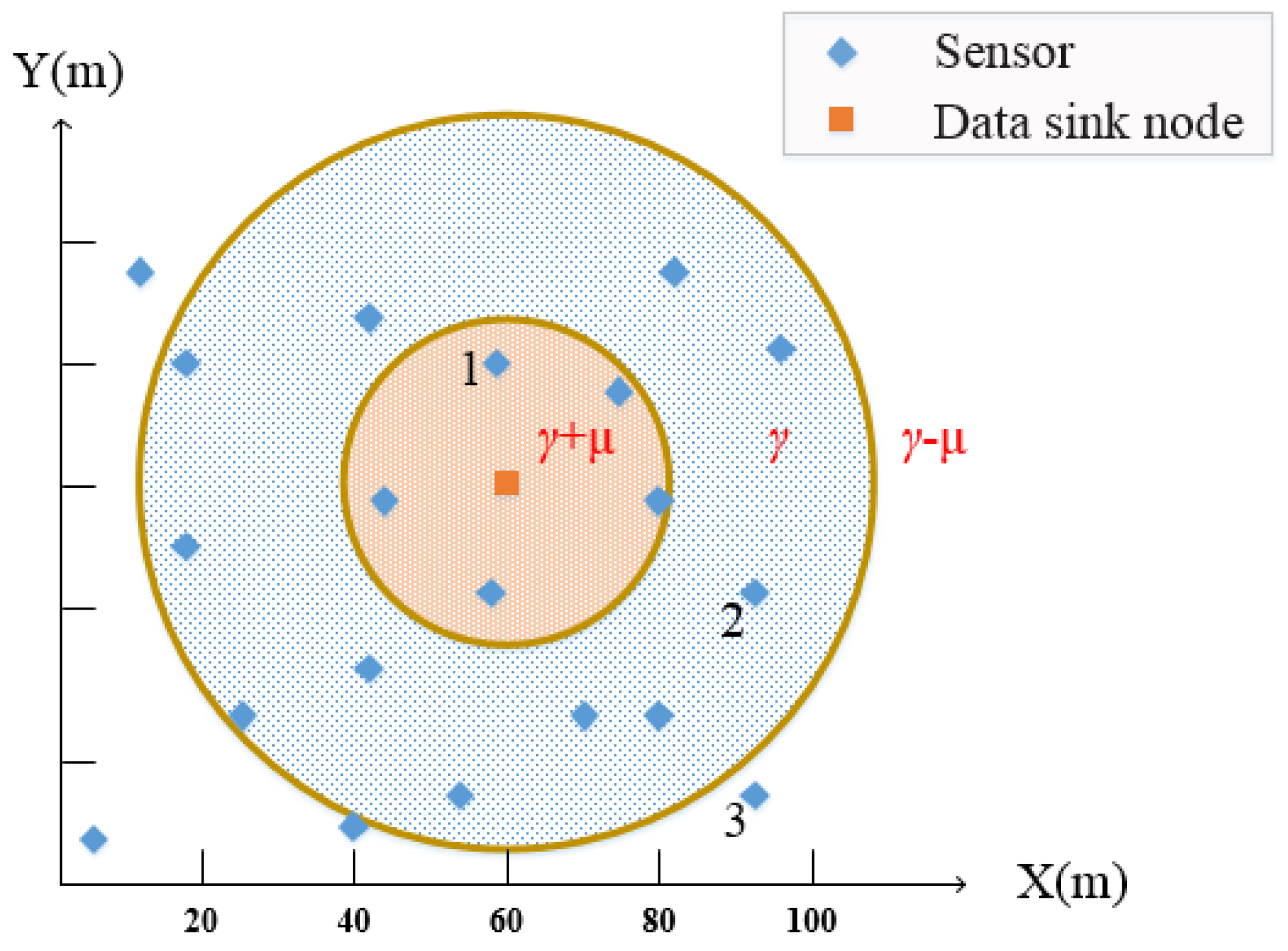
2.1.3. Charging Efficiency and Charging Demand
2.2. Method
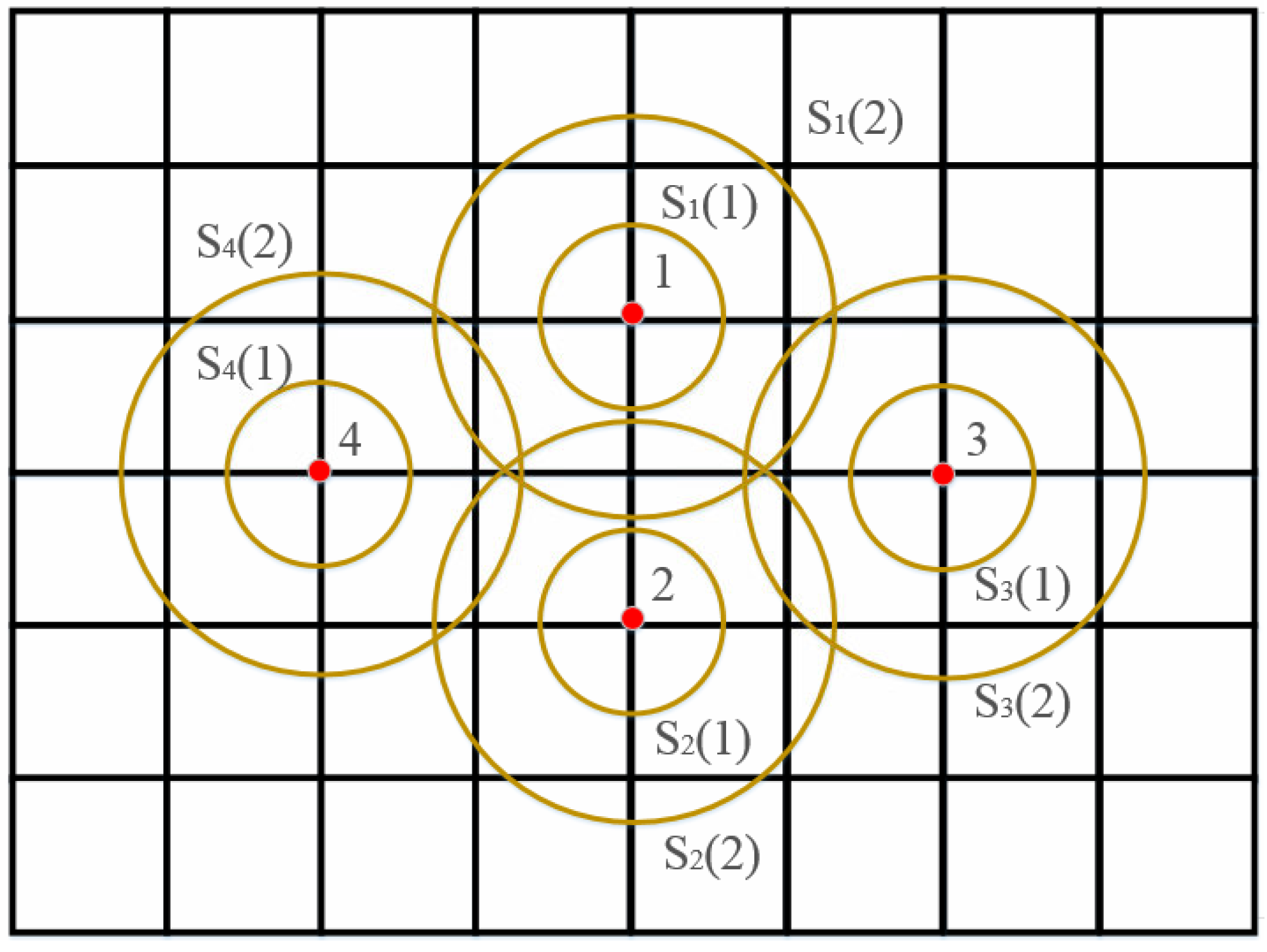
2.2.1. Area Discretization of Charging Power and Charging Demand
2.2.2. Searching for Minimal Dominating Set
| Algorithm 1: Calculate the Coverage Dominating Sets of Given Sensors |
| Input: Directional charger ai, angle θ and the sensor set Si with the locations of all the sensors |
| Output: Coverage Dominating Sets CDSs |
| Step 1. Calculate the included angle between the sensor and the charger; |
| Step 2. Sort sensors using angles, from small to large. θ1 ≤ θ2 ≤…≤ θX with respect to sensors s1, s2,…sX; |
| Step 3. Set a parameter St to record the current coverage set. Two parameters, θmin and θmax, record the minimum and maximum of the current coverage set. Initialize θmin = θ1, θmax = θ1; St = {s1}; |
| Step 4. Starting from second sensors, j = 2; |
| Step 5. Rotate the chargers until no more sensors can be covered. |
| While (θj − θmin ≤ θ){ |
| θmax = θj; |
| Add sj to St; |
| j = (j + 1) mod X; |
| } |
| Step 6. Add the current St to the cover dominating sets CDSs; |
| Step 7. Let θmax = θj and add sj to St; |
| Step 8. Remove the sensor from the smallest angle until the current set can be covered again |
| While(θmax − θmin > θ){ |
| From the St to remove the minimum angle sensor, and θmin update into the current minimum angle value; |
| If(θmin=θ1){ |
| End;} |
| } |
| Go to Step 5. |
| Algorithm 2: Search for the Best Dominating Set |
| Input: Coverage Dominating Sets CDSs |
| Output: The Best Dominating Set BDS |
| Step 1: Calculate the total power P and the charging efficiency W of all Coverage Dominating Sets CDSs using Equations (3) and (4) |
| Step 2: Calculate the charging demand H of all Coverage Dominating Sets CDSs using Equation (5) |
| Step 3: Select the best dominating set BDS with minimum H-W |
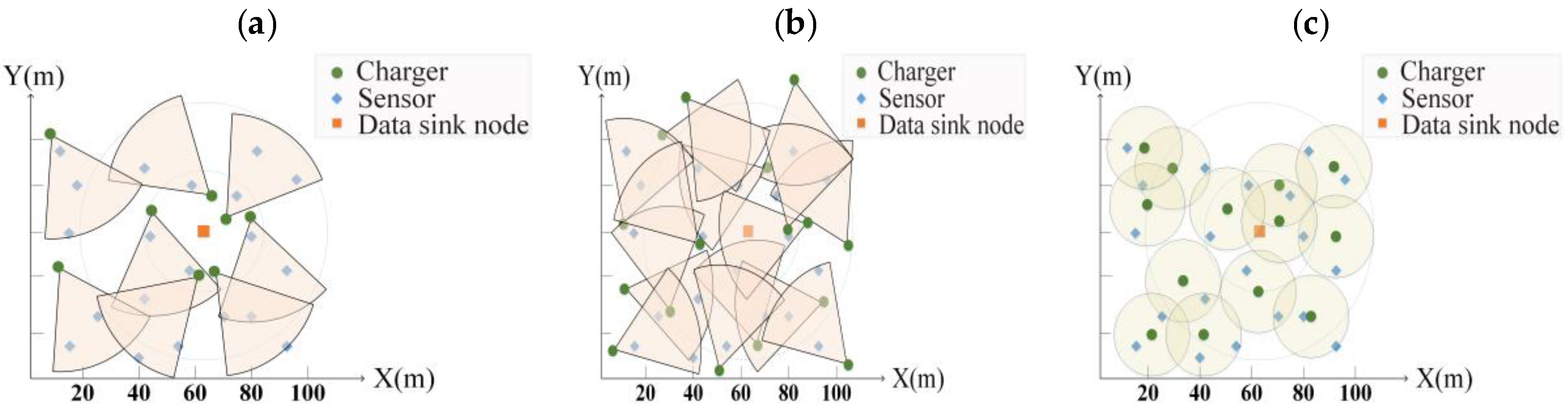
3. Results
3.1. Description of Parameter Setting and Comparisons
3.2. Experimental Results
4. Discussion
4.1. Effects of the Sensor Quantify on Charger Quantity
4.2. Effects of the Adjustment Coefficient of Charging Demand μ
4.3. Effects of the Charging Angle θ
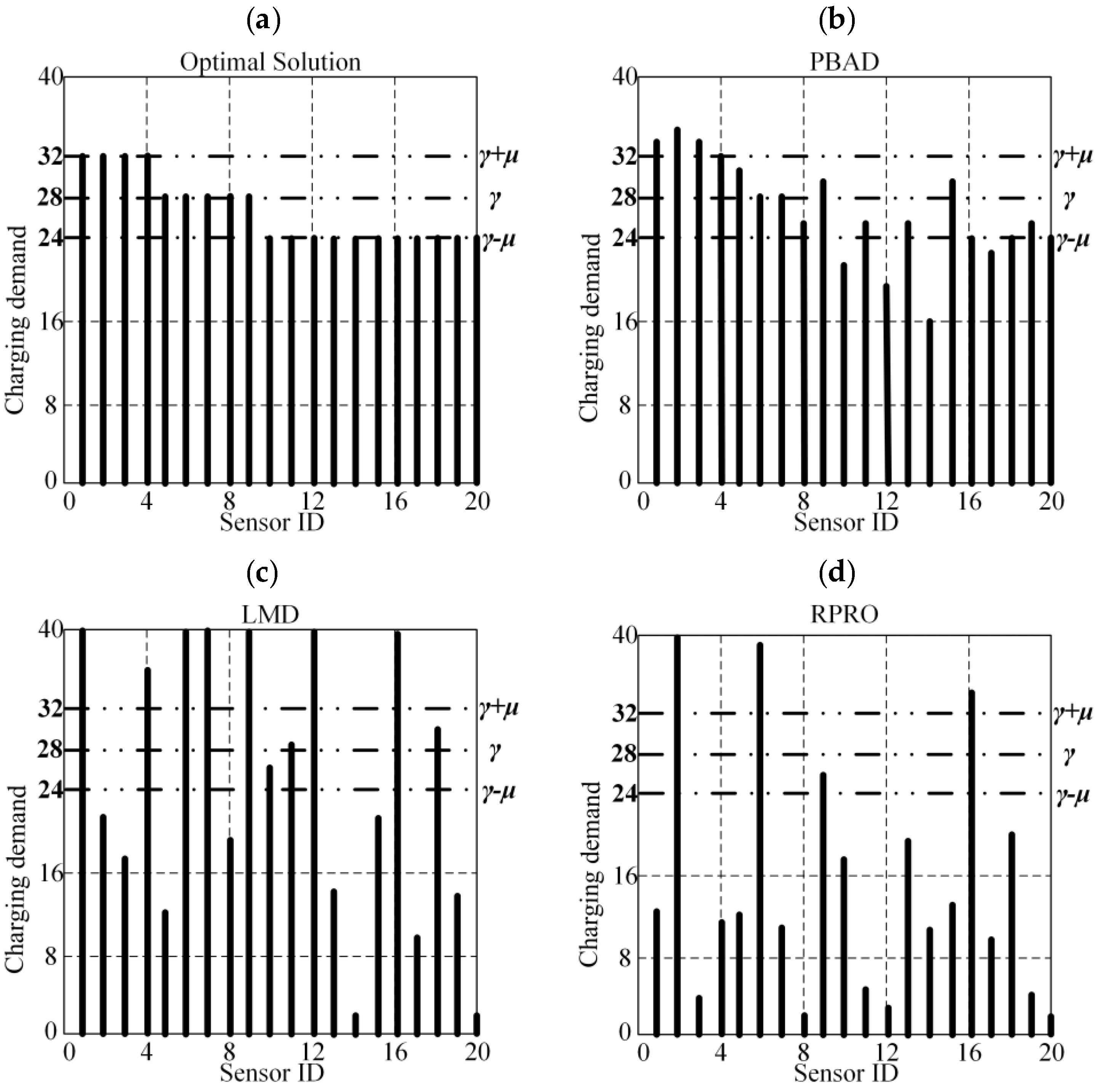
4.4. Charging Efficiency Performance in the Real Case of Each Sensor
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pantazis, N.A.; Nikolidakis, S.A.; Vergados, D.D. Energy-efficient routing protocols in wireless sensor networks: A survey. IEEE Commun. Surv. Tutor. 2013, 15, 551–591. [Google Scholar] [CrossRef]
- Fafoutis, X.; Sørensen, T.; Madsen, J. Energy harvesting—Wireless sensor networks for indoors applications using IEEE 802.11. Procedia. Comput. Sci. 2014, 32, 991–996. [Google Scholar] [CrossRef] [Green Version]
- Sample, A.P.; Meyer, D.T.; Smith, J.R. Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer. IEEE Trans. Ind. Electron. 2010, 58, 544–554. [Google Scholar] [CrossRef]
- Global Wireless Charging Market 2016–2020. Available online: http://www.prnewswire.com/news-releases/global-wireless-charging-market-2016-2020-300196623.html (accessed on 31 July 2016).
- Gilbert, D. Wifi Routers can Wirelessly Charge Batteries, Cameras and Sensors. Available online: http://www.ibtimes.co.uk/wifi-routers-can-wirelessly-charge-batteries-cameras-sensors-1504987 (accessed on 31 July 2016).
- Sendra, S.; Lloret, J.; Garcia, M.; Toledo, J.F. Power saving and energy optimization techniques for wireless sensor neworks. J. Commun. 2011, 6, 439–459. [Google Scholar] [CrossRef]
- Bri, D.; Garcia, M.; Lloret, J.; Dini, P. Real deployments of wireless sensor networks. In Proceedings of the IEEE Third International Conference on Sensor Technologies and Applications, Athens/Glyfada, Greece, 18–23 June 2009; pp. 415–423.
- Li, J.; Mohapatra, P. Analytical modeling and mitigation techniques for the energy hole problem in sensor networks. Pervasive Mob. Comput. 2007, 3, 233–254. [Google Scholar] [CrossRef]
- Lian, J.; Naik, K.; Agnew, G.B. Data capacity improvement of wireless sensor networks using non-uniform sensor distribution. Int. J. Distrib. Sens. Netw. 2006, 2, 121–145. [Google Scholar] [CrossRef]
- He, S.; Chen, J.; Jiang, F.; Yau, D.K.Y.; Xing, G.; Sun, Y. Energy provisioning in wireless rechargeable sensor networks. IEEE Trans. Mob. Comput. 2013, 12, 1931–1942. [Google Scholar] [CrossRef]
- Chiu, T.-C.; Shih, Y.-Y.; Pang, A.-C.; Jeng, J.-Y.; Hsiu, P.-C. Mobility-aware charger deployment for wireless rechargeable sensor networks. In Proceedings of the 14th IEEE Asia-Pacific Network Operations and Management Symposium, Seoul, Korea, 25–27 September 2012; pp. 1–7.
- Liao, J.-H.; Jiang, J.R. Wireless charger deployment optimization for wireless rechargeable sensor networks. In Proceedings of the 7th IEEE International Conference on Ubi-Media Computing, Ulaanbaatar, Mongolia, 12–14 July 2014; pp. 160–164.
- Horster, E.; Lienhart, R. Approximating optimal visual sensor placement. In Proceedings of the 2006 IEEE International Conference on Multimedia and Expo, Toronto, ON, Canada, 9–12 July 2006; pp. 1257–1260.
- Han, X.; Cao, X.; Lloyd, E.L.; Shen, C.-C. Deploying directional sensor networks with guaranteed connectivity and coverage. In Proceedings of the 5th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, San Francisco, CA, USA, 16–20 June 2008; pp. 153–160.
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Minimizing charging delay in wireless rechargeable sensor networks. In Proceedings of the IEEE INFOCOM 2013, Turin, Italy, 14–19 April 2013; pp. 2922–2930.
- Garey, M.R.; Johnson, D.S. Computers and Intractibility: A Guide to the Theory of Np-Completeness; W.H. Freeman and Company: New York, NY, USA, 1979. [Google Scholar]
- Ai, J.; Abouzeid, A.A. Coverage by directional sensors in randomly deployed wireless sensor networks. J. Comb. Optim. 2006, 11, 21–41. [Google Scholar] [CrossRef]
- Dai, H.; Liu, Y.; Chen, G.; Wu, X.; He, T. Safe charging for wireless power transfer. In Proceedings of the IEEE INFOCOM 2014, Toronto, ON, Canada, 27 April–2 May 2014; pp. 1105–1113.







| Name | Type | Contribution | Power Balance Aware |
|---|---|---|---|
| Energy provisioning in wireless rechargeable sensor networks. [10] | Omnidirectional charger | Physical characteristics of wireless charging | No |
| Mobility-aware charger deployment for wireless rechargeable sensor networks. [11] | Omnidirectional charger | A sensing model for optimization of mobile deployment | No |
| Optimized charger deployment for wireless rechargeable sensor networks. [12] | Omnidirectional charger | Charger sleep scheduling | No |
| Minimizing charging delay in wireless rechargeable sensor networks. [15] | Omnidirectional charger | Robot stop locations in discrete areas | No |
| Approximating optimal visual sensor placement. [13] | Directional charger | Grid linear programming | No |
| Deploying directional sensor networks with guaranteed connectivity and coverage. [14] | Directional charger | Considers the fact that the sensors are connected to each other | No |
| Symbol | Corresponding Meaning |
|---|---|
| Z | Selected 2D region |
| x | Number of sensors |
| sj | The sensor j |
| m | The number of chargers |
| ai | The charger i |
| Y | The data sink node |
| θ | Charging angle |
| r | Charger radius |
| Direction vector of a charger | |
| The vector of the charger and sensor | |
| σ | The factor affecting charging effect |
| Wmax | Upper bound value of charging power |
| γ | The average charging demand |
| μ | The charging demand adjustment coefficient |
| f | The specific distance which influences the charging demand |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, T.-L.; Li, S.-L.; Chang, H.-Y. A Power Balance Aware Wireless Charger Deployment Method for Complete Coverage in Wireless Rechargeable Sensor Networks. Energies 2016, 9, 695. https://doi.org/10.3390/en9090695
Lin T-L, Li S-L, Chang H-Y. A Power Balance Aware Wireless Charger Deployment Method for Complete Coverage in Wireless Rechargeable Sensor Networks. Energies. 2016; 9(9):695. https://doi.org/10.3390/en9090695
Chicago/Turabian StyleLin, Tu-Liang, Sheng-Lin Li, and Hong-Yi Chang. 2016. "A Power Balance Aware Wireless Charger Deployment Method for Complete Coverage in Wireless Rechargeable Sensor Networks" Energies 9, no. 9: 695. https://doi.org/10.3390/en9090695
APA StyleLin, T.-L., Li, S.-L., & Chang, H.-Y. (2016). A Power Balance Aware Wireless Charger Deployment Method for Complete Coverage in Wireless Rechargeable Sensor Networks. Energies, 9(9), 695. https://doi.org/10.3390/en9090695