Energy Optimization in Smart Homes Using Customer Preference and Dynamic Pricing
Abstract
:1. Introduction
- Initially, we categorize different homes and appliances by considering electricity prices, person occupancies and environmental conditions to manage energy consumption. Then, we propose mathematical optimization models of major household appliances to manage the energy consumption of all types of appliances. To maximize end user comfort, user-dependent appliances are introduced, which take into consideration human activities.
- We propose a centralized energy optimization algorithm, which considers different constraints to minimize the overall energy consumption and electricity bill up-to ℏ homes (Section 4, Figure 1). However, prior to the selection and implementation of an optimization algorithm, different algorithms are tested and validated using the fmincon and lsqnonlin solvers (Table 3).
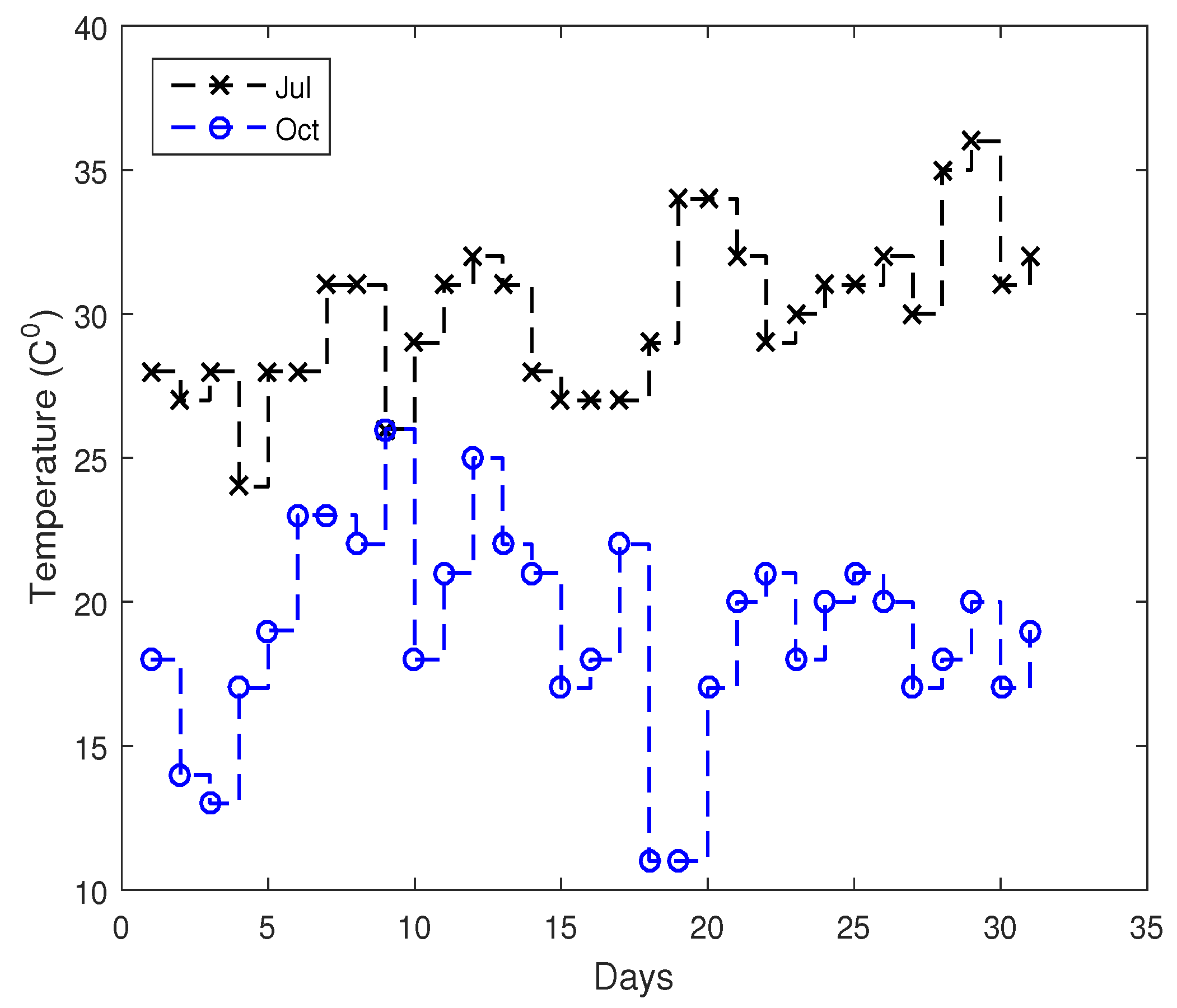
- The influence of external temperature and variations in energy demand on DR programs is also analysed (details are given in Section 5.3). From this analysis, it is concluded that weather has a great impact on the energy consumption and DR programs based on which utilities and consumers manage their schedules.
- Finally, extensive simulations have been performed to evaluate the effectiveness of the proposed algorithm in different scenarios.
2. Related Work
- Price-based DR programs: Most of the published articles focus on DSM and direct load control (DLC) strategies to manage the energy demand during critical peak hours [2,3,4,5]. In these techniques, users may pause or turn-off unnecessary load to reduce their electricity cost. However, these techniques may disturb end user comfort. In [6], the authors have proposed a DR model under a dynamic pricing environment to reduce electricity cost and user discomfort. To maximize end user comfort, appliances are divided into different categories, such as deferrable, curtailable, thermal and critical. To reduce high peaks during low pricing hours, maximum energy consumption limits to restrict the customers to consume energy under the given limits are imposed. Users consuming more energy beyond these limits are charged high prices. In this work, again, the trade-off between user comfort and electricity cost reduction is found. However, the utility gains the benefit in terms of increased system stability. In another similar work, the authors introduce energy consumption limits in each time slot to reduce the electricity cost of end users [7,8]. Although this technique has shown a remarkable impact in terms of cost saving, the major drawback associated with this scheme are frequent disconnections and discouragement of consumers in participating in DR programs. In addition, users may feel discomfort while doing their daily life activities, because most of the DR programs are designed for grid stability and peak reduction [5,6,7,8,9].In [10,11], the authors consider only deferrable appliances, whereas [12] is limited to thermal loads only. In [13], a hybrid technique is proposed, which jointly controls the working of all, thermal, deferrable and non-interruptible, loads. In [14], mathematical models of various types of home appliances are proposed based on their energy demand and operating modes. After appliance classification, the energy management problem is formulated as a mixed integer nonlinear programming (MINLP) problem, which later on is solved using Benders’ decomposition approach. This scheme reduces the electricity cost with maximum appliance utility. However, user comfort has not been modelled in an effective way. In [15,16], the energy consumption of different types of appliances is managed, such that the major focus is on appliance scheduling, Peak to Average Ratio (PAR). and electricity cost reduction, as well as comfort management. However, a significant amount of energy is wasted due to unnecessary appliance operation. In [17,18], appliance scheduling schemes based on customer reward (CR) are proposed to avoid high peaks; customers are given incentives to shift load from on-peak hours to off-peak hours. However, comfort-aware customers cannot take full advantage of these types of schemes due to energy limits imposed by utilities. In conclusion, price based DR programs are efficient in reducing the electricity cost of end users along with PAR reduction, however at the cost of user comfort. The reason is the inconsideration of user behaviour in DSM programs.
- Comfort-aware DR programs: In [19], a user comfort-aware load management algorithm is proposed to schedule the aggregate load of a household. The game theoretic approach is used to solve the optimization problem, aiming at minimizing end user cost while preserving end user comfort. Unlike the other schemes, this scheme gives users the choice to prioritize either comfort or electricity cost reduction. In [20], the authors present a user-aware game theoretic approach for demand management, which considers user preferences. Both hard and soft appliances are considered, including deferrable and non-deferrable categories, where users have options to either choose comfort or cost saving. For this purpose, the authors introduce a weight factor to prioritize comfort over cost. However, users cannot achieve both objectives at the same time. Moreover, appliance scheduling for minimum electricity cost may lead to high peaks during low pricing hours and may disturb user comfort [21]. In [22,23], the Markov chain is used to model a very limited set of user activities; using a personal computer, cooking activity and performing no activity. Based on these activities, total energy demand is calculated. Although these schemes prove to be efficient in terms of energy management, without the DR program, it is difficult to reduce end user cost. In [9], the authors schedule background loads, like refrigerator and humidifiers, by using the early deadline first technique. Non-background loads are not involved in the scheduling process, because these may affect user comfort. Each disconnected appliance is assigned a slack time, which is the maximum time for which any appliance remains disconnected from the power source. Afterwards, appliances with minimum slack time are turned-on. The authors also impose a power limit on aggregated power consumed by the background load. Although this scheme is efficient in terms of cost reduction, end user comfort is disturbed due to the high slack time of appliances and energy consumption limits.
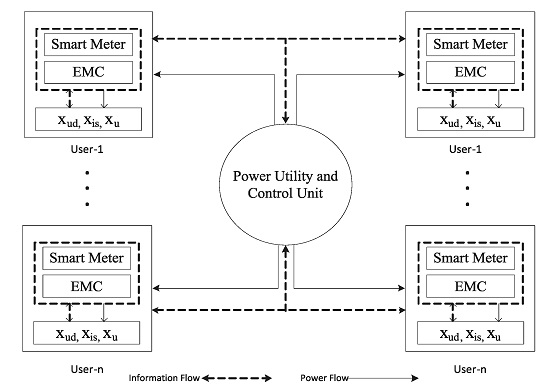
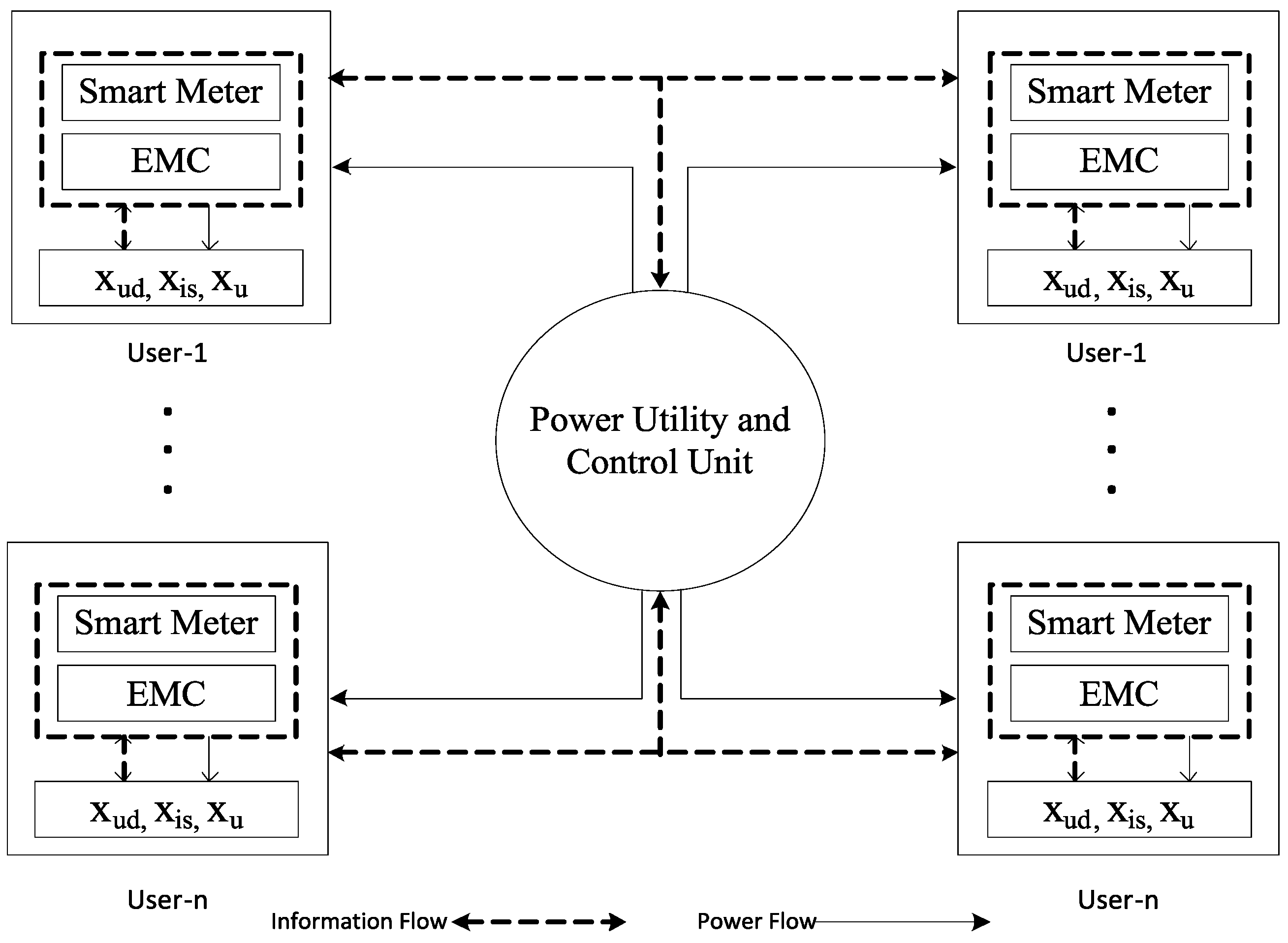
3. System Model
3.1. User Dependent
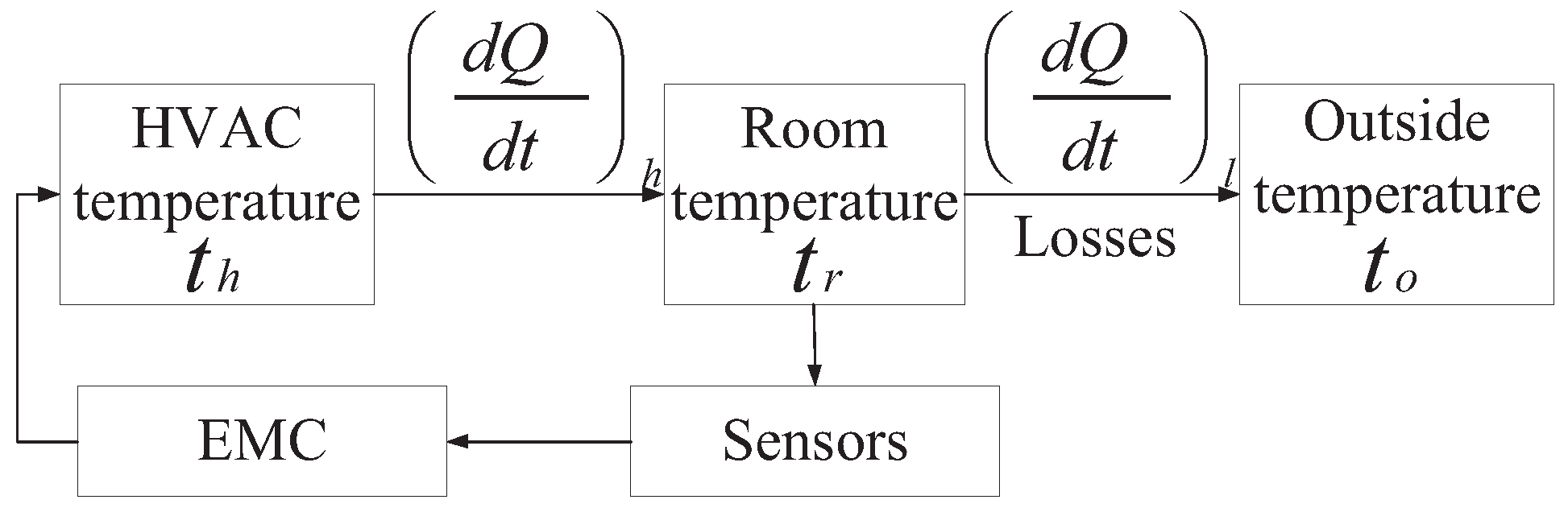
3.1.1. HVAC
| Algorithm 1 Pseudo code of the HVAC working. |
| 1: begin |
| 2: Initialize parameters: , |
| 3: for all do |
| 4: for all do |
| 5: if number of occupants > 0 and () then |
| 6: solve objective Function (6) |
| 7: calculate |
| 8: else |
| 9: if number of occupants ≤ 0 and () then |
| 10: |
| 11: , go to Step 4; till T |
| 12: end if |
| 13: end if |
| 14: end for |
| 15: end for |
| 16: end |
3.1.2. Refrigerator
- = temperature of the refrigerator
- = time interval ()
- τ = duty cycle
- = heat losses during the OFF state
- = cooling effect during the ON state
- = heat loss due to .
3.1.3. Washing Machine
3.1.4. Lights with Controllable Brightness
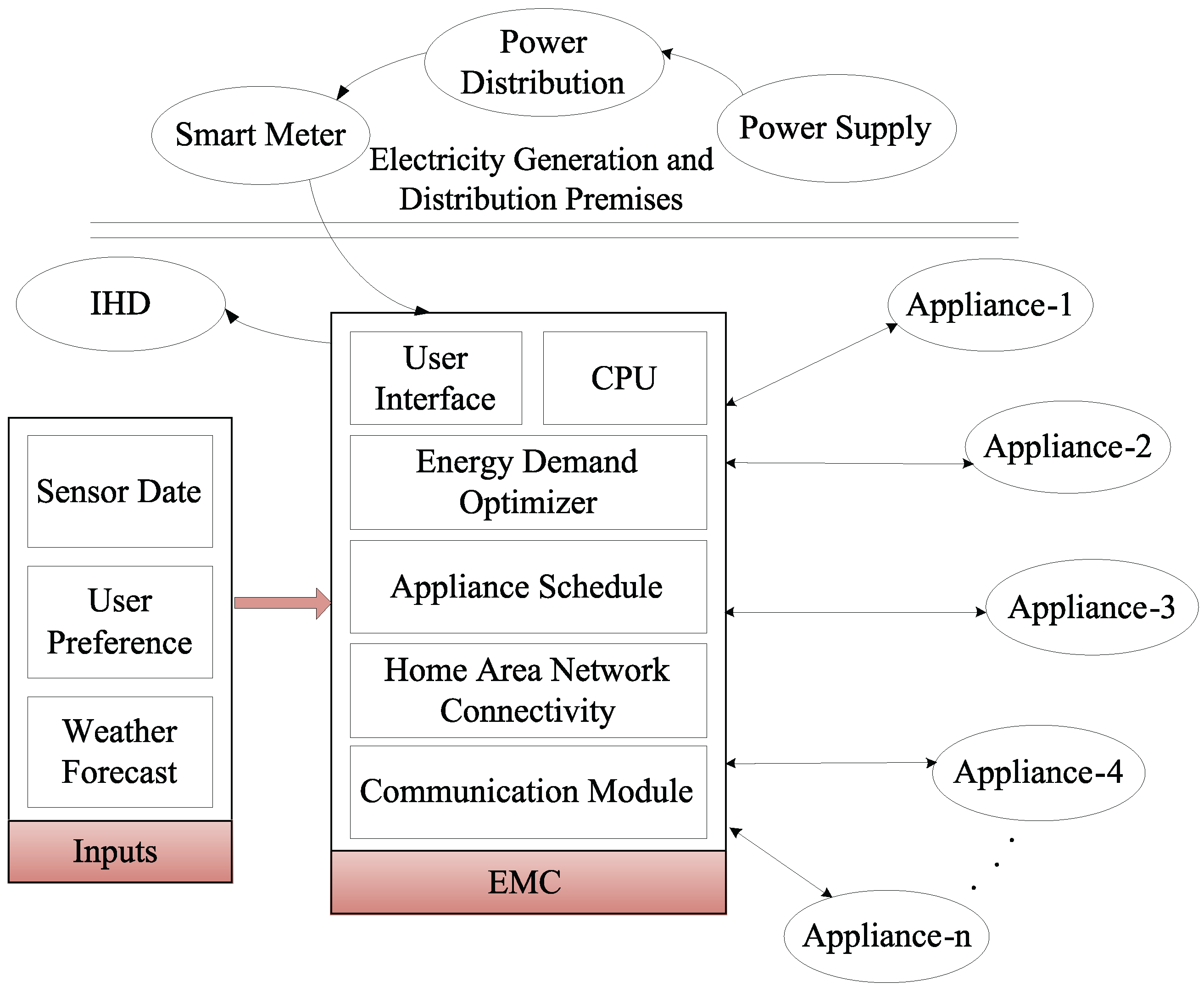
3.2. Interactive Schedulable
3.2.1. Dish Washer
3.2.2. Lights without Controllable Brightness
3.3. Unschedulable
4. Energy Demand Optimization
4.1. The Proposed Scheduling Algorithm
4.2. Load Scheduling
4.3. PAR Reduction
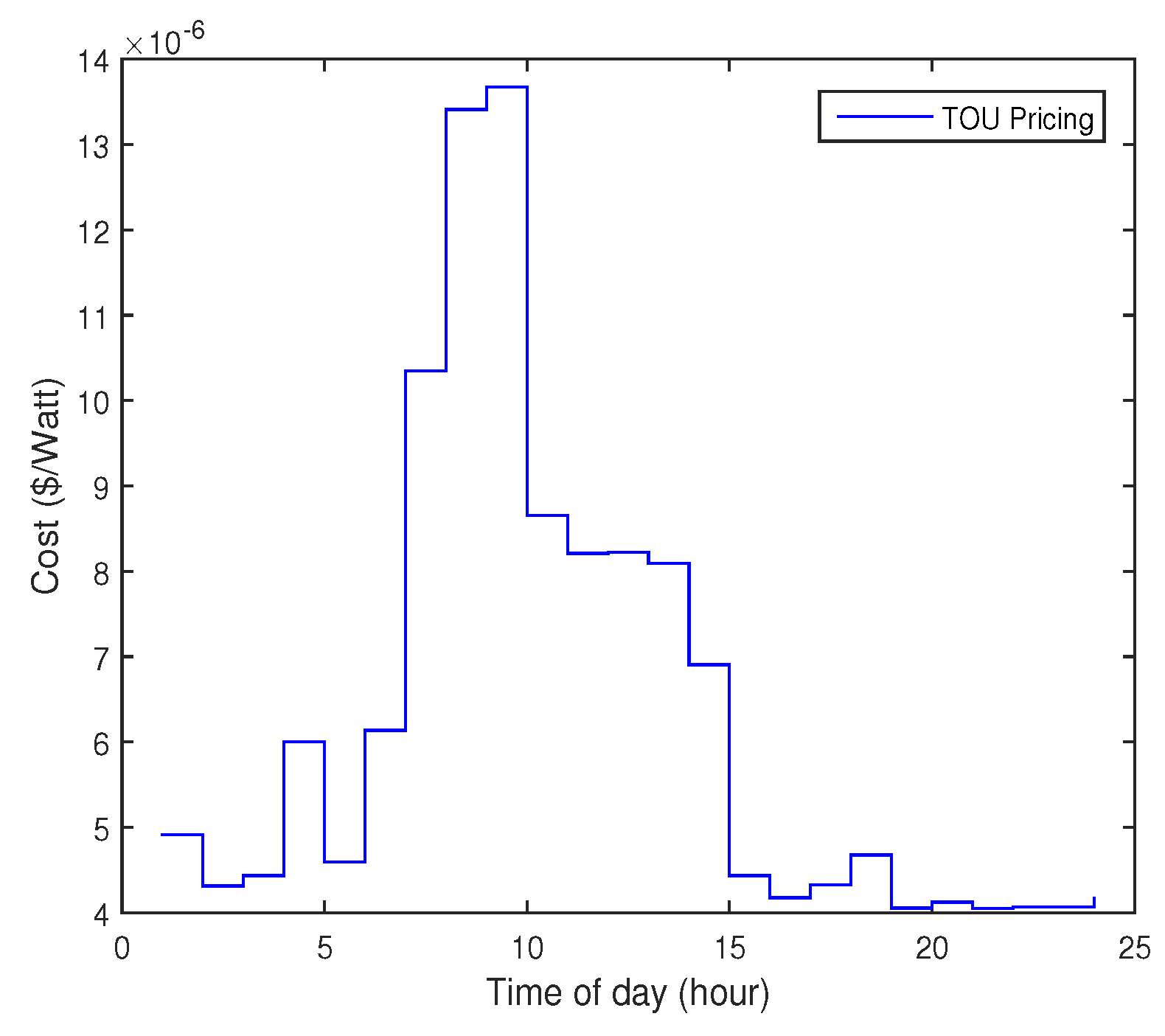
5. Performance Evaluation
5.1. Simulation Set-Up
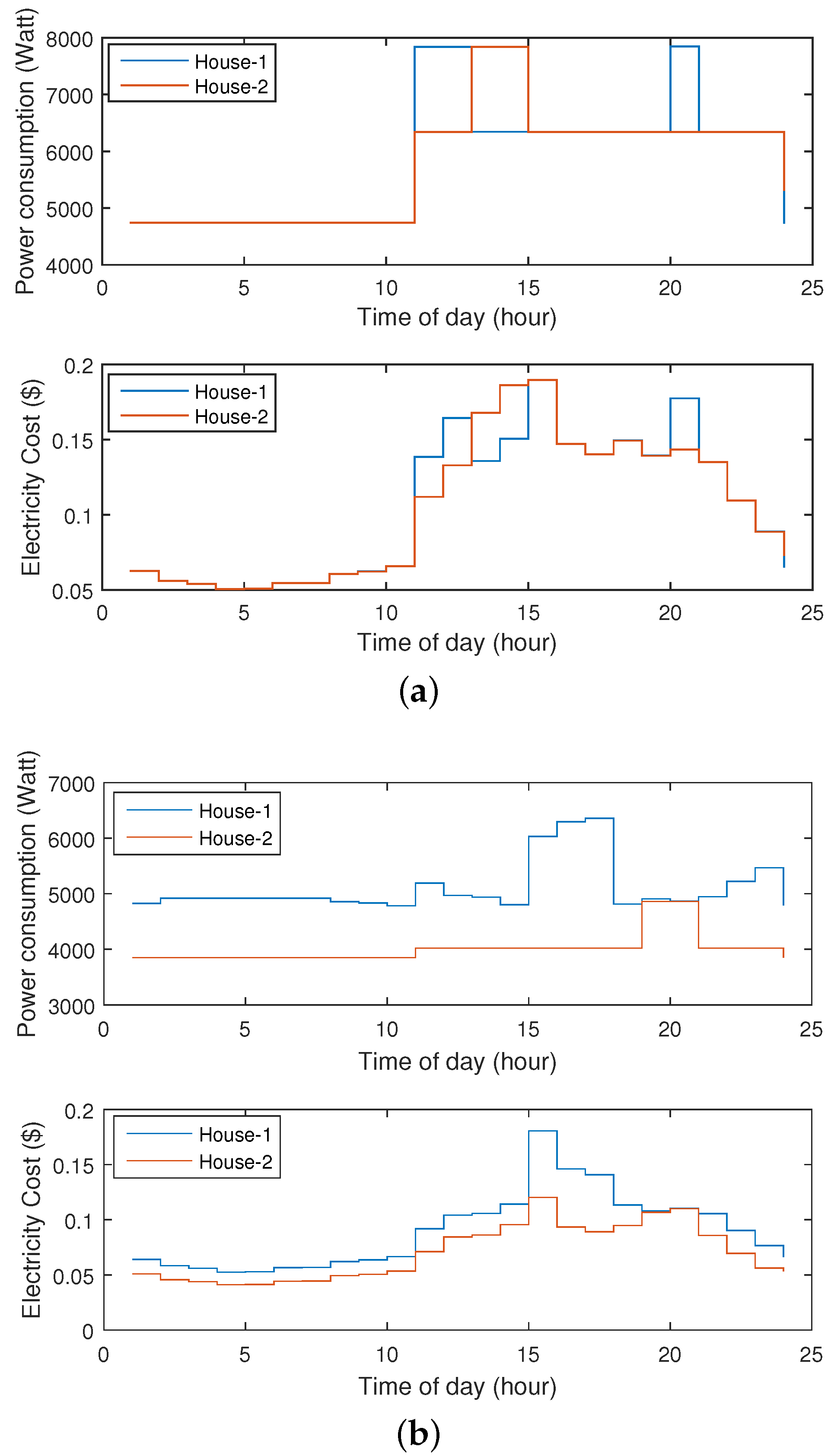
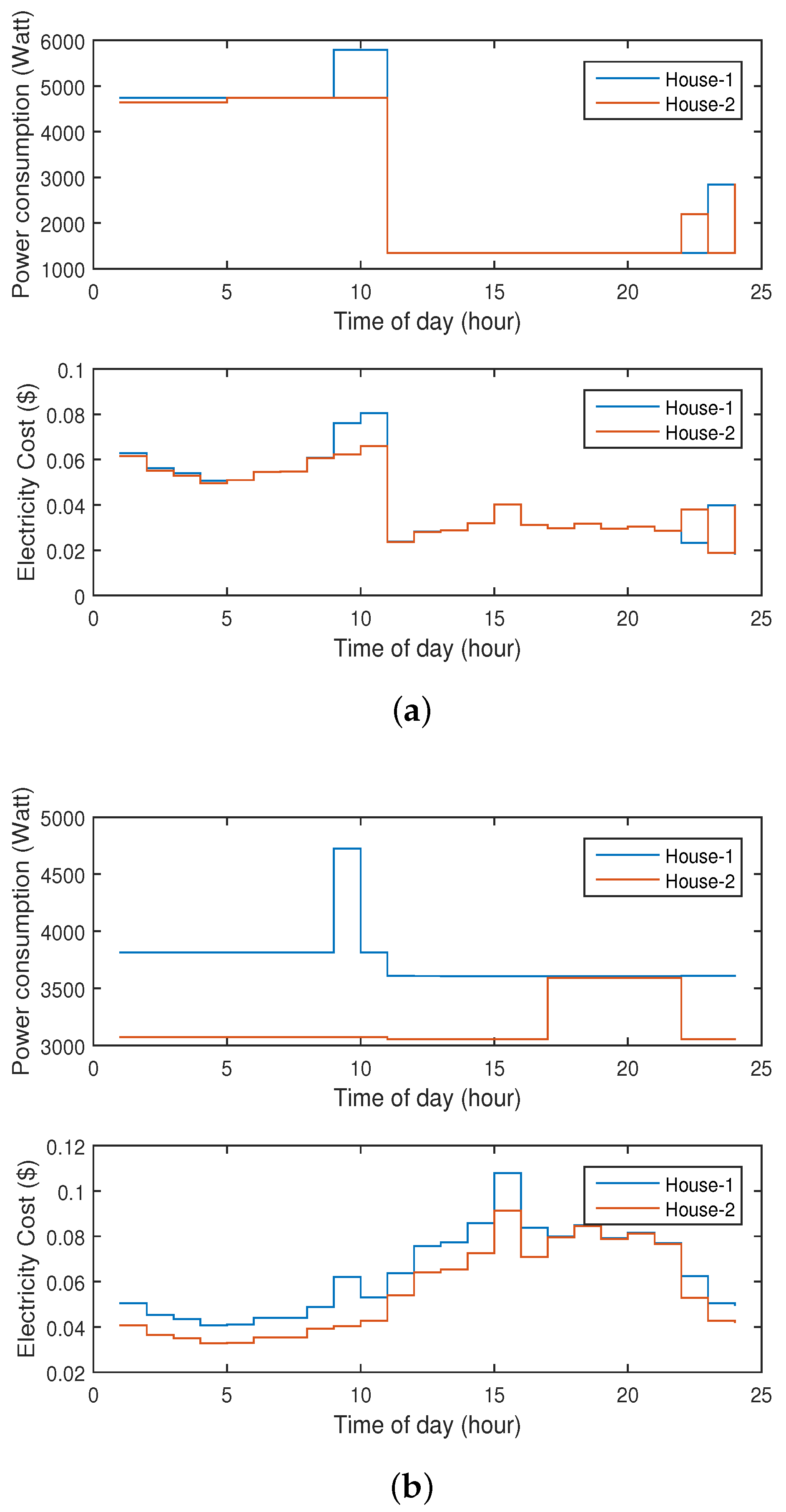
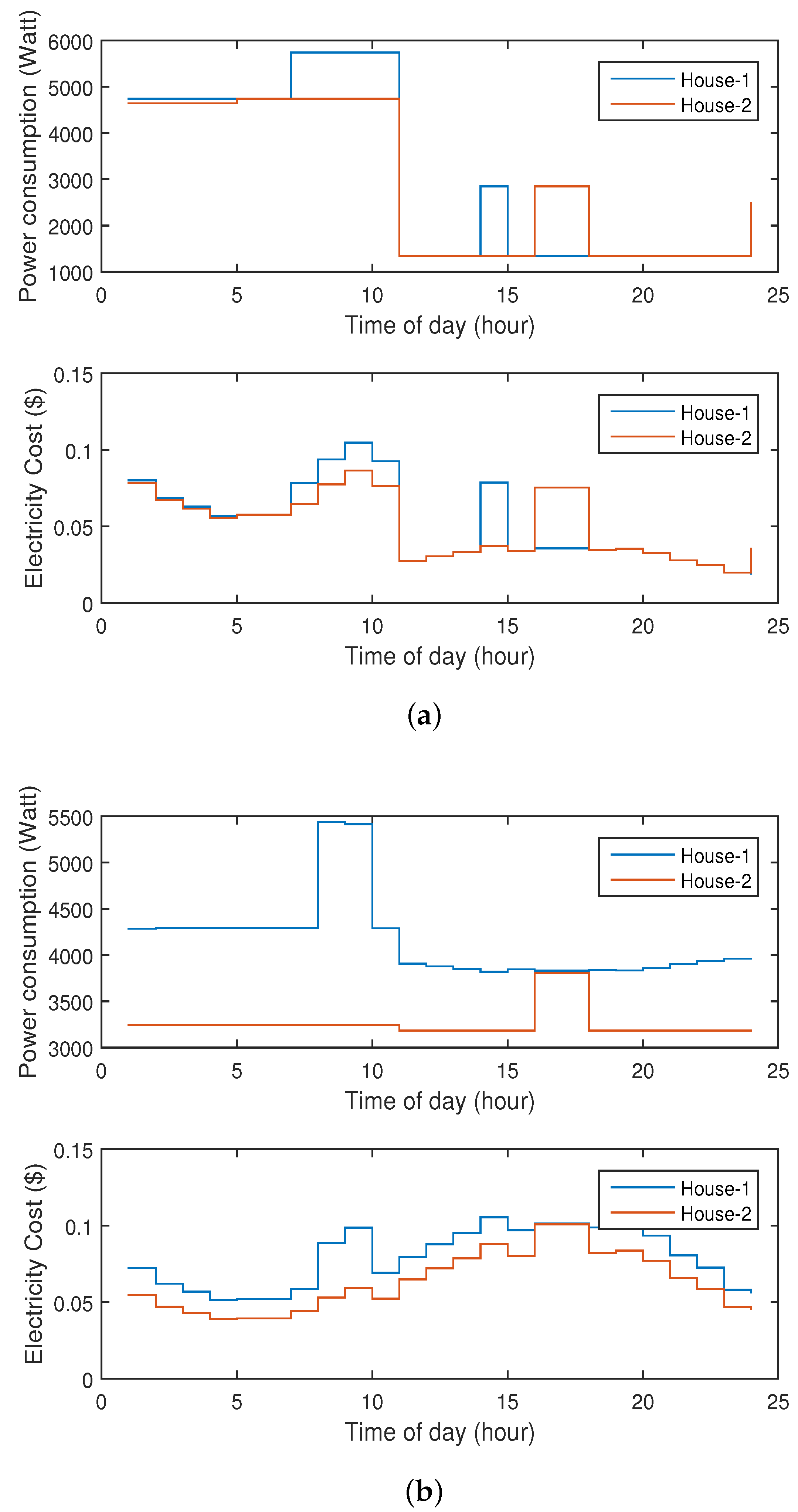
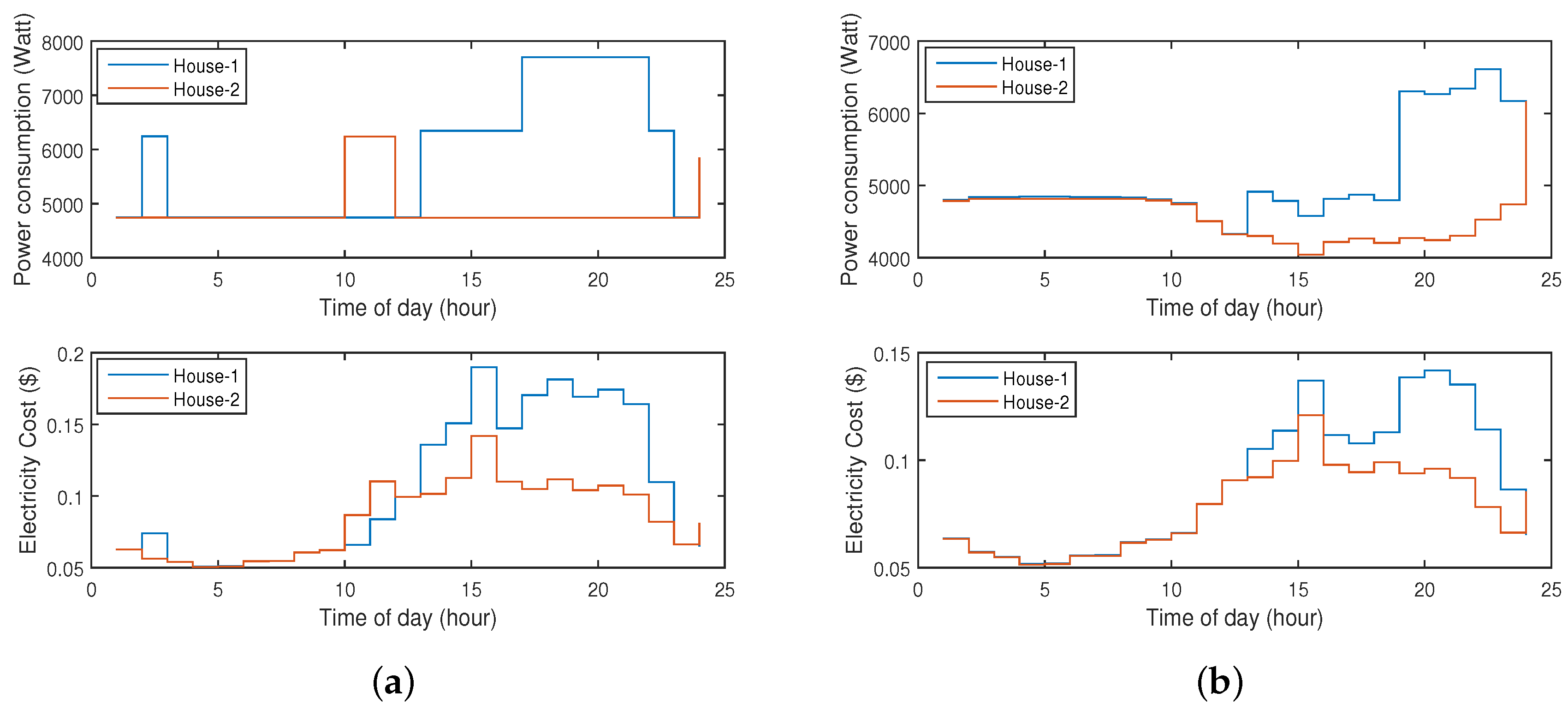
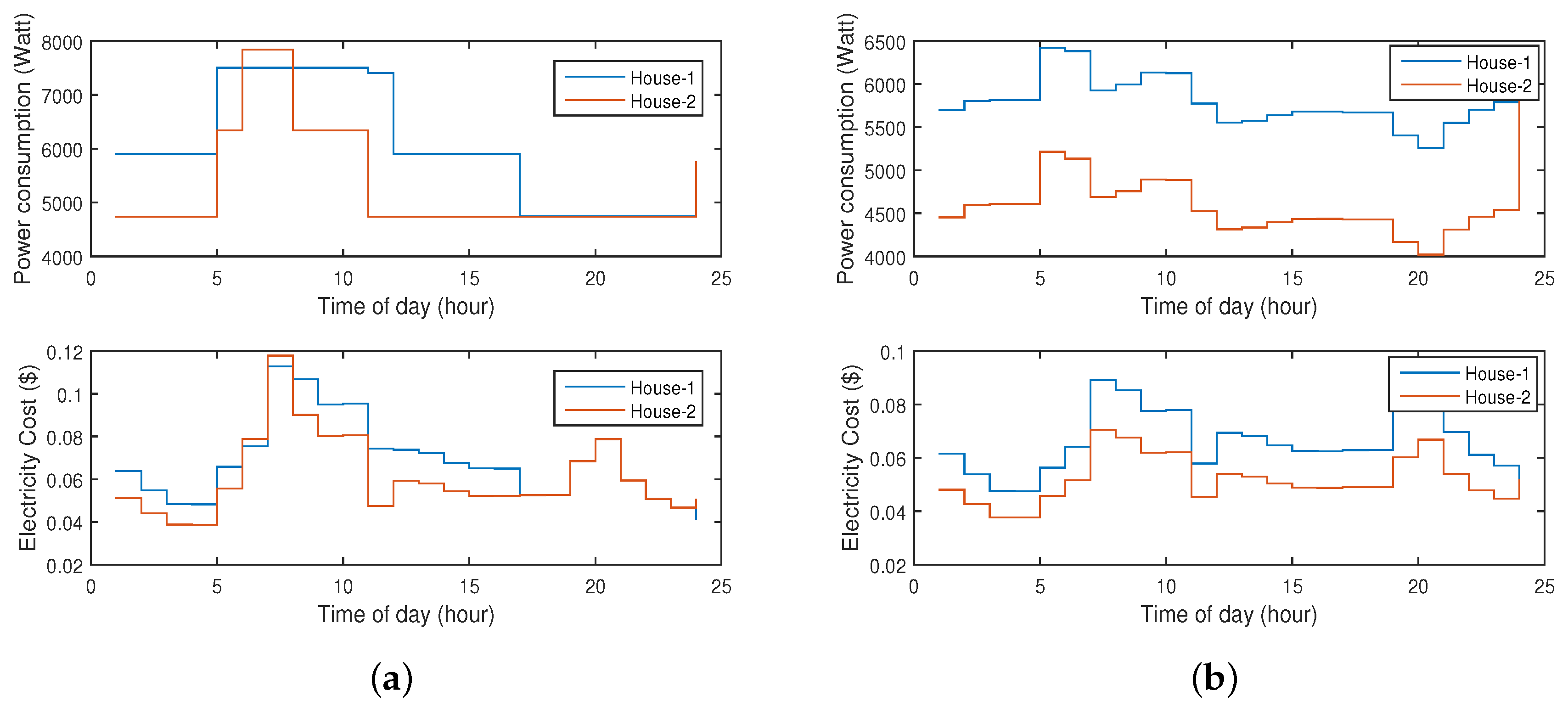
5.2. Results and Discussion
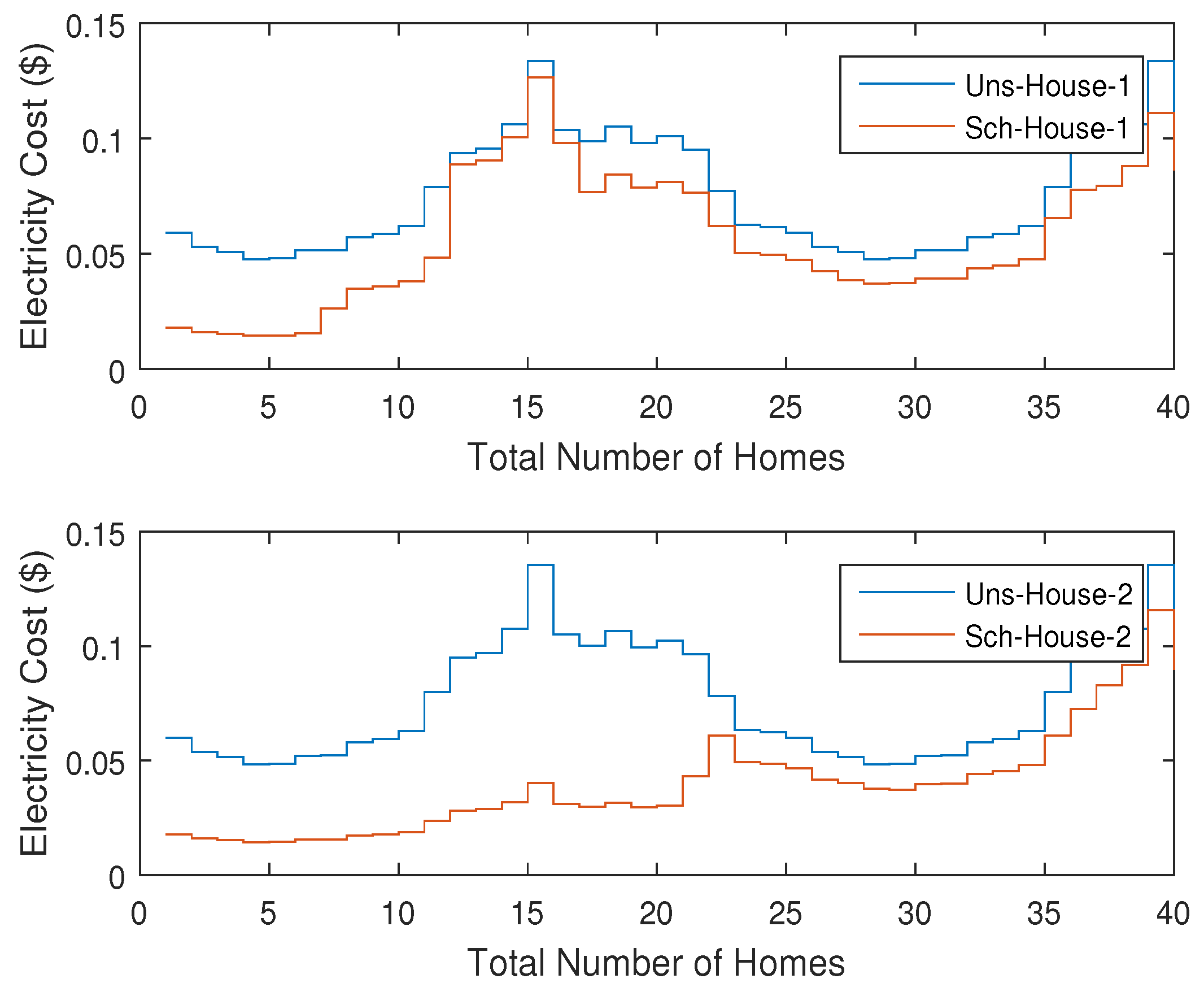
5.3. Impact of Seasons on the Energy Optimization
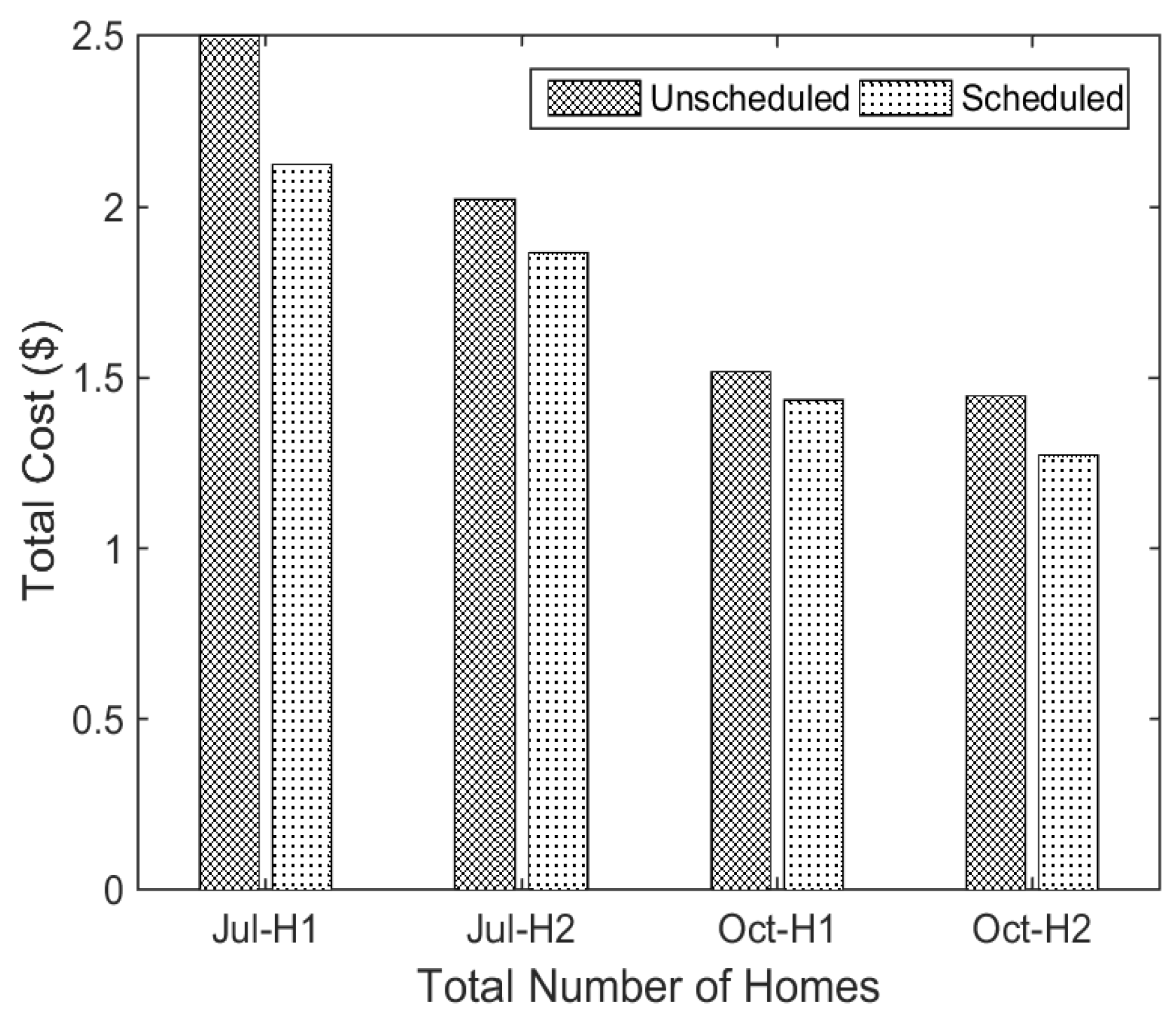
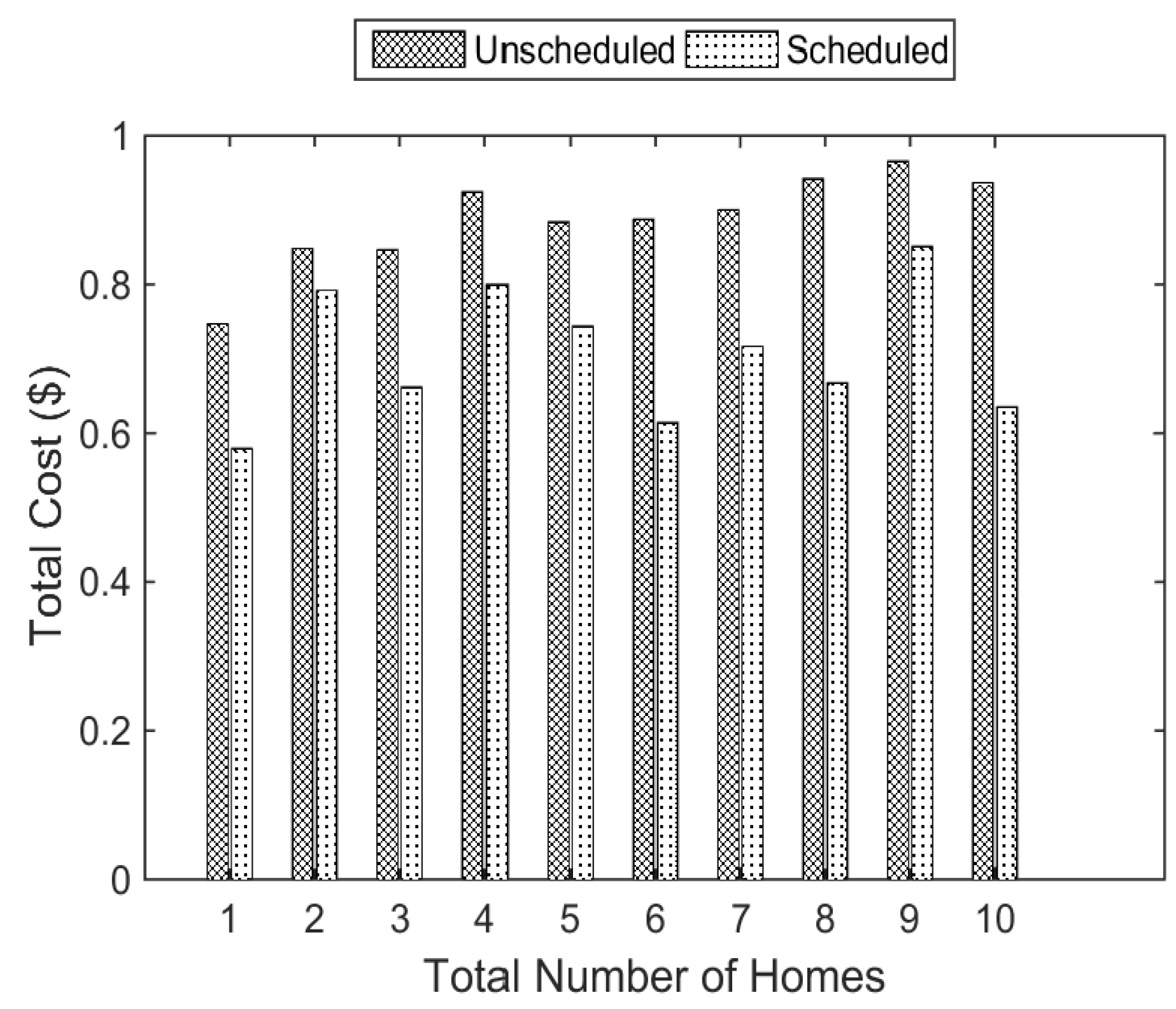
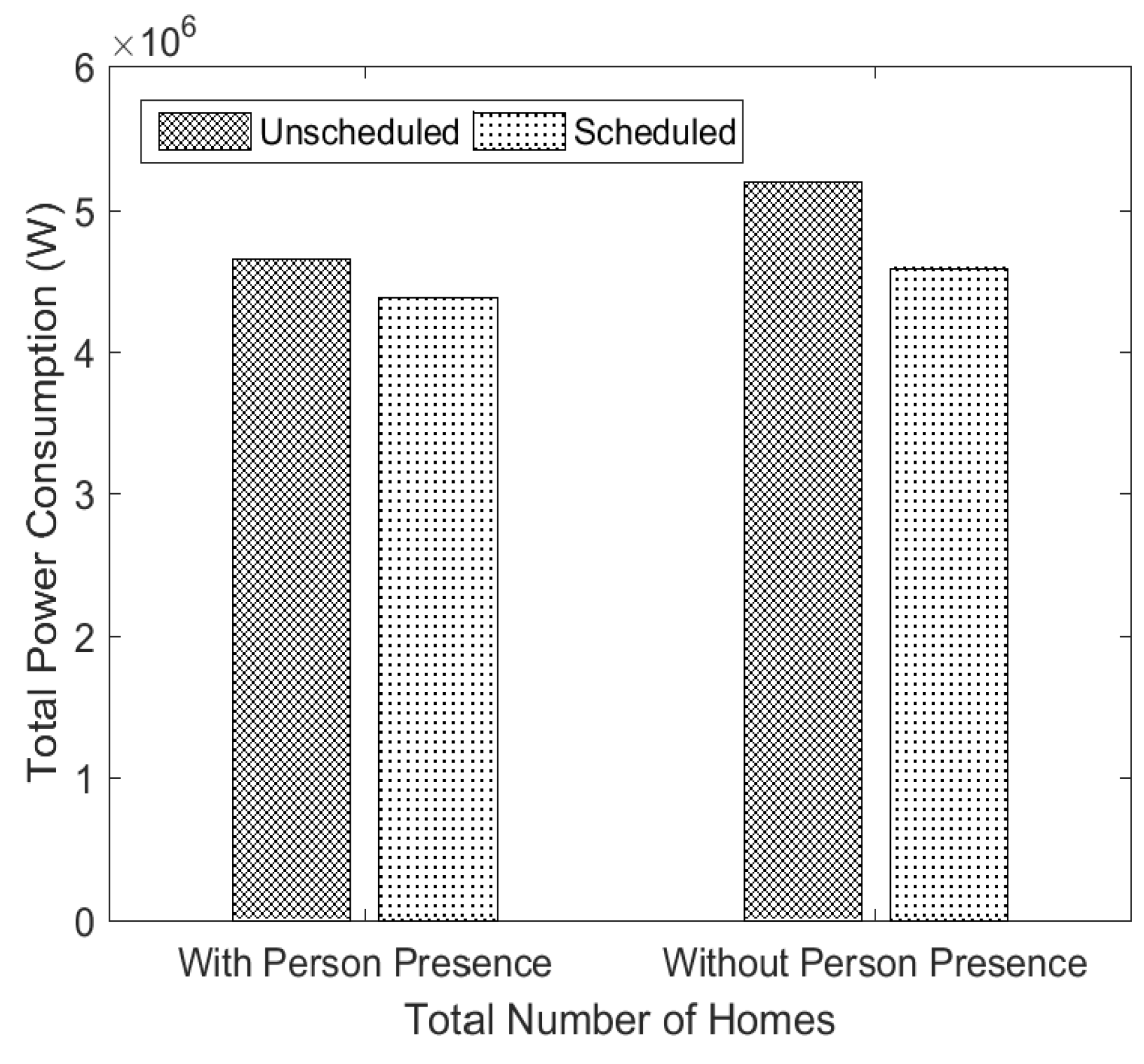
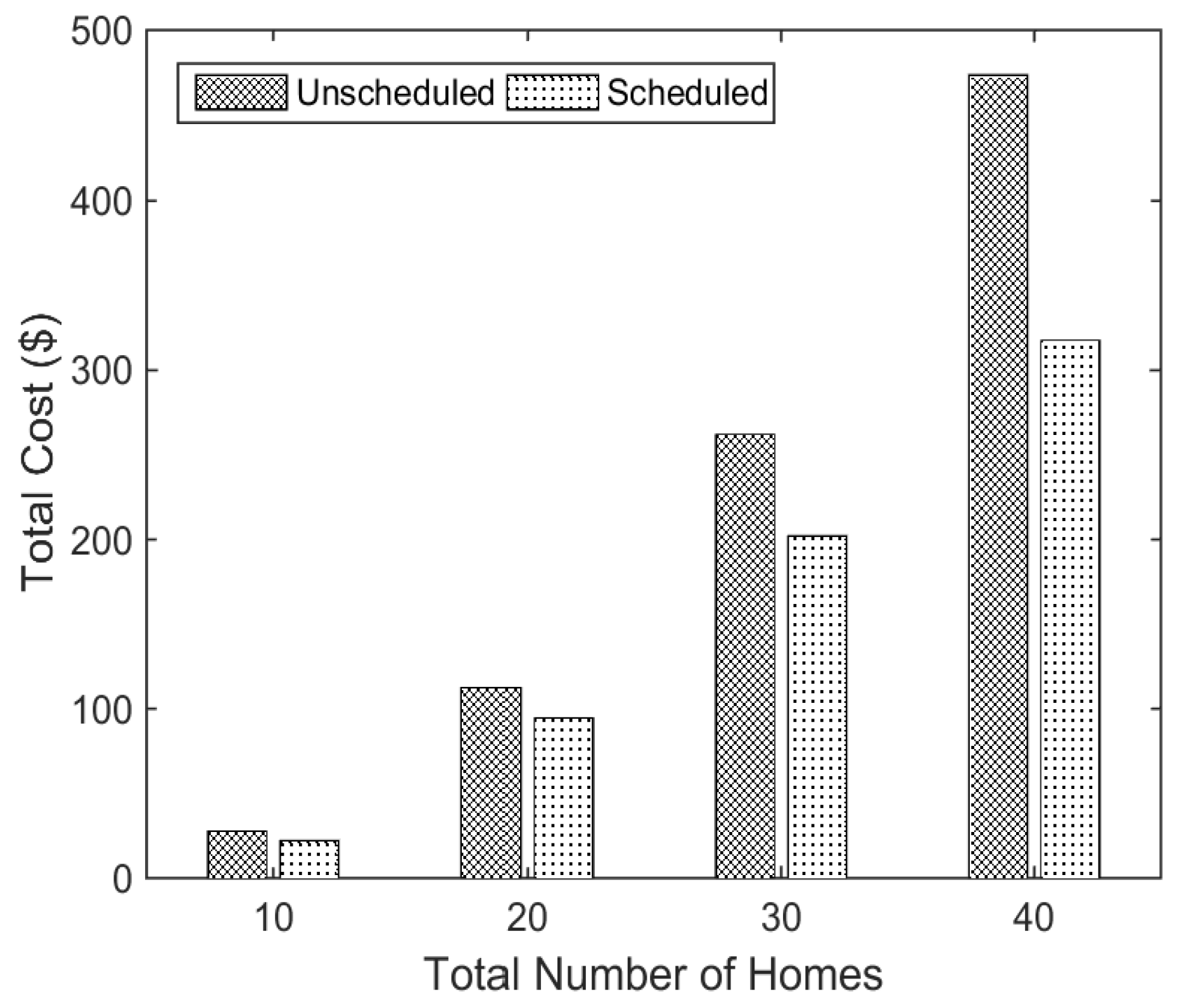
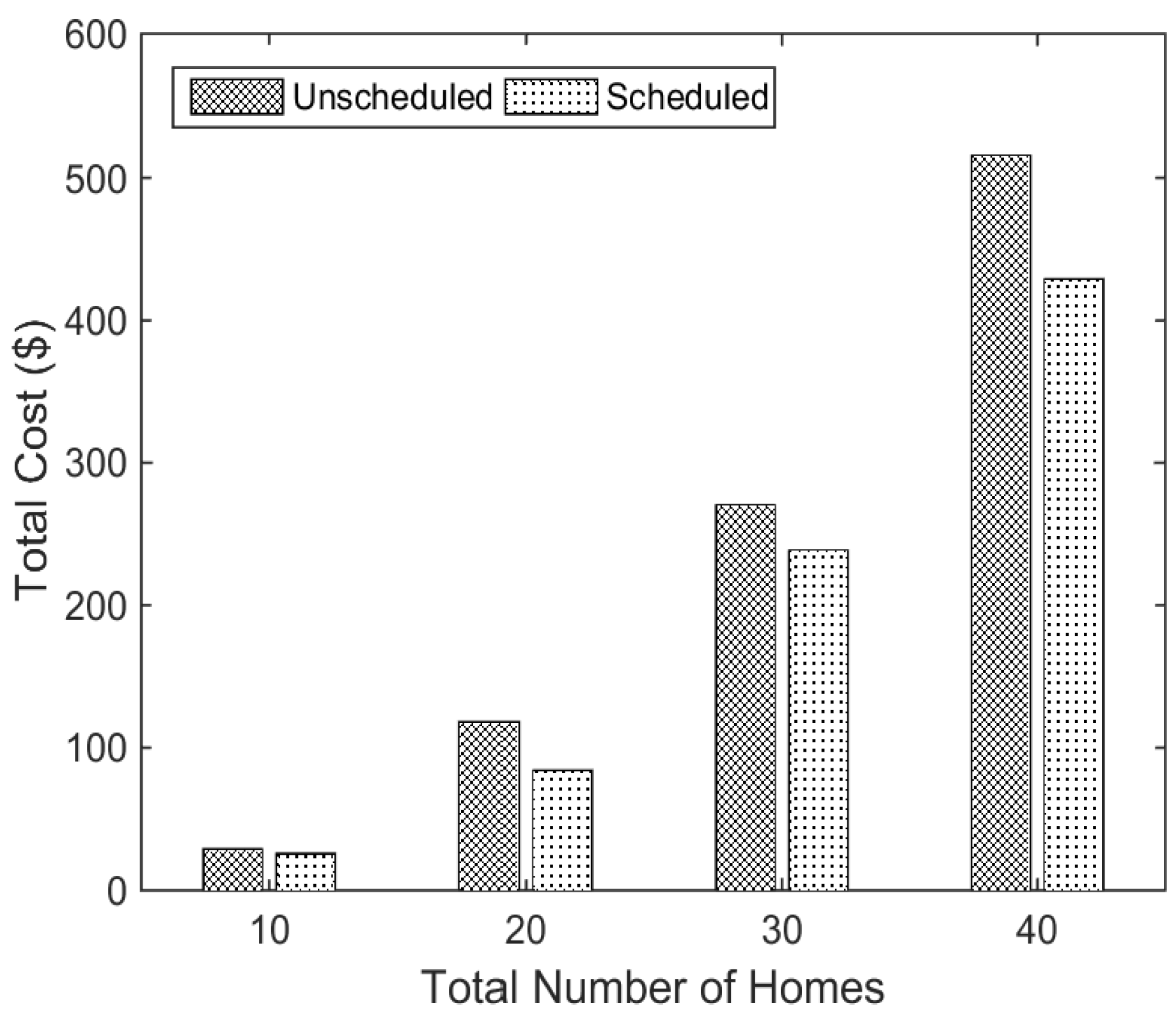
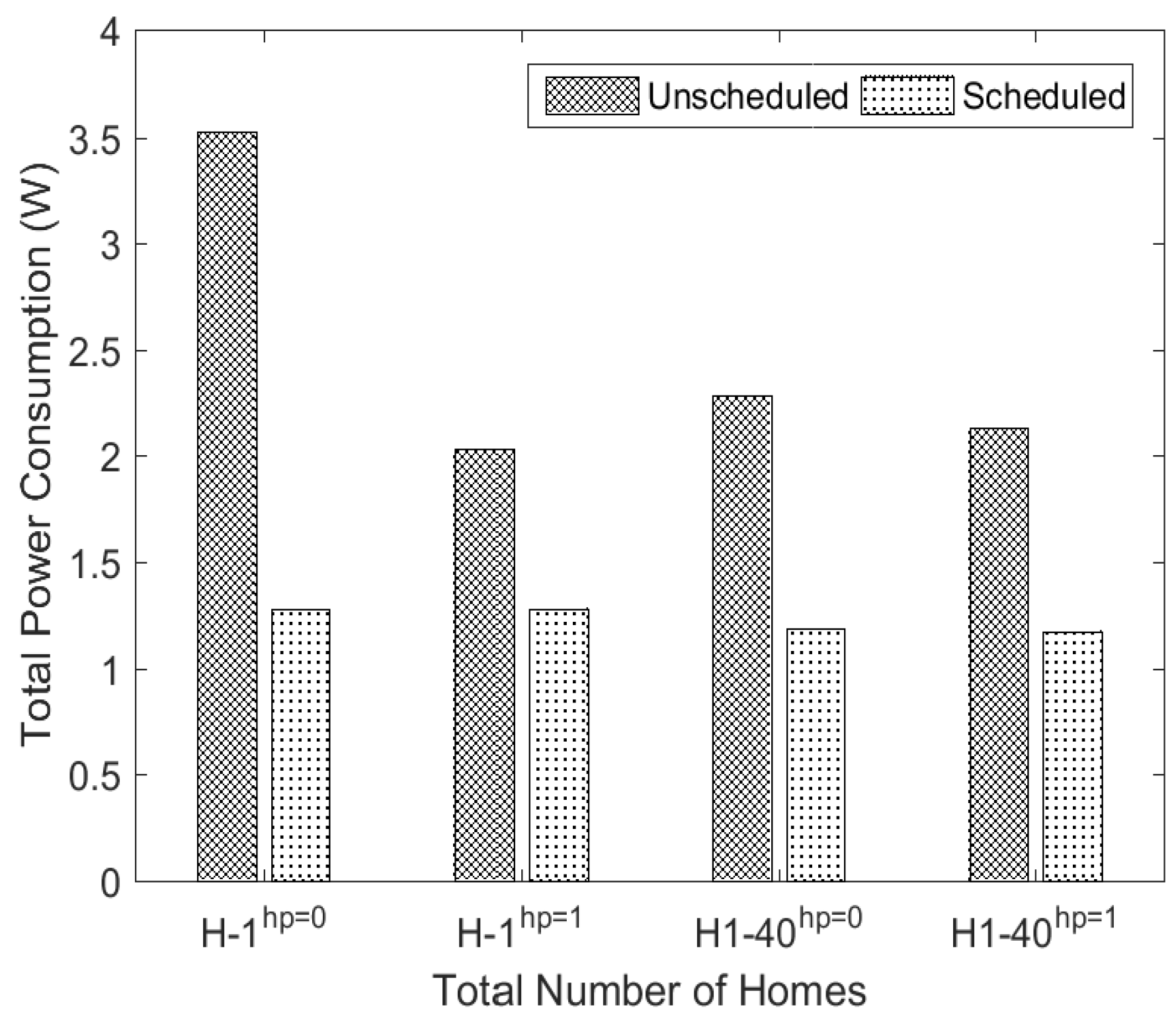
5.4. Impact of Number of Homes
5.5. Impact of PAR
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclatures
| Symbol | Description | Symbol | Description |
| user-dependent appliances | electricity unit price | ||
| interactive schedulable appliances | ψ | appliance ON/OFF status | |
| unschedulable appliances | T | total time horizon | |
| γ | residential units | ζ | energy consumption threshold |
| minimum energy consumption | χ | appliance set | |
| maximum energy consumption | human presence | ||
| minimum temperature | maximum temperature | ||
| scheduling horizon | appliance starting time | ||
| total energy consumption | Boolean variable for ON/OFF status | ||
| ϱ | small change in temperature | equivalence resistance of room | |
| M | HVAC air flow rate | C | specific heat capacity |
| heat exchange | outside temperature | ||
| room temperature | appliance utility function s | ||
| total electricity cost | C | electricity cost | |
| appliance finishing time | homes | ||
| HVAC temperature | temperature difference |
References
- Bose, B.K. Global Warming: Energy, Environmental Pollution, and the Impact of Power Electronics. IEEE Ind. Electron. Mag. 2010, 4, 6–17. [Google Scholar] [CrossRef]
- Ye, F.; Qian, Y.; Hu, R.Q. A Real-Time Information Based Demand-Side Management System in Smart Grid. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 329–339. [Google Scholar] [CrossRef]
- Rasheed, M.B.; Javaid, N.; Ahmad, A.; Khan, Z.A.; Qasim, U.; Alrajeh, N. An Efficient Power Scheduling Scheme for Residential Load Management in Smart Homes. Appl. Sci. 2015, 5, 1134–1163. [Google Scholar] [CrossRef]
- Salehfar, H.; Patton, A. Modeling and evaluation of the system reliability effects of direct load control. IEEE Trans. Power Syst. 1989, 4, 1024–1030. [Google Scholar] [CrossRef]
- Sianaki, O.A.; Hussain, O.; Tabesh, A.R. A Knapsack problem approach for achieving efficient energy consumption in smart grid for endusers’ life style. In Proceedings of the IEEE Conference on Innovative Technologies for an Efficient and Reliable Electricity Supply (CITRES), Waltham, MA, USA, 27–29 September 2010.
- Althaher, S.; Mancarella, P.; Mutale, J. Automated demand response from home energy management system under dynamic pricing and power and comfort constraints. IEEE Trans. Smart Grid 2015, 6, 1874–1883. [Google Scholar] [CrossRef]
- Costanzo, G.T.; Zhu, G.; Anjos, M.F.; Savard, G. A system architecture for autonomous demand side load management in smart buildings. IEEE Trans. Smart Grid 2012, 3, 2157–2165. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Kuzlu, M.; Rahman, S. An algorithm for intelligent home energy management and demand response analysis. IEEE Trans. Smart Grid 2012, 3, 2166–2173. [Google Scholar] [CrossRef]
- Barker, S.; Mishra, A.; Irwin, D.; Shenoy, P.; Albrecht, J. Smartcap: Flattening peak electricity demand in smart homes. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications (PerCom), Lugano, Switzerland, 19–23 March 2012; pp. 67–75.
- Zhao, Z.; Lee, W.C.; Shin, Y.; Song, K.B. An optimal power scheduling method for demand response in home energy management system. IEEE Trans. Smart Grid 2013, 4, 1391–1400. [Google Scholar] [CrossRef]
- Chen, X.; Wei, T.; Hu, S. Uncertainty-Aware household appliance scheduling considering dynamic electricity pricing in smart home. IEEE Trans. Smart Grid 2013, 4, 932–941. [Google Scholar] [CrossRef]
- Lin, Y.H.; Tsai, M.S. An Advanced Home Energy Management System Facilitated by Nonintrusive Load Monitoring with Automated Multiobjective Power Scheduling. IEEE Trans. Smart Grid 2015, 6, 1839–1851. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Heo, Y.; Kishore, S. MPC-Based appliance scheduling for residential building energy management controller. IEEE Trans. Smart Grid 2013, 4, 1401–1410. [Google Scholar] [CrossRef]
- Roh, H.T.; Lee, J.W. Residential Demand Response Scheduling with Multiclass Appliances in the Smart Grid. IEEE Trans. Smart Grid 2016, 7, 94–104. [Google Scholar] [CrossRef]
- Liu, Y.; Yuen, C.; Huang, S.; Hassan, N.U.; Wang, X.; Xie, S. Peak-to-Average Ratio Constrained Demand-Side Management with Consumer’s Preference in Residential Smart Grid. IEEE J. Sel. Top. Signal Process. 2014, 8, 1084–1097. [Google Scholar] [CrossRef]
- Mahmood, D.; Javaid, N.; Alrajeh, N.; Khan, Z.A.; Qasim, U.; Ahmed, I.; Ilahi, M. Realistic Scheduling Mechanism for Smart Homes. Energies 2016, 9, 202. [Google Scholar] [CrossRef]
- Vivekananthan, C.; Mishra, Y.; Ledwich, G.; Li, F. Demand response for residential appliances via customer reward scheme. IEEE Trans. Smart Grid 2014, 5, 809–820. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Xia, X.; Zhang, J. Optimal scheduling of household appliances for demand response. Electr. Power Syst. Res. 2014, 116, 24–28. [Google Scholar] [CrossRef]
- Yaagoubi, N.; Mouftah, H.T. A Comfort Based Game Theoretic Approach for Load Management in the Smart Grid. In Proceedings of the IEEE Green Technologies Conference, Denver, CO, USA, 4–5 April 2013; pp. 35–41.
- Yaagoubi, N.; Mouftah, H.T. User-Aware Game Theoretic Approach for Demand Management. IEEE Trans. Smart Grid 2015, 6, 716–725. [Google Scholar] [CrossRef]
- Ozturk, Y.; Senthilkumar, D.; Kumar, S.; Lee, G. An Intelligent Home Energy Management System to Improve Demand Response. IEEE Trans. Smart Grid 2013, 4, 694–701. [Google Scholar] [CrossRef]
- Cottone, P.; Gaglio, S.; Re, G.L.; Ortolani, M. User activity recognition for energy saving in smart homes. Pervasive Mob. Comput. 2015, 16, 156–170. [Google Scholar] [CrossRef]
- Widen, J.; Wackelgard, E. A high-resolution stochastic model of domestic activity patterns and electricity demand. Appl. Energy 2010, 87, 1880–1892. [Google Scholar] [CrossRef]
- Stamminger, R.; Broil, G.; Pakula, C.; Jungbecker, H.; Braun, M.; Rudenauer, I.; Wendker, C. Synergy Potential of Smart Appliances; Report of the Smart-A Project; University of Bonn: Bonn, Germany, 2008. [Google Scholar]
- Wholesale Solar. Available online: http://www.wholesalesolar.com/solar-information/how-to-save-energy/power-table (accessed on 17 September 2015).
- Nghiem, T. Modeling and Advanced Control of HVAC Systems; University of Pennsylvania: Philadelphia, PA, USA, 2011. [Google Scholar]
- Setlhaolo, D.; Xia, X. Optimal scheduling of household appliances with a battery storage system and coordination. Energy Build. 2015, 94, 61–70. [Google Scholar] [CrossRef]
- Online Weather Report. Available online: http://www.accuweather.com/en/us/new-york-ny/10007/november-weather/349727 (accessed on 17 Septmber 2015).
- Adika, C.O.; Wang, L. Autonomous Appliance Scheduling for Household Energy Management. IEEE Trans. Smart Grid 2014, 5, 673–682. [Google Scholar] [CrossRef]
- Fadlullah, Z.M.; Quan, D.M.; Kato, N.; Stojmenovic, I. GTES: An Optimized Game-Theoretic Demand-Side Management Scheme for Smart Grid. IEEE Syst. J. 2014, 8, 588–597. [Google Scholar] [CrossRef]
- Soliman, H.M.; Leon-Garcia, A. Game-Theoretic Demand-Side Management with Storage Devices for the Future Smart Grid. IEEE Trans. Smart Grid 2014, 5, 1475–1485. [Google Scholar] [CrossRef]
- New York Independent System Operator. Available online: http://www.nyiso.com/public/markets_operations/market_data/pricing_data/index.jsp (accessed on 9 April 2016).
- Yoon, J.H.; Bladick, R.; Novoselac, A. Demand response for residential buildings based on dynamic price of electricity. Energy Build. 2014, 80, 531–541. [Google Scholar] [CrossRef]
- Farid, A.M. Multi-Agent system design principles for resilient operation of future power systems. In Proceedings of the IEEE International Workshop on Intelligent Energy Systems (IWIES), San Diego, CA, USA, 8 October 2014; pp. 18–25.
- Ahmad, A.; Javaid, N.; Alrajeh, N.; Khan, Z.A.; Qasim, U.; Khan, A. A Modified Feature Selection and Artificial Neural Network-Based Day-Ahead Load Forecasting Model for a Smart Grid. Appl. Sci. 2015, 5, 1756–1772. [Google Scholar] [CrossRef]


| Technique | Domain | Achievements | Limitations | E Min. | LC | C Min. | Pricing Scheme | |
|---|---|---|---|---|---|---|---|---|
| Game theory [2] | DSM, various home appliances are considered | Minimize PAR, , power generation electricity cost | User comfort is not considered, focus is towards cost and PAR reductions, environmental conditions are not considered | ✗ | ✗ | ✗ | ✓ | NG |
| BPSO and BWDO [3] | DSM | Minimize electricity cost, PAR, user comfort | User comfort is considered for few appliances, environmental conditions are not considered | ✓ | ✗ | ✓ | ✓ | TOU |
| Monte Carlo [4] | Load control | Minimize end user bill, maximize user comfort | User comfort is affected when users consume more energy, environmental conditions are not considered | ✗ | ✗ | ✗ | ✗ | NG |
| MINOP [6] | DR-based controller for DSM | Minimize end user cost | User comfort is affected due to energy consumption limits, dynamic prices and environmental conditions are not considered | ✗ | ✗ | ✓ | ✓ | DP |
| MIP [7] | Layered architecture for DSM in smart buildings | Minimize end user cost with integration of various energy sources | Due to capacity limit, user comfort is affected, appliances are not categorized based on user preferences | ✗ | ✗ | ✓ | ✓ | DP |
| Simulation tool for DR [8] | An intelligent HEM algorithm for power intensive appliances | Minimize end user cost with energy consumption reduction, user comfort with load prioritization | Due to capacity limit, user comfort is affected, appliances are not categorized based on user preferences | ✓ | ✓ | ✗ | ✓ | NG |
| LSF [9] | EDF -based HEM algorithm for heavy loads | Only background load is scheduled, cost and PAR are reduced through energy consumption scheduling, flexibility is also studied | Active human participation is not involved, which can disturb comfort, other appliances are not considered in HEM | ✗ | ✗ | ✗ | ✓ | NG |
| GA [10] | Home Energy Management | Minimize electricity cost, PAR | Only high consumption appliances are considered, other appliances are neglected due to which it is infeasible solution, temperature and user preferences are not considered | ✗ | ✗ | ✗ | ✓ | RTP + IBR |
| Linear and stochastic programming [11] | A new DSM algorithm for home appliances | Monetary expenses are minimized, uncertainties in appliance operation time and renewable energy are handled | Active user participation is not considered, focus is towards cost reduction | ✗ | ✗ | ✗ | ✓ | DAP |
| NILM and multi-objective NSGA-II [12] | Appliance scheduling in response to DR for automated HEM system, non-intrusive load monitoring, comfort is also considered | Electricity cost is minimized, appliances are automatically selected for operation | No user preferences are involved, historical consumption data for demand analysis, consumption trends are uncertain | ✗ | ✗ | ✗ | ✓ | RTP |
| MPC [13] | Energy management controller for appliance scheduling | Electricity cost is minimized | Two types of loads are considered, thermal constraints are considered, but without user preferences | ✓ | ✗ | ✓ | ✓ | TOU |
| MINLP, GBD [14] | Appliance scheduling for home energy management | Electricity cost is minimized, appliance utility is improved | Only elastic appliances are considered for user comfort, but without user occupancies | ✓ | ✗ | ✓ | ✓ | TOU |
| MOOP based HEMS [15] | HEM considering PAR constraint | Electricity cost, PAR and user discomfort are minimized | Users specify the feasible time for comfort, but varying patterns are not tackled, thermal constraints are not incorporated | ✓ | ✗ | ✓ | ✓ | FRM, FPM |
| BPSO for HEMS [16] | RSMfor appliance scheduling | Reduces electricity cost, appliance utility is improved, user comfort is also improved | Trade-off between comfort and appliance utility, environmental constraints are not considered | ✓ | ✗ | ✓ | ✓ | TOU |
| Bi-level control scheme [17] | CR-based DR program for residential users | Reduces electricity cost, PAR, improves network voltage performance, comfort is also improved | Trade-off between cost and comfort, thermal parameters are not considered | ✗ | ✗ | ✗ | ✓ | TOU |
| MINLP [18] | Appliance scheduling based on CR scheme | Minimize electricity cost and earn incentives | User comfort is not modelled, trade-off between cost and comfort | ✗ | ✗ | ✗ | ✓ | TOU |
| Game theory [19,20] | Appliance scheduling for DSM | Minimize electricity cost and user discomfort | Trade-off between cost and comfort | ✓ | ✗ | ✓ | ✓ | TOU |
| Integrated and self-organizing algorithm [21] | DSM using load shifting | Peak load shifting and DR improvement, run-time schedules based on load prediction | Trade-off between cost and comfort due to predefined comfort zones | ✓ | ✗ | ✓ | ✓ | TOU |
| Information theory [22] | HEM through load shifting | Reduce high peaks, energy consumption and cost of end users through activity recognition | No DR program is used, more activities can consume more energy and high peaks | ✓ | ✓ | ✗ | ✓ | TOU |
| Non-homogeneous Markov chain [23] | DSM through user activities | Reduce energy consumption and cost of end users through activity recognition and modelling | Dynamic prices are not considered, so DR programs cannot be implemented here | ✓ | ✓ | ✗ | ✓ | NG |
| Proposed-Fmincon-SQP | Home energy management through appliance scheduling | Cost, energy and PAR reductions, dynamic schedules based on user activities, user comfort maximization, environmental constraints are considered | Greater No. of users at any particular time can increase electricity cost and PAR | ✓ | ✓ | ✓ | ✓ | RTP, TOU |
| Total Appliances | Appliance Name | Power Rating (kWh) |
|---|---|---|
| 1 | Air Conditioner | 1.6 |
| 2 | Refrigerator | 1.24 |
| 3 | Washing Machine | 3.4 |
| 4 | Light with Controllable Brightness | 0.1 |
| 5 | Dish Washer | 1.5 |
| 6 | Light without Controllable Brightness | 0.1 |
| 7 | Entertainment Station | 1.5 |
| Solver | Algorithm | Local Minimum | Convergence | Constraint Violation |
|---|---|---|---|---|
| fmincon | Sequential quadratic programming | Yes | Yes | No |
| lsqnonlin | Levenberg–Marquardt | Possible | No | No |
| fmincon | Interior-point | Yes | Yes | No |
| Unit Type | House Type | Pricing Scheme | Unscheduled Power (W) | Scheduled Power (W) | % Saving |
|---|---|---|---|---|---|
| Unit 1 | House 1 | RTP | 72,284 | 41,757 | 42.24 |
| Unit 1 | House 2 | RTP | 68,139 | 32,098 | 52.90 |
| Unit 1 | House 1 | TOU | 74,332 | 39,913 | 46.31 |
| Unit 1 | House 2 | TOU | 71,340 | 37,906 | 46.87 |
| Unit 2 | House 1 | RTP | 139,810 | 44,711 | 68.03 |
| Unit 2 | House 2 | RTP | 117,295 | 48,291 | 58.83 |
| Unit 2 | House 1 | TOU | 138,416 | 42,701 | 69.16 |
| Unit 2 | House 2 | TOU | 118,033 | 41,451 | 64.89 |
| Unit Type | House Type | Pricing Scheme | Unscheduled Cost ($) | Scheduled Cost ($) | % Saving |
|---|---|---|---|---|---|
| Unit 1 | House 1 | RTP | 2.5148 | 1.9403 | 22.85 |
| Unit 1 | House 2 | RTP | 2.0243 | 1.8583 | 8.21 |
| Unit 1 | House 1 | TOU | 2.6467 | 2.2626 | 14.52 |
| Unit 1 | House 2 | TOU | 1.9384 | 1.5597 | 19.54 |
| Unit 2 | House 1 | RTP | 1.2210 | 1.2048 | 01.30 |
| Unit 2 | House 2 | RTP | 1.8909 | 1.5162 | 19.82 |
| Unit 2 | House 1 | TOU | 1.0167 | 0.9974 | 01.90 |
| Unit 2 | House 2 | TOU | 1.5323 | 1.3278 | 13.35 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasheed, M.B.; Javaid, N.; Ahmad, A.; Jamil, M.; Khan, Z.A.; Qasim, U.; Alrajeh, N. Energy Optimization in Smart Homes Using Customer Preference and Dynamic Pricing. Energies 2016, 9, 593. https://doi.org/10.3390/en9080593
Rasheed MB, Javaid N, Ahmad A, Jamil M, Khan ZA, Qasim U, Alrajeh N. Energy Optimization in Smart Homes Using Customer Preference and Dynamic Pricing. Energies. 2016; 9(8):593. https://doi.org/10.3390/en9080593
Chicago/Turabian StyleRasheed, Muhammad Babar, Nadeem Javaid, Ashfaq Ahmad, Mohsin Jamil, Zahoor Ali Khan, Umar Qasim, and Nabil Alrajeh. 2016. "Energy Optimization in Smart Homes Using Customer Preference and Dynamic Pricing" Energies 9, no. 8: 593. https://doi.org/10.3390/en9080593
APA StyleRasheed, M. B., Javaid, N., Ahmad, A., Jamil, M., Khan, Z. A., Qasim, U., & Alrajeh, N. (2016). Energy Optimization in Smart Homes Using Customer Preference and Dynamic Pricing. Energies, 9(8), 593. https://doi.org/10.3390/en9080593