A Co-Simulation Framework for Power System Analysis
Abstract
:1. Introduction
2. EMT Co-Simulation Framework
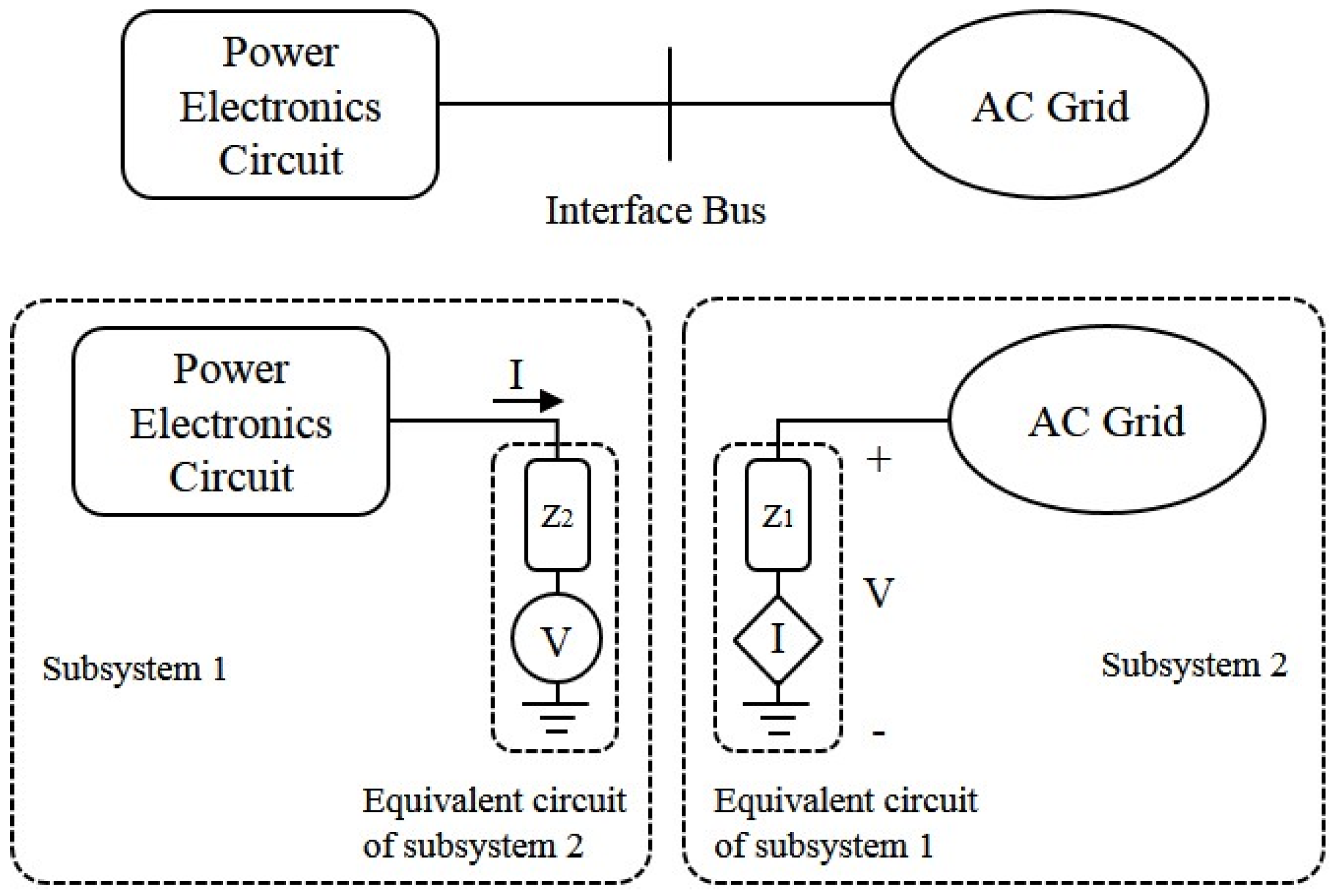
2.1. Network Partitioning
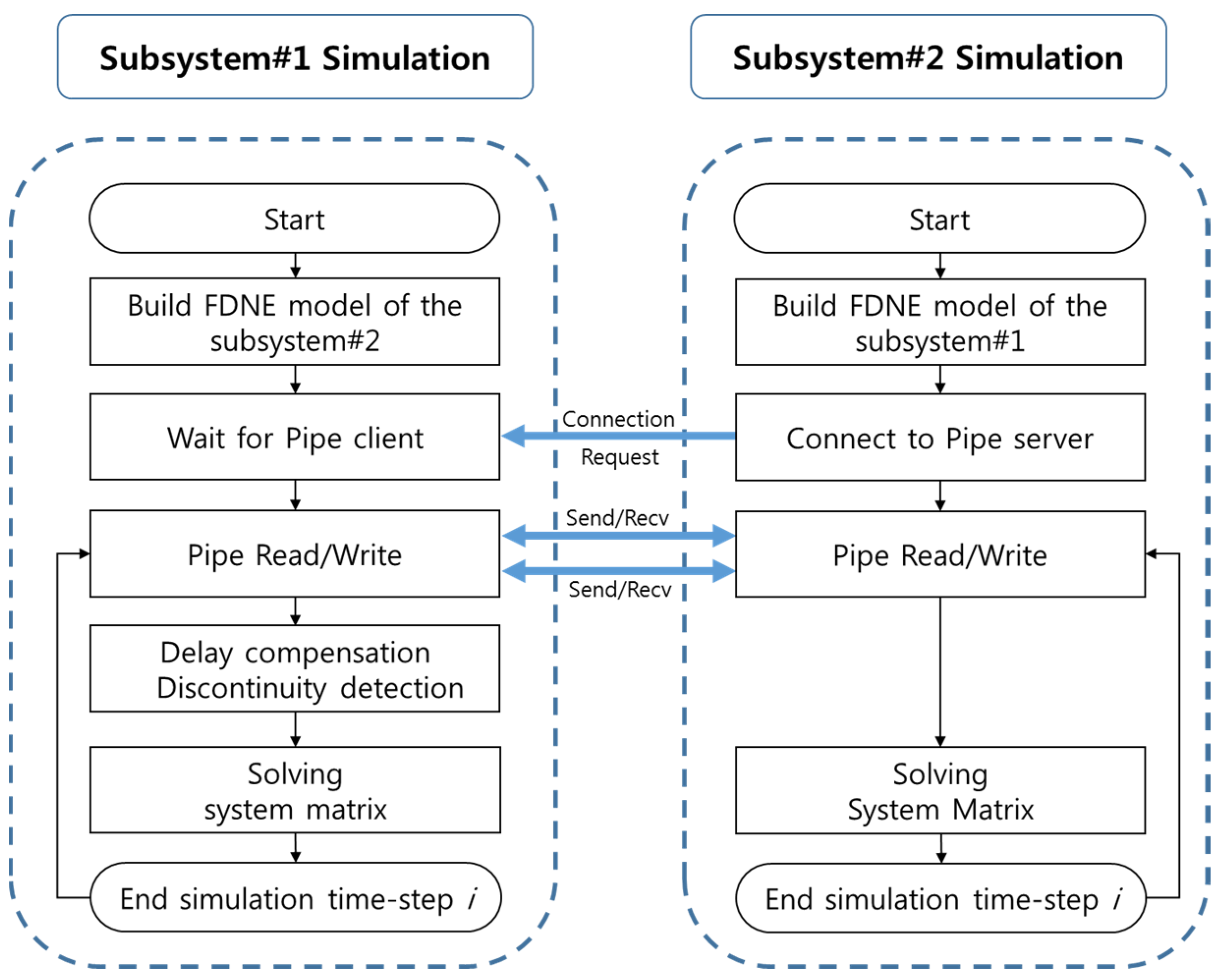
2.2. Interfacing
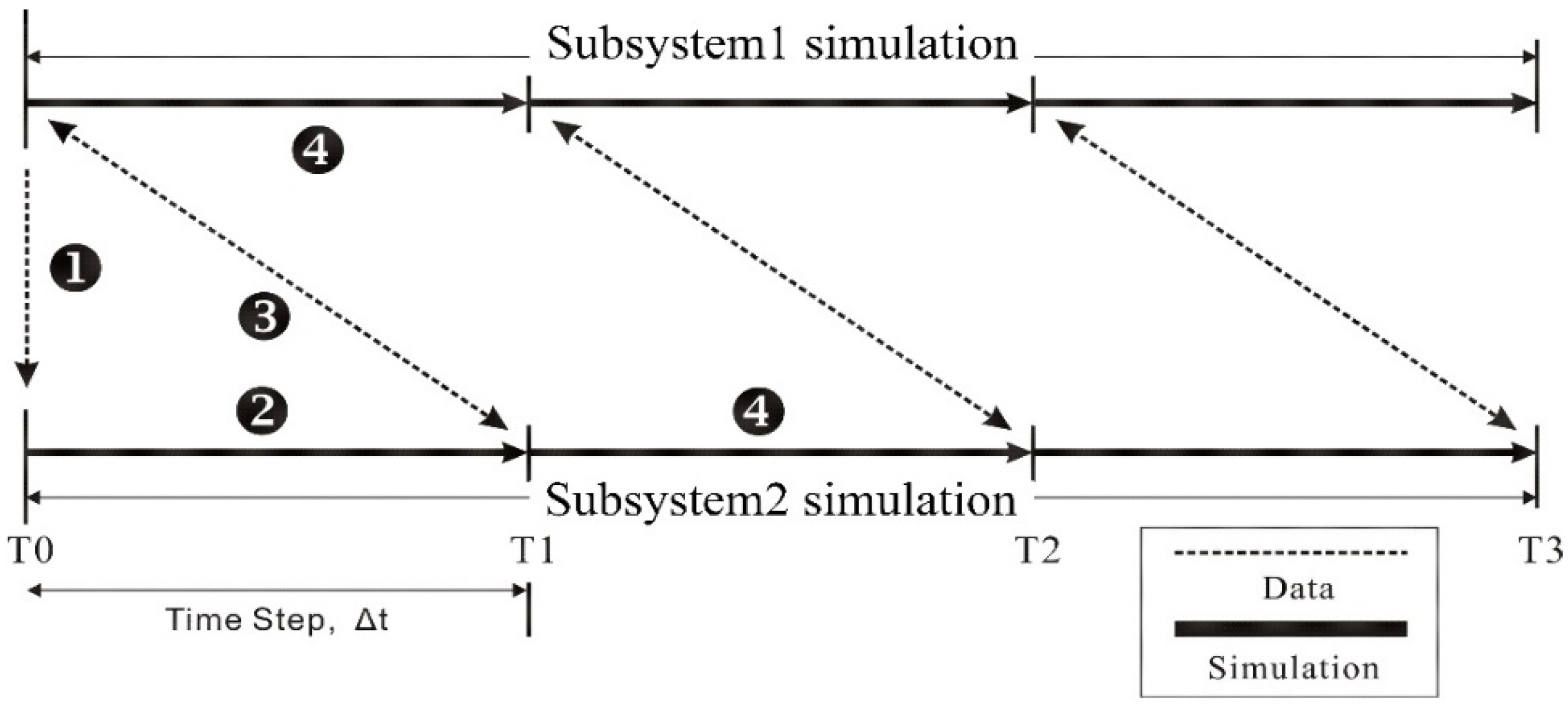
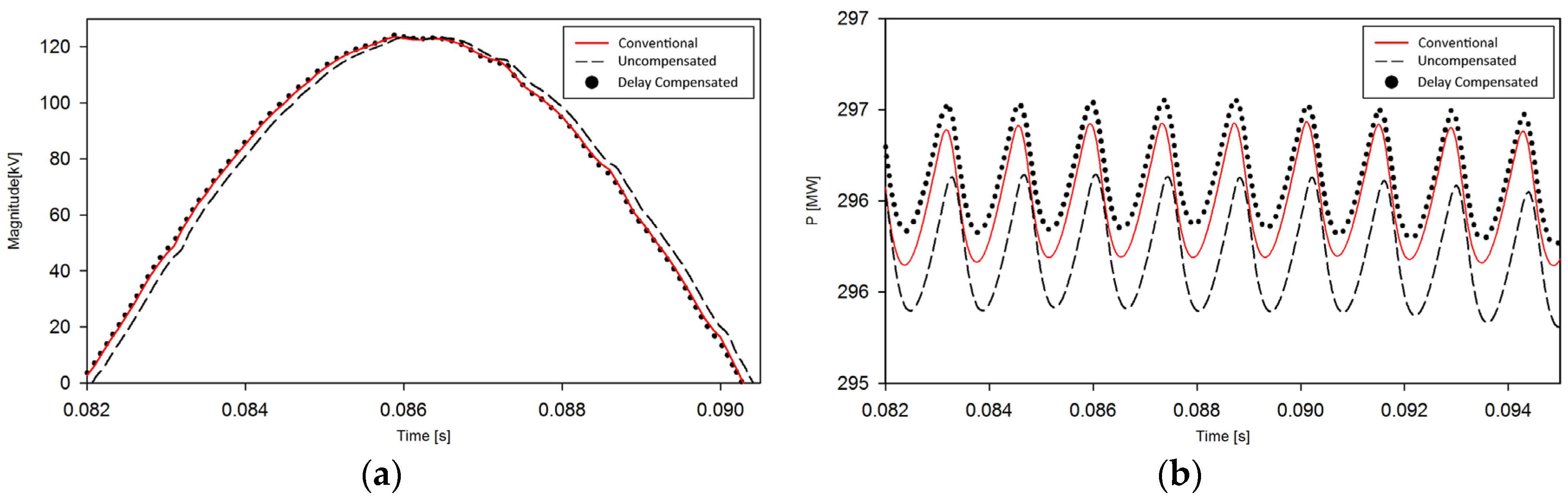
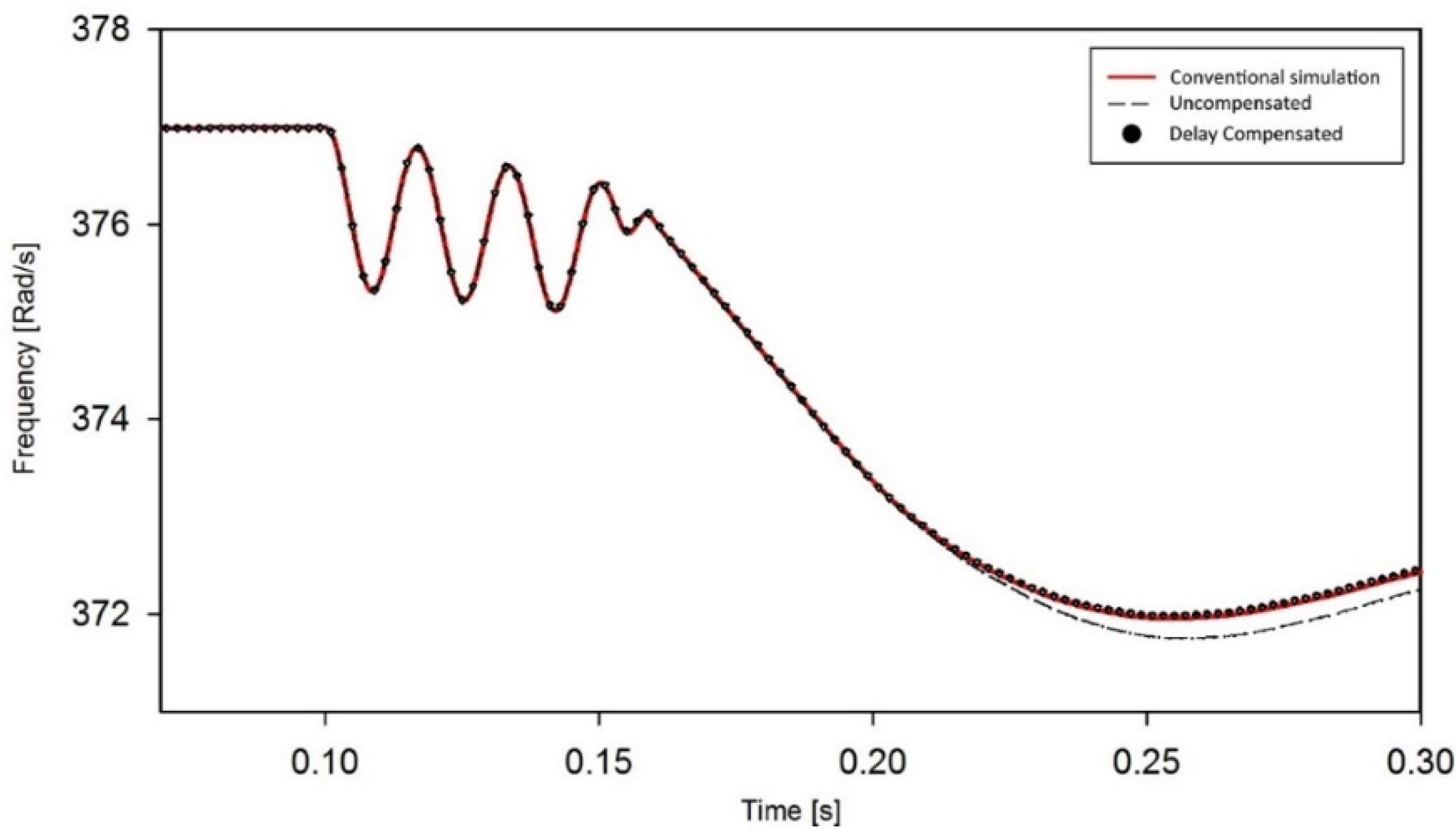
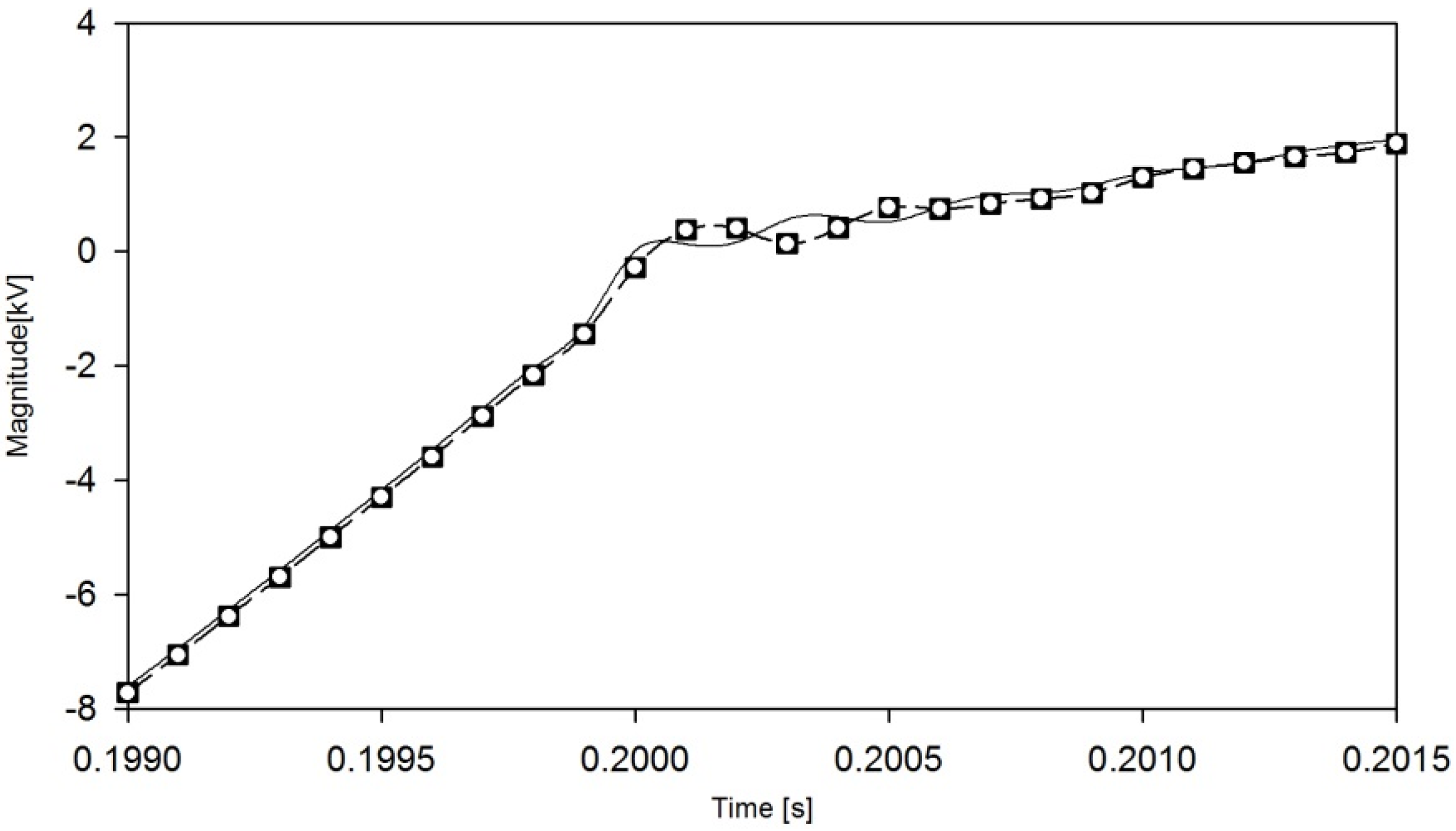
2.3. Time-Step Delay Error
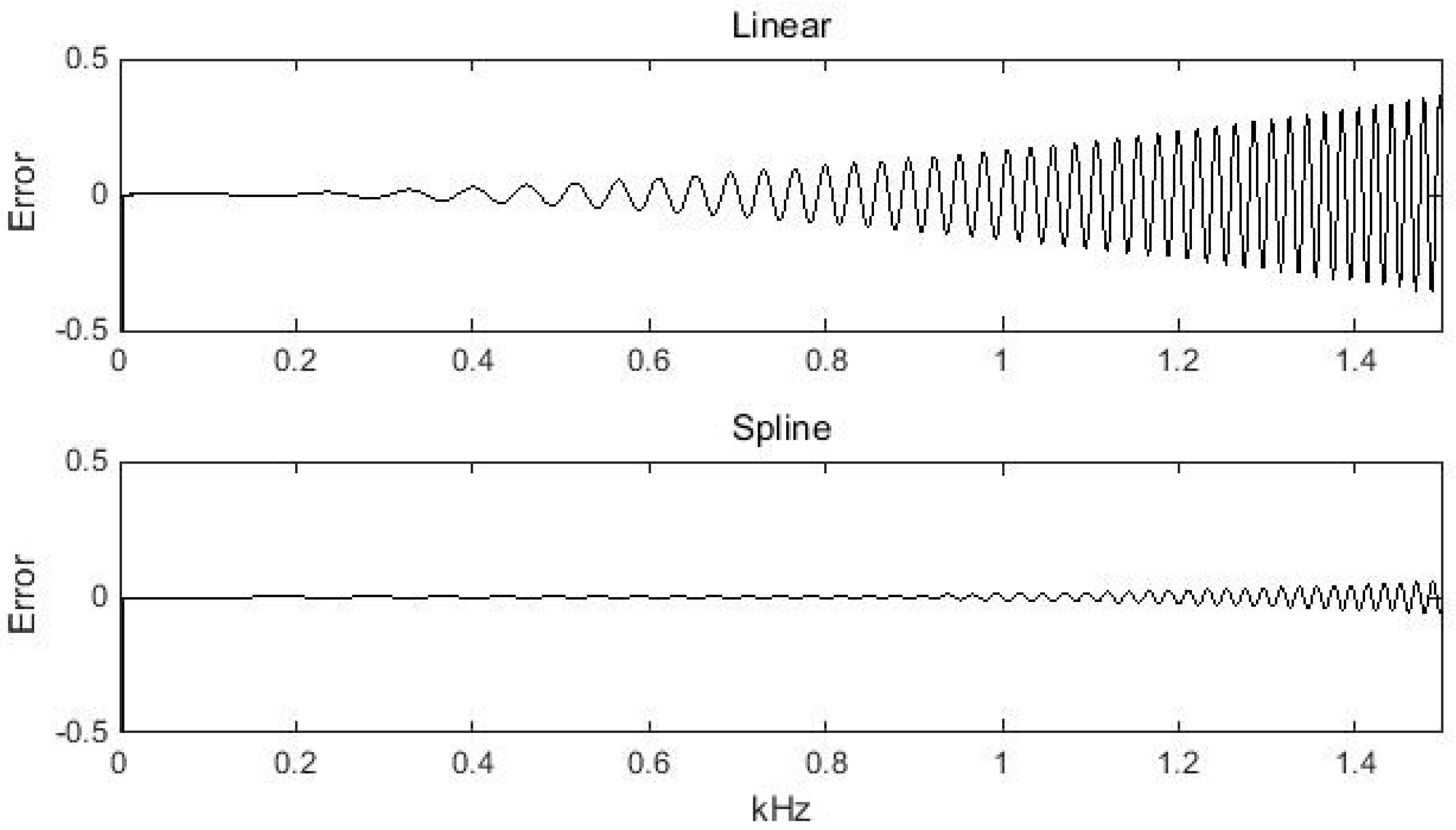
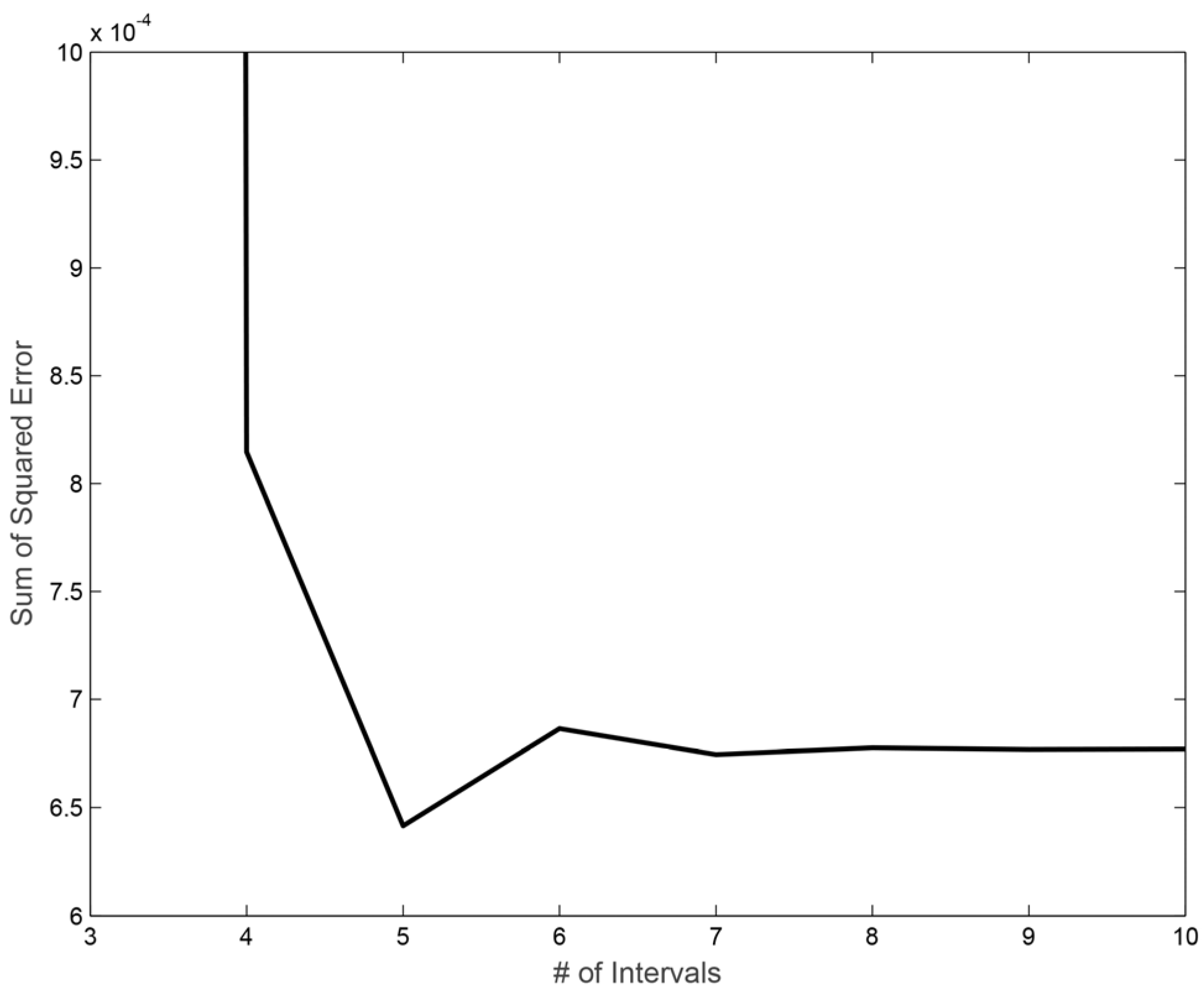
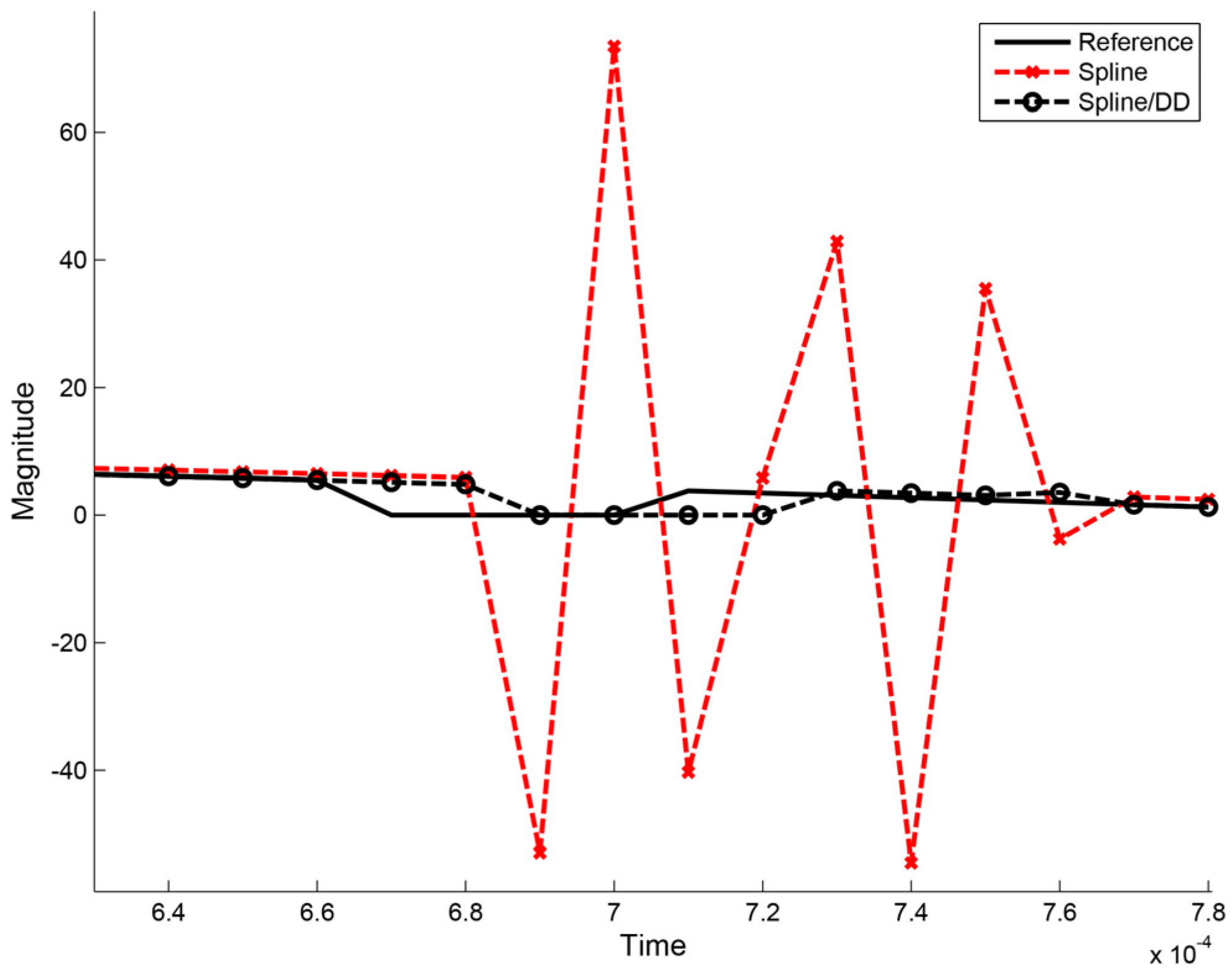
2.4. Data Prediction by Extrapolation
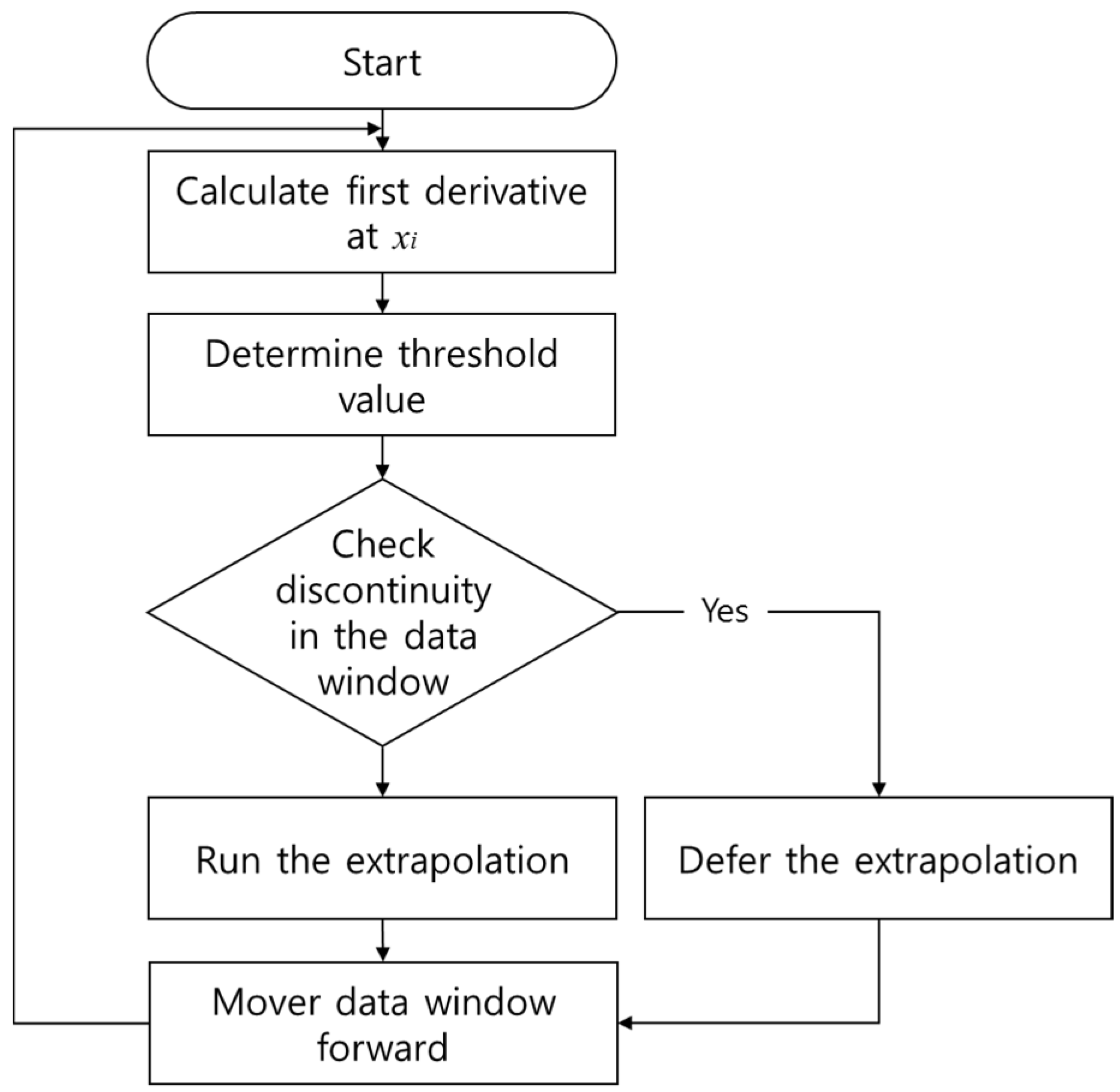
2.5. Discontinuity Detection
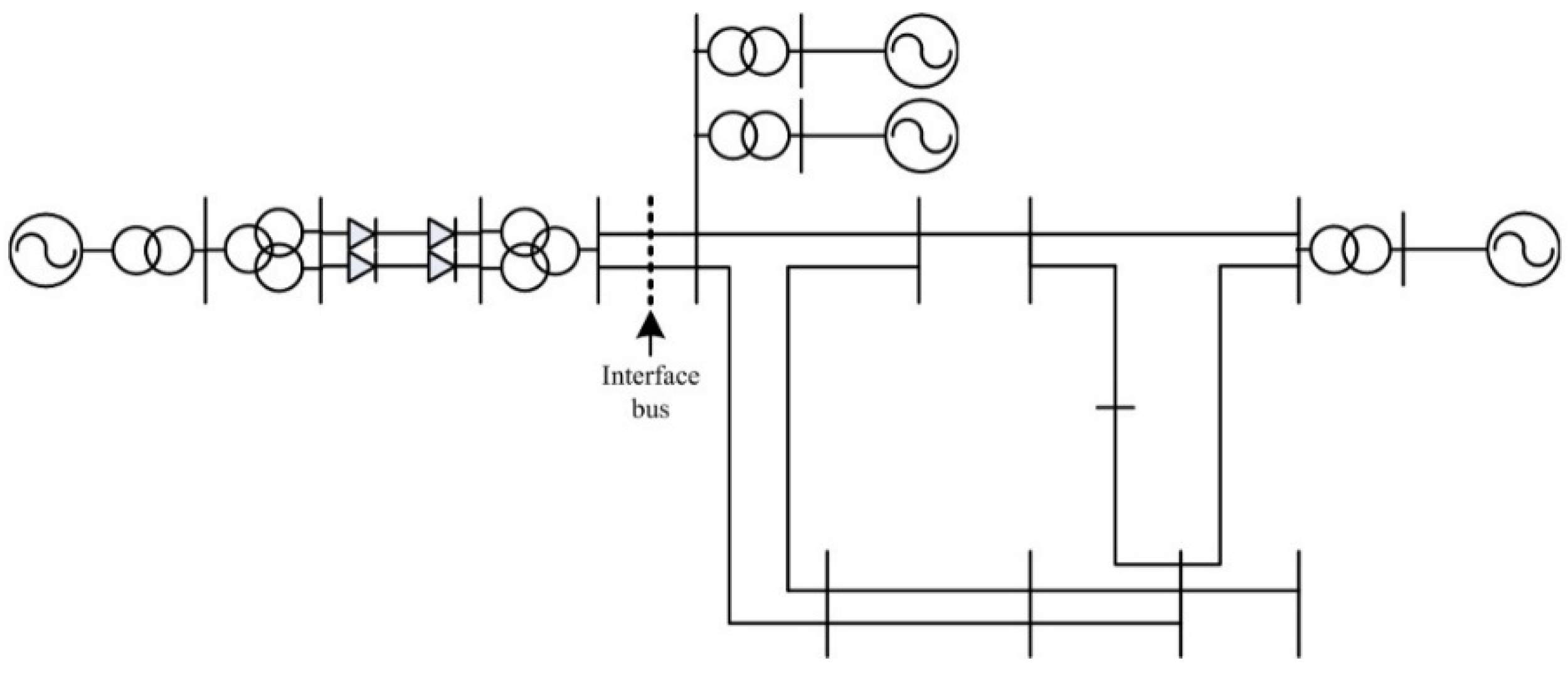
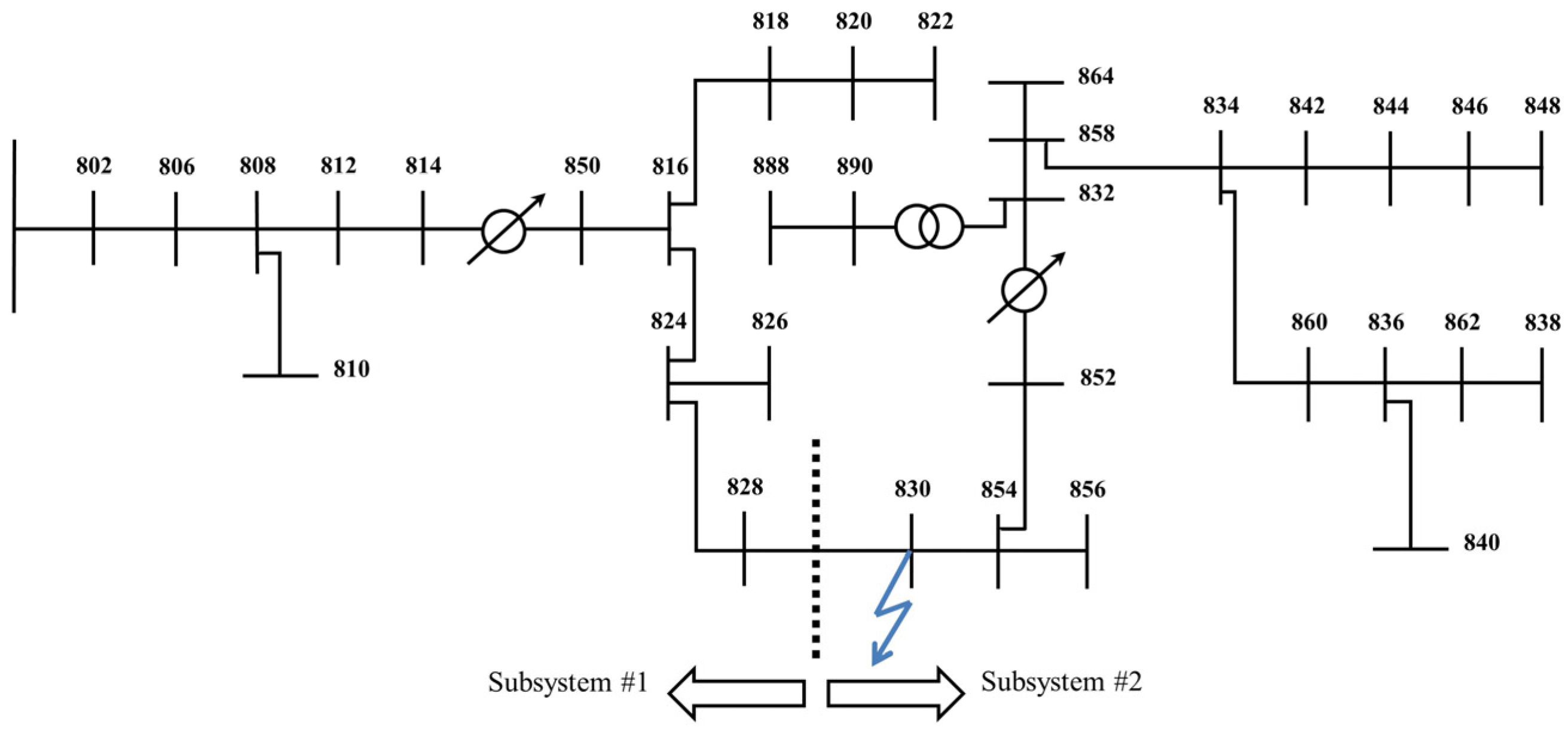
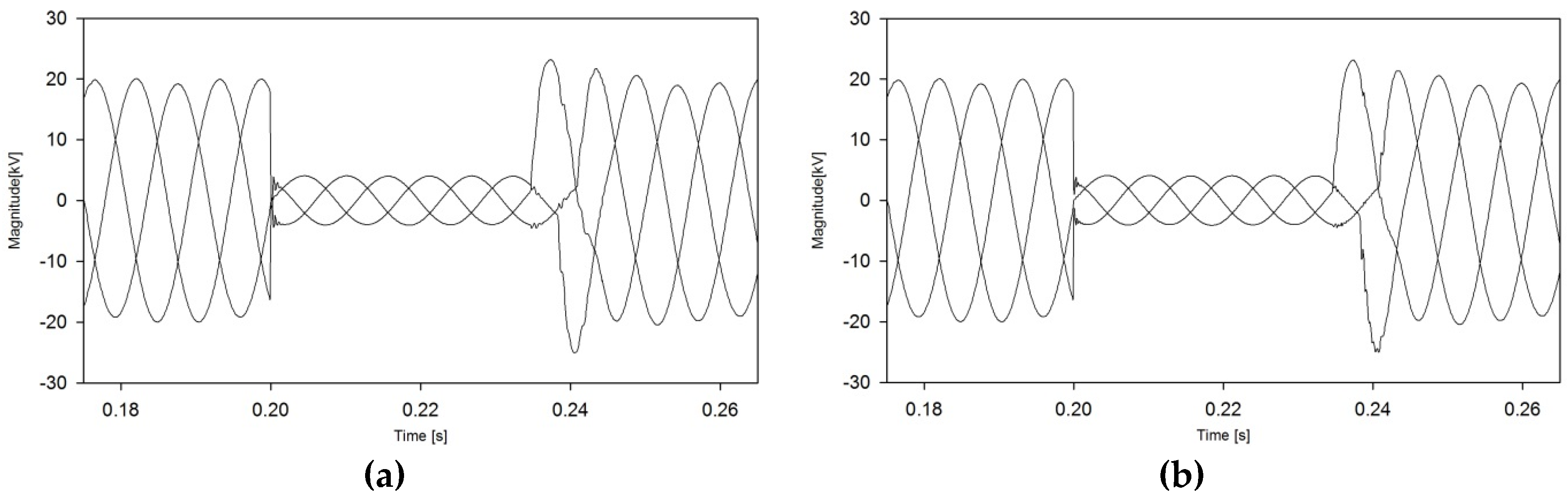
3. Case Study
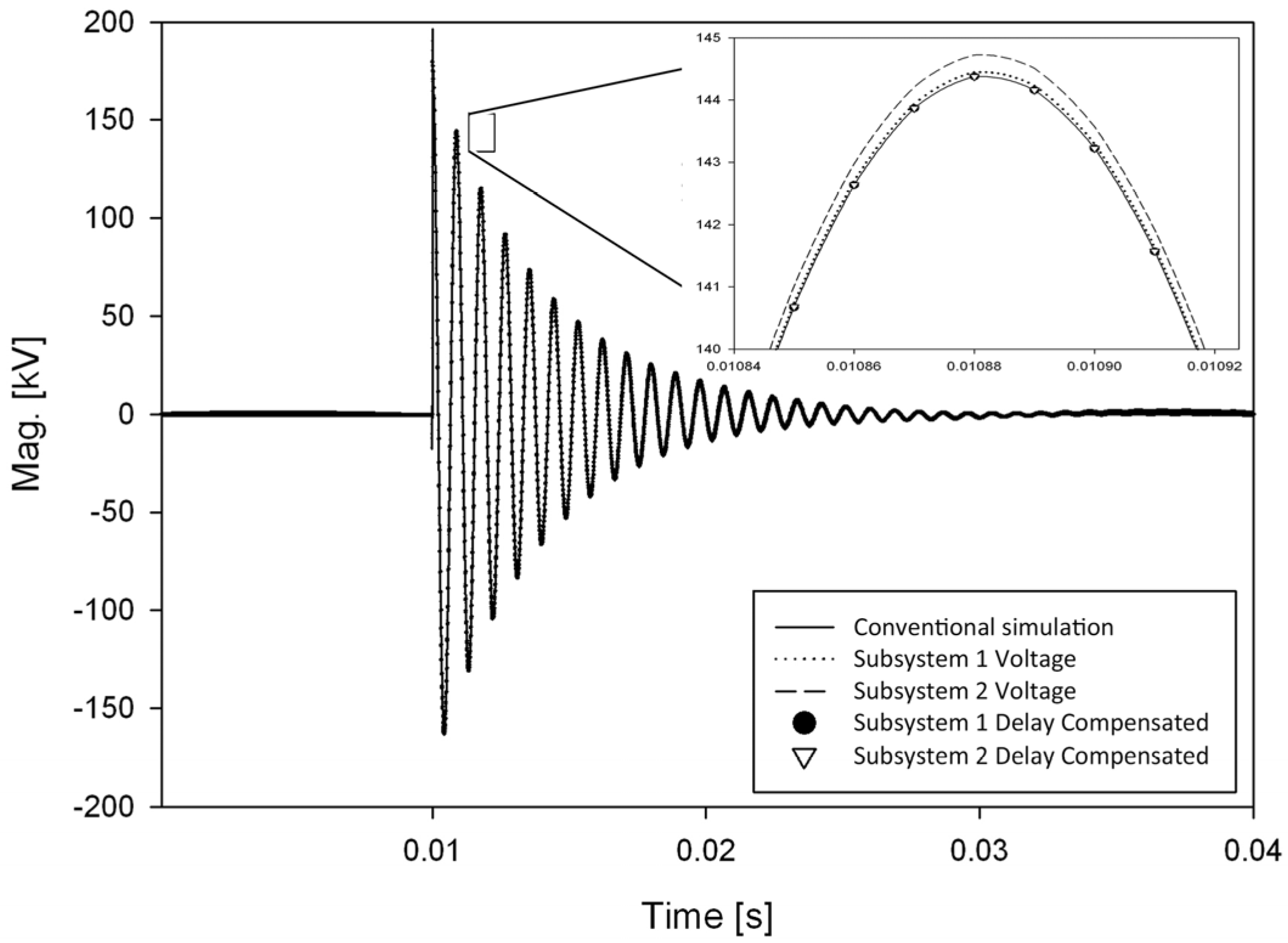
3.1. AC/DC Power System
3.2. AC Distribution System
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CPU | Central processing unit |
| DD | Discontinuity detection |
| EMT | Electromagnetic transient |
| FDNE | Frequency dependent network equivalent |
| GUI | Graphical user interface |
| HVDC | High voltage direct current transmission |
| IPC | Interprocess communication |
| R-L-C | Resistor, Inductor and Capacitor |
| SSE | Sum squared error |
References
- Chowdhury, S.P.; Chowdhury, S.; Crossley, P.A. UK scenario of islanded operation of active distribution networks with renewable distributed generators. Int. J. Electr. Power Energy Syst. 2011, 33, 1251–1255. [Google Scholar] [CrossRef]
- Dommel, H.W.; Meyer, W.S. Computation of electromagnetic transients. Proc. IEEE 1974, 62, 983–993. [Google Scholar] [CrossRef]
- Dommel, H.W. EMTP Theory Book; Bonneville Power Admin: Portland, OR, USA, 1986. [Google Scholar]
- Heffernan, M.D.; Turner, K.S.; Arrillaga, J.; Arnold, C.P. Computation of AC-DC System Disturbances—Part I. Interactive Coordination of Generator and Convertor Transient Models. IEEE Trans. Power Syst. 1981, 11, 4341–4348. [Google Scholar] [CrossRef]
- Gao, F.; Kai, S. Multi-scale simulation of multi-machine power systems. Int. J. Electr. Power Energy Syst. 2009, 31, 538–545. [Google Scholar] [CrossRef]
- Su, H.T.; Snider, L.A.; Chung, T.S.; Fang, D.Z. Recent advancements in electromagnetic and electromechanical hybrid simulation. In Proceedings of the International Conference on Power System Technology, Singapore, 21–24 November 2004; pp. 1479–1484.
- Lefebvre, S.; Mahseredjan, J. Interfacing Techniques for Transient Stability and Electromagnetic Transient Programs. IEEE Trans. Power Deliv. 2009, 24, 2385–2395. [Google Scholar]
- Hui, S.Y.R.; Fung, K.K.; Christopoulos, C. Decoupled simulation of DC-linked power electronic systems using transmission-line links. IEEE Trans. Power Electron. 1994, 9, 85–91. [Google Scholar] [CrossRef]
- Chiocchio, T.; Leonard, R.; Work, Y.; Fang, R.; Steurer, M.; Monti, A.; Khan, J.; Ordonez, J.; Sloderbeck, M.; Woodruff, S.L. A co-simulation approach for real-time transient analysis of electro-thermal system interactions on board of future all-electric ships. In Proceedings of the 2007 Summer Computer Simulation Conference, San Diego, CA, USA, 16 July 2007.
- Cécile, J.F.; Schoen, L.; Lapointe, V.; Abreu, A.; Bélanger, J. A Distributed Real-Time Framework for Dynamic Management of Heterogeneous Co-Simulations. Available online: http://www.rtlab.com/files/scs_article.pdf (accessed on 16 October 2015).
- Tylavsky, D.J.; Bose, A.; Alvarado, F.; Betancourt, R.; Clements, K.; Heydt, G.T.; Huang, G.; Ilic, M.; La Scala, M.; Pai, M.A. Parallel Processing in Power Systems Computation. IEEE Trans. Power Syst. 1992, 7, 629–638. [Google Scholar]
- Tomin, M.A.; De Rybel, T.; Marti, J.R. Extending the Multi-Area Thévenin Equivalents method for parallel solutions of bulk power systems. Int. J. Electr. Power Energy Syst. 2013, 44, 192–201. [Google Scholar] [CrossRef]
- Su, H.T.; Chan, K.W.; Snider, L.A. Parallel interaction protocol for electromagnetic and electromechanical hybrid simulation. IEEE Proc. Gener. Trans. Distrib. 2005, 152, 406–414. [Google Scholar] [CrossRef]
- Marti, J.R.; Linares, L.R.; Calvino, J.; Dommel, H.W.; Lin, J. OVNI: An object approach to real-time power system simulators. In Proceedings of the International Conference on Power System Technology, Beijing, China, 18–21 August 1998; pp. 977–981.
- Sultan, M.; Reeve, J.; Adapa, R. Combined transient and dynamic analysis of HVDC and FACTS systems. IEEE Trans. Power Deliv. 1998, 13, 1271–1277. [Google Scholar] [CrossRef]
- Wang, Y.P.; Watson, N.R. A benchmark test system for testing frequency dependent network equivalents for electromagnetic simulations. Int. J. Electr. Power Energy Syst. 2013, 44, 364–374. [Google Scholar] [CrossRef]
- Annakkage, U.D.; Nair, N.-K.C.; Gole, A.M.; Dinavahi, V.; Noda, T.; Hassan, G.; Monti, A. Dynamic system equivalents: A survey of available techniques. IEEE Trans. Power Deliv. 2009, 27, 411–420. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef]
- Gustavsen, B.; Mo, O. Interfacing convolution based linear models to an electromagnetic transients program. Int. Conf. Power Syst. Trans. 2007, 1, 4–7. [Google Scholar]
- Zhu, W.; Pekarek, S.; Jatskevich, J.; Wasynczuk, O.; Delisle, D. A Model-in-the-Loop Interface to Emulate Source Dynamics in a Zonal DC Distribution System. IEEE Trans. Power Electron. 2005, 20, 438–445. [Google Scholar] [CrossRef]
- Wu, X.; Lentijo, S.; Deshmuk, A.; Monti, A.; Ponci, F. Design and implementation of a power-hardware-in-the-loop interface: A nonlinear load case study. In Proceedings of IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 6–10 March 2005; Volume 2, pp. 1332–1338.
- Ren, W.; Steurer, M.; Woodruff, S.; Andrus, M. Demonstrating the Power Hardware-in-the-Loop through Simulation of a Notional Destroyer-Class AllElectric Ship System during Crashback. In Proceedings of the ASNE Advanced Propulsion Symposium, Arlington, VA, USA, 30 October 2006.
- Noda, T.; Sasaki, S. Algorithms for distributed computation of electromagnetic transients toward pc cluster based real-time simulations. In Proceedings of the International Conference on Power System Transients, New Orleans, LA, USA, 28 September 2003.
- Dufour, C.; Paquin, J.-N.; Lapointe, V.; Be’langer, J.; Schoen, L. PC cluster-based real-time simulation of an 8-synchronous machine network with HVDC link using RT-LAB and TestDrive. In Proceedings of the 7th International Conference on Power Systems Transients, Lyon, France, 4–7 June 2007.
- Ren, W.; Steurer, M.; Woodruff, S. Accuracy evaluation in power hardware-in-the-loop (PHIL) simulation center for advanced power systems. In Proceedings of the 2007 Summer Computer Simulation Conference, San Diego, CA, USA, 16 July 2007.
- Fang, T.; Chengyan, Y.; Zhongxi, W.; Xiaoxin, Z. Realization of electromechanical transient and electromagnetic transient real time hybrid simulation in power system. In Proceedings of the IEEE/PES Transmission and Distribution Conference Exhibition, Dalian, China, 14 August 2005; pp. 1–6.
- Belanger, J.; Snider, L.A.; Paquien, J.; Pirolli, C.; Li, W. A Modern and Open Real-Time Digital Simulator of Contemporary Power Systems. In Proceedings of the International Conference on Power Systems Transients (IPST 2009), Kyoto, Japan, 2 June 2009; pp. 2–6.
- Jang, G.; Oh, S.; Hann, B.-M.; Kim, C.K. Novel reactive power compensation scheme for the Jeju-Haenam HVDC system. IEEE Proc. Gener. Trans. Distrib. 2005, 152, 514–520. [Google Scholar] [CrossRef]
- Kersting, W.H. Radial distribution test feeders. In Proceedings of the 2001 Power Engineering Society Winter Meeting, Columbus, OH, USA, 31 January 2001; Volume 2, pp. 908–912.
- Jang, S.; Kim, K. An islanding detection method for distributed generations using voltage unbalance and total harmonic distortion of current. IEEE Trans. Power Deliv. 2004, 19, 745–752. [Google Scholar] [CrossRef]
- Xin, H.; Qu, Z.; John, S.; Ali, M. A Self-Organizing Strategy for Power Flow Control of Photovoltaic Generators in a Distribution Network. IEEE Trans. Power Deliv. 2011, 26, 1462–1473. [Google Scholar] [CrossRef]

| Specifications | HVDC System | AC System |
|---|---|---|
| Type | Line commutated converter | |
| Rate Voltage | DC ±180 kV | 154 kV |
| Rate Current | 849 A | - |
| Rating | 300 MW | 75 MVA synchronous generator |
| Number of circuits | 2 | - |
| Converter Transformer | 3phase 3winding (YDY) | - |
| Reactive power compensation | 70 MVA synchronous condensers | - |
| Harmonic Filter | DTF 27.5 MVA X 2 for 11, 13th harmonics HPF 27.5 MVA X 2 for 23, 25th harmonics | - |
| Type | Radial |
|---|---|
| Total Number of Bus | 34 |
| Frequency | 60 Hz |
| Voltage | 24.9 kV |
| Number of Loads | Spot: 6, Distributed: 19 |
| Total Load | Active: 1769 kW, Reactive: 1044 kW |
| Transformer | 24.9 kV/4.16 kV, D-Y, 500 kVA |
| Voltage Regulator | Y-Y with OLTC |
| Shunt Capacitor | 750 kVA |
| Type | Conventional | Co-simulation | ||
|---|---|---|---|---|
| Case | Reference | Common time-step | ||
| CPU | Single core (3.2 GHz) | Multi core (2.66 GHz) | Single core (3.2 GHz) | Multi core (2.66 GHz) |
| Time-step | 10 μs | 10 μs | 10 μs | 10 μs |
| Computation time * | 1 | 1.12 | 6.72 | 0.51 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, S.; Chae, S. A Co-Simulation Framework for Power System Analysis. Energies 2016, 9, 131. https://doi.org/10.3390/en9030131
Oh S, Chae S. A Co-Simulation Framework for Power System Analysis. Energies. 2016; 9(3):131. https://doi.org/10.3390/en9030131
Chicago/Turabian StyleOh, Seaseung, and Suyong Chae. 2016. "A Co-Simulation Framework for Power System Analysis" Energies 9, no. 3: 131. https://doi.org/10.3390/en9030131
APA StyleOh, S., & Chae, S. (2016). A Co-Simulation Framework for Power System Analysis. Energies, 9(3), 131. https://doi.org/10.3390/en9030131






