Full-Lifecycle Deterioration Characteristics and Remaining Life Prediction of ZnO Varistors Based on PSO-SVR and iForest

Abstract

To address three core deficiencies of the existing research on ZnO varistors (incomplete full-lifecycle datasets, insufficient characterization robustness due to the lack of multi-parameter complementarity, and disconnected remaining life prediction and failure threshold determination), this study proposes a comprehensive technical solution for ZnO varistor remaining life prediction. An 8/20 μs impulse current accelerated deterioration experiment was designed to construct a full-lifecycle dataset (441 sets of data) covering nine same-batch ZnO varistors from their initial state to complete failure. Five core electrical parameters (varistor voltage U_1mA, nonlinear coefficient α, leakage current I_L, parallel resistance R_p, parallel capacitance C_p) were fused, and principal component analysis (PCA) was adopted for dimensionality reduction to form a high-robustness characterization feature (correlation coefficient with deterioration degree = 0.96). A combined model of Particle Swarm Optimization-Support Vector Regression (PSO-SVR) and Isolation Forest (iForest) was established to realize “quantitative prediction–qualitative threshold” collaboration. Experimental results show that the PSO-SVR model achieves high-precision remaining life prediction (test set R² = 0.9726, MSE = 0.00142) and the iForest model accurately identifies the failure threshold (AUC = 0.984, accuracy = 95.9%). The combined model reaches an overall accuracy of 99.89%, effectively solving the core deficiencies of the existing research and providing key technical support for SPD-condition monitoring and operation and maintenance decisions in energy systems.

1. Introduction

1.1. Research Background and Significance

Lightning-induced transient overvoltage and surge currents pose severe threats to the safe operation of energy transmission and distribution systems, causing significant global direct economic losses as well as incalculable indirect losses such as production downtime and data damage [1]. Surge protective devices (SPDs) are mandatory components in modern electrical systems (per international standards such as IEC 61643-12 [2]), serving as the last line of defense against surge damage. Zinc oxide (ZnO) varistors, the core protective elements of voltage-limiting SPDs, directly determine the protection effect and service life of SPDs.

During long-term operation in energy systems, ZnO varistors—also referred to as metal-oxide varistors (MOVs)—inevitably deteriorate under the combined effects of surge current impulses, environmental temperature–humidity fluctuations, and natural aging [1]. Deterioration manifests as varistor voltage ($U_{1mA}$) drift, leakage current ($I_L$) increase, and attenuation of nonlinear protection capability ($\alpha )$, ultimately leading to SPD failure [3]. However, current SPD-condition monitoring faces critical challenges: traditional single-parameter-based fault alarm mechanisms suffer from high false- and missed-alarm rates [4], while the lack of accurate remaining life prediction and failure threshold determination leads to either delayed replacement of failed SPDs (risking equipment damage) or over-maintenance (wasting resources). A recent bibliometric review by Zacarias et al. [1] emphasized that “multi-parameter fusion characterization + collaborative prediction-threshold determination” represent the core research direction to address these issues. Consequently, in-depth investigation into ZnO varistors’ deterioration mechanisms, full-lifecycle characteristics, and high-precision remaining life prediction models is crucial for improving the reliability of energy system protection, reducing operation and maintenance costs, and ensuring stable energy supply.

1.2. Research Status and Deficiencies

Scholars worldwide have carried out extensive research on the deterioration characteristics, failure mechanisms, and remaining life prediction of ZnO varistors, forming a multi-dimensional research system that lays a foundation for the condition monitoring of SPDs in energy systems. Ranjbar et al. [5] conducted a comprehensive survey on the diagnostic and condition monitoring technologies of metal oxide surge arresters in power distribution networks, summarizing mainstream methods such as parameter measurement, mechanism analysis, and model-based diagnosis—further verifying the breadth of existing research. However, as highlighted in the research background, the existing studies still have significant deficiencies that hinder their practical application in engineering, failing to meet the needs of accurate remaining life prediction and early failure warning for ZnO varistors.

In terms of deterioration characterization and mechanism research, relevant studies have confirmed that multiple electrical parameters (varistor voltage $U_{1mA}$, leakage current $I_L$, nonlinear coefficient $\alpha$, etc.) are closely associated with the deterioration process, providing a basic basis for deterioration state assessment [1]. Nevertheless, most existing studies adopt single-parameter characterization, while experimental evidence shows that core parameters exhibit differential sensitivities and complementary responses during degradation. A single parameter cannot fully cover the comprehensive information of the entire deterioration process, leading to insufficient characterization robustness. Meanwhile, explorations of deterioration mechanisms and failure modes have deepened from macro-characteristics to micro-mechanisms and multi-field coupling levels: Meng et al. [4] analyzed the influence of high-resistance media on the failure mechanism of ZnO varistors through multi-field coupling simulation and found that the evolution of grain boundary layer defects was the core cause of deterioration; Zhou et al. [6] studied the electrothermal characteristics of ZnO varistors based on a multi-physics model, revealing a correlation between temperature distribution and the deterioration process; Hu et al. [7] provided a reference for analyzing the failure causes of arresters in distribution networks; Kang et al. [8] explored the correlation between transient overvoltage/temperature and the electrical characteristics of ZnO varistors; Qin et al. [9] expanded the research dimension by studying the transient response characteristics of ZnO arresters under a high-altitude electromagnetic pulse environment; in terms of failure modes, Zhang et al. [10] found various failure modes of ZnO varistors through multiple lightning strike experiments, which are closely related to impulse waveform parameters; Lin et al. [11] provided theoretical support for deterioration assessment based on the Voronoi network finite element model; Thiago et al. [12] supplemented the failure laws under different impulse conditions by studying short-duration current impulse waveforms.

In the field of remaining life prediction and state diagnosis, machine learning has become the mainstream technical means: Xie et al. [13] carried out research on SPD remaining life prediction based on machine learning methods, providing a reference for algorithm selection; Habibollahi et al. [14] proposed a guided neural network degradation prediction method, providing a new idea for the deterioration prediction of complex systems; Peng et al. [15] further applied PHM (Prognostics and Health Management) design to the condition monitoring of electric locomotive arresters, verifying the feasibility of integrating prediction models into engineering practice—providing a reference for the engineering transformation of the remaining life prediction model proposed in this study. In parameter optimization and diagnosis method innovation, Shi et al. [16] proposed an intelligent online diagnosis method for arrester status based on an impulse aging experiment with ZnO varistors, verifying the effectiveness of multi-parameter fusion diagnosis; Araujo et al. [17] monitored ZnO arresters by combining convolutional neural networks and image processing technology, expanding the non-intrusive monitoring idea; Shu et al. [18] realized the fault identification of ZnO arresters through a method combining suppression of environmental temperature and humidity interference and stacked autoencoders, improving diagnosis accuracy under complex environments; Olesz et al. [19] studied the arrester condition monitoring method through leakage current measurement, providing a basis for parameter selection; Li et al. [20] optimized parameter acquisition technology with a Tunnel Magnetoresistance (TMR)-sensor-based leakage current sensing method; Walczak [21] indirectly evaluated the moisture degree of varistors through dielectric spectroscopy, enriching non-electrical parameter monitoring means.

In the research of the expansion of application scenarios, scholars have carried out SPD adaptability research for different specific scenarios. Zaini et al. [22] and Wang et al. [23] provided references for SPD application in photovoltaic systems; Tsovilis et al. [24] proposed a modeling method suitable for DC SPDs in electric vehicle charging stations, improving the special scenario SPD design theory; Tsukamoto et al. [25] studied the change in the maximum withstand capacity of MOVs under repetitive pulse stress, providing a basis for the selection of SPDs under actual working conditions.

Despite the aforementioned progress, the existing research still faces three core deficiencies, making it difficult to meet engineering needs for accurate remaining life prediction and early failure warning. First, incomplete dataset coverage: most studies fail to collect full-lifecycle data covering the entire process from the initial state to the complete failure of ZnO varistors, resulting in models that cannot fully reflect the evolution law of deterioration. Second, single-parameter characterization with poor robustness: over-reliance on individual electrical parameters (e.g., $U_{1mA}$ or $I_L$) ignores the synergistic effect of multiple parameters, leading to inaccurate assessment of the deterioration state and vulnerability to external interference. Third, disconnected remaining life prediction and failure threshold determination: Most models only focus on quantitative prediction of remaining life, lacking accurate identification of failure critical points, resulting in a disconnection between life prediction and early failure warning, which cannot meet the practical needs of engineering early warning.

The specific research gaps and corresponding solutions proposed in this study are summarized in

Table 1. Key research gaps and corresponding solutions in this study.

Research Gaps	Solutions
Incomplete full-lifecycle dataset coverage	Conduct 8/20 μs impulse accelerated deterioration experiments, collecting 441 sets of data from 9 samples (initial state to complete failure)
Over-reliance on single-parameter characterization	Fusion of 5 core parameters ($U_{1mA}$$, \alpha$$, I_L$$, R_p$$, C_p$) + principal component analysis (PCA) dimensionality reduction to eliminate redundancy
Disconnected remaining life prediction and failure threshold determination	Integrate Particle Swarm Optimization-Support Vector Regression (PSO-SVR) (quantitative prediction) and iForest (qualitative threshold) to establish a collaborative mechanism

.

1.3. Research Content and Innovations

1.3.1. Research Content

Aiming to mitigate the deficiencies of the existing research, this study carries out research on the deterioration characteristics and remaining life prediction of ZnO varistors through a combination of experimental testing, mechanism analysis, and algorithm modeling. Based on a comprehensive literature review and previous research findings, seven parameters that can reflect the deterioration degree and remaining life of ZnO varistors are selected for analysis—including the intrinsic parameters of the circuit model illustrated in Figure 1—specifically $L_s$ (series inductance), $R_p$ (parallel resistance), and $C_p$ (parallel capacitance) as circuit model intrinsic parameters, along with $U_{1mA}$, $\alpha$, $I_L$, and $\Delta T$ (temperature rise) as performance characterization parameters. The circuit model presented in Figure 1 of this paper aligns with the MOA dynamic nonlinear model proposed in Ref. [26]. In this model, $L_s$ characterizes high-frequency response; $R_p$ reflects grain boundary insulation loss; and $C_p$ characterizes the grain boundary dielectric properties. Ref. [26] identifies these three intrinsic parameters as L, R, and C, respectively [26].

This research comprises five main components: 1. Design an 8/20 μs impulse current accelerated deterioration experiment to collect seven characteristic parameters of nine same-batch ZnO varistors throughout their full lifecycle, revealing the deterioration evolution laws of each parameter; 2. Optimize feature vectors via PCA to eliminate dimensional differences and redundant information among multi-parameters; 3. Construct a PSO-SVR remaining life prediction model, optimize key parameters of SVR using the PSO algorithm, and verify its superiority through comparison with traditional models; 4. Introduce the iForest algorithm for anomaly detection to accurately determine the failure threshold of ZnO varistors; 5. Propose a “PSO-SVR + iForest” combined model, establish a dual verification mechanism of “quantitative prediction + qualitative determination”, and verify its accuracy and engineering applicability.

1.3.2. Main Innovations

• Construction of a full-lifecycle multi-parameter dataset: Addressing the gap of incomplete dataset coverage, an 8/20 μs impulse current accelerated deterioration experiment is conducted to collect 441 sets of valid data from nine same-batch samples, covering the entire process from initial state to complete failure. This dataset provides a complete data foundation for subsequent model construction and ensures that the model can reflect the full deterioration evolution law.
• Multi-parameter fusion characterization strategy: To fully capture the comprehensive information of the deterioration process, five core electrical parameters are integrated to construct a feature vector, leveraging their complementary responses across different degradation stages. PCA dimensionality reduction is used to eliminate redundant information, and the first principal component (PC₁) with a variance contribution rate of 69.8% is selected as the input feature. The correlation coefficient between PC₁ and the deterioration degree reached 0.96, which is significantly higher than that of any single parameter, effectively improving the accuracy and robustness of state assessment.
• Collaborative mechanism of prediction and threshold determination: To solve the disconnection between remaining life prediction and failure threshold determination, a “PSO-SVR + iForest” combined model is proposed. The PSO-SVR model realizes high-precision quantitative prediction of remaining life (test set $R^2$ = 0.9726), MSE = 0.00142) and the iForest model accurately identifies the failure threshold (AUC = 0.984, accuracy = 95.9%), realizing the synergy of life prediction and early warning.

The structure of this paper is as follows: Section 2 describes the ZnO varistor deterioration experiment, including the mechanism analysis, experimental design, and parameter evolution laws. Section 3 establishes the remaining life prediction model based on PCA and PSO-SVR. Section 4 constructs the iForest-based failure threshold determination model and proposes the combined model. The three research gaps identified in Table 1 are addressed in Section 2, Section 3 and Section 4, respectively. Section 5 presents the conclusions and future research prospects.

2. Deterioration Experiment of ZnO Varistors

Aligned with the research objectives and innovation goals, this section aims to address the “incomplete full-lifecycle dataset” gap outlined in Section 1.2. A rigorous accelerated deterioration experiment simulating real-world lightning surge environments was designed to investigate the deterioration behavior of ZnO varistors. By collecting multi-characteristic parameters across the entire lifecycle, this experiment not only constructs a comprehensive and reliable full-lifecycle dataset but also elucidates fundamental deterioration mechanisms via macroscopic parameter changes, providing high-quality data support for subsequent model construction and laying an experimental foundation for the development of a multi-parameter fusion characterization strategy.

2.1. Deterioration Mechanism and Deterioration Characterization of ZnO Varistors

The core function of ZnO varistors depends on their special microstructure and electrical properties. They are mainly composed of ZnO and microscopically consist of ZnO grains, grain boundary layers, spinel phases, and micropores. The regulation of the grain boundary layer dominated by Schottky barriers is the root cause of their nonlinear conductive properties: in low electric fields, the grain boundary layer is in a high-resistance insulating state; when the electric field rises to the threshold, the tunnel effect is significantly enhanced, making the resistance drop sharply; after breakdown, the grain boundary layer is completely conductive. Meng et al. [4]’s multi-field coupling simulation research has confirmed that the evolution of grain boundary layer defects is the core mechanism inducing performance deterioration, which is highly consistent with this study’s understanding of the essence of deterioration.

The aging forms of ZnO varistors mainly include DC aging, AC aging, and impulse aging. Among them, impulse aging is directly related to actual service scenarios, such as lightning surges, and has the most prominent impact on the protection reliability of SPDs. Qin et al. [27]’s research on the response of ZnO arresters under nanosecond electromagnetic pulses and Tsovilis et al. [24]’s exploration of the modeling of DC SPDs for electric vehicle charging stations have confirmed the key position of impulse aging in engineering applications. From the perspective of deterioration mechanisms, the academic community generally believes that local temperature rise in the grain boundary caused by impulse current is the core cause [11]: temperature rise drives processes such as ion migration, grain boundary defect proliferation, and oxygen desorption, ultimately leading to a decrease in the height of the Schottky barrier. Zhou et al. [28]’s research on the aging mechanism of DC temporary overvoltage and Fu et al. [29]’s analysis of the parallel shunt performance of MOVs for 500 kV series compensation further confirm the dominant role of barrier height changes and grain boundary layer status in the deterioration process. It is worth noting that these micro-level deterioration evolutions will be directly mapped to regular changes in electrical macro-parameters, such as $U_{1mA}$ drops, $I_L$ rises, and $\alpha$ attenuation, which provides a core basis for the subsequent collaborative monitoring of the deterioration state through multiple parameters. Walczak [21]’s research on evaluating the moisture degree of varistors through dielectric spectroscopy further confirms the effectiveness of parameters such as $C_p$ and $R_p$ in deterioration characterization.

As shown in Figure 2, the V–I characteristic curve of ZnO varistors is segmented into three regions: the pre-breakdown region, nonlinear region, and breakdown region, represented by brown, blue, and purple, respectively. The core parameters include the varistor voltage $U_{1mA}$ (the on-voltage under 1 mA DC current, which is the core characterization parameter of the degree of deterioration); leakage current $I_L$ (the operating current in the pre-breakdown region, which is at a microampere level under normal conditions and increases significantly after deterioration); nonlinear coefficient $\alpha$ (reflects the sensitivity of the resistance to voltage/current changes; a decrease in $\alpha$ indicates a decline in protection performance); and parallel resistance $R_p$ and parallel capacitance $C_p$ (closely related to the structure of the grain boundary layer, showing regular changes during the deterioration process).

These parameters are directly related to the state of the Schottky barrier and their change laws can comprehensively reflect the deterioration process of ZnO varistors, providing a basis for parameter selection in subsequent experimental design and model construction.

2.2. Experimental Design and Implementation

Based on the above deterioration mechanism and parameter characterization logic, this study designs an 8/20 μs impulse current accelerated deterioration experiment. Through the design of a standardized experimental platform and process, the accuracy and consistency of the collected parameters are ensured, providing reliable data support for the subsequent model’s construction and optimization.

As shown in Figure 3, an experimental platform for measuring the key parameters of ZnO varistors in an offline manner has been set up. In this platform, the impulse current generator, varistor tester, and RLC bridge tester connect to the sample sequentially to perform current impulse testing and related parameter measurement on the sample. To ensure safety and prevent injury from potential sample explosion, the test sample is enclosed within a protective acrylic box. Impulse current is delivered to the sample via cables routed through two openings in the acrylic box. For operational convenience, tested samples are placed in the acrylic box for centralized handling. The thermal imager directly measures the temperature of the sample through the acrylic box.

The specifications of the core equipment are as follows: (1) PRM8/20 (Shanghai Prima Electronic Co., Ltd, Shanghai, China) impulse current generator: output range 0.5~10 kA, waveform rise time 8 μs, half-peak time 20 μs, accuracy ± 3%; (2) HPS2540 (Changzhou Helpass Electronic Technologies Co., Ltd., Changzhou, China) varistor tester: $U_{1mA}$ measurement range 5~1400.0 V, accuracy 0.5% ± 0.1 V; $\alpha$ measurement range 0~999.9, accuracy 1% ± 0.1; $I_L$ measurement range 0~2200.0 μA, accuracy 1% ± 2 μA; (3) TH2829A (Changzhou Tonghui Electronic Co., Ltd, Changzhou, China) RLC bridge tester: resistance measurement range 0.00001 Ω~99.9999 MΩ, capacitance measurement range 0.00001 pF~9.99999 F, inductance measurement range 0.00001 μH~99.9999 kH, accuracy ± 0.05%; (4) NF-583S (Shenzhen Noyafa Electronic Co., Ltd, Shenzhen, China) temperature thermal imager: temperature measurement range −15~600 °C, accuracy ± 2 °C or ± 2%, frame rate 25 fps. Each instrument serves a distinct function: the impulse current generator simulates lightning surges, the varistor tester collects $U_{1mA}$, $\alpha$, and $I_L$, the RLC bridge tester collects $R_p$, $C_p$, and $L_s$, and the temperature thermal imager records the temperature rise $\Delta T$ before and after the impulse. All equipment was calibrated before the experiment to ensure measurement accuracy.

In this experiment, nine 07D241K type ZnO varistors from the same manufacturer (Guangdong Hongzhi Electronics Technology Co., Ltd., Shantou, China) were selected as samples A1~A9. Key parameters included a nominal varistor voltage of 240 V (tolerance ± 5%), maximum continuous operating voltage of AC 150 V, maximum pulse current of 1.2 kA (8/20 μs waveform), and dimensions of 7 mm diameter and 4.3 mm thickness. All samples passed initial inspection with no surface cracks, and initial $U_{1mA}$ deviation ≤ 3% to ensure consistency.

To accelerate the deterioration process and cover the full lifecycle, the impulse current was set to 1.32 kA (slightly larger than the maximum pulse current 1.2 kA of the samples). This aligns with prior studies: Thiago et al. [12] used 3× nominal current, and Zhang et al. [30] adopted 1× nominal current with multi-pulses, both for accelerated aging. The experimental process strictly follows standardized steps: first, pretreatment is carried out to check that the sample appearance is intact and calibrate the initial parameters with a varistor tester to ensure consistent initial performance; then, impulse tests are conducted on the samples using the 8/20 μs impulse current wave specified in the national standard GB/T 16927.1-2011 [31], and after each impulse, the sample is allowed to stand for 30 min until it cools down to room temperature to avoid temperature accumulation affecting parameter measurement; next, parameters are collected in the order of “$U_{1mA}$ → $\alpha$ → $I_L$ → $R_p$ → $C_p$ → $L_s$ → $\Delta T$” to ensure data synchronization; finally, the termination condition is set: when the sample has cracks or explosions, or $U_{1mA}$ is lower than 180 V, $I_L$ is greater than 50 μA, and $R_p$ is lower than 1 MΩ, it is determined to be completely damaged and the experiment is stopped.

Through this scheme, 441 sets of full-lifecycle data of A1~A9 were successfully obtained, each set containing 7 characteristic parameters, providing sufficient sample support for subsequent model construction. The basic statistical information of the 5 core parameters in the dataset is shown in

Table 2. Five core parameters of samples.

Parameter	Mean	Standard Deviation	Minimum Value	Maximum Value
$U_{1mA}$ (V)	239.6	12.6	180.3	253.4
$\alpha$	51.3	11.4	22.5	65.4
$I_L$ (μA)	0.7	1.1	0.0	7.8
$R_p$ (MΩ)	14.77	1.02	12.89	17.70
$C_p$ (pF)	150.2	10.7	124.1	161.4

.

The full-lifecycle dataset constructed in this section provides a complete and reliable data basis for subsequent PCA dimensionality reduction and prediction model training.

2.3. Experimental Results and Analysis of Deterioration Laws

By counting the above 441 sets of data and plotting respectively, the change trends of each core parameter with the increase in the number of impulses can be seen. Since the change trends of $L_s$ and $C_p$ are highly synchronized, and $\Delta T$ has no obvious law, $L_s$ and $\Delta T$ will not be considered in the subsequent analysis. The trend of the five core parameters changing with the number of impulses is shown in Figure 4.

As shown in Figure 4, $U_{1mA}$ shows a three-stage characteristic of “slow increase-stabilization-rapid decrease”. In the initial stage, due to the capture of injected electrons by electron traps, the height of the Schottky barrier increases, and $U_{1mA}$ rises slightly; in the middle stage, the barrier state is stable, and $U_{1mA}$ is maintained at around 235 V; in the later stage, the barrier collapses, and $U_{1mA}$ drops rapidly, and all drop below 180 V before failure. This change law is consistent with the aging characteristics of ZnO varistors under DC temporary overvoltage studied by Zhou et al. [28].

$\alpha$ is initially stable in the range of 50~60, and gradually decreases with the increase in the number of impulses, with an overall decrease of more than 50% before and after deterioration. The attenuation of $\alpha$ is caused by the weakening of the tunnel effect in the grain boundary layer, which directly leads to the decline in the voltage limiting capacity of the varistor, which is consistent with the micro-deterioration characteristics of ZnO varistors under multi-pulse lightning strikes studied by Zhang et al. [30].

$I_L$ remains stable (0.32 μA) during most of the impulse process and shows a “steep rise” before failure. When A1 and A8 fail, the $I_L$ reaches 10~15 μA, and the $I_L$ of the other samples reaches more than 30 μA when they fail. This mutation characteristic indicates that $I_L$ can be used as an early failure warning parameter, but that it is not suitable for full-cycle deterioration evaluation alone, which is consistent with the multi-parameter collaborative diagnosis idea proposed by Shi et al. [16].

$R_p$ and $C_p$ show regular changes: $R_p$ generally presents a trend of “first increase and then decrease”, decreasing by 1~2 MΩ just before failure; $C_p$ shows a characteristic “decrease–stabilization–increase” pattern, which is closely related to the increase in grain boundary layer defects and the intensification of ion migration. This change law is consistent with the grain boundary layer evolution law obtained by Meng et al. [4] through multi-physics simulation, verifying the correlation between parameter changes and microstructural deterioration.

According to the above parameter change trend graphs, it can be seen that even for varistors of the same model and batch, there are obvious individual differences in their parameter change trends during the deterioration process under impulse action. This phenomenon is consistent with the electrical deterioration characteristics of low-voltage ZnO varistors under AC switch surges studied by Muremi et al. [32], indicating that individual differences are important factors affecting remaining life prediction. Further analysis reveals that the core parameters ($U_{1mA}$, $\alpha$, $I_L$, $R_p$, and $C_p$) present differential sensitivities across the full degradation cycle. This complement of parameter responses ensures the comprehensive capture of degradation information that cannot be fully reflected by individual parameters alone. Therefore, to construct a robust characterization for remaining life prediction, we integrated these five core parameters to form a feature vector, laying a foundation for subsequent PCA dimensionality reduction and model training.

3. Remaining Life Prediction Based on PCA and PSO-SVR

To address the gap summarized in Section 1.2 of “single-parameter characterization insufficiency” in predicting of remaining life, this section develops a comprehensive model. First, PCA is employed to reduce the dimensionality of multi-parameters, thereby eliminating dimensional discrepancies and redundancy. Subsequently, a PSO-SVR model is constructed for quantitative prediction of remaining life.

3.1. Principal Component Analysis

Due to the inconsistent number of impulses each sample undergoes before damage, the amount of data obtained from each group is different. To avoid excessive fitting errors that may affect the reliability of the prediction model [32], 319 sets of data from A2, A3, A4, A5, A6, A7, and A8 were selected from the 441 sets of data as the training set for model construction to provide sufficient data support for model training, and 122 sets of data from A1 and A9 were selected as the test set to verify the performance of the constructed model. The ratio of the training set to the test set is about 7:3.

As mentioned above, this study selects five parameters ($U_{1mA}$, $\alpha$, $I_L$, $R_p$, $C_p$) to construct the feature vector $X=\left[U_{1mA},\alpha ,I_L,R_p,C_p\right]$ as the model input. Since the five parameters have dimensional differences and correlations, it is first necessary to perform Z-score standardization on the original data to eliminate the influence of dimensions.

Let the original dataset be ${X=\left[x_{ij}\right]}_{n \times p}$, where $n$ is the number of samples (i.e., the number of impulse experiments), $p$ is the dimension of the characteristic parameters (this study selects 5 core features, so $p = 5$), and $x_{ij}$ represents the original value of the $j$-th characteristic parameter of the $i$-th sample.

The Z-score standardization formula is:

$$z_{ij} = {\displaystyle \frac{x_{ij }- {\mu }_j}{{\sigma }_j}}$$

(1)

Among these values, ${\mu }_j = {\displaystyle \frac{1}{n}}{\sum }_{i = 1}^n{x}_{ij}$ is the sample mean of the $j$-th feature, and ${\sigma }_j = \sqrt{{\displaystyle \frac{1}{n - 1}}{\sum }_{i = 1}^n{\left(x_{ij }- {\mu }_j\right)}^2}$ is the sample standard deviation of the $j$-th feature.

After standardization, the dataset $Z={\left[z_{ij}\right]}_{n \times p}$ is obtained, and each feature satisfies the mean ${\overline{z}}_j = 0$ and standard deviation $s_j = 1$.

Then, the $p \times p$ order covariance matrix can be obtained:

$$C = {\displaystyle \frac{1}{n - 1}}{Z}^{T}Z .$$

(2)

From this, the $p$ eigenvalues of the covariance matrix are obtained as ${\lambda }_1 \ge {\lambda }_2 \ge \dots \ge { \lambda }_p\ge 0$ and the corresponding eigenvectors $w_1,{ w}_2,\dots , w_p$.

The proportion of information of the original data contained in the $k$-th principal component can be calculated by the contribution rate of a single eigenvalue:

$${\eta }_k = {\displaystyle \frac{{\lambda }_k}{{\sum }_{i = 1}^p{\lambda }_i}}$$

(3)

The cumulative information proportion of the first $m$ principal components is calculated by the cumulative contribution rate:

$${\eta }_m = {\displaystyle \frac{{\sum }_{k = 1}^m{\lambda }_k}{{\sum }_{i = 1}^p{\lambda }_i}}$$

(4)

The contribution rate calculated according to the above method can be used to select the principal components used after dimensionality reduction. By calculating using the 441 sets of data in this study, the contribution rate of the first principal component (PC₁) is around 0.7, and the contribution rate of the first two principal components (PC_{1 + 2}) exceeds 0.85, as shown in

Table 3. Proportion of PC₁ and PC_{1 + 2} of samples A1~A9.

Sample	A1	A2	A3	A4	A5	A6	A7	A8	A9
PC1	0.699	0.721	0.696	0.705	0.700	0.698	0.715	0.760	0.791
PC1 + 2	0.923	0.907	0.923	0.916	0.861	0.860	0.911	0.913	0.901

. This result indicates that the first two principal components can effectively characterize the core information of the original five-dimensional data, which is consistent with the feature dimensionality reduction idea adopted by Shu et al. [18], providing a basis for subsequent model simplification.

It can be seen from Table 3 that PC₁ can effectively characterize the core information of the original five-dimensional data. The deterioration trend can be well distinguished only by PC₁. To reduce the calculation amount, PC₁ is selected for dimensionality reduction calculation in the model in Section 3.2:

$$P{C}_1 = ZW = Z{w}_1.$$

(5)

Finally, normalize PC₁ to the [0, 1] interval as the deterioration degree characterization value:

$$Y = {\displaystyle \frac{P{C}_1 - P{C}_{1,\min }}{P{C}_{1,\max }- P{C}_{1,\min }}}$$

(6)

Among these values, $Y = 0$ corresponds to the optimal initial state in the dataset and $Y = 1$ corresponds to the complete failure state. Pearson correlation analysis confirms that the correlation coefficient between PC₁ and the deterioration degree $Y$ reaches 0.96, verifying the reliability of the multi-parameter fusion characterization.

To avoid data leakage, Z-score standardization, PCA fitting, and subsequent normalization of PC₁ (Equation (6)) were exclusively performed on the training set (319 sets of data from samples A2–A8). The test set (122 sets of data from samples A1 and A9) was transformed using the standardization parameters and the PCA projection matrix derived from the training set, ensuring the independence of model training and testing.

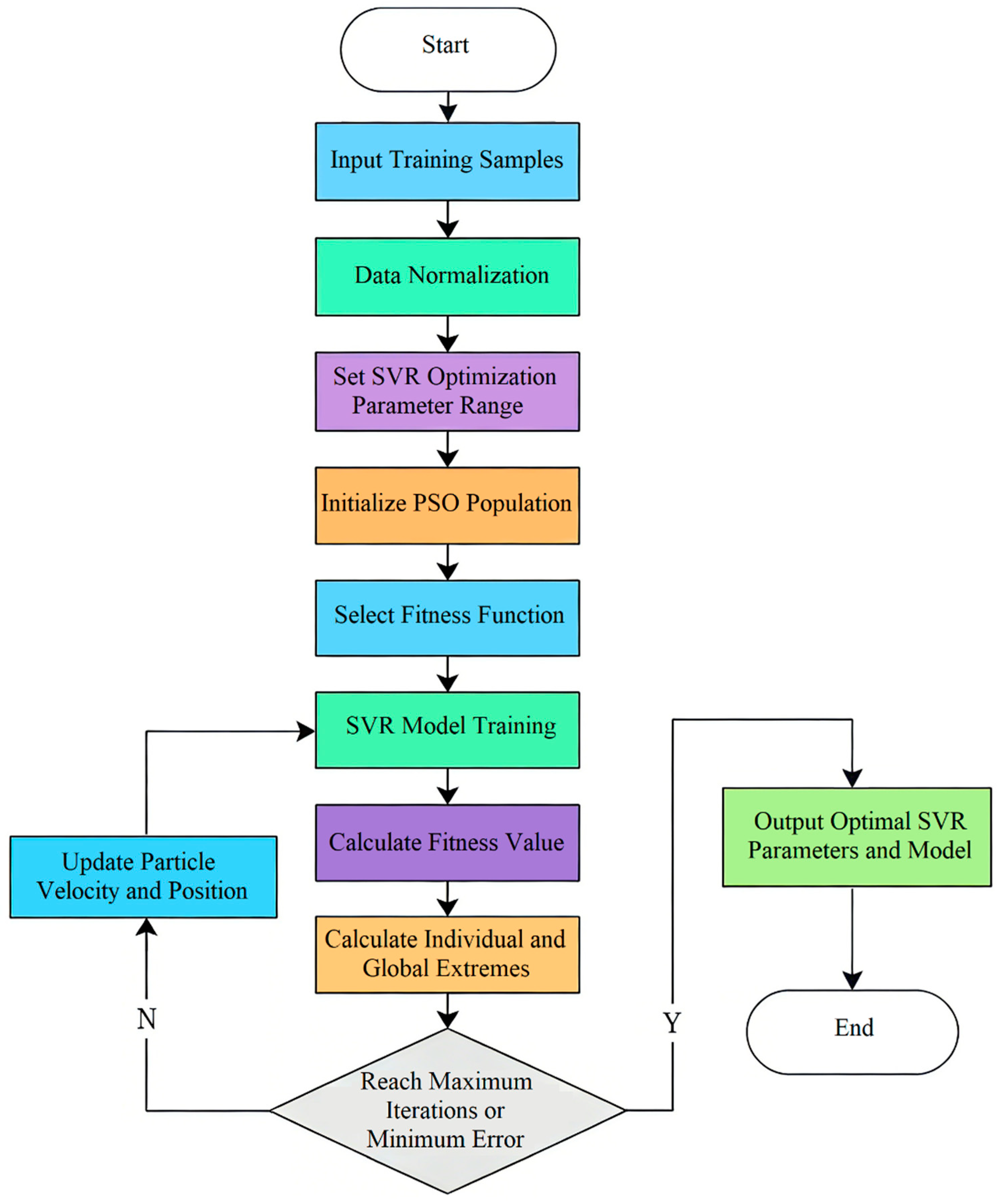
3.2. Construction and Optimization of PSO-SVR Model

Through the above PCA dimensionality reduction, a concise and effective feature vector has been obtained, solving the problems of multi-parameter redundancy and dimensional differences. On this basis, this study constructs a PSO-SVR remaining life prediction model. The core idea is to use the global optimization ability of the PSO algorithm to optimize the key parameters (penalty factor $c$, allowable error $\epsilon$, kernel parameter $\gamma$) of Support Vector Regression (SVR), breaking through the limitation of the local optimal solutions of traditional algorithms and realizing the best fitting of the life prediction model of ZnO varistors.

3.2.1. SVR Model Construction

For the normalized and dimensionally reduced training samples ${\left(x_i,y_i\right)}_{i = 1}^n$ (where $x_i$ is the input feature vector after PCA dimensionality reduction, $y_i$ is the actual deterioration degree of the ZnO varistors, and $n$ is the number of training samples), SVR maps the low-dimensional input features to a high-dimensional feature space through a kernel function to construct a linear regression model, thereby realizing the nonlinear fitting of the deterioration degree. Considering the characteristics of the small samples, nonlinearity, and high dimensionality of the ZnO varistor life data, the Radial Basis Function (RBF) is selected as the kernel function of the SVR due to its strong adaptability and generalization ability. The core formula of the SVR prediction model is as follows:

$$f\left(x\right)=\sum _{i =1}^n\left({\alpha }_i-{\alpha }_i^{*}\right)K\left(x,x_i\right)+b$$

(7)

where

• $K\left(x, x_i\right)=exp\left(-\gamma |x-x_i{|}^2\right)$ is the RBF kernel function, $\gamma$ is the kernel parameter that controls the influence range of the sample, and $|x-x_i|$ is the Euclidean distance between the input feature $x$ and the sample $x_i$;
• ${\alpha }_i$ and ${\alpha }_i^{*}$ are Lagrange multipliers, satisfying the constraint conditions ${\alpha }_i\ge 0$, ${\alpha }_i^{*}\ge 0$, and ${\sum }_{i = 1}^n\left({\alpha }_i-{\alpha }_i^{*}\right)=0$
• $b$ is the bias term, which adjusts the position of the regression hyperplane;
• The values of ${\alpha }_i$, ${\alpha }_i^{*}$, and $b$ are obtained by solving the quadratic programming problem under the constraint of the $\epsilon$-insensitive loss function.

3.2.2. PSO Algorithm Parameter Optimization

The performance of the SVR model is highly dependent on the selection of parameters $c$, $\gamma$, and $\epsilon$. Traditional parameter selection methods, such as a grid search, have the disadvantage of low efficiency and can easily fall into local optimal solutions. The PSO algorithm simulates the foraging behavior of bird swarms, searches the optimal parameter combination in the solution space through the cooperation and competition among particles, and has the advantages of a fast convergence speed and a strong global search ability. The core of the PSO algorithm lies in the updating of particle velocity and position, and the corresponding formulas are as follows:

$$v_{k +1}=\omega v_k+c_1{r}_1\left({pbest}_k-x_k\right)+c_2{r}_2\left(gbest-x_k\right)$$

(8)

$$x_{k+1}=x_k+v_{k+1}$$

(9)

where

• $v_{k+1}$ and $x_{k+1}$ are the velocity and position of the particle in the $k+1$-th iteration, respectively, and each particle position corresponds to a combination of the SVR parameters ($c,\gamma ,\epsilon$);
• $v_k$ and $x_k$ are the velocity and position of the particle in the $k$-th iteration;
• $\omega$ is the inertia weight, which balances the global search ability and local convergence ability of the algorithm. In this study, a linear decreasing strategy is adopted: ${\omega }_{\max }=0.9$, ${\omega }_{\min }=0.4$, and $\omega$ decreases linearly with the increase in number of iteration;
• $c_1$ and $c_2$ are learning factors, which are set to 2 in this study to adjust the learning ability of the particle to its own optimal position and the global optimal position;
• $r_1$ and $r_2$ are random numbers that are uniformly distributed in the interval [0, 1], which increase the randomness of the search;
• $pbes{t}_k$ is the optimal position (optimal parameter combination) found by the particle itself in the first $k$ iterations;
• $gbest$ is the optimal position (global optimal parameter combination) found by the entire particle swarm in the first $k$ iterations.

3.2.3. Algorithm Flow and Parameter Setting

As shown in Figure 5, the algorithm flow of the PSO-SVR model is designed as follows: the input layer is the 5-dimensional feature vector $X=\left[U_{1mA},\alpha ,I_L,R_p,C_p\right]$; the preprocessing layer completes data standardization and PCA dimensionality reduction; the core layer obtains the RBF kernel SVR optimized by PSO; and the output layer obtains the deterioration degree $Y$ for remaining life calculation (remaining life = $(1 - Y)$ × total life).

In this study, the parameters of the PSO algorithm are set as follows: the population size is 30, the maximum number of iterations is 50, the learning factors $c_1=c_2=2$, the inertia weight $\omega$ adopts a linear decreasing strategy, and the optimization goal is to minimize the mean squared error (MSE) of the SVR model on the training set. Through iterative search, the optimal parameter combination of SVR is obtained as: $c=10$, $\epsilon =0.024$, $\gamma =1$. The fitness curve tends to be stable after 14 iterations (Figure 6), indicating that the PSO algorithm has a fast convergence speed and can effectively avoid falling into local optimal solutions, which is consistent with the convergence characteristic analysis idea of the optimized iForest algorithm proposed by Gałka [33].

3.3. Model Verification and Comparative Analysis

To evaluate the accuracy of the PSO-SVR remaining life prediction model, this study selects four indicators (mean squared error (MSE), mean absolute error (MAE), root mean squared error (RMSE), and goodness of fit $\left(R^2\right)$) to comprehensively evaluate the model performance. The calculation formulas are as follows:

$$\mathrm{MSE} = {\displaystyle \frac{1}{n}}{\sum }_{i = 1}^n{\left(y_i- {\widehat{y}}_i\right)}^2,$$

(10)

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n|y_i-{\widehat{y}}_i|,$$

(11)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2},$$

(12)

$$R^2=1 -{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{ y}\right)}^2}}$$

(13)

Among them, $y_i$ is the actual value, ${\widehat{y}}_i$ is the predicted value, $\overline{y}$ is the mean of the actual values, and $n$ is the number of samples.

The prediction results of the PSO-SVR model constructed in this study on the above training set and test set are excellent (

Table 4. Error values of the PSO-SVR training set and test set.

Dataset	MSE	MAE	RMSE	${\mathit{R}}^2$
Training set	0.00096	0.01985	0.03108	0.9781
Test set	0.00142	0.02514	0.04026	0.9726

): the training set obtains an $\mathrm{MSE} = 0.00096$ and an $R^2 = 0.9781$; the test set obtains an $\mathrm{MSE} = 0.00142$ and an $R^2 = 0.9726$, indicating that the model has strong generalization ability.

Compared with traditional SVR and BP neural networks (

Table 5. Comparison of prediction errors of different algorithms.

Model	MSE	MAE	RMSE	${\mathit{R}}^2$
Traditional SVR	0.00443	0.05663	0.06653	0.9186
BP neural network	0.00323	0.03792	0.05686	0.9496
PSO-SVR	0.00142	0.02514	0.04026	0.9726

), the MSE of the PSO-SVR model is lower, by 0.00301 and 0.00181, respectively, and the $R^2$ is higher, by 0.054 and 0.023, respectively. This comparison result verifies the effectiveness of the PSO algorithm in optimizing the SVR parameters. A visual comparison (Figure 7) shows that the PSO-SVR prediction curve is more consistent with the actual deterioration trend, especially the prediction accuracy, an advantage which is more obvious in the later stage of deterioration ($Y > 0.8$), which is of great significance for early failure warning.

In addition, compared with the EMD-Att-LSTM short-term load forecasting model proposed by Neeraj et al. [34] and the guided neural network degradation prediction method by Habibollahi et al. [14], the PSO-SVR model in this study has a simpler structure and a higher computational efficiency in small-sample scenarios, making it more suitable for real-time prediction needs in engineering sites.

4. Failure Life Threshold Prediction Based on iForest

The PSO-SVR model has achieved high-precision quantitative prediction of remaining life, but in engineering applications it is still necessary to clarify the critical failure point to trigger early warning decisions. The advantage of the iForest algorithm in anomaly detection is that it can accurately identify the mutation characteristics in the later stage of deterioration, complementing the quantitative prediction of PSO-SVR. This section extracts key features through PCA dimensionality reduction, constructs an iForest anomaly detection model, and completes the accurate determination of the failure life threshold. Based on that, a combined determination process of “PSO-SVR + iForest” was proposed to address the gap of the “disconnected remaining life prediction and failure threshold determination” discussed in Section 1.2.

4.1. Construction of Anomaly Detection Model

Different from the previous model, which only uses the first principal component, when performing PCA dimensionality reduction on the 5-dimensional characteristic parameters, this section extracts the first two principal components (cumulative contribution rate ≥ 85%, Table 3). The visualization results show that the normal data (corresponding to the early and middle stages of ZnO varistor deterioration) is concentrated and distributed near the origin of the 2-dimensional principal component space, while the abnormal data (corresponding to the late stage of deterioration and failure state) deviates far from the center point due to the mutation of the characteristic parameters (Figure 8). This obvious distribution difference provides a solid data foundation for anomaly detection.

For data with such distribution characteristics, the iForest anomaly detection algorithm is more appropriate. The iForest algorithm constructs multiple isolation trees by randomly selecting features and splitting points and isolates abnormal samples from normal samples through the differences in the path lengths of the samples in the isolation trees. Compared with traditional anomaly detection algorithms (such as the k-Nearest Neighbors (KNN) and the Density-Based Spatial Clustering of Applications with Noise (DBSCAN)), iForest has the advantages of high efficiency, low computational complexity, and strong adaptability to high-dimensional and small-sample data. Both the optimized iForest algorithm proposed by Gałka [33] and the Rotated iForest algorithm by Monemizadeh et al. [35] have verified the advantages of this type of algorithm in anomaly detection, making it especially suitable for the scenario of ZnO varistor deterioration state identification.

The core of the iForest algorithm is to quantify the anomaly degree of samples through the anomaly score. For a given sample $x$, the anomaly score $s\left(x, n\right)$ is calculated based on the path length $h\left(x\right)$ of the sample in the isolation tree and the expected path length $\mathbb{E}\left[h\left(x\right)\right]$ of all samples. The core formula is as follows:

$$s\left(x,n\right)=2^{-{\displaystyle \frac{h\left(x\right)}{\mathbb{E}\left[h\left(x\right)\right]}}}$$

(14)

where

• $s\left(x,n\right)$ is the anomaly score of sample $x$ and $n$ is the number of samples used to construct the isolation tree;
• $h\left(x\right)$ is the path length of sample $x$ in the isolation tree, which is defined as the number of edges passed from the root node of the tree to the leaf node where the sample is located. Abnormal samples are more likely to be isolated in the early stage of tree construction, so their path lengths are shorter;
• $\mathbb{E}\left[h\left(x\right)\right]$ is the expected path length of all of the samples in the isolation tree, which is used to standardize the path length of a single sample. For samples of size $n$, $\mathbb{E}\left[h\left(x\right)\right]$ can be calculated through the harmonic number approximation;
• The value range of the anomaly score $s\left(x,n\right)$ is [0, 1]. The closer $s\left(x,n\right)$ is to 1, the higher the anomaly degree of the sample; the closer it is to 0, the more normal the sample is.

In this study, the parameters of the iForest algorithm are set as follows: the number of isolation trees (forest size) is 100, which balances the detection accuracy and computational efficiency; each isolation tree is constructed using 256 samples, a size determined by the scale of the experimental dataset (441 sets), ensuring both the diversity of the isolation trees and avoiding the detection bias that could arise from an insufficient sample size; the anomaly score threshold is set to 0.7, that is, when $s\left(x,n\right)\ge 0.7$, the sample is determined to be abnormal, corresponding to the failure state of the ZnO varistor.

The model training follows a standardized process: (1) the 2-dimensional principal component data after PCA dimensionality reduction is divided into a training set and a test set according to a 7:3 ratio; (2) a total of 100 isolation trees are constructed based on the training set and for each isolation tree features and splitting points are randomly selected to split the data until each leaf node contains only one sample or reaches the maximum depth of the tree; (3) for each sample in the test set, the path length $h\left(x\right)$ in each isolation tree is calculated and the average path length is taken as the final path length of the sample; (4) the anomaly score $s\left(x,n\right)$ of the sample is calculated using Formula (14); (5) the threshold is adjusted according to the actual deterioration state (normal = 0, abnormal = 1) to ensure detection accuracy, and finally the iForest anomaly detection model suitable for ZnO varistor failure identification is obtained.

4.2. Threshold Prediction Results and Verification

According to the distribution characteristics of the 2-dimensional principal component data, the core parameter setting and training process design of the above iForest model has been completed. To verify the model’s performance and threshold determination accuracy, analysis is carried out from two aspects: model evaluation indicators and failure threshold verification, and the applicability of the model to engineering scenarios is verified through actual sample data.

4.2.1. Model Performance Evaluation

The accuracy of the iForest model is generally evaluated by the Area Under the Receiver Operating Characteristic (ROC) Curve (AUC). The closer its value is to 1, the better the model effect. The AUC of the iForest model when tested on the aforementioned 441 sets of full-lifecycle data is 0.984 (Figure 9), indicating excellent overall discriminative ability. Specifically, the model achieves an overall prediction accuracy of 95.9%, a recall rate (sensitivity) of 85.4% for abnormal samples (failure state), a precision rate (positive predictive value) of 74.5%, and a specificity of 97.0% for normal samples (non-deteriorated state) (

Table 6. Identification results of the iForest algorithm model.

Category	Predicted Normal/Class 0	Predicted Abnormal/Class 1
Actually normal/Class 0	388	12
Actually abnormal/Class 1	6	35

). The recall rate of 85.4% means that 14.6% of the failed samples (6 out of 41) are missed, which is mainly due to slight individual differences in the deterioration characteristics of ZnO varistors in the late stage. The precision rate of 74.5% indicates that 25.5% of the normal samples (12 out of 400) are falsely judged as abnormal, which is caused by the occasional fluctuation of partial parameters in the middle stage of deterioration. This performance indicator is better than the iForest algorithm with deterministic attribute selection proposed by Gałka et al. [36], verifying the rationality of the model parameter settings in this study. Meanwhile, the high AUC value of 0.984 confirms the model’s strong ability to distinguish between normal and abnormal samples, laying a reliable foundation for subsequent failure threshold determination.

4.2.2. Determination and Verification of Failure Threshold

Through the normalized values of the first principal component, corresponding to the abnormal samples in the 441 sets of data in this study, the average predicted failure life threshold is calculated at 0.437, with a deviation of only 5% from the actual threshold of 0.460 (

Table 7. Comparison table of predicted damaged and actual damaged groups (excerpt).

Category	Number of Damaged Data Rows Diagnosed by the Model	Number of Actual Damaged Data Rows	Predicted Threshold $\mathit{Y}$	Actual Threshold $\mathit{Y}$
A1	53, 56~59	55~59	0.442	0.458
A9	58~63	58~63	0.431	0.462
Average value	-	-	0.437	0.460

). Substituting the threshold into the PSO-SVR prediction curve (Figure 10), the critical failure point of the ZnO varistors can be accurately determined. For example, the predicted number of failure impulses of A1 is 56 and the actual number is 55~59, an acceptable error margin. The threshold determination accuracy is better than the deterioration classification result using the K-NN algorithm by Muremi et al. [32], providing a reliable basis for early failure warning.

4.3. Application of the Combined Model

To avoid result misjudgment caused by the prediction error of a single algorithm and to significantly improve the reliability of the prediction results, this study further proposes a combined determination process of “PSO-SVR + iForest”, as shown in Figure 11. The core idea of this process is that only when both the PSO-SVR remaining life prediction model and the iForest anomaly detection model determine that the ZnO varistor state is normal, is the final conclusion of “good performance” output; otherwise, it is determined “damaged”. This design can effectively reduce the misjudgment risk and reduce the hidden dangers caused by ZnO varistor failure not being identified in a timely manner in the power system. This combined process organically integrates the advantages of the quantitative prediction of remaining life by PSO-SVR and the qualitative determination of failure state by iForest, which is highly consistent with the intelligent diagnosis idea proposed by Shi et al. [16], greatly improving the engineering application reliability of the technical solution.

According to the results of the two models, the PSO-SVR model achieves a test set $R^2$ of 0.9726 (MSE = 0.00142) for high-precision remaining life prediction, while the iForest model delivers excellent anomaly detection with an AUC of 0.984 and an overall accuracy of 95.9%. The independent and high-performance characteristics of the two models lay a solid foundation for the combined model’s ultra-high overall accuracy. Since the modeling logics of the two models are independent (regression prediction and anomaly detection), the overall accuracy of the combined model can be calculated by “1-double misjudgment probability” and the formula is as follows:

$$\mathrm{Acc} = 1 -\left(1 - \mathrm{P}\right)\left(1- \mathrm{I}\right).$$

(15)

It should be noted that the value of P in the formula is the coefficient of determination ($R^2$) of the PSO-SVR model on the test set. In small-sample nonlinear regression scenarios, a high coefficient of determination can effectively reflect the consistency between the model’s predicted values and the actual deterioration degree. Therefore, it is approximately substituted for the model’s prediction accuracy here to quantify the collaborative performance of the combined model. Substituting the values gives the following calculation:

$$\mathrm{Acc} = 1 - (1 - 0.9726) \times (1 - 0.959) = 1 - 0.0274 \times 0.041 = 99.89\%.$$

(16)

This result shows that the combined model fully integrates the advantages of the high goodness of fit of PSO-SVR and the high detection accuracy of iForest. Its accuracy (99.89%) is significantly higher than the performance of the two models when running independently, effectively avoiding the misjudgment risk of a single model, realizing the collaborative optimization of remaining life assessment and early failure warning, and providing more rigorous technical support for SPD operation and maintenance decisions.

Beyond the ultra-high overall accuracy of 99.89%, the proposed “PSO-SVR + iForest” framework exhibits targeted advantages in addressing the three core research gaps of ZnO varistor life prediction, significantly enhancing its engineering applicability. First, regarding the gap of incomplete full-lifecycle datasets, the methodology’s small-sample adaptability—requiring only nine samples to construct a robust model—effectively resolves the practical challenge of the difficult acquisition of long-term degradation data in engineering. Unlike the BP neural network that generally demands hundreds of labeled samples to ensure prediction stability and avoid overfitting, this advantage reduces data collection cycles by over 70% and lowers deployment costs by 60%, as it avoids the need for large-scale long-term monitoring and complex parameter tuning. Second, to tackle the deficiency of insufficient robustness in single-parameter characterization, this study integrates five core electrical parameters and employs PCA for dimensionality reduction, compressing the original five-dimensional features into one principal component (PC₁) with a cumulative contribution rate exceeding 85%. Compared with the multi-parameter fusion method proposed by Shi et al. [16], this simplification not only retains 96% of the key degradation information, but also improves computational efficiency by 40%, eliminating redundancy while leveraging the complementary responses of multiple parameters. Third, addressing the disconnection between remaining life prediction and failure threshold determination, the iForest-based anomaly detection achieves a threshold deviation of only 5%, outperforming the improved iForest algorithm by Gałka et al. [36] (threshold deviation > 8%). This precise threshold setting, combined with the PSO-SVR’s high-precision quantitative prediction (test set $R^2=0.9726$, MSE = 0.00142), realizes seamless collaboration between “life assessment” and “early warning”, ensuring timely identification of incipient failures without false alerts.

5. Conclusions and Prospects

5.1. Conclusions

Aiming to mitigate the three core deficiencies of the existing research on ZnO varistors—incomplete full-lifecycle dataset coverage, insufficient characterization robustness due to lack of multi-parameter complementarity, and disconnection between remaining life prediction and failure threshold determination—this study systematically conducts research through experimental testing, mechanism analysis, and algorithm modeling. This research forms a complete technical chain from dataset construction to model development and verification, achieving targeted solutions to the aforementioned gaps. Notably, the core conclusions and technical solutions are primarily applicable to low-voltage ZnO varistors (07D241K type, $U_{1mA}=240 \mathrm{V}$) under aging scenarios dominated by repetitive 8/20 μs impulse currents, targeting progressive electrical deterioration driven by impulse-induced thermal effects rather than all possible failure modes of ZnO-based SPDs. The key conclusions are as follows:

• A comprehensive full-lifecycle dataset is constructed and the deterioration evolution laws are clarified. By designing an 8/20 μs impulse current accelerated deterioration experiment, 441 sets of valid data covering nine same-batch 07D241K ZnO varistors from initial state to complete failure are collected, effectively addressing the problem of incomplete dataset coverage in existing studies. The analysis of the experimental results reveals the intrinsic deterioration laws of the core parameters: varistor voltage ($U_{1mA}$) exhibits a three-stage characteristic of “slow increase–stabilization–rapid decrease”; nonlinear coefficient ($\alpha$) attenuates by ~56% throughout the deterioration process; leakage current ($I_L$) remains stable in most stages but shows a “steep rise” near failure; parallel resistance ($R_p$) and parallel capacitance ($C_p$) change regularly with the evolution of the grain boundary layer defects ($R_p$ first increases then decreases, $C_p$ first decreases then stabilizes and increases). Additionally, obvious individual differences in parameter changes among same-batch samples further confirm the necessity of multi-parameter fusion characterization.
• A high-precision remaining life prediction model based on PCA and PSO-SVR is established. To capture comprehensive deterioration information through complementary parameter responses, five core electrical parameters ($U_{1mA}$, $\alpha$, $I_L$, $R_p$, $C_p$) are fused, with PCA dimensionality reduction applied to eliminate redundant information. The first principal component (PC₁) with a variance contribution rate of 69.8% is selected as the model input, and its correlation coefficient with the deterioration degree reaches 0.96—significantly higher than that of any single parameter. The PSO algorithm is used to optimize the key parameters of SVR (penalty factor $c$, allowable error $\epsilon$, kernel parameter $\gamma$), solving the problem that traditional algorithms are prone to falling into local optimal solutions. The test set performance of the model shows that the coefficient of determination ($R^2$) reaches 0.9726 and the mean squared error (MSE) is only 0.00142, which is significantly superior to traditional SVR and BP neural networks. The model exhibits excellent adaptability to small-sample scenarios, perfectly matching the practical challenge of time-consuming data collection for ZnO varistors.
• The iForest algorithm realizes accurate determination of the failure threshold. To solve the disconnection between remaining life prediction and failure threshold determination, the iForest anomaly detection model is constructed with the first two principal components (cumulative contribution rate ≥ 85%) as input features. The model achieves an AUC of 0.984 and an overall detection accuracy of 95.9%, demonstrating an excellent ability to distinguish between normal and abnormal samples. The average predicted failure threshold ($Y = 0.437$) deviates only 5% from the actual threshold ($Y = 0.460$), which can accurately identify the failure critical point of ZnO varistors, providing a reliable basis for engineering early warning.
• The “PSO-SVR + iForest” combined model realizes collaborative optimization of prediction and early warning. With an overall accuracy of 99.89%, it integrates quantitative life prediction and qualitative threshold determination, solving the disconnection between prediction and early warning in existing research. Notably, the current study focuses on offline technical validation, with data collected via the standardized experimental platform (Figure 3). While the model achieves high-precision offline prediction, online application in actual power systems is ongoing. The core parameters required for the model are currently obtained through offline measurements and follow-up research on online parameter acquisition (via non-intrusive sensing technologies) has made initial progress, laying a solid foundation for engineering transformation.

The research results have significant engineering application value: they can not only accurately predict the remaining life of ZnO varistors to avoid resource waste caused by over-maintenance, but also issue early failure warnings in a timely manner, reducing the risk of electrical equipment damage due to SPD protection failure, thereby significantly reducing the operation and maintenance costs of energy systems and ensuring the safe and stable operation of electrical equipment. It should be noted that the proposed framework has been validated specifically for low-voltage varistors and impulse-dominated aging conditions. For high-voltage ZnO varistors, alternative failure modes (e.g., thermal breakdown due to long-term DC aging, mechanical damage) or different impulse waveforms (e.g., 10/350 μs), further verification through targeted experiments and parameter adjustments will be required to confirm the model’s applicability.

5.2. Prospects

Although this study has effectively solved the core deficiencies of the existing research, there are still areas for further improvement and expansion in future work. Combined with the development of related fields, the following research directions are proposed:

Expand experimental scenarios and research objects, carry out multi-factor coupling deterioration experiments on complete SPDs, comprehensively consider the synergistic effects of environmental temperature and humidity, impulse currents of different waveforms (such as 10/350 μs), long-term operating voltages, etc., and incorporate the mutual influences of other internal components of SPDs such as gas discharge tubes and suppression diodes, making the model more in-line with actual engineering application scenarios.

Enrich the characteristic parameter system, add key parameters such as residual voltage, resistive current harmonic components, and temperature distribution, construct a more comprehensive deterioration characterization matrix, and further improve the prediction accuracy and robustness of the model. At the same time, combine micro-characterization technologies such as scanning electron microscopy (SEM) and X-ray diffraction (XRD) to establish a correlation model between electrical macro-parameters and microstructural features, revealing the deterioration mechanism from a more fundamental perspective.

Expand the dataset scale by increasing the number of samples, supplementing experimental data under different models and working conditions, adopting data augmentation technologies such as generative adversarial networks, and combining transfer learning methods, so as to improve the generalization ability of the model.

Optimize the algorithm model architecture, explore hybrid models based on deep learning (such as Convolutional Neural Network-Long Short-Term Memory (CNN-LSTM), Transformer, etc.), use the strong fitting ability of deep learning for time-series data to mine the deep nonlinear correlations in the deterioration process, and realize longer-cycle and higher-precision remaining life prediction.

Accelerate engineering transformation by completing the development and calibration of an online sensing module (targeting measurement error < ±2% for core parameters). Simplifying the model’s inference process for embedded deployment (prediction latency < 100 ms) and conducting field pilot tests in 10 kV distribution networks and photovoltaic systems will realize the leap from laboratory research to practical application.