Distributionally Robust Game-Theoretic Optimization Algorithm for Microgrid Based on Green Certificate–Carbon Trading Mechanism

Abstract

Aiming at multi-agent interest demands and environmental benefits, a distributionally robust game-theoretic optimization algorithm based on a green certificate–carbon trading mechanism is proposed for uncertain microgrids. At first, correlated wind–solar scenarios are generated using Kernel Density Estimation and copula theory and the probability distribution ambiguity set is constructed combining 1-norm and $\infty$-norm metrics. Subsequently, with gas turbines, renewable energy power producers, and an energy storage unit as game participants, a two-stage distributionally robust game-theoretic optimization scheduling model is established for microgrids considering wind and solar correlation. The algorithm is constructed by integrating a non-cooperative dynamic game with complete information and distributionally robust optimization. It minimizes a linear objective subject to linear matrix inequality (LMI) constraints and adopts the column and constraint generation (C&CG) algorithm to determine the optimal output for each device within the microgrid to enhance its overall system performance. This method ultimately yields a scheduling solution that achieves both equilibrium among multiple stakeholders’ interests and robustness. The simulation result verifies the effectiveness of the proposed method.

1. Introduction

As the global energy crisis and environmental pollution issues become increasingly severe, microgrids—as small-scale power generation, distribution, and consumption systems capable of integrating renewable energy—have emerged as a key development direction for modern power systems [1,2]. However, the output of renewable energy exhibits significant intermittency and volatility. This uncertainty substantially increases the complexity of microgrid dispatch, posing a severe challenge to their safe and stable operation [3,4,5].

Currently, there are two primary optimization scheduling methods for addressing uncertainty: stochastic optimization and robust optimization. Ref. [6] proposes a multi-time scale scheduling strategy incorporating multi-scenario analysis and combining two-stage stochastic optimization (day-ahead) with model predictive control (intraday). Ref. [7] addresses uncertainties in wind and solar power generation by using K-means clustering to identify potential wind power scenarios for the following day based on day-ahead forecasts, then applying stochastic optimization to solve microgrid day-ahead scheduling problems. Stochastic optimization relies on assumptions about probability distributions. However, it is difficult to accurately characterize the variation patterns of uncertainty parameters in practice, which limits the application of stochastic optimization. In contrast, robust optimization adopts uncertainty sets to characterize uncertain parameters without requiring prior knowledge of probability distributions [8], ensuring safe operation under all scenarios. Ref. [9] utilizes a min-max-min three-layer optimization model, which introduces uncertainty adjustment parameters to regulate the conservatism of scheduling schemes, thereby solving economic dispatch problems under worst-case scenarios. Ref. [10] constructs a two-stage robust optimization dispatch model for microgrids based on expected scenarios. This model determines first-stage decisions based on system economic performance under the desired scenario, while the second stage employs robustness testing to ensure feasibility under any scenario, achieving the optimization goal of “expected scenario performance optimal and worst-case feasible.” Ref. [11] proposes a microgrid optimization allocation strategy based on fuzzy scenario clustering. By clustering typical and extreme scenarios, it establishes a two-stage robust optimization model on the load side that minimizes comprehensive costs. However, robust optimization solely considers worst-case scenarios and neglects probabilistic information, often resulting in conservativeness and economically suboptimal solutions. Consequently, researchers have proposed a distributed robust optimization method [12,13,14]. This approach represents a novel strategy for handling uncertainty leveraging historical data to obtain economic efficiency and robustness without requiring precise probability distributions. Ref. [15] constructs a moment set of uncertainty using historical wind power scenarios and adopts distribution-robust optimization for scheduling decisions. Ref. [16] proposes a distribution-robust optimization method based on Wasserstein distance that considers extreme scenarios. Ref. [17] introduces a data-driven distribution-robust optimization model and achieves both economic and reliable system scheduling by adjusting load-side flexibility through integrated demand response mechanisms.

The research above focuses solely on optimizing the economic performance of microgrids. In recent years, the “dual carbon” goals have driven the transformation and upgrading of microgrid operation optimization concepts. Microgrid operation optimization should not be confined to economic considerations. In order to achieve the “dual carbon” goals and promote renewable energy consumption, green certificate trading mechanisms and carbon trading mechanisms can be introduced to facilitate the low-carbon development of microgrids. Ref. [18] introduced a stepwise carbon trading mechanism in a wind–solar hydrogen storage microgrid system, demonstrating that this approach significantly reduces system carbon emissions. Ref. [19] developed an economic dispatch model for wind power systems incorporating green power certificate trading, showing that green certificates progressively increase wind power output in day-ahead dispatch plans and substantially enhancing economic benefits. Ref. [20] introduced a combined green certificate–carbon trading mechanism, achieving comprehensive optimization of system economics, low-carbon performance, and reliability while enhancing renewable energy integration.

Green certificates and carbon trading involve distinct entities, creating conflicts of interest among gas turbines, renewable energy generators, and energy storage systems. Therefore, designing a cooperative mechanism to coordinate the interests of all parties is urgently needed. Ref. [21] proposes a multi-agent, multi-site cooperative game-theoretic optimization scheduling strategy considering carbon–green certificates based on the green certificate–carbon trading mechanism and cooperative game theory. This strategy forms a multi-agent alliance with the site operator as the leader and energy storage plants, wind farms, and the power grid as followers. Ref. [22] proposes an integrated energy system (IES) green certificate–carbon trading interaction model grounded in cooperative game theory. This model addresses synergies across generation, carbon sequestration, and market dimensions. The market segment establishes a green certificate–carbon trading interaction mechanism to enhance overall IES economics. Cooperative game theory is applied to discuss conditions for alliance formation, with Shapley value methods employed for equitable distribution of cooperative surplus. Ref. [23] employs a two-stage robust cooperative game-theoretic optimization scheduling method for community IES based on carbon–green certificate trading, effectively reducing operational costs and carbon emissions while increasing renewable energy absorption rates. Although these studies adopt game-theoretic optimization to balance multi-stakeholder interests under a joint green certificate and carbon trading mechanism, the designed optimization algorithms fail to fully leverage historical scenario data, resulting in performance losses and leaving room for improvement. Motivated by the above, this paper synthesizes game-theory and distributed roust optimization to develop a distributed robust game-theoretic optimization algorithm for microgrids based on green certificate–carbon trading, which employs distributed robust optimization to effectively utilize historical scenario data, introduces the green certificate–carbon trading mechanism to enhance environmental benefits, and balances multi-agent interests through a non-cooperative fully-informed dynamic game. This constructs a distributed robust game-theoretic optimization scheduling model for microgrids, thereby not only effectively utilizing historical scenario data but also improving environmental benefits while accommodating multi-agent interests. This algorithm identifies Nash equilibrium solutions through non-cooperative complete information dynamic games. By employing distributed robust optimization with the C&CG [24] algorithm to formulate strategies for different entities, it calculates optimal outputs for microgrid equipment under worst-case conditions. This approach achieves outstanding microgrid economic performance and robustness while enhancing environmental benefits.

This paper is organized as follows. Section 2 establishes the microgrid model and incorporates the green certificate–carbon trading mechanism. In Section 3, a distributionally robust game-theoretic optimization algorithm for microgrids based on a green certificate–carbon trading mechanism is proposed. In Section 4, the effectiveness of the algorithm is then validated through simulations and comparative analysis. Finally, conclusions are drawn in Section 5.

2. Microgrid Model

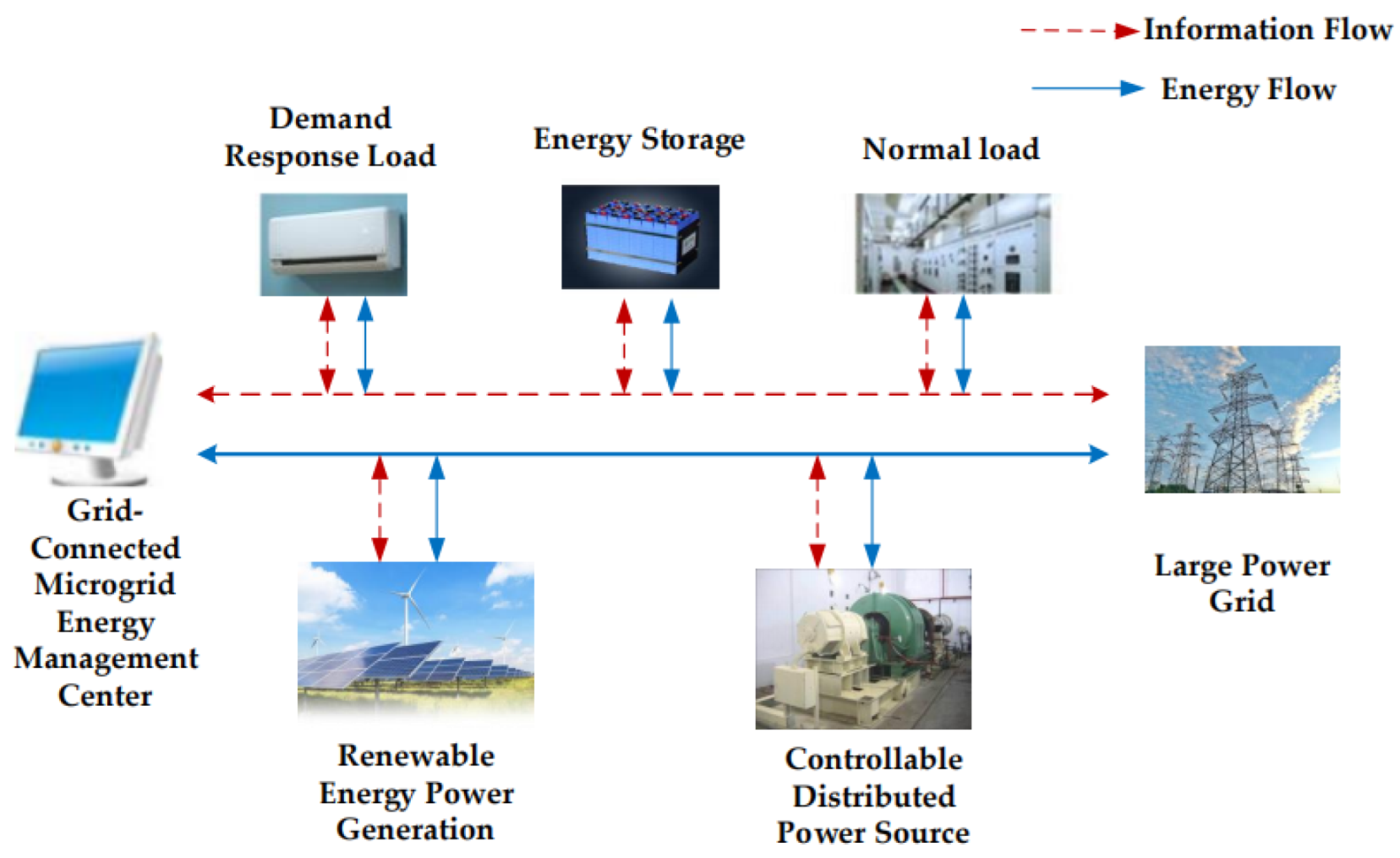
2.1. The Structure of Microgrid

The grid-connected microgrid structure, as shown in Figure 1, comprises controllable distributed power sources, renewable energy generation, energy storage, and local loads.

2.2. Micro Gas Turbine

The micro gas turbine model is described as follows:

$$\left\{\begin{array}{l}{P}_g^{\min }\le P_g(t)\le P_g^{\max }\\ -\Delta P_g^{\max }\le P_g(t)-P_g(t-1)\le \Delta P_g^{\max }\end{array}\right.$$

(1)

where $P_g(t)$ represents the power output of the micro gas turbine at time t; $P_g^{\max }/P_g^{\min }$ denote the maximum and minimum power outputs respectively; and $\Delta P_g^{\max }$ represents the maximum variation in ramping power.

The cost function of a micro gas turbine is:

$$C_g(t)=(C_g^a+C_g^b)P_g(t)\Delta t$$

(2)

where $\Delta t$ is the sample time interval, and $C_g^a$/$C_g^b$ represent the operational and maintenance cost coefficients respectively.

2.3. Energy Storage Unit

An energy storage unit can charge during power surpluses in microgrids and discharge during shortages, thereby providing a solution of peak cutting and valley filling [25,26]. The dynamic equations for the charging and discharging of energy storage units are:

$$E_{\mathit{ES}}(t)=E_{\mathit{ES}}(0)+\rho \sum _{t^{\prime }=1}^t[P_{\mathit{ES}}^{\mathit{ch}}(t^{\prime })\Delta t]-{\displaystyle \frac{1}{\rho }}\sum _{t^{\prime }=1}^t[P_{\mathit{ES}}^{\mathit{dis}}(t^{\prime })\Delta t]$$

(3)

where $\rho$ represents the charge and discharge energy efficiency of the energy storage unit.

The energy storage state-of-charge constraint is:

$$E_{\mathit{ES}}^{\mathit{min}}\le E_{\mathit{ES}}(t)\le E_{\mathit{ES}}^{\mathit{max}}$$

(4)

where $E_{\mathit{ES}}(t)$ represents the state of charge at time t, and $E_{\mathit{ES}}^{\mathit{min}}/E_{\mathit{ES}}^{\mathit{max}}$ represent the minimum/maximum electrical energy values permitted for the energy storage unit.

For scheduling convenience, the state of charge of energy storage is required to remain consistent between the initial and final time points:

$$E_{\mathit{ES}}(0)=E_{\mathit{ES}}(N_T)$$

(5)

It also needs to meet the charge and discharge constraints. Thus, put the charge constraints, discharge constraints, and Equation (5) together:

$$\left\{\begin{array}{l}0\le P_{\mathit{ES}}^{\mathit{ch}}(t)\le U_{\mathit{ES}}(t)P_{\mathit{ES}}^{\mathit{max}}(t)\\ 0\le P_{\mathit{ES}}^{\mathit{dis}}(t)\le [1-U_{\mathit{ES}}(t)]P_{\mathit{ES}}^{\mathit{max}}(t)\\ \rho {\displaystyle \sum _{t=1}^{N_T}}[P_{\mathit{ES}}^{\mathit{ch}}(t)\Delta t]-\frac{1}{\rho }{\displaystyle \sum _{t=1}^{N_T}}[P_{\mathit{ES}}^{\mathit{dis}}(t)\Delta t]=0\end{array}\right.$$

(6)

where $N_T$ is the scheduling period; $P_{\mathit{ES}}^{\mathit{ch}}(t)/P_{\mathit{ES}}^{\mathit{dis}}(t)$ represent charging/discharging power respectively; $P_{\mathit{ES}}^{\mathit{max}}(t)$ represents the maximum allowable charge or discharge power for energy storage; and $U_{\mathit{ES}}(t)$ represents energy storage charging and discharging status, where $U_{\mathit{ES}}(t)=1$ indicates energy storage charging and $U_{\mathit{ES}}(t)=0$ indicates energy storage discharging. The last formulation in Equation (6) means that the total charge of the energy storage unit equals its total discharge in a scheduling period, which can guarantee that Equation (5) is satisfied.

The cost function for the energy storage unit is:

$$C_{\mathit{ES}}(t)=C_{\mathit{ES}}^k[P_{\mathit{ES}}^{\mathit{ch}}(t)·\rho +P_{\mathit{ES}}^{\mathit{dis}}(t)/\rho ]$$

(7)

where $C_{\mathit{ES}}^K$ is the maintenance cost coefficient for energy storage.

2.4. Demand Response Load

Demand response loads can reduce the peak–valley gap and achieve staggering power consumption. Therefore, the rational optimization of demand response loads can enhance the economic benefits of microgrids. During operation, the following constraints must be satisfied:

$$\sum _{t=1}^{N_T}{P}_{\mathit{DR}}(t)=D_{\mathit{DR}}$$

(8)

$$P_{\mathit{DR}}^{\mathit{min}}\le P_{\mathit{DR}}(t)\le P_{\mathit{DR}}^{\mathit{max}}$$

(9)

where $P_{\mathit{DR}}(t)$ represents the actual power of demand response load at time t; $P_{\mathit{DR}}^{\mathit{max}}$/$P_{\mathit{DR}}^{\mathit{min}}$ represent the maximum/minimum values of their power consumption respectively; and $D_{\mathit{DR}}$ represents the total electricity demand during the scheduling process.

Demand response loads may impact user satisfaction during the adjustment process. Therefore, compensation costs are incorporated into the cost function and adjusted as follows:

$$C_{\mathit{DR}}(t)={\omega }_{\mathit{DR}}|P_{\mathit{DR}}(t)-P_{\mathit{DR}}^{\ast }(t)|\Delta t$$

(10)

where $P_{\mathit{DR}}^{\ast }(t)$ represents the expected power consumption of the demand response load during time period t, and ${\omega }_{\mathit{DR}}$ is the unit compensation cost coefficient for demand response load. By introducing auxiliary variables $P_{\mathit{DR}1}(t)$ and $P_{\mathit{DR}2}\left(t\right)$, Equation (10) can be transformed into the following linear form.

$$C_{\mathit{DR}}(t)={\omega }_{\mathit{DR}}[P_{\mathit{DR}1}(t)+P_{\mathit{DR}2}(t)]\Delta t$$

(11)

$$P_{\mathit{DR}}(t)-P_{\mathit{DR}}^{*}(t)+P_{\mathit{DR}1}(t)-P_{\mathit{DR}2}(t)=0$$

(12)

$$P_{\mathit{DR}1}(t)\ge 0,P_{\mathit{DR}2}(t)\ge 0$$

(13)

2.5. Power Interaction with Large Grid

To achieve power balance, the microgrid can engage in electricity purchase and sale transactions with the main grid. During these transactions, the following constraints must be satisfied:

$$U_{\mathit{buy}}(t)+U_{\mathit{sell}}(t)\le 1$$

(14)

$$0\le P_{\mathit{buy}}(t)\le U_{\mathit{buy}}(t)P_{\mathit{buy}}^{\mathit{max}}$$

(15)

$$0\le P_{\mathit{sell}}(t)\le U_{\mathit{sell}}(t)P_{\mathit{sell}}^{\mathit{max}}$$

(16)

where $U_{\mathit{buy}}(t)$/$U_{\mathit{sell}}(t)$ represent the electricity purchase/sale status of the system at time t; $P_{\mathit{buy}}(t)$/$P_{\mathit{sell}}(t)$ represent the power purchased/sold during time period t; and $P_{\mathit{buy}}^{\mathit{max}}$/$P_{\mathit{sell}}^{\mathit{max}}$ represent the maximum power purchase/sale capacity during power exchange between the microgrid and the main grid.

During time interval t, the interaction cost between the microgrid and the main grid can be expressed as:

$$C_M(t)=\lambda (t)[P_{\mathit{buy}}(t)-P_{\mathit{sell}}(t)]\Delta t$$

(17)

where $\lambda \left(t\right)$ represents the electricity price at time t.

2.6. Stepwise Carbon Trading Mechanism

The carbon trading market establishes a controlled carbon emissions trading system, leveraging cost incentives to drive enterprises to reduce carbon emissions. If an enterprise’s actual carbon emissions fall below its allocated carbon quota, it may sell surplus allowances to generate economic returns; conversely, it must purchase carbon emission rights or take other measures to meet assessment requirements [27].

Actual emissions traded in the carbon market are shown as follows:

$$E_{\mathit{free}}(t)=\nu P_g(t)$$

(18)

$$E_a(t)=\varpi P_g(t)$$

(19)

$$E_{{\mathit{co}}_2}(t)=E_a(t)-E_{\mathit{free}}(t)$$

(20)

where $E_{\mathit{free}}(t)$ represents the free carbon emission allowances allocated to coal-fired power units; $E_a(t)$ represents actual carbon emissions; $\nu$ is the carbon allocation coefficient, and $\varpi$ is the carbon dioxide emission factor for coal-fired units.

Stepwise carbon emissions trading costs can be defined as shown in Equation (21).

$$C_{{\mathit{co}}_2}(t)=\left\{\begin{array}{cc}\hfill \mu E_{{\mathit{co}}_2}(t),\hfill & \hfill 0\le E_{{\mathit{co}}_2}<l\hfill \\ \hfill \mu (1+\alpha )(E_{{\mathit{co}}_2}(t)-l)+\mu l,\hfill & \hfill l\le E_{{\mathit{co}}_2}<2l\hfill \\ \hfill \mu (1+2\alpha )(E_{{\mathit{co}}_2}(t)-2l)+\mu (2+\alpha )l,\hfill & \hfill 2l\le E_{{\mathit{co}}_2}<3l\hfill \\ \hfill \mu (1+3\alpha )(E_{{\mathit{co}}_2}(t)-3l)+\mu (3+3\alpha )l,\hfill & \hfill 3l\le E_{{\mathit{co}}_2}<4l\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \end{array}\right.$$

(21)

where $\mu$ represents the base price for carbon trading; $\alpha$ represents the stepwise price growth rate for carbon trading; and $l$ is the step length.

2.7. Green Certificate Trading Mechanism

Currently, a green certificate trading mechanism based on a quota system is adopted. This mechanism mandates that the energy sector fulfill its responsibility to consume renewable energy. If actual renewable energy generation fails to meet quota requirements, entities must purchase green certificates to fulfill their obligations; conversely, they may sell green certificates to generate revenue. The green certificate trading model [21] is as follows:

$$P_{\mathit{res}}(t)={\sigma }_{\mathit{green}}(P_L(t)+P_{DR}(t))$$

(22)

For $P_N(t)\le P_{\mathit{res}}(t)$, it means that the renewable energy quota has not been met, and the cost ($C_{\mathit{green}}(t)$ in Equation (23) takes positive values, meaning expenditures) generated from green certificates is as follows:

$$C_{\mathit{green}}(t)={\displaystyle \frac{P_{\mathit{res}}(t)-P_N(t)}{1000}}{c}_{\mathit{green}}^b+{\beta }_p(P_{\mathit{res}}(t)-P_N(t))$$

(23)

For $P_N(t)>P_{\mathit{res}}(t)$, it means that the renewable energy quota has been met, and the cost ($C_{\mathit{green}}(t)$ in Equation (24) takes a negative value, meaning profit) generated from green certificates is as follows:

$$C_{\mathit{green}}(t)={\displaystyle \frac{P_{\mathit{res}}(t)-P_N(t)}{1000}}{c}_{\mathit{green}}^b$$

(24)

where $P_{res}(t)$ represents the daily renewable energy quota; ${\sigma }_{green}$ represents the renewable energy quota coefficient; $P_L(t)$ represents the normal load demand of the microgrid at time t; $P_N(t)$ represents the actual consumption of renewable energy; $c_{\mathit{green}}^b$ represents the unit price of green certificates; ${\beta }_p$ represents the penalty coefficient; and $C_{\mathit{green}}$ represents the cost or revenue of green certificates. If $C_{\mathit{green}}\ge 0$, it represents the cost of green certificates; otherwise, it represents the revenue of green certificates.

2.8. Renewable Energy Generator

The total cost of renewable energy generators comprises the operating costs of wind and photovoltaic systems, as expressed in Equation (25). Specifically, wind power generation incurs no fuel costs, requiring only maintenance expenses related to output power during operation. Similarly, photovoltaic cells incur only operational maintenance costs during operation.

$$C_{\mathit{res}}(t)={\kappa }_{\mathit{wind}}{P}_{\mathit{wind}}(t)+{\gamma }_{\mathit{pv}}{p}_{\mathit{pv}}(t)$$

(25)

where ${\kappa }_{\mathit{wind}}$/${\gamma }_{\mathit{pv}}$ represent the unit operation and maintenance costs for wind power and photovoltaic power respectively, and $P_{\mathit{wind}}(t)$/$P_{\mathit{pv}}(t)$ represent the output of wind power and photovoltaic power respectively, during time period t.

2.9. Objective Function

The daily operation objective of the microgrid is to minimize the total economic cost, with the specific mathematical expression shown in Equation (26).

$$\min \sum _{t=1}^{N_T}[C_g(t)+C_{\mathit{ES}}(t)+C_{\mathit{DR}}(t)+C_m(t)+C_{co2}(t)+C_{\mathit{green}}(t)+C_{\mathit{res}}(t)]$$

(26)

The constraints that must be satisfied include Equations (1), (3)–(6), (8), (9) and (12)–(16). During operation, the system power balance Equation (27) must also be satisfied.

$$P_{\mathit{DR}}(t)+P_L(t)+P_{\mathit{ES}}^{\mathit{ch}}(t)+P_{\mathit{sell}}(t)=P_g(t)+P_{\mathit{ES}}^{\mathit{dis}}(t)+P_{\mathit{buy}}(t)+P_{\mathit{pv}}(t)+P_{\mathit{wind}}(t)$$

(27)

3. Distributionally Robust Game-Theoretic Optimization Algorithm for Microgrid Based on Green Certificate–Carbon Trading Mechanism (GCDRGO)

3.1. Construction of Multi-Agent Game Model for Microgrid

Game theory is a mathematical framework for competition and cooperation among rational decision-makers, and it has been widely applied in power systems [28]. Game theory is categorized into cooperative games and non-cooperative games. If an agreement is reached, it constitutes a cooperative game; otherwise, it is a non-cooperative game. Furthermore, based on participants’ information and action sequences, non-cooperative games can be subdivided into fully informed static games, partially informed static games, fully informed dynamic games, and partially informed dynamic games [29].

The non-cooperative complete information dynamic games model established in this paper consists of participants, strategies, and revenue functions, which are denoted as $\Lambda =\{N,S,H\}$ and illustrated in detail as follows:

Participants $N$: gas turbine operators, renewable energy operators, and energy storage operators;

Strategies $S=\{S_1,S_2,S_3\}$: $w,n,z$ respectively correspond to the output of gas turbine operators, renewable energy operators, and energy storage operators. $S_1,S_2,S_3$ represent the strategy sets of gas turbine operators, renewable energy operators, and energy storage operators respectively; the game for three established agents is simultaneous. When a participant updates its strategy in iteration m, it treats the strategies of other participants from iteration m-1 as known. This process represents finding the “best response” given the strategies of others.

Payoff functions $H=\{H_1,H_2,H_3\}$: $H_1=H_1(w,n^{\ast },z^{\ast })$, $H_2=H_2(w^{\ast },n,z^{\ast })$, $H_3=H_3(w^{\ast },n^{\ast },z)$, and $H_1,H_2,H_3$ correspond to the total revenue of gas turbine operators, renewable energy operators, and energy storage operators respectively;

$(w^{\ast },n^{\ast },z^{\ast })$ is a Nash equilibrium solution for $\Lambda$; this indicates that under this strategy combination, all three parties can achieve the maximum payoff in the sense of a Nash equilibrium.

$$\left\{\begin{array}{l}{H}_1(w^{\ast },n^{\ast },z^{\ast })\ge H_1(w,n^{\ast },z^{\ast })\\ H_2(w^{\ast },n^{\ast },z^{\ast })\ge H_2(w^{\ast },n,z^{\ast })\\ H_3(w^{\ast },n^{\ast },z^{\ast })\ge H_3(w^{\ast },n^{\ast },z)\end{array}\right.$$

(28)

3.2. Two-Stage Distribution-Robust Optimization Model

3.2.1. Construction of Probabilistic Fuzzy Sets

The effectiveness of scene-based probabilistic distribution-robust optimization methods heavily relies on the generation of a large number of precise scenarios. However, in actual operation, wind and solar power generation are jointly constrained by natural geographical conditions and human factors, often exhibiting significant correlation. The copula function is a statistical tool used to model the dependence structure between multiple random variables, separate from their individual marginal distributions. This paper employs a scenario generation method of wind–solar power based on kernel density estimation and copula theory to yield N raw scenarios that account for wind–solar correlation [30]. Due to the massive volume of data generated by scene generation and the presence of numerous highly similar scenes, this paper employs K-means clustering to group the initially generated N scenes, thereby enabling the effective merging of similar scenes. Ultimately, we obtain $N_s$ typical scenarios ${\mathit{u}}_s$ ($s=1,2,\dots N_s$) along with their corresponding initial probabilities $P_{s0}$.

This paper constructs a distribution-robust optimization model, constraining the fluctuation range of probability distributions with confidence intervals defined by the 1-norm and $\infty$-norm.

The confidence level of the probability distribution P can be expressed as [31]:

$$\mathrm{Pr}({‖P_s-P_{s0}‖}_1\le {\theta }_1)\ge 1-2N_s\exp ({\displaystyle \frac{-2N{\theta }_1}{N_s}})$$

(29)

$$\mathrm{Pr}({‖P_s-P_{s0}‖}_{\infty }\le {\theta }_{\infty })\ge 1-2N_s\exp (-2N{\theta }_{\infty })$$

(30)

where ${\theta }_1$ and ${\theta }_{\infty }$ are the permissible deviation values for the probability distribution.

Let ${\alpha }_1$ and ${\alpha }_{\infty }$ denote the values of $1-2N_S\exp (-2N{\theta }_1/N_s)$ and $1-2N_s\exp (-2N{\theta }_{\infty })$ on the right side of the two inequalities above, respectively. Then ${\alpha }_1$ and ${\alpha }_{\infty }$ represent the confidence levels satisfied by the probability distributions $p$ based on the 1-norm and the $\infty$-norm, respectively. Thus, ${\theta }_1$ and ${\theta }_{\infty }$ can be expressed as:

$${\theta }_1={\displaystyle \frac{N_s}{2N}}\ln {\displaystyle \frac{2N_s}{1-{\alpha }_1}}$$

(31)

$${\theta }_{\infty }={\displaystyle \frac{1}{2N}}\ln {\displaystyle \frac{2N_s}{1-{\alpha }_{\infty }}}$$

(32)

From the above formula, the confidence set of the probability distribution can be derived as:

$$\varphi =\{\begin{array}{ccc}& \left\{P_s\right\}\in R_{+}^{N_s}\hfill & \end{array}\left|\begin{array}{c}{\displaystyle \sum _{s=1}^{N_s}{P}_s=1}\hfill \\ {\displaystyle \sum _{s=1}^{N_s}\left|P_s-P_{s0}\right|}\le {\theta }_1\hfill \\ \underset{1\le s\le N_s}{\max \left|P_s-P_{s0}\right|}\le {\theta }_{\infty }\hfill \end{array}\right.$$

(33)

where $R_{+}^{N_s}$ denotes the set of positive real numbers representing the probability distribution of the scenario s.

3.2.2. Distribution-Robust Optimization Model

This model employs a three-layer nested optimization structure min-max-min to minimize the system’s day-ahead scheduling costs. The proposed two-stage distributed robust optimization model for microgrids can be simplified to:

$$\begin{array}{l}\underset{\mathit{x}}{\min }{\mathit{c}}^T\mathit{x}+\underset{P_s\in \varphi }{\max }\underset{{\mathit{y}}_s\in \Omega (\mathit{x},{\mathit{u}}_s)}{\min }{\displaystyle \sum _{s=1}^{N_s}}{P}_s{\mathit{b}}^T{\mathit{y}}_s\\ \Omega (\mathit{x},{\mathit{u}}_s):\left\{\begin{array}{l}\mathit{F}\mathit{x}+\mathit{G}{\mathit{y}}_s\le \mathit{h}+\mathit{R}{\mathit{u}}_s\\ \mathit{x}=(x_1,x_2,x_3,\dots x_{N_T})\\ x_t\in \{0,1\},\forall t\in 1,2,\dots N_T\\ s=1,2,\dots N_s\end{array}\right\}\end{array}$$

(34)

with the following symbol abbreviations,

$$\left\{\begin{array}{l}\mathit{x}=[U_{\mathit{ES}}(t),U_{\mathit{buy}}(t),U_{\mathit{sell}}(t)]\\ \mathit{y}=[P_{\mathit{DR}}(t),P_{\mathit{DR}1}(t),P_{\mathit{DR}2}(t),P_L(t),P_{\mathit{ES}}^{\mathit{ch}}(t),P_{\mathit{sell}}(t)\\ P_g(t),P_{\mathit{ES}}^{\mathit{dis}}(t),{\mathit{P}}_{\mathit{buy}}(t),P_{\mathit{pv}}(t),P_{\mathit{wind}}(t)]\end{array}\right.$$

(35)

where $\varphi$ denotes the region of the probability distribution set for the scenario, representing the confidence set constrained by the 1-norm and ∞-norm. $P_s$ represents the probability distribution corresponding to scenario $s$; $N_s$ represents the total number of scenarios; discrete variable $\mathit{x}$ represents the charging/discharging state of energy storage and electricity purchase/sale in the first phase; and continuous variable $\mathit{y}$ represents the power output of all the device in the microgrid in the second phase. $\mathit{F},\mathit{G},\mathit{R}$ denotes the coefficient matrix corresponding to variables in the model constraints; $\mathit{h}$ denotes the column vector corresponding to the constraint conditions. The constraints include Equations (1), (3)–(6), (8), (9), (12)–(16) and (27).

3.2.3. Solving Methods of Two-Stage Distribution-Robust Optimization

To enhance computational efficiency, this paper performs distributed robust optimization on three entities: gas turbines, renewable energy sources, and energy storage units. Taking the i-th agent as an example, its first-stage variables are composed of $\mathit{x}=\left\{[{\mathit{x}}_i,{\mathit{x}}_j^{\ast }]:i=1,2,3;j\ne i\right\}$, and its second-stage variables are composed of $\mathit{y}=\left\{[{\mathit{y}}_i,{\mathit{y}}_j^{\ast }]:i=1,2,3;j\ne i\right\}$ where ${\mathit{x}}_i$ denotes the discrete variable for the i-th agent, and ${\mathit{x}}_j^{\ast }$ represents the optimization solution value for the other entities. Similarly, ${\mathit{y}}_i$ denotes the continuous variable for the i-th agent, and ${\mathit{y}}_j^{\ast }$ represents the optimization solution value for the other agents. This paper performs distributed robust optimization for the aforementioned three entities. As is well known, the column and constraint generation (C&CG) algorithm is an advanced, iterative cutting-plane method designed to solve two-stage robust optimization (RO) or adaptive optimization problems with mixed-integer recourse decisions. The column and constraint generation (C&CG) algorithm is adopted to solve the two-stage distributed robust optimization problem, decomposing the original problem into a main problem (MP) and a subproblem (SP) [24]. Compared to the Bender solution, the C&CG algorithm has advantages such as strong applicability, low computational complexity, high solution efficiency, and good convergence properties.

The main problem can be expressed as:

$$\begin{array}{l}\underset{\mathit{x}}{\min }{\mathit{c}}^T\mathit{x}+\eta \\ \eta \ge {\displaystyle \sum _{s=1}^{N_s}{p}_s^{{(\mathcal{l})}^{\ast }}{\mathit{b}}^T{\mathit{y}}_s^{\mathcal{l}}}\\ \mathit{F}\mathit{x}+\mathit{G}{\mathit{y}}_s^{\mathcal{l}}\le \mathit{h}+{\mathit{R}\mathit{u}}_s\\ s=1,2,\dots N_s\\ \mathcal{l}\le k\end{array}$$

(36)

where $\eta$ is the given threshold, k is the total number of iterations, and ${P_s}^{{(\mathcal{l})}^{\ast }}$ is the probability distribution under the worst-case scenario found at iteration $\mathcal{l}$. By solving the main problem, we obtain the variables ${\mathit{x}}^{\ast }$ and the lower bound LM of the original problem.

The subproblem is a two-layer structure of max–min optimization, which can be described as:

$$f({\mathit{x}}^{\ast })=\underset{P_s\in \varphi }{\max }\underset{{\mathit{y}}_s\in \Omega (\mathit{x},{\mathit{u}}_s)}{\min }\sum _{s=1}^{N_s}{P}_s{\mathit{b}}^T{\mathit{y}}_s$$

(37)

From subproblem Equation (37), given the solution of the main problem, the corresponding worst-case probability distribution within the confidence interval can be calculated and returned to he main problem. Thus, the upper bound UM for the original problem can be obtained. Since the outer and inner problems are mutually independent in terms of constraints, Equation (37) can be decomposed as follows: first solve the inner min problem, then solve the outer max problem, corresponding to Equations (38) and (39) respectively.

$$T_s=\underset{{\mathit{y}}_s\in \Omega (\mathit{x},{\mathit{u}}_s)}{\min }{\mathit{b}}^T{\mathit{y}}_s$$

(38)

$$L=\underset{P_s\in \varphi }{\max }\sum _{s=1}^{N_s}{P}_s{T}_s$$

(39)

Based on the value of $T_s$ obtained from Equation (38), it will furtherly solve the optimization problem in Equation (39). Since the absolute value constraint (33) corresponding to $P_s$ is a nonlinear constraint, it must be converted to a linear equivalent form.

$$\left\{\begin{array}{l}{\displaystyle \sum _{s=1}^{N_s}(P_s^{+}+P_s^{-})\le {\theta }_1}\\ P_s^{+}+P_s^{-}\le {\theta }_{\infty }\\ {\sigma }_s^{+}+{\sigma }_s^{-}\le 1\\ 0\le P_s^{+}\le {\sigma }_s^{+}{\theta }_1\\ 0\le P_s^{-}\le {\sigma }_s^{-}{\theta }_1\\ P_s=P_{s0}+P_s^{+}-P_s^{-}\end{array}\right.$$

(40)

where $P_s^{+}$ and $P_s^{-}$ represent the positive and negative offsets of probability distribution $P_s$ relative to $P_{s0}$ respectively; and ${\sigma }_s^{+}$ and ${\sigma }_s^{-}$ denote the 0–1 flags indicating positive and negative offsets for $P_s$ respectively.

Through the above transformation, the original model (34) has been converted into a mixed-integer programming problem, which can be rapidly solved using commercial solvers.

Remark: The optimization problem in Equation (34) has already incorporated the optimization of all participants, including the gas turbine, renewable energy, and energy storage. Then, optimization problem (34) is transformed into optimization problem (36)–(40). That is, the distributed robust optimization problem for each of the gas turbine, renewable energy, and energy storage units can be solved by Equations (36)–(40).

3.3. Flowchart of GCDRGO Algorithm

The specific procedure of the GCDRGO algorithm is as follows:

Step 1: Initialize the number of game iterations $m=0$, game convergence threshold $\vartheta \in [0,1]$, and distribution-robust optimization convergence threshold $\epsilon \in [0,1]$.

Step 2: Using copula functions (a statistical tool used to model the dependence structure between multiple random variables) and nuclear density estimation, generate wind–solar correlation scenarios to obtain initial probabilities $P_{s0}$.

Step 3: Initialize the strategy $S_{im}=\{S_{1,m},S_{2,m},S_{3,m}\}$ for all agents i (gas turbines, renewable energy generators, and energy storage unit), where $S_{i,m}=({\mathit{x}}_{i,m},{\mathit{y}}_{i,m})$ ($i=1,2,3$).

Step 4: For each agent i, with its strategy $S_{i,m}$ as the optimization degree of freedom, the existing strategy $S_{j,m},(j\ne i)$ of other agents is denoted as $S_{j,m}^{\ast },(j\ne i)$. Solve the following distributed robust optimization problem (using master–slave iteration) to obtain its strategy $S_{i,m}$, then compute its payoff function $H_i^m=H_i^m(S_{i,m},S_{j,m}^{\ast })$:

4.1: Set lower bound $L{M}_i=0$, upper bound $U{M}_i=\infty$, and iteration count $k=1$.

4.2: For the agent $i$, solve the main problem (36), obtain the optimal solution $({\mathit{x}}_i^{k,\ast },{LM}_i^{k,\ast })$ and update lower bound value $L{M}_i=L{M}_i^{k,\ast }$.

4.3: Keep ${\mathit{x}}_i^{k,\ast }$ unchanged, solve subproblem (37) to obtain the worst-case probability distribution $P_{s,i}^{k,\ast }$ and objective function value $f_i^{k,\ast }({\mathit{x}}_i^{k,\ast })$, and update upper bound value $U{M}_i=\min (U{M}_i,f_i^{k,\ast }({\mathit{x}}_i^{k,\ast }))$.

4.4: If $U{M}_i-L{M}_i\le \epsilon$, then return the optimal solution ${\mathit{x}}_i^{k,\ast }$, and terminate the distribution-robust optimization solution of the agent i. Otherwise, update the worst-case probability distribution $P_{s,i}^{k+1}=P_{s,i}^{k,\ast }$ in the main problem, and add the new variable constraint (41) to the main problem (36), then proceed to 4.2:

$$\begin{array}{l}\eta \ge {\displaystyle \sum _{s=1}^{N_s}{p}_s^{{(k+1)}^{\ast }}{\mathit{b}}^T{\mathit{y}}_s^{k+1}}\\ \mathit{F}x+\mathit{G}{y}_s^{k+1}\le \mathit{h}+{\mathit{R}\mathit{u}}_s\end{array}$$

(41)

Step 5: If $H_i^m-H_i^{m-1}\le \vartheta$, then the Nash equilibrium is reached, the game terminates, and the Nash equilibrium solution is output $\{({\mathit{x}}_1^{\ast },{\mathit{y}}_1^{\ast }),({\mathit{x}}_2^{\ast },{\mathit{y}}_2^{\ast }),({\mathit{x}}_3^{\ast },{\mathit{y}}_3^{\ast })\}$; otherwise set $m=m+1$, continue the game iteration, and return to Step 3.

4. Simulation and Analysis

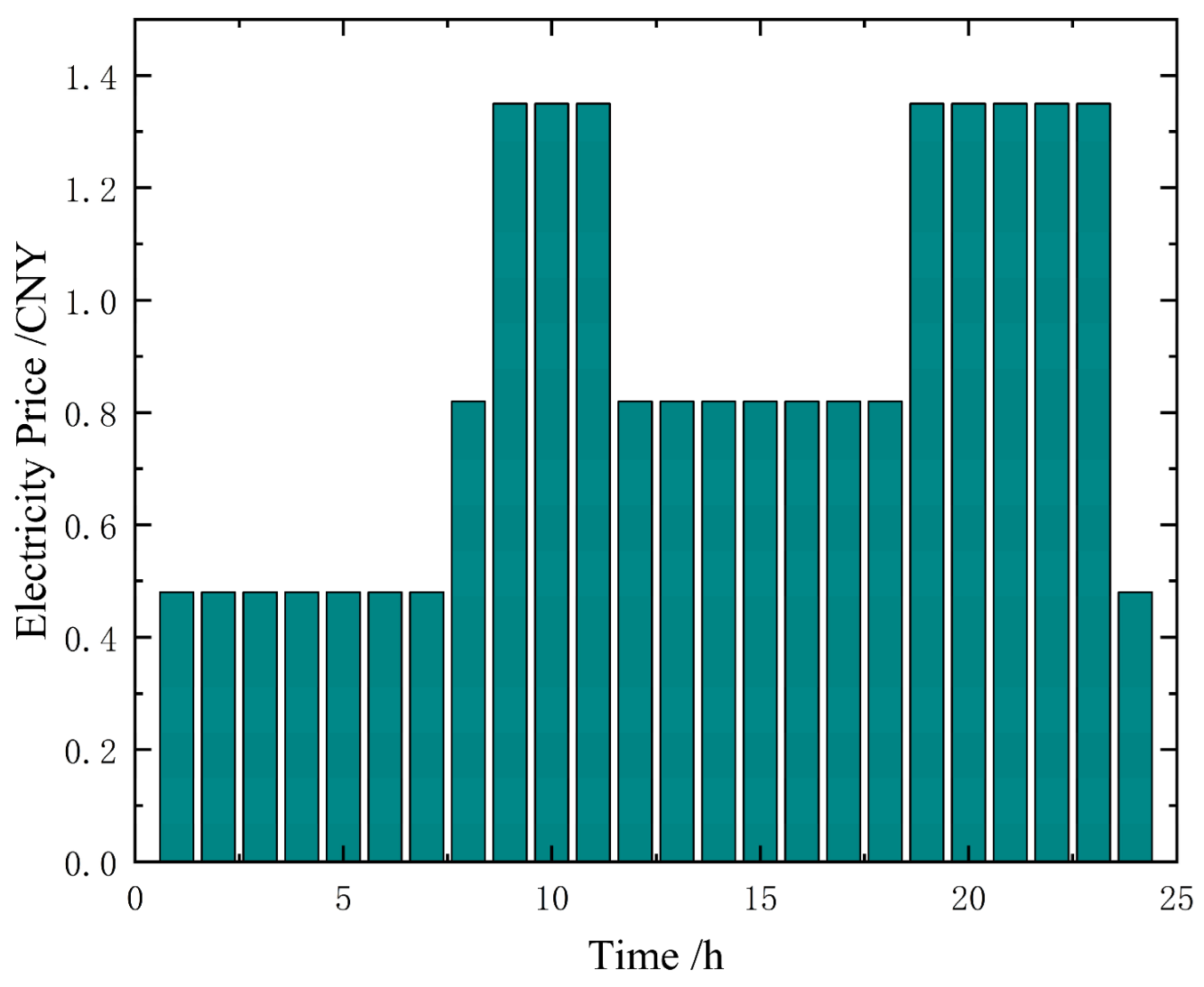
4.1. Parameter Settings

The proposed method will be validated by the grid-connected microgrid model shown in Figure 1. The data in this paper originate from a microgrid system in an industrial park located in a coastal city in China.

Table 1. Microgrid operational parameters.

Equipment	Parameters	Numerical Value
	$P_g^{\min }/\mathrm{k}\mathrm{W}$	80
	$P_g^{\max }/\mathrm{k}\mathrm{W}$	500
Micro gas turbine	$\Delta P_g^{\max }/\mathrm{k}\mathrm{W}$	300
	$C_g^a/[\mathrm{CNY}/(\mathrm{k}\mathrm{W}·\mathrm{h})]$	0.5
	$C_g^b/[\mathrm{CNY}/(\mathrm{k}\mathrm{W}·\mathrm{h})]$	0.15
	$P_{ES}^{\max }/\mathrm{k}\mathrm{W}$	250
	$E_{ES}^{\max }/(\mathrm{k}\mathrm{W}·\mathrm{h})$	900
Energy storage unit	$E_{ES}^{\min }/(\mathrm{k}\mathrm{W}·\mathrm{h})$	200
	$E_{ES}^0/(\mathrm{k}\mathrm{W}·\mathrm{h})$	500
	$C_{ES}^k/[\mathrm{CNY}/(\mathrm{k}\mathrm{W}·\mathrm{h})]$	0.38
	$\rho$	0.95
	$P_{DR}^{\min }/\mathrm{k}\mathrm{W}$	35
Demand response load	$P_{DR}^{\max }/\mathrm{k}\mathrm{W}$	200
	$D_{DR}/(\mathrm{k}\mathrm{W}·\mathrm{h})$	1800
	${\omega }_{\mathit{DR}}/[\mathrm{CNY}/(\mathrm{k}\mathrm{W}·\mathrm{h})]$	0.32

lists the relevant parameters of each device in the microgrid. The transaction electricity prices for this simulation example are based on the time-of-use electricity rates of a certain city, as illustrated in Figure 2. The scheduling period $N_T$ is 24 h and the sample time interval $\Delta t$ is set to 1.

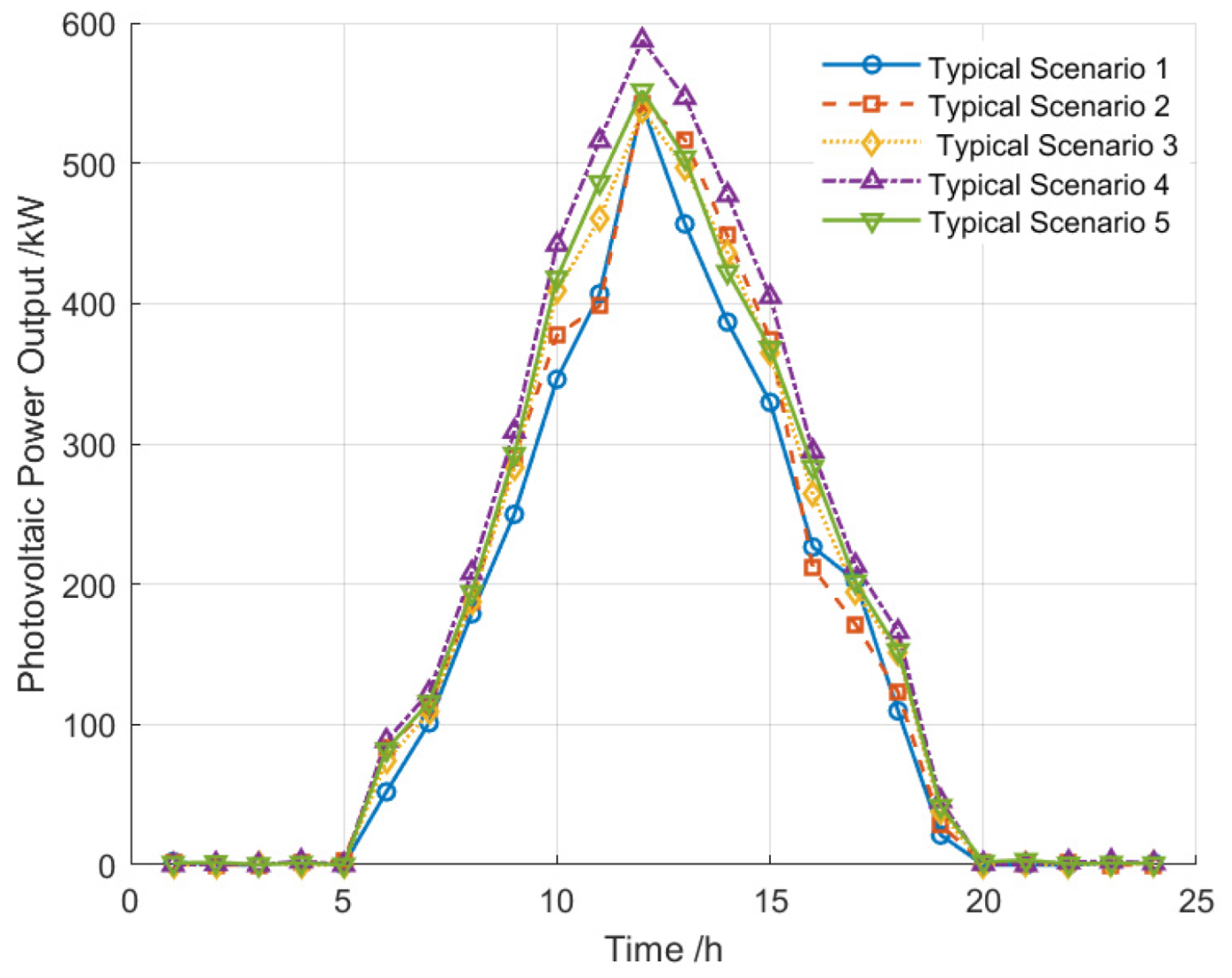
4.2. Analysis of Scenario Generation

The bivariate distribution functions of wind and solar power outputs, normalized using Frank-copula functions based on historical data, are shown in Figure 3. As depicted in Figure 3, the distribution functions of wind and solar power outputs exhibit distinct symmetry, indicating strong correlation between wind and solar power outputs in this region. This correlation provides crucial evidence for generating wind–solar complementary scenarios. Using the wind–solar correlation scenario generation method, N = 500 wind–solar correlation scenarios were generated. Subsequently, it identified $N_s=5$ typical wind–solar correlation scenarios by K-means clustering, as shown in Figure 4 and Figure 5.

4.3. Analysis of Optimization Results

4.3.1. Optimized Dispatch Results for Microgrid

The optimized dispatch results for the microgrid are shown in Figure 6:

As shown in Figure 6, during the periods from 01:00 to 05:00 and 20:00 to 24:00, the photovoltaic output power is zero. During the periods from 01:00 to 07:00 and at 24:00, the day-ahead electricity price (off-peak rate) is lower than the generation cost of the gas turbine. Therefore, the micro gas turbine operates at minimum power during these two periods. During the higher-priced period from 09:00 to 22:00, the gas turbine operates at maximum power to reduce overall operating costs by increasing electricity sales to the utility grid. During off-peak periods at 03:00, 05:00, 06:00, and 24:00, energy storage systems charge; during peak periods at 09:00 and 19:00–21:00, they discharge. During off-peak hours (01:00–07:00 and 24:00), the microgrid purchases electricity from the utility grid to meet load demands and charge the energy storage system. This stored energy is then used to supply loads or sell electricity back to the grid during peak pricing periods for profit. During all other hours, the microgrid sells surplus electricity to the grid while ensuring power requirements are met, thereby maximizing profits.

4.3.2. Comparison Analysis of Different Optimization Run Results

For convenience in subsequent discussion, this paper denotes the distributed robust optimization scheduling scheme without considering the green certificate–carbon trading mechanism as DRO; the distributed robust optimization scheduling scheme incorporating the green certificate–carbon trading mechanism is denoted as GCDRO.

By comparing the three approaches in

Table 2. Comparison of optimization results.

Plan	Total Cost/CNY	Carbon Trading Cost/CNY	Green Certificate Transaction Cost/CNY	Energy Storage Unit Cost/CNY	Carbon Emissions/kg	Renewable Energy Utilization Rate/%
DRO	5292.77	-	-	708.63	45.94	34.65
GCDRO	4853.26	344.26	−457.28	524.62	33.83	72.57
GCDRGO	4993.57	310.28	−385.46	477.31	27.46	67.37

, it can be concluded that the DRO method results in the highest carbon emissions and the highest total costs because it does not incorporate carbon trading and green certificate trading mechanisms. Compared to DRO, the GCDRO method reduces carbon emissions by 26.36% and reduces total cost by approximately 8.30% due to incorporating the green certificate–carbon trading mechanism. At a slightly higher cost than the total cost of the GCDRO method (a difference of 2.89%), the proposed GCDRGO method has achieved the effect of reducing carbon trading costs by 9.87%, reducing energy storage unit costs by 9.02%, and increasing green certificate costs by 15.71%. Moreover, the GCDRGO method can realize the balance of multi-agent interests. These findings not only validate the fact that integrating green certificate–carbon trading mechanism effectively reduces emissions and boosts renewable energy utilization but also highlight the critical role of game theory frameworks in optimizing multi-stakeholder benefit allocation. This provides both theoretical foundations and practical pathways for constructing low-carbon microgrid systems.

4.4. Analysis of the Green Certificate–Carbon Trading Mechanism

4.4.1. Impact Analysis of Different Renewable Energy Quota Coefficients

Changes in the renewable energy quota coefficient also impact green certificate revenues and renewable energy generation. As shown in Figure 7, while increasing the renewable energy quota coefficient boosts renewable energy output, it simultaneously leads to a gradual decline in green certificate trading revenues. Therefore, policy formulation must seek a reasonable quota coefficient that not only effectively incentivizes renewable energy development but also maintains the health and stability of the green certificate market.

4.4.2. Impact Analysis of Different Stepwise Carbon Price Growth Rates

Similarly, the value of the stepwise carbon price growth rate will correspondingly affect carbon transaction costs and carbon emissions. As shown in Figure 8, as the stepwise carbon price growth rate increases, carbon emissions start to decline significantly and then decrease gradually. However, carbon transaction costs rise remarkably in tandem. A higher carbon price growth rate forces the system toward low-carbon transformation by increasing emission costs, which brings about environmental benefits (emission reductions). Simultaneously, this entails higher economic costs for the entire system. Therefore, a compromise must be sought between environmental and economic benefits.

4.5. Analytical Comparison of GCDRGO Optimization Models

4.5.1. Comparative Analysis of Scheduling Results at Different Confidence Levels

As shown in Equations (31) and (32), the choice of confidence level directly impacts the optimization results. With the historical scenario count N set to 500, the optimization scheduling costs under different confidence levels are presented in

Table 3. Optimization dispatch cost under different confidence levels.

Total Cost for Different Confidence Levels/CNY
${\alpha }_1$	${\alpha }_{\infty }=0.50$	${\alpha }_{\infty }=0.70$	${\alpha }_{\infty }=0.99$
0.20	4961.34	4993.57	5026.55
0.50	4999.74	5006.19	5052.54
0.99	5012.45	5031.79	5076.52

. As shown in Table 3, the economic cost of microgrids increases correspondingly with the rise in confidence levels ${\alpha }_1$ and ${\alpha }_{\infty }$. This is because as ${\alpha }_1$ and ${\alpha }_{\infty }$ increase, the confidence interval also expands, leading to heightened system uncertainty and the consequently rising cost of the microgrid.

Remark: Table 3 clearly illustrates the fundamental trade-off between robustness and economic performance inherent in distributionally robust optimization. As the confidence levels ${\alpha }_1$ and ${\alpha }_{\infty }$ increase, the ambiguity set expands to cover a wider range of possible probability distributions, which results in the expensive total costs. Conversely, lower confidence levels yield a more economical schedule but accept a higher risk of performance degradation under adverse distributions. In practice, the parameters ${\alpha }_1$ and ${\alpha }_{\infty }$ can be tuned to reflect the operator’s specific risk tolerance, balancing the desired level of robustness with affordable cost.

4.5.2. Analysis of the Impact of Different Numbers of Historical Scenarios on Optimization Results

Similarly, based on Equations (31) and (32), the quantity change of historical scenarios also leads to significant differences in optimization results. Given confidence levels ${\alpha }_1=0.2$ and ${\alpha }_{\infty }=0.7$, and the number of typical scenarios $N_s=5$, the simulation results are shown in

Table 4. Total cost under different numbers of historical scenarios.

Number of Scenarios	Total Cost/CNY
500	4993.57
2000	4863.56
5000	4808.78
10000	4787.91

. As indicated in Table 4, the total cost of the microgrid gradually decreases along with the increase in the number of historical scenarios. Since a larger number of historical scenarios makes the initial probability distribution closer to the actual values, the economic performance can be improved.

Remark: The proposed algorithm minimizes a linear objective subject to linear matrix inequality (LMI) constraints. It can be solved efficiently by using interior point methods. The fastest interior point algorithms show $O(\chi {\zeta }^3)$ growth in computation, where $\chi$ is the total row size of the LMIs and $\zeta$ is the total number of scalar decision variables. With the increasing of $N_s$, both the total number of scalar decision variables and the total row size of the LMIs will increase. Therefore, the C&CG algorithm’s computational time and iteration count will grow and the computational burden will become much heavier. $N$ is unrelated to computational efficiency, but determines the value of the permissible deviation values for the probability distribution ${\theta }_1$ and ${\theta }_{\infty }$.

5. Conclusions

This paper proposes a distributed robust game-theoretic optimization algorithm for microgrids based on the green certificate–carbon trading mechanism, addressing the multi-agent interests and environmental benefits in uncertain microgrids. The conclusions are as follows:

• Through combining kernel density estimation and copula functions, it can generate typical scenarios and probabilistic fuzzy sets that account for wind–solar correlation to enhance the accuracy of probabilistic fuzzy sets.
• The introduction of the green certificate–carbon trading mechanism can enhance microgrid utilization of renewable energy, achieving energy saving and emission reduction. Analyzing the green certificate–carbon trading mechanism shows the impact of changes in the renewable energy quota coefficient and the carbon trading price growth rate on the environmental and economic benefits of the system. Therefore, appropriate parameters for the green certificate–carbon trading mechanism must be established to significantly enhance the microgrid’s low-carbon economic performance.
• This algorithm synthesizes non-cooperative complete information dynamic games with distributional robust optimization for the solution. The Nash equilibrium solution is found by a non-cooperative dynamic game of complete information, and the strategy of each agent is formulated by distributed robust optimization. It can not only effectively utilize historical scenario data to optimize microgrid performance and enhance computational efficiency but also realize the balance of interests among gas turbines, renewable energy generators, and energy storage units.