A Data-Driven Approach for Distribution System State Estimation Considering Data and Topology Uncertainties

Abstract

With the increasing integration of distributed energy resources and the growing variability of multiple loads, distribution networks face significant uncertainties in measurement data, line parameters, and topology. Traditional state estimation methods, such as weighted least squares, rely on accurate network parameters and are therefore highly sensitive to measurement noise and topology variations. To address these challenges, this work proposes a comprehensive data-driven framework for ADN state estimation that features a novel integration of an improved deep residual network (i-ResNet) and transfer learning. An improved deep residual network (i-ResNet) is developed to enable fast and robust state estimation without dependence on online parameters, even under uncertain data conditions. Furthermore, a transfer learning–based model is introduced to accommodate topology changes by leveraging historical data from multiple network configurations. Experimental studies on the IEEE 33-bus and 118-bus test systems are conducted to evaluate the performance of the proposed approach. The results demonstrate that the proposed method achieves higher accuracy and faster convergence than conventional techniques, with voltage magnitude errors consistently maintained below 1%.

1. Introduction

The distribution network, as the final stage directly connecting to end-users, plays a critical role in ensuring social welfare and economic stability. The global energy landscape is undergoing a profound transformation driven by industrial expansion and the transition from non-renewable to renewable energy sources [1]. Consequently, distribution networks are increasingly integrating distributed energy resources (DERs), variable loads, and energy storage systems. While this integration enhances supply reliability and mitigates energy shortages, the operation process of distribution systems introduces greater complexity and operational uncertainty [2]. Moreover, ongoing electricity market reforms and economic dispatch mechanisms further complicate grid management, making distribution systems more susceptible to unexpected operating conditions [3].

Distribution System State Estimation (DSSE) provides real-time estimates of system states like node voltages, supporting analysis, control, topology, bad data detection, and device planning for the Distribution Management System (DMS). However, conventional DSSE faces three main challenges: (1) Low observability due to limited deployment of high-precision devices like PMUs; (2) data uncertainty caused by noisy measurements and outdated line parameters; and (3) topological uncertainty due to frequent changes in distribution networks from faults, maintenance, or reconfiguration. These issues hinder traditional estimation methods, making accurate DSSE vital for better grid management, stability, and resilience [4,5,6].

Recent research on distribution network state estimation algorithms primarily concentrates on the Weighted Least Squares (WLS) approach, robust algorithms, and new artificial intelligence techniques. These are typically classified into physics-model-based methods and data-driven approaches that use historical data.

Distribution network state estimation uses static and dynamic methods based on physics models. Static estimation employs current measurement data, with the Weighted Least Squares (WLS) method being the most common, refined over time [7]. Enhancements to WLS include incorporating measurement correlations [8], spatiotemporal features [9], and augmented analysis to improve accuracy [10]. Some methods reduce measurement data using intermediate variables [11,12] or split the network into areas [13,14], simplifying calculations at the risk of noise sensitivity and iteration demands [15,16]. With DERs, system dynamics can cause WLS methods to fail locally [17]. To address data issues, alternatives like WLAV and Huber estimators [18] are used, though they involve complex, slower models, impacting real-time performance.

Dynamic state estimation uses current measurement data and the previous state estimate to infer and predict the next state. While mainly based on Kalman Filtering (KF) for linear systems, solutions for nonlinear systems include algorithms like the Extended Kalman Filter (EKF), Unscented Kalman Filter (UKF), Cubature Kalman Filter, and Particle Filter. Reference [19] introduced an adaptive interpolation technique to mitigate nonlinear effects on EKF performance by quantifying the nonlinearity of measurement and state equations. To enhance robustness, reference [20] proposed an improved UKF that adjusts the distribution of Sigma points in real-time via a correction factor, thus increasing estimation accuracy. Reference [21] applied the H∞ criterion from robust control to manage measurement noise uncertainty, developing an H∞-UKF method. Reference [22] addressed false data injection attacks with a hybrid KF-based model, enhancing security across various scenarios. Overall, physics-model-based solutions depend on line parameters and measurement data; however, their iterative process is time-consuming, limiting applications amid high uncertainty in distribution network operations.

With the increasing adoption of various machine learning algorithms, applying artificial intelligence techniques to solve complex power system issues, including state estimation, has garnered growing research interest. Data-driven AI methods analyze the nonlinear relationships between measurement vectors and state variables using historical data to develop models tailored to the data. These methods significantly improve the accuracy and robustness of state estimation, making them a popular research area. This field includes directly modeling the relationship between input measurements and output state variables with data-driven models and using these models to support physics-based solutions. For example, Ref. [18] used historical data and associated states to learn the mapping from current measurements to state variables. By inputting current measurement data into the trained model, an estimate of the current state is obtained. Similarly, Refs. [23,24] combined distributed local measurements with polynomial regression to estimate system voltage magnitude and phase angle, requiring a measurable controller in the distributed energy resource system as input. Reference [25] proposed a fast state estimation method suitable for large systems, where neural networks output node voltage magnitudes and phase angles, with measurements such as branch power, which have strong correlations, serving as inputs selected through correlation analysis. After offline training, the model can generate voltage estimates from measurement data in online operation, although the varying inputs for each node increase the complexity of training. In [26], a deep ensemble approach was introduced to enhance training stability by combining models with linear regression to reduce uncertainty. Meanwhile, Refs. [27,28] employed neural networks to explore the relationship between measurements and state variables, providing initial estimates for Gauss–Newton methods. Given the vast data in distribution network databases, extracting valuable insights and utilizing data-driven methods for state estimation has become a key research focus.

Moreover, the topology of the distribution network changes during real operation, and data for these time-varying topologies are limited, complicating the training of the data-driven models mentioned earlier [29]. Currently, research on state estimation with dynamic topologies is quite limited. The main approach is to leverage abundant data from other topological structures in the database to offset the lack of sample data for the new topology [30]. For instance, reference [31] introduced a model transfer method where the model is initially trained on the original topology, most layers are frozen, and then it is fine-tuned with limited data from the new topology. Similarly, reference [32] combined artificial neural networks with transfer learning to develop a transfer neural state estimation method, allowing the current distribution network state estimator to adapt to other networks. Overall, using data-driven algorithms for distribution network state estimation is increasingly compatible with smart grid development, though research in the context of dynamic topologies still requires more focused exploration.

This paper addresses limitations of current methods, noting that parameter changes and measurement data uncertainty during operation limit traditional physical methods and reduce accuracy. It proposes i-ResNet, a modified residual neural network, to develop a state estimation model based on data analysis, requiring only small real-time and pseudo-measurements without complex parameters. The method is robust to data errors and improves operational efficiency. Due to frequent topology changes from system optimization, a time-varying topology state estimation based on migration learning is proposed, using historical data from source topologies and small new topology datasets to enhance data-driven effectiveness. Simulations across various networks confirm the approach’s efficacy.

The contributions of this paper can be summarized as follows:

(1)

A refined i-ResNet state estimation approach is extended to analyze the influence of measured data and topology uncertainties on the operation state of distribution network. The proposed strategy enhances robustness against measurement noise while significantly improving computational efficiency, thereby meeting both accuracy and speed requirements.

(2)

Experimental evaluations are performed on the IEEE 33-bus and 118-bus benchmark systems to assess the effectiveness of the proposed approach. The results confirm that the method achieves superior accuracy and faster convergence compared with conventional techniques, maintaining voltage magnitude errors consistently below 1%.

The rest of this article is structured as follows. Section 2 introduces the i-ResNet model-based approach for state estimation, which considers data uncertainty. Section 3 explores the impact of topology changes on state estimation outcomes and discusses potential improvements for handling topology uncertainty in practical applications. Case studies are presented in Section 4. The article concludes with Section 5.

2. Distribution Network State Estimation Considering Data Uncertainty

Traditional distribution network state estimation struggles with practical challenges due to uncertainties in line parameters and measurement data arising from equipment aging, maintenance, and measurement errors. These uncertainties reduce estimation accuracy. Additionally, the iterative nature of standard physical models results in long computation times, making them unsuitable for the quick response needed in modern grids. The widespread integration of distributed energy resources has also changed distribution networks from simple, unidirectional power flow systems to complex, bidirectional ones. This shift introduces voltage volatility caused by renewable energy’s intermittency and peak output, potentially endangering grid stability.

This section introduces a new state estimation model using i-ResNet to overcome issues in line parameter accuracy, measurement reliability, and efficiency. It directly links measurements and state variables via offline training on historical data. During real-time use, the trained model quickly produces state estimates from current measurements, removing reliance on line parameters and showing improved resistance to measurement uncertainties.

2.1. Data-Driven State Estimation Model

Using artificial intelligence for power system monitoring and analysis is essential for developing smart grids. As AI technology progresses, diverse machine learning algorithms are increasingly used in the power sector. Data-driven models examine the spatial and temporal correlations in historical data, converting the distribution network state estimation from a problem based on line parameters and measurements into a process that directly addresses the nonlinear relationship between measurement data z and state variables x.

$$x_t=h^{-1}(z_t),$$

(1)

where $z$ is the measurement matrix; $x$ is the state variable matrix at the current time; and the function $h^{-1}(\cdot )$ is a nonlinear mapping function containing weights ($w_1,w_2\dots w_i$), reflecting the relationship between the input measurement values and the output state variables. The task of offline training is to find the weights that minimize the loss between predicted values and the actual states through training.

The AI training usually depends on extensive historical data to capture the nonlinear relationship between measurement and state variables. Distribution network databases hold large amounts of historical data from measurement devices like SCADA and PMUs, satisfying the needs for training data-driven models. Unlike traditional physical models, data-driven models use measurement data as input and state variables as output, eliminating the need for precise topology parameters and directly avoiding issues caused by line parameter uncertainties.

2.2. Variant of Deep Residual Network

This section begins by explaining the principles and benefits of Deep Residual Networks. It then introduces a specialized variant designed for the distribution network state estimation task and concludes by presenting the state estimation model based on this deep residual network.

2.2.1. Deep Residual Network

The Deep Residual Network (ResNet) [33] is one of the most successful deep learning models in recent years. Building residual learning modules helps resolve problems such as vanishing or exploding gradients that can arise during deep neural network training. A deep residual network consists of a series of blocks, with the fundamental residual block shown in Figure 1.

A residual block includes weight layers, activation functions, normalization, and identity mapping. The core component is the identity mapping, which helps lower the number of parameters and computational load. Additionally, residual blocks use skip connections to transfer input information quickly. The formula for a residual block is as follows:

$$x_{l+1}=x_l+F(x_l,W_l),$$

(2)

where $x_l$ and $x_{l+1}$ represent the input and output of the current residual block, respectively; F is the residual function. Each residual unit is a serial connection structure. Based on the above formula, the learned features of the overall residual network are as follows:

$$x_L=x_0+{\displaystyle \sum _{i=0}^{L-1}F(x_i,W_i)},$$

(3)

where $x_0$ is the input to the residual neural network; $x_L$ is the output. The structure of the residual network is shown in Figure 2.

According to the chain rule, the gradient of the backward process can be obtained as

$${\displaystyle \frac{\partial loss}{\partial x_0}}={\displaystyle \frac{\partial loss}{\partial x_L}}\cdot (1+{\displaystyle \frac{\partial }{\partial x_0}}{\displaystyle \sum _{i=l}^{L-1}F(x_i,W_i)}),$$

(4)

where $\partial loss/\partial x_L$ is the gradient reaching the loss function. The “1” in the parentheses indicates that the shortcut mechanism allows gradient propagation without attenuation, while the residual gradient is propagated through the weighted layers, not directly. The residual gradient will not always be −1, and even if the gradient is slight, the shortcut mechanism prevents gradient vanishing. Therefore, residual learning effectively addresses the vanishing/exploding gradient problem, improving efficiency.

For a specific domain, the process of optimizing model parameters can be summarized as the following optimization problem:

$$W_i=\underset{W_i}{\arg \min }{\displaystyle \sum _{t\in T}{\gamma }_{i,t}(f_i(X_{i,t},W_i),y_t)},$$

(5)

where $f_i(\cdot )$ is the target regression function on the domain; $W_i$ represents the parameters of this domain; and $y_t$ represents the actual value.

2.2.2. Variant of Deep Residual Network

A state estimation model utilizing a deep residual neural network can be developed based on the previous discussion. Although deep residual neural networks are mainly used in image recognition and computer vision—areas with different task characteristics from the state estimation task described here—necessary adjustments are made to tailor the network to this study’s environment. This customized network is called i-ResNet, and its architecture is illustrated in Figure 3.

The i-ResNet architecture includes a reshaping layer, multiple residual blocks, and extended residual blocks. The reshaping layer adjusts the dimension of the intermediate feature space. The extended residual block serves as the central component. Compared to traditional deep residual neural networks, the enhancements and their reasons are outlined as follows:

(1)

Replacing the convolutional layers in standard residual blocks with fully connected layers improves processing of one-dimensional input data, such as branch active/reactive power and node injection active/reactive power. Fully connected layers effectively model the input-output relationship and help reduce model complexity [34].

(2)

Incorporating identity mappings on the left, similar to the traditional deep residual network, combines two residual blocks into a single extended residual block. This structure includes two basic residual blocks with skip connections that transfer feature information across non-adjacent layers, representing an improved version of the deep residual network [35,36]. The benefit of this approach is enhanced information flow and reduced information loss, allowing for more effective utilization of the residual network’s optimization potential.

(3)

The Huber function serves as the loss function because of its robustness to outliers. The ReLU function is selected as the activation function, with its expression provided in Equation (6).

$$relu(x)=\left\{\begin{array}{l}x,x>0\\ 0,x\le 0\end{array}\right.$$

(6)

2.2.3. State Estimation Model Based on i-ResNet

Once the i-ResNet model structure is designed, the overall architecture of the proposed i-ResNet-based distribution network state estimation is illustrated in Figure 4. It consists of several components: data preprocessing, offline training of the i-ResNet model, and online implementation. Each element is explained below.

(1)

Data Preprocessing Unit

Initially, historical operational data from the distribution network is gathered, and an initial training dataset is created via random sampling. Next, because the data varies greatly in scale across the network, normalization is performed on all data to reduce the effects of differing variable scales during model training. Specifically,

$$X^1={\displaystyle \frac{X-\min (X)}{\max (X)-\min (X)}},$$

(7)

where $X^1$ represents the normalized data and $\max (X)$ and $\min (X)$ represent the maximum and minimum values in the dataset X, respectively. After standardization, the data $X^1\in \left[0,1\right]$ and is dimensionless. A specific error level is randomly added to the standardized data to simulate the errors of measurement devices in actual operation. Finally, the training set and test set are partitioned.

(2)

Offline Training Phase

During the offline training phase, measurement data from various time points in the dataset are fed into the model through the input layer. Features are extracted with a reshaping layer, mapped to a high-dimensional space and passed through a series of residual blocks. After processing these residual blocks and another reshaping layer, the model outputs a state estimate and calculates if the accuracy meets the standards. If it does not, the loss function—comparing the estimated results with actual values—is computed, and parameters are updated using the optimizer. The Huber loss function is chosen for its robustness to outliers, combining the benefits of MSE and MAE, as shown in Equation (8). The Adam optimizer is used for training. Once the accuracy criteria are satisfied, the network parameters and the model are saved, and training terminates.

$$L_{\delta }(y,f(x))=\left\{\begin{array}{l}{\displaystyle \frac{1}{2}}{(y-f(x))}^2,\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|y-f(x)\right|\le \delta \hspace{0.17em}\hspace{0.17em}\\ \delta \left|y-f(x)\right|-{\displaystyle \frac{1}{2}}{\delta }^2,\hspace{1em}\left|y-f(x)\right|>\delta \end{array}\right.$$

(8)

(3)

Online Application Phase

During the online application phase, the measurement data from the current time step is fed into the trained model to produce the relevant state variable results rapidly. These results help inform the subsequent operation and dispatch of the distribution network.

3. Distribution Network State Estimation Considering Topology Uncertainty

The previously proposed i-ResNet-based model effectively captures the nonlinear relationship between states and measurements using historical data. It removes the need for exact line parameters, offers quick and precise estimates, and is robust against measurement noise. However, in real-world operations, distribution network topologies often change due to dispatch demands or unforeseen events, leading to topological uncertainty. When such changes occur, the lack of sufficient measurement devices often prevents obtaining accurate structural parameters quickly, making traditional physical models unsuitable. Additionally, a new topology’s limited operational history hampers data-driven approaches that depend on extensive historical data for training.

To address the state estimation problem for new topologies, this section introduces a transfer learning-based method. It creates links between source and target topologies, using inductive transfer to harness extensive historical data from source topologies to enhance performance on the target topology.

3.1. Topology Uncertainty in Distribution Networks

Unlike the stable topology of transmission networks, distribution network structures frequently change due to operational scheduling or unexpected events [37], with modifications happening from weeks to months [38]. The growing integration of renewable energy sources and variable loads adds more uncertainty, sometimes causing system state changes hourly [39]. Some adjustments are planned, like network reconfiguration for economic reasons after DER integration [40], but many are unplanned and challenging to predict, such as line aging or fault outages [41].

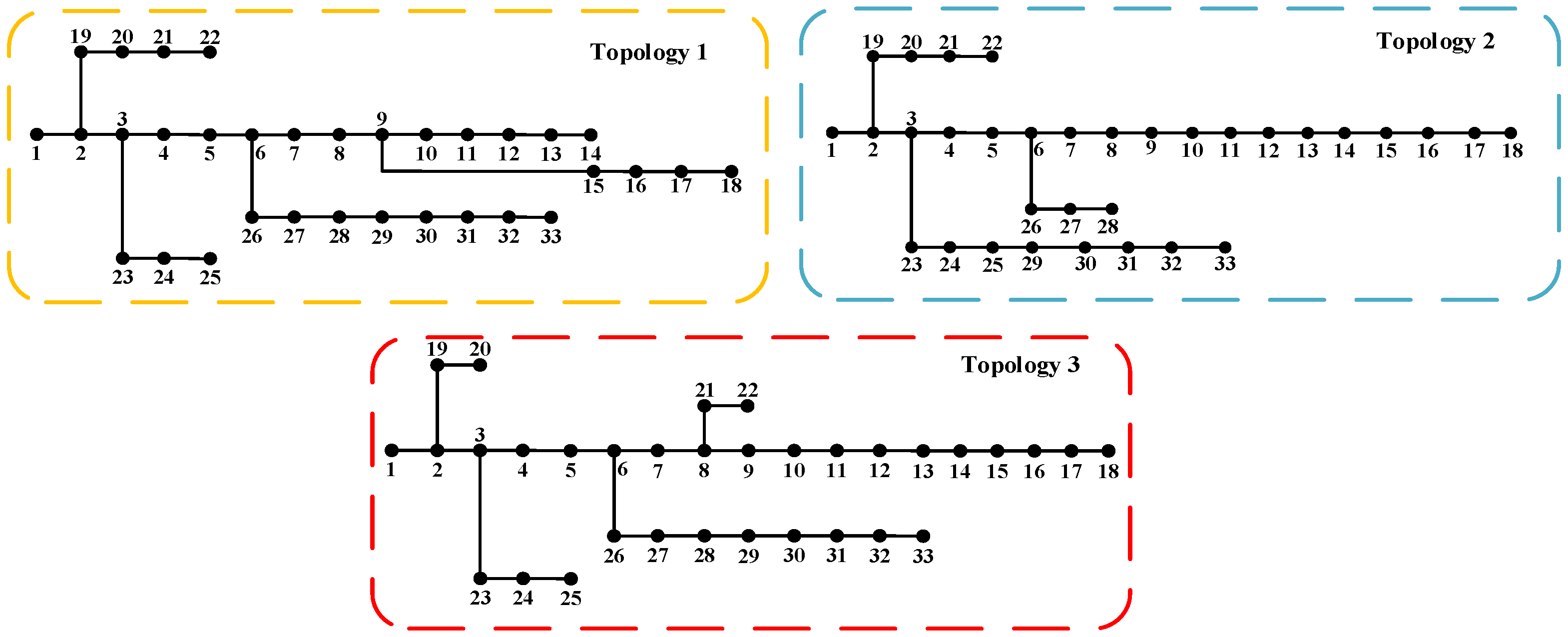
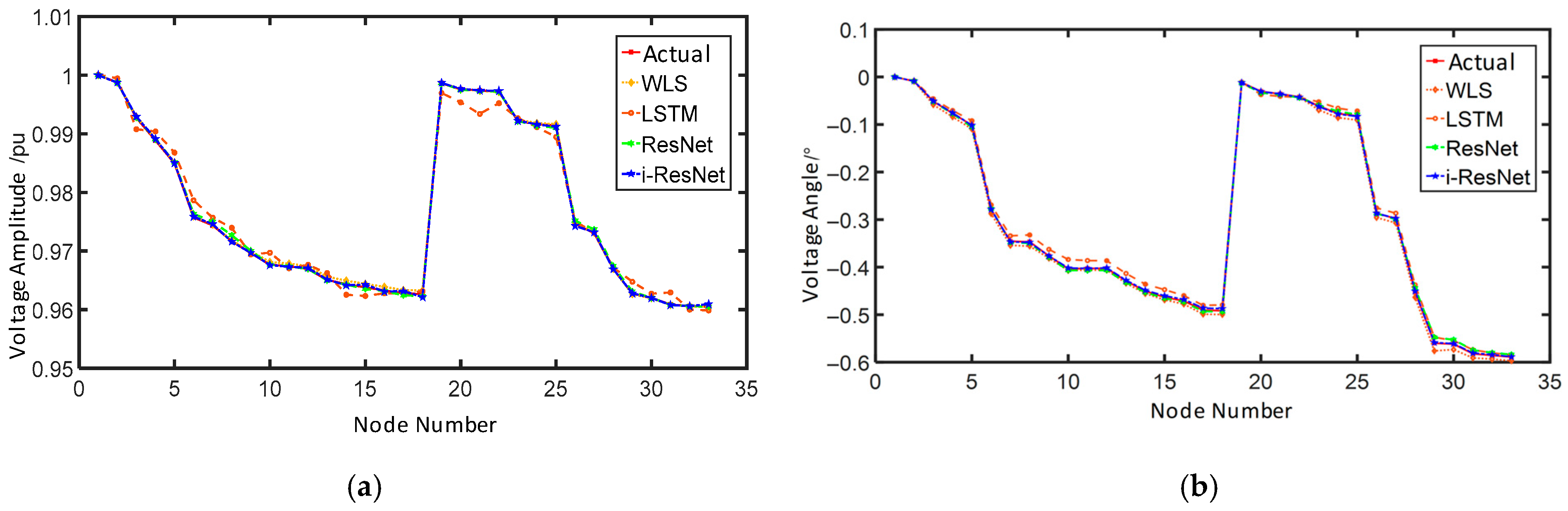
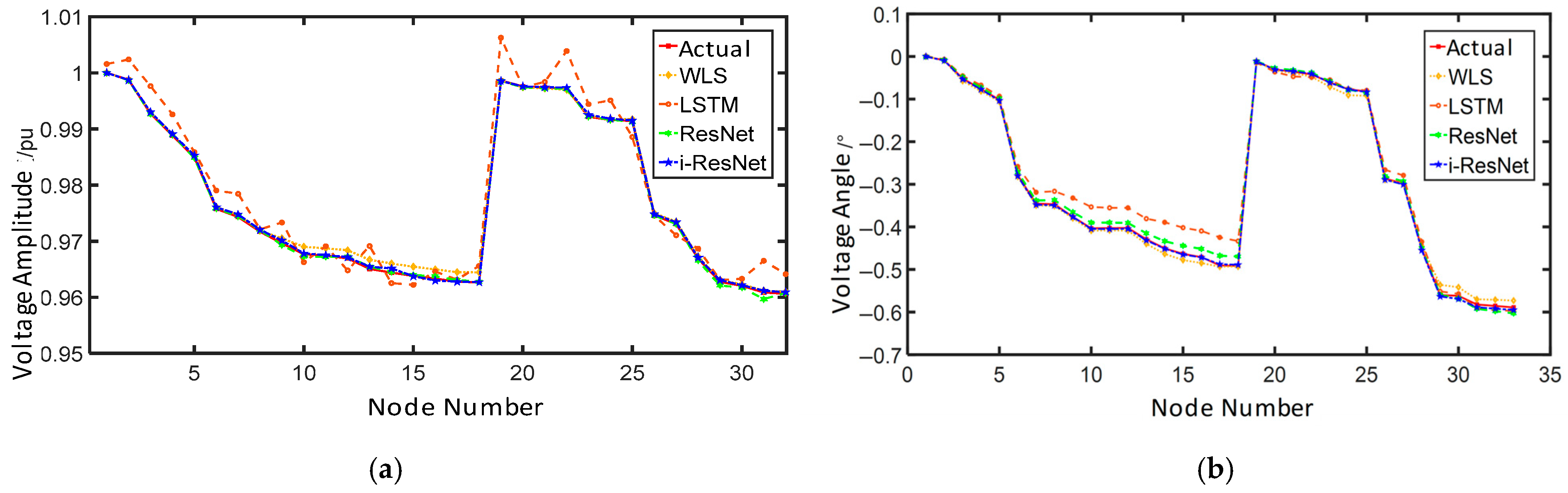
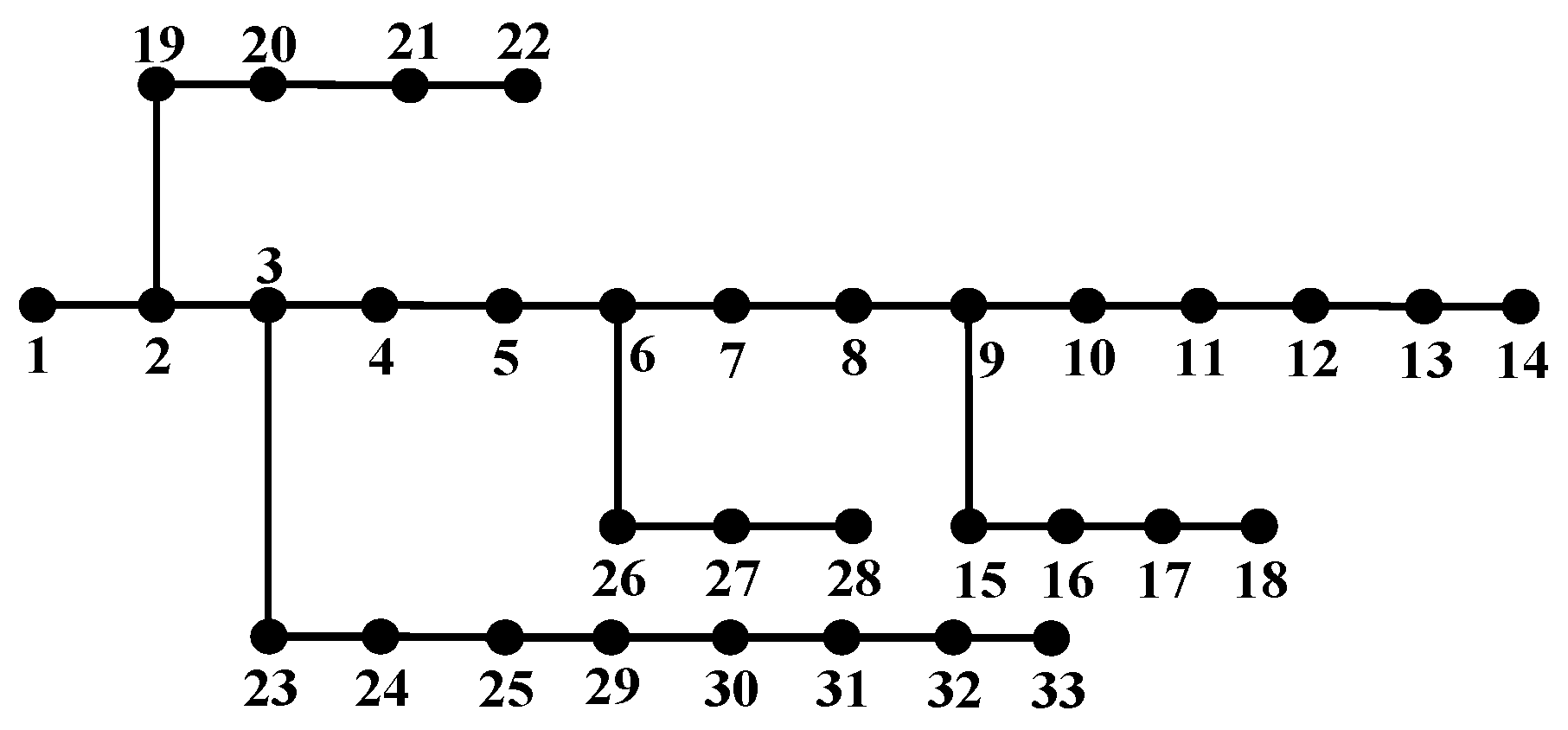
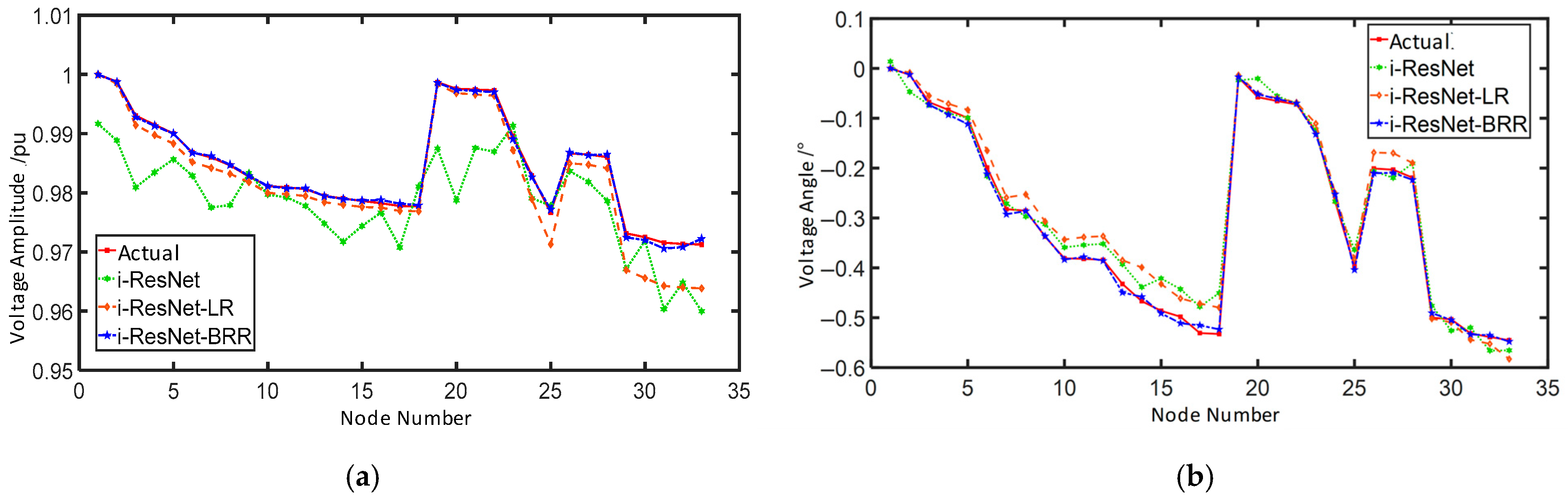
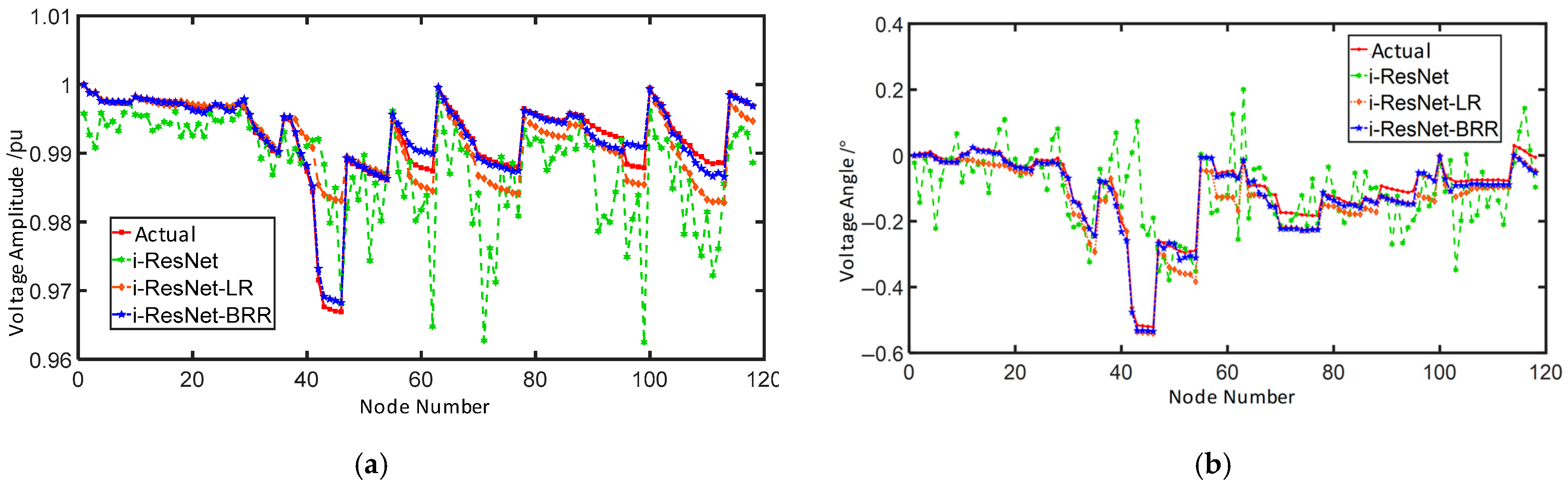
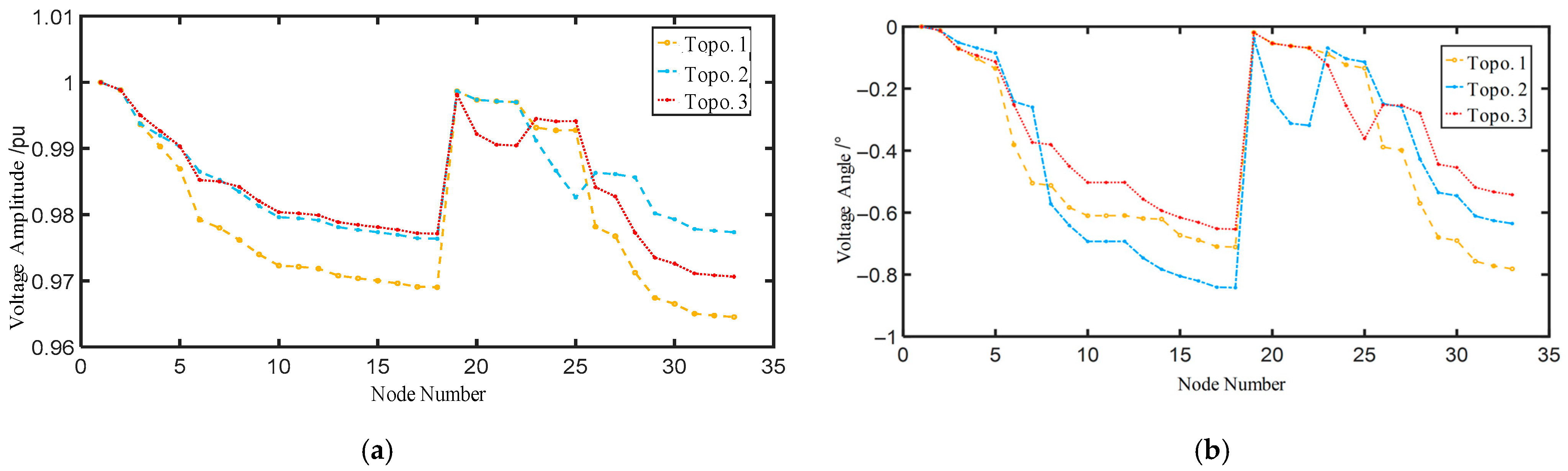
Using the IEEE 33-bus system as an example, Figure 5 illustrates three distinct topological configurations. At the same time, Figure 6 compares their operational states—specifically, node voltage magnitudes and phase angles, which are the state variables considered in this work—at a specific moment.

Figure 6 clearly illustrates how changes in the distribution network topology lead to notable variations in voltage magnitude and phase angle profiles. This demonstrates that a state estimation model trained only on the original topology cannot reliably estimate the operational features of a new target topology.

Frequent topological changes and the absence of real-time measurement devices hinder the acquisition of precise and timely line parameters and topology data, limiting the effectiveness of traditional physical models. The i-ResNet model introduced in previous section, which does not rely on topology parameters, faces difficulties due to limited operational data for new topologies, making accurate training impossible. To overcome the issue of topology uncertainty, this section presents a distribution network state estimation model that leverages transfer learning.

3.2. Transfer Learning-Based State Estimation Model

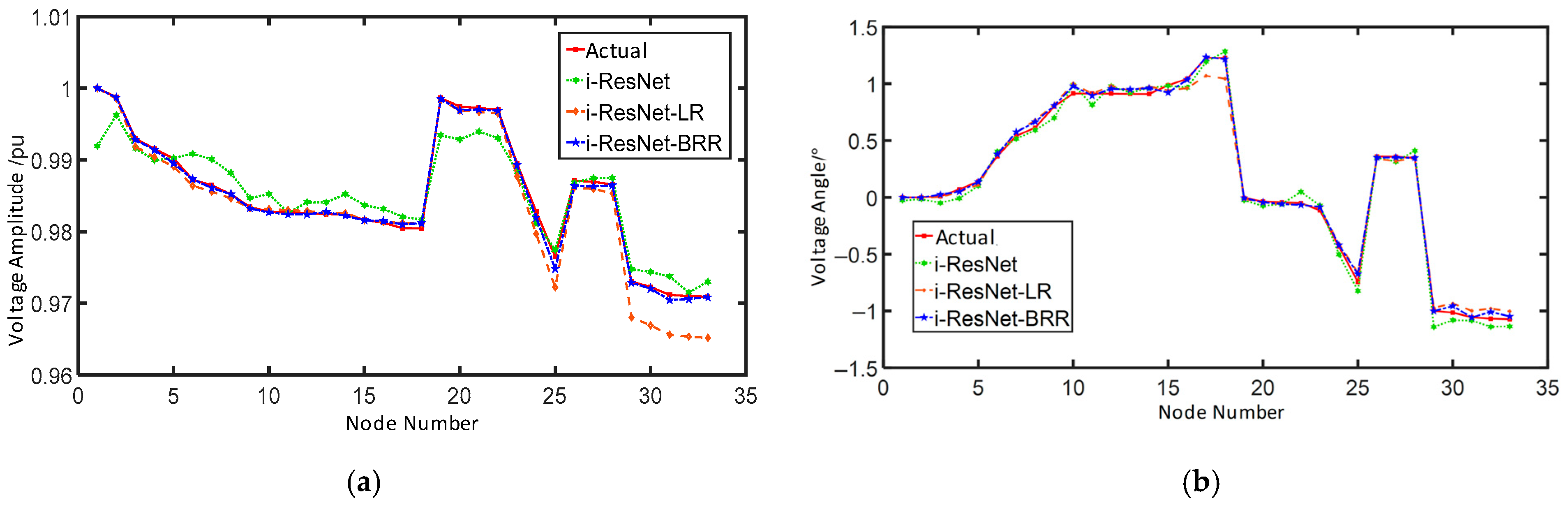
Based on the analysis in Section 4.1 and Section 4.2 and using the IEEE 33-bus system as an example, the potential for applying transfer learning to this problem is evident from Figure 6. While operational states vary significantly across different topologies, certain nodes exhibit similarities. For instance, Topology 2 and Topology 3 show comparable voltage magnitude patterns at nodes 1–18, whereas Topology 1 and Topology 2 are identical at nodes 19–23. Moreover, ample labeled data exists for other topologies, indicating that data from various topologies can compensate for the limited data in a new target topology, making transfer learning highly suitable. For practical purposes, this paper utilizes inductive transfer learning.

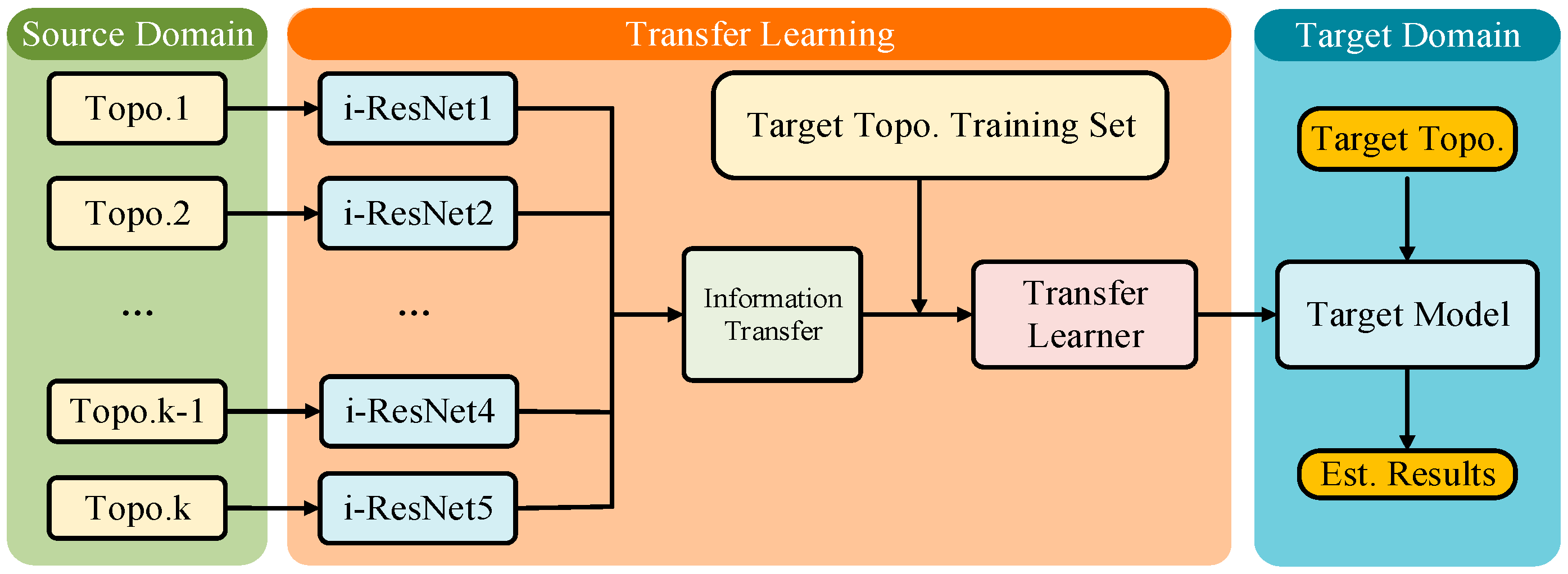
Estimating time-varying topology states involves identifying the recently changed topology as the target domain and linking it to known topologies in a database, which act as source domains. Knowledge transfer is then employed to develop an estimation model for the modified topology. This process is depicted in Figure 7.

The transfer-combined state estimation model involves several steps: initially, historical measurement data from various source topologies are gathered from the database, and corresponding source topology state estimation models are trained using the i-ResNet model introduced in Section 2. Next, a small set of measurement data from the new (target) topology is used to combine these source models and determine their respective weights. Finally, the combined model estimates the state of the target topology. Unlike training a dedicated model for each topology as described in Section 2, this approach primarily leverages pre-trained i-ResNet models from other topologies, which are then combined with limited data from the target topology to create an accurate state estimation model for the current topology. Since the process of generating source domain models with i-ResNet was detailed in the previous section, the following section discusses the model combination strategy.

A traditional linear combination model is often expressed as

$$f(x)=w^{T}x.$$

(9)

The limitation of this method is its reliance on fixed weights wᵢ and the need for a specific causal connection between input and output, which results in subpar performance with nonlinear problems. To overcome this, this paper adopts Bayesian Ridge Regression (BRR) [42].

According to Bayesian regression theory [43], the state estimate at time t is assumed to be

$$x_t={\displaystyle \sum _{i=1}^n{h_i}^{-1}(z_t)w_i}+\epsilon ,$$

(10)

where $w_i$ corresponds to the weight of the$i$-th source topology model; $h_i^{-1}(z_t)$ represents the estimation result of the $i$-th model at time t; $\epsilon$ is the noise, distinguishing it from linear regression, and $\epsilon$ is assumed to follow a Gaussian distribution with zero mean and variance ${\sigma }_n^2$:

$$\epsilon \sim N(0,{\sigma }_n^2).$$

(11)

Based on Equation (11), the probability density of the observed data likelihood function can be expressed as

$$\begin{array}{ll}p(x\left|Z,w,{\sigma }_n^2\right.)& ={\displaystyle \prod _{t=1}^{N}p(x_t\left|h_t^{-1}(z_t),w_i\right.)}\\ & ={\displaystyle \prod _{t=1}^N\frac{1}{\sqrt{2\pi }{\sigma }_n}}\exp \left[{\displaystyle \frac{{(x_t-h_t^{-1}(z_t))}^2}{2{\sigma }_n^2}}\right]\\ & ={\displaystyle \frac{1}{\sqrt{2\pi }{\sigma }_n}}\exp \left(-{\displaystyle \frac{{\left|x-Z^{T}w\right|}^2}{2{\sigma }_n^2}}\right)\end{array},$$

(12)

where $N=\left\{z,x\right\}={\left\{(z_t,x_t)\right\}}_{t=1}^N$ represents the target topology dataset and $w$ is the Bayesian model weight vector. Thus, the model combination problem transforms into deriving the conditional distribution of the weights w.

Applying Bayes’ theorem, and assuming a prior distribution for the parameters $w\sim$N(0,Σ_p), the posterior probability can be derived:

$$p(x\left|Z,w,{\sigma }_n^2\right.)={\displaystyle \frac{p(x\left|Z,w,\right.{\sigma }_n^2)p(w)}{p(x\left|Z,\right.{\sigma }_n^2)}}.$$

(13)

Based on Equation (13), the posterior distribution of w is derived from the likelihood function, observed data, and prior distribution. Hence, the posterior distribution for w is as follows:

$$p(w\left|x,Z\right.)=N(w\left|{\displaystyle \frac{1}{{\sigma }_n^2}}{\Lambda }^{-1}Z\right.x,{\Lambda }^{-1}),$$

(14)

where ${\Lambda }^{-1}={\sigma }_n^{-2}X{X}^T$. Given a test measurement dataset $Z_{*}$, the predictive distribution for the state estimate is obtained by averaging over all parameters and the posterior weight distribution:

$$\begin{array}{ll}p(f_{*}\left|Z,Z_{*}\right.,{\sigma }_n^2)& ={\displaystyle \int p(f_{*}\left|Z_{*},w,{\sigma }_n^2\right.)}p(w\left|Z,x\right.)dw\\ & =N(f_{*}\left|{\displaystyle \frac{1}{{\sigma }_n^2}}{Z}_{*}^T\right.{\Lambda }^{-1}Zx,Z_{*}^T{\Lambda }^{-1}{Z}_{*})\end{array}.$$

(15)

Bayesian Ridge Regression is a common type of Bayesian regression, which assumes that the prior distribution for the weights w is a spherical Gaussian [44,45]:

$$p(w\left|\lambda \right.)=N(w\left|0,{\lambda }^{-1}{I}_P\right.),$$

(16)

where the prior parameter λ follows a Gamma distribution. The resulting model is called Bayesian Ridge Regression. During model fitting, the parameters $w$ and λ are estimated jointly.

As a probabilistic model, Bayesian Ridge Regression may produce parameters that slightly differ from those derived using ordinary least squares. Nonetheless, it generally offers greater stability in complex situations. The derivation process also shows that this method can fully utilize data, which makes it especially effective in scenarios with limited operational data, topological uncertainty, and changing topologies, like those encountered in this study. This advantage is similarly observed in other fields where data is challenging to obtain [46]; for instance, in medical diagnostics, probabilistic models like Naïve Bayes have been successfully applied to migraine classification using limited patient data augmented with synthetic samples [6].

4. Case Analysis and Results

4.1. Validating the State Estimation Performance Under Data Uncertainty

To validate the effectiveness and applicability of the proposed method, an IEEE 33-bus distribution network with a 12.66 kV base voltage is used for initial testing. Its topology features five tie lines (depicted as dashed lines in Figure 8), enabling reconfiguration and illustrating topology uncertainty. The dataset is generated through power flow calculations in MATPOWER combined with random sampling and then split into training and testing sets for the data-driven algorithms. PV generators are attached at nodes 6, 9, 16, and 29 to model the uncertainty in renewable integration, utilizing actual historical generation data (refer to output profile in Figure 9).

The measurement set consists of 18 real-time measurements of branch active and reactive powers, along with 64 pseudo-measurements of node injection powers, totaling 82 dimensions. Pseudo-measurement errors are evaluated under two scenarios: 15% for high accuracy and 50% for low accuracy, reflecting practical uncertainty. The state variables include node voltage magnitudes and phase angles. The real-time measurement locations are summarized in

Table 1. Real-Time Measurement Locations.

Node Injection Power (Pi, Qi)	Branch Power (Pij, Qij)
/ 1	2, 5, 7, 10, 14, 19, 23, 27, 30

¹ “/” means no node injection in this case.

.

To showcase the effectiveness of the proposed method compared to traditional physical techniques, the WLS algorithm, a common choice for state estimation, is used for comparison. Additionally, since residual neural networks are tailored for tackling deep learning problems, other data-driven approaches are included as benchmarks: Support Vector Machine (SVM), Long Short-Term Memory (LSTM), and the original Residual Network (ResNet). The accuracy is assessed using Mean Absolute Error (MAE) and Root Mean Square Error (RMSE).

As a physics-based approach, WLS does not need training data and relies only on measurements and the topological model. Conversely, methods like SVM, LSTM, ResNet, and the proposed i-ResNet are trained on 3000 datasets and do not require topological structure data. Their performance is assessed with a separate test set of 200 samples.

4.1.1. Scenario 1 (15% Pseudo-Measurement Error)

The results in the table clearly show that the proposed method outperforms others in accuracy across all metrics, with the lowest mean error and minimal variation from true values. For estimating node voltage magnitudes, the i-ResNet model decreases the MAE by 97%, 92%, and 55% when compared to SVM, LSTM, and the baseline ResNet, respectively. The poor results from SVM highlight the need to choose suitable data-driven techniques for particular tasks. Although the traditional WLS method can yield fairly accurate results under ideal conditions with exact topology and measurements, it consistently falls short of the performance achieved by our proposed method.

Estimating the phase angle is more difficult, leading to higher errors across all methods. However, i-ResNet still offers the best accuracy, with 92%, 90%, and 69% improvements over SVM, LSTM, and ResNet, respectively. The difference in performance compared to WLS is even greater for phase angles than for voltage magnitudes. These findings demonstrate that deep residual networks outperform LSTM models, and our proposed modifications to the residual structure further enhance data flow and estimation precision.

Visual comparisons serve as an extra validation step. Figure 10 shows the estimated voltages at all 33 nodes at a specific time (excluding SVM for clarity). Even with notable operational changes across the network, the proposed method’s estimates remain closely aligned with the real values at every node. The state estimation errors for both node voltage magnitude and phase angle in Scenario 1 of the IEEE 33-bus system are presented in

Table 2. Node Voltage Magnitude State Estimation Errors in Scenario 1 of IEEE 33 bus system.

Algorithm	MAE	RMSE
WLS	2.4 × 10−4	3.2 × 10−4
SVM	8.2 × 10−3	1.2 × 10−2
LSTM	2.2 × 10−3	3.1 × 10−3
ResNet	4.0 × 10−4	5.5 × 10−4
i-ResNet	1.8 × 10−4	2.6 × 10−4

and

Table 3. Node Voltage Phase Angle State Estimation Errors in Scenario 1 of IEEE 33 bus system.

Algorithm	MAE	RMSE
WLS	8.7 × 10−3	1.2 × 10−2
SVM	2.6 × 10−2	3.3 × 10−2
LSTM	2.3 × 10−2	5.3 × 10−2
ResNet	6.3 × 10−3	9.5 × 10−3
i-ResNet	2.0 × 10−3	3.2 × 10−3

, respectively.

Further analysis of temporal performance (Figure 11) shows that i-ResNet precisely monitors system state changes over time. Although WLS performs well when system parameters are accurate, it falls short compared to our method, especially in phase angle estimation. The ability to track significant voltage fluctuations highlights the effectiveness of our approach and underscores the need for advanced estimation techniques in modern distribution systems.

4.1.2. Scenario 2 (50% Pseudo-Measurement Error)

This scenario tests realistic distribution network operation conditions with reduced pseudo-measurement accuracy, reflecting higher measurement data uncertainty.

Table 4. Node Voltage Magnitude State Estimation Errors in Scenario 2 of IEEE 33 bus test system.

Algorithm	MAE	RMSE
WLS	4.2 × 10−4	6.8 × 10−4
SVM	8.3 × 10−3	1.3 × 10−2
LSTM	3.1 × 10−3	4.0 × 10−3
ResNet	6.2 × 10−4	1.1 × 10−3
i-ResNet	2.4 × 10−4	3.3 × 10−4

and

Table 5. Node Voltage Phase Angle State Estimation Errors in Scenario 2 of IEEE 33 bus test system.

Algorithm	MAE	RMSE
WLS	1.4 × 10−2	2.3 × 10−2
SVM	4.2 × 10−2	6.7 × 10−2
LSTM	3.6 × 10−2	5.8 × 10−2
ResNet	9.0 × 10−3	1.3 × 10−2
i-ResNet	3.8 × 10−3	5.8 × 10−3

show the voltage magnitude and phase angle estimation errors for various algorithms in this scenario.

The tables indicate that all algorithms’ accuracy diminishes as pseudo-measurement errors grow. Although the traditional WLS, which relies on physics, performed similarly to the proposed method with low pseudo-measurement errors in the previous section, its accuracy drops notably when errors reach 50%, mimicking real-world grid conditions. In particular, for voltage phase angles, the difference in performance between WLS and the i-ResNet method becomes roughly tenfold in both metrics, highlighting how physics-based techniques depend heavily on accurate topology and measurement data.

Meanwhile, the i-ResNet-based method introduced in this section achieves high estimation accuracy. It shows that practical data-driven strategies can more effectively manage uncertainties in distribution system state estimation and adapt better to distribution network fluctuations. Additionally, the model provides the best estimates for voltage magnitudes and phase angles.

The state estimation results for all 33 nodes at the same sampling time as in Scenario 1 are shown in Figure 12. Compared to Figure 10, there is a visible decrease in estimation accuracy across the results, highlighting the effect of data uncertainty. Despite this, the proposed method still provides accurate state estimates for every node.

This subsection illustrates the constraints of traditional physical methods regarding accuracy in practical conditions, based on experiments with various pseudo-measurement error levels. The findings confirm that the i-ResNet-based state estimation algorithm introduced here can deliver high accuracy in real distribution network operations and effectively withstand data uncertainty.

4.2. Validating the State Estimation Performance Under Topology Uncertainty

This section demonstrates the method’s effectiveness under Topology Uncertainty through simulation experiments on IEEE 33-bus and 118-bus distribution networks of varying scales.

The measurement data setup follows Section 3.1. Since this section mainly verifies the transfer model’s performance, experiments are conducted with pseudo-measurement errors set at 15%, excluding the 50% error scenario used for comparison. The original topology training data consists of 1000 sets, while the new topology historical data includes only 48 sets, simulating situations with limited operational data under changing topologies. Comparisons are made against the non-transferred i-ResNet and the transfer model i-ResNet-LR. The non-transferred i-ResNet model is trained only on the 48 datasets from the new topology, while i-ResNet-LR follows the same training process as the proposed i-ResNet-BRR in this section. This comparison demonstrates the superiority of the proposed method over traditional data-driven approaches and other transfer learning techniques. Detailed experimental parameters are listed in

Table 6. Transfer Model Parameter Configuration.

Parameter of Testing	Quantity
Source Domain Topologies	12
Source Domain Topology Training Sets	1000
Source Domain Topology Testing Sets	200
Target Domain Topology Training Sets	48
Target Domain Topology Testing Sets	200

. Evaluation metrics MAE and RMSE are chosen to comprehensively reflect the deviation between estimated and actual values.

4.2.1. Validation Under IEEE 33-Bus Distribution Network

This subsection uses the IEEE 33-bus distribution network to demonstrate the advantages of i-ResNet-BRR over other algorithms through simulations on two target topologies. Target Topology 1 is depicted in Figure 13, with system measurement devices aligned with those listed in Table 1. For clearer visualization of the topological changes, measurement devices are not shown in the figure.

After training all models,

Table 7. Voltage Magnitude Estimation Errors for Target Topology 1.

Algorithm	MAE	RMSE
i-ResNet	9.7 × 10−3	1.9 × 10−2
i-ResNet-LR	5.1 × 10−3	7.8 × 10−3
i-ResNet-BRR	1.0 × 10−4	1.8 × 10−3

and

Table 8. Voltage Phase Angle Estimation Errors for Target Topology 1.

Algorithm	MAE	RMSE
i-ResNet	5.0 × 10−2	9.7 × 10−2
i-ResNet-LR	4.3 × 10−2	6.3 × 10−2
i-ResNet-BRR	3.4 × 10−2	5.4 × 10−2

display their performance on the test set. The results show that the non-transferred i-ResNet model, trained with only 48 target topology datasets, produces significant errors in voltage magnitude and phase angle estimation. For example, using RMSE, the proposed method reduces errors in voltage magnitude by 90% and in phase angle by 44%, indicating that training with limited data alone is insufficient for satisfactory state estimation. In contrast, the proposed approach greatly improves accuracy by leveraging knowledge transferred from source topologies stored in the database. Compared to the transfer model i-ResNet-LR, the proposed method increases accuracy by 77% for voltage magnitude and 14% for phase angle. This demonstrates that our model combination approach outperforms traditional linear regression algorithms, effectively mitigating negative transfer effects, utilizing 100% of the data, and reducing overfitting risks.

Figure 14 display test set sampling results to compare voltage magnitude and phase angle estimation performance more intuitively. The standalone i-ResNet model does not achieve the required accuracy and struggles to track operational trends across nodes, mainly due to limited training data. Although both transfer learning approaches broadly approximate the actual values, the proposed method aligns more closely with the real voltage magnitude and phase angle results compared to i-ResNet-LR, highlighting its superiority over other transfer learning models.

Another target topology, Target Topology 2 (Figure 15), is tested to confirm that the methodology is broadly applicable.

Table 9. Voltage Magnitude Estimation Errors for Target Topology 2.

Algorithm	MAE	RMSE
i-ResNet	8.6 × 10−3	1.1 × 10−2
i-ResNet-LR	5.4 × 10−3	8.2 × 10−3
i-ResNet-BRR	1.1 × 10−3	2.2 × 10−3

and

Table 10. Voltage Phase Angle Estimation Errors for Target Topology 2.

Algorithm	MAE	RMSE
i-ResNet	4.8 × 10−2	7.8 × 10−2
i-ResNet-LR	4.1 × 10−2	5.9 × 10−2
i-ResNet-BRR	2.9 × 10−2	5.0 × 10−2

display consistent performance trends across various evaluation metrics, with i-ResNet-BRR consistently achieving optimal results.

Figure 16 displays the test set sampling results for voltage magnitude and phase angle estimation across all nodes. The non-transferred i-ResNet shows considerable volatility and notable deviations from accurate results when training samples are limited. In contrast, the proposed i-ResNet-BRR consistently performs well across various topological structures.

Further validation involves randomly choosing 3, 5, 7, 9, and 12 topological structures as source domains to assess how the number of source topologies affects estimation results.

Table 11. State Estimation Results Under Different Topology Quantities.

Number of Source Domain Topology	MAE of i-ResNet-BRR
3	2.36 × 10−3
5	1.98 × 10−3
7	1.26 × 10−3
9	1.17 × 10−3
12	1.10 × 10−3

shows the voltage estimation MAE at different source domain scales (using voltage magnitude as an example). The results indicate that as the number of source topologies increases, the transfer model’s accuracy improves and stabilizes. Smaller source domains offer limited transferable information, preventing BRR from achieving an optimal combination. Increasing source topologies from 3 to 12 decreases estimation error by 53%, highlighting the need to select an appropriate number of source topologies in practice to provide enough transfer information for effective model combination.

4.2.2. Validation Under IEEE 118-Bus Distribution Network

Additional simulations on the IEEE 118-bus system are performed to test the method’s effectiveness across various distribution network sizes. The experimental parameters shown in

Table 12. Real-Time Measurement Locations in IEEE 118 system.

Node Injection Power (Pi, Qi)	Branch Power (Pij, Qij)
4, 13, 20, 25, 30, 40, 43, 48, 59, 65, 69, 72, 74, 81, 86, 91, 97, 100, 106, 115	1, 5, 10, 13, 19, 22, 28, 31, 35, 40, 43, 48, 52, 55, 65, 69, 73, 78, 81, 86, 89, 93, 97, 102, 108, 110, 116

, and comparison algorithms include non-transferred i-ResNet and transfer model i-ResNet-LR. Figure 17 illustrates the target topology, with red lines showing connected tie lines that are part of the distribution network (for example, Node 17 connected to Node 27 instead of Node 16).

Node voltage magnitude and phase angle estimation results for the target topology are shown in

Table 13. Voltage Magnitude Estimation Errors for Target Topology of IEEE 118 System.

Algorithm	MAE	RMSE
i-ResNet	4.0 × 10−3	6.0 × 10−3
i-ResNet-LR	1.8 × 10−3	2.6 × 10−3
i-ResNet-BRR	1.1 × 10−3	2.2 × 10−3

and

Table 14. Voltage Phase Angle Estimation Errors for Target Topology of IEEE 118 System.

Algorithm	MAE	RMSE
i-ResNet	5.5 × 10−2	7.7 × 10−2
i-ResNet-LR	2.8 × 10−2	4.0 × 10−2
i-ResNet-BRR	2.1 × 10−2	3.2 × 10−2

. The proposed method delivers the best estimation performance compared to other approaches, even in large-scale distribution networks. In terms of MAE, it improves by 73% and 62% over the non-transferred model for voltage magnitude and phase angle, respectively, and by 39% and 25% over the transfer model. For RMSE, it exceeds the non-transferred and transfer models by 63% and 15% in magnitude, and by 58% and 20% in phase angle, confirming its suitability for large-scale distribution networks.

Figure 18 displays a comparison of operational states across all nodes at a specific time sample from the test set. As the system scale increases, the non-transferred i-ResNet becomes highly volatile, performing worse than in the IEEE 33-bus scenario and struggling to accurately track node states. This highlights the challenge of precise state estimation in large-scale distribution networks with limited data, emphasizing the importance of transfer learning. For voltage magnitude and phase angle estimates, i-ResNet-BRR effectively follows the state changes across all nodes, aligning more closely with the actual values. Although i-ResNet-LR generally follows the trend of the true values, its estimates still show notable deviations.

According to literature [46], the main focus for demonstrating the practical utility of the proposed method is the voltage magnitude distribution across distribution network nodes. Since voltage phase angles can be zero, calculating the Mean Relative Error (MRE) can sometimes be undefined, so only voltage magnitude analysis is performed here.

Table 15. Voltage Phase Angle Estimation Errors for Target Topology.

Topology	RMSE
IEEE 33 (Topology 1)	0.10%
IEEE 33 (Topology 2)	0.11%
IEEE 118	0.11%

presents a comparison of voltage magnitude relative errors among different methods, indicating that the proposed estimation model achieves an MRE of 1% (99% accuracy), which aligns with the precision of real-time measurement devices and underscores its practical value in real distribution networks.

Simulation results from both scenarios demonstrate that the i-ResNet-based state estimation approach maintains excellent performance even in large-scale distribution networks. These comprehensive simulations confirm that the proposed method exhibits strong scalability and adaptability across distribution systems of varying scales.

Additionally, the developed i-ResNet state estimation model effectively reduces the computational complexity typically associated with traditional physics-based estimation methods, greatly improving speed.

Table 16. Computational Efficiency of State Estimation with Different Algorithm.

Algorithm	Computational Efficiency (s)
WLS	3.6 s
LSTM	1.12 s
ResNet	0.7 s
i-ResNet	0.39 s

shows the computation times for various state estimation methods on the test system.

The findings highlight a significant difference between the computation times of traditional physics-based methods and data-driven approaches. The proposed approach is nearly nine times faster than WLS. This gap in efficiency arises from the iterative Jacobian matrix calculations in traditional models, a process that becomes much more time-consuming as network size increases, making real-time processing more difficult. Conversely, data-driven methods use multi-threaded parallel processing, where the system size mainly affects offline training time, with little impact on online estimation. Additionally, the i-ResNet shows a 79% increase in efficiency over the standard ResNet, thanks to task-specific modifications that streamline the model and improve computational efficiency.

Regarding offline training costs, each topology-specific i-ResNet model requires approximately 3.5 h (in case of Figure 1) of training on standard GPU hardware (single GPU), This process involves iterative optimization to converge the model parameters. The training process for one model has a peak memory footprint of about 4.2 GB of GPU memory. Each trained model file is about 95 MB in size.

For a utility maintaining about 9 common topologies (typical topology numbers achieved from local utility company), the total initial training time is 33.7 h, this is a one-time, parallelizable investment (we did not use computing cluster with multiple GPUs).

As the comparison, for traditionally used WLS, while a single WLS run is fast (~3.6 s in our tests), it must run continuously, so the cumulative computational burden is significant. Moreover, for WLS any change in topology or parameters requires re-initialization and re-convergence of the WLS algorithm.

To be noted, every time once new topology emerges (not occurred before), the re-training process would be executed. Meanwhile, to avoid the problem of model aging, we recommend periodic retraining using the newly accumulated operational data.

In summary, the method presented in this chapter offers notable benefits in computational efficiency and estimation accuracy compared to traditional physical models and other data-driven methods.

5. Conclusions

The widespread integration of distributed energy resources and variable loads has introduced significant volatility in distribution networks. To maintain stable grid operation, ensure reliable power supply, and build resilient smart grids, this paper addresses operational uncertainties by focusing on distribution system state estimation, primarily exploring two key areas: measurement systems for distribution networks and state estimation algorithms.

To tackle uncertainties in line parameters and measurement data that hinder the application of physical models, an i-ResNet-based state estimation model has been developed. This model trains on historical measurements and state variables from databases, eliminating the need for line parameters and avoiding errors caused by parameter inaccuracies. Experimental results confirm the method’s high accuracy even with substantial measurement errors, demonstrating strong robustness. Furthermore, this model outperforms traditional physical models in computational efficiency, delivering faster results to dispatch centers for operational decisions.

It should be noted that this study primarily addresses measurement uncertainties and limited observability in conventional distribution system operations. While the proposed method exhibits certain robustness to random errors and anomalous data through the Huber loss function and Bayesian ridge regression ensemble characteristics, we recognize that coordinated false data injection attacks represent a distinct category of cybersecurity threats that require specialized protection mechanisms. This important direction will be a focus of our future research.

For scenarios with limited historical data following topology changes during distribution network operation, a transfer learning-based state estimation model is introduced. This approach leverages correlations between source and target topologies to transfer knowledge from data-rich domains to data-scarce scenarios, effectively overcoming limitations of traditional data-driven training and significantly improving estimation accuracy. Tests across networks of varying scales and configurations validate the model’s enhanced performance and consistent accuracy.

While the methods proposed in this paper demonstrate effectiveness across multiple case studies, certain limitations remain. The transfer learning-based time-varying topology state estimation requires some operational data from the target topology, suggesting the need to explore zero-shot learning scenarios in future work. Although this transfer learning method approximates actual operational states reasonably well, its performance still trails models trained with sufficient samples. Subsequent research will focus on further improving estimation accuracy while considering the integration of cybersecurity protection mechanisms to enhance system resilience against various threats.