Review of Active Distribution Network Planning: Elements in Optimization Models and Generative AI Applications

Abstract

Active distribution networks (ADNs) are rapidly evolving with the integration of distributed energy resources, flexible loads, and energy storage systems. Traditional planning methods, based on passive upgrades and worst-case scenarios, are no longer adequate for high DER penetration and dynamic system behavior. This review highlights the key evolution needs that will drive the evolution towards a more dynamic and optimized active distribution planning. Furthermore, this work reviews the core elements in ADN planning, covering time horizons, objectives, decision variables, uncertainty approaches, and optimal power flow formulations. This work also reviews recent generative AI models applied to active distribution networks, presenting a structured classification and definitions of each generative AI category.

1. Introduction

Active distribution networks represent an evolution of traditional distribution networks. The key factors are driven by the increasing integration of distributed energy resources (DERs), including energy storage systems (ESS), electric vehicles (EVs), and demand response mechanisms [1]. This evolution is driven by the global need for decarbonization. The efforts to reduce climate change through DERs offer benefits such as reduced power losses, minimized fuel costs, and lower greenhouse gas emissions.

Traditional distribution systems, characterized by unidirectional power flows and centralized control, are increasingly strained by the variability of renewable sources and fluctuating loads, necessitating flexible, bidirectional operations in ADNs [2]. The rising EV adoption and the need for reliable infrastructure in the face of demand growth and intermittency from sources such as solar PV and wind underscore the relevance of ADN planning in enabling sustainable, cost-effective grid modernization.

Existing literature on distribution system planning has primarily focused on traditional approaches, emphasizing passive infrastructure upgrades, single-objective optimizations, and deterministic models under worst-case scenarios [3]. Key frameworks include linear programming for basic expansion planning and mixed-integer models for asset sizing and placement, often addressing isolated elements such as substation upgrades or feeder reinforcements. Recent studies have begun incorporating DER integration and active management schemes, such as optimal power flow (OPF) formulations and stochastic optimization, to handle uncertainties in generation and demand. Dominant paradigms involve multi-stage planning horizons and bi-level optimizations for coordinating transmission and distribution networks. While several studies have explored DER integration or OPF techniques, they often address isolated aspects without a unified planning framework. Figure 1 illustrates the transition from traditional distribution network planning—characterized by passive actions, a “fit and forget” scheme, and worst-case scenarios to active planning, which emphasizes DER integration, flexibility utilization, and dynamic optimization. Shared aims include objectives, time horizons, network constraints, and investment constraints, while evolution needs encompass AC-OPF formulations, new asset modeling, and uncertainty management. Despite advancements, the literature falls short in providing holistic frameworks that integrate time horizons, decision variables, and constraints across low- and medium-voltage (LV/MV) contexts, particularly under high DER penetration and uncertainties such as load forecast errors, EV charging variability, and cyber threats [4]. Traditional planning’s reliance on passive strategies, rigid design rules, and worst-case assumptions limits adaptability to real-time flexibility and dynamic optimization [5]. Few reviews provide a comprehensive view of the evolving needs and new trends in the application of AI to power system planning. In this work, beyond focusing on the emerging elements in the formulation of the ADN planning problem, the main novelty lies in the potential application of generative AI models in the decision-making processes of operation and planning.

Table 1. Key characteristics of passive and active distribution networks.

Characteristic	Passive Distribution Network	Active Distribution Network
Power flow direction	Unidirectional	Bidirectional
Control and monitoring	Limited, mostly manual	Near real-time control
Flexibility sources	Almost none	Demand response, EVs, storage, DERs
Voltage and congestion control	Network reinforcement	DERs, storage, reactive power control
Investment driver	Infrastructure upgrades	Flexibility + selective reinforcement
System role	Passive	Active system participant

highlights the key characteristics between passive and active distribution networks. Passive networks operate with unidirectional power flow, limited monitoring, and rely almost exclusively on infrastructure upgrades to solve constraints. In contrast, ADN uses bidirectional flows, near real-time control, and monitoring, and the use of flexibility from demand response, EVs, storage, and DERs.

This literature review aims to define the common key elements of passive and active distribution system planning while identifying unresolved challenges and trends in the transition to ADNs. Furthermore, this work provides an overview of generative AI (GenAI) applications for enhancing the operation and planning of distribution networks. The main contributions of this literature review are:

1.

A comprehensive review of key concepts in passive and active distribution system planning, covering time horizons, objectives, decision variables, and technical constraints. This is supplemented by a comparison of different OPF formulations, uncertainty techniques, and flexible planning tools.

2.

A structured review and categorization of generative AI models for power systems, with emphasis on scenario generation, uncertainty modeling, optimization, and decision support, and a focused analysis of their application to planning in ADNs.

2. Elements of the Distribution Network Planning Problem

Formulating a distribution network planning problem means translating complex real-world engineering and economic challenges into a structured, solvable mathematical model. The architectural integrity of this model depends entirely on the precise definition of its fundamental elements. These elements, which include the planning horizon, objectives, decision variables, constraints, and uncertainty, collectively define the problem’s real applicability. Figure 2 shows a summary of the ADN planning elements that this review target. The specific choices made for each component are not trivial; they dictate the model’s mathematical structure and the robustness of the resulting plan. The following subsections provide an examination of each of these elements.

The following review employed a systematic search for this review on distribution network planning optimization elements and generative AI applications. The databases IEEE Xplore, Scopus, Web of Science, ScienceDirect, and Google Scholar were searched mainly from 2020–2025 using structured boolean keywords. Following PRISMA guidelines, about 500 records were initially identified and refined to 104 relevant references after screening, prioritizing simulation-based studies while excluding non-peer-reviewed sources.

2.1. Planning Horizons

Planning horizons in power systems can be classified by duration, reflecting different technical and economic considerations.

Table 2. Planning horizons.

Planning	Horizon	Aim	Actions
Short-Term	1 to 4 years	Expansion planning for immediate or near-term needs, operational improvements.	Conductor sizes, number of feeders, transformer sizes, and locations.
Long-Term	5 to 20 years	Developing infrastructure to meet future demand, aligning with medium-term goals.	System design standards, primary and secondary voltage classes, feeder configurations.
Horizon-Year	20+ years	Strategic, cost-effective infrastructure design to meet long-term consumer needs.	Comprehensive system design, integrating primary and secondary systems.

shows the time horizons, aims, and planning actions.

Short-term planning addresses immediate grid expansion to accommodate new demands. The system expansions include: upgrading feeders, transformers, and conductors to support new connections, such as electric vehicle charging stations. The integration of EV charging infrastructure often leads to multiple connection requests that must be addressed within months, necessitating rapid deployment of capacity. Some recent studies have adopted hybrid planning strategies that integrate traditional and flexible approaches to determine the optimal investment decisions for the next five years [6,7]. This combined perspective enables a more adaptive and cost-effective planning process capable of addressing increasing uncertainty in demand and generation patterns. The Nordic report in [8] highlights the role of short-term flexibility markets in providing immediate solutions for short term planning expansions. The use of distributed flexibility solutions, such as local batteries or demand response systems, can mitigate congestion and manage peak loads.

Long-term planning aims to reinforce the electric power infrastructure based on demand growth over the next 5 to 20 years. This horizon focuses on minimizing total investment costs, including the installation of new assets. Some of the reinforcements include the replacement of underground cables, the replacement of substations, and the deployment of energy storage to manage renewable energy integration and demand growth. The latter has yet to be regulated by DSOs in some countries. In [8] a Finnish project used battery energy storage in long-term investment applications to support reliability and energy markets, thus achieving sustainable grid modernization.

Horizon Year Planning focuses on strategic system design to meet energy needs for time horizons of more than 20 years. For such a long horizon, it is necessary to integrate and coordinate all primary and secondary systems to ensure seamless scalability and flexibility. Uncertainty is very high, and it is necessary to consider solutions that are prepared for widespread electrification, demographic and climate changes, and the integration of technologies aligned with future projections.

2.2. Planning Objectives

The planning objectives for distribution systems can be classified into economic, technical, and environmental objectives.

Table 3. Planning objectives of distribution network models.

Category	Objective and Description
Economic  [7,10,11,12]	1. Minimization of CAPEX and OPEX: Optimizing resources to reduce both initial investment and ongoing operational costs. 2. Maximization of assets capacity with fixed TOTEX: Increasing the ability of the asset capacity in the network to integrate DERs, EVs or load growth within a fixed TOTEX. 3. Maximization of net profit value: Enhancing revenue and profitability by effectively managing flexible resources.
Technical [13,14,15,16]	1. Maximization of system reliability: Ensuring consistent power delivery by minimizing system outages and enhancing redundancy. 2. Improvement of voltage deviation: Stabilizing voltage levels across the network to meet power quality standards and reduce flicker or voltage violations. 3. Minimization of network losses: Reducing energy losses in the network to improve overall efficiency.
Environmental [17,18,19,20]	1. Minimization of carbon emissions: Reducing the carbon footprint of the network by integrating clean energy sources and improving energy efficiency. 2. Maximization of renewable DG penetration: Increasing the share of renewables like solar and wind in the energy mix. 3. Maximization of EV charging stations: Supporting the adoption of electric vehicles by strategically placing charging infrastructure, which can also enhance renewable integration.

shows common planning objectives. The minimization of total investment costs is the most common objective in active distribution planning modeling [9]. The maximization of hosting capacity with a fixed budget and the maximization of net profit by effectively managing resources are also increasing in importance due to the need to integrate electric vehicles into the network.

The objective functions can be single-objective, multi-objective, or bi-level, depending on the problem. Most multi-objective planning models consider weighted coefficient methods and Pareto-based methods. The weighted coefficient method aims to transform a multi-objective problem into a single-objective model by using different weighting approaches. Examples include user-defined fixed weights, the analytic hierarchy process, stochastic weights, fuzzy mathematical methods, and bargaining functions. On the other hand, the Pareto-based method generates a Pareto-optimal frontier by means of a non-dominated ranking algorithm to evaluate possible solutions. A key advantage of this method is that all objectives can be taken into account with equal attention and a reasonable set of optimal solutions can be provided to decision-makers. For this reason, this method is often preferred. However, it requires more computational time compared with the weighted coefficient method.

2.3. Decision Variables

In this subsection, a review of traditional and flexible or active planning decision variables is conducted. The most used decision variables for planning are shown in Figure 3. Furthermore,

Table 4. Decision variables for distribution network planning.

Decision Variable	Description
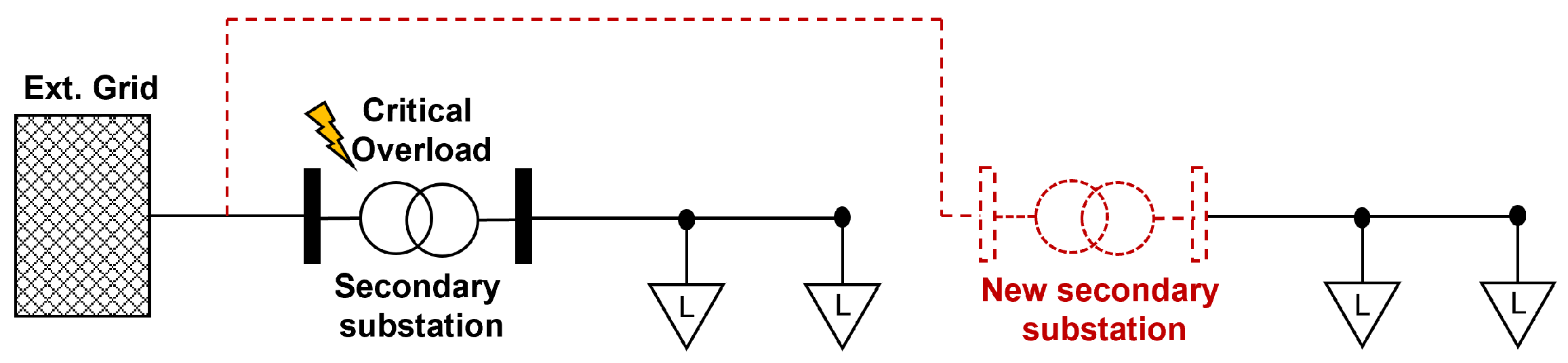
Locations and sizes of new substations	Optimizes voltage regulation and load distribution. Supports network expansion and enhances reliability [21,22,23,24,25].
Upgrade of existing substations for reinforcement	Upgrades ensure the capacity to handle increased demand [23,24,25].
Locations and sizes of new feeders	Expands network capacity and reduces the load on existing feeders. Placement optimized using GIS and power flow analyses [23,24,25,26].
Upgrade of existing feeders for reinforcement	Prevents overloads as demand grows. Employs sensitivity analysis and cost-benefit analysis [24].
Locations of reserve feeders and interconnection switches	Provides flexibility for re-routing power during contingencies. Enhances system reliability and resilience [24].
Locations, sizes, and types of renewable distributed generations	Manages demand fluctuations, providing operational flexibility. Placement optimized for stability and efficiency [23,24].
Locations of new EV charging stations	Strategically placed to prevent local network strain. Supports efficient load balancing with increasing EV adoption [27].
Locations, sizes, and types of ESS	Stabilizes load by storing excess energy. Assists in peak shaving and integration of renewable sources.
Locations and sizes of voltage control devices	Maintains stable voltage levels in high DER penetration areas. Essential for voltage stability and regulatory compliance.

summarizes the main decision variables considered in distribution network planning models. These variables define the elements subject to optimization when expanding, reinforcing, or modernizing the network. They include the locations and sizes of substations and feeders, which determine network topology, load distribution, and expansion capacity; the placement of reserve feeders and interconnection switches, which enhance reliability and flexibility during contingencies; and the integration of renewable distributed generation, energy storage systems, and electric vehicle charging stations, which support flexibility, stability, and decarbonization objectives. Additionally, the locations and sizes of voltage control devices play a critical role in maintaining voltage stability and regulatory compliance, particularly under high renewable penetration scenarios.

2.3.1. Traditional Planning Strategies

Traditional distribution system planning strategies mainly involve upgrading existing infrastructure and adding new infrastructure. However, these approaches focus on adding infrastructure or enhancing existing components rather than adopting dynamic, real-time strategies. Figure 4 shows the upgrade of existing substations that address a critical overload at a secondary substation. This solution involves increasing the capacity of the existing substation, which also involves improving cooling systems. This strategy has the advantage of reinforcing the existing infrastructure without expanding the network, which can be more cost-effective and efficient for areas with space or environmental constraints. Another traditional distribution planning action to deal with capacity overloads in the existing infrastructure is to add new substations to redistribute the load. As shown in Figure 5, the system experiences a critical overload at a secondary substation connected to the external grid. When this occurs, a new secondary substation is added near the overloaded area, and some of this load is transferred from the existing substation to the new substation. This strategy is simple and effective in relieving immediate overload issues, is primarily reactive and requires continual infrastructure expansion by adding more substations as the demand increases to prevent future overloads. However, this approach may lead to a fragmented infrastructure and rising maintenance costs in the long term.

Figure 6 shows the feeder upgrade solution in red, which aims to increase the cross-sectional area for all overloaded branches. The increased feeder capacity allows for larger connected loads, which reduces the risk of outages, losses or voltage drops. Another planning action that addresses feeder overload conditions is adding a new feeder to support the existing infrastructure. As shown in Figure 7, when the main sections of the feeders experience overloads due to high demand from downstream loads, a new feeder is installed to divert a portion of this load. This feeder runs parallel to the existing network to alleviate the stress on the overloaded section of the original feeder, enhancing reliability and preventing potential failures. Lastly, the transformer tap adjustment is primarily used for voltage control, typically over seasonal or short-term planning horizons. In practice, during peak load periods, the tap is set to a higher position to boost downstream voltage and prevent undervoltage violations. During light-load periods or with reverse power flow from PVs, the tap is lowered to avoid overvoltage at the feeder ends.

2.3.2. Flexible Planning Strategies

The flexibility in active distribution networks aims to increase the adaptability and responsiveness of the grid to manage the variable generation and demand.

Table 5. Overview of flexible sources in active distribution networks.

Flexible Source	Impact	Considerations
PV Generation	Voltage rise, reverse power flow under low load	Hosting capacity analysis, inverter-based voltage regulation, local control schemes
ESS	Peak shaving, arbitrage, reliability enhancement	Optimal siting/sizing, cost-benefit trade-offs, multi-period dispatch
EVCS and V2G	Rapid changes in load demand, potential feeder overload	EVCS siting, flexible charging strategies (time-of-use, V2G)
Demand Response	Demand shifting, improved load factor	Tariff and load control schemes

compares the utilization of flexible sources and their impacts in active distribution networks.

The solar PV integration is typically used for local voltage regulation, but it can also be triggered as a problem when generation exceeds local demand. However, modern inverters are able to control the reactive power to help mitigate these impacts. Wu et al. [28] address the challenges of long-term uncertainties and fluctuating load demand by considering flexible and dynamic strategies such as AC/DC feeders, voltage source converters for renewables, and static var generators. Electric vehicles present significant flexibility potential due to their ability to store energy in their batteries and the stationary nature of being parked more than 90% of the time. Vehicle-to-grid (V2G) technology enables the EV to inject stored energy from the battery into the grid. Proper charger siting and scheduling can unlock flexibility while minimizing distribution constraints. Ref. [29] demonstrates the economic value of EV flexibility in reducing peak demand levels and absorbing wind generation variability, and reveals that this value is enhanced with increasing electrification of the transport sector and increasing wind generation capacity. This work considered flexible EVs as a decision variable, and the V2G injections were optimally scheduled on the operational timescale.

Demand response initiatives reduce or shift load to off-peak periods. This flexible approach can be more cost-effective than major infrastructure upgrades in certain scenarios. Through the use of dynamic tariffs, incentives, or load control programs, demand response helps to avoid peak demand overloads and postpone high infrastructure investments. On the other hand, battery storage systems enable peak load shaving and efficient energy management. By storing excess energy during off-peak periods and releasing it during peak periods, this flexible source smooths load profiles and reduces stress on the grid. This is especially important in distribution networks with high levels of renewable energy. Ref. [30] proposed a flexible and stochastic coordinated planning model that uses different flexible sources, such as energy storage systems and demand response. This work also considers different uncertainties related to the loads, wind farms, and energy prices based on Monte Carlo simulations.

Figure 8 shows a new battery installation to address the critical overload at a secondary substation. The battery is optimally sized and placed to reduce the peak demands associated with the simultaneous charging of fast EV charging stations. The battery charging/discharging schedule permits avoiding overload in peak hours and charging the battery during low-demand hours. This planning strategy permits preventing the need for infrastructure upgrades. Another flexible planning alternative is shown in Figure 9. This graphical example shows how demand-side flexibility using dynamic tariffs can be coordinated with distributed energy resources.

2.4. Planning Constraints

The constraints are conditions that limit the solution space to obtain the optimal solution of the objective function. The number of constraints in distribution network planning models depends on the decision variables and scope of the problem.

Table 6. Distribution network constraints.

Category	Constraints
Technical	Power balance equations, voltage magnitude, voltage angle, feeder/substation thermal limits, Battery state of charge limits, PV generation power, N-1 criterion.
Non-Technical	Location of assets, capacity of assets, quantity of assets per location.
Time and Investment	Capital expenditure, operational expenditure, static and dynamic states.

shows four different groups of planning constraints and a representative constraints for each group. The groups are the following: technical constraints, non-technical constraints, time and investment constraints [3,31].

The most common constraints are related to technical constraints, including the bus voltage limits for nodes and buses, the power balance equations given by the Kirchoffs laws, the branch current flow constraints, thermal limits of the lines/substations, and the radiality of the distribution network [32,33,34,35]. Secondly, the non-technical constraints are limitations or requirements related to the practical aspects of distribution network planning. These include the logistical, environmental, allocation, quantity and capacity of transformers, feeders, substations, and circuit breakers, which must be optimized for efficient expansion [36,37]. Thirdly, the investment constraints involve budget limitations, purchased power restrictions, and fuel costs, which must be managed to minimize overall expenses. Also, the time constraints ensure operational stability by setting minimum periods for which a unit must remain on or off before changes in its operational state can occur, addressing scheduling and uncertainty considerations [32,38].

Lastly, the miscellaneous constraints consider the use of a single type of cable or transformer, distributed generation capacity and penetration level, and ramp rate limits for active and reactive power. They also address spatial area constraints, ensuring enough space for future equipment like transformers, and the reuse or removal of existing infrastructure [36,39].

2.5. Type of Planning Variables

In optimal power flow (OPF) planning problems, understanding the types of variables involved is essential for problem formulation, computational efficiency, and the selection of solution techniques. Variables are typically classified into two categories: binary and continuous. This classification is based on their mathematical nature and role in representing different aspects of investment planning.

Table 7. Types of planning variables.

Variable Type	Description
Binary	Installation of new secondary substations, upgrade of secondary substation capacity, installation of new ESS, installation of PV systems, installation of controlled EVCS, installation of parallel feeders, upgrade of feeder capacity, among others.
Continuous	Battery state of charge, substation power injection, voltage magnitude, voltage angle, branch power flow, generation power injection, load shedding, among others.

shows the standard variables used in OPF planning problems. Binary variables represent decisions that involve only two states, such as whether to upgrade an existing asset, install a new asset, or activate a flexible asset. These variables are crucial for modeling investment choices that require a yes-or-no decision framework. Continuous variables represent quantities that can vary within a range of values, such as power losses, distributed generation injected power, branch power flow, bus voltage magnitudes, among others. These variables are critical for modeling the physical and operational behavior of the system, as well as for achieving efficiency and reliability in the network. By categorizing these variables, the figure highlights the diverse nature of the data and decisions involved in OPF planning. This structured approach facilitates the integration of technical, operational, and economic factors into the problem formulation.

2.6. Uncertainty Modelling Techniques

This section reviews techniques for representing uncertainty in the planning of active distribution networks. Adequate planning of active distribution networks requires consideration of modeling uncertainty in their input parameters. Renewable generation, load, and EV charging, exhibit significant variability in magnitude, timing, and location [40,41].

The classification of uncertainty modelling techniques is shown in

Table 8. Uncertainty modelling techniques.

Category	Methods
Probabilistic	1. Stochastic optimization 2. Robust optimization
Possibilistic	1. Possibilistic methods
Hybrid probabilistic-possibilistic	1. Combined probabilistic and possibilistic approaches
Information Gap Decision Theory	1. Decision-making under deep uncertainty
Monte Carlo simulations	1. Sequential: Simulation method with iterative updates 2. Pseudo-sequential: Hybrid approach between sequential and non-sequential 3. Non-sequential: Independent Monte Carlo runs without sequential updates
Analytical	1. Fuzzy-Monte Carlo 2. Fuzzy-scenario-based methods
Approximation of PDF	1. Convolution 2. Cumulants 3. Taylor Series Expansion 4. First-Order Second-Moment 5. Point Estimate Method 6. Unscented Transformation

. At a high level, these can be divided into numerical and analytical approaches. Numerical methods often use Monte Carlo (MC) simulation, in which uncertain parameters are randomly sampled to generate a range of possible scenarios. Some MC simulation variants include sequential, pseudo-sequential, and non-sequential approaches. While these methods accurately capture complex stochastic behavior, they are computationally intensive. In contrast, analytical methods approximate probability distributions for faster evaluation. Examples include linearized expansions (e.g., Taylor series), point estimation techniques, cumulant-based approaches (balancing accuracy and efficiency), and unscented transformations used in active distribution network studies. Probabilistic methods assume that uncertainties, such as load growth and EV charging behavior follow known or estimated distributions, making them appropriate when historical data is available. Possibilistic (fuzzy) approaches use possibility distributions, ideal for sparse or incomplete data. Hybrid frameworks combine probabilistic and possibilistic elements to handle both well-characterized and poorly known uncertainties. Robust and stochastic optimization methods address uncertainty by optimizing network investments and operations under different scenarios, including worst-case conditions. Information Gap Decision Theory explores system performance under increasing uncertainty, making it valuable for long-term planning [41,42,43,44].

In real use cases, DSOs must consider load forecast errors and EV charging uncertainties (such as arrival times, battery charge levels, and charging power). The choice of uncertainty modeling technique depends on data availability, computational resources, and the trade-off between accuracy and tractability [40,41].

3. Literature Review of OPF Planning Models

This section reviews various OPF formulations used in distribution network planning, along with studies that have employed these formulations. Deterministic and heuristic methods for solving OPF are significantly influenced by the underlying mathematical formulation, which may include non-linear programming, second-order cone programming, linear programming, or mixed-integer programming. Selecting the appropriate formulation depends on the application and the type of expansion planning problem. Additionally, the advantages and disadvantages of each OPF model are summarized in the final subsection.

3.1. Linear Programming

Linear Programming (LP) methods, such as DC-based OPF approaches, are widely used due to their simplicity, computational efficiency, and guaranteed convergence. These methods linearize the power flow equations, providing rapid solutions. However, the trade-off lies in reduced modeling accuracy, as linear approximations often fail to capture the non-linear and dynamic behavior of real-world power systems, particularly in distribution networks with high levels of distributed energy resources or electric vehicle integration.

A review of planning models related to substations and distribution feeders was studied in [45]. This work categorizes these models into two main areas: planning under standard operating conditions and planning for emergency scenarios. This classification allows for a structured analysis of how LP methods have been applied to various planning tasks. Moreover, the authors highlight potential research opportunities, particularly in enhancing the adaptability and robustness of these models for modern grid challenges. In [46], authors expand the application of LP methods in power system planning by categorizing distribution expansion models into four approaches based on time horizons and physical structure. For each category, they analyze the cost functions, constraints, and mathematical programming techniques employed. Their work provides valuable insights into the strengths of LP methods, such as computational efficiency and simplicity, as well as their limitations, including the inability to fully capture system non-linearities and complex interactions.

3.2. Mixed-Integer Linear Programming

Mixed-Integer Linear Programming (MILP) is a widely utilized optimization technique for problems that require modeling both continuous and discrete variables. In the context of distribution network planning, MILP is particularly effective for representing decisions such as the selection of asset types, capacities, and operational configurations. By incorporating binary or integer variables, MILP captures the discrete nature of many practical problems, including investment decisions, resource allocation, and system upgrades.

A bi-level optimization model using MILP to address distribution network expansion planning was developed by [47]. This approach integrates investment decisions, distributed energy resources, and energy storage systems into the optimization framework. This enables the model to propose solutions that are both cost-efficient and operationally feasible, using active network management strategies to accommodate real-time constraints. Similarly, ref. [48] expanded the application of MILP by introducing a multi-objective optimization framework that incorporates reliability and economic performance indices. This framework allows planners to evaluate trade-offs between minimizing costs and enhancing system reliability, offering a balanced and informed decision-making approach for distribution network planning. Authors in [49], introduced high penetration of plug-in electric vehicles (PEVs) in distribution networks. The study proposed a multi-stage bilevel MILP optimization model tailored to integrate PEVs into planning processes effectively. This hierarchical approach ensures that both long-term planning and short-term operational considerations are addressed, making it particularly suited to modern power systems with high levels of PEV adoption. The proposed model highlights the potential of MILP in enabling efficient integration of new technologies while maintaining economic and operational sustainability.

3.3. Mixed-Integer Nonlinear Programming

The earliest OPF formulations were inherently non-linear and accurately modeled power system characteristics, although they often relied on approximations, such as treating discrete variables as continuous. Modern non-linear formulations, however, frequently include discrete decision variables, resulting in Mixed-Integer Nonlinear Programming (MINLP). These advanced formulations address the inherent non-linearity while incorporating additional system constraints.

Uncertainties from large-scale deployment of electric vehicles and photovoltaic systems pose challenges to distribution network expansion planning. Work in [50], proposed an optimal planning method integrating PV-grid-EV transactions to mitigate these uncertainties. The study employs a peer-to-peer transactive market cleared via a decentralized algorithm, ensuring privacy and autonomy. Using multiple linearization techniques, the method ensures model convergence and enables cost-effective EV charging station planning while avoiding unnecessary PV curtailment. Results demonstrate improved integration of large-scale EVs and PV, enhancing network efficiency and security. In [51], authors presented an advanced MINLP model for handling the high penetration of electric vehicles in distribution networks, effectively addressing scalability challenges through scenario-based optimization. The study achieved a 42% reduction in computation time, demonstrating significant improvements in efficiency over traditional approaches.

3.4. Convex Relaxation Methods

Convex relaxations have gained prominence for their ability to achieve global optimality with faster convergence. These approaches reduce the solution space to find feasible, globally optimal solutions more reliably and can also provide bounds for the quality of local optima in the original problem. Among these, Second-Order Cone (SOC) relaxations are notable for their computational efficiency and widespread solver support. They are particularly suitable for radial network systems under certain constraints [52,53,54].

In [55], authors proposed a SOC relaxation to address the Optimal Power Flow problem for operational planning in active distribution networks. This approach integrates flexibility models, including On-Load Tap Changers and network reconfiguration, directly into the relaxed operational planning process. The model also considers the short-term economic impacts of utilizing these flexibilities, which are progressively applied in various test scenarios to achieve the goal of reducing operational costs. Authors in [56], the authors introduce a SOC optimization model aimed at minimizing the annualized social cost of the overall EV charging system using a two-step equivalence framework. This approach can solve the optimal planning problem of EVCSs, which comprise multiple types of charging facilities with different charging demand profiles. SOC relaxations are increasingly used for multi-stage ADN planning, ensuring tightness in solutions for DER-rich networks [14].

3.5. Metaheuristic Methods

Inspired by natural processes, meta-heuristic methods offer flexible solutions to complex problems. While they do not guarantee global optimality or error bounds, they can effectively handle discrete variables and large-scale systems. Popular meta-heuristic techniques include Genetic Algorithms, Particle Swarm Optimization, and Simulated Annealing, among others. These methods are particularly valuable for scenarios requiring robust solutions for operational planning. Ref. [57] propose a fuzzy-based meta-heuristic approach for multi-objective optimization in network planning, effectively addressing conflicting priorities like cost minimization and reliability enhancement. In [58] an optimal expansion of MV power networks to minimize the total investment costs was proposed. This work used a hybrid Tabu search/particle swarm optimization algorithm to optimize three electric distribution networks as case studies.

Table 9. Comparison of mathematical formulations in OPF.

Formulation	Advantages	Disadvantages
Linear Programming	Computationally efficient and scalable Guarantees global optimality	Low accuracy; oversimplifies non-linear power flows Solutions may be physically infeasible
Mixed-Integer Linear Programming	Handles discrete decisions (e.g., investment, switching) Can be solved to global optimality (via branch-and-bound)	High computational demand (NP-hard) Relies on linearization, sacrificing physical accuracy
Mixed-Integer Non-Linear Programming	High-fidelity: models AC power flow & discrete variables Most realistic representation of the network	Computationally intensive; complex to solve Non-convex: risk of converging to local optima
Convex Relaxations	Guarantees global optimality (if relaxation is exact) Computationally tractable and reliable	May have a “relaxation gap” (inaccurate solution) Handling discrete variables requires MILP framework
Metaheuristic Methods	Handles non-linear and non-convex models Model-agnostic and good for large-scale problems	No guarantee of global optimality Solution quality is difficult to benchmark or prove

presents the advantages and disadvantages of the distribution network planning formulations analyzed in this chapter. MINLP and MILP optimization models are the most used formulations for optimizing the total investment costs and meeting the operational constraints.

3.6. Dynamic OPF Planning Models and Tools with Flexibility

This section presents some examples of dynamic OPF planning models and tools that integrate flexible planning actions. Ref. [59] presents a comprehensive tool for optimal long-term grid planning considering power flow, demand flexibility model, and grid constraints. The parametrization of the generic flexibility model was based on real load demand data and selected individual demand flexibility resources. Furthermore, this work illustrates effects that are not captured by the more coarse-grained generic flexibility model but that are relevant for long-term grid planning purposes. Ref. [60] proposed FlexiPlan.jl, an open-source tool for holistic planning of transmission and distribution grids considering demand flexibility and storage use. This tool uses stochastic optimization to find robust decisions under different climate conditions and operating hours with respect power generation and demand.

The FlexPlan methodology consists of three input modules. First, the grid data from the transmission and distribution networks is imported to model the AC and DC grids from PowerModels.jl. Second, a list of grid expansion options is provided using AC and DC grid expansions, demand flexibility, and storage investments to determine the optimal investments. Finally, the planning scenarios, number of renewable generation and demand time series are collected. Ref. [61] presented an open-source software tool called eGo, which is able to optimize grid and storage expansion at different voltage levels. Operating and investment costs are minimized by applying a multi-period linear optimal power flow considering the grid infrastructure. This tool performs simulation and optimization at the MV and LV levels to determine grid expansion costs, taking into account the allocation of curtailment requirements, storage integration, and traditional grid expansion measures. Ref. [62] proposes an automated distribution planning framework using the open-source library Pandapower. This library is a simulation model capable of running time series power flows to assess congestion and voltage deviation in the MV and LV network. A heuristic optimization that searches for the best combination of individual actions to solve the defined constraints using a set of reconfiguration, reinforcement and expansion actions is used to solve the potential problems in the network. This framework proposed the following planning actions: replacing existing lines and transformers, adding parallel lines to existing line paths, changing the switch configuration, finding new line paths, using advanced control functions on transformers and PV systems, replacing conventional transformers with On-Load-Tap-Changing transformers. Furthermore, the authors emphasise the benefits of using pandapower as a modular and flexible option, allowing constraints to be added such as, radiality, supply, n-1 and other topological constraints, load flow constraints for bus voltage, line load, transformer load, multiple worst case scenarios, load flow constraints for n-1 operation with optimal supply among others.

4. ADN Trends: Generative AI Models, Applications and Future Asset Expansions

Active distribution networks must manage stochastic and dynamic uncertainties arising from variable renewable generation, fluctuating loads, and bidirectional power flows. Generative AI models have emerged as a powerful alternative to address these short-, mid-, and long-term challenges by generating realistic expansion scenarios, quantifying uncertainties, and supporting robust optimization. These models enable distribution system planners to optimize network expansion while integrating new technologies.

Table 10. Overview of generative AI models and applications.

Category	Type of Generative AI Model	Application	Ref.
GAN-based models	cGAN, WGAN-GP, CycleGAN, StyleGAN, ExGAN, BiGAN	Scenario generation (renewable, load, EV), data augmentation, cyber-resilience, fault diagnosis. Synthetic time-series for PV, wind, load, and EVs to support stochastic and long-term planning	[63,64,65,66,67,68]
Diffusion-based models	DiffCharge, DiffLoad, ExDiffusion, Conditional Diffusion	EV/load scenario generation, uncertainty quantification, extreme event modeling, resilience analysis. Stress-testing, extreme event simulation, reliability planning.	[69,70,71,72,73]
VAE-based models	$\beta$-VAE, Conditional VAE, BiVAE	Probabilistic forecasting, scenario synthesis, energy efficiency planning, voltage stability assessment. Probabilistic load/price forecasting and OPF optimization under uncertainty.	[74,75,76,77]
Flow-based models	RealNVP, Glow, Normalizing Flow	Renewable and load scenario generation, uncertainty modeling, probabilistic OPF, expansion planning.	[78,79,80,81]
Transformer-based models	GPT, LLaMA, eGridGPT, CPGA-BOT, PowerPulse	Planning assistants, data mining, simulation automation, energy management, human-in-the-loop decision support. Decision support via Large Language Models (LLMs), planning chatbots, automated data mining, and simulation scripting.	[82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101]

provides an overview of the main categories of Generative AI models and their applications in energy systems planning and operation. The distinctive attributes and strengths of each category determine their suitability for particular applications. Generative Adversarial Networks (GAN)-based models are widely used for scenario generation due to their ability to learn complex, high-dimensional data distributions through adversarial training, which involves a generator and a discriminator. This setup enables GANs to produce highly realistic synthetic time series for renewable energy generation, electricity demand, or electric vehicle behavior. Their realistic nature and data-driven approach make them ideal for tasks such as data augmentation, cyber-resilience testing, and stochastic planning, where the objective is to expand existing datasets under different conditions [63,64,65,66,67,68]. The Sankey diagram in Figure 10 shows that different generative AI model families are connected to various application areas in the energy domain. The flow widths reflect their relative prevalence in the literature, showing that transformer-based models dominate across most applications—particularly planning and optimization, decision support, and energy management, while other generative models contribute more selectively to tasks such as scenario generation, data augmentation, resilience, and uncertainty modeling. For instance, the conditional style-based GAN proposed in [63] leverages meteorological variables to generate intraday renewable energy scenarios with spatiotemporal correlations, aiding stochastic planning by simulating volatile outputs without relying on extensive historical data. Notably, these models can produce diverse scenarios that capture rare but critical events, such as sudden weather changes. Authors in [64], demonstrated that the the cross-modal cGAN outperforms benchmark models on both PV and wind power datasets, even under missing data conditions. In a case study on stochastic day-ahead economic dispatch, scenarios generated by the cGAN yield an expected cost within 1.43% of the true scenarios, validating its practical applicability.

Diffusion-based models have recently emerged as a robust alternative to GAN models. They work by learning to reverse a gradual noising process: starting from pure random noise, the model iteratively predicts and removes noise in small steps until a coherent, high-fidelity image (or data sample) emerges. This iterative denoising makes them particularly effective at representing uncertainty and extreme events. Their probabilistic formulation naturally lends itself to applications such as uncertainty quantification, stress-testing, and resilience analysis in energy systems, where understanding variability and extreme scenarios is essential for reliability and planning under uncertainty [69,70,71,72,73]. As an example, ref. [69] used a denoising diffusion probabilistic approach to generate realistic EV charging scenarios at both battery-level and station-level, capturing temporal dynamics, station-specific patterns, and intractable uncertainties. Quantitative results show that the proposed DiffCharge model achieves the lowest marginal score, highest discriminative score, and best tail score, enabling accurate uncertainty modeling for distribution network planning. VAE-based models, including $\beta$-VAE, provide probabilistic frameworks for forecasting and optimization under uncertainty. Variational autoencoder (VAE)-based models combine deep learning and probabilistic inference in order to learn how to compress and reconstruct data in a lower-dimensional latent space. They consist of two main parts: an encoder, which maps input data into a distribution in the latent space (typically Gaussian), and a decoder, which reconstructs data samples from points drawn from this latent space. By learning this bidirectional mapping, VAEs can generate realistic and continuous variations of data while maintaining interpretability. Their probabilistic nature makes them well-suited for tasks involving scenario synthesis and forecasting under uncertainty—such as load or price prediction, energy efficiency planning, and voltage stability assessment [74,75,76,77]. Research in [74] applies a VAE-GAN hybrid for synthetic data generation in smart homes, leveraging the latent space to create new data points that preserve privacy while enabling efficient load and price forecasting for optimal power flows in ADNs. Furthermore, VAEs facilitate the compression of high-dimensional data, reducing the need for large datasets and making them suitable for edge computing in distributed ADN environments. Flow-based models, such as RealNVP, offer explicit density estimation for renewable and load scenarios. As explored in [78], these models generate interpretable renewable patterns with controllable diversity, supporting probabilistic OPF and expansion planning by modeling nonlinear correlations and geospatial dependencies in DER placement. Furthermore, this work showed that flow-based models improves coverage probabilities by up to 4 percentage points over VAEs and 3 points over GANs, while reducing interval widths by up to 7% compared to VAEs and 4% compared to GANs, indicating more reliable forecasts with sharper uncertainty intervals.

Unlike GANs, VAEs provide more stable training and a structured latent representation that can be directly exploited for optimization and decision support. Flow-based models use a sequence of invertible transformations to map simple probability distributions into complex data distributions and vice versa. Each transformation is mathematically reversible, allowing both exact likelihood computation and precise control over the generative process. This bidirectional and transparent structure enables direct sampling, density estimation, and interpretation of how data are formed. Such properties make flow-based models highly suitable for renewable and load scenario generation, probabilistic optimal power flow, and expansion planning, where accurate probabilistic modeling and explicit likelihood estimation are required [78,79,80,81].

Finally, Transformer-based models—such as GPT, LLaMA, and specialized versions like eGridGPT and PowerPulse—extend generative AI beyond data synthesis to include reasoning, automation, and decision support. They are built around self-attention mechanisms, which allow the model to weigh the importance of each element in a sequence relative to all others. In practice, this means the model learns which parts of the input are most relevant when generating or interpreting each output token, enabling it to capture long-range dependencies, contextual relationships, and nonlinear interactions across complex datasets. This capability makes transformers highly effective for planning assistance, data mining, simulation management, and human-in-the-loop decision support in energy systems. Their flexibility positions them as foundational tools for next-generation applications that merge language understanding with generative capabilities, such as intelligent planning assistants and simulation chatbots [82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101]. The eGridGPT framework [85] represents one of the first applications of LLMs in power grid control rooms, integrating large language models with digital twins for procedure analysis, scenario simulation, and holistic decision recommendations. Similarly, PowerPulse [100], fine-tuned on power sector data, automates responses to energy-related queries and supports adaptation in dynamic grids. A significant development is their integration into multi-agent systems for VPP coordination, where LLMs can process ambiguous data and enhance security in smart grids.

Each GenAI model category offers distinct strengths: GANs specialize in producing highly realistic data, diffusion models in modeling uncertainty and extreme events through iterative denoising, VAEs in generating interpretable probabilistic representations of complex systems, flow-based models in providing exact and transparent likelihood estimation, and transformers in capturing context, reasoning across data, and enabling automation—together forming a powerful, complementary framework for next-generation intelligent energy system planning and decision support. The ADN planning problem is mainly affected by long-term uncertainty from renewables, EVs, and flexible loads, making traditional planning no longer valid for realistic investment estimations. Generative AI can generate realistic scenarios by capturing complex spatio-temporal patterns from emerging assets, thereby improving robustness and decision-making for system operators. Recent works have integrated generative model into planning of active distribution networks by considering it into the methodology steps. In particular, ref. [102] proposes a cooperative planning method for renewable energy generations and multi-timescale flexible sources in ADN. It uses a Wasserstein generative adversarial network with gradient penalty based scenario generation and a second-order cone relaxation approach for optimization. The case study results in a 69 node network showed a 7.9% reduction over single-timescale planning. The main improvements were found in the reduction of the curtailment/shedding penalties by over 75% and voltage deviation by 2%. Ref. [103] proposes a GAN-assisted two-stage stochastic PV planning framework with coordinated multi-timescale Volt–Var control, validated on IEEE 37- and 123-node systems. Case studies show that, unlike deterministic planning, the stochastic model eliminates voltage violations under critical high-PV/low-load scenarios and reduces total power losses across most time slots, particularly around peak PV hours.

5. Conclusions

This work reviews the key elements of active distribution system planning, classifying critical components from the literature, including planning horizons, objectives, decision variables, constraints, uncertainty modeling, and OPF formulations. The review finds that traditional planning is characterized by passive “fit and forget” reinforcement and worst-case assumptions, whereas emerging active strategies prioritize DER integration, system flexibility, and dynamic optimization. This highlights a critical need for evolution, demanding advancements in AC-OPF formulations, new asset modeling frameworks, and robust uncertainty management. The literature also reveals that addressing complex ADN problems requires enhancing traditional planning with active decision variables, dynamic scenarios, probabilistic methods, and advanced optimization, such as MINLP and convex relaxation.

Furthermore, this review discusses applications of generative AI in active distribution planning, including the creation of realistic, synthetic load profiles to simulate future demand and optimize DER integration. This approach enables privacy-preserving data sharing, helping to bridge the gap between research and industry by facilitating innovative, adapted optimization models for modern power systems. Finally, the review reveals that active distribution planning faces critical challenges from the accelerating integration of data centers, AI factories, renewable energy communities, and fast-charging hubs. While functionally different, these assets create a common, critical threat: the introduction of high-magnitude, fast-ramping events. This new volatility lies outside the design parameters of traditional grid operations, leading to severe, new risks of congestion and instability.

Future research should prioritize the development of advanced integrated ADN planning models that address long-term uncertainty arising from renewables, EV charging, and flexible loads. These models should leverage generative AI for realistic spatio-temporal scenario generation to support robust and stochastic planning. Additionally, multi-timescale and cooperative planning frameworks are needed to jointly optimize investment and operational flexibility for all the planning horizons.